在QRPA理论中，巨共振被视为两准粒子产生、湮灭的相干叠加，相应的产生算符为

其中$ \beta^\dagger $(β)为准粒子a，b的产生(湮灭)算符，$ X_{ab}^{(n)} $, $ Y_{ab}^{(n)} $为本征态n相应的跃迁振幅。根据运动方程的思想^[25]，可以得到QRPA方程

其中$ E_n $为相对于基态的激发能，矩阵元A，B的详细形式见文献[26−27]。由于粒子数守恒破缺，QRPA方程的解$ |n'\rangle $会存在假态，可以通过假态$ |s\rangle $与物理态的正交性，得到去除假态后的真实物理态波函数$ |n\rangle $^[28]，

其中$ |s\rangle $为假态，正比于$ \langle ab|\hat N|0\rangle $，$ \hat N $为粒子数算符，$ |0\rangle $为基态，$ \alpha $通过正交关系$ \langle n| \hat N |0\rangle=0 $得到。

基态$ |0\rangle $到激发态$ |n\rangle $的跃迁强度通过

给出。对于ISGMR，跃迁算符为$ \hat F=\sum\limits_{i=1}^A r_i^2 $。由于QRPA给出的强度为分立的跃迁强度，为了与实验进行比较，通常采用Lorentz平滑处理。相应的k-阶能量权重的求和规则为

在QRPA+QPVC理论中，除包含了两准粒子产生、湮灭的贡献外，还包含了两准粒子与声子态耦合的贡献，相应的产生算符定义为

其中$ Q^\dagger $为QRPA本征态(这里称为声子态)的产生算符，$ X^{(\nu)}, \, Y^{(\nu)}$为QPVC本征态$ \nu $相应的跃迁振幅。根据运动方程的思想^[25]，可以得到QRPA+QPVC方程。进一步将其投影到由QRPA方程本征矢$ \{ n,\bar n\} $(其中$ \bar n $为负能态对应的本征矢)为基矢的空间，可以得到QRPA+QPVC方程为

其中D、$ \bar D $分别为QRPA正、负能本征值构成的对角矩阵，$ \varOmega_\nu $代表QRPA+QPVC方程的本征能量，$ \varGamma_\nu $代表宽度，相应的本征波函数为

${\cal{A}}_i (i=1,\,2,\,3,\,4)$写为

对于i取不同值时有$ s_1s_1' = nn' $, $ s_2s_2' = n\bar n' $, $ s_3s_3' = \bar n n' $, $ s_4 s_4'= \bar n\bar n' $。$ W(E) $写为

其中：H为哈密顿量算符；ε为一个任意小量，在具体求解过程可取为0.5 MeV；$a_1b_1,\, n$为中间态。

值得注意的是，在密度泛函相互作用拟合时，一般要求对原子核性质给出最好的描述，因此在参数中已经隐式包含了一部分来自超越平均场效应的贡献。在QRPA+QPVC计算时，为了避免重复计算，可以采用subtraction方法^[29]，这种方法进一步保证了方程的稳定性。

由于QRPA+QPVC矩阵为复对称矩阵，其强度函数的定义如下：

其中η在计算时可取为0.5 MeV。相应的k-阶能量权重的求和规则为

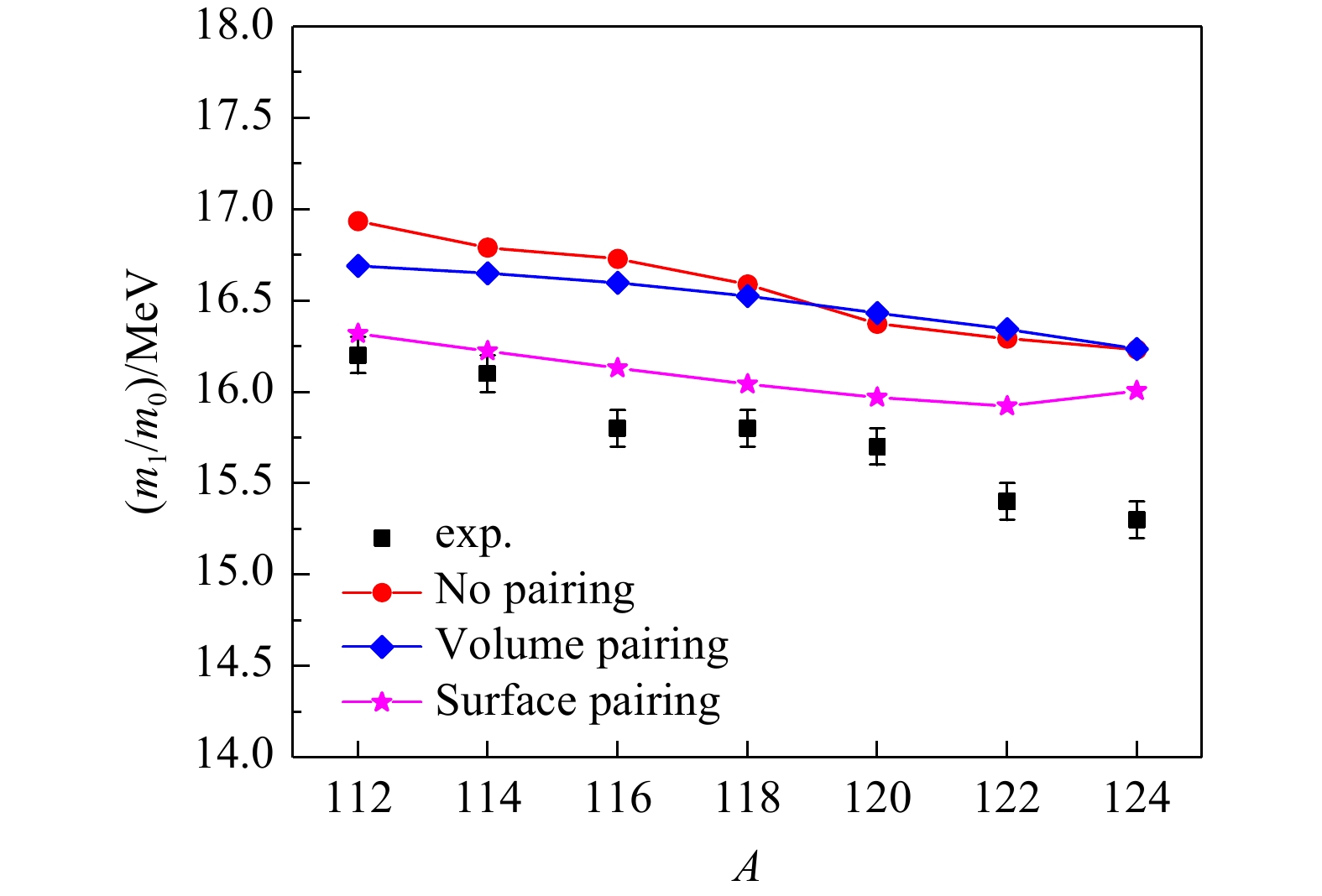
Sn同位素状态方程较“软”这一问题的提出是根据无规相位近似(RPA)理论，没有考虑对关联效应的影响。^112−124Sn同位素中子数为62~74，位于幻数$ N=50 $和82之间，因此，在ISGMR的计算中，需要自洽考虑对关联效应。

文献[30]基于非自洽QRPA理论，利用δ对力指出对关联效应使Sn同位素ISGMR能量约向低能方向移动100~150 keV。文献[28]利用自洽QRPA理论研究了对关联效应对理解“为什么Sn同位素给出的状态方程这么软”这一问题的作用，如图1所示。以Skyrme相互作用SkM*^[31]为例，其中黑色方形为实验值^[32]，红色圆形为没有考虑对关联的RPA模型计算结果，蓝色菱形为采用体积对力的QRPA模型计算结果，紫红色五角星为采用表面对力的QRPA模型计算结果。相关结果取自文献[28]。从图中可以看出，对于^112−118Sn，考虑体积对力后对ISGMR能量的描述略微改善，但仍然高估实验值0.5~0.8 MeV。对于^120−124Sn，考虑体积对力对ISGMR能量的描述没有改善。而考虑表面对力，^112−120Sn同位素的ISGMR能量描述得到了大幅度改善，仅略微高估实验值。然而，对^122−124Sn的描述仅略有改善，仍严重高估实验值。

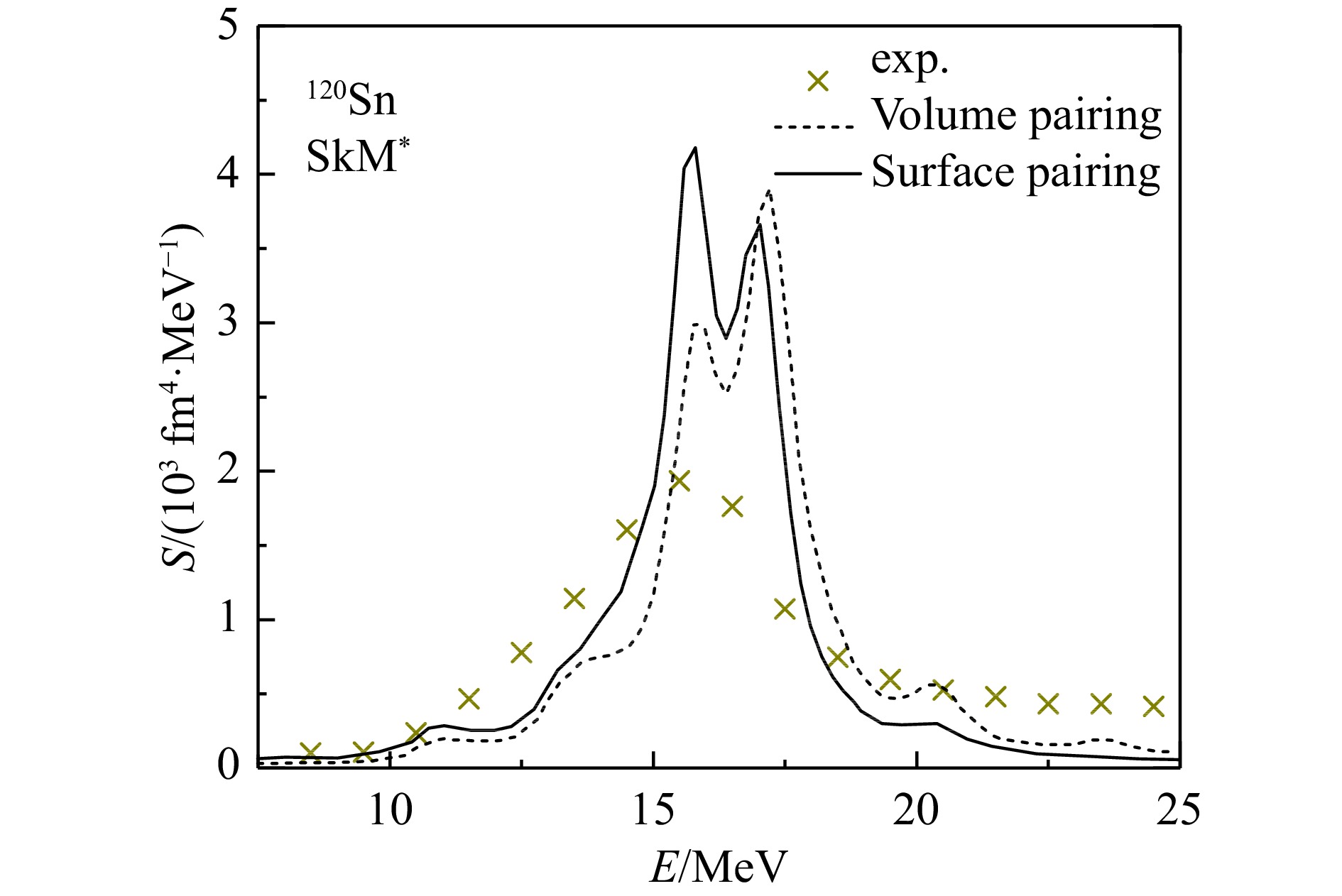
图2给出了QRPA理论对¹²⁰Sn中ISGMR强度分布的描述，采用Skyrme相互作用SkM*。其中土黄色叉号为实验结果^[32]，黑色虚线为采用体积对力的QRPA模型计算结果，黑色实线为采用表面对力的QRPA模型计算结果。相关理论计算结果取自文献[28]。可以发现，¹²⁰Sn强度函数的实验分布呈现单峰结构，且具有较宽共振宽度。而QRPA理论仅考虑了两准粒子激发的叠加，不能够给出巨共振宽度，因此，无法描述实验上宽的共振峰，并呈现出双峰结构。相比于采用体积对力的结果，采用表面对力的计算结果显示，第一个峰强度高于第二个峰，因此对ISGMR中心能量的描述有了大幅度的改进，但是其强度分布仍与实验结果有较大差别。

文献[33]利用约束的Hartree-Fock-Bogoliubov方法，以Skymre相互作用SLy4^[34]为例，采用表面对力，也发现考虑对关联有助于改进Sn同位素给出的状态方程较“软”。文献[35]基于自洽Hartree-Fock-BCS+QRPA理论，通过研究不同形式对力对^106−116Cd和^112−124Sn偶偶核ISGMR能量的影响，发现考虑对关联效应后，Skyrme相互作用参数组SkM*能够对Cd和Sn同位素链给出较好的描述，但相应的不可压缩系数仍然相对较小。文献[36]利用自洽QRPA理论，采用Skyrme相互作用参数组SLy4和UNEDF0^[37]，计算了整条Sn和Pb同位素链的偶偶核，分析了可分离对力对这一问题的影响，发现考虑可分离对力后，仍然高估了Sn同位素的ISGMR能量。

虽然表面对力有助于部分解释“为什么Sn同位素给出的状态方程这么软”这一问题，然而，能够重现Pb同位素ISGMR能量的模型仍然高估了Sn同位素的中心能量。另一方面，目前没有证据表明应该使用表面对力、体积对力或者其它形式的对力。因此，对关联效应并不能完全解释这一问题。

另一方面，文献[38]提出了幻数增强机制来解释这一问题，并预言：若该机制成立，则²⁰⁸Pb的ISGMR能量会显著高于其相邻同位素，如^{206, 210}Pb。然而，对Pb同位素链ISGMR的实验测量结果表明，^{206, 208, 210}Pb的ISGMR能量十分接近^[14]，因此排除了幻数增强机制。文献[39]通过构建混合模型实现了Sn同位素ISGMR强度分布，然而混合模型却低估了²⁰⁸Pb的ISGMR能量。因此，“为什么Sn同位素给出的状态方程这么软”是一个令人长期困扰的开放性问题。

QRPA理论仅考虑了两准粒子组态的贡献，因此有其局限性，主要表现在无法描述巨共振的宽度、能谱的精细结构以及到低激发态的衰变性质等。若要克服这些问题，需要包含更高阶的组态，如二阶无规相位近似(SRPA)理论^[40−42]、准粒子振动耦合(QPVC)理论^[43−47]等。由于两粒子两空穴组态空间非常大，因此SRPA理论计算非常耗时，因此，很难进一步包含对关联效应。然而，QPVC理论通过考虑两准粒子与声子的耦合来引入更高阶的关联效应，近似等价地考虑了四准粒子组态的贡献，计算量相比SRPA要小很多，因此，可以在包含对关联效应的基础上计算从轻到重的原子核。

目前，基于Skyrme密度泛函和相对论密度泛函都发展了自洽的QRPA+QPVC理论，并用于原子核巨共振的计算^[46−47]。探索更高阶多体关联效应对原子核ISGMR的影响具有重要意义。

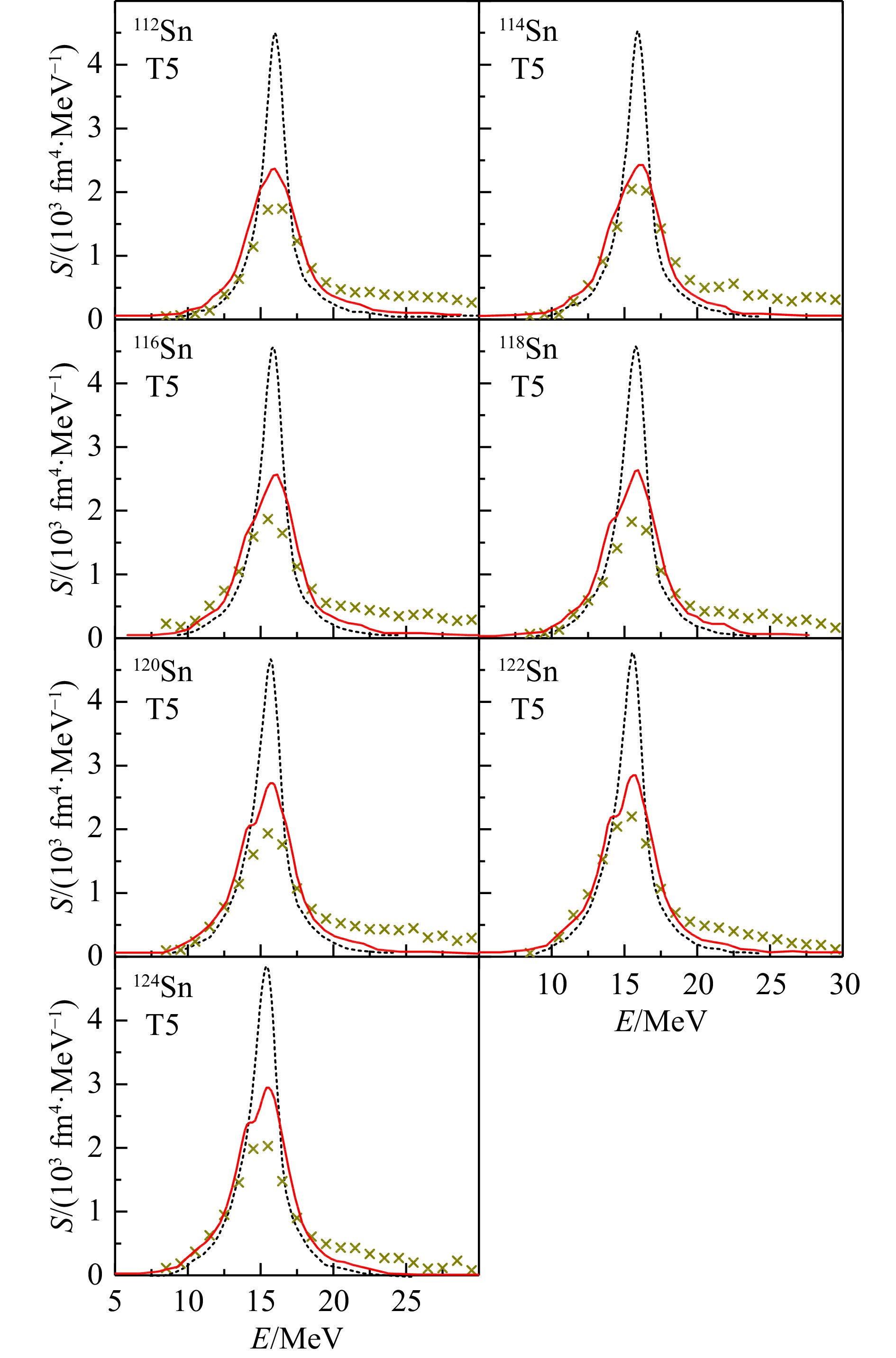
文献[48]利用了基于Hartree-Fock-BCS的QRPA+QPVC理论对这一问题进行了探索。研究采用T5 ($ K_\infty= 202 \;{\mathrm{MeV}} $)和T6 ($ K_\infty=236 \;{\mathrm{MeV}} $)两组Skyrme参数^[49]。然而，由于T5和T6均不能够给出与实验相符的声子态激发能量和跃迁概率，因此，没有采用自洽计算给出声子态。在声子态的计算中，基于T5相互作用，采用了Landau-Migdal近似，并调节了相互作用参数以重$ 2_1^+ $、$ 3_1^- $的实验值。

图3给出了基于QRPA和QRPA+QPVC理论，采用Skyrme T5相互作用，计算得到的Sn同位素链ISGMR强度随能量的分布。其中，土黄色叉号为实验结果^[32]，黑色虚线表示自洽QRPA计算的结果，红色实线为QRPA+QPVC计算的结果。QRPA+QPVC模型中声子态的计算采用了Landau-Migdal近似。相关结果取自文献[48]。从图中可以发现，自洽QRPA理论可以对实验值的中心能量给出很好的描述。由于T5相互作用的不可压缩系数较小($ K_\infty=202 \; {\mathrm{MeV}}$)，因此说明了Sn同位素状态方程较“软”。另一方面，由于QRPA理论不能给出宽度，其强度函数峰值均高估了实验值约1倍。在考虑准粒子振动耦合效应后，能够很好地给出ISGMR宽度。然而，其中心能量基本没有变化，即在非自洽的QRPA+QPVC理论中，仍然存在Sn同位素链给出的状态方程较“软”的问题。

文献[46]基于Skyrme Hartree-Fock-Bogoliubov (SHFB)发展了完全自洽的QRPA+QPVC理论，并将其应用于原子核ISGMR的研究。

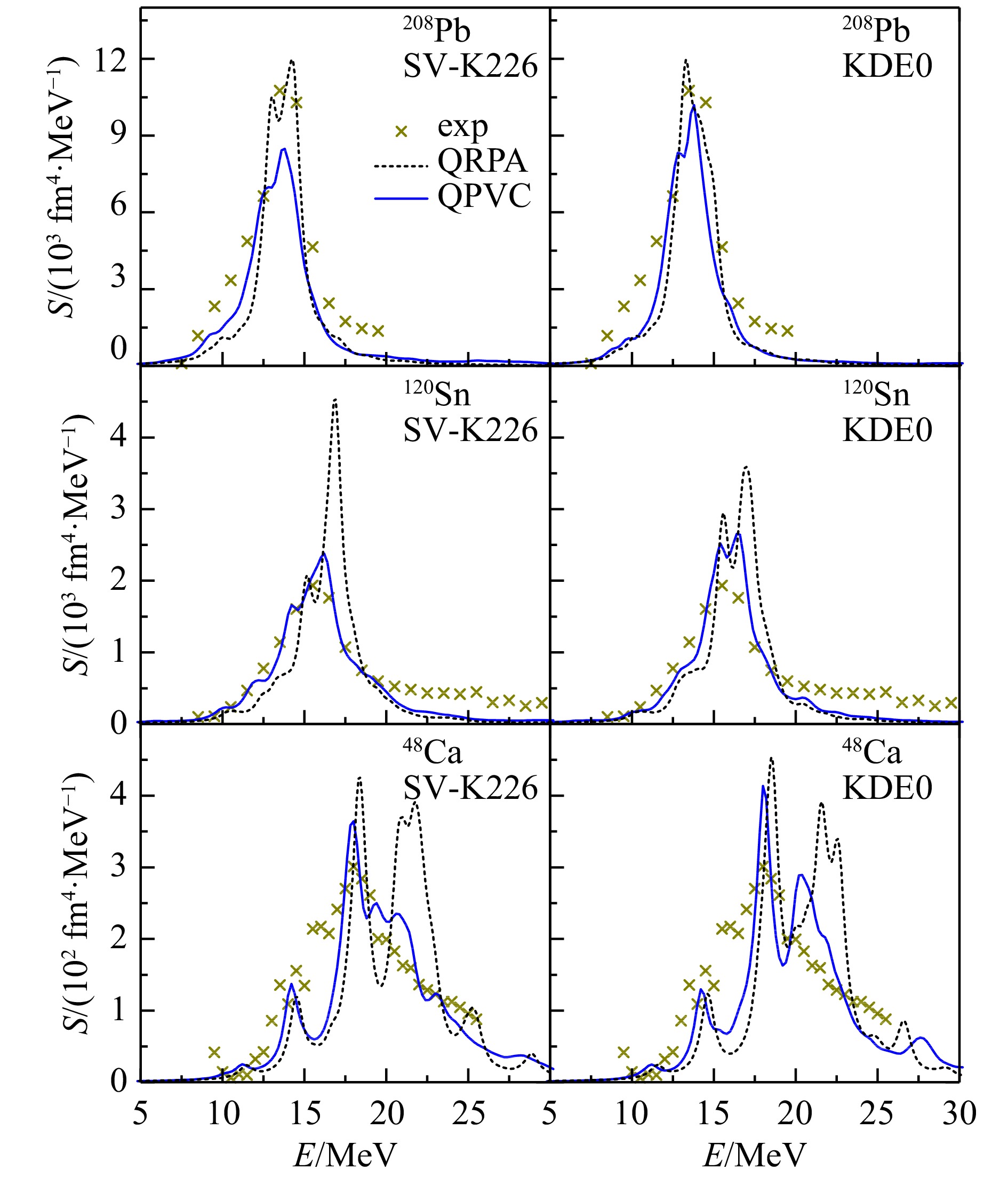
图4给出了QRPA和QRPA+QPVC理论计算的²⁰⁸Pb,¹²⁰Sn和⁴⁸Ca中ISGMR强度函数随能量的分布。左图为采用Skyrme参数组SV-K226^[50]的结果(取自文献[46])，右图为采用Skyrme参数组KDE0^[51]的结果。总体来看，考虑QPVC效应后，两种相互作用对⁴⁸Ca, ¹²⁰Sn和²⁰⁸Pb强度函数的描述均得到了明显改善。在²⁰⁸Pb中，QRPA理论给出了与实验相符的ISGMR能量，然而宽度略低估实验值。考虑QPVC效应后，ISGMR能量略微向低能方向移动，并且给出了较大的宽度，与实验更加符合。在¹²⁰Sn中，实验的强度分布呈现单峰结构，QRPA理论则给出了能量高于实验值的主峰以及能量接近实验值的小峰。ISGMR中心能量比实验值偏大约0.8 MeV，即Sn同位素链给出的状态方程较“软” ，与文献[21−22]一致。考虑QPVC效应后，给出了与实验相符的ISGMR宽度。更进一步，ISGMR中心能量也向低能方向移动了约0.7~0.8 MeV，与实验较为吻合。在⁴⁸Ca中，实验上ISGMR强度分布同样呈现具有较大共振宽度的单峰结构，而QRPA理论则给出多峰结构，并高估实验能量。考虑QPVC效应后，峰的位置向低能方向移动，位于22 MeV能量处的峰被很大程度压低，与实验更为符合。对于⁹⁰Zr，利用SV-K226相互作用，同样很好地重现了ISGMR的强度分布^[46]。

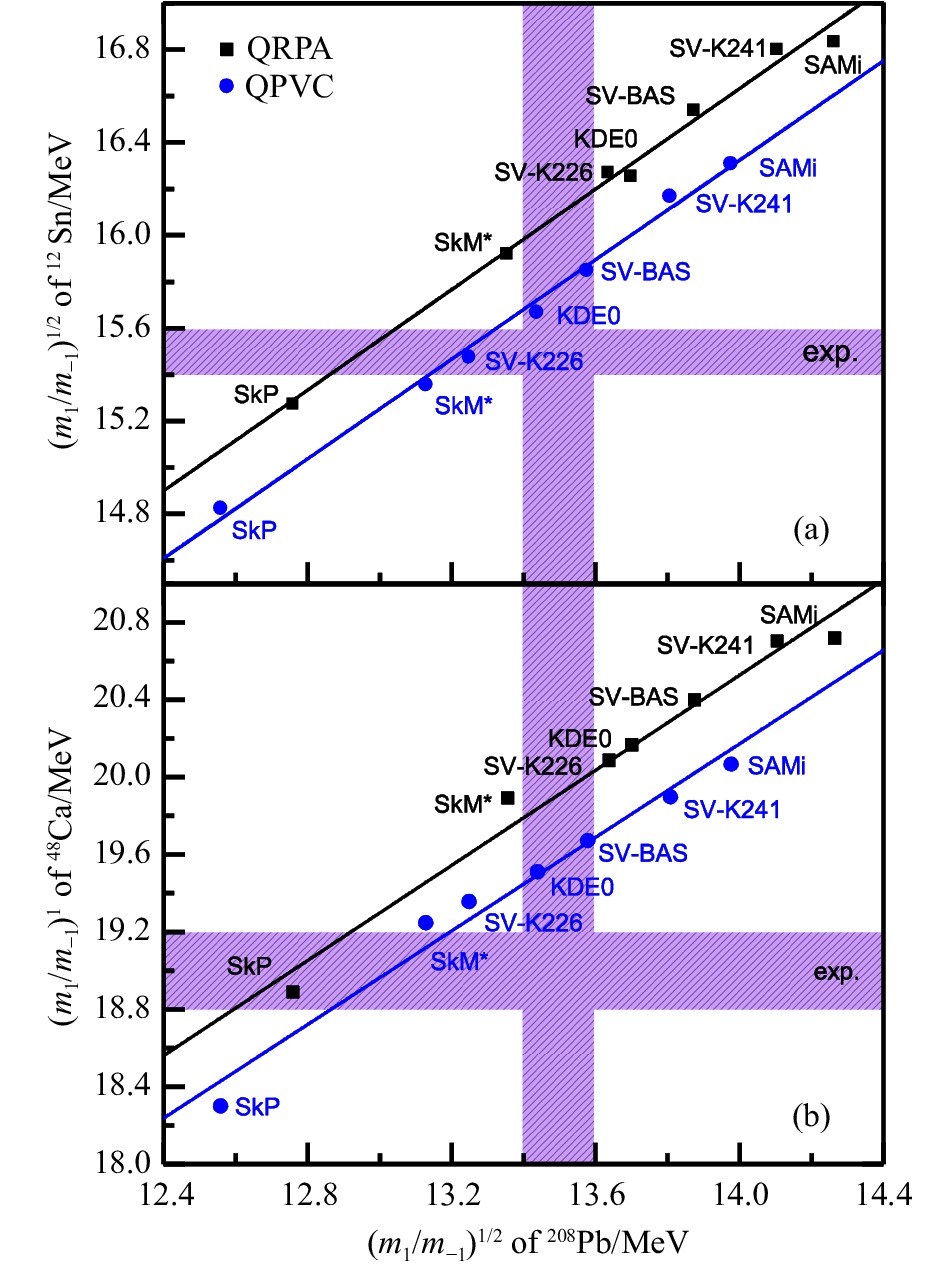
由于不同原子核中均存在ISGMR能量与核物质不可压缩系数的关系$ E_ {\rm{ISGMR}} \propto \sqrt{K_\infty} $，因此可以推测不同原子核的ISGMR能量之间也应存在线性关联，如图5所示。图中给出了¹²⁰Sn [图5(a)]、⁴⁸Ca [图5(b)]中ISGMR能量与²⁰⁸Pb ISGMR能量的关系，取自文献[46]。其中黑色方形代表QRPA理论计算的结果，蓝色圆形代表QRPA+QPVC理论计算的结果，通过最小二乘法给出相应的回归直线，实验值和其不确定度取自文献[14, 32, 53]。采用的Skyrme相互作用为SkP^[54]、SkM*、SV-K226、KDE0、SV-bas、SV-K241^[50]和SAMi^[55]。从图中可以看出，在QRPA理论中，不同模型计算的¹²⁰Sn(或⁴⁸Ca)的ISGMR能量与²⁰⁸Pb的ISGMR能量之间存在较好的线性关联。这一线性关联表明Skyrme相互作用参数组的计算结果均应分布在这条线附近。然而，与实验值相比可以发现，这条线离¹²⁰Sn(或⁴⁸Ca)与²⁰⁸Pb的实验值交叉点较远，即在QRPA理论中无法同时描述¹²⁰Sn(或⁴⁸Ca)与²⁰⁸Pb的ISGMR能量。考虑QPVC效应后，不同核之间ISGMR能量的线性关联仍然成立。值得注意的是，包含QPVC效应后，线性关联给出的直线向实验交叉点大幅度移动，几乎穿过了实验交叉点。这说明了考虑QPVC效应后，对¹²⁰Sn和²⁰⁸Pb ISGMR能量的同时描述并非来自个别相互作用的巧合，而是来源于QPVC所引入的高阶多体关联效应。

采用相互作用参数组SV-K226，考虑QPVC后，²⁰⁸Pb的ISGMR中心能量降低了约0.4 MeV，¹²⁰Sn的ISGMR中心能量下降了约0.8 MeV，这使得QPVC理论成功实现了对²⁰⁸Pb和¹²⁰Sn的ISGMR能量同时描述。文献[46]进一步分析了在¹²⁰Sn和²⁰⁸Pb中，QPVC效应引起ISGMR能量移动大小不同的原因。在²⁰⁸Pb和¹²⁰Sn中，QRPA计算的跃迁强度分布由少数几个本征态主导，取其强度最高的本征态进行分析。此时QPVC能量E满足

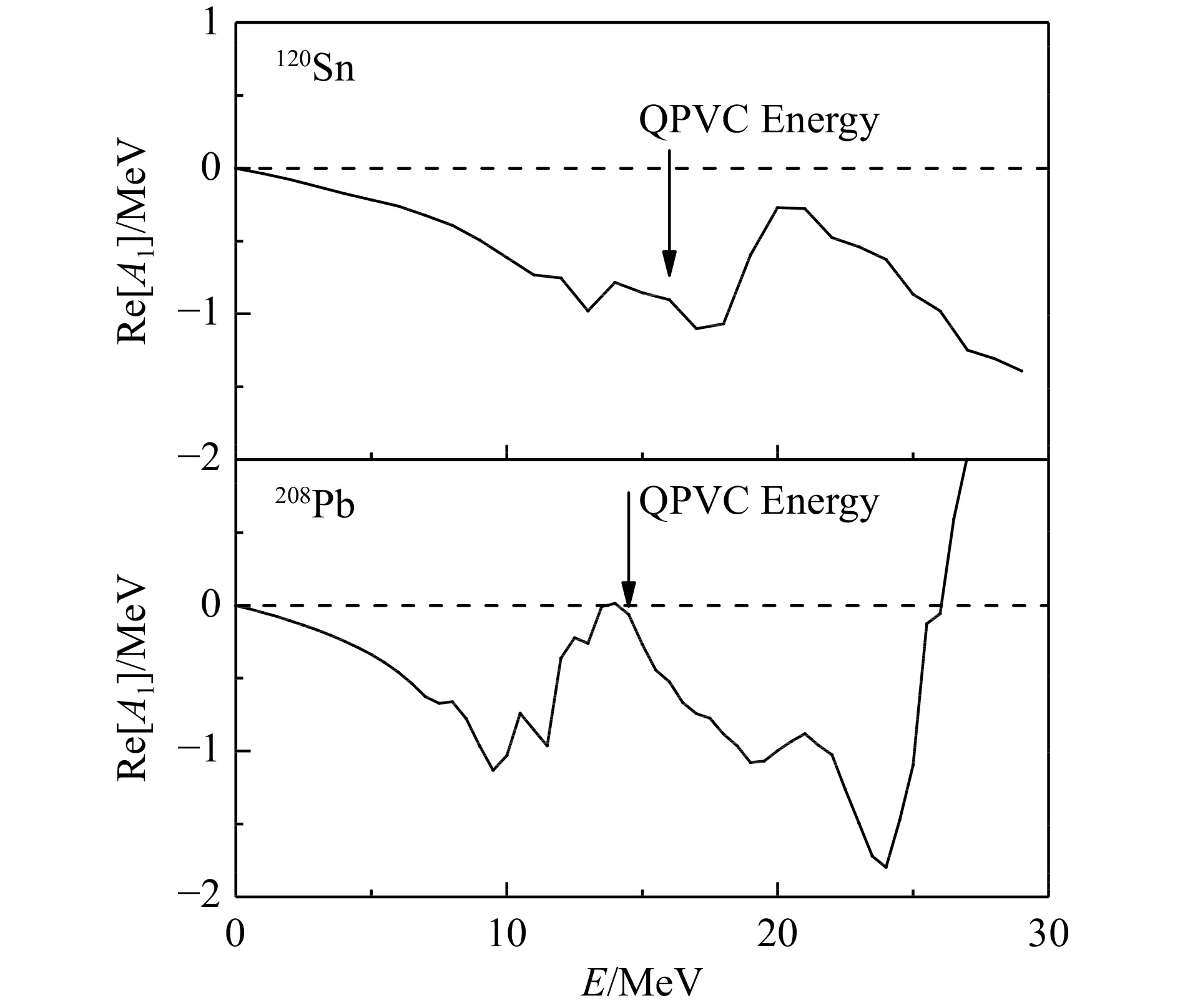
其中$ E_ {\rm{QRPA}} $为待分析的QRPA本征态，对于²⁰⁸Pb为14.33 MeV，对于¹²⁰Sn为16.88 MeV。$ {\rm{Re}} {\cal{A}}_1 (E) $表示自能$ {\cal{A}}_1(E) $的实部。该方程的解给出了QPVC理论中原子核ISGMR的能量$ E_{{\rm{QPVC}}} $，该能量所对应的自能$ {\cal{A}}_1(E_{\rm{QPVC}}) $的实部，给出了QPVC效应带来的能量移动大小。

图6给出了¹²⁰Sn和²⁰⁸Pb中QPVC方程自能$ {\cal{A}}_1(E) $的实部随能量的变化，采用的相互作用为SV-K226，取自文献[46]。可以发现，随着能量的增加，自能总体上有下降的趋势，这是因为一般随着能量的增加，两准粒子与声子态可能耦合的数目在增加。因此，这意味着在更高激发能的位置QPVC效应一般会引起更大的能量移动。然而，某些特殊的两准粒子与声子(称之为中间态)具有很大的自能耦合顶点，在该中间态能量处自能$ {\cal{A}}_1(E) $会出现一个类奇点行为(分母趋近于零)：它的实部会有一个迅速的跳跃，导致自能的实部迅速变大，如图6中17.5~20.0 MeV (¹²⁰Sn)、10.0~15.0 MeV (²⁰⁸Pb)和24.0~27.0 MeV (²⁰⁸Pb)能量范围所示。

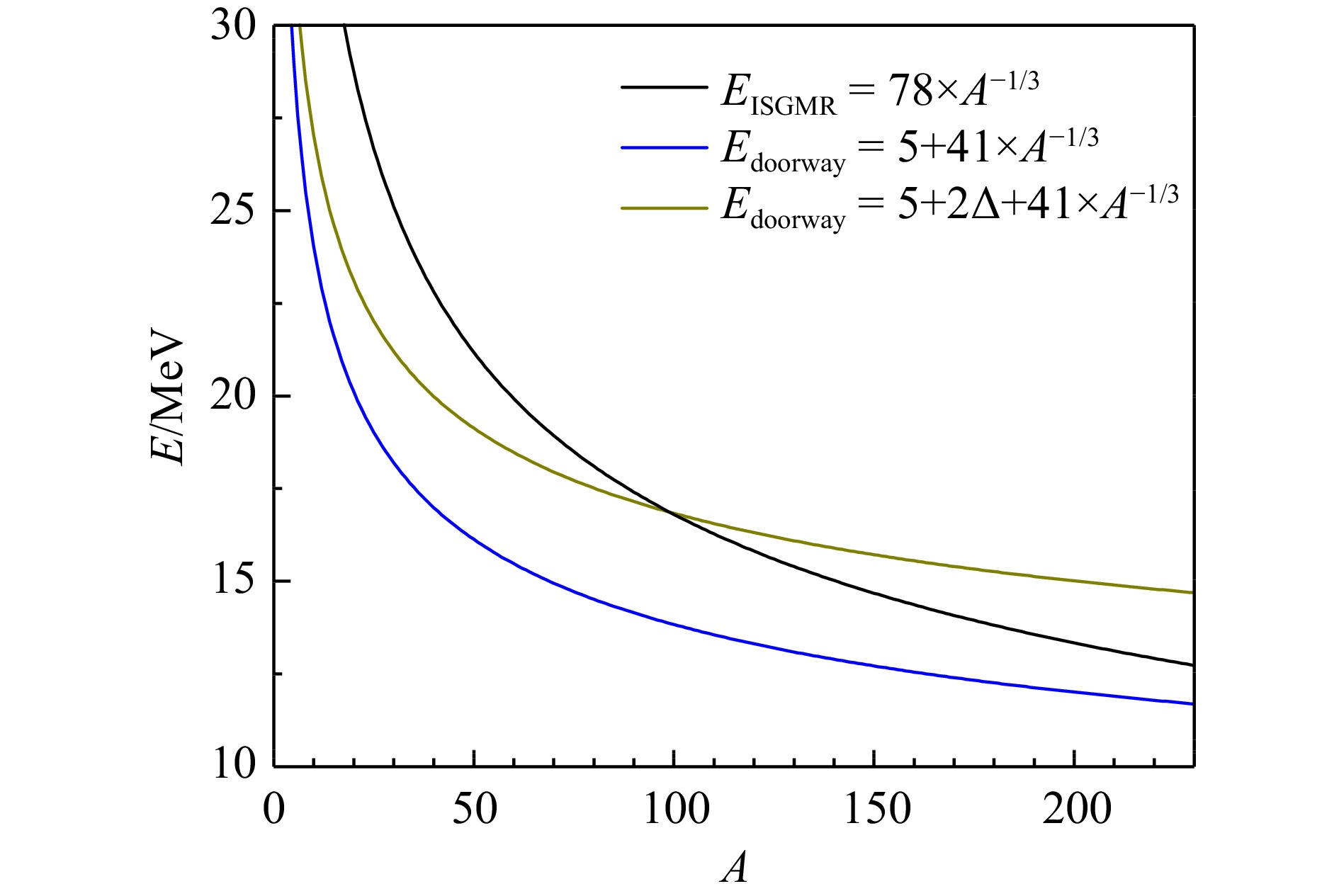
从图6可以发现，对于¹²⁰Sn，ISGMR能量$ E_{\rm{QPVC}} $出现在类奇点行为之前，而对于²⁰⁸Pb，ISGMR能量$ E_{\rm{QPVC}} $出现在类奇点行为之后。这导致了QPVC效应在¹²⁰Sn中引起了较大的移动，而在²⁰⁸Pb中移动则很小。因此，需要理解中间态能量与ISGMR能量的相对位置。中间态由声子与两准粒子组态组成。这里最为重要的中间态声子为低激发3⁻声子，它在¹²⁰Sn和²⁰⁸Pb中有相似的能量，约5 MeV左右。由于声子为奇宇称态，考虑到宇称守恒，两准粒子组态也为奇宇称态，即跨壳激发。对于双幻核(质子数和中子数均为幻数)，两准粒子组态即一粒子一空穴组态，激发能约为一个谐振子壳的能量$ 41 A^{-1/3}\;{\mathrm{MeV}} $，因此中间态的总能量为$ E_ {\rm{doorway}} = 5 + 41 A^{-1/3}\;{\mathrm{MeV}} $。对于需要考虑对关联的原子核，两准粒子组态能量还需要考虑拆散配对粒子的能量贡献$ 2\Delta \;{\mathrm{MeV}}$，其中$ \Delta $为对能隙，因此，中间态的总能量为$ E_ {\rm{doorway}} = 5 + 41 A^{-1/3} + 2 \Delta \;{\mathrm{MeV}} $。另一方面，原子核ISGMR能量可以近似为$ 78A^{-1/3}\; {\mathrm{MeV}} $，它和中间态能量的关系如图7所示。图中给出了ISGMR能量$ E_ {\rm{ISGMR}} $的经验公式随质量数$ A $的变化，以及中间态能量$ E_ {\rm{doorway}} $近似公式在包含和不包含对关联效应时随质量数$ A $的变化，取自文献[46]。可以发现，在²⁰⁸Pb中，ISGMR能量高于中间态能量。由于对能隙的存在，¹²⁰Sn中ISGMR能量小于中间态能量。因此，¹²⁰Sn中(Q)PVC效应引起的ISGMR能量移动要大于²⁰⁸Pb。

在超越平均场层次，零程核力在计算核物质参数时会出现紫外发散的问题^[56]，因此如何准确约束核物质不可压缩系数目前仍是一个开放性问题。然而，由于采用了subtraction方法，QRPA+QPVC保证了系统的静态性质和平均场一致^{[29, 57]}，因此核物质不可压缩系数也应与平均场结果一致。表1中给出了QRPA理论和QRPA+QPVC理论计算的⁴⁸Ca，¹²⁰Sn和²⁰⁸Pb中ISGMR能量与实验数据的偏离[$ |E_c^ {\rm{theo.}} - E_c^ {\rm{exp.}}| $ MeV]，取自文献[46]。从表中可以看出，在QRPA理论中，SkP对⁴⁸Ca和¹²⁰Sn的ISGMR能量给出了最好的描述，其不可压缩系数为$K_\infty=201\; {\mathrm{MeV}}$，但是它却偏离²⁰⁸Pb的ISGMR能量0.74 MeV。SkM*，SV-K226和KDE0对²⁰⁸Pb提供了较好的描述，其不可压缩系数为$K_\infty=217 \sim 229 \; {\mathrm{MeV}}$，而它们却高估了⁴⁸Ca和¹²⁰Sn的ISGMR能量。即QRPA理论对核物质不可压缩系数的约束存在矛盾。考虑QPVC效应后，SkM*和SV-K226对⁴⁸Ca提供了较好的描述，SkM*, SV-K226和KDE0对¹²⁰Sn提供了较好的描述，SV-K226, KDE0和SV-bas对²⁰⁸Pb提供了较好的描述。因此，SV-K226和KDE0对3个核均提供了较好的描述，其相应的不可压缩系数分别为$ K_\infty = 226 \; {\mathrm{MeV}}$和$ 229 \; {\mathrm{MeV}}$。这个结果和之前文献中利用QRPA理论在²⁰⁸Pb中得到的$ K_\infty= (240\pm20) \; {\mathrm{MeV}}$相一致。

除了非相对论的Skyrme密度泛函理论，另一种常用的密度泛函理论为相对论密度泛函理论^[58]。当文献[46]出现在预印本文库(arXiv:2211.01254)之后的2个月，文献[59] (arXiv:2212.14766)采用基于相对论密度泛函的QRPA+QPVC理论对ISGMR强度函数的分布进行了研究，进一步证实了考虑QPVC效应后能够实现²⁰⁸Pb和¹²⁰Sn的统一描述。

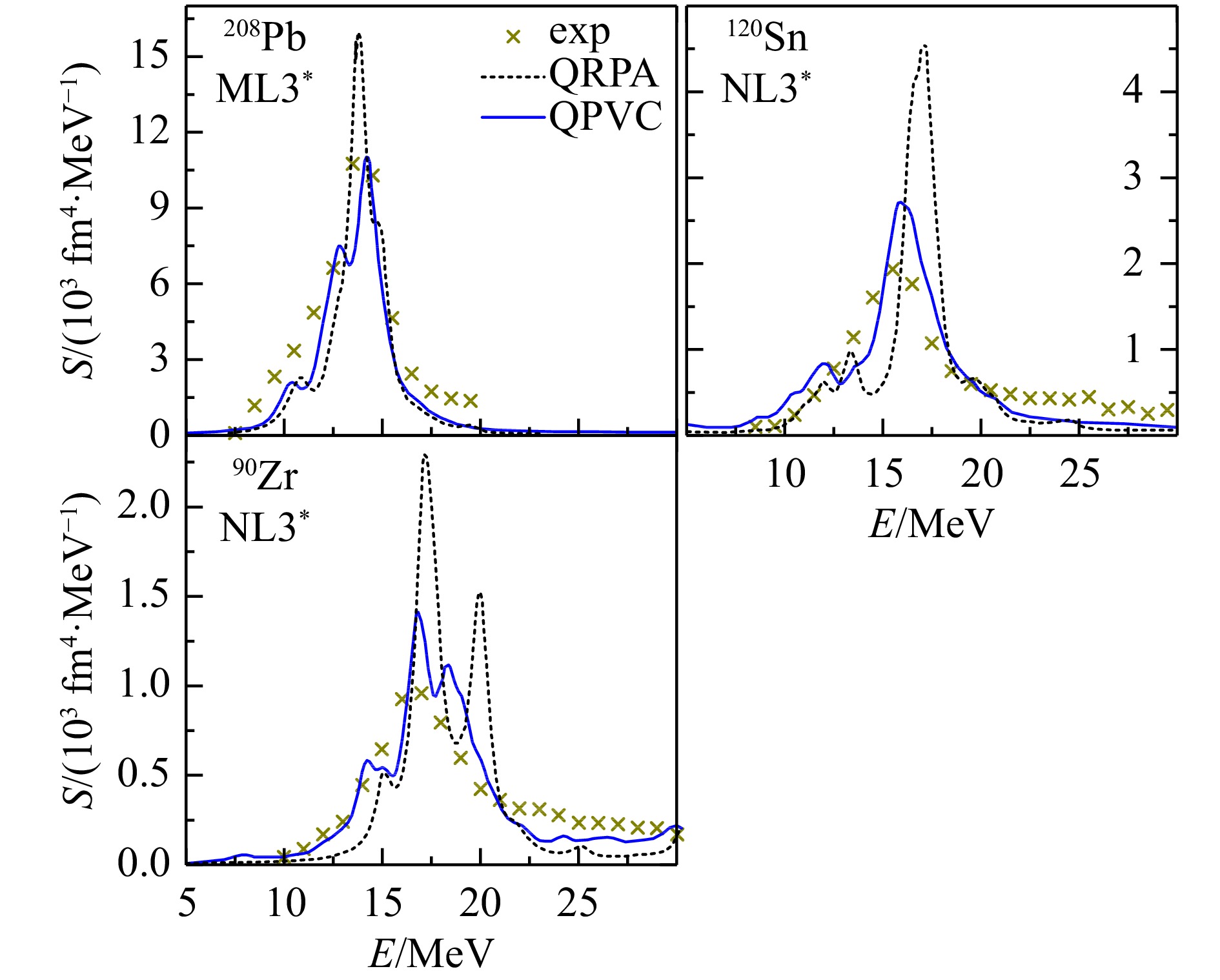
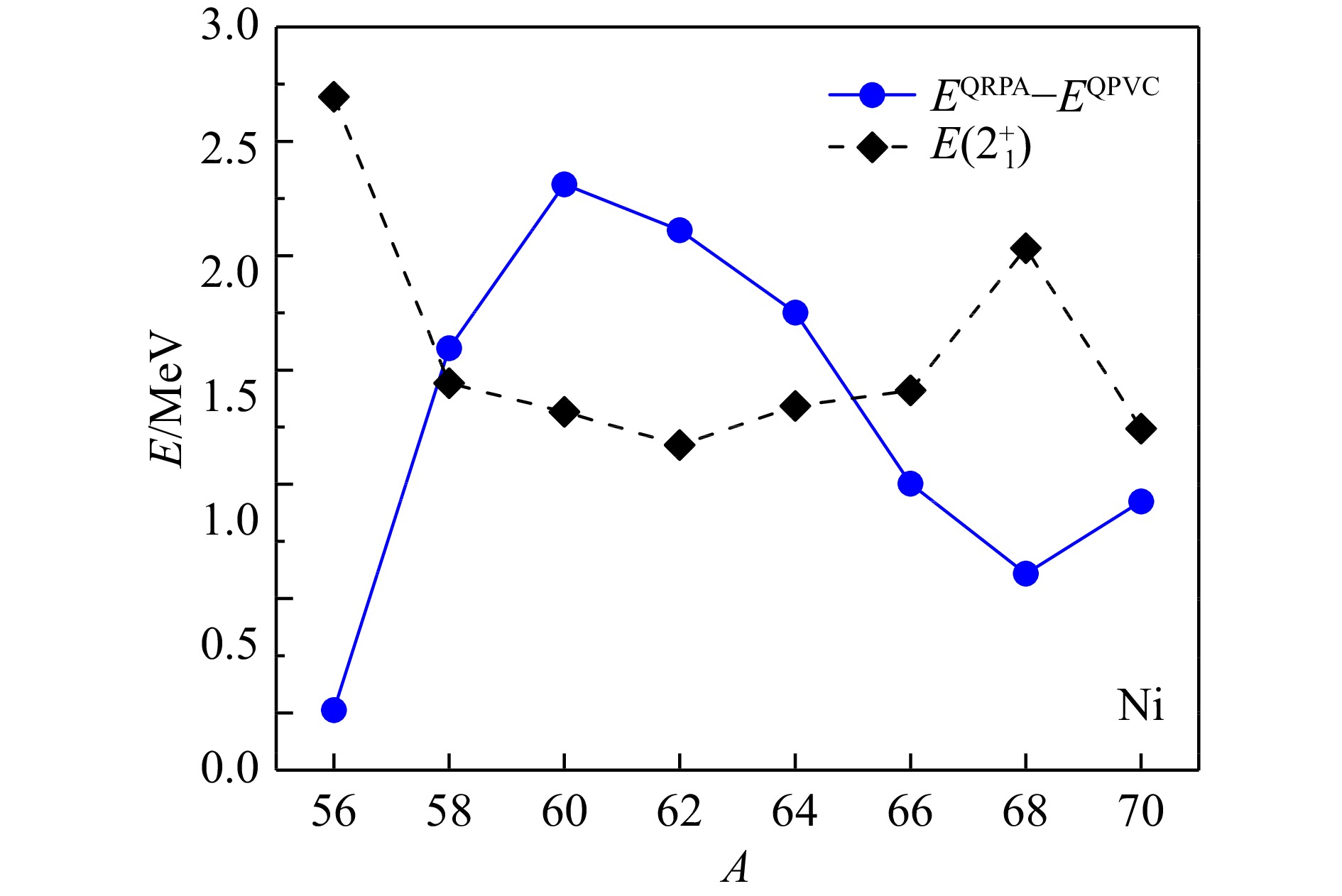
图8给出了采用相对论密度泛函NL3*^[60]，QRPA和QRPA+QPVC理论计算的²⁰⁸Pb，¹²⁰Sn和⁹⁰Zr中同位旋标量ISGMR强度分布。其中，叉号为实验结果^[61]，黑色虚线表示自洽QRPA计算的结果，蓝色实线为QRPA+QPVC计算的结果。相关结果取自文献[59]。NL3*的不可压缩系数$ K_\infty =258 $ MeV。从图中可以看出，在QRPA理论中，它可以对²⁰⁸Pb的ISGMR能量给出与实验相符的结果。考虑QPVC效应后，仍然可以对²⁰⁸Pb的ISGMR能量给出较好的描述。对于¹²⁰Sn，QRPA理论高估了实验ISGMR能量，即存在Sn同位素链状态方程较“软”的问题。考虑QPVC效应后，可以对¹²⁰Sn的ISGMR能量给出较好的描述，说明了QPVC效应对Pb和Sn ISGMR统一描述具有重要作用。进一步，图中给出了QRPA和QRPA+QPVC理论对⁹⁰Zr ISGMR强度分布的描述。可以发现，QRPA理论中⁹⁰Zr出现双峰结构，考虑QPVC效应后，第二个峰和第一个峰距离靠近，几乎合并成了一个峰，因此与实验上的强度分布较为一致。

文献[59]认为，直接理解QPVC效应在²⁰⁸Pb和¹²⁰Sn中带来的ISGMR能量的不同移动较为困难。因此，文献[59]以Ni同位素链为例，分析了QPVC效应在开壳核与闭壳核中的不同。图9给出了采用NL3*相互作用QPVC效应带来的Ni同位素链ISGMR能量的移动$ E^ {\rm{QRPA}} - E^ {\rm{QPVC}} $以及实验上第一个$ 2^+ $激发能$ E(2_1^+) $随着质量数的变化。从图中可以看出，QPVC效应带来的ISGMR能量的移动$ E^ {\rm{QRPA}} - E^ {\rm{QPVC}} $与$ E (2_1^+) $有相反的趋势。$ E(2_1^+) $的减小通常被认为是四极振动集体性增强的体现。因此可以猜测，ISGMR的能量移动与$ E(2_1^+) $密切相关。以此类比，¹²⁰Sn中$ E(2_1^+) = 1.17 \;{\mathrm{MeV}}$，比²⁰⁸Pb $ E(2_1^+)= 4.09 \; {\mathrm{MeV}}$小很多，也许导致了QPVC效应对二者ISGMR能量的影响不同。该机制与文献[46]都认为对关联是导致QPVC效应在²⁰⁸Pb和¹²⁰Sn中影响不同的主要原因，然而文献[59]认为对关联主要通过$ 2_1^+ $态能量起贡献，而文献[46]认为$ 3^- $声子的贡献同样重要，而对关联主要通过对能隙起贡献。

丰中子原子核由于具有较大的中质比，往往表现出不同于β-稳定线附近原子核的性质，比如新的激发模式的出现^{[27, 62−63]}，因此对丰中子原子核的研究具有重要的意义。SV-K226和KDE0的不可压缩系数分别为226 MeV和229 MeV，基于QRPA+QPVC理论，它们对β-稳定线附近的Sn和Pb同位素给出了与实验ISGMR强度分布几乎一致的描述，因此我们可以利用这两组参数进一步对丰中子Sn同位素的电单极激发强度分布进行预测。

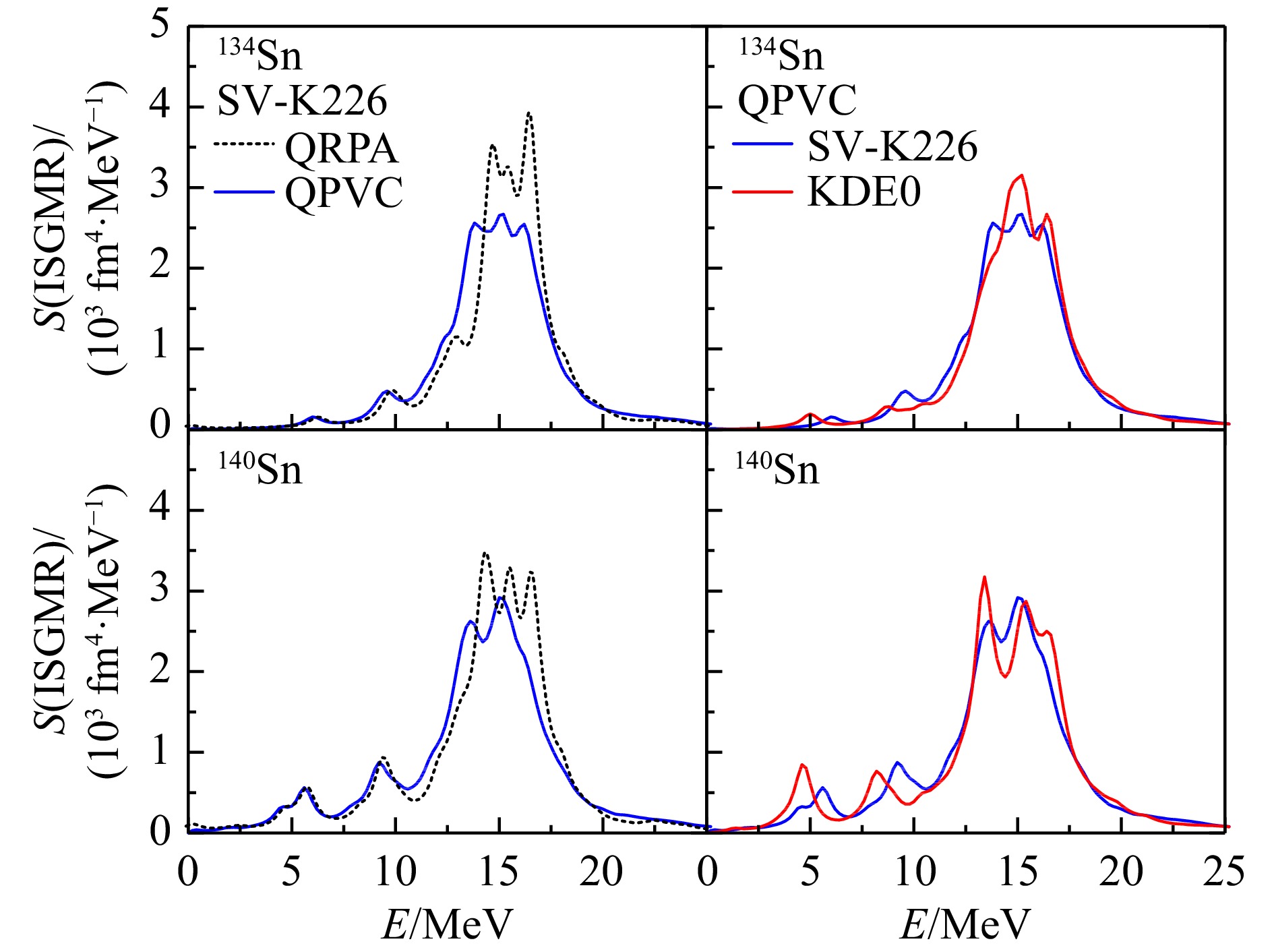
图10的左图给出了基于QRPA和QRPA+QPVC理论采用SV-K226相互作用计算的^{134, 140}Sn中电单极激发强度分布。可以看出，在QRPA理论的计算中，丰中子核素^{134, 140}Sn中除了巨共振区域(10~20 MeV)出现了较宽的ISGMR共振峰外，在低能量区域(小于10 MeV)也出现了明显的电单极激发(为了区别于ISGMR，后面称为软单极激发)强度分布，且在¹⁴⁰Sn中更为显著。考虑QPVC效应后，ISGMR的峰值能量向低能量方向移动，而软单极激发强度分布仅略微向低能方向移动，即QPVC效应对于软单极激发的影响较小，而对于ISGMR的影响较大。右图给出了基于QRPA+QPVC理论采用SV-K226和KDE0相互作用计算的^{134, 140}Sn中电单极激发强度分布。然而，对于软单极激发，SV-K226和KDE0表现出了明显的差异。这是因为软单极激发对应于中子的呼吸模式(而非中子和质子的呼吸模式)^[63]，因此不能被对称核物质的不可压缩系数$ K_\infty $唯一约束。另一方面，由于SV-K226和KDE0具有相近的$ K_\infty $，它们在10~20 MeV的巨共振区域给出了几乎一致的ISGMR强度分布，这表明丰中子原子核的ISGMR强度分布仍然可以约束$ K_\infty $。因此，实验上对丰中子核素ISGMR强度分布的测量将有助于进一步检验在稳定核区对核物质不可压缩系数$ K_\infty $的约束。

原子核巨单极共振的统一描述是核物理研究的一个重要问题：在原子核ISGMR的研究中，能够正确描述²⁰⁸Pb ISGMR能量的理论模型往往高估Sn同位素链的ISGMR能量约1 MeV，这会使得由Sn同位素链提取的不可压缩系数比Pb小约30 MeV，从而引发了核物理中的著名谜题“为什么Sn同位素链给出的状态方程这么软?”。本文综述了QRPA理论和QPVC理论对这一问题的研究。在QRPA理论中，通过考虑表面对力，发现对关联效应能够部分解释Sn同位素状态方程较“软”的问题，但是采用其它类型的对力，比如体积对力时仍然存在问题，不能得到令人满意的解释。最近，基于Skyrme密度泛函理论的自洽QRPA+QPVC理论的发展为这一问题的回答提供了合理的解释，并论证了QPVC效应在解决这一问题时的重要作用。随后，这一结论在相对论QRPA+QPVC的计算中也得到了验证。Sn和Pb同位素中ISGMR的统一描述将核物质不可压缩系数约束为(226~229) MeV。基于QRPA+QPVC理论，本文也对丰中子Sn同位素^{134, 140}Sn的电单极激发强度分布进行了研究，实验上对丰中子核素电单极激发强度函数的测量将有助于进一步检验目前对核物质不可压缩系数的约束。

另一方面，目前的研究工作说明了超越两准粒子组态空间对于巨共振的描述十分重要，进一步探究更高阶组态空间对巨共振的影响是值得讨论的问题。