水下无线通信技术在海洋探测系统的实用化进程中发挥着重要作用, 主要原因在于该技术能够满足水下航行器与传感器之间进行可靠的数据传输的需求^[1,2]. 其中, 水下无线光通信(underwater wireless optical communication, UWOC)技术由于能够在短距离范围内实现高速数据传输而备受关注^[3]. UWOC通常被认为是比声学通信和射频通信更安全的通信技术^[1,3]. 为了进一步提升其传输距离和数据传输速率, UWOC系统已得到广泛的研究与论证^[4]. 然而, 对于UWOC系统的安全性问题很少有相关研究. 2017年, Kong等^[3]研究验证了UWOC系统随着传输距离的增加或水信道浑浊程度的加剧, 信息泄漏的可能性大大增加, 对UWOC系统的安全性构成巨大威胁.

幸运的是, 量子密钥分发(quantum key distribution, QKD)^[5,6]技术基于量子力学的基本定律, 能够保证信息传输的无条件安全, 是解决UWOC信息安全问题的一种有效方法. 通常, QKD主要可分为离散变量(discrete variable, DV)QKD^[7–10]与连续变量(continuous variable, CV) QKD^[11–16]. 相比于DV-QKD, CV-QKD易融于现有光通信系统, 无需使用造价高昂的单光子探测器, 而是采用成本更低的相干探测器, 具有更大的密钥率以及更高的探测效率. 作为CV-QKD应用最广泛的一种类型, 高斯调制相干态(Gaussian modulated coherent state, GMCS)方案在理论安全性^[17–21]和实验^[22–29]方面都已取得显著进展. 此外, GMCS方案也被应用于其他连续变量量子通信方案中, 比如量子秘密共享方案^[30,31], 量子数字签名方案^[32]等.

由于地球约71%的表面积被海洋所覆盖, 因此海水也是一种非常重要的信息传输信道. 水下QKD技术能够用于提升水下信息传输的安全性, 对构建全球量子通信网络至关重要. 因此近年来, 研究人员对水下QKD技术的可行性进行了理论^[33,34]和实验^[35–39]研究. 然而, 上述研究均是基于DV-QKD方案. 最近, 水下CV-QKD技术由于自身独特的优势而备受关注, 并且已进行了相关的理论研究^[40–44]以及实验研究^[45]. 在水下CV-QKD方案的实际部署中, 接收方通常会对所接收到的信息进行零差或外差探测. 在执行零差探测时, 由于只对正则分量X和P的其中之一进行测量, 因此测量基的选择是必不可少的步骤. 然而, 在实际系统的接收端, 由于所采用的数模转换器(digital-to-analog convertor, DAC)其带宽有限, 使得测量基在选择过程中会产生角度偏差^[46]. 这会导致合法通信方在评估海水信道透过率和过噪声时与真实值发生偏差, 影响方案的安全性.

基于上述分析, 本文提出基于非理想测量基选择的水下CV-QKD方案, 并且在实际海水信道条件下对所提出的方案进行安全性分析. 为了对非理想测量基选择所引入的额外过噪声进行定量分析并获得其安全界限, 本文引入对应于DAC中运算放大器环路增益的参数, 构建水下CV-QKD方案的综合安全性框架. 仿真结果表明, 由非理想测量基选择所引入的额外过噪声能够降低水下CV-QKD方案的密钥率与最大传输距离, 影响其安全性. 但所提出的安全性分析框架模型能够有效地解决由非理想测量基选择所带来的安全隐患, 有助于推动水下CV-QKD系统的实用化进程. 本文第2节详细描述了所提出的基于非理想测量基选择的水下CV-QKD方案; 第3节对所提出的方案的安全性进行分析, 包括其渐近安全性与组合安全性; 第4节总结全文.

本节首先介绍基于非理想测量基选择的水下CV-QKD方案, 之后对海水信道的光传播特性进行详细分析.

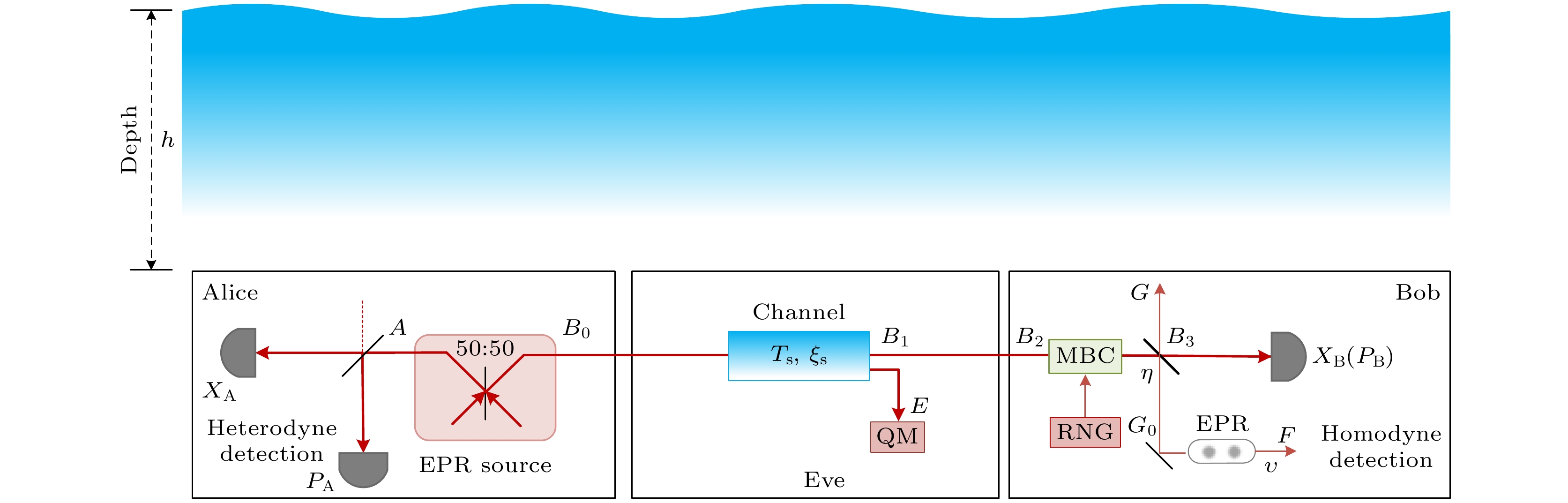
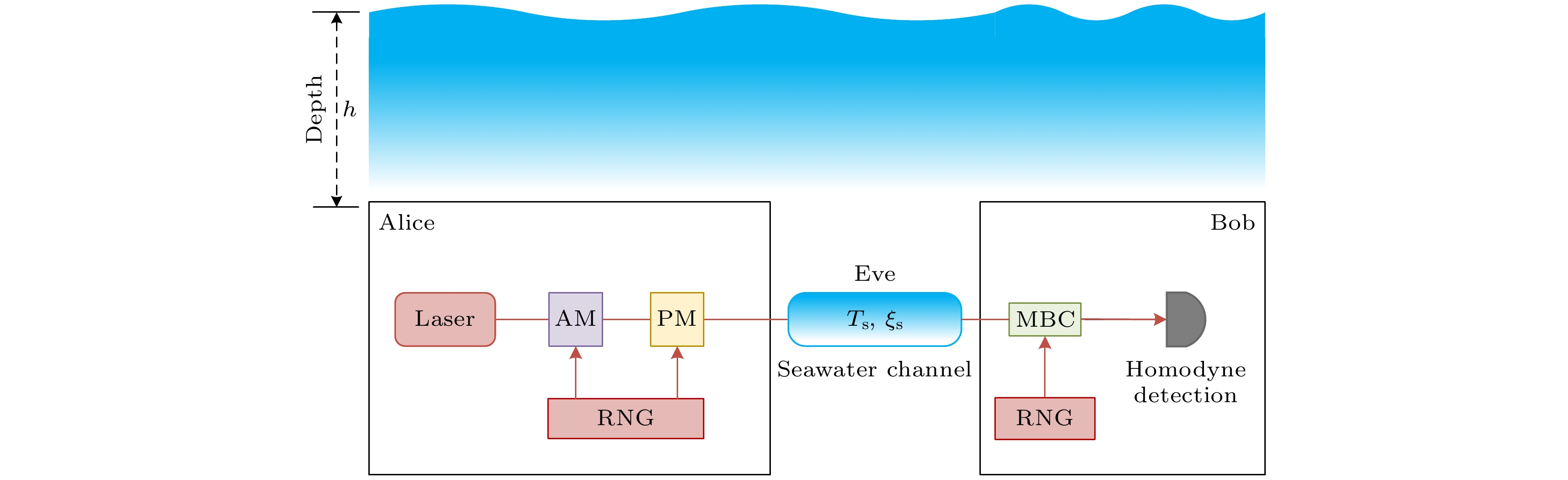
图1给出了基于非理想测量基选择的水下CV-QKD制备-测量(prepare-and-measure, PM)方案图. 发送方Alice采用随机数发生器生成两个高斯随机数${X_{\text{A}}}$与${P_{\text{A}}}$, 两者的均值为0, 方差为${V_{\text{A}}}$. 之后, Alice利用振幅调制器和相位调制器将密钥信息加载到散粒噪声为$(\Delta {X_{\text{A}}}, {\text{ }}\Delta {P_{\text{A}}})$的初始相干态中, 并经海水信道发送给接收方Bob. 海水信道的透过率与过噪声分别为${T_{\text{s}}}$与${\xi _{\text{s}}}$, 此处过噪声可以理解为由于Eve的窃听所引入的噪声. 当Bob接收到由Alice发送的信息后, 采用零差探测器随机对所接收到的相干态其中一个正则分量进行测量. 由于平衡零差探测器能够通过调节量子信号与本振光之间的差分相位$\psi $来测量正则分量${X_{\text{B}}}$或${P_{\text{B}}}$. 因此, Bob可以通过采用相位调制器来进行测量基选择, 即Bob通过在相位调制器上选择0或${{\text{π}} {/ } 2}$来执行测量基选择流程.

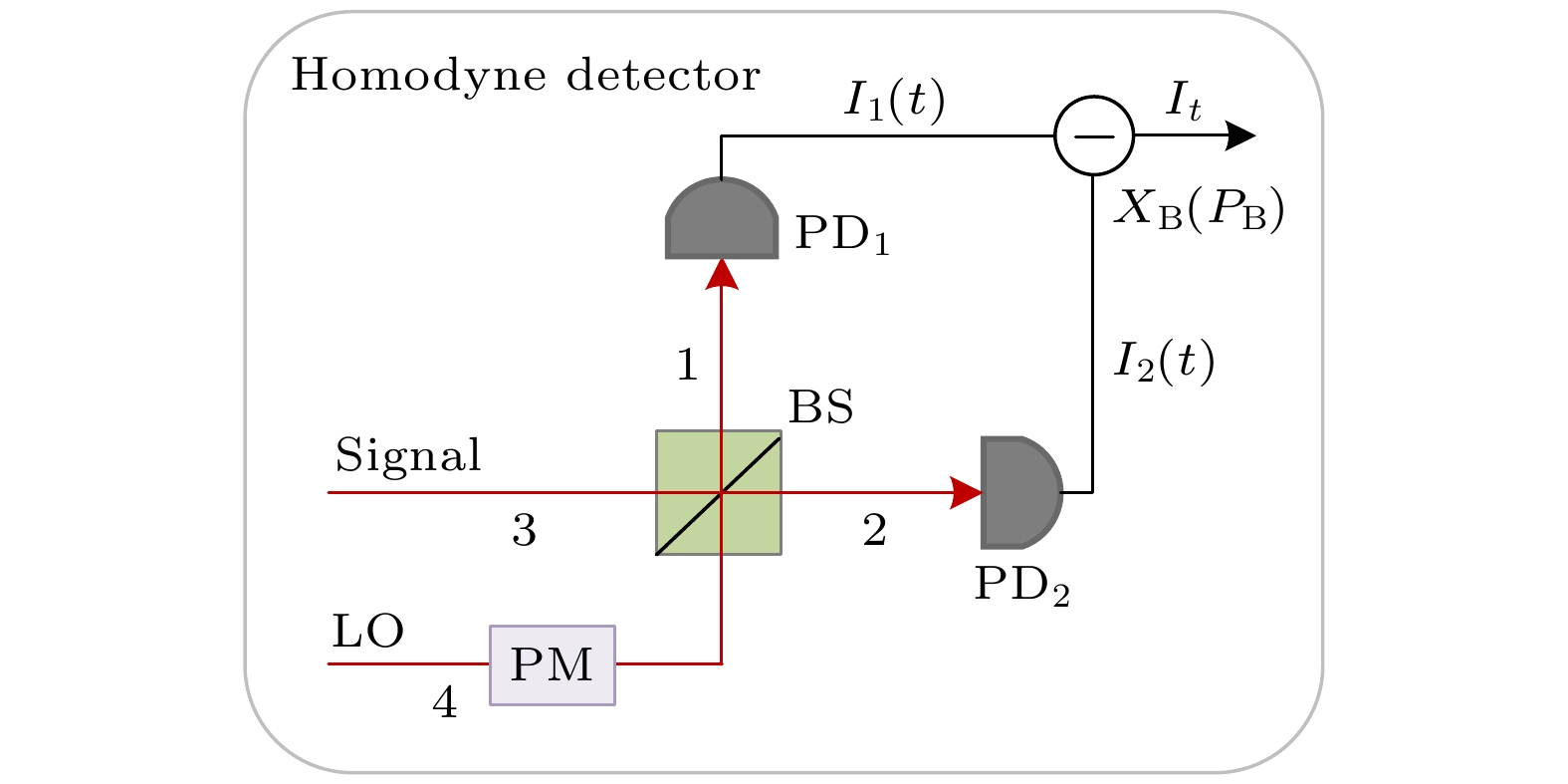
图2给出了与PM方案等价的纠缠模型方案. 在图2中, Alice相干态的制备等价为对双模压缩态(Einstein-Podolsky-Rosen, EPR)其中一个模$ A $进行外差探测, 而另一个模$ {B_0} $则经过海水信道后转换为模B₁, 并以模B₂发送给接收方Bob进行测量, Bob通过在相位调制器上选择0或${\pi {/ } 2}$来执行测量基选择流程. 此外, 模E表示Eve所收集的辅助模, 利用量子存储器对其进行存储. 在Bob端, 用透过率为$ \eta $的分束器表示Bob实际探测器的量子效率, 而探测器电噪声$ {\upsilon _{{\text{el}}}} $则等价于方差为$ \upsilon $的辅助EPR态$ {\rho _{F{G_0}}} $其中一个模$ {G_0} $经分束器后引入的噪声. 模G₀与模B₂经分束器相互作用后得到模B₃和模G, 辅助EPR态另一个模为F.

零差探测器的探测原理图如图3所示. 在图3中, 当量子信号光与本征光(LO)经分束器进行干涉后, 每束出射光束都被引导到光子探测器用于测量光电流$ {I_1}(t) $和$ {I_2}(t) $, 之后进行电子化处理, 并将$ {I_1}(t) $和$ {I_2}(t) $相减. 为了简化分析, 此处假定所测量的光电流$ {I_1}(t) $与光子数$ {n_1} $成正比, 并且$ {I_2}(t) $与光子数$ {n_2} $成正比. 50∶50分束器的两个输出光场模的湮灭算符分别为$ {\hat {\boldsymbol{a}}_1} $与$ {\hat {\boldsymbol{a}}_2} $, 其表达式为

其中$ {\hat {\boldsymbol{a}}_{\text{S}}} $与$ {\hat {\boldsymbol{a}}_{{\text{LO}}}} $分别表示信号光模与本征光模. 则平衡零差探测的输出结果$ {I_t} $(光电流差), 其表达式为^[46]

其中$ \psi $表示信号光与本征光之间的差分相位. 由(2)式可知, 零差探测器的测量值$ {I_t} $取决于本振光的相位, 即所采用的平衡零差探测器可以通过调整信号光与本征光之间的差分相位$ \psi $来选择是测量正则分量$ {X_{\text{B}}} $还是正则分量$ {P_{\text{B}}} $. 因此, 图3中所采用的相位调制器用于实现连续变量测量基的选择. 换言之, 当接收方Bob利用相位调制器令差分相位$ \psi = 0 $时, 则表明Bob测量的是正则分量$ {X_{\text{B}}} $; 当接收方Bob利用相位调制器令差分相位$ \psi = {{\text{π}} {/ } 2} $时, 则表明Bob测量的是正则分量$ {P_{\text{B}}} $. 因此, 在本文所提出的方案中, 连续变量的测量基指的是正则分量$ {X_{\text{B}}} $或$ {P_{\rm B}} $, 测量基选择指的是正则分量$ {X_{\text{B}}} $或$ {P_{\text{B}}} $的选取.

由于相位调制器的调制相位与调制电压线性相关, 因此差分相位$\psi $的表达式可写为

式中${\varOmega _{\text{π}}}$表示Bob端相位调制器的半波电压, 并且其调制电压$\varOmega $的表达式为

其中参数$S$表示支持测量基选择的随机数, 可由DAC导出. 此外, Alice端的相关数据${P_{\text{A}}}$表达式为${P_{\text{A}}} = {I_{\text{A}}}\sin \phi $, 其中${I_{\text{A}}}$表示极坐标下量子信号的强度, $\phi $表示极坐标下量子信号的相位. 假设方案中所采用的DAC是完美的, 并且在实际环境下进行理想测量基选择所得到的测量结果为${P_{\text{B}}}$, 其表达式可写为

其中$\varpi $表示相位漂移. 此外, 假定Alice端的另外一个数据为$P_{\text{A}}^ * = {I_{\text{A}}}\sin \left( {\phi + \vartheta } \right)$, 其中$\vartheta $为已知相位. 对${P_{\text{A}}}{P_{\text{B}}}$与$P_{\text{A}}^ * {P_{\text{B}}}$的期望进行计算, 可得^[46]

然而, 当DAC的带宽有限时, 这表明此时调制电压$\varOmega $和调制相位$\psi $与它们的真实值发生偏离, 则有

其中$\varXi $表示DAC中运算放大器的环路增益, 并且与运算放大器的增益带宽成比例^[46]. 此处, ${\psi ^ * }$的实际值将会与预期值产生差异. 将${\psi ^ * }$代入(5)式, 则有

将(9)式和(5)式进行比较可以发现, 此时所获得的测量基$P_{\text{B}}^*$与实际测量基${P_{\text{B}}}$存在偏差. 在这种情况下, 无论所选择的测量基是$X_{\text{B}}^*$或$P_{\text{B}}^*$, 都与实际测量基${X_{\text{B}}}$或${P_{\text{B}}}$存在偏差, 即由于DAC带宽限制而导致的非理想测量基选择. 则

因此, 当考虑非理想测量基选择的情况时, 海水信道透过率与过噪声的表达式可重新写为

在实际情况下, 不同地区海水所呈现的衰减特性存在差异, 主要原因在于不同地区海水其成分构成不同. 即使在同一地区, 其衰减效应也会随着海水深度和气候等多种因素的变化而变化. 因此, 为了简化分析, 此处假定气候等外部环境不变, 只考虑海水深度和波长在水下CV-QKD系统中对海水信道光吸收和光散射效应的影响. 吸收系数$\gamma \left( {\lambda , h} \right)$作为波长$\lambda $与海水深度$h$的函数, 其表达式为^[47]

其中(13)式中所涉及的具体参数计算和设定见附录A. 而散射系数$\kappa \left( {\lambda , h} \right)$同样作为波长$\lambda $与海水深度$h$的函数, 其表达式可写为^[48]

其中(14)式中所涉及的具体参数计算和设定见附录B. 根据(13)式与(14)式, 总信道衰减系数$\sigma \left( {\lambda , h} \right)$其表达式为

根据Ruan等报道^[42]可知, 在海水的“光传输窗口”中, 即在450—550 nm的波长范围内, 光传输效果最好. 因此, 此处选择波长为520 nm的光来研究水下CV-QKD的系统性能.

由上述分析可知, 不同深度的海水对光的传播特性存在差异, 变化过程是非线性的. 因此, 为了方便分析, 此处只考虑信号光在具有相同深度的水平面中传播的情况. 不失一般性, 假定光的传播特性在短距离传输的情况下以及在同一水平面内保持不变. 则海水信道透过率${T_{\text{s}}}$的表达式可写为

其中$\sigma \left( {\lambda , h} \right)$为信道总衰减系数, $L$为水平传输距离.

需要指出的是, 水下CV-QKD与自由空间大气CV-QKD两者作为全球安全通信网络不可或缺的一部分, 具有一些相似之处, 即两者性能均会受到光吸收和光散射的影响. 但水下CV-QKD与自由空间大气CV-QKD又有本质区别: 在水下连续变量QKD方案中, 光吸收系数和光散射系数与波长和海水深度有关, 并且信号光在水中传播存在一个透过率窗口, 其波长范围在 450—550 nm, 称为蓝绿光, 波长在窗口范围内的光透过率较大^[42]; 而在自由空间大气CV-QKD方案中, 信号光在大气信道中传输同样会受到传输介质的吸收和散射作用, 但该种信道对信号光的吸收和散射作用主要由大气分子与气溶胶粒子的存在而产生, 这与海水信道对信号光的吸收和散射作用机理具有本质区别.

本节在渐近情况^[17]以及组合安全性情况^[20]下对基于非理想测量基选择的水下CV-QKD方案进行安全性分析.

此处考虑方案的渐近安全性, 即在集体攻击下, 水下CV-QKD方案在不考虑实际数据量的情况下所进行的安全密钥率分析计算. 因此, 所提出的方案在反向协商下其渐近密钥率的计算式为^[49]

其中${I_{{\text{AB}}}}$表示Alice与Bob的互信息量, ${\chi _{{\text{BE}}}}$表示Eve从Bob密钥中所窃取的信息量的Holevo界, $\beta $表示反向协商效率. 互信息量${I_{{\text{AB}}}}$的表达式为

这里$V = {V_{\text{A}}} + 1$, ${V_{\text{A}}}$为调制方差. ${\chi _{{\text{tot}}}}$表示归结为信道输入的总噪声, 其表达式为

式中${\chi _{\hom }} = {{\left[ {(1 - \eta ) + {\upsilon _{{\text{el}}}}} \right]} {/ } \eta }$, $\eta $和${\upsilon _{{\text{el}}}}$分别表示零差探测器量子效率和电噪声; ${\chi _{{\text{line}}}}$表示归结于信道输入的总信道附加噪声,

其中参数${T_{\text{s}}}$与${\xi _{\text{s}}}$分别表示海水信道的透过率与过噪声.

为了计算参数${\chi _{{\text{BE}}}}$, 此处假设攻击者Eve无法对Bob系统中的非理想器件进行攻击. 此种噪声评估模型已被广泛应用于CV-QKD实验中^[22,23]. 基于该噪声评估模型, ${\chi _{{\text{BE}}}}$的表达式可写为

式中$G(x) = (x + 1){\log _2}(x + 1) - x{\log _2}x$;

其中

${\omega _{3, 4}}$表达式可写为

其中

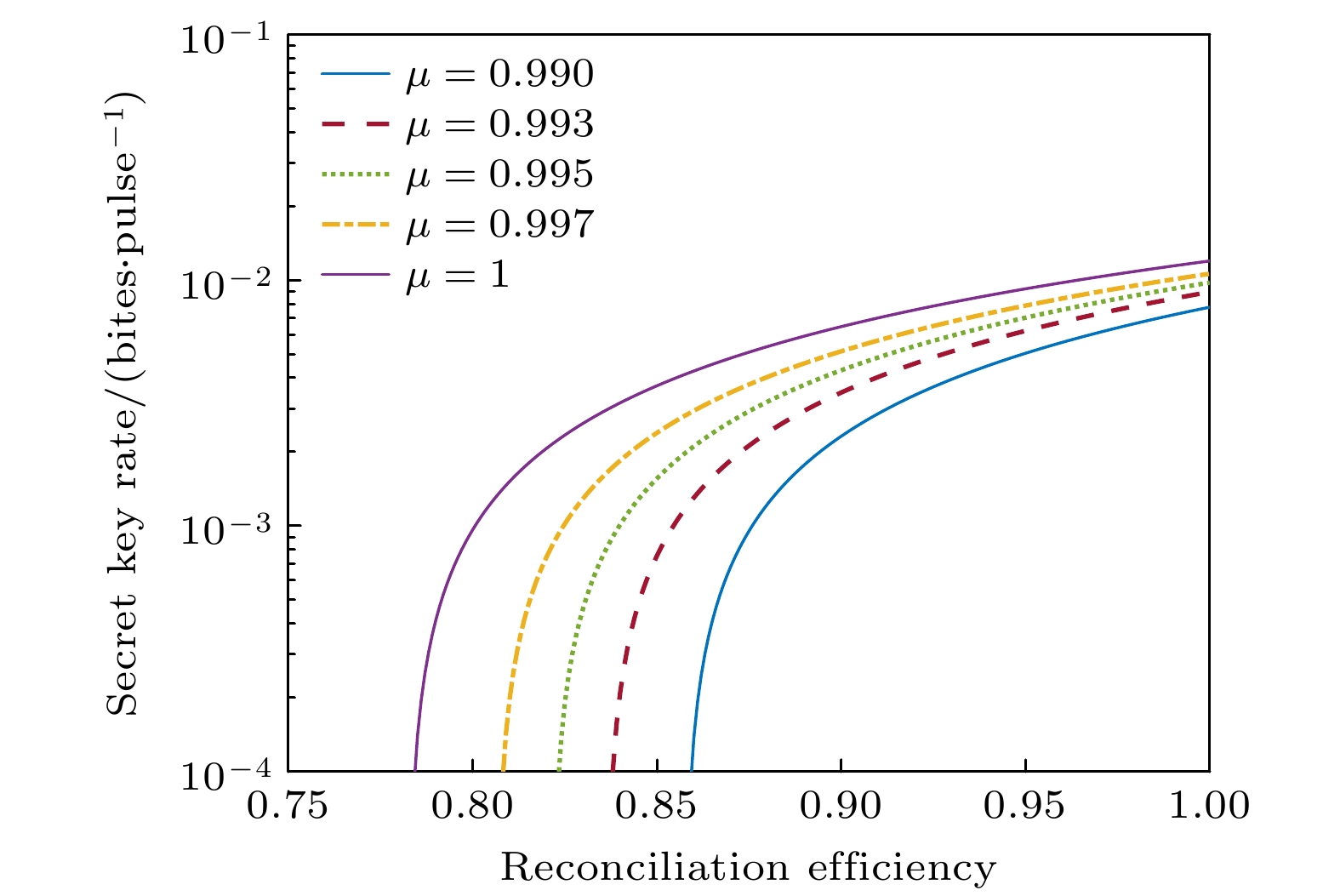
接下来分析基于非理想测量基选择的水下CV-QKD方案在渐近情况下的方案性能. 涉及的仿真系统参数分别设定为$ {V_{\text{A}}} = 3 $, $ \eta = 0.6 $, $ {\upsilon _{{\text{el}}}} = 0.05 $. 根据 2.1节的分析, 如果调制相位不正确并且Alice与Bob都没意识到这一点, 则他们将会获得偏离正确值的参数$ T_{\text{s}}^{\text{*}} $与$ \xi _{\text{s}}^{\text{*}} $. 根据(12)式, 设$ \mu = {\left( {E\left[ {\sin {\psi ^ * }} \right]} \right)^2} $, 即由非理想测量基选择所引入的额外过噪声用参数$ \mu $进行衡量. 则所提出方案的渐近密钥率与传输距离在不同参数$ \mu = 0.990, {\text{ }}0.993, 0.995, {\text{ }}0.997, {\text{ }}1 $下的关系如图4所示, 其中协商效率$ \beta = 0.95 $, 海水深度$ h = 30 $m, 海水信道过噪声$ {\xi _{\text{s}}} = 0.01 $, $ \mu = 1 $表示理想测量基选择. 在所提出的方案中, 不同的参数$ \mu $对应于DAC中运算放大器的不同环路增益. 由图4可知, 所提出方案的渐近密钥率随参数$ \mu $的减小而降低, 并且在海水信道的最大传输距离也随之减小. 比如当参数$ \mu = 1 $时, 所提出方案的最大传输距离为53.46 m; 而当参数$ \mu = 0.993 $时, 所提出方案的最大传输距离为41.76 m.

图5给出了所提出方案的渐近密钥率与协商效率$\beta $在不同参数$ \mu = 0.990, {\text{ }}0.993, {\text{ }}0.995, {\text{ }}0.997, {\text{ }}1 $下的关系, 其中深度$ h $=30 m, 传输距离L=10 m, 信道过噪声$ {\xi _{\text{s}}} = 0.01 $. 由图5可知, 对于所提出的方案, 协商效率$\beta $的可使用范围随着参数$ \mu $的减小而压缩. 例如当$ \mu = 1 $时, 所提出方案的协商效率$\beta $的可使用范围为$ [0.784, {\text{ }}1] $, 即在此种情况下当$\beta < 0.784$时, 所提出的方案无法获得密钥; 而当$ \mu = 0.993 $时, 所提出方案的协商效率$\beta $的可使用范围则压缩至$ [0.838, {\text{ }}1] $, 即在此种情况下当$\beta < 0.838$时, 所提出的方案无法获得密钥.

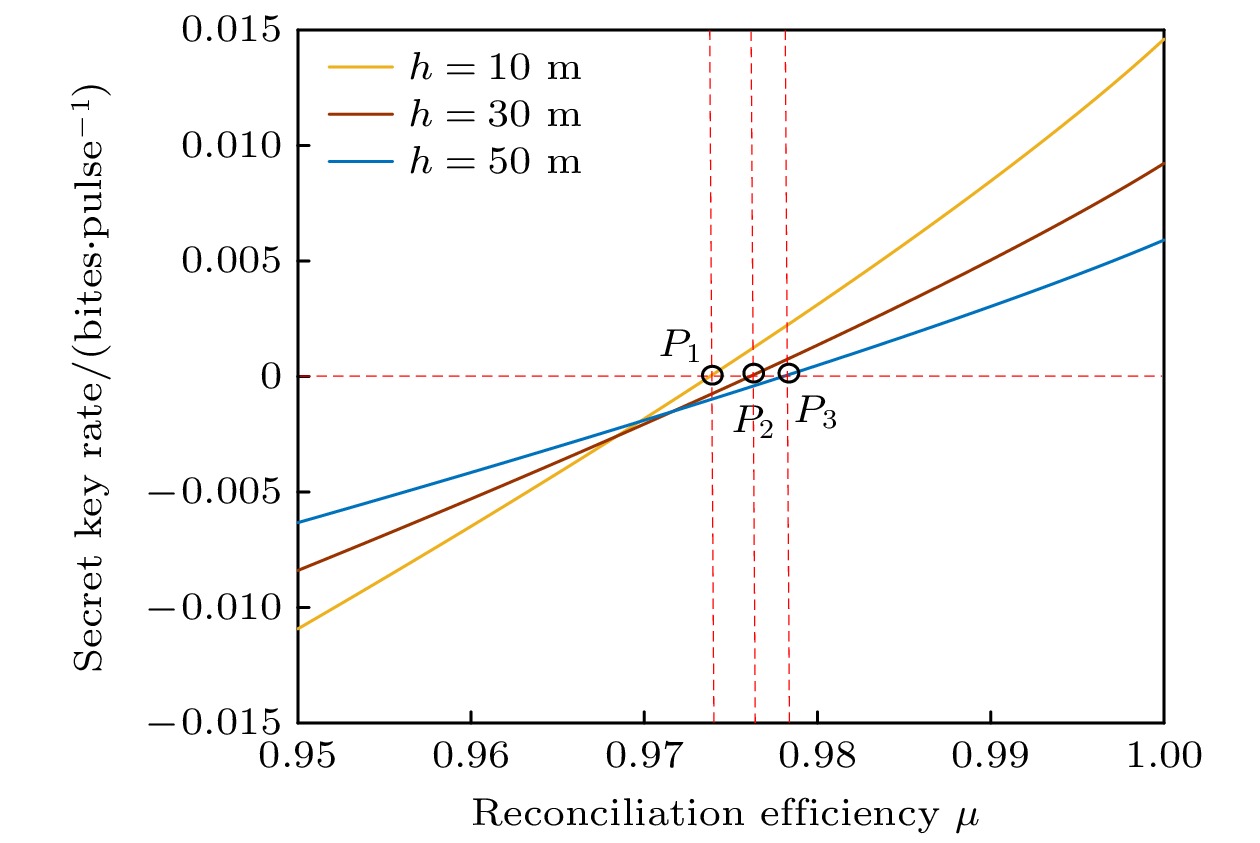
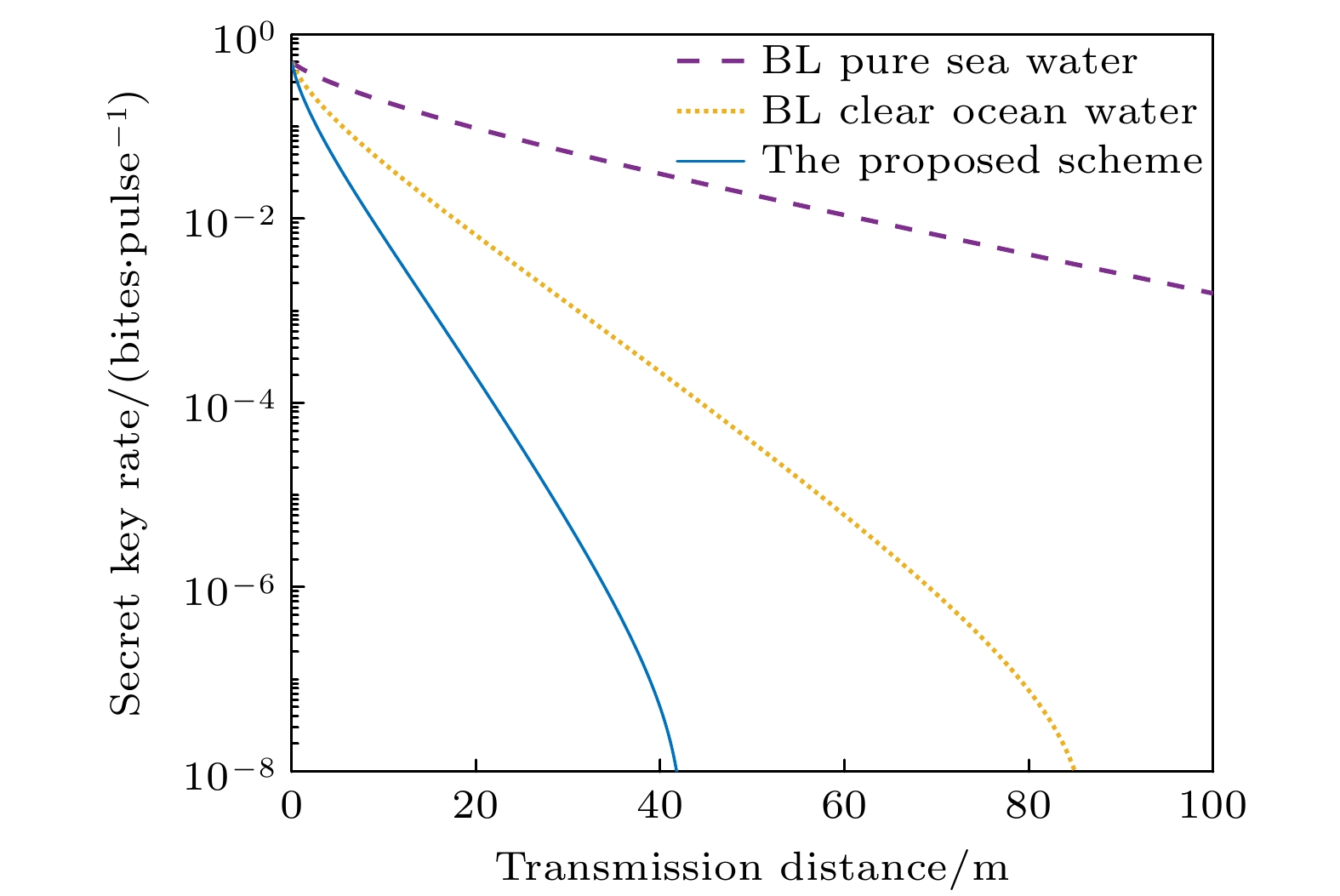
图6给出了所提出方案的密钥率与参数$ \mu $在不同海水深度h = 10, 30, 50 m下的关系, 其中协商效率$ \beta = 0.95 $, 过噪声$ {\xi _{\text{s}}} = 0.01 $, 传输距离L =10 m. 在图6中, 将渐近密钥率$ {K_{{\text{asy}}}} = 0 $的水平虚线与不同海水深度h = 10, 30, 50 m所对应的性能曲线相交, 分别得到纵坐标均为0的点P₁, P₂与P₃, 三个点对应的坐标分别为$ \left( {0.9738, 0} \right) $、$ (0.9761, 0 ) $与$ \left( {0.978, 0} \right) $. 基于此, 可得到海水深度h = 10, 30, 50 m时所对应的参数$ \mu $的阈值下界限, 即$ {\hat \mu _{{\text{th}}}} = 0.9738, 0.9761, 0.978 $. 由图6可以观察到, 随着海水深度$ h $的增加, 参数$ \mu $的阈值下界限也随之增大. 这表明深度$ h $的值越大, 为保证所提出方案的密钥率为正所需要的参数$ \mu $的最小值也越大. 例如当h =10 m时, 参数$ \mu $的阈值下界限为$ {\hat \mu _{{\text{th}}}} = 0.9738 $; 而当$ h $=50 m时, 参数$ \mu $的阈值下界限为$ {\hat \mu _{{\text{fh}}}} = 0.978 $, 显然$ {\hat \mu _{\rm th}} < {\hat \mu _{\rm fh}} $.

图7给出了非理想测量基选择情况下所提出的方案与基于Beer’s law(BL)模型的水下CV-QKD方案性能比较, 基于BL模型的水下CV-QKD方案其密钥率计算详见Ruan 等^[42]的报道, 其中深度h = 30 m(本文所提出的方案), $ \beta = 0.95 ,~ \mu = 0.993 $, 信道过噪声$ {\xi _{\text{s}}} = 0.01 $. 从图7可以发现, 基于BL模型的纯净海水(pure sea water)信道以及清澈海水信道(clear ocean water)信道的CV-QKD其渐近密钥率和传输距离要优于本文所提出方案的渐近密钥率和传输距离. 这在我们的意料之中, 主要原因在于Ruan等^[42]所采用的BL海水信道模型基于这样的假设, 即在短距离传输的情况下, 海水信道可视为线性信道. 由于该模型只是简单将海水信道在短距离传输的情况下等同于线性信道, 这意味着在BL模型中海水对光的衰减系数是固定的, 并没有考虑包括海水深度、海水中叶绿素浓度、有色溶解有机物以及非藻类颗粒等因素对水下CV-QKD方案性能的影响, 因此面对实际情况复杂的海水信道, 该模型并不适用. 而本文所提出的方案其水下信道模型采用叶绿素a浓度模型, 在计算海水信道参数时(吸收和散射系数)充分考虑了海水深度、海水中叶绿素浓度、有色溶解有机物以及非藻类颗粒等因素(计算过程详见附录A与附录B), 更符合实际情况. 因此, 在图7中, 本文所提出方案其性能曲线相比基于BL模型的纯净海水信道以及清澈海水信道的CV-QKD方案的性能曲线更符合实际.

在上述渐近安全性分析中, 对于所提出方案 的渐近密钥率计算的前提是假定Alice和Bob 可以采用无限多的信号进行互换交流. 然而这在实验中是无法实现的, 主要原因是实际安全密钥的 长度是有限的. 由于组合安全性是有限长效应^[18]的不确定性安全的增强, 在集体攻击下, 通过详 细分析水下CV-QKD系统中的每一个步骤, 可以获得一条理论上的最紧安全界限^[20]. 因此本节主要研究所提出的方案在组合安全框架下的性能 表现.

在考虑组合安全性的情况下, 所提出方案的密钥率其表达式为^[20]

其中${\varepsilon _{{\text{rob}}}}$表示协议的鲁棒性. $ F(\varTheta _a^{\max }, \varTheta _b^{\max }, \varTheta _c^{\min }) $表示计算Bob与Eve之间Holevo界的函数, 其表达式为

其中${\nu _1}$与${\nu _2}$为协方差矩阵$\left[ {\begin{array}{*{20}{c}} {\varTheta _a^{\max }{I_2}}&{\varTheta _c^{\min }{\sigma _z}} \\ {\varTheta _c^{\min }{\sigma _z}}&{\varTheta _b^{\max }{I_2}} \end{array}} \right]$的辛特征值, ${I_2} = {\mathrm{diag}}(1, 1)$, ${\sigma _z} ={\mathrm{ diag}}(1, - 1)$, 另一个辛特征值${\nu _3} = \varTheta _a^{\max } - {{{{(\varTheta _c^{\min })}^2}} {/ } {(1 + }}\varTheta _b^{\max })$. 具体而言, 有

此外, $R$表示用于交换的有效脉冲总数, 参数$ {\varDelta _{{\text{AEP}}}} $与$ {\varDelta _{{\text{ent}}}} $的表达式分别为

其中${z_0}$表示离散化参数, 方案的总体安全参数$\varepsilon = \sqrt {{\varepsilon _{{\text{ent}}}} + {\varepsilon _{{\text{PE}}}} + {\varepsilon _{{\text{cor}}}}} + 2{\varepsilon _{{\text{sm}}}} + \bar \varepsilon $. 根据Leverrier ^[20]的研究结果, 这些参数的值可取${\varepsilon _{{\text{sm}}}} = \bar \varepsilon = {10^{ - 21}}$, ${\varepsilon _{{\text{ent}}}} = {\varepsilon _{{\text{PE}}}} = {\varepsilon _{{\text{cor}}}} = {10^{ - 41}}$, ${z_0} = 5$. 需要指出的是当执行参数估计这一步骤的概率至少为0.99时, 本方案的鲁棒性参数$ {\varepsilon _{{\text{rob}}}} \leqslant {10^{ - 2}} $. 基于此, 则与本方案相关的3个随机变量$ \left\| X \right\| $, $ \left\| Y \right\| $和$ \left\langle {X, Y} \right\rangle $的值满足以下3个约束条件:

根据(31)式, 可以得到

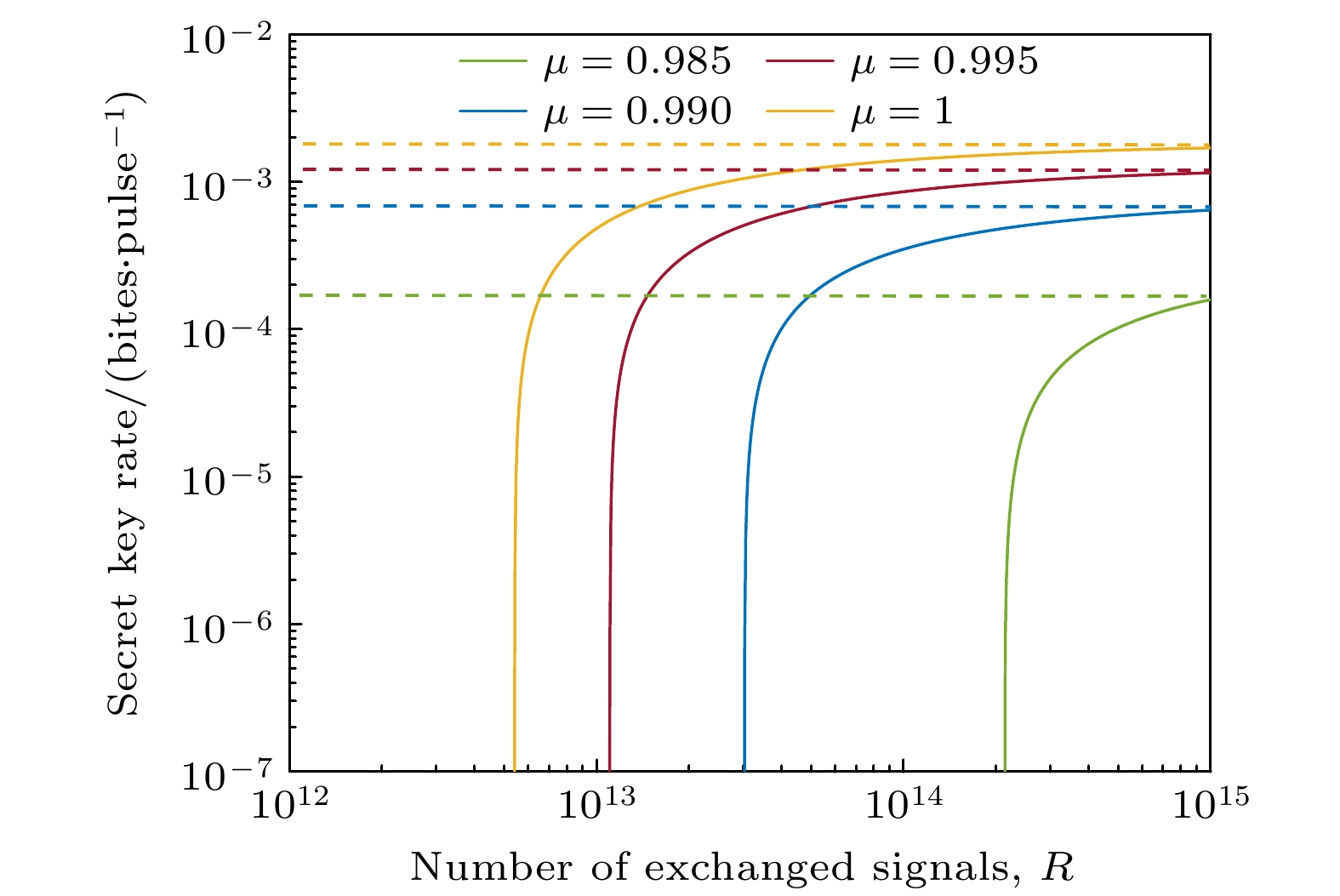
其中$ {\varepsilon _{{\text{PE}}}} $表示参数估计失败的最大概率.

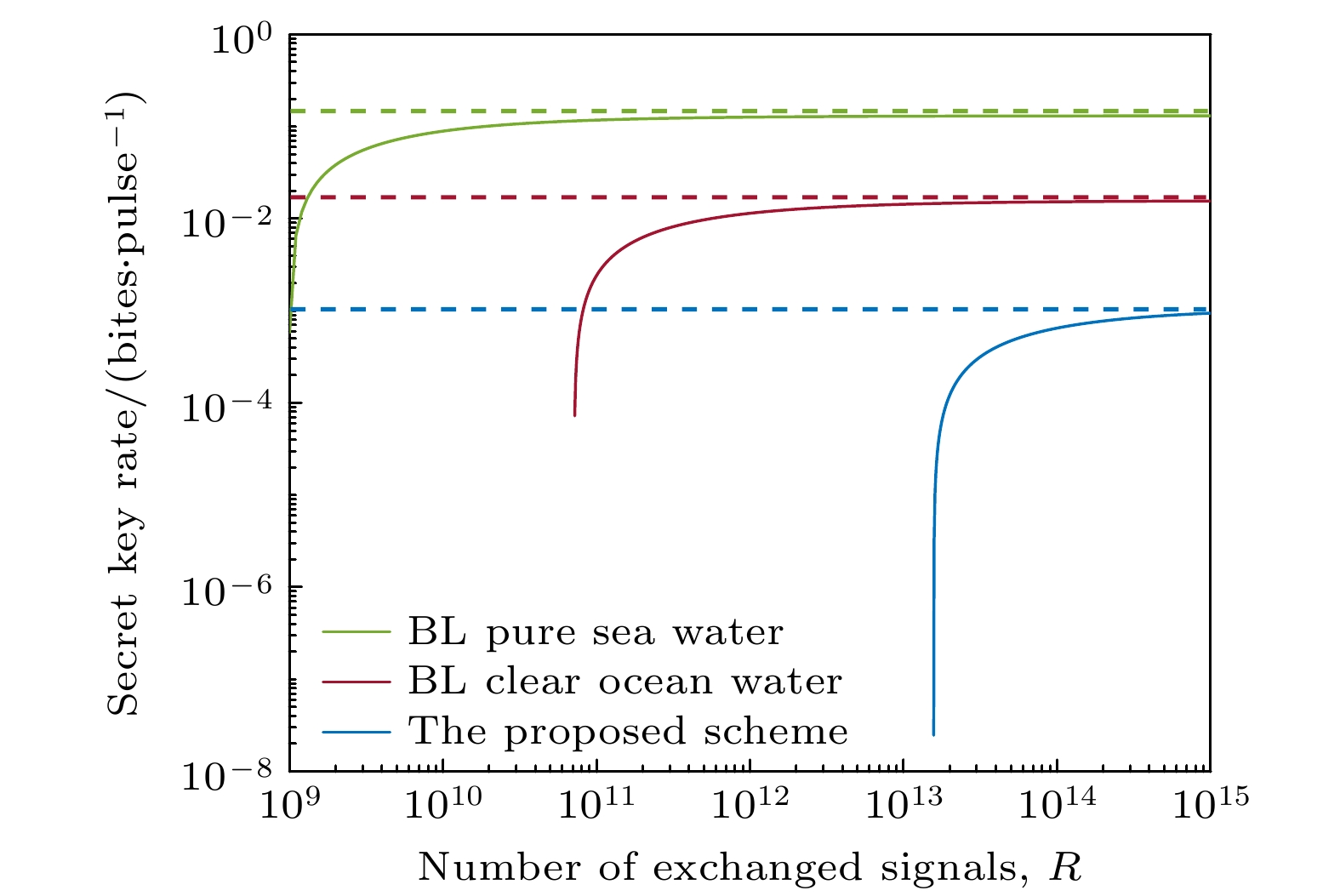
接下来分析所提出的基于非理想测量基选择的水下CV-QKD方案在考虑组合安全性的情况下方案的性能. 涉及全局的仿真系统参数与渐近情情况下所采用的仿真系统参数相同. 图8给出了在组合密钥率与用于交换的有效脉冲总数在不同参数$ \mu = 0.985, {\text{ }}0.990, {\text{ }}0.995, {\text{ }}1 $下的关系, 其中$ \beta = 0.95 $, 深度$ h = 30 $ m, 传输距离L = 15 m, 信道过噪声$ {\xi _{\text{s}}} = 0.01 $, 并且水平虚线表示相对应的渐近密钥率. 从图8可以观察到, 所提出方案的组合密钥率随着参数$ \mu $的减小而降低, 这表明所提出的基于非理想测量基选择的水下CV-QKD方案的组合密钥率会因DAC的有限带宽而降低. 此外, 所提出方案的组合密钥率总是低于其渐近密钥率. 因此, 相比于渐近安全性分析, 采用组合安全性分析可以获得更紧的密钥率曲线.

图9给出了非理想测量基选择情况下所提出的方案与基于BL模型的水下CV-QKD方案组合密钥率比较, 其中深度h = 30 m(本文所提出的方案), $ \beta = 0.95 $, $ \mu = 0.993 $, 传输距离$ L = 15 $m, 信道过噪声$ {\xi _{\text{s}}} = 0.01 $. 从图9可以发现, 在用于交换的有效脉冲总数R相同的情况下, 所提出方案的组合密钥率低于基于BL模型的纯净海水信道以及清澈海水信道CV-QKD方案的组合密钥率, 其原因已在上述分析中给出, 并且三者的组合密钥率均低于各自的渐近密钥率(水平虚线). 由于本文所提出的方案其水下信道模型采用叶绿素a浓度模型, 在计算海水信道参数时(吸收和散射系数)充分考虑了海水深度、海水中叶绿素浓度、有色溶解有机物以及非藻类颗粒等因素. 因此, 在图9中, 本文所提出方案其组合密钥率曲线相比基于BL模型的纯净海水信道以及清澈海水信道的CV-QKD方案的组合密钥率曲线更符合实际.

本文提出基于非理想测量基选择的水下CV-QKD方案, 考虑水下CV-QKD系统的接收端由于DAC的有限带宽所引起的非理想测量基选择对系统性能的影响. 经过研究分析, 发现DAC的有限带宽使得测量基在选择过程中会产生角度偏差, 从而导致合法通信方对海水信道透过率和过噪声的错误估计. 为了对非理想测量基选择所引入的额外过噪声进行定量分析并获得其安全界限, 本方案引入对应于DAC中运算放大器环路增益的参数$ \mu $. 仿真结果表明由非理想测量基选择所引入的额外过噪声能够降低水下CV-QKD方案的性能. 此外, 考虑不同海水深度对所提出方案安全界限的影响, 即随着海水深度的增加, 为保证方案安全性所需要的参数$ \mu $的阈值下界限也随之增大. 因此, 本文所提出的方案可以在不改变水下CV-QKD框架结构的前提下, 有效地解决由接收端DAC带宽限制导致的非理想测量基选择所带来的安全隐患. 此外, 在对所提出的方案进行安全性分析时, 不仅考虑了其渐近安全性, 也考虑了其组合安全性, 因而能够获得更紧的性能曲线.

根据Gilerson等^[47]报道, 可通过采用叶绿素模型来表征吸收系数$ \gamma \left( {\lambda , h} \right) $, 即

这里$ {\gamma _0}\left( \lambda \right) $表示纯净海水的吸收系数并且其值可参考Prieur和Sathyendranath ^[50]研究结果. $ {\gamma _{{\text{acp}}}}\left( \lambda \right) $表示浮游植物的吸收系数, 其中叶绿素a起主要作用, 其表达式为

式中$ {\gamma _1}\left( \lambda \right) $表示400 nm参考波长下叶绿素浓度的光谱吸收系数并且其值可参考Prieur和Sathyendranath ^[50]的研究结果; ${U_1}\left( h \right)$表示深度为$ h $的叶绿素a的浓度,

其中$ {\tilde U_Z} = 0.250\;{\text{mg}} \cdot {{\text{m}}^{ - {3}}} $表示透光层内的总叶绿素a的平均柱集成含量, $ {U_k} = 0.570 $表示表层叶绿素a的背景浓度, $ q = 0.173{\text{ }}{m^{ - 1}} $表示垂直梯度, $ {D_{\text{e}}} = 80.2 $表示透光层深度, $ {U_{\max }} = 0.766 $表示最大浓度, $ {\varUpsilon _{\max }} = {{{U_{\max }}} {/ } {{D_{\rm e}}}} $, $ \Delta \varUpsilon = 0.814 $表示高斯峰的宽度. 上述固定参数的取值都是基于Uitz等^[51]报道. $ {\gamma _{{\text{CDOM}}}}\left( \lambda \right) $表示有色溶解有机物的吸收系数, 主要包括腐殖酸和黄腐酸对光的吸收, 其表达式为

其中参数$ {\gamma _2} = 35.959{{{\text{ }}{{\text{m}}^2}} {/ } {{\text{mg}}}} $与$ {\gamma _3} = 18.828{\text{ }}{{{{\text{m}}^2}} {/ } {{\text{mg}}}} $分别表示黄腐酸和腐殖酸在400 nm参考波长下的光谱吸收系数; 参数$ {\alpha _2} = 0.0189{\text{ n}}{{\text{m}}^{ - 1}} $与$ {\alpha _3} = 0.01105{\text{ n}}{{\text{m}}^{ - 1}} $分别表示黄腐酸和腐殖酸的吸收斜率系数; $ {U_2}\left( h \right) $与$ {U_3}\left( h \right) $分别表示黄腐酸和腐殖酸的浓度, 其表达式可分别写为

$ {\gamma _{{\text{NAP}}}}\left( \lambda \right) $表示非藻类颗粒(nonalgal particulates, NAP)的吸收系数, 其表达式为

其中$ {\gamma _4} = 9.721{\text{ }}{{{{\text{m}}^2}} {/ } {{\text{mg}}}} $表示NAP在400 nm参考波长下的光谱吸收系数, $ {\alpha _4} = 0.012{\text{ n}}{{\text{m}}^{ - 1}} $表示NAP的吸收斜率系数.

由于海水对光的散射作用主要是由纯净海水和NAP的散射引起的, 因此散射系数$\kappa \left( {\lambda , h} \right)$的表达式可写为^[48]

这里${\kappa _{\text{w}}}\left( \lambda \right)$表示纯净海水的散射系数, 其表达式为

${\kappa _{{\text{NAP}}}}\left( {\lambda , h} \right)$表示NAP的散射系数, 包括小颗粒和大颗粒, 其表达式为

其中${\kappa _{\text{s}}}\left( \lambda \right)$与${\kappa _{\text{b}}}\left( \lambda \right)$分别表示小颗粒与大颗粒的散射光谱; ${U_{\text{s}}}\left( h \right)$与${U_{\text{b}}}\left( h \right)$分别表示小颗粒与大颗粒在海水深度为$h$时的浓度, 它们的表达式分别为