首页
登录
注册
下载:
-
扭曲部分相干光场是一类具有自旋转效应并携带轨道角动量的新颖光场, 相较于传统的轴对称部分相干光场(如高斯谢尔模光束[1]), 扭曲部分相干光场在光束整形、微粒捕获、自由空间光通信、光学成像应用领域展现出独特的优势[2–6]. 扭曲部分相干光场的调控理论可以追溯到1993年, Simon 和 Mukunda[7]提出扭曲相位的概念, 并在此基础上构建了扭曲高斯谢尔模光源. 扭曲相位与普通的二次相位有着本质性的差异, 其具有二维属性和手性特性, 且不存在于完全相干光中, 是部分相干光场特有的一种相位. 1994年, Friberg等[8]首次在实验室产生扭曲高斯谢尔模光束, 并观测到光束在传输过程中的旋转效应. 然而, 由于交叉谱密度函数的非负正定性限制, 扭曲相位不能随意加载到已有部分相干光束. 在过去的几十年中, 对扭曲光场的研究主要局限于传统的扭曲高斯谢尔模光场, 这极大地限制了扭曲光场的进一步应用研究. 近年来, 如何构建具有非传统关联结构的新型扭曲光场成为了光调控领域的研究热点[9–24]. Borghi等提出了利用模式分析判断谢尔模型部分相干光场能否携带扭曲相位的方法[9], 并在此基础上构造了几种新型扭曲部分相干光源[10]. Mei和Korotkova[11]在关联函数构建理论的基础上, 构建了具有矩形光斑分布的新型扭曲部分相干光束. Gori和Santarsiero [12]提出了一种不受对称约束的扭曲部分相干光的生成方法. Peng等[13]提出了一类同时携带涡旋相位和扭曲相位的扭曲拉盖尔高斯谢尔模光束, 并证明了这些相位的手性对光场的演化特性有显著影响. Santarisiero等[14]引入了一类高阶扭曲高斯谢尔模光源, 并将它们用作可构建其他扭曲交叉谱密度的基石. Mei和Korotkova[15]阐明了扭曲相位对电磁部分相干光场的光谱密度和光谱偏振度的整形和旋转调控作用, 并证明光谱密度在传播过程中最多可以被整形三次. 另外, Tian 等[16]发展了实验产生扭曲部分相干光束的普遍方法. Wang等[17]利用纯相位空间光调制器实现了随机模式的非相干叠加, 并实验生成了具有可控相位的扭曲高斯谢尔模型光束. 上述研究极大丰富扭曲光场的调控手段, 而且能进一步拓展部分相干扭曲光场的应用研究.
另一方面, Gori等[25]于1988年提出了镜像部分相干光束的概念, 其一维交叉谱密度函数满足如下条件:
$ W\left( { - {x_1}, {x_2}} \right) = W\left( {{x_1}, {x_2}} \right) $ . 不同于绝大多数部分相干光束满足谢尔模型关联分布, 镜像光场独特的关联结构引发了一系列新奇的物理效应. 2015年, Partanen等[26]将高斯谢尔模光束入射到波前折叠干涉仪(WFI), 实验产生了镜像部分相干光束, 并提出反镜像部分相干光束的概念. 近年来, 镜像与反镜像部分相干光场引起多个相关领域的关注并基于其特征展开了深入的研究[27–33]. Guo和Zhao [27]研究了镜像部分相干光场作用在瑞利介质球上的辐射力, 证明了镜像光束在粒子捕获中的优势. Zhou等[28,29]分析了镜像和反镜像高斯谢尔模型光束在大气和海洋湍流中的传输特性. Das等[30]构造了镜像贝塞尔关联部分相干光束理论模型, 并利用改良的WFI从实验中生成该光束. 近期, Tang等[31,32]将镜像变换拓展到矢量领域, 研究了WFI对镜像矢量光场的二阶统计特性, 尤其是偏振特性的调控作用. 这些结果表明, 利用WFI进行镜像变换是重塑和构建特定部分相干光场的有效方法.结合近年的部分相干光研究进展发现, 将特殊相位、关联结构、特殊偏振分布等多种调控手段相结合有助于深入挖掘部分相干光场的新特性, 进一步拓展其应用领域[33–40]. 本文将扭曲相位和干涉仪调制相结合, 利用WFI构造一类镜像与反镜像扭曲高斯谢尔模光场, 并研究光束在自由传输过程中的光谱密度和光谱相干度. 数值模拟结果表明, 该新型光场同时具有“镜像”和“扭曲”效应, 并且可通过调节干涉仪参数和光源扭曲因子, 实现对旋转光斑的中心模式和整体轮廓的精准调控. 本研究结果对于自由空间光通信以及微粒捕获等领域有重要应用价值.
-
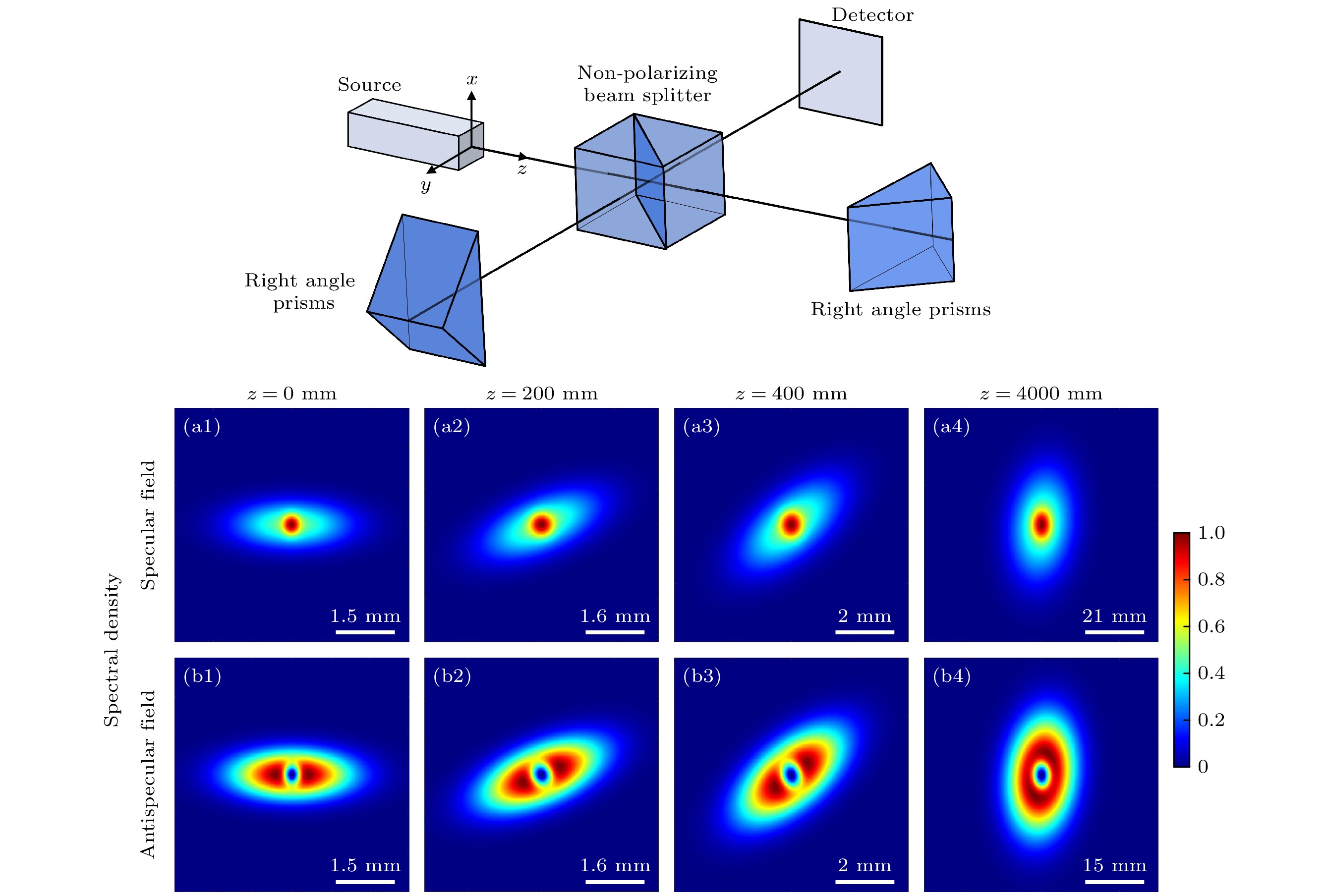
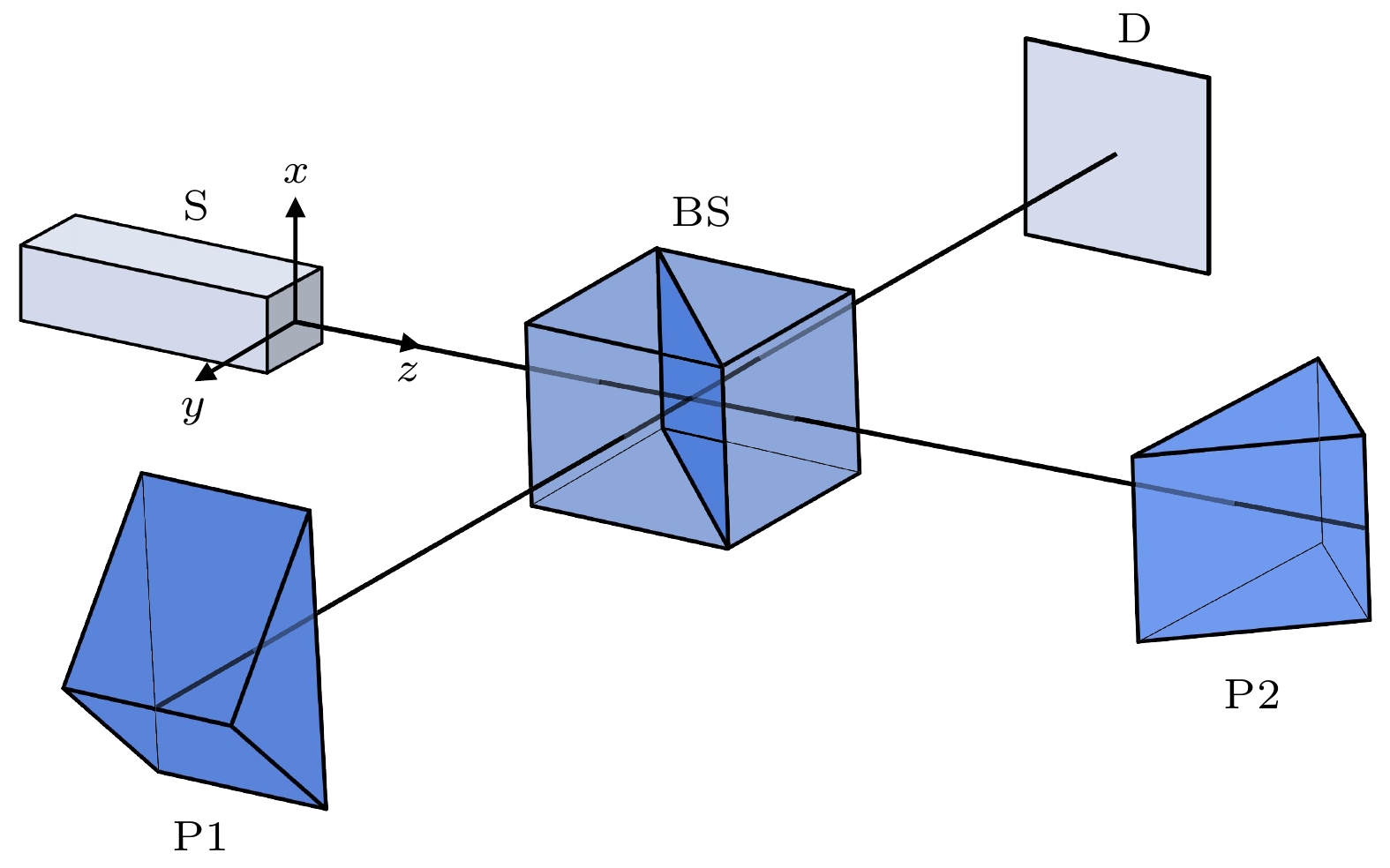
WFI主要用于测量部分相干光场的空间相干特性, 图1是其结构示意图. 该迈克耳孙型干涉仪的核心装置是臂上两个垂直放置的直角棱镜P1和P2, 其中P1在
$x$ 方向反射入射光场, P2则在$y$ 方向反射入射光场. 如果直角棱镜相对于光轴存在微小的倾斜, 则在观察平面上会出现干涉条纹. 本文假设WFI完全垂直放置.考虑将一个具有平面波前的线偏振光
${E_0}\left( {{x_0}, {y_0}} \right)$ 入射到WFI上, 在分光镜处的回射场包含由P1反射生成的光场${E_0}\left( { - {x_0}, {y_0}} \right)$ 和由P2反射生成的${E_0}\left( {{x_0}, - {y_0}} \right)$ . 最后, 探测器处的光场为两个反射光场之和, 可以表示为[25]式中
$\phi $ 表示两光路之间的相位差. 光场的二阶统计特性用交叉谱密度函数来表征:式中,
${E_{10}}\left( {{x_{10}}, {y_{10}}} \right)$ 和${E_{20}}\left( {{x_{20}}, {y_{20}}} \right)$ 分别代表空间部分相干光场上两个任意点的电场, 尖括号表示系综平均. 相应地, WFI输出平面的交叉谱密度函数有如下形式[26]:可以看出, 当
$ \phi = 2{\text{π}}n $ , (3)式满足$ W( - {x_1}, - {y_1}, {x_2}, {y_2} ) = W\left( {{x_1}, {y_1}, {x_2}, {y_2}} \right) $ , 此时光场为镜像光场; 而当$ \phi = {{\text{π}} {/ } {{\text{2 + }}}}{\text{2\pi }}n $ , 满足$ W\left( { - {x_1}, - {y_1}, {x_2}, {y_2}} \right) = - W( {x_1}, {y_1}, {x_2}, {y_2} ) $ , 光场为反镜像光场, 其中的$ n $ 均为整数.考虑将一个各向异性扭曲高斯谢尔模光束入射到WFI, 入射平面上任意两点
$ \boldsymbol{\rho }'_1 = \left( {{x'_1}, y'_1} \right) $ 和$ {\boldsymbol{\rho }}'_{2} = \left( {{x'_{2}}, {y'_{2}}} \right) $ 间的交叉谱密度函数表示形式如下[11]:其中,
$ {w_{x}} $ 和$ {w_{y}} $ 分别为沿$ x $ 轴和$ y $ 轴方向的光束宽度,$ {\delta _x} $ 和$ {\delta _y} $ 为相干长度,$u$ 为扭曲因子.将(4)式代入(3)式, 可得到WFI处的变换扭曲高斯谢尔模光场的交叉谱密度函数:
当
$ \phi = 2{\text{π}}n $ , 变换光场为镜像扭曲高斯谢尔模光场; 当$ \phi = {\text{π+ 2\pi }}n $ , 光场为反镜像扭曲高斯谢尔模光场. 特别地, 当$ \phi = {{\text{π}} {/ } {{\text{2 + }}}}{\text{2\pi }}n $ , 光场退化为变换前光场, 即入射光场.输出平面的光谱密度表示为如下形式:
另外, 输出平面上的光谱相干度表示为
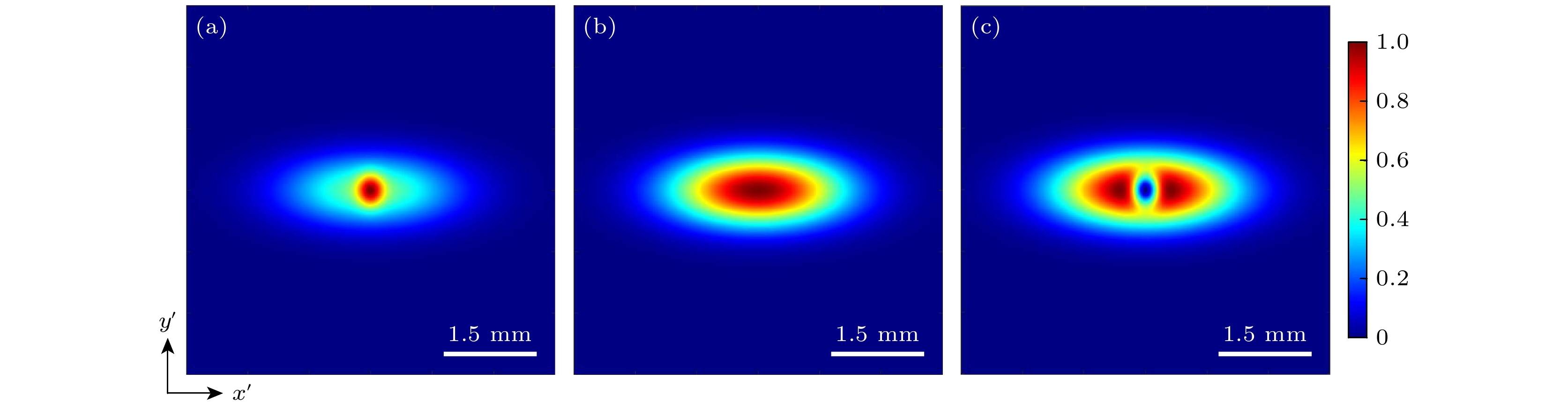
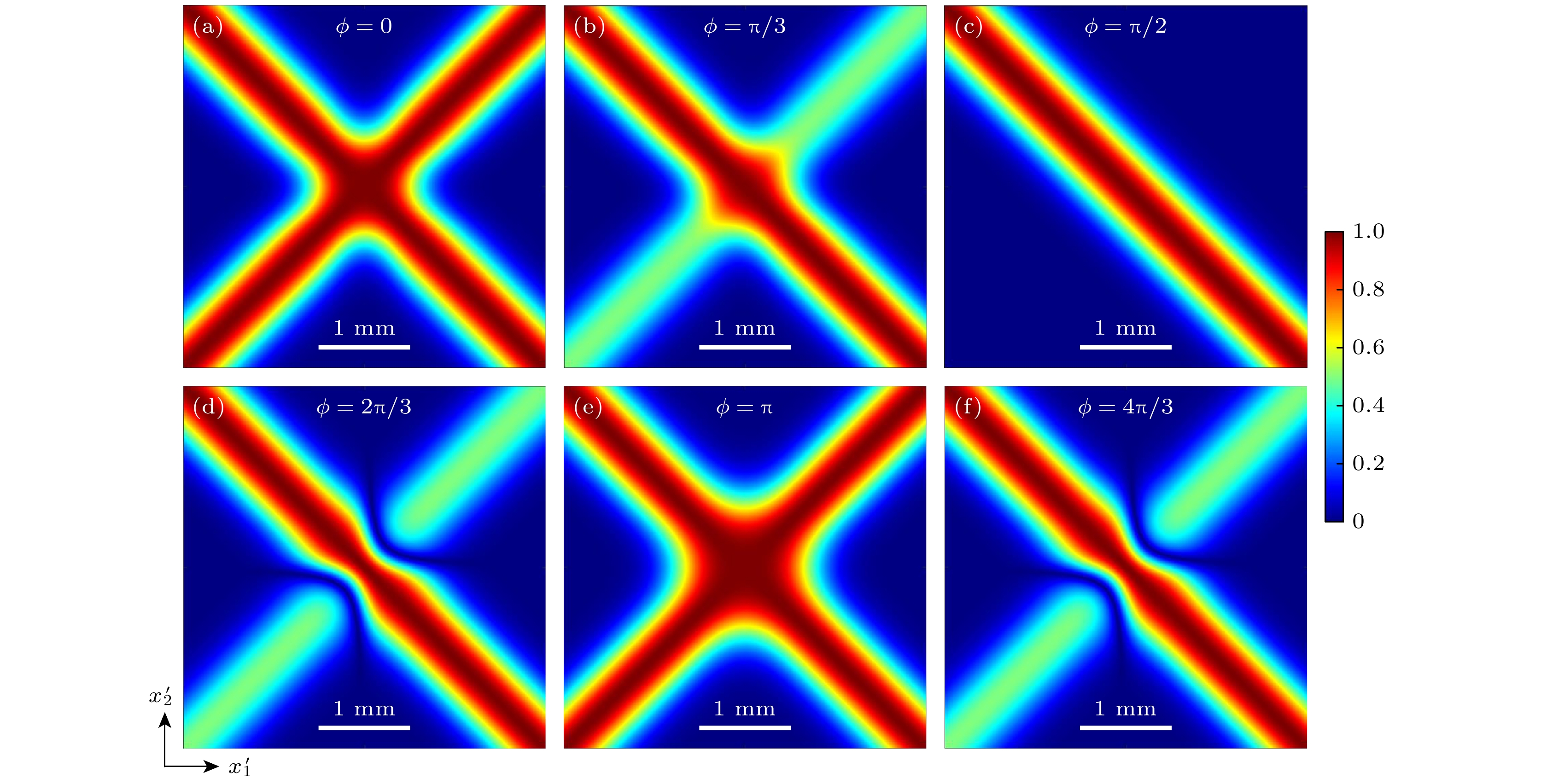
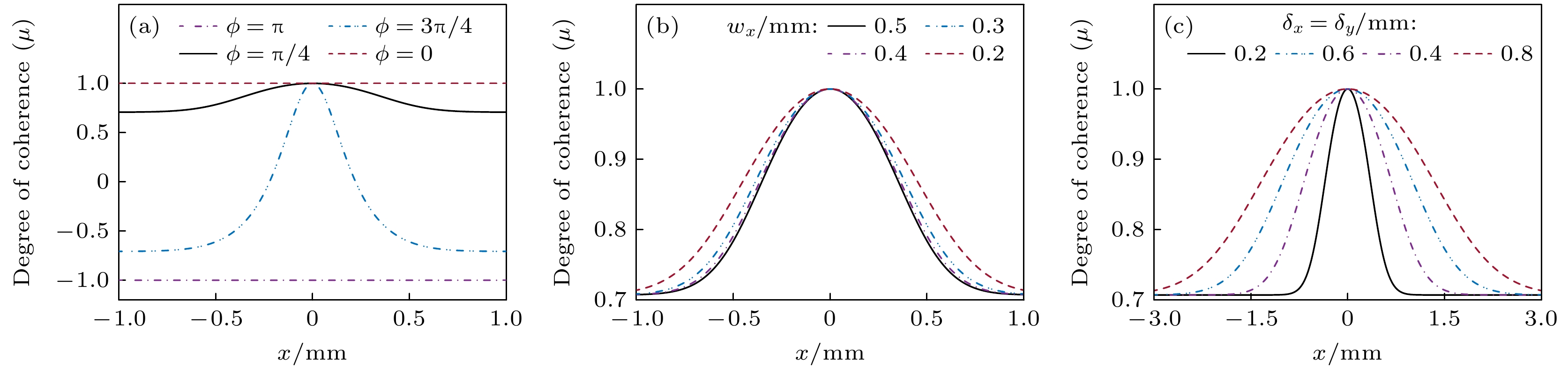
图2 和图3分别展示了WFI输出平面上的光谱密度
$ S\left( {x', y'} \right) $ 和光谱相干度$ \mu \left( {{x'_1}, {0}, {x'_2}, {0}} \right) $ 随不同干涉相位差的分布情况. 光源参数选择如下:$ {w_x} = 0.5 {\text{ mm}} $ ,$ {w_y} = 0.2 {\text{ mm}} $ , 以及$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ . 由图2 中的光谱密度分布可知, 对于镜像扭曲光场$ (\phi = 0) $ , 光束呈现中心亮斑分布; 而对于反镜像扭曲光场$ (\phi = \text{π}) $ , 光束表现为暗中空结构分布. 另外, 当$ \phi = {{\text{π}} {/ } {2}} $ , 光谱密度呈现椭圆高斯分布, 与入射场的光谱密度分布一致. 图3表示输出平面上的光谱相干度随干涉相位差的分布情况. 可以看出, 对于镜像及反镜像光场, 相干表现为轴对称的“十字”结构分布. 对于其他非镜像情况, 沿一三象限的相干性下降, 当$ \phi = {{\text{π}} {/ } {2}} $ , 变换光场退化为入射扭曲高斯谢尔模光束, 此时沿一三象限的相干度为零. -
将干涉仪输出面处的光场作为第二光源, 利用广义惠更斯-菲涅耳公式可计算在任意传输距离
$ z \gt 0 $ 上的交叉谱密度函数:其中,
$ {{\boldsymbol{\rho }}_1} = ({x_1}, {y_1}) $ 和$ {{\boldsymbol{\rho }}_{2}} = ( {{x_{2}}, {y_{2}}} ) $ 分别表示输出横截面上的二维矢量,$ k = {{{\text{2\pi }}} {/ } \lambda } $ 为波数. 将变换后光场的交叉谱密度(5)式代入(8)式, 经过一系列积分运算, 可以得到如下传输中的交叉谱密度函数:其中,
在(9)式的基础上, 可得到镜像和反镜像扭曲部分光场在自由空间传输的光谱密度和光谱相干度. 下文采用数值模拟方法研究光束在传输中的二阶统计特性. 入射光波波长选择为
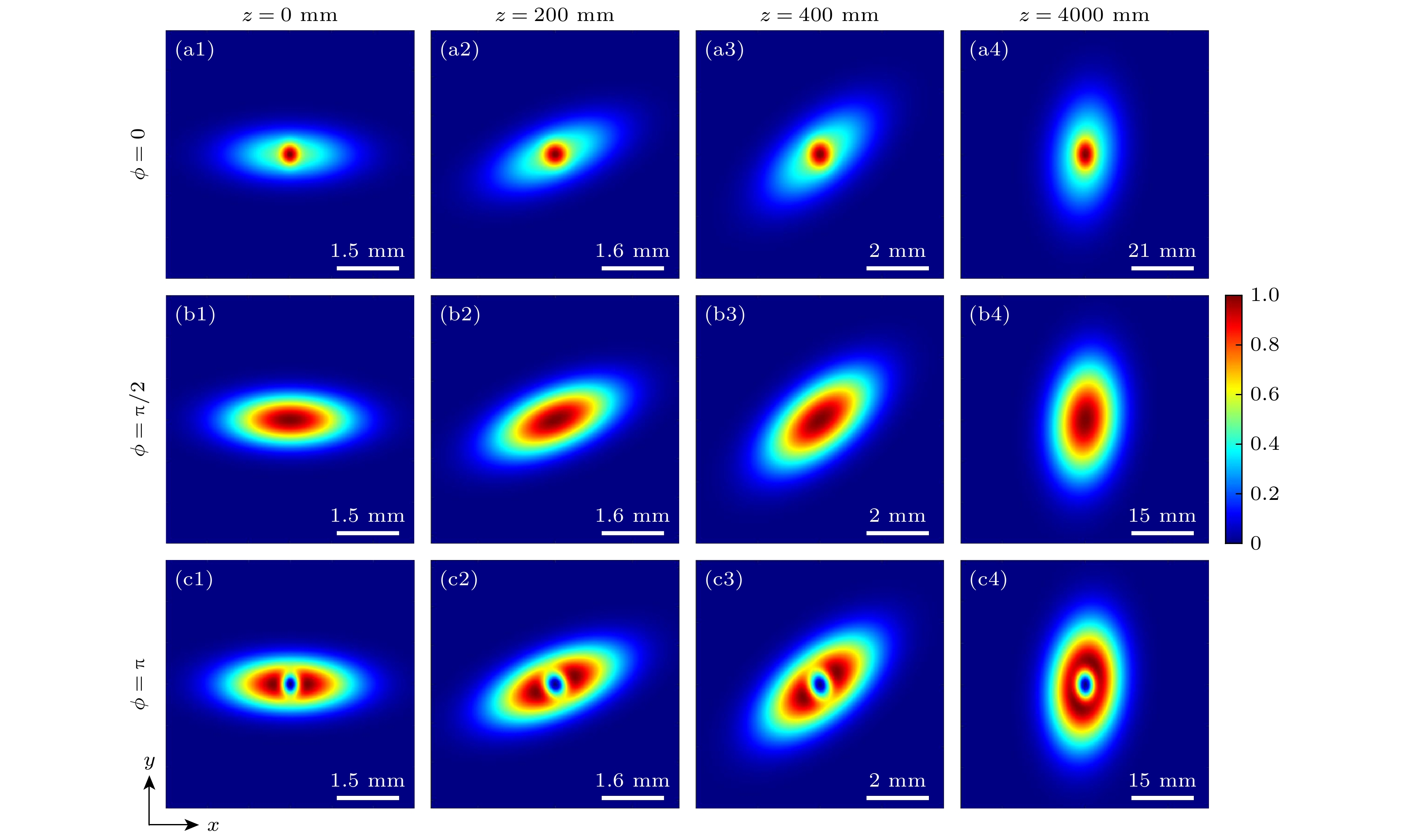
$\lambda = 632.8 {\text{ nm}}$ .图4展示了镜像(上)、非镜像(中)和反镜像(下)扭曲高斯谢尔模光束在自由空间传输的光谱密度演化规律. 由图4可知, 传输距离
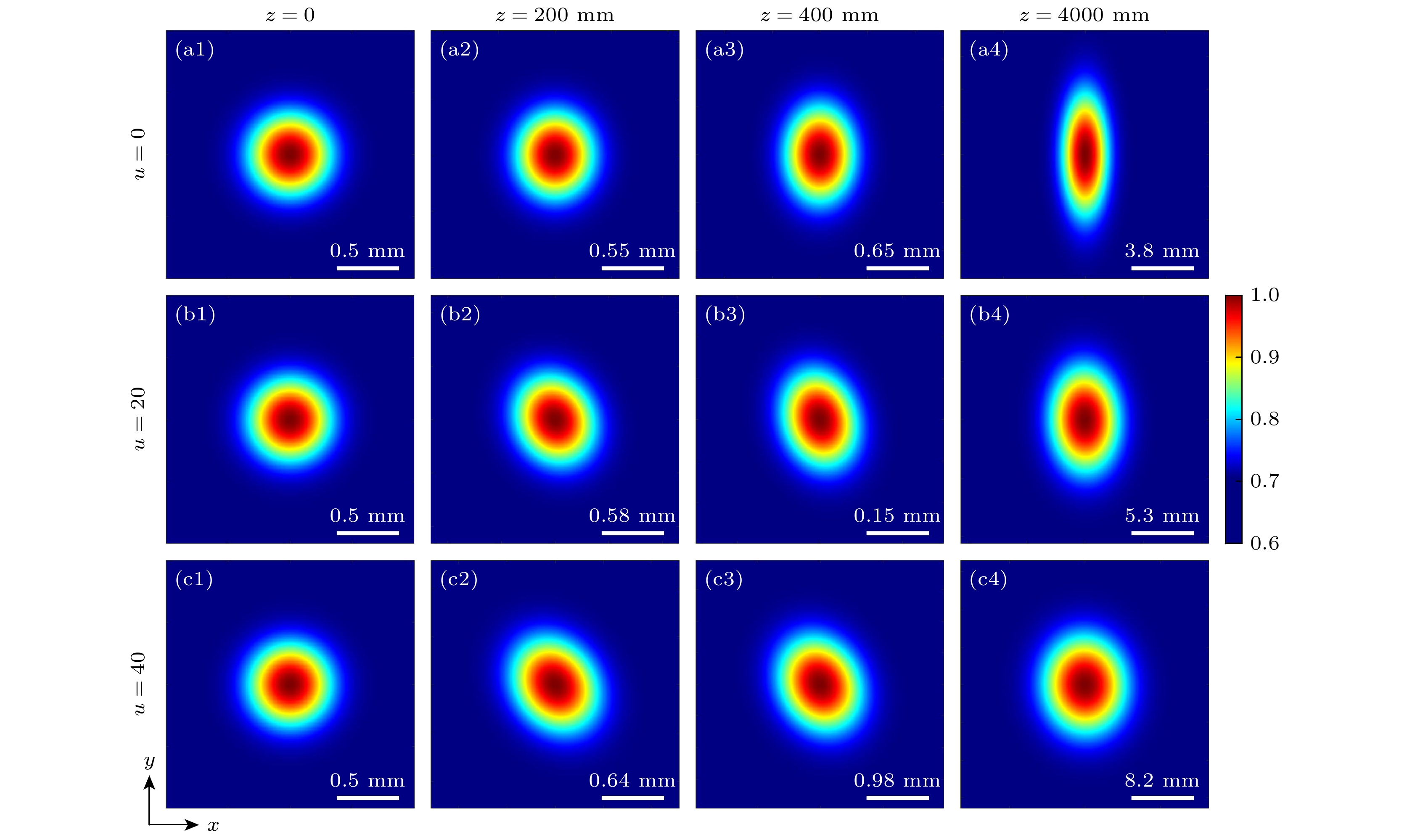
$z$ 的增大, 光束逐渐绕轴逆时针旋转, 最终光斑旋转$ {9}{{0}^ \circ } $ . 该现象说明, 虽然变换光场的表达式中有两项包含扭曲相位((5)式), 但光束整体仍保持“扭曲”效应, 并且旋转规律与一般的扭曲部分相干光场一致. 另外, 在本文中由于扭曲因子$u$ 取值为正, 所以光谱密度分布沿逆时针旋转, 若扭曲因子取值为负, 光斑将沿相反方向旋转. 值得注意的是, 镜像扭曲光场在传输过程中始终保持其镜像特征, 即中心亮斑分布. 类似地, 反镜像光场始终保持其反镜像特性, 即中心暗核分布. 对比3组图像可知, 相位差对光谱密度分布的调控主要集中在光束中心, 造成该现象的原因是干涉效应在中心区域最强.图5展示了扭曲因子
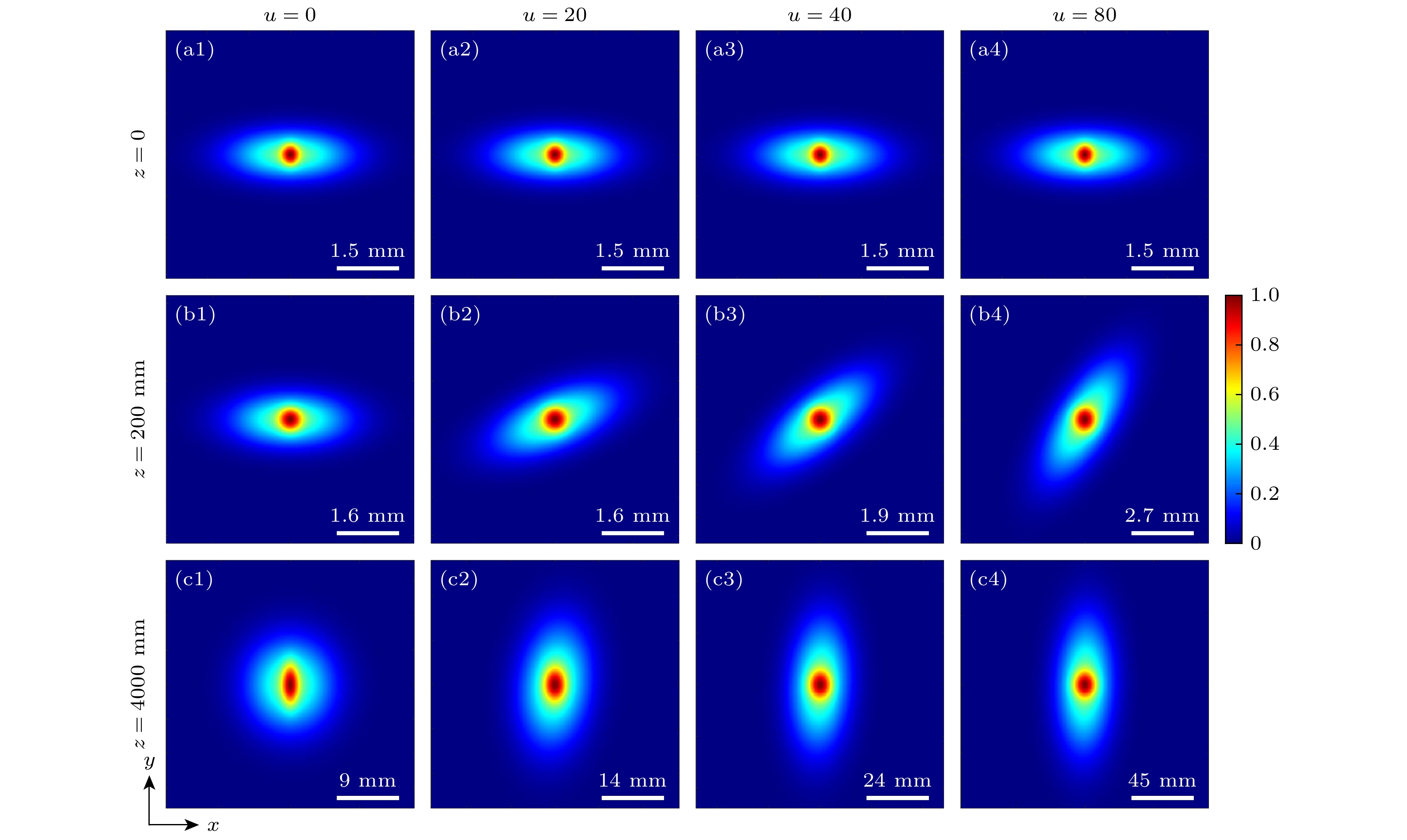
$u$ 对不同传输距离$z$ 的镜像光场的光谱密度的调控作用, 选取了3个典型地传输距离: WFI输出面(上)、传输近场(中)、传输远场(下). 由第1列图像可知, 当扭曲因子$u = 0$ 时, 光束退化为镜像高斯谢尔模型光束. 光束在传输过程中不发生旋转, 只保持镜像特征, 这与之前的研究结果一致[26]. 由图5(a)可知, 扭曲效应的强弱对WFI输出平面上的光谱密度分布不产生影响, 具有不同扭曲因子的光源变换后展现出相同的横向光束模式, 该现象也可通过理论公式(5)得到解释. 随着传输距离的增加, 扭曲因子的作用逐渐展现, 由图5(b)可以看到, 扭曲因子的大小控制了光束旋转的快慢, 即扭曲因子越大, 光斑旋转地越快. 有趣的是, 对于镜像光场, 扭曲因子不仅调控了光束绕轴旋转的速度, 还影响光束在传输过程中的光斑轮廓. 由图5(c)可以看到, 当光束传输到足够远的距离时, 扭曲效应越强, 光斑的椭圆率越小. 在此基础上可以通过调节光源参数获得具有完美圆形中心峰值, 两端极为尖锐的梭形光斑, 这对于微粒操控以及自由空间光通信等领域有着极大的应用潜力.下文讨论两个对称点
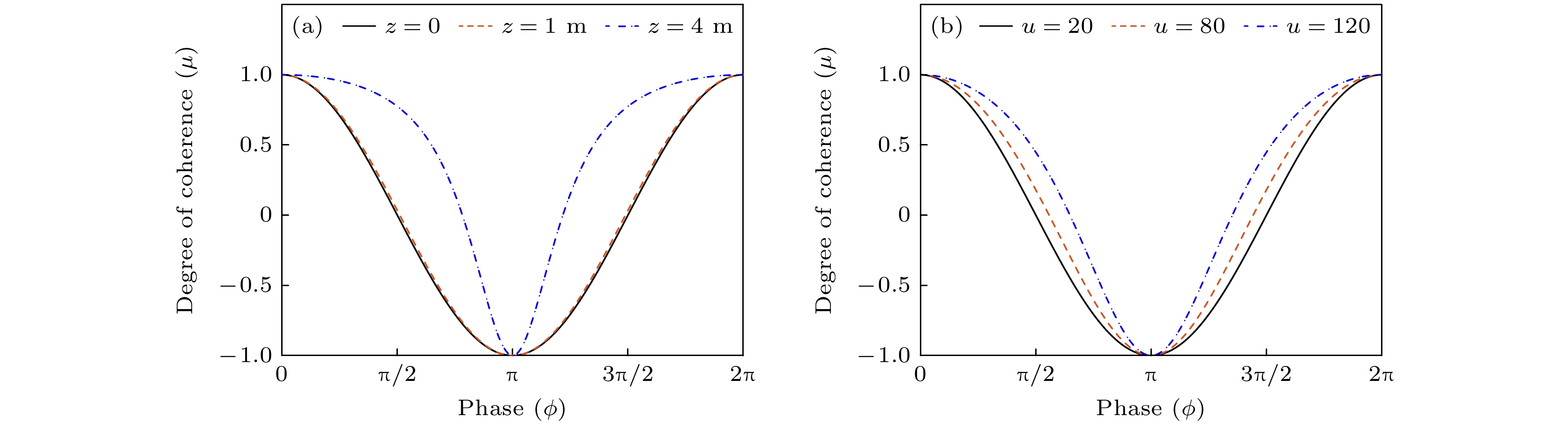
$ {\rho _1} = \left( {{x {/ } 2}, {y {/ } 2}} \right) $ 和$ {\rho _{2}} = \left( { - {x {/ } 2}, - {y {/ } 2}} \right) $ 之间的光谱相干度在自由空间传输时的特性. 图6展示了不同参量对光谱相干度沿$ x $ 轴分布的影响. 图6(a)的结果表明WFI两光路相位差的不同, 会导致光谱相干度的值在–1—1之间变化, 当光场为镜像或反镜像时, 有$\left| \mu \right| = 1$ , 此时光场为完全相干. 图6(b), (c)展示了束宽$ {w} $ 和相干长度$ \delta $ 对横向光谱相干度的影响. 可以看出, 不同于光束宽度的改变仅对相干度分布有微弱影响, 相干长度的大小对相干曲线的轮廓有决定性的影响. 具体来说, 相干曲线随着光源的相干长度的减小而迅速变窄. 图7展示了横向光谱相干度随两光路相位差$\phi $ 的分布情况. 我们再次观察到当光场是镜像或反镜像场时, 两对称点为完全相干, 对于非镜像光场, 两点为部分相干. 另外, 随着传输距离的增大, 两点间的相干性逐渐变好, 而扭曲因子对相干度分布也有一定的调制作用.由于镜像与反镜像扭曲光场为完全相干场, 为了方便起见, 图8所示为相位差为
$\phi = {{\text{π}} {/ } {4}}$ 的变换光场的相干度的演化规律, 并讨论了扭曲因子对横向相干曲线的调控作用. 为了方便比较, 第1行展示了非扭曲部分相干光场的相应情况. 对比第1列$z = 0$ 处的相干度分布可知, 扭曲因子对WFI输出平面上的相干度分布没有影响, 所有相干度图像均呈现各向同性的高斯分布. 随着传输距离的增大, 扭曲效应逐渐展现. 具体来说, 扭曲因子不仅诱导相干度轮廓绕传输轴顺时针旋转, 还能灵活调节横向相干度的分布情况. -
本文通过将扭曲高斯谢尔模光束入射到WFI, 构建了一类镜像与反镜像扭曲高斯谢尔模光束, 并研究了该新型光束在自由空间的传输特性. 研究表明, 变换后的光场仍保持扭曲效应, 其光谱密度和光谱相干度在传输过程中绕轴旋转, 但二者的旋向相反. 值得注意的是, 扭曲相位不仅能决定光场旋转的速度, 还能有效调控光斑的整体轮廓分布. 然而, 中心区域的光斑模式则由WFI相位差调控主导, 具体表现为镜像扭曲光场在传输过程中始终表现为中央亮斑分布, 反镜像扭曲光场则表现为中央暗核分布. 另一方面, 光源参量和干涉仪特性对光谱相干度的调控作用也得到证实. 总之, 镜像与反镜像部分相干光场展现出新奇的物理特性, 并可以通过对入射光参数和干涉仪性质的联合调控, 实现具有灵活可控模式的扭曲光场, 这对于微粒操控等领域有重要的应用前景. 我们的工作证明了WFI可以方便有效地用于构造新型扭曲光场. 虽然本文只考虑了入射光为扭曲高斯谢尔模光束的情况, 但该方法同样适用于入射光为非高斯关联的情况, 在关联结构、扭曲相位和干涉仪的联合调制下, 光场有望展现出更多新效应、新特点. 这将进一步丰富扭曲部分相干光的调控理论, 并拓展其应用范围.
镜像与反镜像扭曲高斯谢尔模光束的传输特性
Propagation properties of specular and antispecular twisted Gaussian Schell-model beams
-
摘要: 通过将扭曲高斯谢尔模光束入射到波前折叠干涉仪(WFI), 构建了一类镜像与反镜像扭曲高斯谢尔模光束, 并研究了光束在传输过程中的二阶统计特性. 结果表明, 变换光场仍保持扭曲效应, 其光谱密度和光谱相干度在传输过程中绕轴旋转, 但二者的旋向相反. 值得注意的是, 扭曲相位不仅能控制光场的旋转速度, 还能有效调控光斑的整体轮廓分布, 而中心区域的光斑模式则由WFI的相位差调控主导, 具体表现为镜像扭曲光场在传输过程中始终表现为中央亮斑分布, 反镜像扭曲光场则表现为中央暗核分布. 此外, 本文证明了光场的光谱相干度可由光源相干性、扭曲相位和WFI相位差等参数灵活调制. 本研究结果对于自由空间光通信以及微粒捕获等领域有重要应用价值.Abstract: We introduce a class of specular and antispecular twisted Gaussian Schell-model beams, which are generated by inserting a twisted Gaussian Schell-model beam into a wavefront folding interferometer (WFI). The analytical expression for the cross-spectral density function of the beam propagating in free space is derived, and the statistical properties of the optical field are investigated in detail. The results show that the twisted effect is still maintained after the transformation, and the spectral density of the light field always rotates to 90 degrees around the axis during propagation. Furthermore, with appropriate optical field adjustment, the twist effect of the spectral degree of coherence (DOC) can be observed, but in opposite directions to the irradiance profile. We also find that the twisted phase not only controls the rotation of the field, but also effectively modulates the overall spot contour. For the far-field spectral density distribution, a larger twist effect will induce a smaller ellipticity of the beam spot. However, the intensity pattern in the central area is mainly determined by the phase difference of WFI. To be specific, the specular twisted field always has a sharp central peak during propagation, and in the antispecular case it has a central dip. Besides, the DOC distribution can be flexibly adjusted by the source coherence, the twisted phase and the phase difference of the WFI. The results of our work have important applications in the fields of free-space beam communication and particle trapping.
-
Key words:
- partially coherent beams /
- specular and antispecular /
- twisted phase /
- propagation .
-
-
图 1 波前折叠干涉仪(WFI), 其中S为光源, BS为非偏振分束器, P1和P2为直角棱镜, D为探测器
Figure 1. Wavefront-folding interferometer (WFI). S is the source, BS is a non-polarizing beam splitter, P1 and P2 are right-angle prisms, and D is a detector.
图 2 WFI输出平面上的归一化光谱密度
$ {{S\left( {x', y'} \right)} {/ } {{S_{\max }}}} $ (a)$\phi = 0$ ; (b)$ \phi = {{\text{π}} {/ } {2}} $ ; (c)$\phi = {\text{π}}$ Figure 2. Normalized spectral density
$ {{S\left( {x', y'} \right)} {/ } {{S_{\max }}}} $ in the WFI output plane: (a)$\phi = 0$ ; (b)$ \phi = {{\text{π}} {/ } {2}} $ ; (c)$\phi = {\text{π}}$ .
图 3 WFI输出平面上的归一化光谱相干度
$ \mu \left( {{x'_1}, {0}, {x'_2}, {0}} \right) $ Figure 3. Spectral degree of coherence
$ \mu \left( {{x'_1}, {0}, {x'_2}, {0}} \right) $ in the WFI output plane.
图 4 变换扭曲光场在自由空间传输过程中的归一化光谱密度
$S\left( {x, y, z} \right)/{S_{\max }}$ 的演变规律Figure 4. Evolution of the normalized spectral density
$S\left( {x, y, z} \right)/{S_{\max }}$ of the transformed twisted field on propagation.
图 5 扭曲因子对镜像扭曲光场的归一化光谱密度
$S\left( {x, y, z} \right)/{S_{\max }}$ 的影响 (a) z = 0 mm; (b) z = 200 mm; (c) z = 4000 mmFigure 5. Influence of the twist factor on the normalized spectral density
$S\left( {x, y, z} \right)/{S_{\max }}$ of the specular twisted field: (a) z = 0 mm; (b) z = 200 mm; (c) z = 4000 mm.
图 6 两个对称点之间的光谱相干度
$\mu \left( {x/2, y/2, - x/2, - y/2, z} \right)$ 在传输距离z = 400 mm处沿$ x $ 轴的二维分布 (a) wx = 0.5 mm,$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ ; (b)$\phi = {{\text{π}} {/ } {4}}$ ,$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ ; (c)$\phi = {{\text{π}} {/ } {4}}$ , wx = 0.5 mmFigure 6. Spectral degree of coherence
$\mu \left( {x/2, y/2, - x/2, - y/2, z} \right)$ between two symmetrical points at the propagation distance z = 400 mm along$ x $ axis: (a) wx = 0.5 mm,$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ ; (b)$\phi = {{\text{π}} {/ } {4}}$ ,$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ ; (c)$\phi = {{\text{π}} {/ } {4}}$ , wx = 0.5 mm.
图 7 两个对称点之间的光谱相干度
$\mu \left( {x/2, y/2, - x/2, - y/2, z} \right)$ 随干涉仪两光路相位差$ \phi $ 的分布情况 (a) wx = 0.5 mm,$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ ; (b) z = 400 mm,$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ Figure 7. Spectral degree of coherence
$\mu \left( {x/2, y/2, - x/2, - y/2, z} \right)$ along$ \phi $ : (a) wx = 0.5 mm,$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ ; (b) z = 400 mm,$ {\delta _x} = {\delta _y} = 0.2 {\text{ mm}} $ .
图 8 两个对称点之间的光谱相干度
$\mu ( {x/2, y/2, - x/2, - y/2, z} )$ 在传输过程中的演化规律, 其中$ \phi = {\text{π}}/4 $ Figure 8. Evolution of the spectral degree of coherence
$\mu ( {x/2, y/2, - x/2, - y/2, z} )$ between two symmetrical points on propagation, and$ \phi = {\text{π}}/4 $ . -
[1] Simon R, Sudarshan E, Mukunda N 1985 Phys. Rev. A 31 2419 doi: 10.1103/PhysRevA.31.2419 [2] Cai Y J, Korotkova O 2009 Appl. Phys. B 96 499 doi: 10.1007/s00340-009-3469-0 [3] Tong Z S, Korotkova O 2012 Opt. Lett. 37 2595 doi: 10.1364/OL.37.002595 [4] Cui Y, Wang F, Cai Y J 2014 Opt. Commun. 324 108 doi: 10.1016/j.optcom.2014.03.030 [5] Cai Y J, Lin Q, Korotkova O 2009 Opt. Express 17 2453 doi: 10.1364/OE.17.002453 [6] Mao Y H, Mei Z R, Wang Y Y, Zhou G Q, Qiu P Z 2020 Opt. Commun. 477 126321 doi: 10.1016/j.optcom.2020.126321 [7] Simon R, Mukunda N 1993 J. Opt. Soc. Am. A 10 95 doi: 10.1364/JOSAA.10.000095 [8] Friberg A T, Tervonen E, Turunen J 1994 J. Opt. Soc. Am. A 11 1818 doi: 10.1364/JOSAA.11.001818 [9] Borghi R, Gori F, Guattari G, Santarsiero M 2015 Opt. Lett. 40 4504 doi: 10.1364/OL.40.004504 [10] Borghi R 2018 Opt. Lett. 43 1627 doi: 10.1364/OL.43.001627 [11] Mei Z R, Korotkova O 2017 Opt. Lett. 42 255 doi: 10.1364/OL.42.000255 [12] Gori F, Santarsiero M 2018 Opt. Lett. 43 595 doi: 10.1364/OL.43.000595 [13] Peng X F, Liu L, Wang F, Popov S, Cai Y J 2018 Opt. Express 26 33956 doi: 10.1364/OE.26.033956 [14] Santarsiero M, Gori F, Alonzo M 2019 Opt. Express 27 8554 doi: 10.1364/OE.27.008554 [15] Mei Z, Korotkova O 2018 Opt. Lett. 43 3905 doi: 10.1364/OL.43.003905 [16] Tian C, Zhu S J, Huang H K, Cai Y J, Li Z H 2020 Opt. Lett. 45 5880 doi: 10.1364/OL.405149 [17] Wang H Y, Peng X F, Zhang H, Liu L, Chen Y H, Wang F, Cai Y J 2022 Nanophotonics-Berlin 11 689 doi: 10.1515/nanoph-2021-0432 [18] Dong S J, Yang Y Z, Zhou Y J, Li X Z, Tang M M 2024 J. Opt. 26 065608 doi: 10.1088/2040-8986/ad4724 [19] Ponomarenko S A 2001 Phys. Rev. E. 64 036618 doi: 10.1103/PhysRevE.64.036618 [20] Wu G F 2016 J. Opt. Soc. Am. A 33 345 doi: 10.1364/JOSAA.33.000345 [21] Zhang C, Zhou Z L, Xu H F, Zhou Z X, Han Y S, Yuan Y S, Qu J 2022 Opt. Express 30 4071 doi: 10.1364/OE.448717 [22] Zhang C Y, Fu W Y 2024 Opt. Appl. 54 15 doi: 10.37190/oa240102 [23] Wan L P, Zhao D M 2019 Opt. Lett. 44 735 doi: 10.1364/OL.44.000735 [24] Cai Y J, Lin Q, Ge D 2002 J. Opt. Soc. Am. A Opt. Image Sci. Vis. 19 2036 doi: 10.1364/JOSAA.19.002036 [25] Gori F, Guattari G, Palma C, Padovani C 1988 Opt. Commun. 68 239 doi: 10.1016/0030-4018(88)90392-6 [26] Partanen H, Sharmin N, Tervo J, Turunen J 2015 Opt. Express 23 28718 doi: 10.1364/OE.23.028718 [27] Guo M W, Zhao D M 2016 Opt. Express 24 6115 doi: 10.1364/OE.24.006115 [28] Zhou Z T, Guo M W, Zhao D M 2016 Appl. Opt. 55 6757 doi: 10.1364/AO.55.006757 [29] Zhou Z T, Guo M W, Zhao D M 2017 Opt. Commun. 383 287 doi: 10.1016/j.optcom.2016.09.013 [30] Das D, Halder A, Partanen H, Koivurova M, Turunen J 2022 Opt. Express 30 5709 doi: 10.1364/OE.452308 [31] Tang M M, Dong S J, Yang Y Z, Zhou Y J, Guo M W, Li X Z 2024 J. Opt. 26 065601 doi: 10.1088/2040-8986/ad3cf2 [32] Guo M W, Zhao D M 2018 Opt. Express 26 8581 doi: 10.1364/OE.26.008581 [33] Tang M M, Feng X X, Liu S Y, Li H H, Li X Z 2021 J. Opt. 23 045605 doi: 10.1088/2040-8986/abedf6 [34] Li C Q, Zhang H Y, Wang T F, Liu L S, Guo J 2013 Acta Phys. Sin. 62 224203 doi: 10.7498/aps.62.224203 [35] 徐华锋, 张兴宇, 王仁杰 2024 物理学报 73 034201 doi: 10.7498/aps.73.20231484 Xu H F, Zhang X Y, Wang R J 2024 Acta Phys. Sin. 73 034201 doi: 10.7498/aps.73.20231484 [36] 王飞, 余佳益, 刘显龙, 蔡阳健 2018 物理学报 67 184203 doi: 10.7498/aps.67.20180877 Wang F, Yu J Y, Liu X L, Cai Y J 2018 Acta Phys. Sin. 67 184203 doi: 10.7498/aps.67.20180877 [37] Liu Y L, Dong Z, Zhu Y M, Wang H Y, Wang F, Chen Y H, Cai Y J 2024 PhotoniX 5 8 doi: 10.1186/s43074-024-00126-7 [38] Yu J Y, Zhu X L, Wang F, Chen Y H, Cai Y J 2023 Prog. Quant. Electron. 91-92 100486 doi: 10.1016/j.pquantelec.2023.100486 [39] Chen Y H, Wang F, Cai Y J 2022 Adv. Phys-X 7 2009742 doi: 10.1080/23746149.2021.2009742 [40] Peng D M, Huang Z F, Liu Y L, Chen Y H, Wang F, Ponomarenko S A, Cai Y J 2021 PhotoniX 2 6 doi: 10.1186/s43074-021-00027-z -
计量
- 文章访问数: 235
- HTML全文浏览数: 235
- PDF下载数: 1
- 施引文献: 0