量子信息与量子计算领域在近几十年取得了巨大的进步^[1]. 这个领域也有一些其他的名称, 比如量子信息科学等, 研究的基本内容是量子信息的性质和应用^[2], 包括量子通信、量子计算、量子模拟、量子传感与计量等研究方向^[3]. 它不仅是现代基础量子物理的一个新的分支, 是物理与信息、计算等的交叉学科, 而且有着极大的应用前景.

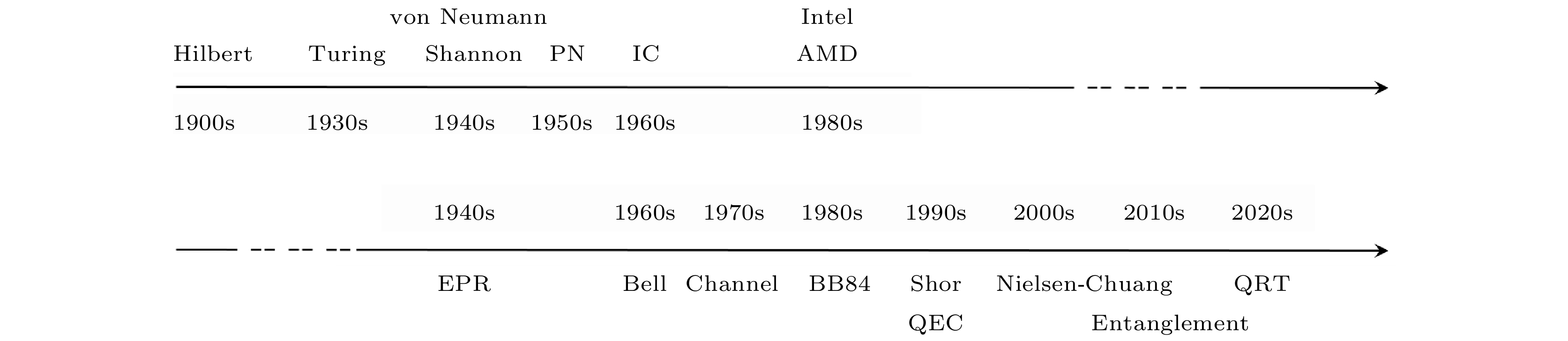
作为经典信息科学和量子物理的交叉, 量子信息科学诞生于20世纪80年代. 经过Bell^[4], Kraus^[5], Holevo^[6]等的奠基, 量子信息和一般量子演化的数学形式逐渐明晰. Feynman等^[7]认识到, 如果用可控的量子系统(即量子计算机)去求解量子问题, 应优于当时还在不断发展的电子计算机. Deustch^[8]做出了关键的一步, 即证明存在通用的量子计算机, 这引起了Yao^[9], Bernstein和Vazirani^[10]等理论计算机学家的进一步研究. 1994年, Shor算法的诞生让整个领域迅速发展起来^[11]. 图1简要勾勒了经典与量子领域的一些发展阶段. 如果把两者平行来看, 量子领域尚处于研发量子芯片的阶段, 距离实现真正的量子计算机、网络系统以及在各个产业中的实际应用尚有一定距离.

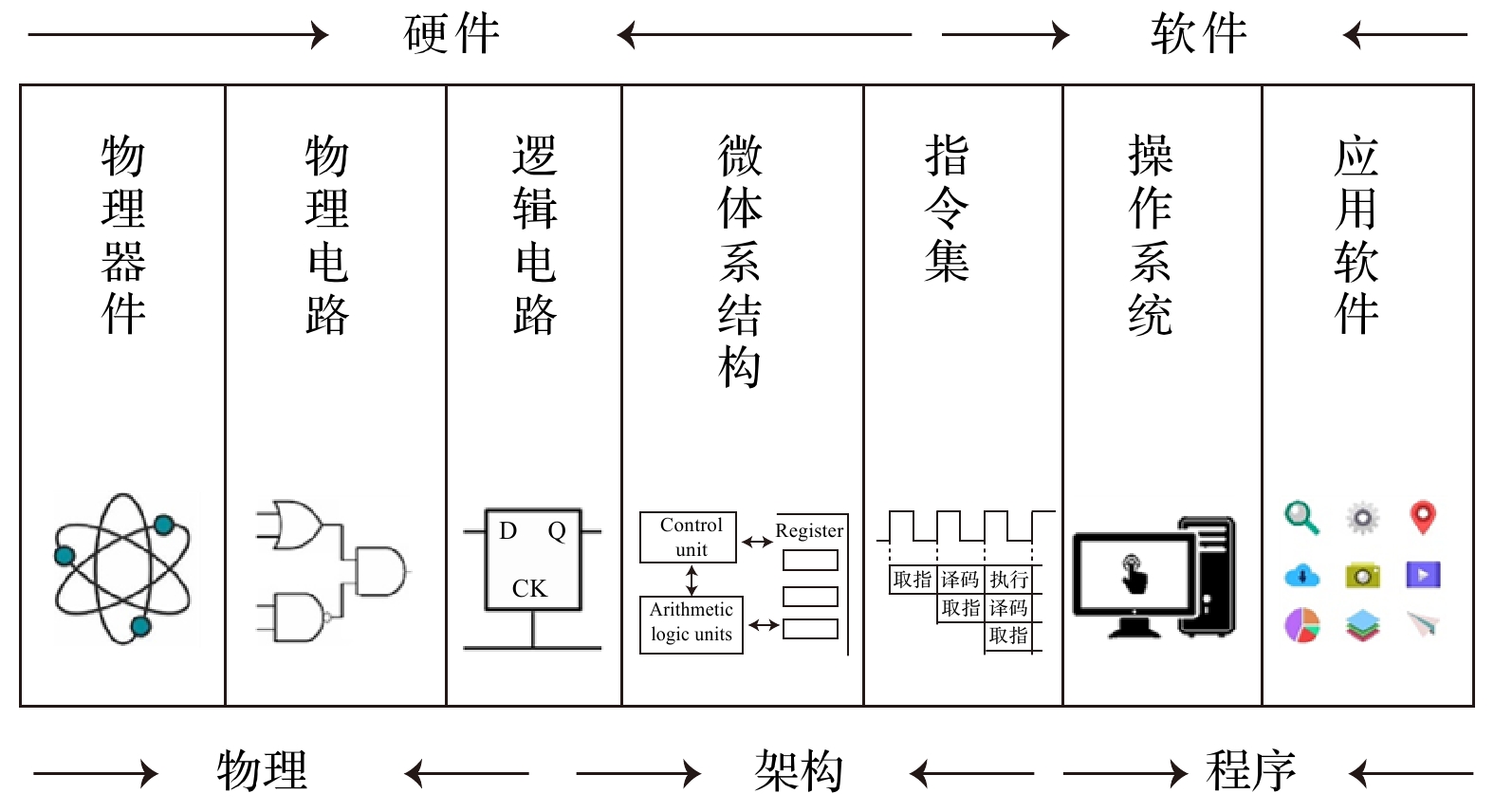
经典信息科学的发展为量子领域提供了很好的借鉴^[12]. Turing, Shannon^[13]建立了计算和信息的理论, von Neumann^[14]提出了通用计算机架构. 基于半导体技术特别是晶体管的发明, Intel, AMD等公司得以大规模地生产集成电路. 借鉴控制论和系统论等理论中的思想, 如今的各种计算系统(包括电脑、手机、单片机等在内) 基本都采用层次化的系统设计, 如图2所示. 底层是电路、晶体管等实现比特存储的基本器件; 然后是实现一些基本操作的数字电路和模拟电路, 包括布尔逻辑门、放大器、整流器等; 接着是实现一些基本功能的线路, 比如加法器、存储器等; 在此基础之上, 构建微体系结构(即冯·诺依曼架构), 包括控制、存储、通信、计算等单元; 最后是软件层次, 包括控制微机的汇编语言层次、控制各个设备的操作系统以及基于高级语言的各种应用软件. 这种结构具有层次化、模块化、规整化的特点^[12], 对软硬件的设计都非常重要.

在物理系统中, 经典比特的两种状态(记为0和1)可以用磁化方向、电压高低、波长大小等较好地表示. 与它们相比, 量子比特允许0和1的叠加态^[2]. 这种叠加以及多比特的量子纠缠可以为量子计算带来很多优势, 然而它的不稳定性(即退相干)一直是一个基本问题^[2]. 人们发展了量子纠错码理论来应对退相干问题^[15], 但在实际中实现真正的纠错码以及相应的容错性还需要一定时间. 在基本物理器件方面, 人们在超导、光子、离子阱、冷原子等系统中取得了很大技术进步^[16]. 但若与经典器件相比, 人们尚不清楚是否存在晶体管的量子对应, 即可以实现信号放大、数据存储和逻辑操作等功能于一体的量子信息器件. 人们在量子算法方面也进行了很多研究, 发现了一些具有量子优势的算法, 比如Shor算法、Grover算法、Harrow-Hassidim-Lloyd算法等^[11,17-20]. 然而, 由于退相干和计算规模等问题, 这些算法尚无法被严格实现. 因而, 相比于经典计算机特别是加上人工智能算法, 量子算法及其优势的实现还面临很大挑战.

理论上, 对量子信息的叠加特性进行刻画并不容易, 人们对量子信息的认识也是不断地深入. 可以说, 这个领域是基础和应用同时发展的, 而不是简单的从基础到应用. 早期的探索可以从Nielsen和Chuang的经典著作中看到^[2]. 然而, 它不包括很多重要的课题, 比如多体纠缠态、通用计算模型、量子香农定理等, 因为这些是在接下来的时间才开始发展的. 这些发展可以在近些年的一些著作中看到^[21-23].

我们知道, 经典信息可以表示为比特串(即数字信号), 其信息量可以由香农熵来度量. 香农证明的三大定理是信息论和编码的基础^[13]. 相应地, 量子信息即是量子比特的量子态, 其信息量一般由冯·诺依曼熵来度量. 然而, 所有纯态的冯·诺依曼熵都为零, 因而需要其他的量来区分不同的纯态. 与经典比特不同, 量子比特的状态存在于希尔伯特空间中, 一个任意的量子态不能被复制(即克隆), 而多个任意的量子态不能被完全区分开来. 人们逐渐发展出了所谓的量子资源理论的框架^[24], 可以用于描述量子信息的不同方面, 包括相干性、纠缠、非定域性、语境性(也称互文性)、互补性以及不确定性等. 我们近期发现, 这个理论框架也可以作为量子计算的基础^[25].

在量子计算中, 人们一般采用所谓的量子线路模型, 即用一系列的量子门来组合成所需的过程或算法^[2]. 这对应于经典的布尔逻辑线路. 经典常用的图灵机模型、元胞自动机(cellular automata)等也有量子对应. 这些模型是所谓的通用计算模型, 即任意的一个经典或量子算法, 都可以在相应的经典或量子的计算模型中被有效实现. 对于经典或量子情况, 通用模型之间是等价的, 即它们实现同一算法的过程可以互相转换(即模拟). 人们也发现了更多的这类所谓的通用量子计算模型, 比如绝热量子计算^[26]、拓扑量子计算^[27]等, 一般是没有经典对应的. 这些模型启发了一些量子算法, 也被不少量子研发公司作为量子计算的架构基础. 然而, 由于是由不同背景的专家在不同时期提出的, 人们对它们的研究并不系统, 研究的侧重点也各有不同. 与量子资源理论所取得的统一描述相比, 之前并不存在一个统一的框架来定义和区分通用量子计算模型.

近期, 我们通过一系列的研究, 发现可以将量子资源理论和通用计算模型结合起来, 并带来多方面的意义. 首先, 它提供了一个统一的框架来定义和分类不同的通用量子计算模型, 这使得对其研究可以系统化. 其次, 它将量子资源放在了通用量子计算的问题之中, 这为如何区分和利用量子资源提供了一个系统的视角. 再次, 通过对计算模型资源理论的刻画, 可以揭示量子算法中的资源是什么, 解决人们关于量子算法是依赖什么核心资源的一些争论. 最后, 它启发了人们对量子冯·诺依曼架构的发现和认识, 这一方面从理论上解决了如何使用量子存储的问题, 也让量子计算从机器语言到汇编语言的发展成为可能, 进而构建完整的量子计算机系统.

需要注意到, 本文采用广义的量子计算概念, 即把其作为最一般的量子信息的演化. 而现实中, 可能采用狭义的概念, 比如, 认为量子信息是对量子态和过程基本性质的研究, 量子计算是对量子算法的研究. 而真正的量子的信息论(即量子香农理论)^[21]是信息学家所关注的, 与物理学家的关注点甚为不同. 我们的研究将资源理论和计算模型结合起来, 即把量子信息研究和量子计算研究方向的语言统一起来, 可以打通不同的研究方向, 促进人们在整体上对量子信息及其演化性质的认识.

本文包括以下基本内容: 第2节回顾量子计算的基础; 第3—5节研究通用量子计算模型的分类, 并简要分析每个模型; 第6节重点分析量子冯·诺依曼架构及其应用; 最后, 第7节讨论几点相关问题, 包括通用和专用架构的关系、一些潜在的问题和发展方向等. 由于一些量子计算模型已经有较好的综述文章, 如绝热量子计算^[26]、拓扑量子计算^[27]、量子游走^[28]、量子元胞自动机^[29]、图态量子计算(也称测量量子计算)^[30], 因而本文的讨论重点不在于模型的细节, 而在于从资源理论的角度讨论模型的分类问题.

人们最常用的量子计算方式是线路模型(circuit model)^[2,8]. 在此模型中, 实现一个计算过程或算法首先要制备简单的初始量子态, 然后有序执行一系列幺正的量子门, 最后对末态进行测量. 测量过程一般要求多次执行此线路, 经过统计分析后得出计算结果. 即若进行测量的对象是厄密算符E, 最终结果表示为其在末态ρ上的期望值:

其中$ e_i $来自于E的本征值分解$ E = \displaystyle \sum\nolimits_i e_i |i \rangle \langle i| $, 概率$ p_i = \langle i|\rho|i \rangle $需要经过统计分析得到.

以上简述的过程类似于通常的量子物理实验. 然而, 量子计算有更多的要求, 这导致一个计算系统与物理实验体系是不同的^[12]. 这里着重讨论三点, 即数字化(digitalization)、通用性(universality) 和可编程性(programmability). 数字化要求量子态要表示为多量子比特的状态, 量子演化过程要表示为一系列基本量子门的组合, 量子测量是对量子比特的简单测量. 其实, 信息及其演化的数字化既是通用性的要求, 也是容错性的要求, 即对噪声或错误的有效控制.

一个重要的结论是, 存在所谓的通用量子门集合, 比如{H, T, CNOT}, {H, CCNOT}, 使得任意的幺正算符都可以被精确地表示为通用门序列^[31]. 这是经典布尔逻辑的量子对应. 其中, H是Hadamard门, 满足${HXH = Z} $, $ {HZH = X} $, X和Z是Pauli算符, T门满足$ {T}^4 = {Z} $. CNOT是常用的两比特控制门, CCNOT代表三比特控制门, 即Toffoli门. 通用门集合的存在是保证线路模型通用的前提. 更一般地, 一个计算模型是否通用也经常归结为能否有效地模拟一个通用门集合. 这也暗含对初态的制备、对末态的测量和对相干时间的要求. 在量子计算的早期, 实现量子计算的这些基本要求一般被称为DiVincenzo基本要求^[32].

可编程性是一个相对隐蔽但更为高级的要求. 从软件的角度来说, 不同的算法表示为不同的线路. 而在硬件上, 为了实现通用性则可能需要大量的不同线路或芯片. 因而, 人们发展了编程的方法使得在同一个芯片上能实现不同的算法. 对于经典情况, 若CPU的操作用G代表, 对于任意的输入数据比特串$ \vec{b} $和程序A的数据表示$ \vec{b}_A $, 需要满足

其中$ A \vec{b} $是所需的结果, $ \vec{b}_A' $可以被用来恢复原程序. 然而, 对于量子情况, 将幺正的G作用在量子数据$ |d \rangle $和程序态$ |p_U \rangle $上,

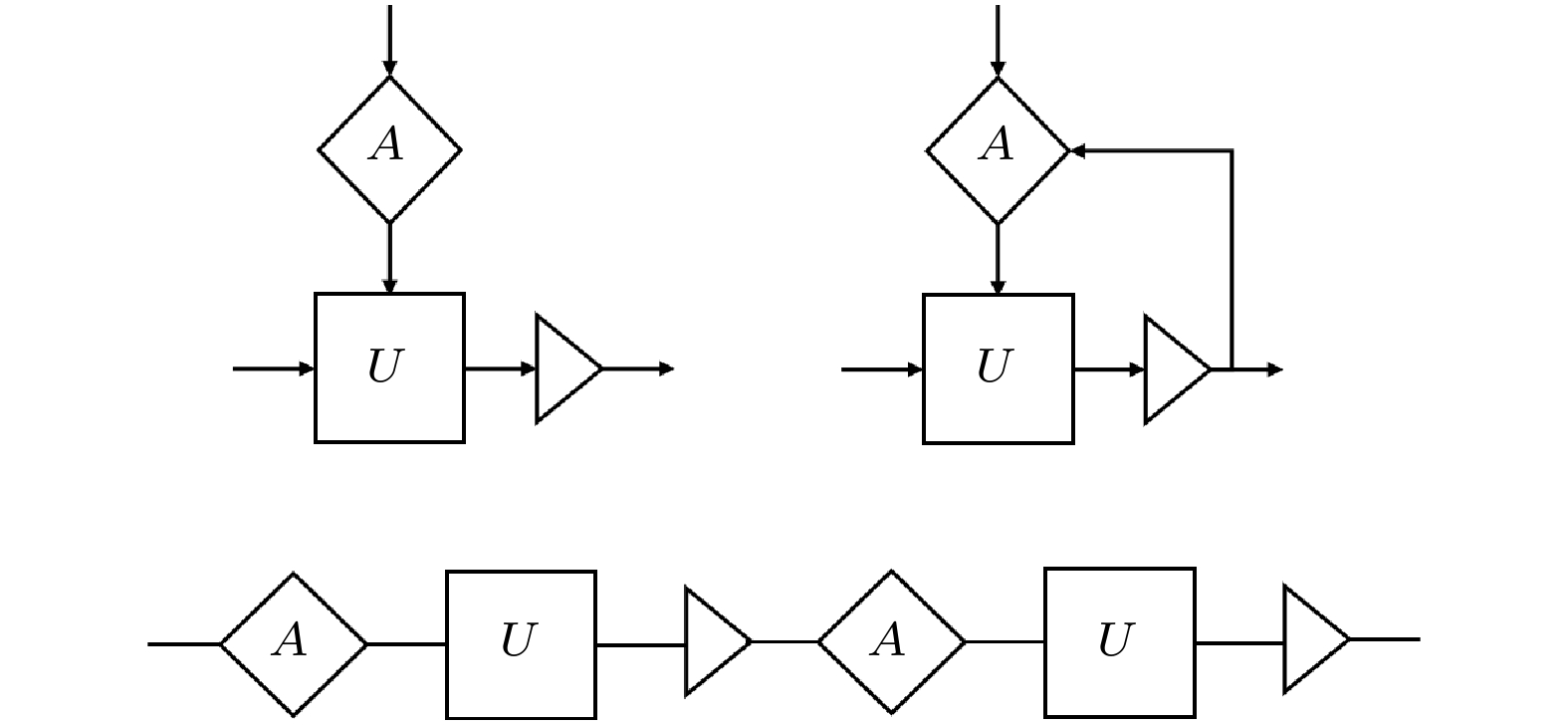
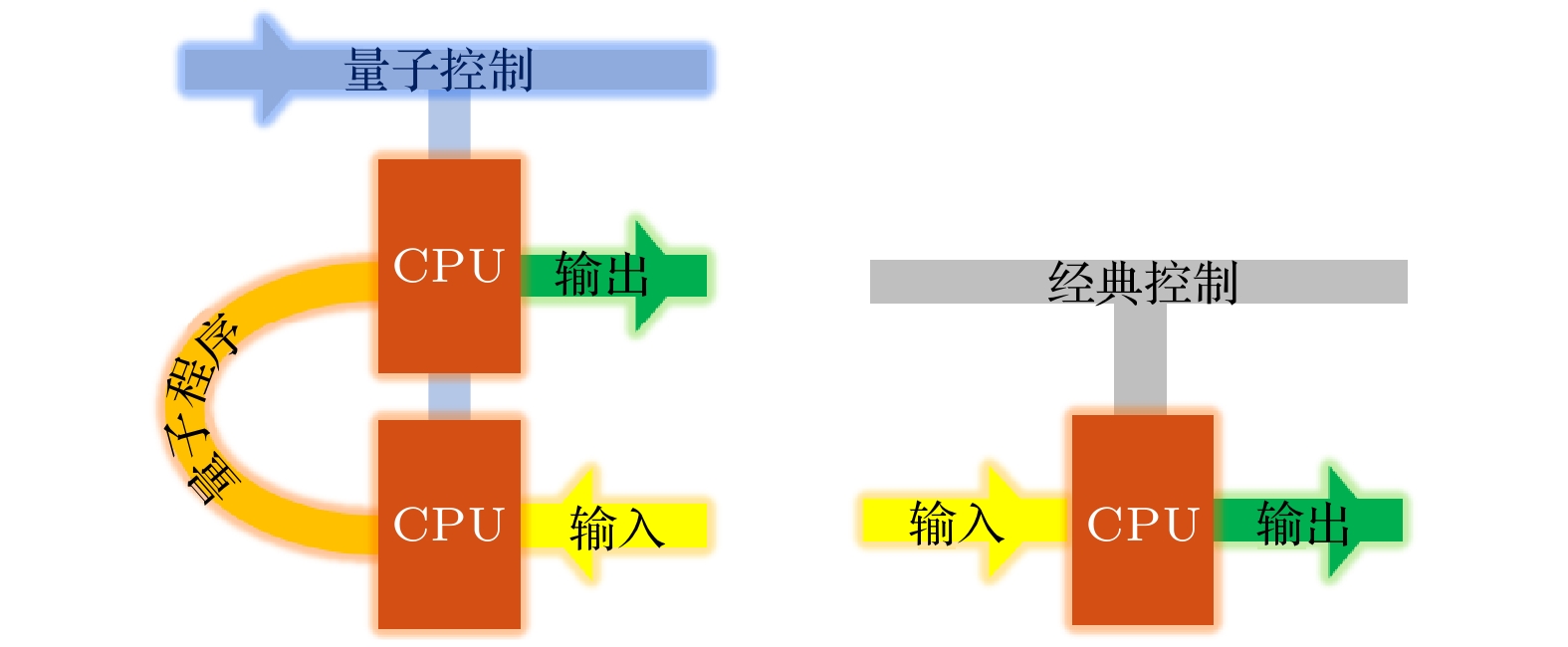
必须满足$ \langle p_V| p_U \rangle = 0, $ $ \forall U\neq V $, 这是Nielsen和Chuang^[33]于1997年证明的所谓量子不可编程定理, 也即量子存储问题. 即不同的量子算法或程序的存储态必须正交, 这其实等价于经典的存储. 由于幺正群的连续性, 导致存储空间迅速增长. 这一定理的限制使得人们只能采取经典-量子混合架构, 即用量子芯片来执行量子算法, 而量子算法的存储是用经典数据. 近期研究表明, 这一定理与量子不可克隆(no cloning)定理在原则上是等价的^[34,35]. 即对未知程序的读取和下载过程是一个计量过程, 如果可以实现, 则可以实现对它的克隆. 如果只要求近似地实现$ U|d \rangle $, 则近似程度受不确定性关系限制^[34].

在线路模型的框架下, 量子算法的设计也需要一个经典的“母”算法, 见图3. 例如, 在Solovay-Kitaev的量子编译算法中^[36], 对于任意的幺正算符U和编译精度ε, 经典算法$ A(U, \varepsilon) $给出量子线路$ U' $的经典表示, 记为$ [U'] $. 量子线路$ U' $本身通过量子门来实现. 算法的有效性一般要求经典算法A和量子算法$ U' $的复杂度, 即计算利用的时间和存储空间, 都不随$ {1}/{\varepsilon} $和U指数增长, 即其消耗

其中$ |U| $代表对U的大小的某种衡量, 比如某种矩阵范数(norm). 随精度的增长$ \log {1}/{\varepsilon} $不一定能达到, 例如, 常用的Trotter-Suzuki矩阵分解只能达到${1}/{\varepsilon} $形式^[37]. 为了计算观测量即得到(1)式中的概率, 还需要进行大量的采样. 采用量子振幅放大算法^[38], 可以将概率转化为振幅, 进而将采样的消耗转化为计算消耗. 对精度的要求, 其实暗含着容错性, 在当前情况下这还无法实现. 因而, 目前大多量子算法的实验实现都是演示性的实验.

容错性(fault-tolerance)的字面含义是对错误的容忍, 它要求采用量子纠错码^[39]以有效地克服退相干、噪声或错误的影响. 严格来讲, 实现通用性也要求实现容错性. 换句话说, 它是指实现任意长寿命的量子比特或者空置量子门(identity), 能将其他的量子门连接起来, 比如前面提到的H, T, CNOT量子门. 在模型的通用性的证明中, 一般假设容错性可以得到保障, 即纠错是另外一个维度的问题.

量子噪声或错误一般被描述为量子信道 (channel)^[2]. 一个信道Φ在态上的作用表示为一组Kraus算子$ \{E_i\} $的叠加:

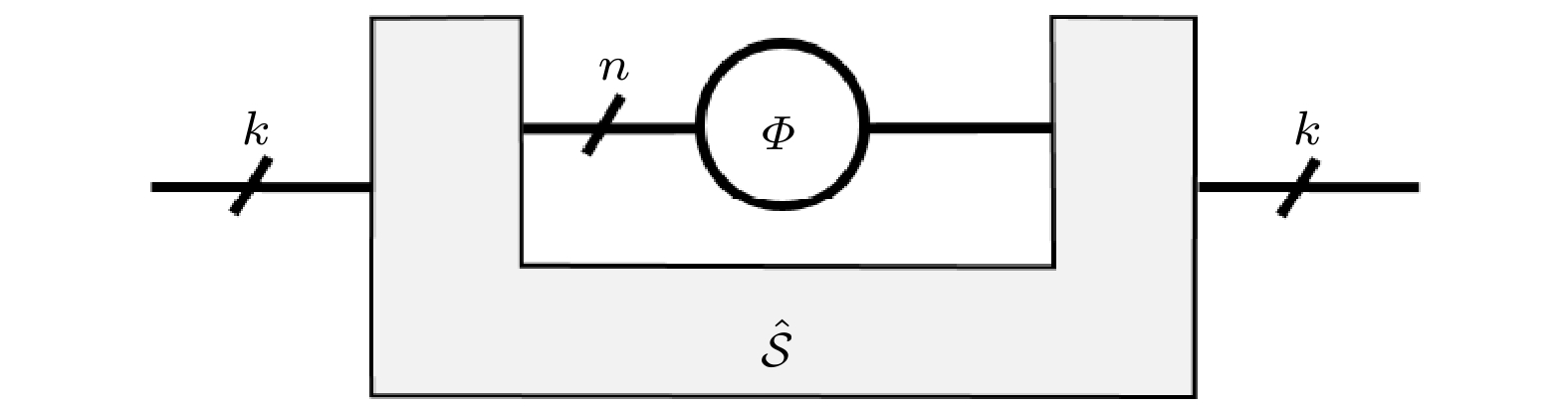
并且$ \displaystyle \sum\nolimits_i E_i^\dagger E_i = {1 1} $^[5]. 更一般地, 采用量子超信道理论^[40-42], 量子纠错是一个量子超信道过程$ \hat{{\cal{S}}} $使得

如图4所示, 其中$ \varepsilon\in [0, 1] $是纠错的准确度或误差, k和n是正整数, 且$ n\geqslant k $, $ r: = k/n $是码率. 超信道的具体形式后面会介绍. 纠缠保真度$ F_E $的形式为$ F_E(\varPhi, \varPsi): = F(\varPhi \otimes {1 1} (\omega), \varPsi \otimes {1 1} (\omega)) $, 而F是通常的态的保真度$ F(\rho, \sigma): = \|\sqrt{\rho}\sqrt{\sigma}\|_1^2 $, $ \|\cdot\|_1 $是迹范数, $ \omega\propto\displaystyle \sum\nolimits_i |ii \rangle $是一个Bell态, 也称为纠缠比特(ebit). 其中,

也称为信道Φ的Choi态, 它的性质和Φ是等价的, 这被称为信道-态对偶原理^[43]. 它和不确定性原理一样, 也是量子物理的基本原理. 这两个原理也会体现在后面讨论的量子冯·诺依曼架构中.

纠错形式(6)包括最早发展的二分形式, 即先用$ {\cal{V}} $编码再用$ {\cal{D}} $解码^[39], 也包括其近似情况^[44]. 为了实现容错性, 需要保证ε可以任意地趋近于0. 误差$ \varepsilon = 0 $的情况对应于严格或精确纠错, 此时噪声算子和编码需要满足Knill-Laflamme条件:

其中$ P = VV^\dagger $, V是等距映射(isometry)编码, $ \{K_i\} $是噪声的Kraus算子集合^[39]. 一大类精确纠错码是所谓的稳定子码(stabilizer codes)^[2,45]. 通常, 稳定子由Pauli算符的直积构成, 编码由一组对易的稳定子构成, 而解码则是通过对稳定子的测量来确定是否发生了比特反转X或相位反转Z错误, 继而将其纠正.

保证ε可以任意地趋近于0并不容易. 我们最近提出^[46,47], 可以通过引入外在参量$ \vec{\lambda} $, 使得$ \varepsilon(\vec{\lambda}) $可以在参量空间中趋近于0. 满足这个条件的纠错码被称为准精确码(quasi-exact), 否则只是一般的近似码. 这些参量包括k, n, 纠错过程$ \hat{{\cal{S}}} $包含的可控参量, 以及噪声Φ本身的一些参量. 我们熟知的一些可控参量包括光学中的压缩系数(squeezing)、光子数、Floquet调控中的外场频率、化学势、温度以及码级联的步数等. 采用准精确码所能实现的容错性被称为“准容错性”, 它处于非容错和严格的容错性之间. 相应地, 通用性也需要约化为准通用性.

结合纠错的一般形式((6)式), 准精确码也可以描述一些广义的纠错机制, 例如纠缠提纯(distillation)、动力学解耦(dynamical decoupling)以及量子密钥分发(quantum key distribution, QKD)提高传输距离的方案等. 具体来讲, 可以将准容错性区分为两种类型. 第一种是$ \varepsilon(\vec{\lambda}) $不能高效地趋近于0. 例如, 近期发展的具有连续对称性的协变码(covariant codes)^[46-49], 其纠错误差和系统大小n的关系具有$ \text{poly}\left({1}/{n}\right) $的形式. 这可以从不确定性关系来理解, 因为协变码可以理解为对未知参量的一种量子计量方式^[50]. 由于不采用额外的辅助比特来降低系统的噪声, 动力学解耦得到的纠错误差不能随解耦的力度而指数式地降低^[51]. 第二种是$ \varepsilon(\vec{\lambda}) $可以高效地趋近于0, 但由于现实原因, 无法随意地调控$ \vec{\lambda} $. 这可以描述目前实验中可以实现的一些有噪声的精确码, 比如表面码(surface code)^[52], 以及可以部分使用纠错码的情况. 这种类型原则上属于容错性的范围. 我们目前所知的准精确码的种类很少, 虽然它们比精确码对码的结构要求更弱.

经典纠错码的发展为我们提供了很好的借鉴^[53]. 目前常用的经典码包括分组(block)码、LDPC码、卷积(convolutional)码、涡轮(Turbo)码、极化(Polar)码等, 它们在计算和通信中扮演重要角色. 人们对量子码的研究主要集中在分组码和LDPC码^[54], 对其他类型的认识较为不足^[15]. 更一般地, 如何从理论上对纠错即编码方式进行分类, 进而系统性地设计纠错码也是重要的课题^[55].

本节先介绍通用量子计算模型的分类方法, 然后分别讨论这些模型的主要性质. 由于历史的原因, 有些计算模型实则是从容错性入手, 比如拓扑量子计算, 即采取特殊的方式来实现量子逻辑门. 我们发现, 不论是通用性还是容错性, 都可以从量子资源理论的角度来刻画.

对于分类问题, 首要的选择是群论. 然而, 计算过程一般不涉及特定的对称性. 我们发现, 通用量子计算模型的分类问题需要采用量子资源理论(resource theory). 从数学上来讲, 量子资源理论可以被描述为一种范畴理论^[56], 其实也可以被理解为一种广义的对称性理论.

一个量子资源理论是定义在一个集合$ {\cal{D}} $上, 并包括三个基本集合: $ {\cal{F}} \subset {\cal{D}} $作为限定子集(free set),$ {\cal{O}}: {\cal{F}} \rightarrow {\cal{F}} $作为限定操作集, $ {\cal{R}}: = {\cal{D}} \backslash {\cal{F}} $作为资源集^[24]. $ {\cal{O}} $和$ {\cal{F}} $的关系可以被看作一种广义的对称性. 为了度量资源量, 定义在$ {\cal{D}} $上的一个函数f需要满足特定的条件, 一般包括:

$ {\rm{i}}) $ 正值性: $ f(\rho) = 0 $, $ \forall \rho \in {\cal{F}} $; $ f(\rho)\geqslant 0 $, $ \forall \rho \in {\cal{D}} $;

$ {\rm{ii}}) $ 连续性: $ f(\rho) \rightarrow f(\sigma) $ if $ \rho \rightarrow \sigma $, $ \forall \rho, \sigma \in {\cal{D}} $;

$ {\rm{iii}}) $ 可加性: $ f(\rho\otimes \sigma) \leqslant f(\rho) + f(\sigma) $, $ \forall \rho, \sigma \in {\cal{D}} $;

$ {\rm{iv}}) $ 单调性: $ f(\rho)\geqslant f(\varPhi(\rho)), $ $ \forall \varPhi \in {\cal{O}} $, $ \forall \rho \in {\cal{D}} $.

度量函数f可以采用距离、熵、Fisher信息等. 例如, 一个熟知的例子是两体纠缠态, 其对应的限定集合是可分态, 限定操作是定域操作外加经典通信, 而两体最大纠缠态是Bell态形式^[57]. 稍晚人们也认识到, 相干性也是一种资源^[58]. 选取一组正交基, 在此基下对角的态构成限定集, 都是非相干态, 而非相干操作也可以被定义. 其实, 冯·诺依曼熵本身就定义了一个最基本的态的资源理论: 选取最大混合态作为限定集, 用负熵($ \log d -S(\rho) $)作为一个态ρ的资源的度量, 则所有纯态的资源度都是最大的, 而限定操作则是无法降低熵$ S(\rho) $的过程.

另外, 集合$ {\cal{D}} $不仅可以是人们一般考虑的态空间, 也可以是其他类型的算符集合, 比如哈密顿量、测量、信道演化、编码等. 考虑不同类型的算符可以给出不同类型的计算模型.

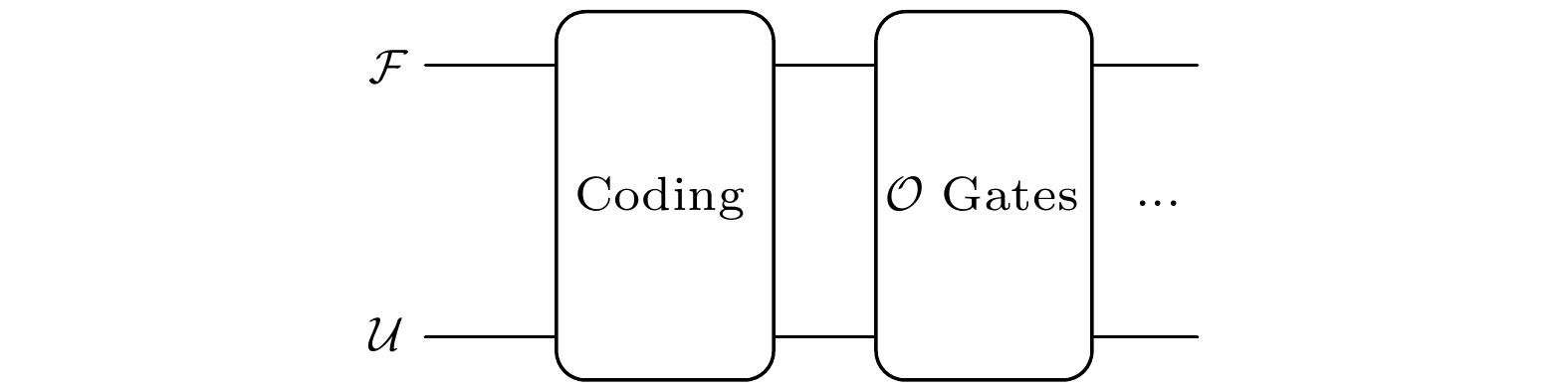
在资源理论的框架下, 定义通用性为采用$ {\cal{O}} ({\cal{F}} \otimes {\cal{R}}) $来实现$ {\cal{D}} $上的任意操作. 为了给通用计算模型分类, 对资源理论的形式做两个扩充^[25]. 首先定义通用资源集合$ {\cal{U}} $, 它们的资源度$ f({\cal{U}}) $达到最大值. 那么, 采用$ {\cal{O}} ({\cal{F}} \otimes {\cal{U}}) $则可以有效模拟其他的$ {\cal{O}} ({\cal{F}} \otimes {\cal{R}}) $过程. 其次, 定义资源序列满足$ {\cal{F}}_1 \subset {\cal{F}}_2 \subset \cdots $, $ {\cal{O}}_1 \subset {\cal{O}}_2 \subset \cdots $, 那么为了实现通用性, 其通用资源的计算能力需要递增, 记为$ {\cal{U}}_1 \succ {\cal{U}}_2 \succ \cdots $. 进而, 对于$ u_{1, 2}\in {\cal{U}}_{1, 2} $, 不同的通用资源之间需要满足如下关系:

这会给出一个系列的计算模型, 我们称之为一个“家族”(family). 原则上, 家族中成员的数量并无上限, 这里考虑只有三个的情况, 而这已经可以产生足够多的计算模型.

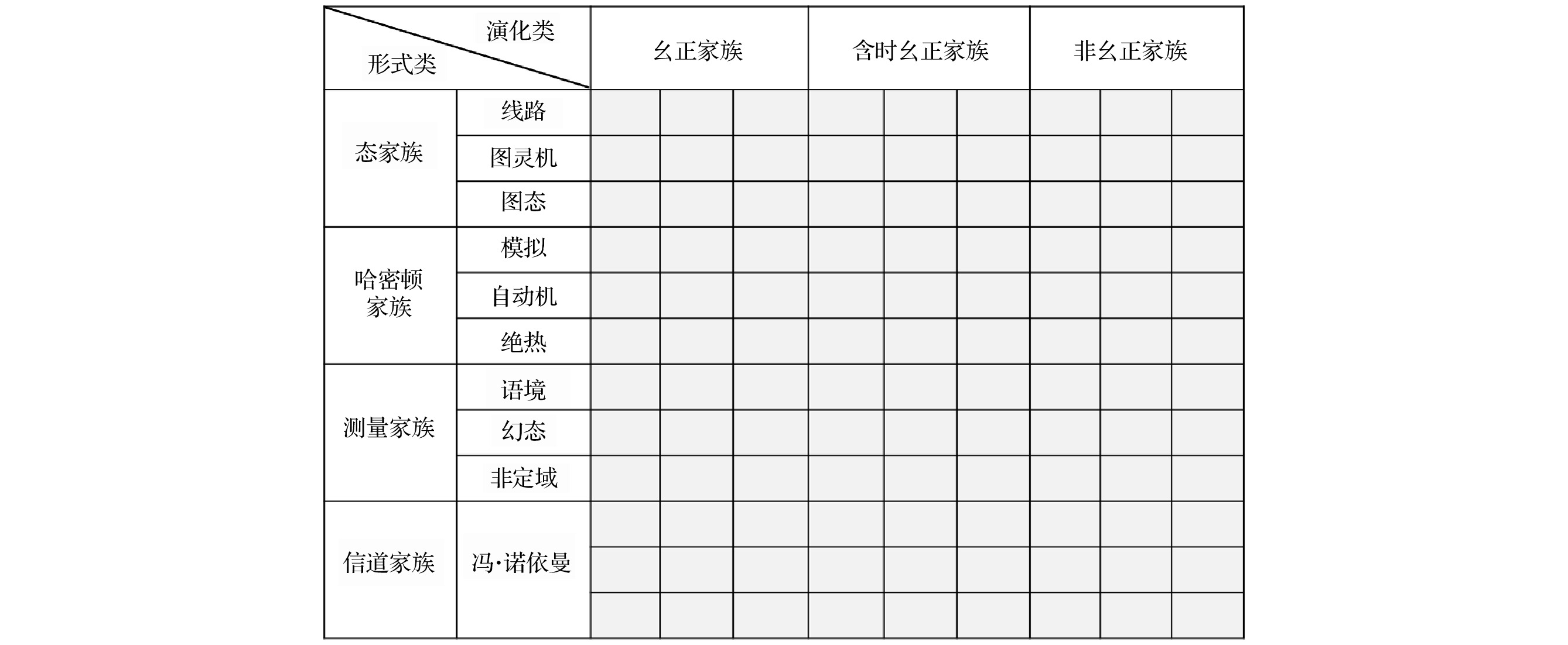
基于以上分析, 这里首先把计算过程抽象为$ {\cal{O}} ({\cal{F}} \otimes {\cal{U}}) $, 外加纠错的过程, 即包括一系列的逻辑和纠错过程, 如图5所示. 考虑量子态、哈密顿量、测量、信道演化以及逻辑门和编码算符分别构成的集合. 从信息的表示形式、演化和保护这三个方面出发, 将通用计算模型分为两大类(category): 依赖信息的不同表示形式的第I类模型; 依赖信息的不同演化形式的第II类模型^[59]. 信息的保护涉及到编码本身的类型, 属于第三个维度, 本文不做讨论^[55]. 通用量子计算模型的分类如图6所示, 其中每个模型的定义和性质是本文讨论的主要内容. 由于篇幅所限, 对于每个模型的分析难以做到详尽, 请参考更多文献了解相应的细节.

第I类模型来自于信息的不同表示形式, 即将信息表示为量子态、哈密顿量、测量和信道的某种性质. 它们分别定义一个家族(family), 每个家族中有三代(generation), 因而一共是12个模型. 第II类模型来自于对量子逻辑门的分类, 按照其实现方式, 即非含时幺正、含时幺正、非幺正演化, 它们分别定义一个家族, 每个家族中有三代, 因而一共是9个模型. 当然还可以进行细分, 这里不进行讨论. 将信息的表示和逻辑演化结合起来, 一共是108种基本模型. 这其中有些方案的研究较为充分, 有些则还没有, 参见文献[59]对其中部分方案的分析. 下面解释这些模型背后的基本逻辑.

例如, 在态家族模型中, 信息表示为量子态即纯态$ |\psi \rangle = \displaystyle\sum\nolimits_i \psi_i |i \rangle $在某组基$ \{|i \rangle\} $下的振幅$ \psi_i $. 计算是对振幅的操作, 也是人们最为熟知的干涉的过程. 混合态可以被看作纯态的概率混合. 当考虑多量子比特的计算过程时, 则可以在资源理论的框架下, 根据定域性来选取不同的受限操作集, 定义一个家族. 我们发现, 态家族包含人们熟知的线路模型, 以及定域图灵机(local Turing machine)模型^[60]和图态(graph state)量子计算, 也称为测量(measurement-based)量子计算^[30,61,62]. 它们的通用计算资源分别对应于相干性^[58]、纠缠^[57]和特定形式的对称性保护的纠缠^[63-65]. 这里, 定域图灵机是对原始的量子图灵机模型的一个简化^[9,10,66], 使得其中相互作用的定域性和量子态的纠缠性质得以凸显.

第II类模型主要依赖于逻辑门的不同形式. 如果将编码表示为某等距映射V, 那么编码后不同类型的逻辑门$ V^\dagger G V $导致不同的模型. 注意, 这里是指某通用逻辑门集合中的基本逻辑门, 例如H和T, 它们的组合可以构成任意的逻辑门. 与通常的考虑不同, 这里的编码可以是静态的(非含时), 也可以是动态的(含时). 例如, 含时幺正类是指$ V(t) $会发生幺正的连续变化, 一个例子是绝热量子过程^[26]. 非幺正类是指编码会发生非幺正的变化, 这里主要考虑编码是一个集合的情况$ \{V_i\} $, 即会从一个码向另一个码转换, 这被称为码转换机制^[67].

逻辑门的一个基本性质是其深度(depth), 这是相对于编码后系统的大小而言的. 顾名思义, 深度是指实现它所需的时间或步数, 对于逻辑门实现过程中的容错性是至关重要的. 例如, 单步(transversal)幺正的形式是$ \otimes_n U_n $, 即全局直积形式, 它不会将局域的噪声扩散, 因而容错性较好. 因而, 本文区分了单步、多步(local finite-depth)和高步(high-depth)三种基本形式, 其中多步是指有限的定域的步数, 高步是指其步数和系统大小相关. 例如, 拓扑量子计算中的非阿贝尔任意子的编织操作(braiding)的深度是线性的, 它属于非含时幺正类家族中的高步类型模型^[27]. 这个家族中的另外两种模型也得到了研究, 其中单步模型可以描述量子计量(metrology)模型^[68], 多步模型可以描述大多数的编码方式, 例如一种基于多粒子的量子游走(quantum walk)模型^[59]. 另外, 也可以采用资源理论来刻画第II类模型, 即对逻辑门的集合$ \{V^\dagger G V\} $进行分类(比如对深度的刻画), 这还有待更深入的研究.

一个完整的既考虑通用性又考虑容错性的 模型需要将以上两类模型结合起来. 例如, 人们 最常用的是结合线路模型和某种固定的编码模 式, 比如一些稳定子码^[2], 但这不一定是最好的方式. 我们看到, 原则上来讲有很多等价的通用量 子计算模型, 如果再考虑到有不同的物理实验平台、不同的实现量子门的物理方式以及模型之间可以有各种混搭方式, 则会产生更多种类的计算方案. 在实际中, 人们会进行特定的选择. 这也说明了量子计算研究的丰富性和复杂性. 总之, 模型的分类表使得对实现通用量子计算的理论方案的研究系统化起来, 可以有原则地去定义和认识一个模型, 发展更多计算方案. 下面重点讨论第I类模型, 介绍每个家族的性质及每个模型的具体形式和 特点.

初始空段落

哈密顿家族依赖于定域的哈密顿量相互作用形式, 并假设每个相互作用项都可以被打开或关闭(on or off). 对于算法而言, 其输入态可以看作是某哈密顿量的本征值:

而算法本身是对哈密顿量的改变, 继而相当于是对态的改变. 那么, 考虑定域哈密顿量相互作用的集合以及对它们的操作, 类比于量子态振幅上的操作, 可以引入哈密顿家族. 它包括哈密顿量子模拟、哈密顿量子元胞自动机和绝热量子计算模型.

哈密顿量子模拟是指用有限的相互作用形式来构造其他的哈密顿量, 在哈密顿家族中, 它允许最一般的构造方式. 如果限制相互作用项的结合方式, 比如只能采取并行(parallel)的办法, 那么就给出了哈密顿量子元胞自动机模型. 根据通用资源的转化关系, 它所依赖的相互作用可以用哈密顿模拟来制备. 若进一步要求只能采取绝热的方式, 则导致绝热量子计算, 其通用的相互作用形式则比较复杂, 比如人们常用的Feynman-Kitaev哈密顿量形式^[88].

哈密顿量子模拟很早就被人们考虑^[7,37,89,90], 但是一般被放在线路模型的框架下. 独立考虑哈密顿量本身的通用性的工作是近些年完成的^[91-93], 即研究什么样的相互作用可以实现其他任意的相互作用形式. 其基本思想是利用Trotter分解形式将所需的哈密顿量:

及其演化$ U = \text{e}^{\text{i}Ht} $表示为一系列$ \text{e}^{\text{i} t_n j_n h_n} $的乘积^[37]. 其中, $ h_n $可以只是有限的几种相互作用形式. 已被证明, 几乎任意的两体相互作用都是通用的^[91-93]. 在实际中, 与线路模型相比, 人们对相互作用的控制不一定优于量子门. 这个模型与多体量子物理的关系可能更为紧密, 比如在哈密顿量复杂性方面^[93].

人们更为熟知的哈密顿演化模拟和仿真模拟可以看作是这个模型的简化应用. 在量子算法中, 哈密顿演化模拟^[94]主要是为了将某演化$ U = \text{e}^{{\mathrm{i}}Ht} $(或含时的形式)分解为一系列更小的演化, 但不采用通用的相互作用集合. 另外一个情况是所谓的仿真模拟(analog simulation或emulation)^[95], 它对局域相互作用的可控性的要求更低. 这种情况主要适用于某些特定的物理系统, 用于对特定的专门问题的研究.

如果对哈密顿项的操作受限, 则可以引入新的计算模型. 一个自然的选择是采用并行的开关这些相互作用. 为了达到通用性, 相应地, 需要的基本哈密顿量形式会更复杂一点, 这就导致了哈密顿元胞自动机模型^[25]. 它需要一维的系统, 其中每个位置上有两个比特(一个是数据比特, 另一个是辅助比特)和一个三能级系统(qutrit), 其基本相互作用为

其中第一部分作用在辅助比特上, 而幺正算符

其第一部分作用在qutrit上. 最后,

作用在两个数据比特上. 其中, Ξ是数据比特上的SWAP门, 与W一起构成通用门集合$ \{\varXi, W\} $^[96]. 那么, 给定任意一个由W和Ξ构成的线路, 都可以由H (16)构成的元胞自动机来模拟. 值得注意的是, 以上复杂的形式只是为了证明其通用性, 在对具体问题的研究中不一定采用这种形式.

这个模型是经典可控的, 即它的并行相互作用可以开关. 虽然名为自动机, 但不是完全自动的演化形式(即$ \text{e}^{{\mathrm{i}}Ht} $). 之前的工作表明, 基于自动演化的模型不能确定性地达到所需的末态, 即使取消掉对并行性的要求^[28,97-100]. 另外, 也有基于门的元胞自动机形式. 总体来讲, 人们对这类模型的研究并不多^[29]. 一个有趣的事情是, 一维的量子模型可以是通用的, 但对经典模型而言, 必须是更高维的^[101]. 与经典情况类似, 元胞自动机模型的应用不如线路模型广泛, 但它常用于对动力学的模拟中^[102].

相比而言, 绝热量子计算得到了较多研究^[26], 这得益于人们对量子绝热过程和量子淬火(annealing)等的研究. 这一模型的通用性证明一般采用Feynman-Kitaev历史态方法^[88]. 即给定一线路$ U = U_L\cdots U_2 U_1 $, 将其转化为一个哈密顿量$ H_\text{FK} $, 其基态是历史态:

其中$ |\gamma_\ell \rangle = |\psi_\ell \rangle|\ell \rangle $, $ |\psi_\ell \rangle = U_\ell'|\psi_0 \rangle $, $ U_\ell' = U_\ell \cdots U_2 U_1 $, $ |\psi_0 \rangle $是初态, $ |\ell \rangle $是时钟态. 然后采用绝热演化使得基态$ |\gamma_0 \rangle\mapsto|\varPhi \rangle $. 历史态中包含真正的末态$ |\gamma_L \rangle $, 其实现概率可以被有效地提高, 但代价是更多的时钟比特和相互作用项. 可以看到, 由于对哈密顿项只能采用绝热的开和关, 它所需的哈密顿量形式即通用资源更为复杂. 在子空间$ \{|\gamma_\ell \rangle\} $中, 可以表示为一维的量子游走形式^[25].

在实际中, 绝热量子计算已被用于探索量子优势. 但是, 由于不能保证计算精度, 因而很难得到确定性的结果^[103,104]. 由于这一模型属于哈密顿类型, 因而它与哈密顿量计算复杂性相关. 例如, 一类哈密顿量是量子随机的(stoquastic), 当定域参数$ k\geqslant2 $时, 是复杂性类StoqMA的完全问题^[105]. 此外, 绝热过程还有更广泛的应用, 例如在绝热几何相和量子门中^[106], 主要是在线路模型的框架下来实现量子门. 由于其几何特性, 对噪声具有一定的鲁棒性, 可以用来增强绝热量子计算的容错性.

下面讨论测量家族. 注意, 这里是把测量作为资源来看待, 而在前面讨论的图态量子计算中测量是自由的操作. 其实, 测量家族也可以称为(准)概率家族, 因为它是基于量子信息的(准)概率表示或者叫相空间表示. 即将态展开为

其中$ \boldsymbol{\sigma} $构成一个厄密算符基, 继而ρ约化为矢量$ \boldsymbol{r} = (r_i) $, 满足$ \text{sum}(\boldsymbol{r}) = \displaystyle\sum\nolimits_i r_i = 1 $^[107]. 如果$ r_i \geqslant 0 $, $ \forall\, i $, 这种态可以被看作经典的概率分布. 那么相应地, 一个态的量子特性被刻画为取负值的$ \boldsymbol{r} $, 即Wigner准概率函数. 这种形式在量子光学、相空间表示理论中有广泛应用. 对于计算模型, 一个重要的结论是$ \boldsymbol{r} $取正值的纯态都是稳定子态^[108], 混合态则不然. 稳定子态上的自由操作是所谓的Clifford操作^[2]. 人们发现, 只需要提供足够多的T门的 “幻态”(magic state)$ |t \rangle: = {T}|+ \rangle $, 就可以实现通用量子计算, 这是所谓的幻态计算模型^[109]. 继而, 可以将其扩展为一个模型的家族, 包括直接依赖于Wigner负值的语境(contextual)计算模型和依赖于Popescu-Rohrlich非定域关联^[110]的模型.

测量的数学描述是POVM^[2]. 它通常是一个集合$ \{M_i\} $, 其中正定算符$ M_i\geqslant0 $满足$ \displaystyle\sum\nolimits_i M_i = {1 1} $. 给定一个态ρ, 对其测量会产生三种信息: 结果i, 它的概率$ p_i = \text{tr}(M_i\rho) $, 以及每个末态$ \rho_i $. 测量可以用信道来实现, 即令Kraus算子满足$ K_i^\dagger K_i = M_i $, 并且保留i的信息. 在实际中, 有很多不同名称的测量, 比如当$ \rho_i $被破坏时被称为破坏性测量, 当需要用辅助比特时导致间接测量, 当其中一个$ M_i $很接近于单位算符$ {1 1} $时, 称为弱测量.

测量家族的第一个模型是我们定义的语境计算模型^[25]. 语境性(contextuality)也称互文性, 等价于Wigner函数的负值性^[111]. 这个模型的核心思想是一类语境量子线路, 可以表示为

其中$ U_1 $, $ U_2 $作用的是辅助端, 也称为控制端或语境端, 另一端是数据端. $ CV $和$ CU $是两个控制门(也称复用门), 取块对角形式

其中$ P_i = |i \rangle \langle i| $是控制端的投影算符, $ U_i $作用在数据端. 整个线路可以看作是利用辅助端在数据上进行的测量来实现演化. 可以发现, 基本的量子门H, T, CNOT都可以表示为这种形式, 并且辅助端的初态都是$ |+ \rangle $, 测量是对Pauli X算符的测量$ M_X $, 所用到的门都是非相干的, 即不能产生叠加. 这就证明了这个模型的通用性.

这个模型的通用资源就是$ M_X $测量. 如果将初态替换为$ |0 \rangle $, $ |1 \rangle $或其概率混合, $ M_X $替换为$ M_Z $, 那么它只能制备经典的概率函数, 即Wigner函数都是正值. $ M_X $测量的作用类似于H门: $ M_X $相当于用H作用后的$ M_Z $, 给定$ |0 \rangle $态, $ M_X $可以产生$ |+ \rangle $. 其实, 它的作用是产生门的叠加. 通俗来讲, 定义量子语境性即为不同语境的叠加. 量子语境是指一个量子操作, 例如态制备、演化或测量^[112]. 当两个算符对易时, 它们就是兼容的, 因此可以同时存在, 可以被归约为经典的数或函数. 量子语境性指的是同时存在(即叠加)不兼容的量子语境. 那么, 经典语境性可以定义为量子语境的混合. 与量子线路模型类似, 其限定集都是经典线路, 因而其通用资源(即相干性和语境性) 是等价的资源.

由于这是一个新的模型, 目前对它的认识尚浅. 这里简要讨论几点. 首先, 语境线路可以看作是对量子传态和门的扩展^[113,114], 后者可以看作是利用测量进行计算或通信的源头, 它突出了测量结果即经典通信的重要性, 这也是贯穿整个测量家族模型的一个性质. 利用控制端产生门的叠加其实源于所谓的LCU算法^[19,115-118], 但它通常需要在控制端进行后选择, 因而是概率性的. 控制端(或单元)也是冯·诺依曼架构中的核心单元, 因而这两类模型之间也可能有某些联系.

量子幻态计算模型是采用一类特殊的Wigner正值态作为限定集, 即稳定子态. 这个模型是研究较早也较为成熟的, 它与稳定子纠错码的结合也比较自然^[109]. 按照在Pauli算符上的作用, 定义第k层的Clifford层级

其中$ {\cal{P}}_n $是n比特的Pauli群^[114]. $ {\cal{C}}^{(2)} $是Clifford群, 它是稳定子态集合上的自由操作. 因而, 为了实现通用性, 至少需要一个高层级的门, 例如T门和CCNOT门, 等价于某非Clifford测量. 采用稳定子码和隐形传态机制, 可以同时实现容错性和通用性^[119]. 然而, 在实际中, 实现容错性并不容易. 一是因为制备稳定子态及实现纠错在实验上是很大的挑战, 二是因为制备隐形传态所需的幻态(比如$ |t \rangle = {T}|+ \rangle $) 也需要提纯或纠错过程.

在以上两个模型中, 为了确定性地实现量子门, 经典通信都是必须的部分, 这其实说明了关联的作用. 有一种更强形式的关联, 称为Popescu-Rohrlich (PR)非定域性^[110], 它可以取代经典通信来实现T门的传递^[120]. 对于二进制的输入$ x, y $, PR过程的输出$ a, b $满足

其违反了CHSH不等式^[121], 超过了量子理论所允许的值. 基于此, 我们引入了非定域幻态(post-magical)计算模型^[25], 这里做简要概述. 非定域幻态计算模型可以看作是对图态量子计算的某种修改, 即把测量反馈的过程用PR关联代替, 因而可以实现即时的非定域计算, 具有单向保密性. 它的限定自由操作集是最小的, 只包括单比特的Pauli算符测量, 以及对测量结果的公布(broadcast)而不是双向通信. 那么相应地, 它需要PR关联以及某种形式的图态来实现通用性.

这一模型使得PR关联显得尤为特殊. 此前研究表明, 如果在隐形传态中不使用经典通信, 那么则需要指数级多的纠缠态^[122], 而这可以用少量PR关联代替. 而且PR关联不需要是完美的, 很小的超越量子的关联就可以取代经典通信^[123]. 目前, 人们对经典通信在量子计算中的作用并不是非常清楚^[124]. 例如, 在纠错和信道容量的研究中, 采用向后的单向经典通信和双向经典通信辅助的量子信道容量并不相同^[125]. 这也与交互式证明过程有关^[126], 一个值得探索的问题是, 是否存在有限次的交互式证明过程来取代PR关联, 并导致测量家族中一个新的模型.

信道家族模型的核心特性是利用量子信道来承载信息, 因而它们是存储程序式的模型即量子冯·诺依曼架构(von Neumann architecture). 根据信道-态对偶原理^[43], 量子信道等价于其Choi态(7)式. 在我们的模型中, 量子程序都表示为Choi态的形式, 计算过程由Choi态上的幺正操作和测量构成. 由于后面会重点分析此类模型, 这里着重讨论其资源理论的刻画^[127].

在前面讨论的三类模型中, 我们看到通用资源是由于采用了不同的定域性导致的: 若自由操作集较大, 那么通用资源就较容易制备. 对于信道的集合, 我们定义的三个模型分别依赖于存储(即单位逻辑门$ {1 1} $)、两体的存储(对应于纠缠逻辑门比如CNOT)和一种依赖于协变的量子测量的非定域操作^[127]. 它们所对应的自由集分别为纠缠损坏(entanglement breaking)信道、两体定域信道和单点信道. 这三个模型统称为量子冯·诺依曼架构, 记为模型I、模型II和模型III.

对于Choi态, 由于是由Bell态得到的, 其基本特性是纠缠. 一类信道是纠缠损坏信道^[128]:

其中$ \{M_i\} $是POVM, $ \sigma_i $是态. 这类信道的Choi态是可分态, 因而不能用于量子信息的传递. 我们知道, 经典计算可以描述为随机过程, 而任一随机过程$ \boldsymbol{p}\mapsto \boldsymbol{q} = S \boldsymbol{p} $都可以用某POVM$ \{M_i\} $来实现:

而这也是一种特殊的纠缠损坏信道. 因而, 我们定义模型I的自由集为纠缠损坏信道, 而所有不损坏纠缠的信道都是资源, 显然其中资源度最大的是幺正的演化, 它们的纠缠等价于Bell态.

实际上, 从存储的角度来看, Bell态是存储的基本单元^[129,130], 可以实现读写功能, 即用测量在其一端写入, 在另一端读出. 根据信道-态对偶, Bell态是作为动力学性质的资源, 这与态家族不同, 在那里纠缠态是作为静态的资源. 而纠缠的动力学对应其实是两体纠缠信道, 它导致我们定义的模型II. 考虑Choi态的定域性, 比如对于$ A|B $划分, 两体信道$ \varPhi^{AB} $是可分的, 当且仅当$ \omega_{\varPhi^{AB}} $是可分的 (注意这里的定域性和模型I不同). 因而, 类比于纠缠, 将两体可分Choi态作为自由集, 其上的定域操作加经典通信作为自由操作, 那么纠缠的两体信道则成为资源, 其中最大的可以用CNOT门来代表. 这个模型可以用来设计量子芯片的结构, 在后面第6节会详细讨论.

那么, 如何构造一个依赖于非定域的存储的模型III呢？一个自然的考虑是采用非定域的存储态, 可以将存储的程序直接恢复出来, 即(3)式可以近似地成立. 而前面两种模型是无法读出程序本身的, 只能得到某些观测结果. 这个问题其实和计量问题等价, 即程序的读取过程即是计量的过程^[34], 并且显然其精度受不确定性关系限制. 如果程序态系统的大小正比于n, 那么计算的精度正比于$ {1}/{n^2} $. 在较弱的意义下即对计算精度要求较低时, 这可以被认为达到了准通用性^[46]. 是否可以修正该模型而达到通用性是一个值得继续探讨的问题. 也不难表明, 这种方案也可以表示为Choi态上的操作^[127]. 后面讨论的量子冯·诺依曼架构主要是依赖于模型I和模型II.

前面在第2.1节已经介绍了量子线路模型的基本内容. 这里再简要讨论一下它的一些特点和不足. 从理论上讲, 不论是经典的还是量子的, 线路模型是非常基本的, 它是设计软硬件的基础, 其他种种计算模型都可以从线路模型的角度来理解. 加上量子线路易于经典控制(即每个逻辑门的时空位置可控), 也易于经典表示(即逻辑门的类型和时空位置可以表示为比特串), 导致它是目前最为流行的模型.

与其他模型相比, 线路模型也有一些比较隐蔽的要求, 比如它要求量子比特之间可以进行相互作用, 比特的相干时间要长, 足以支撑较深的线路. 这一点在实践中是有影响的. 如在超导线路中, 相互作用的量子比特之间的串扰是当前实验中的一个关键问题^[72].

在通用性之外, 线路模型没有很好地考虑其他要求, 包括模块化、可编程性、保密性等. 例如, 一个量子算法若被表示为一个线路图, 其中门的位置和类型是经典的信息, 若不加密则可以被随意地使用, 包括被敌对方使用. 对保密性的考虑是很多保密或安全计算模型的出发点, 如多方安全计算^[73]、盲量子计算^[74]及后面讨论的量子冯·诺依曼架构^[35].

从计算机的设计架构来看(图2), 线路模型主要用于机器语言层次上的硬件线路设计, 比如一些基本的数字和模拟电路. 而为了适应更高级的语言, 需要采用冯·诺依曼模型或架构. 所以, 从硬件的角度来看, 目前量子计算的研究还处于机器语言的层次, 甚至稳定的量子比特(即容错性)还没有严格实现.

在经典计算中, 图灵机模型是最早的模型之一, 对认识可计算性、算法甚至计算机架构都具有重要的意义. 相比而言, 人们对量子图灵机的研究很少. 主要原因是最初的量子图灵机模型较为复杂(例如采用全局相互作用), 且有一些问题^[66,75], 在此不赘述. 这里, 从资源论的角度出发, 即把线路模型依赖的相干性过渡为纠缠, 发现利用量子纠缠作为资源的模型是量子定域图灵机^[60]. 从数学上来看, 刻画纠缠的一个合适的形式是矩阵乘积态(11)式, 也可以表示为

其振幅被表示为对一系列算符A和一个边界算符B的乘积求迹. 这些算符所作用的空间是所谓的“bond space”, 可被称为纠缠空间^[69-71].

需要注意的是, 任意的态都可以写为如上形式, 其纠缠空间的维度可以是常数, 也可以随系统N的大小而改变. 一个态的纠缠对应于其纠缠空间上的性质. 而此纠缠空间可作为图灵机模型中的机器态(machine state)空间, 一个计算过程正是由此系统和数据单元一对一地相互作用完成, 数据单元之间不进行直接相互作用(这与线路模型不同). 然而, 这一模型在实际中的探索还相对较少.

历史上, 矩阵乘积态及其衍生的张量和神经网络主要应用在多体和统计物理中^[76], 在量子计算中的应用其实并不多. 从纠缠的角度来看, 与单纯的计算任务相比, 它在存储、通信等任务中的作用可能更明显, 比如在分布式计算中^[77].

图态量子计算也被称为 “one-way”模型或基于测量的模型, 即测量量子计算^[30,61,62]. 这一模型发现的也较早, 由于具有新颖性, 在当时也引起很大关注. 与线路模型不同, 它不要求设计各种不同的线路以及量子比特间的相互作用, 而是在给定某资源态上进行一系列的带反馈的定域测量, 它们导致的量子传门(gate teleportation)过程可以实现量子门^[78]. 由于测量是破坏性的, 一个计算过程会消耗资源态含有的资源. 这也解释了其名称中“one-way”的由来. 但从资源理论的角度来看, 将其称作基于图态或某种等价的资源态的计算模型则更为合适. 为了避免与测量家族产生混淆, 本文通常将其称为图态量子计算. 另外, 它也带有一点存储程序(stored program)的色彩, 即多比特纠缠门是提前潜在地存储在了初始资源态中. 这些特点其实启发了我们发展量子冯·诺依曼架构, 因为量子传门和存储程序都是其中核心的内容^[79].

同时, 从资源的角度来研究通用模型这一研究思路也是受这一模型的启发. 因为, 人们很早就在研究这个模型中的通用性和通用资源态问题^[80,81], 例如何种图态是通用的. 并且, 人们还发现, 如果任给一个态, 它的纠缠度通常会很大, 但它不是这个模型中的通用资源^[82,83]. 这曾经导致关于量子计算的资源到底是纠缠还是干涉的争论.

近期, 我们首先表明通用资源态需要是特殊的类型^[63-65]. 用MPS表示, 它需要带有边界的形式:

然后满足纠缠空间上的单射条件(injectivity), 即在物理空间上的测量操作会导致纠缠空间上的任意幺正过程, 即态$ |\ell \rangle $可以演化为任意所需的态. 一类例子是具有对称性的情况, 这是多体物理中的对称性保护的态^[84-86]. 前面提到的簇态具有一维$ Z_2\times Z_2 $^[63]或者二维$ Z_2 $ 1-form对称性^[65], 而AKLT态具有SO(3)的全局对称性等^[69]. 参见文献[25]关于更多资源论的刻画.

在实际中, 这一模型在光学系统中广泛使用^[87], 因为相比于相互作用, 对多光子进行测量更好实现. 大规模的资源态的制备并不一定容易, 因而也可以实时地延续产生. 然而, 更理想的情况是资源态是给定的, 比如作为某多体量子物态, 但它对局域测量的要求目前还难以实现.

对于态家族, 根据资源理论, 如果在量子态上所允许的操作非常有限, 比如单比特操作外加经典通信, 那么为了达到通用性则需要某种纠缠态作为通用资源. 这可以用来定义图态量子计算^[30,61,62]. 当操作集扩大为定域操作, 这会使得通常的两体纠缠态成为资源^[57], 而这种计算模型被称为定域图灵机^[60]. 继续扩大操作集至可以实现通用的经典计算(比如采用Toffoli门), 那么能产生叠加的Hadamard门则成为通用资源, 对应于量子相干性^[58], 并用于刻画线路模型.

它们的通用资源符合转化关系(9)式. 即Bell态$ |\omega \rangle $可以由最大相干态$ |+ \rangle =\displaystyle \frac{1}{\sqrt{d}} \sum\nolimits_i |i \rangle $产生:

其中CNOT门在线路模型中是给定的自由操作, 而在定域图灵机中是一种资源. 同样, 采用图灵机中允许的定域操作, 可以从Bell态来产生图态量子计算中所需的纠缠态, 这些特殊形式的态包括二维的簇态(cluster)^[61] 以及AKLT态^[69]等. 它们是矩阵乘积态(MPS)^[69-71]的形式:

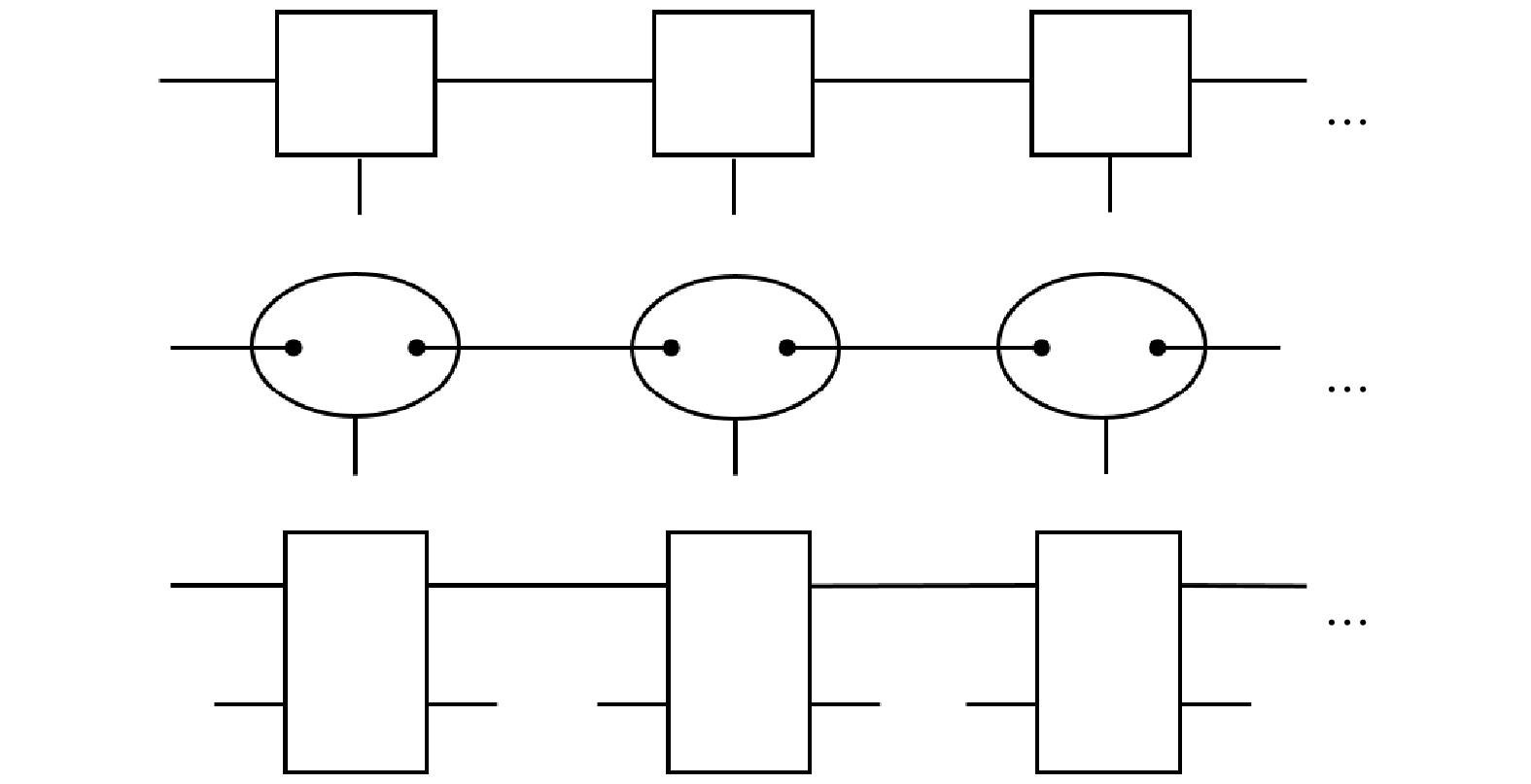
如图7所示, MPS有三种等价的表示方法, 由于其可以有效地表示任意的量子态, 因此有着广泛的应用, 这也可以从后面的论述中看出.

继续讨论第II类模型. 前面指出, 它是根据基本逻辑门的深度做的分类. 这类模型依赖于纠错码的性质, 特别是其支持的逻辑门. 注意, 这里主要是对标I类模型中的线路模型, 因为其他模型中的操作也可以约化为线路模型中的基本逻辑门和测量. 由于人们的认识并不成熟, 因而这里就不一一分析每个模型了, 仅对固定编码的情况进行较为详细的讨论.

在(非含时)幺正家族中, 需要固定一个编码方式, 例如某等距算符V, 它基本决定了最优的解码方式, 虽然在实际中可以采用不同的解码. 在此家族中, 单步模型的编码相对简单. 对于单一固定的精确码, Eastin和Knill^[131]证明, 单步逻辑门无法实现通用性, 因为单步逻辑门的个数是有限的. 在近些年, 人们发现这与对称性有关. 如果允许连续对称性, 比如U(1)或U(d), 这类所谓的协变码只能是近似码^[46-49], 并且纠错精度受到不确定性关系限制. 由于单步幺正操作不改变系统的纠缠, 这个模型所能制备的态的数量是有限的, 因而它不能实现通用性; 相反, 由于协变码是近似码, 它只能实现准通用性^[46].

更一般地, SU(d)群不一定是严格的对称性, 而量子计量(也称精密测量)方案则属于这种情况^[68]. 协变码也可以用在计量任务中, 它们的计算精度都受到不确定性关系限制. 计量不假设对称性, 它一般是指某含有未知参量λ的过程$ O(\lambda) $采用单步的形式作用在某资源态$ |\psi \rangle $上, 然后通过对某力学量的观测来估计λ的值.

另外, 在领域内人们有时候会把精密测量和量子计算并列作为不同的研究方向^[132], 这是在狭义的意义上, 前者更关注模拟信号(比如λ)的处理, 并且精度有限, 而后者更关注数字化的信息. 但广义上来讲, 它们都属于通用量子计算或量子信息科学的研究范围.

多步模型可以描述更多的纠错码情况. 比如, 对于一般的稳定子码, 其逻辑的Pauli X和Z一般是单步的, 有时H, S, CNOT, 甚至T门也可以做到单步, 但是不能同时做到单步^[131]. 在多步门的实现过程中会存在纠错的问题, 因为它远离了码空间. 这是一个重要的问题, 一个解决办法是结合码转换的思想, 在实现过程中形成其他的纠错码, 这样依然可以进行纠错^[133].

另外一种值得关注的方法是借用哈密顿模拟和时空转化的思想, 即将线路演化的方向看作空间, 将逻辑门看作哈密顿量的演化, 将逻辑比特看作哈密顿量的激发态. 这样, 单一的逻辑门都是多步的形式, 这其实是哈密顿形式的多粒子量子游走模型^[28]. 例如, 哈伯德(Hubbard)模型被证明是通用的模型. 当然, 也可以把空间方向打散, 即不采用规整的晶格结构来排列比特, 而是类似于线路模型, 依然将时间方向作为真实的演化方向, 而每个逻辑比特和逻辑门则被存储在一小块系统中, 类似于光学系统. 这需要对系统的激发态及其相互作用的精准控制^[59].

从纠缠的角度来看, 多步的有限深操作可以改变系统的短程纠缠, 而高步操作可以改变系统的长程拓扑纠缠^[134]. 在高步模型中, 发展最为成熟的是拓扑量子计算^[27], 它也有望成为未来通用量子计算机的硬件基础. 对于阿贝尔任意子的情况, 例如表面码^[52], 编织操作并不是高步的, 它也不能实现通用性. 真正通用的是非阿贝尔任意子(例如Fibonacci)的编织操作, 这种过程需要准绝热地实现, 其步数和系统大小成正比^[135]. 但拓扑系统无法实现自纠错^[136], 即在有限温度下, 系统的拓扑信息会被破坏, 热激发有一定的概率导致逻辑错误. 在编织过程中, 需要避免任意子与热涨落产生的任意子相互影响. 虽然拓扑系统(例如分数量子霍尔体系)在实验上已经实现, 但实现任意子的编织是一大挑战^[137].

对于动态码, 人们的认识较浅. 相比于静态码, 动态码的好处是增加了一个可控的维度, 因而更容易实现纠错和通用性. 但它为外加的控制(幺正或非幺正)提出了更高的要求. 人们已经发展了很多较为成熟的含时的控制方法, 包括动力学解耦^[51]、Floquet控制^[138]、绝热演化^[26]、几何相^[106]以及采用测量的方法等^[67]. 其中, 动力学解耦由于不消耗额外的辅助比特, 其纠错能力是近似的^[139]. Floquet控制可以看作是对它的一个延伸. 例如, 在多体码方面, Floquet多体物态可以用作纠错码. 绝热演化主要是被看作I类模型, 但也可以用绝热手段实现码空间的演化. 目前采用几何相主要是在物理层面构建量子门, 但也可以推广到逻辑层面, 这还有待于继续研究.

对于动态码非幺正转换的情况, 也可以区分为连续和不连续两类, 与前者相关的是有耗散计算模型^[140], 与后者相关的是测量量子计算^[61]和基于测量的码转换方法^[67]. 目前, 耗散计算模型主要用于量子态的制备, 对于如何在逻辑层面实现码的转换研究较少. 测量量子计算主要是被看作I类模型, 但也可以看作是一种单步的基于测量的码转换方法, 例如从一个图态码到另一个图态码的变化. 基于测量的码转换可以看作是对其推广, 并导致了通用量子计算方案, 例如将Reed-Muller码和Steane码结合可以实现通用的单步逻辑门集合^[141], 这对于单一的码是不可能的. 动态码的转换过程可以看作是实现逻辑门的消耗, 计入其门的深度, 因而也可以区分为三类模型.

总之, 相对于静态码而言, 动态码具有更大的自由度, 在技术上与静态码相比有不同的要求. 由于它是将很多码结合起来, 因而可以优于单一的码, 这是未来值得发展的方向.

本节着重讨论量子冯·诺依曼架构^{[35,79,127,142]}, 包括量子的输入、输出、通信、控制、存储和计算单元. 理论上, 它需要克服在量子程序存储单元^[33]和量子控制单元^[143]构建上的不可能定理. 近期的理论研究表明, 这些困难是可以克服的, 进而使得通用的量子冯·诺依曼架构成为可能. 其通用性也是由对量子线路的模拟来证明, 即任给一个量子线路, 都可以由冯·诺依曼架构中的基本操作来实现, 包括由测量驱动的读写即输入输出, 以及基于量子传门过程的门的组合. 与线路模型乃至其他模型相比, 冯·诺依曼架构更多地考虑到了模块化、可编程性、保密性等要求. 这里重点分析与存储和控制相关的过程. 另外, 我们的分析只局限于理论上, 不涉及如何在具体系统上的实现以及更多细节, 比如存储的类型等.

前面的研究表明, 采用Choi态来存储程序可以绕过Nielsen-Chuang的不可能定理^[33]. 即与得到某程序U在态上的作用不同, 我们只要求得到其在某力学量上的观测结果. 根据信道-态的对偶原理, 信道或程序$ {\cal{E}} $在态ρ上的作用通过如下方式实现:

其中$ \rho^{\mathrm{t}} $是ρ的转置, $ \text{tr}_\text{B} $作用在$ \omega_{{\cal{E}}} $的第二部分. 我们一般只考虑幺正的程序过程, 有$ |\omega_{U} \rangle = (U\otimes {1 1}) |\omega \rangle $, 或简记为$ |U \rangle $. (27)式中$ \rho^{\mathrm{t}} $可以由测量过 程$ \{\sqrt{\rho^{\mathrm{t}}}, \sqrt{ {1 1}-\rho^{\mathrm{t}}}\} $实现, 这是一个初态的写入过程. 计算结果是对于某观测量的测量, 即$ \text{tr}(A\rho_{\mathrm{f}}) $, 这要低于得到整个末态$ \rho_{\mathrm{f}} $的要求.

例如, 对于纯态的情况, 假设初态为$ |0 \rangle $, 则需要计算

那么, 初态是由$ \{P_0, P_{\bar{0}}\} $写入, $ P_{\,\bar{0}} = {1 1} - P_0 $. 读取是由$ \{|\psi_i \rangle \langle \psi_i|\} $实现. 这里, 测量的随机性已经被考虑进去: $ P_0 $会得到$ p_i $, $ P_{\,\bar{0}} $会得到$ p_i' = 1-p_i $, 二者是等价的^[79]. 当初态维度较大时, 也可以将初态有效地用一个二元的测量过程实现. 因而可以看到, 程序态都是二分的, 其中一端是写入端, 一端是读出端.

在模型中, 程序态可能是由经销商或他人制备并通过网络进行发送. 由于它是量子态, 因而对于外界具有保密性, 后文会详细分析这一点.

量子信息的通信(上传、下载等)是此模型中重要的部分, 它的实现也可以有多种方式. 这里讨论涉及到量子隐形传态和传门的过程. 量子传态可以表示为

即某未知态$ |\psi \rangle_\text{S} $经Bell测量$ M_\text{AS} $^[2], 其结果i用于Pauli算符$ \sigma_{i} $的纠正, 则可以把态从S传递到B系统上.

量子传态具有一个重要的对称性, 这表现在其Pauli纠正发生的概率都相同. 在输入端S上的Pauli的X和Z作用, 可以表示为末态上的Pauli的作用, 其对称性为$ Z_{\mathrm{d}} \times Z_{\mathrm{d }}$, 这其实也是一维的图态的全局对称性^[78], 我们知道, 它在计算中的应用就是基于量子传态机制. 更进一步, 利用通用量子传门机制^[79], 即根据对称性

其中$ U \in SU(d) $, $ [T_{ij}]\in {{SU}}( d^2) $是U的仿射表示^[144], 输入端的U可以通过测量端T的作用而传递到输出端, 使得

注意, 这里U已知, 在标准基下的测量是在T作用后进行的. $ |\omega_{U^{\mathrm{t}}} \rangle $需要用U的转置是因为性质$ (U\otimes {1 1}) |\omega \rangle = ( {1 1} \otimes U^{\mathrm{t}}) |\omega \rangle $. 那么, 采用这一机制以及程序上的读写, 就可以实现对任意算法过程(比如$ \langle \psi_f | U_n \cdots U_2 U_1 |\psi_i \rangle $) 的有效模拟, 进而证明这一模型的通用性. 在硬件上, 这一机制可以用于量子芯片的构造, 在6.3节进行详细介绍.

给定量子程序, 除了测量也可以对其进行更多的操作, 这也是冯·诺依曼架构中算法设计的基础. 由于程序是Choi态, 其上的一般操作是超信道^[40-42], 可以表示为

其中 ρ 是初态, $ {\cal{U}} $, $ {\cal{V}} $是幺正演化, a是辅助系统. 其中V的维度可以比U的大^[145]. (32)式也可以表示为在Choi态上的作用:

其中$ \tilde{{\cal{U}}} $与$ {\cal{U}} $等价^[35]. $ \text{tr}_{\bar{\text{S}}} $不作用在数据端S上, 一系列的超信道级联在一起得到所谓的量子梳(comb). 我们统称为超信道. 将信道-态对偶原理反复利用, 就会得到高阶的超信道. 可以看到, 纠缠比特(ebit)在实现超信道中起了关键的作用, 这也是其资源理论刻画的依据^[127].

量子控制单元是指一个可以控制量子程序实现的量子系统, 它的一个基本作用是将一个门U转换为受控$ \wedge_U $的形式. 起初, 人们发现, 对于任意的未知的量子门过程, 这是不可能实现的, 被称为不可控制定理^[143]. 因为它违反了量子的基本原则, 即它会把U的全局相位转变为有物理意义的相对相位. 其实, Kitaev^[88]最早发现, 如果假设知道U的某一个本征值和本征态, 则可以利用它作为辅助来实现控制过程, 即

其中$ U|\lambda \rangle = |\lambda \rangle $, $ f(U) = \wedge_\varXi ( {1 1}\; {1 1}\; U)\wedge_\varXi $, $ \wedge_\varXi $是受控交换门. 这一辅助排除了U的全局相位的因素. 因而, 与量子程序不同, 量子控制单元不需要借助测量来实现, 而是可以直接作为量子的输入信号. 整个量子冯·诺依曼架构的结构如图8所示. 与经典情况不同, 这里量子的控制流和信息流之间可以产生纠缠. 量子控制其实也可以被看作一类超信道过程, 只是其控制辅助端和数据端同样重要. 量子控制单元的作用还有待于进一步深入研究.

本节分析量子冯·诺依曼架构的基本特点, 包括模块化、保密性、可编程性以及整体的MPS结构. 这些特点可以通过与其他模型的一些对比中看出.

首先, 模块化是构造冯·诺依曼架构的一个基本出发点. 这在制造真正的计算机硬件方面是重要的, 当然在软件设计当中也有模块化的要求. 模块以及模块之间的接口是现在的计算设备中重要的组成部分^[12], 通常的线路模型并没有考虑这一点, 因为一般只考虑通用性这一个基本的理论要求. 模块化(与数字化, 参见2.1节)也是区分一个计算系统和一个物理系统的重要指标, 因为一个自然的物理系统(比如原子分子)一般不会按照功能区分为几个可替换的部分.

保密性是量子冯·诺依曼架构区别于经典计算以及其他量子计算模型的一个重要特点. 这里所说的保密性主要是基于量子的存储(以及量子通信), 或者说是通信中的保密性在存储方面的延伸^[146]. 由于量子程序是存储为Choi态的形式, 外在的窃听者只能通过测量获取Choi态的信息, 这将破坏程序. 在通信中, 程序制造商将Choi态发送给用户, 用户需要进行验证. 理论表明, 一定量的Choi态的份数可以满足验证的要求^[126,147], 同时保证不向用户泄露足够多的Choi态的信息, 即程序制造商可以同时做到对用户和第三方的保密.

保密性与所谓的盲量子计算不甚相同^[74]. 在盲量子计算任务中, 用户要委托给计算中心或经销商一个计算任务, 并不让它知道是什么计算(输入输出以及计算过程). 即用户知道程序的经典表示$ [U] $, 但经销商有能力实现U甚至制备$ |U \rangle $. 在冯·诺依曼架构中, 经销商一般同时知道$ [U] $和U, 用户只是可以利用$ |U \rangle $但不完全知道它的信息$ [U] $. 盲量子计算方式可能适用于量子计算的某个阶段或场景, 比如有限的量子计算中心向广大的用户提供安全的服务.

可编程性是对硬件的一个要求, 即同一个硬件构造可以实现不同的功能, 这在通用计算机的建造中起了关键作用, 同时也促进了很多技术中从模拟信号到数字信号的转变. 这里, 可编程的要求是一个过程或功能可以被存储为数据, 即将硬件转换为软件, 然后被进一步使用. 在线路模型中, 程序被表示为一个经典的线路“图”, 即$ [U] $. 例如, 在超导平台中, 可编程性是指同一个平台可以执行不同的程序$ [U] $, 这是经典的可编程性. 在我们的模型中, 量子程序被表示为Choi态的形式, 量子的可编程性是指同一个平台可以执行不同的程序$ |U \rangle $. 另外, Choi态的组合也是可控的. 例如, 可以根据控制信号选择是否将一个特定的Choi态组合进来^[127,142], 即它对应的门的开或关. 如果采用量子控制信号, 那么它也构成整个量子算法的一部分, 增强量子的可编程性.

从整体来看, 一系列的Choi态上的组合与MPS态的形式相关, 而后者在定域图灵机和测量量子计算中也扮演重要角色(见第4节). 我们知道, MPS态可以表示为一系列的张量(见图7), 一个张量既有物理指标, 也有虚拟即纠缠指标. 在冯·诺依曼架构中, Choi态可以看作是纠缠空间上的, 而CPU中的操作是构造了张量, 并对指标进行测量. 定域图灵机是只假设给定简单的纠缠比特, 然后通过构造张量来制备MPS态. 而测量量子计算一般是假设给定了MPS态, 通过对物理指标的测量来进行计算. 从这个角度来看, 冯·诺依曼架构可以看作是对这两个模型的扩展.

现有的经典电子芯片一般是根据冯·诺依曼架构来设计的. 硬件基础是半导体二极管、三极管等组成的电路. 从硬件的角度来看, 一个硬件可以执行多种功能, 例如存储数据、程序, 也可以作为逻辑门甚至模拟电路的部分. 如前所述, 其结构是模块化和层次化的, 有很多可编程的逻辑模块. 这为量子芯片的发展做了很好的范例.

下面举例说明当前量子芯片的一些结构特点. 在超导芯片中^[148], 量子比特作为硬件, 而量子门是根据比特和控制系统的相互作用实时产生的, 前面提到, 其可编程性是经典意义上的. 在量子光芯片中^[149], 量子门作为硬件, 而量子比特是利用激光实时产生的, 当然光子也可以在光纤或光腔等硬件中存储. 当前都是采用经典-量子的混合架构, 即把量子芯片作为计算单元, 而其他的数据处理部分都采用经典计算机.

采用量子冯·诺依曼架构理论可以对量子芯片的结构进行扩充, 即加入量子的程序和控制模块. 例如在超导平台中, 程序存储模块和控制模块都可以由超导比特组成, 这就打破了门和比特与空间和时间的对应, 即量子门既存在于空间(即硬件)中, 又存在于时间中(实时), 量子比特也是如此. 其实, 经典芯片已经做到了这一点. 程序模块中可以有体系较大的程序, 也可以是一些基本的门程序. 利用量子传门机制和超信道过程, H, T, CNOT门程序可以组成可编程的门阵列, 作为量子的FPGA的基本结构. 另外, 在硬件上也可以采用多种系统混搭的方式, 可以将不同物理系统的特性结合起来, 这也是目前人们探索的一个方向^[150].

与经典类似, 存储的类型也可以有多种, 例如内存、外存、闪存, 采用电、磁、光等物理方式. 外存一般采用磁盘或光盘, 由于其运行速度较慢, 现在的芯片都有内存. 当运行一个程序时, 一般是从外存中把数据导入到内存中, 最后才把最终结果存入外存中. 对于快速的计算, 内存或芯片中的量子比特的寿命其实不需要任意长. 然而, 如果需要稳定的量子外存, 那么需要从原则上克服退相干. 与磁盘的磁性状态对应, 人们并未发现能自纠错的量子系统^[136]. 若采用主动的量子纠错, 则需要较大的开销. 因而, 研究合适的量子存储器件也是实验上的一个重要方向^[151].

上面并没有严格区分程序、算法或过程这几个概念, 因为在数学上它们都可以被表示为幺正演化或信道. 在计算机中, 算法(algorithm)和程序(program)并不一样. 编程或程序的实现要依赖于编程语言, 例如机器语言、汇编语言和高级语言, 而算法是数学意义上的, 同一个算法可以用不同的程序实现. 笼统来讲, 两者都是计算机的软件方面.

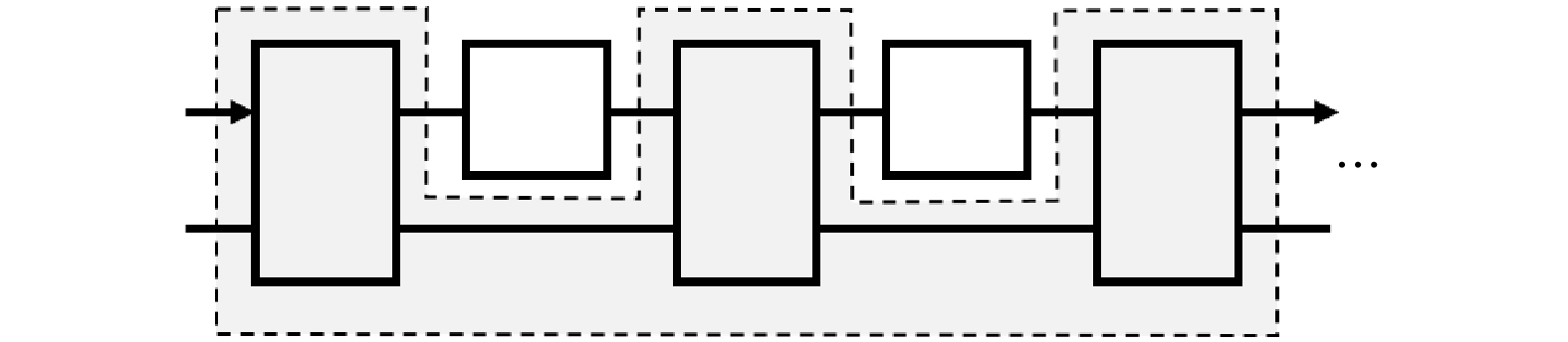
量子冯·诺依曼架构对软件的影响也可以区分为两点. 在程序方面, 它使得量子汇编语言成为可能, 而目前还处于量子机器语言阶段. 对语言的发展, 主要依赖于计算机科学家. 在算法方面, 类比于超信道之于信道的意义, 它使得设计量子超算法(super-algorithm)成为可能. 量子超算法的结构如图9所示, 是用一个量子的“母”算法去设计一个量子的“子”算法. 我们提到的线路模型中的算法结构(图3) 是它的特例: 其母算法是经典的或经典-量子混合型的. 需要注意, 虽然超算法也可以被当作普通的算法来看待, 就好比任意一个计算模型都可以用线路模型来模拟, 但将其作为超算法则会提供新的思路. 从资源理论来看, 它利用了量子存储或记忆作为资源^[127]. 在经典算法中, 超算法早已经被广泛应用, 例如人们熟知的机器学习算法.

人们已经发现的一些量子算法或方案都可以被看作是量子超算法. 例如, 量子信道区分方案是量子超信道理论最早的应用之一, 采用超信道而不是简单的信道可以提升某些信道区分的成功率^[152]. 近期提出的量子奇异值变换(QSVT)^[20]可以统一描述几种量子算法, 也是一种量子超算法^[59]. 其他包括量子博弈理论^[153]、计量方案^[154]、 量子优化^[155]、特别是量子机器学习^[156-159]. 机器学习是通过对大量样本的学习之后, 形成一个算法去解决问题. 相比于经典机器学习, 量子机器学习算法在某些高精度的计算问题中具有指数级的加速^[159,160].

本文从量子资源理论的角度研究了通用量子计算模型的分类问题, 并具体分析了某些模型, 例如量子冯·诺依曼架构. 其中有些模型的发展较为成熟, 而有些模型的发展才刚开始.

自DiVincenzo^[32]在21世纪初提出实现通用量子计算的基本要求以来, 人们发展了诸多通用量子计算模型或架构, 用于探究量子计算机的实现. 这些模型在量子算法设计、物理实现、应用场景等方面展现出了比通常的线路模型更为丰富的图景. 本文试图从量子资源理论的角度来系统地认识通用量子计算模型, 但至目前为止, 该研究尚不充分, 本文提到了存在的若干问题. 比如, 在非定域计算模型中用到了PR关联, 这超出了量子理论的范围, 是否能将其修正是值得研究的一个问题. 另外也忽略了对资源的度量问题. 发展最为成熟的是量子态的资源度量, 比如相干、纠缠等. 虽然其他类型的资源也可以转换为态的资源来度量, 但尚需具体研究. 由于篇幅所限, 本文未能详细分析分类表中将两类模型结合起来的具体方案, 这与所采用的纠错码密切相关.

在结束之前, 再来讨论量子资源与量子优势、通用与专用等问题, 以期对通用量子计算有一个更广泛的认识.

在量子计算发展的早期, 人们对量子计算的核心特性的认识并不清晰. 例如, 基于Shor算法、Grover算法等, 一些计算机学家认为量子加速的原因在于量子干涉^[161]. 然而, 在量子隐形传态、量子加密通信乃至量子计算中, 量子纠缠也起到关键作用^{[113,162,163]}. 稍后, 人们一方面在测量量子计算模型中表明大量的纠缠并不能导致通用性^[82,83], 一方面在线路模型中表明少量的纠缠就足以保证通用性^[164]. 与此同时, 也有研究认为量子加速的基础是量子的语境性^[165]. 我们的系统研究表明, 量子资源需要放在一个通用量子计算模型的框架中来认识, 它们之间并不能做简单的对比或替换. 相反, 它们都是可以被利用的量子资源, 研究它们之间的互相转换也是有益的.

量子优势来自于对量子资源的合理利用. 人们一般将量子优势等同于量子加速, 但它也可以体现在存储、保密、能耗、计量等其他方面^[142]. 例如, 保密是人们最早认识到的一点^[146], 量子通信的保密性和安全性, 以及与量子计算的结合依然是领域内研究的重要方向^[73,74,166]. 这有可能会避免现有的非量子网络中的一些安全问题. 在存储方面, Holevo^[167]从信息论的角度最先研究了量子比特和信道的通信能力(也是存储能力). 近期人们发现, 利用量子存储(或记忆)使得量子机器学习算法在某些问题中显著地优于经典算法^[159,160]. 人们也开始重点研究在能耗^[168,169]和计量精度^[68,132]等方面的量子优势. 然而, 人们目前尚不能以任意高的精度控制所需的量子体系, 这对近期量子优势的实现提出了挑战.

在通用量子计算的研究范式之外, 还存在专用的量子计算这一方向. 专用, 顾名思义, 是面向某类特定的问题, 它并不需要同时满足数字化、通用性、可编程性等要求. 但是, 也很难界定专用量子计算的范围, 一些研究方向的例子包括量子模拟^[95]、连续变量量子信息处理等^[170]. 在经典计算中也是如此, 并且, 专用计算模式也越来越受到了重视. 如图10所示, GPU、光芯片、忆阻器等在一些计算任务中展现出了优于现有CPU架构的一些优点. 这些专用计算模式可以看作从经典到量子通用计算的合理过渡.

由于当前实现容错性是有困难的, 因而发展专用量子计算也很重要. 例如, 在量子模拟中, 对某些量子多体物理现象的可靠模拟将有助于科学研究, 这些现象或模型(例如超导、哈伯德模型)大多很难在现有的计算机上求解^[171]. 为了提高模拟的可靠性, 也需要发展对错误的控制技术, 在这方面可以采用动力学解耦^[51]、错误估计和处理等方法^[172,173]. 另外, 对连续变量(光子、声子等)的研究也是必要的. 须知在经典领域, 模拟(即连续变量)电路一直伴随着数字电路, 在各种电子设备中扮演着重要角色.

尽管量子计算领域已经发展了30余年, 但依然面临着很多核心的挑战. 这些挑战大致属于基础理论、硬件和软件三个方面. 在理论方面, 量子信道的一些性质尚未完全清楚. 例如, 量子信道容量非常难以计算, 这是由某些奇特的性质(比如不可加性)导致的^[174], 这使得香农信息论的量子版本尚未最终建立. 信道容量是通信码率(带宽)的上确界, 对高效率的纠错码的设计具有重要的指导意义. 另外, 采用矩阵乘积态形式, 量子态的性质可以归结为信道的性质, 而少体量子纠缠态的分类问题尚未得到解决^[175], 这个问题与分布式量子计算也密切相关. 在硬件方面, 依然需要从根本上克服退相干, 实现大规模的量子纠错^[176], 而在软件方面, 需要发现更多的量子算法, 发展量子编程和应用软件等. 总之, 对通用量子计算模型的研究表明, 尚有很多量子信息的基本性质和应用等待我们去发掘.

感谢中国科学技术大学韩永建、北京量子信息科学研究院张江、李琳、山东大学仝殿民、于晓东、西安电子科技大学王云江、中国科学院数学与系统科学研究院骆顺龙和中国科学院物理研究所范桁等专家的宝贵意见, 感谢刘沅东、王楷等同学参与的讨论.