首页
登录
注册
-
超材料是由周期性或准周期性排列的亚波长大小的基本单位细胞组成的人工材料, 由于具有优异的电磁波操纵能力而引起了相关研究人员的极大兴趣[1]. 超材料可以通过波前整形[2]、极化转换[3]、相位调控[4]、幅度调控[5]等方式对电磁波进行自由操纵, 并产生了生物传感器[6]、雷达隐身[7]等诸多应用. 超表面作为超材料的二维对应体, 由于其低损耗、易于制造以及多用途等优点, 成为现代电磁调控领域的研究热点[8]. 2014年, “编码超表面”概念提出使超表面从模拟时代进入数字时代, 实现了电磁波的高效调控[9].
太赫兹波由于其独特的频谱特性已经在室内通信[10]、光谱成像[11]、医疗诊断[12]等多个领域展现出优异的应用潜力. 如何灵活有效地控制太赫兹波的振幅、相位、传播方式等特性实现多种波束调控功能被广泛关注[13–19]. Fan和Cheng[20]通过调整单元结构的几何参数得到不同相位, 并对得到的结构进行编码排列模拟实现了太赫兹波段的多种波束形态控制. 与改变单元结构的几何参数来调相的传统方法相比, 几何相位(PB)超表面可以通过旋转超表面单元结构顶层图案构造无色散相位梯度. 该方法不仅具有宽带特性, 而且避免了传统方法中复杂和繁琐的几何参数调整过程, 可有效提高设计和制造效率. 然而一旦设计完成, PB超表面的功能将固定无法动态调制, 这将限制PB超表面的可重用性, 造成资源浪费. 近年来, 基于相变材料的超表面被提出, 如Ge2Sb2Te5 (GST)[21]、二氧化钒(VO2)[22,23]、液晶[24]和石墨烯[25]等. 相变材料对环境非常敏感, 在外界条件的刺激下会改变其晶格态, 具有快速相变切换和相保持能力特性, 在PB超表面单元设计中加入相变材料实现PB超表面的可调性, 增强超表面的功能性和灵活性, 能够适应多样化的应用场景和需求.
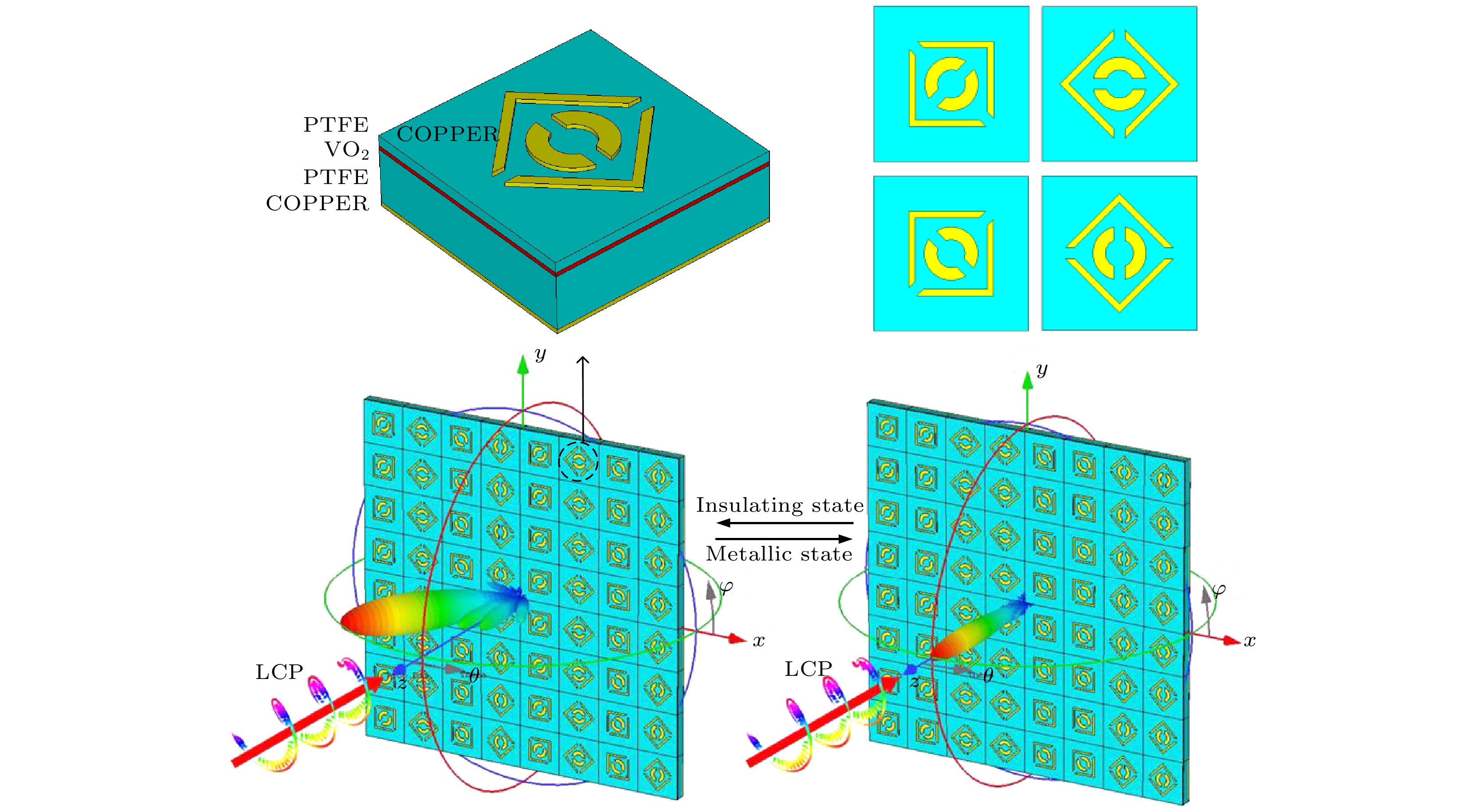
本文提出的波束转向可控反射型超表面, 结合几何相位和相变材料VO2两种相位调控手段, 在1.1—2.0 THz较宽频段内, 超表面可异常偏转垂直入射的圆极化(circularly polarized, CP)波, 且反射效率始终高于80%, 通过控制VO2绝缘态-金属态的转变, 可重构超表面的相位梯度, 实现偏转功能的开-关. 所设计的复合相位调控超表面可为太赫兹波束调控提供新的思路和方法.
-
当超表面单元结构关于X, Y方向镜面对称时, 各向异性反射型超表面单元的反射系数可以通过以线极化为基底的琼斯矩阵表示[26]
其中
$ \left| {{{r} _{xx}}} \right| $ ($ \left| {{{r} _{yy}}} \right| $ )/$ {\varphi }_{{xx}} $ ($ {\varphi }_{{yy}} $ )分别为x和y极化波入射下同极化反射系数的幅值和相位响应, 单元结构旋转角度α, 反射矩阵可以表示为当圆极化波入射到超表面单元时, 反射矩阵可以表示为
此时, 获得圆极化波入射到超表面单元上的反射系数为
式中, rLL和rRR分别表示LCP波和RCP波垂直入射到超表面单元上的同极化反射系数, rRL和rLR分别表示LCP波和RCP波垂直入射到超表面单元上的交叉极化反射系数. 从(4)式可以看出, 要实现最理想的反射性能, 单元需满足
$ \left| {{{r} _{xx}}} \right| \approx \left| {{{r} _{yy}}} \right| \approx 1 $ , (4)式可化简为由(5)式可以看出, 单元的同极化相位响应由x, y线极化波的相位响应和旋转角度α同时控制, 交叉极化的相位响应仅由x, y线极化波的相位响应控制. 基于以上理论分析为满足单元的同极化相位响应仅由旋转角度α单独控制, 单元设计需要满足3个条件: 1) 超表面单元结构关于X, Y方向镜面对称; 2)
$ \left| {{{r} _{xx}}} \right| \approx \left| {{{r} _{yy}}} \right| \approx 1 $ ; 3)$ {\varphi _{xx}} - {\varphi _{yy}} = {\text{π}} $ . -
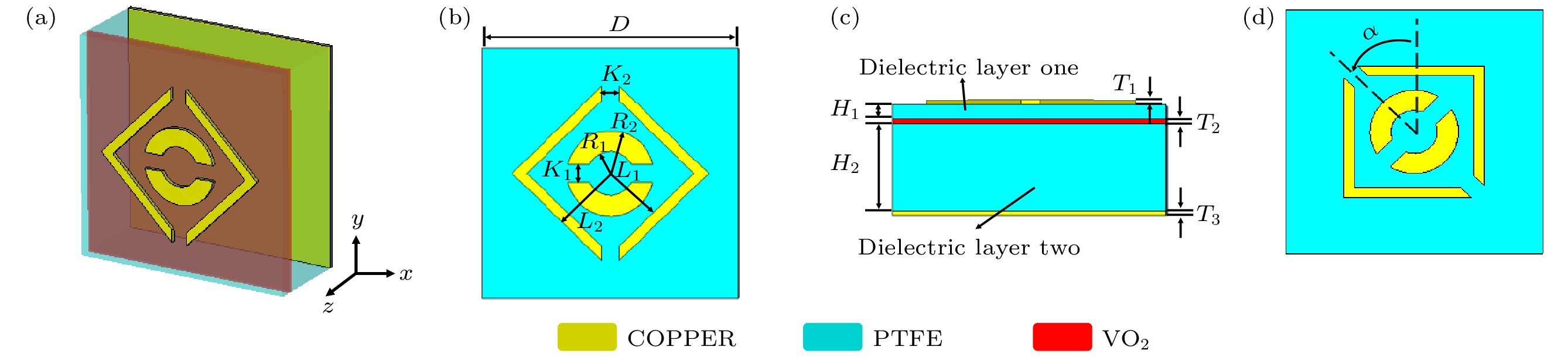
本文拟利用PB相位原理和VO2相变材料的复合相位调控机制, 在宽频带范围内实现太赫兹波束转向的控制. 基于上文理论分析, 本文设计的镜面对称单元结构如图1所示. 超表面单元的顶层和底层金属由Cu组成, 介质层一和介质层二材料相同, 为聚四氟乙烯(PTFE), 其相对介电常数为
${\varepsilon _{\text{r}}}$ = 2.1+0.0002i, 介质层一和介质层二的中间夹层材料为VO2, α为逆时针旋转角度. 表1列出了设计的超表面单元的主要参数.设计的超表面单元中加入VO2, 在太赫兹频率范围内, VO2的介电常数可以使用Drude模型表示[27]:
其中
$\gamma $ = 2.75×1013 rad/s,${\sigma _{0}}$ = 3×105 S/m,${\varepsilon _\infty }$ = 12,$ {\omega _{\text{p}}}\left( {{\sigma _{0}}} \right) $ =1.4×1013 rad/s. 常温时, VO2处于绝缘态, 电导率${\sigma _{{\text{V}}{{\text{O}}_{2}}}}$ = 200 S/m. 当温度超过68 ℃时, VO2转化为金属态, 电导率${\sigma _{{\text{V}}{{\text{O}}_{2}}}}$ =2×105 S/m[28].当VO2为绝缘态时, 结构单元的顶层贴片结构使x极化波和y极化波产生不同的相位响应, 可实现独立相位调控. 为了拓展超表面单元的工作带宽, 采用CST优化器和参数扫描工具进行优化. 首先, 设置优化目标为
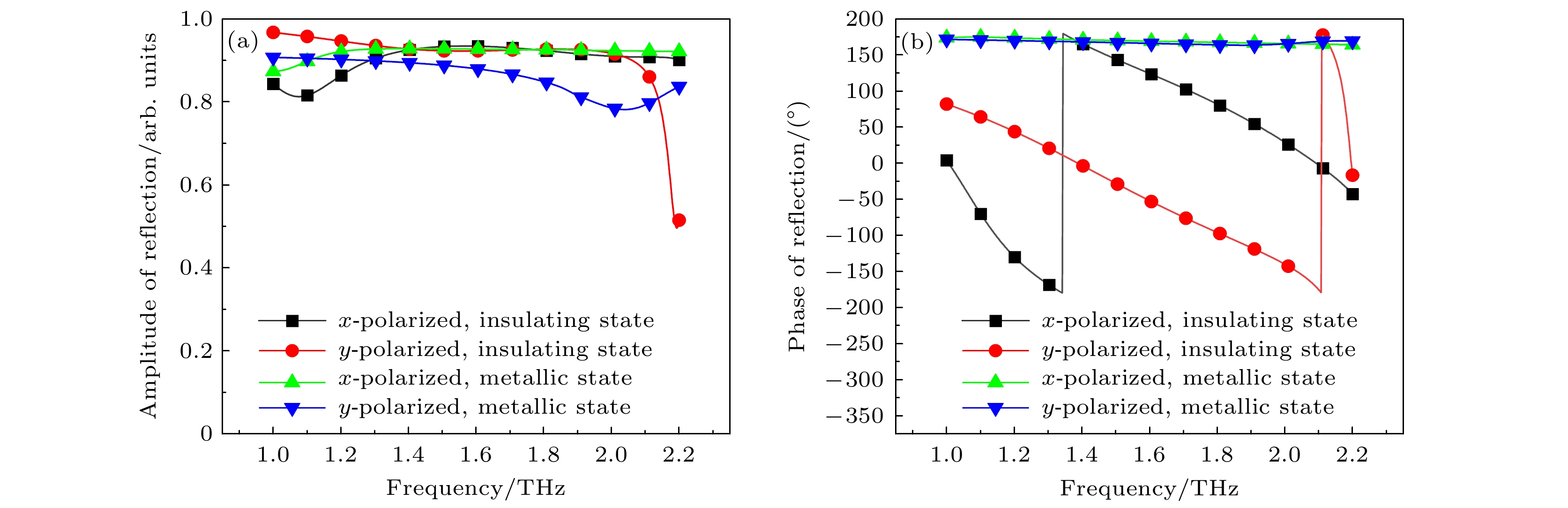
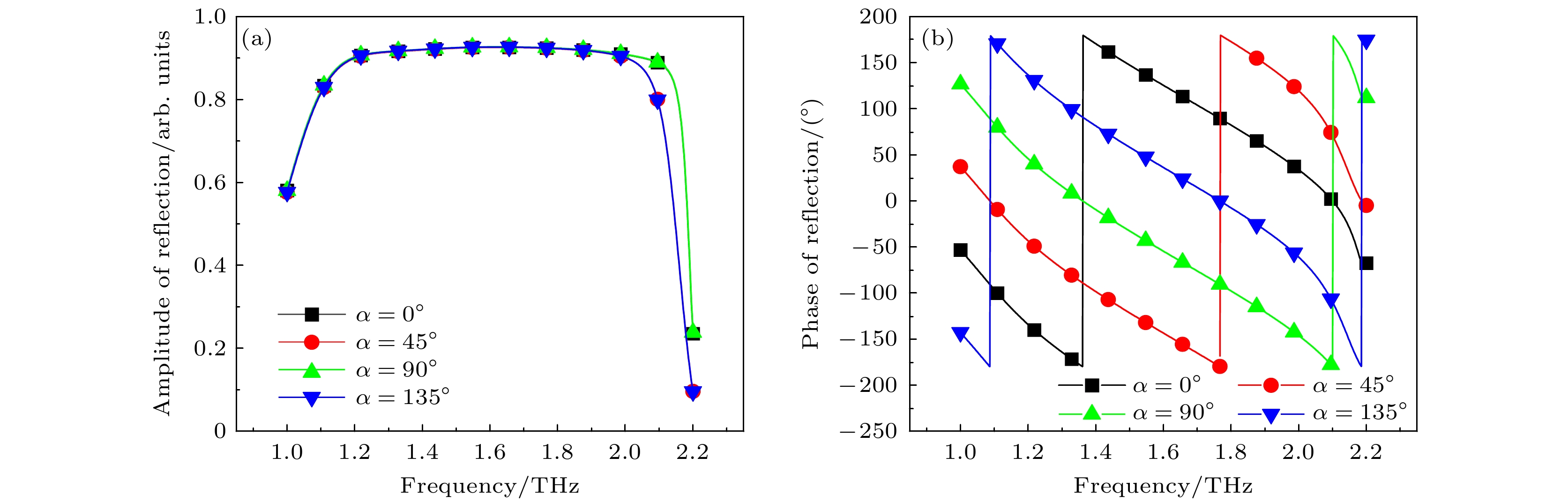
$ {\varphi _{xx}} - {\varphi _{yy}} = {\text{π}} $ 和$ \left| {{{r} _{xx}}} \right| \approx \left| {{{r} _{yy}}} \right| > 0.8 $ , 利用优化器获得一组结构参数. 随后在该组参数附近利用参数扫描功能, 选取了相位差约为180°的最宽范围, 确定了最终的参数设置, 如表1所示, 此时单元的同极化反射幅度和相位如图2所示, 单元的工作频带范围为1.1—2.0 THz. 当VO2处于绝缘态时, 对于垂直入射的x极化波和y极化波, 设计的镜面对称单元结构在1.1—2.0 THz的频率范围内反射幅度大于0.9且相位差始终接近180°, 满足PB相位原理. 因此超表面单元的顶层结构旋转一定角度α时, 将产生相应的相移$ \pm 2\alpha $ . 调整旋转角度得相邻相位差为90°超表面单元, 对应的旋转角度和俯视图见表2.对得到的超表面单元进行仿真分析, 左旋圆极化(left-circularly polarized, LCP)波垂直入射时, 不同旋转角下的编码超表面单元的反射幅度和相位如图3所示, 图3(a)说明在1.1—2.0 THz的频率范围内, 不同旋转角度的超表面单元反射幅度基本一致, 图3(b)说明当旋转角以45°为间隔从0°变化至135°时, 相邻的超表面单元之间的同极化反射相位差恒定90°. 编码超表面单元对入射的LCP波和右旋圆极化(right-circularly polarized, RCP)波具有相似的特性, 本文仅分析LCP波入射的情况. 而当VO2处于金属态时, 在1.1—2.0 THz的频率范围内, 相邻的单元结构的反射幅度大于0.8, 但相位基本一致无相位差, 不满足PB相位原理.
-
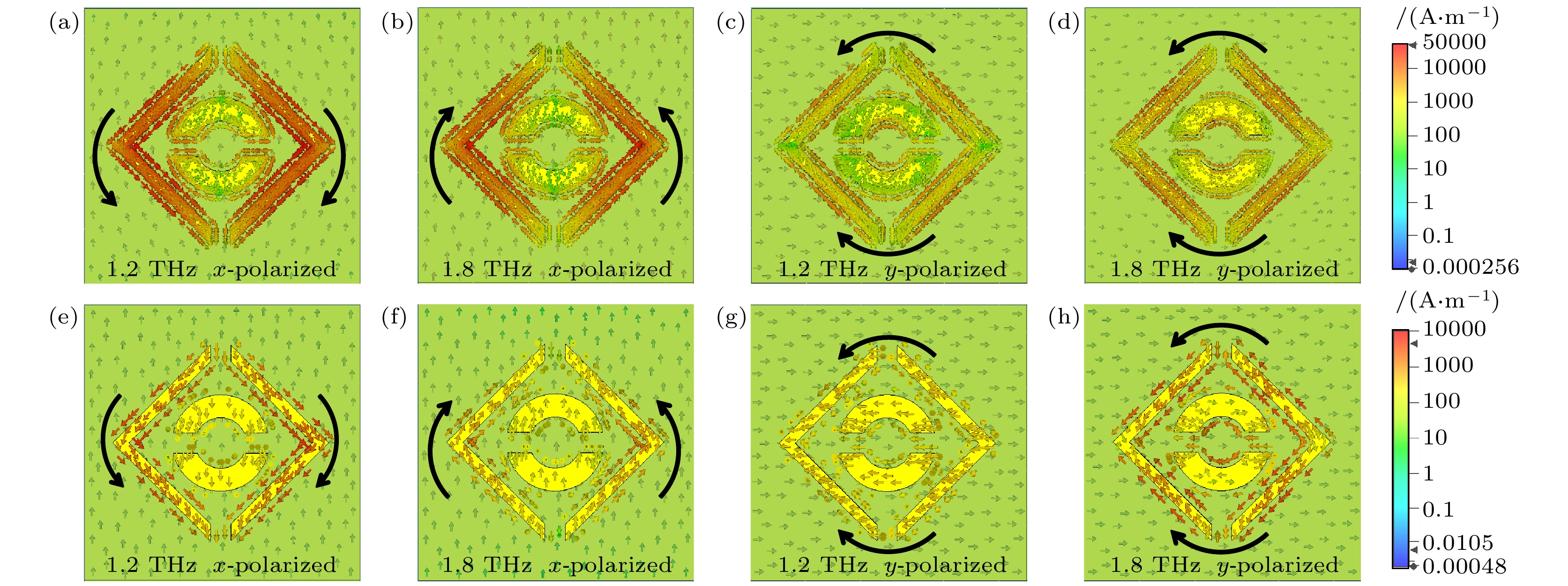
若超表面单元顶层结构具有某个方向上的对称性, 就可以视为该方向上的偶极子[29,30], 本文设计顶层镜面对称的超表面单元结构, 该结构沿着x轴和y轴均对称, 因此可以看作是这两个方向上的偶极子. 采用CST软件对设计的超表面单元结构进行仿真分析, 计算单元结构的电流分布等参数. 当VO2为绝缘态时, 图4(a)—(d)绘制了1.2 THz, 1.8 THz正交极化波垂直入射下顶层金属图案和底板的电流分布, 当VO2变为金属态时, 图4(e)—(h)显示了同样条件下的电流分布情况. 从图4(a)可以看出, 此时单元顶层金属图案和底层的电流方向存在反向平行关系, 产生磁偶极共振; 图4(b)中单元顶层外结构和单元底层的电流方向相同, 产生电偶极共振; 图4(c), (d)可以发现此时单元顶层结构和单元底层的电流方向均反向平行, 产生磁偶极共振. 单一的共振模式一般只在特定的频率范围内有效, 设计的结构在不同的频率处激发电偶极和磁偶极共振可以覆盖更宽的频率范围, 扩展整体的响应带宽[31]. 因此, 当VO2为绝缘态时, 设计的超表面单元结构具有宽带宽特性. 图4(e)—(h)表明, 超表面单元顶层结构和底层的电流方向同样反向平行或相同, 形成偶极共振, 这说明VO2的相变不影响单元结构的宽带宽特性.
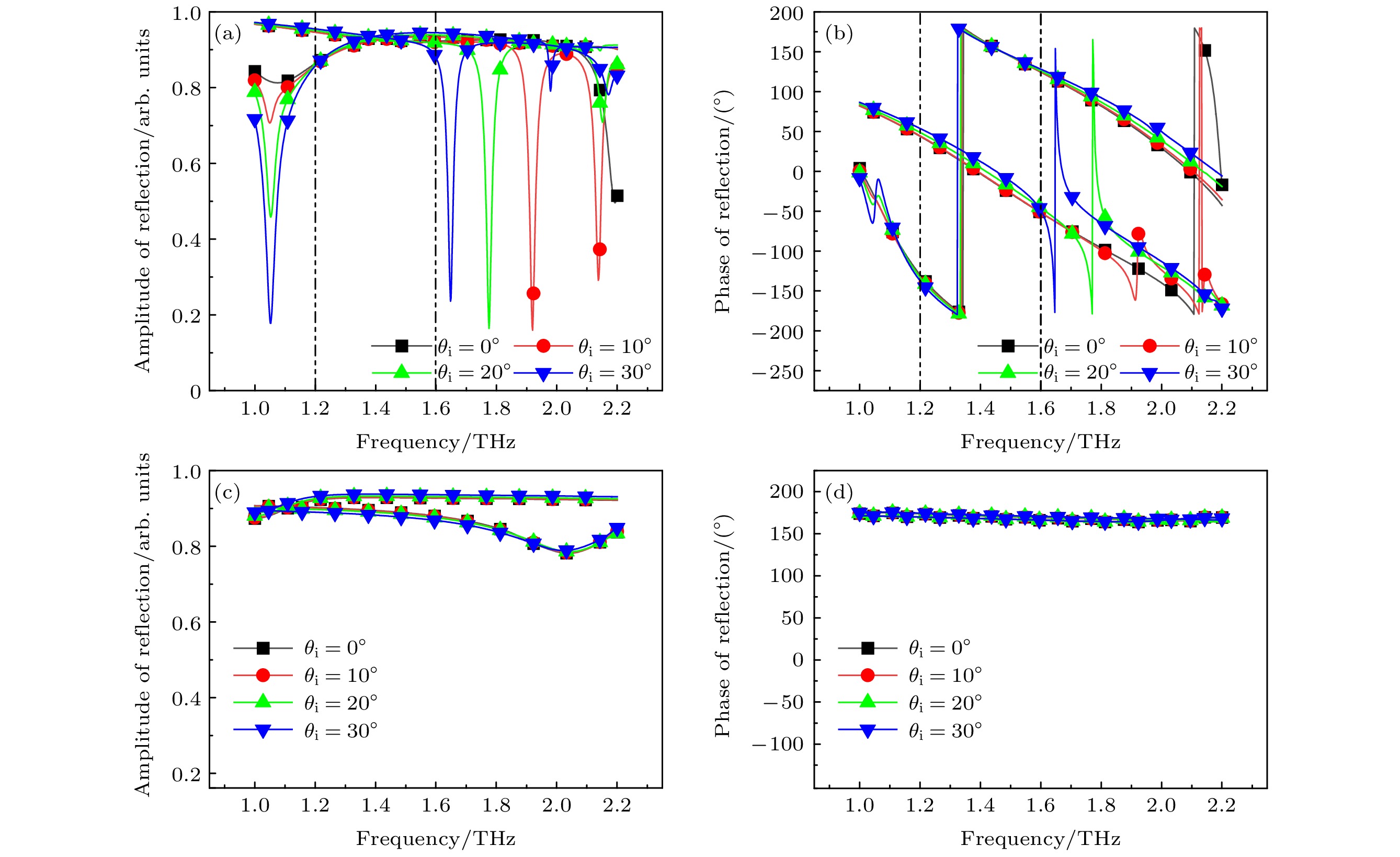
为对超表面单元结构的反射和相位调控能力验证, 我们对该单元在30°内线极化波斜入射下的激励情况进行全波仿真. 仿真结果如图5所示, 图5(a), (b)说明, 当VO2处于绝缘态时, 斜入射角度对单元结构的反射和相位调控能力有一定影响, 但当入射角
$ {\theta _{\text{i}}} $ < 30°时, 该超表面单元在1.2—1.6 THz能够保持较为稳定的相位差且幅度基本一致. 当VO2处于金属态时, 图5(c), (d)说明当入射角$ {\theta _{\text{i}}} $ < 30°时, 斜入射角度对单元结构的反射能力和相位调控能力基本无影响. 因此得出结论, 当入射角$ {\theta _{\text{i}}} $ < 30°, VO2处于绝缘态时, 设计的超表面单元满足PB相位原理, 超表面偏转功能可在1.2—1.6 THz范围内正常工作; 当VO2处于金属态时, 超表面反射功能可在1.1—2.0 THz范围内正常工作. 仿真结果验证, 该超表面具有一定的角度稳定性. -
当平面波垂直入射编码超表面时, 其远场函数可用(7)式来表示[9]:
式中θ和φ为俯仰角和方位角, K为传播常数, D为单元尺寸,
${f_{\text{e}}}\left( {\theta , {\text{ }}\varphi } \right)$ 为单个单元的远场函数,$\varphi \left( {m, n} \right)$ 为第(m, n)个单元的相位.依据(7)式和(8)式可以设计具有固定相位差的超表面单元从而实现多样化的太赫兹远场波束形式, 且随着bit数增大, 编码超表面调控太赫兹波的形式更加灵活.
费马定理表明光是沿着光程为极值(极大、极小或常量)的路径传播的, 可表示为[32]
式中
$ {\theta _{\text{i}}} $ 为入射角,$ {\theta _{\text{r}}} $ 为反射角,$ {n_{\text{i}}} $ 和$ {{n} _{\text{t}}} $ 分别为入射空间和出射空间介质的折射率,$ {\text{d}}\varphi $ 和dx分别表示光路在分界面上相邻点的相位差和距离, 当分界面x轴方向上的相位变化率$ {\text{d}}\varphi $ /dx固定时, 可推导出广义斯涅尔反射定律[33]:由(10)式可知, 通过不同的相位差
$ {\text{d}}\varphi $ 或不同的编码序列周期dx获得不同的相位梯度, 可以任意控制反射波束的传播路径. 因此, 通过建立相位梯度超表面, 可利用广义斯涅耳反射定律获得反射波束偏转角为 -
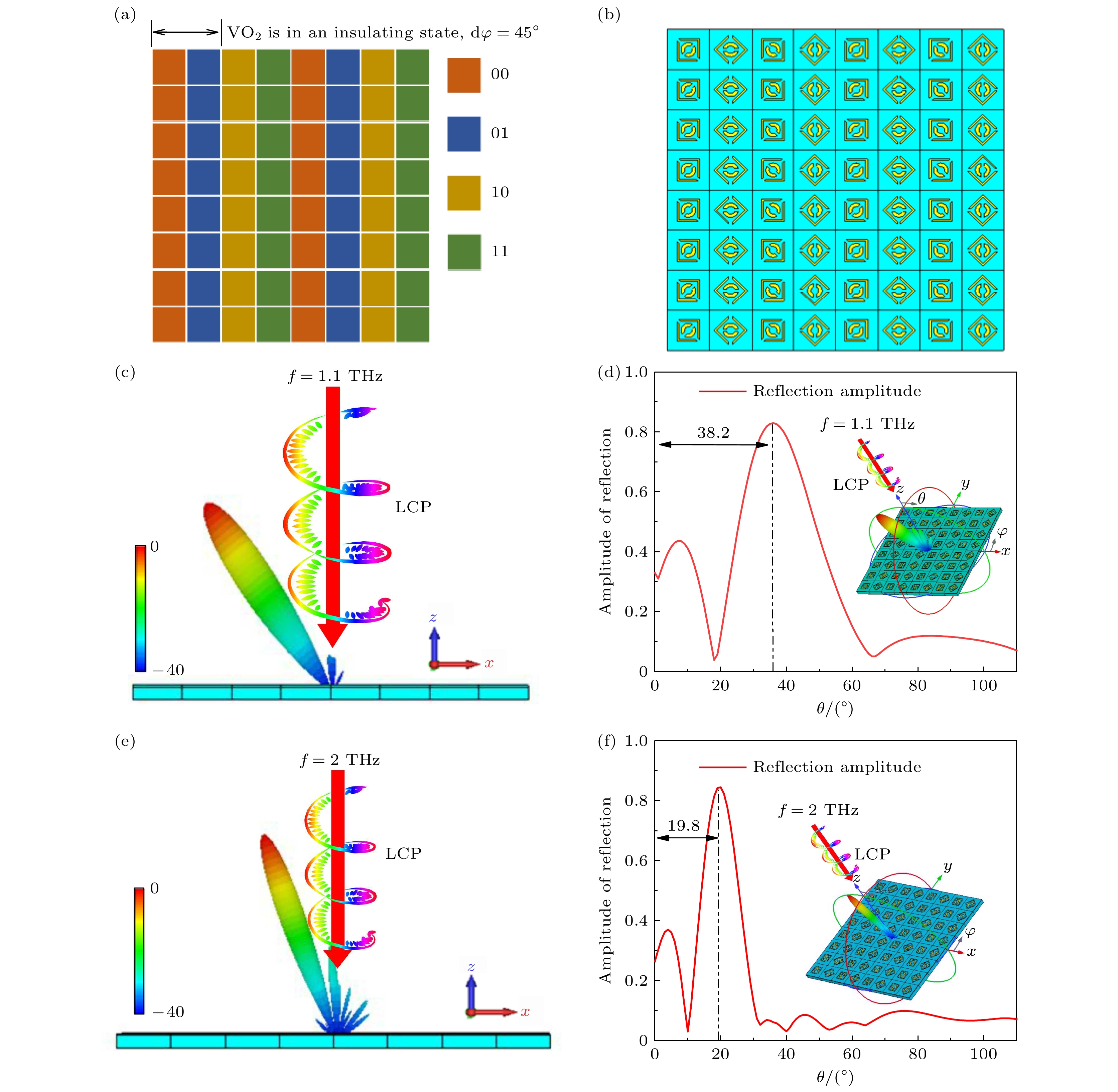
通过编码超表面控制太赫兹圆极化波的反射波束方向和角度可以应用于定向无线通信和雷达探测等领域. 对2.2节中获得超表面单元进行二维排布基于广义斯涅耳反射定律设计所需要的相位梯度
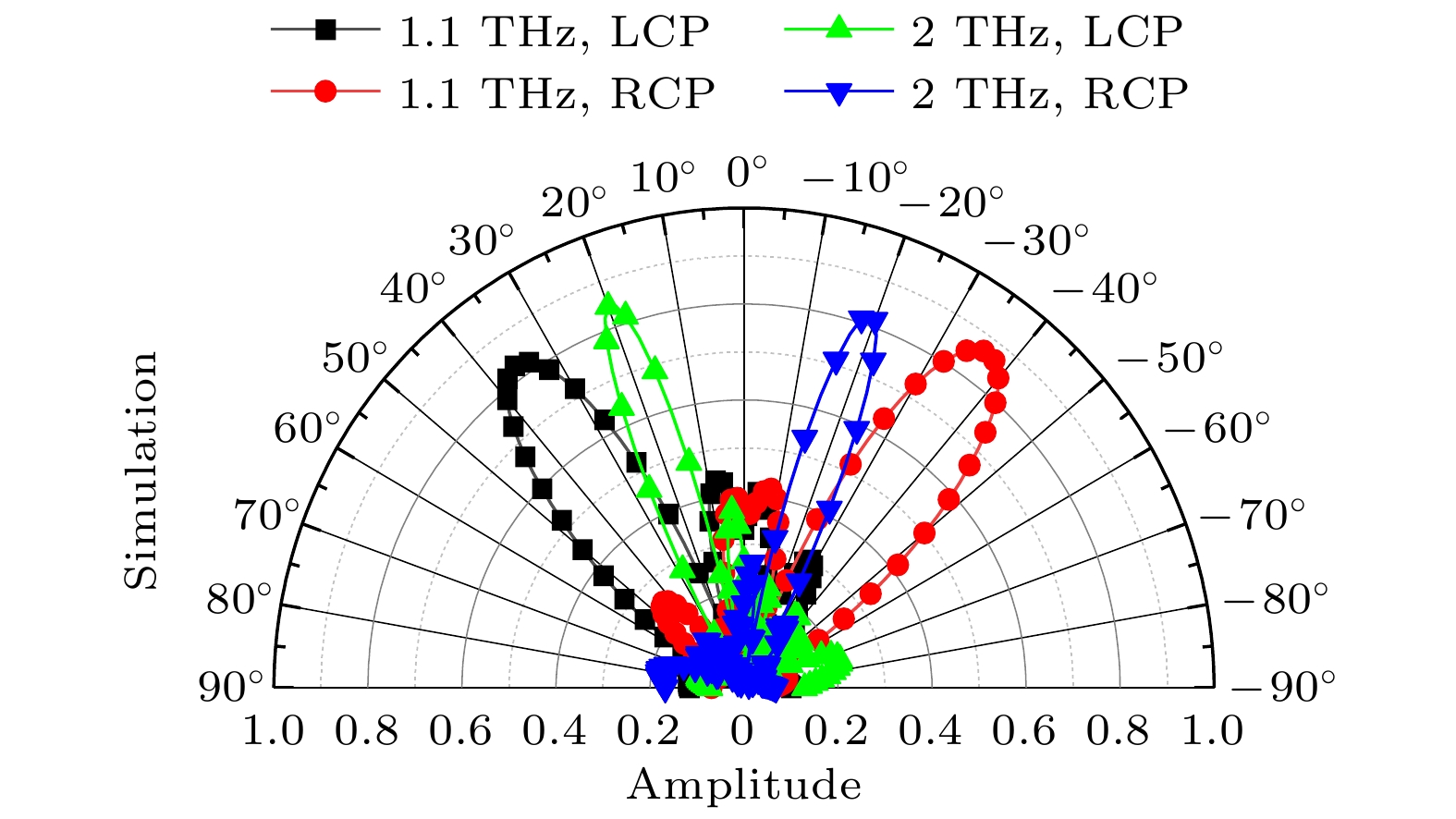
$ {\text{d}}\varphi $ /dx以控制反射波束的传播路径. 当VO2处于绝缘态, 圆极化波垂直入射时, 设计超表面排布序列周期为“00-01-10-11⋅⋅⋅/00-01-10-11⋅⋅⋅”, 如图6(a), (b)所示, 此时相位差$ {\text{d}}\varphi $ = 45°, 编码序列周期dx = 440 μm. 对于垂直入射的LCP波, 反射波束发生偏转, 在1.1 THz处其3D远场图如图6(c)所示. 图6(d)给出了1.1 THz处反射模式下的归一化幅度曲线, 可以看出偏转角θ约为38°, 与理论计算值$ {\theta _{\text{r}}} $ = 38.3°一致. 在2.0 THz处其3D远场图如图6(e)所示, 图6(f)给出了2.0 THz处反射模式下的归一化幅度曲线, 偏转角约为20°, 仿真与理论一致.对于垂直入射的RCP波, 超表面反射波束的偏转角相同, 偏转方向相反, 图7给出了xz平面的归一化远场辐射图, 表明当VO2处于绝缘态时, 随着入射太赫兹圆极化波频率从1.1 THz增至2 THz, 超表面可将入射的太赫兹CP波从±20°转向±38.2°. 仿真结果验证, 当VO2处于绝缘态, 太赫兹CP波垂直入射时, 设计的编码超表面在1.1—2.0 THz频率范围内可使太赫兹圆极化反射波束发生偏转, 偏转角可由(11)式计算得出.
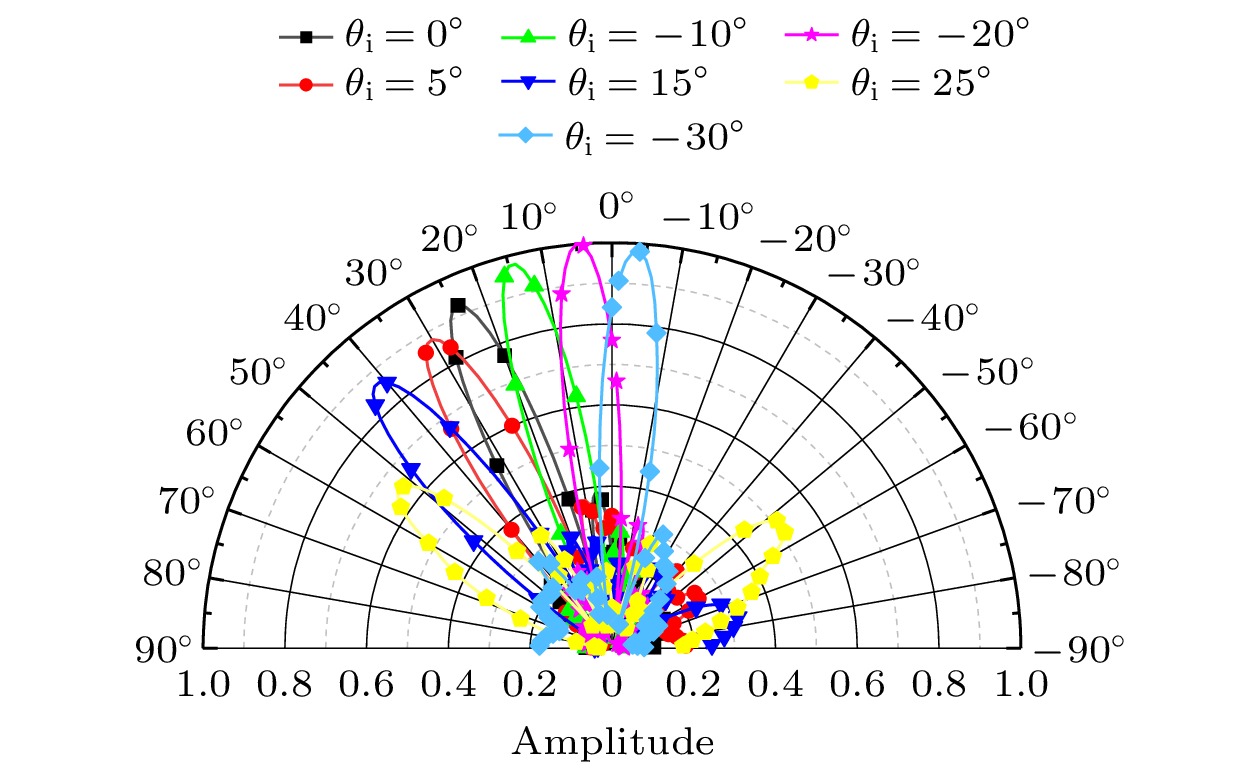
为进一步分析所设计的超表面对非垂直入射电磁波的反射情况, 设置LCP波入射角
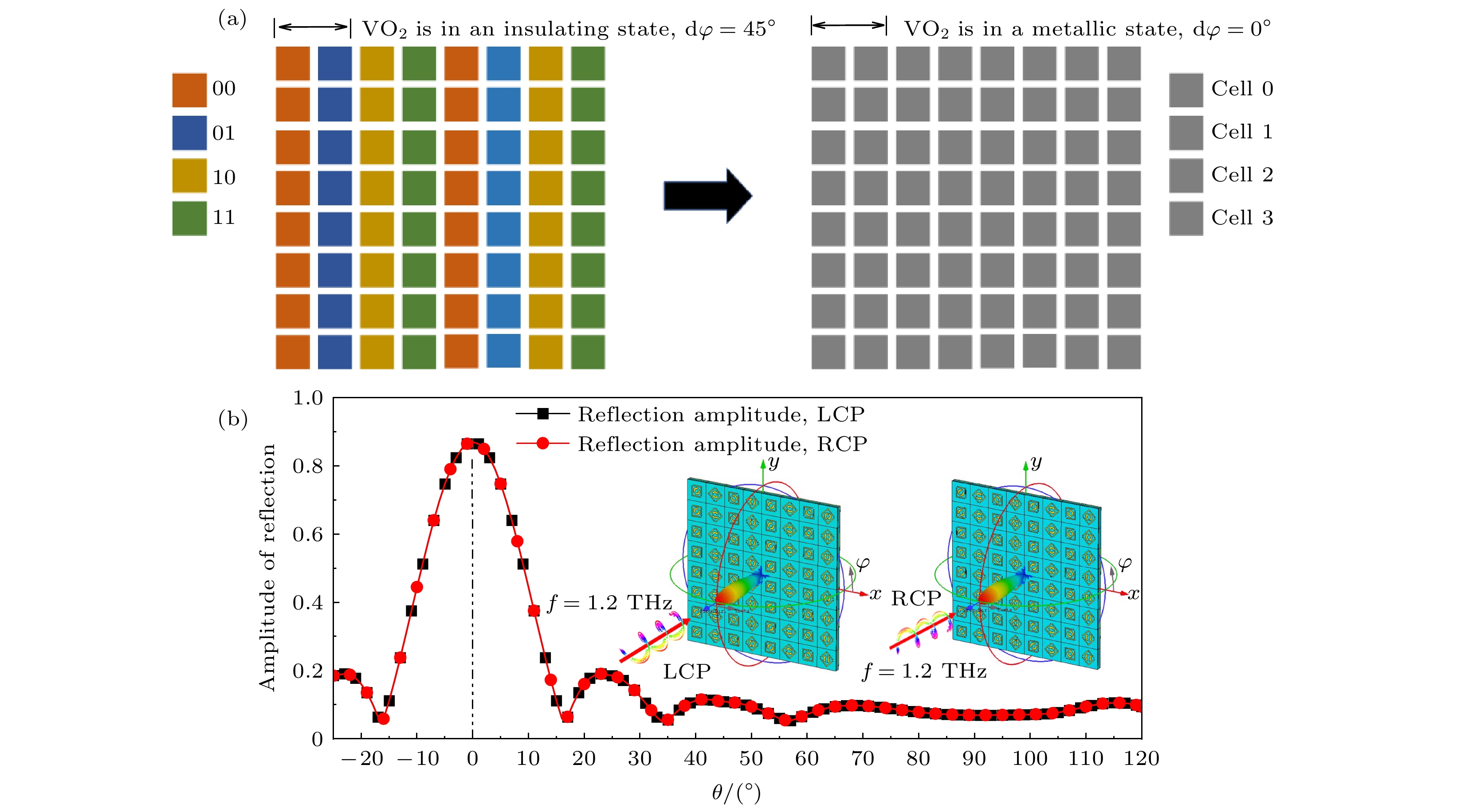
$ {\theta _{\text{i}}} $ 分别为0°, 5°, –10°, 15°, –20°, 25°和–30°, 图8给出了1.6 THz处的归一化远场辐射图, 可以得到1.6 THz处其异常反射角分别为25°, 30°, 15°, 42°, 5°, 54°, –4°与理论计算结果(25.22°, 30.88°, 14.62°, 43.23°, 4.82°, 58.07°, –4.23°)基本吻合, 这说明在0°—30°的范围内, 设计的超表面的偏转功能可正常使用, 超表面有一定的角度稳定性, 与上文理论分析一致.当VO2处于金属态时, 各单元的相位差dφ变为0°, 如图9(a)所示, 设计的超表面相位梯度发生改变, 4个单元结构可视为无相位差的单元0, 1, 2和3, 超表面功能模式由偏转切换为镜面反射. 图9(b)展示了超表面的反射功能, 当CP波垂直入射时其反射波束方向为0°. 仿真结果验证, 太赫兹CP波垂直入射时, VO2绝缘-金属态的切换可使编码超表面在1.1—2.0 THz的频率范围由偏转功能(偏转角20°—38.2°)转为镜面反射功能(偏转角0°), 实现太赫兹圆极化反射波束方向的调控.
-
本文结合几何相位原理和相变材料VO2两种相位调控手段, 提出了一种反射波束方向可控的反射型超表面, 有效实现太赫兹反射波束方向的调控. 基于几何相位原理旋转单元顶层结构并进行编码排序, 在工作频段内, 随着垂直入射的太赫兹CP波的频率的改变, 可实现20°—38°的异常偏转. 通过控制VO2绝缘态-金属态的转变, 该超表面可在CP波入射时实现异常偏转和镜面反射两种功能之间的切换. 仿真结果表明, 设计的超表面可实现波束转向控制, 为太赫兹反射波束调控领域提供了新的可能性, 将在太赫兹无线通信和雷达系统具有潜在的应用价值[34,35].
复合相位调控的波束转向可控反射型超表面
Composite phase modulated beam steering controllable reflective metasurface
-
摘要: 基于Pancharatnam-Berry相位原理和相变材料VO2的复合相位调控机制, 设计了一种波束转向可控的反射型超表面. 基于Pancharatnam-Berry相位原理对超表面单元顶层结构进行旋转编码, 获得所需的相位梯度, 而超表面VO2层绝缘态-金属态的转换, 可使预设超表面的相位梯度改变, 进而改变反射波束的转向. 仿真测试结果表明: 当VO2处于绝缘态时, 在1.1—2.0 THz工作频段内, 超表面可使垂直入射的圆极化波以特定的角度出射, 其反射效率大于80%; 当VO2处于金属态时, 对于同一超表面的相同工作频段, 超表面将入射的太赫兹波镜面反射, 反射效率接近100%. 这一设计对未来太赫兹反射波束调控领域具有潜在的应用价值.Abstract: Terahertz metasurface functional devices as an effective method to control terahertz waves have attracted extensive attention from researchers. In order to enhance the functionality and flexibility of the metasurface and adapt to diverse application scenarios and demands, a beam-steering controllable reflective metasurface is designed by combining the Pancharatnam-Berry phase principle and the phase change material vanadium dioxide in this work. The metasurface unit consists of five layers, they being the top layer that is a metal patterned layer, the third layer that is made of vanadium dioxide and located between the dielectric layers with different thickness, the dielectric layer that is made of polytetrafluoroethylene (PTFE), and the bottom layer that serves as a metal reflective layer. The metasurface units are rotated based on the Pancharatnam-Berry phase principle to obtain four metasurface units with fixed phase differences in between, after which the metasurface units are arranged in two dimensions based on the generalized Snell reflection law to obtain the desired phase-gradient deflected reflection beam. The insulating state-metallic state transition of the vanadium dioxide layer on the metasurface can change the phase gradient of the preset metasurface, thereby realizing the on/off function of deflection. The simulation results show that when the vanadium dioxide is in the insulating state, the phase gradient of the designed metasurface appears, and the metasurface can deflect the vertically incident circularly polarized wave with specific angle anomalies in a operating band of 1.1–2.0 THz; when the vanadium dioxide is in the metallic state, for the same operating band of the same metasurface, the phase gradient of the metasurface disappears, and the metasurface mirror reflects the vertically incident circularly polarized waves, thereby realizing the function switching. This design provides new possibilities for modulating the terahertz reflected beam, which will have potential applications in terahertz wireless communication and radar systems.
-
Key words:
- terahertz /
- encoding metasurfaces /
- beam control .
-
-
图 1 超表面单元 (a)三维示意图; (b)俯视图; (c)正视图; (d)旋转结构
Figure 1. Metasurface units: (a) 3D schematic diagram; (b) top view; (c) front view; (d) rotating structure.
图 2 x极化波和y极化波垂直入射时, 超表面单元的同极化反射幅度(a)和相位(b)
Figure 2. The co-polarized reflection amplitude (a) and phase (b) of the metasurface unit when x-polarized and y-polarized waves are vertically incident.
图 3 VO2处于绝缘态, LCP波垂直入射时, 不同旋转角α对应的超表面单元的同极化反射幅度(a)和相位(b)
Figure 3. VO2 is in an insulating state, with different rotation angles when LCP waves are vertically incident α, the amplitude (a) and phase (b) of co-polarized reflection of corresponding metasurface units.
图 4 表面电流分布 (a)—(d) VO2处于绝缘态; (e)—(h) VO2处于金属态
Figure 4. Surface current distribution: (a)–(d) VO2 is in an insulating state; (e)–(h) VO2 is in a metallic state.
图 5 不同入射角度下, 线极化波激励下超表面单元的反射相位和幅度 (a), (b) VO2处于绝缘态时, 不同入射角度下的幅度变化和相位变化; (c), (d) VO2处于金属态时, 不同入射角度下的幅度变化和相位变化
Figure 5. Reflection phase and amplitude of metasurface elements under linearly polarized wave excitation at different incident angles: (a), (b) Amplitude variation and phase change of VO2 at different incident angles when it is in an insulating state; (c), (d) amplitude variation and phase change of VO2 at different incident angles when it is in a metallic state.
图 6 2-bit反射编码超表面, LCP波垂直入射 (a)超表面排布示意图; (b)超表面结构; (c) 1.1 THz处的三维远场散射图; (d) 1.1 THz处的归一化反射振幅图; (e) 2.0 THz处的三维远场散射图; (f) 2.0 THz处的归一化反射振幅图
Figure 6. 2-bit reflection encoding metasurface, LCP wave vertically incident: (a) Schematic diagram of metasurface layout; (b) metasurface structure; (c) 3D far-field scattering map at 1.1 THz; (d) normalized reflection amplitude map at 1.1 THz; (e) 3D far-field scattering map at 2.0 THz; (f) normalized reflection amplitude map at 2.0 THz.
图 8 归一化远场辐射图, 1.6 THz处不同入射角对应的反射角
Figure 8. Normalized far-field radiation pattern, reflection angles corresponding to different incident angles at 1.6 THz.
图 9 反射超表面 (a)超表面相位梯度改变示意图; (b)三维远场散射图
Figure 9. Reflective metasurface: (a) Schematic diagram of phase gradient change on metasurface; (b) 3D far-field scattering map.
表 1 超表面单元的主要参数
Table 1. Main parameters of metasurface units.
Parameter D R1 R2 L1 L2 K1 K2 T1 T2 T3 H1 H2 Value/μm 110 10 19 60 51 8 8 0.2 0.3 0.2 3 26 
下载: 导出CSV
-
[1] Zhang Q, Cherkasov A V, Arora N, Hu G, Rudykh S 2023 Extreme Mech. Lett. 59 101957 doi: 10.1016/j.eml.2023.101957 [2] Zeng J W, Luk T S, Gao J, Yang X D 2017 J. Opt. 19 125103 doi: 10.1088/2040-8986/aa95dc [3] Liu S, Cui T J, Xu Q, Bao D, Du L L, Wan X, Tang W X, Ouyang C M, Zhou X Y, Yuan H, Ma H F, Jiang W X, Han J G, Zhang W L, Cheng Q 2016 Light-Sci. Appl. 5 e16076 doi: 10.1038/lsa.2016.76 [4] Zeng Y J, Feng C H, Li Q, Su X, Yu H B 2019 IEEE Photonics J. 11 4601212 doi: 10.1109/JPHOT.2019.2926499 [5] Wang B X, Qin X F, Duan G Y, Yang G F, Huang W Q, Huang Z M 2024 Adv. Funct. Mater. 34 2402068 doi: 10.1002/adfm.202402068 [6] Zhou J, Zhao X, Huang G R, Yang X, Zhang Y, Zhan X Y, Tian H Y, Xiong Y, Wang Y X, Fu W L 2021 ACS Sens. 6 1884 doi: 10.1021/acssensors.1c00174 [7] Shi M Y, Xu C, Yang Z H, Liang J, Wang L, Tan S J, Xu G Y 2018 J. Alloy. Compd. 764 314 doi: 10.1016/j.jallcom.2018.06.093 [8] Wang H, Ling F, Zhang B 2020 Opt. Express 28 36316 doi: 10.1364/OE.405885 [9] Cui T J, Qi M Q, Wan X, Zhao J, Cheng Q 2014 Light-Sci. Appl 3 e218 doi: 10.1038/lsa.2014.99 [10] Zhang Y G, Yin K H, Liang L J, Yao H Y, Yan X, Hu X F, Huang C C, Qiu F, Zhang R, Li Y P, Wang Y R, Li Z H, Wang Z Q 2024 Curr. Appl. Phys. 58 21 doi: 10.1016/j.cap.2023.11.013 [11] Orlov S, Ivaskeviciute-Povilauskiene R, Mundrys K, Kizevicius P, Nacius E, Jokubauskis D, Ikamas K, Lisauskas A, Minkevicius L, Valusis G 2024 Laser Photon. Rev. 18 2301197 doi: 10.1002/lpor.202301197 [12] Bai S S, Yang H Y 2022 Chin. J. Integr. Med. 28 366 doi: 10.1007/s11655-022-2886-3 [13] Imai R, Kanda N, Higuchi T, Zheng Z, Konishi K, Kuwata-Gonokami M 2012 Opt. Express 20 21896 doi: 10.1364/OE.20.021896 [14] Fedotov V 2021 Nat. Photonics 15 715 doi: 10.1038/s41566-021-00887-8 [15] Liang H, Zeng H, Zhao H, Wang L, Liang S, Feng Z, Yang Z, Zhang Y 2024 J. Phys. D-Appl. Phys. 57 085104 doi: 10.1088/1361-6463/ad0bc5 [16] Zhao F, Xu J, Song Z 2022 IEEE Photonics J. 14 1 doi: 10.1109/JPHOT.2022.3175811 [17] Sun S, Ma H F, Gou Y, Zhang T Y, Wu L W, Cui T J 2023 Adv. Opt. Mater. 11 2202275 doi: 10.1002/adom.202202275 [18] 汪静丽, 董先超, 尹亮, 杨志雄, 万洪丹, 陈鹤鸣, 钟凯 2023 物理学报 72 098101 doi: 10.7498/aps.72.20222321 Wang J L, Dong X C, Yin L, Yang Z X, Wan H D, Chen H M, Zhong K 2023 Acta Phys. Sin. 72 098101 doi: 10.7498/aps.72.20222321 [19] Wu L W, Ma H F, Gou Y, Wu R Y, Wang Z X, Xiao Q, Cui T J 2022 Nanophotonics 11 2977 doi: 10.1515/nanoph-2022-0190 [20] Fan J, Cheng Y 2019 J. Phys. D-Appl. Phys. 53 025109 doi: 10.1088/1361-6463/ab4d76 [21] Ding Z P, Su W, Ye L P, Zhou Y H, Li W L, Zou J F, Tang B, Yao H B 2024 Phys. Chem. Chem. Phys. 26 8460 doi: 10.1039/D3CP05689A [22] Jiang H, Wang J Y, Zhao S L, Ye L H, Zhang H, Zhao W R 2023 Opt. Commun. 536 129380 doi: 10.1016/j.optcom.2023.129380 [23] Zhao S L, Jiang H, Wang J Y, Zhu W C, Zhao W R 2023 Photonics 10 893 doi: 10.3390/photonics10080893 [24] Sharma M, Hendler N, Ellenbogen T 2020 Adv. Opt. Mater. 8 1901182 doi: 10.1002/adom.201901182 [25] Sorathiya V, Patel S K, Katrodiya D 2019 Opt. Mater. 91 155 doi: 10.1016/j.optmat.2019.02.053 [26] Menzel C, Rockstuhl C, Lederer F 2010 Phys. Rev. A 82 053811 doi: 10.1103/PhysRevA.82.053811 [27] Zhao Y, Huang Q P, Cai H L, Lin X X, Lu Y L 2018 Opt. Commun. 426 443 doi: 10.1016/j.optcom.2018.05.085 [28] Driscoll T, Kim H T, Chae B G, Kim B J, Lee Y W, Jokerst N M, Palit S, Smith D R, Di Ventra M, Basov D N 2009 Science 325 1518 doi: 10.1126/science.1176580 [29] Zheng Q, Zhang J, Li Y, Zheng L, Sui S, Qu S 2017 International Applied Computational Electromagnetics Society Symposium (ACES) pp1–2 [30] 杨森, 王佳云, 张婷, 于新颖 2022 光学学报 42 233 doi: 10.3321/j.issn.0253-2239.2022.13.gxxb202213031 Yang S, Wang J Y, Zhang T, Yu X Y 2022 Acta Opt. Sin. 42 233 doi: 10.3321/j.issn.0253-2239.2022.13.gxxb202213031 [31] Li J S, Yao J Q 2018 IEEE Photonics J. 10 1 [32] Born M, Wolf E 2013 Phys. Today 53 77 [33] Yu N, Genevet P, Kats M A, Aieta F, Tetienne J P, Capasso F, Gaburro Z 2011 Science 334 333 doi: 10.1126/science.1210713 [34] Ai H, Kang Q, Wang W, Guo K, Guo Z 2021 Sensors 21 4784 doi: 10.3390/s21144784 [35] Monnai Y, Lu X, Sengupta K 2023 J. Infrared Millim. Terahertz Waves 44 169 doi: 10.1007/s10762-022-00902-1 -
计量
- 文章访问数: 354
- HTML全文浏览数: 354
- PDF下载数: 2
- 施引文献: 0