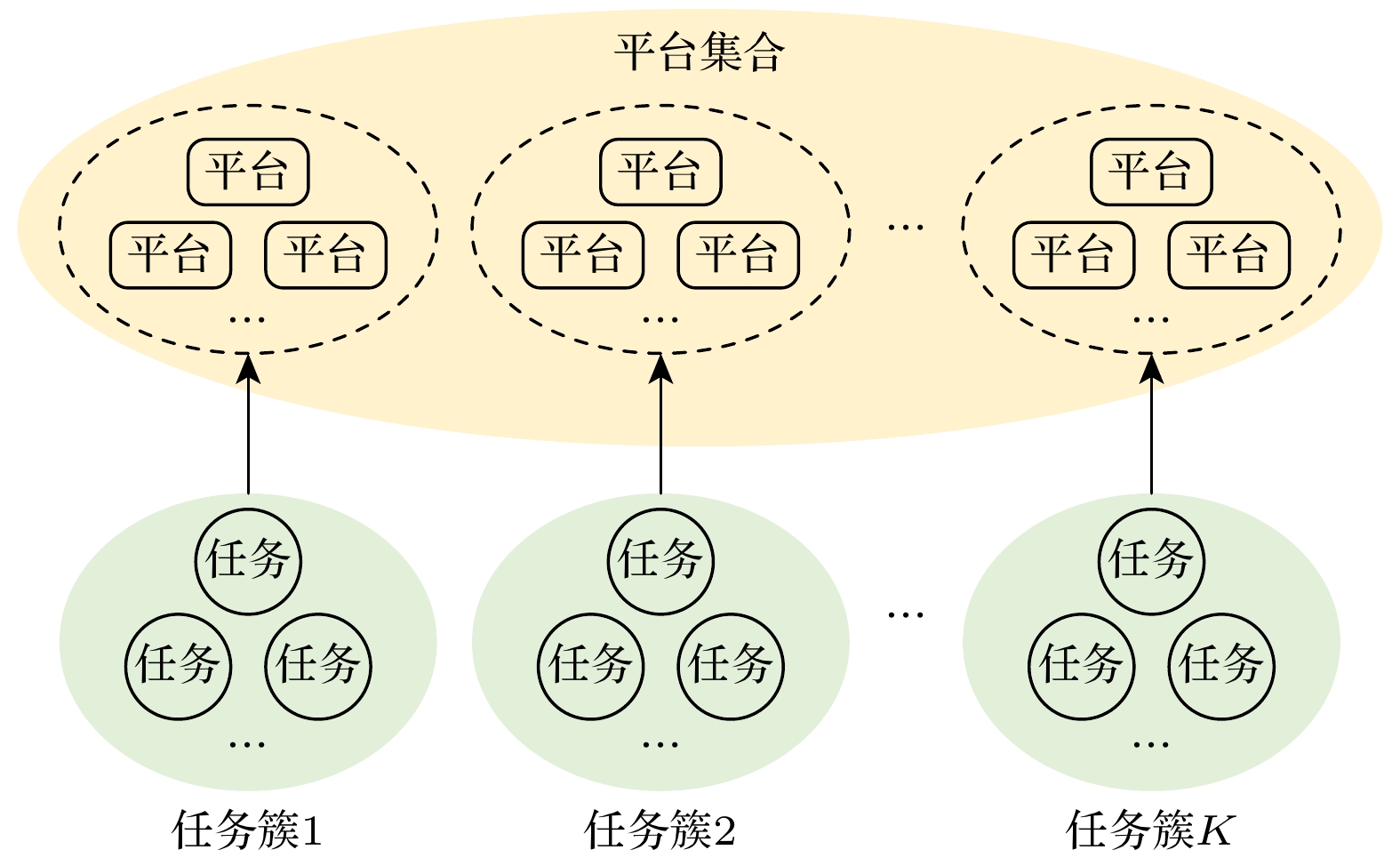
平台聚类编组问题作为军事C2组织资源调度中重点研究问题之一, 一直受到国内外研究人员的广泛关注^[1,2]. 在联合作战中, 由于涉及的平台数量庞大、类型多样, 资源供给数量众多、种类丰富, 在进行平台聚类编组时不但需要考虑大量的武器平台元素, 还需要考虑平台位置信息、提供的资源规模等属性, 因此联合作战中平台聚类编组问题属于组合优化问题中的NP (non-deterministic polynomial)问题^[3,4]. 由于军事C2组织资源调度中一般要求任务簇与平台簇一一对应, 所以通常情况下联合作战中任务分组的数量就决定了平台编组的数量, 据此可以利用无监督聚类优化算法求解联合作战中平台聚类编组问题.

目前, 无监督聚类优化算法主要有K-means算法^[5–7]、层次聚类^[8–10]、Mean-shift聚类算法^[11–13]、高斯混合模型EM算法^[14–16]等. 与其他方法相比, K-means算法因具有算法思路简单、聚类效果优良等特点, 加之在处理大数据情况下, 具有很好的伸缩性, 算法复杂度相对较低等优点, 使其在实际应用中广受青睐^[17,18]. 该算法作为数据挖掘领域的十大算法之一, 已成功应用于特征分析^[19–21]、商业智能^[22–24]、图像分组^[25–27]、文档聚类^[28–30]等多个领域. 随着大数据时代的到来, 问题所包含的聚类数据量呈指数级增长, 给K-means算法的计算速率带来了巨大挑战. 一些学者尝试将量子计算与K-means算法相结合, 利用量子天然所具有的并行计算能力来加速K-means算法的聚类过程, 达到量子增强的目的, 使得K-means算法的时间复杂度有较大幅度地降低^[31–33].

在上述研究成果的启发下, 本文针对联合作战战役行动中平台聚类编组问题提出了一种基于量子K-means的量子增强求解方法. 首先, 该方法在K-means算法的基础上, 利用已确认的任务簇数量确定平台聚类的类别数量, 再以每个任务簇中所含任务的位置信息为基准, 通过推导计算, 求解出每个初始聚类中心点位置; 其次, 以欧氏距离作为衡量平台数据与各聚类中心点间相似度的指标, 对平台数据进行量子化处理, 将平台数据转化成对应的量子态形式表示, 根据理论推导将欧氏距离求解转化成量子态内积求解, 通过设计构造通用的量子态内积求解量子线路完成对欧氏距离的求解; 接着, 根据平台数据与各聚类中心之间的相似度, 将各平台划归到对应的聚类中心并对聚类中心位置信息进行更新, 不断迭代直至达到类簇的误差平方和数值或者预先设定的迭代阈值, 完成聚类并取得平台聚类编组结果.

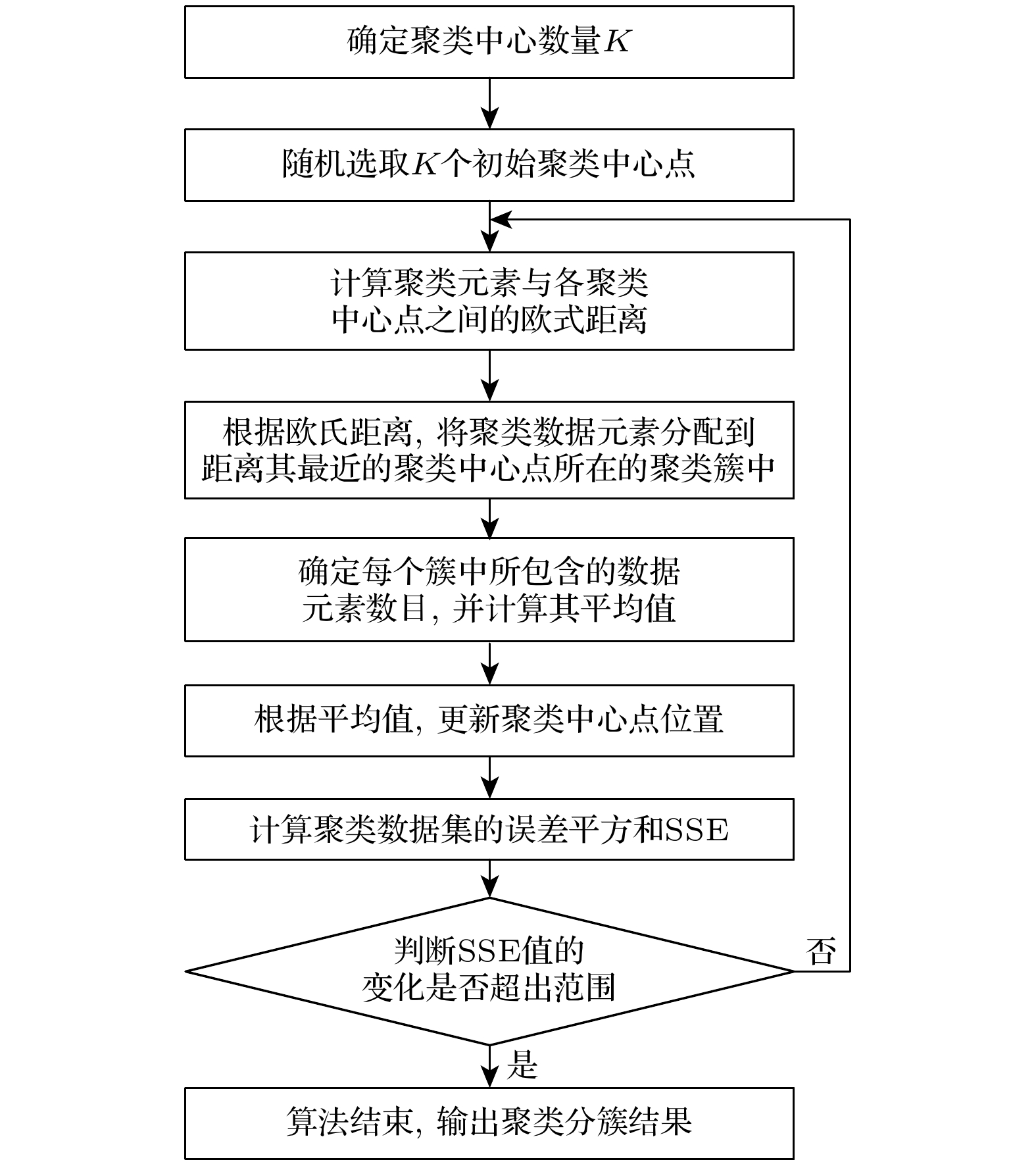
经典K-means算法的基本思想为: 首先, 根据相关依据和经验, 预先确定聚类类别数目K, 并从聚类数据集中随机选取K个初始聚类中心点; 其次, 依次计算其余聚类数据元素与各聚类中心点之间的欧氏距离, 通过欧氏距离找出距离目标数据元素最近的聚类中心点, 并将该聚类数据元素划归到该聚类中心点所对应的簇中; 接着, 通过求解每个簇中的聚类数据元素的平均值, 计算该簇对应的新聚类中心点; 最后, 根据聚类效果, 进行反复迭代, 直至聚类中点位置相对稳定或者迭代次数达到设定次数.

设聚类数据集合为$X = \left\{ {{x_1}, {x_2}, \cdots , {x_N}} \right\}$, 其中N为聚类数据数量, 初始聚类中心点有K个, 每个聚类中心点表示为${c_k}$, 其中$k \in \left\{ {1, 2, \cdots , K} \right\}$, 每个聚类数据维度为M. 则可以定义如下公式:

其中$D\left( {{x_i}, {c_k}} \right)$表示聚类数据${x_i}$与聚类中心点${c_k}$ 之间的欧氏距离, ${x_{ij}}$和${c_{kj}}$分别表示聚类数据 ${x_i}$和聚类中心点${c_k}$第j个维度对应的属性值, $j \in \{ 1, 2, \cdots , M \}$.

其中${c'_k}$表示通过求平均值得到的新聚类中心点, ${C_k}$表示聚类数据划归到聚类中心点${c_k}$所组成的集合, ${N_k}$表示聚类集合${C_k}$所含聚类数据的数量.

其中SSE表示整个聚类数据集的残差平方和.

经典K-means算法的具体步骤如下:

步骤1　根据具体问题, 结合实际经验具体分析, 确定将要划分聚类中心数目K;

步骤2　在聚类数据集中, 初始聚类中心点通过随机选定的K个数据元素来确定;

步骤3　根据(1)式计算其余聚类样本元素和各聚类中心点之间的欧氏距离;

步骤4　对欧氏距离计算结果进行比较, 将聚类数据元素划归到与其欧氏距离最小的聚类中心点所在的簇中;

步骤5　确定每个簇中的聚类数据元素数目, 并通过(2)式对簇中聚类数据元素的均值进行计算;

步骤6　将均值计算结果作为新的聚类中心点位置, 并进行更新;

步骤7　根据(3)式, 计算整个聚类数据集的残差平方和;

步骤8　对聚类数据集的残差平方和变化进行判断, 若变化超出所设定的范围, 则跳转到步骤3, 根据新的聚类中心点重新进行聚类分簇. 如果变化在所设定的范围内, 则结束聚类, 将聚类分簇结果进行输出. 图1为K-means算法的具体聚类流程图.

设${{\boldsymbol{x}}_i} = {\left[ {{x_{i1}}, {x_{i2}}, \cdots , {x_{iM}}} \right]^{\text{T}}}$为聚类数据集合X中的任意数据元素, ${{\boldsymbol{c}}_k} = {\left[ {{c_{k1}}, {c_{k2}}, \cdots {c_{kM}}} \right]^{\text{T}}}$为聚类中心集合${C_k}$中的任意一个聚类中心点. 根据(1)式, ${{\boldsymbol{x}}_i}$与${{\boldsymbol{c}}_k}$之间的欧氏距离具体推导如下:

根据(4)式, 整个聚类数据集的残差平方和SSE公式也可以进一步推导:

通过对经典K-means算法的计算复杂度分析, 可以发现该算法对计算资源的消耗主要集中在计算聚类数据元素与聚类中心点之间的欧氏距离部分(步骤3)和计算整个聚类数据集的残差平方和部分(步骤7). 随着数据量和维度的不断增大, 该算法所消耗的计算资源会急剧增加, 算法的计算复杂度也会指数级提升. 根据(4)式和(5)式的推导结果, 可以建立起欧氏距离与内积计算之间的联系, 将计算欧氏距离转化为内积计算. 但是, 针对内积计算问题采用目前常用的经典算法进行求解需要消耗较大的计算资源, 并且算法的计算复杂度都比较高. 所以, 本文从新兴的量子技术角度出发, 考虑在量子理论体系下, 利用量子增强技术来提升经典K-means算法处理问题的能力.

本文提出的基于量子K-means的量子增强求解方法是将量子力学基础理论和量子计算相关理论与经典K-means算法的主要步骤相结合, 在充分发挥量子并行计算优势基础上提升经典算法的执行效率和准确度. 针对经典K-means算法, 本文提出的方法主要做了3个方面的优化和改进. 一是根据具体问题对聚类分簇K值和初始聚类中心点位置进行优化处理; 二是对所有聚类数据元素和聚类中心点进行量子化处理, 建立经典内积与量子态内积之间的联系; 三是制备量子态, 设计构建通用的量子态内积求解量子线路, 通过对量子态内积的求解实现对应欧氏距离的求解.

经典K-means算法较为明显的缺点就是聚类分簇K值难以确定和初始聚类中心点随机选取. 如果聚类分簇K值和初始聚类中心点选取不当往往会严重影响到最终聚类结果, 使其陷入局部最优.

对于聚类分簇K值, 在算法聚类过程中, 如果K值选择过大, 会导致各簇之间数据特征的差异性很小, 如果K值选择过小, 会导致每个簇内部的数据特征差异性很大. 同时, K值过大或者过小都会导致聚类结果不理想, 难以实现全局最优. 对平台进行聚类的目标就是想实现任务簇与平台簇的一一对应关系, 因此本文从实际出发以已知的任务簇数量作为初始聚类分簇K的取值(如图2所示). 这样选取的K值不但与实际相符, 也更容易求出全局较优解.

在K-means算法聚类过程中, 初始聚类中心点的选取对聚类效果起着关键性作用, 当初始聚类中心点位置不理想时, 不但影响聚类效果, 还会使算法的迭代次数增加, 从而提高算法的计算复杂度. 本文在确定聚类分簇K值的基础上, 对每个任务簇中的任务数据元素平均值进行计算, 并将该平均值对应的位置作为对应平台簇的初始聚类中心点位置. 这样选取的聚类中心点不仅与实际问题相结合, 具体操作还比较简单, 一定程度上降低了算法的操作复杂度.

在希尔伯特空间中, 一个量子位对应的量子态可以表示成一个二维向量, 根据张量积运算, 两个量子位对应的量子态就可以表示一个四维向量, 以此类推, n个量子位对应的量子态就可以表示一个${2^n}$维向量. 当聚类数据元素的特征维度为$N'$时, 需要的量子位数为$\left\lceil {{{\log }_2}N'} \right\rceil $. 当量子态对应的向量形式中出现多余的维度时, 将其对应的振幅数值设置为0即可. 下面进行具体的计算推导.

设聚类数据元素与聚类中心点的特征维度都为$N'$, 设一个聚类数据元素${{\boldsymbol{x}}_1} = [ {x_{11}}, {x_{12}}, \cdots , {x_{1 N'}} ]^{\text{T}}$与一个聚类中心点${{\boldsymbol{c}}_1} = {\left[ {{c_{11}}, {c_{12}}, \cdots , {c_{1 N'}}} \right]^{\text{T}}}$. 设两个量子态分别为$\left| {\boldsymbol{\eta}} \right\rangle = {\left[ {{e_1}, {e_2}, \cdots , {e_L}} \right]^{\text{T}}}$, $\left| {\boldsymbol{\vartheta}} \right\rangle = {\left[ {{f_1}, {f_2}, \cdots , {f_L}} \right]^{\text{T}}}$, 其中$L = {2^{\left\lceil {{{\log }_2}N'} \right\rceil }}$. 令$E = \left\| {{x_1}} \right\| = \sqrt {\displaystyle\sum\nolimits_{i = 1}^{N'} {x_{1 i}^2} } $, $F = \left\| {{c_1}} \right\| = \sqrt {\displaystyle\sum\nolimits_{i = 1}^{N'} {c_{1 i}^2} } $. 将E代入${x_1}$的表达式, ${x_1}$的表达形式可以转化为

将F代入${c_1}$的表达式, ${c_1}$的表达形式可以转化为:

当$L = N'$时, 令${e_1} = \dfrac{{{x_{11}}}}{E}, {e_2} = \dfrac{{{x_{12}}}}{E}, \cdots , {e_L} = \dfrac{{{x_{1 N'}}}}{E}$, 令${f_1} = \dfrac{{{c_{11}}}}{F}, {f_2} = \dfrac{{{c_{12}}}}{F}, \cdots , {f_L} = \dfrac{{{c_{1 N'}}}}{F}$. 可以得到如下表达式:

根据(8)式和(9)式, 计算量子态$\left| \eta \right\rangle $与$\left| \vartheta \right\rangle $的内积可以得到如下表达式:

当$L \gt N'$时, 令${e_1} = \dfrac{{{x_{11}}}}{E} $, $ {e_2} = \dfrac{{{x_{12}}}}{E}, \cdots $, $ {e_{N'}} = \dfrac{{{x_{1 N'}}}}{E}, \; {e_{N' + 1}} = 0$, ${e_{N' + 2}} = 0, \cdots , {e_L} = 0 $. 令${f_1} = \dfrac{{{c_{11}}}}{F} $, $ {f_2} = \dfrac{{{c_{12}}}}{F}, \cdots , {f_{N'}} = \dfrac{{{c_{1 N'}}}}{F}$, ${f_{N' + 1}} = 0, {f_{N' + 2}} = 0, \cdots , {f_L} = 0 $. 可以得到如下表达式:

根据(11)式和(12)式, 计算量子态$\left| \eta \right\rangle $与$\left| \vartheta \right\rangle $的内积可以表示为

这样无论L大于或者等于$N'$, 都可以建立起经典内积与量子态内积之间的联系, 使接下来构建量子线路进行内积求解成为可能.

设任意两个量子态分别为$\left| \varphi \right\rangle = [ {q_1}, {q_2}, \cdots , {q_L} ]^{\text{T}}$, $\left| \phi \right\rangle = {\left[ {{p_1}, {p_2}, \cdots , {p_L}} \right]^{\text{T}}}$, 其中L表示量子比特位数, ${\displaystyle\sum\nolimits_{i = 1}^L {\left| {{q_i}} \right|} ^2} = 1$, ${\displaystyle\sum\nolimits_{i = 1}^L {\left| {{p_i}} \right|} ^2} = 1$. 以生成量子态$\left| \varphi \right\rangle $为例, 设计其对应的通用量子线路. 根据量子基础理论, 量子态$\left| \varphi \right\rangle $可以写成如下形式:

其中, 结合本文实际问题应用, 设${a_{11}}$, ${b_{11}}$为任意实数, 且$a_{11}^2 + b_{11}^2 = 1$.

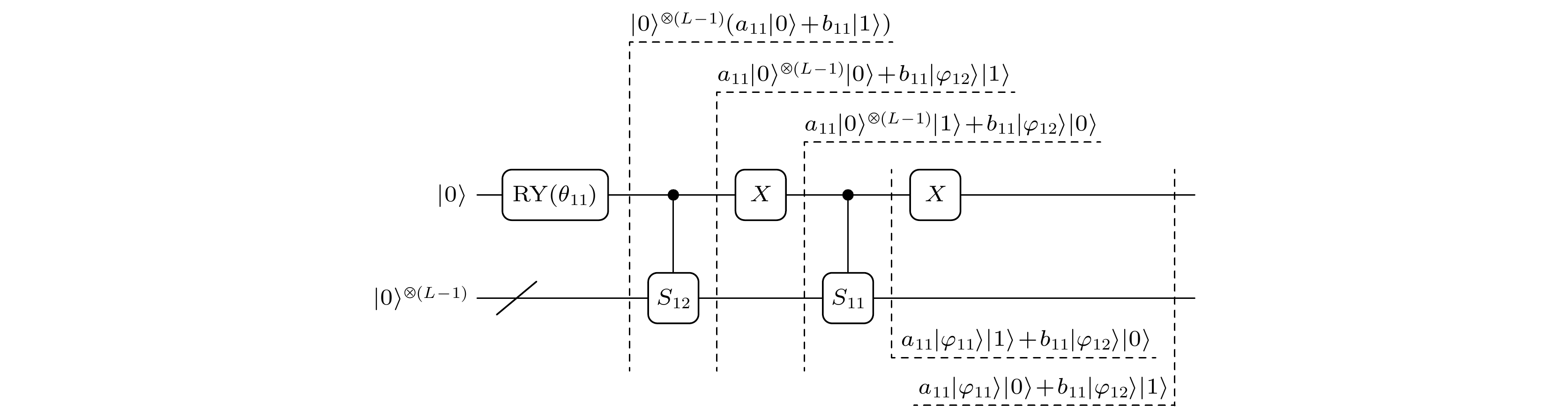
根据(14)式中$\left| \varphi \right\rangle $的表达形式, 参考文献[34]量子态制备过程中量子逻辑门选择方法, 经过量子酉变换计算推理, 利用量子逻辑门设计出了制备$\left| \varphi \right\rangle $对应的量子线路. 如图3所示, 在量子初始基态${\left| 0 \right\rangle ^{ \otimes L}}$的基础上, 经过RY(i)量子逻辑门、X量子逻辑门等操作后, 得到$\left| \varphi \right\rangle $对应的量子态. 具体计算推导过程如下:

RY(i)量子逻辑门的矩阵形式为

X量子逻辑门的矩阵形式为

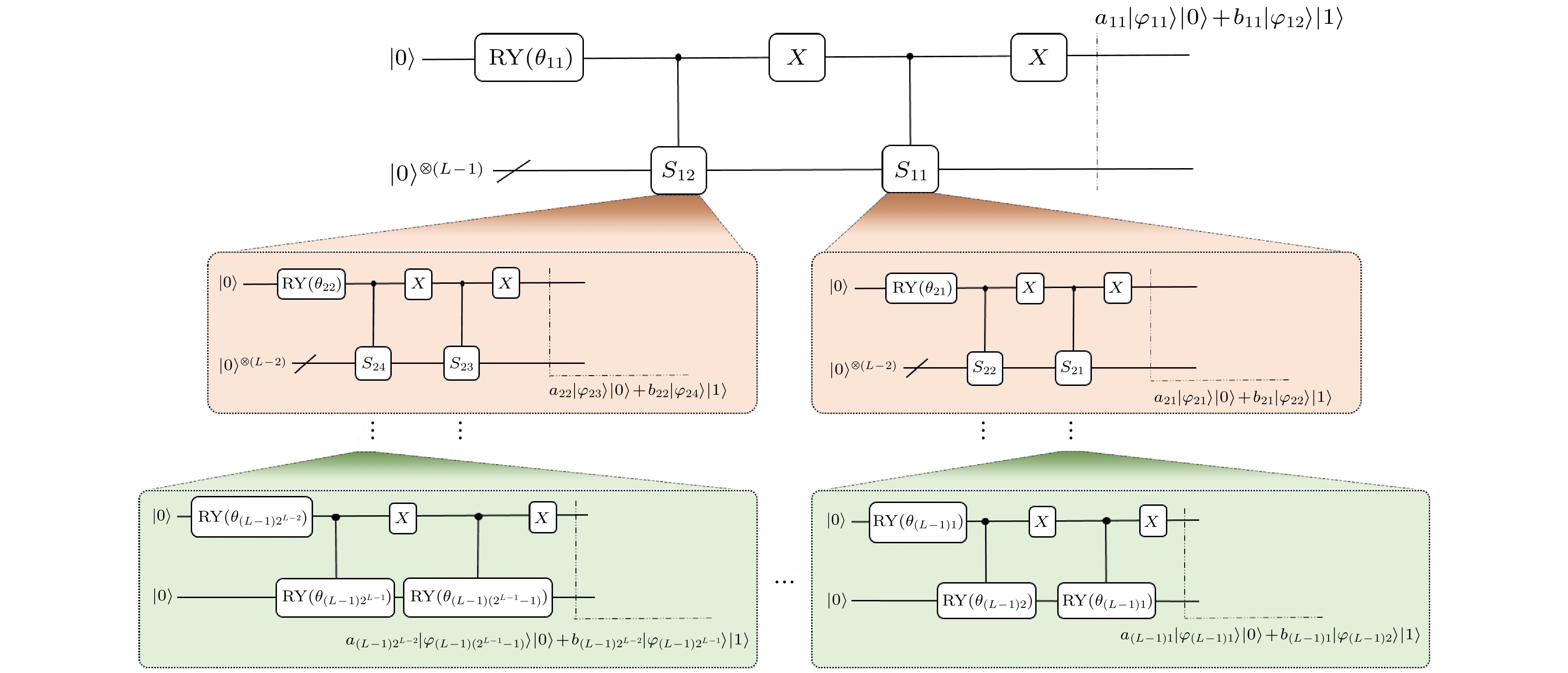
从上述计算推导过程和图3显示的信息可以看出, 图中量子逻辑门模块${S_{11}}$和${S_{12}}$的主要作用就是演化生成量子态$\left| {{\varphi _{11}}} \right\rangle $和$\left| {{\varphi _{12}}} \right\rangle $. 在设计量子线路过程中, 直接实现量子逻辑门模块${S_{11}}$和${S_{12}}$比较困难, 本文可以采用相同的原理, 将量子态$\left| {{\varphi _{11}}} \right\rangle $和$\left| {{\varphi _{12}}} \right\rangle $的表达式写成$\left| {{\varphi _{11}}} \right\rangle = {a_{21}}\left| {{\varphi _{21}}} \right\rangle \left| 0 \right\rangle + {b_{21}}\left| {{\varphi _{22}}} \right\rangle \left| 1 \right\rangle $和$\left| {{\varphi _{12}}} \right\rangle = {a_{22}}\left| {{\varphi _{23}}} \right\rangle \left| 0 \right\rangle + {b_{22}}\left| {{\varphi _{24}}} \right\rangle \left| 1 \right\rangle $的形式, 其中${a_{21}}$, ${b_{21}}$, ${a_{22}}$, ${b_{22}}$为实数, 且$a_{21}^2 + b_{21}^2 = 1$, $a_{22}^2 + b_{22}^2 = 1$. 这样就可以采用递归方法, 对量子线路中较为复杂的量子逻辑门模块${S_{11}}$和${S_{12}}$进行进一步分解设计, 最终得到如图4所示的制备量子态$\left| \varphi \right\rangle $的通用量子线路图. 该量子线路图可以适用于任意量子态的制备.

根据量子力学基础理论, 量子态$\left| \phi \right\rangle $也可以写成如下形式:

其中${c_{11}}$, ${d_{11}}$为任意实数, 且$c_{11}^2 + d_{11}^2 = 1$. 采用同样的计算推导方法, 本文也可以设计出制备量子态$\left| \phi \right\rangle $的通用量子线路.

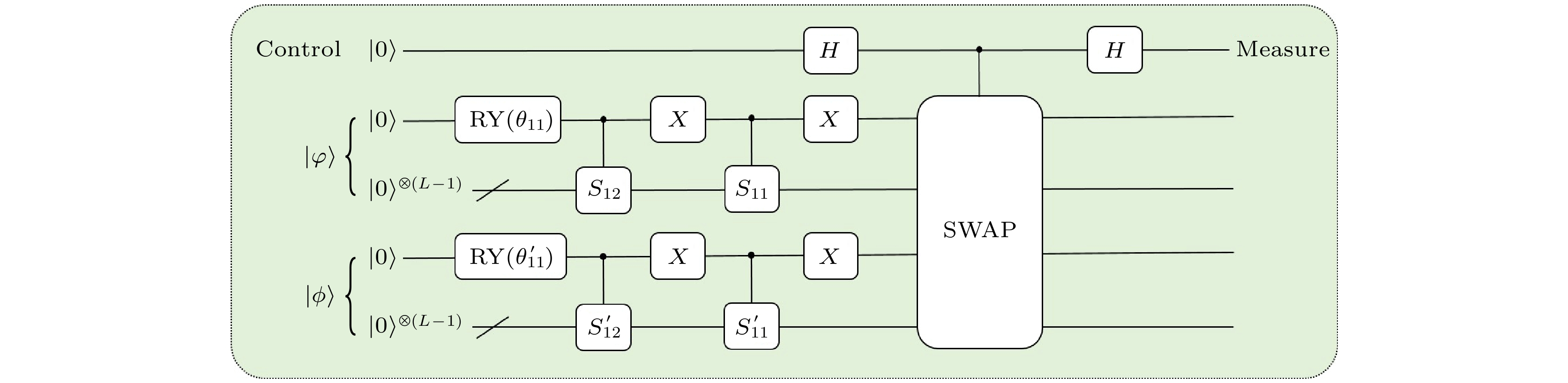
在完成两个量子态$\left| \varphi \right\rangle $和$\left| \phi \right\rangle $的制备后, 接下来就是设计实现两个量子态内积的通用量子线路. 因为受控SWAP量子逻辑门可以实现两个量子比特状态之间的转换, 所以在量子态演化过程中, 在量子线路中增加控制位, 主要利用H量子逻辑门、受控SWAP量子逻辑门实现两个量子态$\left| \varphi \right\rangle $和$\left| \phi \right\rangle $之间的转换, 形成量子纠缠态, 通过对控制位量子态的测量求得两个量子态的内积. $\left| \varphi \right\rangle $和$\left| \phi \right\rangle $的量子态内积求解线路如图5所示, 其中H量子逻辑门的矩阵形式为

SWAP量子逻辑门的矩阵形式为

求解量子态内积的计算推导如下:

用标准基态$\left| 0 \right\rangle $测量控制位得到0的概率为

用标准基态$\left| 1 \right\rangle $测量控制位得到1的概率为

为了对本文提出的基于QK-means的量子增强求解方法进行有效性和准确性验证, 本节首先选取UCI(University of CaliforniaIrvine)数据库中的Haberman, Iris, Diabetes, Wine四个公共数据集作为本次实验的测试数据集, 并结合经典K-means算法在相同条件下进行仿真实验与分析; 其次, 以某多军兵种联合作战登陆战役模拟演习中收集的关于作战平台实验数据为研究对象, 将本文提出的方法与经典的K-means算法同时用于求解平台聚类问题, 并对结果进行分析研究; 最后, 对本文提出的基于QK-means的量子增强求解方法的计算复杂度与经典K-means算法的计算复杂度进行对比分析.

Haberman, Iris, Diabetes, Wine四个公共数据集的基本信息如表1所示, 本文依次将其作用于两种算法进行实验验证. 实验结果重点从准确率、运行时间和迭代次数等方面对两种算法进行对比分析. 由于在对这两种算法进行实验测试时, 在初始聚类中心选取环节都具有一定的随机性, 造成单次实验结果可能出现较大偏差, 为了避免这种误差影响, 本文设定在每个数据集上运行算法10次, 求其平均值作为最终结果. 本文提出的方法的伪代码如表2所示.

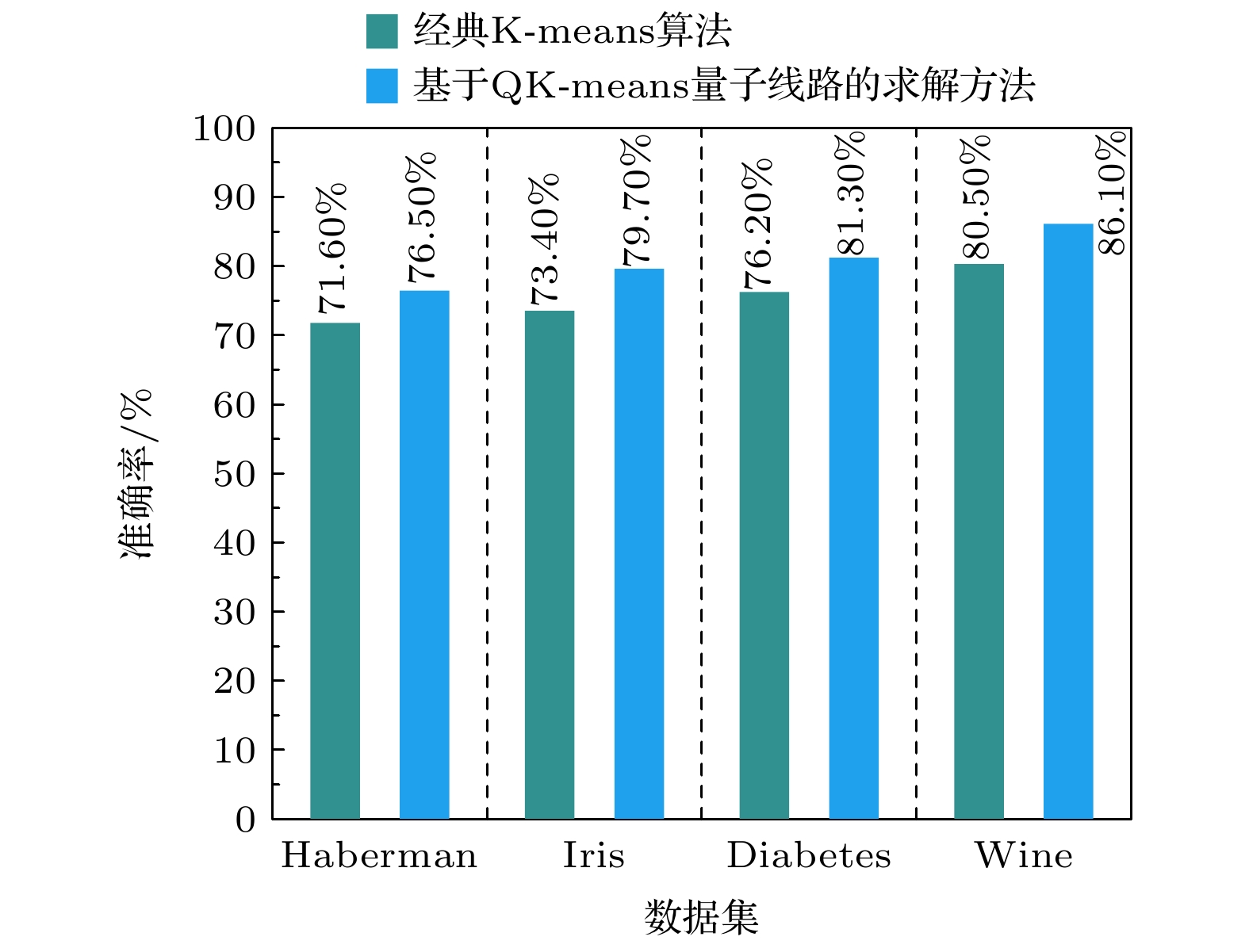
图6所示为基于QK-means的量子增强求解方法和经典K-means算法在4种公共数据集上进行聚类分簇的准确率比较图. 由于选用的4个公共数据集都是带标签的, 每个数据样本都有自身对应的分类标签, 所以这里以结果实现正确划分的数据样本个数与数据样本总数量的比值作为衡量两个算法的准确程度. 从图中通过分析可以得出, 在4种数据集下本文提出的方法比经典K-means算法都有较为显著的提升, 主要原因是经典K-means算法在确定初始聚类中心点位置时, 采用的是随机在所有数据样本中选取, 而初始聚类中心点位置很容易影响到聚类结果, 造成实验结果与数据集自身标签分类结果之间有偏差, 容易陷入到局部最优解. 而本文针对初始聚类中心点位置选取方式进行了优化, 在确保合理性的前提下, 缩小每个聚类中心点选择范围, 避免了不良初始聚类中心点数据带来的较大实验结果误差.

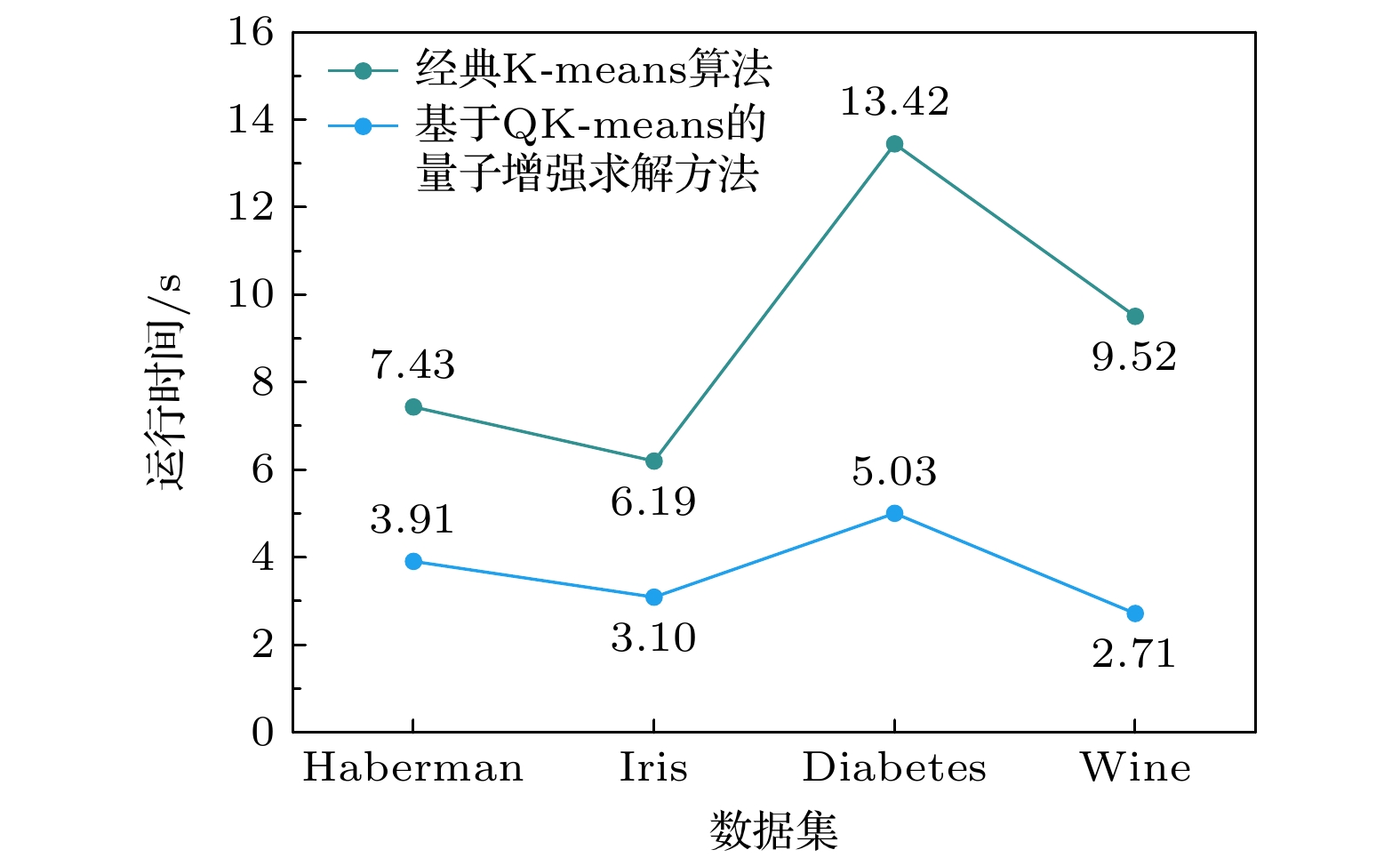
图7为在4种公共数据集下两种算法的运行时间对比图. 从图7可以分析得出, 在4种数据下本文提出的方法的运行时间明显低于经典K-means算法的运行时间, 特别是当数据样本较大或者数据维度较大时, 两种算法的运行时间对比更为明显. 通过分析认为主要原因是本文提出的方法利用量子增强技术使其具有并行计算的能力, 大大缩短了算法的运行时间, 而这种并行计算能力, 随着数据量和数据维度增大, 表现出的优势更为明显. 另一个原因是本文提出的方法优化了初始聚类中心点的选取方式, 一定程度上通过减少迭代次数缩短了算法的运行时间.

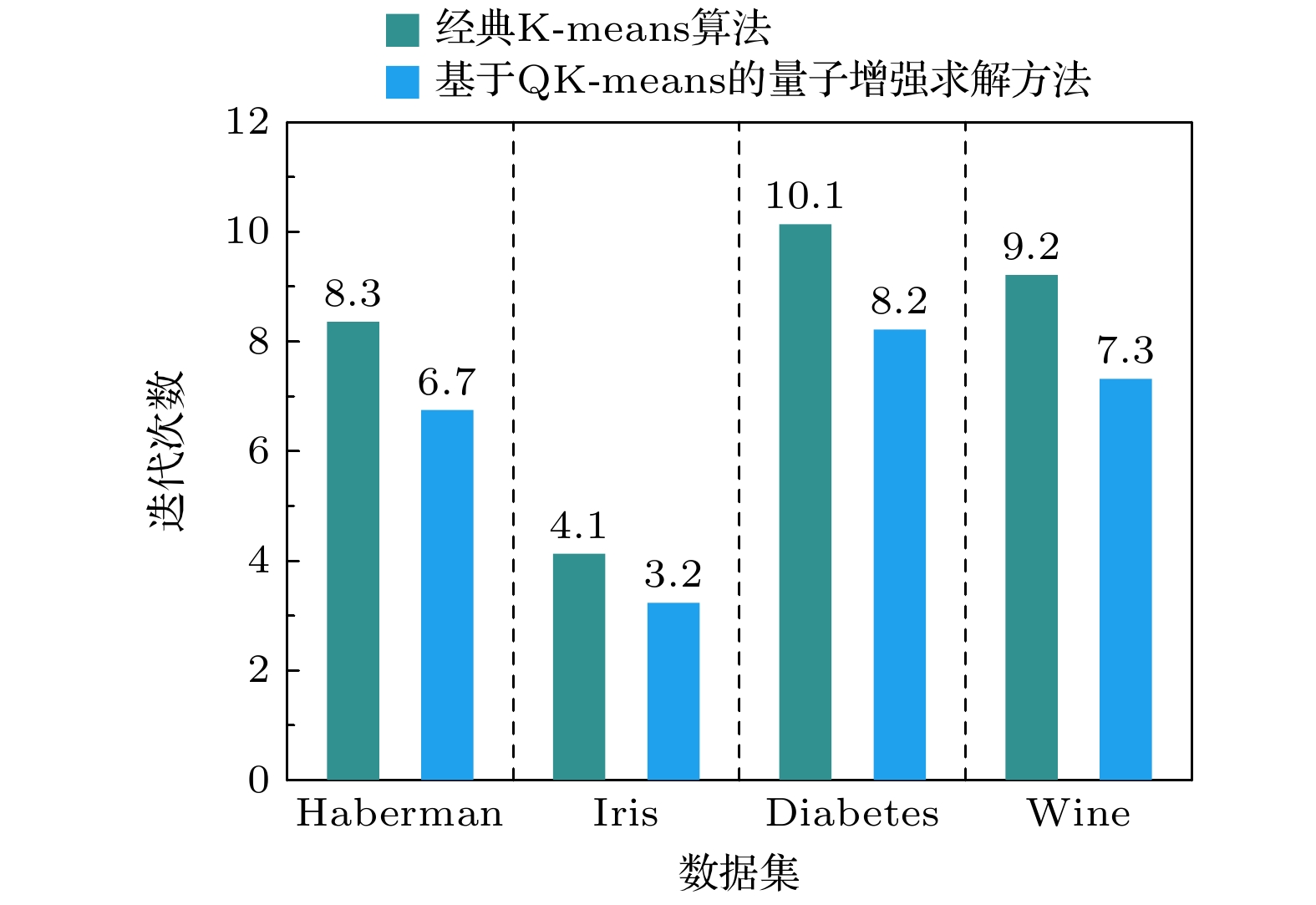
图8为在4种公共数据集下两种算法的迭代次数对比图, 图中迭代次数是多次试验测试的平均值, 所以不一定是整数值. 从图中分析可以得出, 在4种数据下本文提出的方法的迭代次数少于经典K-means算法的迭代次数, 特别是当数据样本较为复杂时, 与经典K-means算法相比, 本文提出的方法具有较大优势. 分析原因主要是本文提出 的方法在选择初始聚类中心点时, 通过缩小每个 聚类中心点选取范围, 将其限制在一个较优的数 值范围, 降低了随机性给聚类结果带来的影响, 从而使算法可以较早取得较优解, 减少了算法的迭 代次数. 当数据样本变得复杂时, 经典K-means算法通过随机方式选取初始聚类中心点的局限性和不确定性就越为突出, 造成了算法迭代次数增多, 而本文提出的方法则基本不受数据样本复杂度的影响.

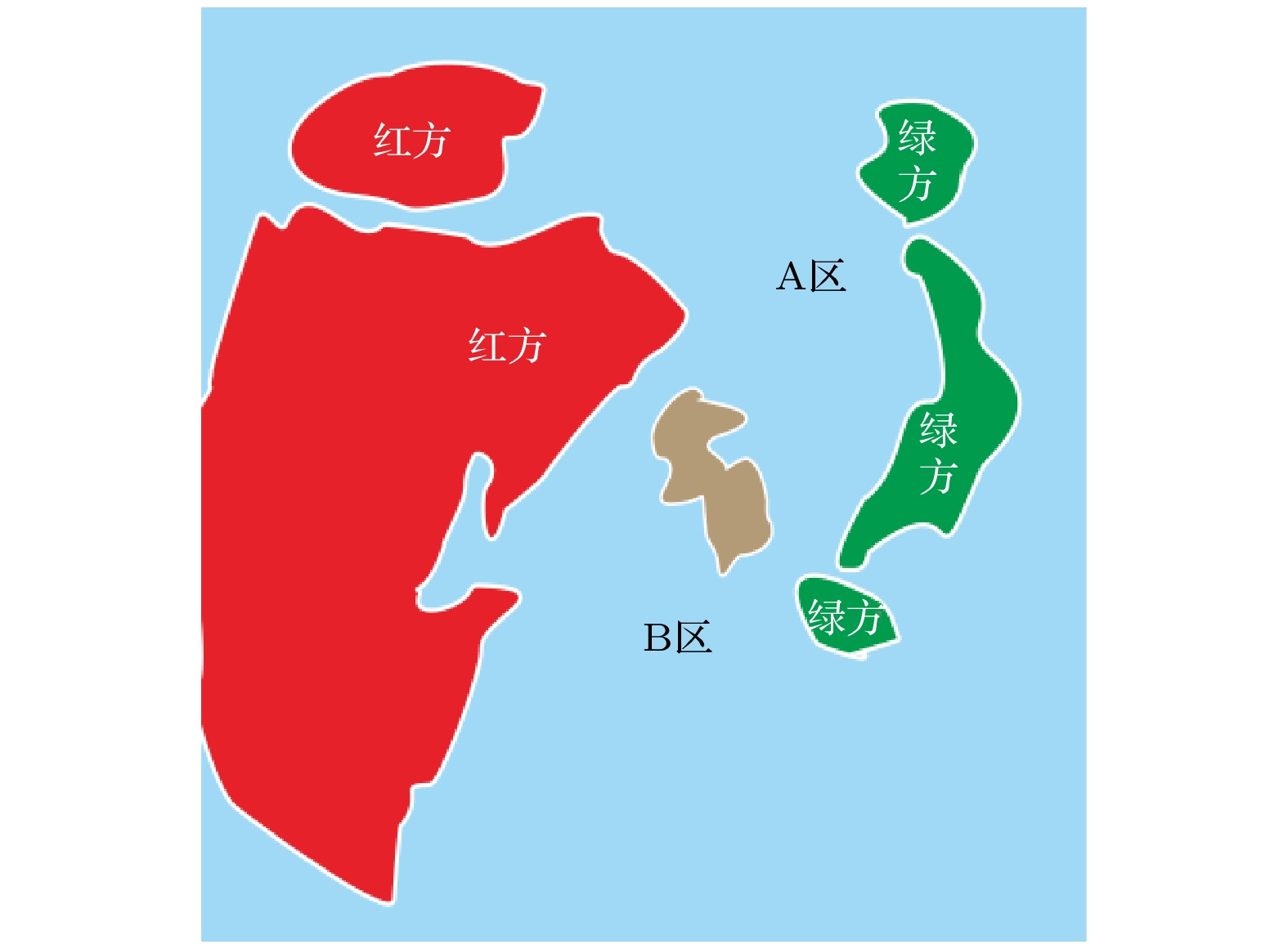
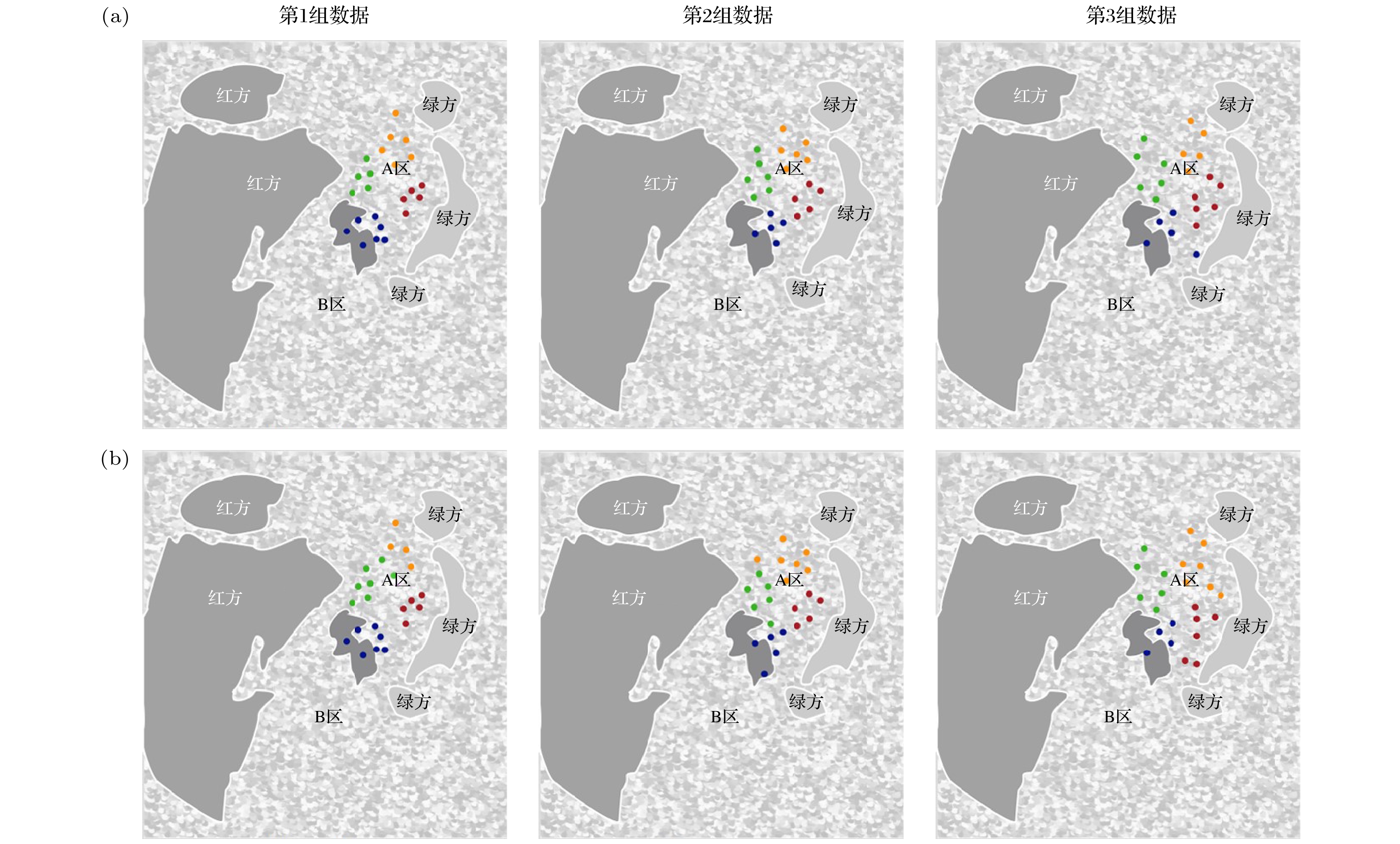
如图9所示为某多军兵种联合作战登陆战役模拟演习项目的作战任务区域图. 该项目作战区域主要由A区域与B区域组成, 本文只对A区域中的作战平台开展联合作战战役行动中平台聚类问题研究. 实验过程中, A区共有作战平台类型12种, 数量23个, 各平台包含的具体资源属性类型有12种, 同类型的不同平台采用不同字符进行表示. 实验所需的数据是在战役演习项目中对A区域作战平台数据进行收集整理的基础上, 随机选取的3组作战平台数据, 每组数据包含23个平台数据样本.

针对联合作战战役行动中平台聚类问题, 实验所需搭建环境以及所采用的实验原理和方法都与4.1节实验基本相同, 这里不再赘述. 针对本文提出方法的伪代码, 程序在执行中将聚类中心点选取方式调整为利用每个任务簇的任务数据平均值进行确定, 并将该值作为对应平台簇的初始聚类中心点.

图10为在3组平台数据下两种算法的实验结果比较图. 图10(a)为基于QK-means的量子增强求解方法的实验结果, 图10(b)为经典K-means算法的实验结果. 从图中可以分析得出, 两种算法都可以对3组平台数据进行聚类分簇, 但本文提出的方法在聚类效果上要优于经典K-means算法, 其主要原因就是经典K-means算法在初始聚类中心点选取时随机性较大, 容易陷入局部较优解.

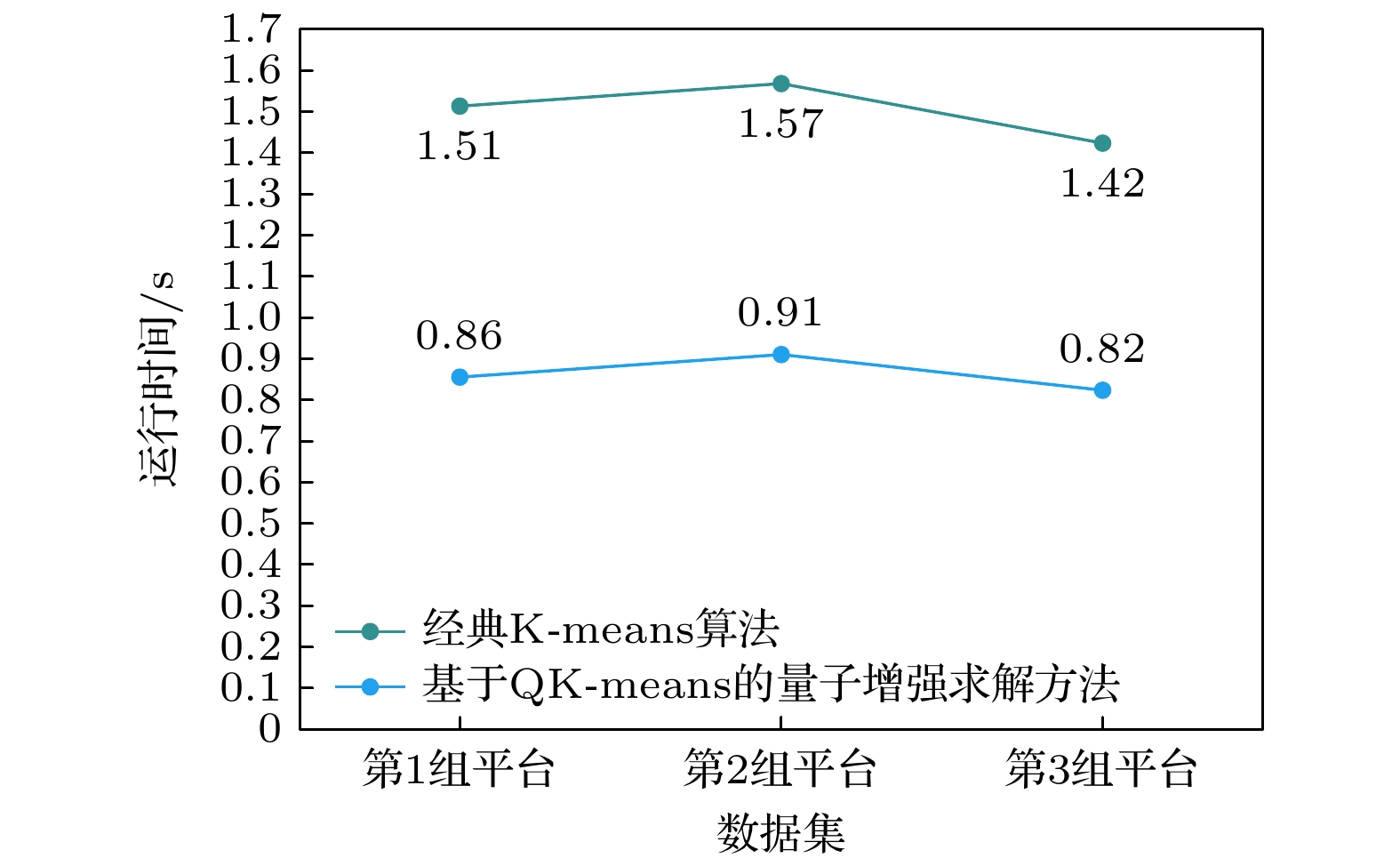
图11为在3组平台数据下两种算法的运行时间对比图. 从图中可以分析得出, 在3组平台数据下本文提出的方法的运行时间低于经典K-means算法的运行时间, 再次验证了本文提出的方法的量子并行计算优势. 此外, 由于3组平台数据的规模相同, 所以两种算法在3组数据下的运行时间也基本相等.

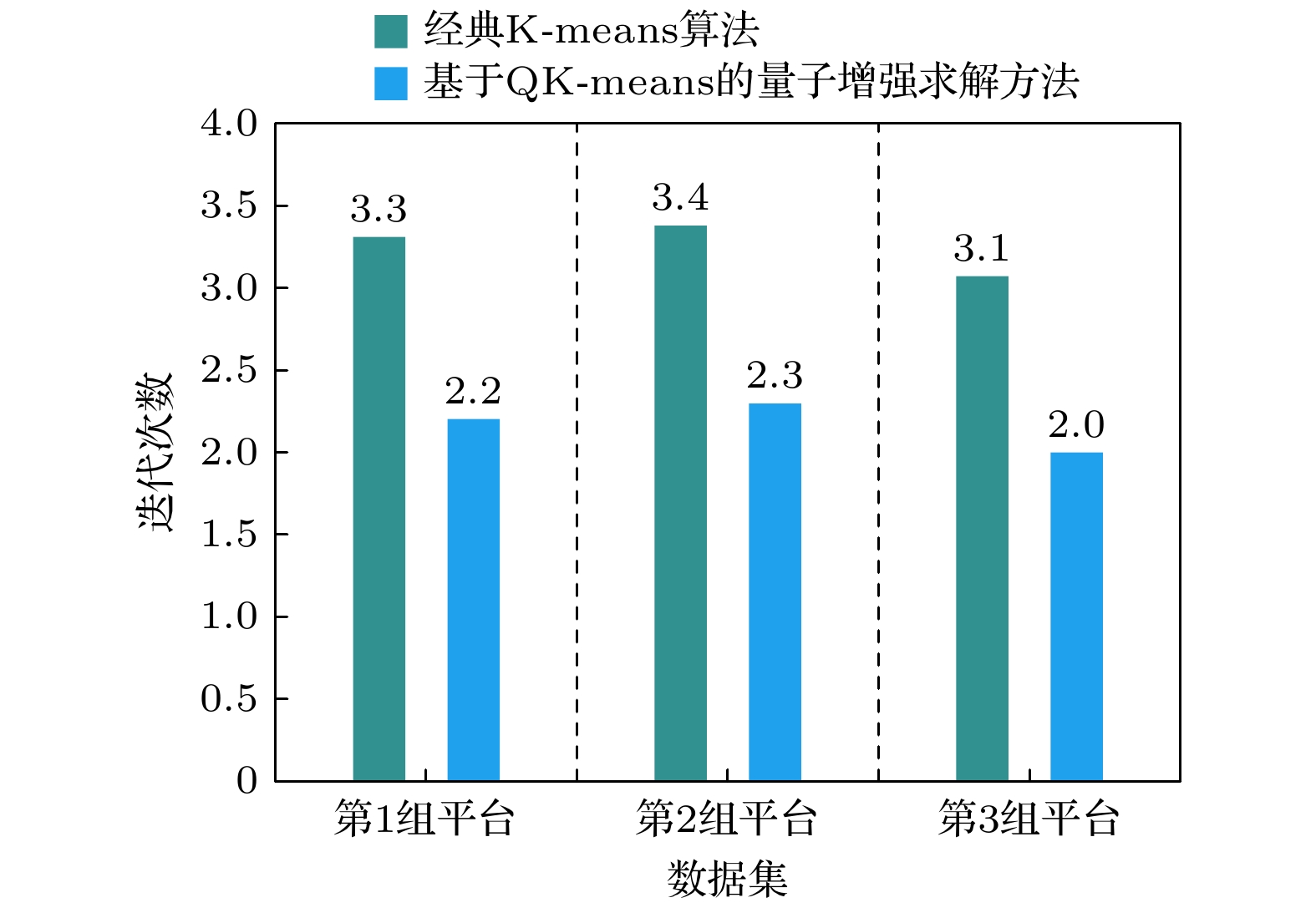
图12为在3组平台数据下两种算法的迭代次数对比图. 由于图中迭代次数是经过多次试验测试得到的平均值, 所以不一定是整数值. 从图12分析可以得出, 在3组数据下本文提出的方法的迭代次数少于经典K-means算法的迭代次数, 且由于3组平台数据的规模相同, 两种算法在3组数据下的迭代次数也基本相等.

根据经典K-means算法流程图(图1), 经典K-means算法中主要消耗资源的步骤为计算聚类数据样本与各聚类中心点之间的欧氏距离、计算聚类数据集的残差平方和等. 根据文献[35]相关内容, 计算聚类数据样本与各聚类中心点之间的欧氏距离部分的时间复杂度为$O\left( {KMN} \right)$, 计算聚类数据集的残差平方和部分的时间复杂度也为$O\left( {KMN} \right)$, 其中K为聚类中心点数量, M为数据样本维度数量, N为数据样本数量. 所以如果算法迭代次数为Z, 则经典K-means算法总的时间复杂度为$O\left( {2 ZKMN} \right)$. 而根据基于QK-means的量子增强求解方法的伪代码(表2), 该方法主要针对经典K-means算法的计算聚类数据样本与各聚类中心点之间的欧氏距离部分和计算聚类数据集的残差平方和部分进行量子增强, 实现并行计算. 根据文献[36]相关内容, 在基于QK-means的量子增强求解方法中, 计算聚类数据样本与各聚类中心点之间的欧氏距离部分的时间复杂度为$O\left( {KN\log M} \right)$, 计算聚类数据集的残差平方和部分的时间复杂度也为$O\left( {KN\log M} \right)$, 其中K为聚类中心点数量, N为数据样本数量, M为数据样本维度数量. 如果算法迭代次数为Z, 则该方法总的时间复杂度为$O\left( {2 ZKN\log M} \right)$. 从分析的结果可以看出本文所提方法与经典K-means算法相比, 较大幅度地缩短了算法的时间复杂度, 实现了量子增强.

通过对经典K-means算法运行结构进行仔细分析, 该算法在进行聚类数据样本与各聚类中心点之间的欧氏距离计算以及聚类数据集的残差平方和计算时需要分配较多额外的辅助存储空间. 根据文献[35]相关内容, 分析得出计算聚类数据样本与各聚类中心点之间的欧氏距离部分空间复杂度为$O\left( {MK} \right)$, 计算聚类数据集的残差平方和部分空间复杂度为$O\left( {M\left( {N + K} \right)} \right)$, 所以经典K-means算法总的空间复杂度应该取较大值为$O\left( {M\left( {N + K} \right)} \right)$, 其中K为聚类中心点数量, N为数据样本数量, M为数据样本维度数量. 而本文提出的方法在计算欧氏距离时需要先对数据样本量子化, 通过量子化可以减少计算所需的空间资源, 根据文献[35]相关内容, 该方法中的计算聚类数据样本与各聚类中心点之间的欧氏距离部分空间复杂度为$O\left( {K\log M} \right)$, 计算聚类数据集的残差平方和部分空间复杂度为$O\left( {\left( {N + K} \right)\log M} \right)$, 所以该方法总的空间复杂度为$O\left( {\left( {N + K} \right)\log M} \right)$. 与经典K-means算法相比, 本文提出的方法在算法空间复杂度方面具有明显降低.

针对联合作战战役行动中平台聚类编组问题, 本文提出了基于QK-means的量子增强求解方法. 首先, 该方法在经典K-means算法基础上, 结合具体实际问题, 对算法结果影响较大的初始聚类分簇数量与初始聚类中心点位置等环节进行了优化处理, 降低了随机选取给算法带来的误差影响, 避免算法结果陷入局部最优解; 其次, 该方法针对经典K-means算法中需要消耗较大计算资源计算聚类数据样本与各聚类中心点之间的欧氏距离部分和计算聚类数据集的残差平方和部分, 构建对应的量子线路进行求解, 实现量子增强与加速; 最后, 在公共数据集上和具体的战役平台编组中对经典K-means算法和基于QK-means的量子增强求解方法进行仿真验证与分析, 实验结果表明, 本文提出的方法能较好地解决联合作战战役行动中平台聚类编组问题, 与经典K-means算法相比, 在时间复杂度和空间复杂度两个方面都有较大幅度降低. 该方法虽然便于理解, 有较高的准确率, 算法的复杂度也大幅度降低, 但该方法量子化程度有限, 需要较多的计算资源. 如何提升基于QK-means的量子增强求解方法的量子化程度是下一步我们重点需要研究的方向.