高级搜索

基于迁移学习的共形超构表面散射场高效智能计算方法

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

刘凯越, 李腾耀, 郑娜娥, 田志富, 蔡通, 王彦朝, 曹超华. 基于迁移学习的共形超构表面散射场高效智能计算方法[J]. 物理学报, 2024, 73(23): 234101-1. doi: 10.7498/aps.73.20241160
引用本文: 刘凯越, 李腾耀, 郑娜娥, 田志富, 蔡通, 王彦朝, 曹超华. 基于迁移学习的共形超构表面散射场高效智能计算方法[J]. 物理学报, 2024, 73(23): 234101-1. doi: 10.7498/aps.73.20241160
shu
Kai-Yue Liu, Teng-Yao Li, Na-E Zheng, Zhi-Fu Tian, Tong Cai, Yan-Zhao Wang, Chao-Hua Cao. Efficient intelligent calculation method for conformal metasurface scattering field based on transfer learning[J]. Acta Physica Sinica, 2024, 73(23): 234101-1. doi: 10.7498/aps.73.20241160
Citation: Kai-Yue Liu, Teng-Yao Li, Na-E Zheng, Zhi-Fu Tian, Tong Cai, Yan-Zhao Wang, Chao-Hua Cao. Efficient intelligent calculation method for conformal metasurface scattering field based on transfer learning[J]. Acta Physica Sinica, 2024, 73(23): 234101-1. doi: 10.7498/aps.73.20241160
shu

基于迁移学习的共形超构表面散射场高效智能计算方法

  • 1.

    信息工程大学五院, 郑州　450001

  • 2.

    信息工程大学四院, 郑州　450001

  • 3.

    空军工程大学防空反导学院, 西安　710051

  • 4.

    中国人民解放军95607部队, 成都　610000

    • 作者简介: 刘凯越. E-mail: lky_930128@163.com .
    通讯作者: E-mail: caitong326@sina.cn.; 

  • 中图分类号: 41.20.Jb, 42.25.Bs, 81.05.Xj

Efficient intelligent calculation method for conformal metasurface scattering field based on transfer learning

  • 1.

    Fifth College, Information Engineering University, Zhengzhou 450001, China

  • 2.

    Fourth College, Information Engineering University, Zhengzhou 450001, China

  • 3.

    Air and Missile Defense College, Airforce Engineering University, Xi’an 710051, China

  • 4.

    Unit 95607 of the People’s Liberation Army, Chengdu 610000, China

    • Corresponding author: E-mail: caitong326@sina.cn.; 

  • MSC: 41.20.Jb, 42.25.Bs, 81.05.Xj

  • 摘要: 共形超构表面具有灵活的外形, 便于适应复杂的平台结构, 在移动载体散射调控方面具有显著的应用优势. 但共形超构表面散射场电磁仿真时间周期长、优化复杂, 难以支撑共形超构表面的敏捷设计. 本文提出了一种基于迁移学习的共形超构表面散射场高效智能计算方法. 首先, 根据天线理论和全波电磁仿真在物理机理上的同一性, 预先用大量理论数据训练源域模型, 构建相位分布与散射场的初始映射模型; 然后, 将少量全波仿真训练数据作为目标域样本, 依托预训练、参数冻结和模型微调实现初始模型的有效迁移, 完成超构表面相位分布到散射场映射模型的构建; 最后, 针对不同的共形几何结构, 在迁移学习模型基础上进行了二次迁移. 结果表明, 本文所提方法的散射场计算时间较全波仿真下降3个数量级, 在少样本条件下应用迁移学习后散射场计算精度平均提升19.8%, 训练数据量仅占未迁移学习模型的42.9%, 数据集收集时间缩短50.1%, 同时在超构表面共形结构发生改变时具有一定泛化性.
    Abstract: Conformal metasurfaces with flexible structures can fit complicated platforms and have obvious advantages in moving platforms scattering manipulations. However, the far-field simulation of conformal metasurface is time-consuming and difficult to optimize, thereby making the its agile design difficult. Here, an efficient and intelligent scattering field calculation method is proposed based on transfer learning for conformal metasurfaces. Firstly, according to the consistency in physical mechanism between antenna theory and full wave simulation, an initial mapping model between phase distribution and far-field of metasurface is constructed and pre-trained based on a large quantity of theoretical data in source domain. Secondly, by pre-training, parameter freezing and model fine-tuning, the far-field prediction model for full wave simulation is transferred and achieved successfully, based on a small quantity of full wave simulation data in target domain. Finally, the transfer learning model for far-field prediction is transferred once again for conformal metasurfaces with different structures. Results indicate that the proposed method only consumes 0.1% of full wave simulation time for conformal metasurface far-field calculation. In fewer samples, the model with transfer learning can improve the average accuracy by 19.8%, and the training data account for only 42.9% for the models without transfer learning, which reduces the training data collection time by 50.1%. Moreover, our far-field calculation method demonstrates good transfer performance between conformal metasurfaces with different structures.
  • 加载中

  • 图 1  共形超构表面迁移学习框架

    Figure 1.  Transfer learning framework of conformal metasurface.

    下载: 全尺寸图片 幻灯片

    图 2  共型超构表面剖面结构和单元电磁特性　(a) 茹科夫斯基翼型函数曲线; (b) 共型超构表面结构; (c) 超构单元结构及其仿真设置, 其中x和y方向设置为unit cell边界, z方向为open边界; (d) 超构单元的同极化反射相位和幅度

    Figure 2.  The structure of conformal metasurface and electromagnetic response of meta-atom: (a) Жуковский airfoil function; (b) the structure of conformal metasurface; (c) prototype of the meta-atom and simulation setup, where unit cell conditions are applied in x and y directions and open condition is applied in z direction; (d) reflection phase and amplitude of co-polarization.

    下载: 全尺寸图片 幻灯片

    图 3  源域训练数据生成和模型构建　(a) 基于天线理论计算得到大量相位分布和散射场数据; (b) 预训练模型${\mathcal{M}_0}$的网络架构

    Figure 3.  Training data generation and model network construction of source domain: (a) Numerous phase distribution and scattering data can be generated based on antenna theory; (b) paradigm of pre-trained network ${\mathcal{M}_0}$.

    下载: 全尺寸图片 幻灯片

    图 4  全波仿真数据获取设置　(a) 联合自动化仿真流程; (b) 共形超构表面全波仿真设置

    Figure 4.  Configurations of full wave simulations: (a) The flowchart of associated automation simulation; (b) the full wave simulation setup of conformal metasurface.

    下载: 全尺寸图片 幻灯片

    图 5  迁移学习策略

    Figure 5.  Transfer learning strategy.

    下载: 全尺寸图片 幻灯片

    图 6  模型结构分析　(a) 卷积块数量取1, 2, 3时模型的平均测试损失值; (b) 全连接层数量为1, 2, 3, 4, 5时模型的平均测试损失值; (c) 激活函数分别为ReLU, ReLU6, ELU, Leaky ReLU和Soft Plus模型平均测试损失值

    Figure 6.  Network structure analysis. Model average train loss with (a) convolution blocks number of 1, 2, 3, (b) fully connected layer number of 1, 2, 3, 4, 5, and (c) activation function of ReLU, ReLU6, ELU, Leaky ReLU and Soft Plus.

    下载: 全尺寸图片 幻灯片

    图 7  模型超参数寻优. 测试集的平均损失随 (a) 学习率, (b) 批大小, (c) 迭代轮次变化曲线

    Figure 7.  Model hyperparameter optimization. The average loss of the test set varies with (a) learning rate, (b) batch size, and (c) iteration rounds.

    下载: 全尺寸图片 幻灯片

    图 8  迁移学习冻结层数对测试集损失值的影响

    Figure 8.  The impact of transfer learning frozen layers numbers on loss value.

    下载: 全尺寸图片 幻灯片

    图 9  模型${\mathcal{M}_0}$, ${\mathcal{M}_1}$和${\mathcal{M}_2}$的平均损失值和效果验证 模型${\mathcal{M}_0}$(a), ${\mathcal{M}_1}$(b), ${\mathcal{M}_2}$(c)的损失值随迭代轮次的变化曲线以及两种测试算例下的拟合效果

    Figure 9.  Loss value and verification of ${\mathcal{M}_0}$, ${\mathcal{M}_1}$ and ${\mathcal{M}_2}$: Loss over the epoch and prediction results under two testing instances of ${\mathcal{M}_0}$(a), ${\mathcal{M}_1}$(b), ${\mathcal{M}_2}$(c).

    下载: 全尺寸图片 幻灯片

    图 10  迁移学习模型与全波仿真时间对比　(a) 结构1共形超构表面在软件中进行全波仿真计算散射场, 与利用模型${\mathcal{M}_1}$计算散射场的时间对数值; (b) 结构2共形超构表面在软件中进行全波仿真计算散射场, 与利用模型${\mathcal{M}_2}$计算散射场的时间对数值

    Figure 10.  Time comparison of transfer learning model and full-wave simulation: (a) Logarithmic value of full-wave simulation time in CST and model ${\mathcal{M}_1}$ calculation time for conformal metasurface with structure 1; (b) logarithmic value of full-wave simulation time in CST and model ${\mathcal{M}_2}$ calculation time for conformal metasurface with structure 2.

    下载: 全尺寸图片 幻灯片

    图 11  迁移学习模型和未迁移学习模型性能对比分析　(a) 模型精度随训练数据量的变化关系; (b) 数据集收集时间柱状图

    Figure 11.  Performances comparative analysis of models with and without transfer learning: (a) Model accuracy varies with the amount of training data; (b) bar chart of dataset collection time.

    下载: 全尺寸图片 幻灯片

    图 12  结构2共形超构表面散射场计算模型平均损失函数及效果验证　(a) 基于结构2全波仿真数据直接训练得到的远场计算模型${\mathcal{M}'_2}$(未迁移学习); (b) 基于结构1理论数据散射场计算模型${\mathcal{M}_0}$迁移训练得到的结构2共形超构表面远场计算模型${\mathcal{M}''_2}$(经历一次迁移学习); (c) 基于结构1迁移学习模型${\mathcal{M}_1}$迁移训练得到的结构2共形超构表面远场计算模型${\mathcal{M}_2}$(经历两次迁移学习)

    Figure 12.  Average loss value and performance verifications of structure 2 conformal metasurface far-field prediction models: (a) Far-field prediction model ${\mathcal{M}'_2}$(without transfer learning) for structure 2 conformal metasurface, trained based on structure 2 conformal metasurface full wave calculation data; (b) far-field prediction model ${\mathcal{M}''_2}$ (with once transfer learning) for structure 2 conformal metasurface, transferred from the structure 1 conformal metasurface theoretical far-field prediction model ${\mathcal{M}_0}$; (c) far-field prediction model ${\mathcal{M}_2}$ (with twice transfer learning) for structure 2 conformal metasurface, transferred from the structure 1 conformal metasurface full wave calculation far-field prediction model ${\mathcal{M}_1}$.

    下载: 全尺寸图片 幻灯片

    图 13  不同轮廓方程结构迁移学习效果　(a) 轮廓方程为圆弧的共形超构表面散射场预测模型${\mathcal{M}_{\text{c}}}$的平均损失值和效果验证; (b) 轮廓方程为的二次曲线的共形超构表面散射场预测模型${\mathcal{M}_{\text{q}}}$的平均损失值和效果验证. 其中左图中的插图表示结构1轮廓和圆弧、二次曲线结构对比图

    Figure 13.  The transfer learning performance of different contour equation structures: (a) Average loss value and performance verifications of far-field prediction model ${\mathcal{M}_{\text{c}}}$ for conformal metasurface with contour equation of a circular arc; (b) average loss value and performance verifications of far-field prediction model ${\mathcal{M}_{\text{q}}}$ for conformal metasurface with contour equation of a quadratic curve. The illustration in the left figure represents the comparison between the outline of structure 1 and the structure of arc and quadratic curves.

    下载: 全尺寸图片 幻灯片

    表 1  模型结构的搜索空间

    Table 1.  Search space of model structure.

    序号控制变量候选集合
    1卷积块数量$ \{1, 2, 3\} $
    2全连接块数量(不含输出层)$ \{1, 2, 3, 4, 5\} $
    3激活函数类型{ReLU, ReLU6, ELU, LeakyReLU, SoftPlus}
    下载: 导出CSV

    表 2  模型超参数的搜索空间

    Table 2.  Search space of model hyperparameters.

    序号控制变量候选集合
    1学习率{0.0001, 0.0002, . .., 0.0099, 0.01}, 步长为0.0001
    2批量大小{32, 64, 128, 256, 512, 1024}
    3迭代轮次{5, 10, 15, 20, . .., 90, 95, 100}, 步长为5
    下载: 导出CSV

    表 3  模型迁移关系

    Table 3.  The transfer relationship between models.

    序号模型预训练模型迁移次数
    1${\mathcal{M}_0}$无0
    2${\mathcal{M}_1}$${\mathcal{M}_0}$1
    3${\mathcal{M}'_2}$无0
    4${\mathcal{M}''_2}$${\mathcal{M}_0}$1
    5${\mathcal{M}_2}$${\mathcal{M}_1}$2
    下载: 导出CSV
  • [1] Liu K Y, Wang G M, Cai T, Guo W L, Zhuang Y Q, Liu G 2018 Chin. Phys. B 27 084101 doi: 10.1088/1674-1056/27/8/084101
    [2] Liu K T, Wang G M, Cai T, Dai B J, Xiao Y, Li H P, Guo W L 2019 J. Phys. D: Appl. Phys. 52 255002 doi: 10.1088/1361-6463/ab12ba
    [3] Bai H, Wang G M, Zou X J , Xie P, Shi Y P 2022 Chin. Phys. B 31 054102 doi: 10.1088/1674-1056/ac373b
    [4] Liu K Y, Wang G M, Cai T, Li H P, Li T Y 2021 IEEE Trans. Antennas Propag. 69 3349 doi: 10.1109/TAP.2020.3037647
    [5] Germain D, Seetharamdoo D, Burokur S N, de Lustrac A 2013 Appl. Phys. Lett. 103 124102 doi: 10.1063/1.4821357
    [6] Wang Y C, Feng Q, Kong X D, Liu H X, Han J Q, Li L 2024 IEEE Antennas Wirel. Propag. Lett. 23 970 doi: 10.1109/LAWP.2023.3340682
    [7] Fu B, Yu S X, Kou N, Ding Z, Zhang Z P 2022 Chin. Phys. B 31 40703 doi: 10.1088/1674-1056/ac3a65
    [8] Gupta E, Bonner C, Lazarus N, Mirotznik M S, Nicholson K J 2023 IEEE Antennas Wirel. Propag. Lett. 22 2629 doi: 10.1109/LAWP.2023.3282556
    [9] Fu C, Han L, Liu C, Lu X, Sun Z 2022 IEEE Trans. Antennas Propag. 70 2352 doi: 10.1109/TAP.2021.3112618
    [10] Wang Y, Su J, Li Z, Guo Q, Song J 2020 IEEE Antennas Wirel. Propag. Lett. 19 631 doi: 10.1109/LAWP.2020.2974018
    [11] Luo X Y, Chen K, Guo W L, Feng Y J 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT) Guangzhou China, May 19–22, 2019 p1
    [12] Xu H X, Hu G W, Wang Y Z, Wang C H, Wang M Z, Wang S J, Huang Y J, Genevet P, Huang W, Qiu C W 2021 Light Sci. Appl. 10 75 doi: 10.1038/s41377-021-00507-8
    [13] 王朝辉, 许河秀, 逄智超, 王明照, 王少杰 2022 红外与毫米波学报 41 210 doi: 10.11972/j.issn.1001-9014.2022.01.015 Wang C H, Xu H X, Pang Z C, Wang M Z, Wang S J 2022 J. Infrared Millimeter Waves 41 210 doi: 10.11972/j.issn.1001-9014.2022.01.015
    [14] Srilatha K., Madhav B. T. P., babu B. Anil, Das Sudipta, Rao M. C. 2022 Appl. Phys. A 128 1091 doi: 10.1007/s00339-022-06247-9
    [15] 刘梦蛟, 李添悦, 戈钦, 王漱明, 王振林, 祝世宁 2022 光学学报 42 21260049 Liu M J, Li T, Ge Q, Wang S, Wang Z, Zhu S 2022 Acta Opt. Sin. 42 21260049
    [16] Xu H X, Tang S, Sun C, Li L, Liu H, Yang X, Yuan F, Sun Y 2018 Photonics Res. 6 782 doi: 10.1364/PRJ.6.000782
    [17] 杨斯雯, 黄玲玲, 王涌天 2023 光学技术 49 522 Yang S, Huang L, Wang Y 2023 Opt. Tech. 49 522
    [18] Ma Y C, Chen S, Ermon S, Lobell David B 2024 Remote Sens. Environ. 301 113924 doi: 10.1016/j.rse.2023.113924
    [19] Fu S Y, Tao S Y, Fan H T, He K, Liu X T, Tao Y L, Zuo J X, Zhang X, Wang Y, Sun Y J 2024 Appl. Energy 353 121991 doi: 10.1016/j.apenergy.2023.121991
    [20] Chen L C, Zhu Y, Papandreou G, Schroff F, Adam H, 2018 European Conference on Computer Vision Berlin Germany, September 8–14, 2018 p833
    [21] Treviso M, Lee J, Ji T, Aken B, Cao Q, Ciosici M, Hassid M, Heafield K, Hooker S, Martins P, Martins A, Milder P, Raffel C, Simpson E, Slonim N, Dodge J,Strubell E, Balasubramanian N, Derczynski L, Gurevych I, Schwartz R 2023 Trans. Assoc. Comput. Linguist. 11 826 doi: 10.1162/tacl_a_00577
    [22] Zhu R C, Qiu T S, Wang J F, Sui S, Hao C L, Liu T, Li Y F, Feng M D, Zhang A X, Qiu C W, Qu S B 2021 Nat. Commun. 12 2974 doi: 10.1038/s41467-021-23087-y
    [23] Xu Y, Li F, Gu J, Bi Z, Cao B, Yang Q, Han J, Hu Q, Zhang W 2024 Adv. Photonics Nexus 3 026002
    [24] Qu Y R, Jing L Shen Y C, Qiu M, Soljačić M 2019 ACS Photonics 6 1168 doi: 10.1021/acsphotonics.8b01526
    [25] Xu D, Luo Y, Luo J, Pu M, Zhang Y, Ha Y, Luo X 2021 Opt. Mater. Express 11 1852 doi: 10.1364/OME.427426
    [26] Zhang J, Qian C, Fan Z X, Chen J T, Li E P, Jin J M, Chen H S 2022 Adv. Opt. Mater. 10 2200748 doi: 10.1002/adom.202200748
    [27] 张森, 席德科, 李华星 2019 工程热物理学报 40 1058 Zhang S, Xi D, Li H 2019 J. Eng. Thermophys. 40 1058
    [28] Jia Y T, Qian C, Fan Z X, Ding Y Z, Wang Z D, Wang D P, Li E P, Zheng B, Cai T, Chen H S 2022 Adv. Funct. Mater. 32 2109331 doi: 10.1002/adfm.202109331
  • 加载中
图( 13) 表( 3)
计量
  • 文章访问数:  233
  • HTML全文浏览数:  233
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-08-20
  • 刊出日期:  2024-12-05

基于迁移学习的共形超构表面散射场高效智能计算方法

    通讯作者: E-mail: caitong326@sina.cn.; 
    作者简介: 刘凯越. E-mail: lky_930128@163.com
  • 1. 信息工程大学五院, 郑州　450001
  • 2. 信息工程大学四院, 郑州　450001
  • 3. 空军工程大学防空反导学院, 西安　710051
  • 4. 中国人民解放军95607部队, 成都　610000
  • 收稿日期:  2024-08-20

摘要: 共形超构表面具有灵活的外形, 便于适应复杂的平台结构, 在移动载体散射调控方面具有显著的应用优势. 但共形超构表面散射场电磁仿真时间周期长、优化复杂, 难以支撑共形超构表面的敏捷设计. 本文提出了一种基于迁移学习的共形超构表面散射场高效智能计算方法. 首先, 根据天线理论和全波电磁仿真在物理机理上的同一性, 预先用大量理论数据训练源域模型, 构建相位分布与散射场的初始映射模型; 然后, 将少量全波仿真训练数据作为目标域样本, 依托预训练、参数冻结和模型微调实现初始模型的有效迁移, 完成超构表面相位分布到散射场映射模型的构建; 最后, 针对不同的共形几何结构, 在迁移学习模型基础上进行了二次迁移. 结果表明, 本文所提方法的散射场计算时间较全波仿真下降3个数量级, 在少样本条件下应用迁移学习后散射场计算精度平均提升19.8%, 训练数据量仅占未迁移学习模型的42.9%, 数据集收集时间缩短50.1%, 同时在超构表面共形结构发生改变时具有一定泛化性.

English Abstract

    全文HTML

    1.   引　言

    • 超构表面通过周期或准周期地排布亚波长超构单元, 能够对电磁波极化、幅度、相位等属性进行调控, 凭借其独特性能被广泛应用在波束奇异折反射、涡旋波生成、新颖天线制备等方面[1–3]. 共形超构表面相较于平面超构表面, 在结构设计上更加灵活, 通过将超构表面与曲面结合, 可实现对电磁波的调控, 能够更好地适应载体外形, 在无人机、飞机等目标雷达散射截面(radar cross section, RCS)减缩和增强等方面具有潜在应用.

      目前, 已经涌现出基于共形超构表面的新颖天线设计[4–8]、RCS减缩[9–11]、共形隐身衣[12–14]等创新应用. 传统共形超构表面设计主要根据传播相位调控原理[15]叠加因曲面造成的波程差, 通过实现相位补偿构建相位分布和超构表面散射场之间的关系[16,17]. 该方法依赖于超构单元之间相互独立的假设条件, 对单元的宏观排布序列进行设计, 没有考虑结构弯曲造成超构单元电磁性能变化以及单元间耦合和相互作用带来的影响. 但实际上相邻超构单元潜在相互耦合作用将导致电磁特性发生一定变化, 特别是在结构发生共形弯曲时, 必将对超构表面整体电磁特性带来不可预测的影响. 为充分考虑结构弯曲、单元耦合等复杂影响要素, 深度学习方法逐步应用到超构表面设计等方面, 通过深度学习的非线性拟合能力实现超构表面散射场的计算. 然而, 这些深度学习方法往往依赖大量的训练数据进行模型训练, 超构表面散射场训练数据的收集需要耗费大量的时间和计算资源. 且对于特定的设计任务, 一旦超构表面几何参数发生轻微变化, 经过训练的网络模型往往难以适配新的问题, 需要重新建立训练数据集和训练模型.

      为解决训练数据集和几何参数变化引起的模型重新构建问题, 迁移学习逐渐应用到电磁领域, 通过迁移训练可将源任务知识和经验与目标任务共享[18–21], 例如, 利用GoogleNet网络进行迁移学习并对超构单元相位响应进行预测[22], 依托迁移学习对不同光谱范围内的单元电磁响应进行预测[23], 在不同多光子单元[24]、不同结构的介质超构单元[25,26]进行知识迁移等. 但是, 这些迁移学习方法主要聚焦单个超构单元结构参数和电磁响应之间的关系研究, 而在超构表面整体相位分布与散射场之间映射关系方面研究较少. 这主要是因为超构表面尺寸更大、结构更复杂、计算复杂度更高, 专业电磁计算软件对超构表面的仿真时间要远远大于超构单元仿真时间, 并且随着超构表面维数增加, 仿真时间和复杂度会显著增加. 因此, 在少样本条件下对超构表面整体相位分布与散射场之间的映射关系进行精准建模, 日益成为支撑共形超构表面高效设计的关键挑战.

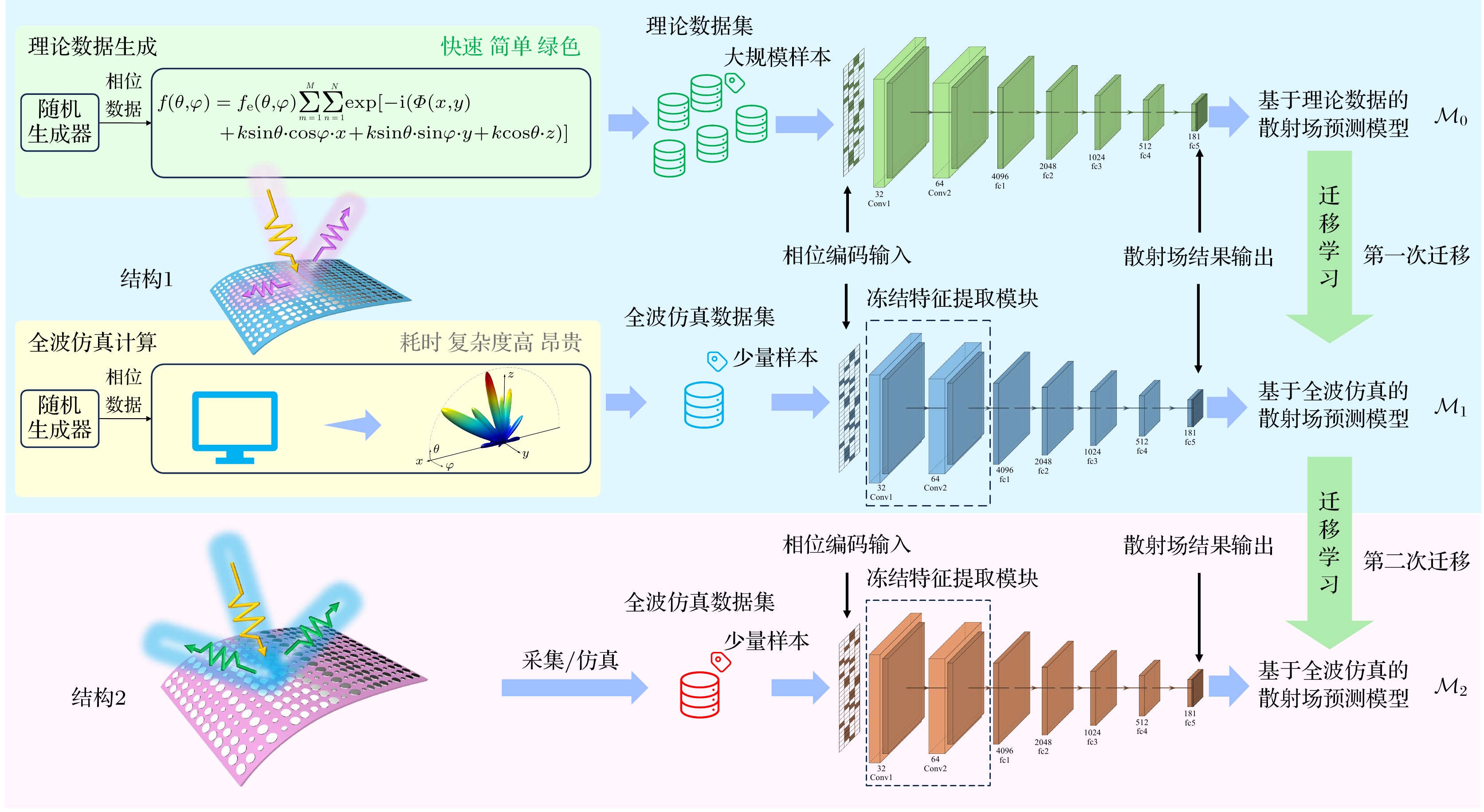
      为此, 本文提出一种基于迁移学习的共形超构表面散射场高效智能计算方法, 总体思路和方法框架如图1所示. 依托大量理论数据构建共形超构表面散射场计算模型, 通过模型预训练、参数冻结和模型微调等迁移学习策略, 在少量全波仿真数据样本条件下将模型迁移到目标域, 建立当前超构表面的高精度散射场计算模型. 在超构表面的几何参数发生变化时, 对散射场计算模型进行快速二次迁移, 实现了不同共形结构超构表面整体散射场的高效智能计算.

    2.   工作机理

    • 本文依托迁移学习来解决少样本条件下的散射场快速精准计算问题, 其中源域为理论数据, 通过输入相位分布并根据公式计算对应散射场理论值的方式可快速构建大量理论训练数据, 源域数据具有经济、运算复杂度低、时间消耗少的优点, 但缺点是没有考虑单元之间耦合等因素, 因此结果与实际电磁响应相差较大. 目标域是全波仿真数据, 在电磁软件中构建共形超构表面, 通过改变单元结构控制输入相位并进行全波仿真得到更准确的超构表面散射场, 目标域数据与实际电磁响应相符且精度较高, 但数据获取昂贵、运算复杂、时间花销大.

      本文利用大量源域数据进行模型预训练, 然后在目标域利用少量数据进行模型参数优化, 总体框架如图1所示. 首先, 利用大量理论数据训练得到相位分布到散射场的映射模型${\mathcal{M}_0}$; 接着, 依托少量超构表面散射场全波仿真数据, 在预训练模型$ \mathcal{M}_{0} $基础上进行模型参数优化得到迁移模型${\mathcal{M}_1}$; 最后, 针对新的共形超构表面结构, 生成新的少量全波仿真数据, 并在${\mathcal{M}_1}$的基础上进行模型迁移, 构建新结构下相位分布与散射场之间的映射模型${\mathcal{M}_2}$. 本文基于该框架建立共形超构表面相位分布到散射场的精确映射关系, 克服共形超构表面因为结构弯曲、耦合等原因带来的影响, 构建可快速适应多种超构表面散射场的高精度、高效率智能计算方法. 下面, 分别从超构表面单元与共形结构、源域散射场计算模型、目标域计算模型迁移对本文方法进行分析.

      • 2.1.   超构表面单元与共形结构

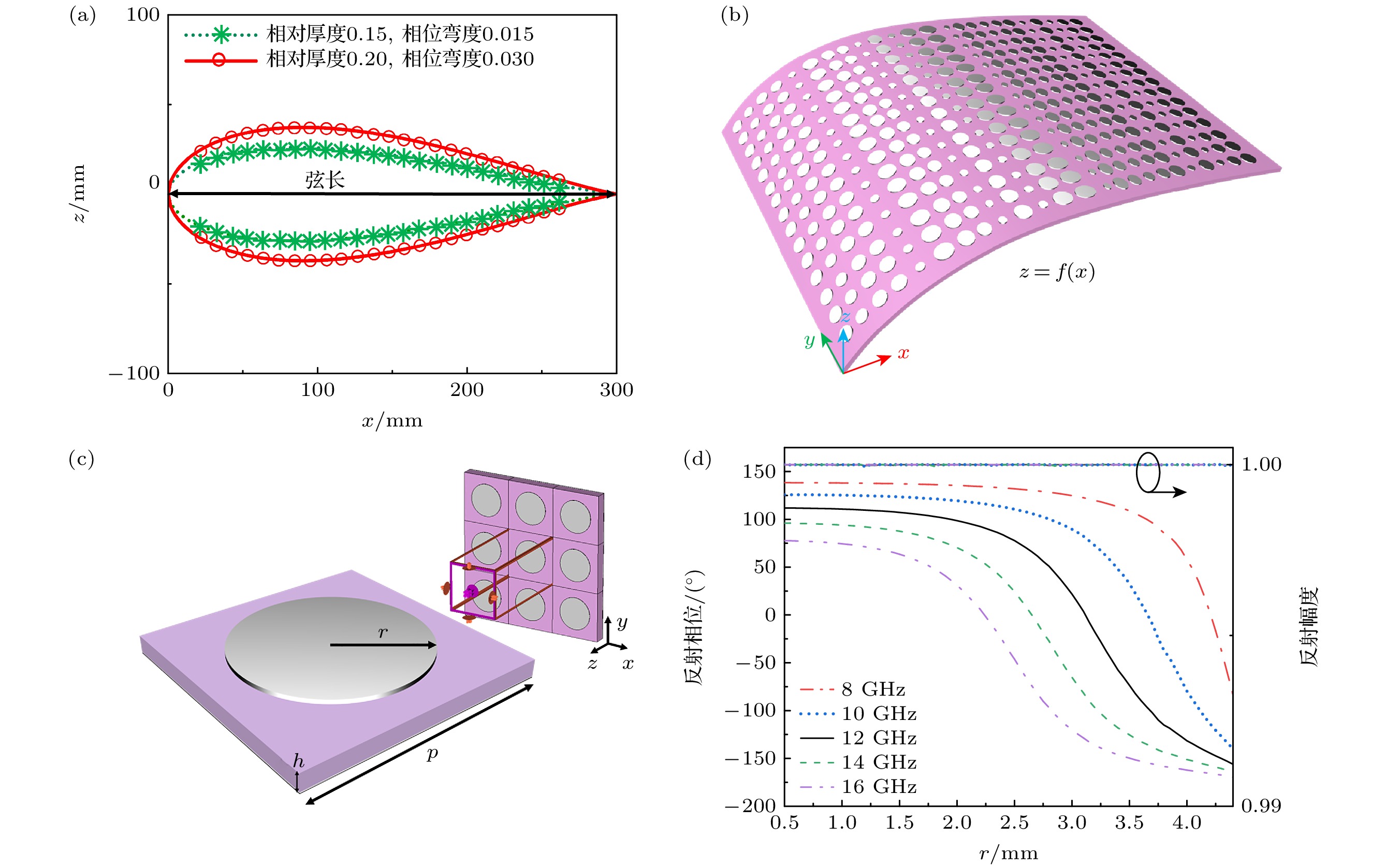
    • 随着无人机在无线通信中继、对抗、保障等多领域的广泛应用, 针对电磁散射场的分析逐渐成为无人机目标特性调控的关键, 对于无人机而言, 机翼结构是其散射主要贡献源之一, 本文以经典的低速翼型茹科夫斯基翼型[27]为例, 设计超构表面共形结构, 超构表面横截面轮廓可以表示如下:

      其中参数$l$表示翼型的弦长, 取值为300 mm; $\delta $表示机翼最大厚度与弦长的比值, 即相对厚度; $\varepsilon $表示机翼中弧线到翼弦的最大距离与弦长的比值, 即相对弯度. 根据(1)式绘制出两种对称翼型如图2(a)所示, 其相对厚度和相对弯度分别取$\delta $ = 0.15, $\varepsilon $ = 0.015和$\delta $ = 0.2, $\varepsilon $ = 0.03. 由于翼型上表面和下表面对称, 因此本文选取其中的上表面作为超构表面的共形结构. $x$, $z$分别是超构单元坐标, 根据翼型弦长, 设置24个超构单元沿着弦长展开, 单元沿着翼型型线等间隔排布, 图2(a)中“o”和“*”分别表示单元中心所在位置, 超构单元坐标按照作者提出的方法求解[4], 在y轴方向上单元沿着直线等间隔排布, 坐标为单元周期$p$的整数倍, 共形超构表面结构如图2(b)所示.

      本文选取的超构单元如图2(c)所示, 上层为圆形金属贴片, 中间是介电常数为2.65, 电损耗正切为0.001的介质层, 底层为金属背板. 利用CST对单元进行仿真, 得到反射相位和幅度随参数r变化的反射频谱如图2(d)所示, 可以看出通过控制半径r可以调控反射波相位, 幅度在8—16 GHz频率范围内均接近于1. 为了便于构建深度学习网络模型, 采用2-bit编码单元进行超构表面的设计, 选取r = 1, 3, 3.47, 4.4 mm四种结构作为2-bit编码超构单元, 在频率为12 GHz时, 相邻单元存在90°相位差. 需要说明的是, 虽然本文用了圆形金属贴片超构单元和茹科夫斯基翼型的共形剖面曲线, 但是本文方法并不局限于上述结构和曲线, 在具体设计的过程中可以根据需要选择合适的超构单元结构和共型剖面函数f.

      • 2.2.   源域散射场计算模型

    • 本文结合源域数据的特点预先利用大量源域数据样本对网络进行模型预训练, 建立源域共形超构表面散射场计算模型, 作为目标域模型迁移的预训练基础.

      • 2.2.1.   理论数据生成

    • 准确且充足的训练数据是确保有监督深度学习模型有效训练的关键, 根据天线理论, 在平面波入射条件下, 超构表面相位分布与散射场之间的关系可以表示为

      其中$\theta $和$\varphi $代表俯仰角和方位角; $M$和$N$为单元阵列大小, $M$和$N$均为正整数; $\varPhi \left( {M, N} \right)$为相位分布矩阵; $x, y, z$为单元在超构表面上的坐标, 可根据共形表面轮廓函数计算得出; $k$为波数, $k = 2\pi /\lambda $, $\lambda $为波长. 根据2-bit超构单元编码, 相位分布矩阵$\varPhi $元素分别有0, 90, 180, 270四种取值. 通过随机生成$G$组相位分布样本, 代入(2)式可快速得到大量相位分布与散射场的成对数据.

      • 2.2.2.   源域数据预处理

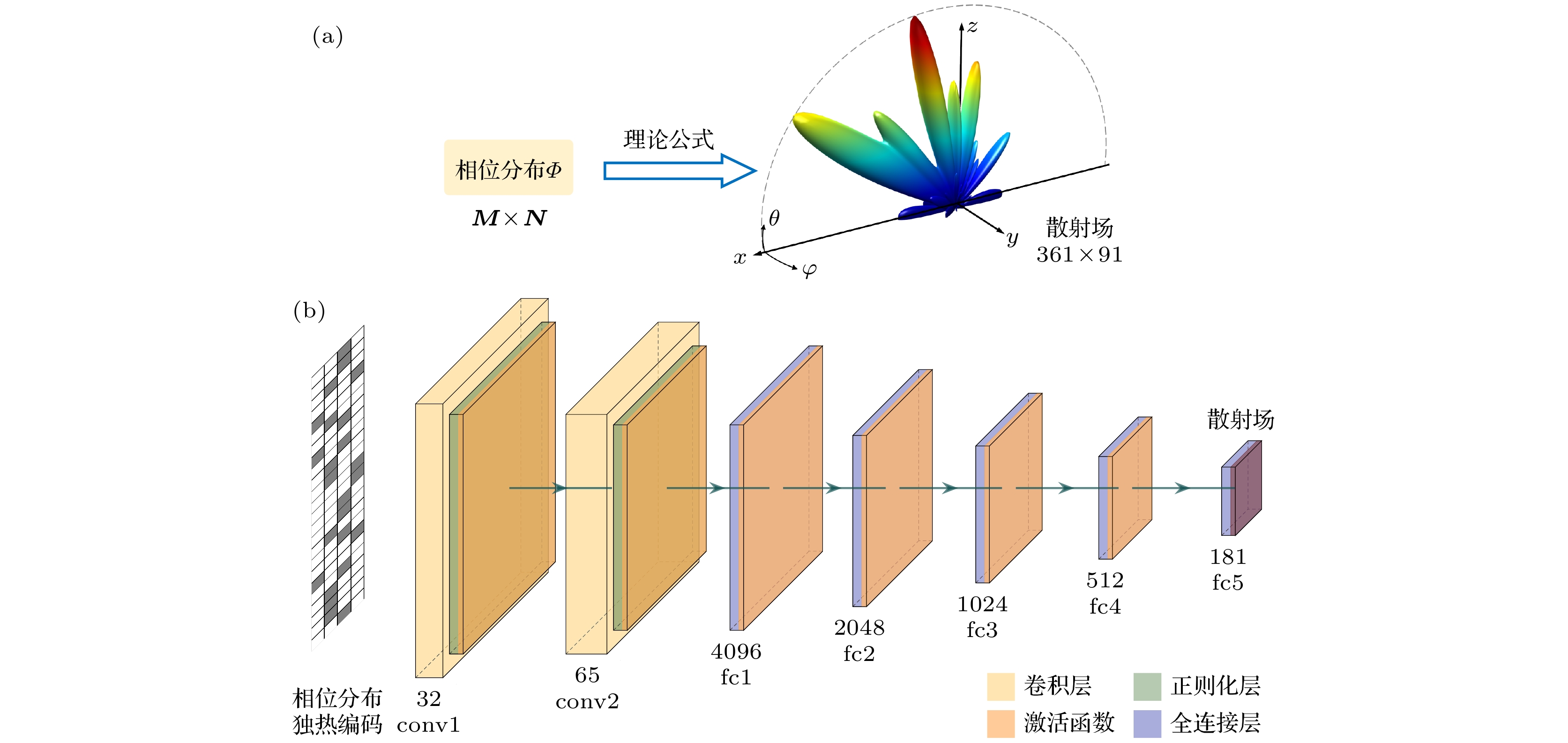
    • 对于相位分布的预处理, 采用先降维再进行 独热编码的处理策略. 本文中相位分布只在一个 维度上具有梯度, 即沿着共形结构弯曲的方向($x$轴方向)存在相位梯度, 在$y$方向没有相位梯度, 为减少数据的冗余性, 将相位分布用$1 \times N ~(N = 24)$的一维向量表示. 同时, 为挖掘不同向量元素间的局部相关性, 使非偏序关系的变量取值不具 有偏序性, 本文对相位分布数据进行了独热编码, 将离散的相位分布映射到欧氏空间[28]. 一维向量被 拓展为$N \times 4$的二维矩阵, 得到独热编码后的相 位分布${{\boldsymbol{X}}_{\mathrm{s}}}$, 其中$N$为相位维度大小, 4为独热编码长度.

      散射场数据为181维的向量, 表示在xoz面俯仰方向以1°为步长俯仰角在0—180°范围内的远场数据, 如图3(a)所示. 基于(3)式对散射场数据进行归一化预处理并记为$ {{\boldsymbol{Y}}_{\text{s}}} $, 此处选用最大最小规则完成散射场归一化,

      预处理完毕的相位分布和散射场数据分别表示为${{\boldsymbol{X}}_{\text{s}}}, {\text{ }}{{\boldsymbol{Y}}_{\text{s}}}$, 其构成大规模源域理论训练数据集${\mathcal{D}_{\text{s}}} = \left( {{{\boldsymbol{X}}_{\text{s}}}, {{\boldsymbol{Y}}_{\text{s}}}} \right)$, 其中${{\boldsymbol{X}}_{\mathrm{s}}}$为24×4的二维矩阵, $ {{\boldsymbol{Y}}_{\text{s}}} $为181×1的一维向量.

      • 2.2.3.   源域模型构建

    • 通过天线理论数据训练深度学习模型, 建立由相位分布到理论散射场之间的非线性映射关系${f_{\text{s}}}:{{\boldsymbol{X}}_{\text{s}}} \to {{\boldsymbol{Y}}_{\text{s}}}$. 以24×4的相位分布独热编码作为输入, 归一化的181×1的散射场数据作为输出, 构建散射场计算模型${\mathcal{M}_0}$网络架构如图3(b)所 示, 该模型包含2个卷积块和5个全连接块. 其中, 卷积块由二维卷积层、正则化层、激活函数构成, 激活函数采用LeakyReLU函数, 卷积块构成了相位分布数据的特征提取模块; 全连接块由全连接层和激活函数构成, 5个全连接层的神经元个数分别为4096, 2048, 1024, 512, 181, 前4个全连接层用于从高维特征中提取散射场的数值映射关系, 最后1个全连接层用于散射场数据的预测输出.

      依托理论训练数据集对散射场计算模型${\mathcal{M}_0}$进行训练, 损失函数采用均方差损失函数, 如(4)式所示:

      其中$n$为样本个数; ${\hat y_i}$和${y_i}$分别为第$i$个样本的预测值和目标值.

      • 2.3.   目标域计算模型迁移

    • 理论数据是理想情况下的散射场, 并未考虑超构单元之间的耦合影响和由于单元共形弯曲带来的电磁响应的变化, 因此散射场与实际情况之间存在差异, 基于天线理论散射场预测知识${f_{\text{s}}}$不能准确地实现目标域散射场计算. 迁移学习将从理论数据${\mathcal{D}_{\text{s}}} = \left( {{{\boldsymbol{X}}_{\text{s}}}, {{\boldsymbol{Y}}_{\text{s}}}} \right)$学到的知识迁移应用到目标域中, 使用少量全波仿真散射场数据样本, 建立更加准确的共形超表面散射场预测模型.

      • 2.3.1.   仿真数据获取

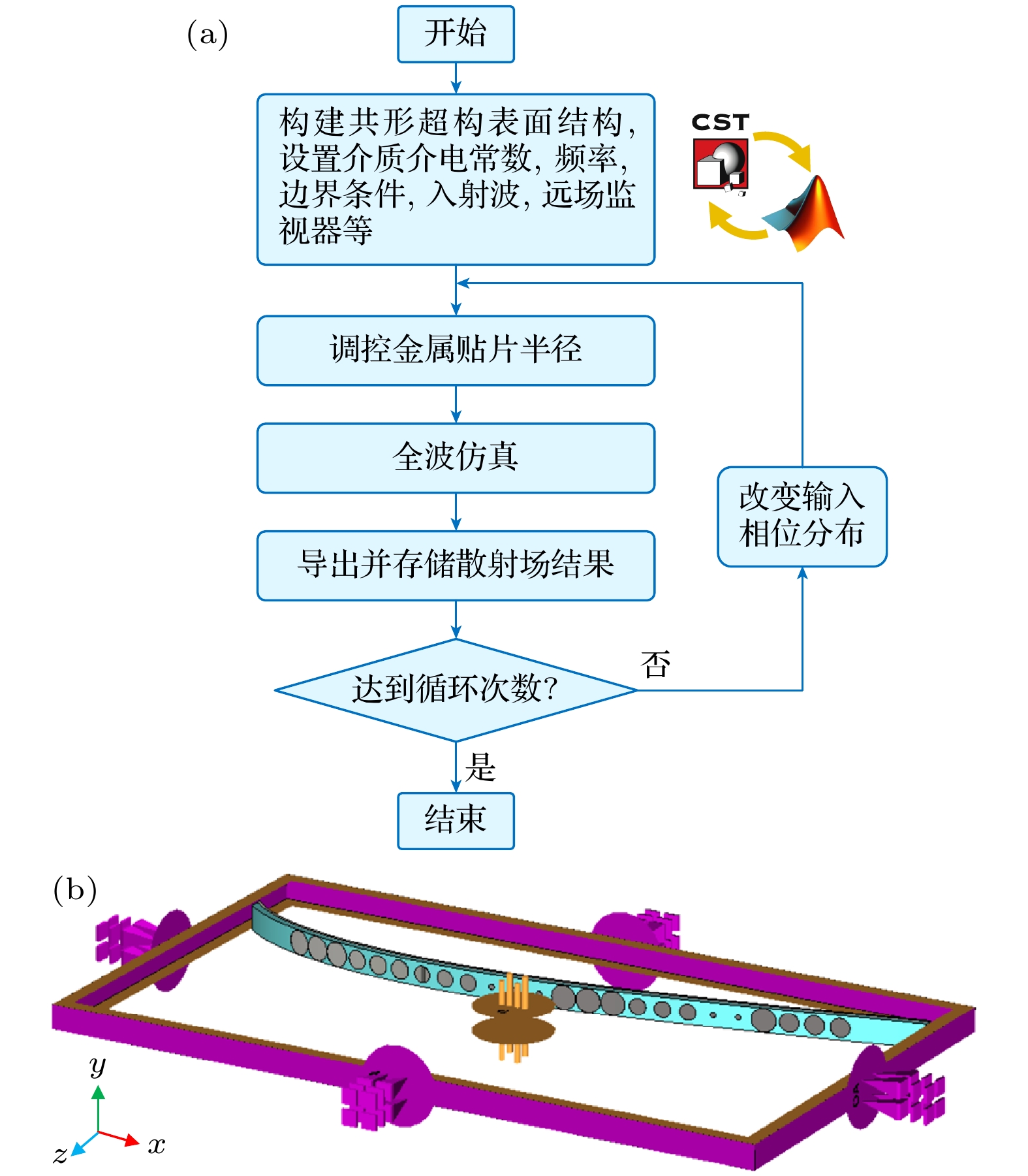
    • 全波仿真是一种基于Maxwell方程的数值分析算法, 在不做任何简化假设的情况下求解完整的Maxwell方程组, 能够精确分析三维射频电磁场分布. 利用电磁仿真软件CST进行全波仿真可以得到超构表面更准确的散射场, 但这会消耗大量的计算资源, 时间花销远远大于理论计算, 难以进行大规模的数据收集. 因此, 本文利用MATLAB和CST联合自动化全波仿真收集少量样本数据, 仿真流程如图4(a)所示. 全波仿真设置如图4(b)所示, 其中共形几何结构按照(1)式表示的翼型型线构建, $x$和$z$方向采用open (add space)边界条件, 在$ y $方向采用periodic边界条件, 同时用沿着$ - z$方向传播的线极化平面波照射共形超构表面. 通过MATLAB自动控制输入相位分布来调控CST共形超构表面结构单元金属贴片半径, 从而获取不同相位分布下对应的全波仿真散射场结果. 经过$w\left( {w < 0.2 G} \right)$轮次循环仿真得到目标域数据, 并按照2.2.2节的方法对数据进行预处理, 得到目标域的训练数据集${\mathcal{D}_{\text{t}}} = \left( {{{\boldsymbol{X}}_{\text{t}}}, {{\boldsymbol{Y}}_{\text{t}}}} \right)$. 由于全波仿真考虑了单元之间的相互作用和耦合的情况, 因此利用电磁仿真软件得到的远场数据更真实.

      • 2.3.2.   模型迁移学习

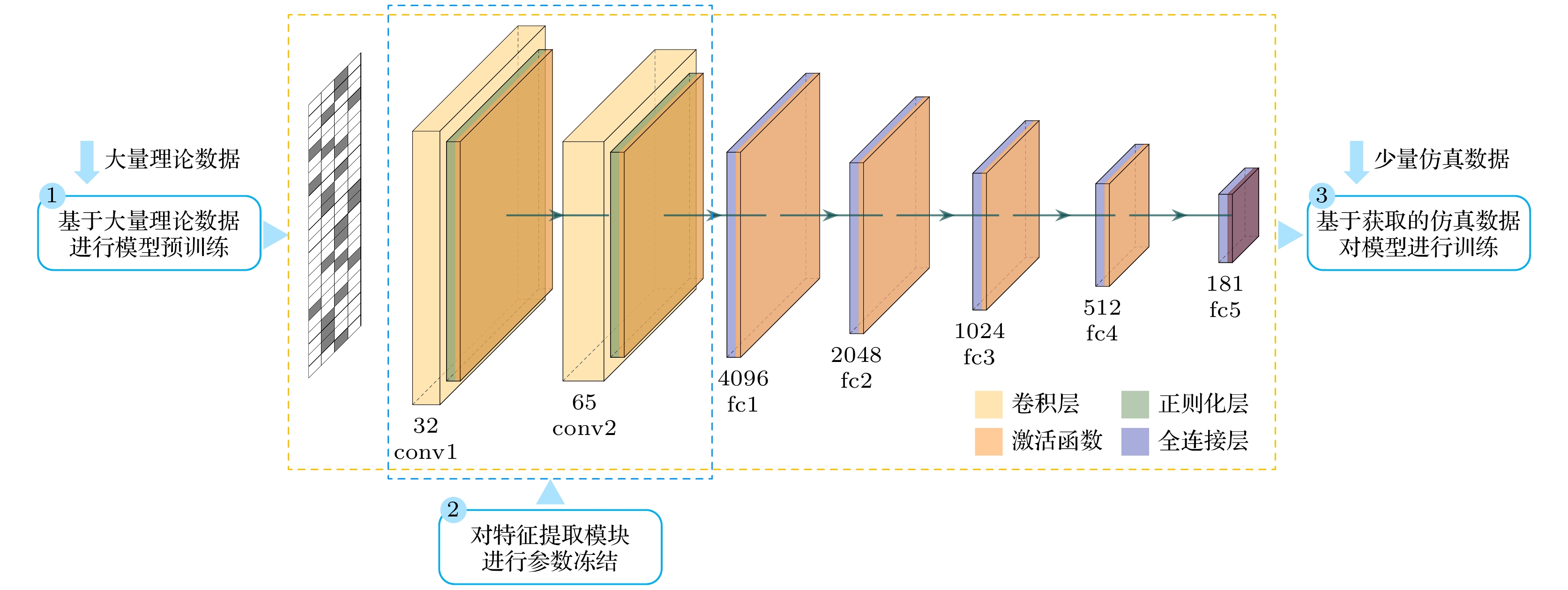
    • 为了使源域模型能够适应当前共形超构表面结构, 按照模型预训练、特征提取模块参数冻结、模型微调的迁移学习策略, 对源域模型进行迁移, 如图5所示.

      首先, 基于大量理论数据对散射场计算模型进行预训练, 以预训练模型${\mathcal{M}_0}$为基础, 对真实电磁模型${\mathcal{M}_1}$进行参数初始化. 此刻, 散射场计算模型具备了拟合(2)式的建模能力, 模型参数较随机初始化更加接近当前超构表面散射场的预测模型, 能够有效地弥补少样本条件下模型收敛速度慢、甚至是无法收敛的问题. 进而, 针对预训练模型${\mathcal{M}_0}$中的特征提取模块参数进行冻结, 进一步提高模型的训练效率. 由于特征提取过程在理论数据和全波仿真数据之间具有一定的相似性, 理论数据拟合的卷积块已经具备较好的模型提取特征提取能力, 所以冻结卷积块有助于进一步加速模型收敛. 最后, 将模型${\mathcal{M}_0}$学习到的知识迁移到${\mathcal{M}_1}$, 依托数据集${\mathcal{D}_{\text{t}}}$对${\mathcal{M}_1}$进行训练, 迭代更新散射场计算模型中的全连接层参数, 实现模型全波仿真数据的迁移适配, 最终得到能够有效预测目标域散射场数据的迁移学习模型${\mathcal{M}_1}$, 从而建立真实的相位分布到散射场之间的非线性映射${f_{\text{t}}}:{{\boldsymbol{X}}_{\text{t}}} \to {{\boldsymbol{Y}}_{\text{t}}}$.

      当超构表面的共形几何结构发生改变时, 为获得新结构下的散射场计算模型, 可对模型${\mathcal{M}_1}$进行二次迁移. 首先, 对新的共形超构表面按照2.3.1节的方法进行全波仿真, 得到新结构的少量训练数据, 记为$ {\mathcal{D}'_{\text{t}}} = \left( {{{\boldsymbol{X}}'_{\text{t}}}, {{\boldsymbol{Y}}'_{\text{t}}}} \right) $. 然后, 以原结构的散射场计算模型${\mathcal{M}_1}$作为新结构模型迁移学习的预训练模型, 冻结特征提取模块, 对全连接层的参数进行更新. 最后, 以${\mathcal{D}'_{\text{t}}}$为基础, 对散射场计算模型进行迁移训练, 得到新结构的散射场求解模型${\mathcal{M}_2}$, 从而实现新结构散射场求解的快速迁移和自动适配.

    3.   结果分析

    • 本文从模型参数选择优化、模型计算结果分析、迁移效果对比分析、二次迁移效果分析等方面对本文提出的方法进行性能分析与验证. 其中, 模型参数选择优化从模型结构、超参数选择等方面进行模型优化; 模型计算结果分析对模型${\mathcal{M}_0}, {\text{ }}{\mathcal{M}_1}, {\mathcal{M}_2}$的散射场计算效果进行验证; 迁移效果对比分析从预测精度、模型效率等方面对迁移学习带来的性能提升效果进行分析; 二次迁移效果分析探讨了共形超构表面结构改变时模型的泛化迁移能力.

      • 3.1.   数据集与评价指标构建

    • 为支撑基于迁移学习的共形超构表面散射场高效智能计算方法性能的分析及验证, 本文构建了包含相位分布和散射场成对数据的3个主要数据集${\mathcal{D}_{\text{s}}}$, ${\mathcal{D}_{\text{t}}}$和${\mathcal{D}'_{\text{t}}}$, 这些数据集的生成选用的GPU为Nvidia RTX 4090, CPU为Intel Core i9-13900KF. 1) 结构1理论数据集${\mathcal{D}_{\text{s}}}$, 其相位分布数据采用 随机生成策略得到, 散射场数据依托(2)式生成; 2) 结构1全波仿真数据集${\mathcal{D}_{\text{t}}}$, 其全波仿真数据集的相位分布数据采用随机生成策略得到, 散射场数据由全波仿真获取; 3) 结构2全波仿真数据集${\mathcal{D}'_{\text{t}}}$, 数据集获取方式与${\mathcal{D}_{\text{t}}}$相同.

      为有效评价散射场计算模型的性能, 本文设计并采用了模型在测试集中的平均损失、散射场数据预测值与真值的皮尔逊相关系数(Pearson correlation coefficient, PCC)、数据获取时间等构建模型性能的主要分析指标. 模型在测试集中的平均损失评估了预测所得散射场在各个角度的预测精度; 散射场数据预测值与真值之间的PCC评估了预测所得远场分布整体的分布相似性, 构成了对散射场数据全角度分布属性的评价, 其表达式如下所示:

      其中${T_i}, {\text{ }}{Y_i}$分别表示真值和预测值数据. 训练数据获取时间评估了模型构建所需的样本量规模和训练效率, 对少样本场景的适应性进行评价.

      • 3.2.   模型参数选择优化

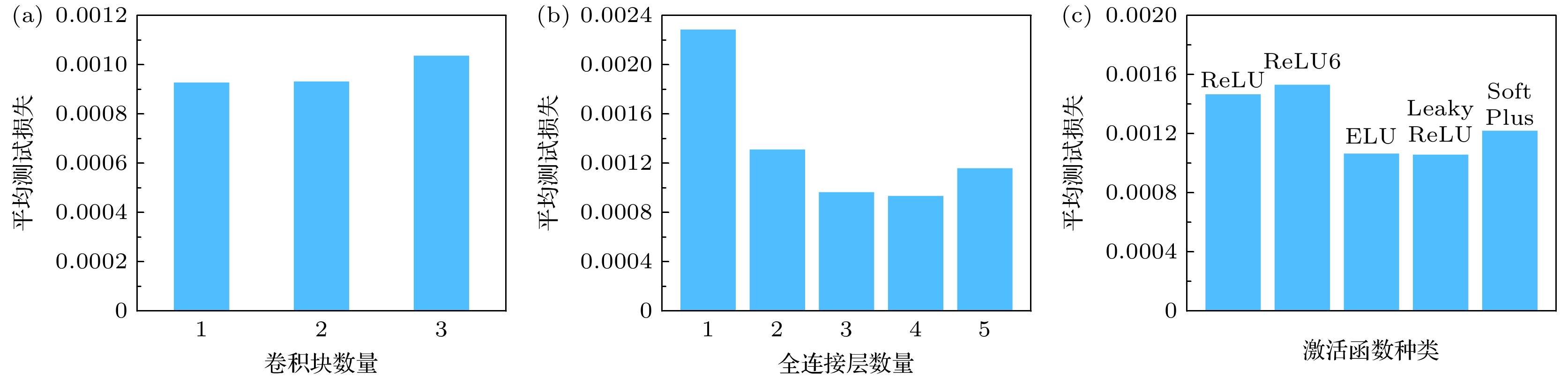
    • 本文基于图3(b)给定的网络模型结构, 依托结构1理论数据集训练得到了散射场计算模型${\mathcal{M}_0}$, 通过修改模型结构对模型结构的最优解进 行分析验证. 如表1所列, 本文从卷积块数量、全连接块数量和激活函数类型3个维度对模型结 构的候选集合进行优化求解, 分析确定模型的最优结构.

      首先, 对模型结构中的卷积块数量进行控制分析, 图6(a)给出了卷积块取1, 2, 3时的平均测试损失, 随着卷积块的增加, 平均损失略有增加, 但增加幅度有限, 综合考虑计算量和特征提取的需求, 本文卷积块数量选取为2. 其次, 对模型结构中的全连接块进行控制分析. 由于最后一个全连接层用于将高维向量映射到181长度的远场分布数据, 属于模型的必要输出层, 因此该层保持不变, 对其他全连接块进行增减. 全连接块的主要作用是实现从相位编码所提取的特征到散射场的映射. 全连接块取不同数量的平均损失值如图6(b)所示, 随着全连接层的增加, 损失值先变小后增大, 主要原因是随着全连接块的增加, 模型表达能力增强, 但同样也带来潜在的过拟合问题, 会造成损失值在测试集中进一步增大. 综合考虑, 本文模型全连接块数量选取为4, 此时平均测试损失最小. 最后, 对激活函数类型进行控制分析. 激活函数主要对全连接块的输出进行非线性转换, 使得模型能更好地学习输入相位编码和输出散射场之间的非线性关系. 图6(c)给出了选取不同激活函数的测试结果, 根据平均测试损失结果, 本文选取LeakyReLU作为模型的激活函数.

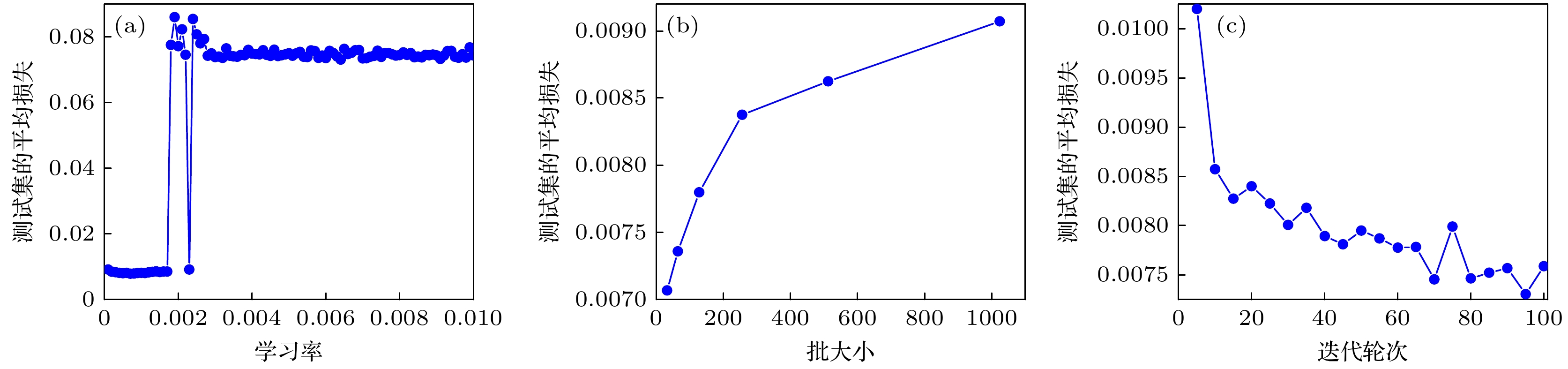
      在模型训练过程中, 学习率、批量大小和迭代轮数作为模型的超参, 影响着模型的收敛速度和预测精度. 因此, 本文针对这些超参数进行寻优, 通过选择合适的超参数, 达到提升模型预测精度的效果, 这些超参数的搜索空间如表2所列.

      平均损失随学习率的变化曲线如图7(a)所示, 学习率选在0.0001—0.0017之间时, 模型在测试集上的平均损失在0.008—0.009之间浮动. 当学习率超过0.0018之后, 模型在测试集上的平均损失大幅提升, 并出现大幅振荡, 达到0.0749左右, 因此本文选择0.0002作为模型的学习率, 此时模型在测试集上的平均损失为0.0085. 平均损失随批大小的变化曲线如图7(b)所示, 模型在测试集上的平均损失值随着批大小的增长, 出现单调递增的变化. 过大的批量大小会导致梯度过于稳定, 不利于寻找预测的最优值, 过小的批量大小会导致梯度随机性较高, 因此本文选择128作为批量大小. 平均损失随迭代轮次的变化曲线如图7(c)所示, 当迭代轮次小于30时, 模型在测试集上的损失快速下降, 表明此时模型尚未收敛; 当迭代轮次大于50后, 模型在测试集上的损失小幅回升后出现振荡, 表明此时可能出现过拟合现象. 因此, 本文选择50作为迭代轮次取值.

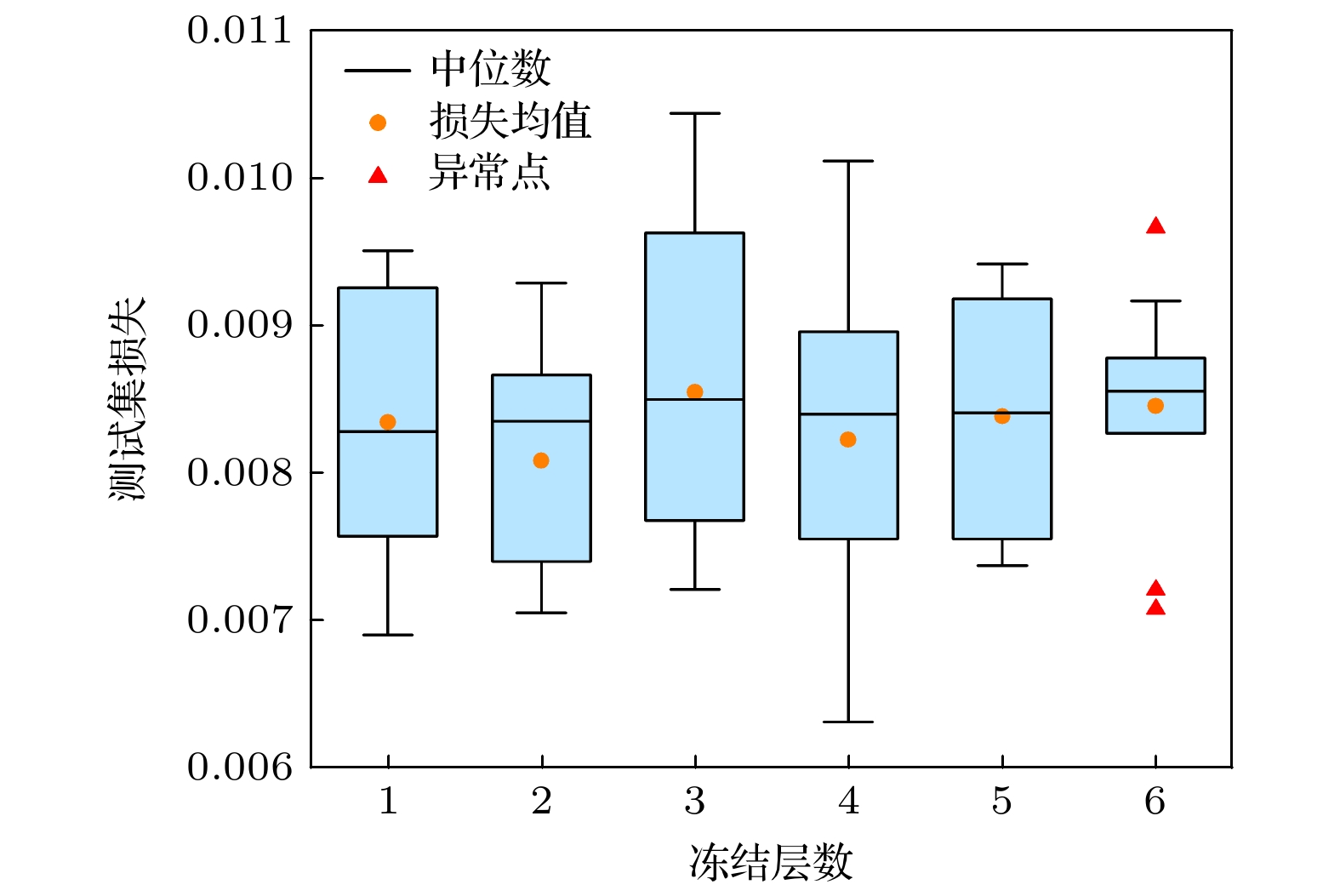
      在模型迁移过程中, 参数冻结有助于优化模型的迁移学习能力, 提升模型迁移的性能. 为此, 本文针对除输出层外的2个卷积块和4个全连接块进行了参数冻结分析. 以相同的源域模型作为预训练模型, 在给定结构的目标域中进行模型迁移, 分别冻结第1个卷积块(冻结1层)、前2个卷积块(冻结2层)、所有卷积块和第1个全连接块(冻结3层)、所有卷积块和前2个全连接块(冻结4层)、所有卷积块和前3个卷积块(冻结5层)、所有卷积块和前4个全连接块(冻结6层), 得到不同层参数冻结条件下迁移模型的测试集损失, 为了便于分析, 绘制不同冻结层数模型损失值的箱线图如图8所示, 其中横坐标表示冻结层数. 当仅冻结卷积块时, 损失值更加集中在较小的损失值附近. 而冻结2个卷积块时, 相较于仅冻结1个卷积块可获得更低的损失均值, 且更小的损失波动范围. 当将全连接块的参数纳入冻结范围时, 迁移模型的损失值出现了较大波动, 损失值均值高于冻结2个卷积块的情况, 在冻结所有卷积块及4个全连接块时, 甚至出现了少量的异常点. 综合考虑, 本文选择冻结2个卷积块, 在该情况下可获得稳定且较低的测试集损失, 有助于将预训练模型获得的特征提取能力迁移到新的数据集中, 确保迁移模型的性能获得改善和优化.

      • 3.3.   模型计算结果分析

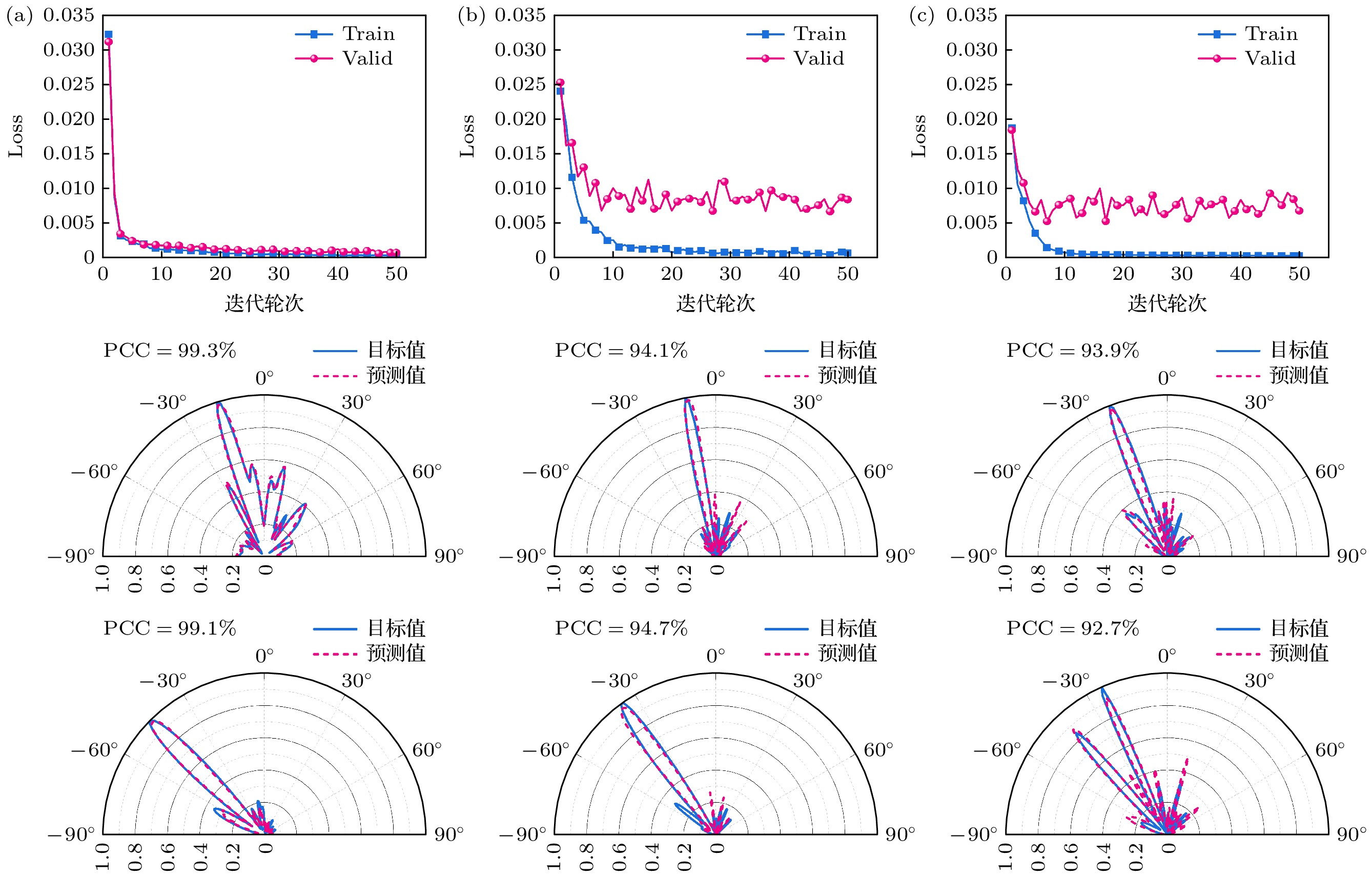
    • 根据上述网络结构和训练超参数分析, 对源域结构1共形超构表面理论数据散射场计算模型${\mathcal{M}_0}$、目标域结构1共形超构表面全波仿真数据散射场计算模型${\mathcal{M}_1}$和结构2共形超构表面全波仿真数据散射场计算模型${\mathcal{M}_2}$进行构建并训练. 训练过程中数据集按照8∶1∶1的比例分成训练集、验证集和测试集. 模型${\mathcal{M}_0}$, ${\mathcal{M}_1}$和${\mathcal{M}_2}$的训练集和验证集的损失函数随迭代轮次的变化曲线如图9(a), (b), (c)中左列子图所示, 可以看出随着迭代轮次的增加损失函数均趋于收敛, 其中${\mathcal{M}_0}$网络的收敛速度最快, 在训练5轮次即开始收敛, 平均损失值从0.0326快速收敛到0.0047, 并最终下降至0.0003左右. 在大规模理论数据集条件下, 本文模型收敛速度快, 在验证集中也取得了较好的收敛效果. 而${\mathcal{M}_1}$和${\mathcal{M}_2}$在10轮次和7轮次左右开始收敛, 训练集(验证集)中${\mathcal{M}_1}$平均损失值从0.025(0.024)下降到0.0015(0.0088)并最终稳定在0.0006(0.008)左右, ${\mathcal{M}_2}$平均损失值从0.019(0.18)下降到0.0006(0.008)并最终稳定在0.0002(0.006)左右. ${\mathcal{M}_0}$的验证集损失值与训练集损失值相接近, 而${\mathcal{M}_1}$和${\mathcal{M}_2}$的验证集损失值略大于训练集损失值, 造成这种差异的主要原因是${\mathcal{M}_0}$的训练数据集规模大, 模型可以实现更好的拟合预测, 因而收敛较快、损失值更小.

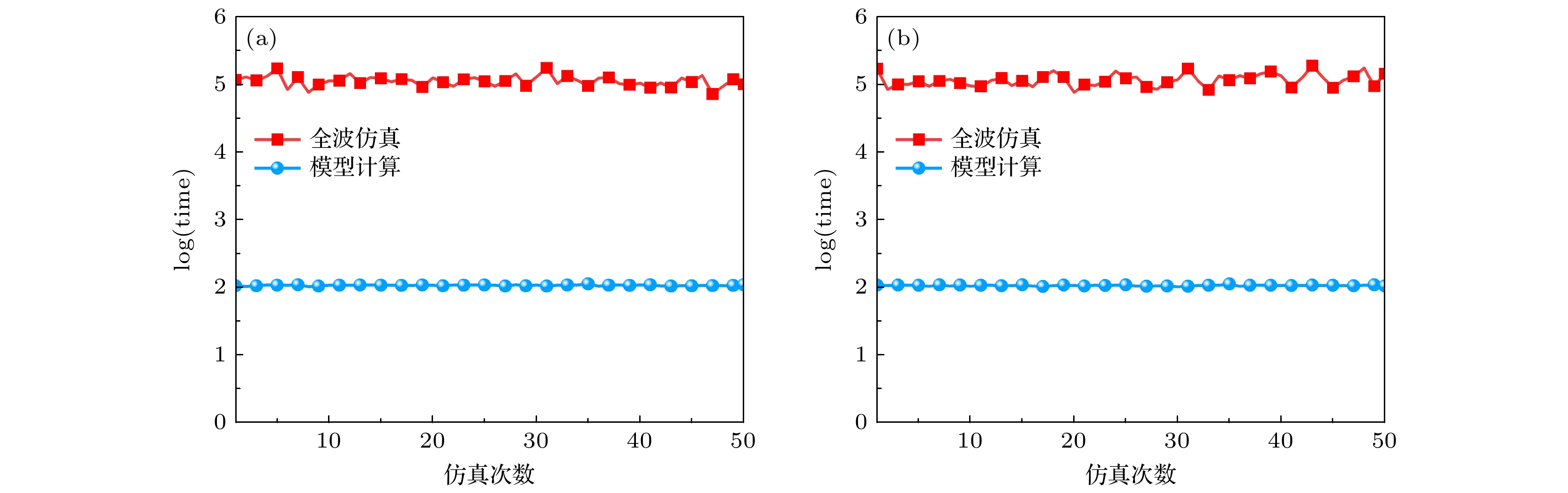
      为验证模型计算准确性, 对上述三个模型分别随机选取2种测试算例进行验证, 其中${\mathcal{M}_0}$的测试算例在结构1共形超构表面理论散射数据中选取, ${\mathcal{M}_1}$的测试算例在结构1共形超构表面全波仿真散射数据中选取, ${\mathcal{M}_2}$的测试算例在结构2共形超构表面全波仿真散射数据中选取, 模型拟合结果如图9(a), (b), (c)中右列子图所示, 其中虚线表示模型预测得到的共形超构表面在xoz面上的散射场数值, 实线表示散射场目标数值. 由图9(a), (b), (c)中右列子图可以看出, ${\mathcal{M}_0}$, ${\mathcal{M}_1}$和${\mathcal{M}_2}$预测的散射场数值均与目标结果符合良好, 特别是在主瓣方向上, 目标值与预测值几乎重合. 为定量地分析网络预测效果, 利用PCC表示目标值与预测值之间的拟合精度, 计算得出${\mathcal{M}_0}$, ${\mathcal{M}_1}$和${\mathcal{M}_2}$模型预测数据与目标数据在两种测试算例上的PCC分别为99.3%和99.1%, 94.1%和94.7%, 93.9%和92.7%, 其中${\mathcal{M}_0}$模型的预测精度最高, 这主要是因为理论训练数据集规模大, 模型学习效果最好, 该现象也与损失值结果相符合.

      为分析模型计算效率, 对网络模型计算散射场与利用电磁仿真软件进行全波仿真计算散射场的时间消耗进行分析和比较. 为了避免共形超构表面样本个体差异带来的误差, 随机选取50个结构1共形超构表面和50个结构2共形超构表面, 并分别在迁移学习模型和软件中进行了仿真计算. 从结果可知, 利用电磁计算软件进行全波仿真大约需要80—200 s, 而利用网络模型计算散射场所需时间仅需100 ms左右. 为了便于分析, 将网络模型和全波仿真散射场计算时间取对数并进行比较, 时间对数值曲线如图10所示, 其中时间均以ms为单位. 由图10可以看出, 对于两种结构的共形超构表面, 迁移学习模型${\mathcal{M}_1}$和${\mathcal{M}_2}$的计算时间对数值稳定在2左右, 全波仿真时间对数值稳定在5左右, 迁移学习模型计算时间比全波仿真时间消耗下降3个数量级, 大大提升了共形超构表面散射场的计算效率.

      • 3.4.   迁移效果对比分析

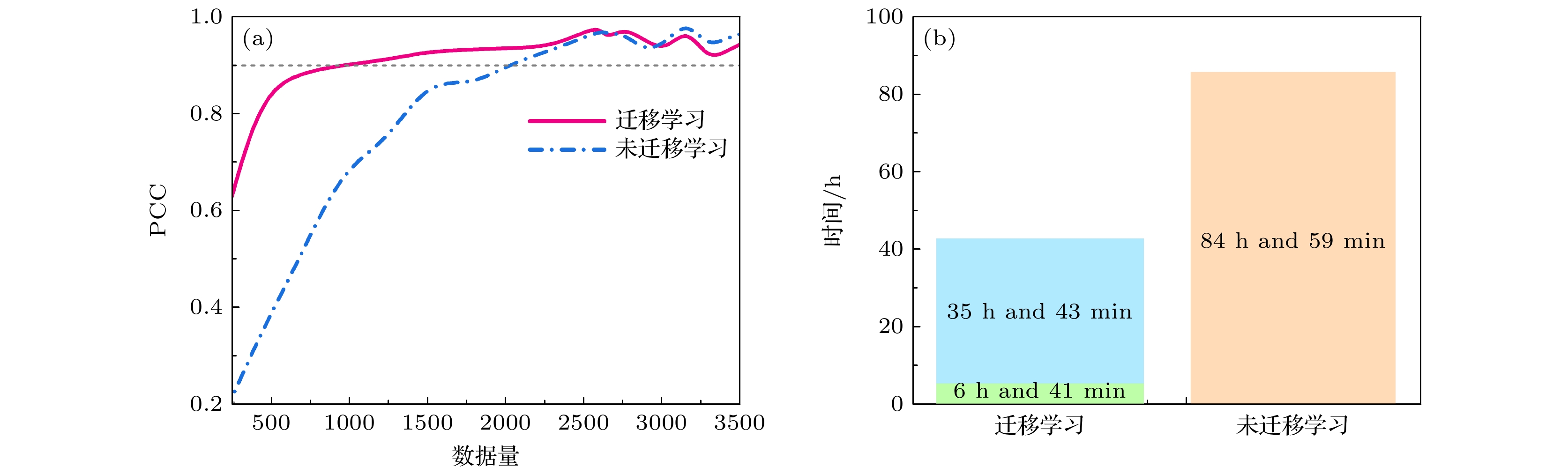
    • 在迁移学习过程中, 本文对特征提取模块进行了参数冻结, 冻结后模型的训练时间减少3%—5%, 模型在测试集上的平均损失值相较于不使用参数冻结时浮动$ \pm 2.03 {\text{%}}$. 为了讨论迁移学习对模型预测精度的影响, 将迁移模型与未迁移模型进行对比分析. 以共形超构表面结构1为例, 直接在少量全波仿真样本数据训练得到未迁移学习模型${\mathcal{M}'_1}$.

      图11(a)给出了两种模型预测数据与目标数据之间的PCC随着训练数据量的变化曲线, 可以看出随着数据量的增大, 两种网络的预测精度均有明显提升, 但需要注意的是在数据量较小时, 经过迁移学习的模型${\mathcal{M}_1}$预测精度要明显优于未经过迁移学习的模型${\mathcal{M}'_1}$. 在仅有400组训练数据的情况下, ${\mathcal{M}_1}$预测精度已达到81%, 而${\mathcal{M}'_1}$预测精度仅有35%, 迁移学习使预测精度提升了46%, 当目标域数据量为990时, ${\mathcal{M}_1}$预测精度已达到90%, 而${\mathcal{M}'_1}$预测精度仅有71.4%, 预测精度提升了18.6%, 当数据量为2310时, 未迁移学习模型基本达到迁移学习模型的预测精度, 并随着数据量的进一步增长, 两种模型的预测精度基本保持一致. 从上述分析可以看出, 迁移学习模型${\mathcal{M}_1}$在目标域训练样本规模较小的情况下具有良好的性能, 计算精度比未迁移学习模型平均提升19.8%, 在相同模型精度下(PCC = 90%)所需训练数据量仅占未迁移学习模型的42.9%, 大大减小了对训练数据量的需求.

      在数据集收集时间上, 源域理论数据集由MATLAB软件仿真生成, 获取57000组数据所需时间约为6 h 41 min, 结构1目标域全波仿真数据集由联合自动化全波仿真生成, 获取990组数据所需时间约为35 h 43 min, 获取2310组数据所需时间约为84 h 59 min. 从图11(b)可以看出, 在同样达到90%的模型计算精度时, 迁移学习训练数据获取时间仅占未迁移学习的49.89%, 数据获取时间减少50.1%, 大大缩减了数据生成时间, 有效地提升了模型构建效率.

      • 3.5.   二次迁移效果分析

    • 模型${\mathcal{M}_1}$的高计算精度证明了同一共形结构下散射场理论数据与全波仿真数据之间良好的知识迁移效果, 本文继而探索不同结构之间网络模型的迁移效果. 改变相对弯度和相对厚度参数, 使超构表面共形结构轮廓线变为图2(a)中红色曲线($\delta $ = 0.2, $\varepsilon $ = 0.03). 为得到结构2共形超构表面的散射场计算模型, 本文以结构1共形超构表面全波仿真计算模型${\mathcal{M}_1}$作为预训练模型, 利用1200组结构2共形超构表面全波仿真数据对${\mathcal{M}_1}$进行迁移训练, 得到新结构下的散射场计算模型${\mathcal{M}_2}$. 除此之外, 构建结构2散射场计算模型还有以下两种思路: 1) 直接利用结构2共形超构表面的全波仿真数据进行训练; 2) 在结构1理论散射场计算模型${\mathcal{M}_0}$的基础上进行迁移训练. 为了便于分析, 将结构2全波仿真数据直接训练得到的远场计算模型, 即未迁移模型记为${\mathcal{M}'_2}$, 将从结构1理论散射数据迁移到结构2全波仿真数据的散射场计算模型记为${\mathcal{M}''_2}$. 模型之间的迁移关系如表3所列, 其中${\mathcal{M}_2}$的预训练模型是${\mathcal{M}_1}$, 而${\mathcal{M}_1}$是从${\mathcal{M}_0}$迁移得来的, ${\mathcal{M}''_2}$是从${\mathcal{M}_0}$迁移得到, ${\mathcal{M}'_2}$没有进行迁移学习.

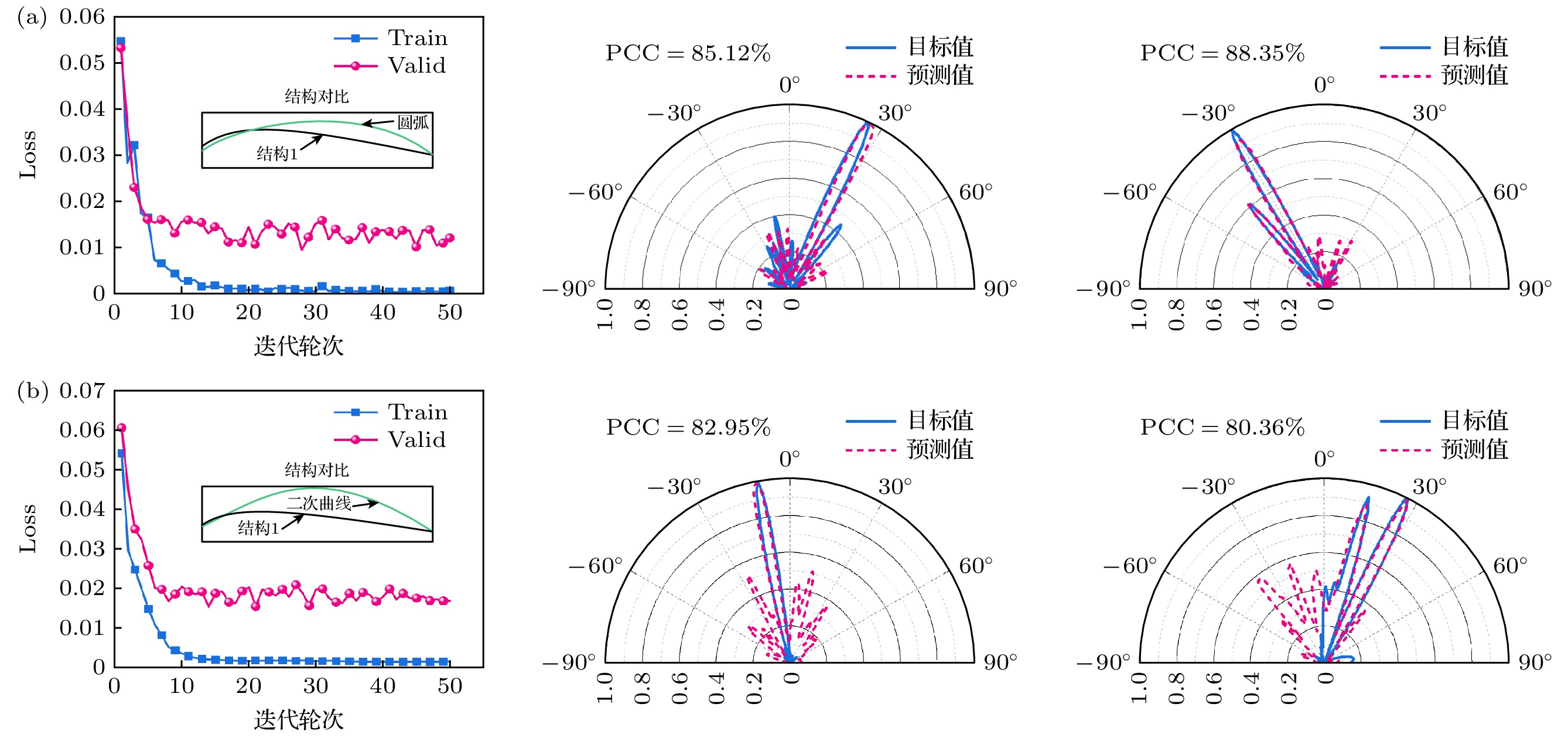
      作为对比, 对上述结构2共形超构表面散射场计算模型的两种思路进行了实验, 分别构建模型${\mathcal{M}'_2}$和${\mathcal{M}''_2}$, 得到模型平均损失值, 并在结构2共形超构表面全波仿真散射数据中随机选取两个测试算例, 将${\mathcal{M}'_2}$, ${\mathcal{M}''_2}$和${\mathcal{M}_2}$的散射场计算结果分别与测试算例进行比较, 如图12所示. 从图12中可以看出, ${\mathcal{M}'_2}$的平均损失值在25轮次左右开始收敛, 最终验证集上的损失值稳定在0.01左右; ${\mathcal{M}''_2}$的平均损失值在10轮次左右开始收敛, 最终验证集损失值稳定在0.008左右; ${\mathcal{M}_2}$的平均损失值在7轮次左右开始收敛, 最终验证集损失值稳定在0.006左右. 二次迁移模型${\mathcal{M}_2}$的损失值最低, ${\mathcal{M}_2}$和${\mathcal{M}''_2}$的收敛速度比${\mathcal{M}'_2}$快, 主要是因为预训练模型加速了收敛. 同时, 从图12中测试算例拟合效果来看, 在训练样本数量有限的情况下, ${\mathcal{M}_2}$的散射场预测值与目标值更接近, 精度更高, 迁移模型${\mathcal{M}''_2}$次之, 未迁移模型${\mathcal{M}'_2}$的精度最低, 这与损失值结果相吻合. 造成这种现象的主要原因是, ${\mathcal{M}_2}$是从结构1全波仿真散射场计算模型迁移而来的, 源域与目标域相似性较高, 而${\mathcal{M}''_2}$的预训练模型是结构1的理论散射场计算模型, 与前者相比, 源域与目标域差异性略大, 而未迁移模型${\mathcal{M}'_2}$因为没有预训练模型学习到的知识可以利用, 模型计算精度最低. 本实验分析了模型在超构表面轮廓函数参数改变时的迁移学习效果, 验证了模型的有效性, 可以提升训练效率.

      进一步, 本文讨论共形超构表面剖面结构改变时模型的适应性能. 选取与2.1节超构表面横截面轮廓方程不同的曲线, 以圆弧和二次曲线作为超构表面共形结构, 其与结构1轮廓对比如图13左列子图所示. 本文以结构1共形超构表面全波仿真计算模型${\mathcal{M}_1}$作为预训练模型, 按照同样的方法分别对圆弧和二次曲线共形超构表面散射场预测模型进行迁移训练, 得到模型${\mathcal{M}_{\text{c}}}$和${\mathcal{M}_{\text{q}}}$. 如图13所示, ${\mathcal{M}_{\text{c}}}$和${\mathcal{M}_{\text{q}}}$模型均能有效收敛, 并且验证集损失值稳定在0.013和0.017左右. 同时对上述两个模型分别随机抽取2种测试算例进行验证, 可以看出${\mathcal{M}_{\text{c}}}$和${\mathcal{M}_{\text{q}}}$模型预测散射场结构与目标结果基本符合, 计算得PCC分别为85.12%, 88.35%和82.95%, 80.36%, 较${\mathcal{M}_2}$在精度上有所下降, 这主要是由于结构轮廓方程变化带来的物理特性的不同, 因此在个别旁瓣上预测值与目标值存在一定偏差, 从而降低了PCC值, 但在主要辐射方向上依然吻合较好, PCC分别能达到89.08%, 95.02%和92.37%, 89.16%. 本实验说明模型在超构表面横截面轮廓方程完全不同时, 在主要辐射方向上能够进行有效预测, 验证了其在不同结构之间具有一定的泛化性.

    4.   总　结

    • 为解决共形超构表面散射场的高效计算问题, 本文提出了一种基于迁移学习的共形超构表面散射场高效智能计算方法, 构建了从相位分布到散射场的映射模型, 建立了包含模型预训练、参数冻结、模型微调等在内的迁移学习策略, 实现了散射场的快速精准预测, 且当超构表面几何参数发生变化时能够快速迁移适配. 本文所提方法可有效地提升深度学习模型构建效率, 大大缩减共形超构表面散射场计算时间, 为共形超构表面的快速设计提供了新的思路和方法.

    参考文献 (28)

目录

/

返回文章
返回