-
经颅聚焦超声因其无创、安全、穿透深度大等优点[1], 具有重大发展潜力. 超声波在穿过头骨时能够保持较高的穿透深度, 使其能直接影响到深层脑组织, 并且聚焦超声产生的热效应[2], 有助于治疗更深部位的疾病. 因此, 相较于传统跨颅骨的手术治疗方法, 经颅聚焦超声技术能够在不进行开颅手术的前提下实现手术治疗, 大大降低了感染出血的风险, 在生物医学领域具有广阔的应用场景. 比如, 在低强度下, 经颅聚焦超声可以在组织不消融的情况下可逆地打开血脑屏障[3,4], 在高强度下, 经颅聚焦超声可产生组织消融, 并且组织消融的结果与组织在高强度聚焦超声下暴露的时间有关[5].
然而, 当超声穿过颅骨时, 由于颅骨自身的性质以及结构复杂性, 会带来强烈的超声散射和衰减[6], 使得经颅声场产生严重的失真和畸变[7,8]. 近些年出现了一种通过单片声全息透镜来生成任意复杂声场的技术[9], 可以以一种廉价的方式解决该问题. 全息技术因其精准、实时、低功耗等特征, 被广泛运用于各类能量场调控工作中, 该方法通过对所需波面的相位或振幅进行空间存储[10], 从而当全息透镜被合适的能量源照射时, 通过干涉重建波面. 如今, 现代计算机全息技术[11]不再需要从真实的物理场景中记录波面的相位或者振幅, 就可以在数值仿真中计算出波面的相位或者振幅, 并基于此进行重建. 在通过单片声全息透镜来生成复杂声场这项技术中, 超声的相位或振幅通过计算机数值仿真计算得到, 存储在声全息图中. 声全息透镜放置于超声传播路径上, 可以通过改变超声波的相位生成复杂的声场[12]. 目前, 该技术已经被证明可以克服超声跨颅传播带来的失真和畸变, 在颅骨内任意位置产生焦点[13]. 对比目前主流的基于相控阵进行经颅聚焦的方法[14,15], 该技术不依赖于复杂的电子设备, 具有成本低廉, 操作便捷等优势[16].
然而, 现有的基于声全息透镜的经颅聚焦方法依然面临严峻的应用问题. 单片声全息透镜往往只能重建单一聚焦声场, 在实际应用场景下缺乏灵活性. 因此, 本文提出了一种用于经颅聚焦的多频声全息透镜的设计方法, 通过提取不同工作频率的两片聚焦到不同位置的声全息透镜中的有效信息, 将其整合到单片声全息透镜, 从而实现基于单一全息透镜的多频经颅聚焦. 基于本文所提出方法设计制造的声全息透镜能根据不同的驱动频率, 在聚焦平面重建出对应的焦点, 从而提高了声全息透镜在经颅聚焦这一应用中的灵活性, 提升其应用潜力.
-
由于颅骨自身性质与结构的复杂性, 当超声波穿过颅骨时, 会经历严重的衰减和散射[17], 从而导致严重的声场畸变[18]. 为了对跨颅声场传播过程进行准确数值仿真, 本文使用MATLAB中的k-wave[19]开源工具箱, 使用完美匹配层来吸收边界反射, 借助k空间伪谱法[20,21]以描述超声在颅骨这类非均匀介质中的传播. k空间伪谱法将声场转化为频域空间中的积分方程来求解声场分布, 与传统方法相比, 在处理非均匀介质情况时表现出更高的计算效率, 在声学仿真领域得到了广泛应用. 该方法通过求解以下方程来描述非均匀介质中的声传播[22]:
其中,
$ u $ 代表声学粒子速度,$ d $ 为声学粒子位移,$ p $ 代表声压,$ \rho $ 是声密度,$ {\rho _0} $ 为介质密度,$ {c_0} $ 是等熵声速, 通过线性算子L引入了随频率变化的声学吸收和色散[23]:其中,
$ \tau = - 2{\alpha _0}c_0^{\gamma - 1} $ ,$ \eta = - 2{\alpha _0}c_0^\gamma \tan ({\text{π}}\gamma /2) $ 分别为吸收和色散比例系数,$ {\alpha _0} $ 为幂律前因子,$ \gamma $ 是幂律吸声指数. -
目前, 时间反演法是一种主流的经颅聚焦声全息透镜设计方法, 该方法利用声传播的时间反转不变性[24], 通过在聚焦位置设置一系列虚拟声源, 通过数值模拟来获得反向传播场[25]. 首先, 在颅骨内部设置虚拟声源, 在颅骨模型外的全息面记录来自虚拟源的超声信号. 然后, 对传感器记录得到的信号进行傅里叶变换, 提取工作频率下的相位作为声全息图. 为了基于单个声全息透镜实现多频声场控制, 本文尝试将两组不同频率驱动, 聚焦到不同位置的声全息图中的有效信息进行整合. 具体而言, 利用时间反演法, 在不同位置设置不同频率的虚拟源, 在全息面接收声压值
$ {p_{\text{f}}}(x, y) $ , 随后对接收的信号进行傅里叶变换并提取工作频率下的相位作为声全息图, 记为$ {H_1}(x, y) $ 和$ {H_2}(x, y) $ , 定义如下成本函数[26]:其中,
$ E(|{p_{\text{f}}}(x, y)|) $ 为在某频率驱动下, 在全息面上某素点$ (x, y) $ 处接收到的平均声压值,$ {\text{std(|}}{p_{\text{f}}}(x, y)|) $ 为在某频率驱动下, 在全息面上某个像素点$ (x, y) $ 处接收到的声压值的标准差.$ S $ 是用拉普拉斯算子的二阶精确有限差分近似求得的平滑项,$ \alpha $ 和$ \beta $ 为权重参数. 首先, 将多频全息图$ H(x, y) $ 置零初始化, 随后逐一遍历$ H(x, y) $ 中的每一个像素点, 将其设置为$ {H_1}(x, y) $ 或$ {H_2}(x, y) $ 中对应像素点的值. 具体来说, 将$ {H_1}(x, y) $ 和$ {H_2}(x, y) $ 对应的$ {p_{\text{f}}}(x, y) $ 分别代入 (5)式中, 计算并比较两者的成本函数, 将成本函数较高的分配给$ H(x, y) $ , 重复此操作直到所有像素都被更新. 重复迭代, 每次迭代后重新计算$ S $ , 当与前一次迭代相比改变的像素数量低于表面总像素的0.5%时, 终止迭代. 初始迭代时令$ \beta $ =0, 迭代后每次计算更新$ \beta $ , 使$ E(|{p_{\text{f}}}(x, y)|) = - 0.5\beta S $ , 变量$ \alpha $ 始终设置为0.3. 在得到多频声全息图后, 参考He等[27]通过(6)式, 将提取到的相位信息转化为声全息透镜表面每个像素对应的高度值$ \xi (x, y) $ :其中,
$ {c_{{\text{water}}}} $ 和$ {c_{{\text{lens}}}} $ 分别为在水中和全息透镜材料中的声速, 分别为2495 m/s和1500 m/s.$ f $ 为多频声全息透镜对应的两种频率的均值, 为1.5 MHz. -
为了评估基于本文提出方法设计的多频声全息透镜的声场聚焦性能, 将生成的声全息透镜分别在仿真中和实验中进行测试. 用不同频率的平面波进行经颅聚焦实验, 并测量聚焦平面上的声压值, 并通过对比聚焦面上的焦点与预设的目标焦点之间的距离来验证基于该方法生成的多频声全息透镜的声场聚焦准确性. 除此之外, 分别计算在两种频率下重建的声场分布与预设的目标声场分布之间的峰值信噪比(PSNR), 从而评估基于该方法的声场聚焦质量, 验证所提出的方法的性能. PSNR的计算公式如下[28]:
其中MAX代表声压图像中像素点的最大值, MSE代表均方误差. PSNR值越高, 说明声场聚焦质量越好.
-
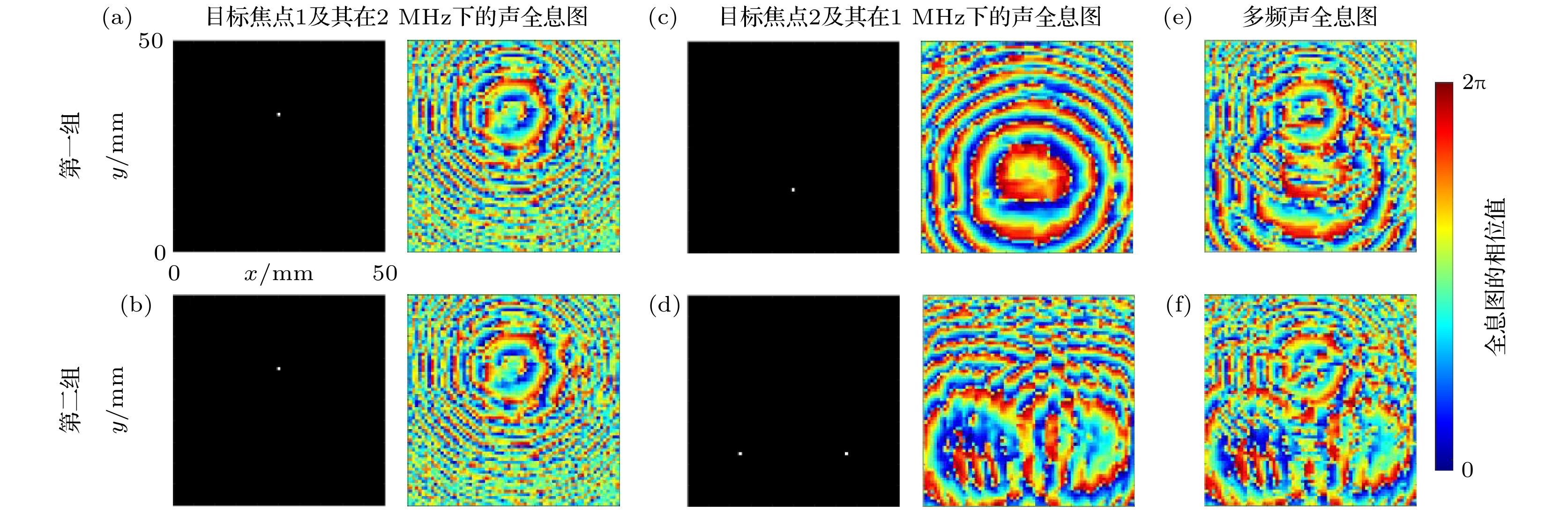
在数值仿真中, 设置仿真网格大小为0.25 mm, 库朗数为0.2, 数值仿真通过MATLAB中的k-wave工具包实现. 具体来说, 利用时间反演法, 在聚焦平面目标焦点的位置设置点源, 在声全息透镜所在的平面接收时域信号并提取在工作频率下的相位来获取声全息图. 分别获取两组目标焦点在1 MHz和2 MHz频率下的声全息图, 如图1所示.
-
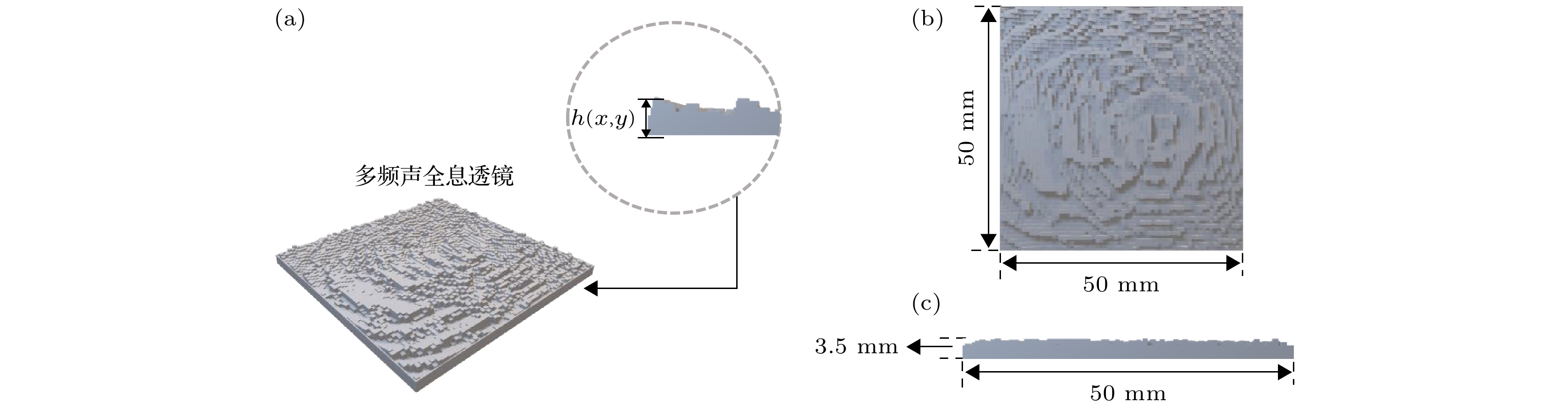
在获得多频声全息图后, 基于(6)式可以获得多频声全息透镜每个像素的高度, (6)式的频率参数设置为两种频率的均值, 即1.5 MHz, 制成的声全息透镜如图2所示.
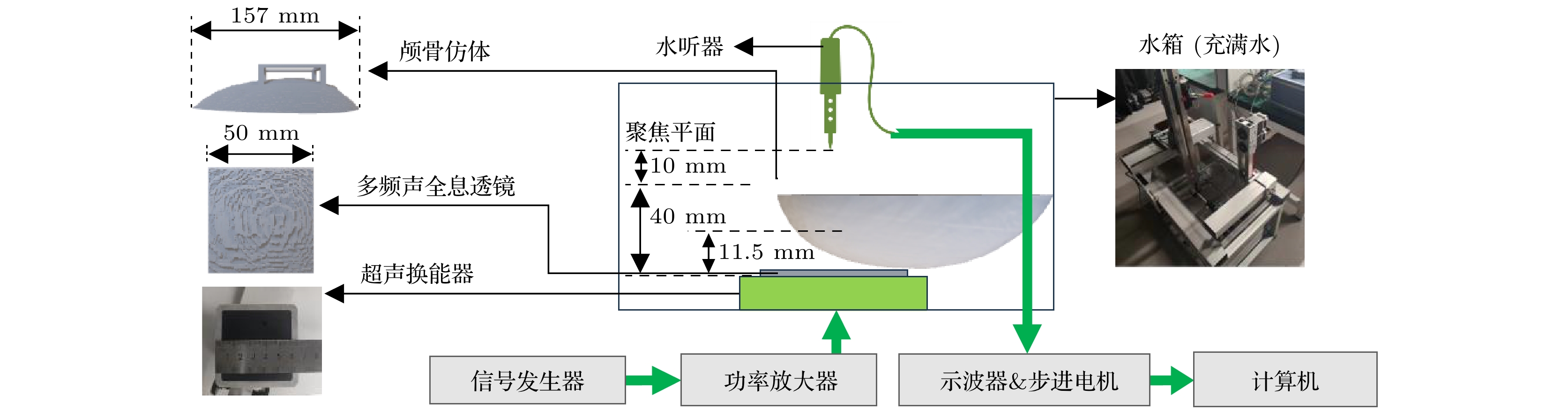
为了验证该全息透镜的聚焦性能, 建立了经颅聚焦的仿真和实验平台. 在仿真和实验中, 颅骨、全息面、聚焦平面之间的相对位置设置如图3所示. 仿真平台利用MATLAB中的k-wave工具包搭建, 仿真参数与3.1节一致. 实验平台以针式水听器(ONDA-HNP-0400)为核心, 如图3所示. 多频声全息透镜和颅骨仿体由3D打印技术制造得到. 材料选用Verowhite, 其中声速为2495 m/s[29], 密度为1175 kg/m3. 颅骨模型的制造分辨率为750 μm. 颅骨模型上配有支架, 可与声全息透镜一同安装在超声换能器上. 使用信号发生器(KEYSIGHT MXG N5182 B), 发射1 MHz或2 MHz的正弦脉冲, 并通过线性射频放大器连接到超声换能器. 整套实验装置被浸没在充满水的水箱中. 利用针式水听器扫描虚拟源所在的平面, 扫描区域大小为50 mm×50 mm, 步长为0.5 mm. 通过对获得的信号进行滤波处理, 采集到时变信号并计算其能量, 以绘制声压图.
-
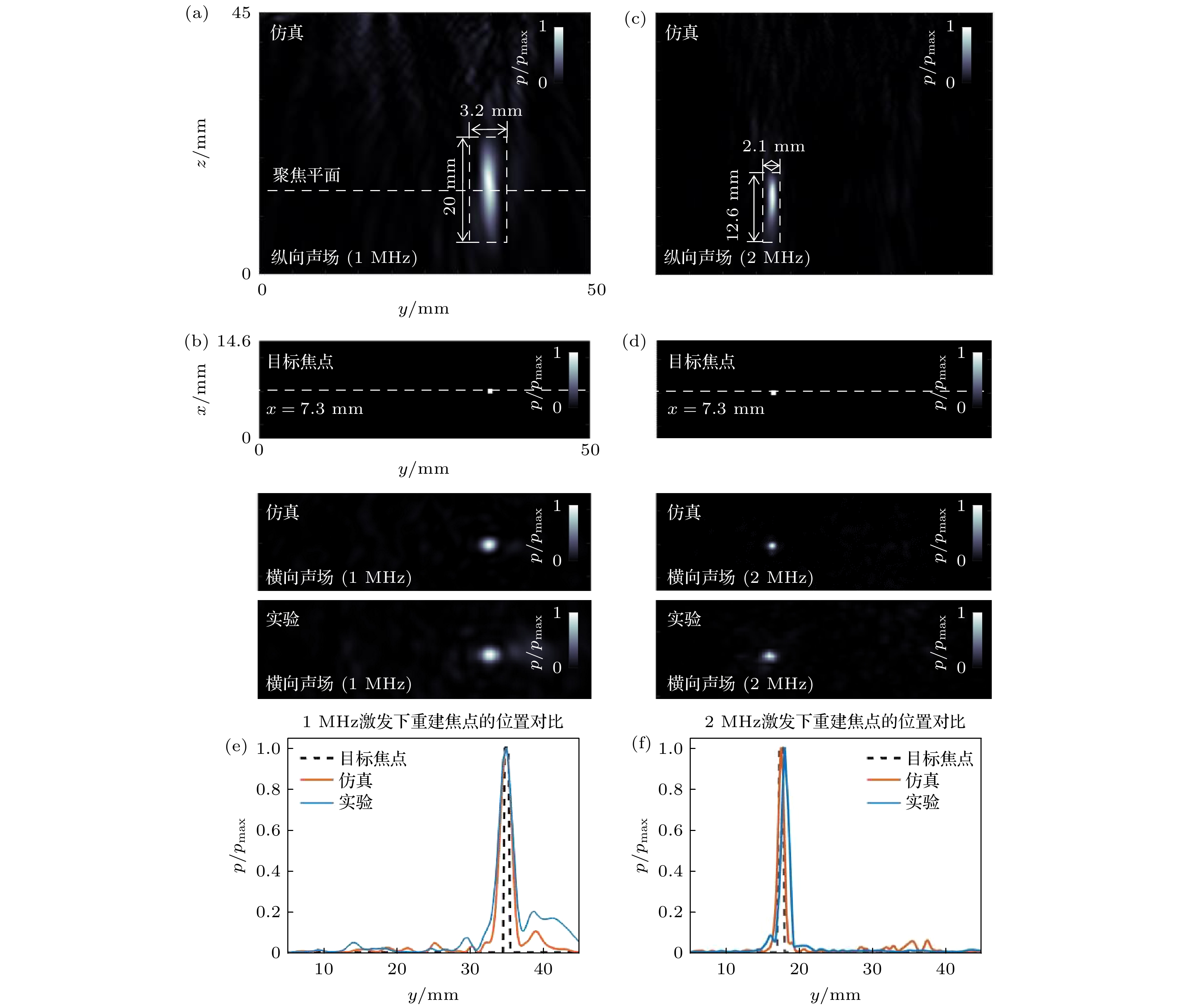
经过仿真和实验, 基于本文设计的多频声全息透镜得到一系列经颅聚焦声场. 基于此, 通过2.3节所提出的量化指标对聚焦结果进行评估, 以验证该方法的可靠性. 图4为对应的仿真与实验结果. 图4(a), (c)分别为在1 MHz和2 MHz的平面波激发下, 在聚焦平面附近的纵向声场, 图4(b), (d)分别为在1 MHz和2 MHz的平面波激发下, 目标焦点的位置与在仿真和实验中在聚焦平面上的横向声场. 图4(e), (f)分别为在1 MHz和2 MHz的平面波激发下, 仿真与实验中聚焦平面上的横向声场在x = 7.3 mm的虚线处的声压对比. 根据图4结果可知, 通过本文所提出的方法生成的多频声全息透镜在不同频率的超声激发下, 能够在仿真中在聚焦平面的不同位置处生成精准的声聚焦点, 并且通过实验验证该多频声全息透镜在实际应用场景下依旧具备良好的性能, 具有灵活的应用性.
此外, 为了评估基于本文提出方法的超声聚焦质量, 在数值仿真和实验中, 皆对聚焦声场与目标焦点之间的PSNR进行了计算, 如表1所示. 相对而言, 在仿真和实验中, 较高的PSNR证明该声全息透镜可以在不同频率的超声激励下在聚焦平面重建出不同的高质量焦点.
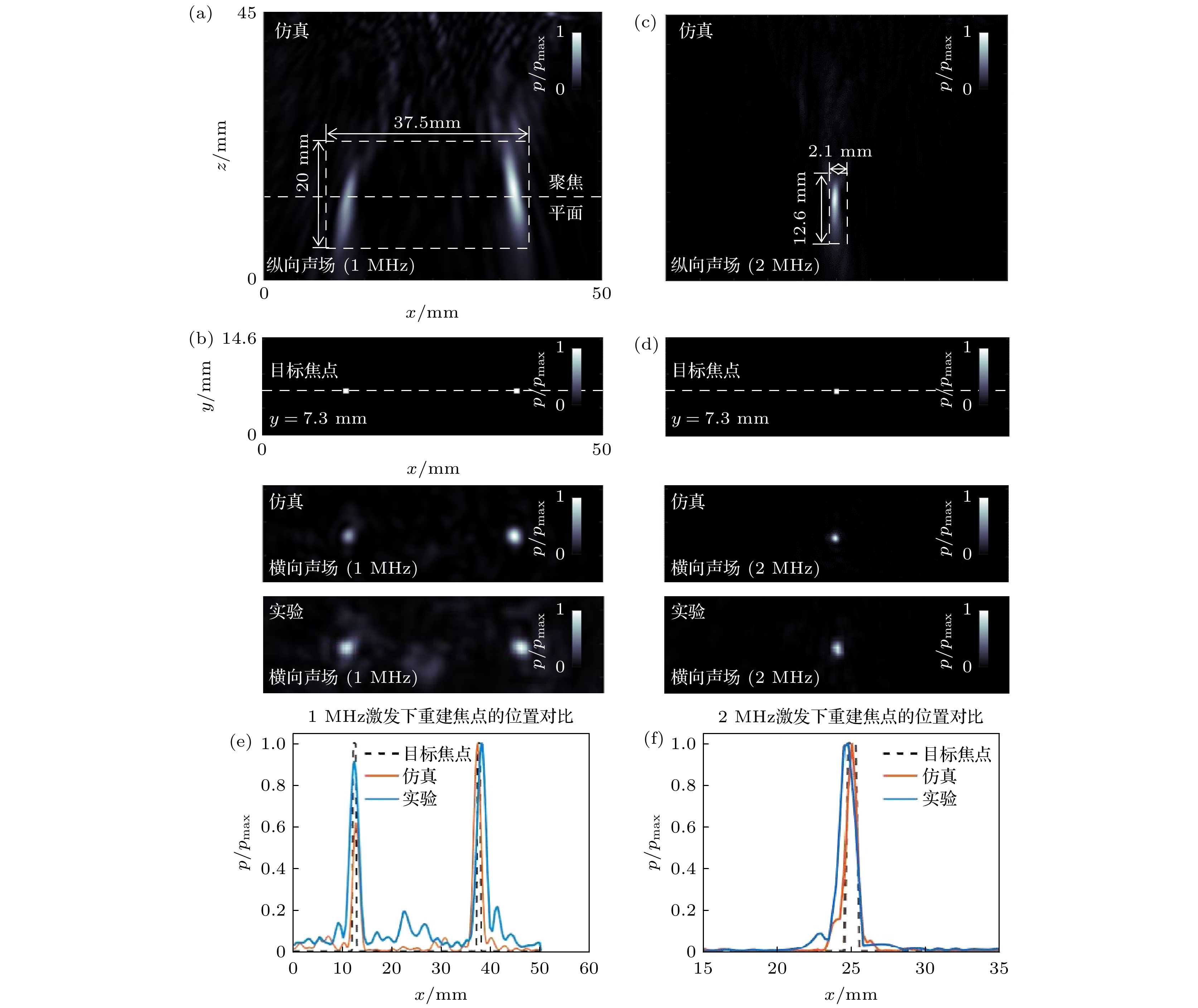
为了验证通过该方法制作的声全息透镜在多焦点情况下, 仍旧可以生成高质量的焦点, 在1 MHz场景下的聚焦平面中设置多个焦点, 设计了第2片用于经颅聚焦的声全息透镜来进行重复实验以验证该方法在多焦点的情况下仍旧具备可行性. 仿真和实验结果如图5所示. 图5(a), (c)分别为在仿真中, 在1 MHz和2 MHz激发下焦点平面的纵向声场. 图5(b), (d)分别为在1 MHz和2 MHz的激发下, 仿真和实验中在聚焦平面处形成的焦点和目标焦点. 图5(e), (f)分别为在1 MHz和2 MHz的激发下, 仿真与实验中聚焦平面上的横向声场在y = 7.3 mm的虚线处的声压对比. 由结果可知, 即使在多点情况下, 用不同频率的超声激发多频声全息透镜, 仍能在不同频率超声激发下, 生成准确的经颅聚焦点.
同样, 计算了在数值仿真和实验中在聚焦平面重建的聚焦声场与目标图像之间的PSNR, 如表2所示. 在仿真中和实验中, 较高的PSNR证明该多频声全息透镜即使在多焦点的情况下, 仍旧能在不同频率的超声激发下生成高质量的焦点.
综上所述, 本文所设计的多频声全息透镜, 在单焦点和多焦点情况下均能在相应频率的激发下生成高质量焦点, 其物理原因在于通过对全息透镜相位分布的相干叠加设计实现对复合声波束干涉和衍射效应的特殊控制. 在1 MHz的超声激发下进行的数值仿真中, 两个多频声全息透镜在聚焦平面上分别形成了单个焦点和多个焦点. 相较于单焦点, 多焦点中的能量较高的焦点和较低的焦点分别为单焦点能量的0.63倍和0.44倍, 主要原因在于多焦点聚焦需要通过控制不同区域的相位信息来使多个焦点处的波前相干叠加, 这导致能量在多个焦点之间分散, 从而引发能量损失. 此外, 随着激发频率从1 MHz增大到2 MHz, 生成的焦点的分辨率明显提高, 同时PSNR也得到了显著提升, 这一现象可归因于频率的增加导致波长缩短, 同时全息透镜相对于波长而言的数值孔径变大, 从而使声波的聚焦点更加精确, 体现了较短的波长在提高聚焦分辨率和聚焦质量方面的优势.
-
针对目前用于经颅聚焦的声全息透镜只生成单一声场, 缺乏应用灵活性这一问题, 在本文中, 我们提出了一种用于经颅聚焦的多频声全息透镜的设计方法, 通过提取不同频率下, 聚焦在不同焦点位置的声全息透镜的有效信息, 生成用于经颅聚焦的多频声全息透镜. 数值仿真与实验结果证明, 无论在单焦点还是多焦点任务下, 该透镜均能在不同频率的平面波激励下, 克服颅骨造成的声波散射问题, 能够跨骨形成对应的精确且高质量的焦点. 在一定程度上提高了声全息透镜在经颅聚焦这一领域的应用灵活性. 但是值得一提的是, 该工作目前只应用于颅骨仿体中, 在真实的颅骨中需要考量更复杂的情况, 比如松质骨和皮质骨对聚焦精度产生的影响, 这些将在之后的工作进行研究.
基于声透镜的多频经颅聚焦
Multifrequency transcranial focusing based on acoustic lensing
-
摘要: 经颅聚焦超声是一种具有发展前景的技术, 具有无创、安全、穿透深度大等优点. 声全息透镜作为一种低成本且便捷的经颅聚焦方法, 具有较大的发展潜力. 然而, 基于单片声全息透镜通常只能实现单一经颅聚焦声场的重建, 在实际应用场景下缺乏应用灵活性. 针对该问题, 本文提出了一种用于经颅聚焦的多频声全息透镜的设计方法, 通过提取在不同频率下设计的聚焦到不同位置的两片声全息透镜中的有效信息, 并将其整合到一片声全息透镜中来实现, 生成的声全息透镜可以在不同频率的激发下聚焦到不同位置. 仿真和实验结果表明, 通过此方法设计的声全息透镜在不同频率的超声波激发下, 可以克服颅骨对超声波的散射效应, 在颅骨后方精确地形成高质量的声聚焦点.Abstract: Transcranial focused ultrasound (tFUS) possesses significant advantages such as non-invasiveness and high tissue penetration depth, making it a promising tool in the field of brain science. Acoustic holographic lenses can manipulate the sound field through phase modulation, providing a low-cost and convenient approach for realizing transcranial focusing. Acoustic holographic lenses have been successfully utilized for achieving precise transcranial focusing in living mice to open the blood-brain barrier and for performing neural modulation, which shows considerable application potential. However, existing transcranial acoustic holographic lenses can only be driven by specific ultrasound frequencies and focused at predetermined positions, which limits their flexibility in complex applications. To address this issue, this study establishes a multi-frequency transcranial focusing method based on acoustic holographic lenses to enhance its adaptability in the field of tFUS. By integrating acoustic holographic lenses designed for different focal positions at various frequencies, we generate multi-frequency acoustic holographic lenses suitable for transcranial focusing and conduct experiments to evaluate their performance. In simulations, for single-focus tasks, the peak signal to noise ratio(PSNR) of the proposed method achieves 32.16 dB under 1 MHz ultrasound excitation, and 40.18 dB and 2 MHz ultrasound excitation, respectively; for multi-focus tasks, the PSNR values are 29.39 dB and 39.89 dB, respectively. In experiments, for single-focus tasks, the PSNR value of the proposed method is 27.48 dB under 1 MHz ultrasound excitation, and 32.33 dB under 2 MHz ultrasound excitation, respectively; for multi-focus tasks, the PSNR values are 23.30 dB and 32.17 dB, respectively. These results demonstrate that the multi-frequency transcranial acoustic holographic lens can effectively modulate the sound field under varying ultrasound frequencies and create high-quality focal points at different locations behind the skull, which significantly enhances the application flexibility of transcranial acoustic holographic lenses.
-
Key words:
- transcranial ultrasound /
- ultrasound focusing /
- acoustic holography /
- holographic lens .
-

-
图 2 用于经颅聚焦的多频声全息透镜 (a)多频声全息透镜的3D视图; (b)多频声全息透镜俯视图; (c)多频声全息透镜的正视图
Figure 2. Multi-frequency acoustic holographic lens for transcranial focusing: (a) 3D view of the multi-frequency acoustic holographic lens; (b) top view of the multi-frequency acoustic holographic lens; (c) front view of the multi-frequency acoustic holographic lens.
图 4 多频声全息透镜的仿真与实验结果 (a) 1 MHz仿真中, 焦点附近的纵向声场; (b)1 MHz激发下的仿真与实验重建的聚焦平面与目标焦点; (c) 2 MHz仿真中, 焦点附近的纵向声场; (d) 2 MHz激发下的仿真与实验重建的聚焦平面与目标焦点; (e) 1 MHz激发的情况下, 在仿真和实验中, 沿着x = 7.3 mm的虚线上的声压对比; (f) 2 MHz激发的情况下, 在仿真和实验中, 沿着x = 7.3 mm的虚线上的声压对比
Figure 4. Simulation and experimental results of multi-frequency acoustic holographic lenses: (a) Longitudinal acoustic field near the focal point in 1 MHz simulation; (b) focusing plane and target foci reconstructed by simulation and experiment under 1 MHz excitation; (c) longitudinal acoustic field near the focal point in 2 MHz simulation; (d) focusing plane versus target foci reconstructed from simulation and experiment under 2 MHz excitation; (e) sound pressure comparison along the dashed line at x = 7.3 mm in simulation and experiment for the case of 1 MHz excitation; (f) sound pressure comparison along the dashed line at x = 7.3 mm in simulation and experiment for the case of 2 MHz excitation.
图 5 多频声全息透镜在多焦点情况下的仿真与实验结果 (a) 1 MHz仿真中, 焦点附近的纵向声场; (b)1 MHz激发下的仿真与实验重建的聚焦平面与目标焦点; (c)在2 MHz仿真中, 焦点附近的纵向声场; (d) 2 MHz激发下的仿真与实验重建的聚焦平面与目标焦点; (e)1 MHz激发的情况下, 在仿真和实验中, 沿着y = 7.3 mm的虚线上的声压对比; (f)2 MHz激发的情况下, 在仿真和实验中, 沿着y = 7.3 mm的虚线上的声压对比
Figure 5. Simulation and experimental results of multi-frequency acoustic holographic lenses in the case of multiple focal points: (a) Longitudinal acoustic field near the focal point in the 1 MHz simulation; (b) focused plane and target foci reconstructed by simulation and experiment for the 1 MHz excitation; (c) longitudinal acoustic field near the focal point in the 2 MHz simulation; (d) focused plane and target foci reconstructed by simulation and experiment for the 2 MHz excitation; (e) sound pressure comparison in the 1 MHz excitation case in the simulation and experiment along the y = 7.3 mm dashed line; (f) sound pressure comparison along the dashed line at y = 7.3 mm in simulation and experiment for the case of 2 MHz excitation.
表 1 聚焦平面的声场与目标图像之间的PSNR
Table 1. PSNR between the sound field at the focal plane and the target image
频率/MHz PSNR(仿真) PSNR(实验) 1 32.16 27.48 2 40.18 32.33 表 2 聚焦平面的声场与目标图像之间的PSNR
Table 2. PSNR between the sound field at the focal plane and the target image.
频率/MHz PSNR(仿真) PSNR(实验) 1 29.39 23.30 2 39.89 32.17 -
[1] Landhuis E 2017 Nature 551 257 doi: 10.1038/d41586-017-05479-7 [2] 张玫玫, 吴意赟, 于洁, 屠娟, 章东 2023 物理学报 72 084301 doi: 10.7498/aps.72.20230068 Zhang M M, Wu Y Y, Yu J, Tu J, Zhang D 2023 Acta Phys. Sin. 72 084301 doi: 10.7498/aps.72.20230068 [3] Ballantine H, Bell E, Manlapaz J 1960 J. Neurosurg. 17 858 doi: 10.3171/jns.1960.17.5.0858 [4] Vykhodtseva N, Hynynen K, Damianou C 1995 Ultrasound Med. Biol. 21 969 doi: 10.1016/0301-5629(95)00038-S [5] Elias W J, Khaled M, Hilliard J D, Aubry J F, Frysinger R C, Sheehan J P, Wintermark M, Lopes M B 2013 J. Neurosurg. 119 307 doi: 10.3171/2013.5.JNS122327 [6] 张芸芸, 李义方, 石勤振, 许乐修, 戴菲, 邢文宇, 他得安 2023 物理学报 72 154303 doi: 10.7498/aps.72.20230581 Zhang Y Y, Li Y F, Shi Q Z, Xu L X, Dai F, Xing W Y, Ta D A 2023 Acta Phys. Sin. 72 154303 doi: 10.7498/aps.72.20230581 [7] Yang Y, Wang C Z, Li Y C, Huang J Q, Cai F Y, Xiao Y, Ma T, Zheng H R 2019 IEEE Trans. Neural Syst. Rehabil. Eng. 28 361 [8] Tufail Y, Yoshihiro A, Pati S, Li M M, Tyler W J 2011 Nat. Protoc. 6 1453 doi: 10.1038/nprot.2011.371 [9] Melde K, Mark A G, Qiu T, Fischer P 2016 Nature 537 518 doi: 10.1038/nature19755 [10] Leith E N, Upatnieks J 1962 J. Opt. Soc. Am. 52 1123 doi: 10.1364/JOSA.52.001123 [11] 钟志, 赵婉婷, 单明广, 刘磊 2021 物理学报 70 154202 doi: 10.7498/aps.70.20210190 Zhong Z, Zhao W T, Shan M G, Liu L 2021 Acta Phys. Sin. 70 154202 doi: 10.7498/aps.70.20210190 [12] Andrés D, Jiménez-Gambín S, Jiménez N, Camarena F 2020 IEEE International Ultrasonics Symposium Las Vegas, NV, USA, November 17, 2020 p1 [13] Jiménez-Gambín S, Jiménez N, Benlloch J M, Camarena F 2019 Phys. Rev. Appl. 12 014016 doi: 10.1103/PhysRevApplied.12.014016 [14] Shah B R, Lehman V T, Kaufmann T J, Blezek D, Waugh J, Imphean D, Yu F F, Patel T R, Chitnis S, Dewey Jr R B 2020 Brain 143 2664 doi: 10.1093/brain/awaa107 [15] Yin Y, Yan S, Huang J, Zhang B 2023 Sensors 23 9702 doi: 10.3390/s23249702 [16] Jiménez-Gambín S, Jiménez N, Pouliopoulos A N, Benlloch J M, Konofagou E E, Camarena F 2021 IEEE Trans. Biomed. Eng. 69 1359 [17] Pouliopoulos A N, Wu S Y, Burgess M T, Karakatsani M E, Kamimura H A, Konofagou E E 2020 Ultrasound Med. Biol. 46 73 doi: 10.1016/j.ultrasmedbio.2019.09.010 [18] Tillander M, Hokland S, Koskela J, Dam H, Andersen N P, Pedersen M, Tanderup K, Ylihautala M, Köhler M 2016 Med. Phys. 43 1539 doi: 10.1118/1.4942378 [19] Treeby B E, Cox B T 2010 J. Biomed. Opt. 15 021314 doi: 10.1117/1.3360308 [20] Mast T D, Souriau L P, Liu D L, Tabei M, Nachman A I, Waag R C 2001 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 48 341 doi: 10.1109/58.911717 [21] Tabei M, Mast T D, Waag R C 2002 J. Acoust. Soc. Am. 111 53 doi: 10.1121/1.1421344 [22] Kook G, Jo Y, Oh C, Liang X, Kim J, Lee S M, Kim S, Choi J W, Lee H J 2023 Microsyst. Nanoeng. 9 45 doi: 10.1038/s41378-023-00513-3 [23] Treeby B E, Cox B T 2010 J. Acoust. Soc. Am. 127 2741 doi: 10.1121/1.3377056 [24] Thomas J L, Fink M A 1996 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 43 1122 doi: 10.1109/58.542055 [25] Aubry J F, Tanter M, Pernot M, Thomas J L, Fink M 2003 J. Acoust. Soc. Am. 113 84 doi: 10.1121/1.1529663 [26] Brown M D, Cox B T, Treeby B E 2017 Appl. Phys. Lett. 111 244101 doi: 10.1063/1.5004040 [27] He J R, Wu J W, Zhu Y Y, Chen Y, Yuan M D, Zeng L M, Ji X R 2021 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 69 662 [28] Tanchenko A 2014 J. Vis. Commun. Image Represent. 25 874 doi: 10.1016/j.jvcir.2014.01.008 [29] Bakaric M, Miloro P, Javaherian A, Cox B T, Treeby B E, Brown M D 2021 J. Acoust. Soc. Am. 150 2798 doi: 10.1121/10.0006668 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: