首页
登录
注册
下载:
-
20世纪50年代初, 意大利物理学家Fermi, Pasta, Ulam三位科学家及学生Tsingou在第一代大型计算机上模拟由64个谐振子组成的非线性系统的演化, 期望证明统计物理学中的能量均分原理, 初始时刻这些谐振子所有的能量都集中于某一振子上, 其他振子的初始能量为零, 按照能量均分原理, 系统最后应达到一种平衡态, 即能量应均等地分配到所有振子上, 但是模拟结果事与愿违, 他们发现该非线性系统的大部分能量能周期性地回归到初始态, 此即著名的Fermi-Pasta-Ulam-Tsingou现象, 简称FPUT现象[1]. 该现象的发现曾极度地推动了非线性物理学的发展. 早期的FPUT现象研究主要集中在流体力学领域, 由于其实验观测需要庞大的船只等实验设备, 所需成本较高, 因此FPUT现象研究逐渐被搁置. 随着光学精密仪器的发展和实验技术的进步, 2001年得以在实验室首次实现光纤中FPUT现象的观测[2], 自此以后, 非线性物理学界掀起了对FPUT现象的研究热潮[3–15].
FPUT现象的形成与非线性系统的双周期波态和调制不稳定性相关[3–15]. 调制不稳定性描述加在系统平面波上的微小扰动随传输距离的增加而指数增长的这一过程, 它可有效地解释FPUT现象中一阶扰动信号振幅随传输距离的初始增长过程[16–18], 高阶扰动成分振幅的增长可由级联调制不稳定性解释[6,19,20], 当多个扰动成分振幅增至最大值后出现振幅的快速衰减, 其原因至今还未能得到有效的物理解释. 理论方面, 人们还研究了不同类型的FPUT现象和调制不稳定性的关系[21]、讨论了高阶效应对FPUT现象的影响及高阶效应下FPUT现象的频率谱特点[22,23]、探索了三波截断法分析FPUT现象等工作[13]. 近年, 人们还发现FPUT现象不仅能在调制不稳定性区域内(称为传统调制不稳定性)激发, 还能在调制不稳定性区域外(称为非传统调制不稳定性)激发[24–26], 这可能与调制不稳定性的计算过程中忽略了扰动的非线性效应有关. 除此之外, 人们还将FPUT现象的研究推广到了两耦合非线性系统, 基于Manakov模型方程发现两耦合系统具有非对称频谱的特点, 主要结果包括相关非对称光谱的解析计算[27]、非简并Akhmediev呼吸子解的求解[28]以及复杂的高阶调制不稳定性演化[29]. 实验方面, 近年来, 人们采用不同的技术手段实现光纤中的FPUT现象的观测, 如具有破坏性的“回切”测量术[30]、基于光时域反射仪系统的全光纤测量方法[31–33]、基于周期性放大作用的循环光纤环方法[16, 34]等不同技术手段.
稳定的非线性波是实验观测的关键, 然而据我们所知, 目前对FPUT现象稳定性的研究还非常少, 相关研究主要通过分析某个特定的双周期波的稳定性来讨论FPUT现象的稳定性[26, 35], 分析结果只局限于某一特定的解析双周期波解, 且不能直接地从实际的实验条件出发分析FPUT现象的稳定性. 本文则考虑实验中的实际条件, 以加入一定噪声的正弦扰动平面波作为入射条件, 通过数值模拟方法分析光纤中FPUT现象的稳定性. 研究中, 我们并不局限于某一特定值的“扰动”振幅和“扰动”频率(很多相关文献在研究中都采用能引起最佳增益的最佳扰动频率作为正弦“扰动”频率, 且具有较小的“扰动”振幅), 而是采用较大频率域内的值, 横跨了调制不稳定性区域内外的频率空间, “扰动”振幅的值也不限于小量, 因此我们的研究结果具有广泛性、可推广性、可为光纤中FPUT现象的理论和实验研究提供有益的帮助.
-
描述电场慢变包络在非线性单模光纤中传输的控制方程为经典的非线性薛定谔方程, 即
其中a表示电场的慢变包络振幅; z代表传输距离; t代表群速度参考系下的时间坐标; β2是群速度色散参量, 其值可正可负(β2 > 0代表正常色散, β2 < 0代表反常色散); γ代表光纤克尔效应的非线性系数.
不失一般性, 为方便分析, 我们可将模型方程(1)归一化为
其中
(3)式中Ld为色散长度, T0为初始脉冲宽度.
本文后面的分析将依归一化方程(2)展开讨论. 方程(2)的平面波解为
其中A0表示入射平面波的振幅, 依线性稳定性分析方法知, 在正常色散情况下, 即当β2 > 0 (或sgn(β2) = 1)时, 光纤不具备调制不稳定性, 在反常色散情况下, 即当β2 < 0 (或sgn(β2) = –1)时, 光纤具有调制不稳定性, 基于归一化模型方程(2)的光纤增益谱为
其中K为正弦扰动波束; Ω为正弦扰动频率; Im(K)代表K的虚部, 最佳增益为
我们在本文中采用实验中比较容易实现的初始条件, 即
其中方程(7)右侧第2和第3项分别代表在泵浦光频率两侧所加的两个正弦扰动信号(
$ \pm \varOmega $ 频率成分), 其振幅均为$ \sqrt \delta $ , φ0代表正弦信号与泵浦光的相位差, 第三项代表实验条件下不可避免的白色噪声, 在模拟中, 令其中rand代表[0, 1]范围内均匀分布的一系列随机数, 该噪声的振幅为泵浦光振幅的1%.
-
本文采用的模拟方法为经典的谱方法与自适应步长的龙格库塔方法相结合的模拟方法. 在本文的模拟结果中, 不失一般性, 令平面波振幅A0 = 1(对应的最佳扰动频率为
$ {\varOmega _{\text{m}}} = \sqrt 2 $ , 临界扰动频率为$ {\varOmega _{\text{c}}} = 2 $ ), 为使结果具有普适性, 同时不激发高阶谐波, 在我们的研究中, 正弦扰动频率Ω > Ωc/2 = 1, 其值不仅可以位于调制不稳定性区域内(Ω < 2), 也可以位于调制不稳定性区域外(Ω > 2); 正弦扰动振幅δ不局限于无穷小量, 其值任意. -
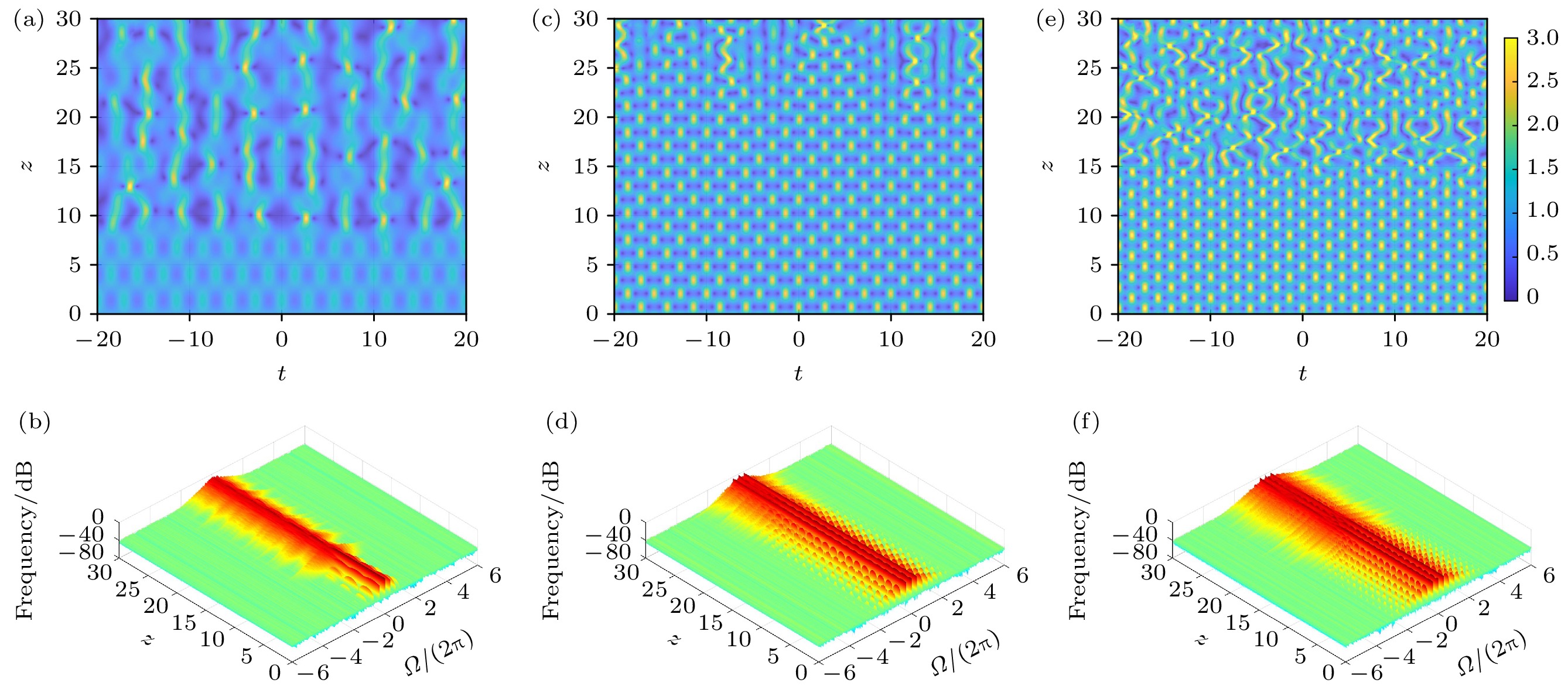
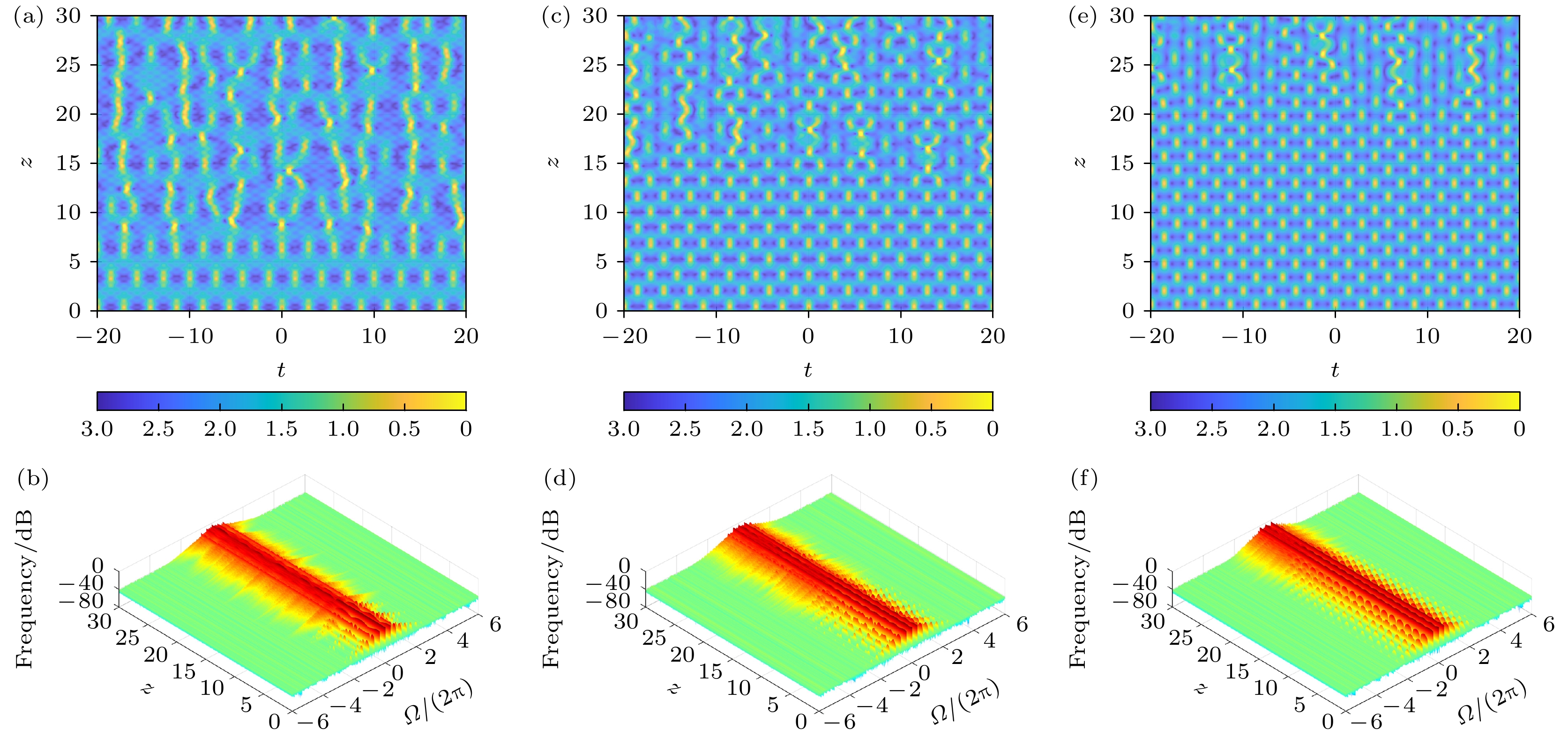
通过大量的数值模拟, 可以发现对一给定扰动频率, 扰动振幅可以极大地影响FPUT现象的稳定性. 图1(a)和图1(b)分别反应当扰动频率Ω = 1.5, φ0 = 0.5π, 扰动振幅δ = 0.01时扰动平面波随传输距离的时空和频率谱演化, 可看出在该参数条件下, 扰动平面波振幅可周期性的回归到初始态(z = 0处), 此即FPUT现象, 稳定的FPUT现象可传输至约z = 15处, 当z > 15, FPUT现象逐渐消失, 波形很快变得杂乱无章; 随着扰动振幅δ的增加, 发现FPUT现象的稳定性逐渐增强, 当增加至δ = 0.1, FPUT现象的稳定性增至最强, 如图1(c)和图1(d)所示(δ = 0.1), 稳定的FPUT现象可传输至约z = 22.5处; 随着扰动振幅的进一步增加, FPUT现象稳定性逐步减弱, 如图1(e)和图1(f)所示, 其中 δ = 0.25, 这时稳定的FPUT现象只可传输至约z = 15.
由图1可看出, 随着传输距离的增加, 规则的双周波演化(也即FPUT现象)最终都变得杂乱无章, 这应该与调制不稳定性及级联调制不稳定性相关. 由级联调制不稳定性效应所出现的高阶频率谱成分也具有调制不稳定性增益, 当这些高频成分的振幅长到一定值, 彼此之间及与低频率成分之间就产生相互作用, 从而改变波形演化的动力学特征; 另一方面, 噪声在实验中不可避免, 而噪声中也存在众多具有非零增益的频率成分, 这些频率成分的振幅随传输距离增加而快速增长, 当其增加到一定程度, 彼此之间都会产生相互作用. 故图1中规则的双周期波随着传输距离的增加都会变得杂乱无章. 这里的论述可用于解释下文中所有相关图中规则双周波演化最终都变得杂乱无章的原因.
通过比较图1可看出: 第一, 在给定的扰动频率下, 随着扰动振幅的增加, FPUT现象的稳定性先增强再减弱; 第二, 在给定的扰动频率下, 存在一个临界的扰动振幅δcr, 当δ < δcr时, 随着δ的增加, FPUT现象的稳定性逐渐增强; 当δ = δcr时, FPUT现象稳定性增至最强; 当δ > δcr时, 随着δ的增加, FPUT现象稳定性逐渐减弱.
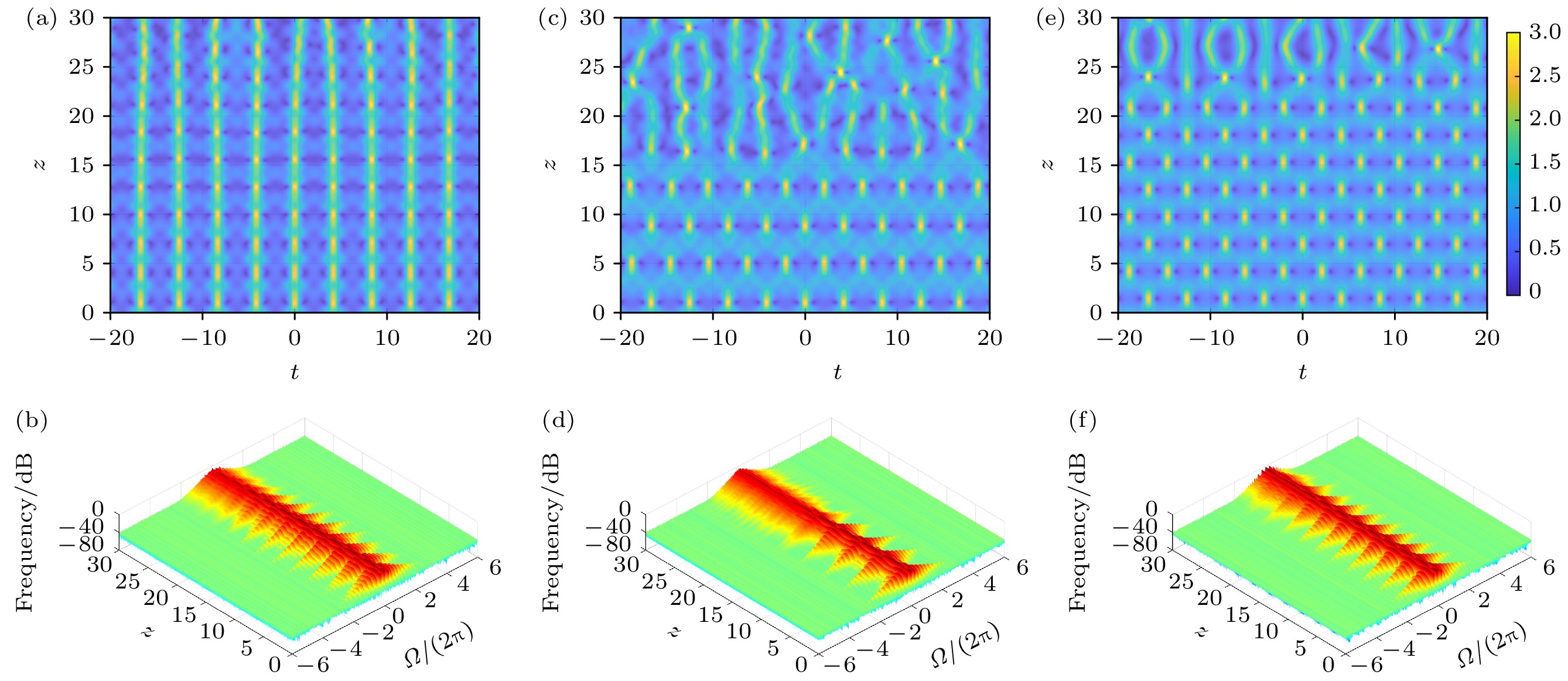
上述结论也适用于扰动频率位于调制不稳定性带外的情况, 如图2所示(所用参数为Ω = 2.2 > Ωc = 2, φ0 = 0.5π, 扰动振幅从上到下依次是δ = 0.01, 0.25, 0.5). 当δ = 0.01时, 稳定的FPUT现象只可传输至距离约z = 9处, 当δ = 0.25时, 稳定的FPUT现象可传输距离增至约z = 22处, 当δ = 0.5时, 稳定的FPUT现象可传输距离减至约z = 13处.
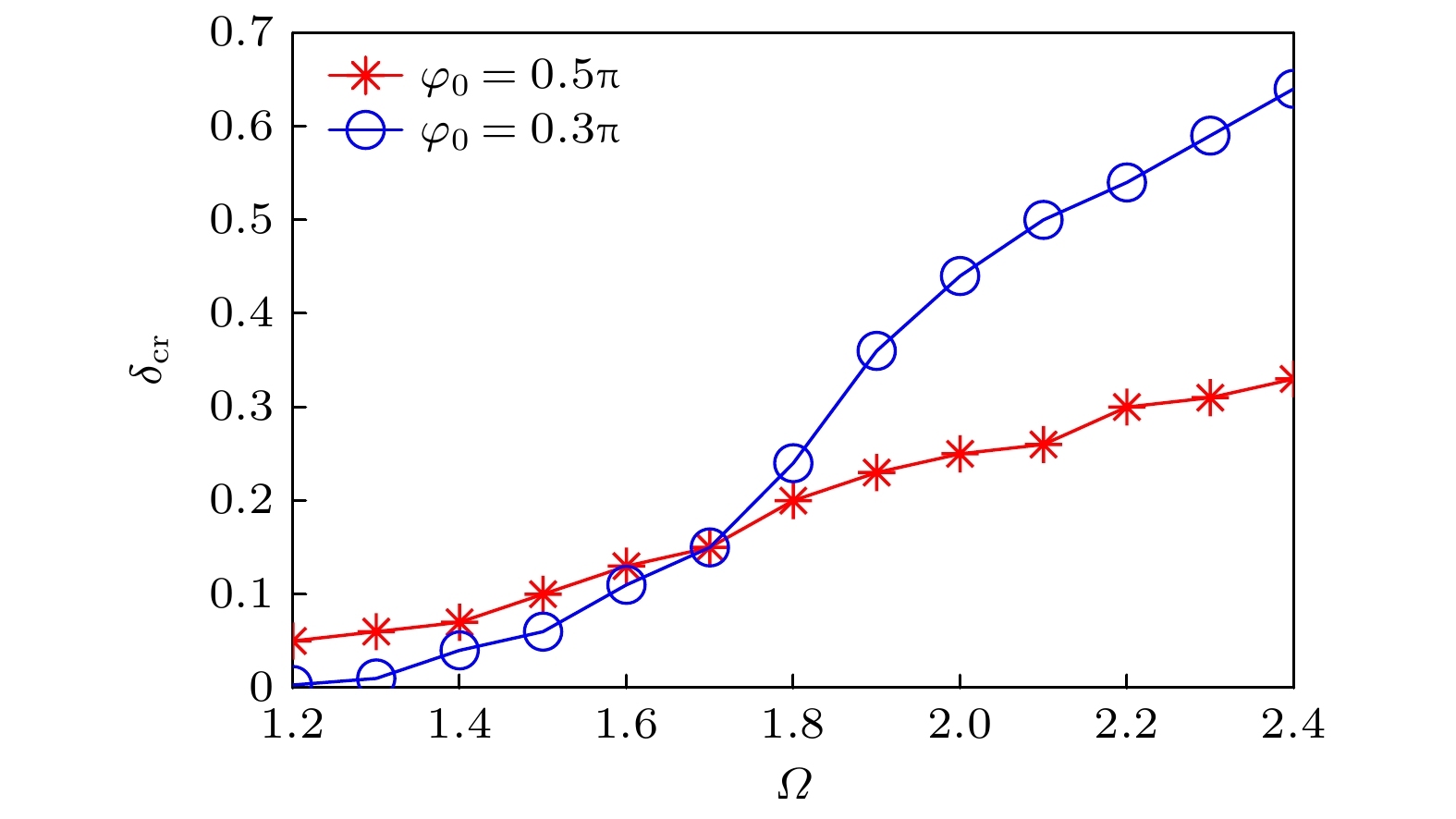
临界扰动振幅δcr值与扰动频率密切相关, 其值随着扰动频率的增加而增加, 如图3所示. 此结论不仅适用于扰动信号与泵浦光之间相位差φ = 0.5π的情况, 还适用于其他相位差的情况, 主要区别是随着φ的减小, 较小扰动频率所需的临界扰动振幅δcr相对较小(比较图3中Ω < 1.7时φ = 0.5π和φ =0.3π对应的δcr值曲线), 反之则比较大(比较图3中Ω > 1.7时φ = 0.5π和φ =0.3π对应的δcr值曲线).
-
扰动信号与泵浦光之间相位差(φ0)是影响FPUT现象演化规律的另一个非常重要的物理 参量, 在图1和图2中, φ0 = 0.5π, 下面将探讨扰动振幅一定时, 相位差φ0从0逐渐增加至0.5π时所引起的对FPUT现象稳定性的影响, 为突出相位差φ0的影响, 我们在该部分的研究中令扰动振幅保持不变.
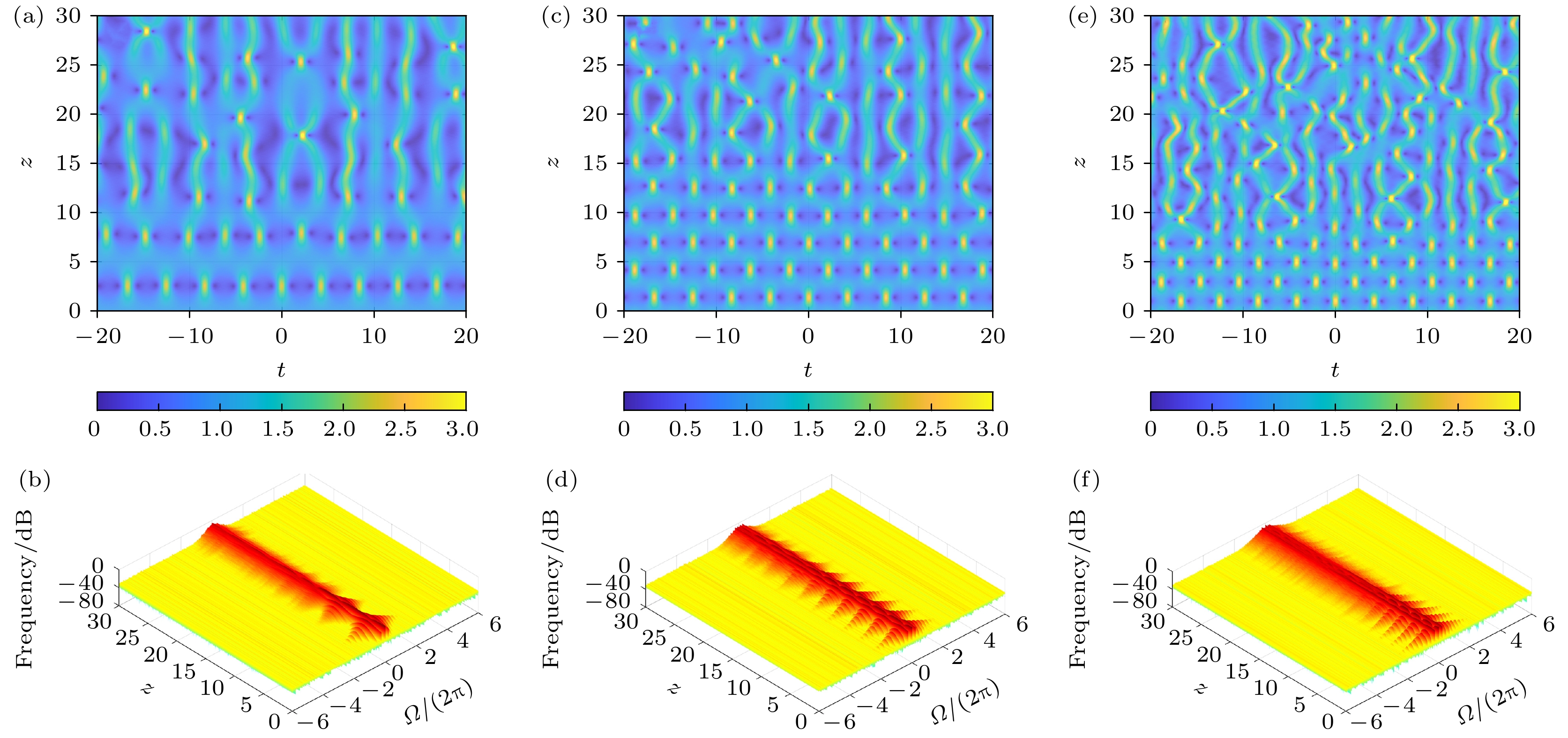
图4展示了当扰动频率位于调制不稳定性带内时相位差φ0对FPUT现象稳定性的影响. 如图4(a)所示, 当φ0 = 0.1π时, FPUT现象可比较稳定的传输到z = 25处; 当相位差φ0增至0.3π时, FPUT现象只可以较稳定的传输到z = 15处(图4(b)); 当相位差φ0继续增至0.5π时, 稳定的FPUT现象可传输距离又增至z = 20处(图4(c)). 由此可见, 相位差φ0可极大程度地影响FPUT现象的稳定性, 通过大量的数值模拟, 我们发现当φ0从0开始逐渐增加时, FPUT稳定性先逐渐减弱, 当φ0增加至某临界值φ0cr, FPUT稳定性减至最弱, 当φ0继续增加时, FPUT稳定性又逐步增强. 上述结论适用于调制不稳定性带内的其他扰动频率值.
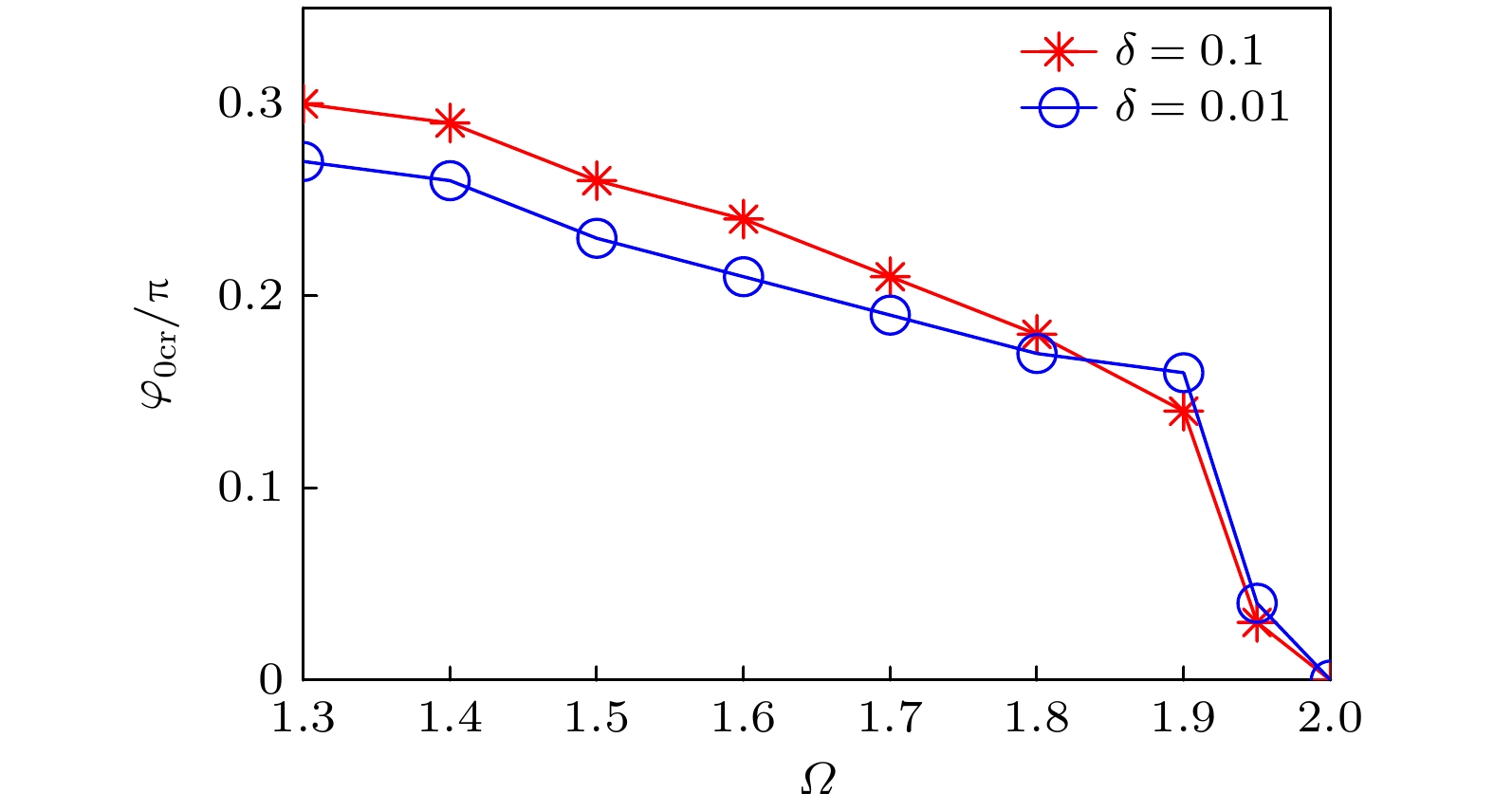
图5显示了当扰动振幅分别为δ = 0.1 和δ =0.01时, 临界值φ0cr随扰动频率的变化关系. 由图5可见, 临界值φ0cr随扰动频率的增加而快速减小, 且在较大的频率范围内, 临界值φ0cr随扰动振幅δ的增加而增加. 在此值得注意的是当扰动频率接近截止频率时, 即当Ω → 2时, φ0cr → 0, 也就是说当扰动频率接近截止频率, 且当扰动信号和泵浦光同相时, FPUT现象的稳定性最差.
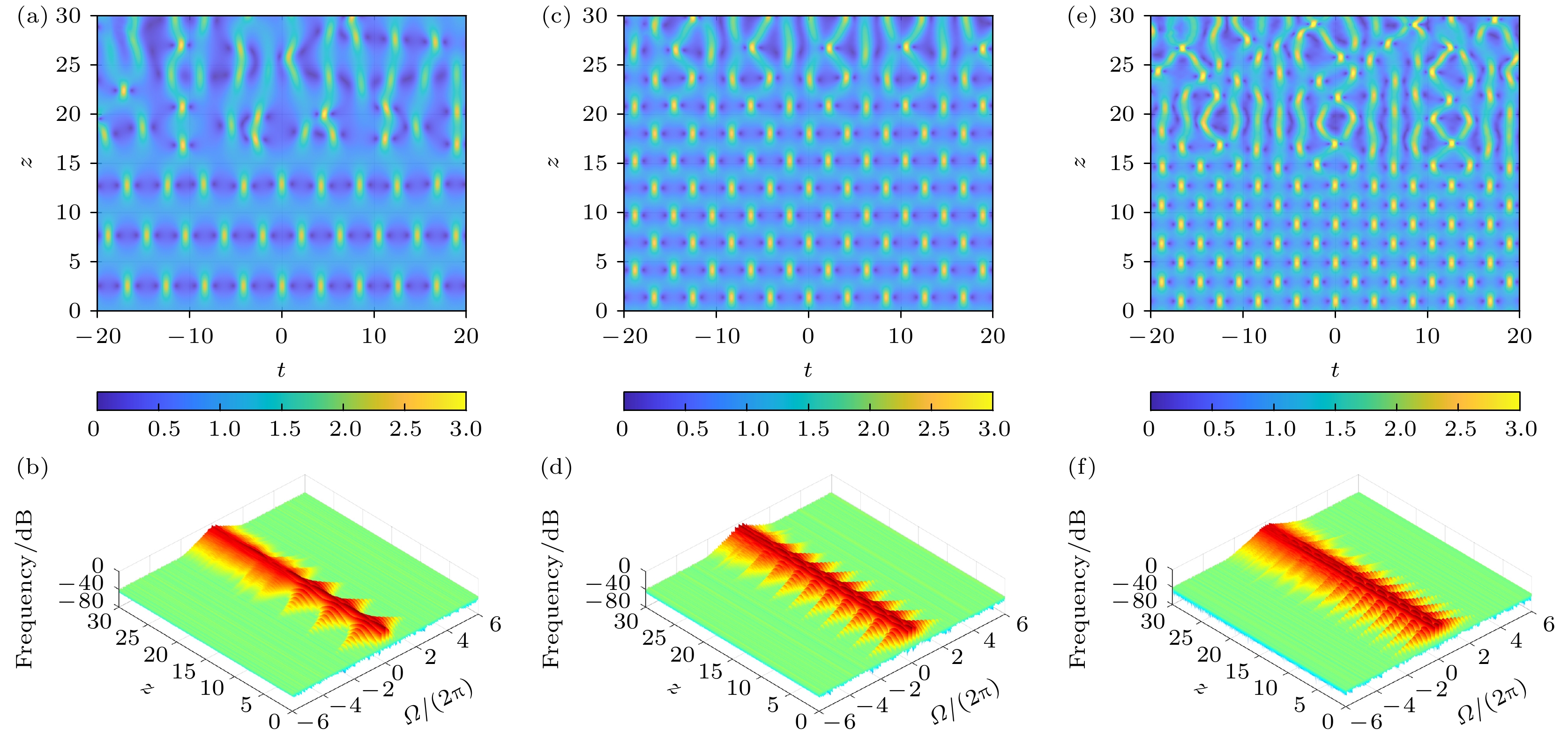
当扰动频率位于调制不稳定性带外时, 相位差对FPUT现象稳定性的影响与扰动频率位于带内的情况截然不同, 随着相位差φ0的增加, FPUT现象稳定性呈现单调增强的趋势, 如图6所示, 当φ0 = 0.1π时(图6(a)), FPUT只可稳定的传输至约z = 5; 当φ0 = 0.3π时(图6(b)), FPUT可稳定的传输至约z = 15; 当φ0 = 0.5π时(图6(c)), FPUT可稳定传输距离增至约z = 20.
-
噪声在实验中是不可避免的, 同时, 在数值模拟中, 也会因数值方法的不稳定性引起, 故在研究工作中必须考虑噪声对FPUT现象稳定性的影响. 图7展示了当(8)式中噪声系数为0.1时, 即当噪声的振幅为泵浦光振幅的10%时, 扰动平面波随传输距离的时空和相应的频谱演化, 其他参数与图1(噪声系数为0.01)完全相同. 比较图7与图1可看到噪声越大, 所观察到的FPUT现象循环数越少, FPUT现象稳定性越差, 该结论与Wabnitz和Wetzel研究的[5]结论一致. 物理上这是可以完全理解的, 噪声中有众多不稳定性增益频率成分, 其振幅随着传输距离的增加而增加, 当振幅达到一定量值, 彼此之间以及与一阶扰动频率成分之间均会产生相互作用, 从而破坏FPUT现象的稳定性演化. 当噪声系数增加时, 噪声中所有频率成分的初始振幅都将增加, 这时所有具有非零增益的频率成分的振幅都会随着传输距离的增加而极速增加, 故在较短的传输距离内就能彼此之间以及与一阶及级联的高阶扰动频率成分之间发生强相互作用, 从而快速破坏FPUT现象的稳定性传输.
上述扰动振幅及扰动信号与泵浦光之间相位差对FPUT现象的稳定性影响, 不能由调制不稳定性及级联调制不稳定性来解释, 它们只能用来解释一阶及高阶扰动振幅的初始增长, 由于能量守恒, 其振幅并不会无限的增加, 当振幅增加到一定值, 就会出现衰减至初始态的现象, 衰减的物理原因至今尚未清楚, 我们认为扰动振幅对FPUT现象的稳定性影响可能主要与其关联的严格双周期波的稳定性紧密相关. 经典的非线性薛定谔模型方程(1)是可积系统, 理论上讲, 具有非常多的严格双周期波解, 其中一些解在一定条件下可退化到(7)式的初始态, 该些解的稳定性可能均与(7)式中的扰动振幅δ和相位差φ0紧密相关, 而且与本文上述结论一致.
-
FPUT现象的稳定性是影响其实验观测的一个重要特性, 本文结合实验中的实际条件, 通过大量的仿真模拟研究了扰动振幅及扰动信号与泵浦光间相位差对FPUT现象稳定性的影响, 研究发现二者均可以极大程度地影响FPUT现象的稳定性.
当扰动振幅从无穷小量逐渐增加时, FPUT现象的稳定性逐渐增强; 当扰动振幅值达到临界扰动振幅值, FPUT现象的稳定性增至最强; 当扰动振幅继续增加时, FPUT现象的稳定性又逐渐减弱, 该临界扰动振幅值随扰动频率的增加而增加.
扰动信号与泵浦光间相位差对调制不稳定性带内和带外的FPUT现象稳定性影响不同. 当扰动频率位于调制不稳定性带内时, 随着相位差的增加, FPUT现象的稳定性逐步减弱; 当相位差增至临界值, FPUT现象的稳定性减至最弱; 随着相位差的继续增加, FPUT现象的稳定性又开始逐步增强. 临界相位差值随扰动频率的增加而减弱. 当扰动频率位于调制不稳定性带外时, FPUT现象的稳定性随着相位差的增加而增强.
噪声的强度并不影响上述主要结论, 但是噪声的存在将降低FPUT现象的稳定性, 噪声振幅越大, FPUT现象的稳定性越差.
利用上述主要结论, 可以用来指导FPUT现象的实验观测. FPUT现象并不能无限的周期性传输, 它的周期性总是在一定传输距离后被破坏掉, 由上述主要结论, 我们得知在实验中设置的扰动振幅要适当大, 不能受到调制不稳定性的局限性而把扰动振幅总设置在非常小的范围值内, 同时, 扰动信号与泵浦光的相位差要适当, 当扰动频率位于传统调制不稳定性区域内时, 该相位差要尽量避免中间值, 即要么使其为0, 要么为0.5π, 但是当扰动频率位于传统调制不稳定性区域外时, 该相位差要位于0.5π为最佳.
综上, 我们在研究中并不局限于某一特定值的扰动振幅和扰动频率, 其中扰动振幅任意, 扰动频率横跨了调制不稳定性区域内外的频率空间, 故我们的研究结果具有广泛性、可推广性、可为光纤中FPUT现象的理论和实验研究提供有益的帮助.
非线性光纤中Fermi-Pasta-Ulam-Tsingou现象的稳定性分析
Stability analysis of Fermi-Pasta-Ulam-Tsingou phenomenon in nonlinear optical fibers
-
摘要:
稳定性是影响Fermi-Pasta-Ulam-Tsingou(FPUT)现象实验观测的一个十分重要的因素, 针对文献中FPUT现象稳定性分析贫乏的问题, 本文主要通过数值模拟方法研究非线性光纤中影响FPUT现象稳定性的主要因素. 本文采用的初始条件为实验上比较容易实现的正弦扰动平面波加上白色噪声, 发现增加扰动振幅及扰动信号与泵浦光之间的相位差均可极大程度的影响FPUT现象的稳定性. 结果表明: 1) 当扰动振幅从零逐渐增加时, 所观察到的FPUT现象的稳定性逐渐增强; 当扰动振幅增加至临界值, FPUT现象的稳定性增至最强; 当扰动振幅大于该临界值, FPUT现象的稳定性开始逐渐减弱. 2) 当扰动频率位于传统调制不稳定性区域时, 随着扰动信号与泵浦光之间相位差从0增加至π/2, FPUT现象的稳定性先减弱, 当相位差增加至某临界值, FPUT现象的稳定性减至最弱, 当相位差大于临界值, FPUT现象的稳定性又出现逐步增强的规律. 当扰动频率位于非传统调制不稳定性区域时, 与传统情况不同, FPUT现象的稳定性随扰动信号与泵浦光之间的相位差的增加而增强. 以上结果表明, 在FPUT现象的实验中, 为观察到更稳定的FPUT现象, 扰动振幅的值不能太小, 且扰动信号与泵浦光之间相位差也要适宜. Abstract:Stability plays a significant role in successfully observing Fermi-Pasta-Ulam-Tsingou (FPUT) phenomenon in experiment. However, there are few relevant studies in the literature. The primary object of this work is to study the stability of FPUT phenomenon in the nonlinear fibers numerically. In this study, we take the sinusoidally perturbed continuous waves (CWs) with white noise as the imposed initial condition, which can be readily realized in real experiments. We find that both the perturbation amplitude and phase difference between the perturbation and pump can drastically affect the stability of the resulting FPUT phenomenon. Firstly, as the perturbation amplitude increases, the FPUT phenomenon becomes much more stable. When the perturbation amplitude reaches a critical value, the most stable FPUT phenomenon can be observed. With the further increase of the perturbation amplitude, the stability of the resulting FPUT phenomenon weakens. Secondly, the phase difference between the perturbation and pump takes distinct effects on the stability of FPUT phenomenon for perturbation frequency located inside and outside the conventional modulation instability (MI) band. For the perturbation frequency located inside the conventional MI band, as the phase difference between the perturbation and pump increases from zero, the corresponding FPUT phenomenon first is less stable, and then becomes most instable at a critical phase difference; after that, the stability of the FPUT phenomenon is enhanced again. For the perturbation frequency located outside the conventional MI band, the stability of FPUT phenomenon is enhanced monotonically as the phase difference increases from 0 to π/2. In order to observe a much more stable FPUT phenomenon, as shown in the above results, the perturbation amplitude should be moderately large, and the phase difference between the perturbation and the pump should be appropriate to avoid the most instable FPUT phenomenon. -
Key words:
- modulation instability /
- Fermi-Pasta-Ulam-Tsingou recurrence .
-
-
图 1 非线性光纤中扰动平面波随传输距离的时空和相应的频谱演化(1%噪声), 参数为Ω = 1.5, φ0 = 0.5π (a), (b) δ = 0.01; (c), (d) δ = 0.1; (e), (f) δ = 0.25
Figure 1. The evolution of perturbed plane waves in nonlinear fibers with the propagation distance in the temporal and spectral domain (1% noise) with Ω = 1.5, φ0 = 0.5π: (a), (b) δ = 0.01; (c), (d) δ = 0.1; (e), (f) δ = 0.25.
图 2 非线性光纤中扰动平面波随传输距离的时空和相应的频谱演化(1%噪声), 参数为Ω = 2.2, φ0 = 0.5π (a), (b) δ = 0.01; (c), (d) δ = 0.25; (e), (f) δ = 0.5
Figure 2. The evolution of perturbed plane waves in nonlinear fibers with the propagation distance in the temporal and spectral domain (1% noise) with Ω = 2.2, φ0 = 0.5π: (a), (b) δ = 0.01; (c), (d) δ = 0.25; (e), (f) δ = 0.5.
图 3 临界扰动振幅δcr与扰动频率的依赖关系(1%噪声)
Figure 3. The dependence of the critical perturbation amplitude (δcr) on the perturbation frequency (1% noise).
图 4 非线性光纤中扰动平面波随传输距离的时空和相应的频谱演化(1%噪声), 参数为Ω = 1.5, δ = 0.1 (a), (b) φ0 = 0.1π; (c), (d) φ0 = 0.3π; (e), (f) φ0 = 0.5π
Figure 4. The evolution of perturbed plane waves with the propagation distance in the temporal and spectral domain (1% noise) with parameters Ω = 1.5, δ = 0.1: (a), (b) φ0 = 0.1π; (c), (d) φ0= 0.3π; (e), (f) φ0 = 0.5π.
图 5 扰动信号与泵浦光之间的临界相位差与扰动频率的依赖关系(1%噪声)
Figure 5. The dependence of the critical phase difference between the perturbation and the pump on the perturbation frequency (1% noise).
图 6 非线性光纤中扰动平面波随传输距离的时空和相应的频谱演化(1%噪声), 参数为Ω = 2.2, δ = 0.25 (a), (b) φ0 = 0.1π; (c), (d) φ0 = 0.3π; (e), (f) φ0 = 0.5π
Figure 6. The evolution of perturbed plane waves with the propagation distance in the temporal and spectral domain (1% noise) with parameters Ω = 2.2, δ = 0.25: (a), (b) φ0 = 0.1π; (c), (d) φ0= 0.3π; (e), (f) φ0 = 0.5π.
图 7 非线性光纤中扰动平面波随传输距离的时空和相应的频谱演化(10%噪声), 参数为Ω = 1.5, φ0 = 0.5π (a), (b) δ = 0.01; (c), (d) δ = 0.1; (e), (f) δ = 0.25
Figure 7. The evolution of perturbed plane waves in nonlinear fibers with the propagation distance in the temporal and spectral domain (10% noise) with Ω = 1.5, φ0 = 0.5π: (a), (b) δ = 0.01; (c), (d) δ = 0.1; (e), (f) δ = 0.25.
-
[1] Fermi E, Pasta P, Ulam S, Tsingou M 1955 Studies of the Nonlinear Problems Los Alamos, May 1, 1955 pLA-1940 [2] Van Simaeys G, Emplit G, Haelterman M 2001 Phys. Rev. Lett. 87 033902 doi: 10.1103/PhysRevLett.87.033902 [3] Akhmediev N N 2001 Nature 413 267 doi: 10.1038/35095154 [4] Devine N, Ankiewicz A, Genty G, Dudley J M, Akhmediev N 2011 Phys. Lett. A 375 4158 doi: 10.1016/j.physleta.2011.10.006 [5] Wabnitz S, Wetzel B 2014 Phys. Lett. A 378 2750 doi: 10.1016/j.physleta.2014.07.018 [6] Chin S A, Ashour O A, Blic M R 2015 Phys. Rev. E 92 063202 doi: 10.1103/PhysRevE.92.063202 [7] Bao C, Jaramillo-Villegas J A, Xuan Y, Leaird D E, Qi M, Weiner A M 2016 Phys. Rev. Lett. 117 163901 doi: 10.1103/PhysRevLett.117.163901 [8] Kimmoun O, Hsu H C, Branger H, Li M S, Chen Y Y, Kharif C, Onorato M, Kelleher E J R, Kibler B, Akhmediev N, Chabchoub A 2016 Sci. Rep. 6 28516 doi: 10.1038/srep28516 [9] Deng G, Li S, Biondini G, Trillo S 2017 Phys. Rev. E 96 052213 doi: 10.1103/PhysRevE.96.052213 [10] Pierangeli D, Flammini M, Zhang L, Marcucci G, Agranat A J, Grinevich P G, Santini P M, Conti C, DelRe E 2018 Phys. Rev. X 8 041017 doi: 10.1103/PhysRevX.8.041017 [11] Naveau C, Szriftgiser P, Kudlinski A, Conforti M, Trillo S, Mussot A 2019 Opt. Lett. 44 763 doi: 10.1364/OL.44.000763 [12] Vanderhaegen G, Szriftgiser P, Kudlinski A, Conforti M, Trillo S, Droques M, Mussot A 2020 Opt. Express 28 17773 doi: 10.1364/OE.391560 [13] Sheveleva A, Andral U, Kibler B, Colman P, Dudley J M, Finot C 2022 Optica 9 656 doi: 10.1364/OPTICA.445172 [14] Chen S C, Liu C 2022 Physica D 438 133364 doi: 10.1016/j.physd.2022.133364 [15] Sinthuja N, Rajasekar S, Senthilvelan M 2023 Nonlinear Dyn. 111 16497 doi: 10.1007/s11071-023-08722-1 [16] Kraych A E, Agafontsev D, Randoux S, Suret P 2019 Phys. Rev. Lett. 123 093902 doi: 10.1103/PhysRevLett.123.093902 [17] Chowdury A, Ankiewicz A, Akhmediev N, Chang W 2018 Chaos 28 123116 doi: 10.1063/1.5053941 [18] Copie F, Suret P, Randoux S 2022 Opt. Lett. 47 3560 doi: 10.1364/OL.462389 [19] Kimmoun O, Hsu H C, Kibler B, Chabchoub A 2017 Phys. Rev. E 96 022219 doi: 10.1103/PhysRevE.96.022219 [20] Yin H M, Chow K W 2021 Physica D 428 133033 doi: 10.1016/j.physd.2021.133033 [21] Mussot A, Naveau C, Conforti M, Kudlinski A, Copie F, Szriftgiser P, Trillo S 2018 Nat. Photonics 12 303 doi: 10.1038/s41566-018-0136-1 [22] Liu C, Wu Y H, Chen S C, Yao X, Akhmediev N 2021 Phys. Rev. Lett. 127 094102 doi: 10.1103/PhysRevLett.127.094102 [23] Yao X K, Liu C, Yang Z Y, Yang W L 2022 Phys. Rev. Res. 4 013246 doi: 10.1103/PhysRevResearch.4.013246 [24] Conforti M, Mussot A, Kudlinski A, Trillo S, Akhmediev N 2020 Phys. Rev. A 101 023843 doi: 10.1103/PhysRevA.101.023843 [25] Vanderhaegen G, Naveau C, Szriftgiser P, Kudlinski A, Conforti M, Mussot A, Onorato M, Trillo S, Chabchoub A, Akhmediev N 2021 Proc. Natl. Acad. Sci. U.S.A. 118 e2019348118 doi: 10.1073/pnas.2019348118 [26] Cheung V Y Y, Yin H M, Li J H, Chow K W 2023 Phys. Lett. A 476 128877 doi: 10.1016/j.physleta.2023.128877 [27] Chen S C, Liu C, Yao X, Zhao L C, Akhmediev N 2021 Phys. Rev. E 104 024215 doi: 10.1103/PhysRevE.104.024215 [28] Liu C, Chen S C, Yao X K, Akhmediev N 2022 Chin. Phys. Lett. 39 094201 doi: 10.1088/0256-307X/39/9/094201 [29] Chen S C, Liu C, Akhmediev N 2023 Phys. Rev. A 107 063507 doi: 10.1103/PhysRevA.107.063507 [30] Hammani K, Wetzel B, Kibler B, Fatome J, Finot C, Millot G, Akhmediev N, Dudley J M 2011 Opt. Lett. 36 2140 doi: 10.1364/OL.36.002140 [31] Naveau C, Vanderhaegen G, Szriftgiser P, Martinelli G, Droques M, Kudlinski A, Conforti M, Trillo S, Akhmediev N, Mussot A 2021 Front. Phys. 9 637812 doi: 10.3389/fphy.2021.637812 [32] Hu X Y, Chen W, Lu Y, Yu Z J, Chen M, Meng Z 2018 IEEE Photon. Technol. Lett. 30 47 doi: 10.1109/LPT.2017.2773615 [33] Vanderhaegen G, Szriftgiser P, Kudlinski A, Armaroli A, Conforti M, Mussot A, Trillo S 2023 Phys. Rev. A 108 033507 doi: 10.1103/PhysRevA.108.033507 [34] Goossens J W, Hafermann H, Jaouën Y 2019 Sci. Rep. 9 18467 doi: 10.1038/s41598-019-54825-4 [35] Yin H M, Li J H, Zheng Z, Chiang K S, Chow K W 2024 Chaos 34 013120 doi: 10.1063/5.0157966 -
计量
- 文章访问数: 190
- HTML全文浏览数: 190
- PDF下载数: 3
- 施引文献: 0