-
中子的发现可以追溯到20世纪20年代, Rutherford[1]在研究原子核组成时提出了原子核中可能存在中性粒子的理论预测. 而中子的实验确认是在1932年由Chadwick[2]完成的, 他也因此获得了1935年的诺贝尔物理学奖. 之后, Halban[3]、Elsasser[4]和Mitchell等[5]证实了中子具有波动性, 并实现了中子衍射实验. 同时, Bloch[6]从理论上进一步提出中子的自旋为1/2, 具有磁矩, 其大小与质子相当, 并于1940年从实验上测得了中子的磁矩[7], 20世纪40年代末和50年代初中子衍射被成功应用于测定磁性材料的磁结构[8]. 后来在物质结构、磁结构的探索中, 中子衍射是极其重要的研究手段.
在非弹性中子散射过程中, 中子与散射系统之间的能量和动量转移是表征材料内部动力学性质的重要指标. 自1950年前后首次用于研究固体材料的声子谱以来[9], 随着实验技术和中子源的不断进步, 这项技术已被广泛应用于液体和非晶态材料的动力学性质研究[10–13]. 进入21世纪后, 非弹性中子散射技术已成为多个研究领域不可或缺的工具, 尤其在超导声子谱和各种磁激发研究中发挥了关键作用[14,15]. 本文主要介绍非弹性中子散射的原理、谱仪的发展及其在不同领域的应用.
-
在中子散射实验中, 直接测量的是散射截面
$ \dfrac{{\mathrm{d}}^2\sigma}{{\mathrm{d}}\varOmega {\mathrm{d}}E'} $ , 即单位时间内在立体角$ {\mathrm{d}}\varOmega $ 内、能量在$ E' $ 到$ E'+{\mathrm{d}}E' $ 之间的中子数. 通过这一散射截面, 可以确定样品的物理性质. 在玻恩近似条件下, 可以认为在样品内发生的入射束流和出射束流的折射、多次散射现象以及初级束流的消光等问题都可以忽略. 因此, 散射强度与样品物性之间的关系得以简化处理. 同时, 中子散射过程本质上是量子跃迁过程, 利用费米黄金定则可以推导出散射截面.对于非弹性中子散射, 其本质是材料中声子在产生和湮灭过程中与中子之间能量和动量的转 移. 在能量较低时, 通常由单声子散射过程主导, 此处仅考虑单声子散射过程. 相干单声子散射截面 为[16]
其中,
$ \sigma_{{\mathrm{coh}}}=4\pi{\overline b}^2 $ ,$ b $ 为散射长度;$ v_0 $ 为原胞体积;$ {\mathrm{e}}^{-2 W} $ 为Debye-Waller因子;$ {\boldsymbol{Q}} = {\boldsymbol{k}} - {\boldsymbol{k'}} $ ,$ {\boldsymbol{k}} $ 和$ {\boldsymbol{k'}} $ 分别为入射中子和散射中子的波矢;$ {\boldsymbol{e}}_{\mathrm{s}} $ 为简正模式的极化矢量;$ \omega = (E - E') / \hbar $ ,$ E $ 和$ E' $ 分别为入射中子和散射中子的能量;$ {\boldsymbol{\tau}} $ 为晶格的倒格矢. 只有在满足条件$ \omega = \omega_{\mathrm{s}} $ ,$ {\boldsymbol{Q}} = {\boldsymbol{\tau}} + {\boldsymbol{q}} $ 或$ \omega = -\omega_{\mathrm{s}} $ ,$ {\boldsymbol{Q}} = {\boldsymbol{\tau}} - {\boldsymbol{q}} $ 时, 散射才会发生. 前者的散射过程是散射系统从中子获得能量并激发出一个声子, 称为声子发射; 后者对应于散射系统湮灭一个声子并将能量转移给中子, 称为声子吸收. 因此, 通过非弹性散射的截面可以测量出发生散射时声子对应的能量和动量转移, 即材料中声子的色散谱.在凝聚态物理研究中, 磁性材料在各个前沿领域扮演着重要角色. 为了深入了解这些材料的性质, 研究其自旋激发是必不可少的, 这也是非弹性中子散射实验的独特优势. 进一步考虑自旋的影响后, 散射截面为[16]
其中
$ \gamma $ 为中子的旋磁比;$ r_0 = \dfrac{\mu_0 e^2}{4 \pi m_{\mathrm{e}}} $ ;$ S $ 为原子自旋;$ g $ 为朗德$ g $ 因子;$ F({\boldsymbol{Q}}) $ 为磁形状因子. 与单声子散射过程类似, 散射只在满足条件$ \omega = \omega_q $ ,$ {\boldsymbol{Q}} = {\boldsymbol{\tau}} + {\boldsymbol{q}} $ 或$ \omega = -\omega_q $ ,$ {\boldsymbol{Q}} = {\boldsymbol{\tau}} - {\boldsymbol{q}} $ 时发生. 这两组条件分别对应磁振子的产生和湮灭. 因此, 通过非弹性中子散射可以测量材料中磁振子的能量和动量关系, 即自旋激发谱. -
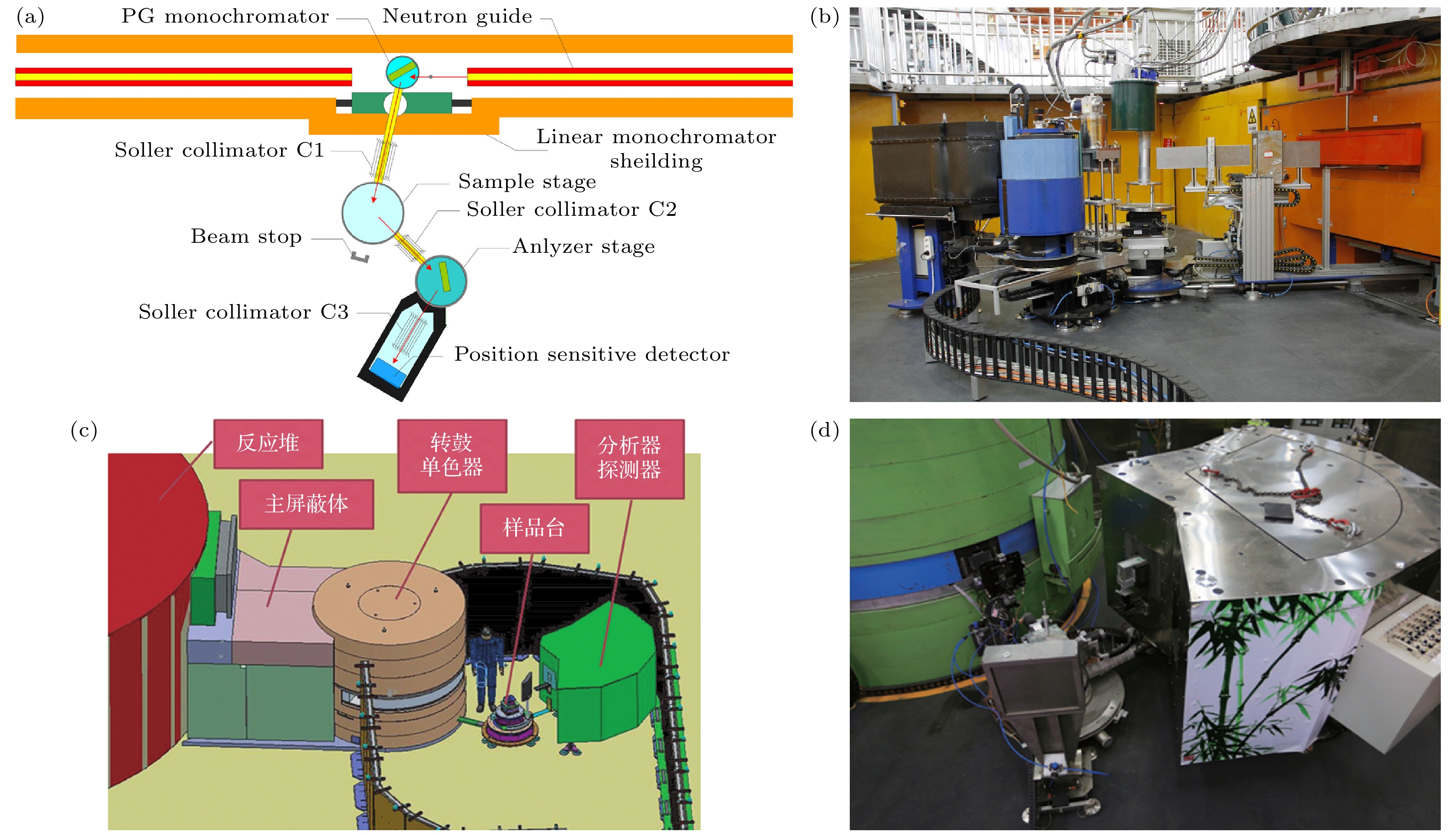
三轴谱仪由加拿大Chalk River实验室的Brockhouse和Stewart[17]在二轴中子衍射谱仪的基础上发展而来, 并与中子衍射共同获得了1994年诺贝尔奖, 表彰这一发现帮助解答了原子在做什么的问题, 至今仍然是各大反应堆源还广泛使用的非弹性中子散射谱仪. 三轴谱仪构造图如图1(a)所示, 具有单色器、样品台和分析器三个转动轴. 三轴谱仪运行的基本原理如下: 1)采用单晶作为单色器, 利用布拉格定律将慢化器源的白光中子筛选为单色中子, 入射至样品, 入射中子波矢为
$ {\boldsymbol{k}_{\mathrm{i}}} $ ; 2)将样品调整至测量的目标散射角度; 3)调整分析器与样品轴之间的夹角, 筛选出射中子波矢$ {\boldsymbol{k}_{\mathrm{f}}} $ 的方向和大小; 4)探测器接收在该条件下中子散射信号强度. 根据实验的结果, 利用矢量运算法则计算入射和出射中子波矢产生的中子动量转移, 根据入射和出射中子波矢大小的变化计算中子能量转移, 从而获得样品在动量转移$ {\boldsymbol{Q}} $ 和能量转移$ \hbar\omega $ 下的中子散射强度. 通过不断调整三个轴的夹角, 可以测量样品在$ {\boldsymbol{Q}} $ 恒定下, 散射强度随$ \hbar\omega $ 的变化(Constant$ {\boldsymbol{Q}} $ 模式)或在$ \hbar\omega $ 恒定下, 散射强度随$ {\boldsymbol{Q}} $ 的变化(Constant$ E $ 模式), 从而获取样品的声子、磁色散关系等性质. 三轴谱仪的探测器单次测量中, 入射中子为固定能量中子束, 收集的出射中子也为单能中子的信号, 因此单次只能测量倒易空间的一个点, 测量效率较低. 然而, 三轴谱仪具有较强的束流强度和较高的信噪比, 其优势在于能够监测倒易空间某些特定位置的信号随温度或磁场等外部条件变化时的演化趋势.三轴谱仪根据入射中子能量的范围可分为冷中子三轴谱仪和热中子三轴谱仪. 冷中子三轴谱仪的入射能量范围一般为0.1—10 meV, 热中子三轴谱仪的入射能量范围为5—100 meV. 三轴谱仪的能量测量范围由入射和出射中子能量差所决定, 由于三轴谱仪普遍采取的是能量损失模式来测量, 即
$ E_{\mathrm{i}} > E_{\mathrm{f }}$ , 在固定出射中子能量$ E_{\mathrm{f}} $ 情形下, 入射中子能量$ E_{\mathrm{i}} $ 决定了测量激发谱的最大能量转移值. 人们根据研究的科学目标来建造特定入射能量的三轴谱仪, 如科学目标为研究量子材料中的低能磁激发、低能的声子激发等, 需要使用低能中子, 以提供较高的分辨率来测量该能量段的激发信号. 在这种情况下, 应用低能慢化器可以将反应堆发射的高能中子慢化, 从而保证高低能中子通量. 相应地, 当科学目标是研究较高能的磁激发、超导样品的高能激发或声子中的高能光学支时, 则需采用高能慢化器.三轴谱仪的主要部件包括单色器、样品台、分析器、准直器、探测器和屏蔽体等, 同时配备低温、高温和磁场等个性化样品环境以满足不同的实验需求. 三轴谱仪一般采用热解石墨、锗、硅和铍等单晶作为单色器, 单色器通过布拉格衍射从白光中子中筛选出单色中子. 由于高阶中子波长(
$ {\lambda_i}/{2} $ ,$ {\lambda_i}/{3} $ 等)由布拉格衍射通过单色器, 因此通过适当添加各种滤波器, 例如较厚的热解石墨、低温下的铍或氧化铍等材料, 可以有效解决布拉格衍射时产生的高阶中子波长引起的干扰信号. 分析器同样使用定向好的单晶, 利用布拉格衍射筛选出射中子的能量和动量. 中子探测器包括闪烁体探测器和3He探测器等, 其中3He探测器对中子的探测效率更高. 由于非弹性中子信号较弱, 一般非弹性中子谱仪都使用高压3He气体探测器, 以提高探测效率. 在中子散射路径中放置具有一定间隙的中子吸收材料(如涂硼或镉)构成的平行板, 这种装置被称为准直器. 准直器的作用是减小中子束流的发散度, 从而提高谱仪的动量分辨率. 屏蔽体通常由吸收高能中子、减少背景辐射等作用的材料(如硼或镉)制成, 用于降低背景噪声.目前在世界上的反应堆中子源中, 建设了多台三轴谱仪, 覆盖不同的入射能量, 如美国国家标准局(NIST)建设了冷中子三轴谱仪MACS[18]和热中子三轴谱仪BT-7[19], 以及橡树岭国家实验室(ORNL)的HFIR反应堆的冷中子三轴谱仪CTAX和热中子三轴谱仪HB-3; 法国的郎之万研究所(ILL)建设了冷中子三轴谱仪ThALES[20]和热中子三轴谱仪IN8[21]; 澳大利亚的核科学与技术组织(ANSTO)建设了冷中子三轴谱仪Sika[22]和热中子三轴谱仪Taipan[23]; 日本的原子力科学研究所(JRR-3)建设了冷中子三轴谱仪HER[24]和热中子三轴谱仪GPTAS[25]; 瑞士散裂中子源(SINQ)作为连续型中子源, 也建有冷中子三轴谱仪TASP[26]和热中子三轴谱仪EIGER[27]. 我国建有中国先进研究堆(CARR)和中国绵阳研究堆(CMRR)两个反应堆中子源, 均建设有多台三轴中子散射谱仪. 它们是CARR上的“行知”冷中子三轴谱仪[28]、“翠竹”热中子三轴谱仪和中德热中子三轴谱仪SV30[29], CMRR上的“鲲鹏”冷中子三轴谱仪[30]和热中子三轴谱仪TTAS. 其中“翠竹”谱仪独创地在单色器之前放置了一台速度选择器, 极大地降低了高能中子辐射和高阶波长中子背景噪声, 并且拓展了出射中子能量
$ E_{\mathrm{f}} $ 的选择自由度, 使得测量的能量-动量范围得以最大化(图1(c)和图1(d))[29,31].三轴谱仪是最经典的非弹性中子散射谱仪(以下简称“非弹谱仪”), 但它最大的不足在于实验效率, 每次实验只能测量一个入射能量、出射能量和散射角, 仅对应于倒易空间中的一个点. 因此三轴谱仪方便追踪小范围倒易空间内序参量随温度、磁场等环境变化的关系, 但无法高效获得材料完整的倒空间色散特征及与相关理论模拟进行对比.
为了提高谱仪的实验效率, 原理上可以从三个方面入手: 增加入射中子束的数量、增加出射中子束的数量以及增加散射角的数量. 由于采用单晶片作为单色器, 反应堆非弹谱仪通常不能输出多个入射中子能量, 但可以通过增加散射角通道和分析器单晶片的方式来提高实验效率, 这类谱仪称为广谱(multiplexing)中子谱仪[32]. 国外的代表性谱仪有NIST的MACS[18], ILL在三轴谱仪上增加了多通道分析部件FlatCone[33], 柏林BER-II的MultiFLEXX[34], 德国莱布尼兹研究中心MLZ的冷中子三轴谱仪PANDA[35]和热中子三轴谱仪PUMA[36], 日本在JRR-3最新建造的HODACA谱仪[24]等, 国内的代表谱仪有中国人民大学在CARR建造的“博雅”广谱谱仪[37].
由于单晶片的排列需要一定的空间, 且穿透多层单晶后会出现衰减, 因此要进一步提高实验效率, 需要在原理上进行突破, 飞行时间谱仪因此应运而生.
-
这个原理上的突破就是飞行时间法[38]. 飞行时间法是采用中子飞行时间来确定中子入射及出射能量的一种方法, 即固定中子飞行的距离, 测量中子飞行的时间, 从而计算中子速度及能量. 一般有两种构型, 第一种构型为采用单色中子入射样品, 通过二维探测器采集多方向、多能量出射中子的方法, 即单次测量中单色中子入射, 但收集多出射中子信号的方法, 可测量样品较大范围的倒易空间, 该方法称为直接几何法. 进一步, 通过采取先进的中子斩波技术, 还可以实现多个非连续的入射中子能量(即多束不同的单色中子)来实现直接几何飞行时间测量; 第二种构型为采用白光中子入射样品, 探测器采集确定能量大小和方向的出射中子, 即单次测量中入射中子呈连续能量分布, 出射中子为单能, 也可实现较大范围的测量倒易空间, 该方法称为逆几何法. 本文主要介绍采用直接几何法建造的谱仪.
在实验中, 通常通过安装在束线上的束流监控器或测量样品在探测器上的衍射峰位置来确定中子入射能量. 根据中子从样品到探测器的飞行时间, 可以确定出射能量, 从而计算能量转移. 二维探测器能够覆盖较大的立体角. 在二维探测器的特定位置上, 将与样品形成一个特定的夹角, 这样在该位置收集到的中子的出射波矢方向将由该夹角决定, 而出射波矢的大小则由中子从样品飞行到探测器的飞行时间决定. 通过这些参数, 可以计算出射波矢的大小和方向, 从而利用动量守恒定律计算样品的动量转移大小. 因此, 通过中子的飞行时间和夹角等参数, 可以得出散射中子的能量和动量转移信息, 从而获得样品的非弹性散射信号的分布.
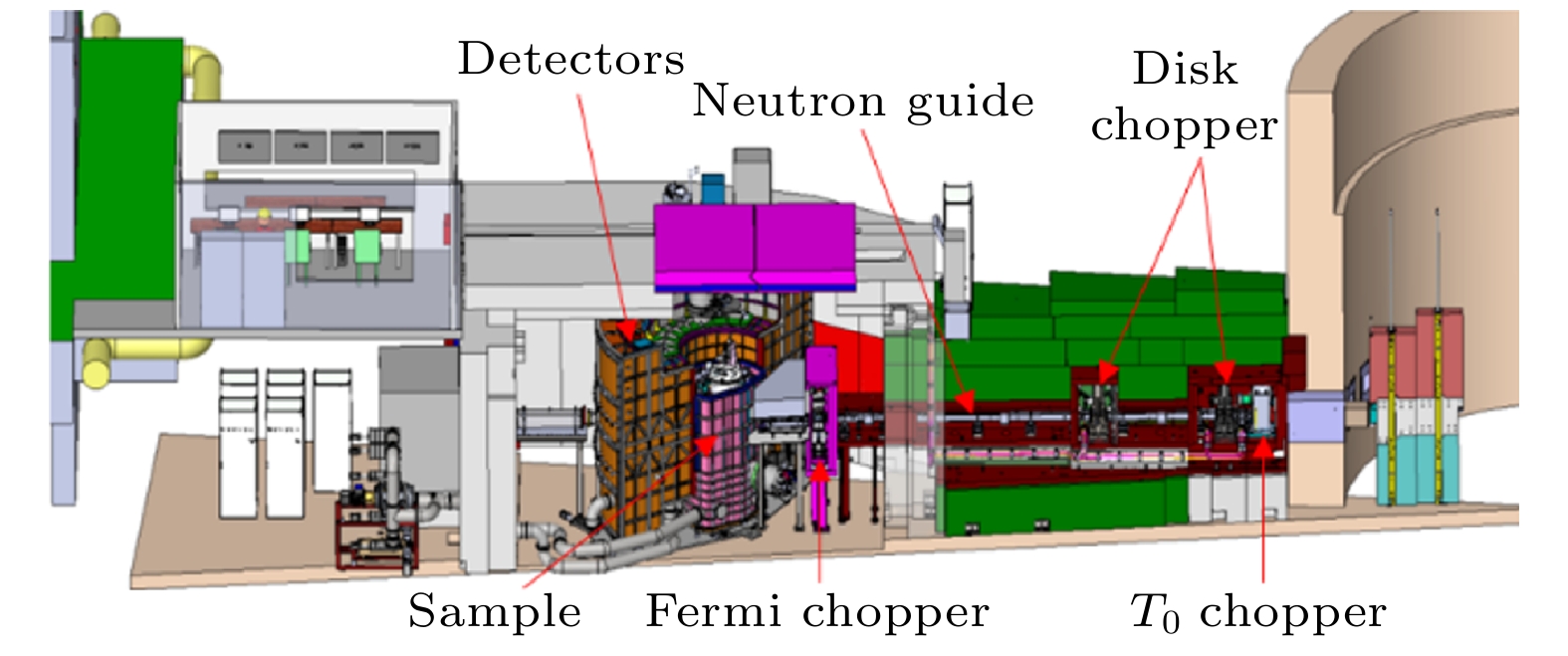
图2展示了直接几何飞行时间谱仪的构造. 主要部件包括慢化器、屏蔽系统、真空系统、中子导管、斩波器、样品环境、样品腔、散射腔和探测器等, 数据采集和处理需要电子学系统和数据获取系统等设备. 慢化器用于降低打靶后中子的能量, 常采用的材料有液氢和水. 屏蔽系统包括位于谱仪外部的混凝土屏蔽墙, 用于吸收杂散中子, 降低对外部环境的辐射. 进行中子散射实验时, 谱仪内部的各个部件也会对入射中子产生散射并被探测器收集, 由于非弹性中子散射的信号较弱, 这种杂散射的信号可能对样品的本征信号产生干扰. 因此谱仪内部也需要在部件表面等位置安装各种屏蔽材料(包括碳化硼、隔等吸收中子的材料), 以吸收这些背底信号. 中子散射需要在真空中进行, 减少空气等对中子的散射, 真空系统用于保持样品腔和散射腔的高真空状态, 主要用到的真空泵包括机械泵、分子泵、低温泵等.
直接几何飞行时间谱仪的分辨率受多种因素影响, 包括中子入射的能量、慢化器到单色斩波器的距离、单色斩波器到探测器的距离, 以及中子束流的时间宽度(这包括从慢化器发射的中子的时间宽度和经过单色斩波器后中子束流的时间宽度). 在中子散射实验中, 分辨率与样品处的中子束流强度通常无法同时达到最佳. 提高分辨率通常意味着束流强度的降低. 因此, 设计谱仪时需要考虑谱仪参数之间的平衡, 以及实验对分辨率和通量的需求, 以获得谱仪分辨率与通量之间的良好平衡.
飞行时间谱仪技术仍在不断发展中, 谱仪设计上也采取了多种方法以提高实验的效率, 包括增强中子源的打靶功率、优化导管设计以增加束流强度、采用多入射中子能量模式以及扩大探测器的立体角覆盖范围. 此外, 为了提高信噪比, 谱仪需采用碳化硼等材料来吸收杂散中子, 优化斩波器的设计和频率选择, 使用准直器去除杂散中子, 并通过调整狭缝大小来改变中子束流的面积, 以适应不同样品大小的需求. 为了拓展适用领域和实验多样性, 目前的发展方向包括扩大入射中子能量范围、建设更长谱仪以提高分辨率, 以及开发更多样的样品环境, 例如扩宽温区范围、使用超高磁场、增大均匀磁场面积和发展高压样品条件, 以满足样品测量的需求.
由于散裂中子源产生脉冲白光中子, 利用飞行时间法可以在单周期内筛选白光或单色光进行实验. 此外, 可以通过带宽斩波器等手段将相邻周期的中子吸收, 从而降低相邻周期中子的污染, 最大限度地利用束流. 因此, 飞行时间法与散裂中子源的脉冲打靶获取脉冲中子束流的方法相得益彰. 直接几何飞行时间谱仪一般根据入射能量的范围分为高能非弹谱仪(入射能量范围为10—2000 meV)、低能非弹谱仪(入射能量范围为1—50 meV)以及准弹性中子散射谱仪(入射能量为
$1\;{\text{μ}}{\mathrm{eV}} $ —5 meV). 入射能量的选择与其科学目标相关, 且与三轴谱仪的入射能量选择方式一致.飞行时间谱仪搭配脉冲中子源采用中子的飞行时间来判定中子能量, 这一点和采用单晶片的三轴和广谱谱仪在原理上不同. 事实上飞行时间谱仪并不只在采用加速器的散裂中子源上建设, 国外一些反应堆中子源上也通过斩波器将时间连续的中子束流斩成脉冲模式, 例如澳大利亚ANSTO的Pelican[39], 法国ILL的PANTHER[40]和IN5[41], 不过这样会牺牲反应堆连续源的通量优势.
目前, 世界上的散裂中子源中均建设有多台直接几何飞行时间谱仪, 覆盖不同的入射能量范围, 以满足不同的实验需求. 例如, 日本散裂中子源 J-PARC建设了高能非弹谱仪4SEASONS[42]和低 能非弹谱仪AMATERAS[43]; 英国散裂中子源ISIS建设了高能非弹谱仪MARI和MERLIN[44,45]以及低能非弹谱仪LET[46]; 美国散裂中子源SNS建设了高能非弹谱仪ARCS[47]和低能非弹谱仪CNCS[48]等.
-
中国散裂中子源(CSNS)是国内首个、世界上第四个脉冲型散裂中子源, 计划建设三台直接几何非弹性散射谱仪, 分别是高能非弹谱仪、冷中子非弹谱仪和极化非弹谱仪. 首台为高能非弹谱仪 (HD), 从2019年开始和中山大学合作建设[49]. 该谱仪于2020年完成物理设计, 目前已完成建设并转入调试阶段(图3). 其设计入射中子能量范围为10—1500 meV, 分辨率在10—200 meV范围内达到能量的3%—5%; 在200—1500 meV范围内达到能量的4%—10%, 探测器角度覆盖范围达到水平–30°—130°(前期–30°—60°), 竖直: –30°—30°. 该谱仪的设计参考了当前国际上同类谱仪的设计经验, 在此基础我们做了两点改进, 一是突破了重复率倍增(repetition-rate multiplication, RRM) 模式和高分辨模式在中低能量区域无法共存的原理禁区, 得到最多10个可用的入射能量, 这是目前国际上最多的; 二是设计了更为便捷安全的单束模式. 表1为中国散裂中子源的高能非弹谱仪和其他同类谱仪的对比.
对于入射能量超过百毫电子伏特的飞行时间非弹性谱仪, 通常采用费米斩波器作为单色器, 以满足分辨率的要求. 与常见的盘式斩波器相比, 费米斩波器的物理机制更加复杂, 同时也为我们提供了创新的机会.
费米斩波器由斩波器转轴和转子组成, 如图4所示, 图中狭缝堆积的结构就是转子, 亦称为吸收包. 左图为Sloppy斩波器, 右图为钆斩波器, 都是通道材料和吸收材料组成三明治结构. 费米斩波器都能做成直通道和弯通道形式, 在数学处理上, 直通道可以看作是曲率半径无限大的弯通道. 根据图4, 费米斩波器的几何参数包括狭缝长度L、狭缝宽度w、吸收层厚度d、狭缝曲率半径R和费米转速f等, 另外通道材料通常为Si或Al, 吸收材料通常为Gd或B. 这些参数和材料, 再加上费米斩波器前的束流特征和谱仪分辨率要求, 共同决定 了费米斩波器有波长依赖关系的各种参数指标, 包括费米斩波器的开门时间和注量透过率函数等. 为了覆盖不同的入射中子能量范围以满足不同实 验模式, 高能非弹谱仪一共配备了三个费米斩波器吸收包, 此外, 还可以将费米斩波器移出束流实现白光模式.
对于速度为
$ \nu $ 的入射中子, 相邻两支单色中子在费米斩波器处的时间差需要大于一定值, 以确保其能量转移覆盖范围在探测器上的重叠处于允许范围内. 通常, 在出射能量减小的情况下, 出射能量大约为入射能量的1/4; 而在出射能量增加的情况下, 根据细致平衡原理, 能量获得模式的信号通常较弱. 当出射能量为入射能量的两倍时, 可以满足绝大多数测量要求.对于相邻两支中的低能支, 其时间差为
其中
$ \alpha_{{\mathrm{gain}}} $ 为能量获得比例, 此处讨论时设为2;$ \alpha_{{\mathrm{loss}}} $ 为能量丢失比例, 此处设为0.25.我们默认费米斩波器的开门时间间隔都按直通道类型处理, 即转速加倍. 因此, 使用RRM模式, 费米斩波器的转速应满足以下关系:
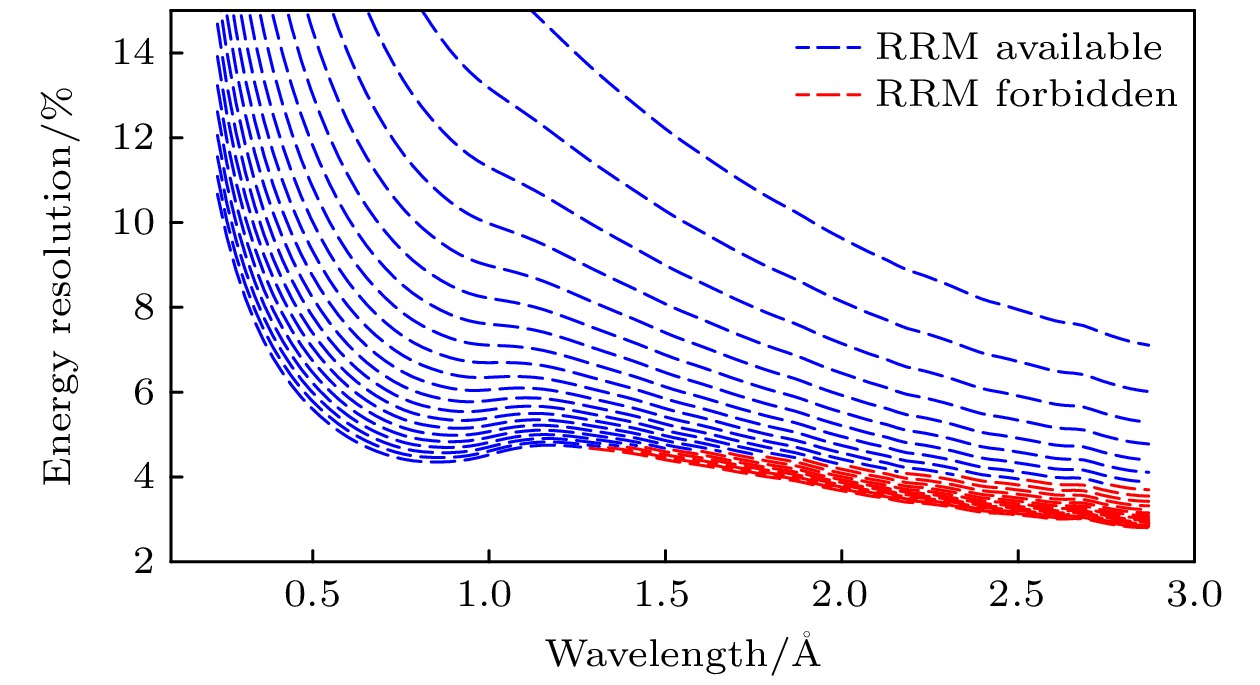
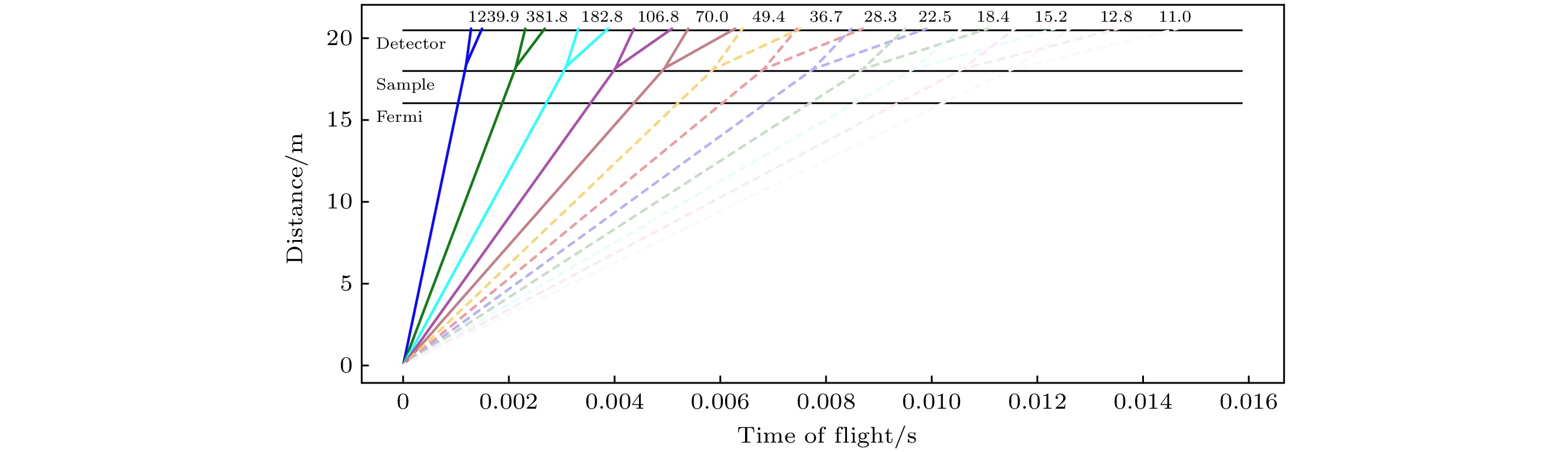
不满足该关系的区域被称为费米斩波器的RRM模式禁区, 如图5中的红色区域所示. 由于费米斩波器的转速需要与CSNS的25 Hz加速器频率匹配, 因此可用的转速仅限于25的倍数. 图中虚线表示费米斩波器在不同转速下的能量分辨率, 上沿为200 Hz, 下沿为600 Hz. 可以看到, RRM模式下的禁区主要出现在右下角, 即低能高分辨区域. 该区域具有丰富的物理应用, 是最受关注的部分. 为了突破这一原理上的禁区, 我们提出了一种弯通道费米斩波器的设计.
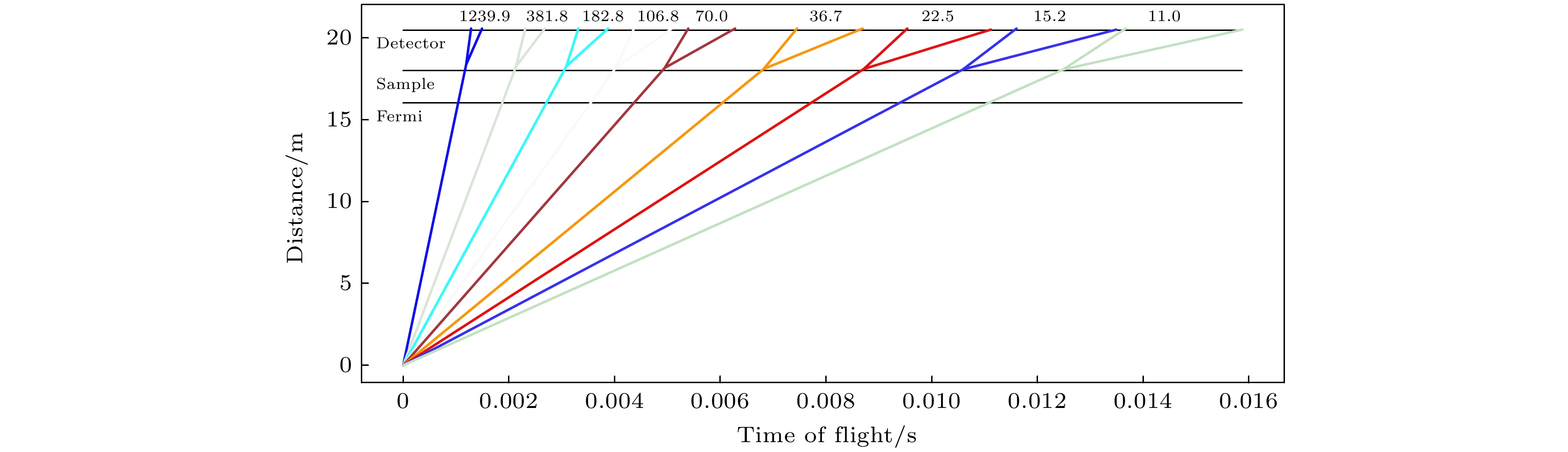
如图6所示, 当费米斩波器的几何参数确定后, 对于不同能量的入射中子, 最高透过率存在差异. 最高透过率与中子波长的关系曲线称为费米斩波器的带宽曲线. 该曲线随着波长的增加最终会降至零, 这一波长被称为费米斩波器的截止波长. 带宽曲线和截止波长是费米斩波器与盘式斩波器之间的主要区别. 与直通道相比, 弯曲通道的费米斩波器的带宽曲线分为两支, 其中一支的衰减速率更快, 称为前置零点; 另一支在某些波长范围内得到了增强. 前置零点对应的波长与费米转速呈正相关, 同时, 多束模式在中低能段的重叠程度也与费米转速呈正相关. 因此, 通过精心设计费米的几何参数, 可以确保在多束重叠发生时, 由于前置零点的出现, 减少一支单色束, 从而达到避开能量分析区间重叠的效果(图7). 与此同时, 由于另一支的带宽曲线增强, 显著提高了中低能区域的中子通量.
针对能量转移超出设计范围的情况, 我们设计了更为便捷安全的单束模式. 国际上同类谱仪也具备单束模式, 通常通过两个带宽斩波器来实现, 这两个斩波器分别限制中子飞行时间窗口的两端. 然而, 由于移动两个带宽斩波器的相位, 存在长波泄漏的风险. 为此, 利用穷举法计算了所有费米转速和离散化入射能量的组合, 并调整了三个斩波器的位置和参数, 最终得到了第二带宽斩波器上180°位置的单束狭缝. 当在RRM模式下出现能量转移超出范围的情况时, 可以立即调整第二带宽斩波器的相位, 通过单束狭缝排除该干扰, 从而无需担心长波泄漏的风险.
目前, 该谱仪正处于调试阶段. 经实测, 能量分辨率等指标已达到设计要求, 单束模式也经过了束流验证. 预计该谱仪将在2024年底完成验收, 随后将面向全球开放中子束流实验申请.
-
非弹性中子散射是一种强大的实验技术, 可以提供材料中各种激发态的关键物理信息, 如声子、磁激发、自旋子、晶体场激发等, 在材料科学和物理学等领域有着广泛的应用.
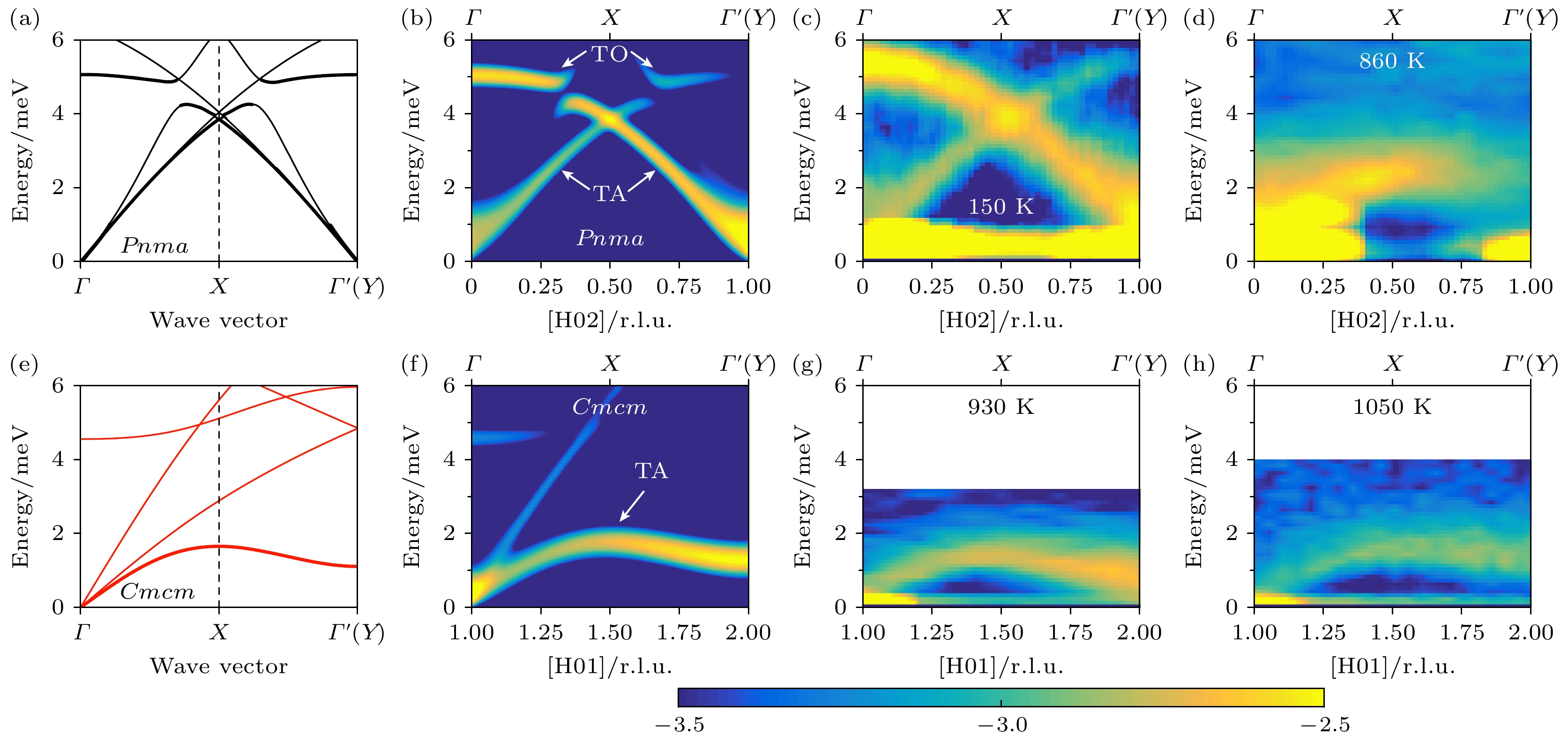
非弹性中子散射实验可以用于研究材料中原子的振动模式, 包括晶格振动、声子谱和局域振动模式等. 这在了解材料的热性质、声子输运和热导率等方面具有重要意义. 例如, 在热电材料SnS和SnSe的晶格动力学行为与温度及各向异性相关的研究中(如图8所示), 在Pnma结构的[100]方向上观察到了TAc和TOc色散的大幅软化, 在Cmcm相中则持续存在极为软化的TAc分支, 然而, 重整化效应并不仅限于这些色散, 它在整个布里渊区内均显著存在, 导致强烈的重整化和明显的各向异性群速度变化[50]. 非弹性中子散射能够精确给出完整的声子振动谱, 包括色散关系、谱权重分布以及随温度的演变行为等, 这是其他谱学手段难以实现的. 基于铍滤波器等技术, 非弹性中子散射可以一次性测量粉末样品的声子态密度分布, 是热电材料研究的重要手段.
非弹性中子散射是定量研究材料中磁性相互作用的关键实验手段, 在多种关联电子材料的研究中具有不可替代的作用. 例如, 非弹性中子散射技术被广泛应用于研究铜氧化物、铁基和镍氧化物等高温超导材料, 可以定量给出磁性相互作用参数、自旋共振模行为以及整体自旋涨落强度等关键信息[51–54]. 高温超导材料具有广阔的应用前景, 已在信息技术、生物医学、科学仪器、电力和交通运输等多个领域展现出潜在的应用价值. 然而, 高温超导的微观机制仍然是前沿科学中悬而未决的一大难题, 其关键在于理解磁性相互作用在高温超导形成过程中的作用, 因此定量测量磁激发并探讨其与超导电性的关系是必不可少的. 科学家通过非弹性中子散射测量了具有条纹序的铜氧化物超导体La1.875Ba0.125CuO4, 发现其激发与YBa2Cu3O6–x极其相似, 该激发行为能够很好地被具有量子激发的条纹模型理解[55], 这一结果表明在铜基高温超导体中, 条纹磁性关联有着极其重要的作用. 在铁基超导体中, 非弹性中子散射实验给出了能量尺度相近的次交换耦合参数、巡游与局域共存的磁性涨落行为, 以及普遍与超导共生的自旋共振模[56–58]. 特别是自旋共振模的行为与铜氧化物超导体相似, 虽然细节上存在差异, 但说明两者的超导机制可能存在统一的物理图像[59,60]. 近年来, 新一代镍氧化物高温超导体被发现[61,62], 特别是双层镍酸盐
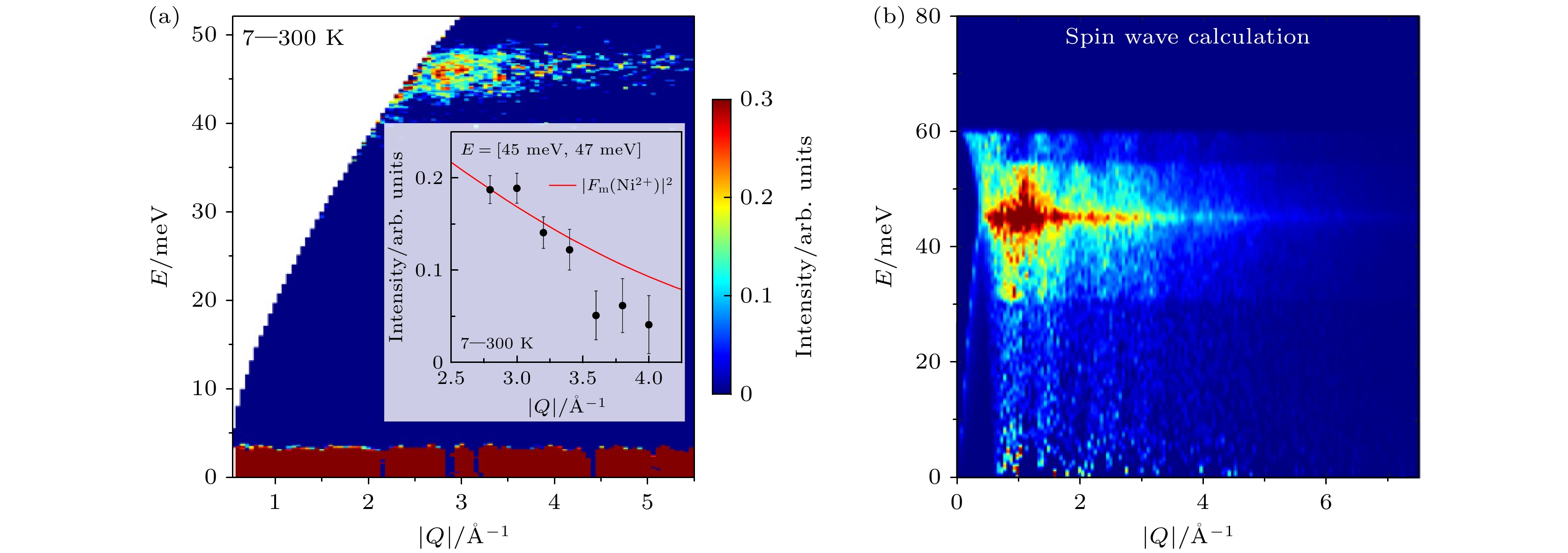
${\mathrm{La}}_3 {\mathrm{Ni}} _2 {\mathrm{O}}_{7-\delta} $ 在高压下出现了80 K以上的超导电性[63,64], 这为高温超导机制的研究提供了一个新的平台. 理论预言镍基超导体将具有与铜氧化物超导体及铁基超导体相似的强自旋交换相互作用[65], 但这亟需非弹性中子散射实验提供相关证据. 如图9所示, 在${\mathrm{La}}_3 {\mathrm{Ni}} _2 {\mathrm{O}}_{7-\delta}$ 粉末样品的非弹性中子散射谱中观察到约45 meV处出现平坦的自旋涨落信号, 这一特征可理解为条纹型反铁磁在强层间和弱层内磁耦合的结果, 为理解高温超导机制提供了实验依据[54].量子自旋液体是凝聚态物理中一个热门的研究领域. 其基态是具有长程纠缠的无序态, 并且具有分数化的激发, 被视为发展量子计算的理想平台, 同时与高温超导也有着密切的联系. 因此, 探索量子自旋液体材料不仅在基础科学研究中具有重要的科学意义, 而且在量子技术和材料科学等领域也展现出广阔的前景. 其首要问题是如何判别量子自旋液体态, 在凝聚态物理研究中通常利用比热、磁化率、热导率和
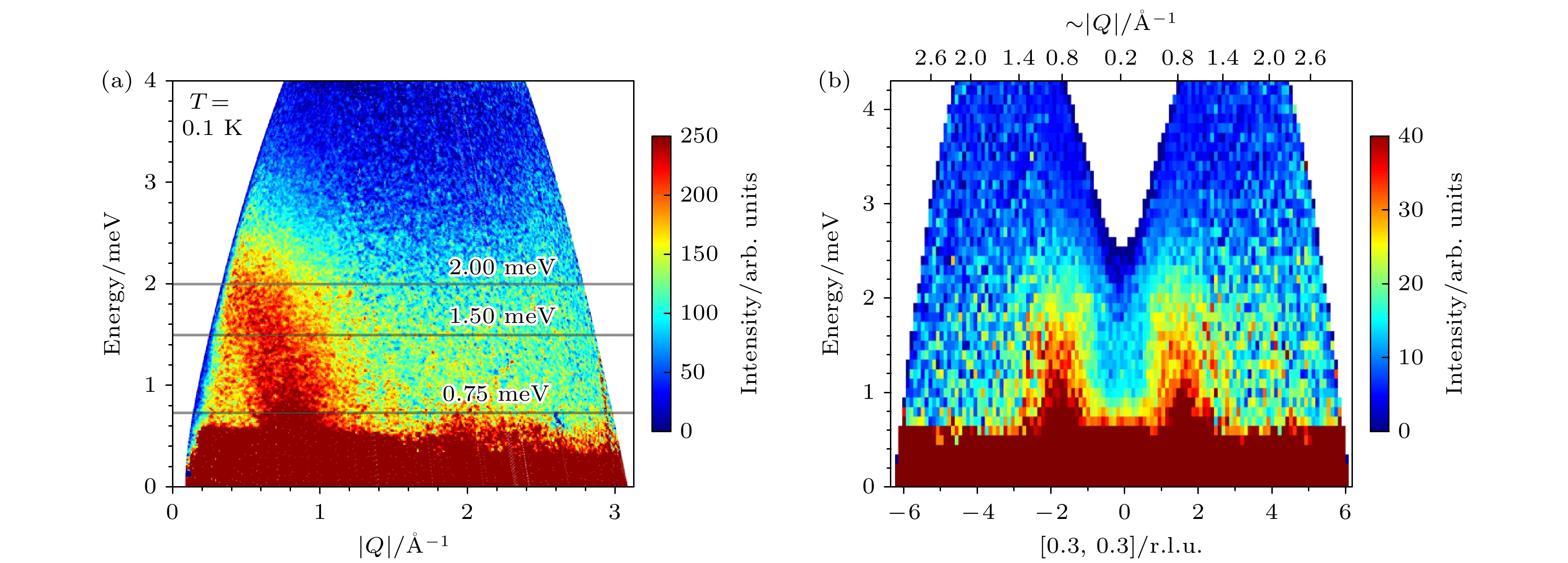
${\text{μ}}{\mathrm{SR}}$ 等手段, 可以提供极低温下磁无序及强自旋涨落的证据[66–70]. 但对于量子自旋液体的自旋子激发, 还没有一种实验手段 能够进行直接测量, 目前比较常用的方法就是通过非弹性中子散射测量是否有连续激发谱进行判 定. 在备受关注的自旋液体候选材料${\mathrm{YbMgGaO}} _4 $ 和$ {\text{α}}\text{-}{\mathrm{RuCl}}_3 $ 的研究中, 通过非弹性中子散射实验, 揭示了连续的磁激发谱的存在[15,71], 这是量子自旋液体的重要实验标志. 随着该领域的深入研究, 更多的量子自旋液体候选材料被相继发现, 非弹性中子散射实验技术也得到广泛应用. 比如在三维阻挫晶格材料PbCuTe2O6中, 通过粉末和单晶的非弹性中子散射实验均发现了如图10所示的连续谱磁激发, 并结合密度泛函理论计算表明其具有一个三维量子自旋液体基态[72].非弹性中子散射除了可以测量材料的声子谱和磁激发谱之外, 在许多其他领域也有广泛的应用. 如在磁电耦合材料研究中, 通过对原子结构和声子的综合测量, 为其机理研究提供帮助[73]; 在热电、压卡、磁卡等应用材料中, 非弹性中子散射可以帮助厘清亚晶格、电荷、自旋等之间的关联作 用[74–76]; 非弹性中子散射也可以用于研究催化剂表面上的吸附分子与表面原子之间的相互作用, 了解催化反应机制和表面吸附动力学[77]; 非弹性中子散射技术在研究生物大分子的动力学行为方面也取得了显著成果, 例如用于研究蛋白质在不同环境条件下的动力学变化, 帮助理解蛋白质的功能和机制[78,79].
非弹性中子散射谱仪具有高灵敏度、无损测量、高能量分辨率、能够提供关于材料中原子和分子的动态信息等优点, 在各个研究领域中具有独特的优势, 但也存在一些局限性, 这需要非弹谱仪的不断发展改进以满足不同研究领域的需求, 拓展其在材料科学、生命科学等领域的应用范围. 比如相较于弹性散射, 非弹性中子散射的信号强度通常较弱, 需要大量样品和长时间的测量来获取准确的数据, 针对这点, 一方面可以投资高强度的中子源, 使用更先进的加速器技术, 通过提高中子束流强度来提高信号强度和数据质量; 二是尽力降低本底以提高信噪比, 并开发和推广用户友好的数据处理和分析软件, 集成机器学习和高级统计方法, 提高结果的准确性, 同时降低使用门槛. 另外, 随着前沿科研的不断发展, 对样品的测量环境的要求也不断提高, 如极低温、强磁场、高压等, 这些都要求谱仪不断发展以扩大实验的适用范围和实验条件的可靠性, 对于促进材料科学和物理学的发展以及相关领域的研究具有重要意义.
-
非弹性中子散射作为一种强大的实验手段, 能够通过测量中子与物质相互作用时的能量和动量转移, 深入洞察材料的微观结构和动力学性质. 三轴谱仪和飞行时间谱仪的发展显著提高了非弹性散射实验的效率和精度. 特别是中国散裂中子源的高能非弹谱仪, 采用创新的费米斩波器设计, 实现了在不同能量范围内的高分辨率和多能量测量, 为材料动力学性质的研究提供了新的实验平台.
尽管非弹性中子散射技术经过几十年的发展已经相当成熟, 但硬件上的提升需要一些原理上的突破, 因此仍具有巨大发展潜力. 数据分析方法的革新也将成为另一个重要的发展方向. 随着机器学习和人工智能技术的快速发展, 新算法能够在海量数据中快速识别有意义的物理信号, 并自动处理和分析实验数据. 这不仅提高了实验效率, 也使结果的准确性大大提升, 进一步推进材料研究的进展. 另外, 非弹性中子散射技术将在新型材料的研究中扮演关键角色. 由于新型材料独特的动力学性质, 通常难以通过其他手段进行深入研究. 非弹性中子散射可以提供这些材料微观机制的详细信息, 从而为理论模型提供实验证据. 随着前沿科学研究的不断深入, 非弹性中子散射技术正在逐步扩大其应用范围.
总之, 非弹性中子散射技术随着技术进步和研究领域的扩展, 预计未来将迎来更多重大突破与创新. 无论是在材料科学、物理学等基础科学领域, 还是在能源、环境等实际应用中, 非弹性中子散射技术将发挥越来越重要的作用, 为科学研究和社会发展提供强大的动力.
非弹性中子散射谱仪及其应用
Inelastic neutron scattering spectrometer and its applications
-
摘要: 非弹性中子散射谱是材料科学和物理学研究中的关键工具, 其通过观测中子与物质相互作用后的能量和动量变化, 揭示材料的微观动力学特性. 该技术为定量描述材料的声子色散和磁性激发提供了重要信息. 非弹性中子散射谱仪根据单色中子的选择方法, 可分为三轴谱仪和飞行时间谱仪. 三轴谱仪具有高信噪比、高灵活性, 并且对特定测量点能进行精确追踪; 而飞行时间谱仪则通过多种手段显著提升实验效率. 非弹性中子散射谱仪的应用范围相当广泛, 在磁性、超导、热电、催化等诸多材料的机理研究方面, 均体现出在推动前沿科学发展中的不可或缺性. 中国散裂中子源的高能非弹性谱仪是国内首台飞行时间中子非弹性谱仪, 凭借其创新的费米斩波器设计, 成功实现了高分辨率与多能量的共存, 同时实验可用的单束中子支数达到了国际领先水平.
-
关键词:
- 非弹性中子散射 /
- 三轴中子散射谱仪 /
- 飞行时间中子散射谱仪 /
- 费米斩波器
Abstract: Inelastic neutron scattering is a pivotal technique in materials science and physics research, revealing the microscopic dynamic properties of materials by observing the changes in energy and momentum of neutrons interacting with matter. This technique provides important information for quantitatively describing the phonon dispersion and magnetic excitation of materials. Inelastic neutron scattering spectrometers can be divided into triple-axis spectrometers and time-of-flight spectrometers, according to the method of selecting monochromatic neutrons. The former has high signal-to-noise ratio, flexibility, and precise tracking capabilities for specific measurement points, while the latter significantly improves experimental efficiency through various measures. The application of inelastic neutron scattering spectrometers is quite extensive, playing an indispensable role in advancing frontier scientific research in the study of mechanisms in various materials such as magnetism, superconductivity, thermoelectrics, and catalysis. The high-energy inelastic spectrometer at the China Spallation Neutron Source is the first time-of-flight neutron inelastic spectrometer in China, achieving high resolution and multi-energy coexistence with its innovative Fermi chopper design. Additionally, the number of available single neutron beams in the experiment of this facility has reached the international leading level. -

-
图 1 (a)三轴谱仪平面图; (b) CMRR的“鲲鹏”冷三轴谱仪[30]; (c) “翠竹”热中子谱仪的构造图[31]; (d) “翠竹”热中子谱仪的照片[29]
Figure 1. (a) Triple-axis spectrometer plane diagram; (b) the cold triple-axis spectrometer “Kunpeng” at CMRR[30]; (c) construction diagram of the thermal triple-axis spectrometer IOP-CIAE[31]; (d) photograph of the thermal triple-axis spectrometer IOP-CIAE[29].
图 5 通过费米斩波器的中子飞行时间-距离图. 其中虚线表示相邻两支单色中子的能量分析区间存在重叠. 颜色的透明度代表费米斩波器在该能量的透过率
Figure 5. The neutron flight time-distance diagram of the Fermi chopper. The dashed lines indicate that there is an overlap in the energy analysis ranges of two adjacent monochromatic neutrons. Transparency of the colors represents the transmission rate of the Fermi chopper at that energy.
图 8 SnS声子色散和动态磁化率
$ (\chi''(Q, E)) $ 随结构相变的演化 (a)—(d) Pnma相; (e)—(h) Cmcm相. 图(a)和图(e)分别为在Pnma相和Cmcm相中用谐波近似计算的低能色散[50]Figure 8. The SnS phonon dispersion and dynamic magnetic susceptibility
$ (\chi''(Q, E)) $ evolve with structural phase transitions: (a)–(d) The Pnma phase; (e)–(h) the Cmcm phase. The low-energy dispersion calculated using harmonic approximation in the Pnma phase and Cmcm phase are shown[50] in panels (a) and (e).图 9 (a)通过非弹性中子散射测量
$ {\mathrm{La}}_3 {\mathrm{Ni}}_2 {\mathrm{O}}_{7-\delta} $ 的能谱, 强度为低温减去高温数据; (b)通过自旋波计算得到的自旋激发谱[54]Figure 9. (a) Energy spectrum of
${\mathrm{La}}_3{\mathrm{Ni}} _2{\mathrm{O}} _{7-\delta} $ was measured through inelastic neutron scattering, with intensity being the low-temperature data subtracted from the high-temperature data; (b) spin excitation spectrum obtained through spin wave calculations[54].图 10 (a)通过非弹性中子散射测量的
$ {\mathrm{PbCuTe}}_2{\mathrm{O}} _6 $ 粉末的磁激发; (b)$ {\mathrm{PbCuTe}}_2{\mathrm{ O}}_6 $ 单晶的磁激发谱[72]Figure 10. (a) Magnetic excitations of
${\mathrm{PbCuTe}} _2{\mathrm{O}} _6 $ powder measured by inelastic neutron scattering; (b) magnetic excitation spectrum of$ {\mathrm{PbCuTe}}_2{\mathrm{O}} _6 $ single crystal[72].表 1 各个非弹谱仪的参数对比. 其中L1, L2和L3分别为慢化器到费米斩波器的距离、样品到费米斩波器的距离和样品到探测器的距离
Table 1. Parameter comparison of various non-elastic spectrometers. Among them, L1, L2 and L3 are the distance from the moderator to the Fermi chopper, the distance from the sample to the Fermi chopper and the distance from the sample to the detector respectively.
谱仪 HRC 4SEASONS SEQUOIA ARCS MERLIN HD 中子源 J-PARC J-PARC SNS SNS ISIS CSNS 慢化器 DHM CHM DWM DWM DWM DWM Ei/meV 1—2000 5—300 8—2000 10—1500 7—2000 10—1500 Q/Å–1 — — — 0.15—22 — 0.1—41.5 水平角度 –31°—62° –35°—130° –30°—60° –28°—135° –45°—135° –30—130°
前期(–30°—60°)垂直角度 20°—20° –25°—27° –18°—18° –27°—26° –30°—30° –30—30° 分辨率 >2% >5% 1%—5% 3%—5% 4%—7% 3%—10% L1/L2/L3 14/1/4 16.3/1.7/2.5 18/2/5.53 11.6/2/3—3.4 10/1.8/2.5 16/2/2.5 样品尺寸 5 cm×5 cm 4.5 cm×4.5 cm
or 2 cm×2 cm5 cm×5 cm 5 cm×5 cm 5 cm×5 cm 5 cm×5 cm
or 3 cm×3 cm -
[1] Rutherford E 1920 Proc. R. Soc. London, Ser. A 97 374 doi: 10.1098/rspa.1920.0040 [2] Chadwick J 1932 Nature 129 312 doi: 10.1038/129312a0 [3] Von Halban H 1936 Acad. Sci. Paris 203 73 [4] Elsasser W 1936 CR Acad. Sci 202 1029 [5] Mitchell D P, Powers P N 1936 Phys. Rev. 50 486 doi: 10.1103/PhysRev.50.486.2 [6] Bloch F 1936 Phys. Rev. 50 259 doi: 10.1103/PhysRev.50.259 [7] Alvarez L W, Bloch F 1940 Phys. Rev. 57 111 doi: 10.1103/PhysRev.57.111 [8] Shull C G, Smart J S 1949 Phys. Rev. 76 1256 doi: 10.1103/PhysRev.76.1256.2 [9] Brockhouse B, Hurst D 1952 Phys. Rev. 88 542 doi: 10.1103/PhysRev.88.542 [10] Brockhouse B 1958 Il Nuovo Cimento (1955-1965) 9 45 doi: 10.1007/BF02824229 [11] Besnard M, Dianoux A J, Lalanne P, Lassegues J C 1977 J. Phys. 38 1417 doi: 10.1051/jphys:0197700380110141700 [12] Janik J A 1982 Adv. Liq. Cryst. 5 215 doi: 10.1016/B978-0-12-025005-9.50012-6 [13] Gaskell P H, Saeed A, Chieux P, Mckenzie D R 1991 Phys. Rev. Lett. 67 1286 doi: 10.1103/PhysRevLett.67.1286 [14] Loong C K, Vashishta P, Kalia R K, Degani M H, Zheng Y 1989 Phys. Rev. Lett. 62 2628 doi: 10.1103/PhysRevLett.62.2628 [15] Banerjee A, Yan J, Knolle J, Bridges C A, Stone M B, Lumsden M D, Mandrus D G, Tennant D A, Moessner R, Nagler S E 2017 Science 356 1055 doi: 10.1126/science.aah6015 [16] Squires G L, Lynn J W 1978 Phys. Today 32 69 doi: 10.1063/1.2995246 [17] Brockhouse B, Stewart A 1955 Phys. Rev. 100 756 doi: 10.1103/PhysRev.100.756 [18] Rodriguez J A, Adler D M, Brand P C, Broholm C, Cook J C, Brocker C, Hammond R, Huang Z, Hundertmark P, Lynn J W, Maliszewskyj N C, Moyer J, Orndorff J, Pierce D, Pike T D, Scharfstein G, Smee S A, Vilaseca R 2008 Meas. Sci. Technol. 19 034023 doi: 10.1088/0957-0233/19/3/034023 [19] Lynn J, Chen Y, Chang S, Zhao Y, Chi S, Ratcliff II W, Ueland B G, Erwin R W 2012 J. Res. Nat. Inst. Stand. Technol. 117 61 doi: 10.6028/jres.117.002 [20] Boehm M, Hiess A, Kulda J, Roux S, Saroun J 2008 Meas. Sci. Technol. 19 034024 doi: 10.1088/0957-0233/19/3/034024 [21] Jimenez-Ruiz M, Hiess A, Currat R, Kulda J, Bermejo F 2006 Physica B 385 1086 doi: 10.1016/J.PHYSB.2006.05.373 [22] Wu C M, Deng G, Gardner J, Vorderwisch P, Li W H, Yano S, Peng J C, Imamovic E 2016 J. Instrum. 11 P10009 doi: 10.1088/1748-0221/11/10/P10009 [23] Danilkin S A, Yethiraj M, Saerbeck T, Klose F, Ulrich C, Fujioka J, Miyasaka S, Tokura Y, Keimer B 2012 J. Phys. Conf. Ser. 340 012003 doi: 10.1088/1742-6596/340/1/012003 [24] Kikuchi H, Asai S, Sato T J, Nakajima T, Harriger L, Zaliznyak I, Masuda T 2024 J. Phys. Soc. Japan 93 091004 doi: 10.7566/JPSJ.93.091004 [25] Nawa K, Okuyama D, Wu H C, Murasaki R, Matsuzaka S, Kinjo K, Sato T J 2024 J. Phys. Soc. Japan 93 091001 doi: 10.7566/JPSJ.93.091001 [26] Fischer W 1997 Physica B 234 1202 doi: 10.1016/S0921-4526(97)00260-3 [27] Stuhr U, Roessli B, Gvasaliya S, Rnnow H, Filges U, Graf D, Bollhalder A, Hohl D, Bürge R, Schild M, Holitzner L, C K, Keller P, Mühlebach T 2017 Nucl. Instrum. Methods Phys. Res., Sect. A 853 16 doi: 10.1016/j.nima.2017.02.003 [28] Cheng P, Zhang H, Bao W, Schneidewind A, Link P, Grünwald A, Georgii R, Hao L, Liu Y 2016 Nucl. Instrum. Methods Phys. Res., Sect. A 821 17 doi: 10.1016/j.nima.2016.03.045 [29] 李天富, 武梅梅, 焦学胜, 孙凯, 陈东风 2020 原子核物理评论 37 364 doi: 10.11804/NuclPhysRev.37.2019CNPC36 Li T F, Wu M M, Jiao X S, Sun K, Chen D F 2020 Nucl. Phys. Rev. 37 364 doi: 10.11804/NuclPhysRev.37.2019CNPC36 [30] Song J M, Luo W, Liu B Q, et al. 2020 Nucl. Instrum. Methods Phys. Res., Sect. A 968 163929 doi: 10.1016/j.nima.2020.163929 [31] 戴鹏程, 李世亮 2011 物理 40 33 Dai P C, Li S L 2011 Physics 40 33 [32] Demmel F, Fleischmann A, Gläser W 1998 Nucl. Instrum. Methods Phys. Res., Sect. A 416 115 doi: 10.1016/S0168-9002(98)00559-2 [33] Kempa M, Janousova B, Saroun J, Flores P, Boehm M, Demmel F, Kulda J 2006 Physica B 385-386 1080 doi: 10.1016/j.physb.2006.05.371 [34] Groitl F, Toft-Petersen R, Quintero-Castro D L, et al. 2017 Sci. Rep. 7 13637 doi: 10.1038/s41598-017-14046-z [35] Utschick C, Skoulatos M, Schneidewind A, Böni P 2016 Nucl. Instrum. Methods Phys. Res., Sect. A 837 88 doi: 10.1016/j.nima.2016.08.060 [36] Sobolev O, Hoffmann R, Gibhardt H, Jünke N, Knorr A, Meyer V, Eckold G 2015 Nucl. Instrum. Methods Phys. Res., Sect. A 772 63 doi: 10.1016/j.nima.2014.11.007 [37] Wang J, Liu J, Xu D, Grünauer F, Hao L, Liu Y, Zhang H, Cheng P, Bao W 2024 Chin. Phys. B 33 057801 doi: 10.1088/1674-1056/ad3629 [38] Firk F 1979 Nucl. Instrum. Methods 162 539 doi: 10.1016/0029-554X(79)90732-8 [39] Yu D, Mole R, Noakes T, Kennedy S, Robinson R 2013 J. Phys. Soc. Japan 82 SA027 doi: 10.7566/JPSJS.82SA.SA027 [40] Cicognani G, Mutka H, Sacchetti F 2000 Physica B 276 83 doi: 10.1016/S0921-4526(99)01366-6 [41] Ollivier J, Mutka H, Didier L 2010 Neutron News 21 22 doi: 10.1080/10448631003757573 [42] Kajimoto R, Yokoo T, Nakajima K, et al. 2007 J. Neutron Res. 15 5 doi: 10.1080/10238160601048742 [43] Nakajima K, Ohira-Kawamura S, Kikuchi T, Nakamura M, Kajimoto R, Inamura Y, Takahashi N, Aizawa K, Suzuya K, Shibata K, et al. 2011 J. Phys. Soc. Japan 80 SB028 doi: 10.1143/JPSJS.80SB.SB028 [44] Le M D, Guidi T, Bewley R, et al. 2023 Nucl. Instrum. Methods Phys. Res., Sect. A 1056 168646 doi: 10.1016/j.nima.2023.168646 [45] Bewley R, Eccleston R, McEwen K, Hayden S, Dove M, Bennington S, Treadgold J, Coleman R 2006 Physica B 385-386 1029 doi: 10.1016/j.physb.2006.05.328 [46] Bewley R, Taylor J, Bennington S 2011 Nucl. Instrum. Methods Phys. Res., Sect. A 637 128 doi: 10.1016/j.nima.2011.01.173 [47] Abernathy D L, Stone M B, Loguillo M, Lucas M, Delaire O, Tang X, Lin J, Fultz B 2012 Rev. Sci. Instrum 83 015114 doi: 10.1063/1.3680104 [48] Ehlers G, Podlesnyak A A, Niedziela J L, Iverson E B, Sokol P E 2011 Rev. Sci. Instrum. 82 085108 doi: 10.1063/1.3626935 [49] Luo W, Feng Y, Liu X, et al. 2023 Nucl. Instrum. Methods Phys. Res., Sect. A 1046 167676 doi: 10.1016/j.nima.2022.167676 [50] Lanigan-Atkins T, Yang S, Niedziela J L, Bansal D, Delaire O 2020 Nat. Commun. 11 4430 doi: 10.1038/s41467-020-18121-4 [51] Sidis Y, Pailhès S, Hinkov V, Fauquxe B, Ulrich C, Capogna L, Ivanov A, Regnault L P, Keimer B, Bourges P 2007 C. R. Phys. 8 745 doi: 10.1016/j.crhy.2007.07.003 [52] Fujita M, Hiraka H, Matsuda M, Matsuura M, M Tranquada J, Wakimoto S, Xu G, Yamada K 2012 J. Phys. Soc. Japan 81 011007 doi: 10.1143/JPSJ.81.011007 [53] Dai P 2015 Rev. Mod. Phys. 87 855 doi: 10.1103/RevModPhys.87.855 [54] Xie T, Huo M, Ni X, Shen F, Huang X, Sun H, Walker H C, Adroja D, Yu D, Shen B, He L, Cao K, Wang M 2024 Sci. Bull. 69 3221 doi: 10.1016/j.scib.2024.07.030 [55] Tranquada J, Woo H, Perring T, Goka H, Gu G, Xu G, Fujita M, Yamada K 2004 Nature 429 534 doi: 10.1038/nature02574 [56] Dai P, Hu J, Dagotto E 2012 Nat. Phys. 8 709 doi: 10.1038/nphys2438 [57] Si Q, Yu R, Abrahams E 2016 Nat. Rev. Mater. 1 1 doi: 10.1038/natrevmats.2016.17 [58] Zhou X, Lee W S, Imada M, Trivedi N, Phillips P, Kee H Y, Törmä P, Eremets M 2021 Nat. Rev. Phys. 3 462 doi: 10.1038/s42254-021-00324-3 [59] Wang M, Zhang C, Lu X, et al. 2013 Nat. Commun. 4 2874 doi: 10.1038/ncomms3874 [60] Hong W, Song L, Liu B, Li Z, Zeng Z, Li Y, Wu D, Sui Q, Xie T, Danilkin S, Ghosh H, Ghosh A, Hu J, Zhao L, Zhou X, Qiu X, Li S, Luo H 2020 Phys. Rev. Lett. 125 117002 doi: 10.1103/PhysRevLett.125.117002 [61] Gu Q, Wen H H 2022 Innovation 3 100202 doi: 10.1016/j.xinn.2021.100202 [62] Wang M, Wen H H, Wu T, Yao D X, Xiang T 2024 Chin. Phys. Lett. 41 077402 doi: 10.1088/0256-307X/41/7/077402 [63] Sun H, Huo M, Hu X, et al. 2023 Nature 621 493 doi: 10.1038/s41586-023-06408-7 [64] Wang N, Wang G, Shen X, et al. 2024 Nature 634 579 doi: 10.1038/s41586-024-07996-8 [65] Wxu W, Luo Z, Yao D X, Wang M 2024 Sci. China Phys. Mech. 67 117402 doi: 10.1007/s11433-023-2300-4 [66] Zhou Y, Kanoda K, Ng T K 2017 Rev. Mod. Phys. 89 025003 doi: 10.1103/RevModPhys.89.025003 [67] Zhu Z, Pan B, Nie L, et al. 2023 Innovation 4 100459 doi: 10.1016/j.xinn.2023.100459 [68] Lin G, Ma J 2023 Innovation 4 100484 doi: 10.1016/j.xinn.2023.100484 [69] Broholm C, Cava R J, Kivelson S A, Nocera D G, Norman M R, Senthil T 2020 Science 367 eaay0668 doi: 10.1126/science.aay0668 [70] 王颖, 殳蕾 2024 物理学报 73 197601 doi: 10.7498/aps.73.20240940 Wang Y, Shu L 2024 Acta Phys. Sin. 73 197601 doi: 10.7498/aps.73.20240940 [71] Paddison J A, Daum M, Dun Z, Ehlers G, Liu Y, Stone M B, Zhou H, Mourigal M 2017 Nat. Phys. 13 117 doi: 10.1038/nphys3971 [72] Chillal S, Iqbal Y, Jeschke H O, Rodriguez-Rivera J A, Lake B 2020 Nat. Commun. 11 2348 doi: 10.1038/s41467-020-15594-1 [73] Bansal D, Niedziela J L, Sinclair R, Garlea V O, Abernathy D L, Chi S, Ren Y, Zhou H, Delaire O 2018 Nat. Commun. 9 15 doi: 10.1038/s41467-017-02309-2 [74] Wei B, Sun Q, Li C, Hong J 2021 Sci. China Phys. Mech. 64 117001 doi: 10.1007/s11433-021-1748-7 [75] Ren Q, Gupta M K, Jin M, et al. 2023 Nat. Mater. 22 999 doi: 10.1038/s41563-023-01560-x [76] Han S, Dai S, Ma J, et al. 2023 Nat. Phys. 19 1649 doi: 10.1038/s41567-023-02188-z [77] Kofu M, Hashimoto N, Akiba H, Kobayashi H, Kitagawa H, Iida K, Nakamura M, Yamamuro O 2017 Phys. Rev. B 96 054304 doi: 10.1103/PhysRevB.96.054304 [78] Shrestha U R, Mamontov E, O’Neill H M, Zhang Q, Kolesnikov A I, Chu X 2022 Innovation 3 100199 doi: 10.1016/j.xinn.2021.100199 [79] Hong L, Jain N, Cheng X, Bernal A, Tyagi M, Smith J C 2016 Sci. Adv. 2 e1600886 doi: 10.1126/sciadv.1600886 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: