-
当今许多前沿科学研究和先进制造领域,比如宇航科学[1-2]、表面科学[3-4]、精密仪器制造[5-8]等,需要超高/极高真空(UHV/XHV)条件下的环境保障。冷原子真空测量技术有望在UHV/XHV范围内实现更加精确的真空测量并建立室温下的原级真空标准,该技术利用囚禁在阱中的冷原子和背景气体碰撞造成的损失率与压力之间的关系来反演真空度。
冷原子真空测量的关键是观测传感器原子在阱中的衰减,通过数值拟合提取碰撞损失率,进而反演气体压力。阱作为囚禁原子的有效手段和真空测量的必要前提分为磁光阱(MOT)和磁阱。MOT中传感器原子的衰减规律会受到激光束加热效应以及量子碰撞衍射效应[9]的影响。
磁阱阱深较浅(<1 mK),在与背景气体分子发生碰撞过程中,由量子碰撞衍射导致的阱加热效应可以忽略不计;理想磁阱中测得的真空度仅取决于基本原子特性(碰撞截面),因此可以用来构建UHV/XHV范围内的冷原子原级标准(CAVS)[10];理想磁阱中更加精确的测量有利于UHV/XHV测量下限的扩展。
本文简述了磁捕获原理和磁阱囚禁特性,在描述不同磁阱磁场强度,磁捕获势能的基础上,分析了调控磁阱性能的磁捕获参数,对比总结了各类型的磁阱束缚性能;其次论述了磁阱中冷原子真空测量的国内外研究现状,对损失率系数测定的实验以及磁阱设备研发的样机进行了归纳,介绍了基于磁阱的冷原子原级真空标准。最后针对测量程序优化和磁阱设备构建对磁阱中的冷原子真空测量进行了展望。
-
磁捕获依赖于原子磁偶极子与空间变化磁场的相互作用,对于具有磁矩的碱金属原子,可以施加外磁场来实现磁捕获。在磁场强度B作用下磁矩为
$\mu $ 时产生的相互作用能为[11-12]$ \theta $ 表示磁矩$\mu $ 与磁场强度$B$ 之间的夹角。在磁捕获场中产生的力可以表示为不同能级磁矩的大小和方向存在差异,根据式(2)可知,磁场强度必须在空间中递变,以配合磁矩产生递变的势能和力,形成磁阱。
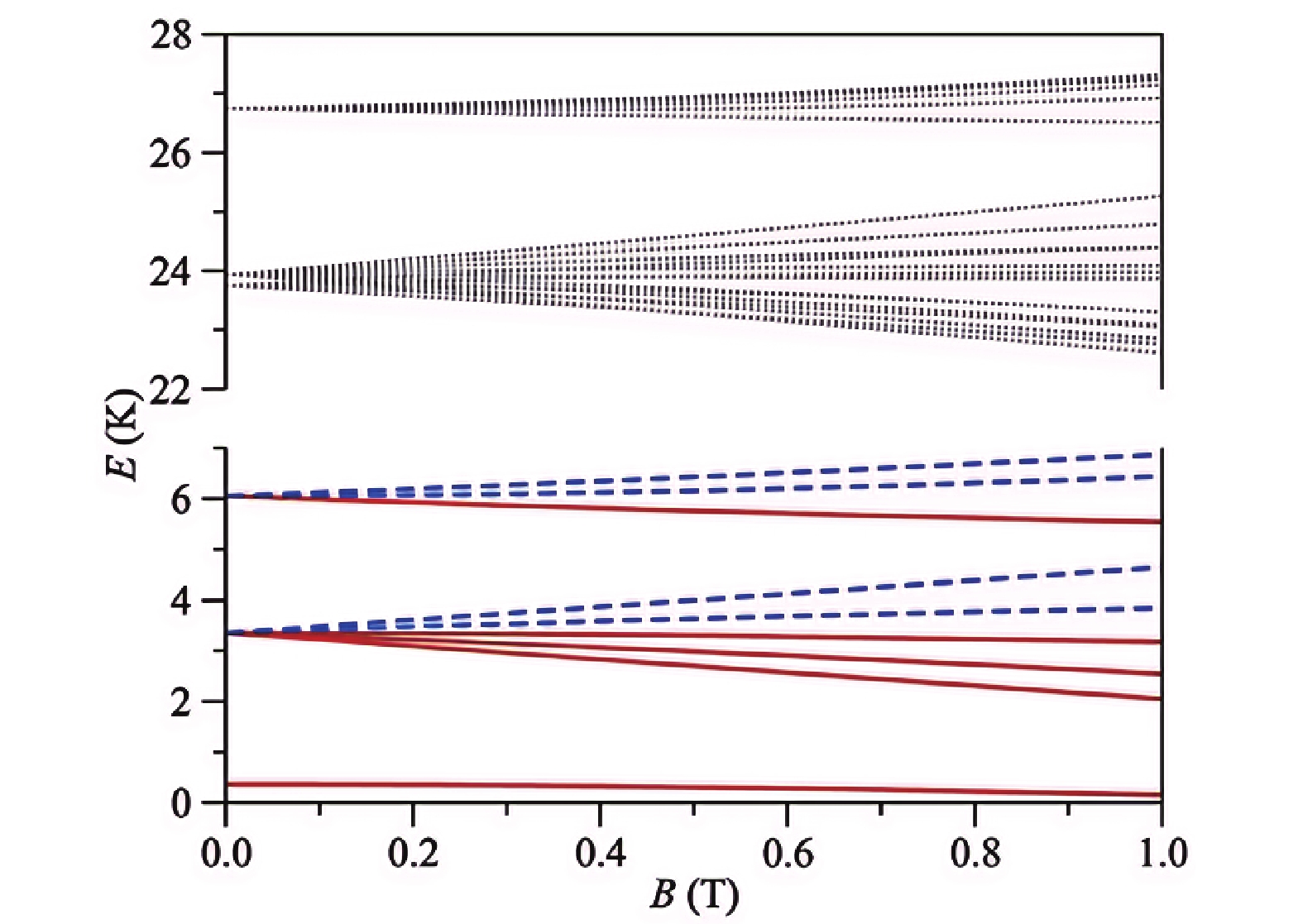
当原子能级分裂后,内部出现两种不同的响应,如图1所示。即能级能量随磁场强度的增大而增大或者随磁场强度的增大而减小,前者被称为弱场趋寻态,后者被称为强场趋寻态。由于原子趋向于在能量最低处保持稳定,在弱场趋寻态下,原子会受到趋向低场的力,原子在场强最小的区域保持稳定;在强场趋寻态下,原子会受到趋向高场的力,原子在场强最大的区域保持稳定。根据恩肖定理[14-15],处在强场趋寻态的原子无法被捕获,因此,磁阱的设计可归结为在局部区域内构造最小磁场强度不为零的磁场,用以捕获弱场趋寻态的原子。
-
目前对UHV/XHV的测量主要集中在磁阱和MOT上。MOT具有更高的压力测量上限(10−5 Pa),正好满足磁悬浮转子真空计(SRG)的测量下限,通过连接MOT和SRG可以连接高真空压力和超高真空压力主要标准和水银压力计主要标准;MOT的阱深更深(MOT为1 K,磁阱为1 mK),阱中的原子数更多,MOT的荧光信号也更容易在更高的背景压力下被检测到[16]。然而MOT在压力测量过程中也存在许多严重的问题:
(1)在MOT中,存在被捕获的基态原子以及激发态原子,激发态原子和基态原子与测试气体粒子之间的速度平均碰撞损失截面不同,在固定的背景气压下,激发态与基态原子数占比变化也会导致MOT测量的损失率发生变化。
(2)MOT的阱深易受到用于形成MOT的激光束的功率、失谐、尺寸和对准的强烈影响[17-19]。
(3)MOT校准复杂,MOT的阱深一般在1−2 K范围内[20],由于阱较深,对于基态和激发态的原子,碰撞引起的损耗可能会受到相互作用势以及非弹性碰撞通道的显著影响,需要对损失率系数重新进行复杂计算[21-22]。磁阱相较于MOT作为传输标准具有以下优势:
(1)当原子从MOT转移到磁阱时,原子被冷却并通过泵浦光进入超精细基态,单一状态保证了磁阱的损失率通过单一阱深测量。
(2)磁阱由通电线圈产生的磁场构成,阱深仅由通电导线的电流进行调控。
(3)磁阱的阱深较浅,一般在1 mK左右,由量子衍射碰撞导致传感器原子碰不出磁阱的比例不足千分之一,当背景温度和阱深被确定后,其对真空测量造成的不确定度可以忽略不记。
(4)由于理想磁阱中对于UHV/XHV测量仅取决于基本原子特性(碰撞截面),因此可以用来构建CAVS。
(5)理想磁阱具有更高的测量精度,可以在更低的压力范围内实现对UHV/XHV的测量;加拿大英属哥伦比亚大学(UBC)也通过基于磁阱的冷原子原级真空标准对MOT传输标准进行校准[16],基于磁阱的CAVS对于真空下限的扩展至关重要。
-
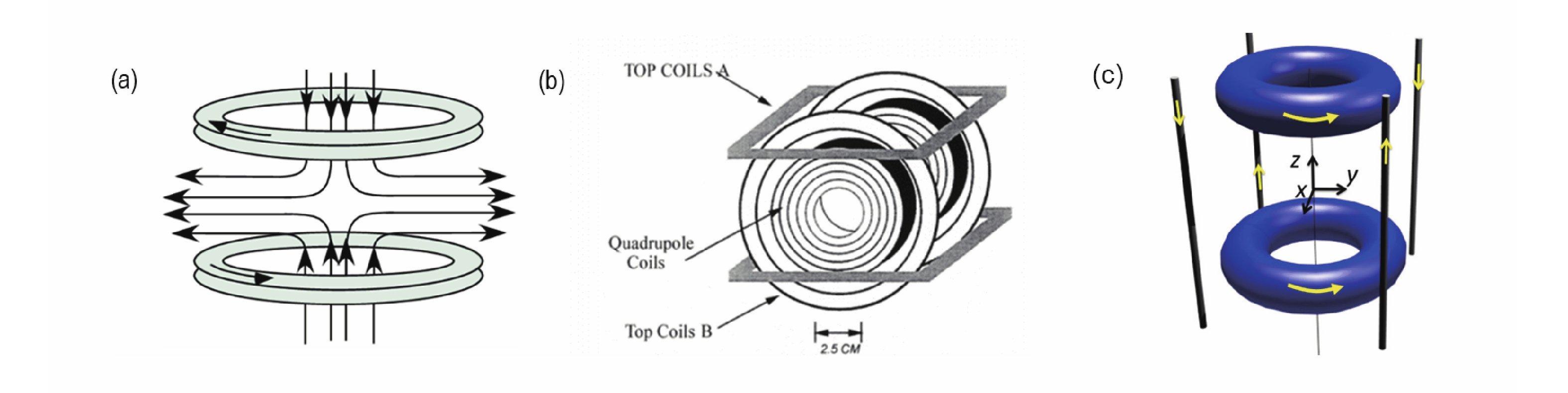
目前已研发出多种用于囚禁原子的磁阱,按照原理可以分为三种类型:四极磁阱[23-26],时间平均轨道势能(TOP)磁阱[27-29], Ioffe-Pritchard(IP)磁阱[30-34]。本节主要针对这三类磁阱的原理和性能进行简要介绍。
-
四极磁阱的结构如图2(a)所示,由两个通相反电流的线圈构成,磁场强度可以表示为
可推断出磁场为空间范围内沿任意方向随距原点距离线性变化的梯度磁场,在磁阱中心场强为零,轴向梯度为径向梯度的两倍,在原点附近的磁场轮廓大致呈球形。
磁阱中的非理想损失会影响对真空度的测量,在四极磁阱中的原子经过磁场零点时,原子磁矩相对于磁场的取向可能会发生变化而导致原子发生马约拉纳(Majorana)自旋翻转损失[23, 25, 35]。
-
TOP磁阱在四极磁阱的径向内添加一个旋转偏置场Bb来实现,结构如图2(b)。Bb会在空间中产生旋转的均匀场,偏移四极磁阱中心的零点,使被捕获的原子远离零点[29]。TOP磁阱的平均磁场强度可以近似表示为
平均磁场强度的最小值位于磁阱中心且不为零,避免了Majorana损失。TOP磁阱中心附近的磁捕获势能可以表示为
其中B″ρ=B′2/2Bb,B″z=4B′2/Bb,ρ2=x2+y2,B″ρ表示径向曲率,B″z表示轴向曲率,ρ表示径向坐标。在Bb作用下,囚禁原子的线性势能变为局部磁场强度不为零的抛物线势能。为了保证TOP磁阱的正常运行,Bb的角频率Ω必须满足一定条件[13]:Ω应大于被捕获原子的振荡频(102 Hz量级),使原子在磁场一个旋转周期内的平均有效势能中运动。Ω应小于与两个连续内部量子态之间的跃迁频率(106 Hz量级),防止Majorana损失。
-
IP磁阱结构如图2(c)所示,由四根轴向载流直导线以及一对载流线圈构成,在磁阱中心附近的磁场强度不为零,形成抛物线势能束缚原子。IP磁阱的磁场强度可以表示为[30]
B0表示总偏置磁场,B′表示径向磁场梯度,B″表示轴向磁场曲率[36]。在调节磁场时,B0应大于零,防止Majorana损失。IP磁阱的捕获势能可以表示为
-
四极磁阱的有效曲率可以表示为B″eff=B′/r=B″R/r,R表示线圈半径,r表示原子云半径,有效曲率远大于TOP磁阱或IP磁阱[37]。相同径向梯度下,TOP磁阱的径向曲率比IP磁阱小两个数量级[33],轴向曲率比IP磁阱大两个数量级[13],取轴向与径向曲率的平均值可以得出IP磁阱的束缚更强[32]。由此可得四极磁阱能实现对原子的最强束缚,但存在Majorana损失。TOP磁阱和IP磁阱可以对Majorana损失进行有效抑制,特别是IP磁阱平均曲率值比TOP磁阱大约一个数量级,因此,综合考虑,IP磁阱在对冷原子的束缚效率方面具有更显著的优势。
-
目前基于磁阱真空测量的国外研究机构有美国家标准与技术研究院(NIST)和加拿大英属哥伦比亚大学(UBC),国内研究机构有兰州空间技术物理研究所,本节将介绍这些机构的相关研究。
-
近年来,NIST不仅在理论上对损失率系数进行计算与测定,而且对磁阱CAVS设备进行持续开发,并搭建了动态膨胀系统来验证CAVS。
-
NIST对于CAVS理论研究主要基于两个方面:对不同种类传感器原子和不同种类背景气体组成系统的损失率系数进行理论测定;将国际单位制(SI)可追溯性从计算已知的碰撞截面转移到通过实验测定的碰撞截面[38-39]。
NIST使用初始基态电子Born-Oppenheimer势能面进行量子紧耦合散射计算,对基于7Li和87Rb原子并引入稀有气体原子、H2分子或14N2分子的CAVS系统的损失率系数进行理论确定;并对损失率系数进行了不确定度评估,包括相对论自旋轨道校正估计和范德华系数不确定度,损失率系数的相对不确定度为1%至2%[40]。通过实验表明半经典近似与量子计算的损失率系数一致[41-43],误差为10%。
在扩展测量下限方面,NIST基于初始计算确定的Li+H2系统损失率系数,通过实验确定的相对灵敏度系数SGAS可以扩展得到Li+任意气体或Rb+任意气体的损失率系数[41, 44]。这样对于任意背景气体系统的真空度反演,无需计算损失率系数,不依赖于校准仪表,可通过实验测量的SGAS获得。
-
NIST制作了一套实验原理样机(L-CAVS)和两套便携式样机(pCAVS)。L-CAVS利用MOT、磁阱和射频(RF)天线来冷却和捕获传感器原子,通过真空测量室与动态膨胀系统相连。在真空测量室中,2D MOT的原子被进一步冷却,并捕获在3D MOT中,之后转移到四极或IP磁阱中。87Rb原子具有单一可捕获态
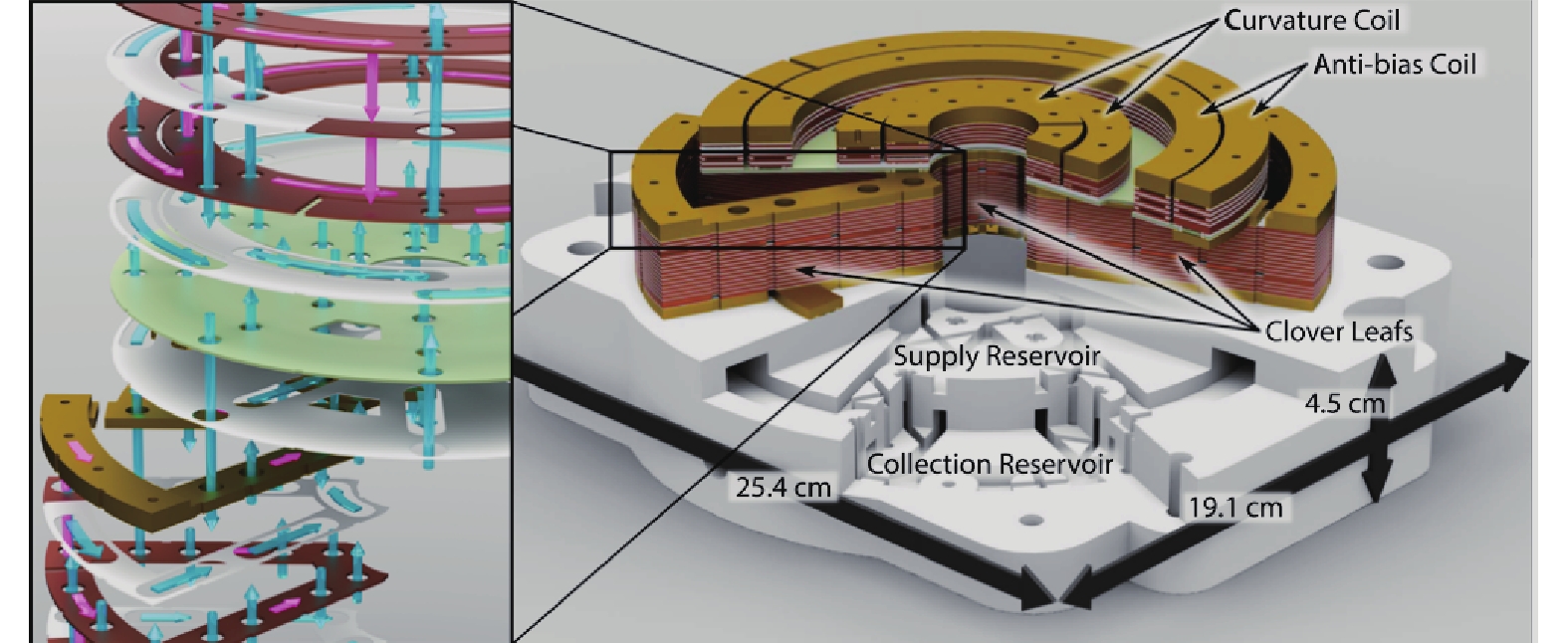
$ \left|F=1,m_{\mathrm{F}}=-1\right\rangle $ ,保证了磁阱损失率从单一阱深测量,且87Rb可用的阱深范围相较于7Li更大;L-CAVS中最多可以捕获5×107个100 μK的87Rb原子。测量室上下设置Bitter式电磁[46-48]来产生两种磁阱,Bitter式电磁铁可冷却强电流产生的热量,不会使磁阱过热或变形[49-51]。Bitter式电磁铁堆叠成三叶草结构[52],如图3所示,由曲率线圈,反偏置线圈和三叶草线圈构成,通过调节各线圈电流使IP磁阱产生偏置磁场以抑制Majorana损失。
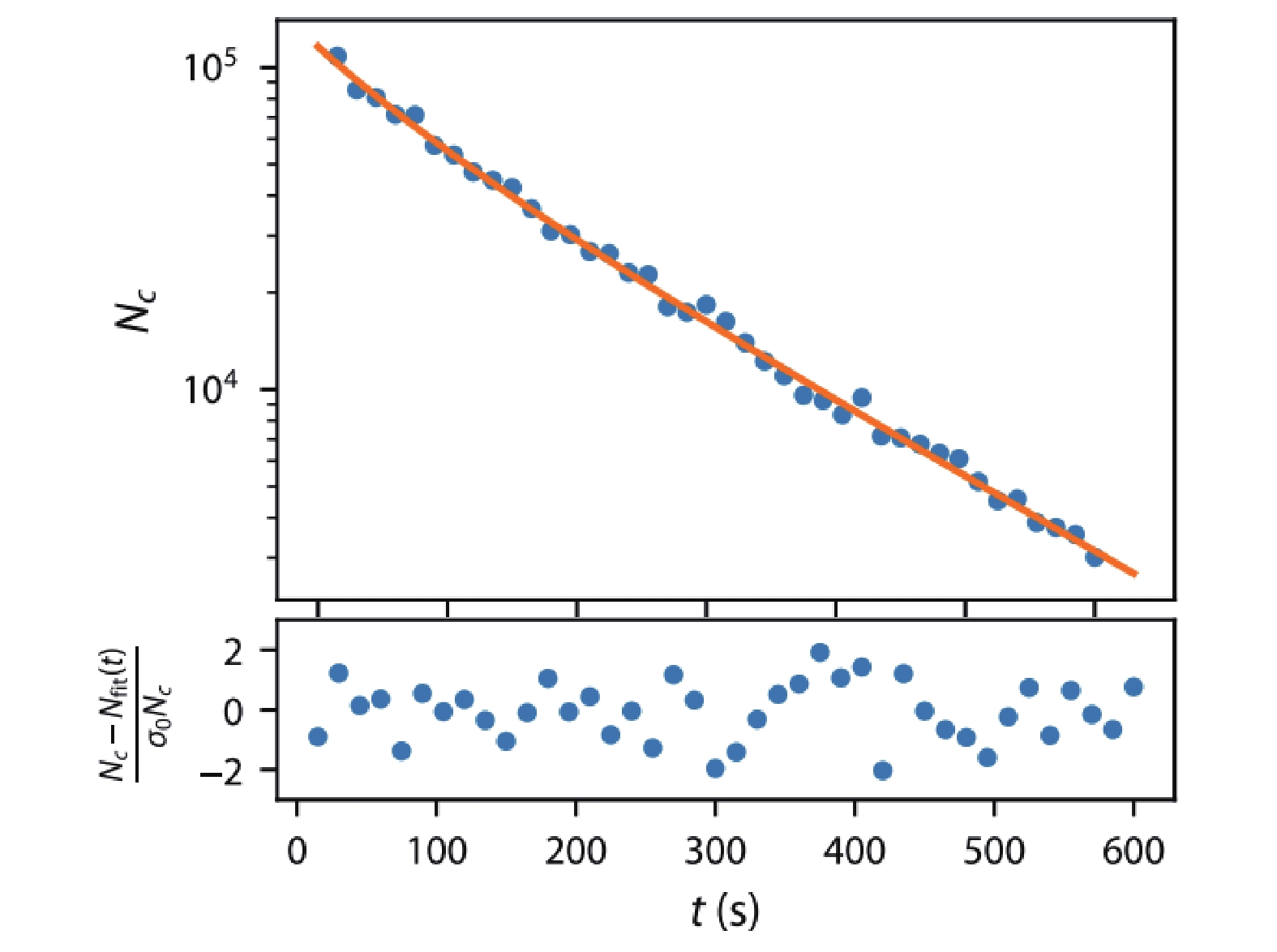
NIST基于87Rb的CAVS在四极磁阱中87Rb原子损失率,测量了动态膨胀室中的基准压力(≤10−9 Pa的纯H2)[53-55]。结果如图4所示,根据半经典理论给出87Rb+H2系统损失率系数可以估计系统压强为4.3 nPa,与基准压力接近。其中主要不确定度为87Rb+H2系统半经典估计中假设的25%不确定度。
由于L-CAVS不便携,不易于使用,且用于激光冷却和捕获原子的设备需要大量组件,需要提高集成度,对CAVS的小型化设计进行探索[57]。NIST开发了比L-CAVS更小、复杂度更低、成本更低的pCAVS。
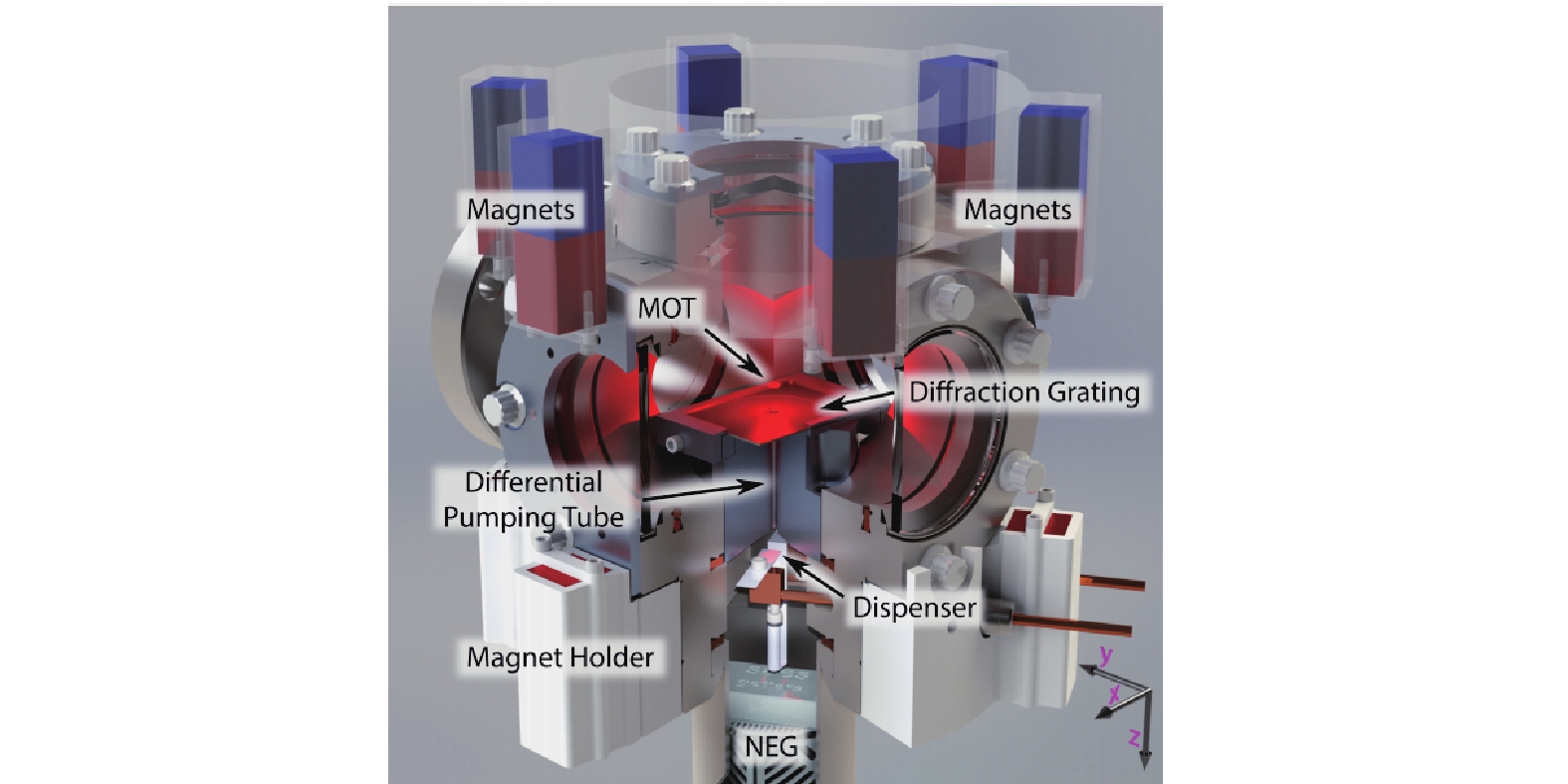
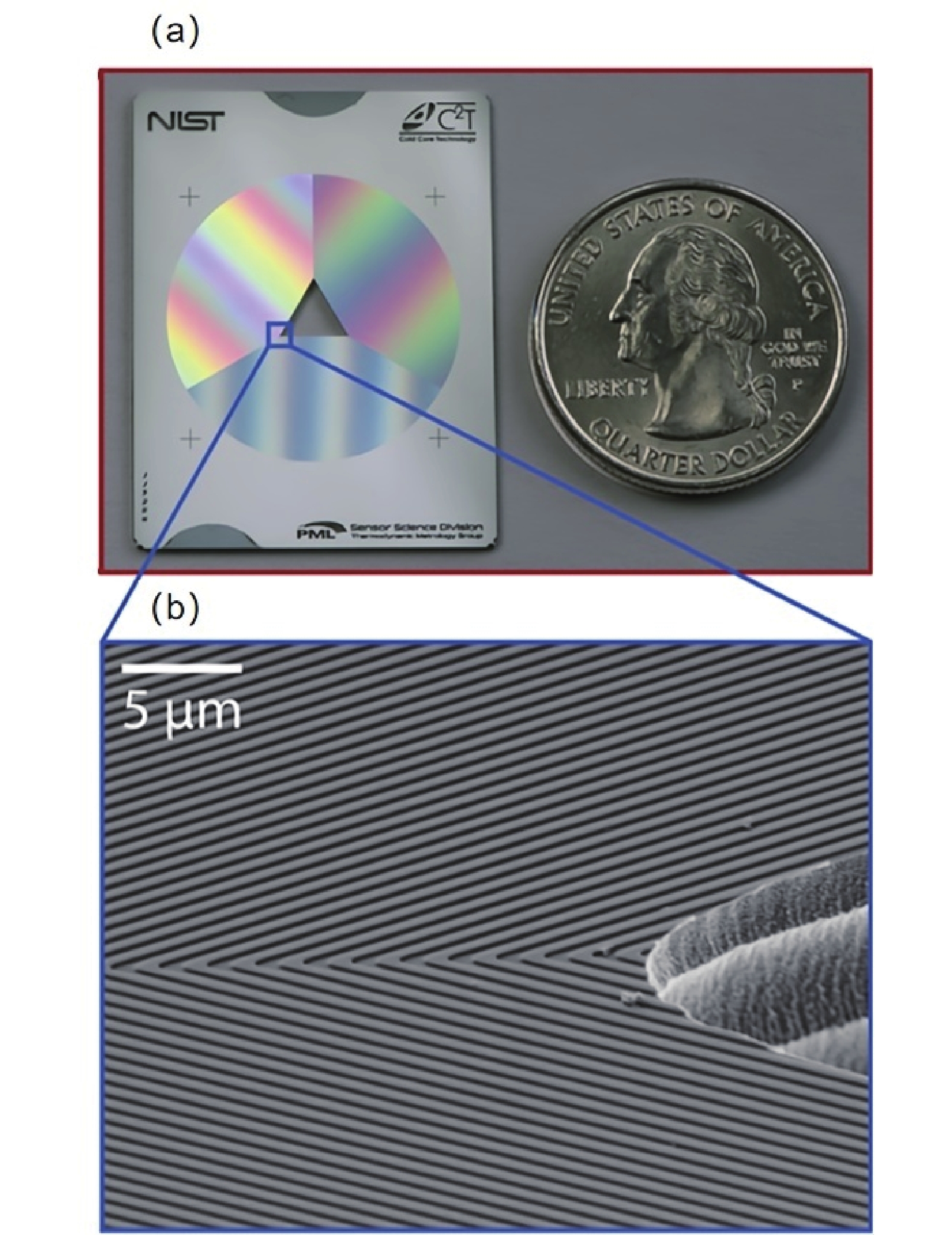
L-CAVS需要在2 m2的实验平台上进行搭建,而pCAVS除激光系统外的尺寸在15 cm×35 cm×50 cm以内。pCAVS由一个源室和一个测量室构成,N52型NdFeB永磁体安装在测量室外部,为磁阱产生四极磁场,结构如图5所示。测量室中采用纳米衍射光栅芯片[59]将2 m3的光学系统缩小至单根光纤发射器,结构如图6所示。输入激光束照射光栅芯片时会产生三束与输入光束相交的反射光束,形成光栅MOT(gMOT)所需的四束相交光束。gMOT对通过差分泵浦管的热7Li原子进行减慢、冷却和捕获[60-62];未被捕获的7Li会粘附在室温真空室壁上而限制加载率[63],NIST通过设计短7Li塞曼减速器与光栅芯片配合使用来优化捕获速度。
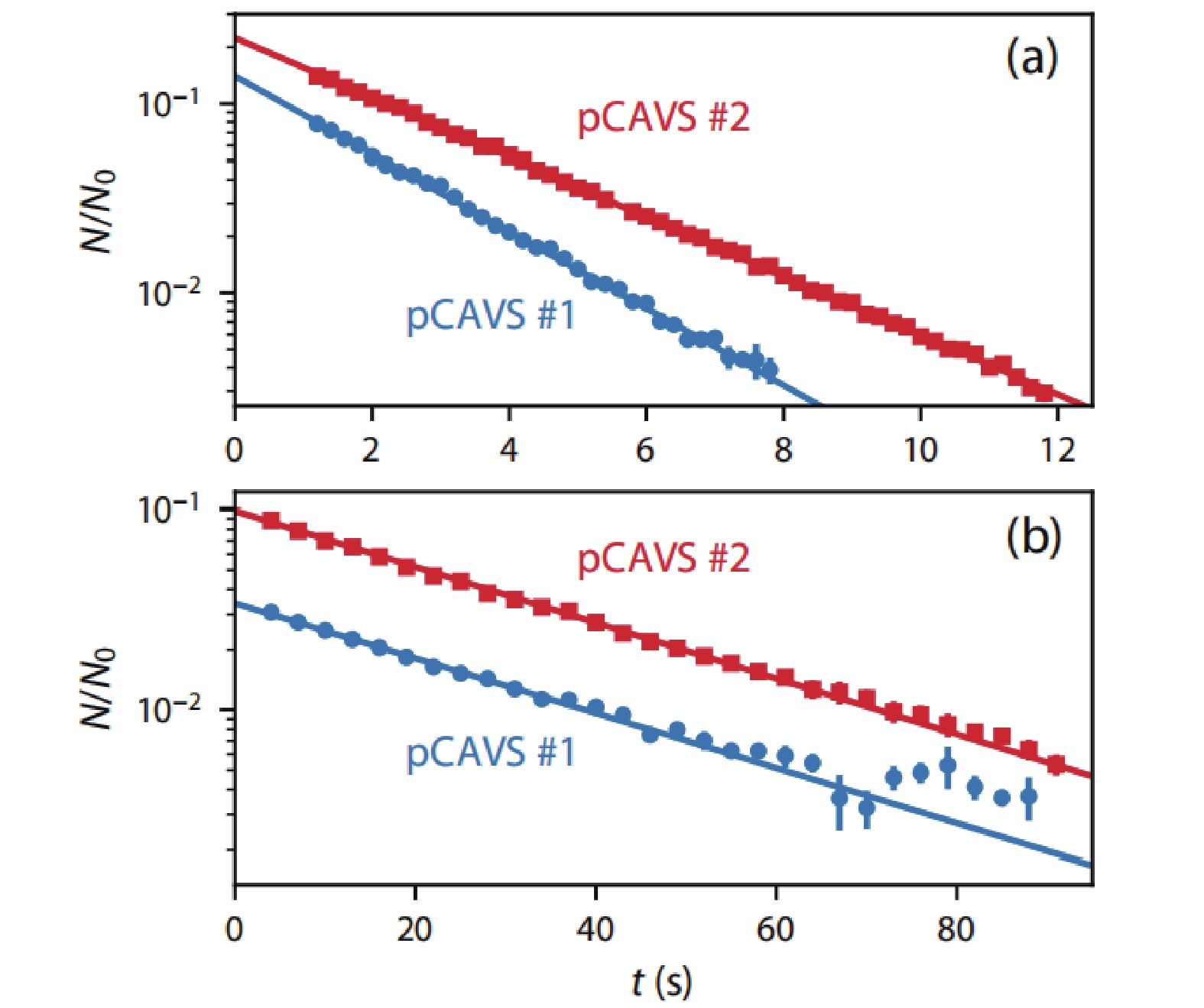
NIST使用两台基于7Li的pCAVS测量同一真空压力。两台pCAVS被安装在同一真空室中,并通入相同功率的激光束,原子云之间相距20 cm。测量到7Li原子数随时间的初始衰减曲线如图7(a)所示,由于连接到pCAVS # 1的视口中存在泄漏,两个pCAVS测量的衰减率不同。修复泄漏后测得两个pCAVS衰减率如图7(b)所示,假设背景气体为H2,根据半经典理论给出7Li+H2系统损失率系数可得[64],pCAVS # 1压力为41.5 nPa、pCAVS # 2压力为42.2 nPa。对于41.8 nPa的真空室压力,两台pCAVS测量结果基本一致,其中主要不确定度为7Li +H2系统理论值中2%不确定度。
-
NIST将pCAVS连接到动态膨胀系统,从而对四个标准进行比较:L-CAVS、pCAVS和流量计/动态膨胀系统。为了验证CAVS,NIST构建了一种动态膨胀系统,可以在超高真空范围内产生捕获原子所需的低不确定度压力,以对冷原子真空传感器与动态膨胀标准进行高精度比较。
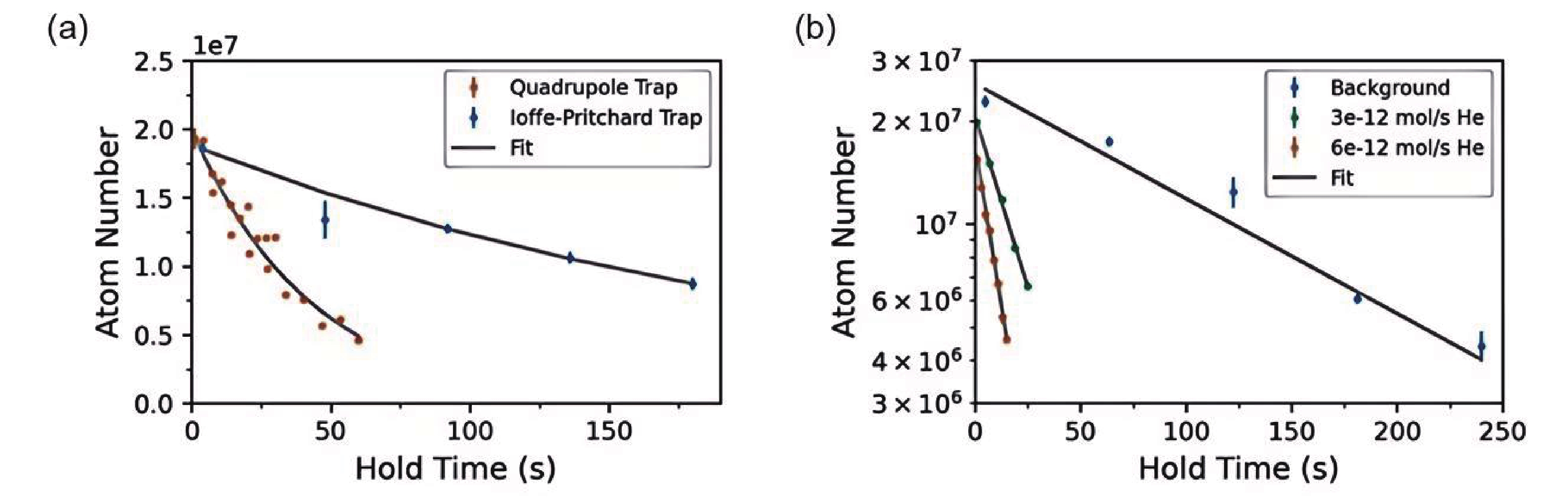
在L-CAVS中相同真空条件下测量IP磁阱和四极磁阱中的Rb原子的衰减率,结果如图8(a)。较低的传感器原子云密度可以抑制蒸发、偶极弛豫和三体损耗。由于Majorana损失,四极磁阱中原子数衰减更快,而IP磁阱由于存在偏置磁场损失率更低。NIST结合CAVS和动态膨胀流标准进行初步测试,在IP磁阱中通入不同流量He测量Rb原子在磁阱中的衰减,由于磁阱偏置磁场低于图8(a)中的偏置磁场,因此Majorana损失不可忽略。测量结果如图8(b)所示,当XHV流量计向与L-CAVS相连的动态膨胀室供应He时,磁阱的损失率会急剧增加。对于3×10−12 mol/s和6×10−12 mol/s的He,损失率分别为4.6×10−2 s−1和8.7×10−2 s−1。表明Rb+He碰撞造成的损失在背景损失中占主导地位。
-
UBC基于粒子之间量子衍射碰撞的普遍定律描述了磁阱中的损失率系数,并在已知深度的磁阱中建立了冷原子原级标准。
-
UBC使用Rb原子在不同阱深下测量了87Rb+40Ar的碰撞横截面,对室温背景碰撞产生的阱损失率进行研究,并使用Rb+Ar系统模型相互作用势证实了在不同阱深处实验测量的损失率与由C6系数表征的已知势的长程吸引部分一致。
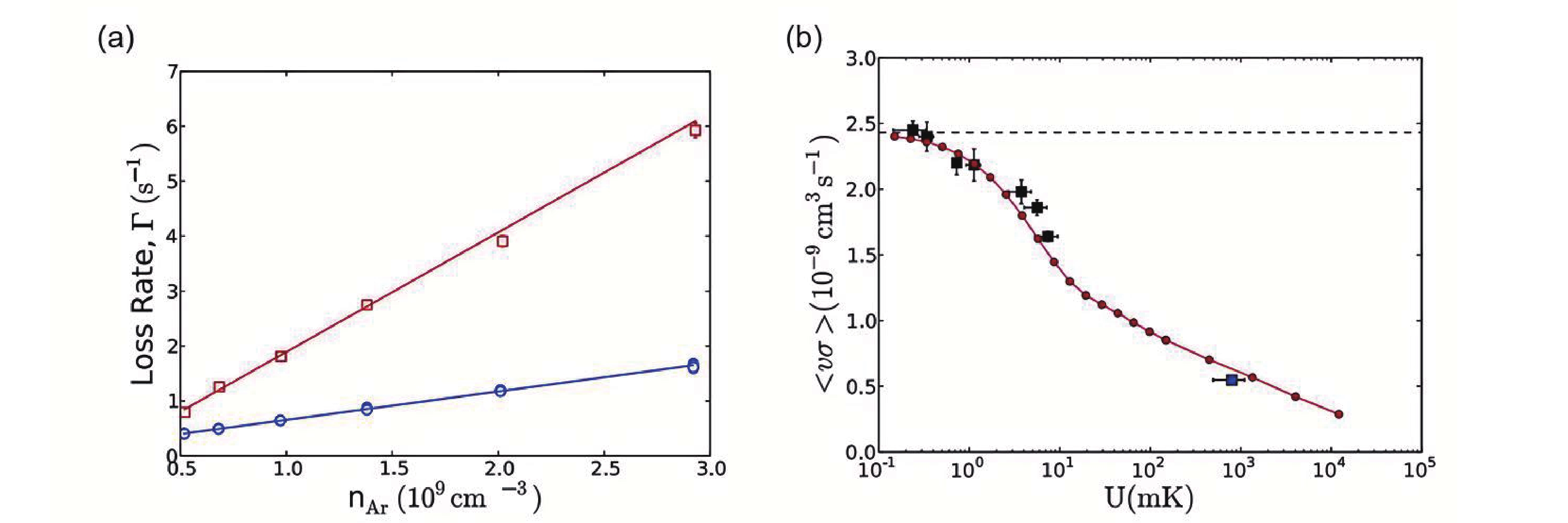
在MOT和四极磁阱中测量87Rb损失率与氩气密度的关系,结果如图9(a)。Rb原子被限制在1 K的MOT中;处于
$ \left|F=1,m_{\mathrm{F}}=-1\right\rangle $ 态的Rb原子在79 G/cm磁场梯度下,被限制在0.64 mK的磁阱中[68]。通过对数据进行拟合可以得到速度平均碰撞系数$\left\langle {{\sigma _{{\text{Rb,Ar}}}}{v_{{\text{Ar}}}}} \right\rangle $ 。在MOT和四极磁阱中拟合损失率系数与阱深的关系,结果如图9(b)所示,在大于800 mk范围内,87Rb损失率系数随阱深变化明显;在小于10 mk范围内,87Rb损失率系数基本不发生变化。由此表明通过测量阱损失率来推断总碰撞截面时,更浅的阱深可以产生更小的不确定度。 -
2011年UBC首次提出可以使用限制在磁阱中的原子或分子云来创建原级真空标准[69]。2020年UBC基于量子衍射碰撞的物理性质,通过拟合不同阱深下测量得到的阱损失率函数来提取由量子衍射碰撞传递的能量谱。利用量子衍射碰撞的普遍定律,实现了第一个也是唯一一个适用于高真空和超高真空(UHV)状态(p<10−7 Pa)的原级量子压力标准。
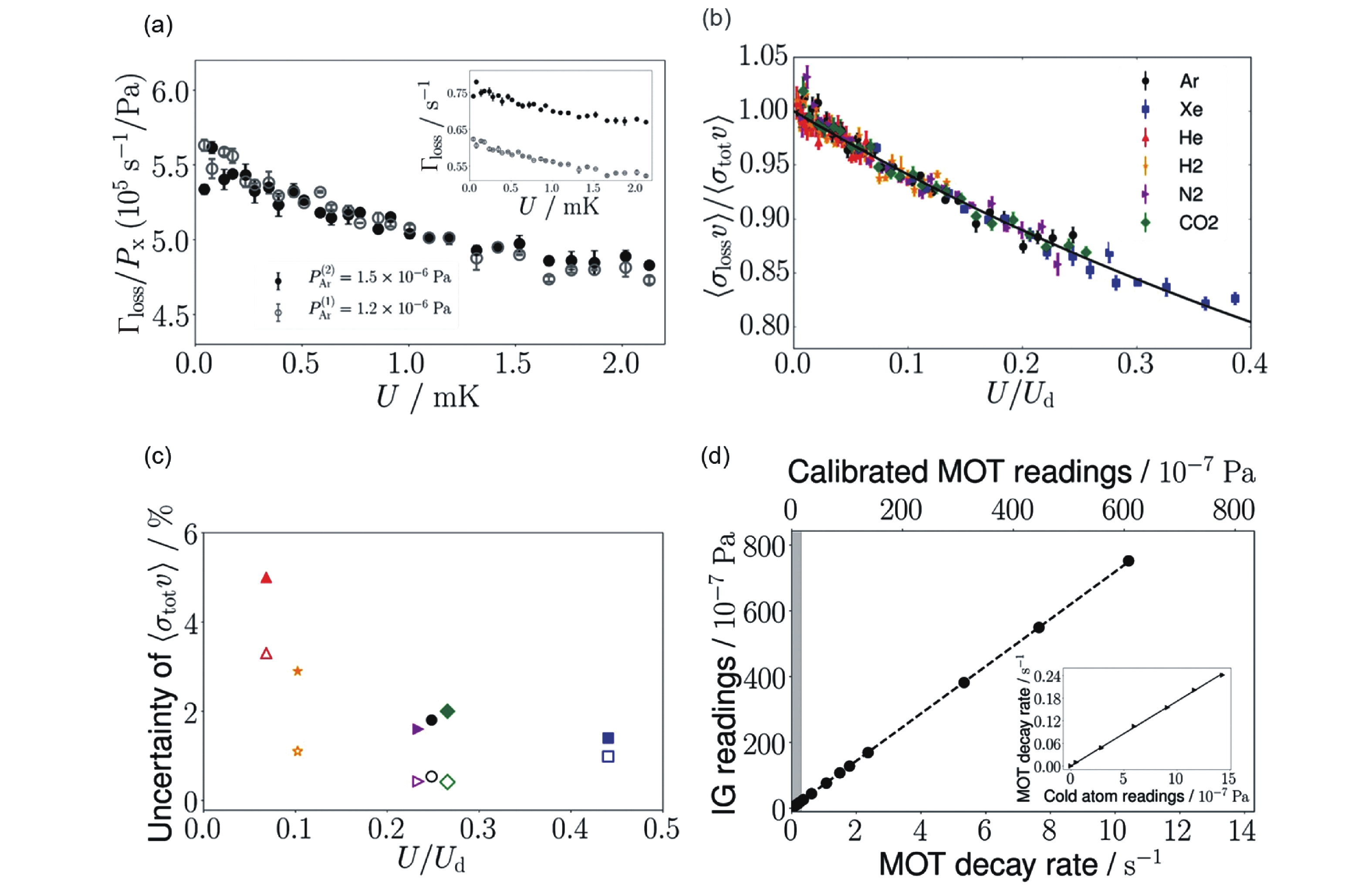
UBC针对捕获的87Rb与(He、Ar和Xe)原子和(H2、N2和CO2)分子气体之间的碰撞进行<σtot v>的测定。通过测量磁阱损失率Гloss(U)作为固定气体压力下阱深的函数,对每种气体的标准进行校准[70-71]。首先在两组不同压力的Ar下测量了归一化损失率Гloss/px随磁阱阱深U的变化曲线,结果如图10(a)所示,不同压力下归一化损失率曲线重叠,表明<σloss(U) v>值不随气压变化。随后,为了验证量子衍射碰撞的普遍性,测量了(He、Ar和Xe)原子和(H2、N2和CO2)分子<σloss(U) v>/<σtot v>与U/Ud之间的关系曲线,<σtot v>表示速度平均总碰撞截面,Ud为量子衍射能;结果如图10(b)所示,不同气体在不同U/Ud下的测量值都遵循相同的线性函数,表明量子衍射碰撞只依赖于势的长程部分C6的解析形式,量子衍射碰撞传递能量太少,不足以使碰撞粒子之间的内部状态发生变化[72]。通过多次对通用多项式进行实验拟合,可以降低测量的<σtot v>不确定度[73],统计(拟合)不确定度与U/Ud范围的函数如图10(c)所示,对于较轻的(He和H2),Ud明显大于其他校准的物质(Ar、Xe、CO2和N2),从而限制了U/Ud≤0.1的范围,导致统计拟合误差较大。考虑系统不确定度后,校准的最佳范围为0.1≤U/Ud≤0.4。
对于MOT在测量过程中存在许多严重问题,UBC使用基于磁阱中的CAVS对基于MOT的传输标准进行校准,如图10(d)所示,将MOT损失率读数与Ar气体离子计“a”读数之间的直接比较,表明可以根据MOT损失率将压力校准到6.0×10−5 Pa范围。
-
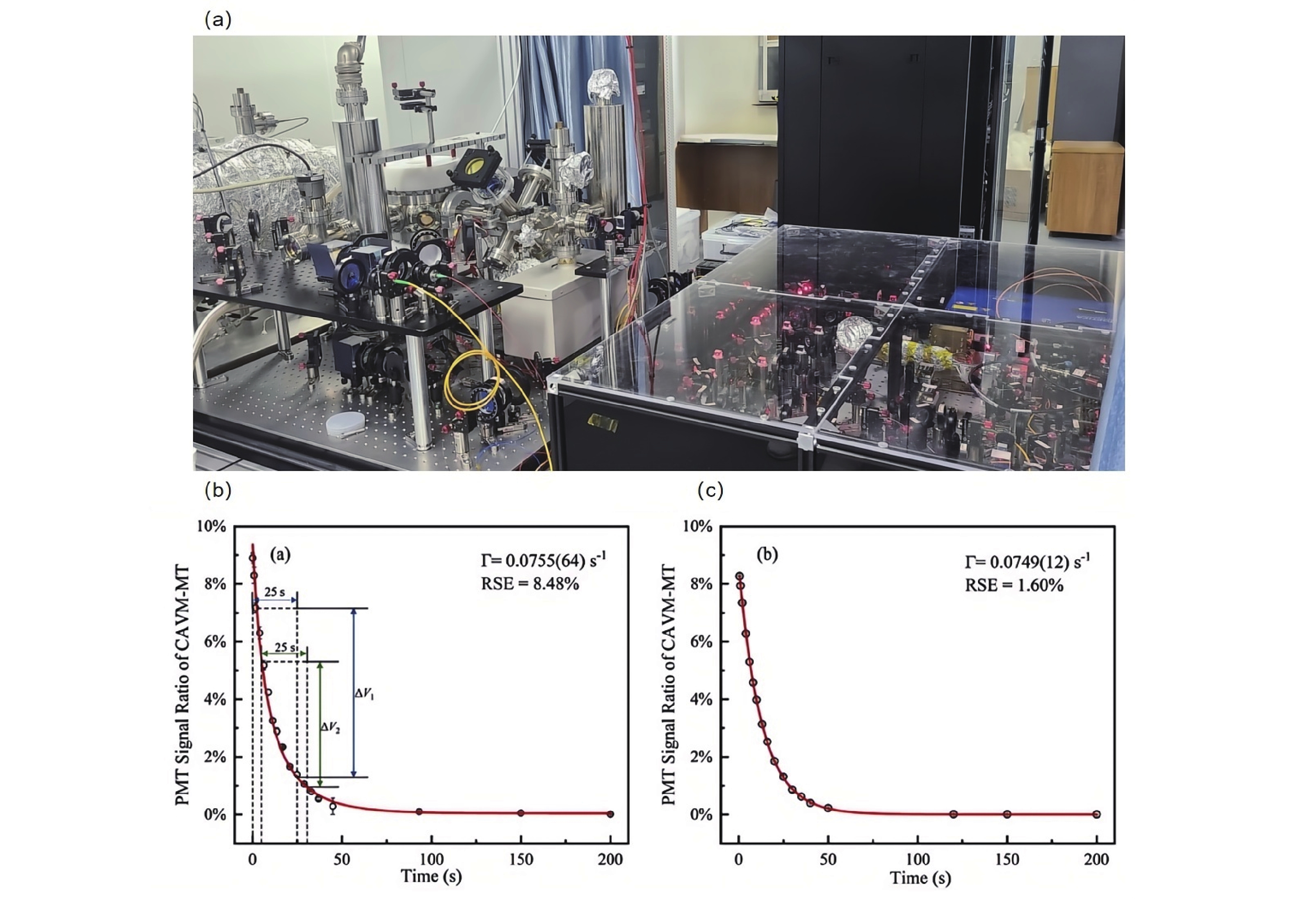
兰州空间技术物理研究所在国家重大项目的支持下,研制出了我国首台锂冷原子超高/极高真空测量装置,如图11(a)所示。基于该装置,在四极磁阱中开展了实验研究[74]。磁阱中冷原子数目的不连续测量会导致损失率提取的拟合误差较为显著,兰州空间技术物理研究所采用四极磁阱拟合得到的损失率如图11(b)所示,损失率拟合为0.0755 s−1,相对标准误差(RSE)约为8.48%,在1.15×10−7 Pa下会给测量结果造成9.67×10−9 Pa的误差。通过严格控制每次实验的初始装载V0,并将推动光束关闭由定时触发改为条件触发,重复磁阱测量过程得到的损失率如图11(c)所示,损失率拟合为0.0749 s−1,RSE明显降低,仅为1.60%,该RSE对应在1.14×10−7 Pa真空度下引入1.82×10−9 Pa的影响,与背景真空度相近,与不控制初始装载V0的情况相比,拟合结果的RSE明显偏低,通过优化数据处理和调整测量方法提高了测量精度。
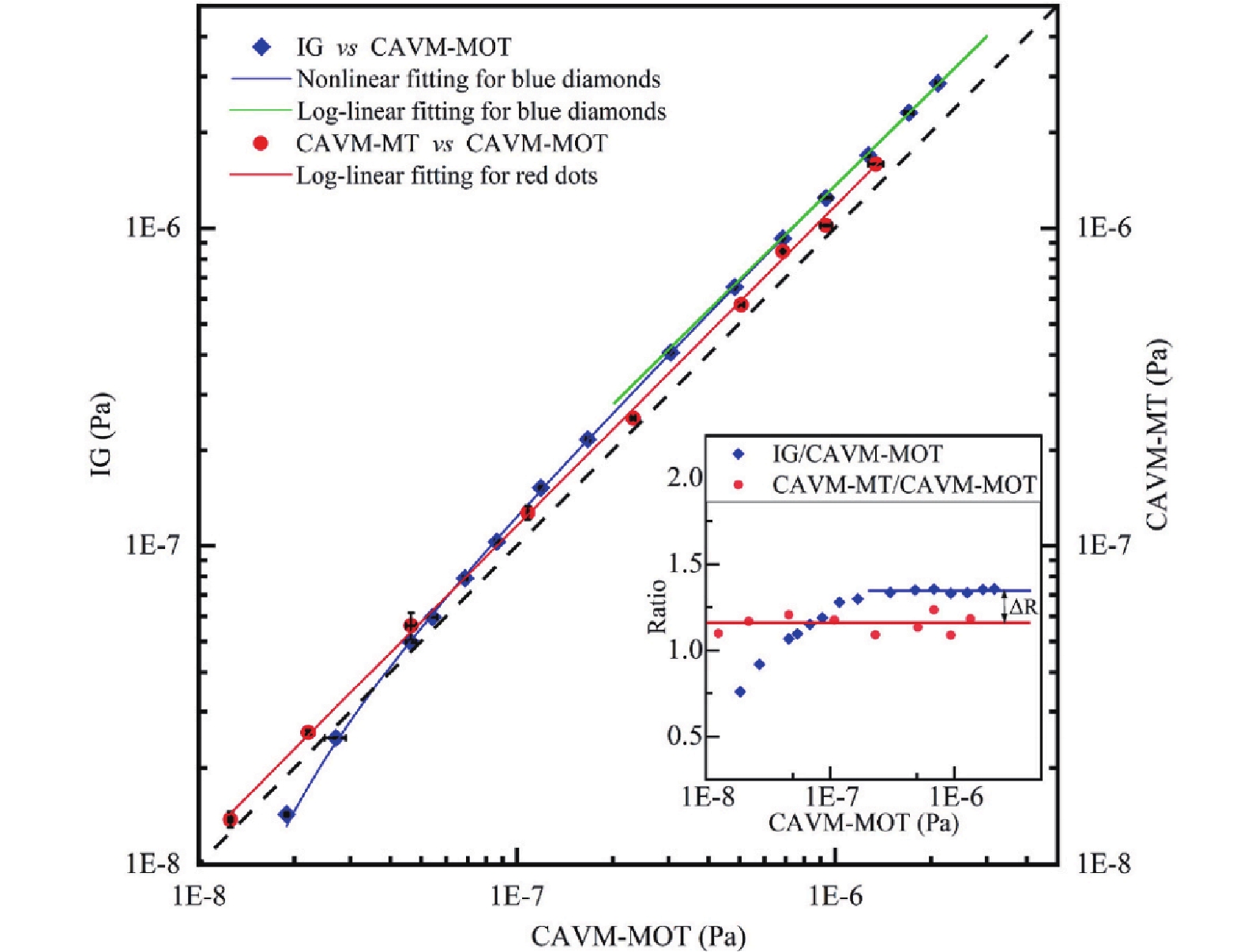
将磁阱和MOT中的冷原子真空测量与电离规示数进行三者比对,对比结果如图12所示。MOT中冷原子真空测量和电离规测量的比对结果在整个测量真空范围内比值稳定,通过线性拟合表明两次测量具有良好的线性关系。MOT和磁阱中冷原子真空测量的比对结果表明,在2×10−7 Pa至5×10−6 Pa的真空范围内,比值较为稳定,但在低于2×10−7 Pa的真空范围内,两者之间的比值发生明显变化,由此验证基于原子基本性质原理和光学方法的磁阱中冷原子真空测量在超高真空范围内较传统真空计具有线性计量优势。
-
本文介绍了各类型磁阱的结构以及磁场分布,对比分析得出IP磁阱能够产生更好的束缚并且更适用于冷原子真空测量。总结了国内外机构基于磁阱真空测量的理论研究,实验测定以及设备开发。面对在UHV/XHV建标需求,为解决磁阱中非理想损耗导致测量不确定性的问题,迫切需要优化测量程序和构建新型设备,可以在以下方面进行深入研究。
对于L-CAVS磁阱存在不连续测量损失率提取拟合误差,其一需尽量消除和降低实验环境造成的误差,确保每次加载的初始条件相同;其二可以设计反馈电路主动控制来保持光学装置稳定。L-CAVS磁阱中还存在测量时间过长的问题,在10−8 Pa量级以上可以达到100 s至1000 s。过长的测量时间会使应用范围受限,真空标准也无法实现100 s至1000 s范围内的绝对稳定,后续需要研究在较短时间内提取损失率的技术。
对于在pCAVS磁阱中使用永磁体构建四极磁阱而存在马约拉纳损失,首先可以结合磁阱类型,磁场分布来选择在pCAVS中磁阱的搭建思路。其次针对小型化和便携性这一主题,结合与真空设备间的装配方式,在不干涉小型MOT操作的基础上来确定磁阱的结构设计,最后根据已有的磁阱结构和磁阱类型对新设计的磁阱的可靠性进行评估,结合实际加工条件对新磁阱进行修改。
磁阱中冷原子真空测量的研究进展
Recent Developments in Magnetic Traps Using Cold-Atom Vacuum Measurements
-
摘要: 冷原子真空测量是一种超高/极高真空度测量的新技术,理想磁阱中冷原子真空测量可溯源至原子基本性质,能够建立真空原级计量标准。通过不同磁阱磁场强度、磁捕获势能和磁捕获参数的对比分析,对各类磁阱的束缚性能进行总结。调研了国内外在磁阱中冷原子真空测量的研究,综述了实现冷原子原级真空标准的理论参数计算和设备研制实验。从优化和构建磁阱方面对磁阱中的冷原子真空测量进行展望。Abstract: The cold atom vacuum measurement is a new technique for ultra-high/extreme-high vacuum (UHV/XHV) measurements, which is traceable to the fundamental properties of atoms in an ideal magnetic trap and can establish vacuum primary metrology standards. Firstly, we summarize the binding performance of various types of magnetic traps by comparing and analyzing the magnitude of the magnetic field, magnetic trapping potential, and magnetic trapping parameters of different magnetic traps. Secondly, we investigated the domestic and international research on cold-atom vacuum measurements in magnetic traps. We reviewed the theoretical parameter calculations and equipment development experiments for realizing cold-atom primary vacuum standards. Finally, we provide an outlook on cold atom vacuum measurements in magnetic traps in terms of optimization and construction of magnetic traps.
-
Key words:
- Magnetic traps /
- Cold atoms /
- Vacuum measurement /
- Primary metrology standards /
- Ultra-high/Extreme-high vacuum .
-

-
图 9 磁阱中87Rb的损失率与室温氩气密度之间的关系曲线(a),实验测量的损失率斜率
$\left\langle {{\sigma _{{\text{Rb,Ar}}}}{v_{{\text{Ar}}}}} \right\rangle $ (正方形)和理论计算的损失率斜率(圆圈),关于87Rb-40Ar碰撞的阱深函数(b)[67]Figure 9. Loss rate of trapped 87Rb versus room temperature argon gas density (a), the experimentally measured(squares) and theoretically computed(circles)loss rate slope,
$\left\langle {{\sigma _{{\text{Rb,Ar}}}}{v_{{\text{Ar}}}}} \right\rangle $ , as a function of trap depth for 87Rb-40Ar collisions (b)[67]图 10 不同阱深下测得的
$ {\Gamma}_{\text{loss}}/p_{\text{x}} $ 值(a),不同U/Ud下的$ \left\langle {{\sigma _{{\text{loss}}}}(U)v} \right\rangle $ /$ \left\langle {{\sigma _{{\text{tot}}}}v} \right\rangle $ 值(b),不同U/Ud下$ \left\langle {{\sigma _{{\text{tot}}}}v} \right\rangle $ 的不确定度(c),氩气的IG读数与MOT衰减率的关系(d)[16]Figure 10.
${\Gamma}_{\text{loss}}/p_{\text{x}} $ values measured at different trap depths (a), the value of$ \left\langle {{\sigma _{{\text{loss}}}}(U)v} \right\rangle $ /$ \left\langle {{\sigma _{{\text{tot}}}}v} \right\rangle $ under different U/Ud (b), (c) shows a plot of the uncertainty in the determination of$ \left\langle {{\sigma _{{\text{tot}}}}v} \right\rangle $ as a function of the range of U/Ud accessed for the measurement, the relationship between IG reading in argon and MOT decay rate (d)[16]图 11 锂冷原子真空测量装置实物照片(a),冷原子真空测量初始装载装置控制优化之前(b)和之后(c),磁阱中冷原子真空测量的衰变曲线随时间变化的比较[75]
Figure 11. Lithium cold-atom vacuum measurement device physical photo (a), comparison of the decay curves of cold atoms vacuum measurement in magnetic trap with time before (b) and after (c) optimization of the cold atoms vacuum measurement initial loading control, comparison plots between cold atoms vacuum measurement in magnetic trap[75]
-
[1] Brockwell T G, Meech K J, Pickens K, et al. The mass spectrometer for planetary exploration (MASPEX)[C]//2016 IEEE Aerospace Conference. Big Sky: IEEE, 2016: 1−17 [2] Dekoulis G. Space flight[M]. IntechOpen, 2018 [3] Mozetič M, Vesel A, Primc G, et al. Recent developments in surface science and engineering, thin films, nanoscience, biomaterials, plasma science, and vacuum technology[J]. Thin Solid Films,2018,660:120−160 doi: 10.1016/j.tsf.2018.05.046 [4] Palmberg P W. Ultrahigh vacuum and surface science[J]. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films,1994,12(4):946−952 [5] Ellefson R E. Methods for in situ QMS calibration for partial pressure and composition analysis[J]. Vacuum,2014,101:423−432 [6] Joyce B A. Molecular beam epitaxy[J]. Reports on Progress in Physics,1985,48(12):1637−1697 [7] Kibbel H, Kasper E. Industrial aspects of silicon molecular beam epitaxy[J]. Vacuum,1990,41(4-6):929−932 doi: 10.1016/0042-207X(90)93825-4 [8] Te Sligte E, Koster N, Molkenboer F, et al. EBL2: high power EUV exposure facility[C]//Proceedings of SPIE 9985, Photomask Technology 2016. San Jose: SPIE, 2016: 259−266 [9] 张苏钊, 孙雯君, 董猛, 等. 基于磁光阱中6Li冷原子的真空度测量[J]. 物理学报,2022,71(9):094204 (in Chinese) doi: 10.7498/aps.71.20212204 Zhang S Z, Sun W J, Dong M, et al. Vacuum pressure measurement based on 6Li cold atoms in a magneto-optical trap[J]. Acta Physica Sinica,2022,71(9):094204 doi: 10.7498/aps.71.20212204 [10] Scherschligt J, Fedchak J A, Barker D S, et al. Development of a new UHV/XHV pressure standard (cold atom vacuum standard)[J]. Metrologia,2017,54(6):S125−S132 doi: 10.1088/1681-7575/aa8a7b [11] Schwinger J, Deraad Jr L L, Milton K, et al. Classical electrodynamics[M]. Boca Raton: CRC Press, 2019 [12] Temple G. Static and dynamic electricity[J]. Nature,1940,146(3701):446 [13] Pérez-Ríos J, Sanz A S. How does a magnetic trap work?[J]. American Journal of Physics,2013,81(11):836−843 doi: 10.1119/1.4819167 [14] Earnshaw S. On the nature of the molecular forces which regulate the constitution of the luminiferous ether[J]. Transactions of the Cambridge Philosophical Society,1848,7:97−112 [15] Wing W H. On neutral particle trapping in quasistatic electromagnetic fields[J]. Progress in Quantum Electronics,1984,8(3-4):181−199 doi: 10.1016/0079-6727(84)90012-0 [16] Shen P R, Madison K W, Booth J L. Realization of a universal quantum pressure standard[J]. Metrologia,2020,57(2):025015 doi: 10.1088/1681-7575/ab7170 [17] Gensemer S D, Sanchez-Villicana V, Tan K Y N, et al. Trap-loss collisions of 85Rb and 87Rb: dependence on trap parameters[J]. Physical Review A,1997,56(5):4055−4063 [18] Prentiss M, Cable A, Bjorkholm J E, et al. Atomic-density-dependent losses in an optical trap[J]. Optics Letters,1988,13(6):452−454 doi: 10.1364/OL.13.000452 [19] Steane A M, Chowdhury M, Foot C J. Radiation force in the magneto-optical trap[J]. Journal of the Optical Society of America B,1992,9(12):2142−2158 [20] Van Dongen J, Zhu C, Clement D, et al. Trap-depth determination from residual gas collisions[J]. Physical Review A,2011,84(2):022708 doi: 10.1103/PhysRevA.84.022708 [21] Beijerinck H C W. Rigorous calculation of heating in alkali-metal traps by background gas collisions[J]. Physical Review A,2000,61(3):033606 doi: 10.1103/PhysRevA.61.033606 [22] Beijerinck H C W. Heating rates in collisionally opaque alkali-metal atom traps: role of secondary collisions[J]. Physical Review A,2000,62(6):063614 [23] Brink D M, Sukumar C V. Majorana spin-flip transitions in a magnetic trap[J]. Physical Review A,2006,74(3):035401 [24] Davis K B, Mewes M O, Joffe M A, et al. Evaporative cooling of sodium atoms[J]. Physical Review Letters,1995,74(26):5202−5205 doi: 10.1103/PhysRevLett.74.5202 [25] Majorana E. Atomi orientati in campo magnetico variabile[J]. Il Nuovo Cimento (1924-1942),1932,9(2):43−50 doi: 10.1007/BF02960953 [26] Maruyama R. Optical trapping of ytterbium atoms[D]. Washington: University of Washington, 2003 [27] Kozuma M, Deng L, Hagley E W, et al. Coherent splitting of Bose-Einstein condensed atoms with optically induced Bragg diffraction[J]. Physical Review Letters,1999,82(5):871−875 [28] Petrich W, Anderson M H, Ensher J R, et al. Stable, tightly confining magnetic trap for evaporative cooling of neutral atoms[J]. Physical Review Letters,1995,74(17):3352−3355 [29] Rolston S L. Magnetic trapping, evaporative cooling, and Bose Einstein Condensation[J]. AIP Conference Proceedings,1999,464(1):91−110 [30] Bergeman T, Erez G, Metcalf H J. Magnetostatic trapping fields for neutral atoms[J]. Physical Review A,1987,35(4):1535−1546 doi: 10.1103/PhysRevA.35.1535 [31] Ketterle W, Durfee D S, Stamper-Kurn D M. Making, probing and understanding Bose-Einstein condensates[M]. arXiv: cond-mat/9904034, 1999 [32] Ketterle W, Van Druten N J. Bose-Einstein condensation of a finite number of particles trapped in one or three dimensions[J]. Physical Review A,1996,54(1):656−660 doi: 10.1103/PhysRevA.54.656 [33] Mewes M O, Andrews M R, Van Druten N J, et al. Bose-Einstein condensation in a tightly confining dc magnetic trap[J]. Physical Review Letters,1996,77(3):416−419 [34] Thomas N R, Wilson A C, Foot C J. Double-well magnetic trap for Bose-Einstein condensates[J]. Physical Review A,2002,65(6):063406 doi: 10.1103/PhysRevA.65.063406 [35] Sukumar C V, Brink D M. Spin-flip transitions in a magnetic trap[J]. Physical Review A,1997,56(3):2451−2454 [36] Courteille P W, Muniz S R, Magalhães K, et al. Magnetic field tomography[J]. The European Physical Journal D- Atomic, Molecular, Optical and Plasma Physics,2001,15(2):173−180 [37] Ketterle W, Van Druten N J. Evaporative cooling of trapped atoms[J]. Advances in Atomic, Molecular, and Optical Physics,1996,37:181−236 [38] Makrides C, Barker D S, Fedchak J A, et al. Elastic rate coefficients for Li+ H2 collisions in the calibration of a cold-atom vacuum standard[J]. Physical Review A,2019,99(4):042704 doi: 10.1103/PhysRevA.99.042704 [39] Scherschligt J, Fedchak J A, Ahmed Z, et al. Review article: quantum-based vacuum metrology at the National Institute of Standards and Technology[J]. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films, 2018, 36(4): 040801 [40] Kłos J, Tiesinga E. Elastic and glancing-angle rate coefficients for heating of ultracold Li and Rb atoms by collisions with room-temperature noble gases, H2, and N2[J]. The Journal of Chemical Physics,2023,158(1):014308 [41] McCulloh K E, Tilford C R, Ehrlich C D, et al. Low‐range flowmeters for use with vacuum and leak standards[J]. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films,1987,5(3):376−381 [42] Partridge H, Stallcop J R, Levin E. Potential energy curves and transport properties for the interaction of He with other ground-state atoms[J]. The Journal of Chemical Physics,2001,115(14):6471−6488 doi: 10.1063/1.1385372 [43] Ury G B, Wharton L. Absolute total scattering cross sections of 7Li–Ar[J]. The Journal of Chemical Physics,1972,56(12):5832−5837 doi: 10.1063/1.1677124 [44] Berg R F, Fedchak J A. NIST calibration services for spinning rotor gauge calibrations[R]. NIST, 2015: 93 [45] Siegel J L, Barker D S, Fedchak J A, et al. A Bitter-type electromagnet for complex atomic trapping and manipulation[J]. Review of Scientific Instruments,2021,92(3):033201 doi: 10.1063/5.0026812 [46] Long Y, Xiong F, Gaire V, et al. All-optical production of Li6 molecular Bose-Einstein condensates in excited hyperfine levels[J]. Physical Review A,2018,98(4):043626 [47] Luan T, Zhou T W, Chen X Z, et al. A modified Bitter-type electromagnet and control system for cold atom experiments[J]. Review of Scientific Instruments,2014,85(2):024701 doi: 10.1063/1.4864051 [48] Sabulsky D O, Parker C V, Gemelke N D, et al. Efficient continuous-duty Bitter-type electromagnets for cold atom experiments[J]. Review of Scientific Instruments,2013,84(10):104706 doi: 10.1063/1.4826498 [49] McKay Parry N, Baker M, Neely T, et al. Note: high turn density magnetic coils with improved low pressure water cooling for use in atom optics[J]. Review of Scientific Instruments,2014,85(8):086103 doi: 10.1063/1.4892375 [50] Ricci L, Martini L M, Franchi M, et al. A current-carrying coil design with improved liquid cooling arrangement[J]. Review of Scientific Instruments,2013,84(6):065115 doi: 10.1063/1.4811666 [51] Roux K, Cilenti B, Helson V, et al. Compact bulk-machined electromagnets for quantum gas experiments[J]. SciPost Physics,2019,6(4):048 doi: 10.21468/SciPostPhys.6.4.048 [52] Davis K B, Mewes M O, Andrews M R, et al. Bose-einstein condensation in a gas of sodium atoms[J]. Physical Review Letters,1995,75(22):3969−3973 [53] Ensher J R. The first experiments with Bose-einstein condensation of 87Rb[D]. Colorado: University of Colorado, 1999 [54] Herold C D. Ultracold mixtures of rubidium and ytterbium for open quantum system engineering[D]. College Park: University of Maryland, 2014 [55] Kastler A. Quelques suggestions concernant la production optique et la détection optique d'une inégalité de population des niveaux de quantifigation spatiale des atomes. Application à l'expérience de Stern et Gerlach et à la résonance magnétique[J]. Journal de Physique et Le Radium,1950,11(6):255−265 doi: 10.1051/jphysrad:01950001106025500 [56] Barker D S, Acharya B P, Fedchak J A, et al. Precise quantum measurement of vacuum with cold atoms[J]. Review of Scientific Instruments,2022,93(12):121101 doi: 10.1063/5.0120500 [57] Eckel S, Barker D S, Fedchak J A, et al. Challenges to miniaturizing cold atom technology for deployable vacuum metrology[J]. Metrologia,2018,55(5):S182−S193 doi: 10.1088/1681-7575/aadbe4 [58] Sitaram A, Elgee P K, Campbell G K, et al. Confinement of an alkaline-earth element in a grating magneto-optical trap[J]. Review of Scientific Instruments,2020,91(10):103202 [59] McGilligan J P, Griffin P F, Riis E, et al. Diffraction-grating characterization for cold-atom experiments[J]. Journal of the Optical Society of America B,2016,33(6):1271−1277 doi: 10.1364/JOSAB.33.001271 [60] Barker D S, Norrgard E B, Klimov N N, et al. Single-beam Zeeman slower and magneto-optical trap using a nanofabricated grating[J]. Physical Review Applied,2019,11(6):064023 doi: 10.1103/PhysRevApplied.11.064023 [61] Nshii C C, Vangeleyn M, Cotter J P, et al. A surface-patterned chip as a strong source of ultracold atoms for quantum technologies[J]. Nature Nanotechnology,2013,8(5):321−324 [62] Cotter J P, McGilligan J P, Griffin P F, et al. Design and fabrication of diffractive atom chips for laser cooling and trapping[J]. Applied Physics B,2016,122(6):172 doi: 10.1007/s00340-016-6415-y [63] Haw M, Evetts N, Gunton W, et al. Magneto-optical trap loading rate dependence on trap depth and vapor density[J]. Journal of the Optical Society of America B,2012,29(3):475−483 doi: 10.1364/JOSAB.29.000475 [64] Arpornthip T, Sackett C A, Hughes K J. Vacuum-pressure measurement using a magneto-optical trap[J]. Physical Review A,2012,85(3):033420 doi: 10.1103/PhysRevA.85.033420 [65] Ehinger L H, Acharya B P, Barker D S, et al. Comparison of two multiplexed portable cold-atom vacuum standards[J]. AVS Quantum Science,2022,4(3):034403 [66] Barker D S, Klimov N N, Tiesinga E, et al. Progress towards comparison of quantum and classical vacuum standards[J]. Measurement: Sensors,2021,18:100229 doi: 10.1016/j.measen.2021.100229 [67] Fagnan D E, Wang J C, Zhu C C, et al. Observation of quantum diffractive collisions using shallow atomic traps[J]. Physical Review A,2009,80(2):022712 doi: 10.1103/PhysRevA.80.022712 [68] Ladouceur K, Klappauf B G, Van Dongen J, et al. Compact laser cooling apparatus for simultaneous cooling of lithium and rubidium[J]. Journal of the Optical Society of America B,2009,26(2):210−217 doi: 10.1364/JOSAB.26.000210 [69] Booth J L, Fagnan D E, Klappauf B G, et al. Method and device for accurately measuring the incident flux of ambient particles in a high or ultra-high vacuum environment: 8803072[P]. 2014 [70] Bennett J R J, Hughes S, Elsey R J, et al. Outgassing from stainless steel and the effects of the gauges[J]. Vacuum,2004,73(2):149−153 [71] Hong S S, Shin Y H, Arakawa I. Investigation of gas species in a stainless steel ultrahigh vacuum chamber with hot cathode ionization gauges[J]. Measurement Science and Technology,2004,15(2):359−364 doi: 10.1088/0957-0233/15/2/007 [72] Booth J L, Shen P R, Krems R V, et al. Universality of quantum diffractive collisions and the quantum pressure standard[J]. New Journal of Physics,2019,21(10):102001 doi: 10.1088/1367-2630/ab452a [73] Derevianko A, Porsev S G, Babb J F. Electric dipole polarizabilities at imaginary frequencies for hydrogen, the alkali–metal, alkaline–earth, and noble gas atoms[J]. Atomic Data and Nuclear Data Tables,2010,96(3):323−331 doi: 10.1016/j.adt.2009.12.002 [74] Hoffmann D, Bali S, Walker T. Trap-depth measurements using ultracold collisions[J]. Physical Review A,1996,54(2):R1030 [75] Sun W, Wu X, Cheng Y, et al. Cold atom technology applied to ultra-high vacuum (UHV) measurements[J]. Vacuum,2024,222:113079 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: