首页
登录
注册
下载:
-
电感耦合等离子体(ICP)具有高温、高晗、高化学活性以及不受任何污染的优异特性[1-2]，已被用于各种工业领域，如材料加工、废物处理和等离子体合成纳米颗粒等[3]，因其具有广阔的应用前景，多年来受到了国内外学者的广泛关注。
电感耦合等离子体炬内的温度场是其最重要的物理性质之一[4]，实验证明在远离等离子体射流中心的区域，等离子体的电子温度(Te)会明显高于重粒子温度(Th)，出现热力学非平衡(NLTE)的现象 [5]。但是由于电感耦合等离子体炬内部的空间狭小，并且温度过高，采用实验的方式来测量等离子体参数面临着诸多困难，因此目前多用数值模拟的方法对等离子体的非平衡特性的进行研究[6]。Javad Mostaghlmi建立了二维的双温度电感耦合等离子体模型，研究了压力的变化对等离子体炬内电子温度与重粒子温度空间分布的影响[7]。一些学者为了能够得到电感耦合等离子体炬内部更加真实的数据，在热力学非平衡和化学非平衡的条件下进行了数值模拟，并且获得的结果与实验数据较为吻合；Zhang W等[8]建立了电感耦合等离子体的热化学非平衡模型，在不同的压力条件下评估了不同化学动力学的模型对等离子体温度场以及粒子的空间分布产生的影响。Tanaka Y以及Watanabe T研究小组[9-12]在热化学非平衡模型的基础上研究了不同工作气体成分的参数变化对电感感应耦合等离子体炬内部的流场以及温度场的影响。Lu B X等[13]基于Comsol建立了电感耦合等离子体的热化学非平衡的二维模型，研究了不同的感应频率、工作压力以及不同流量的工作气体对电子温度和等离子体速度的影响。
但上述研究小组研究均是假设热等离子体处于层流状态，并未考虑其湍流效应。而实际上，在工业应用中用到的等离子体通常处于湍流状态，特别是需要相对较高功率水平的情况下，湍流现象更为明显，湍流模型已被证明对等离子体内的质量和热输运现象有显著影响[14-16]。然而湍流效应对电感耦合等离子体热力学非平衡的影响也只是在少数的研究中被考虑在内[17]。因此研究在湍流条件下等离子体炬内温度空间分布规律有着十分重要的意义。
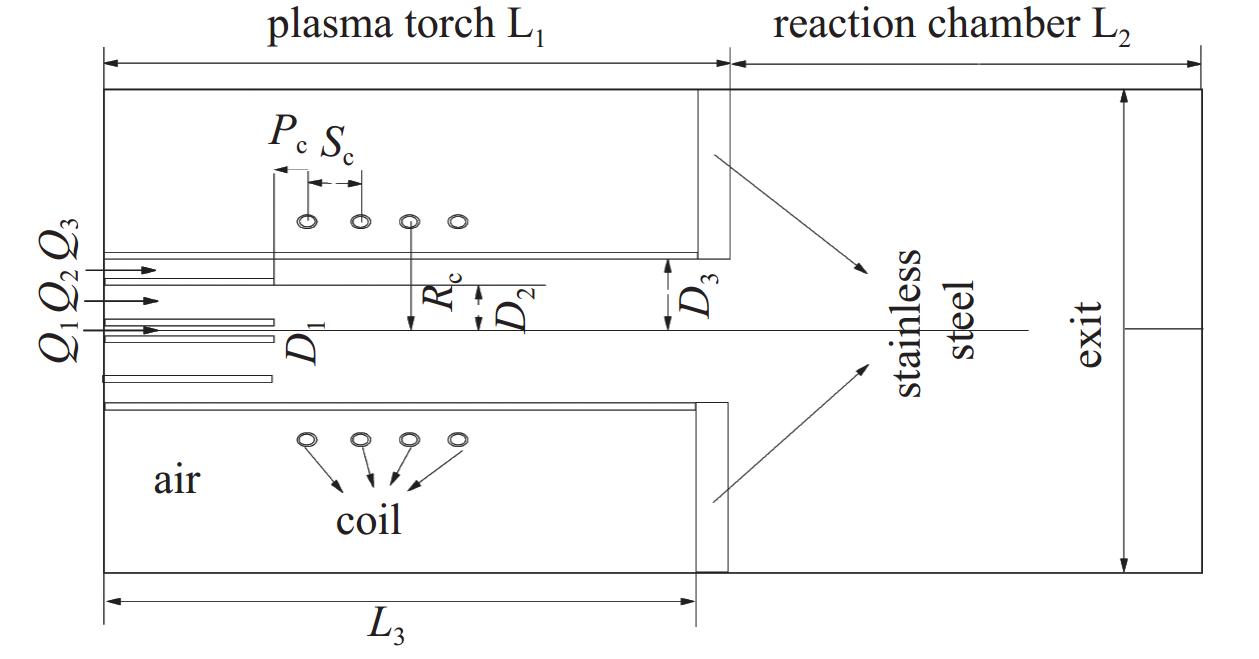
本文使用的装置模型为核工业西南物理研究院自行研制的高功率电感耦合等离子体炬，通过 Ansys Fluent商业仿真软件进行双温度数值模拟，讨论了不同的工作参数对等离子体炬内电子以及重粒子温度空间分布的影响规律。
-
根据对电感耦合等离子体的流动特性以及物理的分析，模型所采用的基本假设为：
(1)等离子体为定常的湍流流动；
(2)纯氩等离子体处于热力学非平衡状态，电子温度与重粒子温度分开计算，未考虑化学非平衡；
(3)等离子体只考虑体积辐射损失；
(4)等离子体的各项物性参数均为温度的函数。
-
可将等离子体当成具有导电特性的流体，柱坐标(r-z)系下的磁流体动力学方程组(MHD)[18-19]:
质量守恒方程：
动量守恒方程：
电子能量守恒：
重粒子能量守恒方程：
磁矢量势方程：
上述方程中σ为等离子体的电导率、ρ为密度、μ为粘滞系数、cp为常压下的比热容、λe为电子热导率、λh为重粒子热导率（以上数据均为Murphy 教授提供）。
u和v分别表示轴向及径向的速度分量，μ0为真空的磁导率，ω为角频率，Jc电流密度[20]；Te与Th分别为电子温度与重粒子温度，kB为玻尔兹曼常数，角向电场
$ {E}_{\theta }=-i\alpha {A}_{\theta } $ ；Fz代表洛伦兹力(Lorentz force)的轴向分量，Fr代表洛伦兹力的径向分量，两者与磁矢位Aθ的系为：在能量守恒方程中，Ur表示体积辐射损失，在建立双温度模型时，体积辐射损失可以表示为电子中性自由辐射、电子自由辐射和线辐射的和[15]
式中
$ {\hat n_e} $ 为1020 m−3,$ {\hat n_a} $ 为1024 m−3 。式中mj为重粒子质量、me为重粒数密度 、ne为电子，式中未考虑粒子间的非弹性碰撞[21]。
-
标准k-ε方程
其中k、ε分别为湍流的动能与耗散率，G为动能的产生率；
$ {\mu _t} = \rho {C_\mu }{k^2}/\varepsilon $ 是湍流粘度。采用的湍流模型常数为Cμ=0.09、C1=1.44、C2=1.92、σk=1.0、σε=1.30以及σt=0.85。 -
本文主要使用Fluent软件对以氩气为反应气体的电感耦合等离子体炬进行双温度数值模拟，图1为等离子体炬的装置结构示意图。将计算得出的温差比值Theta (Te/Th)、电子温度(Te)下等离子体各输运参数以及MHD方程的各源项编写成C++代码，然后通过用户自定义函数(UDF)技术将代码写入到Fluent的求解器中，用 SIMPLE算法进行求解，数值模拟时的边界条件如下所示。
(1)等离子体炬入口的边界条件：
Te=Tk=300 K，v=0；
湍流动能与耗散率的计算式为：
(2) 不锈钢壁及陶瓷管壁:
(3)中心轴:
(4)出口:
-
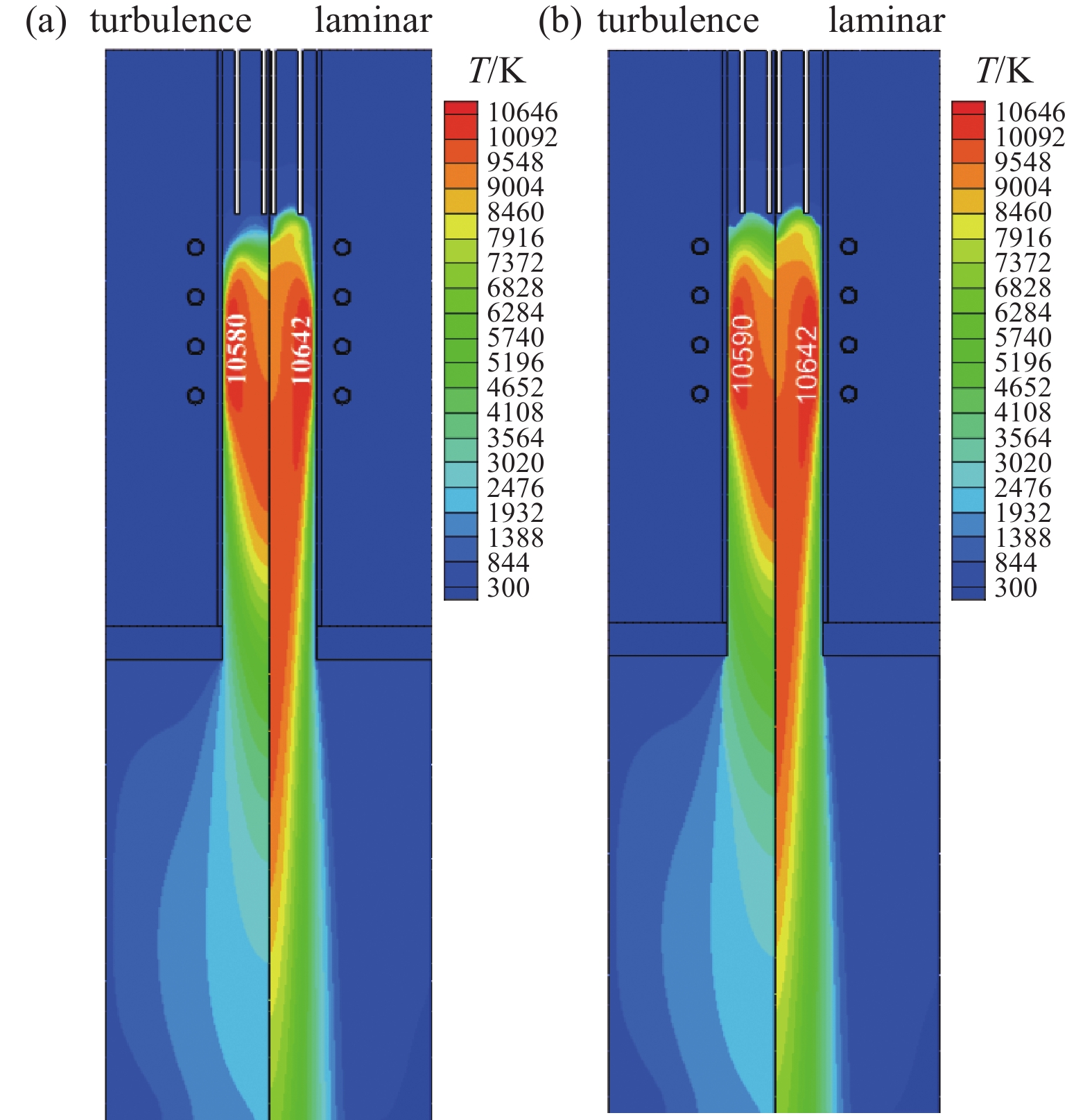
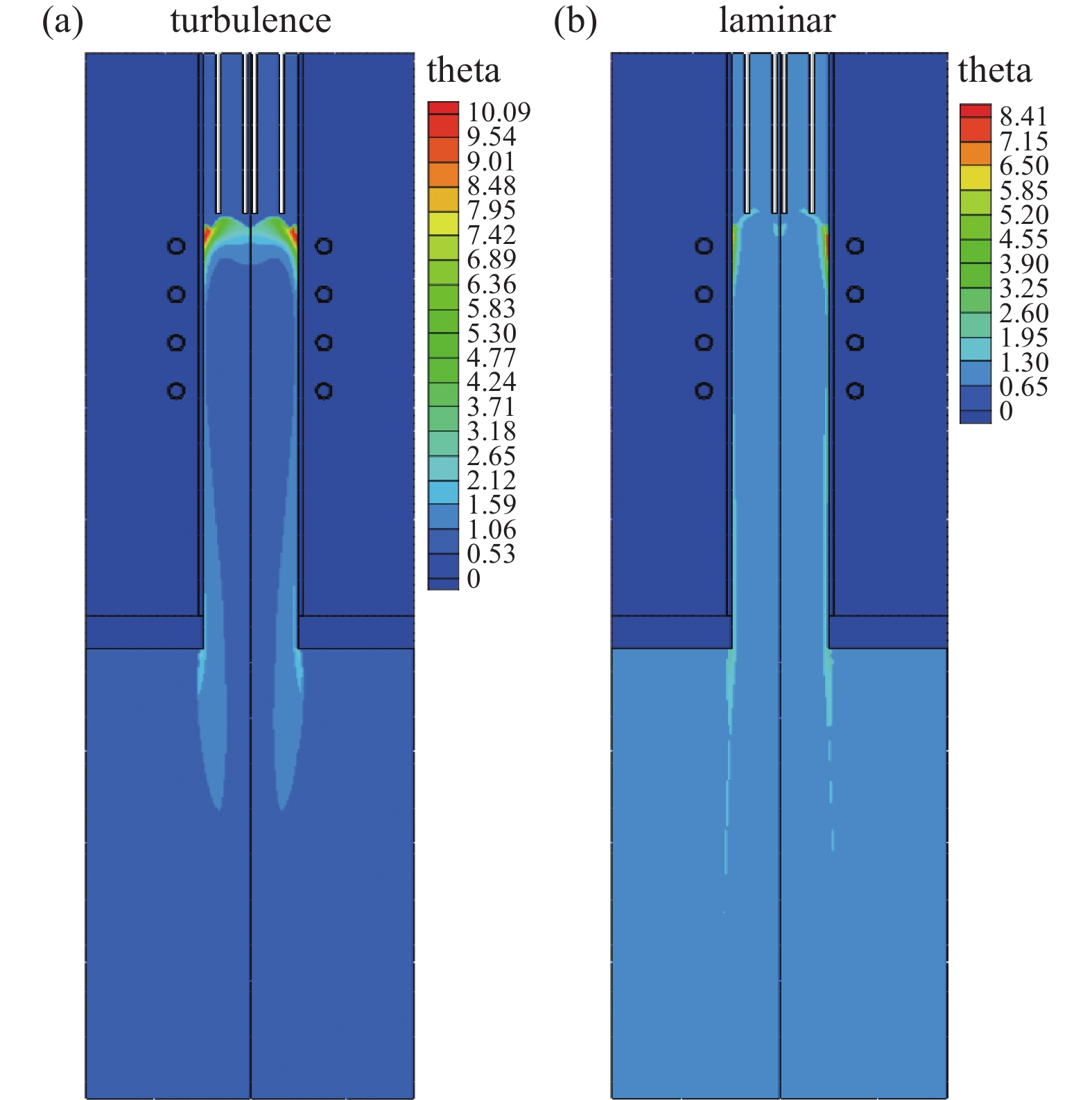
首用讨论了湍流与层流两种不同模型的对等离子体炬内电子温度与重粒子温度分布的影响。Q1为粉末携带气流量， Q2为反应气流量， Q3为冷却气流量，分别设置为0.05 m3/h，0.1 m3/h以及 4 m3/h，同时根据实验数据将等离子体炬的功率设置为60 kW是一个较为理想的数据，其余参数均不做改变，模拟结果如图2所示，分别给出了湍流模型与层流模型的电子与重粒子温度分布的对比。可以看出湍流模型比层流模型得到的高温弧区的面积更小，等离子体的温度也更低，其中在等离子体炬入口的位置电子与重粒子温度的空间分布有较大的差异。从图3可以看出双温度等离子体非平衡区域主要在等离子体炬入口位置，特别是靠近冷却气出口的位置会出现温差的极大值、沿着陶瓷管壁以及等离子体炬出口的位置。层流模型的温差(Theta)的极值和径向的范围更小，可以看出湍流与层流模型结果有明显的差别，因此有必要对更符合实际应用的湍流模型进行数值模拟研究。
-
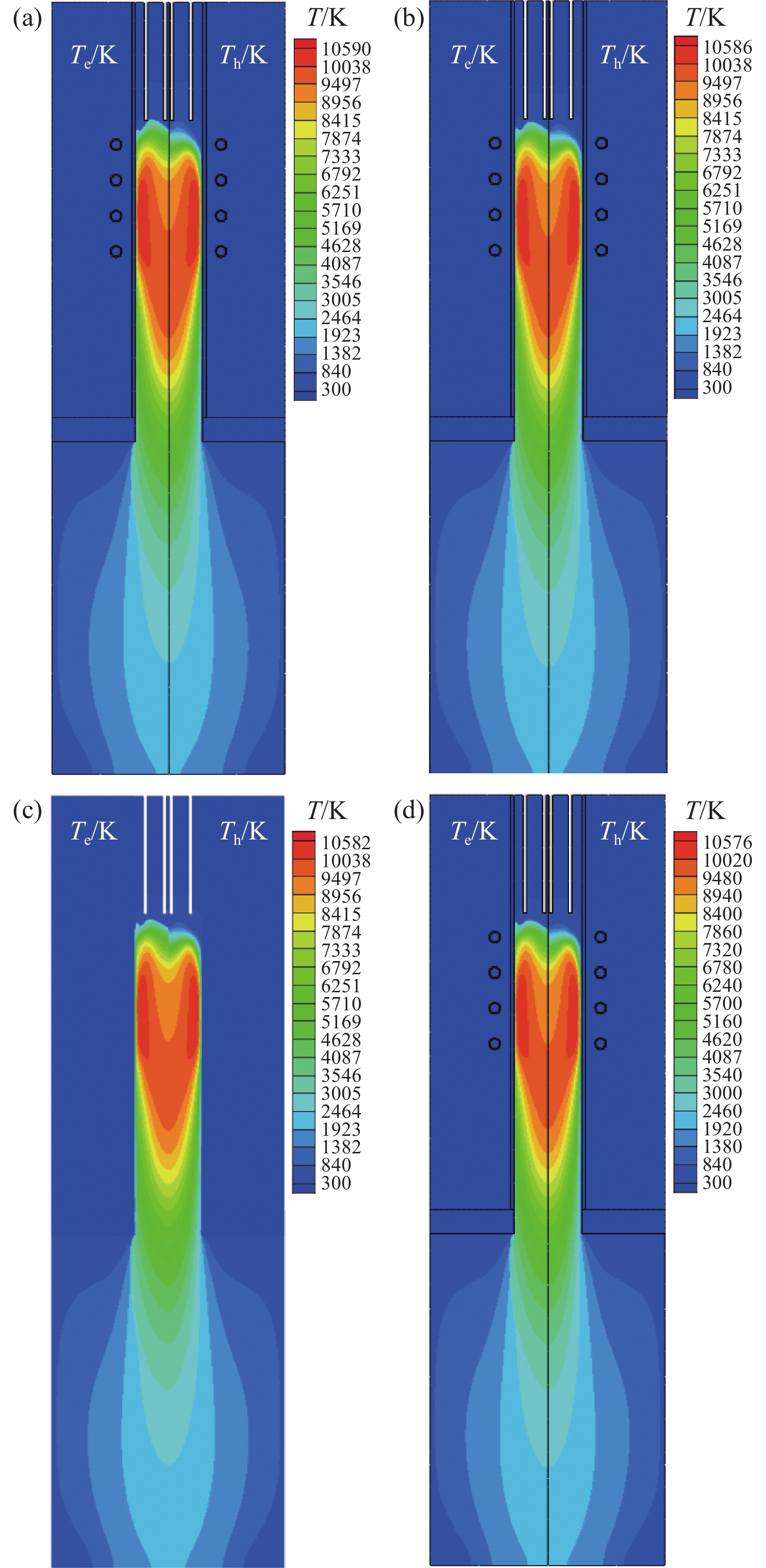
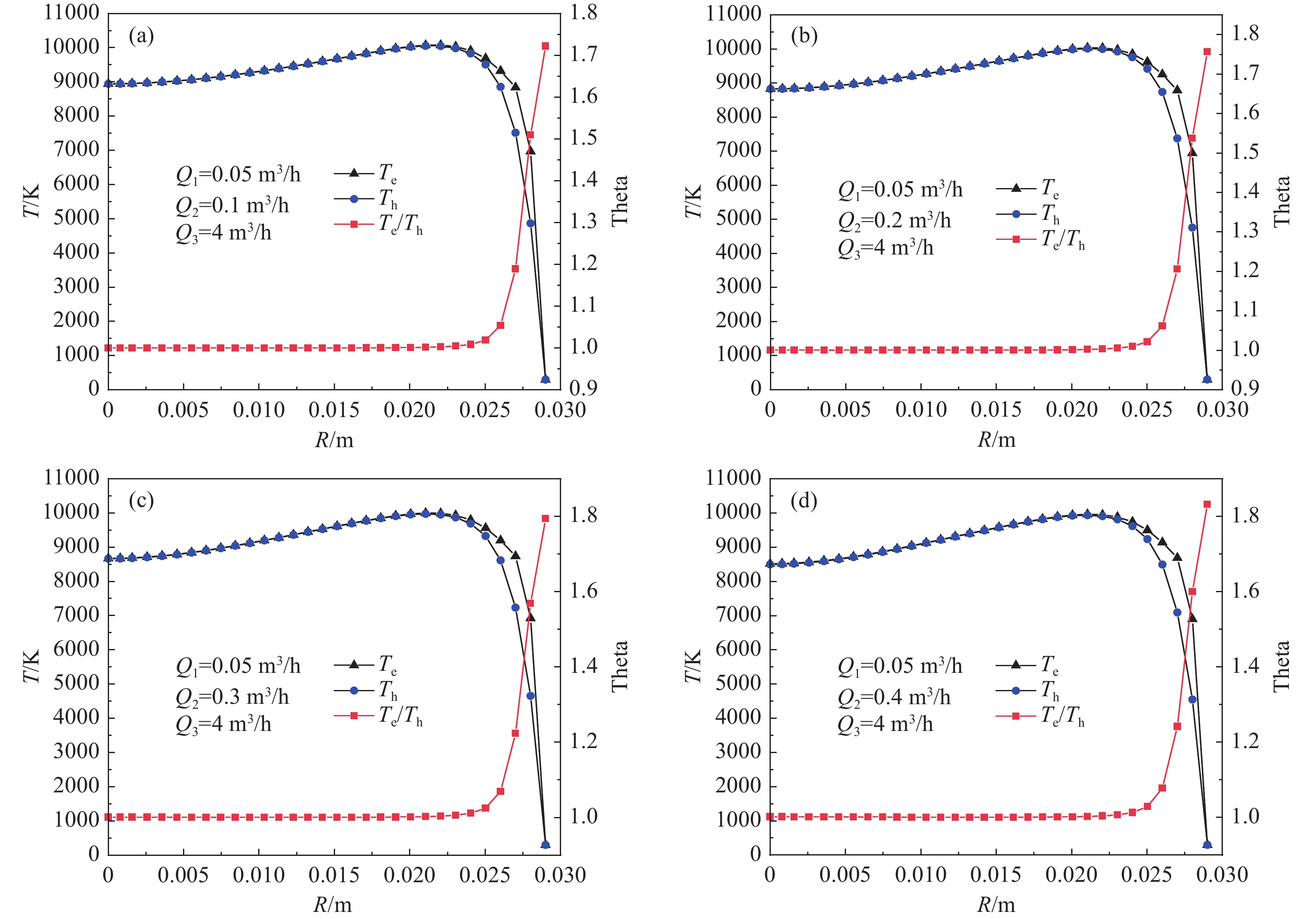
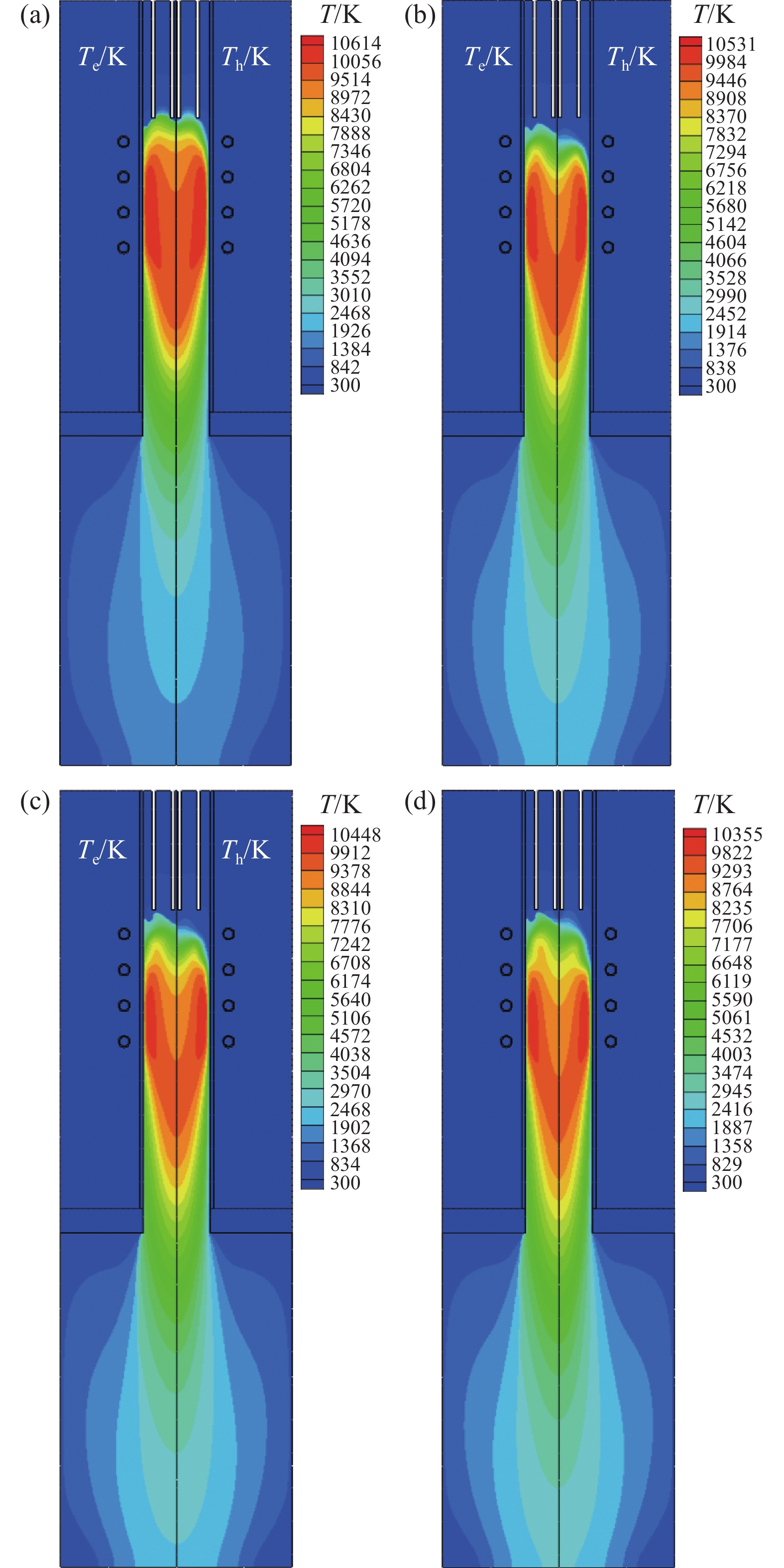
模拟当Q1设置为0.05 m3/h， Q3为 4 m3/h，功率为60 kW，其余参数均不做改变时，反应气体积流量Q2取值在0.1~0.4 m3/h范围内变化时等离子体炬的电子与重粒子温度分布。模拟得到的电子和重粒子温度云图以及第二匝线圈(z=0.15 m)处的径向温度以及差值如图4~5所示。
从图4中可以看出，在等离子体射流的中心区域，电子温度与重粒子温度几乎相等，符合热平衡(LTE)的假设，但是在等离子体射流边缘区域，特别是在陶瓷管壁附近以及等离子体炬出口位置，电子温度明显高于重粒子温度，出现了热非平衡(NLTE)
的现象。随着反应流量的加大，电子温度和重粒子温度反而逐渐降低，等离子体弧区出现沿着中心轴向下移动的现象，在反应流量达到0.3 m3/h时，电子与重粒子弧都已经被吹离了粉枪位置。在工作气体出口的位置电子温度与重粒子温度的差值在逐渐增大，非平衡的区域也在扩张,可以看到重粒子弧区比电子温度的弧区先脱离粉枪的位置。图5为第二匝线圈处的径向温度分布对比，在中心轴的位置随着气流量的增加，等离子体温度有小幅的下降趋势，但在管壁处的温差(Theta)随着反应气流量的增加逐渐增大。上述现象说明在实际应用中控制反应气体积流量是很重要的，可以小范围内改动反应气的流量，如果过度的增加，不仅会导致灭弧现象的产生[20]，还可能导热非平衡的区域与温差极值的增大。
-
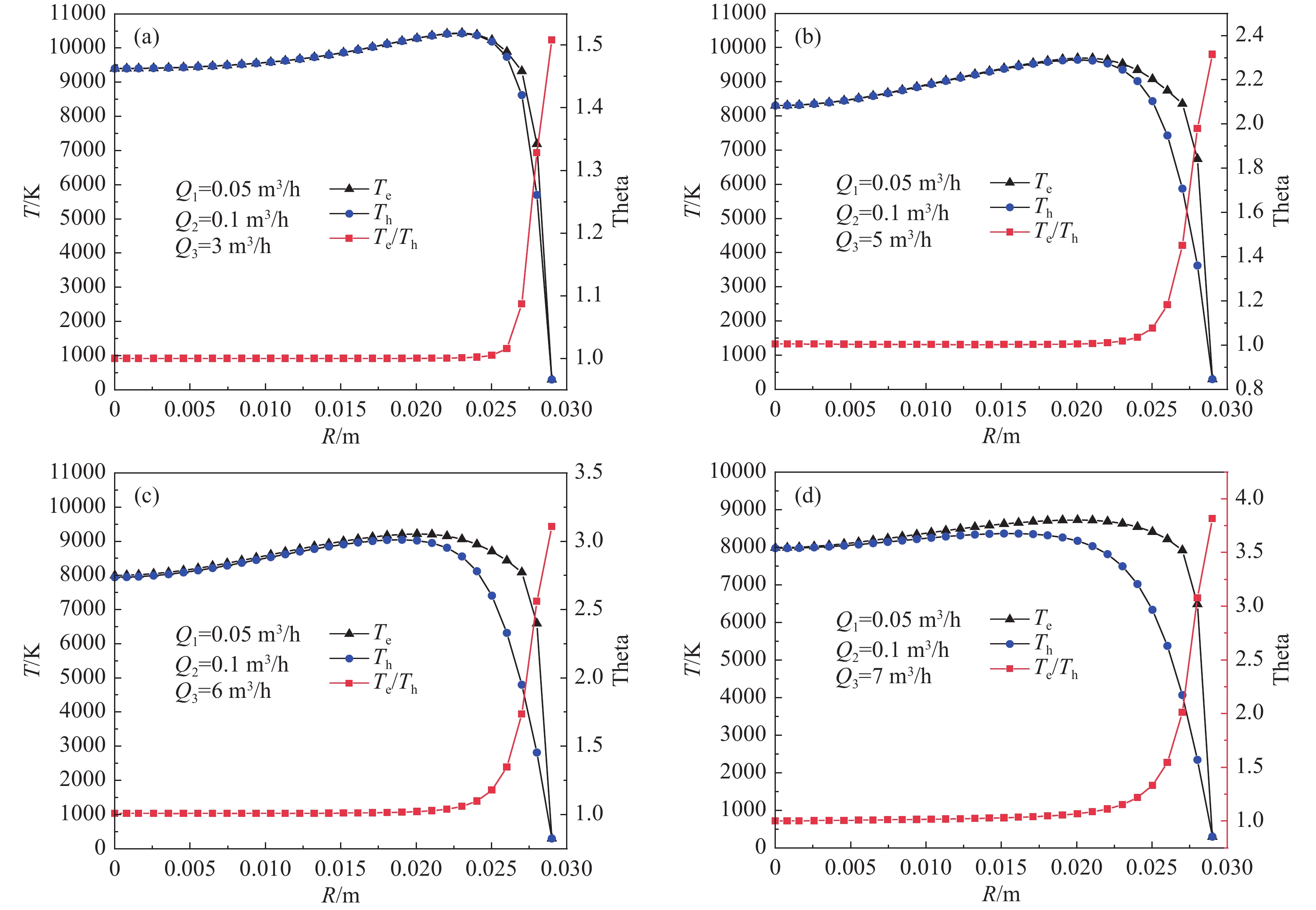
对冷却气体流量Q3在3～6 m3/h范围内变化时等离子体炬内温度的空间分布进行研究。模拟时将Q1设置为0.05 m3/h， Q2为 0.1 m3/h，功率为60 kW，其余参数均不做改变。计算得到的温度云图以及第二匝线圈(z=0.15 m)的等离子体径向温度对比分别如图7～8所示。
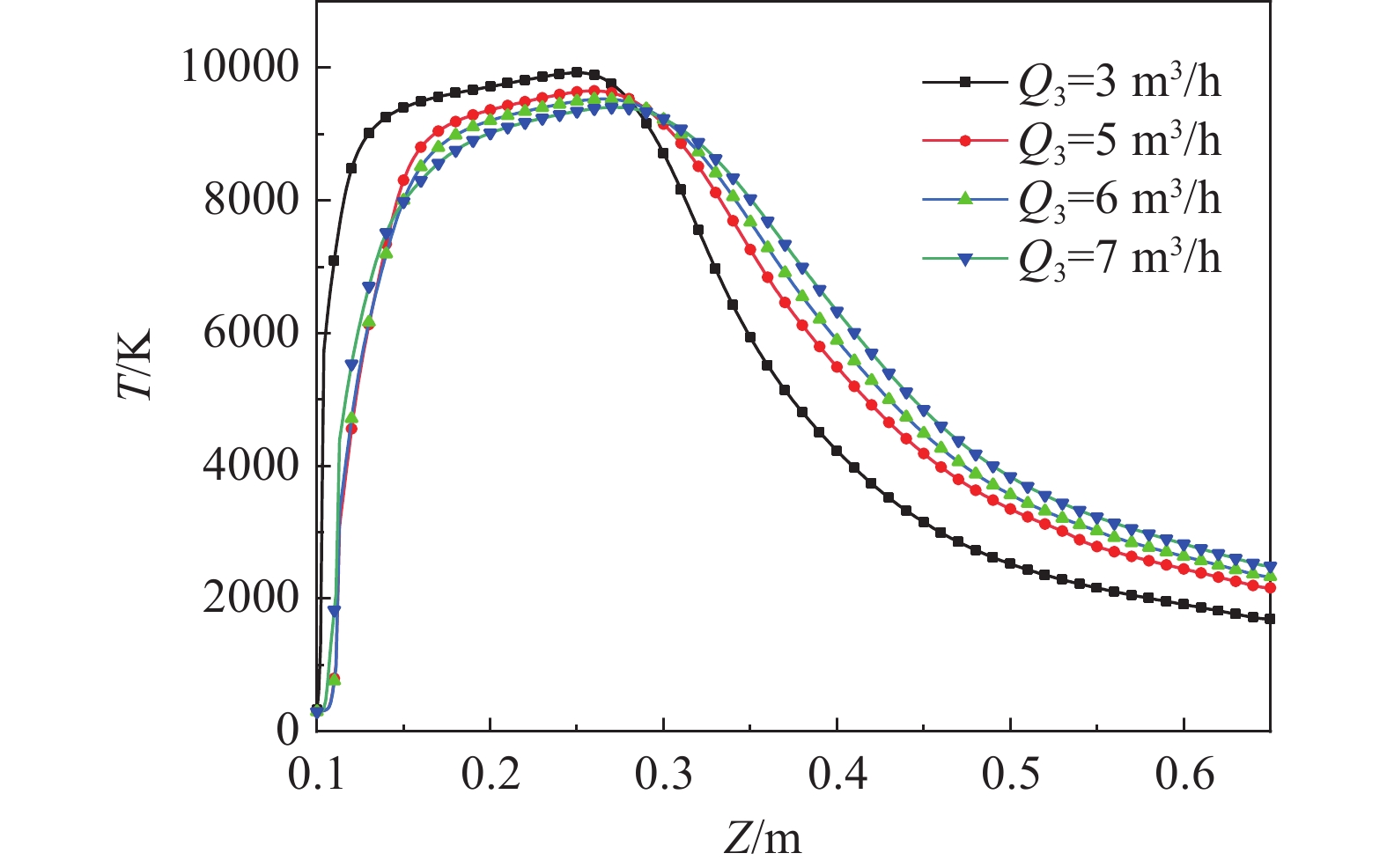
如图6所示随着不断加大冷却气体流量，在靠近等离子体炬入口处的温度快速下降，在反应室内的等离子体温度却有逐渐增大的趋势。如图7所示，随着不断加大冷却气的流量，电子温度与重粒子温度都大大降低，但等离子体射流却逐渐增长。这是由于冷却气流的增大将等离子体射流向中间不断压缩，导致了上述现象的发生。在等离子体炬入口位置，电子与重粒子的温度分布出现了明显的差异，在冷却气流量达到5 m3/h时，重粒子弧区已脱离了粉枪的位置，这导致了热非平衡的面积在不断增加。
从图8可以看出，随着冷却气体积流量的增大，等离子体径向温差也在逐渐增大，且非平衡区域有向等离子体中心移动的趋势。电子温度的下降速度明显低于重粒子温度下降速度，这是由于重粒子受到冷却气流的影响导致温度迅速下降，而电子由于粒子间的碰撞而得以保持较高温度。在实际的操作中，加入冷却气是为了防止陶瓷管因温度过高而出现破裂，从而延长其使用寿命，同时如果需要较低的电子温度以及较高的等离子体流速可以通过适当增加冷却气体流量的方式实现。但如果冷却气体积流量过大可能会导致等离子体中心出现非平衡现象，这种温度的不平衡会极大影响非平衡等离子体的特性与化学反应。在材料处理领域，许多材料对于温度的变化十分敏感，可能导致材料良品率下降。
-
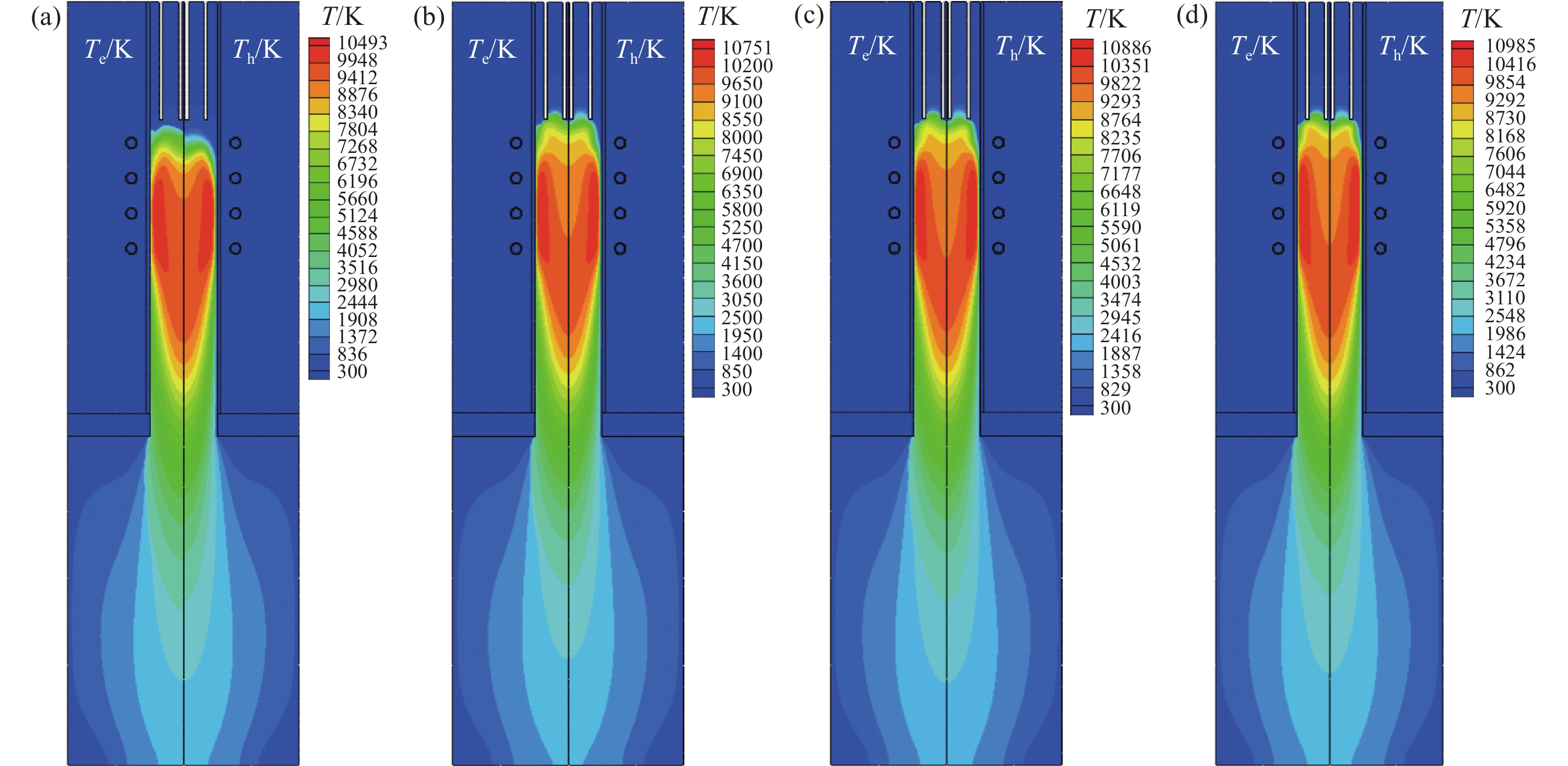
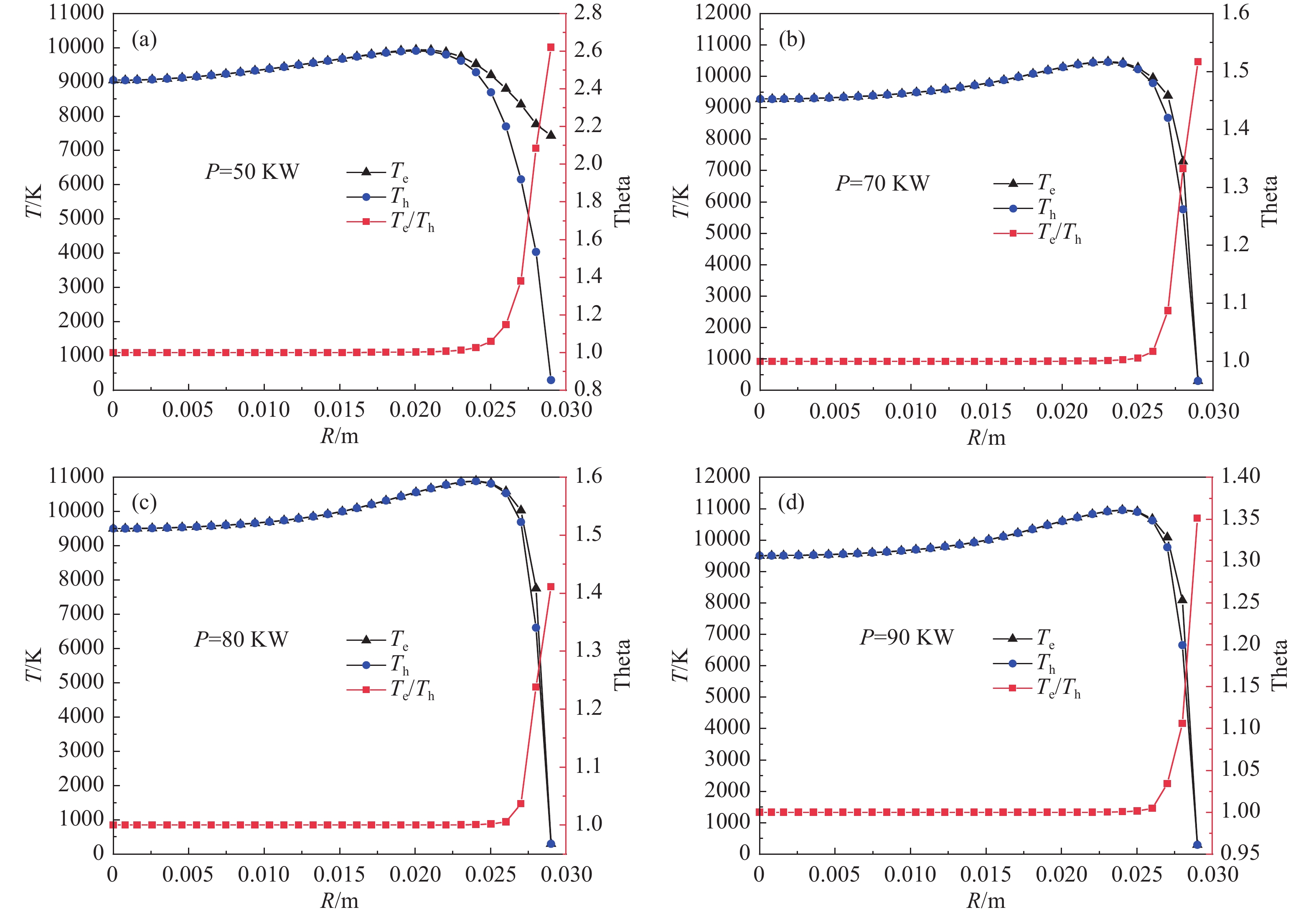
模拟在Q1设置为0.05 m3/h， Q2为 0.1 m3/h， Q3为4 m3/h，线圈功率在50～90 KW变化，其他参数不变时对双温度等离子体炬内部温度分布的影响。
从图9和图10的计算结果可以发现，加大线圈的功率会使电子和重粒子核心区域温度显著增大，等离子体的面积也会沿着轴向和径向扩大，在第二匝线圈处非平衡区域以及温差(Theta)有所减小。其可能的原因是随着线圈功率的增大会导致电子与重粒子的碰撞更频繁与充分，从而使得两种粒子的温度变得接近。在等离子体炬入口的位置，电子与重粒子的温度分布也与功率为50~60 KW（其他条件相同）时有明显差别，重粒子温度的分布更加靠近气体进口的位置，温差(Theta)也有所减小，而功率由70~90 KW电子与重粒子温度明显增大，但空间分布变化并不明显。因此在材料加工时可以适当的提高线圈的功率使得到的等离子体非平衡区域减小。
-
(1)双温度电感耦合等离子体在中心区域满足热平衡，而在远离中心的区域，呈现出热非平衡的现象，产生非平衡现象的区域主要是等离子体炬入口附近、陶瓷管壁附近以及等离子体炬出口附近，其中靠近冷却气出口的位置是Theta(Te/Th)的极大值。
(2)反应气流量的增加会对温度分布造成一定的影响，不仅会将等离子体吹离粉枪区域，造成灭弧的现象，还会使等离子体电子温度与重粒子温差加大，在等离子体炬入口的位置非平衡现象更为明显，Theta (Te/Th)的极值也会增加。
(3)冷却气流量的增加会导致等离子体温度快速降低，陶瓷管边沿温度下降，对延长装置的使用寿命有较好的效果，但是流量的增加也会导致在冷却气体出口的位置Theta (Te/Th)的极值快速增加，非平衡区域向等离子体中心扩张。
(4)线圈功率的增加会使等离子体温度快速上升，同时等离子体会沿着轴向和径向扩张，Theta (Te/Th)的极值则会逐渐下将，非平衡区域有所减小，特别是由60 KW提升到70 KW时变化最为明显。
高功率电感耦合等离子体双温非平衡数值模拟
Numerical Simulation of Two-Temperature Non-Equilibrium for High Power Inductively Coupled Plasmas
-
摘要: 湍流是等离子体在实际工作中的一种常见现象，为了研究湍流模型对等离子体炬内温度空间分布的影响，建立了一个双温度(2T)的热非平衡模型，并将其用于对湍流条件下的电感耦合等离子体(ICP)的数值模拟。通过改变注入反应气和冷却气流量以及输入功率等参数，讨论了不同的工作条件下等离子体的电子温度和重粒子温度的空间分布。研究结果表明：湍流与层流模型的模拟结果有显著的差别，过高的反应气流量会造成灭弧现象，等离子体炬入口处非平衡现象会更加明显；而加大冷却气流量会使整体的等离子体温度快速下降，非平衡区域有向等离子体中心扩张的趋势；加大线圈功率会使等离子体温度快速上升，非平衡区域有所减小，在等离子体炬入口处表现最为明显。该数值模型有助于确定产生所需等离子体的最佳条件。Abstract: A two-temperature (2T) thermal non-equilibrium model is established and applied to the numerical simulation of inductively coupled plasma (ICP) under turbulent conditions. The spatial distribution of electron temperature and heavy particle temperature of plasma under different working conditions is discussed by changing the flow of injected reaction gas and cooling gas and input power. The results show that there are significant differences between the simulation results of turbulent flow and laminar flow model. The high volume flow of reaction gas will cause the arc extinguishing phenomenon, and the non-equilibrium area at the inlet of the plasma torch will increase. However, increasing the volume flow of cooling gas will make the overall plasma temperature drop rapidly, and the non-equilibrium region has a tendency to expand to the plasma center. With the increase of coil power, the plasma temperature will rise rapidly and the non-equilibrium area at the inlet of the plasma torch will decrease. The numerical model helps to determine the optimal conditions for generating the desired plasma.
-
Key words:
- Inductive coupling /
- Double temperature /
- Numerical simulation /
- Argon plasma .
-
-
图 1 感应耦合等离子体发生器结构示意图
Figure 1. Structure diagram of inductively coupled plasma generator
图 2 湍流模型（左）与层流模型（右）的电子温度（Te）以及重粒子温度（Th）温度分布 。（a）电子温度，（b） 重粒子温度
Figure 2. Electron temperature (Te) and heavy particle temperature (Th) temperature distributions of turbulence model (left) and laminar flow model (right). (a) Electron temperature, (b) heavy particle temperature
图 3 湍流模型（左）与层流模型（右）的Theta（Te/Th）计算结果比较。（a）湍流模型Theta值, （b） 层流模型Theta值
Figure 3. A comparison of Theta (Te/Th) calculations from the turbulence model (left) and laminar flow model (right). (a) Theta value of turbulence model, and (b) Theta value of laminar flow model
图 4 不同反应气流量Q2下等离子体电子温度（Te）以及重粒子温度（Th）分布 。（a） Q2=0.1 m3/h，（b） Q2=0.2 m3/h，（c） Q2=0.3 m3/h，（d） Q2=0.4 m3/h
Figure 4. Plasma electron temperature (Te) and heavy particle temperature (Th) distribution under different reaction gas flow Q2。(a) Q2=0.1 m3/h，(b) Q2=0.2 m3/h，(c) Q2=0.3 m3/h，(d) Q2=0.4 m3/h
图 5 不同反应气流量Q2下第二匝线圈处（轴向0.15m处）沿径向温度对比。（a） Q2=0.1 m3/h，（b） Q2=0.2 m3/h，（c） Q2=0.3 m3/h，（d） Q2=0.4 m3/h
Figure 5. Comparison of radial temperature at the second turn coil (axial 0.15m) of different reaction gas flow Q2。(a) Q2=0.1 m3/h，(b) Q2=0.2 m3/h，(c) Q2=0.3 m3/h，(d) Q2=0.4 m3/h
图 7 不同冷却气流量Q3下等离子体炬内电子温度（Te）及重粒子温度（Th）分布图。（a） Q3=3 m3/h，（b） Q3=5 m3/h，（c） Q3=6 m3/h，（d） Q3=7 m3/h
Figure 7. Distribution of electron temperature (Te) and heavy particle temperature (Th) in plasma torch under different cooling gas flow rate Q3。(a) Q3=3 m3/h，(b) Q3=5 m3/h，(c) Q3=6 m3/h，(d) Q3=7 m3/h
图 8 不同冷却气流量Q3下第二匝线圈处（轴向0.15m处）径向温度对比。（a） Q3=3 m3/h，（b） Q3=5 m3/h，（c） Q3=6 m3/h，（d） Q3=7 m3/h
Figure 8. Comparison of radial temperature at the second turn coil (axial 0.15m) of different cooling gas flow Q3. (a) Q3=3 m3/h，(b) Q3=5 m3/h，(c) Q3=6 m3/h，(d) Q3=7 m3/h
图 6 不同冷却气流量Q3下沿中心线轴向温度对比
Figure 6. Comparison of axial temperature along the center line under the flow of different cooling gases Q3
图 9 不同线圈功率下等离子体炬内电子温度（Te）及重粒子温度（Th）分布图。（a）功率P=50 KW，（b）功率P=70 KW，（c）功率P=80 KW，（d）功率P=90 KW
Figure 9. Distribution of electron temperature (Te) and heavy particle temperature (Th) in plasma torch under different coil power. (a) P=50 KW, (b) P=70 KW, (c) P=80 KW, (d) P=90 KW
-
[1] 陈熙. 热等离子体传热与流动[M]. 北京: 科学出版社, 2009: 353−378 (in Chinese) Chen X. Thermal plasma heat transfer and flow[M]. Beijing: Science Press, 2009: 353−378 [2] Boulos M I. The role of transport phenomena and modeling in the development of thermal plasma technology[J]. Plasma Chemistry and Plasma Processing,2016,36(1):3−28 doi: 10.1007/s11090-015-9660-7 [3] Kim K S, Moradian A, Mostaghimi J, et al. Synthesis of single-walled carbon nanotubes by induction thermal plasma[J]. Nano Research,2009,2(10):800−817 doi: 10.1007/s12274-009-9085-9 [4] Zhengxin Y I N, Deping Y U, Yana W E N, et al. Numerical investigation on the flow characteristics of a reverse-polarity plasma torch by two-temperature thermal non-equilibrium modelling[J]. Plasma Science and Technology, 2021, 23(9): 095402. [5] 黄勇, 刘林, 王新鑫, 等. TIG电弧等离子体双温度数值模拟[J]. 焊接学报,2018,39(10):6−10,34 (in Chinese) Huang Y, Liu L, Wang X X, et al. A two-temperature modeling of TIG arc plasma[J]. Transactions of the China Welding Institution,2018,39(10):6−10,34 [6] Boulos M I, Fauchais P, Pfender E. Thermal plasmas: fundamentals and applications[M]. New York: Springer, 1994: 56−71 [7] Mostaghimi J, Proulx P, Boulos M I. A two-temperature model of the inductively coupled rf plasma[J]. Journal of Applied Physics,1987,61(5):1753−1760 [8] Zhang W B, Lani A, Panesi M. Modeling of non-equilibrium plasmas in an inductively coupled plasma facility[C]//45th AIAA Plasmadynamics and Lasers Conference, Atlanta: AIAA, 2014: 2235 [9] Shigeta M, Atsuchi N, Watanabe T. Numerical investigation of a local oxygen injection effect on argon induction plasmas using a chemically non-equilibrium model[J]. Journal of Chemical Engineering of Japan,2006,39(12):1255−1264 doi: 10.1252/jcej.39.1255 [10] Tanaka Y. Thermally and chemically non-equilibrium modelling of Ar–N2–H2 inductively coupled plasmas at reduced pressure[J]. Thin Solid Films,2009,518(3):936−942 doi: 10.1016/j.tsf.2009.07.173 [11] Watanabe T, Sugimoto N. Numerical analysis of oxygen induction thermal plasmas with chemically non-equilibrium assumption for dissociation and ionization[J]. Thin Solid Films, 2004, 457(1): 201-208. [12] Tanaka Y. Two-temperature chemically non-equilibrium modelling of high-power Ar–N2 inductively coupled plasmas at atmospheric pressure[J]. Journal of Physics D: Applied Physics,2004,37(8):1190−1205 doi: 10.1088/0022-3727/37/8/007 [13] Lu B X, Feng Q K. Numerical simulation of thermochemically non-equilibrium inductively coupled plasmas under different operating parameters[J]. Physics of Plasmas,2018,25(9):093510 doi: 10.1063/1.5028204 [14] Ye R B, Proulx P, Boulos M I. Turbulence phenomena in the radio frequency induction plasma torch[J]. International Journal of Heat and Mass Transfer,1999,42(9):1585−1595 doi: 10.1016/S0017-9310(98)00260-9 [15] Cheng K, Chen X, Pan W X. Comparison of laminar and turbulent thermal plasma jet characteristics—a modeling study[J]. Plasma Chemistry And Plasma Processing,2006,26(3):211−235 [16] Punjabi S B, Sahasrabudhe S N, Joshi N K, et al. Comparative study of laminar and turbulent flow model with different operating parameters for radio frequency-inductively coupled plasma torch working at 3 MHz frequency at atmospheric pressure[J]. Physics of Plasmas,2014,21(1):013506 doi: 10.1063/1.4862238 [17] Chang C H, Pfender E. Nonequilibrium modeling of low-pressure argon plasma jets; part I: laminar flow[J]. Plasma Chemistry and Plasma Processing,1990,10(3):473−491 doi: 10.1007/BF01447204 [18] 陈文波, 陈伦江, 刘川东, 等. 高频电感耦合等离子体炬内速度及温度空间分布的数值计算[J]. 高电压技术,2018,44(9):3035−3042 (in Chinese) Chen W B, Chen L J, Liu C D, et al. Numerical calculation of spatial distribution of temperature and velocity in inductively coupled plasma torch[J]. High Voltage Engineering,2018,44(9):3035−3042 [19] Tanaka Y. Time-dependent two-temperature chemically non-equilibrium modelling of high-power Ar–N2 pulse-modulated inductively coupled plasmas at atmospheric pressure[J]. Journal of Physics D: Applied Physics,2006,39(2):307−319 doi: 10.1088/0022-3727/39/2/011 [20] 陈文波, 陈伦江, 刘川东, 等. 工作频率及装置结构对射频感应等离子体特性影响的数值研究[J]. 高电压技术,2019,45(1):316−323 (in Chinese) Chen W B, Chen L J, Liu C D, et al. Numerical study on influence of operating frequency and plasma torch structure on characteristics of radio-frequency-inductive coupled plasma[J]. High Voltage Engineering,2019,45(1):316−323 [21] 钱海洋, 吴彬. 直流电弧等离子体双温度化学非平衡数值模拟[J]. 核聚变与等离子体物理,2011,31(2):186−192 (in Chinese) Qian H Y, Wu B. A two-temperature chemical non-equilibrium modeling of DC arc plasma[J]. Nuclear Fusion and Plasma Physics,2011,31(2):186−192 -
计量
- 文章访问数: 176
- HTML全文浏览数: 176
- PDF下载数: 2
- 施引文献: 0