-
超快激光脉冲凭借其超短时间尺度和超宽频率范围, 成为探索和理解光与物质相互作用中快速动态过程的重要工具, 使得研究者能够捕捉到快速的物理、化学和生物过程[1–3], 例如分子中的化学反应动态、光激发下的电子运动、分子振动和能量转移等[4–7]. 在超快强场与分子的相互作用过程中, 会产生一系列有趣的非线性物理现象, 如准直[8–10]、取向[11–14]、解离[15–18]、阈上电离[19–22]、非次序双电离[23,24]、高次谐波生成[25–27]和强场光电子全息 [28–30]等. 随着激光技术的快速发展, 尤其是飞秒激光和阿秒激光的出现, 可以在极短的时间尺度上观测并操控分子内部的动态过程[31,32]. 超快强场控制分子解离的研究是现代物理和化学领域中的重要课题之一, 涉及到量子力学、分子动力学以及激光技术的融合.
分子解离是指分子在外部能量(如激光场)的作用下, 发生原子间的分离, 形成自由原子或更小的分子片段. 解离过程可以是直接的, 如通过吸收激光能量而导致的瞬间解离[31], 也可以是通过激发到不稳定状态然后自发解离的方式[33]. 超快强场调控分子解离主要可以分为时域控制和频域控制两大类. 时域控制主要通过调节激光脉冲的持续时间、强度和延迟来影响分子的激发态, 从而实现对分子解离路径和产物的控制[34,35]. 频域控制则侧重于激光频谱的调控, 激光脉冲的频率成分可以表示为其时间域信号的傅里叶变换. 具体来说, 可以通过以下数学表达式来表示含时激光脉冲场
$ \mathcal{E}(t) $ 的频谱特征:这里
$ \mathcal{A}(\omega) $ 为谱振幅,$ \phi(\omega) $ 为谱相位[36–40]. 改变激光脉冲的频谱宽度可以影响分子的解离动态, 宽频谱激光能激发多重能级, 促进复杂的解离机制, 而谱相位调控可以使得不同频率成分之间相互干涉, 从而影响能量转移和分子解离的选择性[41–43]. 谱相位分布刻画了脉冲中不同频率成分之间的相对相位差. 若保持谱振幅不变, 改变激光脉冲的谱相位, 其时间轮廓发生改变. 从能量角度看, 仅由谱相位调制超短脉冲整形技术并不改变脉冲的总输出能量, 而是改变脉冲的能量分布、强度和形状, 因而对研究光与原子分子相互过程中纯的量子相干和干涉效应具有独特的优势, 受到了越来越多理论和实验研究者的关注[44,45].针对最初处于基电子态本征态的孤立气相分子, 相关的解离研究主要集中于弱场极限下的单光子相干控制解离过程[46–51], 探究激光光谱相位与生成碎片信息之间的关系. 多个研究结论表明, 在长时间极限下, 各种可观测量(如碎片的产量和能量分布)与激光光谱的相位无关. 这一发现对于理解分子响应的机制非常重要, 表明在某些条件下, 激光光谱的相位对最终结果的影响是有限的[52,53]. 近期也有研究突破了这一传统观点, 揭示了谱相位控制在解离过程中的重要性. 通过控制激光光谱的相位, 研究者能够在分子解离的不同阶段对反应中间体进行干预, 从而改变瞬态碎片的分布[54]. 当考虑稳态相干叠加激发时, 观察到的与固定带宽相位调制脉冲相关的相位依赖性, 进一步强调了相位对于分子动力学的重要性[55]. 这意味着, 在相干光场中, 通过适当设计相位, 可以有效控制反应过程, 不仅限于最终的产物分布, 也包括反应动态的多样性. 在极端强场的条件下, 分子的解离过程变得愈加复杂, 因此, 研究谱相位对解离碎片的影响成为了一个新的研究课题. 对于多原子分子而言, 它们具有多个振动自由度, 并且电子态与振动态之间存在复杂的相互作用, 以及多个势能面之间的非绝热耦合[56–59]. 这些因素共同构成了一个高度复杂的量子系统, 使得研究光解离反应的相干调控问题变得更加困难. 通过对初始处于基振动态的卤代甲烷分子在强场下的解离进行分析, 最近的研究发现, 在长时间极限下, 总解离概率和分支比都依赖于激光光谱相位[60]. 此外, 还有研究表明, 不同的初始态选择会导致振动模的优先拉伸, 从而优先解离特定的化学键[61]. 尽管在超快光场下关于分子解离方面的研究已经取得了显著进展, 但初始振动态、强场相位调制与分子解离动力学之间复杂关系的探索, 尤其是在多原子分子体系中, 仍面临许多未解的难题, 亟待进一步的研究与探索.
卤代甲烷(如氯仿、溴仿及其衍生物)因在紫外线(UV)辐射的作用下发生光解反应, 释放出卤素原子, 参与臭氧层的消耗反应, 成为全球气候变化和环境保护中关注的重点, 也因此成为研究光解离反应的典型模型[62–64]. 本文将以超短强紫外光诱导三态氯溴甲烷分子(CH2BrCl)为例[65–68], 研究超快强场相干调控多原子分子解离问题. 该模型包括基电子态和两个最低的激发态. 在吸收约200 nm的UV光子后, CH2BrCl分子从基电子态跃迁至激发电子态, 随后分解生成卤素原子和卤甲基自由基. 先前的研究表明, 在第一激发态相关的吸收带(
$ \tilde{\rm{A}} $ 带)中, 主要的光解产物为Br+CH2Cl [62]; 而在第二激发态($ \tilde{\rm{B}} $ 带)的吸收带中, 激发态之间的非绝热耦合促使分子从第二激发态转移至第一激发态, 导致光解产物为Cl+CH2Br [65]. 研究结果表明, 在170—180 nm波长范围内, 改变波长不会显著影响解离过程中分支比Br/Cl的比值. 而当波长大于180 nm时, 分支比Br/Cl会随着波长的增大而增大. 本文针对波长不敏感区域解离, 通过对比研究卤代甲烷分子在强场极限区域解离机理与弱场极限区域的不同, 并着重探讨不同初始振动态下, 解离概率和分支比对谱啁啾的依赖性. 研究发现, 在强场极限区域, 初始振动态的选择导致强场极限下诱导的共振拉曼散射(resonance Raman scattering, RRS)现象产生显著差异, 导致了差异化的解离总概率和解离分支比; 而在弱场极限区域, 主要是发生单光子吸收解离过程, RRS过程对解离的过程影响可以忽略. 此外, 啁啾脉冲对RRS现象的调控效果也因初始振动态而异, 这为选择性断裂Cl+CH2Br键提供了更大的可控性. 本文通过分析振动态布居变化与总解离概率及Cl/Br分支比之间的关系, 解释了如何在强场极限下通过调控啁啾参数有效调控分子解离过程. 本文的研究结果将揭示初始振动态、啁啾参数与分子解离动力学之间的内在联系, 深化对超快强场谱相位调控多原子分子解离机理的理解. -
本文考虑一个三态CH2BrCl分子模型, 来研究外场调控光解离问题. 由于考虑的激光激发时间尺度远小于分子的转动时间尺度, 并且主要考虑电子态间的共振激发, 因而由超短脉冲诱导的基电子态转动激发带来的准直和取向效应予以忽略. 进一步地, 该模型忽略C—H键高频振动的影响, 仅考虑Br—CH2, Cl—CH2两个伸缩振动自由度, 因而CH2BrCl可以简化为由Br, CH2和Cl组成的伪三原子模型. 在该模型中, Br—CH2和Cl—CH2的键长分别用
$ r_\text{b} $ 和$ r_\text{c} $ 表示. 此外, Br—C—Cl之间的固定键角$ \theta = 113. 5^{\circ} $ , 忽略弯曲振动模式的影响. CH2BrCl分子的光解离发生在基电子态a1A' 和两个最低单重态b1A'和c1A', 如图1所示. 为了方便, 本文用$ {\mathrm{S}}_{0} $ ,${\mathrm{ S}}_{1} $ ,$ {\mathrm{S}}_{2} $ 分别标记这三个态. 在外场作用下, 含时哈密顿量可以写为[60,65,66]其中,
$ m_\text{b} $ ,$ m_\text{c} $ ,$ m_\text{h} $ 分别表示振动模Br—CH2, Cl—CH2, CH2的约化质量, 表示为这里,
$ M_{\rm{Br}} $ ,$ M_{\rm{Cl}} $ 和$ M_{\rm{CH_{2}}} $ 分别表示Br, Cl原子的质量(这些原子的平均原子质量)和自由基CH2的质量. 对角元$ V_{ij}(r_\text{b}, r_\text{c})(i=j) $ 表示电子态$ {\mathrm{S}}_{0} $ -$ {\mathrm{S}}_{2} $ 非绝热势能面,$ \mu_{ij}{(r_\text{b}, r_\text{c})}(i=j) $ 表示电子态$ {\mathrm{S}}_{0} $ -$ {\mathrm{S}}_{2} $ 的固有偶极矩; 非对角元$ V_{ij}(r_\text{b}, r_\text{c})(i\neq j) $ 描述交叉电子态$ {\mathrm{S}}_{1} $ 和$ {\mathrm{S}}_{2} $ 之间的非绝热相互作用,$ \mu_{ij}{(r_\text{b}, r_\text{c})} (i \neq j) $ 表示$ {\mathrm{S}}_{0} $ 与$ {\mathrm{S}}_{1} $ ,$ {\mathrm{S}}_{2} $ 之间的跃迁偶极矩. 假设分子预定向, 即Cl—C—Br原子位于实验室坐标系的XZ平面, 并且C—Br键平行于Z轴, 则跃迁偶极矩$ \mu_{ij}{(r_\text{b}, r_\text{c})} $ 有两个非零的分量$ \mu_{ij}^x{(r_\text{b}, r_\text{c})} $ 和$ \mu_{ij}^z{(r_\text{b}, r_\text{c})} $ . 本文考虑激光场极化方向与Z轴平行(即平行C—Br矢量), 因此, 在后续计算中, 仅考虑跃迁偶极矩$ \mu_{01}^z{(r_\text{b}, r_\text{c})} $ 和$ \mu_{02}^z{(r_\text{b}, r_\text{c})} $ , 其余偶极矩项均设为零. 由于计算复杂度的限制, 只对Franck-Condon (FC)区域, 即$ 1. 86 \;\text{Å} \leqslant r_\text{b}\leqslant 2. 05 \;\text{Å} $ 以及$1. 68\; \text{Å} \leqslant r_\text{c}\leqslant 1. 88 \;\text{Å}$ 的偶极矩采用从头计算的方式获得; 对于FC区域外的跃迁偶极矩, 采用FC区域边界上从头计算值代替[65,66].本文考虑激光脉冲谱振幅具有高斯分布, 且谱相位可用二次函数描述. 则相应的含时激光场
$ \mathcal{E}(t) $ 可表示为式中,
$ \mathcal{R} $ 表示取实数部分;$ \mathcal{A}_{0} $ ,$ \omega_0 $ ,$ \Delta\omega $ 和$ \beta_0 $ 分别表示频谱的强度(振幅)、中心频率、带宽和啁啾率. 可以发现, 脉冲能量完全由参数$ \mathcal{A}_{0} $ 和$ \Delta\omega $ 决定, 与光谱相位参数$ \beta_0 $ 无关. 通过计算(4)式的积分, 可以获得含时激光场为其中, 电场峰值强度
$ \mathcal{E}_0=\dfrac{\mathcal{A}_{0}}{\tau_0} $ ,$ \tau_0=\dfrac{1}{\Delta\omega} $ , 线性啁啾$ \beta =\dfrac{\beta_0}{\tau_0^4+\beta_0^2} $ , 脉冲持续时间$ \tau^2 = \tau_0^2 \Big(1 + \dfrac{\beta_0^2}{\tau_0^4}\Big) $ , 半高全宽$ \tau_{{\mathrm{FWHM}}}=\tau_0\sqrt{8 \ln 2} $ .本文通过兰索斯代数方法[69–71]获得基电子态不同振动态
$ |\nu'\nu''\rangle $ 的本征函数$ \varphi_{\nu'\nu''}(r_{\text{b}},r_{\text{c}}) $ . 数值计算中将两个振动坐标空间划分为$ 512\times 512 $ 份网格, 所用的空间步长为0.01 Å. 通过使用快速傅里叶变换技术和分裂算符方法对不同振动态波函数进行含时演化[72], 获得第i ($ i=\text{S}_0, \text{S}_1, \text{S}_2 $ )个态的含时波函数$ \varPsi_i(r_\text{b}, r_\text{c}, t) $ , 所用的演化时间步长为0.01 fs, 对应的收敛精度为10–3水平. 边界处可能引入的非物理效应通过引入吸收函数来予以消除[33]. 基电子态上振动态的含时布居及各电子态的含时布居可以计算如下[60,66]:利用时间积分通量方法计算激发电子态上Br+CH2通道和Cl+CH2通道的解离概率为[60,66]
和
式中通量算符
$ \hat{J_{k}}(k=\text{b}, \text{c}) $ 为其中,
$ \hat{p}_{k} $ 是第k个振动模的动量算符,$ m_{k} $ 为相应的约化质量, 非绝热耦合区域外的渐近点选取为$ r^{\mathrm{d}}_\text{b} $ = 6.23 Å和$ r^{\mathrm{d}}_\text{c} $ = 6.05 Å. 通过以上计算, Cl和Br解离碎片的含时分支比可以定义为 -
本文将研究CH2BrCl分子的初始振动态
$ |\nu'\nu''\rangle $ 和激光脉冲谱相位$ \beta_0 $ 如何影响Br+CH2Cl和Cl+CH2Br两个解离通道的解离概率以及分支比R (Cl/Br). 在计算中, 仅考虑Br—CH2和Cl—CH2键伸缩振动模式, 选择基电子态的六个不同振动态$ |00\rangle $ ,$ |10\rangle $ ,$ |01\rangle $ ,$ |20\rangle $ ,$ |11\rangle $ 和$ |02\rangle $ 作为初始态, 选择基振动态的能量为0, 其他各个振动态的振动频率分别为575, 757, 1149, 1330, 1506 cm–1. 为保持基电子态不同振动态激发到第二激发电子态的激发能量相同, 选择的UV脉冲波长分别对应为177, 178.8, 179.4, 180.7, 181.3, 181.8, 182.5 nm. 这些参数选择避免了波长对解离概率的影响, 从而凸显非绝热交叉耦合机制在谱相位调控中的重要角色.首先对比研究了弱场极限区域(只发生单光子吸收解离且解离概率与强度呈线性关系)和强场极限区域(解离概率与强度不再呈线性关系)下变换极限脉冲(
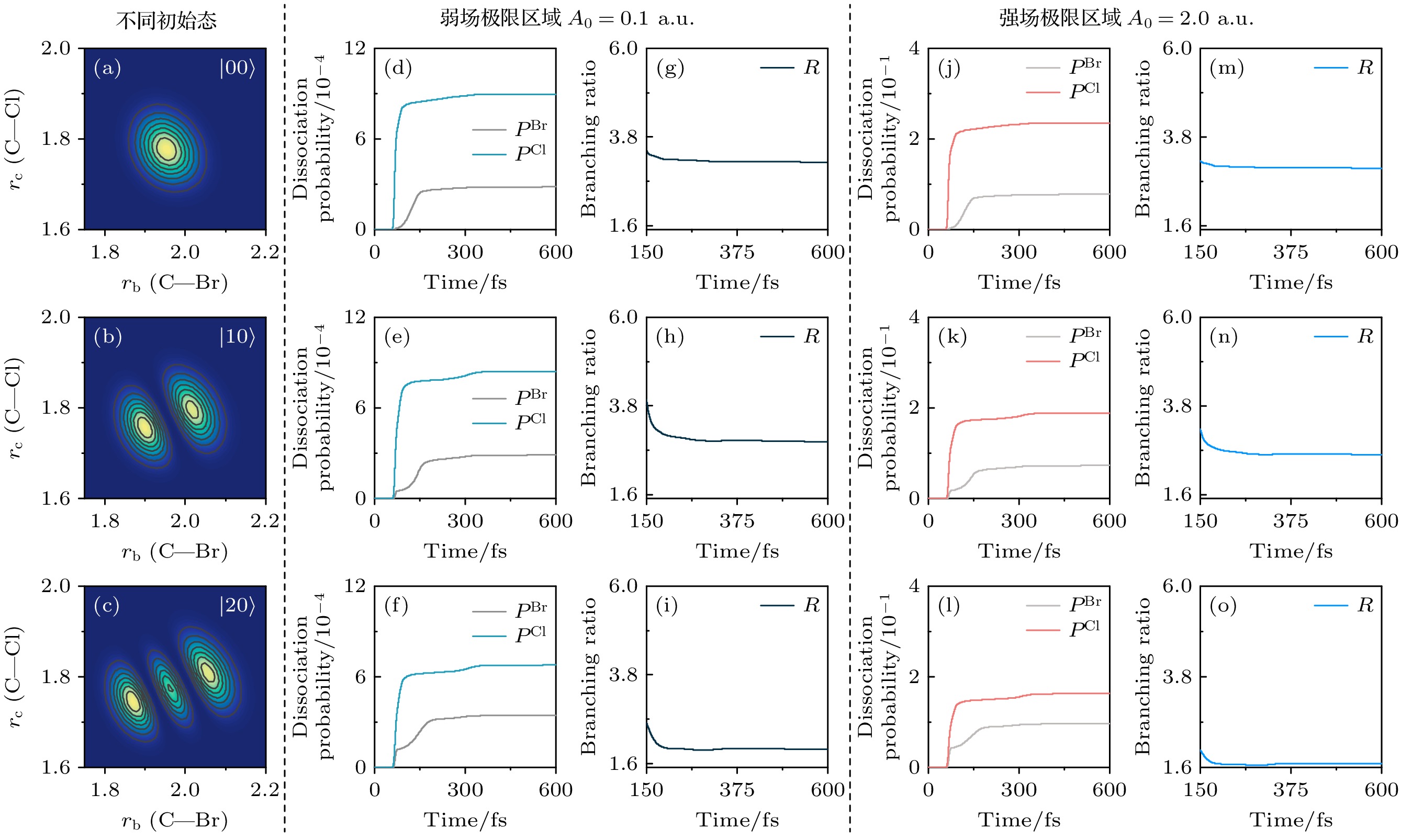
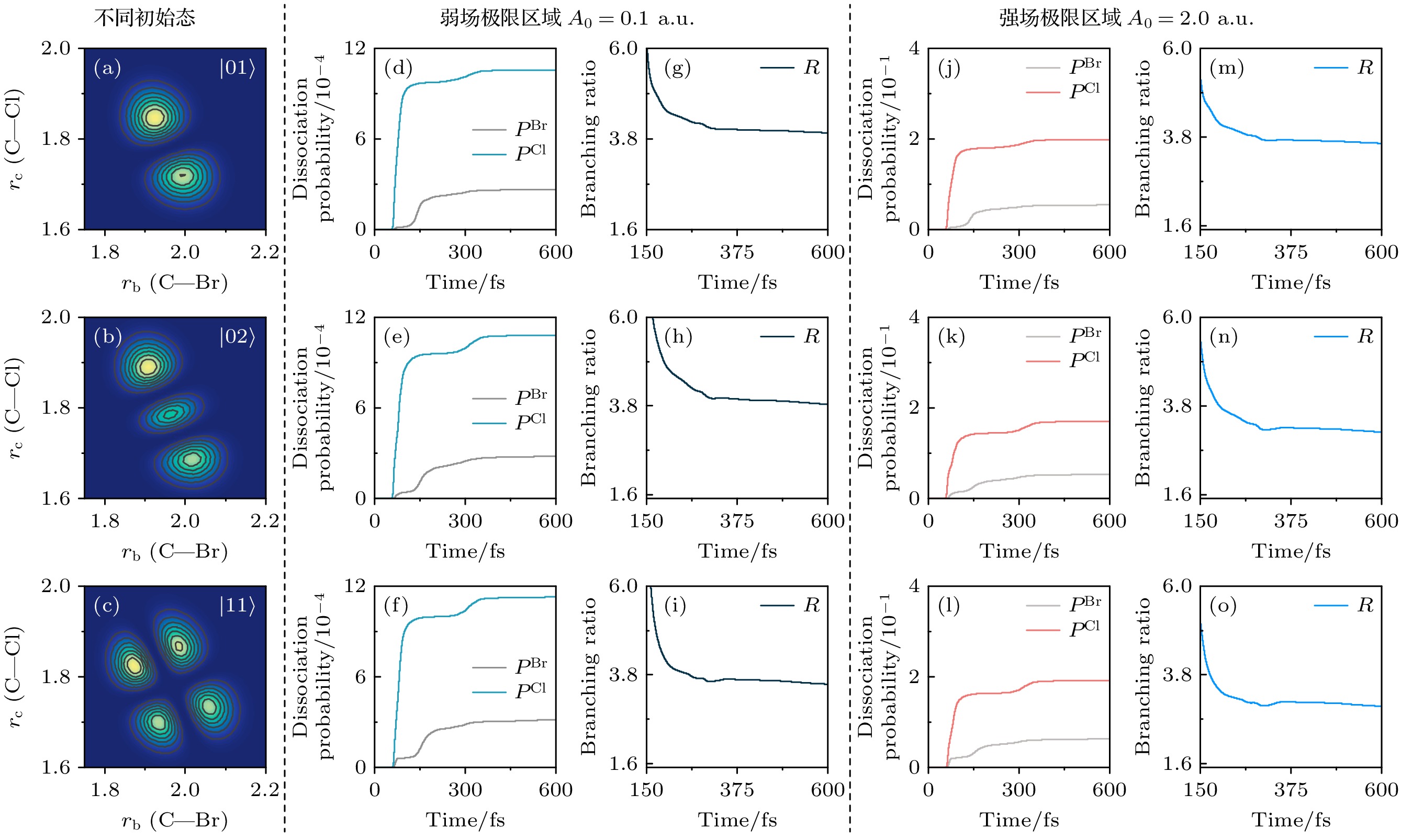
$ \beta_0 =0 $ , 也就是谱相位函数为0的脉冲)分子的解离情况. 弱场极限下的激光脉冲频谱强度为$ \mathcal{A}_{0}=0. 1\; \text{a.u.}$ , 对应的含时电场峰值强度为$ \mathcal{E}_{0}\approx0. 46\times10^{11} \;{\rm W/cm^2}$ ; 为有效避免强场电离现象, 强场极限下的激光脉冲频谱强度为$ \mathcal{A}_{0}= 2. 0\; \text{a.u.}$ , 对应的含时电场峰值强度为$ \mathcal{E}_{0}\approx1. 82\times 10^{13}\;{\rm W/cm^2} $ . 由于研究体系对应的激发态解离过程很快, (4)式选取的脉冲带宽为$ \Delta\omega=2500\;{\mathrm{cm}}^{-1} $ , 对应(5)式中$ \tau_0 = \dfrac{1}{\Delta\omega} \approx 2 \;{\rm fs}$ , 以及半高全宽为$ \tau_{\mathrm{FWHM}} = \tau_0\sqrt{8\ln2} = 5 \;\text{fs} $ . 为了研究单个振动模改变所带来的影响, 图2给出了在保持Cl—CH2振动模处于基振动态的情况下, 改变Br—CH2振动模量子数时的初始波函数密度分布、以及在弱场和强场极限下变换极限脉冲导致激发态产生的含时解离概率$ P^{\mathrm{Br}}(t) = P^{\mathrm{Br}}_{\text{S}_1}(t) + P^{\mathrm{Br}}_{\text{S}_2}(t) $ 和$P^{\mathrm{Cl}}(t)= P_{\text{S}_1}^{\mathrm{Cl}}(t)+ P_{\text{S}_2}^{\mathrm{Cl}}(t) $ , 以及对应的含时解离分支比$ R(t) $ . 从初始态波函数的分布来看, 处于更高激发振动态的Br—CH2振动偏离基态平衡位置越明显. Br—CH2的拉伸有助于Br+CH2Cl通道的解离, 同时抑制Cl+CH2Br通道的解离. 此外, 可以观察到这两种振动模式之间存在着强耦合(图2(a)—(c)). 在不同场强下, 150 fs之前的主要解离产物为Cl+CH2Br. 此后, 由于${\rm S}_1 $ 和$ {\rm S}_2$ 激发态之间的非绝热耦合相互作用, 150 fs后沿Br+CH2Cl通道的解离产物有所增强. 因此, 在相同振动态下, 150 fs后, 随着时间的增加, 解离分支比下降至稳定. 而随着Br—CH2振动模的增大, Br+CH2Cl通道的解离概率逐渐增加, 更高的激发振动态对应着更小的解离分支比. 相比于弱场极限, 在强场极限下, Br+CH2Cl通道和Cl+CH2Br通道的解离概率均有所增加, 但解离分支比却明显降低.图3给出了在保持Br—CH2振动模处于基振动态的情况下, 改变Cl—CH2振动模量子数, 以及同时改变Br—CH2和Cl—CH2振动模量子数时的初始波函数密度分布, 以及在弱场和强场极限下变换极限脉冲导致激发态产生的含时解离概率
$ P^{\mathrm{Br}}(t) $ 和$ P^{\mathrm{Cl}}(t) $ 以及解离分支比$ R(t) $ . 在150 fs附近, 解离行为与图2相似, 但在300 fs后, Cl+CH2通道的解离概率进一步提升. 由于初始态$ |01\rangle $ 和$ |02\rangle $ 对应Cl—CH2键的优先拉伸,$ |11\rangle $ 对应Br—CH2键和Cl—CH2键的共同拉伸. 这种键的优先拉伸现象使得振动态波包从非平衡位置被激发. 由于激发态势能面$ {\mathrm{S}}_2 $ 与基态$ {\mathrm{S}}_1 $ 之间存在非绝热交叉, 有利于Cl—CH2键的解离. 因此, 从非平衡位置激发到$ {\mathrm{S}}_2 $ 势能面的电子波包会在势阱中振荡. 当振荡至非绝热耦合区时, 部分电子波包会泄漏到排斥势能面$ {\mathrm{S}}_1 $ , 促进Cl—CH2键的进一步解离. 这一过程导致了Cl+CH2Br通道的解离概率在300 fs之后出现阶梯型增强的现象. 阶梯的宽度与电子波包在势阱中的振荡周期密切相关. 类似的阶梯型解离现象在NaI分子的解离过程中也有所体现[52]. 可以看到, Cl+CH2Br通道的解离概率和分支比均高于图2中各初始态对应的解离概率和分支比. 与图2类似, 相比于弱场极限, 在强场极限脉冲激发下, 两个通道的解离概率均有所增加, 但解离分支比均减小. 此外, 在强场极限下, 与$ |00\rangle $ 初始振动态相比,$ |01\rangle $ ,$ |02\rangle $ 和$ |11\rangle $ 初始振动态下Br+CH2Cl通道和Cl+CH2Br通道的解离概率均有所减少.通过以上模拟可以发现, 在变换极限脉冲与分子作用下, 不同初始振动态导致了键的不同优先拉伸方向以及拉伸程度, 从而调控了不同解离通道的优先性和解离概率, 这为选择性控制C—Cl和C—Br键的断裂提供了可能的途径. 此外, 在强场极限下, 尽管解离概率普遍增加, 但解离分支比却有所降低. 接下来, 将利用啁啾脉冲进一步研究不同强度区域及不同初始振动态对解离概率和分支比的影响.
-
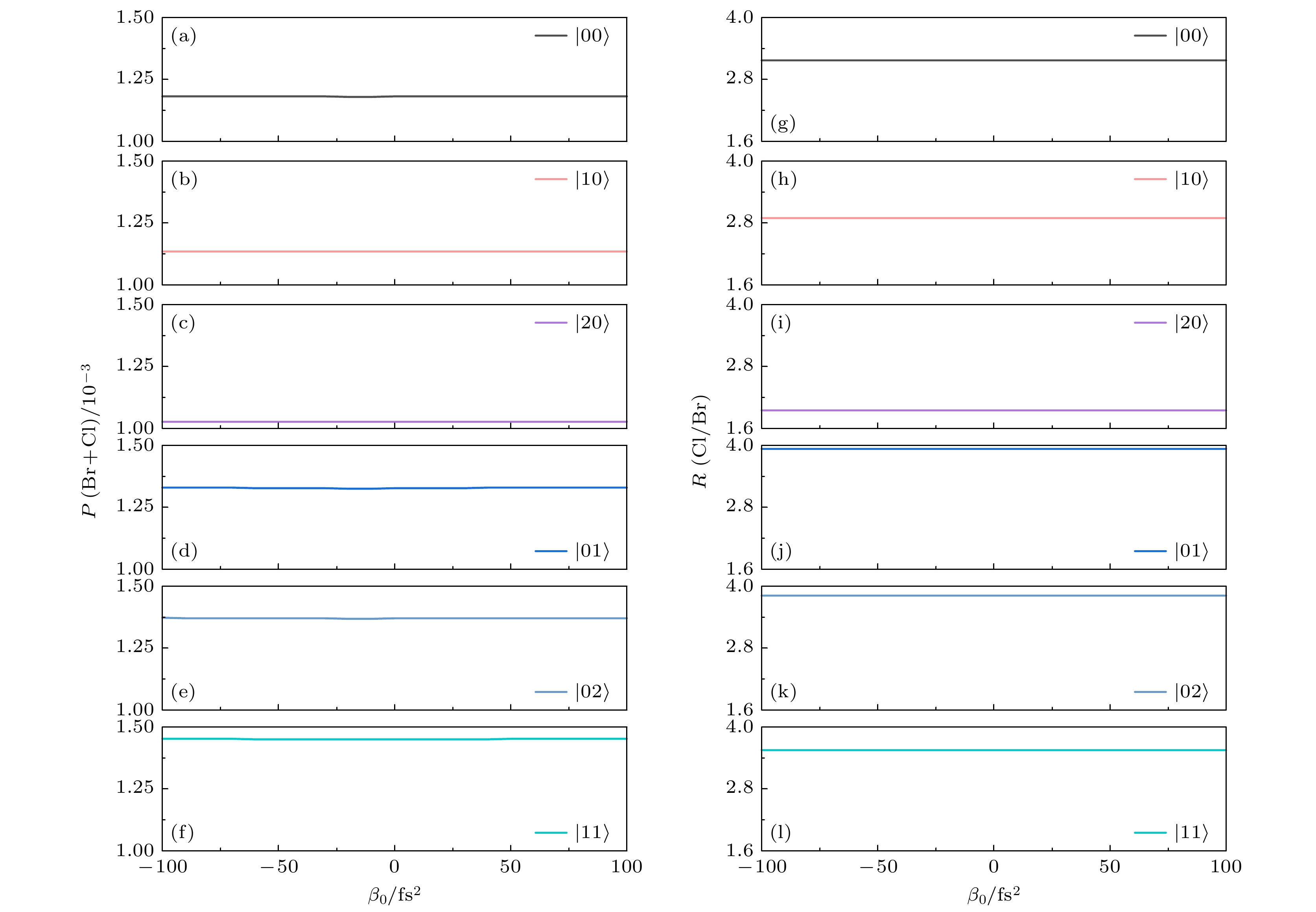
图4给出了弱场极限下
$ (\mathcal{A}_{0} = 0. 1 \; \text{a.u.} )$ 总解离概率P (Br+Cl) 和分支比R (Cl/Br) 与不同初始振动态$ |\nu'\nu''\rangle $ 以及啁啾率$ \beta_0 $ 之间的关系, 其中啁啾率$ \beta_0 $ 在–100—100 fs2范围内变化. 如图4所示, 对于变换极限脉冲, 总解离概率P (Br+Cl) 和分支比R (Cl/Br) 对初始振动态的选择表现出明显的依赖性. 与基振动态$ |00\rangle $ 相比, 当$ |10\rangle $ 和$ |20\rangle $ 振动态作为初始态时, Br—CH2的振动模量子数逐渐增大, 导致对应的总解离概率和分支比均逐渐减小; 相反, 当$ |01\rangle $ 和$ |02\rangle $ 振动态作为初始态时, Cl—CH2振动模量子数的增大导致总解离概率和分支比均增大. 值得注意的是, 分支比R (Cl/Br) 在$ |01\rangle $ 振动态作为初始态时达到了最大值. 这一现象与Cl—CH2振动模的优先拉伸密切相关; 当$ |11\rangle $ 振动态作为初始态时, Br—CH2和Cl—CH2振动模量子数同时增加, 从而导致总解离概率达到最大值, 同时分支比R (Cl/Br) 也随之增大. 这表明分子内部的振动模式对解离过程具有显著影响, 而不同振动态的选择对于研究分子解离动力学具有重要意义. 此外, 对于不同的基电子态振动态, 在长时间极限下, 改变啁啾率$ \beta_{0} $ 并不能有效调控总解离概率和分支比. 这与先前关于初始处于基电子态基振动态的双原子和多原子分子的研究结果一致[52,60]. 这些发现揭示了在弱场极限下, 啁啾率对CH2BrCl分子光解离动力学的重要影响. -
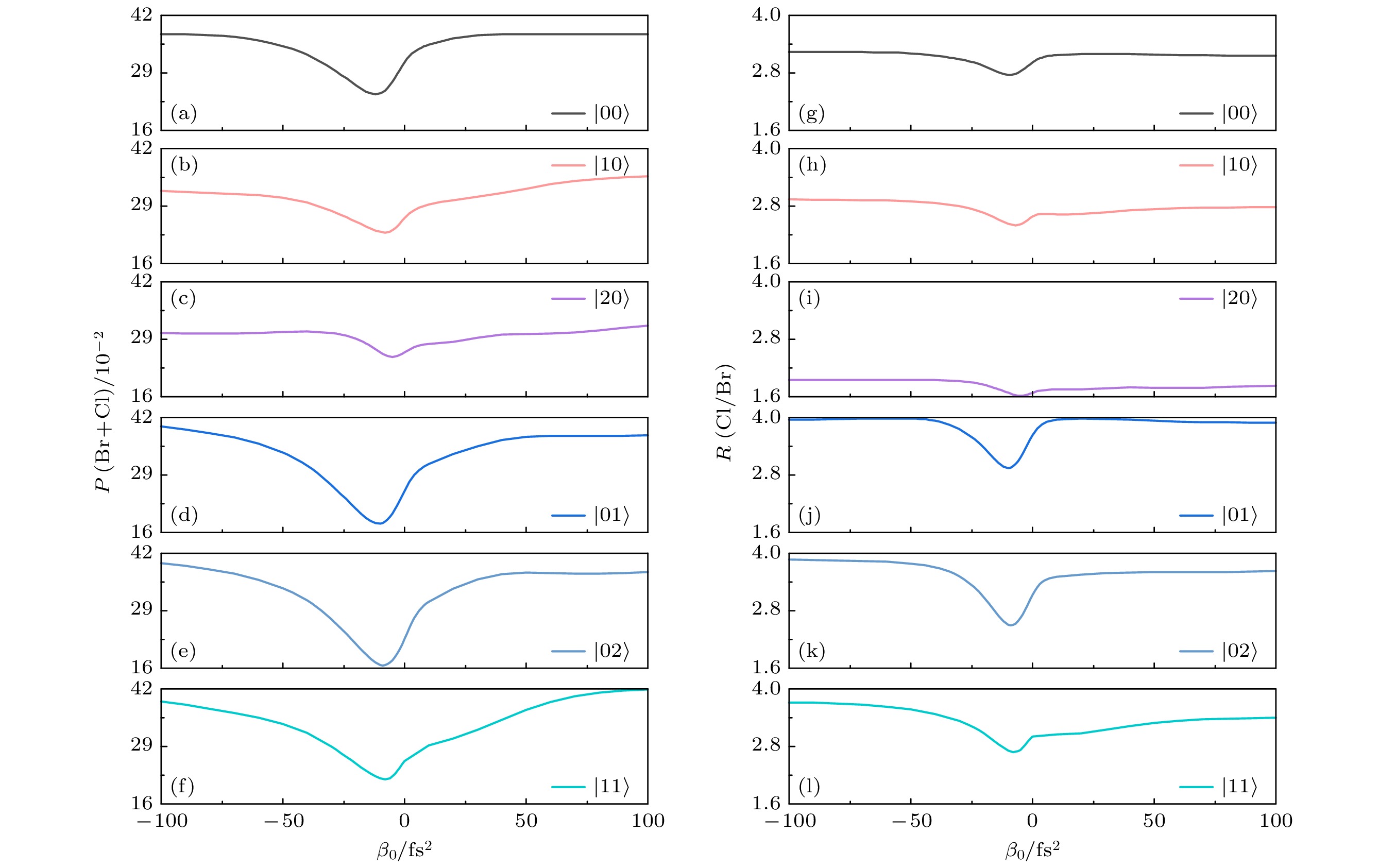
图5给出了强场极限下
$ (\mathcal{A}_{0} = 2. 0 \;\text{a.u.} )$ 不同初始振动态$ |\nu'\nu''\rangle $ 的总解离概率P (Br+Cl) 和分支比R (Cl/Br) 随啁啾率$ \beta_0 $ 的变化, 其中啁啾率$ \beta_0 $ 在–100—100 fs2范围内变化. 对于所有初始振 动态$ |\nu'\nu''\rangle $ , 相比于弱场极限, 在变换极限脉冲下, 强场极限虽然提高了分子总解离概率P (Br+Cl), 但却降低了分支比R (Cl/Br). 这表明仅仅增加变换极限脉冲的强度并不能有效提高Cl+CH2Br通道的解离概率. 相对而言, 啁啾脉冲不仅显著提高了总解离概率, 更重要的是将分支比提升至接近弱场极限的值. 因此, 啁啾脉冲有效促进了Cl+CH2Br通道的解离. 啁啾脉冲的效应也依赖于初始振动态$ |\nu'\nu''\rangle $ , 其对$ |01\rangle $ ,$ |02\rangle $ 和$ |11\rangle $ 振动态的调控效果尤为明显. 不同振动态$ |\nu'\nu''\rangle $ 对应的最佳啁啾率值及其符号各不相同. 这些结果揭示了在强场极限下, 通过调控啁啾率可以有效控制光解离过程, 特别是对于特定初始振动态. 这种调控不仅影响总解离概率, 还能调节不同解离通道的相对产率. -
为了深入理解强场极限下光解离对光谱啁啾率
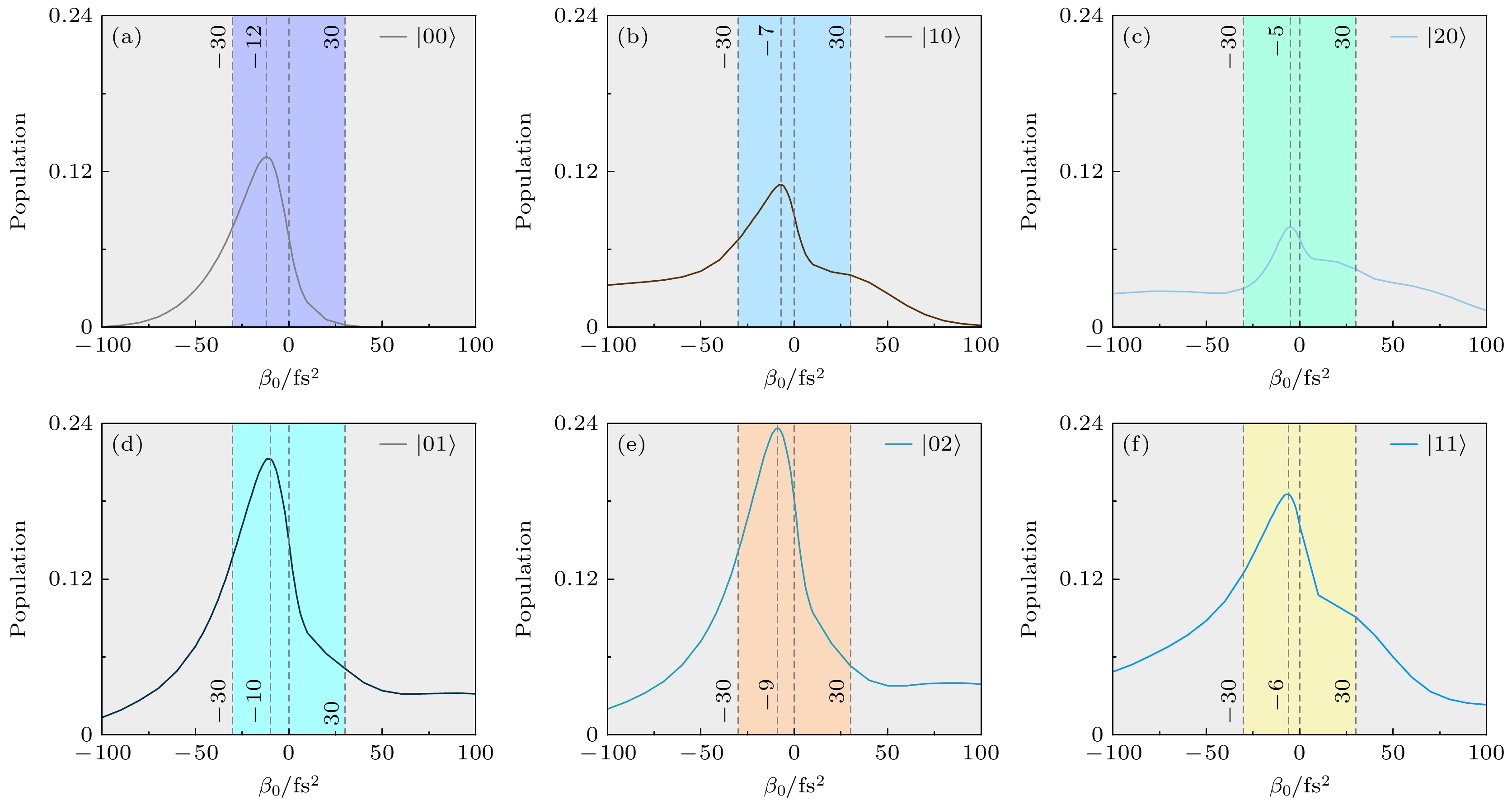
$ \beta_{0} $ 依赖性的潜在物理机制, 本节首先计算了在初始振动态$ |\nu'\nu''\rangle $ 下, 基电子态其余振动态末态布居之和$ P(t_\text{f}) $ , 定义为其中
$ P_{\nu'\nu''}(t) $ 表示初始振动态$ |\nu'\nu''\rangle $ 的含时布居,$ t = t_\text{f} $ ,$ t_\text{f} $ 为激光脉冲结束时刻. 图6给出了$ P(t_\text{f}) $ 与啁啾率$ \beta_{0} $ 之间的关系. 从图6可以看出, 在变换极限脉冲作用时,$ P(t_\text{f}) $ 显著填充, 不同初始振动态$ |\nu'\nu''\rangle $ 的布居填充程度不同. 具体来说, 当初始振动态为$ |20\rangle $ 时, 布居填充最少, 而$ |02\rangle $ 振动态作为初始态时, 布居填充最多. 通过调控啁啾率的值和符号, 可以有效地抑制或增强$ P(t_\text{f}) $ . 如图6中虚线所示, 在变换极限脉冲附近的负啁啾率处,$ P(t_\text{f}) $ 达到最大值. 对于初始振动态$ |00\rangle $ , 当啁啾率$ |\beta_0 | > 100 \;{\rm fs^2}$ 时,$ P(t_\text{f}) = 0 $ ; 对于初始振动态$ |10\rangle $ , 当啁啾率$ \beta_0 > 100 \;{\rm fs^2}$ 时,$ P(t_\text{f}) = 0 $ ; 而对于其他初始振动态$ |\nu'\nu''\rangle $ , 较大的啁啾率明显抑制$ P(t_\text{f}) $ 的大小.图7进一步给出了在不同初始振动态
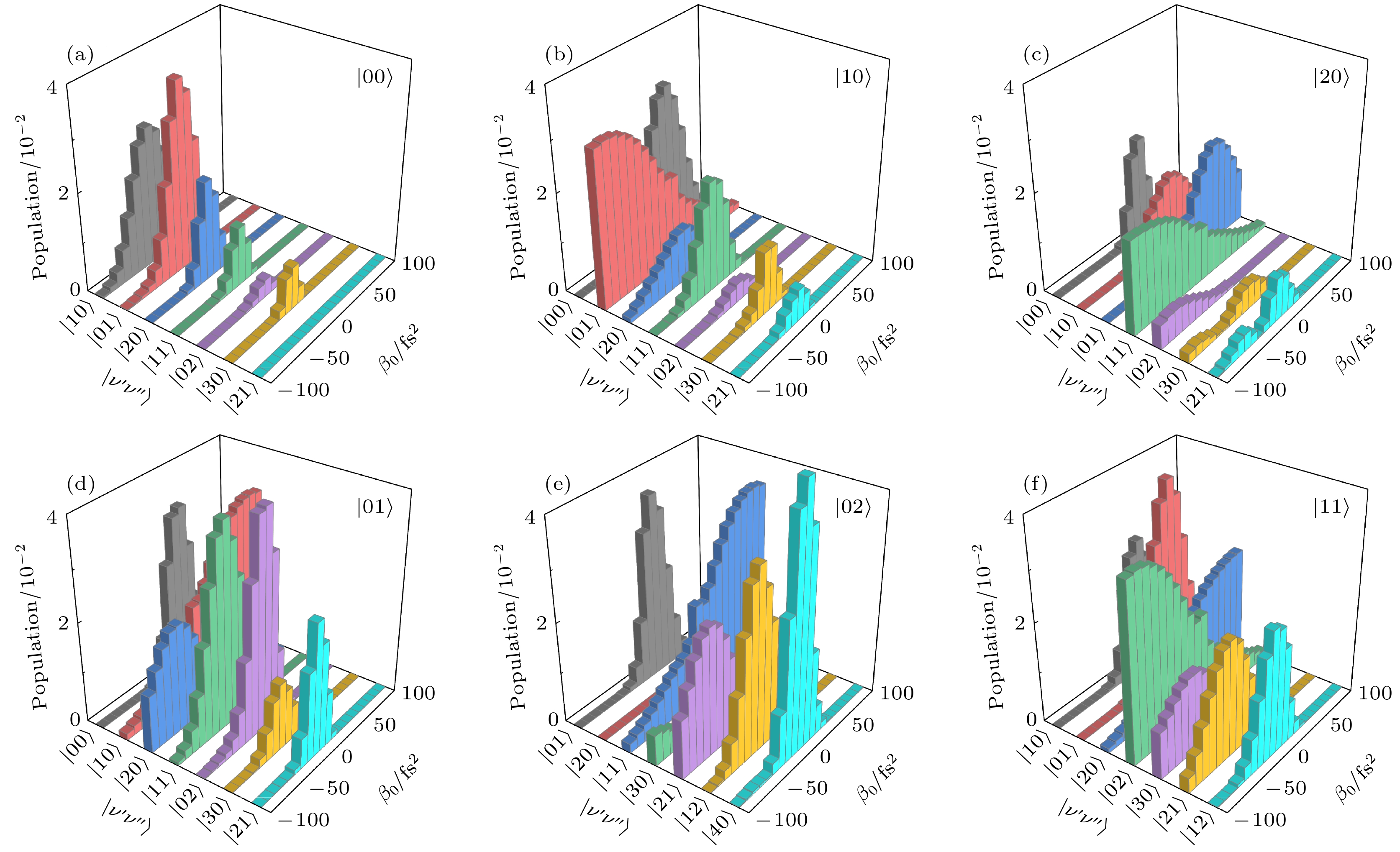
$ |\nu'\nu''\rangle $ 下, 基电子态不同振动态的末态布居分布$ P_{\nu'\nu''}(t_{\mathrm{f}}) $ 与啁啾率$ \beta_{0} $ 的关系. 当初始态为振动态$ |00\rangle $ 时, 较低的激发振动态$ |10\rangle $ 到$ |30\rangle $ 都有明显的布居分布, 其中较低激发振动态的布居填充尤为显著. 这表明在强场作用下, 分子容易被激发到这些低激发态. 当初始态为$ |10\rangle $ ,$ |20\rangle $ 和$ |01\rangle $ 时, 从基振动态$ |00\rangle $ 到$ |21\rangle $ 振动态都有布居分布, 且各振动态的布居分布呈现显著差异. 值得注意的是, 当初始态为$ |20\rangle $ 时, 各振动态的布居分布相对较少, 这可能与该初始态下分子的能级结构和跃迁概率有关. 当初始态为$ |02\rangle $ 时, 基态和最低激发振动态几乎没有布居分布, 主要分布在振动态$ |01\rangle $ 到$ |40\rangle $ 上. 这表明在该初始态下, 分子更倾向于被激发到这些特定的振动态. 当初始态为$ |11\rangle $ 时, 基振动态布居分布较少, 主要集中在振动态$ |10\rangle $ 到$ |12\rangle $ 上. 这可能与该初始态下分子的振动模式和能量分布有关. 此外, 对于不同初始振动态$ |\nu'\nu''\rangle $ , 基电子态不同振动态布居分布明显依赖于啁啾率的值和符号, 且这种依赖性各不相同. 这些结果深化了对分子振动态动力学的理解, 通过调节啁啾率, 可以实现对特定振动态布居的选择性控制. 这种控制方法有望在分子光物理和光化学领域找到重要的应用, 例如通过优化啁啾率来提高特定化学反应的产率或选择性.从先前的研究可以发现, 宽带强脉冲可以通过中间激发态
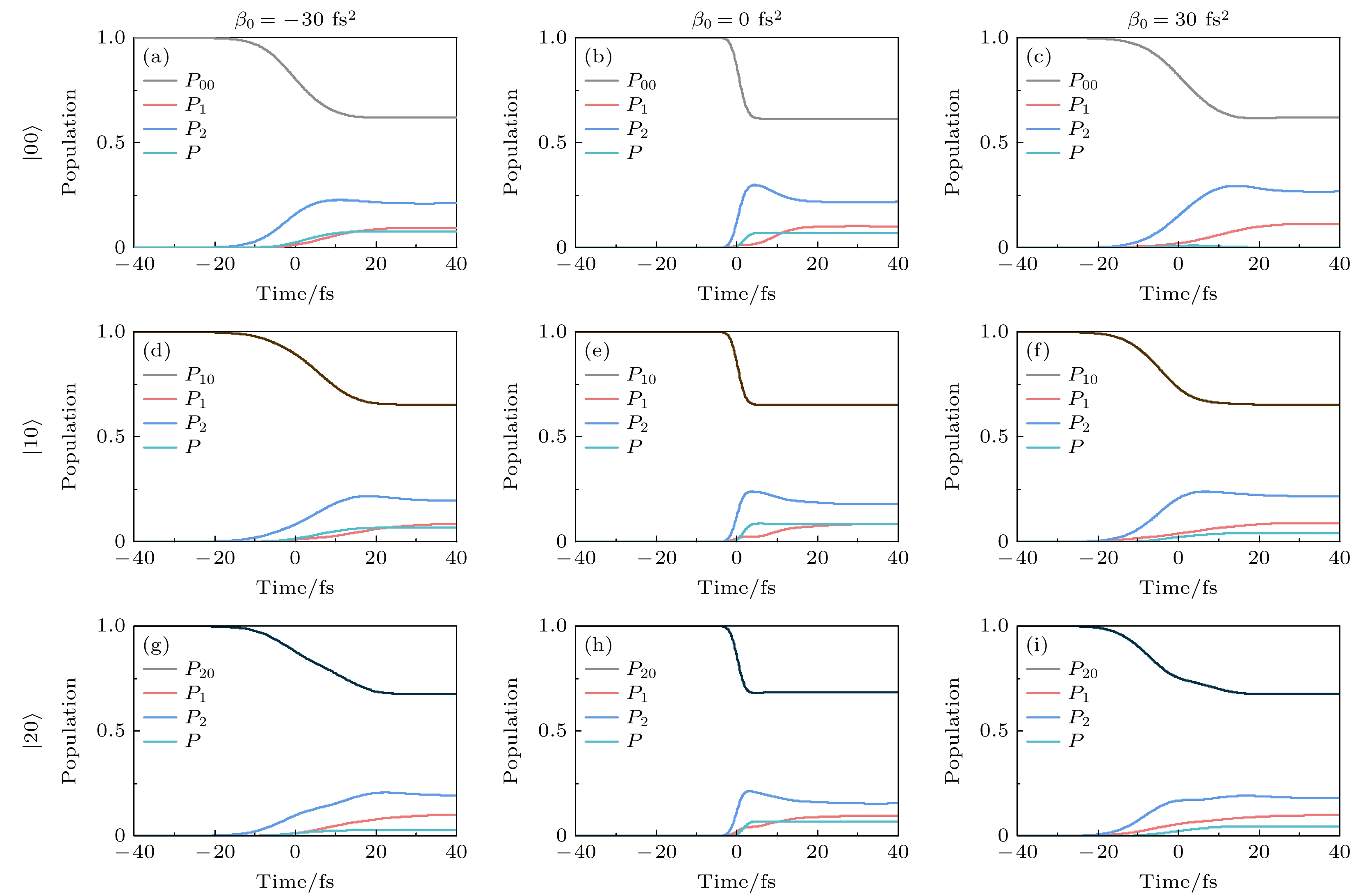
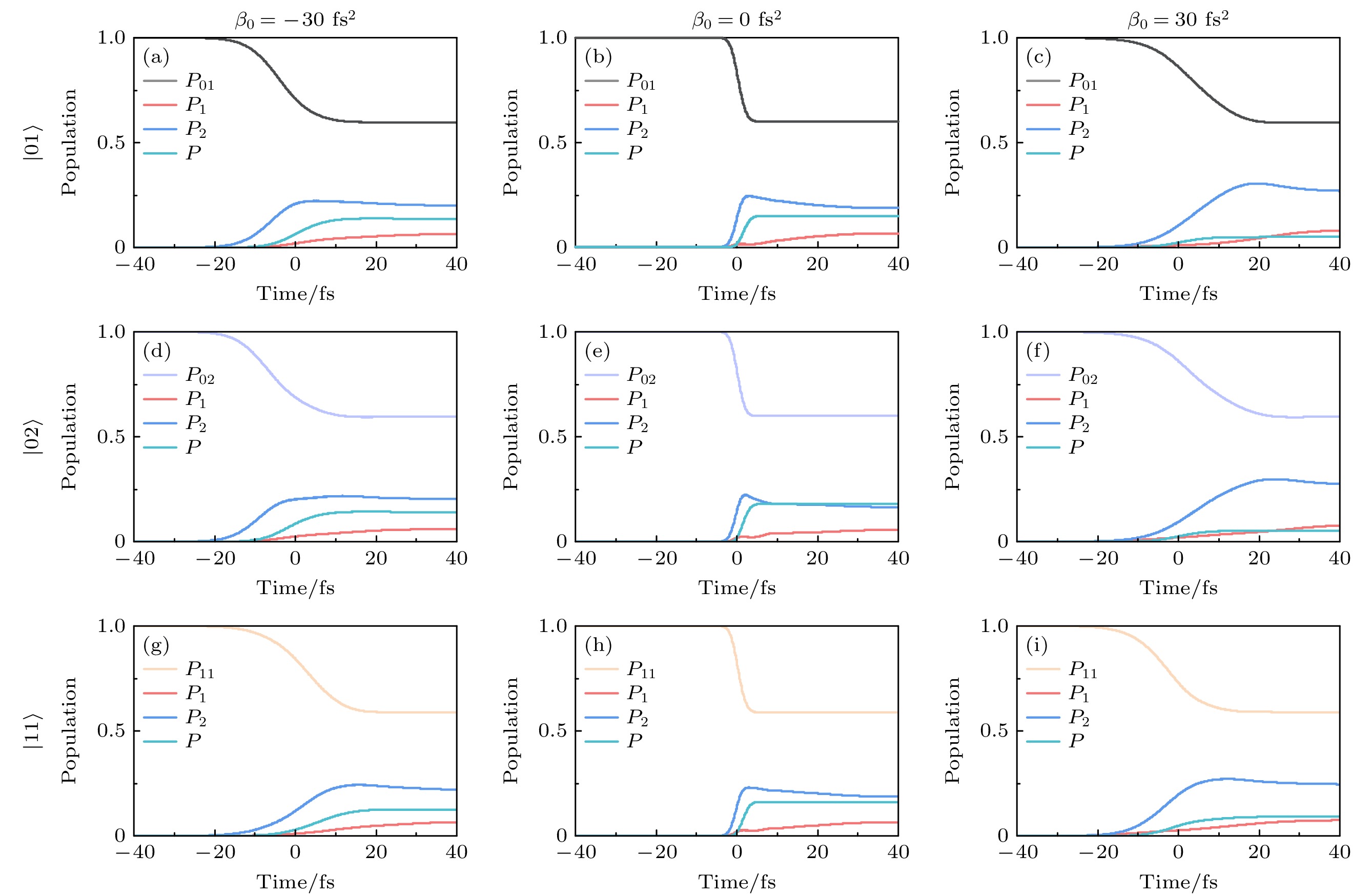
${\mathrm{ S}}_{1} $ 和$ {\mathrm{S}}_{2} $ 发生共振拉曼散射(RRS), 从而有效驱动布居从初始态$ |00\rangle $ 转移到基电子态$ {\mathrm{S}}_{0} $ 的激发振动态上[60,73,74], 如图1(b) 和图1(c) 所示. 在强场极限下, RRS改变了激发态$ {\mathrm{S}}_{1} $ 和$ {\mathrm{S}}_{2} $ 的相对布居, 从而影响了解离分支比. 在上述研究中发现, 谱啁啾率$ \beta_0 $ 可以有效调控基电子态不同振动态上的末态布居. 为此, 图8和图9给出了不同初始振动态在不同啁啾脉冲下, 与共振拉曼散射现象相关的不同态的含时布居变化. 可以看出, 啁啾脉冲有效调控了强场RRS现象. 具体来说, 当初始振动态为$ |00\rangle $ 时, 与变换极限脉冲相比, 较小的正啁啾脉冲($ \beta_0 = 30 \, \text{fs}^2 $ )明显抑制了基电子态激发振动态的RRS, 使更多布居分布在激发电子态上; 而较小的负啁啾脉冲$( \beta_0 = -30 \, \text{fs}^2) $ 增强了基电子态激发振动态的RRS, 同时激发电子态布居分布减少(见图8(a)—(c)). 当初始态振动态为$ |10\rangle $ 时, 与变换极限脉冲相比, 较小的正负啁啾脉冲均有效减弱了基电子态不同振动态的RRS现象, 如图8(d)—(f)所示. 对于初始振动态$ |20\rangle $ , 较小的负啁啾脉冲($ \beta_0 = -30 \, \text{fs}^2 $ )明显抑制了基电子态激发振动态的RRS, 而较小的正啁啾脉冲$ (\beta_0 = 30 \, \text{fs}^2) $ 同样有效减弱了基电子态激发振动态的RRS (见图8(g)—(i)). 特别地, 对于初始振动态$ |01\rangle $ 和$ |02\rangle $ , 与$ \beta_0 = 0 \, \text{fs}^2 $ 相比,$ \beta_0 = 30 \, \text{fs}^2 $ 时, 啁啾脉冲显著抑制了基电子态激发振动态的RRS现象, 使激发电子态的布居大幅度增加(图9(c)和图9(f)).从图3(a)—(c) 中计算的基电子态不同振动态的概率密度分布可知,
$ |01\rangle $ 和$ |02\rangle $ 振动态对应了Cl—CH2振动模的拉伸. 啁啾脉冲有效抑制了基电子态激发振动态RRS现象的发生, 不仅提高了总解离概率, 更主要的是提高了Cl—CH2的解离概率, 从而提升了解离分支比$ R\;(\mathrm{Cl}/\mathrm{Br}) $ . 同样地, 当$ \beta_0 = -30 \, \text{fs}^2 $ 时, 啁啾脉冲也抑制了基电子态激发振动态的RRS现象. 因此, 通过调控啁啾率, 可以有效抑制强场极限下的RRS现象, 使解离分支比$ R\;(\mathrm{Cl}/\mathrm{Br}) $ 提升至接近弱场极限下的值, 如图5右栏所示. 当初始态为$ |11\rangle $ 时, 与变换极限脉冲相比, 较小的正负啁啾脉冲均有效减弱了基电子态不同振动态的RRS现象(见图9(g)—(i)). 这些结果表明, 调控啁啾脉冲的方式对激发态的动态过程有显著的影响, 为优化分子解离过程提供了一种有效途径.RRS过程涉及基电子态初始振动态与特定激发振动态之间的共振双光子跃迁, 不同的中间激发电子态会产生不同的RRS路径. 通过调控啁啾率的值和符号, 可以改变不同路径之间的延迟, 从而导致量子干涉效应的相长或相消[60,75]. 由于分子在激发态上的快速解离, 长激光脉冲会导致不同时间激发的波包发生退相干. 当应用较大的啁啾率时, 脉冲持续时间显著延长, 在此延长的时间内, 激发态的快速解离导致不同RRS通道的相消干涉, 最终消除或者抑制RRS, 如图6所示. 值得注意的是, 当初始态为
$ |00\rangle $ ,$ |10\rangle $ ,$ |20\rangle $ 和$ |11\rangle $ 时, 较大的正啁啾加速了激发电子态波包的退相干, 因此正啁啾脉冲比负啁啾脉冲导致的RRS抑制更快. 相反, 当初始振动态为$ |01\rangle $ 和$ |02\rangle $ 时, 较大的负啁啾脉冲加速了激发电子态波包的退相干, 导致RRS抑制更明显. 这主要是不同振动模的拉伸造成波包的动量不同, 进而影响量子干涉效应, 从而使RRS现象对啁啾脉冲的符号和大小的依赖性表现出不同的特征. 相比之下, 在弱场极限下, 几乎没有发生共振拉曼散射现象, 因此总解离概率和分支比对啁啾率的值和符号不敏感. 这种通过啁啾操控量子干涉的能力, 为在强场极限下探索分子光解反应提供了另一种方法. 通过合理调控啁啾率, 可以有效控制量子干涉效应, 从而实现对分子光解反应路径的选择性调控. -
本文理论研究了单束飞秒脉冲的谱相位对CH2BrCl分子光解离的相干调控机制. 通过对比研究强场极限区域解离与弱场极限区域的不同, 揭示了强场极限区域不同初始振动态及光谱相位对CH2BrCl分子总解离概率和分支比的调控机理. 研究结果显示, 当选择的Cl—CH2Br振动模式相对于Br—CH2Cl振动模式显著拉伸时, 该初始振动态会促进Cl+CH2Br通道的解离. 通过分析基电子态振动态布居分布, 证明了强场极限下诱导的RRS现象, 并观察到啁啾脉冲对RRS的抑制效果在不同初始振动态下表现不同. 调控啁啾率的大小和符号, 可以有效控制激发电子态的量子退相干效应, 从而显著提高光解产率. 这一效果在初始振动态为
$ |01\rangle $ 和$ |02\rangle $ 时尤为明显, 尤其对Cl+CH2Br通道的解离过程. 这些发现对研究超快光场调控三原子或多原子系统的光解离问题具有重要的参考价值.
超快强场相干调控氯溴甲烷分子的解离研究
Dissociation of chlorobromomethane molecules coherently controlled by ultrafast strong field
-
摘要: 超快强场相干调控分子解离在原子与分子物理、物理化学、量子调控等多个领域引起了重要关注, 在现象理解、机理探究和调控方案等多个方面仍然存在许多值得深入研究的问题. 近期研究表明, 在保持光谱振幅分布不变的条件下, 对最初处于基电子态纯本征态的分子, 通过调制单个超快强紫外激光脉冲的光谱相位分布, 可以有效调控总解离概率和分支比. 本文采用含时量子波包方法, 进一步探讨了光谱相位调控氯溴甲烷(CH2BrCl)分子的光解离反应, 着重探究了初始振动态对解离反应的影响. 为了凸显超快强场脉冲调控解离机理与弱场的不同, 本文展示了在弱场极限下, 改变单个超快脉冲的谱相位不会影响总解离概率和分支比; 然而在强场极限下, 总解离概率和分支比对单个超快脉冲的谱相位有明显依赖性. 通过分析基电子态振动态布居分布, 发现啁啾脉冲可以有效调控强场极限下诱导的共振拉曼散射(resonance Raman scattering, RRS)现象, 从而导致解离概率和分支比对初始振动态的选择性. 研究结果进一步表明, 通过选择合适的初始振动态并调控啁啾率的值和符号, 可以实现Cl+CH2Br键的优先断裂. 该研究为理解超快光场相干控制多原子分子光解反应提供了新的视角.Abstract: Coherent control of molecular dissociation in ultrafast strong fields has received considerable attention in various scientific disciplines, such as atomic and molecular physics, physical chemistry, and quantum control. Many fundamental issues still exist regarding the understanding of phenomena, exploration of mechanisms, and development of control strategies. Recent progress has shown that manipulating the spectral phase distribution of a single ultrafast strong ultraviolet laser pulse while maintaining the same spectral amplitude distribution can effectively control the total dissociation probability and branching ratio of molecules initially in the ground state. In this work, the spectral phase control of the photodissociation reaction of chlorobromomethane (CH2BrCl) is studied in depth by using a time-dependent quantum wave packet method, focusing on the influence of the initial vibrational state on the dissociation reaction. The results show that modifying the spectral phase of a single ultrafast pulse does not influence the total dissociation probability or branching ratio in the weak field limit. However, these factors exhibit significant dependence on the spectral phase of the single ultrafast pulse in the strong field limit. By analyzing the population distribution of vibrational states in the ground electronic state, we observe that chirped pulses can effectively control the resonance Raman scattering (RRS) phenomenon induced in strong fields, thereby selectively affecting the dissociation probability and branching ratio based on initial vibrational states. Furthermore, we demonstrate that by selecting an appropriate initial vibration state and controlling both the value and sign of the chirp rate, it is possible to achieve preferential cleavage of Cl+CH2Br bonds. This study provides new insights into understanding of ultrafast coherent control of photodissociation reactions in polyatomic molecules.
-
Key words:
- photodissociation /
- coherent control /
- initial vibrational states /
- resonance Raman scattering .
-

-
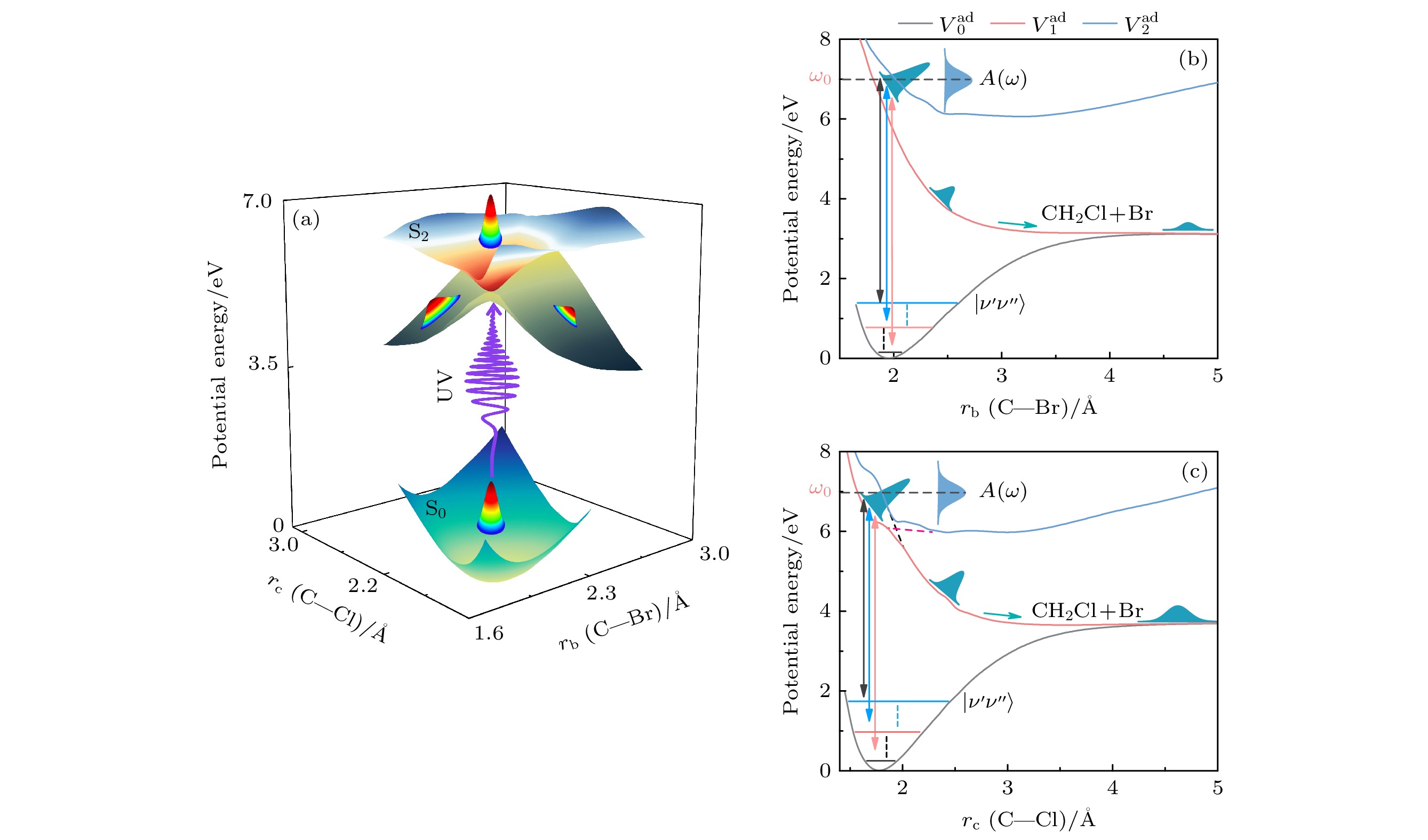
图 1
$ \rm {CH_{2}BrCl} $ 光解离激光控制示意图 (a)基电子态$ \text{S}_0(\text{a}^{1}\text{A}') $ 、激发态$ \text{S}_1(\text{a}^{1}\text{A}') $ 和$ \text{S}_2(\text{a}^{1}\text{A}') $ 的光解离动力学模型; (b)不同初始振动态$ |\nu'\nu''\rangle $ 沿着Br—CH2反应坐标描绘的光解离通道; (c)不同初始振动态$ |\nu'\nu''\rangle $ 沿Cl—CH2反应坐标的光解离通道. 其中黑色线、红色线和蓝色线分别表示基电子态$ \text{S}_0(V_0^\text{ad}) $ 、第一激发电子态$ \text{S}_1(V_1^\text{ad}) $ 和第二激发电子态$ \text{S}_2(V_2^\text{ad}) $ 的绝热势能曲线, 红色虚线和黑色虚线分别表示非绝热势能曲线$ V_1^{{\mathrm{di}}} $ 和$ V_2^{{\mathrm{di}}} $ Figure 1. Schematic illustration of laser control in the photodissociation process of
$ \rm {CH_{2}BrCl} $ . (a) The model showcasing the photodissociation dynamics involving the ground electronic state$ \text{S}_0(\text{a}^{1}\text{A}') $ , as well as the excited adiabatic electronic states$ \text{S}_1(\text{b}^{1}\text{A}') $ and$ \text{S}_2(\text{c}^{1}\text{A}') $ . (b) Photodissociation channel along the Br—CH2 reaction coordinate for different initial vibrational states$ |\nu'\nu''\rangle $ . (c) The channel along the Cl—CH2 reaction coordinate for the same initial states$ |\nu'\nu''\rangle $ . The black, red, and blue solid lines represent the adiabatic potential energy curves of ground electronic state$ \text{S}_0(V_0^\text{ad}) $ , the first excited electronic state$ \text{S}_1(V_1^\text{ad}) $ , and the second excited electronic state$ \text{S}_2(V_2^\text{ad}) $ , respectively. Notably, the red-dashed line and the black-dashed line represent the non-adiabatic potential$ V_1^{\mathrm{di}} $ and$ V_2^{\text{di}} $ .图 2 CH2BrCl分子初始振动态为
$ |00\rangle $ ,$ |10\rangle $ 和$ |20\rangle $ 时, (a)—(c)基电子态的二维振动本征函数密度分布; (d)—(f)弱场极限下Br+CH2Cl通道和Cl+CH2Br通道的含时解离概率(分别用$ P^{\mathrm{Br}} $ 和$ P^{\mathrm{Cl}} $ 标记), (g)—(i)相应的含时分支比R; (j)—(l) 强场极限下Br+CH2Cl和Cl+CH2Br两个通道的含时解离概率, (m)—(o)相应的含时解离分支比Figure 2. For the initial vibrational states of
$ |00\rangle $ ,$ |01\rangle $ and$ |02\rangle $ , (a)–(c) two-dimensional vibrational eigenfunction density distributions; (d)–(f) the dissociation probabilities of Br+CH2Cl and Cl+CH2Br channels in the weak-field limit (marked with$ P^{\mathrm{Br}} $ and$ P^{\mathrm{Cl}} $ , respectively), and (g)–(i) the corresponding time-dependent dissociation branching ratios R; (j)–(l) and (m)–(o) as well as in the strong-field limit.图 3 CH2BrCl分子初始振动态为
$ |01\rangle $ ,$ |02\rangle $ 和$ |11\rangle $ 时, (a)—(c)基电子态的二维振动本征函数密度分布; (d)—(f)弱场极限下Br+CH2Cl通道和Cl+CH2Br通道的含时解离概率(分别用$ P^{\mathrm{Br}} $ 和$ P^{\mathrm{Cl}} $ 标记), (g)—(i)相应的含时分支比R; (j)—(l)强场极限下Br+CH2Cl和Cl+CH2Br两个通道的含时解离概率, (m)—(o)相应的含时解离分支比Figure 3. For the initial vibrational states of
$ |00\rangle $ ,$ |01\rangle $ and$ |02\rangle $ , (a)–(c) two-dimensional vibrational eigenfunction density distributions; (d)–(f) the dissociation probabilities of Br+CH2Cl and Cl+CH2Br channels in the weak-field limit (marked with$ P^{\mathrm{Br}} $ and$ P^{\mathrm{Cl}} $ , respectively), and (g)–(i) the corresponding time-dependent dissociation branching ratios R; (j)–(l) and (m)–(o) as well as in the strong-field limit.图 4 弱场极限下CH2BrCl分子总解离概率(a)—(f)和分支比(g)—(l)作为啁啾率
$ \beta_{0} $ 和不同初始振动态$ |\nu'\nu''\rangle $ 的函数Figure 4. Dependence of (a)−(f) total dissociation probability and (g)−(l) branching ratio of CH2BrCl on the chirp rate
$ \beta_{0} $ and different initial state$ |\nu'\nu''\rangle $ in the weak-field limit.图 5 强场极限下, CH2BrCl分子总解离概率(a)—(f)和分支比(g)—(l)作为啁啾率
$ \beta_{0} $ 和不同初始振动态$ |\nu'\nu''\rangle $ 的函数Figure 5. (a)–(f) Total dissociation probability and (g)–(l) branching ratio in CH2BrCl as a function of chirp rate
$ \beta_{0} $ and different initial state$ |\nu'\nu''\rangle $ in the strong-field limit.图 6 (a)
$ |00\rangle $ , (b)$ |10\rangle $ , (c)$ |20\rangle $ , (d)$ |01\rangle $ , (e)$ |02\rangle $ , (f)$ |11\rangle $ 分别作为初始振动态时, 基电子态其余振动态末态布居之和$ P(t_{\mathrm{f}}) $ 随啁啾率$ \beta_{0} $ 的变化行为. 对于所有不同的初始振动态,$ P(t_{\mathrm{f}}) $ 的最大值都出现在$ \beta_0=0 $ 附近Figure 6. (a)–(f) Sum of the remaining vibrational states populations
$ P(t_{\mathrm{f}}) $ of the ground electronic state for the initial vibrational state (a)$ |00\rangle $ , (b)$ |10\rangle $ , (c)$ |20\rangle $ , (d)$ |01\rangle $ , (e)$ |02\rangle $ and (f)$ |11\rangle $ as a function of$ \beta_0 $ , respectively. The maximum of$ P(t_{\mathrm{f}}) $ appears near$ \beta_0=0 $ for all different initial vibrational states.图 7 随着啁啾率
$ \beta_{0} $ 的改变, (a)$ |00\rangle $ , (b)$ |10\rangle $ , (c)$ |20\rangle $ , (d)$ |01\rangle $ , (e)$ |02\rangle $ , (f)$ |11\rangle $ 分别作为初始振动态时, 基电子态不同振动态$ |\nu'\nu''\rangle $ 的末态布居分布Figure 7. Final population distributions of different vibrational states
$ |\nu'\nu''\rangle $ for the different initial vibrational state (a)$ |00\rangle $ , (b)$ |10\rangle $ , (c)$ |20\rangle $ , (d)$ |01\rangle $ , (e)$ |02\rangle $ and (f)$ |11\rangle $ , varying with the chirp rate$ \beta_0 $ .图 8 强场极限下啁啾脉冲诱导的基电子态振动态共振拉曼散射现象. 初始振动态为
$ |00\rangle $ ,$ |10\rangle $ 和$ |20\rangle $ 时, (a)—(i)啁啾率$ \beta_0=0 $ ,$ \pm30 $ fs2时的初态含时布居$ P_{\nu'\nu''} $ 、基电子态其余振动态布居之和$ P(t) $ 、两个激发电子态的含时布居$ P_{1} $ 和$ P_{2} $ Figure 8. Resonance Raman scattering phenomenon of the vibrational states of the ground electronic state induced by a chirped pulse in the strong-field limit. For the initial vibrational states of
$ |00\rangle $ ,$ |10\rangle $ and$ |20\rangle $ , (a)–(i) the time-dependent populations of the initial state$ P_{\nu'\nu''} $ , the total of remaining vibrational states of the ground electronic state$ P(t) $ , and the two excited electronic states$ P_{1} $ and$ P_{2} $ with three different chirp rates$ \beta_0=0 $ ,$ \pm30 $ fs2.图 9 强场极限下啁啾脉冲诱导的基电子态振动态共振拉曼散射现象. 初始振动态为
$ |01\rangle $ ,$ |02\rangle $ 和$ |11\rangle $ 时, (a)—(i)啁啾率$ \beta_0=0 $ ,$ \pm30 $ fs2时的初态含时布居$ P_{\nu'\nu''} $ 、基电子态其余振动态布居之和$ P(t) $ 、两个激发电子态的含时布居$ P_{1} $ 和$ P_{2} $ Figure 9. Resonance Raman scattering phenomenon of the vibrational states of the ground electronic state induced by a chirped pulse in the strong-field limit. For the initial vibrational states of
$ |01\rangle $ ,$ |02\rangle $ and$ |11\rangle $ , (a)–(i) the time-dependent populations of the initial state$ P_{\nu'\nu''} $ , the total of the remaining vibrational states of the ground electronic state$ P(t) $ , and the two excited electronic states$ P_{1} $ and$ P_{2} $ with three different chirp rates$ \beta_0=0 $ ,$ \pm30 $ fs2. -
[1] Mokhtari A, Cong P, Herek J, Zewail A 1990 Nature 348 225 doi: 10.1038/348225a0 [2] Brumer P, Shapiro M 1992 Annu. Rev. Phys. Chem. 43 257 doi: 10.1146/annurev.pc.43.100192.001353 [3] King W E, Campbell G H, Frank A, Reed B, Schmerge J F, Siwick B J, Stuart B C, Weber P M 2005 J. Appl. Phys. 97 111101 doi: 10.1063/1.1927699 [4] Sun Z, Wang C, Zhao W, Yang C 2018 J. Chem. Phys. 149 224307 doi: 10.1063/1.5052514 [5] Yang J, Zhu X, Wolf T J, Li Z, Nunes J P F, Coffee R, Cryan J P, Gühr M, Hegazy K, Heinz T F, Jobe K, Li R, Shen X, Veccione T, Weathersby S, Wilkin K J, Yoneda C, Zheng Q, Martinez T J, Centurion M, Wang X 2018 Science 361 64 doi: 10.1126/science.aat0049 [6] Sun Z, Liu Y 2023 Phys. Chem. Chem. Phys. 25 17397 doi: 10.1039/D3CP00962A [7] Rubio-Lago L, Chicharro D V, Poullain S M, Zanchet A, Koumarianou G, Glodic P, Samartzis P C, García-Vela A, Bañares L 2023 Phys. Chem. Chem. Phys. 25 11684 doi: 10.1039/D2CP05082J [8] Kranabetter L, Kristensen H H, Ghazaryan A, Schouder C A, Chatterley A S, Janssen P, Jensen F, Zillich R E, Lemeshko M, Stapelfeldt H 2023 Phys. Rev. Lett. 131 053201 doi: 10.1103/PhysRevLett.131.053201 [9] Lian Z, Hu Z, Qi H, Fei D, Luo S, Chen Z, Shu C C 2021 Phys. Rev. A 104 053105 doi: 10.1103/PhysRevA.104.053105 [10] Xu S, Lian Z, Hong Q Q, Wang L, Chen H, Huang Y, Shu C C 2024 Phys. Rev. A 110 023116 doi: 10.1103/PhysRevA.110.023116 [11] Zhang H, Lavorel B, Billard F, Hartmann J M, Hertz E, Faucher O, Ma J, Wu J, Gershnabel E, Prior Y, Averbukh I S 2019 Phys. Rev. Lett. 122 193401 doi: 10.1103/PhysRevLett.122.193401 [12] Hong Q Q, Fan L B, Shu C C, Henriksen N E 2021 Phys. Rev. A 104 013108 doi: 10.1103/PhysRevA.104.013108 [13] Shu C C, Henriksen N E 2013 Phys. Rev. A 87 013408 doi: 10.1103/PhysRevA.87.013408 [14] Hong Q Q, Lian Z Z, Shu C C, Henriksen N E 2023 Phys. Chem. Chem. Phys. 25 32763 doi: 10.1039/D3CP03115B [15] Zhang W, Gong X, Li H, Lu P, Sun F, Ji Q, Lin K, Ma J, Li H, Qiang J, He F, Wu J 2019 Nat. Commun. 10 757 doi: 10.1038/s41467-019-08700-5 [16] Lu P, Wang J, Li H, Lin K, Gong X, Song Q, Ji Q, Zhang W, Ma J, Li H, Zeng H, He F, Wu J 2018 Proc. Natl. Acad. Sci. 115 2049 doi: 10.1073/pnas.1719481115 [17] Guo Z, Fang Y, Ge P, Yu X, Wang J, Han M, Gong Q, Liu Y 2021 Phys. Rev. A 104 L051101 doi: 10.1103/PhysRevA.104.L051101 [18] Yu X, Zhang X, Hu X, Zhao X, Ren D, Li X, Ma P, Wang C, Wu Y, Luo S, Ding D 2022 Phys. Rev. Lett. 129 023001 doi: 10.1103/PhysRevLett.129.023001 [19] Sansone G, Kelkensberg F, Pérez-Torres J, Morales F, Kling M F, Siu W, Ghafur O, Johnsson P, Swoboda M, Benedetti E, Ferrari F, Lépine F, Sanz-Vicario L J, Zherebtsov S, Znakovskaya I, L’Huillier A, Ivanov Y M, Nisoli M, Martín F, Vrakking M J J 2010 Nature 465 763 doi: 10.1038/nature09084 [20] Kang H, Quan W, Wang Y, Lin Z, Wu M, Liu H, Liu X, Wang B B, Liu H J, Gu Y Q, Jia X Y, Liu J, Chen J, Cheng Y 2010 Phys. Rev. Lett. 104 203001 doi: 10.1103/PhysRevLett.104.203001 [21] 罗嗣佐, 陈洲, 李孝开, 胡湛, 丁大军 2019 光学学报 39 0126007 doi: 10.3788/AOS201939.0126007 Luo S Z, Chen Z, Li X K, Hu Z, Ding D J 2019 Acta Opt. Sin. 39 0126007 doi: 10.3788/AOS201939.0126007 [22] Li X, Liu Y, Zhang D, He L, Luo S, Shu C C, Ding D 2023 Phys. Rev. A 108 023114 doi: 10.1103/PhysRevA.108.023114 [23] Zhang W, Yu Z, Gong X, Wang J, Lu P, Li H, Song Q, Ji Q, Lin K, Ma J, Li H, Sun F, Qiang J, Zeng H, He F, Wu J 2017 Phys. Rev. Lett. 119 253202 doi: 10.1103/PhysRevLett.119.253202 [24] Guo Z, Zhang Z, Deng Y, Wang J, Ye D, Liu J, Liu Y 2024 Phys. Rev. Lett. 132 143201 doi: 10.1103/PhysRevLett.132.143201 [25] McFarland B K, Farrell J P, Bucksbaum P H, Guhr M 2008 Science 322 1232 doi: 10.1126/science.1162780 [26] Chen Y J, Fu L B, Liu J 2013 Phys. Rev. Lett. 111 073902 doi: 10.1103/PhysRevLett.111.073902 [27] Huang Y, Meng C, Wang X, Lü Z, Zhang D, Chen W, Zhao J, Yuan J, Zhao Z 2015 Phys. Rev. Lett. 115 123002 doi: 10.1103/PhysRevLett.115.123002 [28] Yang W, Sheng Z, Feng X, Wu M, Chen Z, Song X 2014 Opt. Express 22 2519 doi: 10.1364/OE.22.002519 [29] He M, Li Y, Zhou Y, Li M, Cao W, Lu P 2018 Phys. Rev. Lett. 120 133204 doi: 10.1103/PhysRevLett.120.133204 [30] Xie W, Yan J, Li M, Cao C, Guo K, Zhou Y, Lu P 2021 Phys. Rev. Lett. 127 263202 doi: 10.1103/PhysRevLett.127.263202 [31] Zewail A H 2000 J. Phys. Chem. A 104 5660 doi: 10.1021/jp001460h [32] Kobayashi Y, Chang K F, Zeng T, Neumark D M, Leone S R 2019 Science 365 79 doi: 10.1126/science.aax0076 [33] Shu C C, Yuan K J, Dong D, Petersen I R, Bandrauk A D 2017 J. Phys. Chem. Lett. 8 1 doi: 10.1021/acs.jpclett.6b02613 [34] Yang D, Cong S L 2011 Phys. Rev. A 84 013424 doi: 10.1103/PhysRevA.84.013424 [35] Jia Y W, Yuen C, Jing W Q, Zhou Z Y, Lin C, Zhao S F 2024 Phys. Rev. A 110 023112 doi: 10.1103/PhysRevA.110.023112 [36] Shapiro M, Brumer P 2001 J. Phys. Chem. A 105 2897 doi: 10.1021/jp003878l [37] Csehi A, Halász G J, Cederbaum L S, Vibók Á 2015 J. Chem. Phys. 143 014305 doi: 10.1063/1.4923441 [38] Liebel M, Kukura P 2017 Nat. Chem. 9 45 doi: 10.1038/nchem.2598 [39] Wilma K, Shu C C, Scherf U, Hildner R 2018 J. Am. Chem. Soc. 140 15329 doi: 10.1021/jacs.8b08674 [40] Morichika I, Murata K, Sakurai A, Ishii K, Ashihara S 2019 Nat. Commun. 10 3893 doi: 10.1038/s41467-019-11902-6 [41] Csehi A, Halász G J, Cederbaum L S, Vibók Á 2016 J. Chem. Phys. 144 074309 doi: 10.1063/1.4941847 [42] Tiwari A K, Henriksen N E 2016 J. Chem. Phys. 144 014306 doi: 10.1063/1.4939247 [43] Sun Z, Wang C, Zhao W, Zheng Y, Yang C 2018 Phys. Chem. Chem. Phys. 20 20957 doi: 10.1039/C8CP02449A [44] Spanner M, Arango C A, Brumer P 2010 J. Chem. Phys. 133 151101 doi: 10.1063/1.3491366 [45] Weigel A, Sebesta A, Kukura P 2015 J. Phys. Chem. Lett. 6 4032 doi: 10.1021/acs.jpclett.5b01748 [46] Brumer P, Shapiro M 1986 Chem. Phys. Lett. 126 541 doi: 10.1016/S0009-2614(86)80171-3 [47] Shapiro M, Brumer P 2003 Principles of the Quantum Control of Molecular Processes (New York: Wiley [48] Garcia-Vela A, Henriksen N E 2015 J. Phys. Chem. Lett. 6 824 doi: 10.1021/acs.jpclett.5b00129 [49] García-Vela A 2016 Phys. Chem. Chem. Phys. 18 10346 doi: 10.1039/C6CP01267A [50] Serrano-Jiménez A, Bañares L, García-Vela A 2019 Phys. Chem. Chem. Phys. 21 7885 doi: 10.1039/C9CP01214A [51] Dey D, Henriksen N E 2020 J. Phys. Chem. Lett. 11 8470 doi: 10.1021/acs.jpclett.0c02273 [52] Shu C C, Henriksen N E 2011 J. Chem. Phys. 134 164308 doi: 10.1063/1.3582928 [53] Tiwari A K, Dey D, Henriksen N E 2014 Phys. Rev. A 89 023417 doi: 10.1103/PhysRevA.89.023417 [54] Liu Y, Meng J Q, Sun Z, Shu C C 2024 J. Phys. Chem. Lett. 15 8393 doi: 10.1021/acs.jpclett.4c01901 [55] García-Vela A 2018 Phys. Rev. Lett. 121 153204 doi: 10.1103/PhysRevLett.121.153204 [56] Abrashkevich D G, Shapiro M, Brumer P 2002 J. Chem. Phys. 116 5584 doi: 10.1063/1.1457440 [57] Nichols S R, Weinacht T C, Rozgonyi T, Pearson B J 2009 Phys. Rev. A 79 043407 doi: 10.1103/PhysRevA.79.043407 [58] Luo S, Zhou S, Hu W, Li X, Ma P, Yu J, Zhu R, Wang C, Liu F, Yan B, Liu A, Yang Y, Guo F, Dajun D 2017 Phys. Rev. A 96 063415 doi: 10.1103/PhysRevA.96.063415 [59] Esposito V J, Liu T, Wang G, Caracciolo A, Vansco M F, Marchetti B, Karsili T N, Lester M I 2021 J. Phys. Chem. A 125 6571 doi: 10.1021/acs.jpca.1c03643 [60] Jing W Q, Sun Z P, Zhao S F, Shu C C 2023 J. Phys. Chem. Lett. 14 11305 doi: 10.1021/acs.jpclett.3c03143 [61] Sarma M, Adhikari S, Mishra M K 2008 J. Phys. Chem. A 112 13302 doi: 10.1021/jp803690r [62] Geißler D, Marquetand P, González-Vázquez J, González L, Rozgonyi T, Weinacht T 2012 J. Phys. Chem. A 116 11434 doi: 10.1021/jp306686n [63] Corrales M E, de Nalda R, Bañares L 2017 Nat. Commun. 8 1345 doi: 10.1038/s41467-017-01139-6 [64] Bouallagui A, Zanchet A, Bañares L, García-Vela A 2023 Phys. Chem. Chem. Phys. 25 20365 doi: 10.1039/D3CP01460F [65] Rozgonyi T, González L 2008 J. Phys. Chem. A 112 5573 doi: 10.1021/jp8011427 [66] Shu C C, Rozgonyi T, González L, Henriksen N E 2012 J. Chem. Phys. 136 174303 doi: 10.1063/1.4706603 [67] Chicharro D, Marggi Poullain S, González-Vázquez J, Bañares L 2017 J. Chem. Phys. 147 013945 doi: 10.1063/1.4984789 [68] Muthiah B, Kasai T, Lin K C 2021 Phys. Chem. Chem. Phys. 23 6098 doi: 10.1039/D0CP06350A [69] Lanczos C 1950 J. Res. Natl. Bur. Stand 45 255 doi: 10.6028/jres.045.026 [70] Park T J, Light J 1986 J. Chem. Phys. 85 5870 doi: 10.1063/1.451548 [71] Sun Z, Yang C, Zheng Y 2015 J. Chem. Phys. 143 224309 doi: 10.1063/1.4936832 [72] Kosloff R 1988 J. Phys. Chem. 92 2087 doi: 10.1021/j100319a003 [73] Simpson J R, Roslyak O, Duque J G, Hároz E H, Crochet J J, Telg H, Piryatinski A, Walker A R H, Doorn S K 2018 Nat. Commun. 9 637 doi: 10.1038/s41467-018-03057-7 [74] Guo Y, Shu C C, Dong D, Nori F 2019 Phys. Rev. Lett. 123 223202 doi: 10.1103/PhysRevLett.123.223202 [75] Shapiro M, Brumer P 2012 Quantum Control of Molecular Processes (New York: John Wiley & Sons) pp95–152 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: