自从1984年发现C₆₀团簇以来, 由于其具有许多优异性能, 如超导、强磁性、耐高压、抗化学腐蚀, 在光、电、磁等领域有潜在的应用前景, 因此备受人们关注. 自20世纪末以来, 人们对碳团簇的结构和动力学特性进行了深入的探讨, 尤其是小型碳阴离子团簇, 因其在燃烧、热解过程以及天体物理学中的关键作用而引起了人们的兴趣^[1–4]. 随着碳原子数目的递增, 碳团簇的异构体多样性显著增加; Helden等^[5–7]与Gotts等^[8]通过离子色谱技术结合计算机模拟, 对碳团簇可能的几何结构及其含量进行了详尽的分析, 揭示了线性结构在碳原子数目较少时的普遍性, 以及随着碳原子数目的进一步增加, 环形结构逐渐成为主导形态; Giuffreda等^[9]则通过密度泛函方法(density functional theory, DFT)研究了C₃—C₁₃碳团簇的转动和振动特性.

$ {{\mathrm{C}}}_{4}^{-} $作为最基本的小型碳阴离子团簇之一, 已经引起了广泛的研究兴趣. Adamowicz^[10]和Schmatz与Botschwina^[11]使用考虑单双激发以及非迭代三激发的耦合簇方法(coupled cluster singles, doubles, and perturbative triples, CCSD(T))分别研究了$ {{\mathrm{C}}}_{4}^{-} $线性构型的激发态, 报道了低激发态的垂直激发能. Dreuw与Cederbaum^[12]则使用局域近似方法讨论了$ {{\mathrm{C}}}_{4}^{2-} $中通过垂直发射电子转变为$ {{\mathrm{C}}}_{4}^{-} $离子的排斥库仑势垒(the repulsive coulomb barrier, RCB). Padellec等^[13]通过溅射离子源在重离子储存环上产生稳定的$ {{\mathrm{C}}}_{4}^{-} $离子, 测量了电子与$ {{\mathrm{C}}}_{4}^{-} $碰撞脱附截面, 并研究了生成C, C₂, C₃和C₄的绝对解离截面. 他们在脱附截面上发现近阈处寿命为0.7 fs的共振态, 与此同时采用涉及双替代的耦合簇方法理论预测了存在四种$ {{\mathrm{C}}}_{4}^{-} $同分异构体. 随后他们提高了测量的统计性, 再次测量了其脱附截面^[14], 观测到在8.85 eV处有宽度为1.45 eV的共振峰. 然而由于缺乏理论计算结果, 无法说明该共振态的形成机制. 另一方面由于$ {{\mathrm{C}}}_{4}^{-} $离子存在多种同分异构体, 这些异构体因结构差异可能表现出不同的截面特征, 进一步给分析指认实验结果带来挑战.

本研究采用从头算R-矩阵方法^[15,16]研究电子与$ {{\mathrm{C}}}_{4}^{-} $离子的散射动力学过程. 该方法已被证实在处理复杂分子体系的散射问题时具有高效性和准确性. 研究低能电子分别与$ {{\mathrm{C}}}_{4}^{-} $离子的四种异构体发生弹性散射的积分截面, 标识存在的电子离子共振态. 通过细致比较这些异构体的散射截面, 分析结构变化如何影响共振态的位置和宽度, 以及对散射截面的影响. 最后, 根据计算得到各异构体的散射截面和丰度, 拟合常温下$ {{\mathrm{C}}}_{4}^{-} $离子的低能电子弹性散射截面, 并与已有的实验测量结果进行对比, 分析截面的组成成分.

R-矩阵方法通过定义在质心的球将坐标空间划分为内区和外区. 内区与多中心积分紧密相关, 采用高斯型轨道来解析地求解束缚态和散射态电子. 靶波函数及其相应的电荷密度完全被包含在球内, 电子与靶之间的相互作用可以通过交换势和相关势来表征, 能够精确描述电子与靶分子的散射体系^[17–19]. 因此, 选择内区半径必须确保所有短程相互作用均被包含在内. 通过内区将靶分子和散射电子的哈密顿量对角化, 获得在内外区边界处的边界条件. 外区通过单中心耦合近似来考虑散射电子在靶的长程多极相互作用下的运动. 将前面求解内区得到的边界条件代入外区散射方程, 结合无穷远处的渐进条件, 即可求解外区方程. 这里外区的范围设定为100a₀ (a₀代表玻尔半径), 这一半径足以满足每个通道中散射电子径向波函数的渐近展开式要求.

R-矩阵方法开展散射计算的特点是: 内区与散射能量无关, 这意味着内区的求解只需要执行一次, 并且入射电子能量只与物理上更简单的外区有关. 外区可以使用十分精细的能量步长, 这对于发现和标识共振很重要. 内区中N+1电子波函数由下列公式描述:

这里, ${\phi _i}$表示由n电子靶态构造的通道函数; $\mathcal{A}$是反对称算符; ${\chi _n}$是第n个电子的空间和自旋坐标, 表示n电子靶的第i个状态; ${B_j}(r)$表示连续轨道; 系数${a_{ijk}}$和${b_{ik}}$是由矩阵对角化得到的变分参数. 方程(1)的第2项求和反映了短程相互作用和极化效应, 这些效应作用于N + 1电子结构的函数上. 在这个结构中, 电子被允许跃迁到靶分子的占据轨道和虚分子轨道上. 为了精确描述电子结构, 必须考虑正交弛豫效应以及由虚激发引起的更高电子态的相关效应. 因此, 合理选择变分参数${\chi _i}$对于构建准确的电子散射模型至关重要.

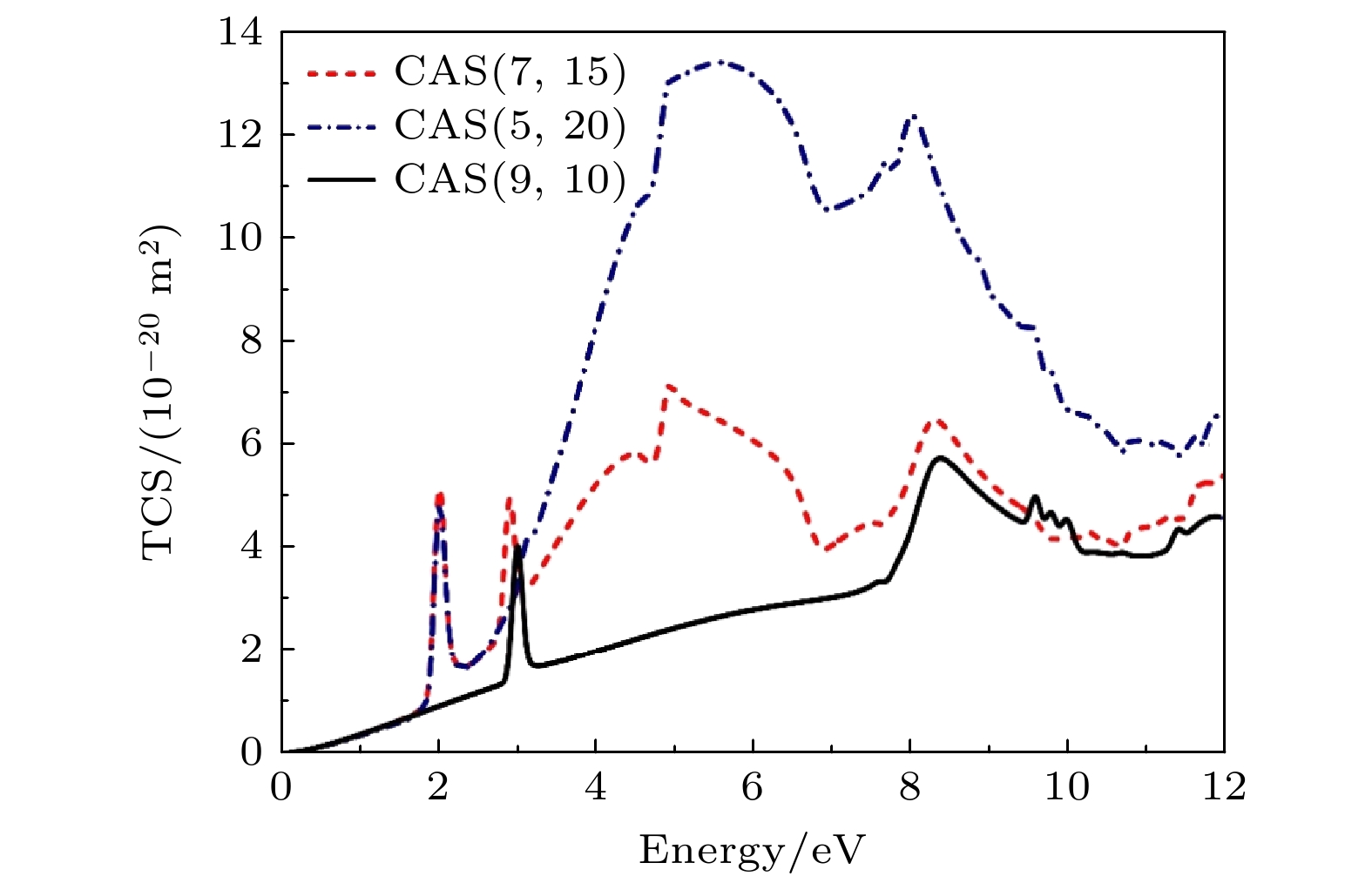
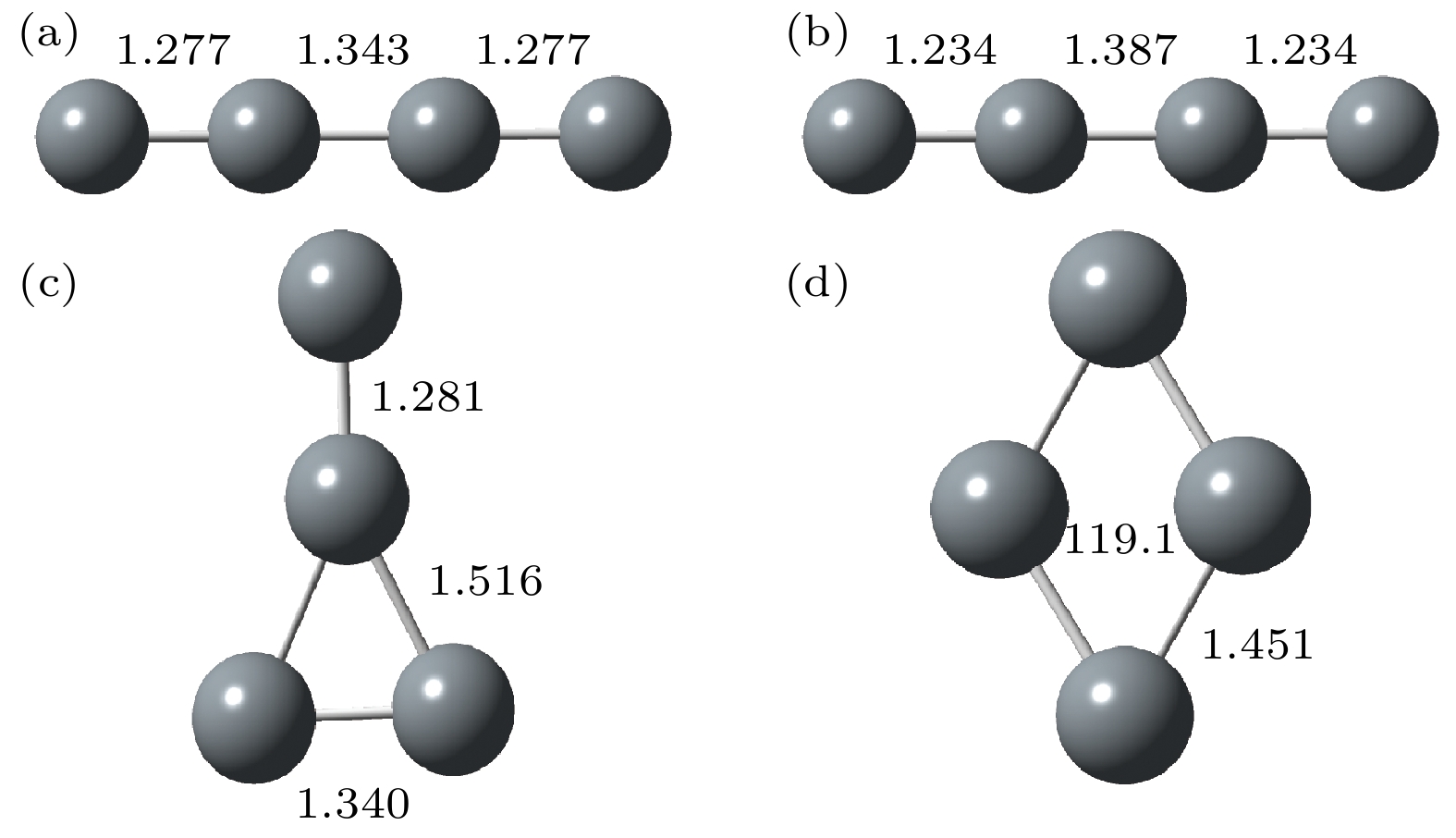
$ {{\mathrm{C}}}_{4}^{-} $阴离子存在四种不同的异构体, 不同理论计算结果预测最稳定异构体A的结构非常相似, 如图1所示. Padellec等^[13]使用CCD计算得到的中心键长为1.343 Å和两端键长为1.277 Å; Watts等^[20]通过四阶多体微扰理论计算得到的中心和两端键长分别为1.343 Å和1.283 Å. 我们使用密度泛函理论B3LYP/aug-cc-pVTZ方法^[21–23]重新对异构体A进行了结构优化, 得到中心键长为1.333 Å, 两端键长为1.277 Å, 如表1所列. 这与Padellec等和Watts等的结果十分接近, 因此我们采用Padellec等得到的四种异构体结构开展散射研究. 为了提高计算能量的准确度, 采用CCSD(T)方法结合aug-cc-pVQZ基组重新计算了四种异构体的相对能量. 结果显示异构体A的能量最低, 是线性结构, 基态为²Π_g, 电子组态为$ 3{{\mathrm{\sigma }}}_{{\mathrm{g}}}^{2} 3{{\mathrm{\sigma }}}_{{\mathrm{u}}}^{2}{4{\mathrm{\sigma }}}_{{\mathrm{g}}}^{2}{1{\mathrm{\pi }}}_{{\mathrm{u}}}^{4}{4{\mathrm{\sigma }}}_{{\mathrm{u}}}^{2}{5{\mathrm{\sigma }}}_{{\mathrm{g}}}^{2}{1{\mathrm{\pi }}}_{{\mathrm{g}}}^{3} $. 异构体B同样是线性结构, 其电子组态为$3 {{\mathrm{\sigma }}}_{{\mathrm{g}}}^{2} $ $ 3{{\mathrm{\sigma }}}_{{\mathrm{u}}}^{2}{4{\mathrm{\sigma }}}_{{\mathrm{g}}}^{2}{1{\mathrm{\pi }}}_{{\mathrm{u}}}^{4}{4{\mathrm{\sigma }}}_{{\mathrm{u}}}^{2}{1{\mathrm{\pi }}}_{{\mathrm{g}}}^{4}{5{\mathrm{\sigma }}}_{{\mathrm{g}}}^{1} $, 中心键长为1.387 Å, 两端键长为1.234 Å. 异构体B的能量比A高出1.09 eV. 异构体C为C_2v对称性的三角形平面构型, 其基态电子组态为$2 {{\mathrm{b}}}_{2}^{2}6{{\mathrm{a}}}_{1}^{2}1{{\mathrm{b}}}_{1}^{2}7{{\mathrm{a}}}_{1}^{2}8{{\mathrm{a}}}_{1}^{2}3{{\mathrm{b}}}_{2}^{2} 2{{\mathrm{b}}}_{1}^{1} $. 在构型C中, 第四个碳原子与三角形的顶点相连, 三角形底边的键长为1.34 Å, 两腰的键长为1.156 Å, 而顶点与第四个碳原子之间的键长为1.281 Å. 异构体C的能量比A高出1.36 eV. 异构体D是D_2h对称性的菱形结构, 基态电子组态为$ 2{{\mathrm{b}}}_{2{\mathrm{u}}}^{2}4{{\mathrm{a}}}_{{\mathrm{g}}}^{2}{1{\mathrm{b}}}_{1{\mathrm{g}}}^{2}{{1{\mathrm{b}}}_{1{\mathrm{u}}}^{2}3{{\mathrm{b}}}_{3{\mathrm{u}}}^{2}5{{\mathrm{a}}}_{{\mathrm{g}}}^{2}1{\mathrm{b}}_{2{\mathrm{g}}}^{1}} $. 其四条边长相等, 均为1.451 Å. 异构体D的能量与C相当, 比A高出1.39 eV.

在靶态计算中, 对小分子通常Hartree-Fock (HF)方法可以得到较好的靶态波函数. 初始采用HF自洽场方法来描述靶态, 进一步采用完全活性空间组态相互作用方法来提高对靶态描述的准确性. 单态密耦合(close couple, CC)模型中, 四种异构体均冻结能量最低的八个轨道, 其余的9个电子可以跃迁到10个活性轨道中, 针对异构体A活化空间为(5a_g, 1b_3u-2b_3u, 2b_2u, 4b_1u-5b_1u, 1b_2g-2b_2g, 1b_3g-2b_3g), 形成了一个包含9个活性电子和10个活性轨道的活性空间, 记为CAS(9, 10). 理论上, 更大的活性空间能够增加电子相关效应, 提高计算结果的准确性. 然而, 考虑到计算资源的限制, 需要在精度和可行性之间做出权衡. 我们测试了几种不同的活性空间: CAS(9, 10), CAS(7, 15)和CAS(5, 20). 截面结果如图2所示, CAS(7, 15)在小于3 eV的低能区预测了两个共振态, 然而在其他两个活化空间中只看到一个共振态, 预示着该活化空间不能充分地描述极化作用. 与CAS(9, 10)的结果相比, CAS(5, 20)在4—6 eV预测了很强的共振峰, 与实验测量在该区域的截面平坦且强度接近零的结果严重不符. 因此, 我们采用CAS(9, 10)的活化空间开展散射计算. 在CC模型中, 异构体C的偶极矩为0.22 Debye. 由于异构体A, B和D这三个结构的对称性, 他们不存在偶极矩.

为了准确模拟电子分子的散射过程, 讨论电子相关效应对散射过程的影响, 采用不同的散射模型. 其中, 静态交换(static exchange, SE)模型是一种最简单的散射模型. 在SE模型中, 靶分子被冻结, 散射电子可占据在虚轨道上, 形成特定的组态表达式, 如(2)式所示:

由于SE模型忽略了靶分子的极化效应, 它通常预测的势形共振态位置偏高. 静态交换加极化(static exchange plus polarization, SEP)模型在SE的基础上增加了极化效应, 靶分子占据轨道同样被冻结, 散射电子占据在虚轨道上, 如(3)式所示:

这里, N为电子总数, N_c为冻结电子数. 通常, SEP模型选择的活性轨道数量应尽可能得多, 以便更准确地描述势形共振和费什巴赫共振. SEP模型中, 为确保足够的极化效应, 取23个空轨道作为上述的虚轨道.

进一步地, CC模型考虑了更多的靶态, 并采用完整的活性空间来描述这些状态, 如(4)式所示:

CC模型是描述电子激发的有效工具, 也是研究费什巴赫共振的理想选择. CC模型对费什巴赫共振以及核激发势形共振态十分敏感, 然而, CC模型的计算成本通常远高于SE或SEP模型. 在某些情况下, CC模型也可以简化为只使用一个靶态, 此时主要计算与基态相关的弹性散射截面.

在散射计算中采用高斯函数来描述连续态, R-矩阵半径为13a₀. 为测试该半径是否包含足够多的靶态电子密度分布, 计算了R-矩阵半径为15a₀的结果, 发现两者之间没有显著差异. 这表明R-矩阵半径选为13a₀已经足够大. 外区半径设定为100a₀, 能量范围为0—12 eV, 扫描步长为0.1 eV. 当前我们采用SEP和CC单态模型来开展散射计算研究.

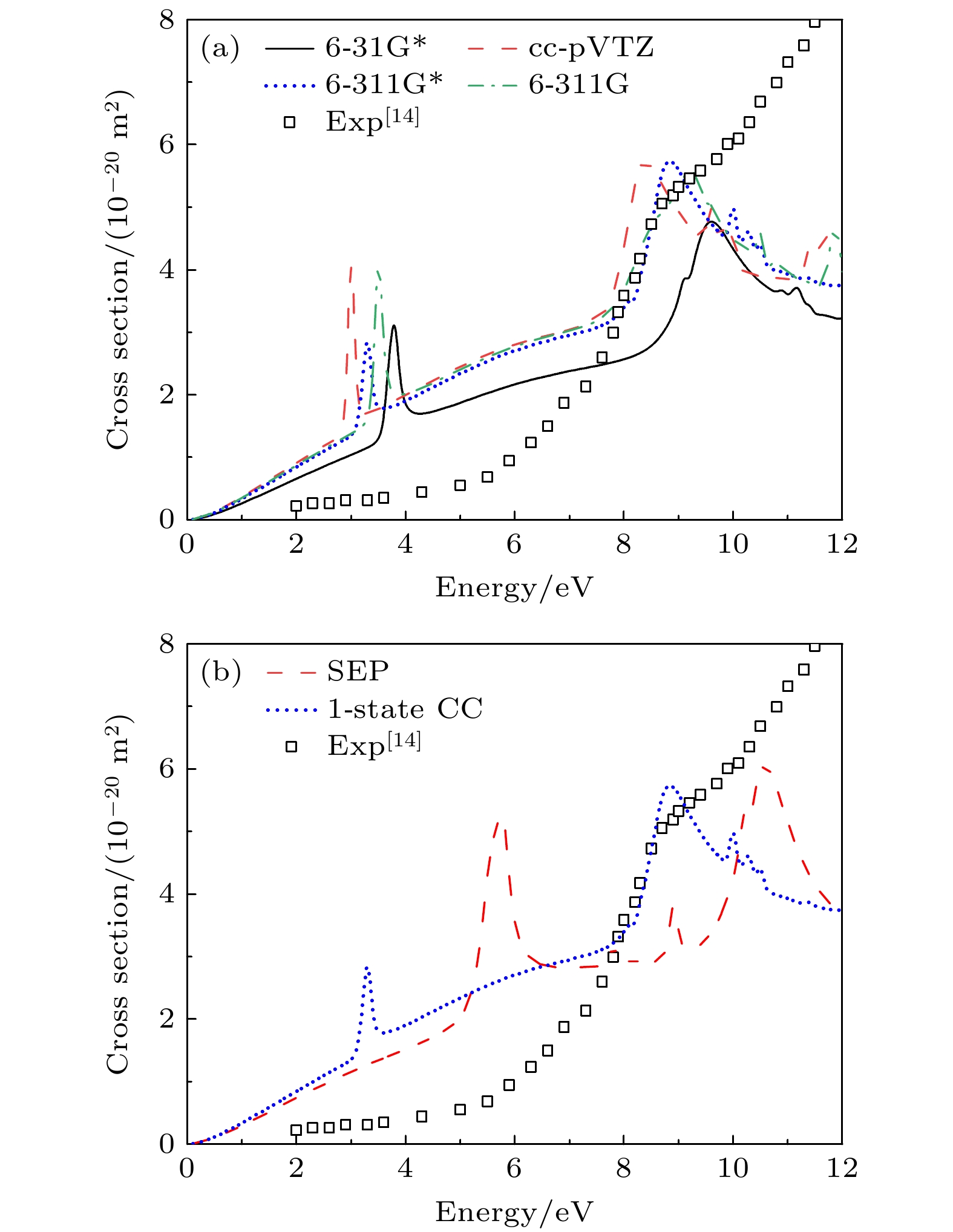
为了准确模拟散射过程, 以最稳定的异构体A为研究对象, 测试了不同的散射模型和基组. 考虑到精确度和计算速度, 中小zeta基组是较为合适的, 因而基组的选择上使用6-31G*, 6-311G, 6-311G*, cc-pVTZ四种不同基组来计算CC单态模型在下的弹性散射截面, 如图3所示. 由图3可以看出, 不同基组的计算结果均预测两个明显的共振峰. 对于第一个共振峰, 这四个基组预测的位置分别在3.8 eV, 3.5 eV, 3.3 eV和3.1 eV. 对于第二个共振峰, 四个基组预测的位置分别在9.7 eV, 9.2 eV, 8.82 eV和8.3 eV. 在Fritioff等^[14]实验测量的解离截面上, 观察到一个位于8.8 eV处的宽共振峰, 该共振峰与6-311G*的计算结果吻合很好. 因此, 将采用此基组计算SEP和单态CC模型的散射截面. 需要指出的是我们预测的位于3—4 eV的低能共振峰并没有在Fritioff等^[14]的实验中观测到. 这主要是由于该共振峰较小的共振宽度以及处于较低的能区, 实验测量时较大的能量扫描步长可能探测不到该共振峰. 图3同样给出了我们在6-311G*基组下采用SEP和单态CC两种散射模型的截面结果. SEP模型同样预测了两个明显的势形共振态, 分别位于5.7 eV和10.6 eV. 第二个共振态高出实验观测值1.8 eV. 在CC模型中, 这两个共振态分别向能量更低的位置移动, 位于3.3 eV和8.82 eV处. 这主要是与SEP模型相比, CC模型考虑了多通道耦合效应, 该效应同样会提供额外的极化作用使得共振态的能量位置更低. 因此在后面对所有异构体的计算中, 均采用单态CC模型和6-311G*基组计算散射截面.

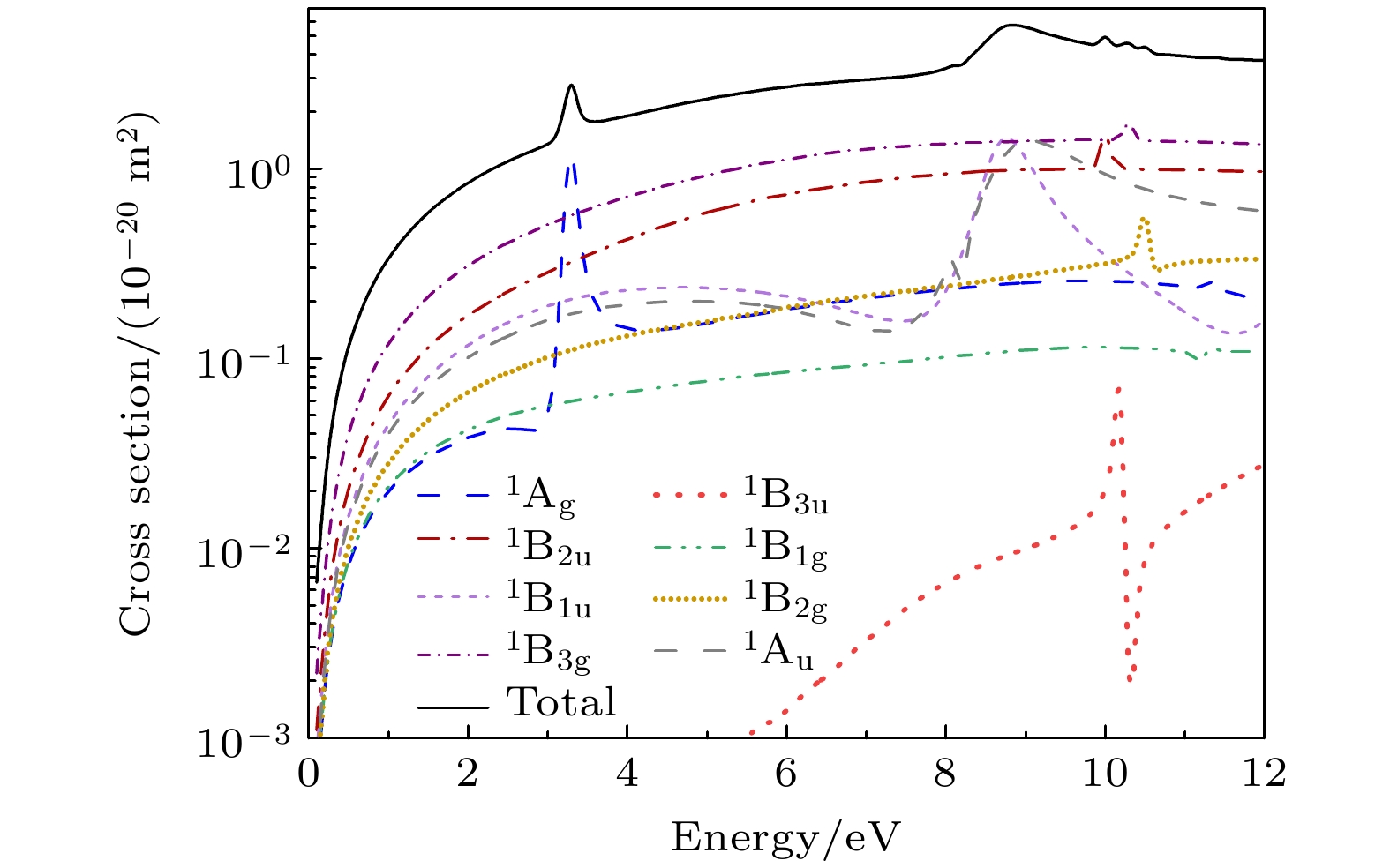
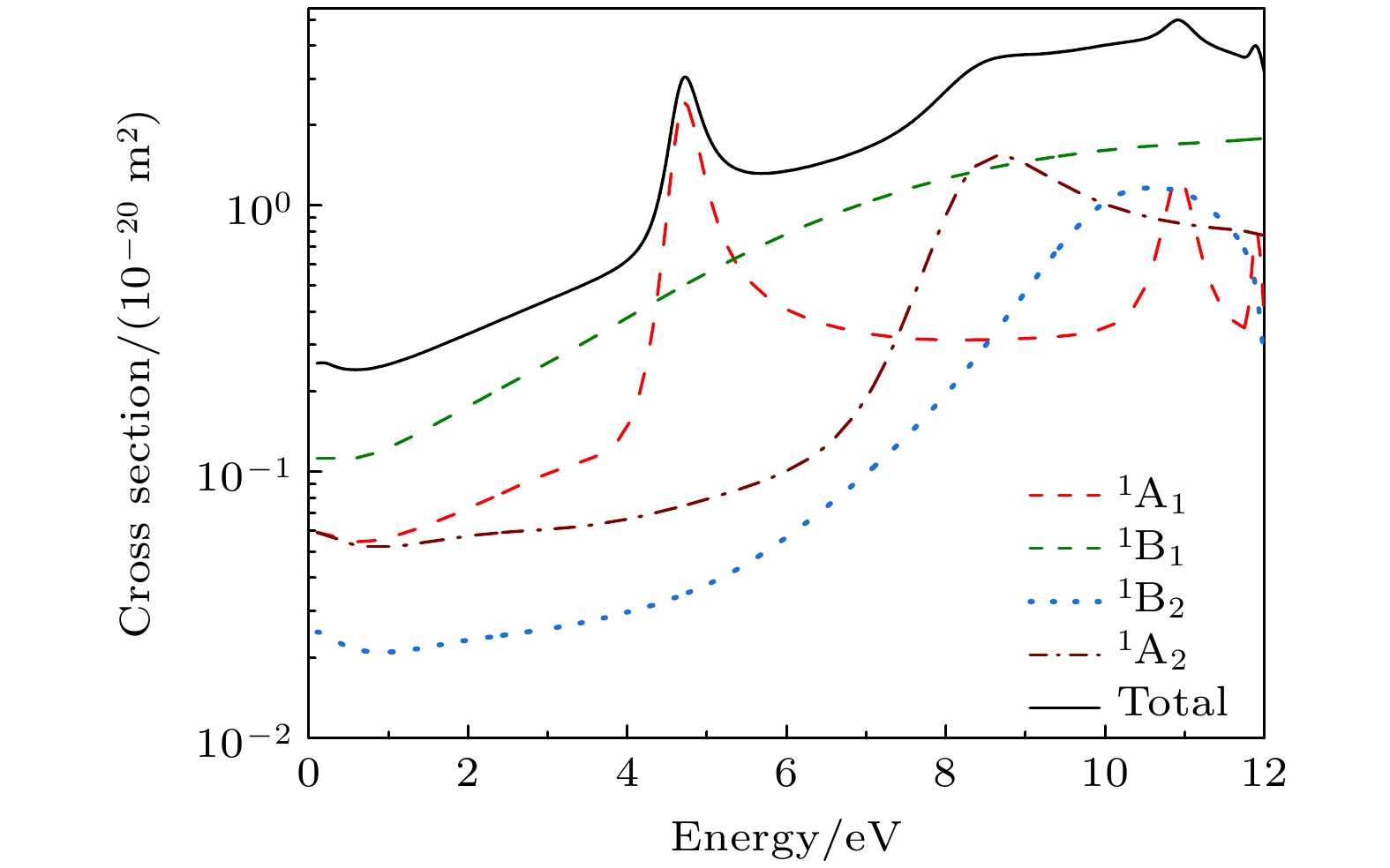
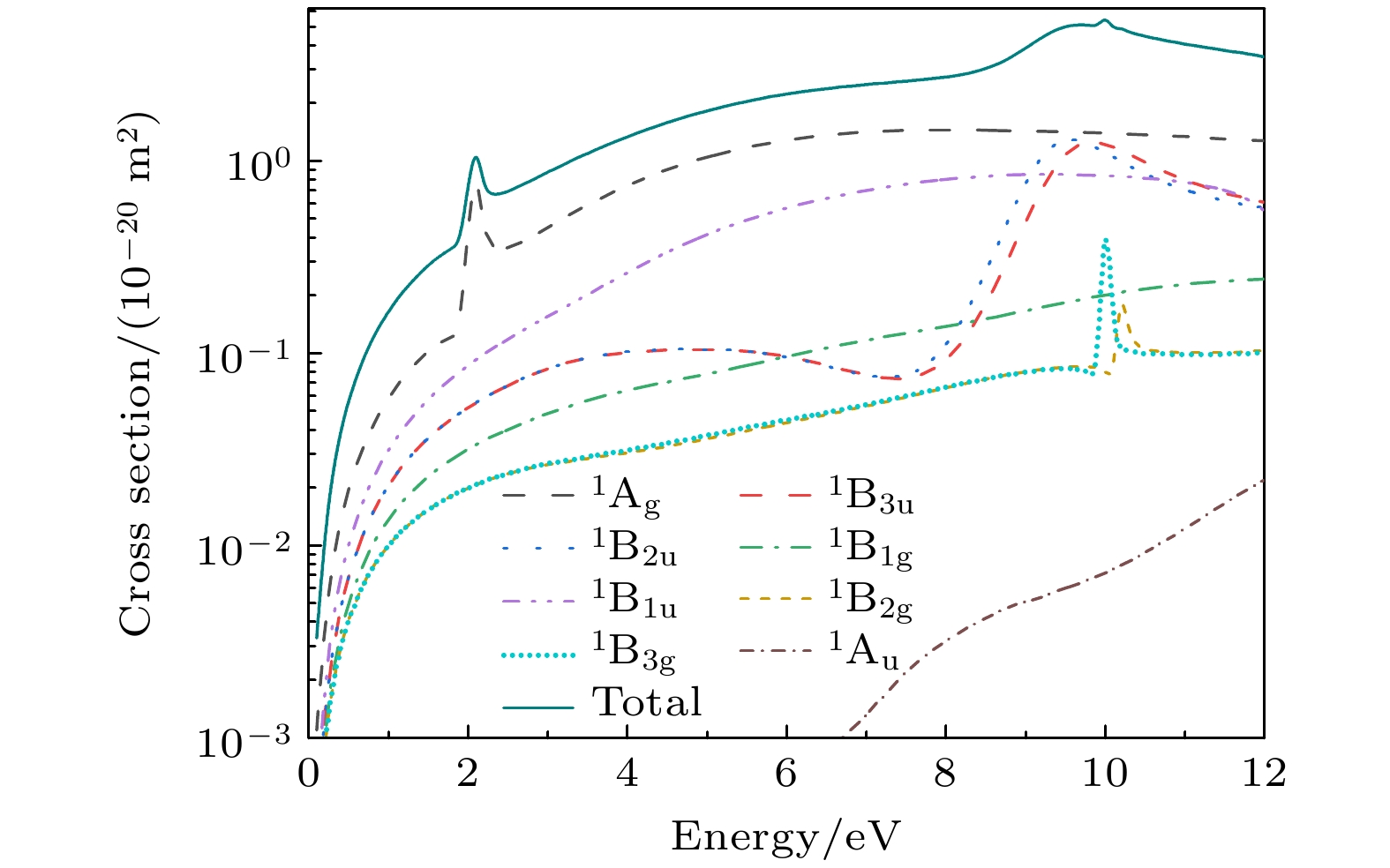
为了更好地分析共振态, 计算了各种对称成份对散射截面的贡献. 图4给出了异构体A在单态CC模型下的低能电子弹性散射各种对称成份的截面结果. 总截面上第一个共振峰位于3.3 eV处, 来自$ {{{\Sigma }}}_{{\mathrm{g}}}^{+} $对称性, 宽度为0.20 eV; 第二个峰位于8.83 eV处的, 主要来自8.8 eV处的$ {{{\Sigma }}}_{{\mathrm{u}}}^{+} $成份和9.1 eV处$ {{{\Sigma }}}_{{\mathrm{u}}}^{-} $对称性的贡献, 宽度分别为0.75 eV和1.76 eV; 第三个峰位于10.1 eV, 来自$ {{{\Pi }}}_{{\mathrm{u}}} $对称性, 宽度为0.15 eV; 第四个峰位于10.4 eV, 由$ {{{\Pi }}}_{{\mathrm{g}}} $组成, 宽度为0.15 eV. 表2列出了我们根据相移拟合的共振态位置和宽度参数. 由此可知: Fritioff等^[14]研究中所观察到的8.8 eV处的共振峰, 主要来自$ {{{\Sigma }}}_{{\mathrm{u}}}^{+} $和$ {{{\Sigma }}}_{{\mathrm{u}}}^{-} $共振态的贡献. 此外, 我们还发现位于3.3 eV处宽度为0.20 eV的$ {{{\Sigma }}}_{{\mathrm{g}}}^{+} $共振态, 在Fritioff等的实验中没有被探测到. 当前的结果为进一步的实验研究提供了理论参考.

采用与A异构体相同的活化空间, 我们也计算了异构体B包括各种对称成份的散射截面, 如图5所示. 由于同为线性结构, 故两者的截面有很多相同之处, 第一个能峰位于2.10 eV, 具有$ {{{\Sigma }}}_{{\mathrm{g}}}^{+} $对称性, 宽度为0.23 eV; 第二个能峰位于大约9.60 eV, 来自$ {{{\Pi }}}_{{\mathrm{u}}} $共振态, 宽度为2.20 eV; 第三个能峰位于10.10 eV, 宽度大约为0.14 eV, 具有$ {{{\Pi }}}_{{\mathrm{g}}} $对称性. 与异构体A相比, 异构体B的共振特性表现出显著不同. 首先, 异构体B的$ {{{\Sigma }}}_{{\mathrm{g}}}^{+} $共振峰能量位置更低, 并且其宽度增加了0.03 eV. 异构体A在9.0 eV附近的$ {{{\Sigma }}}_{{\mathrm{u}}}^{+} $和$ {{{\Sigma }}}_{{\mathrm{u}}}^{-} $共振峰并没有在异构体B中图示的能区内出现, 转移到了能量更高的能区, 超出了当前研究的能量范围. $ {{{\Pi }}}_{{\mathrm{u}}} $和$ {{{\Pi }}}_{{\mathrm{g}}} $共振峰位置与异构体A相比略微向低能量端移动, 前者共振峰的宽度显著增加. 根据海森伯不确定性原理, 表明该位置的共振态寿命与异构体A相比有显著减少. $ {{{\Pi }}}_{{\mathrm{g}}} $共振峰的宽度则减小了0.1 eV, 变化不大. 表3列出了我们根据相移拟合的共振态位置和宽度.

在异构体C的散射计算中, 冻结了能量最低的8个轨道, 允许9个靶电子和1个散射电子在10个活性轨道中(7a₁—9a₁, 1b₁—3b₁, 3b₂—5b₂, 1a₂)跃迁, 即CAS(10, 10)模型. 计算得到的散射截面结果如图6所示. 表4列出了我们根据相移拟合的共振态位置和宽度参数. 异构体C的截面上前两个能峰位于4.7 eV和8.6 eV, 宽度分别为0.42 eV和1.36 eV, 分别来自A₁和A₂共振态. 第三个能峰位于10.8 eV, 主要是由于10.6 eV的B₂共振态和位于11.0 eV的 A₁共振态的贡献, 它们的宽度分别为3.23 eV和0.56 eV. 异构体C与异构体A和B在结构上存在显著差异, 其结构呈现出环形特征. 这种差异导致了共振态能量位置与异构体A和B相比发生了显著变化. 在8.6 eV处观察到的宽度为1.36 eV的A₂共振峰与Fritiofff等^[14]的实验结果非常接近. 这一共振态可能对Fritiofff等实验共振峰有贡献.

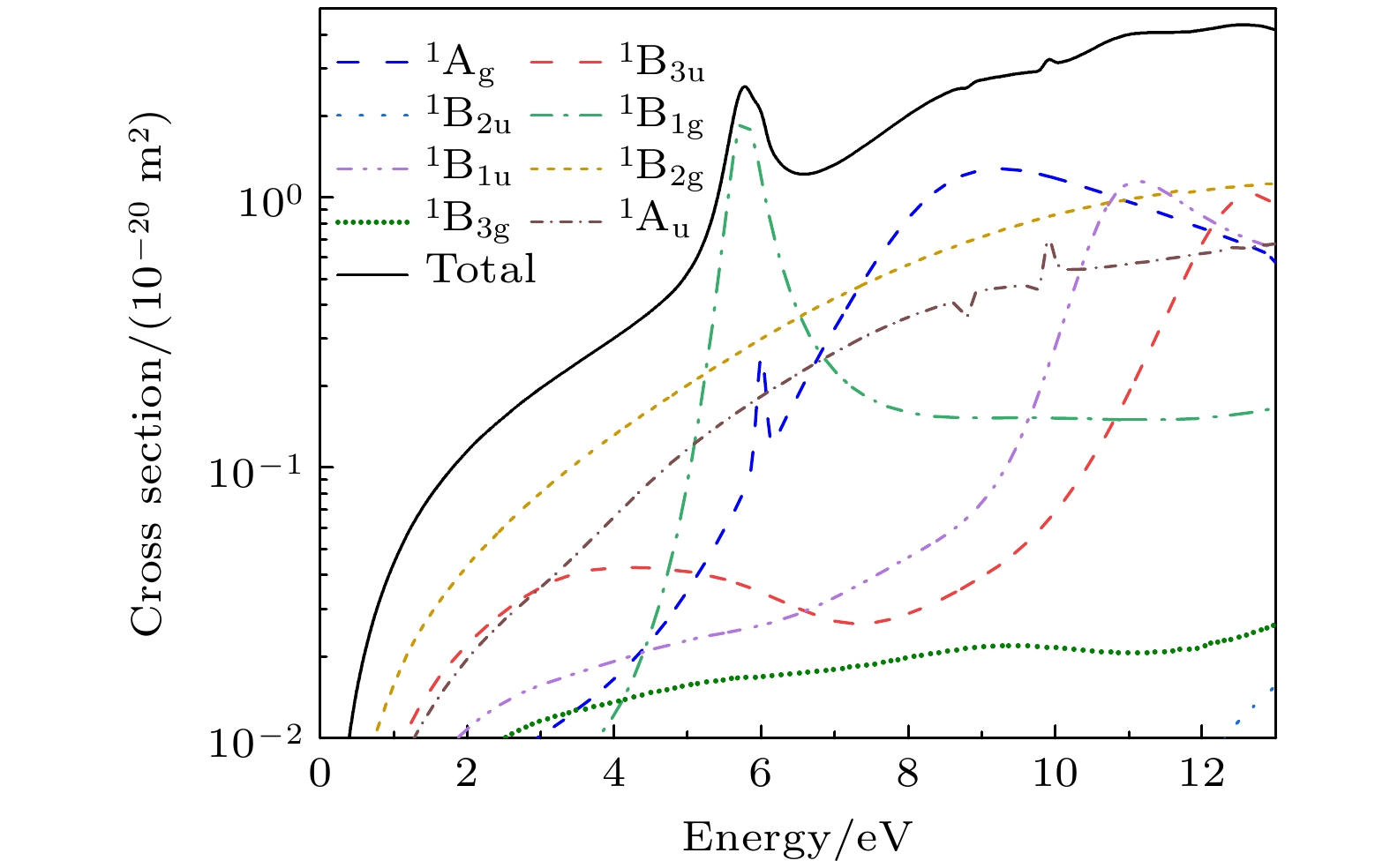
对异构体D, 我们同样冻结能量最低的8个轨道上的16个电子, 其余10个电子可以跃迁到10个活性轨道中(5a_g-6a_g, 3b_3u-4b_3u, 3b_2u, 1b_1g, 1b_1u-2b_1u, 1b_2g, 1b_3g), 得到的截面结果如图7所示. 总截面上第一个能峰位于5.7 eV, 主要来自B_1g共振态, 宽度为0.47 eV. 该能峰右侧位于6.0 eV处的肩膀是由于宽度为0.14 eV的A_g共振态的贡献. 随着能量的增加, 总截面不断抬升, 暗示着可能存在着不同的共振态. 根据我们的计算, 在该能区发现了位于9.2 eV的A_g共振态, 宽度为5.20 eV; 位于11.00 eV宽度为1.80 eV的B_1u共振态. 与异构体C具有三角形结构相比, 异构体D是菱形, 结构发生了显著变化, 导致其共振态位置和对称性发生变化. A_g和B_1u对称性的共振态具有相当大的宽度, 其中A_g共振态的宽度达到了5.20 eV. 表5列出了共振态参数.

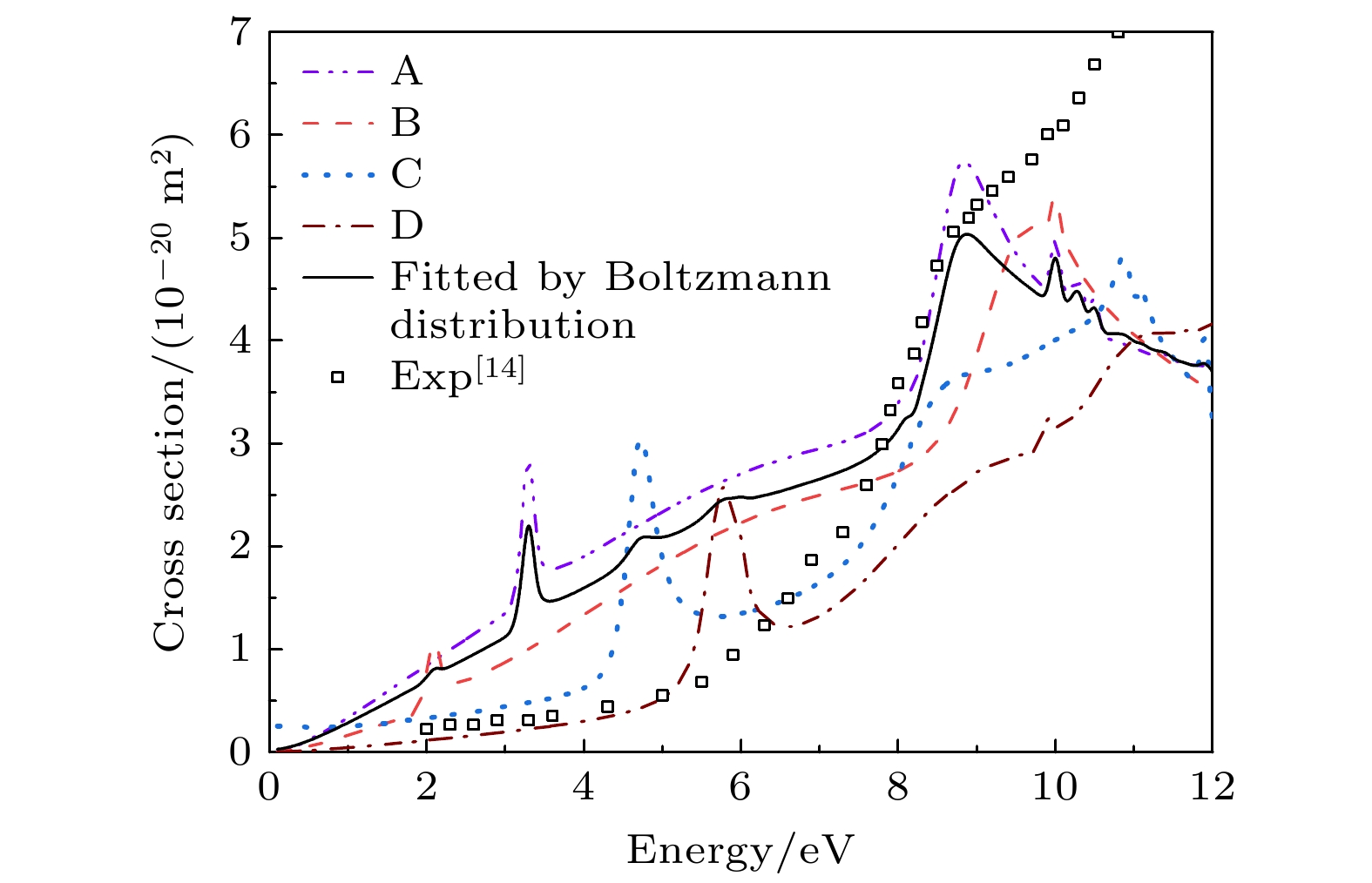
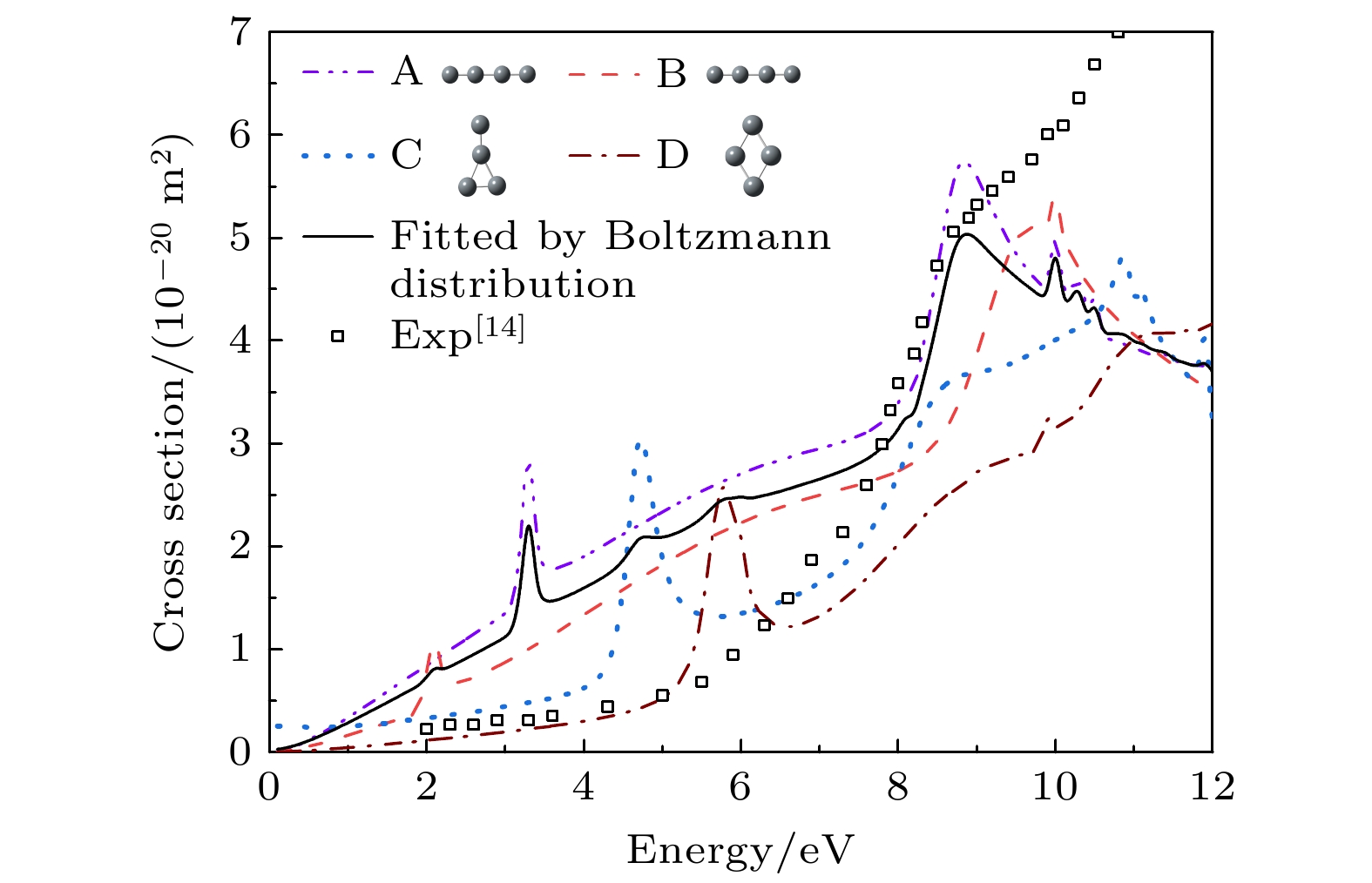
图7列出了四种异构体的弹性散射总截面. 可以看出, 四种异构体均存在一个低能σ*共振态, 随着构型结构由B, A, C到D变化, 该共振态位置由2.1 eV升高到5.8 eV. 共振态表现出明显依赖构型结构的特征. 与此同时, 散射截面也随着异构体结构的变化呈现明显不同, 随着A, B, C到D变化, 截面逐渐减小, 同样呈现出依赖结构的特征. 根据这四种异构体的相对能量, 我们利用Boltzmann分布计算出某一温度下各个异构体丰度, 公式为

其中$ {p_{ij}} $是异构体$ i $相对异构体$ j $的丰度比, $ {n_i} $和$ {n_j} $是两种构型的分子数, $ \Delta E $是两种构型的能量差, $ R $是玻尔兹曼常数, $ T $是温度(单位K). 表6列出了在玻尔兹曼分布下$ {{\mathrm{C}}}_{4}^{-} $四种异构体丰度随温度的变化. 可见在常温(25 ℃)条件下, 异构体A的丰度占比为74.15%, B占比为11.47%, C为7.49%, 而D为6.89%. 基于这一丰度结果和前面计算四种异构体的散射截面, 拟合了在常温下$ {{\mathrm{C}}}_{4}^{-} $异构体四种混合物的电子弹性散射总截面, 如图8所示. 为便于比较, Fritioff等^[14]实验测量的截面也在图中给出. 由图8可以看出, 我们拟合的总截面在小于8.0 eV的低能区, 高于实验测量截面. 我们在8.8 eV处预测一个宽峰结构, 在实验测量中也同样被观察到. 在更高的能区10.0 eV处, 实验测量的截面不断增大, 这主要来自构象A和B的$ {{{\Pi }}}_{{\mathrm{u}}} $以及$ {{{\Pi }}}_{{\mathrm{g}}} $共振态的贡献.

本研究选取了在实验数据上相对缺乏, 但在科学和应用上具有重要性的$ {{\mathrm{C}}}_{4}^{-} $离子作为研究对象. 由于$ {{\mathrm{C}}}_{4}^{-} $离子的散射截面的理论结果尚未有报道, 本文采用R-矩阵方法研究了电子与$ {{\mathrm{C}}}_{4}^{-} $离子的低能碰撞过程. 采用CC单态模型, 研究了0—12 eV能量范围内四种异构体的低能电子弹性积分散射截面. 此外, 还利用玻尔兹曼分布拟合了常温下的弹性积分散射截面. 计算结果显示, 异构体A有5个共振态, 异构体B存在3个共振态、C和D各有4个共振态. Fritiofff等^[14]实验测得位于8.8 eV的共振峰, 重要来自异构体A的$ {{{\Sigma }}}_{{\mathrm{u}}}^{+} $和$ {{{\Sigma }}}_{{\mathrm{u}}}^{-} $共振态的贡献, 以及少部分来自异构体C的A₂共振态贡献. 此外, 当线性异构体A的键长发生变化, 过渡到异构体B时, 可以观察到部分共振态的位置和宽度发生了变化, 表现出明显的依赖构型结构的特征. 另一方面, 本研究提供了$ {{\mathrm{C}}}_{4}^{-} $离子的理论电子散射截面, 报道了可能存在的2价负离子共振态, 为进一步的实验探测提供了可能. 同时报道了共振态的宽度, 为进一步实验测量负离子寿命提供了理论参考. 特别需要指出, 我们预言在3.3 eV的低能区处存在一个势形共振态, 有待实验工作者的进一步证实.