首页
登录
注册
-
石墨烯, 一种由碳原子以sp2杂化轨道组成六角型呈蜂巢状的二维碳纳米材料[1], 以其单层碳原子的极致薄度和高物理特性备受瞩目. 纯净无缺陷石墨烯展现出高达1 TPa的弹性模量[2], 约130 MPa的抗拉强度[2], 以及6%的延伸率[3]. 作为目前制备石墨烯的主流方法, 化学气相沉积(chemical vapor deposition, CVD)法通过精确控制生长过程, 能够大规模生产大尺寸、晶体结构完整的单层或多层石墨烯[4,5]. 然而, 无缺陷石墨烯在实际制备中难以实现, 生长和制备过程中不可避免地会引入空位、位错和晶界等缺陷[6,7]. 这些缺陷对石墨烯的电学、热学和机械性能有着显著影响[8], 缺陷引起的晶格畸变降低了材料的抗拉强度, 增加了裂纹起裂和扩展风险, 使得石墨烯的实际强度很难达到其理论极限[9]. 因此, 深入研究石墨烯的晶界结构和位错运动机理, 对于优化制备工艺和提高性能具有重要意义.
目前普遍认为石墨烯的断裂行为机制与晶界有关, 由于多晶石墨烯晶粒内部无缺陷, 没有残余应力, 使用分子动力学模拟发现多晶石墨烯断裂从晶界处开始, 初始裂纹以晶内或者晶间的方式扩展到多晶的其余部分[10]. 此外, 石墨烯晶界的断裂失效从晶界或畴内开始, 这取决于缺陷排列以及石墨烯畴的晶格取向[11]. 并且, 石墨烯材料的断裂强度与晶界密度有关, 例如无三晶交线(triple-junction-free)的多晶石墨烯随着晶界的密度增大, 断裂强度增大[12]. 在拉伸变形中石墨烯对称倾侧晶界的断裂强度随晶界角的增大而增大[13]. 然而, 晶界对于石墨烯断裂强度的影响通常是复杂的, 晶界处缺陷既可以增强也可以削弱石墨烯的拉伸断裂强度, 这取决于缺陷的密度及其排列[14]. 周文权[9]采用晶体相场法(phase field crystal, PFC)研究了对称和非对称倾侧石墨烯双晶拉伸断裂模式, 沿晶界拉伸变形时, 双晶在变形后期呈穿晶断裂模式, 主要表现为晶界5|7位错处有C—C断裂、纳米微裂纹形核及裂纹向晶内扩展的过程. 然而, 晶界角及位错排列方式与外载荷作用下的石墨烯位错演化行为仍不清晰, 因此有必要深入研究晶界角与位错以及应变石墨烯晶界结构缺陷运动的一般规律. 深入理解石墨烯晶界和位错的变形演化过程, 了解石墨烯的变形与破坏机制, 进而可以通过调控生长条件来控制石墨烯的晶界角和位错密度, 从而优化石墨烯的力学性能, 使其满足特定领域的需求, 并且助于建立更加准确和全面的石墨烯力学模型, 为未来的研究提供坚实的理论基础.
球差校正高分辨率透射电子显微镜[15]、高分辨率透射电子显微镜[16]、原子力显微镜[2]、原位高分辨透射电镜[6]等技术手段支持在原子尺度上对外场作用下的石墨烯结构行为进行探究. 作为实验研究的有效补充, 原子模拟技术已在材料科学领域研究中展现出巨大潜力, 用以揭示材料微观结构的形成过程及其与性能的内在联系[17,18]. 随着计算机模拟技术的快速发展, 分子动力学[19,20]、第一性原理计算[21]、相场法[22–28]、PFC[29]等方法已成为描述材料微观结构演化的强大工具.
分子动力学被用于模拟应力诱导下的石墨烯缺陷行为[30], 但其缺点是模拟中应用的应变速率可能与实际结果相差几个数量级. 传统相场模型可以用于描述石墨烯的外延生长动力学行为, 但很难在原子尺度上描述石墨烯的结构细节[31]. 近年来基于密度泛函理论提出的PFC模型, 由于其原子分辨率和扩散时间尺度被广泛用于晶体结构缺陷行为的研究[32,33], 例如晶界和位错运动[34,35]、晶界预熔、微裂纹的扩展等行为. 通常, 在石墨烯晶界中具有相邻五边形-七边形对的5|7位错[36]. 而在某些取向角度下, 也可能存在其他的缺陷类型, 如5|8|7缺陷等[37,38]. 三模晶体相场模型(three-mode phase-field crystal, PFC3)是标准PFC模型的泛 化[38], 能够产生与振幅、单模、结构PFC模型相同的5|7位错以及更多的欠配位和过配位碳原子的缺陷. 因此, 相较于其他PFC模型, 采用PFC3构建石墨烯晶界的效果更理想.
本文以单层石墨烯为研究对象, 采用三模晶体相场方法建立了石墨烯双晶模型, 深入探究了石墨烯不同角度对称倾侧晶界的结构和位错行为. 针对弛豫和变形过程, 在原子尺度研究了石墨烯晶界上各种位错数量与晶界角的关系, 揭示了拉伸载荷作用下双晶石墨烯的变形与破坏机制, 并从能量角度进行了展开讨论.
-
三模晶体相场模型[30]的无量纲自由能泛函可表述为
式中, F和ρ分别为无量纲的自由能和原子密度; µ为化学势;
$\kappa $ 是表征体系过冷度的参量; λ是唯象参数, 控制体系相对稳定性, 由特定系统的粒子间势决定; L为哈密顿算符;${{\boldsymbol{q}}_{{i}}}$ 和${{\boldsymbol{b}}_{{i}}}$ 为与波矢有关的参量,${{\boldsymbol{q}}_{{i}}}$ 为晶体衍射峰在倒易空间中的位置,${{\boldsymbol{q}}_{0}}$ 控制平衡晶格常数,${{\boldsymbol{b}}_{{i}}}$ 的值由体系中粒子间的相互作用势所决定, 控制石墨烯结构因子中3个峰的相对高度;${\nabla ^2}$ 为拉普拉斯算子. -
在变形过程中采用了等面积条件假设[39,40], 对
$y$ 方向施加拉应变, 无量纲应变速率$\dot \varepsilon $ . 根据等面积条件假设得式中,
$\Delta {x_0}$ 和$\Delta {y_0}$ 代表初始空间步长,$\Delta x$ 和$\Delta y$ 代表形变过程中的空间步长, 模拟$n$ 个时间步长后的空间步长为 -
守恒场序参量
$\rho $ 满足Cahn-Hillard动力学方程[40], 三模晶体相场模型的动力学方程为其中, 在傅里叶空间中
${\nabla ^2} = - {{\boldsymbol{k}}^2}$ . 采用半隐式傅里叶方法对(6)式进行计算:式中,
${\rho _t}$ 和${\rho _{t + \Delta t}}$ 分别表示傅里叶空间中时刻$t$ 和$t + \Delta t$ 的原子密度. 六角晶格的振幅为${A_{{\text{hex}}}} = {1}/{{15}}\left( {3{\rho _0} + \sqrt { - 15\kappa - 36{\rho _0}^2} } \right)$ . 它是表征晶体结构的一个重要参数, 反映了原子或分子的振动强度与晶格稳定性的关联以及原子或分子间的相互作用. 将六角晶格的振幅取反得蜂窝状晶格振幅${A_{{\text{gra}}}} = - {1}/{{15}}\left( {3{\rho _0} + \sqrt { - 15\kappa - 36{\rho _0}^2} } \right)$ [9].采用周期性边界条件, 样品区域为
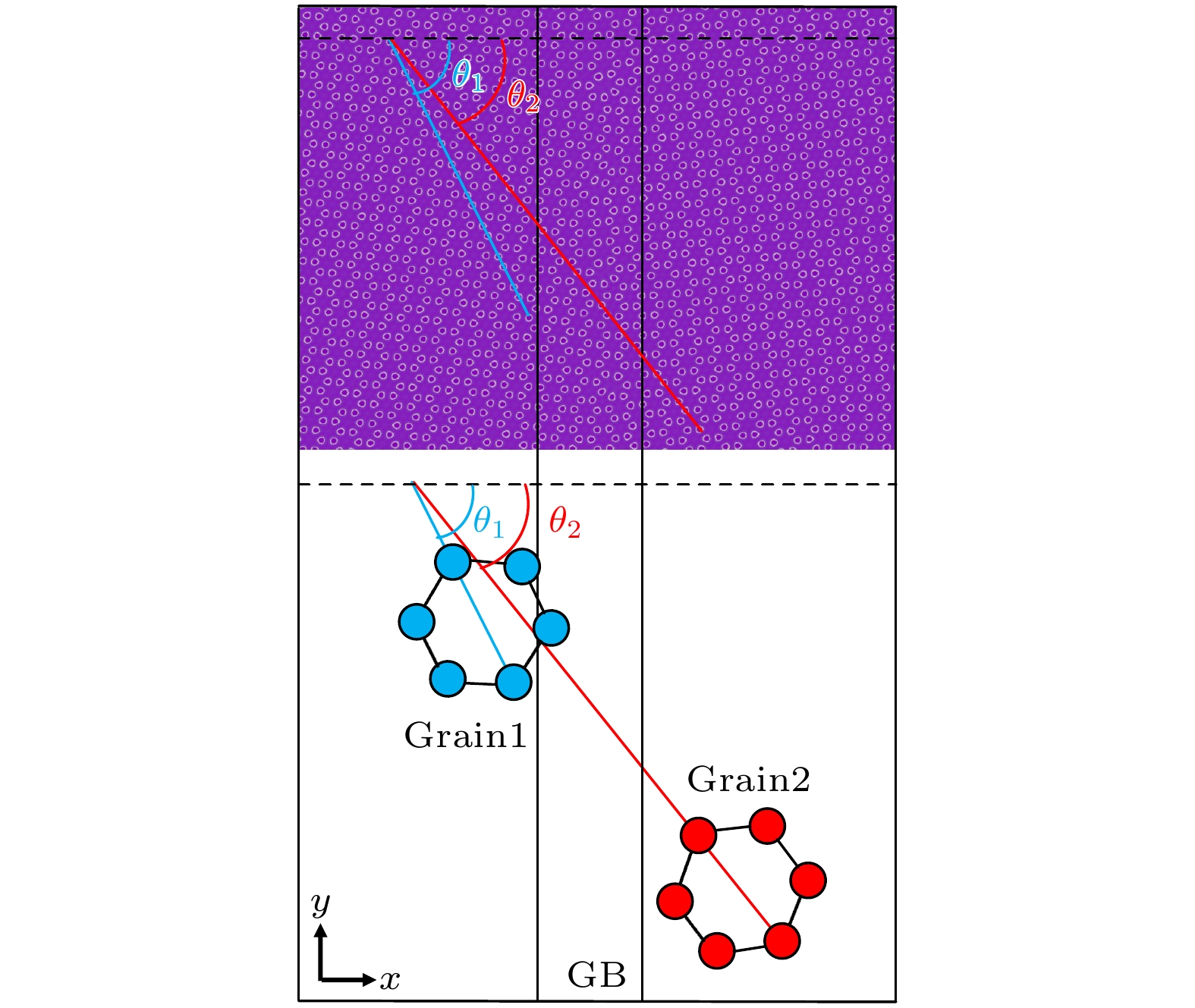
${L_x} \times {L_y} = 500\Delta x \times 500\Delta y$ , 时间步长为$\Delta t = 0.5$ , 空间步长为$\Delta x = \Delta y = 0.5$ . 图1所示为模拟体系结构的示意图, 在模拟区域分别设置两个晶粒, 晶粒1的初始模拟区域设置为${1}/{4}{L_x} - 20 < x < {1}/{4}{L_x} + 20$ , 晶粒2的初始模拟区域设置为${3}/{4}{L_x} - 20 < x < {3}/{4}{L_x} + 20$ , 晶粒1和2的取向角分别设为${\theta _1}$ ,${\theta _2}$ , 晶界角$\theta = {\theta _1} - {\theta _2}$ . 具体模型参数$\kappa $ ,$\rho_0 $ ,$\dot \varepsilon $ ,$\mu $ ,${{\boldsymbol{q}}_{0}}$ ,${{\boldsymbol{q}}_1},{{\boldsymbol{q}}_2},{{\boldsymbol{b}}_0},{{\boldsymbol{b}}_1},{{\boldsymbol{b}}_2}$ 分别为–0.22, –0.2767,$ 1.1 \times 10^{-5}$ , –0.56915, 1,$\sqrt 3 $ , 2, 0, –0.15, 0.2, 施加应力应变的参数如表1所列. 系统弛豫$2 \times {10^4}$ 时间步长以获得结构平衡. -
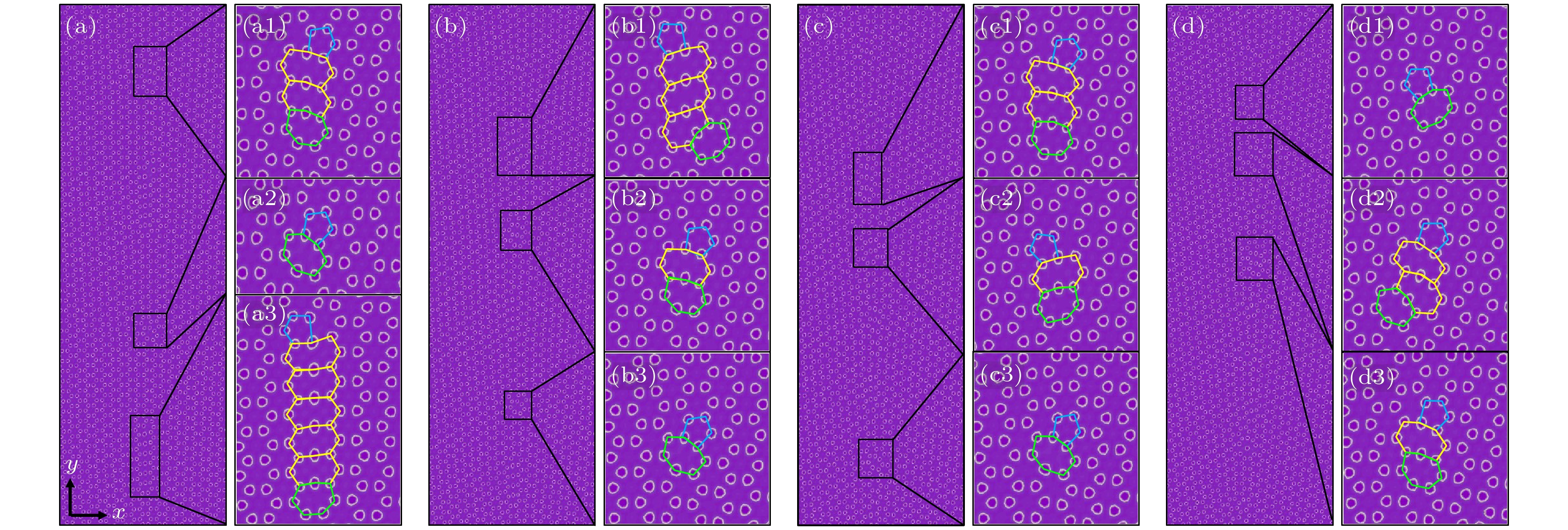
建立石墨烯气相结晶模型, 在温度系数
$\kappa = - 0.22$ 条件下, 初始石墨烯晶核长大并消耗周围气相组织, 形成石墨烯双晶结构.从图2可以看到, 在晶界角度
$\theta = 4^\circ $ 的双晶体系1中, 石墨烯晶界处位错主要为5|7, 5|8|8|7, 5|8|8|8|8|8|7位错; 在晶界角度$\theta = 6^\circ $ 的双晶体系2中, 石墨烯晶界处位错主要为5|7, 5|8|7, 5|8|8|8|7位错. 在晶界角度$\theta = 8^\circ $ 的双晶体系3中, 石墨烯晶界处位错主要为5|7, 5|8|7, 5|8|8|7位错; 在晶界角度$\theta = 10^\circ $ 的双晶体系4中, 石墨烯晶界处位错主要为5|7, 5|8|7, 5|8|8|7位错.5|7位错是石墨烯最常见的位错结构, 5和7分别代表一个五边形和七边形碳元环(五角元胞和七角元胞), 是相邻的五边形-七边形结构; 5|8|7位错中的5, 8, 7分别代表一个五边形、八边形和七边形碳元环(五角元胞、八角元胞和七角元胞), 是相邻的五边形-八边形-七边形结构; 5|8|8|7, 5|8|8|8|7, 5|8|8|8|8|8|7位错也同理.
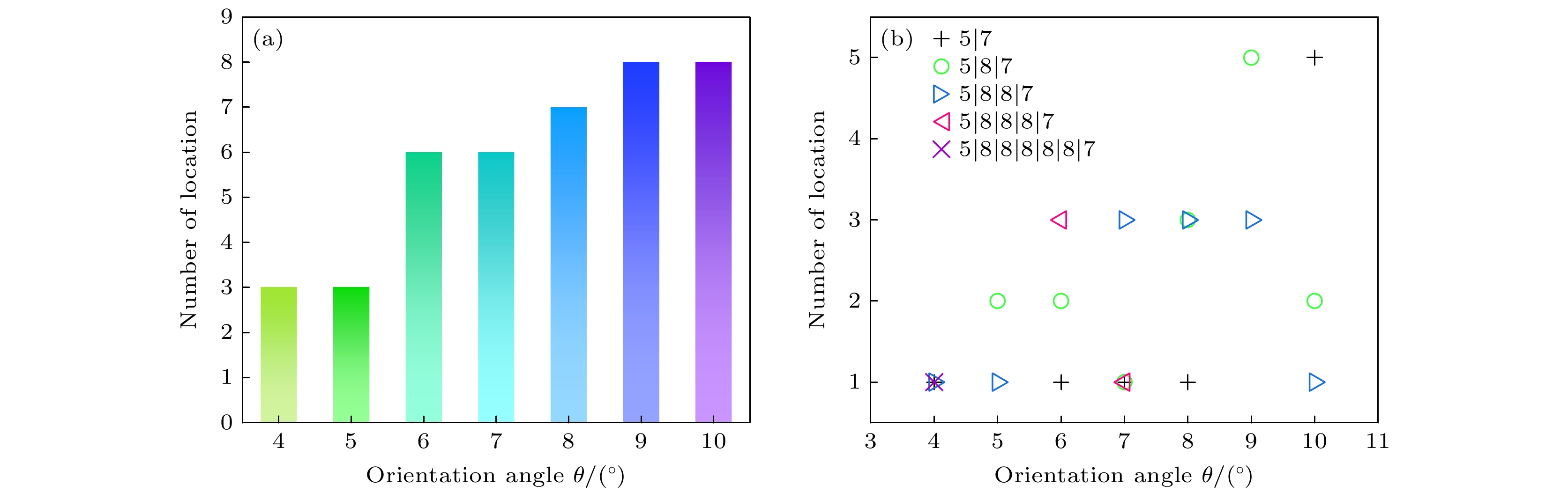
图3是双晶石墨烯体系晶界角与晶界位错个数的关系图. 图3(a)中晶界角为 4°—10°时, 两晶粒间形成由不连续位错构成的小角度晶界, 可以直观地看出随着晶界角的增大, 晶界上的位错数目递增. 从图3(b)可以看出, 晶界角为4°, 6°, 8°, 10°的双晶石墨烯晶界中均有5|7位错, 且随着晶界角θ增大, 5|7位错数量呈增大趋势. 而在晶界角为6°, 7°和4°的双晶石墨烯体系中, 晶界处分别存在5|8|8|8|7位错与5|8|8|8|8|8|7位错.
-
对
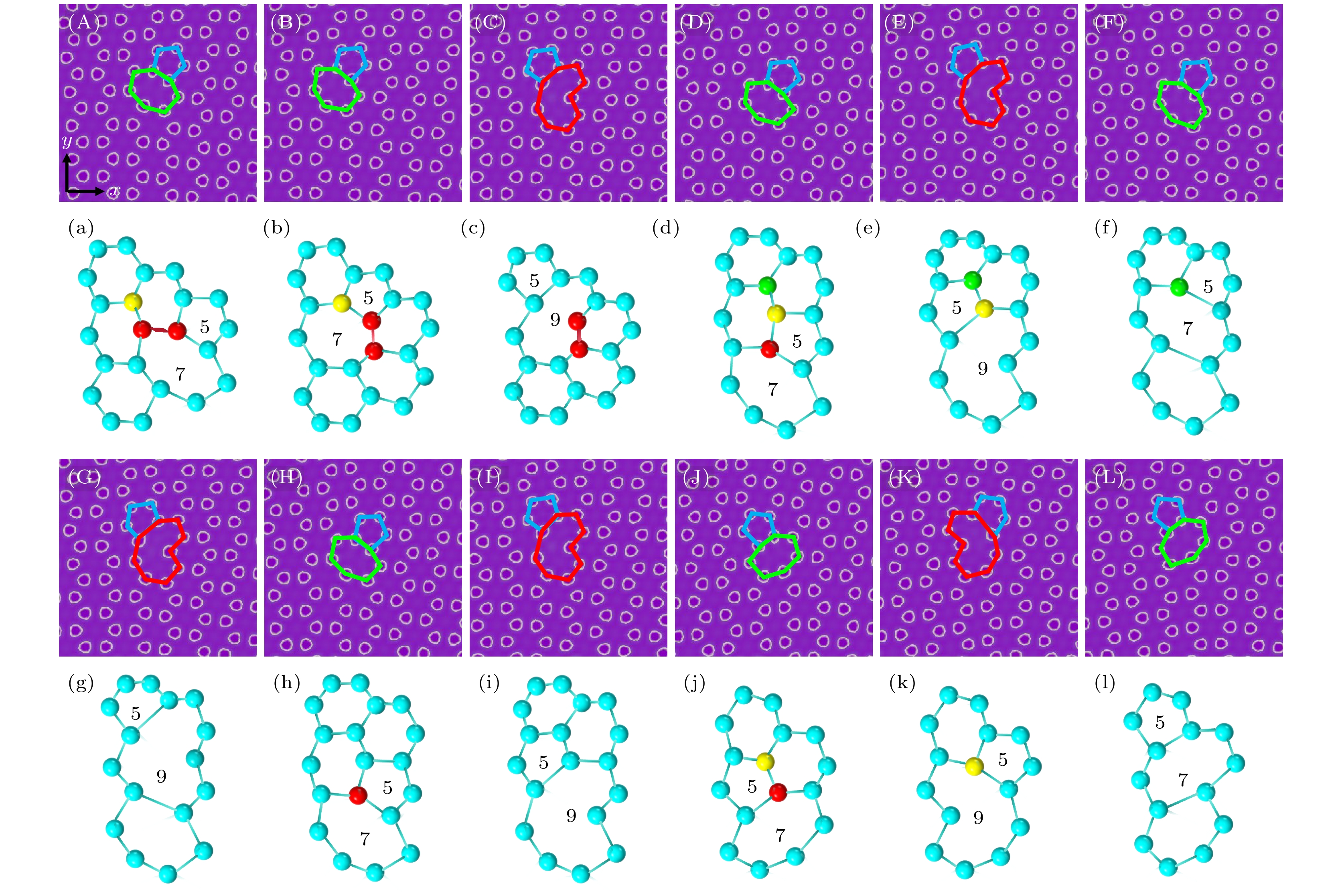
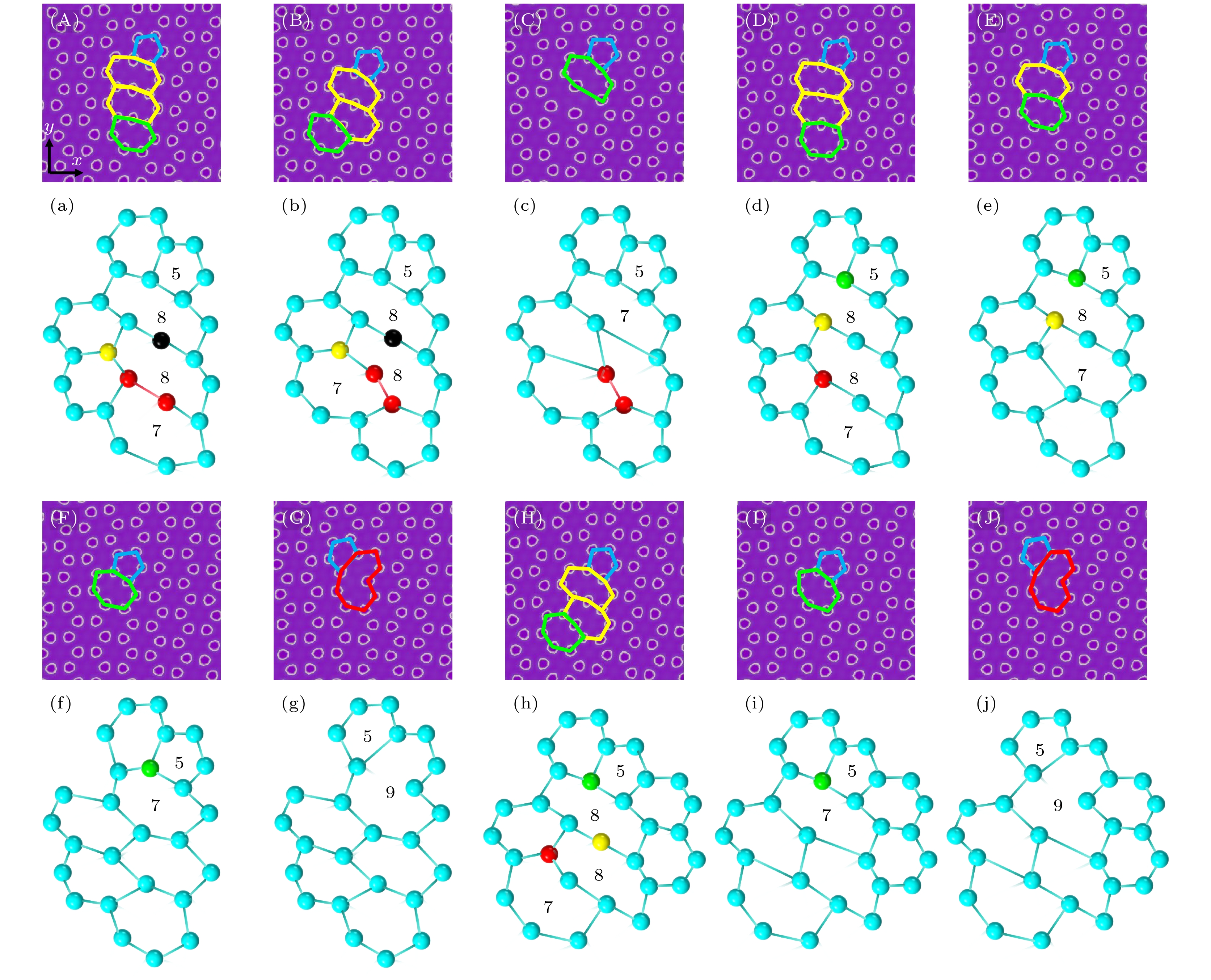
$y$ 方向施加拉应变, 晶界角为4°, 6°, 8°, 10°时, 5|7位错的演变过程分别对应图4(a)—(c)、图4(d)—(g)、图4(h)和图4(i), 图4(j)—(l).随着应变的施加, 图4(a)—(c)中, 5|7位错的C—C键(红色)顺时针旋转90°, 即发生Stone-Wales变换(5|7位错滑移)形成图4(b); 随后因C—C键断裂, 5|7位错的一个C原子(黄色原子)丢失, 形成5|9位错. 图4(d)—(g)中, 5|7位错的两个C原子(红色和黄色原子)丢失, 先后形成5|9位错和5|7位错, 图4(d)—(f)的演化即5|7位错的攀移(5|7位错丢失了C—C键); 最后5|7位错丢失C原子(绿色原子)形成5|9位错. 图4(h)和图4(i)中, 5|7位错的C原子(红色原子)丢失, 形成5|9位错. 图4(j)—(l)中, 5|7位错在应力加载下会进行2次攀移.
-
对
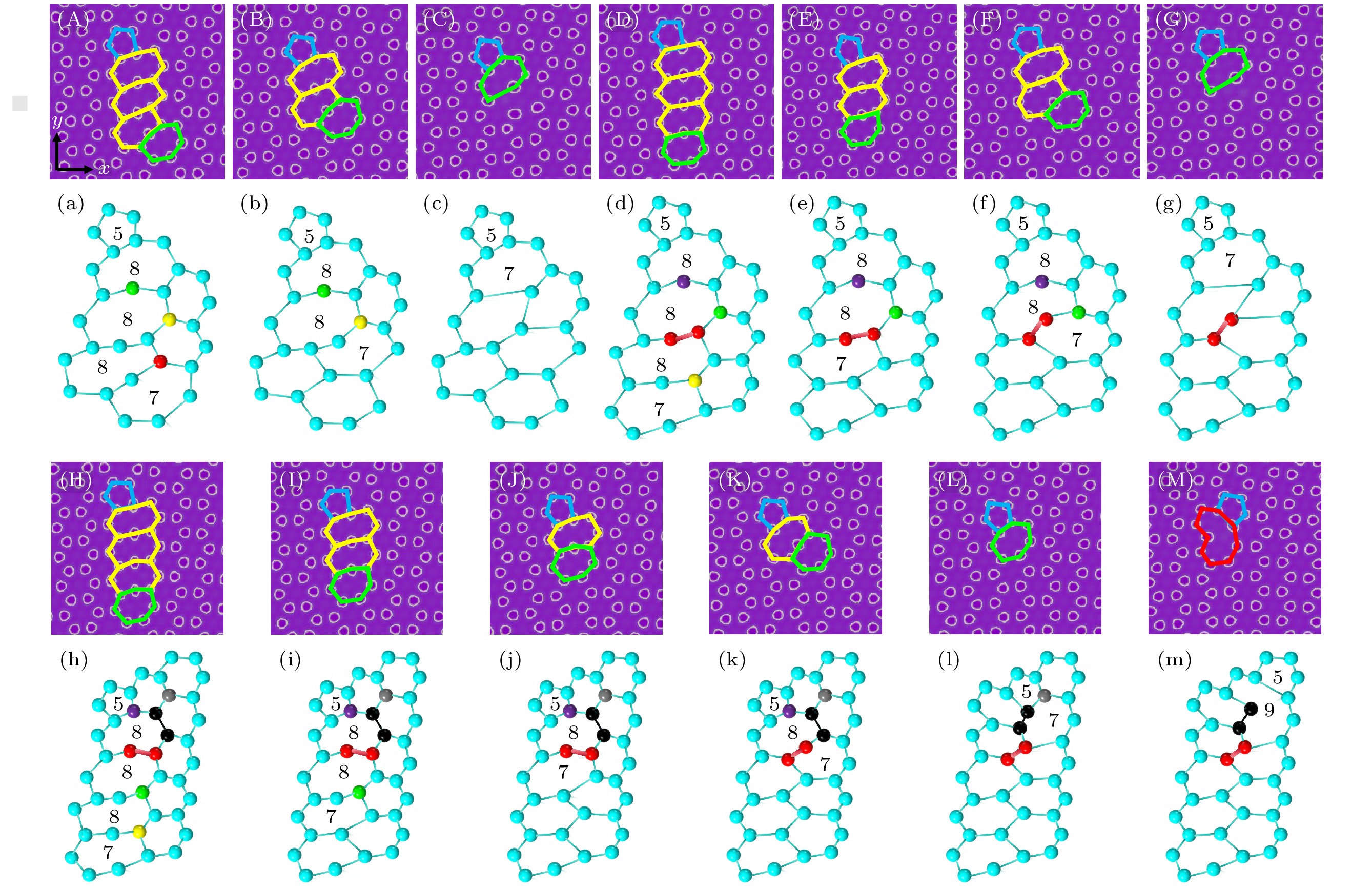
$y$ 方向施加拉应变, 晶界角为6°, 8°和10°时, 5|8|7位错的演变过程分别对应图5(a)—(d)、图5(e)—(h)和图5(i)—(k).随着应变的施加, 图5(a)—(d)中, 5|8|7位错的C—C键(红色)顺时针旋转90°, 变成图5(b)中的5|8|7位错; 然后两个C原子(黄色和绿色原子)丢失, 先后形成5|7位错和5|9位错. 图5(e)—(h)中, 5|8|7位错中C—C键(红色)先逆时针旋转60°, 然后一个C原子(黄色原子)丢失; 接着C—C键(黑色)顺时针旋转60°, 变成5|7位错; 最后5|7位错丢失一个C原子(绿色原子)形成5|9位错. 图5(i)—(k)中, 5|8|7位错丢失两个C原子(黄色和绿色原子)分别形成5|7, 5|9位错.
-
对
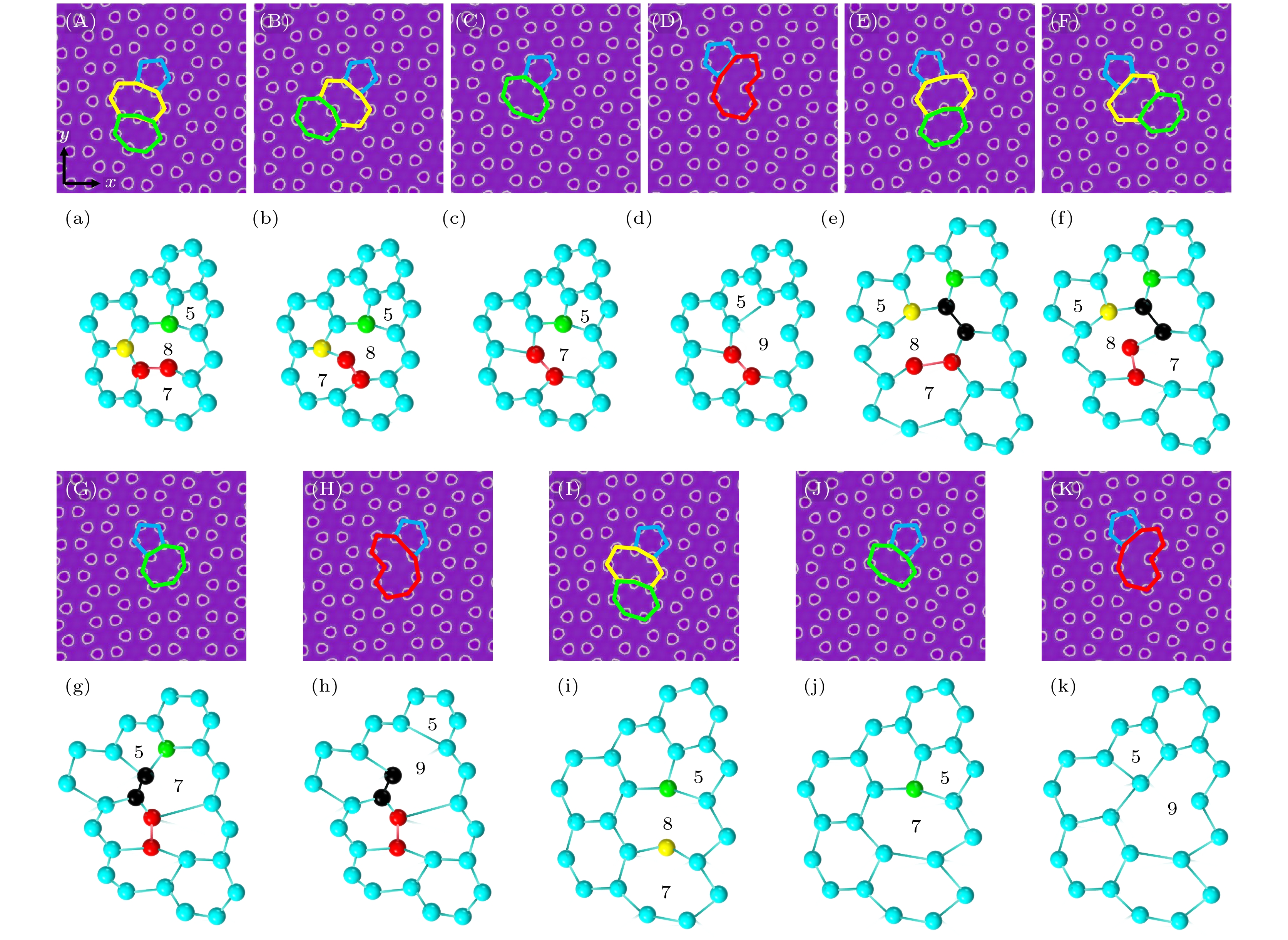
$y$ 方向施加拉应变, 晶界角为4°, 8°和10°时, 5|8|8|7位错的演变过程分别对应图6(a)—(c)、图6(d)—(g)和图6(h)—(j).随着应变的施加, 图6(a)—(c)中, 5|8|8|7位错的C—C键(红色)顺时针旋转30°, 变成图6(b)的5|8|8|7位错; 然后两个C原子(黑色和黄色原子)先后丢失, 形成5|7位错. 图6(d)—(g)和图6(h)—(j)中, 5|8|8|7位错的3个C原子(红色、黄色和绿色原子)丢失, 先后形成5|8|7位错、5|7位错和5|9位错.
-
对
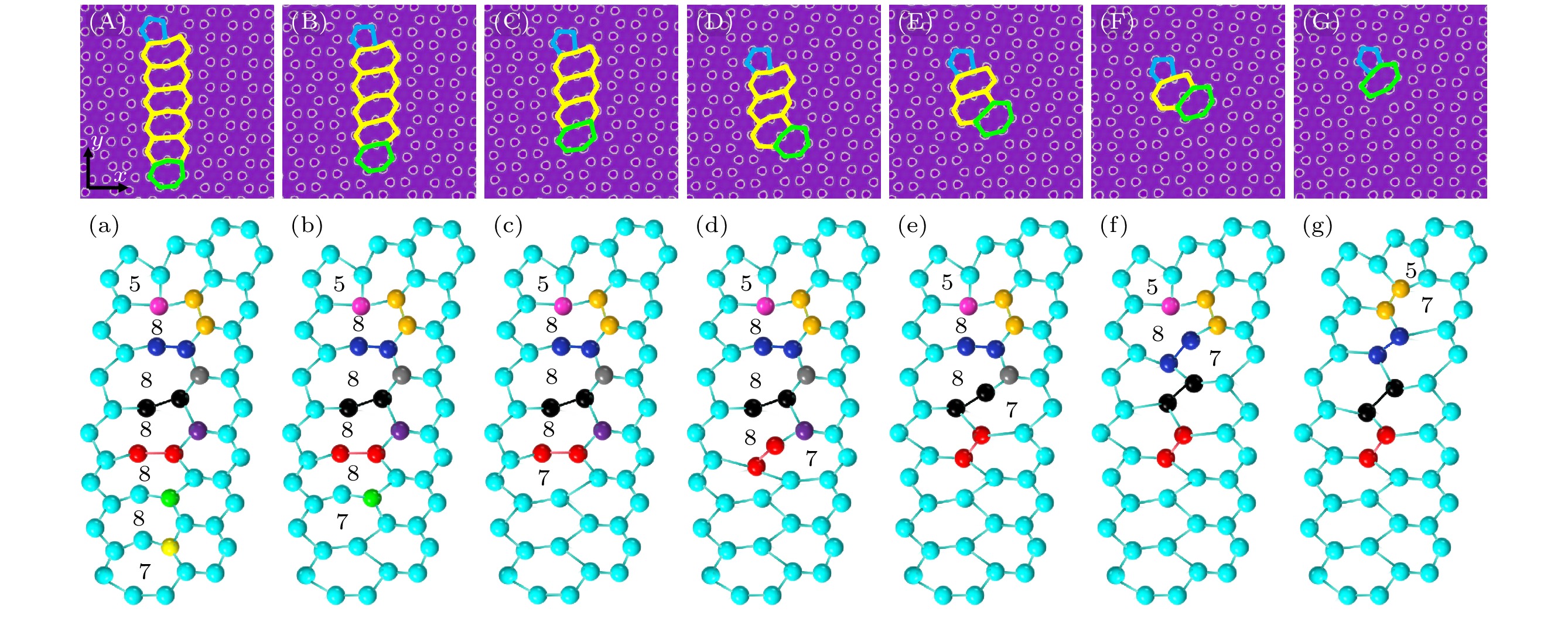
$y$ 方向施加拉应变, 晶界角为6°时, 5|8|8|8|7位错的演变过程有3种情况, 分别对应图7(a)—(c)、图7(d)—(g)和图7(h)—(m).随着应变的施加, 图7(a)—(c)中, 5|8|8|8|7位错的3个C原子(红色、黄色和绿色原子)丢失, 先后形成5|8|8|7位错和5|7位错. 图7(d)—(g)中, 5|8|8|8|7位错的C原子(黄色原子)丢失, 形成5|8|8|7位错; 然后C—C键(红色)逆时针旋转60°, 变成图7(f)的5|8|8|7位错; 接着两个C原子(绿色和紫色原子)丢失, 先后变成5|8|7位错和5|7位错. 图7(h)—(m)中, 5|8|8|8|7位错的两个C原子(黄色和绿色原子)丢失, 先后形成5|8|8|7位错和5|8|7位错; 接着C—C键(红色)逆时针旋转60°, 形成图7(k)的5|8|7位错; 然后C原子(紫色原子)丢失, 同时C—C键(黑色)顺时针旋转90°, 形成图7(l)的5|7位错; 最后一个C原子(灰色原子)丢失, 形成5|9位错.
-
对
$y$ 方向施加拉应变, 晶界角为4°时, 5|8|8|8|8|8|7位错的演变过程如图8所示. 随着应变的施加, 两个 C原子(黄色和绿色原子)丢失, 先后变成5|8|8|8|8|7位错和5|8|8|8|7位错; 接着C—C键(红色)逆时针旋转60°, 形成图8(d)的5|8|8|8|7位错; 然后C原子(紫色原子)丢失, 接着C—C键(黑色)逆时针旋转30°, 形成图8(e)的5|8|8|7位错; 然后C原子(灰色原子)丢失, 接着C—C键(蓝色)逆时针旋转30°, 形成图8(f)的5|8|7位错; 然后C原子(粉色原子)丢失, 接着C—C键(金色)顺时针旋转30°, 形成图8(g)的5|7位错. -
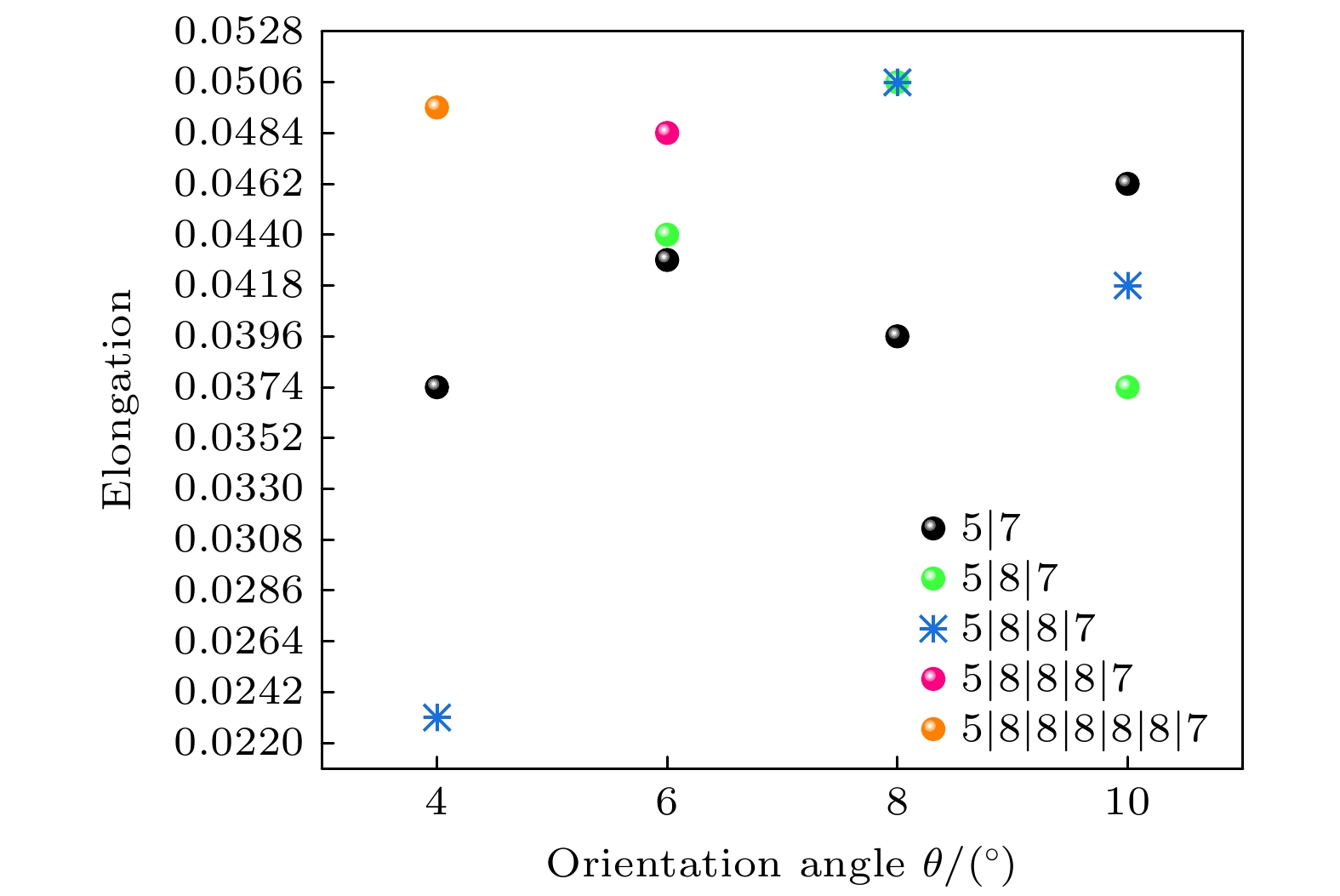
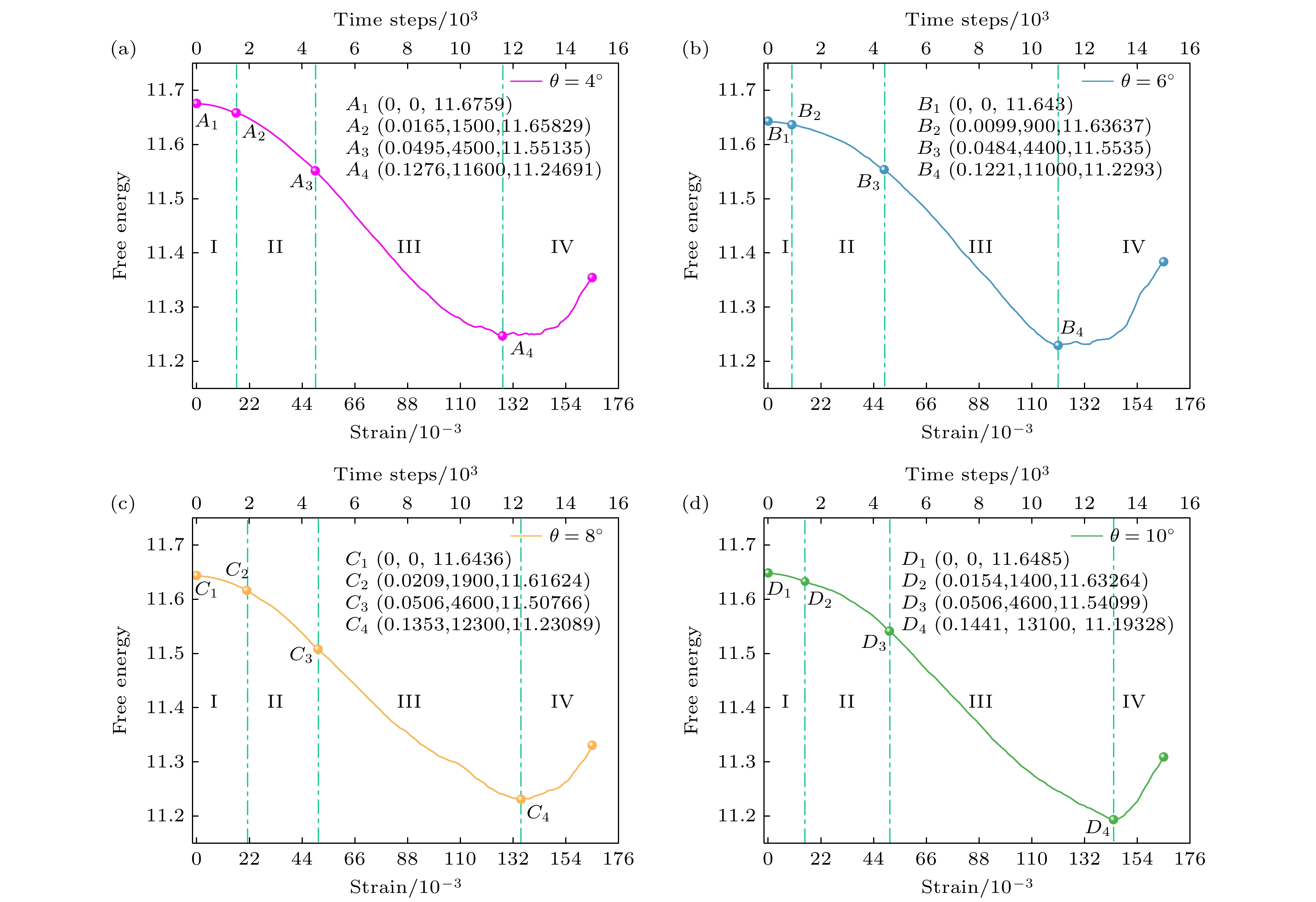
分析了石墨烯小角对称倾侧晶界各种位错失效需要的应变量及自由能的变化(图9和图10所示). 随着应变的施加, 4种不同角度晶界处的各种位错都会经历因C—C键的断裂造成的C原子丢失以及C—C键的旋转, 且最后会演化成5|7或5|9位错.
图9中, 晶界角为4°的5|8|8|8|8|8|7位错在
$\varepsilon = 0.0495$ 后失效, 晶界角为6°的5|8|8|8|7位错在$\varepsilon = 0.0484$ 后失效, 晶界角为8°的5|8|7位错和5|8|8|7位错在$\varepsilon = 0.0506$ 后失效; 4种体系中5|7位错的最大$\varepsilon = 0.0462$ . 前者位错较5|7位错都可以有利于石墨烯性能的提高.图10给出了等面积变形下不同体系的自由能密度曲线随演化时间的响应关系. 结合晶界位错演化特征, 根据自由能密度曲线斜率的变化以及晶界位错是否开始发生结构的变化、失效, 将其自由能曲线划分为4个阶段.
(I)位错反应孕育期. 施加应力释放晶界能, 外力输入的能量微小于系统消耗的能量, 这一时期只有能量的减小且自由能降低缓慢, 其中晶界位错发生微变形, 但并未改变其结构.
(II)位错反应期. 施加应力的能量小于系统消耗的能量, 当应变达到一定值(即第(I), (II)阶段分界点的应变值)时, 晶界的位错在拉伸变形下开始发生成5|8|8|8|8|8|7, 5|8|8|8|7, 5|8|8|7, 5|8|7, 5|7到5|7或5|9位错的转变, 体系缺陷密度大幅度降低, 此时内应力得到松弛, 体系自由能降低, 降低速度快于第(I)阶段. 这一阶段位错演化主要原因是系统中具“不相容位错”, 即与蜂窝晶格不相容(文中为5|8|8|8|8|8|7, 5|8|8|8|7和5|8|8|7位错)和5|8|7位错, 由于应力的施加, 演化为比“不相容位错”和5|8|7位错更小能量的位错, 即5|7, 5|9位错, 在文献[38]中可以得到验证. 由于“不相容位错”具有更高能量, 则其更有利于石墨烯抗拉性能的提高.
(III)变形后期. 施加应力的能量远小于系统消耗的能量, 系统晶界的单个位错, 即5|7及5|9位错开始失效, 体系自由能呈大幅度降低趋势.
(IV)变形终期. 应变达到0.1221—0.01441左右时, 施加应力的能量远高于系统能量的消耗, 体系自由能升高, 此时双晶石墨烯体系已经完全失效.
研究发现在拉伸变形过程中, 4种晶界位错演化过程的自由能变化趋势是相同的, 都是逐渐降低到拐点后再升高, 最后位错行为不能有效缓解体系因持续加载造成的应力集中, 导致失效. 可以看出在(I)和(II)阶段应变最多(0.0506)且自由能下降最多(0.13594)的是晶界角为8°的双晶石墨烯体系, 此体系晶界包括3个5|8|8|7和3个5|8|7位错, 在第(I)和(II)阶段抗拉能力较强. 第(III)阶段变形继续增大, 则系统能量继续降低, 此阶段自由能降低最多(0.34771)的是晶界角为10°的双晶石墨烯体系, 这个体系在(III)阶段的抗拉能力强. 第(IV)阶段, 晶界角为6°的双晶石墨烯体系自由能增加的最多, 这个阶段体系已经完全失效. 相比较下, 可以明显看出在(I), (II), (III)阶段中, 晶界角为10°的石墨烯体系所承受应变最大为0.1441, 自由能下降最多为0.45528, 且在拐点处自由能最低, 即总体抗拉能力最强.
在实际制备石墨烯时, 可通过调控石墨烯的晶界角, 使系统具有更优秀抗拉能力的位错密度及位错结构组合, 使其在第(I), (II), (III)阶段所承受的应变更大, 从而优化石墨烯的力学性能.
-
利用三模PFC模型在原子尺度上模拟了石墨烯小角对称倾侧晶界各种位错在应变作用下的演化过程, 得到了如下主要结论.
1)在不同晶界角的石墨烯气相结晶的模拟结果中, 随着晶界角的增大, 石墨烯晶界位错数量增多, 且5|8|8|8|8|8|7, 5|8|8|8|7和5|8|8|7位错减少, 5|8|7和5|7位错增多.
2)随着应变的施加, 4种晶界的各种位错都会因C—C键的断裂而丢失C原子以及C—C键的旋转演化成5|7或5|9位错, 然后失效.
3) 5|8|8|8|8|8|7, 5|8|8|8|7, 5|8|8|7, 5|8|7位错较5|7位错都有利于石墨烯性能的提高.
4)在拉伸变形过程中, 4种晶界位错演化过程的自由能变化趋势是相同的, 都是逐渐降低到拐点后再升高, 相比较下晶界角为10°的体系在(I), (II), (III)阶段中自由能下降最多, 且总体抗拉能力最强.
三模晶体相场法研究应变诱导石墨烯晶界位错演化
Strain induced dislocation evolution at graphene grain boundary by three-mode phase-field crystal method
-
摘要: 晶界结构在石墨烯变形过程中的演变规律及作用机制对理解石墨烯变形行为具有重要意义. 本文采用三模晶体相场模型, 在原子尺度上深入研究了石墨烯小角对称倾侧晶界处位错在应变作用下的演化机理. 结果发现, 随着晶界角的增大, 晶界位错密度降低, 特定类型的位错(5|8|7位错和5|7位错)数量上升. 在与晶界平行的应力加载下, 晶界处位错因C—C键断裂或旋转, 转化为5|7或5|9型位错, 这是由于较大自由能的位错在拉伸下演化为小能量的位错, 这有利于石墨烯性能的提高. 拉伸载荷下, 含不同角度晶界的体系自由能变化呈现相同趋势: 初始下降至拐点后出现异常上升, 位错行为不能有效缓解体系因持续加载造成的应力集中, 导致失效. 本工作有助于从原子尺度理解石墨烯微观力学行为.Abstract:
The evolution law and mechanism of grain boundary structure in the deformation process of graphene are of great significance for understanding the deformation behavior of graphene and optimizing its mechanical properties. In this work, single-layer graphene is taken as the research object and a double crystalline graphene model is established by using the three-mode phase-field crystal method, thereby in depth ascertaining the evolution mechanism of dislocations at small-angle symmetrical tilt grain boundaries in graphene under strain. In view of the relaxation and deformation process, the relationship between the number of multiple dislocations and the grain boundary angle of graphene is studied on an atomic scale, and the deformation and failure mechanism of double crystalline graphene under tensile load are revealed, and also discussed from the perspective of the free energy. It is found that, after relaxation, with the increase of grain boundary angle, the density of dislocations at the grain boundary decreases, and the number of specific types of dislocations (5|8|7 and 5|7 dislocations) increases. Under stress loading parallel to the grain boundary, the changes of free energy of the systems containing grain boundaries with different angles show the same trend: at first, they fall to the inflection point and then rise abnormally, and the dislocation behavior cannot effectively alleviate the stress concentration caused by continuous loading in the system, leading to failure finally. Under tensile load, the free energy changes of the systems are divided into four stages, they being stage (I), in which the dislocations at grain boundaries are slightly deformed but do not change their structure, stage (II), in which dislocations at the grain boundaries are transformed into 5|7 or 5|9 dislocation due to C—C bond fracture or rotation, and the dislocations that are “incompatible” have higher energy, making them more conducive to improving the tensile properties of graphene, stage (III), in which the 5|7 and 5|9 dislocations begin to fail, and the free energy shows a tendency to decrease significantly, and stage (IV), in which the double crystalline graphene systems are completely in failure. The system with a grain boundary angle of 10° exhibits the most substantial deduction in free energy in stages (I), (II), and (III), and possesses the highest overall tensile strength. This work contributes to understanding the micromechanical behavior of graphene on an atomic scale. -
Key words:
- phase-field crystal method /
- graphene /
- grain-boundaries /
- dislocations .
-
-
图 1 模拟结构示意图(
${\theta _1}$ 为晶粒1取向角,${\theta _2}$ 为晶粒2取向角)Figure 1. Schematic diagram of simulation structure,
${\theta _1}$ is grain 1 orientation angle,${\theta _2}$ is grain 2 orientation angle.
图 2 石墨烯气相结晶图(蓝、绿、黄色标记石墨烯的五角元胞、七角元胞、八角元胞) (a)—(d)晶界角分别为4°, 6°, 8°, 10°, 其中黑框中为晶界处位错; (a1)—(a3), (b1)—(b3), (c1)—(c3), (d1)—(d3)是对应的放大图
Figure 2. Vapor crystallization diagram of graphene: (a)–(d) Grain boundary angles are 4°, 6°, 8° and 10°, respectively, dislocations at grain boundaries are shown in the black box; (a1)–(a3), (b1)–(b3), (c1)–(c3), (d1)–(d3) are the corresponding enlarged images. Blue, green, yellow labeled graphene pentagonal cells, heptagonal cells, octagonal cells
图 3 双晶石墨烯体系中晶界处位错数目统计结果 (a) 晶界角为4°—10°的总位错数目; (b) 晶界角为4°—10°的各种位错数目
Figure 3. Statistical results of the number of dislocations at the grain boundaries in the double crystalline graphene system: (a) Total number of dislocations at grain boundary angles of 4°–10°; (b) number of various dislocations at grain boundary angles of 4°–10°.
图 4 石墨烯晶界5|7位错在应变下的演化图 (A)—(C), (D)—(G), (H)—(I), (J)—(L)分别对应晶界角为4°, 6°, 8°, 10°的石墨烯晶界5|7位错在应变下的演化图; (a)—(c), (d)—(g), (h)—(i), (j)—(l)为对应的演化过程示意图; (A)—(C)的应变
$\varepsilon $ 分别为0, 0.0297, 0.0352; (D)—(G) 的应变$\varepsilon $ 分别为0, 0.0286, 0.0308, 0.0352; (H), (I) 的应变$\varepsilon $ 分别为0, 0.0363; (J)—(L) 的应变$\varepsilon $ 分别为0, 0.0297, 0.0363 (演化过程示意图中标记的5, 7, 8, 9分别代表石墨烯五、七、八、九角元胞, 分别对应相应演化图中石墨烯蓝、绿、黄、红色标记的五、七、八、九角元胞, 图5—8中标记解释与此相同)Figure 4. Evolution diagram of 5|7 dislocations at graphene grain boundaries under strain: (A)–(C), (D)–(G), (H)–(I), (J)–(L) are the evolution diagrams of 5|7 dislocations at graphene grain boundaries under strain for corresponding grain boundary angles of 4°, 6°, 8° and 10°; (a)–(c), (d)–(g), (h)–(i), (j)–(l) are the evolution process diagrams. The strains
$\varepsilon $ of (A)–(C) are 0, 0.0297, 0.0352, (D)–(G) are 0, 0.0286, 0.0308, 0.0352, (H), (I) are 0, 0.0363, and (J)–(L) are 0, 0.0297, 0.0363. The 5, 7, 8, 9 marked in the evolution diagram represent the graphene pentagonal, heptagonal, octagonal, and nougonal cells respectively, corresponding to the pentagonal, heptagonal, octagonal, and nougonal cells marked in the corresponding evolution process diagram in blue, green, yellow, and red respectively. The explanations of labels in Figure 5-8 are the same as those in Figure 4.
图 5 石墨烯晶界5|8|7位错在应变下的演化图 (A)—(D), (E)—(H), (I)—(K)分别对应晶界角为6°, 8°, 10°的石墨烯晶界5|8|7位错在应变下的演化图; (a)—(d), (e)—(h), (i)—(k)是对应的演化过程示意图; (A)—(D)的应变
$\varepsilon $ 分别为0, 0.0209, 0.0352, 0.0407, (E)—(H) 的应变$\varepsilon $ 分别为0, 0.0209, 0.0429, 0.0473, (I)—(K) 的应变$\varepsilon $ 分别为0, 0.0165, 0.0319Figure 5. Evolution diagram of 5|8|7 dislocations at graphene grain boundaries under strain: (A)–(D), (E)–(H), (I)–(K) are the evolution diagrams of 5|8|7 dislocations at graphene grain boundaries under strain for corresponding grain boundary angles of 6°, 8° and 10°; (a)–(d), (e)–(h), (i)–(k) are the corresponding evolution process diagrams; the strains
$\varepsilon $ of (A)–(D) are 0, 0.0209, 0.0352, 0.0407, (E)–(H) are 0, 0.0209, 0.0429, 0.0473, (I)–(K) are 0, 0.0165, 0.0319.
图 6 石墨烯晶界5|8|8|7位错在应变下的演化图 (A)—(C), (D)—(G), (H)—(J)分别对应晶界角为4°, 8°, 10°的石墨烯晶界5|8|8|7位错在应变下的演化图; (a)—(c), (d)—(g), (h)—(j)是对应的演化过程示意图; (A)—(C)的应变
$\varepsilon $ 分别为0, 0.0165, 0.022, (D)—(G)的应变$\varepsilon $ 分别为0, 0.0253, 0.0363, 0.0473, (H)—(J)的应变$\varepsilon $ 分别为0, 0.0154, 0.0242Figure 6. Evolution diagram of 5|8|8|7 dislocations at graphene grain boundaries under strain: (A)–(C), (D)–(G), (H)–(J) are the evolution diagrams of 5|8|8|7 dislocations at graphene grain boundaries under strain for corresponding grain boundary angles of 4°, 8° and 10°; (a)–(c), (d)–(g), (h)–(j) are the corresponding evolution process diagrams; the strains
$\varepsilon $ of (A)–(C) are 0, 0.0165, 0.022, (D)–(G) are 0, 0.0253, 0.0363, 0.0473, (H)–(J) are 0, 0.0154, 0.0242.
图 7 石墨烯晶界5|8|8|8|7位错在应变下的3种演化图 (A)—(C), (D)—(G), (H)—(M) 是晶界角为6°的石墨烯晶界5|8|8|8|7位错在应变下的3种演化图; (a)—(c), (d)—(g), (h)—(m)是对应的演化过程示意图; (A)—(C) 的应变
$\varepsilon $ 分别为0, 0.0132, 0.0209, (D)—(G)的应变$\varepsilon $ 分别为0, 0.0132, 0.0242, 0.0297, (H)—(M)的应变$\varepsilon $ 分别为0, 0.099, 0.0187, 0.0264, 0.0407, 0.0462Figure 7. Three evolution diagrams of 5|8|8|8|7 dislocations at graphene grain boundaries under strain: (A)–(C), (D)–(G), (H)–(M) are three evolution diagrams of 5|8|8|8|7 dislocations at graphene grain boundaries under strain for the grain boundary angle of 6°; (a)–(c), (d)–(g), (h)–(m) are the corresponding evolution process diagrams; the strains
$\varepsilon $ of (A)–(C) are 0, 0.0132, 0.0209, (D)–(G) are 0, 0.0132, 0.0242, 0.0297, (H)–(M) are 0, 0.099, 0.0187, 0.0264, 0.0407, 0.0462.
图 8 石墨烯晶界5|8|8|8|8|8|7位错在应变下的演化图 (A)—(G)晶界角为4°的石墨烯晶界5|8|8|8|8|8|7位错在应变下的演化图; (a)—(g)是演化过程示意图; (A)—(G)的应变
$\varepsilon $ 分别为0, 0.0231, 0.0281, 0.0319, 0.0341, 0.0374, 0.0473Figure 8. Evolution diagram of 5|8|8|8|8|8|7 dislocations at graphene grain boundaries under strain: (A)–(G) are the evolution diagrams of 5|8|8|8|8|8|7 dislocations at graphene grain boundaries under strain for grain boundary angles of 4°; (a)–(g) are the evolution process diagrams; the strains
$\varepsilon $ of (A)–(G) are 0, 0.0231, 0.0281, 0.0319, 0.0341, 0.0374, 0.0473.
图 9 晶界角为4°, 6°, 8°, 10°的石墨烯晶界各种位错的延伸率
Figure 9. Elongation of various dislocations of graphene grain boundaries with grain boundary angles of 4°, 6°, 8° and 10°
图 10 变形过程中双晶石墨烯自由能-应变曲线 (a)—(d)晶界角分别为4°, 6°, 8°, 10°
Figure 10. Free energy curves of double crystalline graphene during deformation: (a)–(d) The grain boundary angles are 4°, 6°, 8°, 10°.
表 1 施加应力应变的参数
Table 1. Parameters for applying stress and strain.
试样 拉伸应
变方向晶粒取向角 晶界角 $\theta $ /(°)${\theta _1}$ /(°)${\theta _2}$ /(°)A $y$ 2 –2 4 B $y$ 3 –3 6 C $y$ 4 –4 8 D $y$ 5 –5 10 
下载: 导出CSV
-
[1] 林彰乾, 郑伟, 李浩, 王东君 2021 金属学报 57 111 doi: 10.11900/0412.1961.2020.00186 Lin Z Q, Zhen W, Li H, Wang D J 2021 Acta. Metall. Sin. 57 111 doi: 10.11900/0412.1961.2020.00186 [2] Lee C, Wei X, Kysar J W, Hone J 2008 Science 321 385 doi: 10.1126/science.1157996 [3] Cao K, Feng S Z, Han Y, Gao L B, Hue Ly T, Xu Z P, Lu Y 2020 Nat. Commun. 11 284 doi: 10.1038/s41467-019-14130-0 [4] Liu J, Hei L F, Song J H, Li C M, Tang W Z, Chen G C, Lu F X 2014 Diam. Relat. Mater. 46 42 doi: 10.1016/j.diamond.2014.04.008 [5] Huang P Y, Ruiz-Vargas C S, van der Zande A M, et al. 2011 Nature 469 389 doi: 10.1038/nature09718 [6] Hashimoto A, Suenaga K, Gloter A, Urita K, Iijima S 2004 Nature 430 870 doi: 10.1038/nature02817 [7] Meyer J C, Kisielowski C, Erni R, Rossell M D, Crommie M F, Zettl A 2008 Nano Lett. 8 3582 doi: 10.1021/nl801386m [8] He L C, Guo S S, Lei J C, Sha Z D, Liu Z H 2014 Carbon 75 124 doi: 10.1016/j.carbon.2014.03.044 [9] 周文权 2019 博士学位论文(西安: 西北工业大学) Zhou W Q 2019 Ph. D. Dissertation (Xi’an: Northwestern Polytechnical University [10] Shekhawat A, Ritchie R O 2016 Nat. Commun. 7 10546 doi: 10.1038/ncomms10546 [11] Zhang J F, Zhao J J, Lu J P 2012 ACS Nano 6 2704 doi: 10.1021/nn3001356 [12] Heo J, Han J 2023 Nanotechnology 34 415704 doi: 10.1088/1361-6528/ace44e [13] Grantab R, Shenoy V B, Ruoff R S 2010 Science 330 946 doi: 10.1126/science.1196893 [14] Wei Y J, Wu J T, Yin H Q, Shi X H, Yang R G, Dresselhaus M 2012 Nat. Mater. 11 759 doi: 10.1038/NMAT3370 [15] Lehtinen O, Kurasch S, Krasheninnikov A V, Kaiser U 2013 Nat. Commun. 4 2098 doi: 10.1038/ncomms3098 [16] Liu Z, Suenaga K, Harris P J F, Iijima S 2009 Phys. Rev. Lett. 102 015501 doi: 10.1103/PhysRevLett.102.015501 [17] Zhao Y H, Tian X L, Zhao B J, et al. 2018 Sci. Adv. Mater. 10 1793 doi: 10.1166/sam.2018.3430 [18] Zhang J B, Wang H F, Kuang W W, Zhang Y C, Li S, Zhao Y H, Herlach D M 2018 Acta Mater. 148 86 doi: 10.1016/j.actamat.2018.01.040 [19] Guo Q W, Hou H, Wang K L, Li M X, Liaw P K, Zhao Y H 2023 npj Comput. Mater. 9 185 doi: 10.1038/s41524-023-01139-9 [20] Xin T Z, Zhao Y H, Mahjoub R, Jiang J X, Ferry M 2021 Sci. Adv. 7 eabf3039 doi: 10.1126/sciadv.abf3039 [21] Xin T Z, Tang S, Ji F, Cui L Q, He B B, Lin X, Tian X L, Hou H, Zhao Y H, Ferry M 2022 Acta Mater. 239 118248 doi: 10.1016/j.actamat.2022.118248 [22] Zhao Y H, Zhang B, Hou H, Chen W P, Wang M 2019 J. Mater. Sci. Technol. 35 1044 doi: 10.1016/j.jmst.2018.12.009 [23] Chen L Q, Zhao Y H 2022 Prog. Mater. Sci. 124 100868 doi: 10.1016/j.pmatsci.2021.100868 [24] Zhao Y H, Xin T Z, Tang S, Wang H F, Fang X D, Hou H 2024 MRS Bull. 49 613 doi: 10.1557/s43577-024-00720-x [25] Zhao Y H, Xing H, Zhang L J, et al. 2023 Acta Metall. Sin. (Engl. Lett. ) 36 1749 doi: 10.1007/s40195-023-01593-w [26] Zhao Y H 2024 npj Comput. Mater. 2 e44 doi: 10.1002/mgea.44 [27] Zhao Y H 2023 npj Comput. Mater. 9 94 doi: 10.1038/s41524-023-01038-z [28] Kuang W W, Wang H F, Li X, Zhang J B, Zhou Q, Zhao Y H 2018 Acta Mater. 159 16 doi: 10.1016/j.actamat.2018.08.008 [29] Song Z, Li H Q, Wang X N, Tian X L, Hou H, Zhao Y H 2023 J. Mater. Res. Technol. 27 6501 doi: 10.1016/j.jmrt.2023.10.187 [30] Zhong L, Gao H J, Li X Y 2020 Extreme Mech. Lett. 37 100699 doi: 10.1016/j.eml.2020.100699 [31] Meca E, Lowengrub J, Kim H, Mattevi C, Shenoy V B 2013 Nano Lett. 13 5692 doi: 10.1021/nl4033928 [32] Li H Q, Wang X N, Zhang H B, Tian X L, Hou H, Zhao Y H 2022 Front. Mater. 9 875519 doi: 10.3389/fmats.2022.875519 [33] Elder K R, Katakowski M, Haataja M, Grant M 2002 Phys. Rev. Lett. 88 245701 doi: 10.1103/PhysRevLett.88.245701 [34] Tian X L, Zhao Y H, Gu T, Guo Y L, Xu F Q, Hou H 2022 Mater. Sci. Eng. 849 143485 doi: 10.1016/j.msea.2022.143485 [35] Zhao Y H, Liu K X, Zhang H B, Tian X L, Jiang Q L, Murugadoss V, Hou H 2022 Adv. Compos. Hybrid Mater. 5 2546 doi: 10.1007/s42114-022-00522-2 [36] Kim K, Lee Z, Regan W, Kisielowski C, Crommie M F, Zettl A 2011 ACS Nano 5 2142 doi: 10.1021/nn1033423 [37] Akhukov M A, Fasolino A, Gornostyrev Y N, Katsnelson M I 2012 Phys. Rev. B 85 115407 doi: 10.1103/PhysRevB.85.115407 [38] Hirvonen P, Ervasti M M, Fan Z, et al. 2016 Phys. Rev. B 94 035414 doi: 10.1103/PhysRevB.94.035414 [39] Guo H J, Zhao Y H, Sun Y Y, Tian J Z, Hou H, Qi K W, Tian X L 2019 Micro Nanostruct. 129 163 doi: 10.1016/j.spmi.2019.03.020 [40] Elder K R, Grant M 2004 Phys. Rev. E 70 051605 doi: 10.1103/PhysRevE.70.051605 -
计量
- 文章访问数: 112
- HTML全文浏览数: 112
- PDF下载数: 5
- 施引文献: 0