高级搜索

质子累积辐照效应对CMOS图像传感器饱和输出的影响

,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

彭治钢, 白豪杰, 刘方, 李洋, 何欢, 李培, 贺朝会, 李永宏. 质子累积辐照效应对CMOS图像传感器饱和输出的影响[J]. 物理学报, 2025, 74(2): 024203-1. doi: 10.7498/aps.74.20241352
引用本文: 彭治钢, 白豪杰, 刘方, 李洋, 何欢, 李培, 贺朝会, 李永宏. 质子累积辐照效应对CMOS图像传感器饱和输出的影响[J]. 物理学报, 2025, 74(2): 024203-1. doi: 10.7498/aps.74.20241352
shu
Zhigang PENG, Haojie BAI, Fang LIU, Yang LI, Huan HE, Pei LI, Chaohui HE, Yonghong LI. Effect of proton cumulative radiation on saturation output in CMOS image sensors[J]. Acta Physica Sinica, 2025, 74(2): 024203-1. doi: 10.7498/aps.74.20241352
Citation: Zhigang PENG, Haojie BAI, Fang LIU, Yang LI, Huan HE, Pei LI, Chaohui HE, Yonghong LI. Effect of proton cumulative radiation on saturation output in CMOS image sensors[J]. Acta Physica Sinica, 2025, 74(2): 024203-1. doi: 10.7498/aps.74.20241352
shu

质子累积辐照效应对CMOS图像传感器饱和输出的影响

  • 西安交通大学核科学与技术学院, 西安　710049

    • 作者简介: 彭治钢.E-mail: pengzg@stu.xjtu.edu.cn .
    通讯作者: E-mail: yonghongli@xjtu.edu.cn.

  • 中图分类号: 42.88.+h, 85.60.Dw, 61.72.J-

Effect of proton cumulative radiation on saturation output in CMOS image sensors

  • School of Nuclear Science and Technology, Xi’an Jiaotong University, Xi’an 710049, China

    • Corresponding author: E-mail: yonghongli@xjtu.edu.cn

  • MSC: 42.88.+h, 85.60.Dw, 61.72.J-

  • 摘要: 本文通过辐照实验和TCAD仿真, 研究了质子累积辐照导致四晶体管钳位光电二极管(4T PPD)CMOS图像传感器的饱和输出变化机理. 实验采用的质子能量为12 MeV和60 MeV, 最高质子注量为2×1012 cm–2. 实验结果表明: 12 MeV和60 MeV质子最高注量辐照后分别导致转换增益增大8.2%和7.3%, 满阱容量分别减小7.3%和3.8%. 饱和输出在12 MeV质子辐照下变化趋势不显著, 在60 MeV质子辐照下增大3%. 在TCAD仿真中, 建立了单个三维4T PPD像元模型, 开展了质子累积辐照效应仿真来分析损伤机理. 仿真结果表明像元饱和输出的变化由满阱容量、复位晶体管的物理特性和浮置扩散区的电容决定, 但它们具有不同的影响. 具体而言, 满阱容量的降低导致饱和输出减小, 而复位晶体管的辐照效应导致饱和输出增大. 辐照导致浮置扩散区的电容减小, 从而使转换增益增大, 进而饱和输出增大. 上述工作较为全面地揭示和分析了辐照后饱和输出的变化机理, 研究成果对CMOS图像传感器的辐射损伤分析具有一定的指导意义.
    Abstract: Complementary metal oxide semiconductor (CMOS) image sensors have been increasingly widely used in the field of radiation environments due to their numerous advantages, and their radiation effects have also attracted much attention. Some experimental studies have shown that the saturation output of CMOS image sensors decreases after irradiation, while others have reported that it increases. In this work, the further in-depth research on the inconsistent results is conducted based on the proton irradiation experiments and TCAD simulations, and the degradation mechanism in full well capacity, conversion factor, and saturation output of the 4T pinned photodiode (PPD) CMOS image sensors due to proton cumulative radiation effects are also analyzed. In experiments, the sensors are irradiated by 12 MeV and 60 MeV protons with a fluence up to 2× 1012 cm–2. The sensors are unbiased during irradiation. The experimental results show that proton irradiation at 12 MeV and 60 MeV result in an increase of 8.2% and 7.3% in conversion factor, respectively, and a decrease of 7.3% and 3.8% in full well capacity, respectively. The saturation output shows no significant change trend under 12 MeV proton irradiation, but increases by 3% under 60 MeV proton irradiation. In the TCAD simulation, a three-dimensional 4T PPD pixel model is constructed. A simulation method that combines the trap and gamma radiation model in TCAD with the mathematical model of minority carrier lifetime is used to simulate global and local cumulative proton irradiation in order to analyze the degradation mechanism. It is proposed that the degradation of saturation output at the pixel level is determined by the full well capacity of PPD, the physical characteristics of the reset transistor and the capacitance of floating diffusion, but they have opposite effects. Proton irradiation leads to the accumulation of oxide-trapped positive charges in the shallow trench isolation on both sides of PPD, resulting in the formation of leakage current path in silicon, thereby reducing the full well capacity. A decrease in full well capacity leads to a decrease in saturation output. While, the radiation effect of the reset transistor causes the potential of floating diffusion (FD) to increase during the FD reset phase, further leading to an increase in saturation output. The irradiation causes the capacitance of the floating diffusion to decrease, resulting in an increase in conversion factor and consequently increasing the saturation output. The difference in radiation sensitivity among the three influence factors at the pixel level may result in a decrease or increase in saturation output with proton fluence increasing. The above work comprehensively reveals and analyzes the mechanisms of degradation in full well capacity, conversion factor and saturation output after irradiation, and the research results have certain guiding significance for analyzing the radiation damage to CMOS image sensors.
  • 加载中

  • 图 1  (a) CIS芯片及图像采集卡; (b) 测试系统的程控暗箱; (c) 质子辐照实验示意图

    Figure 1.  (a) CIS and image acquisition card; (b) the dark box of test system; (c) schematic diagram of CIS proton irradiation experiment setup.

    下载: 全尺寸图片 幻灯片

    图 2  系统增益随质子注量变化

    Figure 2.  Overall system gain versus the proton fluence.

    下载: 全尺寸图片 幻灯片

    图 3  (a) 平均输出信号; (b) 满阱容量随质子注量变化

    Figure 3.  (a) Mean signal level; (b) full well capacity versus proton fluence.

    下载: 全尺寸图片 幻灯片

    图 4  平均饱和输出随质子注量变化

    Figure 4.  Mean saturation outputs versus the proton fluence.

    下载: 全尺寸图片 幻灯片

    图 5  TCAD中建立的4T PPD像元模型　(a) 三维模型, STI和PMD略去以便于展示; (b) 沿(a)图X = 1.2 μm的横截面

    Figure 5.  The 4T PPD CIS pixel model built in TCAD: (a) 3D model, STI, and PMD removed for visualization; (b) 2D cross section taken along the X = 1.2 μm surface in (a).

    下载: 全尺寸图片 幻灯片

    图 6  仿真时序及FD电势输出

    Figure 6.  Simulation driving timings and the potential output of FD.

    下载: 全尺寸图片 幻灯片

    图 7  4T PPD像元输出电压随光照强度变化

    Figure 7.  Output variation of the 4T PPD CIS model with light intensity.

    下载: 全尺寸图片 幻灯片

    图 8  全局质子辐照前后氧化物中陷阱正电荷分布　(a) 辐照前; (b) 质子注量1.0×1012 cm–2

    Figure 8.  Distribution of trapped positive charges in the oxide: (a) Before irradiation; (b) proton fluence of 1.0×1012 cm–2.

    下载: 全尺寸图片 幻灯片

    图 9  12 MeV全局质子辐照　(a) PPD内电子数量; (b) 满阱容量

    Figure 9.  Global irradiation simulation by 12 MeV protons: (a) Total electron count within the PPD; (b) FWC.

    下载: 全尺寸图片 幻灯片

    图 10  辐照前后PPD两侧氧化物陷阱正电荷和电子浓度分布　(a) 辐照前陷阱正电荷; (b) 辐照后陷阱正电荷; (c) 辐照前电子浓度; (d) 辐照后电子浓度

    Figure 10.  Distribution of oxide-trapped positive charges in STI on both sides of the PPD during FD reset stage: (a) Positive charges before irradiation; (b) positive charges after irradiation; (c) electron concentration distribution before irradiation; (d) electron concentration distribution after irradiation.

    下载: 全尺寸图片 幻灯片

    图 11  12 MeV全局质子辐照　(a) FD电势; (b) 饱和输出

    Figure 11.  Global irradiation simulation by 12 MeV protons: (a) FD potential; (b) saturation output.

    下载: 全尺寸图片 幻灯片

    图 12  质子局部辐照(Y > 2.1 μm)　(a) 12 MeV质子辐照PPD内电子数量; (b) 满阱容量

    Figure 12.  Local irradiation (Y > 2.1 μm): (a) Total electron count within the PPD irradiated by 12 MeV protons; (b) FWC.

    下载: 全尺寸图片 幻灯片

    图 13  质子局部辐照(Y > 2.1 μm)　(a) 12 MeV质子辐照FD电势; (b) 饱和输出

    Figure 13.  Local irradiation (Y > 2.1 μm): (a) FD potential irradiated by 12 MeV protons; (b) saturation output.

    下载: 全尺寸图片 幻灯片

    图 14  质子局部辐照(Y < 2.1 μm)　(a) 12 MeV质子辐照PPD内电子数量; (b) 满阱容量

    Figure 14.  Local irradiation (Y < 2.1 μm): (a) Total electron count within the PPD irradiated by 12 MeV protons; (b) FWC.

    下载: 全尺寸图片 幻灯片

    图 15  质子局部辐照(Y < 2.1 μm)　(a) 12 MeV质子辐照FD电势变化; (b) 饱和输出变化

    Figure 15.  Local irradiation (Y < 2.1 μm): (a) FD potential irradiated by 12 MeV protons; (b) saturation output.

    下载: 全尺寸图片 幻灯片

    图 16  质子局部辐照(Y < 2.1 μm)前后浮置扩散区耗尽层厚度　(a) 辐照前; (b) 12 MeV质子辐照后; (c) 60 MeV质子辐照后

    Figure 16.  Depletion region of FD region before and after local proton irradiation simulation (Y < 2.1 μm): (a) Before irradiation; (b) after irradiation by 12 MeV protons; (b) after irradiation by 60 MeV protons.

    下载: 全尺寸图片 幻灯片

    图 17  60 MeV质子局部辐照(Y < 2.1 μm) TG下方沟道和浮置扩散区的电子浓度

    Figure 17.  Electron density in the channel below TG and FD region after local proton irradiation simulation (Y < 2.1 μm).

    下载: 全尺寸图片 幻灯片

    表 1  辐照参数

    Table 1.  Irradiation parameters.

    CIS编号质子能量/MeV最大质子注量/cm–2DDD/(TeV·g–1)TID/krad(Si)
    CIS_1122.0×101217638962
    CIS_2, 3, 4602.0×10128286275
    下载: 导出CSV

    表 2  12 MeV和60 MeV质子等效计算结果

    Table 2.  Equivalent results for 12 MeV and 60 MeV protons.

    质子能量
    /MeV    		 质子注量
    /(1011cm–2)    		 等效中子注量
    /(1011 cm–2)    		 等效TID
    /krad(Si)
    12 1.0 3.0 48.1
    4.0 12.0 192.3
    7.0 21.0 336.6
    10.0 30.0 480.8
    60 1.0 1.0 13.7
    4.0 4.0 55.1
    7.0 7.0 96.4
    10.0 10.0 137.4
    下载: 导出CSV
  • [1] 王祖军, 刘静, 薛院院, 何宝平, 姚志斌, 盛江坤 2017 半导体光电 38 1 Wang Z J, Liu J, Xue Y Y, He B P, Yao Z B, Sheng J K 2017 Semiconductor Optoelectronics 38 1
    [2] Goiffon V, Estribeau M, Magnan P 2009 IEEE Trans. Electron Devices 56 2594 doi: 10.1109/TED.2009.2030623
    [3] Virmontois C, Goiffon V, Magnan P, Girard S, Inguimbert C, Petit S, Rolland G, Saint-Pe O 2010 IEEE Trans. Nucl. Sci. 57 3101
    [4] Le Roch A, Virmontois C, Paillet P, Belloir J M, Rizzolo S, Marcelot O, Dewitte H, Van Uffelen M, Casellas L M, Magnan P, Goiffon V 2020 IEEE Trans. Nucl. Sci. 67 1241 doi: 10.1109/TNS.2020.3003451
    [5] 汪波, 李豫东, 郭旗, 刘昌举, 文林, 玛丽娅, 孙静, 王海娇, 丛忠超, 马武英 2014 物理学报 63 056102 doi: 10.7498/aps.63.056102 Wang B, Li Y D, Guo Q, Liu C J, Wen L, Ma L Y, Sun J, Wang H J, Cong Z C, Ma W Y 2014 Acta Phys. Sin. 63 056102 doi: 10.7498/aps.63.056102
    [6] 王帆, 李豫东, 郭旗, 汪波, 张兴尧, 文林, 何承发 2016 物理学报 65 024212 doi: 10.7498/aps.65.024212 Wang F, Li Y D, Guo Q, Wang B, Zhang X Y, Wen L, He C F 2016 Acta Phys. Sin. 65 024212 doi: 10.7498/aps.65.024212
    [7] Rizzolo S, Goiffon V, Estribeau M, Paillet P, Marcandella C, Durnez C, Magnan P 2018 IEEE Trans. Nucl. Sci. 65 84 doi: 10.1109/TNS.2017.2778760
    [8] 汪波, 李豫东, 郭旗, 文林, 孙静, 王帆, 张兴尧, 玛丽娅 2015 强激光与粒子束 27 210 doi: 10.11884/HPLPB201527.094001 Wang B, Li Y D, Guo Q, Wen L, Sun J, Wang F, Zhang X Y, Ma L Y 2015 High Power Laser Part. Beams 27 210 doi: 10.11884/HPLPB201527.094001
    [9] 汪波, 李豫东, 郭旗, 刘昌举, 文林, 任迪远, 曾骏哲, 玛丽娅 2015 物理学报 64 084209 doi: 10.7498/aps.64.084209 Wang B, Li Y D, Guo Q, Liu C J, Wen L, Ren D Y, Zeng J Z, Ma L Y 2015 Acta Phys. Sin. 64 084209 doi: 10.7498/aps.64.084209
    [10] Fu J, Feng J, Li Y D, Guo Q, Wen L, Zhou D, Zhang X, Cai Y L, Liu B K 2021 Radiat. Phys. Chem. 182 109384 doi: 10.1016/j.radphyschem.2021.109384
    [11] Wang Z J, Xue Y Y, Guo X Q, Bian J Y, Yao Z B, He B P, Ma W Y, Sheng J K, Dong G T, Liu Y 2018 Nucl. Instrum. Methods A 895 35 doi: 10.1016/j.nima.2018.04.002
    [12] Goiffon V, Estribeau M, Marcelot O, Cervantes P, Magnan P, Gaillardin M, Virmontois C, Martin-Gonthier P, Molina R, Corbiere F, Girard S, Paillet P, Marcandella C 2012 IEEE Trans. Nucl. Sci. 59 2878 doi: 10.1109/TNS.2012.2222927
    [13] Wang Z J, Ma W Y, Huang S Y, Yao Z B, Liu M B, He B P, Liu J, Sheng J K, Xue Y 2016 AIP Adv. 6 035205 doi: 10.1063/1.4943674
    [14] Meng X, Stefanov K D, Holland A D 2020 IEEE Trans. Nucl. Sci. 67 1107 doi: 10.1109/TNS.2020.2990081
    [15] Virmontois C, Durnez C, Estribeau M, Cervantes P, Avon B, Goiffon V, Magnan P, Materne A, Bardoux A 2017 IEEE Trans. Nucl. Sci. 64 38 doi: 10.1109/TNS.2016.2641162
    [16] Lai S K, Wang Z J, Huang G, Xue Y Y, Nie X, Tang N, Yan S X, Wang X H 2023 Nucl. Instrum. Methods A 1050 168069 doi: 10.1016/j.nima.2023.168069
    [17] 杨勰, 霍勇刚, 王祖军, 尚爱国, 薛院院, 贾同轩 2022 光学学报 42 0723002 doi: 10.3788/AOS202242.0723002 Yang X, Huo Y G, Wang Z J, Shang A G, Xue Y Y, Jia T X 2022 Acta Opt. Sin. 42 0723002 doi: 10.3788/AOS202242.0723002
    [18] Peng Z G, Fu Y J, Wei Y, Zuo Y H, Niu S L, Zhu J H, Guo Y X, Liu F, Li P, He C H, Li Y H 2024 AIP Advances 14 015211 doi: 10.1063/5.0184659
    [19] Wang Z M, Chen W, Qiu M T, Yan Y H, Zhang H, Wang M W, Wang B C, Yang Y, Wang D, Liu W L, Wang M C, Lv W, Zhao M T, Zhao C, Wei C Y, Yao H J, Zheng S X, Wang X W, Guan X L, Xing Q Z, Cheng C, Du T B, Zhang H Y, Lei Y, Wang D, Du C T, Ma P F, Liu X Y, Li Y, Ye W B, Yu X D 2022 Nucl. Instrum. Methods A 1027 166283 doi: 10.1016/j.nima.2021.166283
    [20] Khan U, Sarkar M 2018 IEEE Trans. Electron Devices 65 2892 doi: 10.1109/TED.2018.2831719
    [21] Wang Z J, Xue Y Y, Wang Z M, Chen W, Yin L Y, Wang X H, Nie X, Lai S K, Huang G, Wang M C, Ding L L, He B P, Ma W Y, Gou S L 2024 Nucl. Instrum. Methods A 1058 168784 doi: 10.1016/j.nima.2023.168784
    [22] Petrosyants K O, Kozhukhov M V 2016 IEEE Trans. Nucl. Sci. 63 2016 doi: 10.1109/TNS.2016.2572658
    [23] Poivey C, Hopkinson G 2009 ESA—EPFL Space Center Workshop June, 2009 p9
    [24] Wang C H, Bai X Y, Chen W, Yang S C, Liu Y, Jin X M, Ding L L 2015 Nucl. Instrum. Methods A 796 108 doi: 10.1016/j.nima.2015.03.062
    [25] Gregory B L, Gwyn C W 1970 IEEE Trans. Nucl. Sci. 17 325 doi: 10.1109/TNS.1970.4325813
    [26] Marshall C J , Marshall P W 1999 Nuclear and Space Radiation Effects Conference, Short Course Norfolk, Virginia, July 12–16, 1999 p50
    [27] Lee M S, Lee H C 2013 IEEE Trans. Nucl. Sci. 60 3084 doi: 10.1109/TNS.2013.2268390
    [28] Johnston A H, Swimm R T, Allen G R, Miyahira T F 2009 IEEE Trans. Nucl. Sci. 56 1941 doi: 10.1109/TNS.2009.2019273
    [29] Hu Z Y, Liu Z L, Shao H, Zhang Z X, Ning B X, Chen M, Bi D W, Zou S C 2011 IEEE Trans. Nucl. Sci. 58 1332 doi: 10.1109/TNS.2011.2142323
  • 加载中
图( 17) 表( 2)
计量
  • 文章访问数:  273
  • HTML全文浏览数:  273
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-26
  • 刊出日期:  2025-01-20

质子累积辐照效应对CMOS图像传感器饱和输出的影响

    通讯作者: E-mail: yonghongli@xjtu.edu.cn.
    作者简介: 彭治钢.E-mail: pengzg@stu.xjtu.edu.cn
  • 西安交通大学核科学与技术学院, 西安　710049
  • 收稿日期:  2024-09-26

摘要: 本文通过辐照实验和TCAD仿真, 研究了质子累积辐照导致四晶体管钳位光电二极管(4T PPD)CMOS图像传感器的饱和输出变化机理. 实验采用的质子能量为12 MeV和60 MeV, 最高质子注量为2×1012 cm–2. 实验结果表明: 12 MeV和60 MeV质子最高注量辐照后分别导致转换增益增大8.2%和7.3%, 满阱容量分别减小7.3%和3.8%. 饱和输出在12 MeV质子辐照下变化趋势不显著, 在60 MeV质子辐照下增大3%. 在TCAD仿真中, 建立了单个三维4T PPD像元模型, 开展了质子累积辐照效应仿真来分析损伤机理. 仿真结果表明像元饱和输出的变化由满阱容量、复位晶体管的物理特性和浮置扩散区的电容决定, 但它们具有不同的影响. 具体而言, 满阱容量的降低导致饱和输出减小, 而复位晶体管的辐照效应导致饱和输出增大. 辐照导致浮置扩散区的电容减小, 从而使转换增益增大, 进而饱和输出增大. 上述工作较为全面地揭示和分析了辐照后饱和输出的变化机理, 研究成果对CMOS图像传感器的辐射损伤分析具有一定的指导意义.

English Abstract

    全文HTML

    1.   引　言

    • 随着半导体技术的发展, CMOS图像传感器(CMOS image sensor, CIS)的性能得到了进一步提升. 由于其高集成度、低功耗和较强的抗辐射性能等诸多优点, 在航空航天领域中发挥着越来越重要的作用[1,2]. 然而, 空间环境中的各种辐射粒子, 如质子、电子和高能重粒子, 在电子设备的整个服役周期内都可能对其造成损伤[3].

      质子作为空间辐射的重要来源, 对CIS既能产生电离效应又能产生位移损伤效应, 分别用电离总剂量(total ionizing dose, TID)和位移损伤剂量(displacement damage dose, DDD)来衡量[4]. 总剂量效应会导致CIS中的暗信号增大[5], 以及满阱容量(full well capacity, FWC)[6]和电荷转移效率[7]的退化. 位移损伤效应同样会影响CIS的特征参数, 如暗信号和暗信号非均匀性等[8,9]. 对于质子累积辐照效应, 它可以看作是总剂量效应和位移损伤效应的协同效应[3,4,10,11], 因此会影响暗电流、暗信号非均匀性、饱和输出、满阱容量等多个参数.

      目前, 关于CIS的饱和输出的相关研究较少, 特别是对于质子辐照效应. 已有的文献[12,13]表明, 饱和输出随着γ辐照剂量的增大而减小, 这归因于γ辐照引起的满阱容量退化. 然而, 文献[1,14]表明饱和输出随着γ剂量的增大而增大, 文献[14,15]表明饱和输出随着质子注量的增大而增大, 这两者都归因于辐照引起像元中复位晶体管的退化. 饱和输出辐照后变化规律并不一致, 相关研究对其分析仅着眼于单一影响因素, 对饱和输出的变化机理开展进一步分析具有意义.

      由于CIS的高集成度和辐照实验的局限性, 目前对累积辐照效应引起的饱和输出变化缺乏全面的了解. 与实验研究相比, 数值模拟可以提供更深入的理论分析, 以弥补实验的局限性. Sentaurus TCAD是CIS辐照效应仿真采用的最常用的仿真软件[12,16–18]. 然而, 大多数TCAD仿真采用二维像元模型[16,17], 没有纳入驱动时序或在时序下进行瞬态仿真. 因此, 目前的仿真工作无法为CIS累积辐照效应中的一些关键问题, 特别是为饱和输出的变化提供合理的解释.

      在这项工作中, 首先通过实验研究了质子辐照对CIS的全局系统增益、满阱容量和饱和输出的影响. 随后, 在TCAD中建立了4T PPD像元的三维模型, 模拟质子累积辐照效应. 最后, 结合实验和仿真结果, 深入分析了质子辐照后满阱容量、复位管的物理特性和浮置扩散区电容对CIS饱和输出的耦合效应.

    2.   CIS质子辐照实验方法

      2.1.   CIS样品

    • 实验样品为某国产CMOS图像传感器, 采用0.13 μm CMOS工艺. 分辨率为2048×2048, 像素尺寸为 6.0 μm×6.0 μm, 有效图像尺寸为 12.8 mm×12.3 mm. 模数转换器输出为14位, 快门类型为卷帘快门.

      • 2.2.   CIS测试系统

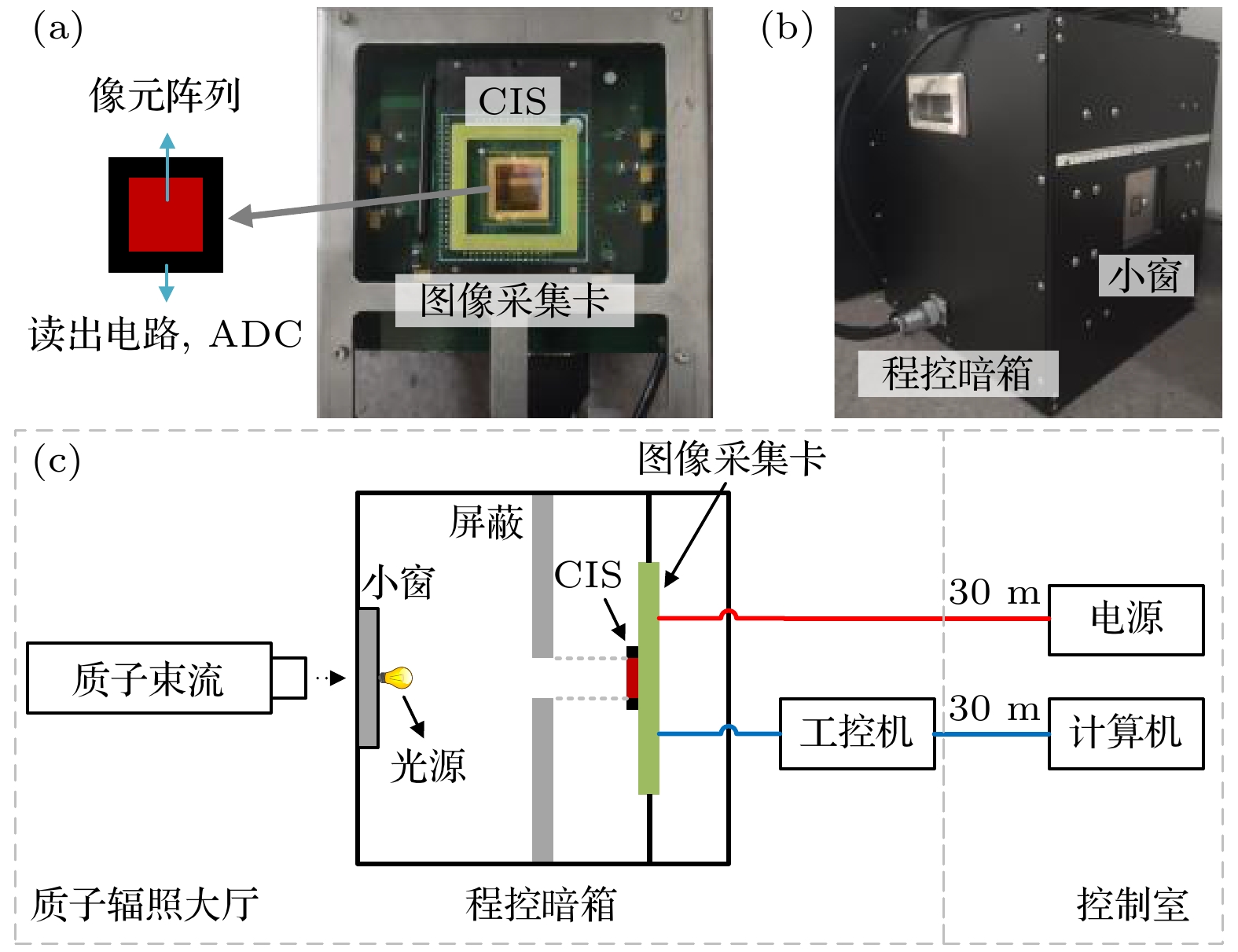
    • 实验中采用了CIS在线测试系统, 如图1所示. 该系统主要包括图像采集卡、程控暗箱和工控机. 在暗箱的一侧安装有由工控机控制的小窗. 当开始辐照时, 远程开启小窗, 使质子束能够准确地辐照样品. 测试系统中采用了10 mm厚的不锈钢屏蔽板, 对CMOS图像传感器进行了局部屏蔽, 仅保留像元阵列裸露于质子束流, 读出电路和ADC等器件不受质子辐照影响. 当辐照注量达到预定值, 暂停质子束流并关闭小窗. 通过工控机中的程序对CIS的各项特性参数进行测试, 程序依据欧洲机器视觉协会(European Machine Vision Association, EMVA) 1288标准. 在小窗后设计了一个强度可控的光源, 以辅助测试. 工控机通过30 m网线远程连接到计算机. 因此, 在实验过程中, 只需操作计算机即可完成测试和数据存储.

      • 2.3.   实验设置

    • 质子辐照实验在西北核技术研究院200 MeV质子应用装置[19]进行. 质子能量为12 MeV和60 MeV. 质子注量率约为1.0×108 cm–2·s–1, 最大累积质子注量为2×1012 cm–2. 在实验过程中, CIS样品处于离线状态. 具体辐照参数如表1所示.

    3.   CIS质子辐照实验结果与分析

    • 本文质子辐照实验重点监测全局系统增益、满阱容量和饱和输出随质子注量的变化. 系统增益和满阱容量通过测试系统直接测量, 饱和输出通过对实验中每个注量点存储的50帧原始数据进行后处理得到.

      • 3.1.   全局系统增益

    • 全局系统增益K是指从输入光子到数字输出信号的整个过程中的增益. 它涵盖了包括光电转换、模拟信号处理和数字信号处理的整个过程. 根据EMVA1288标准, 系统增益K的单位为DN/e– (DN: digital number), 其表达式为

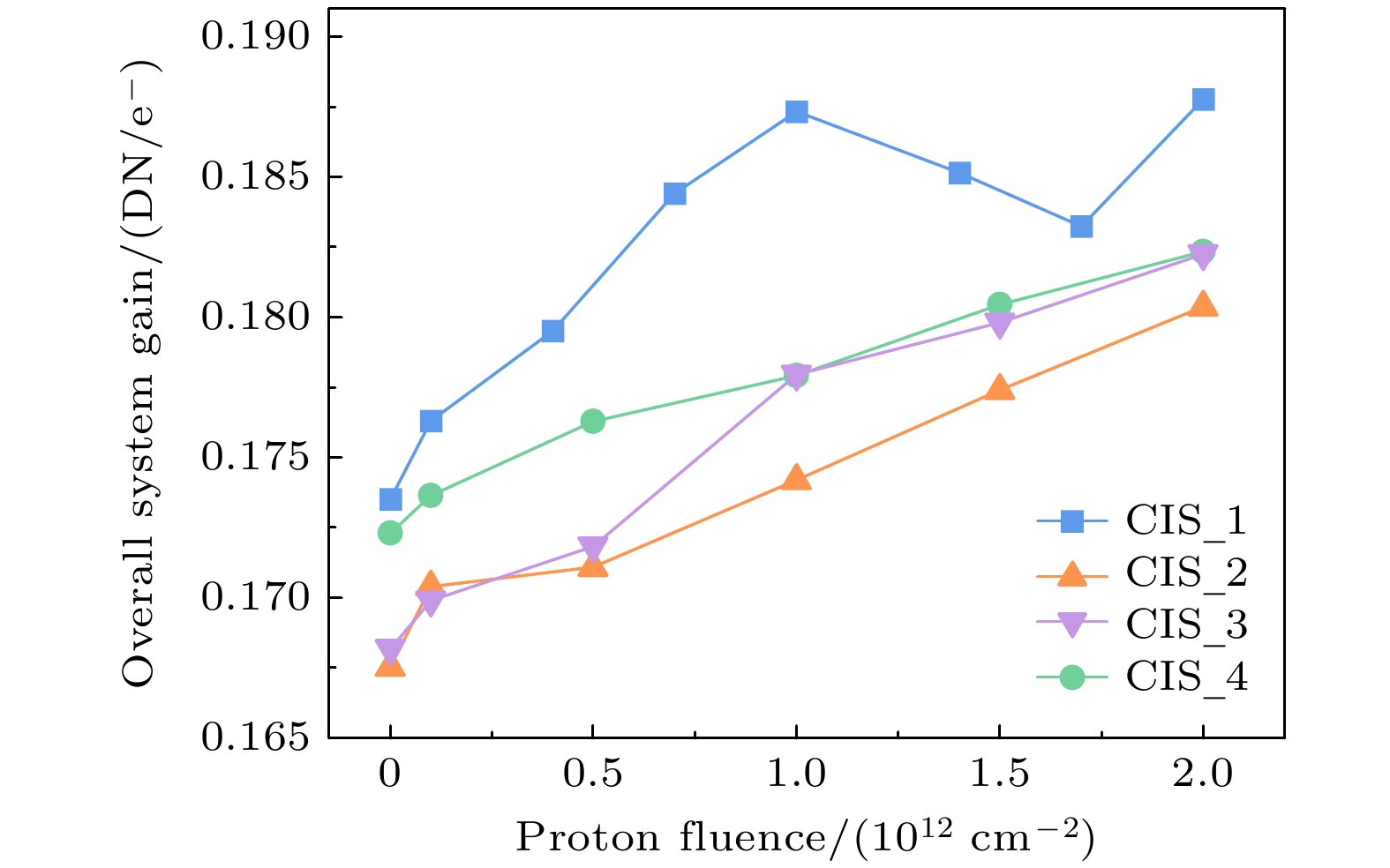
      其中, µy为平均灰度值, µy, dark为平均暗信号, $\sigma _{\text{y}}^2 $为噪声方差, $ \sigma _{{\text{y, dark}}}^2 $为暗信号方差. 绘制光传递曲线, 并在0%—70%饱和范围内进行线性拟合以获得系统增益.

      图2为实验中测得系统增益随质子注量的变化关系. 结果表明, 系统增益随质子注量的增大总体呈增大趋势, CIS_1在12 MeV质子辐照2×1012 cm–2注量后增大8.2%, CIS_2, CIS_3和CIS_4在60 MeV质子辐照后平均增大7.3%. 实验仅对像元阵列进行辐照, 因此系统增益的变化可视为转换增益(conversion factor, CVF)的变化, 而外围模拟或数字电路的增益保持不变. 第4节将通过TCAD仿真分析CVF增大的原因.

      • 3.2.   满阱容量

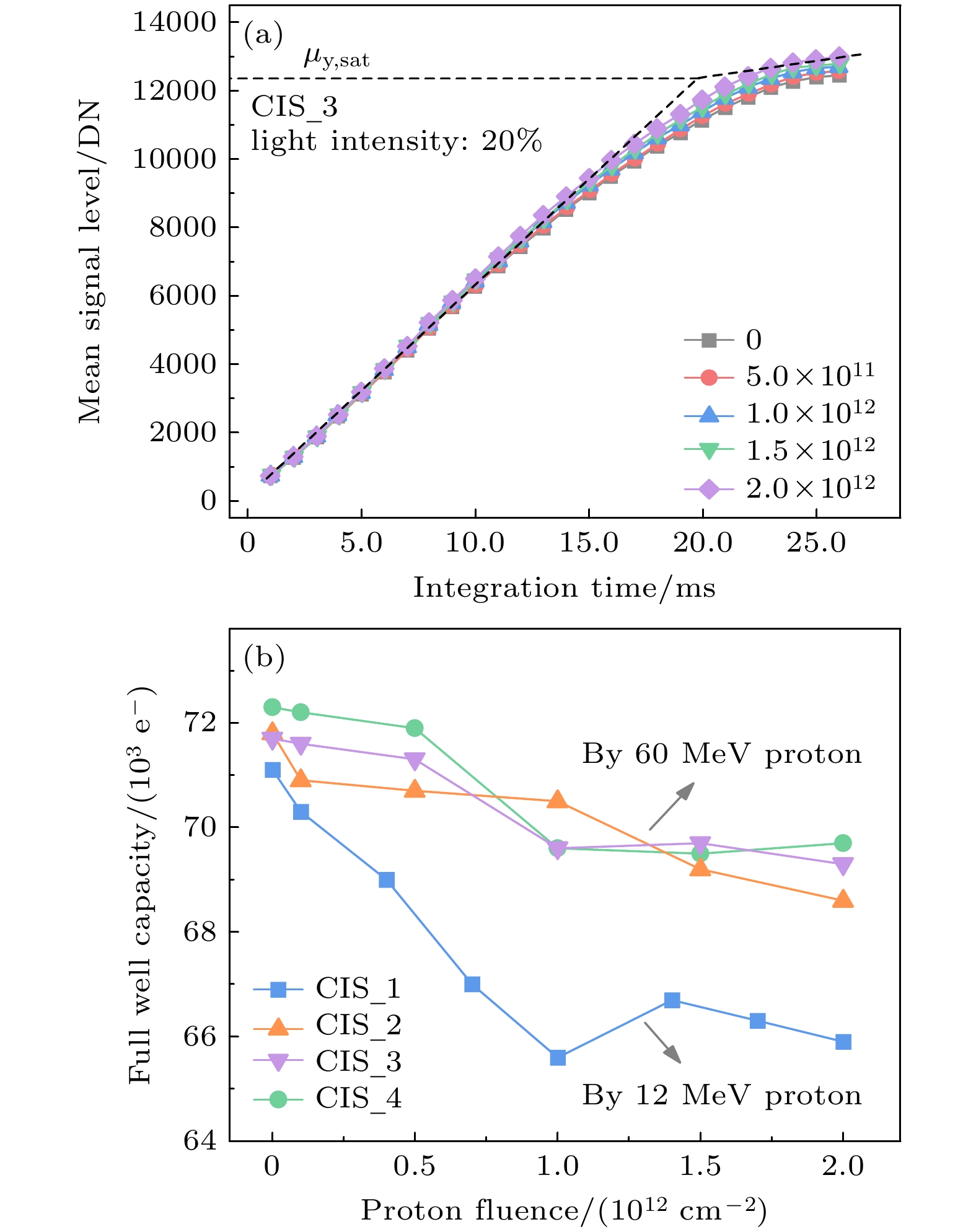
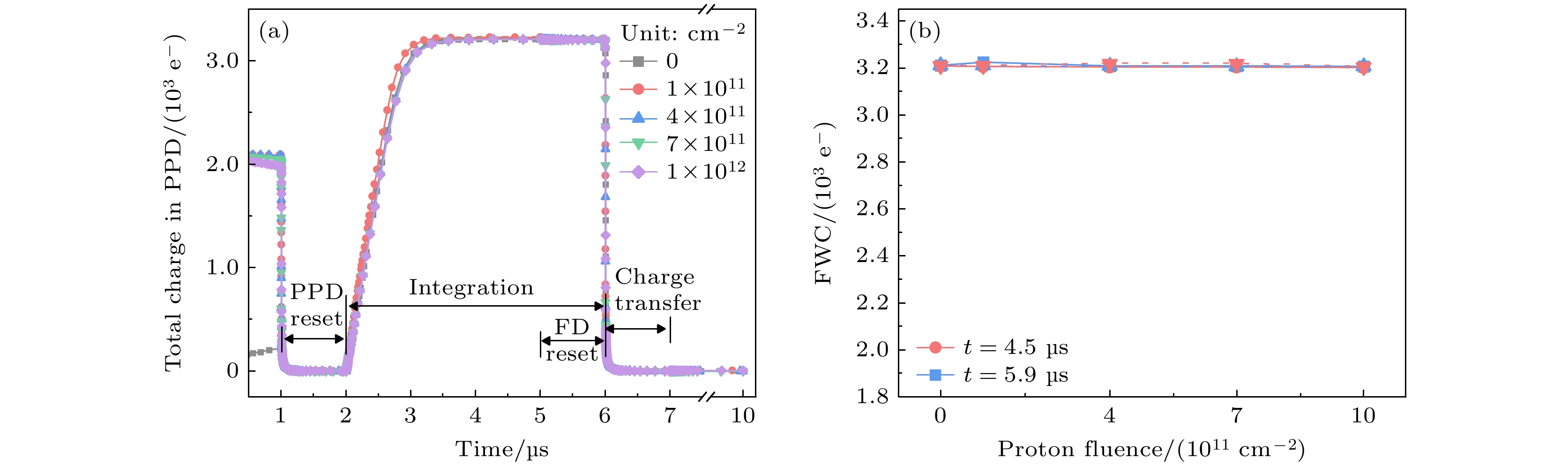
    • 满阱容量是指在钳位光电二极管中能够积累的最大光生电荷量[20]. 它极大程度决定了CIS的饱和输出并影响图像质量. 满阱容量通过将μy,sat除以K获得, μy,sat的提取方法如图3(a)所示. 图中光强为20%, 测试CIS在不同积分时间下的平均输出信号变化曲线. 将曲线从线性区过渡到非线性区的点确定为μy,sat. 图3(a)还表明输出信号随质子注量的增大而增大. 图3(b)为实验测得满阱容量随质子注量的变化关系. 结果表明, 满阱容量随质子注量的增大总体呈减小趋势, 2×1012 cm–2质子注量下CIS_1减小7.3%, CIS_2, CIS_3和CIS_4平均减小3.8%. 这是由于质子能量越高, 等效电离和非电离能量损失越小[21], 如表1所示. CIS_1由12 MeV质子辐照, 其余CIS由60 MeV质子辐照, 因此, CIS_1的满阱容量表现出更显著的退化.

      • 3.3.   饱和输出

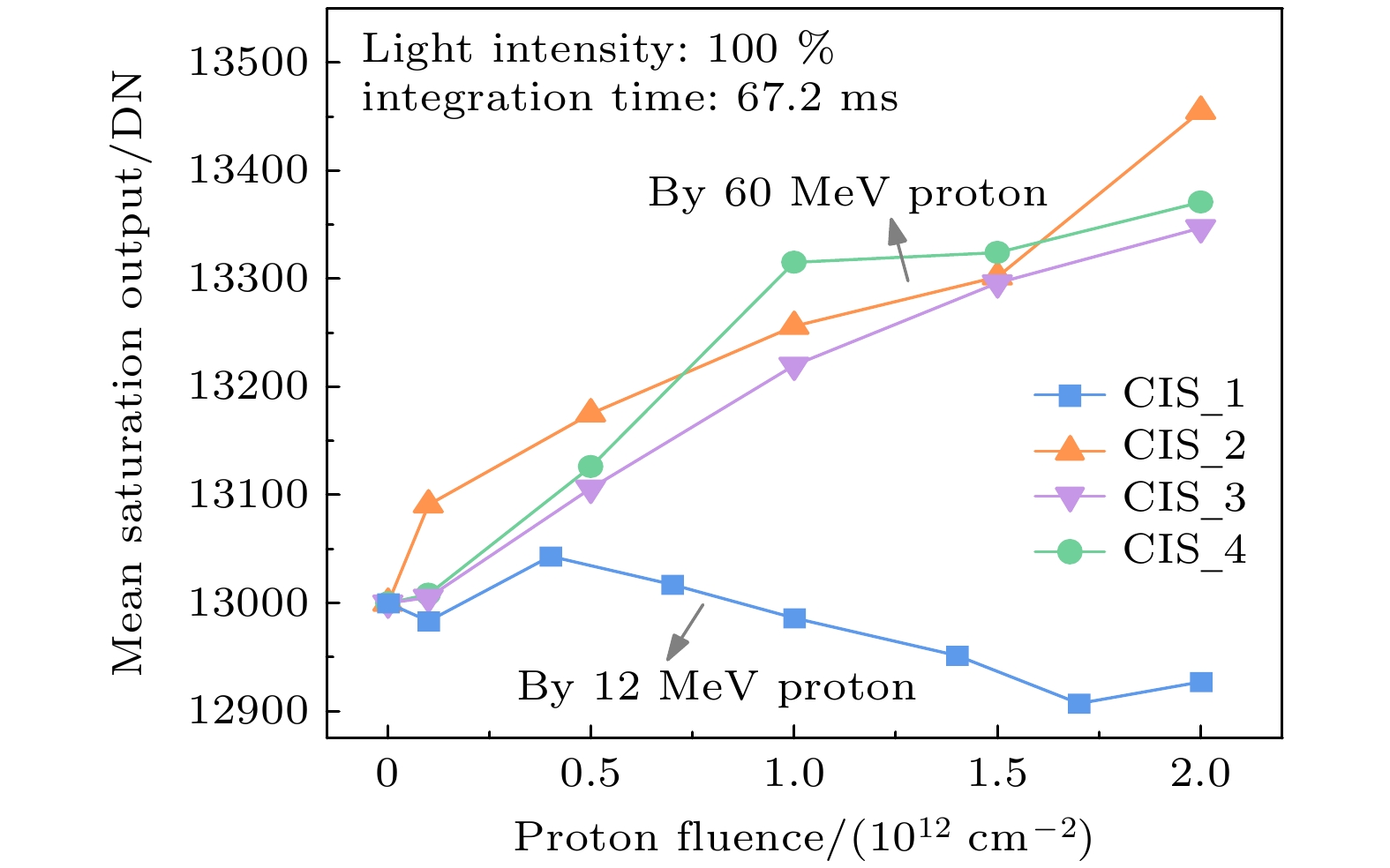
    • CIS的输出信号是一个基本参数, 直接表征其光电转换结果. 如图3(a)所示, 当光强为20%且积分时间大于25 ms时, CIS的输出信号趋于饱和. 为确保其输出确实饱和, 在测试饱和输出时, 将光强设置为100%, 积分时间设置为67.2 ms. 图4展示了饱和输出随质子注量的变化. 由于所测试的CIS中的列级模数转换器为14位, 其理论最大输出为16383 DN. 实际上, 该样品像元阵列的输出信号从左到右逐渐降低, 左侧输出约为16000 DN, 右侧输出仅约为10000 DN, 导致整个像素阵列的平均饱和输出约为13000 DN. 为了更好地观察多个CIS饱和输出的变化规律, 在质子辐照前将图4中的饱和输出调整为13000 DN.

      图4 的结果表明, CIS_1的饱和输出随质子注量的增大没有明显的增大或减少趋势. 相比之下, CIS_2, CIS_3和CIS_4的饱和输出随质子注量的增大而增大, 最高注量辐照后平均增大3%. 造成两组样品饱和输出的差异主要由于低能量质子辐照导致CIS_1的满阱容量显著减小, 如图3(b)所示. 满阱容量的减小在一定程度上导致饱和输出的减小. 相比之下, CIS_2, CIS_3和CIS_4的满阱容量减小相对较小, 因此对其饱和输出的影响也较小. 饱和输出随质子注量增大而增大的现象在已发表的关于CIS的γ和质子辐照实验中也有报道, 相关作者解释为辐射引起的复位晶体管特性的退化[14,15]. 然而, 相关实验结果也显示了饱和输出随γ剂量增大而减小的现象, 归因于满阱容量的降低[12,13]. 因此, CIS的饱和输出存在着复杂的影响机制, 各参数的辐射退化机理及其对饱和输出的综合影响将在下一节的TCAD仿真中进一步分析.

      此外, 实验中也测试了CIS的噪声、暗信号和暗电流等参数. 以暗电流为例, CIS_1在12 MeV能量质子辐照2×1012 cm–2注量后, 暗电流由0.03 nA/cm2增大至78.2 nA/cm2. CIS_2, CIS_3和CIS_4在60 MeV能量质子辐照2×1012 cm–2注量后的平均暗电流由0.03 nA/cm2增大至17.5 nA/cm2. 在质子辐照前后, 所有样品的工作电压与电流无显著变化, 辐照后样品仍可工作, 但成像质量显著退化. 综合样品多个参数在高质子注量辐照下的退化情况, 认为该CMOS图像传感器的抗辐射性能较好.

    4.   TCAD仿真设置

      4.1.   4T PPD CIS仿真模型

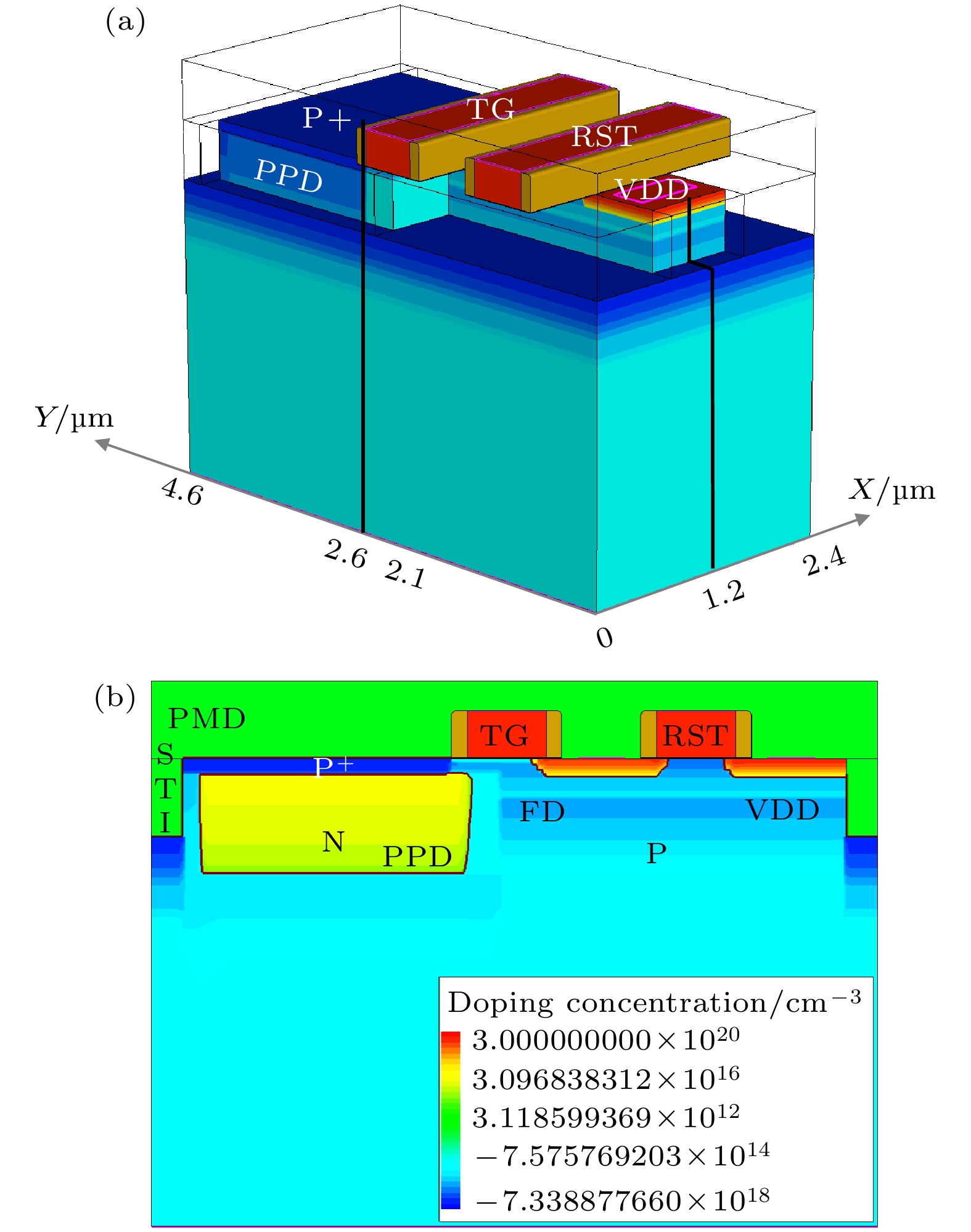
    • 参考已发表的文献[16–18], 在TCAD中建立三维的像元器件模型, 如图5所示. 该模型涉及像元的核心结构, 具体包括钳位光电二极管(pinned photodiode, PPD)、复位晶体管(reset transistor, RST)、传输门(transfer gate, TG)、浮置扩散区(floating diffusion, FD)、金属前介质氧化层(pre-metal dielectric, PMD)、浅沟槽隔离氧化层(shallow trace isolation, STI)等. 在辐照效应仿真前, 对器件模型进行了有效性验证, 包括PPD内N区的全耗尽、光电转换、光生电子转移、RST管漏电流及I-V特性和偏置条件等.

      • 4.2.   仿真条件与模型常态输出

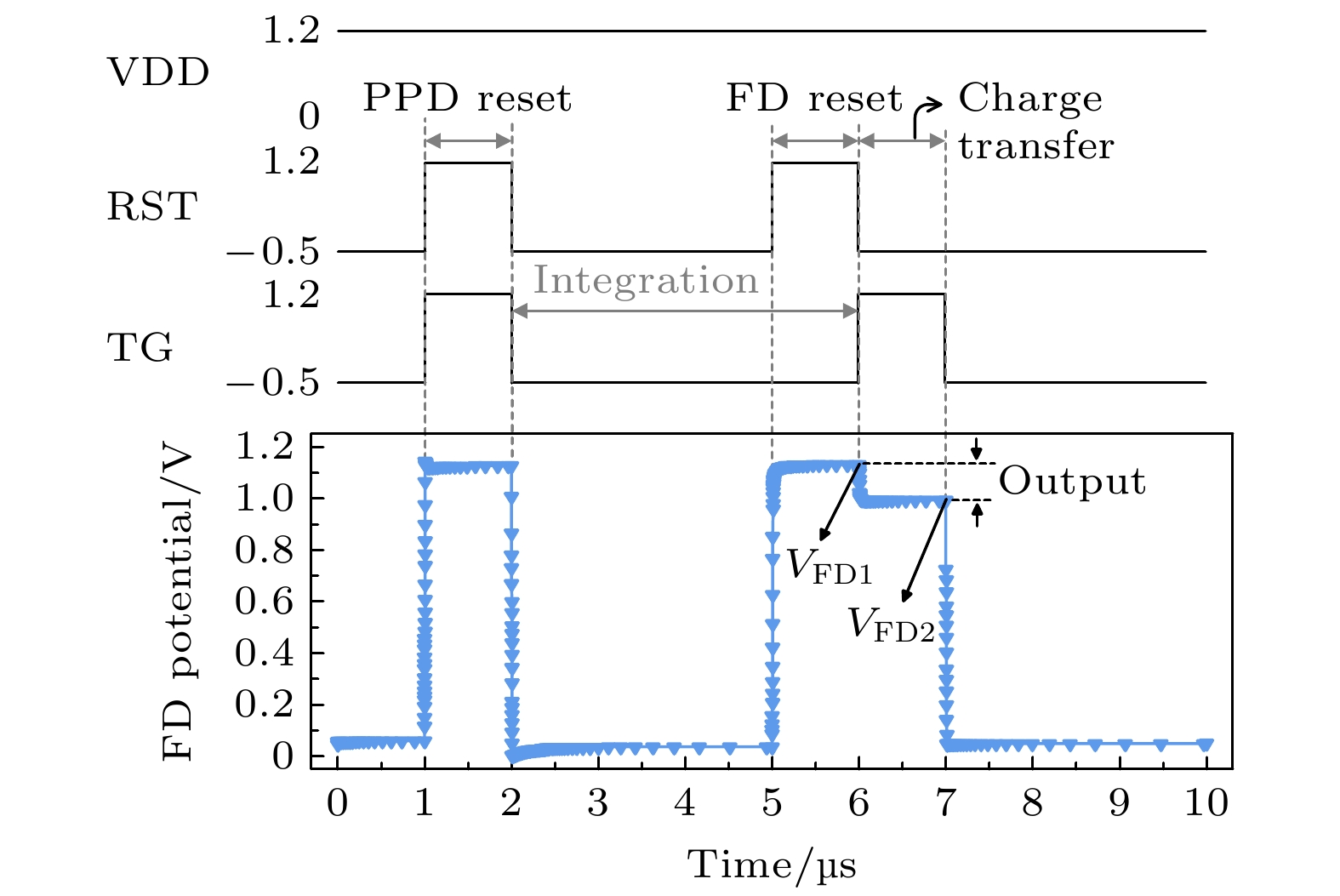
    • TCAD仿真中设置像元模型单个时序周期为10 μs, 由PPD复位、积分、FD复位和电荷转移4个阶段组成, 如图6所示. 在PPD复位阶段, RST和TG都处于高电平导通状态, FD电位升高, PPD区域中的剩余电子被转移到VDD, 完成PPD复位. 在积分阶段, RST和TG都处于低电平截止状态, PPD区域收集光电效应产生的电子. 在FD复位阶段, TG处于低电平截止状态, 而RST处于高电平导通状态, 将FD复位到高电位VFD1. 在电荷转移阶段, TG处于高电平导通状态, RST处于低电平截止状态, PPD中的光电子转移到FD区域, 导致FD电位下降到VFD2. 在实际的CIS中, 相关双采样(CDS)和ADC等读出电路将收集并处理VFD1和VFD2以获得输出. 由于本工作仅考虑像元的辐照效应, 而不考虑外围电路. 因此, 通过VFD1和VFD2之间的电压差来表征输出, 即输出 = VFD1 – VFD2.

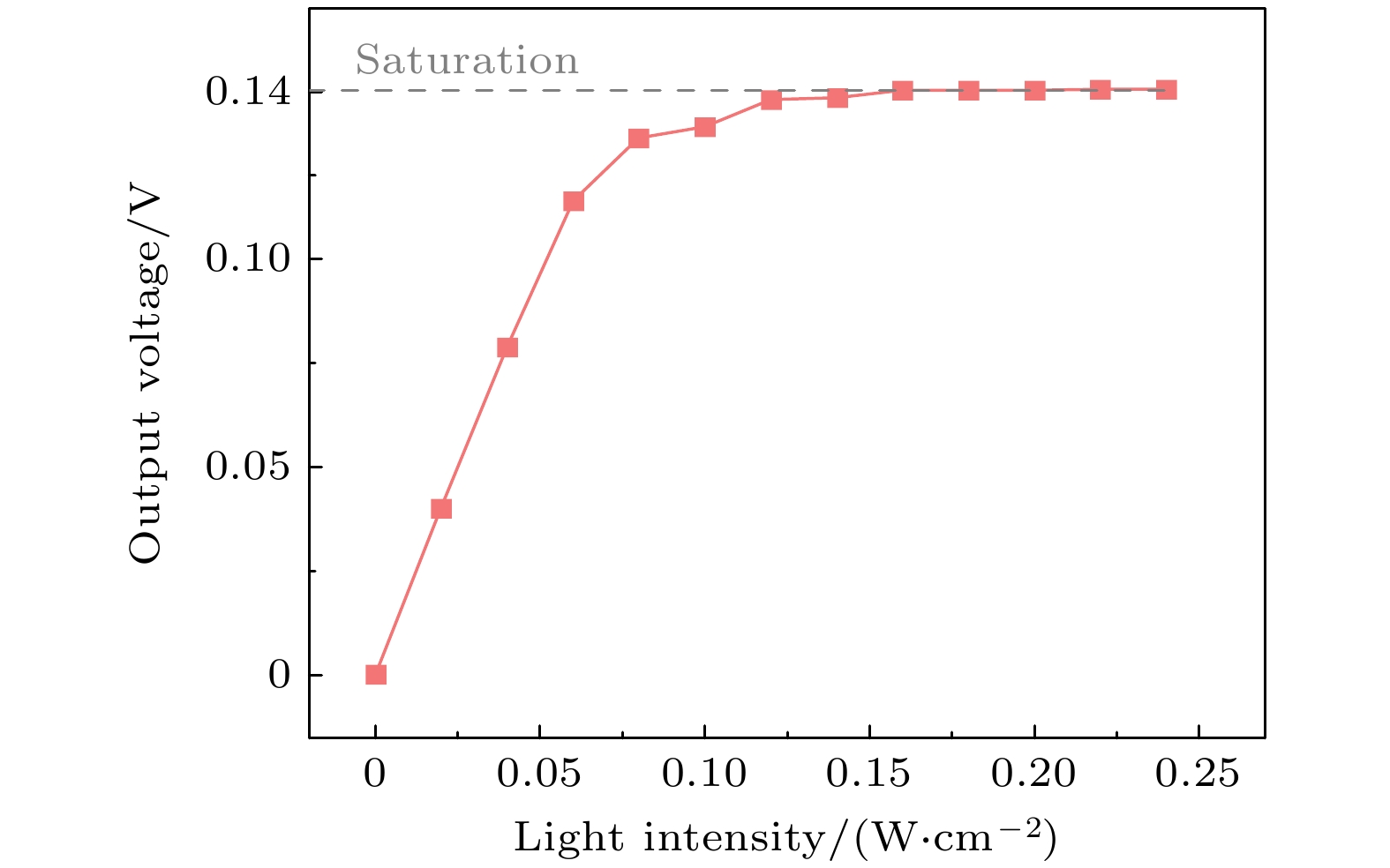
      图7给出了该像元模型的输出电压与光强之间的关系. 在积分时间固定为4 μs的情况下, 输出信号随着光强先线性增大, 后饱和于0.14 V. 因此, 在4.3节的TCAD质子辐照效应仿真中, 对应饱和光照条件的光强设置为0.20 W/cm².

      • 4.3.   质子辐照效应仿真方法

    • TCAD仿真质子累积辐照效应的基本思路是将其等效为中子位移损伤剂量和γ电离总剂量, 并分别添加相应的辐射效应模型.

      对于位移损伤剂量, 需要将质子注量Φp转换为中子注量Φn, 两者的关系如(2)式所示[22]:

      式中, KD是质子和中子的非电离能量损失(NIEL)之间的转换因子, 参考文献[23]可进一步计算出在12 MeV和60 MeV能量下KD分别约为3和1. 采用经典的少数载流子寿命数学模型来模拟中子位移损伤效应[22,24], 其表达式为

      式中, τΦ为中子辐照后的少数载流子寿命, τ0是初始少数载流子寿命, Φn是质子的等效中子注量, Kτ是使用Gregory半经验模型的辐射引起的载流子寿命变化系数[25].

      对于电离总剂量, 12 MeV和60 MeV能量质子的电离能量损失分别为30.2 MeV·cm²/g和8.6 MeV·cm²/g[26], 进一步计算出相应质子注量下的总剂量. 当器件特征尺寸达到深亚微米及以下时, 辐射产生的空穴不能被困在薄栅氧化层[27]. 然而, 空穴被困在STI内靠近其与硅的界面处, 形成一个显著的泄漏电流路径, 这是主要且必须考虑的损伤因素[27–29]. 在本文中, 同时使用TCAD内部Traps和Radiation模型来模拟总剂量效应. 该方法的主要思路如下: 1)在氧化物(对于 4T PPD像元为STI和PMD)中添加hNeutral缺陷[16]; 2)设置γ射线剂量, 并通过Radiation模型产生电子-空穴对. 随后, 缺陷捕获空穴, 形成氧化物陷阱正电荷; 3)固定总剂量辐照后器件状态, 仿真辐照后CIS的电学特性. Radiation模型产生的电子-空穴对(Gr)取决于电子-空穴产生率(g0)、剂量率(D)和产额函数Y(E ), 其表达式为

      由于该模型仅在半导体材料中有效, 因此模型中的STI和PMD的材料需要修改为“OxideAsSemiconductor”.

      TCAD仿真中辐照效应质子注量点对应等效中子注量和γ剂量如表2所示. 在仿真中, 设置γ射线剂量率为100 rad(Si)/s.

    5.   CIS质子辐照仿真结果与分析

      5.1.   全局质子辐照仿真

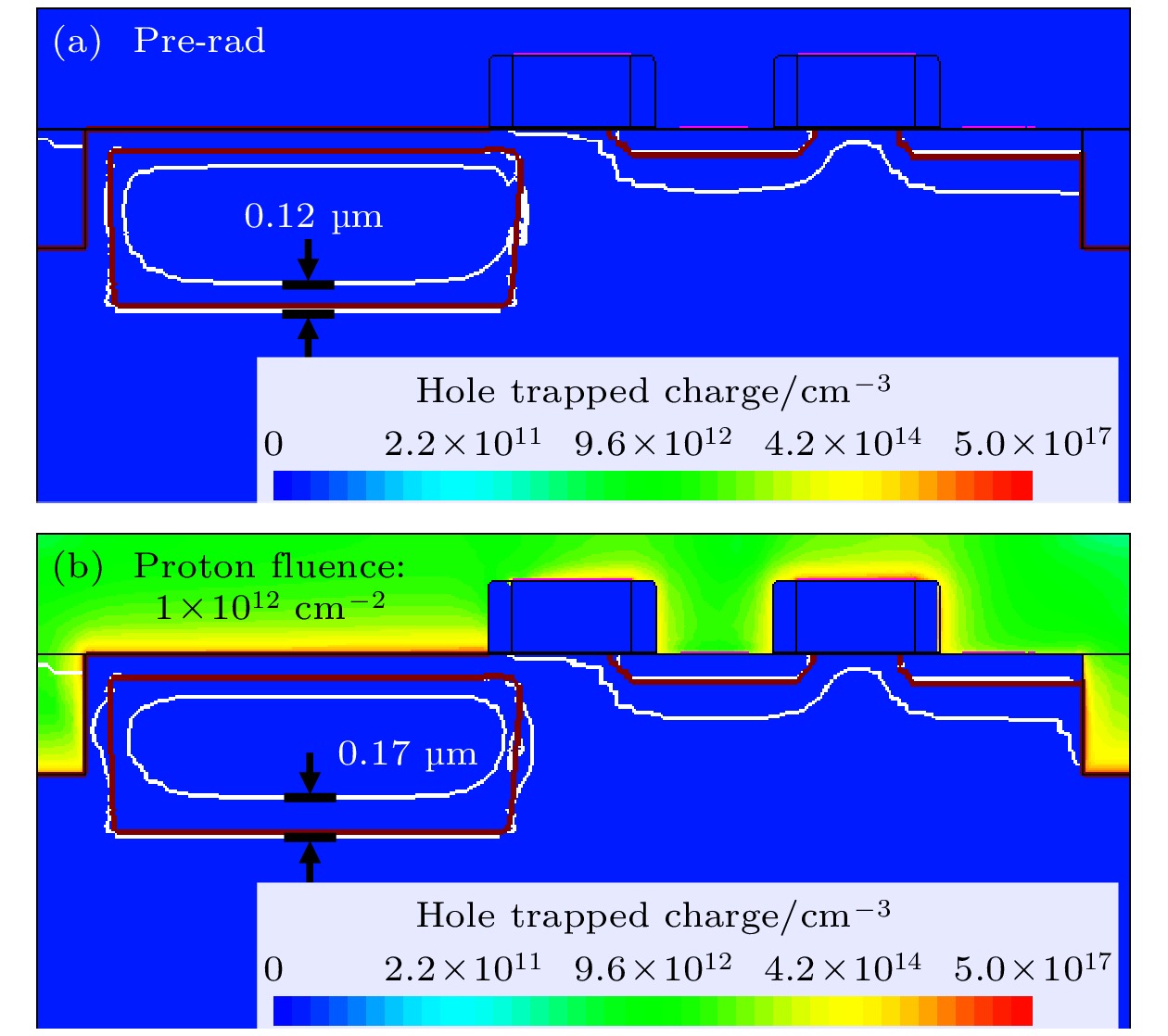
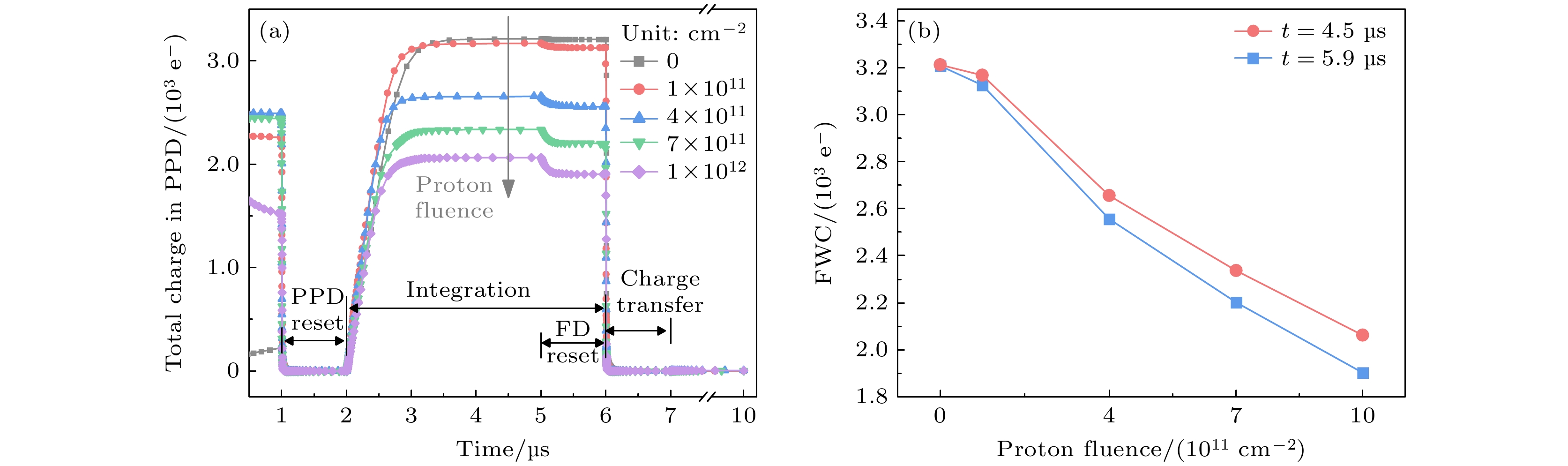
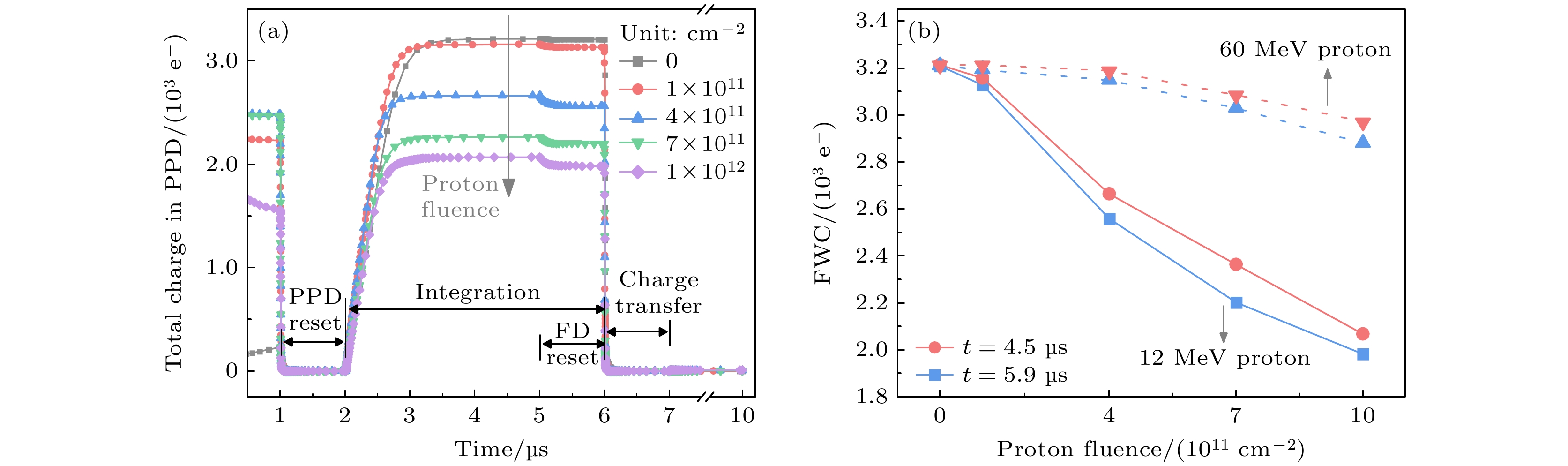
    • 在TCAD中, 首先对像元模型进行预定时间的12 MeV质子辐照, 然后在饱和光照条件下进行驱动时序仿真. 图8显示了FD复位阶段((T+5.9) μs, 其中T为质子辐照时间), 质子辐照前后氧化物中陷阱正电荷的分布. 可见, 正电荷主要分布在硅的界面附近的氧化层(PMD和STI)内. 在饱和光照条件下, PPD内N区中的电子总数对应于满阱容量. 在辐照之前, PPD中的耗尽区厚度为0.12 μm, 而辐照后增大到0.17 μm, 表明辐照后PPD中存储电子减少. 为了进一步研究满阱容量的退化情况, 绘制了整个周期中N区的总电子数变化曲线, 如图9(a)所示. 在t = 1—2 μs的PPD复位阶段, N区域的电子几乎耗尽. 在t = 2—6 μs, 当曝光开始时, 由于高光照强度, N区的电子迅速增大, 最终达到饱和. 在t = 6 μs时, 电荷转移过程开始, 电子转移到FD, N区电子迅速减少.

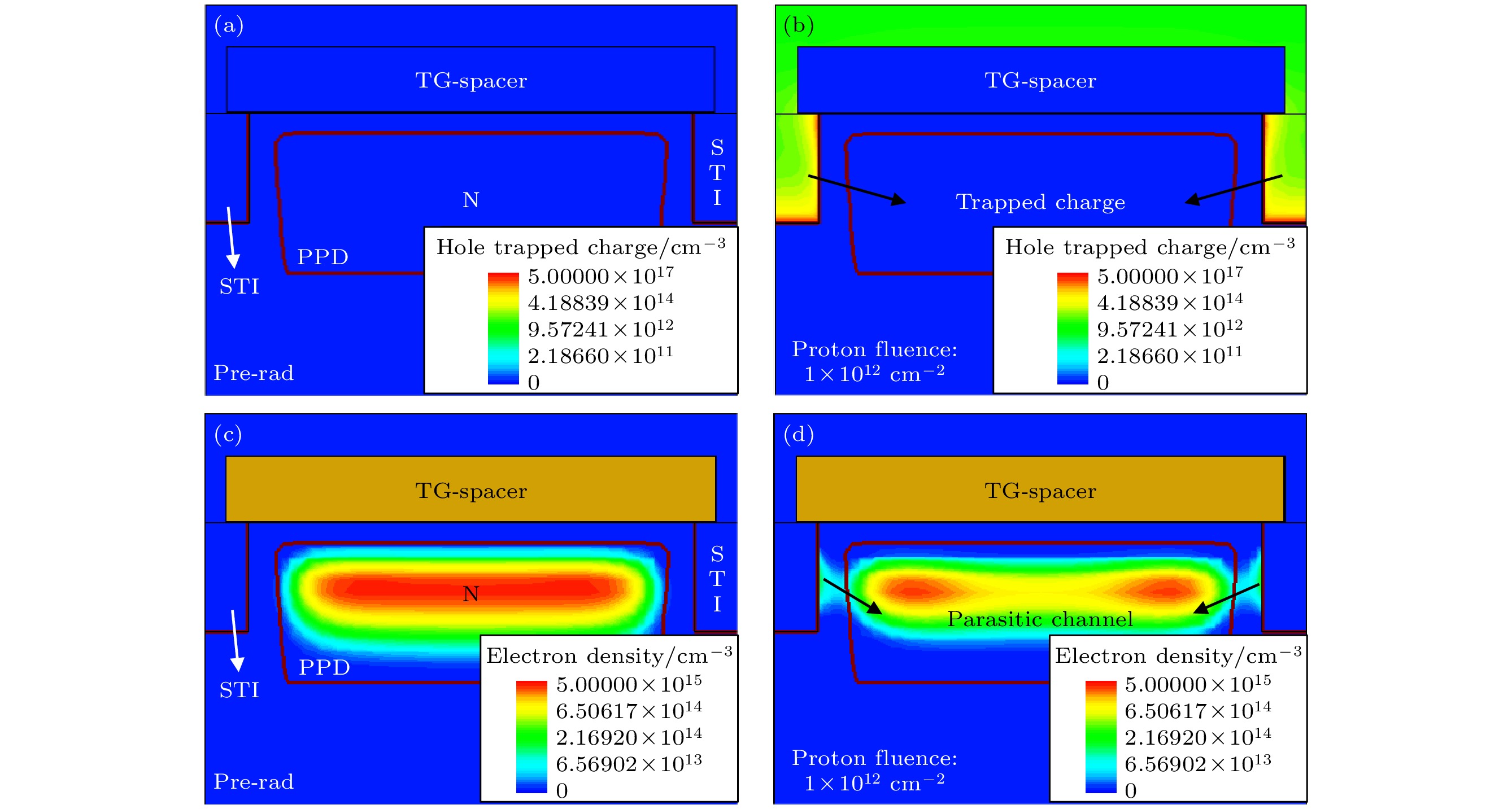
      图9(b)描绘了在t = 4.5 μs和t = 5.9 μs两个时间点, N区的饱和电子数量随质子注量的变化. 随质子累积注量的增大, 饱和电子数量减少, 表明满阱容量减小, 在1×1012 cm–2质子注量下减小38.24%. 图10显示了在FD复位阶段((T+5.9) μs), 沿着Y = 2.6 μm截面的CIS器件模型在辐照前后的氧化物陷阱正电荷和电子浓度的分布. 可见, 大量的氧化物陷阱正电荷在PPD两侧与硅的界面附近的STI中积累(图10(b)). 由此吸引硅中电子向两侧的STI漂移, 在STI界面附近的硅中形成寄生泄漏通道(图10(d)). N区中的一些电子通过寄生泄漏通道转移到FD区域, 导致满阱容量减小. 此外, 随着质子辐照注量的增大, STI中的氧化物陷阱正电荷浓度增大, 加剧了寄生漏电. 因此, 满阱容量随着质子注量的增大而减小.

      此外, 回顾图9(a)中的曲线, 可以观察到在FD复位阶段N区的饱和电子数量略有下降. 5.9 μs时刻的饱和电子数量低于4.5 μs时刻, 且两者的差值随质子注量的增大而增大, 如图9(b)所示. 这是因为在FD复位阶段, RST开启, 拉高FD的电位, 促使更多PPD的电子通过寄生通道转移到FD区域, 进一步降低了满阱容量.

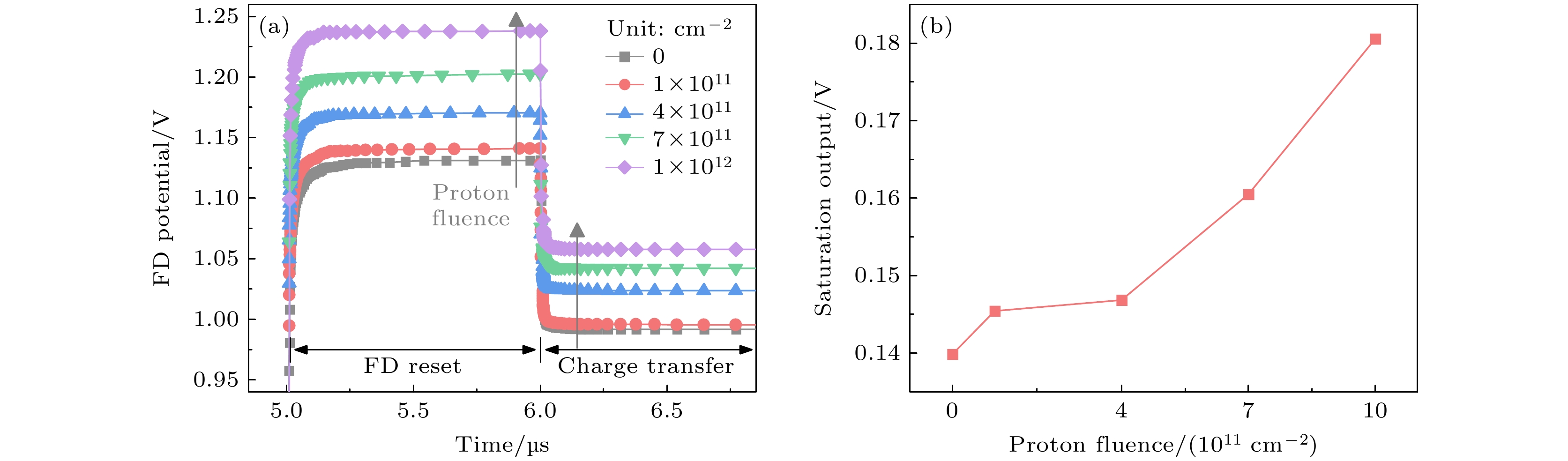
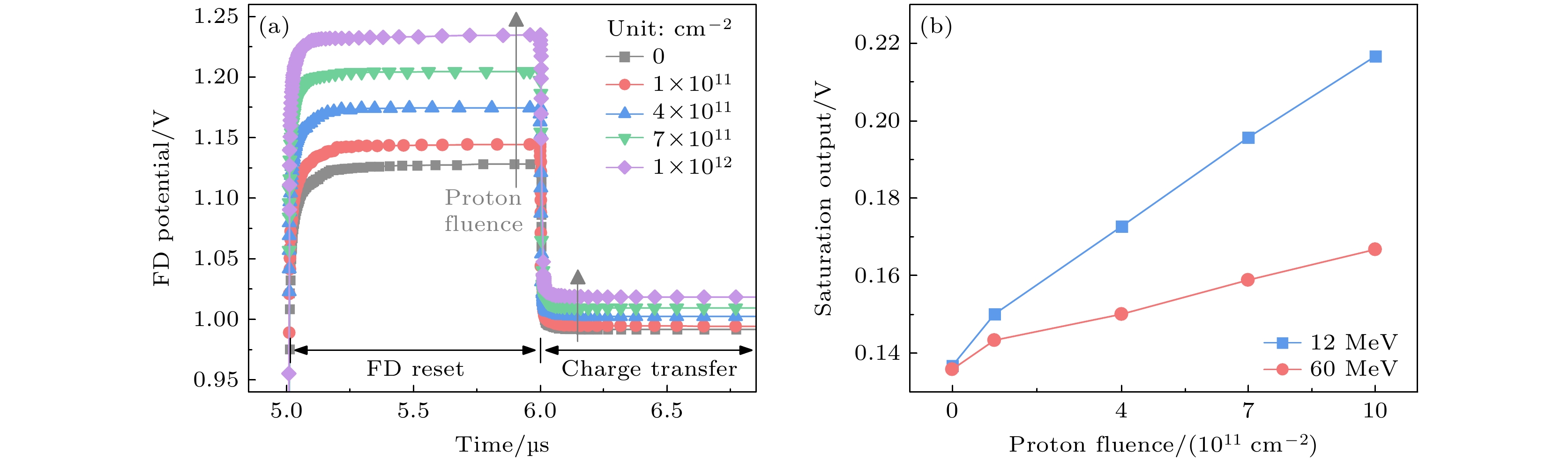
      图11(a)给出了在FD复位和电荷转移阶段(t = 5—7 μs)FD电势随质子注量的变化曲线. CIS的输出信号由VFD1和VFD2决定, 所以在分析饱和输出时, 重点是这两个阶段FD的电势变化. 可见, 在这两个阶段, FD电势整体随着质子注量的增大而抬高. 特别地, FD复位阶段电势VFD1的增大解释了图9(b)中两个时间点之间饱和电子数量差值逐渐增大的现象. 计算并绘制了饱和输出随质子注量的变化, 如图11(b)所示. 可见, 饱和输出随着质子注量的增大呈增大趋势, 在1×1012 cm–2质子注量下增大29.07%.

      • 5.2.   局部质子辐照仿真

    • 为进一步研究辐照导致饱和输出变化的机理, 本节对像元模型开展12 MeV和60 MeV质子局部辐照仿真. 如图5所示, 以Y = 2.1 μm为边界, 可以将整个模型分为两部分: Y > 2.1 μm的部分仅包括PPD和TG区域, 而Y < 2.1 μm的部分仅包括FD和RST区域. 需要注意的是, 在质子累积辐射效应中电离效应占主导地位[25]. 因此, 局部质子辐照仿真指局部添加电离辐射效应, 而位移效应仍然是全局添加.

      • 5.2.1.   局部辐照PPD和TG

    • 考虑质子对PPD和TG的局部辐射效应(即图5中Y > 2.1 μm的部分), 分别于图12和图13中绘制了满阱容量和饱和输出的变化曲线.

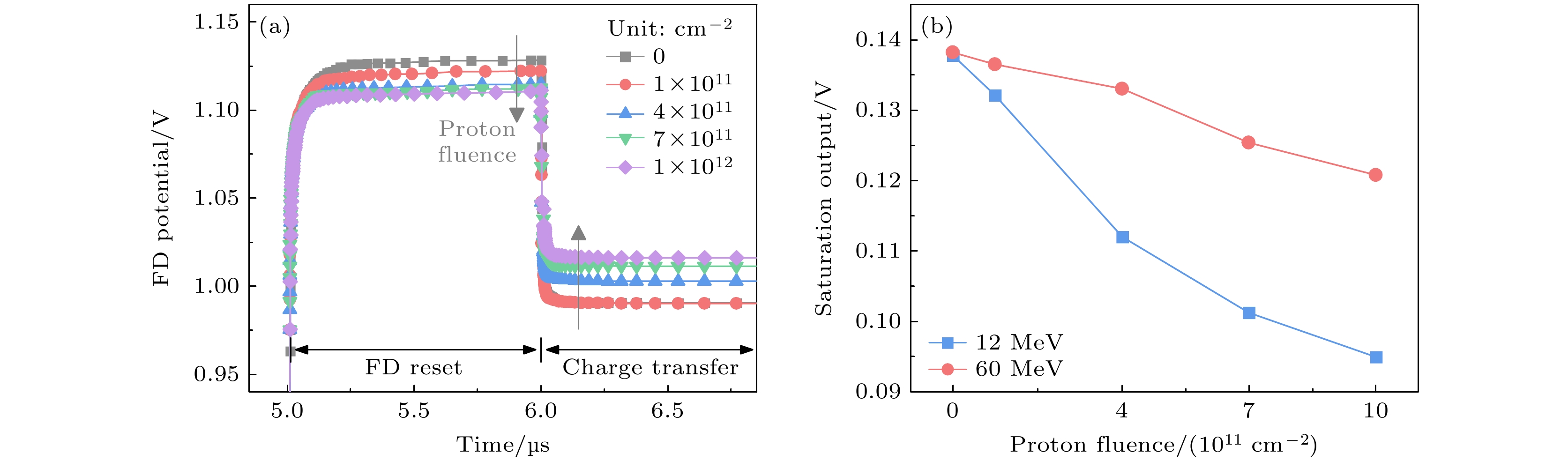
      对比图9和图12, PPD和TG区域的局部质子辐照引起的满阱容量退化与全局辐照的情况近乎一致, 这表明满阱容量的退化主要是由PPD和TG的辐照效应引起的, 在1×1012 cm–2注量下12 MeV和60 MeV质子辐照分别减小38.21%和10.32%, 低能质子辐照导致满阱容量退化更显著, 与实验结果定性一致. 两种情况之间唯一的区别在于FD复位阶段开始时进一步丢失的电子数量: 在全局辐照中, 随着质子注量的增大, FD复位电势的升高导致丢失的电子数量单调增大. 然而, 在PPD和TG的局部辐照中, 进一步丢失的电子数量并不单调增大. 一方面, 由于不考虑RST的辐照效应, 在FD复位期间一些电子从PPD转移到FD, 导致FD电势略有下降, 如图13(a)所示. 另一方面, FD复位电势的轻微下降反过来导致从PPD进一步丢失到FD的电子数量略有减少. FD的复位电势(VFD1)可表示为

      其中Vdd是施加到RST漏极的电源电压, Vth_RST是RST的阈值电压, ΔVsubth_TG和ΔVsubth_RST分别为亚阈值泄漏电流在TG和RST上的电压降. 由于局部辐照PPD和TG, 所以可以忽略Vth_RST和ΔVsubth_RST的辐照响应. 随着质子注量的增大, TG的漏电流增大, ΔVsubth_TG相应增大, 导致FD复位电位下降.

      质子辐照后, 由于满阱容量的降低, 在t = 6—7 μs时从PPD转移到FD的电子总数减少, 这导致电荷转移后FD电位(VFD2)的下降量减少(图13(a)), 进一步导致饱和输出的减少(图13(b)), 在1×1012 cm–2质子注量下, 12 MeV和60 MeV质子辐照分别减小31.08%和12.61%.

      • 5.2.2.   局部辐照FD和RST

    • 考虑质子对FD和RST的局部辐照效应(即图5中Y ＜ 2.1 μm的部分), 分别在图14和图15中绘制了满阱容量和饱和输出的相关曲线.

      图14为该条件下PPD内部的电子总数和满阱容量随质子注量的变化曲线. 随着注量增大, 满阱容量没有显著变化, 进一步证明了满阱容量的退化与RST的辐照效应没有直接关系. 图15为该条件下FD电势和饱和输出随质子注量的变化曲线. 同样, 根据(5)式分析, 由于局部辐照FD和RST, 忽略ΔVsubth_TG的辐照响应. 随着质子注量的增大, ΔVsubth_RST增大, 而Vth_RST减小, 导致FD复位电势增大. 此外, 饱和输出随着质子注量的增大显著增大, 在1×1012 cm–2注量下12 MeV和60 MeV质子辐照分别增大58.50%和22.79%.

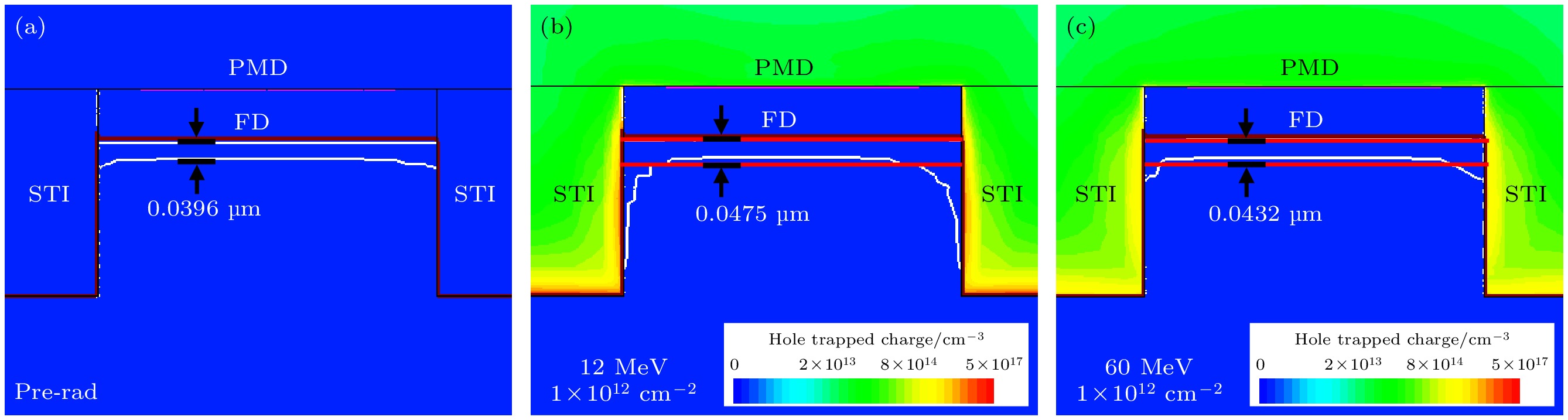
      虽然图14表明质子局部辐照FD和RST区域不会导致满阱容量发生变化, 但图15(b)表明饱和输出随着注量的增大而增大. 图16展示了辐照前后FD耗尽区的变化. 以12 MeV质子辐照为例, 辐照前耗尽层厚度为0.0396 μm, 而辐照后由于STI中的氧化物陷阱为正电荷, 两侧的耗尽区扩展, 导致有效耗尽区厚度增大至0.0475 μm. 电容CD和电势差ΔV可分别由(6)式和(7)式表示:

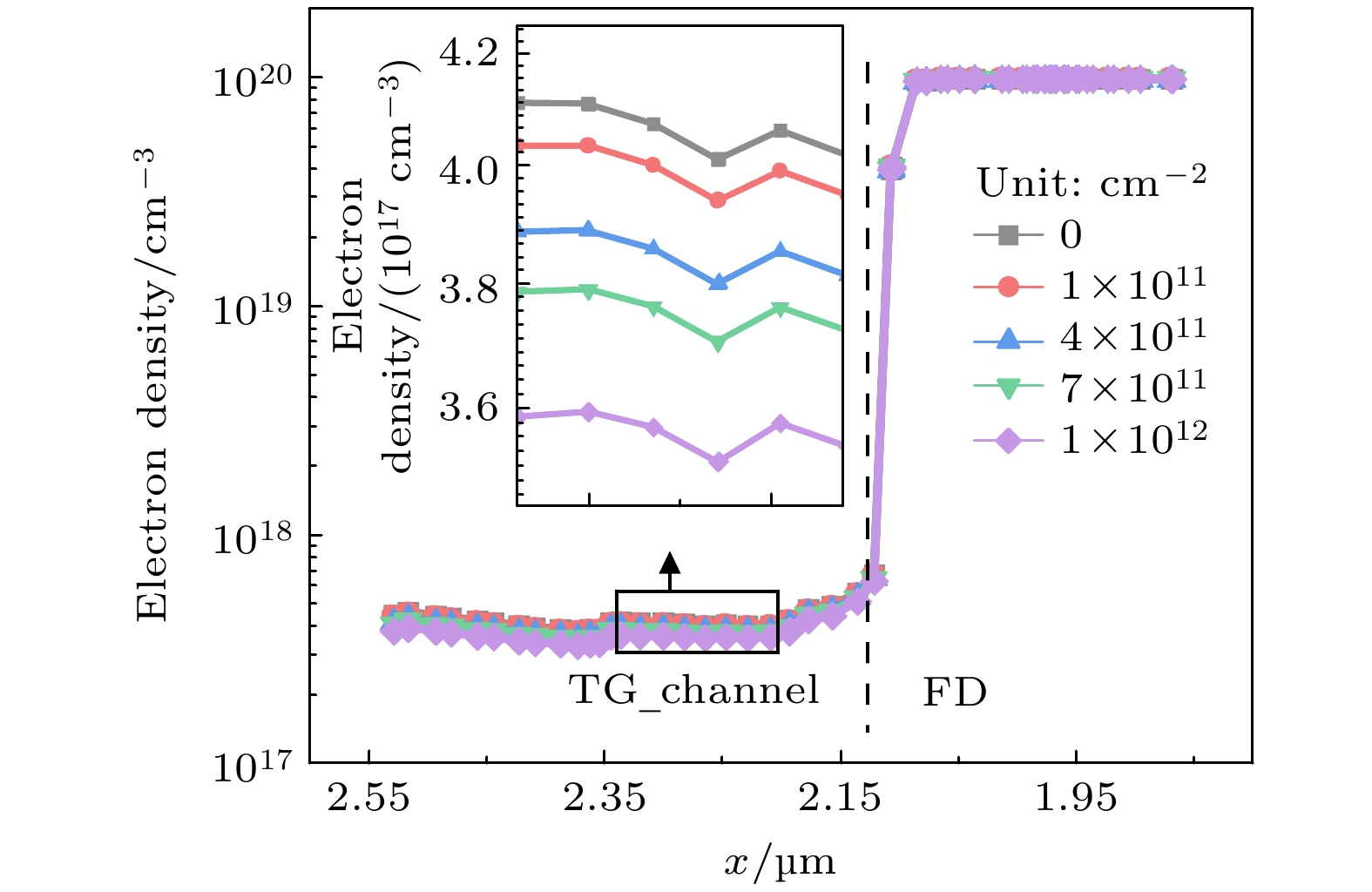
      式中, ε0为真空介电常数8.854×10–12 F/m, εr为硅的相对介电常数11.7, A为FD面积取0.72 μm2, WD为耗尽层厚度, ΔQ表示转移到FD的电子数量. 耗尽区电容随着耗尽层厚度的增大而减小, 因此耗尽区电容随着质子注量的增大而减小. 进一步基于(6)式可以计算出12 MeV和60 MeV质子辐照导致转换增益分别增大了20%和9.1%, 与实验结果(图2)定性一致. 图17为TG下方沟道和浮置扩散区的电子浓度曲线. 可见, 随着质子注量的增大, VFD1增大, TG下方沟道中剩余的电子数量减少, 这些电子转移到浮置扩散区, 导致浮置扩散区中实际获得的电子数量ΔQ略有增大, 进而饱和输出增大.

      根据(6)式和(7)式, 当电容CD减小且电子数量ΔQ增大时, 会导致浮置扩散区的电势差ΔV增大. 因此, 即使满阱容量不变, 饱和输出仍会随着质子注量的增大而增大.

    6.   讨　论

    • TCAD质子辐照仿真结果表明: 1)质子局部辐照PPD和TG导致满阱容量降低, 从而导致饱和输出减小; 2)质子局部辐照FD和RST导致FD复位电势和转换增益增大, 从而导致饱和输出增大. 因此, 在质子辐照实验中观察到的饱和输出增大和无显著变化趋势的现象是1)和2)的耦合结果.

      由于质子能量越高, 等效电离和非电离能量损失越小, 在局部质子辐照仿真中12 MeV质子辐照导致的满阱容量、饱和输出和转换增益的退化均较60 MeV质子辐照显著, 其中满阱容量和转换增益的仿真结果均定性地验证了实验结果. 由于仿真模型与真实器件具有不可避免的差异, 仿真结果与实验结果在定量上存在一定差异.

    7.   结　论

    • 通过辐照实验和TCAD仿真研究了CMOS图像传感器的质子累积辐照效应, 对满阱容量、转换增益展开研究分析, 并着重针对辐照后饱和输出的变化机理进行深度剖析. 研究结果表明, 辐照会诱导PPD和TG两侧的STI氧化物中陷阱正电荷积累, 进而在硅中形成寄生漏电通道, 致使满阱容量降低. 在像元层次, 饱和输出的变化由满阱容量、复位晶体管的物理特性和转换增益共同决定. 具体而言, 辐照使得满阱容量的降低会导致饱和输出减小; 复位晶体的辐照效应则会使FD复位电势增大, 进而饱和输出增大; 辐照使得浮置扩散区的电容减小, 转换增益增大, 进而饱和输出增大. 三者在辐射敏感性上的差异使得饱和输出可能随着质子注量的增大而减小或增大.

    参考文献 (29)

目录

/

返回文章
返回