量子力学与经典引力场理论在其各自适用范围内都能有很好的验证, 但若考虑到引力的量子描述, 即考虑引力是否需要量子化, 或者说如何验证引力相互作用是否确实需要被量子化, 这一问题目前仍存在争议^[1]. 有人认为导致两个系统间产生纠缠的相互作用必须是量子的, 因此, 引力量子化的充分证据是探测到由引力相互作用引起的有质量粒子系统间纠缠^[2,3]. 除此之外, 是否有一个独立于特定模型的实验提议, 可以确定引力是否具有量子力学性质的相互作用? 从粒子物理学的角度看, 引力的量子效应只有在极高能量和小尺度上才能探测到, 这对现有的实验技术来说是一个很大的挑战. 然而, 在较低的能量下, 质量比原子质量尺度高几个数量级的量子系统正逐渐在实验室中实现, 在这些尺度上, 目前的理论预测引力能够影响量子态的动力学, 包括引力场的叠加、由外部引力场引起的退相干以及引力场本身的量子性质等一些新颖的想法被提出^[4–6], 其中部分想法在短期内很有可能在实验和技术上实现. 关于引力量子性的讨论, 2017年Bose等^[7]与Marletto和Vedral^[8]考虑到了由两个有质量量子系统之间的牛顿势所产生的量子纠缠, 文章利用量子信息论中的局域操作和经典通信(local operation and classical communication, LOCC)不能增加系统的纠缠这一原理, 提出在相邻的物质波干涉仪中, 2 μm大小的测试质量的引力相互作用引起的相位演化可以探测到纠缠; 此方案是迄今为止通过实验室建立验证引力量子性的最简便方案. 近年来光力学领域的快速 发展也为上述实验的实现提供了巨大的帮助^[9–11]. 鉴于目前引力量子性的研究, 本文主要致力于分析引力相互作用对有质量粒子间的量子关联动力学行为的影响.

在量子力学中, 一个有质量粒子原则上可以处于两个空间分离位置的叠加状态, 这种引力的叠加态被称为“引力猫态”^[12]. 最近, 已有文章研究了在热平衡场中“引力猫态”的量子关联以及在热平衡场下“引力猫态”中的可提取功^[13–15], 也有相关文章研究了两关联退相干信道间的经典相关性对双“引力猫态”退相干的影响^[16]. 量子关联是量子理论中的一个关键概念, 也是量子计算、量子计量、量子电池和量子通信^[17–22]等量子技术的一个重要物理资源. 由于不同类型的噪声影响, 导致了量子系统退相干和量子关联损失, 这会使我们无法对量子系统特有的非经典性质加以利用, 因此非常有必要研究存在环境噪声时引力相互作用耦合下的有质量量子系统量子态的动力学行为. 提高量子态演化速率能有效保持量子系统关联的鲁棒性, 量子速率极限时间定义了量子系统演化过程中的最大演化速率, 本文针对外部环境噪声影响下的双“引力猫态”量子系统, 采用量子速率极限时间(quantum speed limit time, QSLT)来描述量子态演化速率, 采用几何量子失协^[23–25]来度量双“引力猫态”间量子态的量子失协. 研究结果表明: 无论是在稳定经典场噪声还是衰减场噪声的影响下, 通过增强双“引力猫态”间的引力耦合强度, 能有效减小量子速率极限时间, 从而达到加速量子态演化的目的, 与此同时, 引力耦合增强会改变系统量子失协振荡的周期; 在衰减场的影响下, 调节场的衰减率在一定程度上也能加速量子态演化. 值得注意的是, 在衰减场影响下, 在任意初始时刻开始演化的量子态演化加速的潜能与量子系统失协动力学行为有着一定的对应关系.

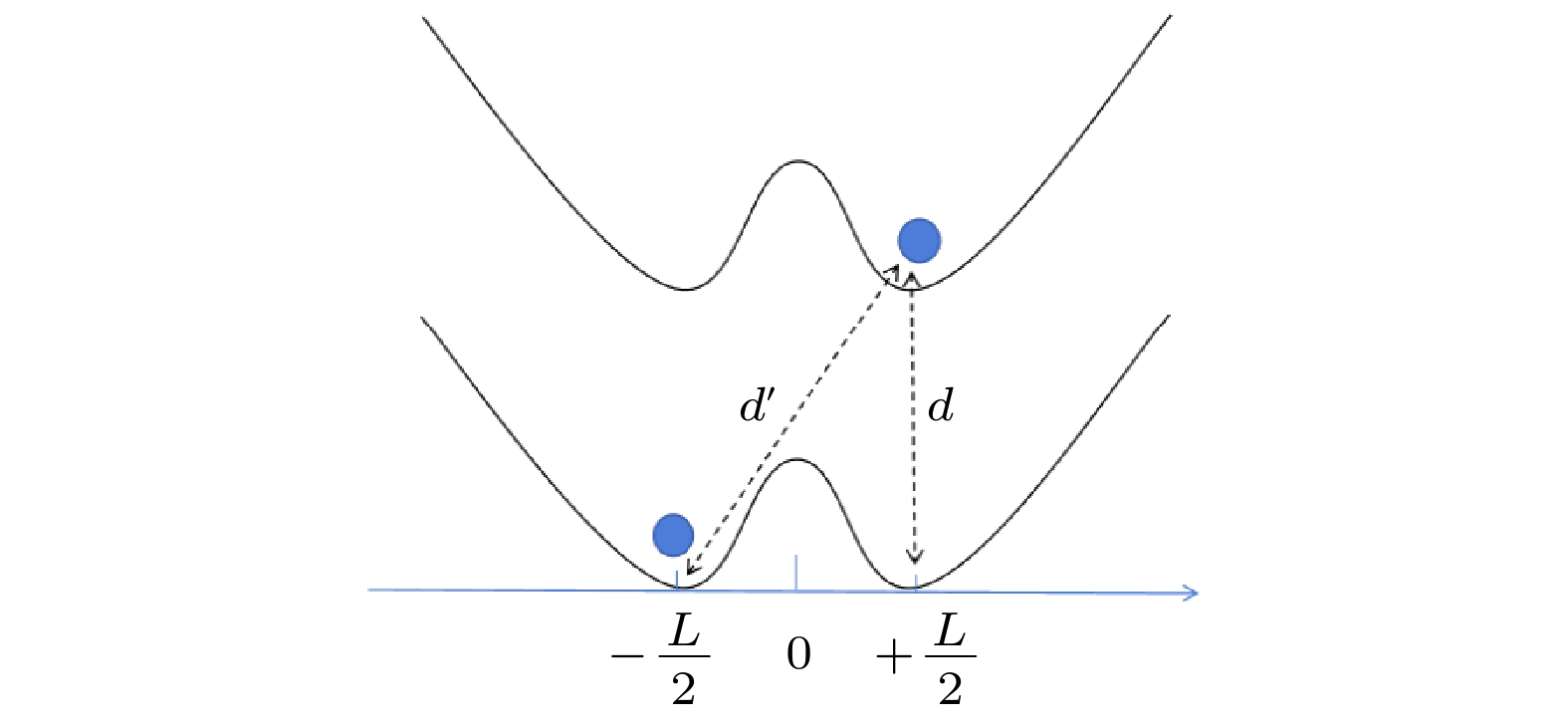
本文考虑两个质量为$ m $的粒子分别被限制在各自的一维双势阱里, 势阱在$ x = {{ \pm L} {/ } 2} $处有最小值, 如图1所示, 每个粒子对应一个量子比特, 通过引力相互作用耦合在一起, 这样的系统称为双“引力猫态”. 双势阱的势能是偶函数, 每个势阱的最小值对应的本征态$ \left| \pm \right\rangle $, 其满足$ \hat x\left| \pm \right\rangle = \pm L{{\left| \pm \right\rangle } {/ } 2} $, $ \hat x $是位置算符, 在Landau-Lifschitz近似下^[12], $ \left| \pm \right\rangle = ( | g \rangle \pm \left| e \right\rangle ) {/ } {\sqrt 2 } $, 其中$ \left| g \right\rangle $和$ \left| e \right\rangle $对应能量为$ - {\omega {/ } 2} $和$ {\omega {/ } 2} $的基态和激发态. 系统的哈密顿量可以写为

式中, $ \omega $是基态与激发态之间的能量差, $ {\sigma _x} $和$ {\sigma _z} $是泡利算符, $ I $是单位算符. $ \gamma $是两个粒子之间引力相互作用强度, 可以表示为

其中, G是引力常数, $ d $和$ d' $是两粒子在势阱相同位置和不同位置时的距离.

为了探究双“引力猫态”量子系统的动力学行为, 将考虑两种情况. 第一种是将上述系统置于经典场中, 系统哈密顿量变为

其中,

$ \lambda $是经典场与双“引力猫态”系统之间的耦合强度, ${\boldsymbol{ I}} $是单位矩阵^[26]. 为了简单起见, 考虑子系统各自处于相同的经典场环境中.

考虑双“引力猫态”系统初始被制备在双量子比特的X态:

任意时刻系统的密度矩阵可以由$ \rho \left( t \right) = U\left( t \right)\times \rho \left( 0 \right){U^ + }\left( t \right) $得到, 其中幺正演化算符为

为简便起见, 考虑稳定经典场$ {\delta _i}\left( t \right) = {\delta _j}\left( t \right) = \delta $, 则任意时刻的密度矩阵可以写为

式中,

其次, 考虑环境是具有$ {\delta _k}\left( t \right) = \delta {{\mathrm{e}}^{ - \chi t}} $形式的经典衰减场, $ \delta $为经典场的固有参数, $ \chi $表示场的衰减率^[26]. 此时哈密顿量变为

在此含时哈密顿量作用下, 时间演化算子具有以下形式:

式中$ \hat T $是编时算子. 根据Magnus展开^[27], 时间演化算符$ U\left( t \right) $可写成以下形式:

式中,

其中$ [A, B] = AB - BA $是A和B的对易式, 这里忽略高阶项, 只取到二阶近似$ {U_{{\text{eff}}}}\left( t \right)= \exp [{\varLambda _1}\left( t \right) + {\varLambda _2}\left( t \right)] $, 通过计算可以得到

至此, 得到了衰减场影响下的双“引力猫态”系统的动力学过程. 在此有效演化下得到任意时刻密度矩阵. 由于过于复杂, 因此在对后续的量子速率极限时间以及迹距离量子失协的计算中, 采用数值模拟的方法绘制了相关数据图.

系统量子态的最大演化速率可以用量子速率极限时间(QSLT)来描述. QSLT定义了一个量子态从初始$ \tau $时刻的状态演化到$ \tau + {\tau _{\mathrm{D}}} $时刻的目标状态的最小演化时间, $ {\tau _{\mathrm{D}}} $是实际演化时间. 2013年, Taddei等^[28]从量子Fisher信息的角度出发, 给出了存在噪声信道的量子系统的QSLT的MT界. Deffner和Lutz^[29]利用Bures角的度量方法给出了开放量子系统中QSLT的MT和ML界. Zhang等^[30]利用相对纯度给出了任意初始态的QSLT. 本文采用Zhang等^[30]的QSLT, 对初始态$ {\rho _\tau } $到目标态$ {\rho _{\tau + {\tau _{\mathrm{D}}}}} $有

其中,

$ {\rho _i} $是初始时刻密度矩阵$ {\rho _\tau } $的奇异值, $ {\sigma _i} $是任意时刻$ \tau \lt t \leqslant \tau + {\tau _{\mathrm{D}}} $系统密度矩阵$ {{\boldsymbol{\rho}} _t} $的奇异值.

2001年, 量子失协由Hendersoon和Vedral^[31]与Ollivier与Zurek^[32]提出, 用来量化量子态中的非经典关联. 即使对纠缠为零的可分离态, 其非经典关联也不一定是零, 不同于量子纠缠, 量子失协能更全面的对量子态中的非经典关联进行量化. 2010年, Modi等^[33]通过相对熵定义了不同量子关联的统一化方法. 2011年, Dakić等^[34]从量子态之间不同的测量距离的角度出发提出用最小希尔伯特-施密特距离的平方定义几何量子失协, 即

但是基于上述施密特–2范数定义的量子失协不满足局域操作下的单调性, 有学者提出了由施密特–1范数定义的失协, 又称迹距离量子失协^[24](trace distance discord, TDD), 即

其中,

$ \left\{ {\prod _i^A} \right\} $是子系统A的一组正交完备的投影基, $ {\boldsymbol{\rho}} _i^B $是子系统B的约化密度矩阵, $ \left\{ {{p_i}} \right\} $为概率分布. 对于一般的量子态, $ D\left( \rho \right) $是不易计算的, 但对于两比特X态:

则$ D\left( {{{\boldsymbol{\rho}} _X}} \right) = {{\mathrm{int}}} \left( {\left| {{c_1}} \right|, {\text{ }}\left| {{c_2}} \right|, {\text{ }}\left| {{c_3}} \right|} \right) $, int表示取$ \left|{c}_{1}\right|, \left|{c}_{2}\right|, \; \left|{c}_{3}\right| $里的中位值. 对于两比特X态密度矩阵有以下形式:

$ D\left( {{{\boldsymbol{\rho}} _X}} \right) $有更严格的解析解^[25,35]:

其中,

首先, 我们分析了双“引力猫态”处于稳定经典场噪声中的情形. 研究了$ \tau = 0 $时引力相互作用强度$ \gamma $和经典场参数$ \delta $对双“引力猫态”演化过程中QSLT的影响. 本节中, 双“引力猫态”系统的初始态是X态, 通过设置初始参数$ {c}_{1}, {c}_{2}, {c}_{3} $, 当$ \left| {{c_2}} \right| \leqslant {c_1}={c_3} $时, QSLT为

其中场与系统间的耦合强度为$ \lambda = 1 $. 接下来选定贝尔态为系统初始态, 即$ \left( {{c_1}, {\text{ }}{c_2}, {\text{ }}{c_3}} \right) = \left( {1, {\text{ }} - 1, {\text{ }}1} \right) $.

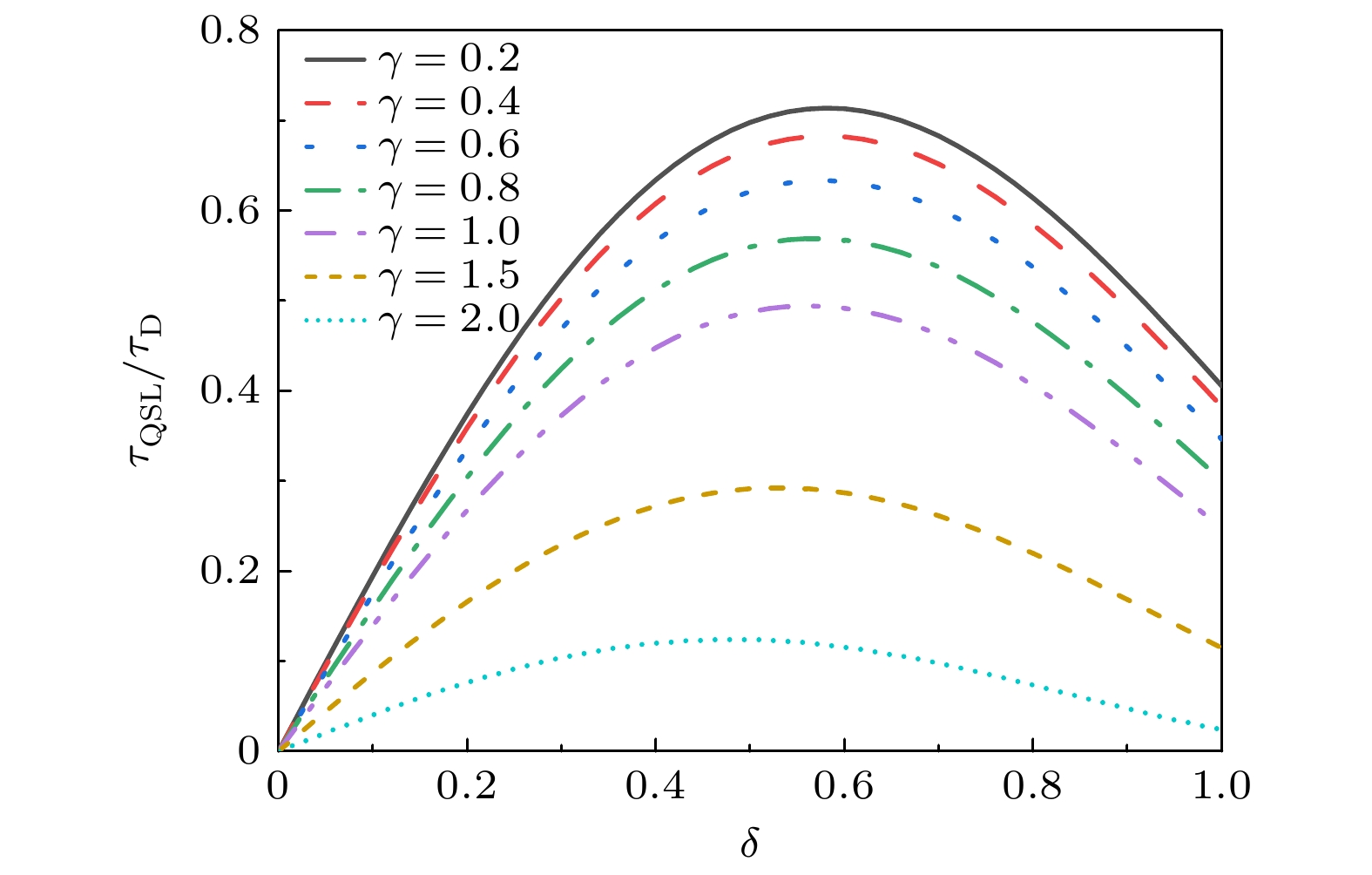
首先分析稳定经典场噪声对双“引力猫态”动力学行为的影响. QSLT关于经典场参数$ \delta $是偶函数, 因此这里只分析了$ \delta \gt 0 $的部分. 如图2所示, 对于相同的耦合强度$ \gamma $, 随着$ \delta $的增加, QSLT与实际演化时间的比值$ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}} } $先增加到一个最大值, 然后减小, 但$ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}} } $都是小于1的, 即量子态演化具备加速的潜力. 对于给定的$ \delta $值, $ \gamma $越大, $ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}} } $越小, 即量子态演化加速的潜力更大, 可以通过调节双“引力猫态”的相互作用强度实现量子态演化的加速.

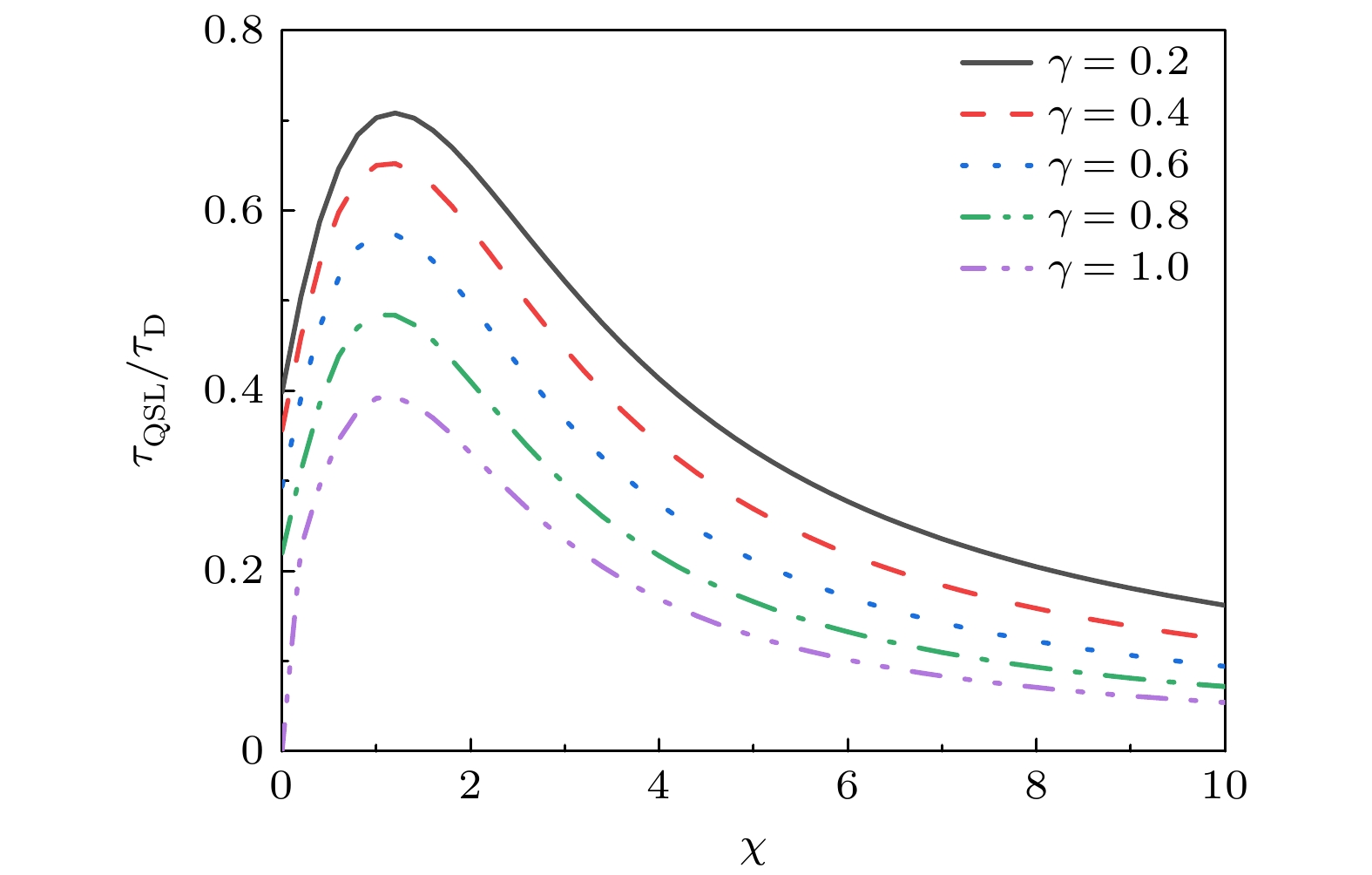
当场存在衰减时, 分析了双“引力猫态”之间的耦合强度$ \gamma $与场的衰减率$ \chi $对QSLT的影响. 如图3所示, 在给定的$ \delta $与衰减率$ \chi $下, 同样是更强的耦合强度$ \gamma $有着更小的QSLT, 意味着更强的耦合对量子态的加速有积极影响. 不同于耦合强度$ \gamma $, 衰减率$ \chi $对QSLT的影响不是单调的, 随着$ \chi $的增加, QSLT是先增大后减小, 因此可以将场的衰减率控制在一定范围内来加速量子态的演化.

图4给出了引力耦合强度较弱时($ \gamma = 0.1 $), $ \delta $与衰减率$ \chi $对QSLT的影响. 从图4(a)可以看到, 当$ \delta $小于一定值时, 随着$ \delta $的增加, QSLT整体上是变大的, 即量子态被加速的潜力会变小; 同时, 随着衰减率$ \chi $增加, QSLT呈下降趋势, 也就是说通过调节衰减率$ \chi $可以实现量子态演化的加速. 而当$ \delta $大于一定值时, 如图4(b)所示, 随着$ \chi $增加QSLT不再是单调的, 会先变大后减小. 也就是说, 影响双“引力猫态”演化快慢的因素是多方面的, 通过调节衰减率来实现对量子态演化加速的调控还需要考虑到经典场参数$ \delta $的影响.

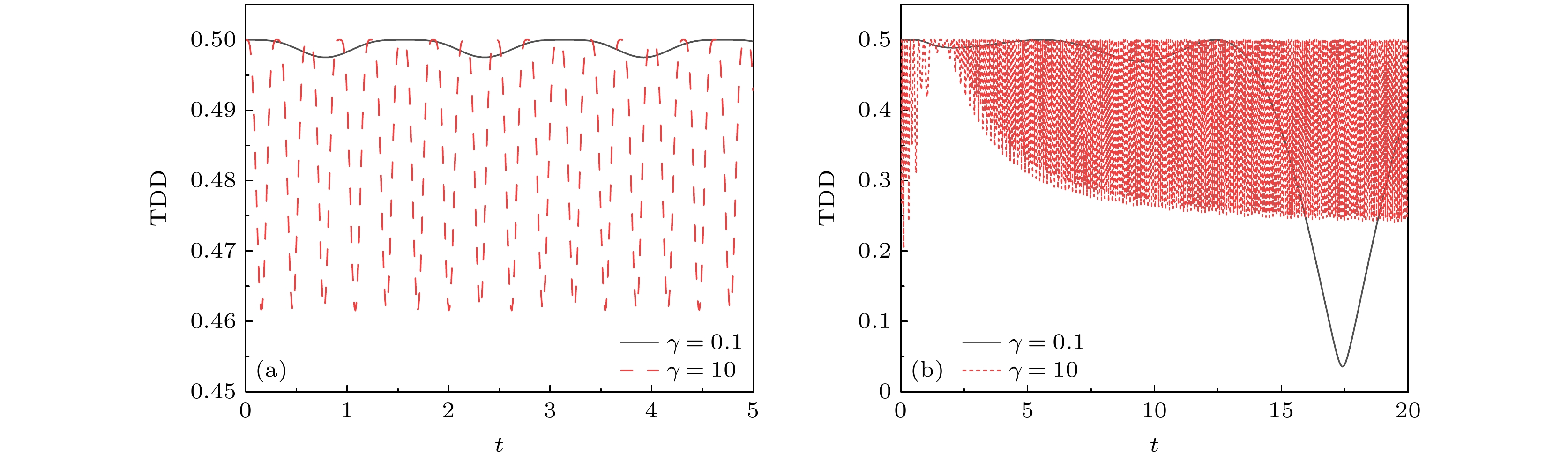
首先, 分析了稳定经典场影响下双“引力猫态”系统的TDD的动力学行为. 这里将双 “引力猫态”系统与环境之间的耦合强度$ \lambda $定为1. 图5分别展示了强耦合与弱耦合时稳定经典场参数$ \delta $对双“引力猫态” TDD动力学的影响. 随着时间的演化, 两比特之间的TDD先减小然后恢复到原值, 具有一定的周期性. 如图5(a)所示, 当两个比特之间的引力耦合强度较弱, $ \gamma $ = 0.1时, 随着$ \delta $的增大, TDD动力学振荡幅度越来越小, 振荡周期越来越短. 相比之下, 当耦合较强时, 在图5(b)中, $ \gamma $ = 10, 随着$ \delta $的增大, TDD随时间衰减得越快, 动力学振荡幅度越大, 但振荡周期不随$ \delta $的变化而改变.

为了更直观地看到双“引力猫态”间引力耦合强度对量子失协动力学的影响, 比较了两种噪声影响下强耦合与弱耦合时TDD随时间的变化曲线. 如图6(a)所示, 在稳定经典场的影响下, 更强的耦合会使得TDD振荡的频率更快, 振荡幅度不变. 对于衰减场的情形, 如图6(b)所示, 情况亦是耦合越强TDD动力学振荡得越快, 但不同的是, 弱耦合时系统TDD在开始的一段时间内波动较小, 在失协最大值附近维持了较长时间, 随后再随时间衰减到最小值后开始恢复; 强耦合时, TDD在短时间内经历快速的衰减-恢复这一振荡过程, TDD振荡幅度随时间的推移越来越小, 在恢复到初值后再随时间振荡衰减且振幅越来越大直至振幅趋于不变, 最终振幅稳定在一定范围内.

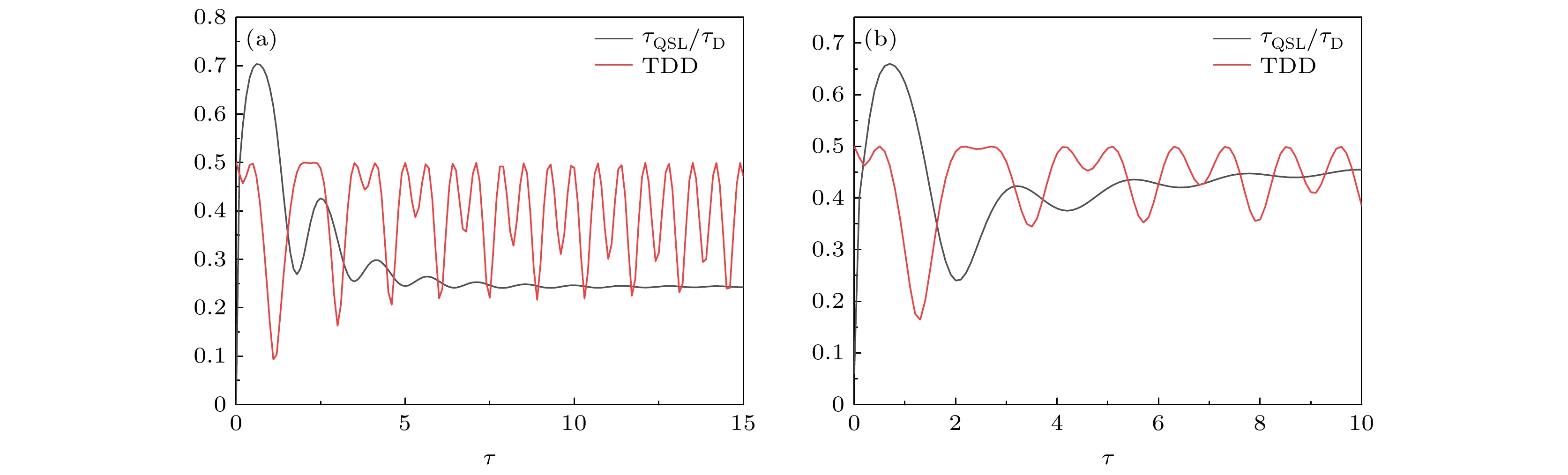
值得注意的是, 对于衰减场的情形, 我们还研究了双“引力猫态”的含时密度矩阵从任意时刻开始, 经由实际演化时间$ {\tau _{\mathrm{D}}} = 1 $的演化, QSLT与实际演化时间的比值随时间的变化. 如图7所示, 选定$ \delta = 1 $, $ \gamma = 1 $, 发现$ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $随时间呈现振荡的趋势, 在短时间内迅速增大到一定值后开始下降, 随后振荡直至趋于平稳值, 即量子态的演化经历了先减速后加速然后再减速再加速的振荡过程, 直至一定时间后演化速率趋于稳定. 同时将其与同条件下系统量子态的TDD进行对比发现, TDD的动力学也存在类似的振荡行为. 并且对比二者发现, 在系统量子失协增加的过程中对应QSLT值的减小过程, 在失协振荡具有规律性时, QSLT趋于一定值, 双“引力猫态”系统量子失协与量子速率极限时间有一定的关系: 即量子失协一定程度上会影响量子态演化的速率, 系统间量子失协的增加会更有利于量子态的演化.

本文研究了一对分别被限制在双势阱中的有质量粒子构成的所谓“引力猫态”系统, 在外部经典场与衰减场噪声影响下的量子失协动力学与量子态演化速率. 通过利用QSLT描述量子态演化速率, 利用TDD度量除纠缠之外的非经典关联, 得到了相关结论: 增大两粒子之间引力相互作用强度对加速双“引力猫态”系统的量子态演化有积极作用. 但对于衰减场的情形, 场的衰减率对系统演化速率的影响不是单一的, 在一定范围内适当增大场的衰减率有利于量子态的加速演化. 实验上可以通过调节有质量粒子的质量和两者之间的距离来改变引力耦合强度, 从而达到调控量子态演化的快慢.

对系统双“引力猫态”的量子失协动力学行为的研究发现, 无论是稳定经典场还是衰减场的情况下, 引力场的耦合强度会影响TDD动力学振荡的周期, 耦合越强, 振荡周期越短; 在稳定经典场噪声影响下, TDD动力学受场的影响会由最大值减小后再增加, 具有周期性地如此反复. 而对于衰减场的情形, 强耦合时TDD会随时间振荡幅度越来越小直至恢复到初始最大值, 然后再随时间振荡衰减直至振幅不随时间变化. 值得注意的是, 对于衰减场的情形, 我们还发现双“引力猫态”的引力耦合强度在一定值时, 量子系统的TDD与在任意初始时刻演化的系统QSLT有相对应的关系, 即随着时间的演化, TDD增加对应着QSLT的减小, 也就是说, 量子失协的增加有利于双“引力猫态”系统的动力学加速.