具有时间反演对称性的光学互易性(optical reciprocity, OR)表现为光传播的可逆性, 其本质是遵从洛伦兹互易定理. 相对地, 时间反演对称性的破缺, 使得介质呈现出光学非互易性(optical nonreciprocity, ONR), 指光在该介质中延某一方向传播时透射率很高, 而沿着该方向的反向传播时无法穿过介质或透射率很低, 即对同一传输通道下光的响应表现为非对称的性质^[1]. 具有ONR特性的光学器件在保证以光为载体的量子信息实现单向传输过程中可避免光反馈对系统的干扰, 因而在量子通信、量子计算和光信息处理等方面具有重要的应用^[2–4]. 而传统的基于磁光法拉第效应的ONR传输^[5], 由于其所需较大的磁体材料而严重制约了非互易器件的芯片集成化和小型化^[6,7]. 近年来, 随着光纤技术及磁材料技术的发展, 基于光纤耦合的小型磁致光隔离器件在商用化得到了快速的发展, 但其较强的磁场极易对磁场敏感的光学器件产生影响, 从而引起光学系统性能的不稳定^[8,9]. 相比之下, 无磁ONR传输则更容易集成, 性能稳定且应用范围更广^[10–12]. 因此, 基于无磁过程的ONR逐渐成为研究热点, 包括利用非线性光学实现ONR^[13–16]、手性量子光学系统^[17–19]、介电常数的时空调制^[1,20,21]、光机力学系统^[22–24]、“移动”的光子晶体或Bragg反射^[25], 以及利用热原子系统实现单光子量级及相干光的高隔离度的光隔离^[26]等.

考虑热原子的无规则运动, 辅以特定方向相干光场的作用, 也可作为产生完美ONR的重要资源, 在实现多通道量子态操控及量子纠缠源制备等领域获得了长足的发展. 例如, 将Λ型三能级热原子置于一个环型腔中, 通过控制单向耦合场的作用方向, 可实现基于极化率-动量锁定的ONR系统^[27], 在此基础上通过引入双向耦合场并控制其频率失谐, 可实现多信道的互易-非互易转换操控^[28]. 基于三能级原子系统, 通过设置耦合场强度随位置阶梯型变化来破坏极化率空间对称性来实现完美非互易反射光放大, 再引入相位调制, 即可通过改变相位能够切换探测光增益和吸收的频率域, 从而更灵活地调节对反射光的放大^[29]. 另外, 利用热原子的多普勒频移效应, 由于对称性破缺可控制激光产生定向的电磁感应透明(electromagnetically induce transparancy, EIT), 以及仅在EIT方向上产生光放大^[30]. 基于双Λ型原子系统, 通过受激辐射的四波混频(four wave mixing, FWM)过程^[31], 可制备原子吸收线附近的非互易纠缠光子对^[32], 结合单向级联FWM, 又可实现多组分连续变量量子纠缠源的制备^[33]. 特别地, 考虑热原子的多普勒频移效应, 利用强光泵浦诱导极化率方法, 可实现高隔离度、宽隔离带宽的无磁ONR传输^[34].

上述研究主要是对基模高斯光束的非互易操控, 而空间分布更复杂的高阶模具有携带更多信息、抑制抖振、提高系统控制精度、适应复杂动态系统和增强系统鲁棒性等优势^[35–37], 因而针对高阶模的无磁ONR研究具有重大意义. 特别是携带轨道角动量(orbital angular momentum, OAM)的拉盖尔-高斯(Laguerre-Gaussian, LG)涡旋光束, 由于其相位波前呈螺旋形分布并绕涡旋中心旋转, 且具备携带OAM的独特性质, 因此在光学微操控、光学成像和量子编码等领域得到广泛应用^[38,39]. 由于原子介质具有良好的吸收、色散和衍射特性, 其与涡旋光的相互作用中对涡旋奇点产生、转换和操控也成为了最近研究的热点^[40,41], 特别是通过单向级联FWM过程, 实现了基于LG模的OAM复用的多组分连续变量纠缠源的制备^[42], 这为构建连续变量并行量子网络开辟了新途径^[43].

本文通过简并二能级热原子系统, 提出并实现了一种基于多重FWM的双通道无磁非互易-互易放大传输方案, 并研究分析了该过程对LG光束OAM的影响. 在单向泵浦场作用下, 考虑热原子的多普勒效应, 实现双路简并FWM场的非互易放大(nonreciprocal amplification, NRA); 在此基础上再引入一束对向共线传播的泵浦场, 形成了空间复用的多重FWM过程, 从而实现了双路FWM信号的互易放大(reciprocal amplification, RA). 进一步地, 利用螺旋相位片分别对信号光和泵浦光加载螺旋相位, 产生携带OAM的高阶LG光束, 并参与到四波混频过程中, 进一步分析了各路FWM场在NRA-RA转换下OAM的转移特性.

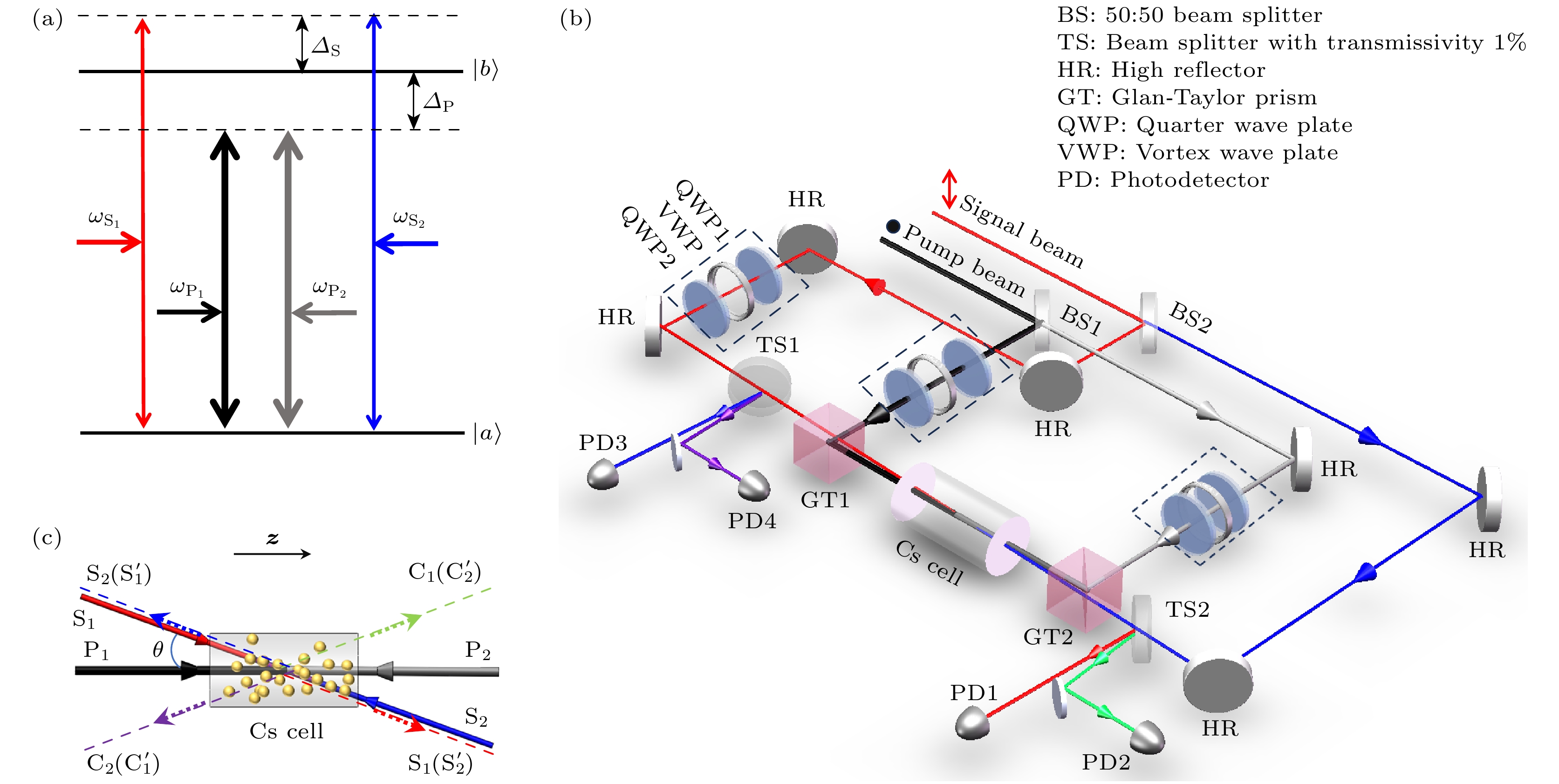
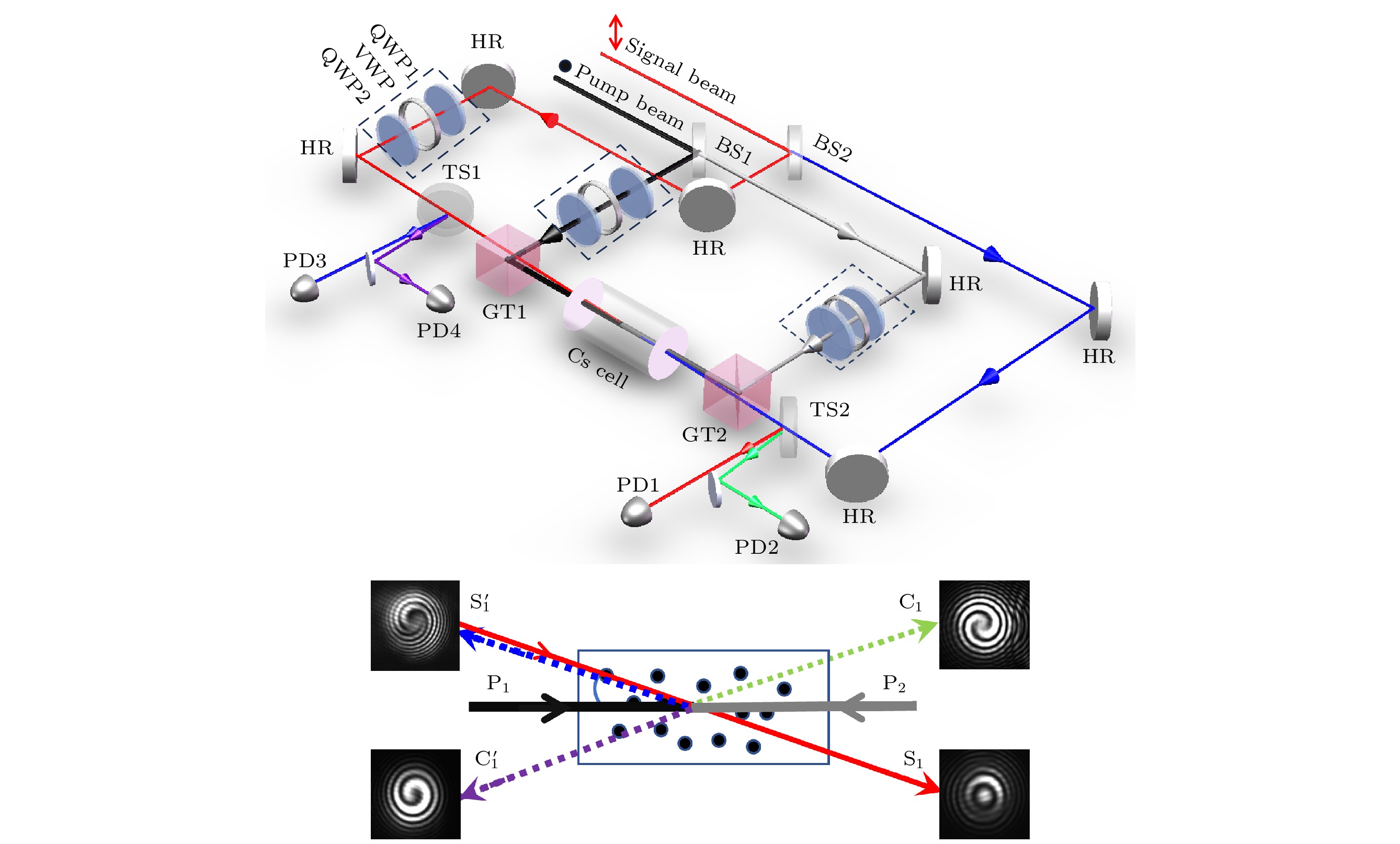
如图1(a)所示, 实验选择¹³³Cs原子D1线的两个跃迁能级$ \left| a \right\rangle $($ 6{{\mathrm{S}}_{1/2}}, {F_{\mathrm{g}}} = 4 $)和$ \left| b \right\rangle $($ 6{{\text{P}}_{1/2}}, {F_{\mathrm{e}}} = 4 $)构成简并二能级系统(屏蔽外界磁场条件下, 各能级的Zeeman子能级频率相同). 频率相同的两束泵浦光P₁光和P₂光($ {\omega _{{{\text{P}}_1}}} = {\omega _{{{\text{P}}_2}}} = {\omega _{\text{P}}} $)作用于$ \left| a \right\rangle \leftrightarrow \left| b \right\rangle $能级跃迁, 定义其频率失谐为$ {{{\varDelta }}_{\mathrm{P}}} = {\omega _{\mathrm{P}}} - {\omega _{ba}} $, $ {\omega _{ba}} = {\omega _b} - {\omega _a} $代表能级$ \left| a \right\rangle $和$ \left| b \right\rangle $之间的能级差. 频率相同的两束信号光S₁光和S₂光($ {\omega _{{{\text{S}}_1}}} = {\omega _{{{\text{S}}_2}}} = {\omega _{\text{S}}} $)同样作用于$ \left| a \right\rangle \leftrightarrow \left| b \right\rangle $能级跃迁, 频率失谐为$ {{{\varDelta }}_{\mathrm{S}}} = {\omega _{\mathrm{S}}} - {\omega _{ba}} $.

实验系统主光路如图1(b)所示. 一束光强较强的垂直偏振光作为泵浦光(pump light, P), 光斑模式为圆形基模高斯光束(TEM₀₀模), 通过一50/50分束镜BS1分为两束, 前向泵浦光(P₁光, 黑线)和后向泵浦光(P₂光, 灰线), P₁光和P₂光分别通过两个消光比为10⁵∶1的格兰-泰勒棱镜(GT1和GT2)反射, 共线对向射入Cs原子气室. Cs原子气室长度L = 25 mm, 气室温度稳定在T_c = 100 ℃左右, 气室侧壁裹有三层磁屏蔽材料(μ箔), 以屏蔽外界磁场对原子的影响. 一束光强较弱的水平偏振光作为信号光(signal light, S), 同样为TEM₀₀模, 经BS2也分为两束, 前向信号光(S₁光, 红线)和后向信号光(S₂, 蓝线). S₁光和S₂光分别经两个透射率为1%的分束镜TS1和TS2透射后, 分别经GT1和GT2透射, 共线对向穿过Cs原子气室, 再分别经TS2和TS1反射后, 通过两个光电探测器PD1和PD3探测. PD2和PD4分别用于探测前、后向新产生的共轭场信号. 如图1(c)所示, 定义P₁光的波矢量$ {{\boldsymbol{k}}_{{{\mathrm{P}}_1}}} $沿z轴正向传播为前向, 则P₂光为后向$ {{\boldsymbol{k}}_{{{\mathrm{P}}_2}}} = - {{\boldsymbol{k}}_{{{\mathrm{P}}_1}}} $, S₁(S₂)光的波矢量$ {{\boldsymbol{k}}_{{{\mathrm{S}}_1}}} $($ {{\boldsymbol{k}}_{{{\mathrm{S}}_2}}} $)与P₁光同(反)向并且以小角度θ角传播(θ ≈ 4 mrad). 实验中, 我们分别在S₁, P₁和P₂三束光的传播路径上放置了由两个四分之一波片(QWP1, QWP2)和一个涡旋片(VWP)组成的光斑调制器件, 其中QWP1和VWP用于操控光的偏振和波前, 将TEM₀₀模转化为LG模, QWP2使LG模调回至原来的偏振状态.

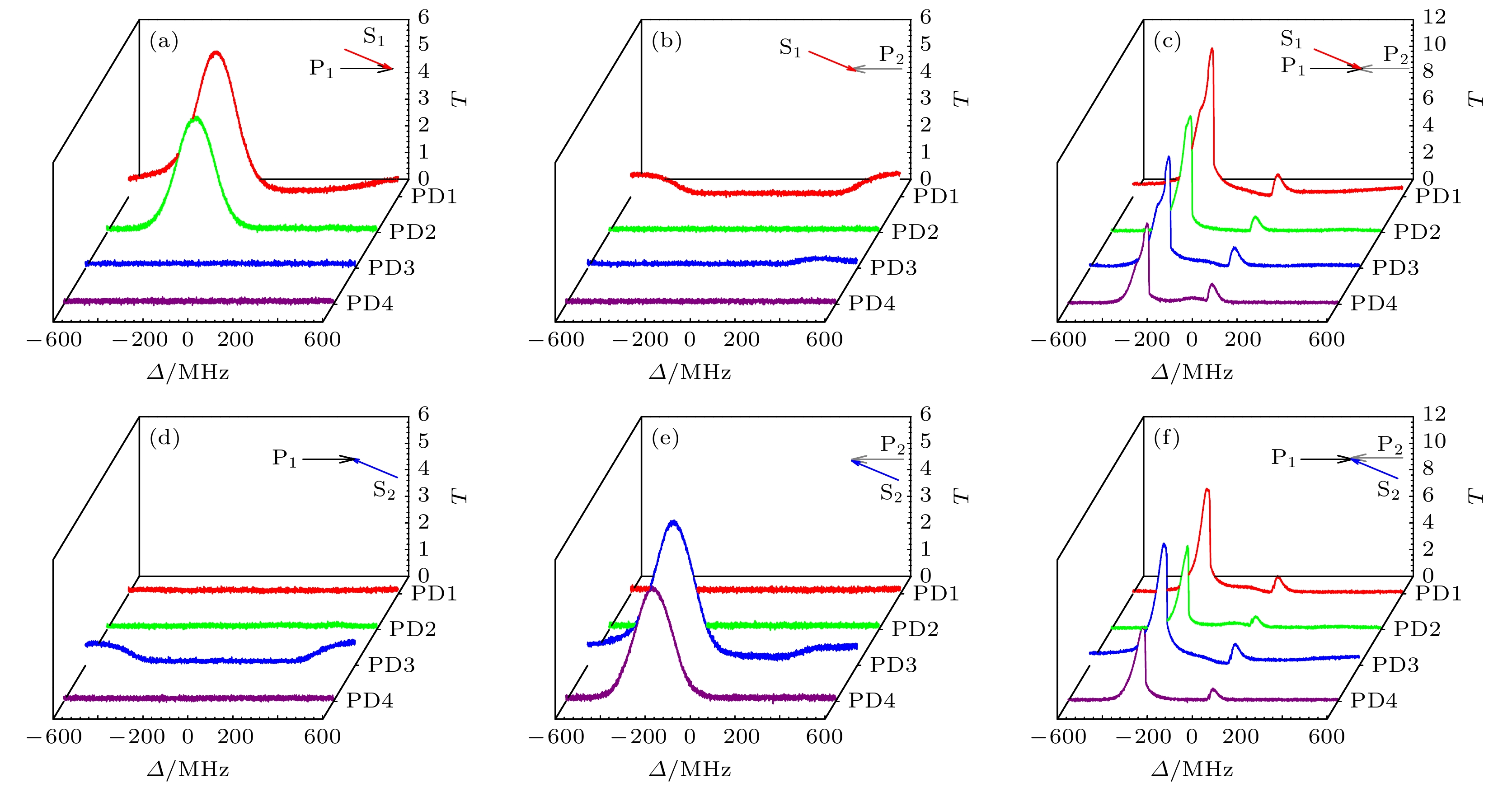
首先在光场横模为TEM₀₀的基础上, 实验测量分析了不同泵浦场条件诱导的FWM过程. 由于泵浦光和信号光作用于相同的能级跃迁, 因此实验选择二者来自同一台激光器, 这使得二者的频率始终保持相同, 即$ {{{\varDelta }}_{\mathrm{P}}} = {{{\varDelta }}_{\mathrm{S}}} = {{\varDelta }} $, 且有$ \left| {{{\boldsymbol{k}}_{\mathrm{P}}}} \right| = \left| {{{\boldsymbol{k}}_{\mathrm{S}}}} \right| = k $. 值得强调的是, 在简并跃迁条件下, 根据动量守恒定律, 理论上只有泵浦光信号光共线传播时, 才能严格满足相位匹配条件, 但这难以将FWM信号从空间上分离. 因此, S₁(S₂)光和P₁(P₂)光在实验中以小角度传播, 其代价是损失了一部分FWM效率.

图2给出了不同方向的泵浦光和信号光注入Cs原子气室时, 四路探测器测量的归一化透射谱T随单光子失谐Δ的分布情况(T = P_out/P_in, 其中P_out代表经Cs原子气室输出的放大光场的强度, P_in代表注入Cs原子气室前信号光的强度). 当只有前向P₁光和前向S₁光作用时(P₁-S₁), 在Δ ≈ –400—0 MHz范围内, S₁光被放大的同时, 其相对P₁光对称的另一侧产生一束新的共轭光(conjugate light) C₁光, 即发生前向FWM过程. 放大的S₁光和产生的C₁光分别被PD1和PD2探测, 如图2(a)中的红色和绿色曲线所示. 相对地, 当前向P₁光被反向P₂光代替时(P₂-S₁), 前、后向均无FWM发生, 经PD1探测的穿过Cs原子气室后的S₁光只有多普勒吸收背景, 见图2(b)中的红色曲线所示. 至此, 一对共轭光场S₁光和C₁光, 在单束泵浦作用下表现出明显的双通道NRA特性. 而在双向泵浦场条件下(P₁-P₂-S₁), 虽然S₁光和C₁光出现增益放大的频率范围变窄(Δ = –400—–200 MHz), 但增益比P₁光条件下提高了近2倍, 如图2(c)中红色和绿色曲线所示; 与此同时, 分别在S₁光和C₁光反向传播方向上, 产生了新的FWM信号$ {{\text{S}}'_1} $光(PD3探测)和$ {{\text{C}}'_1} $光(PD4探测), 见图2(c)中的蓝色和紫色曲线所示. 这表明在双向泵浦场作用下, Cs原子对前向FWM信号S₁光和C₁光表现为RA特性. 当前向S₁光替换为后向S₂光时也会产生相似的结果. 例如, 在P₁-S₂条件下, Cs原子对注入的S₂光表现为强吸收(PD3探测), 见图2(d)蓝色曲线所示, 此时无其他FWM信号产生. 而在P₂-S₂条件下, 可产生后向FWM过程, 即S₂被放大的同时, 又产生一束后向的共轭光C₂光(PD4探测), 见图2(e)中蓝色和紫色曲线所示. 同样地, 在P₁-P₂-S₂条件下, 四路探测器均可以测到放大信号, 即产生双通道的RA, 如图2(f)所示. 其中, S₂光的反向放大光$ {{\text{S}}'_2} $刚好与S₁光的传播方向重合(PD1探测), 而C₂光的反向放大光$ {{\text{C}}'_2} $光与C₁光重合(PD2探测), 如图1(c)所示. 这进一步佐证了热原子在单向泵浦光作用下, 对同向弱信号光可产生基于单向FWM的NRA; 而在双向泵浦条件下, NRA转化为RA.

另外, 从图2(a)和图2(e)可以看出, 在单泵浦光诱导的NRA条件下, 同向放大的信号光和共轭光的增益随单光子失谐整体呈非对称分布, 且主要发生在原子共振中心的负失谐区域. 在靠近原子共振中心的增益较小, 主要是由被放大的光场在穿出原子气室之前又被原子产生较强的吸收损耗导致的. 若继续升高Cs原子气室的温度(即提高粒子数密度)或提高泵浦强度, 则增益强度会变大, 其分布范围也会变宽^[44]. 然而在双向泵浦诱导的RA条件下, 4路放大光场的增益相比单泵浦时虽有所增强, 但其随单光子失谐分布变窄, 且在靠近原子共振中心附近(Δ ≈ –200—0 MHz范围内)出现较宽的缺口, 如图2(c)和图2(f)所示. 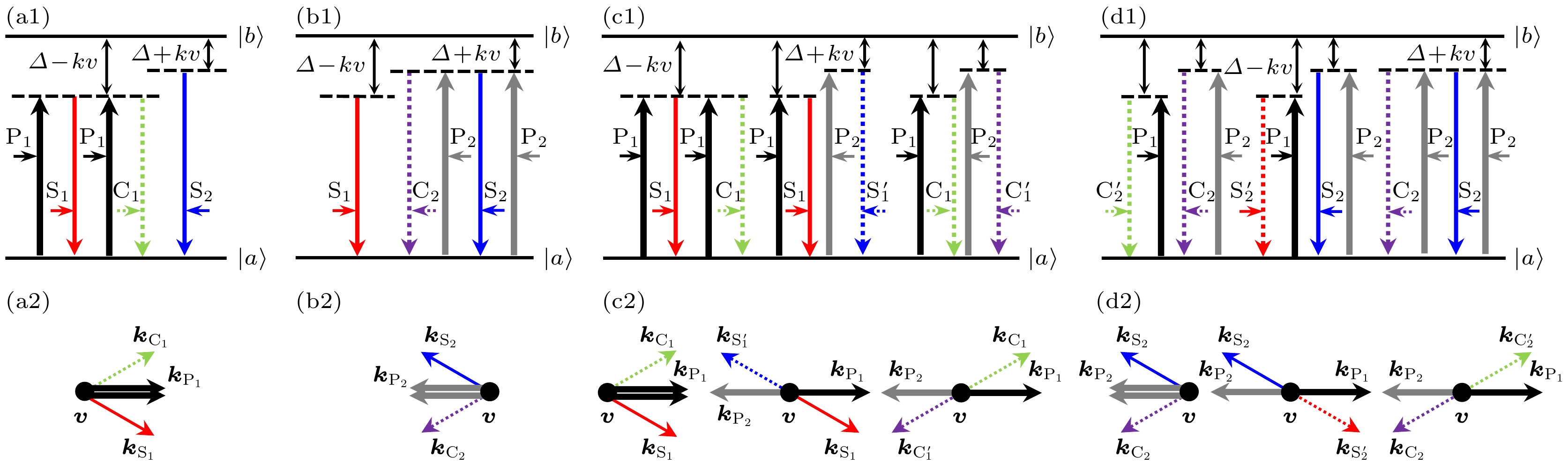在RA条件下, 各路放大光场的增益变高是由于双向泵浦场诱发的多个FWM过程叠加的结果; 而增益分布范围变窄, 则是处于较高温度下的原子气体在原子共振中心附近对驻波泵浦场的横场模式产生了较强的热透镜(自聚焦)效应, 具体表现为强光诱导原子介质折射率的横向分布发生变化: $ \delta n \propto N\mu _{ab}^4{E^2}/{\left( {h{{\varDelta }}} \right)^3} $ (其中N为原子数密度), 在高斯光束横截面中心区域所引起的折射率增量较大, 而边缘区域引起的折射率增量较小. 此时原子介质就像是一个会聚透镜, 使得入射光束发生自聚焦现象^[45]. 该效应导致处于气室内的泵浦光的光斑大小和偏振发生急剧变化, 导致其在与信号光的交叠区域的强度减弱, 严重抑制了FWM的发生. 另外, 由于在Cs原子气室内P₁光与P₂光的光斑大小不完全相同, 二者与注入信号光交叠区作用的原子数不同, 从而导致各路放大光场之间的强度略有差异.

在我们的实验方案中, 单泵浦光诱导的双通道NRA是建立在基于热原子相干效应的FWM基础上. 如图3(a1)所示, 在P₁-S₁条件下, 对于以速度v前向运动的原子, P₁光与S₁光的频率差为$ {{{\varDelta }}'_{{{\mathrm{P}}_1}}} - {{{\varDelta }}'_{{{\mathrm{S}}_1}}} = ({{\varDelta }} - kv) - ({{\varDelta }} - kv) = 0 $, 满足双光子共振条件, 从而发生前向FWM; 而在P₁-S₂条件下, 二者的频率差为$ {{{\varDelta }}'_{{{\mathrm{P}}_1}}} - {{{\varDelta }}'_{{{\mathrm{S}}_2}}} = ({{\varDelta }} - kv) - ({{\varDelta }} + kv) = - 2 kv \ne 0 $, 所以不发生FWM. 前向FWM的具体过程为: 处于基态$ \left| a \right\rangle $的原子吸收一个前向泵浦光子P₁跃迁到激发态$ \left| b \right\rangle $, 受激原子向前发射一个信号光子S₁落回基态$ \left| a \right\rangle $, 然后再吸收一个前向泵浦光子P₁到激发态$ \left| b \right\rangle $, 最后, 受激原子再发射一个前向共轭光子C₁而回到基态$ \left| a \right\rangle $. 上述过程可描述为

整个过程满足能量守恒和动量守恒, 即$ \omega_{\mathrm{C}_1}= \omega_{\mathrm{S}_1}=\omega_{\mathrm{P}_1} $, $ \Delta {k_{\mathrm{f}}} = 2{{\boldsymbol{k}}_{{{\mathrm{P}}_1}}} - {{\boldsymbol{k}}_{{{\mathrm{S}}_1}}} - {{\boldsymbol{k}}_{{{\mathrm{C}}_1}}} \approx 0 $(下标f表示前向FWM过程), 相位匹配过程对应图3(a2). 同理, 在P₂-S₂条件下发生后向FWM, 见图3(b1), 该过程描述为

整个过程同样满足能量和动量守恒, 即$ {\omega _{{{\mathrm{C}}_2}}} = {\omega _{{{\mathrm{S}}_2}}} = {\omega _{{{\mathrm{P}}_2}}} $和$ \Delta {k_b} = - 2{{\boldsymbol{k}}_{{{\mathrm{P}}_2}}} + {{\boldsymbol{k}}_{{{\mathrm{S}}_2}}} + {{\boldsymbol{k}}_{{{\mathrm{C}}_2}}} \approx 0 $ (下标b表示后向FWM), 其相位匹配如图3(b2)所示.

然而, 对于由双向泵浦光驱动产生的双通道RA效应, 其物理机制可看作是在一个同向(前向或后向) FWM的基础上, 又分别以放大的信号光和共轭光为种子光, 诱发了另外两个双向抽运的FWM过程. 以P₁-P₂-S₁条件为例, 如图3(c1)所示, 首先产生前向FWM, 其相互作用过程与P₁-S₁条件的相同, 即S₁被放大的同时, 产生C₁光. 在此基础上, 原子在双向P₁和P₂光驱动下诱发另外两个FWM: 一个产生S₁光的RA, 其相互作用过程表示为

该过程的能量关系为$ {\omega _{{{\mathrm{S}}_1}}} = {\omega _{{{\mathrm{P}}_1}}} $和$ {\omega _{{{{\text{S}}}'_1}}} = {\omega _{{{\mathrm{P}}_2}}} $, 动量关系为$ \Delta {k_{{{\mathrm{S}}_1}}} = ({{\boldsymbol{k}}_{{{\mathrm{P}}_1}}} - {{\boldsymbol{k}}_{{{\mathrm{S}}_1}}}) - ({{\boldsymbol{k}}_{{{\mathrm{P}}_2}}} - {{\boldsymbol{k}}_{{{{\mathrm{S}}}'_1}}}) \approx 0 $; 另一个产生C₁光的RA, 其相互作用过程表示为

该过程的能量关系为$ {\omega _{{{\mathrm{C}}_1}}} = {\omega _{{{\mathrm{P}}_1}}} $和$ {\omega _{{{{\text{C}}}'_1}}} = {\omega _{{{\text{P}}_2}}} $, 动量关系为$ \Delta {k_{{{\mathrm{C}}_1}}} = ({{\boldsymbol{k}}_{{{\mathrm{P}}_1}}} - {{\boldsymbol{k}}_{{{\mathrm{C}}_1}}}) - ({{\boldsymbol{k}}_{{{\mathrm{P}}_2}}} - {{\boldsymbol{k}}_{{{{\mathrm{C}}}'_1}}}) \approx 0 $. $ {{\mathrm{S}}'_1} $光和$ {{\text{C}}'_1} $光分别表示S₁光和C₁光反向放大的光场, 其相位匹配关系如图3(c2)所示. 值得注意的是, 在此分析过程中, $ {{\text{S}}'_1} $($ {{\text{C}}'_1} $)光虽然被看作是S₁(C₁)光的RA, 但其频率却严格依赖P₂光的频率. 在P₁-P₂-S₂条件下同样会产生相似的三个FWM过程, 其相互作用过程和相位匹配关系如图3(d1)和图3(d2)所示.

在图2中产生增益的频率范围内, 固定单光子失谐为某一确定值(比如Δ ≈ –260 MHz), 并且分别在前向探测(PD1和PD2)和后向探测(PD3和PD4)区域放置两个图像传感器(CCD), 可观察到不同泵浦条件下FMW信号的光斑图样, 如图4所示. 在P₁-S₁条件下, 因消多普勒而发生前向FWM, 因此在前向CCD处可观测到三个光斑, 分别为放大的S₁光及产生的C₁光光斑, 中间的光斑为GT棱镜不完美的偏振分光导致漏出的P₁光光斑, 如图4(a1)所示. 而此时在后向CCD处无任何光斑产生, 如图4(a2)所示. 相反地, 在P₂-S₂条件下, 前向方向无任何信号产生, 而在后向可观察到S₂, C₂和P₂三个光斑, 如图4(b1)和图4(b2)所示. 这进一步佐证了单泵浦诱导的NRA特性. 然而, 在P₁-P₂-S₁条件下, 除了前向CCD观察到S₁和C₁光光斑外, 见图4(c1), 与其方向传播的反向CCD处同样也观察到相应新产生的$ {{\text{S}}'_1} $光和$ {{\text{C}}'_{1}} $光光斑, 见图4(c2). 相似地, 在P₁-P₂-S₂条件下, 反向CCD观察到反向FWM产生的S₂和C₂光光斑, 见图4(d2), 而前向CCD观察到相应新产生的$ {{\text{S}}'_{2}} $光和$ {{\text{C}}'_{2}} $光光斑, 见图4(d1). 这进一步验证了双向泵浦诱导的RA特性.

在图4实验结论的基础上, 利用三组QWP和VWP组合, 分别对前向信号光S₁光和双向泵浦光P₁光和P₂光进行空间调制(见图1(b)), 生成携带有不同拓扑电荷数l的LG模涡旋光参与FWM, 实验进一步研究在NRA和RA过程中, OAM在四波混频信号中的转移特性. 由于放大的信号光与产生的共轭光均可能会携带OAM, 于是将放大的各路FWM信号分别通过马赫-曾德尔(Mach-Zehnder, M-Z)干涉仪与球面波进行同轴干涉(此部分光路未在图1中画出), 通过干涉图样可判断输出各路FMW信号携带的OAM信息, 同时也可验证OAM在通过FWM转移过程的守恒性. 对于LG光束而言, 与球面波干涉时, 干涉图样为明暗相间的螺旋状干涉条纹. 当l值大于0时, 代表拓扑电荷数为正数, 螺旋状条纹按照顺时针的方向旋转; 而当l值小于0时, 拓扑荷数为负数, 螺旋状条纹则是按照逆时针方向旋转, 且螺旋条纹的数量与l的绝对值相同.

首先实验测量分析在NRA过程中各路放大FWM场OAM的转移变化. 在P₁-S₁条件下, 当调节S₁光的拓扑电荷数为${l_{{{\text{S}}_1}}} = - 1$的LG光, P₁光依然保持TEM₀₀模(${l_{{{\text{P}}_1}}} = 0$), 则此时被放大的S₁光和新产生的C₁光均为LG光, 见图5(a1). 将S₁光和C₁光通过M-Z干涉仪分别与球面波干涉, 均可得到只有一条旋转臂的螺旋状干涉条纹, 其中S₁光的干涉条纹为逆时针旋转, 即${l_{{{\text{S}}_1}}} = - 1$, 见图5(a2), 而C₁光的为顺时针旋转, 即${l_{{{\text{C}}_1}}} = 1$, 见图5(a3). 相似地, 当调节P₁光为${l_{{{\text{P}}_1}}} = - 1$的LG光, S₁光保持${l_{{{\text{S}}_1}}} = 0$, 则经前向FWM过程, 被放大的S₁光依然保持TEM₀₀模, 而C₁光为LG模, 见图5(b1). 经M-Z干涉仪鉴别可得, 放大的S₁光的干涉条纹为同心干涉圆条纹, 证明其${l_{{{\text{S}}_1}}} = 0$, 见图5(b2); 而C₁光的干涉条纹为具有2条旋臂的螺旋干涉条纹, 且逆时针旋转, 证明其${l_{{{\text{C}}_1}}} = - 2$, 见图5(b3). 两种情况说明, 在前向FMW过程中, 无论P₁光的拓扑电荷数为何值, 其被原子吸收跃迁并受激辐射产生S₁光时, 必然转移为与注入的S₁光相同的拓扑电荷数, 同时将等值相反的拓扑电荷数转移至新产生的共轭光C₁光中, 而整个过程满足OAM守恒, 即$ \Delta {l_{\mathrm{f}}} = 2{l_{{{\mathrm{P}}_1}}} - ({l_{{{\mathrm{S}}_1}}} + {l_{{{\mathrm{C}}_1}}}) = 0 $. 同样地, 在P₂-S₂条件下, 调节P₂光为拓扑电荷数${l_{{{\mathrm{P}}_2}}} = 2$的LG光, S₂光保持TEM₀₀模, 则经FWM过程被后向CCD观测的光斑图如图5(c1)所示, 被放大的S₂光依然保持基模圆光斑, 而新产生的C₂光为LG模. 同样利用M-Z干涉仪检测, 放大的S₂光的干涉条纹为同心干涉圆条纹, 证明其${l_{{{\mathrm{S}}_2}}} = 0$, 见图5(c2); 而C₂光的干涉条纹为具有4条旋臂的螺旋干涉条纹, 且顺时针旋转, 证明其${l_{{{\text{C}}_2}}} = 4$, 见图5(c3). 这说明在后向FWM过程中, P₂光的拓扑电荷数也分别向S₂光和C₂光转移, 且该过程也满足OAM守恒, 即$ \Delta {l_{\mathrm{b}}} = - 2{l_{{{\mathrm{P}}_2}}} + ({l_{{{\mathrm{S}}_2}}} + {l_{{{\mathrm{C}}_2}}}) = 0 $.

由于在双向泵浦场和单向信号光同时作用下, 相干原子会产生多重FWM过程, 从而产生双通道的RA, 该过程同样会诱发泵浦光的OAM向放大的FWM场转移. 以P₁-P₂-S₁条件为例, 首先调制前向S₁光的拓扑电荷数为${l_{{{\text{S}}_1}}} = - 1$, P₁光和P₂光为${l_{{{\text{P}}_1}}} = {l_{{{\text{P}}_2}}} = 0$, 此时在前、后向产生的FWM信号均为LG模, 见图6(a1)和图6(b1). 通过M-Z干涉法, 检测出此时前向的S₁光和C₁光的OAM与单向泵浦条件下的状态保持不变, 即${l_{{{\text{S}}_1}}} = - 1$, ${l_{{{\text{C}}_1}}} = 1$, 如图6(a2)和图6(a3)所示. 而对于后向产生的$ {{\text{S}}'_1} $光和$ {{\text{C}}'_{1}} $光, 其拓扑电荷数分别为${l_{{{{\text{S}}}'_{1}}}} = - 1$和${l_{{{{\text{C}}}'_1}}} = 1$, 如图6(b2)和图6(b3)所示. 对于S₁光的RA过程, 其角动量变化$ \Delta {l}_{{\text{S}}_{1}}=({l}_{{{\mathrm{P}}}_{1}}-{l}_{{{\mathrm{S}}}_{1}})- ({l}_{{\text{P}}_{2}}- {l}_{{{{\mathrm{S}}}}'_{1}})=0 $; 对于C₁的RA过程, $ \varDelta {l}_{{{\mathrm{C}}}_{1}}=({l}_{{{\mathrm{P}}}_{1}}- {l}_{{{\mathrm{C}}}_{1}})- ({l}_{{{\mathrm{P}}}_{2}}- {l}_{{{{\mathrm{C}}}}'_{1}})=0 $, 二者同样均满足OAM守恒. 当调制S₁光的拓扑电荷数为${l_{{{\text{S}}_1}}} = 0$, P₁光和P₂光分别为${l_{{{\text{P}}_1}}} = - 1$, ${l_{{{\text{P}}_2}}} = 2$时, 前向的S₁光和C₁光的光斑模式及干涉图样同样与单泵浦条件下相似, 即${l_{{{\text{S}}_1}}} = 0$和${l_{{{\text{C}}_1}}} = - 2$, 见图6(c1)—(c3), 说明该前向FWM过程的OAM守恒. 对于后向产生的RA场, 由于受P₂光的影响, $ {{\text{S}}'_{1}} $光和$ {{\text{C}}'_{1}} $光均呈现为LG光, 如图6(d1)所示. 经M-Z干涉, $ {{\text{S}}'_{1}} $光的干涉条纹为具有3条旋臂且顺时针旋转的螺旋干涉条纹, 表明其拓扑电荷数为${l_{{{{\text{S}}}'_{1}}}} = 3$, 见图6(d2); 而$ {{\text{C}}'_{1}} $光的为具有1条旋臂且也是顺时针旋转的螺旋干涉条纹, 表明其拓扑电荷数为${l_{{{{\text{C}}}'_{1}}}} = 1$, 见图6(d3), 此时对于S₁光和C₁的RA过程同样均满足OAM守恒.

图6结果表明, 在双向泵浦条件下, 当改变P₂光的OAM时, S₁光和C₁光相应的RA光场$ {{\text{S}}'_1} $光和$ {{\text{C}}'_{1}} $光的OAM也会发生相应变化. 对于P₁-P₂-S₂条件下同样会发生与图6相似的实验现象, 这里不再赘述. 表1列出了注入的S₁(S₂)光为TEM₀₀条件下, 当泵浦光P₁光和P₂光的拓扑电荷数为不同值时, 四路FWM光对应的拓扑电荷数值, 其均满足OAM守恒.

基于铯原子D1线的简并二能级原子系统, 通过引入对向入射的驻波泵浦场实现了基于多重FWM的双通道无磁非互易-互易放大传输方案. 在此基础上, 将信号光和泵浦光调制为携带OAM的高阶LG光束参与到FWM过程中, 在非互易-互易放大转换条件下分析并验证了OAM在各路放大共轭光场之间的转移及守恒性, 从而为光学互易-非互易放大实验系统下利用OAM进行信道容量扩充提供了可行的方案. 由于光学非互易器件如光隔离器、环行器和移相器等是全光通信的基本单元, 因此, 该结论在实现高容量光通信和多通道信号处理领域具有潜在的应用前景.