首页
登录
注册
-
近年来, 声黑洞结构作为一种新型的振动和噪声抑制结构受到了广泛的关注. 它是一种特殊的变厚度几何结构, 存在独特的弯曲波慢速效应. 当厚度趋近于零时, 弯曲波速也趋近于零, 波的累积相位与振幅无限增大, 使得弯曲波在结构尖端位置集中, 这就是声黑洞结构的声波捕获效应与能量聚集效应. 在实际应用中, 尽管声黑洞结构具有截断厚度, 但仍具有较为可观的声波捕获与能量聚集效应[1–4]. 得益于此, 声黑洞结构在各个领域得到了广泛应用. 除减振降噪[5–7]、能量收集[8–12]等领域外, 在器件性能提升方面, Remillieux等[13,14]将声黑洞结构应用到叠片式压电换能器设计中, 实现了更高效的空气辐射. 刘洋等[15]将声黑洞结构嵌入径向复合换能器设计中, 使其机电转换性能与声辐射性能有所提升, 并呈现出一定的辐射指向性. Chen等[16]设计了一种新型声黑洞超声化学反应器, 显著扩大了超声空化区域, 增强了声辐射强度, 从而大大提高了声化学处理效率. 在多功能粒子操纵方面, Liu等[17]在椭圆形聚甲基丙烯酸甲酯板上的声黑洞凹陷中滴入聚苯乙烯微粒悬浮液, 利用二维声黑洞结构所激发的声流效应实现了聚苯乙烯微粒的富集与图案化. Yin等[18]利用声黑洞结构超声微针在液体中激发声流效应, 实现了对丙烯酸微粒的捕获、转移与图案化. 以上研究表明, 声黑洞结构可显著增强器件辐射能力, 进而在多功能声场构造与粒子操纵等方面极具潜力.
基于声黑洞结构的声波捕获与能量聚集效应, 本文提出了一种新型声黑洞楔形结构振动模式转换超声换能器. 建立了辐射板弯曲振动理论分析模型, 将其计算得到的振动频率与有限元仿真频率进行了对比. 使用有限元方法(finite element method, FEM)对换能器的电阻抗频率响应特性、振动模态以及空气中近场辐射声压分布进行了仿真模拟. 加工了换能器样机, 并对其进行阻抗分析、激光测振、空气中辐射声场测量实验, 将实验测得的结果与有限元仿真结果进行了对比, 以分析出换能器的振动性能与辐射性能. 最后进行了超声悬浮实验, 以验证该声黑洞换能器构造多功能声场的潜力. 本文旨在探索声黑洞结构在超声悬浮技术中的潜在应用, 并提供器件设计理论方法和实验参考.
-
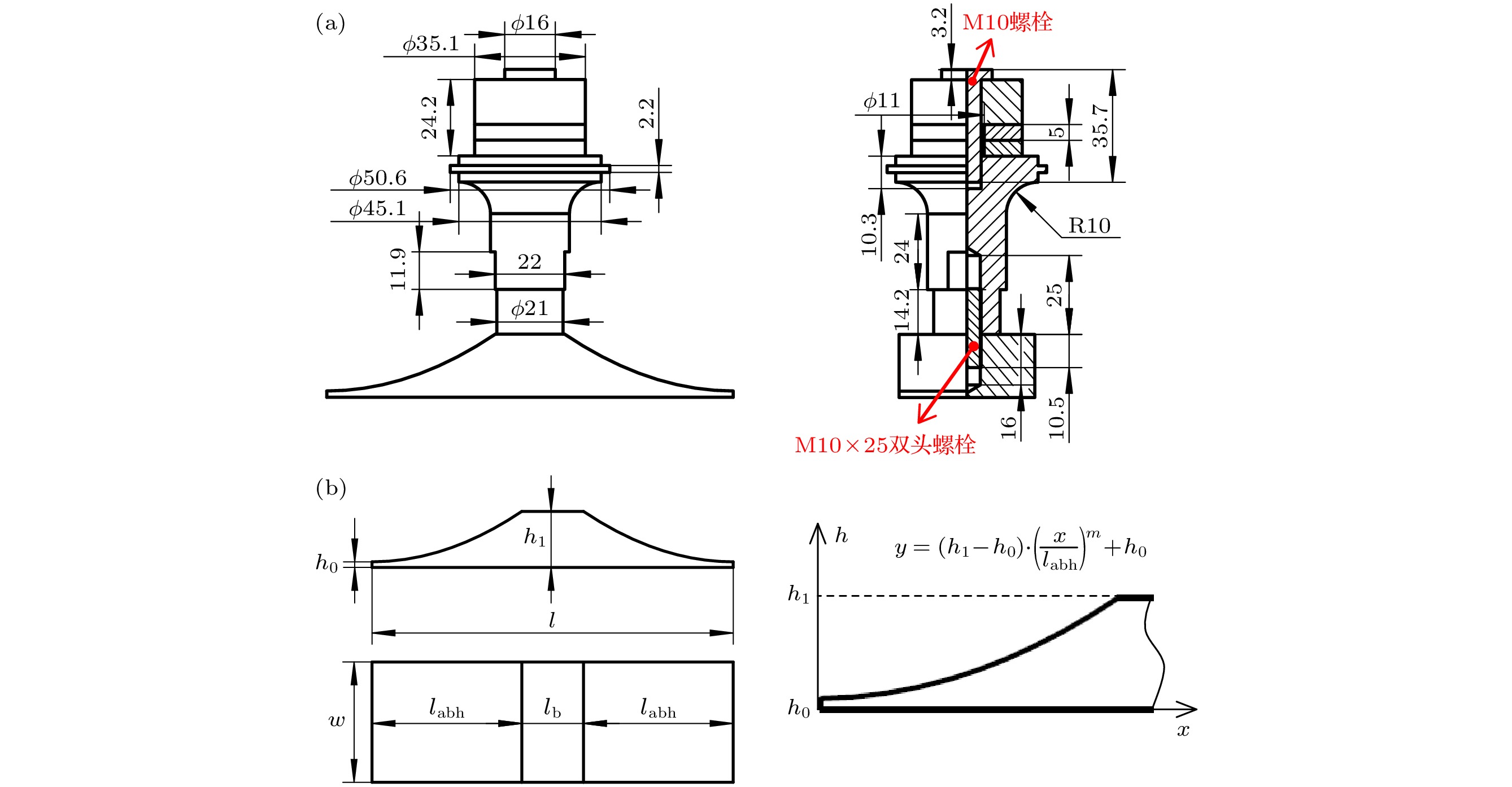
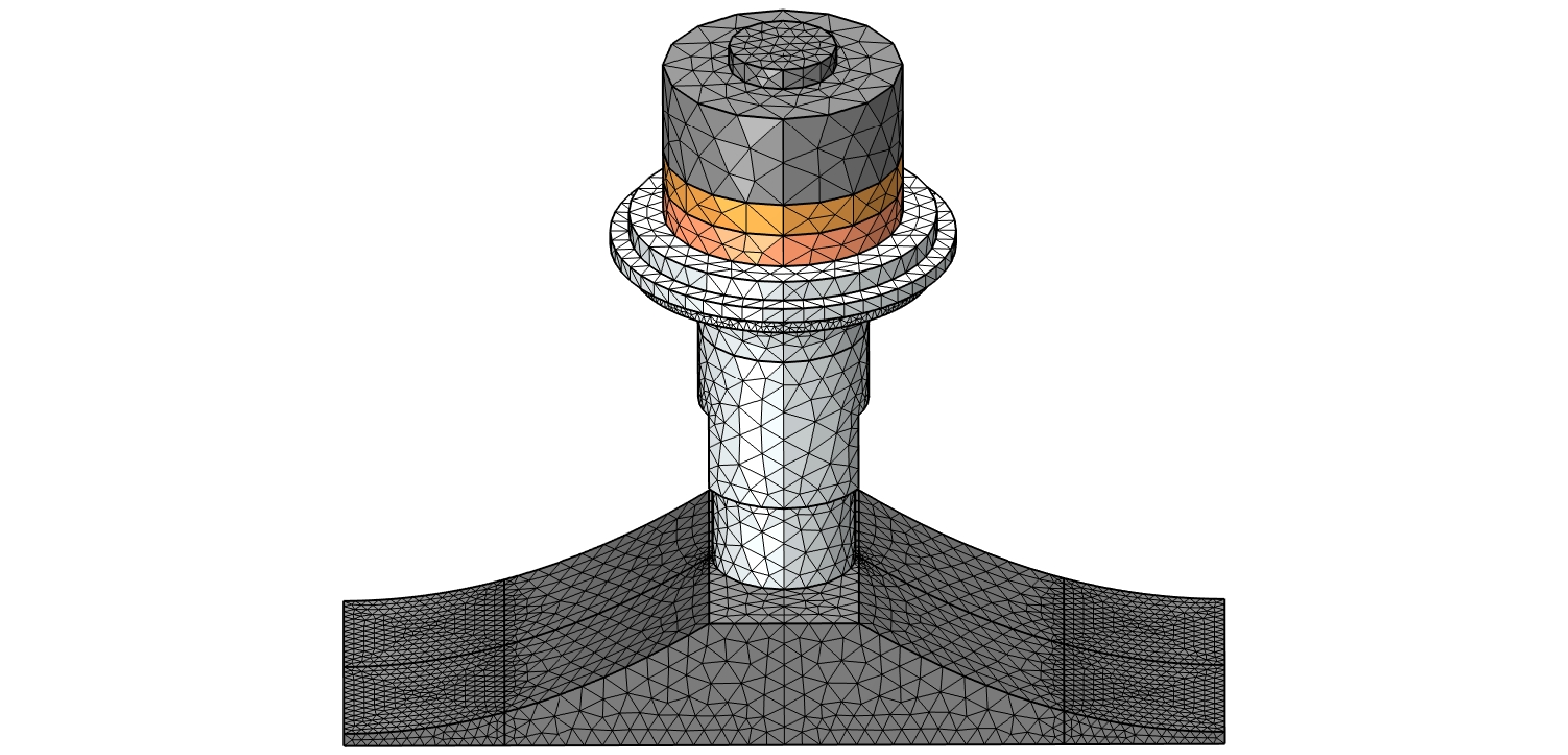
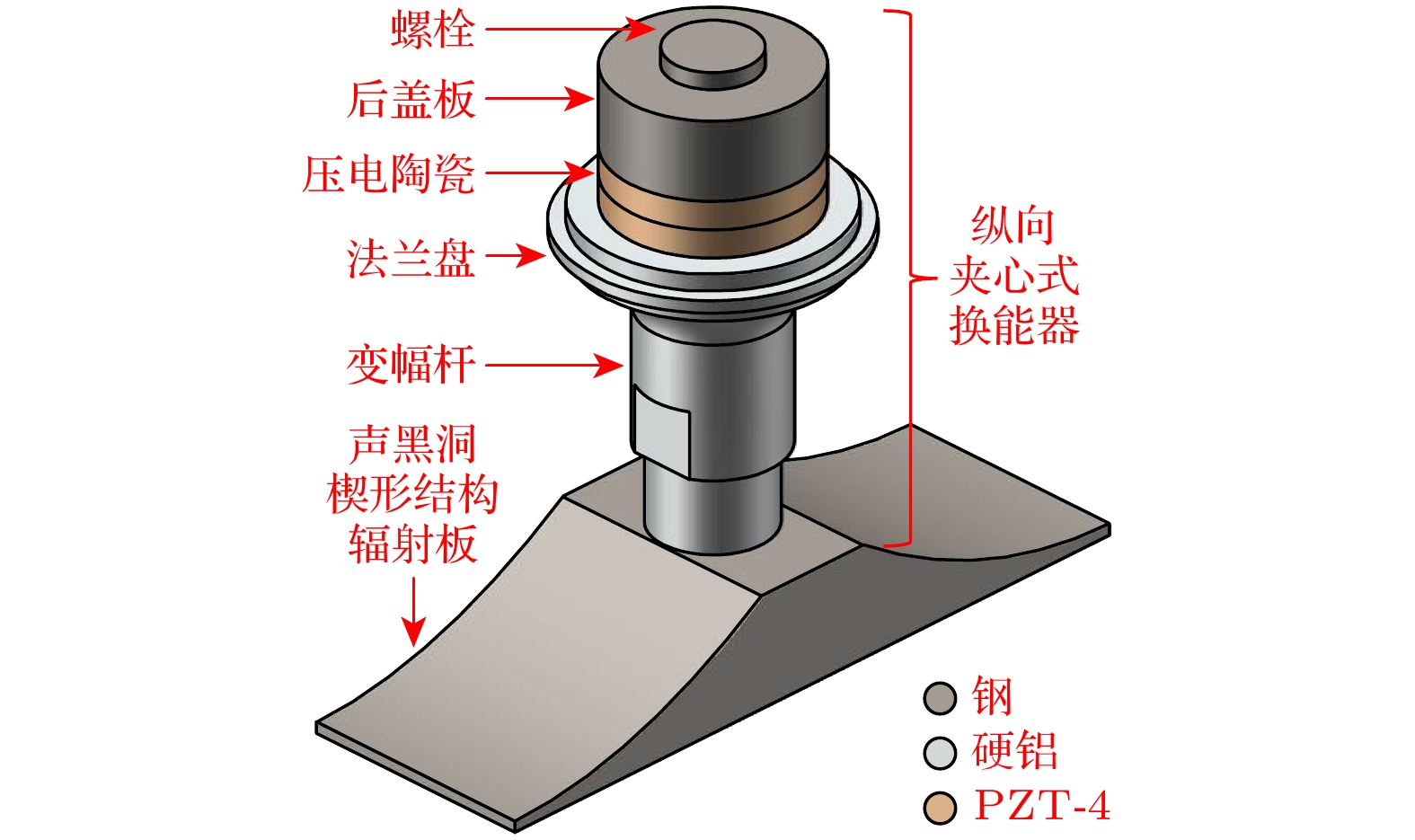
本文提出的声黑洞换能器几何结构如图1和图2所示. 图1中灰色部分的材质为钢, 银白色部分的材质为硬铝, 黄色部分的材质为PZT-4压电陶瓷. 图2(a)为纵向夹心式换能器的几何尺寸. 图2(b)中
$ {h_1} $ 为声黑洞辐射板等厚度部分的厚度,$ {h_0} $ 为截断厚度,$ {l_{{\text{abh}}}} $ 为声黑洞部分的长度,$w$ 为辐射板宽度,$ l $ 为辐射板总长,$ {l_{\text{b}}} $ 为等厚度部分的长度,$ m $ 为指数, 方程式为声黑洞轮廓曲线所遵循的幂律.根据共振系统设计原理, 令纵向夹心式换能器一阶纵向振动与辐射板弯曲振动同频[19]. 基于纵向夹心式换能器一般设计理论, 设计出图1和图2(a)中的纵向夹心式换能器, 其一阶纵向振动频率为26055 Hz[20]. 因辐射板的低阶一维弯曲振动模态存在的耦合程度较小, 故选择使用铁木辛柯梁理论为声黑洞楔形结构辐射板建立传输矩阵理论模型, 以快速设计出对称弯曲振动频率与26055 Hz接近的辐射板.
-
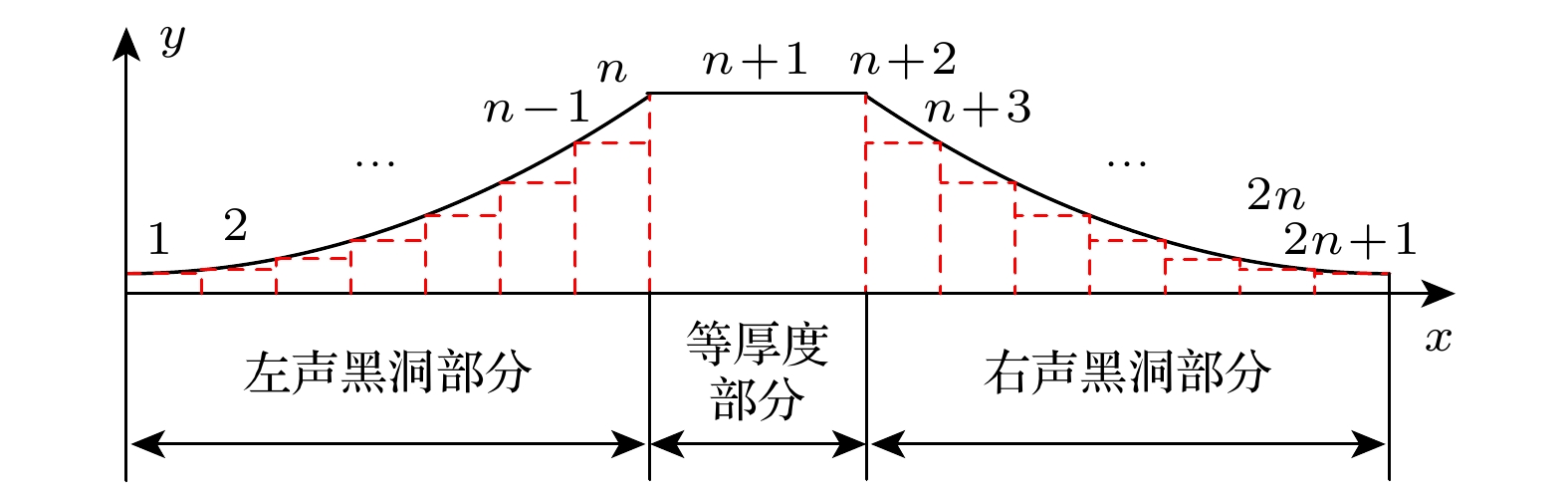
首先需要将辐射板的变厚度部分等间距地划分为若干个等厚度振动单元. 划分方式如图3所示, 左、右声黑洞部分都被划分为n个振动单元, 另外将辐射板单独视为一个振动单元[21].
$x$ 坐标表示长度方向,$y$ 坐标表示横向位移方向.根据铁木辛柯梁理论, 辐射板受到的弯曲横向位移
${Y_{\text{b}}}$ 和剪切横向位移$ {Y_{\text{s}}} $ 为[22,23]其中,
其中
$ E $ 为杨氏模量,$ G $ 为剪切模量,$ \rho $ 为密度,$ I $ 为截面的转动惯量,$ {A_0} $ 为截面面积,$ K' $ 为剪切系数,$ {C_{\text{O}}} $ 为纵波的传播速度,$ {C_{\text{S}}} $ 为横波的传播速度, 其余参数为替代量, 用以简化运算过程. 设$Y$ ,$\varPhi $ ,$M$ ,$Q$ 分别为总横向位移、转角、弯矩、剪力:梁的振动参数可写作如下形式:
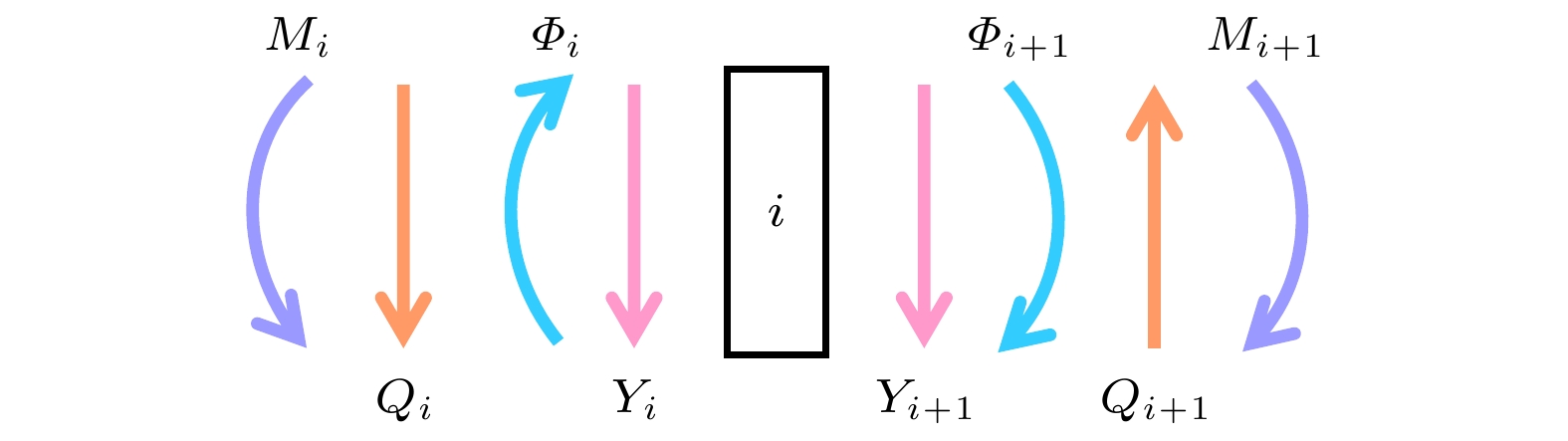
如图4所示, 以
$ {Y_i} $ ,${\varPhi _i}$ ,$ {M_i} $ ,$ {Q_i} $ 和$ {Y_{i + 1}} $ ,${\varPhi _{i + 1}}$ ,$ {M_{i + 1}} $ ,$ {Q_{i + 1}} $ 分别表示第i个振动单元左右两端的横向位移、转角、弯矩、剪力$ ( 1 \leqslant i \leqslant 2 n + 1,\; i \in {N^{\text{*}}})$ , 有式中,
$a_{ij}^i$ 是第i个振动单元的4$ \times $ 4矩阵, 与材料、尺寸和振动频率有关, 详见附录.在任意两个相邻振动单元之间的界面上, 位移和转角连续, 且满足弯矩和剪力的平衡, 因此有
其中
${{\boldsymbol{A}}_{ij}}$ 为辐射板的总矩阵, 即因辐射板的两端自由, 弯矩与剪力为零, 即
$ {M_{2 n + 1}} = {Q_{2 n + 1}} = {M_1} = {Q_1} = 0 $ , 代入(8)式得 -
首先确定辐射板的几何参数. 取单个声黑洞轮廓长度
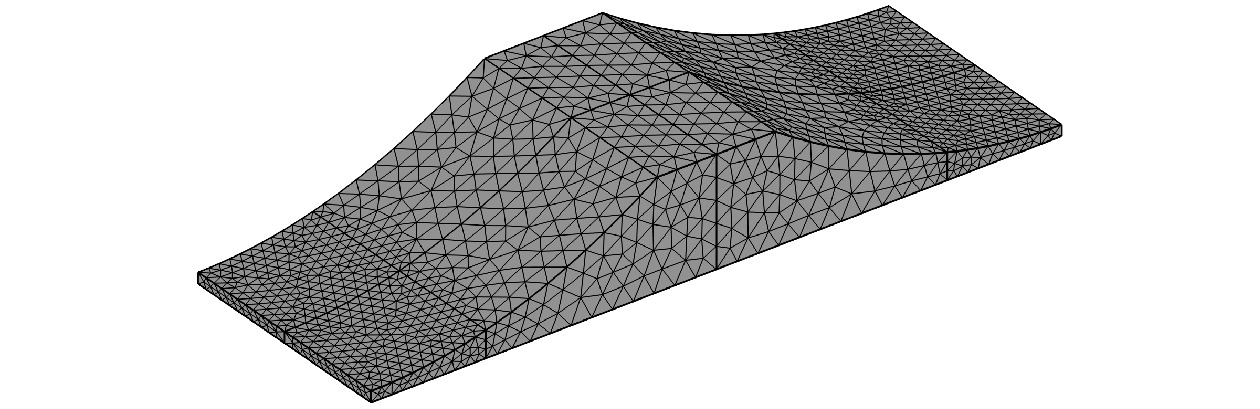
${l_{{\text{abh}}}}$ = 53.4 mm, 等厚度部分长度${l_{\text{b}}}$ = 22 mm, 辐射板总长度$l = 128.8{\text{ mm}}$ , 等厚度部分厚度$ h_1 $ = 20 mm, 板宽$ w $ = 40 mm, 截断厚度$ h_0 $ = 2 mm. 所用钢材料密度$\rho $ = 7850 kg/m3, 杨氏模量$E$ = 205 GPa, 泊松比$ \nu $ = 0.28. 然后对辐射板进行有限元仿真建模. 忽略螺孔及装配预应力, 使用固体力学模块. 其中, 辐射板两端的最大网格单元大小设置为1.75 mm, 辐射板剩余部分则设置为3.5 mm (图5). 随后计算出辐射板的弯曲振动频率, 并与由MATLAB R2022a软件求解频率方程(10)得到的频率进行对比, 结果见表1,${f_{\text{T}}}$ ,${f_{\text{F}}}$ 分别为传输矩阵法和有限元仿真得到的弯曲振动频率,${\varDelta _1} = \left( {{f_{\text{T}}} - {f_{\text{F}}}} \right)/{f_{\text{F}}}$ 为传输矩阵法和有限元仿真计算结果之间的相对误差. 结果显示, 理论计算相对于有限元仿真结果吻合较好, 相对误差均小于4%, 证明了基于铁木辛柯梁理论建立的传输矩阵理论模型的实用性与准确性. 此外, 该理论模型计算速度快, 占用计算机资源更少, 可大大提高设计过程的计算效率. 存在的误差主要是因为该理论模型仅考虑一维弯曲振动, 忽略了不同模态间的耦合效应. -
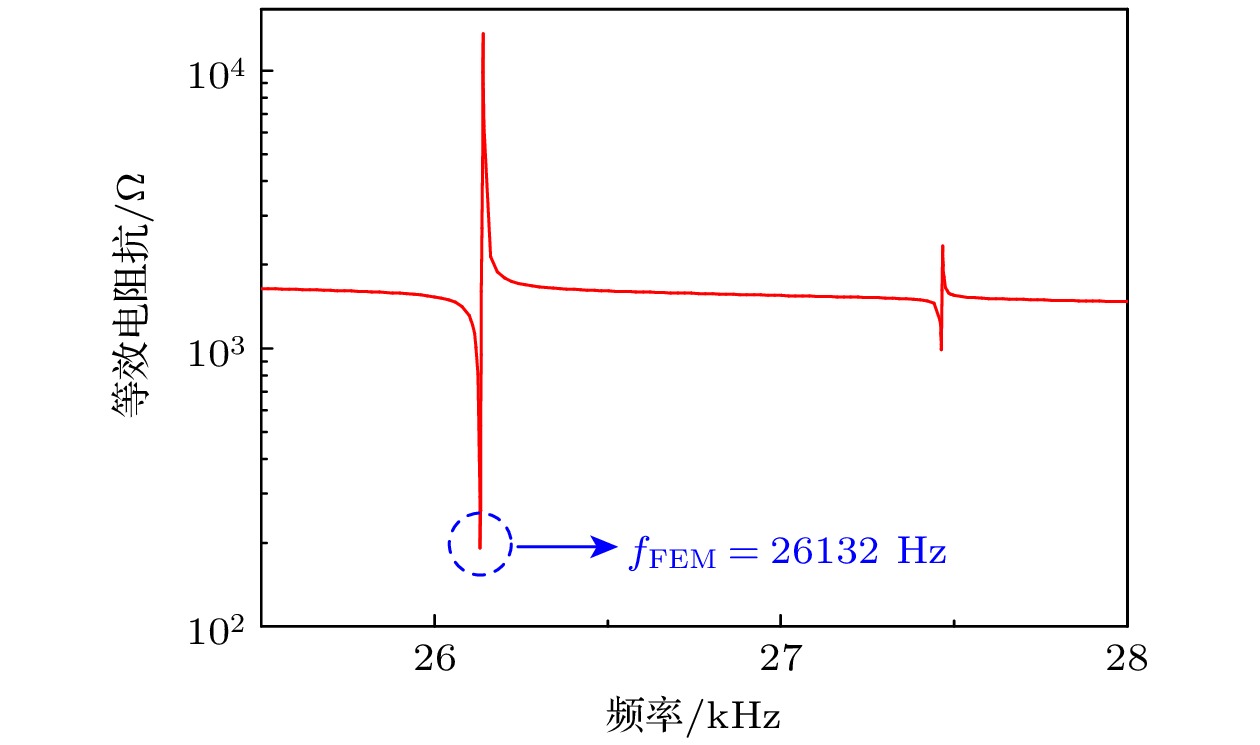
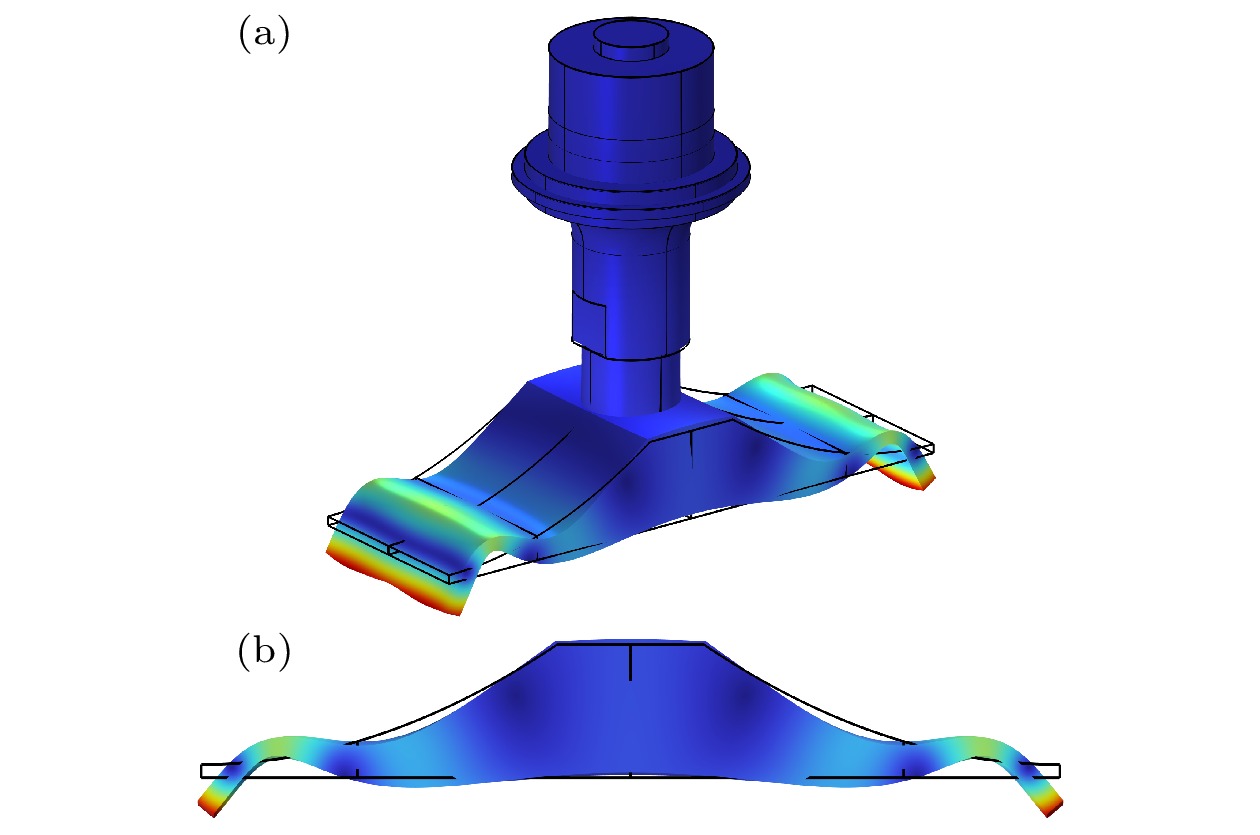
由表1可知, 辐射板三阶对称弯曲振动的频率与纵向夹心式换能器一阶纵振频率基本一致, 故可选用辐射板的该模态进行声黑洞换能器的设计. 在COMSOL软件中对声黑洞换能器进行有限元仿真建模. 其中, 辐射板的网格划分设置与2.2节一致, 纵向夹心式换能器的最大网格单元大小设置为8 mm (见图6). 使用固体力学与静电模块, 设置激励电压为1 V. 由换能器电阻抗频率响应曲线及振动模态(图7和图8)可知, 声黑洞换能器的振动频率
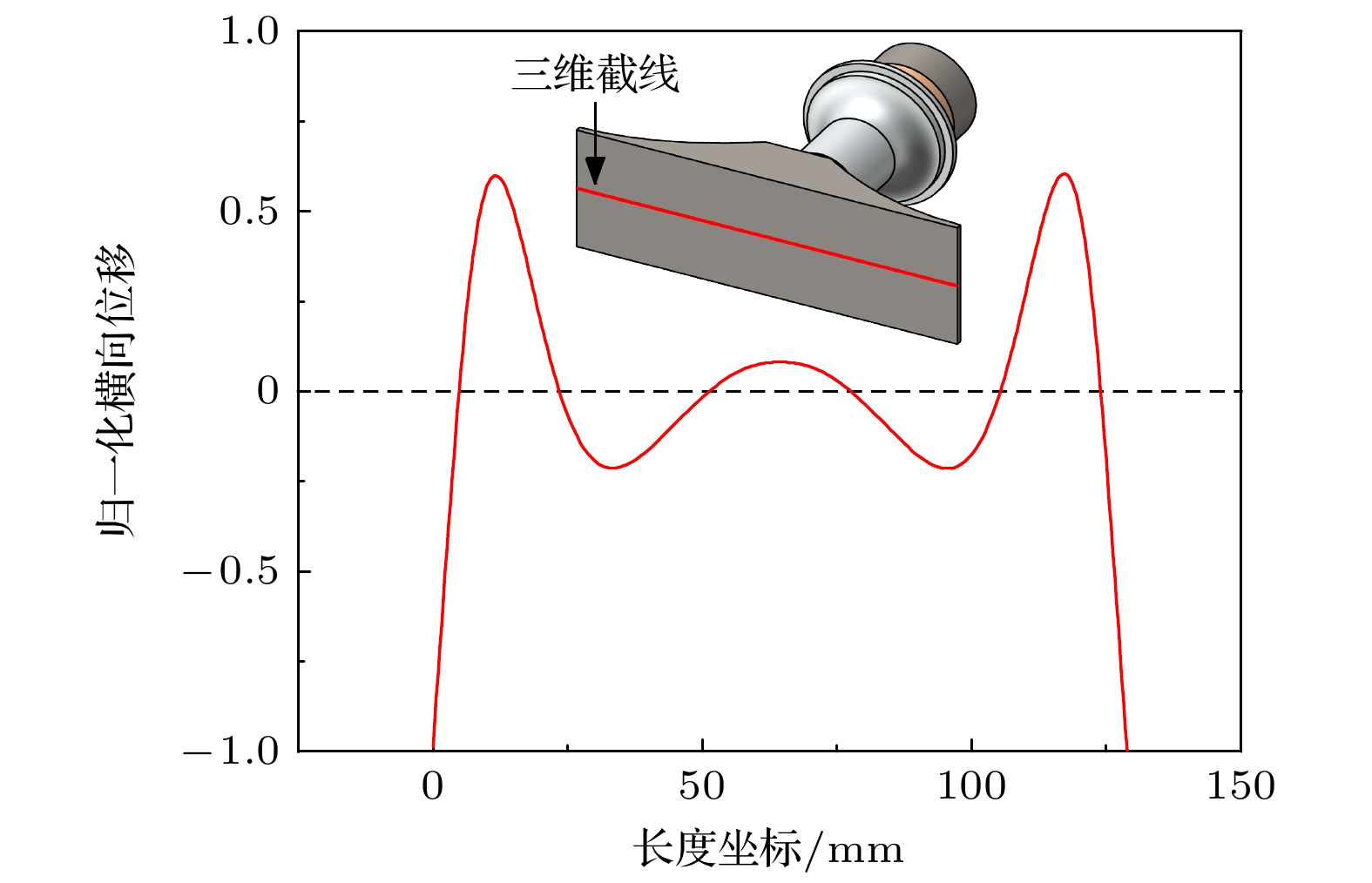
${f_{{\text{FEM}}}}$ 为26132 Hz, 与纵向夹心式换能器一阶纵振频率26055 Hz之间相对误差仅为0.30%, 验证了本文设计方法的可行性.沿长度方向, 取辐射面中轴线作为三维截线, 通过有限元仿真计算得到其归一化的横向位移分布曲线, 以反映整个辐射板的振动位移分布. 如图9所示, 从中间到两端, 振幅逐级增大, 于两端达到最大, 验证了声黑洞结构的能量聚集效应.
-
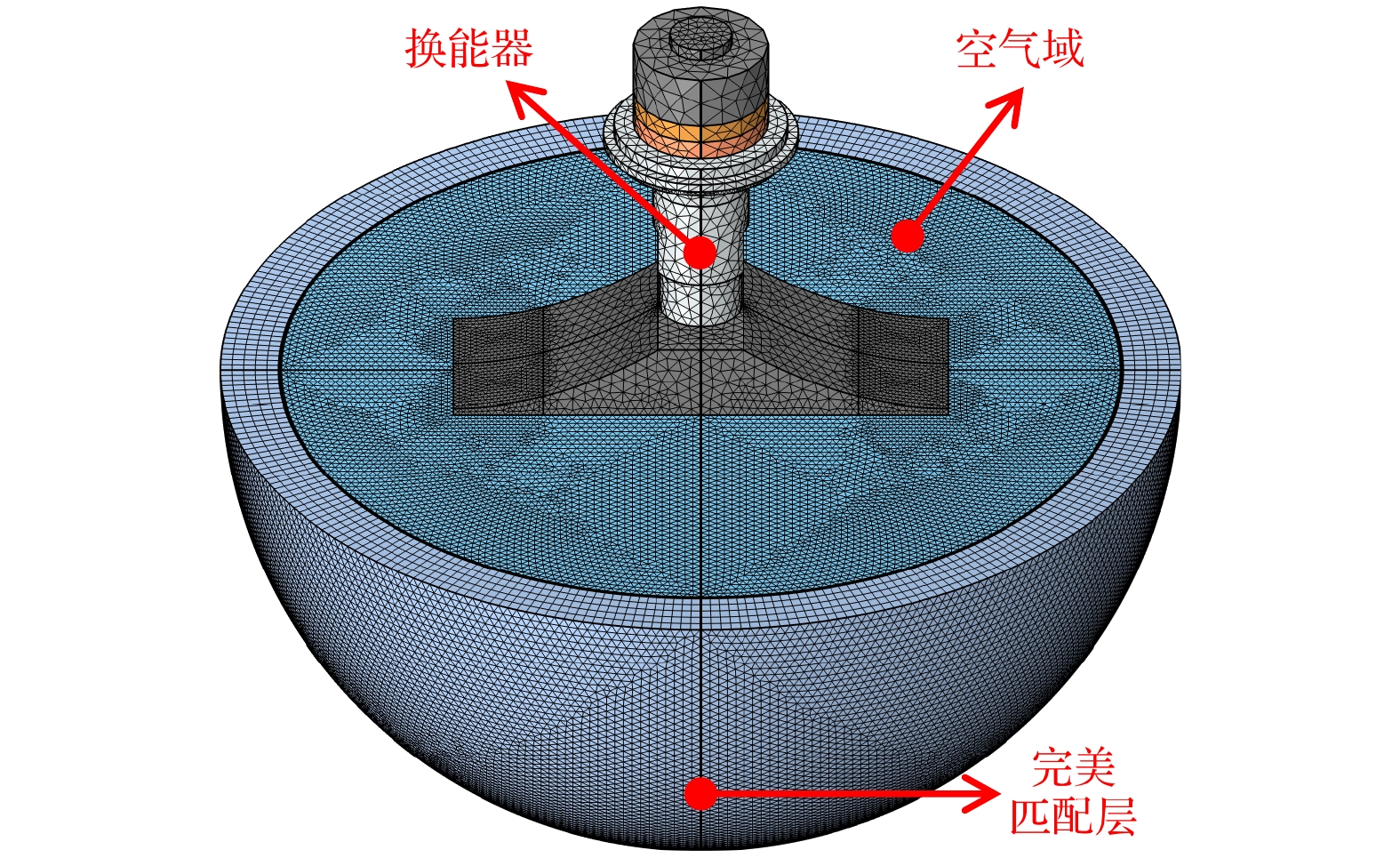
为研究换能器在空气中的辐射近声场, 如图10所示, 在COMSOL软件中使用压力声学模块, 添加半径为110 mm的半球体作为空气域, 并在其外表面上添加厚度为15 mm的完美匹配层(PML), 以吸收入射声波. 空气域划分网格最大单元大小为相应波长的1/6, 以保证空气中声波的仿真精度, 然后将完美匹配层划分为5层网格, 并在与空气域的界面上创建厚度为0.01倍相应波长的边界层, 以保证入射声波被充分吸收.
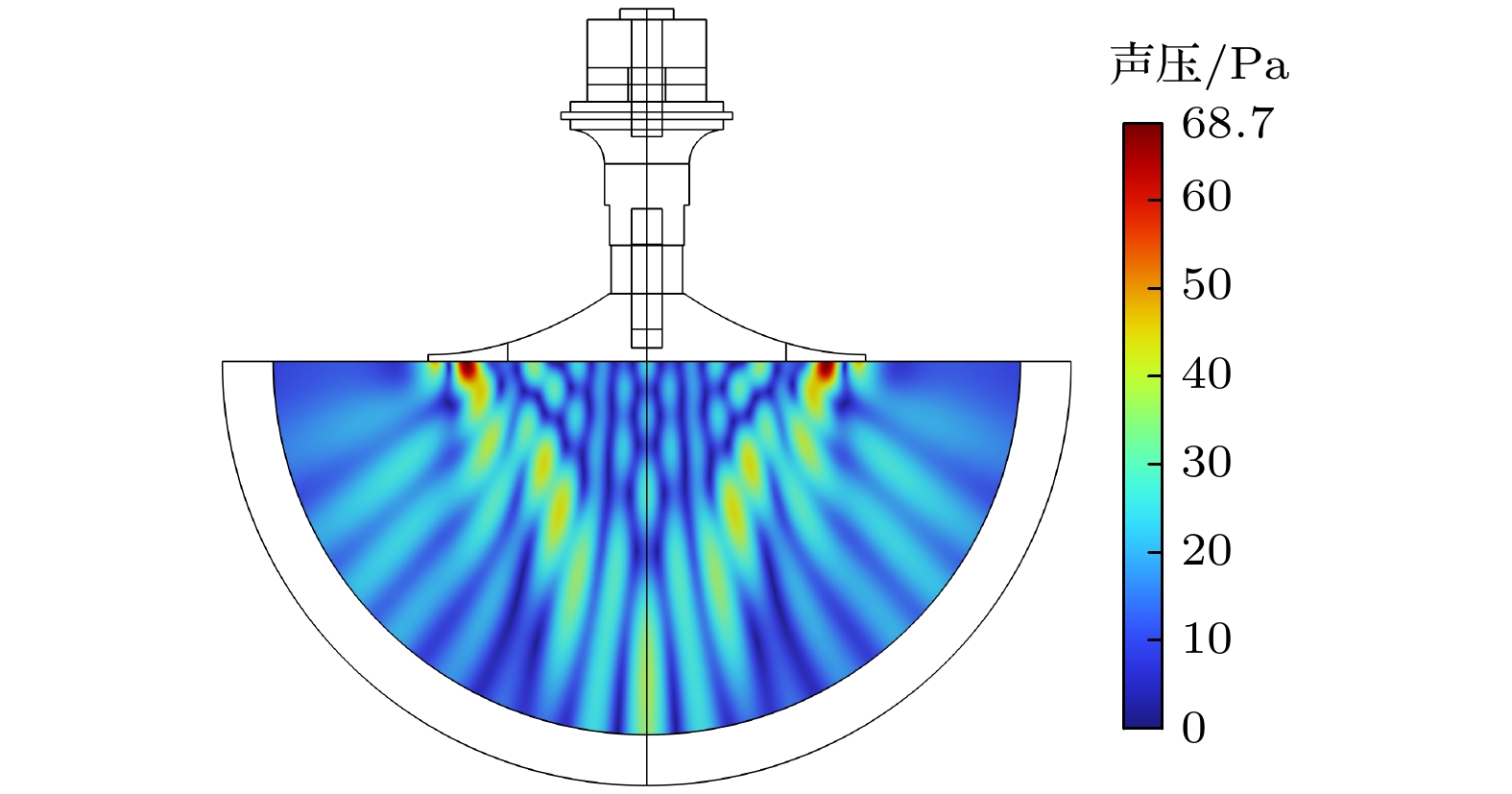
设置激励电压为1 V, 激发频率为26132 Hz. 由图11可知, 声压分布在一定程度上呈现出了梯度分布特征, 最大声压出现在辐射板振幅最大的两端, 且辐射板前方存在多样化能量势阱, 有望在这种非均匀近场声压分布下实现对粒子的梯度悬浮.
-
为验证声黑洞换能器设计的可行性, 制作了如图12所示的换能器样机. 螺栓、后盖板和辐射板材质为钢, 变幅杆材质为硬铝, 压电陶瓷为PZT-4, 电极片由铜制成. 利用阻抗分析仪与激光测振仪测量换能器样机的电参数特性及振动模态, 并利用传声器测量换能器样机在空气中的近场辐射声压, 最后进行超声悬浮实验测试.
-
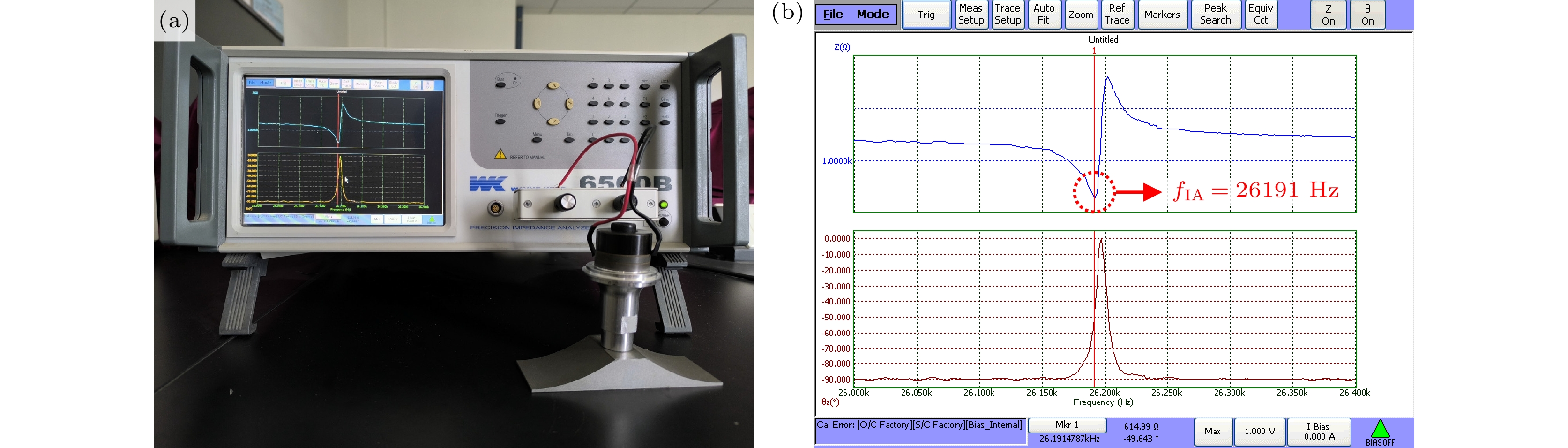
为验证有限元仿真结果, 使用图13(a)中的WK6500B精密阻抗分析仪对换能器的电阻抗进行测量, 设置激励电压为1 V. 由图13(b)所示的电阻抗频率响应曲线可知换能器样机的谐振频率
${f_{{\text{IA}}}}$ = 26191 Hz, 同有限元仿真得到的谐振频率$ {f_{{\text{FEM}}}} $ 之间相对误差${\Delta _2} = \left( {{f_{{\text{IA}}}} - {f_{{\text{FEM}}}}} \right)/{f_{{\text{IA}}}} = 0.23{\text{%}}$ , 吻合较好, 验证了有限元仿真频率结果的可靠性. 误差的主要来源有以下3点:1)实际加工材料参数与有限元仿真使用的标准材料参数之间存在偏差;
2)有限元仿真忽略了换能器的机械损耗、介电损耗, 以及螺栓所带来的预应力;
3)样机加工精度有限, 换能器存在装配误差.
-
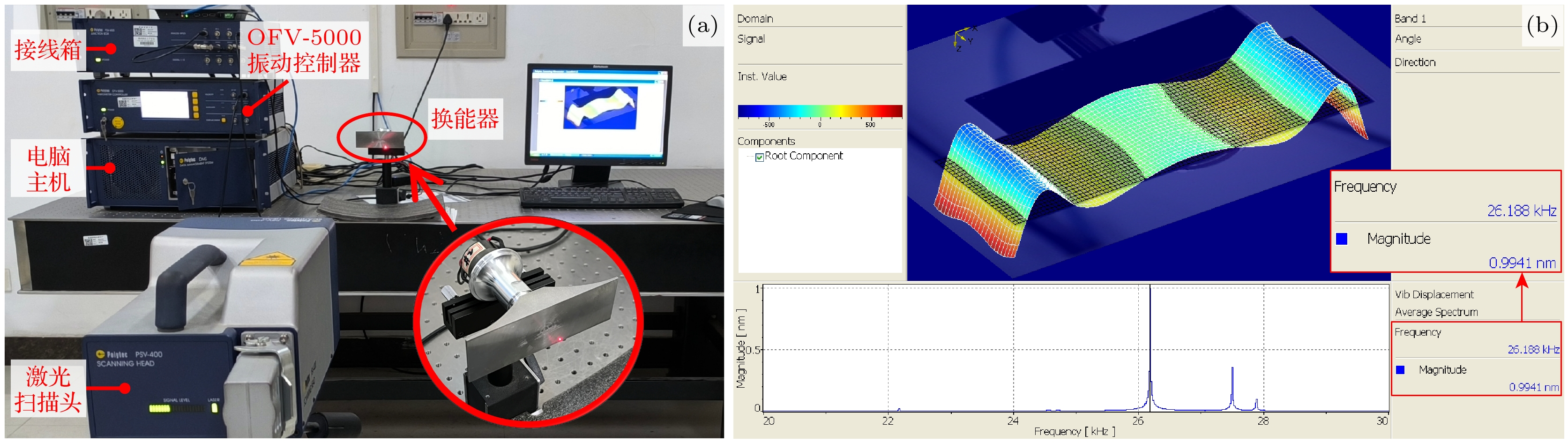
使用图14(a)所示Polytec PSV-400全场扫描式激光振动测量系统对换能器的振动模态进行测量. 设置激励电压为1 V, 扫频范围为20—30 kHz. 由图14(b)所示, 实验测得的振动模态与有限元仿真所得模态较为吻合, 证明目标模态能够被有效激发.
-
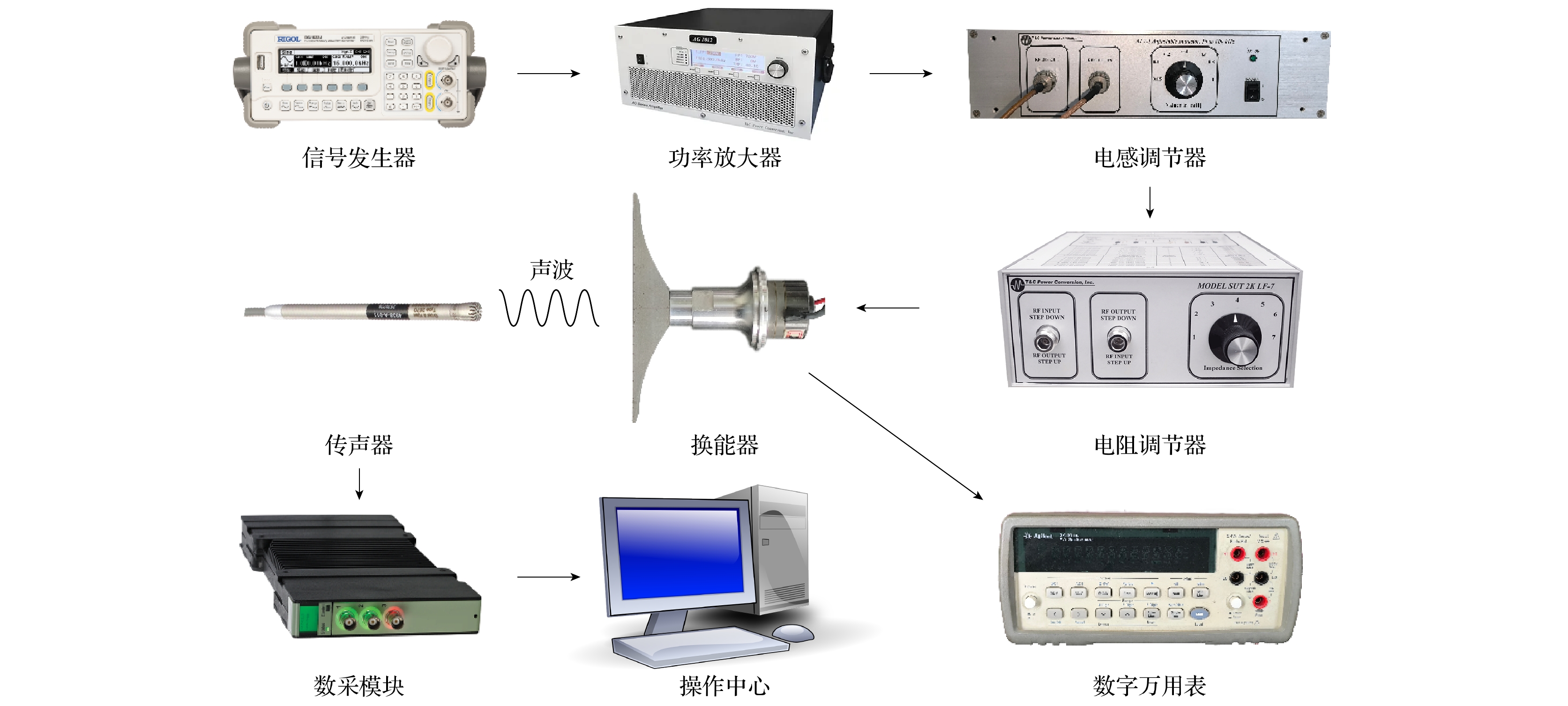
声场测量系统的搭建如图15所示. 首先对换能器进行电激励, 由信号发生器(RIGOL DG1022U)产生26161 Hz, 500 mVpp的正弦电信号, 经功率放大器(T&C AG 1012)放大, 得到有效输出功率为4 W. 然后通过电感调节器、电阻调节器(T&C AI 7-1, MODEL SUT 2K LF-7)对换能器进行电匹配. 将传声器放置于辐射面正前方, 并将传声器连接至Brüel & Kjær 3052-A-030数采模块, 设置取20 s内所采集数据的平均值. 使用Agilent 34401A 6位半数字万用表测量换能器的电压.
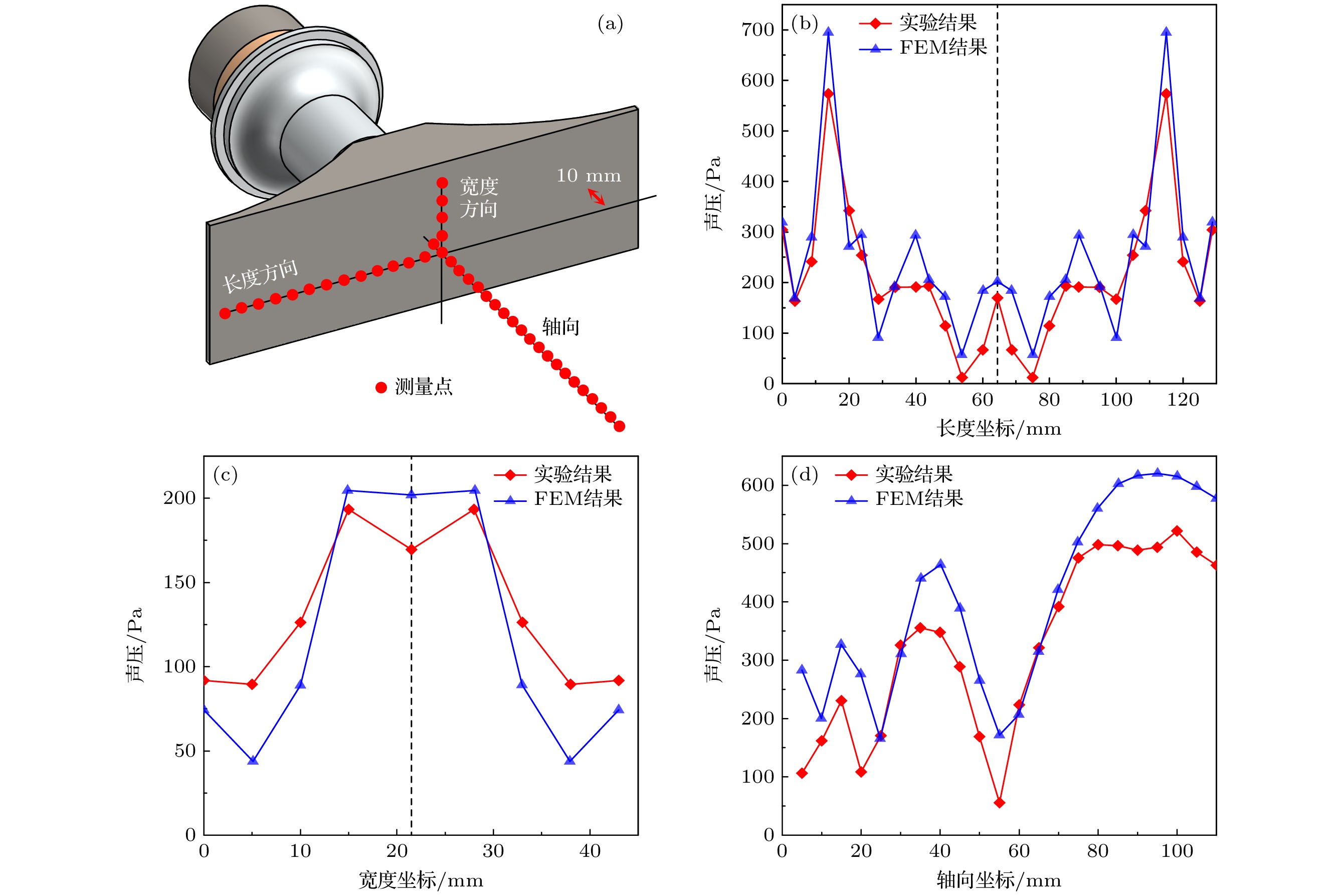
如图16(a)所示, 在距离辐射面10 mm处的平面上, 沿长度方向、宽度方向, 以及沿换能器的轴向分别测量空气中的近场辐射声压. 由于近声场分布的对称性, 在长度方向上的一侧均匀地取14个测量点, 宽度方向上的一侧均匀地取5个测量点. 此外, 在轴向上均匀地取22个测量点. 如图16(b)—(d)所示, 有限元仿真与实验得到的近场声压分布总体上较为一致, 部分数据的偏差主要来源于实验中声波的反射与折射. 近场声压分布图显示, 在轴向上, 近场声压振幅起伏较大, 且随距离增大, 声压极大与极小之间的间距逐渐扩大, 极大值逐级递增; 在宽度方向上, 声压呈现中间高、两侧低的分布特征; 在长度方向上, 声压从中间向两侧逐步增强, 最大声压出现在两端. 这种现象归因于声黑洞结构的能量聚集效应, 该效应逐级放大了辐射板两侧的振动幅度, 使得越接近两端的位置辐射声压越强, 从而导致辐射器的近场声压分布呈现出梯度增大的规律. 这一特性可用于实现粒子的梯度悬浮.
-
图17(a)为搭建的超声悬浮实验平台. 将换能器辐射面朝下, 在下方放置一立方体铝块作为反射障板, 在换能器与铝块间形成驻波声场. 设置信号发生器产生26161 Hz , 500 mVpp的正弦电信号, 功率放大器有效输出功率为4 W. 将若干直径为4 mm的发泡聚苯乙烯(EPS)小球悬浮于声场中. 如图17(b)所示, 当辐射面与反射障板相隔约20.3 mm时, 从左到右依次悬浮有5个、4个、3个、4个、5个小球. 可见, 由于声黑洞结构对弯曲振幅的累积放大效果, 辐射面与反射障板之间的驻波声场在长度方向上为梯度分布, 声辐射力从中间到两侧逐级增大, 悬浮的小球也逐渐增多, 有望实现粒子筛选.
-
本文基于声黑洞结构的能量聚集效应, 设计了一种声黑洞楔形结构振动模式转换超声换能器. 基于铁木辛柯梁理论, 利用传输矩阵法建立了理论模型, 能快速、准确地计算辐射板的弯曲振动频率, 大大提升了辐射板的设计效率. 根据有限元仿真与实验测量结果, 辐射板从中间到两端的振幅逐级增大, 使得近场辐射声压呈现出梯度分布的特点, 且声场中存在多样化势阱. 实验测得的振动频率及模态、近场声压分布结果与有限元仿真结果吻合较好, 验证了本文设计方法的可行性. 粒子梯度悬浮实验验证了该声黑洞换能器构造多功能声场的潜力, 有望在粒子筛选等技术中得到进一步应用. 未来, 我们将持续优化声黑洞结构的工程设计, 探索声黑洞结构在多功能粒子操纵方面的应用潜力.
-
已知正文(7)式中的各个元素
$ a_{mn}^i $ 是一个4$ \times $ 4矩阵, 该矩阵的各个元素如下:这里,
声黑洞楔形结构振动模式转换超声换能器
An ultrasonic transducer for vibration mode conversion of wedge-shaped structure of acoustic black hole
-
摘要: 基于声黑洞结构独特的声波捕获与能量聚集效应, 提出了一种新型声黑洞楔形结构振动模式转换超声换能器. 该换能器由一个纵向夹心式换能器和一个声黑洞楔形结构辐射板组成. 基于铁木辛柯梁理论, 利用传输矩阵法建立了辐射板弯曲振动的理论模型, 计算得到的振动频率与有限元仿真频率吻合较好. 对换能器的电阻抗频率响应特性、振动模态以及空气中近场辐射声压分布进行了仿真模拟, 结果显示, 声黑洞楔形结构辐射板的振幅逐级增大, 近场辐射声压呈现出梯度分布的特点. 加工了换能器样机, 并对其进行实验测试, 测试结果验证了设计方法的可行性. 最后进行了超声悬浮实验, 结果表明声黑洞设计可以赋能于超声悬浮技术, 构造出声压梯度分布的声场, 实现粒子筛选.Abstract: Acoustic black hole (ABH) structure has been extensively used in vibration mitigation, noise reduction, energy harvesting and so on, owing to its unique sound wave trapping and energy concentration effects. Besides, ABH structure holds emerging potential in improving the performance of ultrasonic device and constructing multifunctional acoustic field. Hence, an ultrasonic mode-conversion transducer consisting of a longitudinal sandwich transducer and an ABH wedge radiant plate is proposed in this work, in order to explore the potential applications of ABH in ultrasonic levitation and multifunctional particle manipulation. The theoretical model of flexural vibration of the radiant plate is established by utilizing Timoshenko beam theory and transfer matrix method, and the calculated vibration frequencies are in good agreement with those obtained by finite element method (FEM). The electrical impedance frequency response characteristics, vibration modes and the near-field sound pressure distribution of the transducer in air are also simulated. The results indicate that the amplitude of the ABH wedge radiant plate increases stepwise, and the sound pressure exhibits a gradient distribution. A prototype of the transducer is fabricated and experimentally tested, confirming the accuracy of FEM simulations and the feasibility of the design approach. Finally, the result of the ultrasonic levitation experiment indicates that the ABH design can give rise to gradient distribution of sound pressure in standing wave sound field for achieving precise particle sorting.
-
-
图 1 声黑洞楔形结构振动模式转换超声换能器
Figure 1. Ultrasonic transducer with acoustic black hole wedge structure based on vibration mode-conversion.
图 2 换能器尺寸参数示意图 (a)纵向夹心式换能器; (b)声黑洞楔形结构辐射板
Figure 2. Schematic diagram of the transducer’s dimensions: (a) The longitudinal sandwich transducer; (b) the ABH wedge radiant plate.
图 7 有限元仿真得到的换能器电阻抗频率响应曲线
Figure 7. Electrical impedance frequency response curve of the transducer obtained by FEM.
图 8 (a)换能器整体模态; (b)辐射板弯曲振动模态
Figure 8. (a) Vibration mode of the whole transducer; (b) the flexural vibration mode of the radiant plate.
图 9 归一化的辐射板横向位移分布曲线
Figure 9. Curve of normalized transverse displacement distribution of the radiant plate.
图 10 空气中辐射近声场建模的网格划分
Figure 10. Meshing of the modeling of radiated near sound field in air.
图 11 空气中近场声压分布有限元仿真结果
Figure 11. Near-field sound pressure distribution in air obtained by FEM.
图 12 声黑洞楔形结构振动模式转换换能器样机
Figure 12. Prototype of the ultrasonic transducer with acoustic black hole wedge structure based on vibration mode-conversion.
图 13 阻抗分析实验 (a) WK6500B精密阻抗分析仪及换能器样机; (b)换能器输入电阻抗及相位的频率响应曲线
Figure 13. Impedance analysis experiment: (a) The WK6500B precision impedance analyzer and the transducer prototype; (b) frequency response curve of the input electric impedance and phase of the transducer.
图 14 激光测振实验 (a) Polytec PSV-400全场扫描式激光振动测量系统及换能器样机; (b)辐射板弯曲振动模态
Figure 14. Laser vibrometry experiment: (a) The Polytec PSV-400 full-field scanning laser vibrometry system and the transducer prototype; (b) flexural vibration mode of the radiant plate.
图 15 空气中声场测量实验系统
Figure 15. Experimental system for acoustic field measurement in air.
图 16 空气中近场声压分布实验测量与有限元仿真结果对比 (a)测量点示意; (b)距辐射面10 mm处长度方向上声压分布; (c)距辐射面10 mm处宽度方向上声压分布; (d)轴向上声压分布
Figure 16. Comparison of the experimental and FEM’s results of near-field sound pressure distribution in air: (a) Schematic diagram of measuring points; (b) sound pressure distribution in the length direction 10 mm away from the radiant surface; (c) sound pressure distribution in the width direction 10 mm away from the radiant surface; (d) axial sound pressure distribution.
图 17 (a)超声悬浮实验平台; (b) EPS小球的梯度悬浮
Figure 17. (a) Platform of ultrasonic levitation experiment; (b) gradient levitation of EPS pellets.
表 1 辐射板弯曲振动频率计算结果对比
Table 1. Comparison of calculated flexural vibration frequency of the radiant plate.
参数 一阶 二阶 三阶 四阶 五阶 六阶 ${f_{\text{T}}}$ /Hz5575 13909 26722 43370 62585 83304 ${f_{\text{F}}}$ /Hz5431 13402 26101 43287 62847 83737 ${\varDelta _1}$ /%2.65 3.78 2.38 0.19 0.42 0.52 
下载: 导出CSV
-
[1] Krylov V V 2014 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 1296 doi: 10.1109/TUFFC.2014.3036 [2] Bowyer E P, Krylov V V 2015 Appl. Acoust. 88 30 doi: 10.1016/j.apacoust.2014.07.014 [3] Chong B M P, Tan L B, Lim K M, Lee H P 2017 Int. J. Appl. Mech. 9 1750078 doi: 10.1142/S1758825117500788 [4] Zhao C, Prasad M G 2019 Acoustics 1 220 doi: 10.3390/acoustics1010014 [5] Krylov V V, Winward R 2007 J. Sound Vib. 300 43 doi: 10.1016/j.jsv.2006.07.035 [6] Deng J, Guasch O, Maxit L, Gao N S 2022 J. Sound Vib. 526 19 doi: 10.1016/j.jsv.2022.116803 [7] Deng J, Gao N S, Chen X 2023 Thin Walled Struct. 184 6 doi: 10.1016/j.tws.2022.110459 [8] Zhao L, Conlon S C, Semperlotti F 2015 Smart Mater. Struct. 24 065039 doi: 10.1088/0964-1726/24/6/065039 [9] Liang Y K, Ji H L, Qiu J H, Cheng L, Wu Y P, Zhang C 2018 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM) Auckland, New Zealand, July 9–12, 2018 pp1372–1377 [10] Li H, Doaré O, Touzé C, Pelat A, Gautier F 2022 Int. J. Solids Struct. 238 111409 doi: 10.1016/j.ijsolstr.2021.111409 [11] Zhang L, Kerschen G, Cheng L 2022 Mech. Syst. Signal Process. 177 109244 doi: 10.1016/j.ymssp.2022.109244 [12] Zhang L, Tang X, Qin Z, Chu F 2022 Appl. Phys. Lett. 121 013902 doi: 10.1063/5.0089382 [13] Remillieux M C, Anderson B E, Le Bas P Y, Ulrich T J 2014 Ultrasonics 54 1409 doi: 10.1016/j.ultras.2014.02.017 [14] Anderson B E, Remillieux M C, Le Bas P Y, Ulrich T J, Pieczonka L 2015 Ultrasonics 63 141 doi: 10.1016/j.ultras.2015.07.002 [15] 刘洋, 陈诚, 林书玉 2024 物理学报 73 084302 doi: 10.7498/aps.73.20231983 Liu Y, Chen C, Lin S Y 2024 Acta Phys. Sin. 73 084302 doi: 10.7498/aps.73.20231983 [16] Chen C, Liu Y, Wang C H, Guo J Z, Lin S Y 2024 Ultrason. Sonochem. 111 107106 doi: 10.1016/j.ultsonch.2024.107106 [17] Zhan L P, Hua T Z, Chun Y K, Naquin T D, Jing H N, Yu H H, Yan C J, Xia M Q, Bachman H, Ran Z P, Hong X X, Hui H J, Huang T J 2022 Sci. Adv. 8 eabm2592 doi: 10.1126/sciadv.abm2592 [18] Yin Q, Yong S H, Long W Z, Chao M Z, Ming Z W 2024 Microsyst. Nanoeng. 10 144 doi: 10.1038/s41378-024-00789-z [19] 林书玉, 张福成, 郭孝武, 董胜林 1995 陕西师范大学学报(自然科学版) 23 43 Lin S Y, Zhang F C, Guo X W, Dong S L 1995 J. Shaanxi Normal Univ. (Nat. Sci. Ed.) 23 43 [20] 林书玉 2004 超声换能器的原理及设计 (北京: 科学出版社) 第91—111页 Lin S Y 2004 The Theory and Design of Ultrasonic Transducers (Beijing: Science Press) pp91–111 [21] Williams F W, Banerjee J R 1985 J. Sound Vib. 99 121 doi: 10.1016/0022-460X(85)90449-3 [22] Miklowitz J 2021 J. Appl. Mech. 20 511 doi: 10.1115/1.4010756 [23] Mori E 1989 Ultrasonics International 89 Conference Proceedings Madrid, Spain, July 3–7, 1989 p256 [24] Zhou G, Li M 2000 J. Acoust. Soc. Am. 107 1358 doi: 10.1121/1.428423 -
计量
- 文章访问数: 352
- HTML全文浏览数: 352
- PDF下载数: 5
- 施引文献: 0