微机电系统(MEMS)在机械制造、航天航空、信息通信、生物化学等众多科学和工程领域^[1,2]均有涉及, 尤其近年来得到了快速发展. MEMS尺寸较小, 内部通道一般位于微米或纳米级, 气体的输运可能涵盖整个流动区域, 即从连续流到自由分子流. 微纳尺度下气体的流动和传热过程会表现出与宏观连续尺度时诸多不同的特性, 如速度滑移、温度跳跃以及浓度分离等^[3]. 特别地, 热蠕流是一种非平衡条件下由温差引起的流动, 构成多种微型器件的工作原理, 如克努森泵、微型热加速度计等^[4–6]. 微小空间内气体热蠕流动行为的准确预测对相关器件性能的优化升级十分关键. 但是, 一方面由于稀薄气体的热质传递不满足连续介质假设, 采用常规数值方法模拟时遇到挑战; 另一方面, 热蠕流动机制十分复杂^[7,8], 这对微尺度下流动和传热过程的理解造成了一定的困难.

许多学者采用数值模拟研究了微尺度下的气体流动特性^[9–11]. Nabapure^[12]采用直接模拟蒙特卡罗(DSMC)方法模拟了稀薄气体在四壁面驱动方腔中的流动过程. 结果表明, 壁面驱动模式对腔内流体速度和流动结构影响较大, 传热强度随Kn的增大而减小. Wu等^[13]通过求解线性化Boltzmann方程, 研究了二维振动板驱动方腔内的稀薄气体流动, 发现了稀薄气体的反共振现象, 此时移动平板的阻尼力最小. Ogata和Kawaguchi^[14]采用约束插值剖面(CIP)法模拟了滑移区方腔内的稀薄气体流动. 数值结果表明, 带滑移边界条件的Navier-Stokes (NS)方程可适用于模拟克努森数10^–3 < Kn < 10^–1的流动. Palharini等^[15]采用DSMC对稀薄气体在三维空腔过渡流区中的流动进行了研究. 结果发现, 不同长深比下空腔内的流体具有不同的流动结构, 如单次再循环和二次再循环. Yang等^[16]采用矩方法研究了3种不同类型的非平衡气体流动问题, 包括外力驱动的泊肃叶流、顶盖驱动的和热诱导的空腔流. 研究表明, 矩方法在前两种流动中具有很好的准确性, 但是在后一种热驱流动中其可靠性当Kn > 0.5后迅速下降.

微器件中的气体流动常常伴随着热量的传递, 因而有不少学者开展了微尺度条件下的流动耦合传热研究^[17–20]. Yamaguchi等^[21]测量了由热蠕流动引起的通过矩形微通道的流量, 通道两端分别连接一个温度不同的腔体. 结果表明, 气体在过渡流状态下的流速比滑移流时小. Barbera和Brini ^[22]采用有理扩展热力学方程, 研究了两个同轴圆柱体之间稀薄气体的稳态流动. 他们发现, 即使只规定圆柱体径向温度梯度, 热通量的切向分量和轴向分量也不会消失. Akhlaghi等^[23]采用DSMC模拟了顶盖驱动空腔内稀薄气体的反傅里叶传热现象. 他们将热通量分解为弹道部分和碰撞部分, 分别来源于边界的无碰撞粒子和进入流场后至少发生一次碰撞后的粒子进行抽样, 结果发现弹道和碰撞部分均有助于低温向高温的逆向热传递发生. Han等^[24]使用DSMC方法研究了通道壁面上温度不连续分布对气体热蠕流动的影响. 结果发现, 冷壁面气体沿着通道向热壁面流动. Roohi等^[25,26]同样采用DSMC模拟了等腰三角形空腔中的稀薄气体流动. 研究表明, 热通量本构关系的傅里叶项和剪切应力梯度分量之间的竞争导致了三角形空腔中的反傅里叶热传递. 最近, Wang等^[27]采用DUGKS探究了非线性振动板驱动矩形空腔内的稀薄气体流动, 结果显示气体的流场结构呈现非对称性, 且温度场将产生二次谐波振荡. Zhu等^[28]使用DUGKS系统研究了从滑移到自由分子区的气体在顶盖以恒定速度驱动下的流动和传热特性, 其结果解释了非平衡条件下反傅里叶传热现象的发生. 此外, Wang等^[29]根据不同的热蠕流动机制对克努森泵进行分类, 并从克努森泵的配置、性能和应用这3个方面的研究现状进行了全面回顾和分析, 总结得到, 微通道上温度的配置和调节是控制克努森泵流动性能的关键因素.

上述研究在一定程度上揭示了受限空间中稀薄气体流动和传热的内在机理, 但多数工作着眼于运动边界或恒定温度条件^[30]的情况. 一些实际应用则涉及脉动加热驱动, 如热剪应力传感器^[31]中通过加热膜元件引起流体流动从而产生电阻变化、多组分气体的浓度分离^[32]以及声传感器中由热激励产生的声波^[33]. 相关应用还包括用于DNA分子反应检测的纳米机械谐振器, 其由高频电压或局部激光加热金属电阻器形成的热振荡驱动^[34,35], 以及由脉冲激光烧灼弹性材料形成热振荡而驱动纳米颗粒的声学谐振器^[36]. 关于这类由变温边界驱动的稀薄气体的流动机理研究目前还较少. 因此, 本文使用DUGKS方法模拟壁面温度周期变化条件下封闭方腔内的热蠕流动, 讨论温变频率和振幅对腔内稀薄气体流动和传热特性的影响机制.

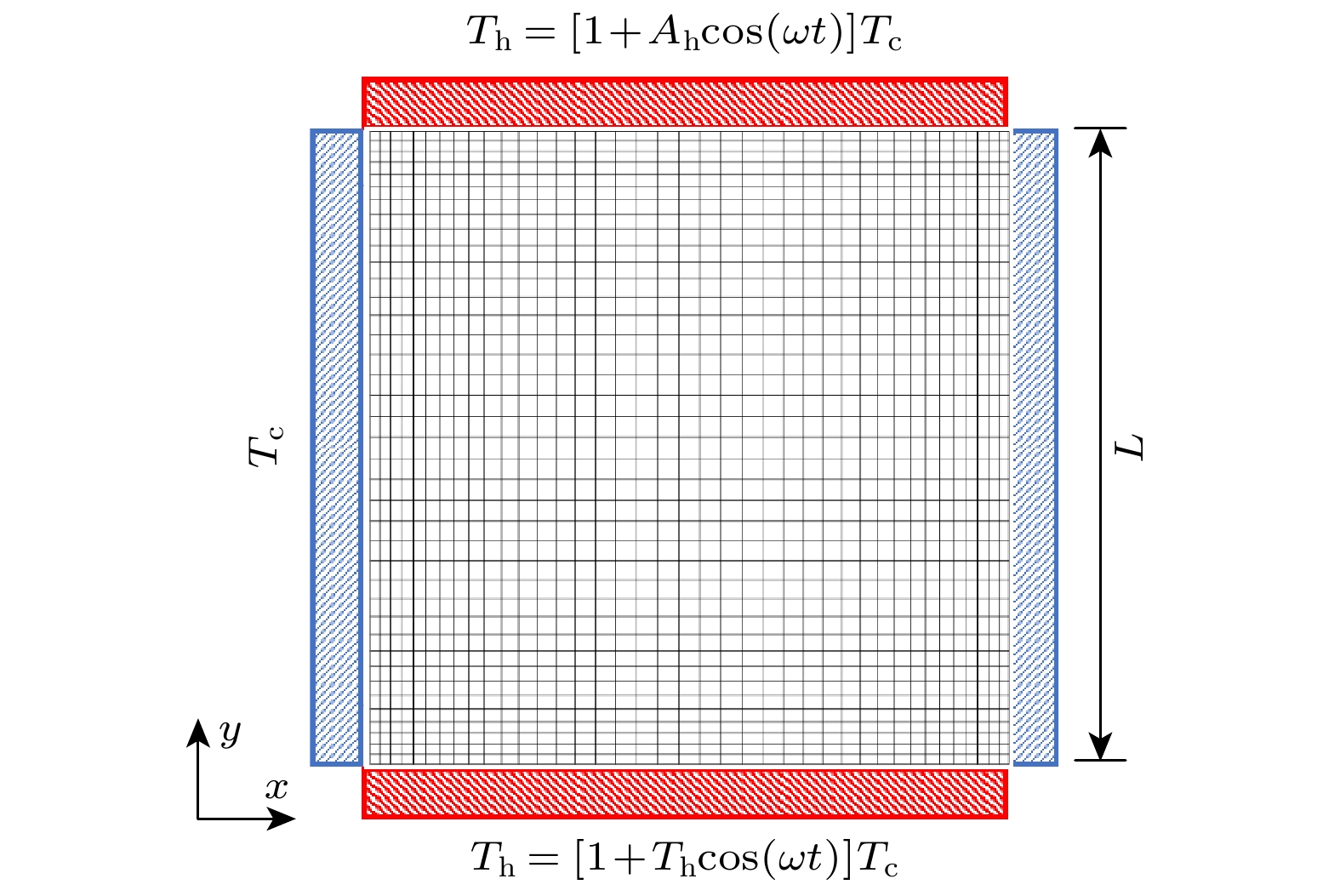
本文研究的矩形方腔内热蠕流动问题如图1所示. 边长L = 1 m的方腔中充满稀薄程度为Kn的单原子氩气. 腔体四周为静止固壁. 左、右壁面温度保持不变, T_c = 273 K. 上、下壁面温度也呈均匀分布, 但是大小随时间作周期性变化,

式中, A_h为温度变化的振幅, ω为变温频率, t为时间. 所有壁面均为Maxwell漫反射边界. 该问题主要受变温振幅A_h、斯托克斯数St以及克努森数Kn控制. St和Kn分别定义如下:

其中, $ {v}_{{\mathrm{m}}}=\sqrt{2 R{T}_{{\mathrm{c}}}} $为分子最概然速率, $ \lambda $是分子 平均自由程:

文中, 变温频率ω由$ St $调节. 上述无量纲控制参数的变化范围分别为0.1 ≤ A_h ≤ 0.8, 0.5 ≤ St ≤ 5.0以及0.01 ≤ Kn ≤ 10. 在模拟中, 物理空间离散使用40 × 40的正交非均匀网格系统, 网格分辨率从腔体中心到墙壁逐渐细化. 网格中心的位置$ \left({x}_{i}, {y}_{j}\right) $由表达式$ {x}_{i}=\dfrac{{\zeta }_{i}+{\zeta }_{i+1}}{2},\; {y}_{j}=\dfrac{{\zeta }_{j}+{\zeta }_{j+1}}{2}, 0\leqslant i\leqslant {{39, 0}}\leqslant j\leqslant 39 $给出, 其中$ {{z}}_{i} $定义为^[27]

其中, a是一个决定网格疏密分布的常数, a越大, 两端网格尺寸越小. 本文选取a = 2. 速度空间离散采用Newton-Cotes数值积分结合张量积法则, 其中单向在区间[$ -4{v}_{{\mathrm{m}}} $, $ 4{v}_{{\mathrm{m}}}] $内均匀布置101个积分点. 时间步长dt由CFL数确定, 即$ {\mathrm{d}}t= {\mathrm{C}}{\mathrm{F}}{\mathrm{L}}\cdot {\Delta x}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}} $/$ {\left(\left|\boldsymbol{u}\right|+\left|\boldsymbol{\xi }\right|\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $, 其中$ {\Delta x}_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}} $为最小网格尺寸, $ \left|\boldsymbol{u}\right|{\mathrm{和}}\left|\boldsymbol{\xi }\right| $分别为流体宏观速度和微观速度; CFL设置为0.8.

本文采用Guo等^[37]提出的DUGKS数值求解上述热蠕流动问题. 该方法不依靠NS方程中连续介质假设, 通过在物理、时间和速度空间上进行离散求解Sharkhov-BGK形式的Boltzmann模型方程^[38,39], 并通过守恒律准确建立了介观量与宏观量之间的联系. 特别地, 基于特征线理论来构造界面分布函数, 耦合了分子自由迁移和局部碰撞效应, 适合全尺度流域模拟.

在DUGKS中, 控制方程为Shakhov-BGK模型形式的连续Boltzmann方程:

式中, $ f=f\left(\boldsymbol{x}, \boldsymbol{\xi }, \boldsymbol{\eta }, t\right) $为$ D $维空间中在时刻$ t $具有速度$ \boldsymbol{\xi }= ({\xi }_{1}, {\xi }_{2}, \cdots , {\xi }_{D}) $和坐标$ \boldsymbol{x}=\left({x}_{1}, {x}_{2}, \cdots , {x}_{D}\right) $的粒子分布函数. 文中, $ D = 2 $. $ \boldsymbol{\eta} = (\xi_{D+1},\cdots,\xi_3) $是3维空间中粒子除$ \boldsymbol{\xi } $之外的速度分量. $ \tau $为松弛时间, 其大小与气体的宏观动力黏度$ \mu $和压力$ p $相关, $ \tau = \mu /p $. $ {f}^{{\mathrm{S}}} $为Sharkhov-BGK平衡态分布函数.

为消除分布函数对被动变量$ \boldsymbol{\eta } $的依赖, Huang等^[40]建议引入两个约化分布函数:

进而可由(5)式得到$ g $和$ h $的演化方程为

这里, $ {g}^{{\mathrm{S}}} $和$ {h}^{{\mathrm{S}}} $是约化后的Sharkhov-BGK平衡态分布函数:

式中,

式中, $ \rho , \boldsymbol{u}, T, \boldsymbol{q} $分别为气体的宏观密度、速度、温度和热流密度, $ R $为气体常数, $ Pr $是普朗特数. $ \boldsymbol{c}=\boldsymbol{\xi }-\boldsymbol{u} $为粒子的本征速度. 由理想气体状态方程有, $ p=\rho RT $. 此外, 本文采用如下幂律模型描述动力黏度与温度之间的关系^[41]:

其中, 根据可变硬球模型VHS取$ \omega =0.81 $, $ {\mu }_{{\mathrm{r}}{\mathrm{e}}{\mathrm{f}}} $是参考温度$ {T}_{{\mathrm{r}}{\mathrm{e}}{\mathrm{f}}} $时的气体动力黏度.

本节简述采用DUGKS离散求解约化后的Boltzmann模型方程. 为了方便, (7)式记为

其中, $ \phi =g $或$ h $. 分别使用中点和梯形积分法处理对流项和碰撞项, 可从时间$ {t}_{n} $到$ {t}_{n+1} $将(11)式在控制体$ {V}_{j} $进行二阶有限体积离散为

式中, $ j $号单元的体积和中心分别为$ \partial \left|{V}_{j}\right| $, $ {\boldsymbol{x}}_{j} $, 时间步长为$ \Delta t={t}_{n+1}-{t}_{n} $. $ {F}^{n+1/2}\left(\boldsymbol{\xi }\right) $是界面通量. 其根据界面分布函数确认, 形式为

其中, $ \partial {V}_{j} $为单元$ j $的表面, $ \boldsymbol{n} $是由表面指向流体域的法向单位向量.

不难发现, (13)式给出的分布函数更新规则是隐式的. 为了构造显示格式, 这里引入一个辅助分布函数$ \tilde{\phi } $:

(13)式进而可改写为|

此处,

在实际计算中可以迭代求解$ \tilde{\phi } $, 而不是原始分布函数$ \phi $.

分布函数更新的另一个关键点在于重构界面上半步长的分布函数$ {\phi }^{n+1/2} $, 从而计算微观通量$ {F}^{n+1/2} $. 为此在半时间步$ s=\Delta t/2 $内沿特征线对(12)式积分:

式中再次使用了梯形法则计算碰撞项. $ {\boldsymbol{x}}_{{\mathrm{b}}}\in \partial {V}_{j} $为单元格j的界面中心. 值得注意的是, (18)式由于右侧碰撞项$ \varOmega \left({\boldsymbol{x}}_{{\mathrm{b}}}, \boldsymbol{\xi }, {t}_{n}+s\right) $也是隐式的. 同理, 引入另一个分布函数$\bar{\phi } $来得到显示迭代格式:

由此, (18)式可改写为

其中,

在得到$ {\bar{\phi }}^{+, n}\left({\boldsymbol{x}}_{{\mathrm{b}}}-\boldsymbol{\xi }s, \boldsymbol{\xi }\right) $后, 就可以由(19)式确定分布函数$ {\bar{\phi }}^{n+1/2}\left({\boldsymbol{x}}_{{\mathrm{b}}}, \boldsymbol{\xi }\right) $, 并进一步根据界面的宏观量计算出$ {\phi }^{{\mathrm{S}}, n+1/2}\left({\boldsymbol{x}}_{{\mathrm{b}}}, \boldsymbol{\xi }\right) $. 最后, 界面原始分布函数就可以得到:

整数倍时间步的分布函数$ {\bar{\phi }}^{+, n}\left({\boldsymbol{x}}_{{\mathrm{b}}}-\boldsymbol{\xi }s, \boldsymbol{\xi }\right) $可由泰勒公式确定:

$ {\mathrm{式}}{\mathrm{中}}{\boldsymbol{\sigma }}_{{\mathrm{b}}} $为界面上$ {\bar{\phi }}^{+} $的斜率, 而$ {\bar{\phi }}^{+} $与辅助分布函数$ \tilde{\phi } $有如下关系:

此外, 分布函数更新(14)式中的$ {\tilde{\phi }}^{+} $也可根据$ {\bar{\phi }}^{+} $和$ \tilde{\phi } $求得

接着进行速度空间离散. 本文选择Newton-Cotes数值积分公式, 一维时速度离散个数为$ N $(要求$ N-1 $是4的整数倍), 离散速度和相应的权系数$ {\left({\boldsymbol{\xi }}_{i}, {\omega }_{i}\right)}_{i={\mathrm{0, 1}}, 2, \cdots , N-1} $, 继而可由张量积得到二维离散速度. 这样, 宏观量就可以根据(26)式计算:

其中, $ E={u}^{2}/2+\varepsilon $表示单位质量气体总能, $ \varepsilon= {c}_{{\mathrm{v}}}T $为内能, $ {c}_{{\mathrm{v}}} $为定容比热容. 恒压和恒容下的比热容分别为$ {c}_{{\mathrm{p}}}=5 R/2 $和$ {c}_{{\mathrm{v}}}=3 R/2 $, 则比热比$ \gamma ={c}_{{\mathrm{p}}}{/c}_{{\mathrm{v}}}= 5/3 $. 需要注意的是, 由于碰撞项的相应速度矩为零, 故仍可根据(26)式利用$\bar{\phi } $替换$ \tilde{\phi } $来计算界面处气体的宏观量, 除了热流q$ \left({x}_{{\mathrm{b}}}, {t}_{n+1/2}\right) $需要更改为

热流密度与传热强度特征参数Nu相关:

其中$ {\lambda }_{{\mathrm{l}}} $为气体导热系数, $ \Delta T $为特征温差.

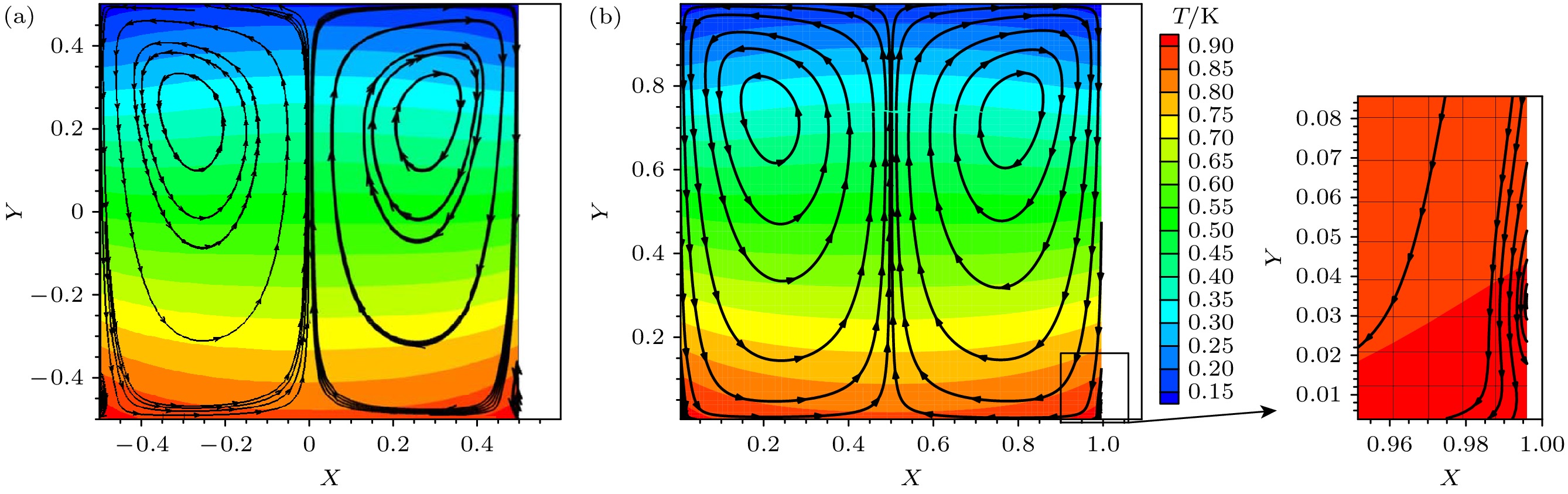
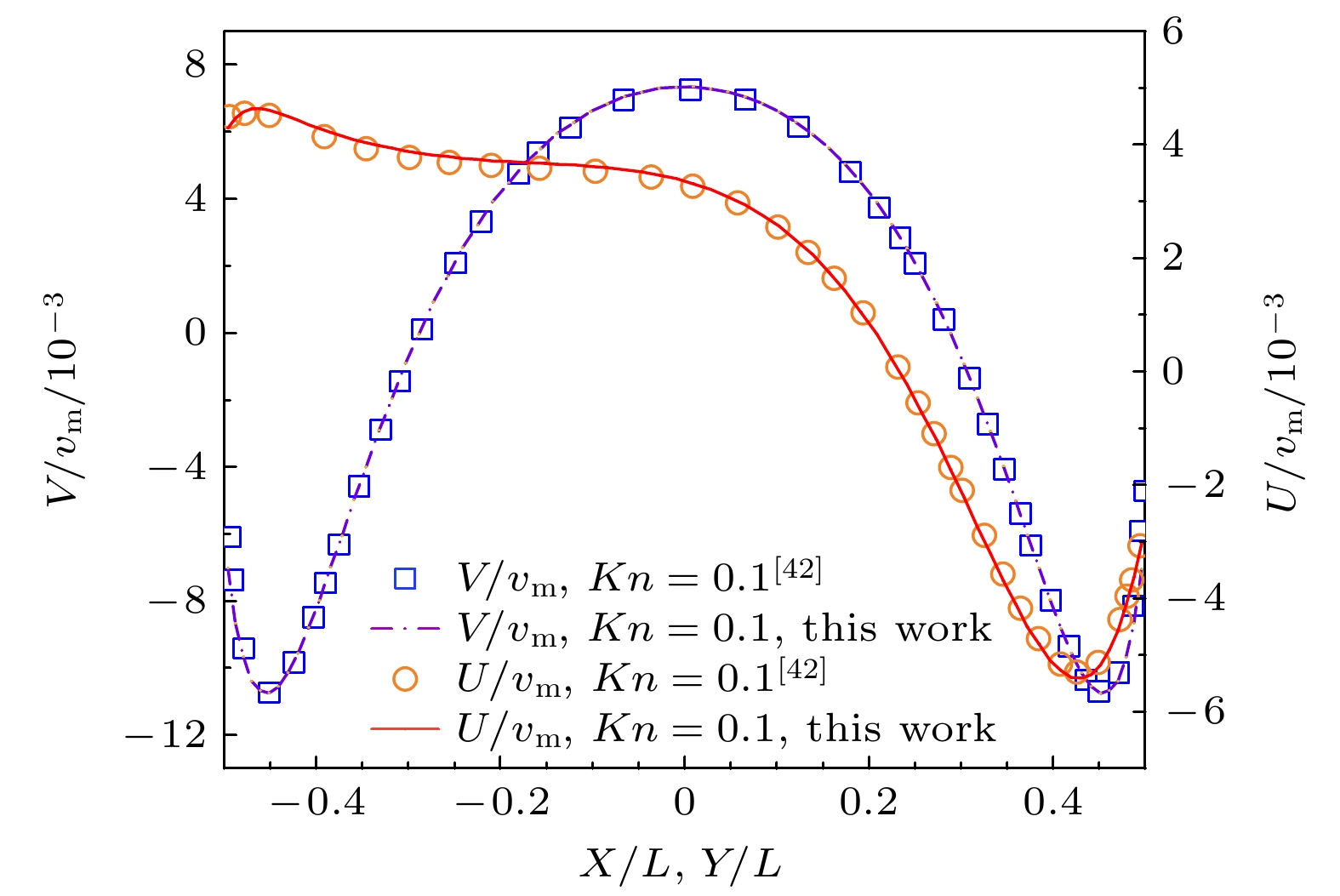
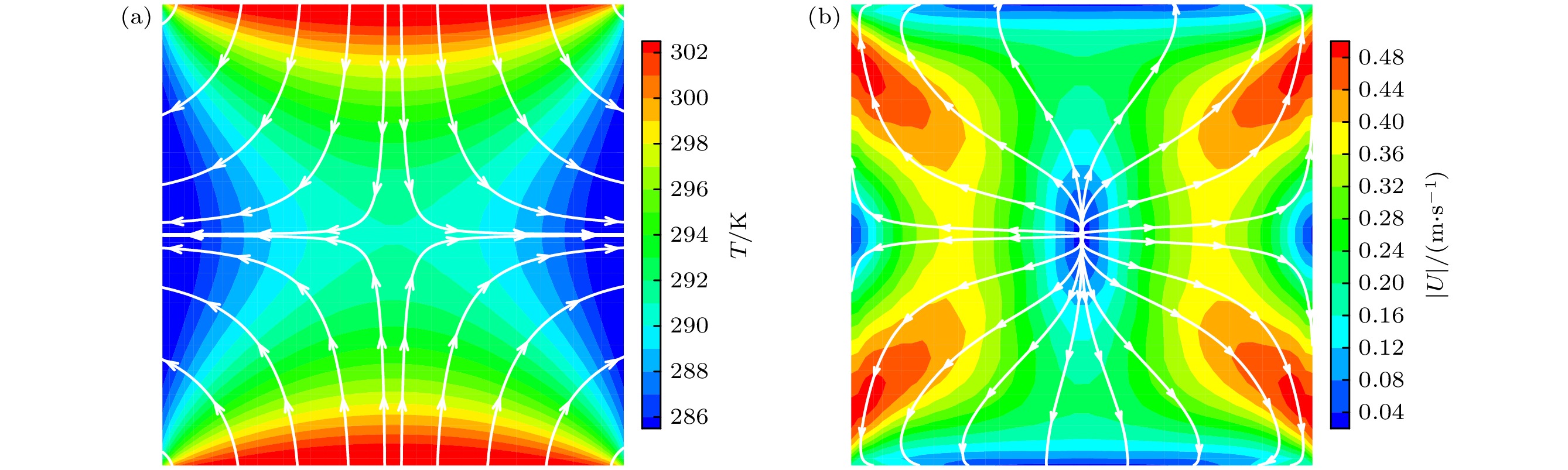
为验证数值方法的准确性, 本节考虑封闭方腔中由竖直壁面上温度线性分布引起的热蠕流动. 为了方便对比, 根据已有文献[42,43]将参数设置如下: 方腔边长L = 1 m; 上、下壁面温度之比为T_c/T_h = 0.1; 竖直侧壁温度与坐标$ y $有关, $ T\left(y\right)= {T}_{{\mathrm{h}}}-y({T}_{{\mathrm{h}}}-{T}_{{\mathrm{c}}}) $, 其中0 ≤$ y $≤ 1; 所有壁面均为Maxwell漫反射边界; 根据参考温度$ {T}_{{\mathrm{r}}{\mathrm{e}}{\mathrm{f}}}={T}_{{\mathrm{h}}} $的克努森数Kn = 0.1; 黏度-温度关系中根据硬球模型HS取$ \omega =0.5 $. 物理空间离散使用70 × 70的正交非均匀网格, CFL数设置为0.8, 速度空间采用57 × 57的均匀离散点集.

图2给出了稳态时方腔内温度云图和速度场流线. 从中可以发现, 竖直壁面上端温度低、下端温度高, 气体对壁面施加向上的作用力, 壁面对流体的反作用力向下, 从而导致气体在竖直壁面附近从上往下流动. 同时, 由于水平壁面的阻碍, 气体到达下壁面后将逐渐向上偏转, 最终在腔内形成两股大的回流区. 此外, 等温线及流线均关于腔体垂直中心线对称. 特别地, 除腔体中心部分的大涡旋外, 方腔左、右底角处出现了二级小涡. 上述定性现象与文献[42,43]报道的结果相一致. 图3进一步给出了通过左侧一级主涡中心的水平和竖直线上的无量纲速度分布, 可发现本文结果和Zhu等^[42]的结果吻合良好.

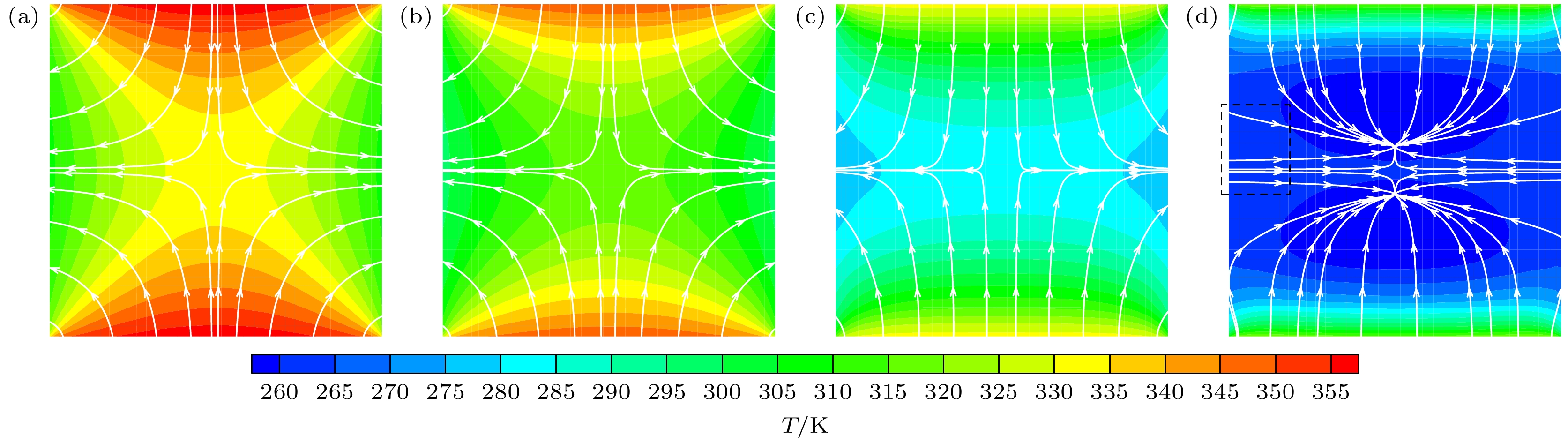
本节研究不同St下方腔内气体流动与传热特性的变化. 此时固定稀薄参数Kn = 1、振幅A_h = 0.5. 图4展示了t = 0时刻不同频率下方腔内的温度场和热流线. 可以看出, 温度场与热流线沿方腔中心线对称. 热流线由高温指向低温, 即常规傅里叶传热现象, 没有出现平板驱动时的反傅里叶热传递^[25–28]. 此外, 随着St增大, 气体T减小, 等温线弯曲程度减弱, 并有与变温的上下壁面呈平行的趋势, 而热流线由弯曲状态逐渐趋于竖直状态. 这是由于当St增大时, 上下壁面T到达最大值所需的时间减小, 热量传递时间缩减导致气体获得热量变少, T提升较小. 由于温度传播存在延时现象, St越大温度延时传播越突出. 当St < 5时, 热流线从上下壁面指向左右壁面. 当St = 5时, 左右壁面中心处附近的热流线出现反向现象, 表现为从壁面指向方腔内部. 这是因为热量未能及时传递到方腔中心, 气体温度还停留在上半周期的低温状态.

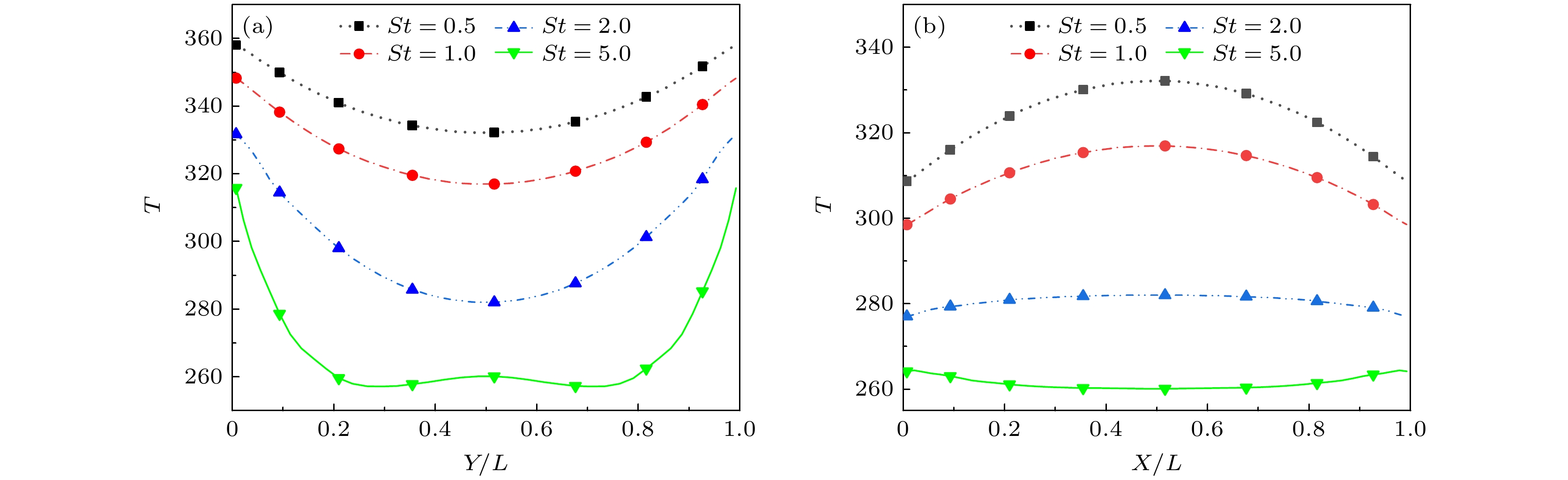
图5给出了t = 0时刻不同St情况下水平和竖直中心线上的温度T分布. 如图5所示, 竖直和水平中心线上T都关于方腔中心对称. 整体来说, 前者T中间低, 两侧高; 后者T中间高, 两侧低. 结合图4不难看出, 非中心的竖直和水平线上T分布也呈现出该趋势. 当St变大时, 竖直中心线上T降低, 且随St非线性变化. 同样, 水平中心线上T随St增大而减小. 特别地, 端点处流体与壁面的T不一致, 表明出现温度跳跃. 对于上下壁面中心, 温度跳跃现象随St增大而越显著, 且流体温度始终低于壁面温度; 而左右壁面中心处流体温度随St增大逐渐减小到低于壁面温度. 上述结果均是由于热量传递的迟滞效应造成的. 特别地, 当St = 5.0时, 竖直中心线中点处T略高于其附近温度, 水平中心线T则出现了中间低两端高的相反情形, 这一现象与图4中热量呈现四周向内传输的状态相符.

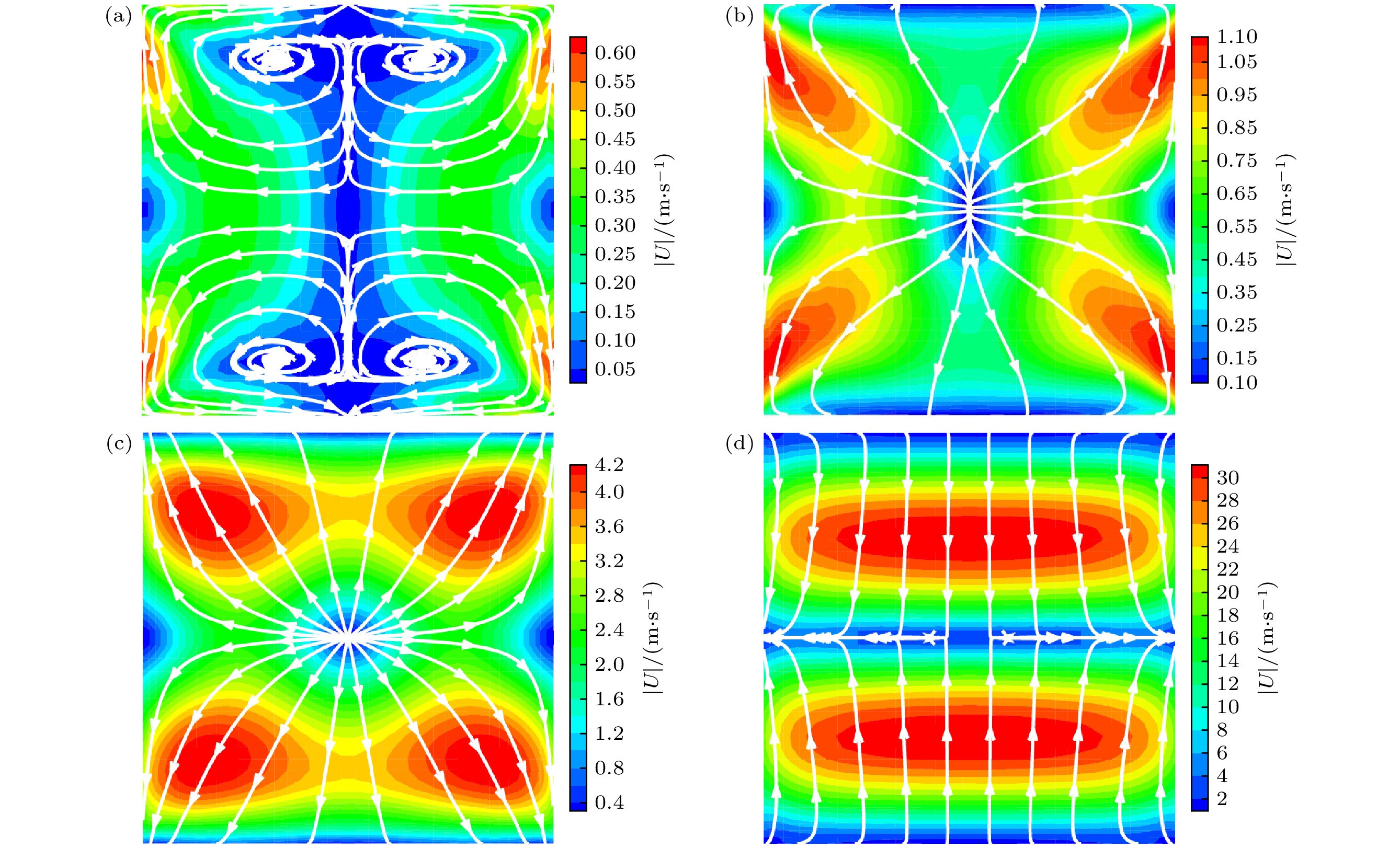
在本文边界条件下, 方腔内流场结构呈上下、左右对称, 如图6中给出的t = 0时刻不同St下速度场和流线所示. 可以看出, 方腔中心、左右壁面中心附近以及上下壁面处速度较小. 随着St增大, 腔内流体速度变大, 整体流动呈增强趋势, 但是水平方向流动逐渐减弱, 这可能是由于周期变短时气体需要更快回到初始状态, 使得流动速度加快. 当St = 0.5时, 气体的温差梯度较小, 热蠕运动较为平缓. 竖直中心线上壁面附近和水平中心线上中心处的气体T较高, 运动分别表现为由上下壁面流向方腔中心以及方腔中心流向左右壁面. 这样导致流体在1/4腔内循环而出现涡流. 当1 ≤ St ≤ 2时, 流线从方腔中心指向四周壁面. 这是因为上下壁面T较大, 而方腔中心处气体T较低, 稀薄气体的热膨胀效应造成气体由冷向热流动. 当St = 5.0时, 上下壁面附近气体T提升较慢, 腔内气体呈现温度分层现象, 流动表现为由上下壁面流向方腔中心.

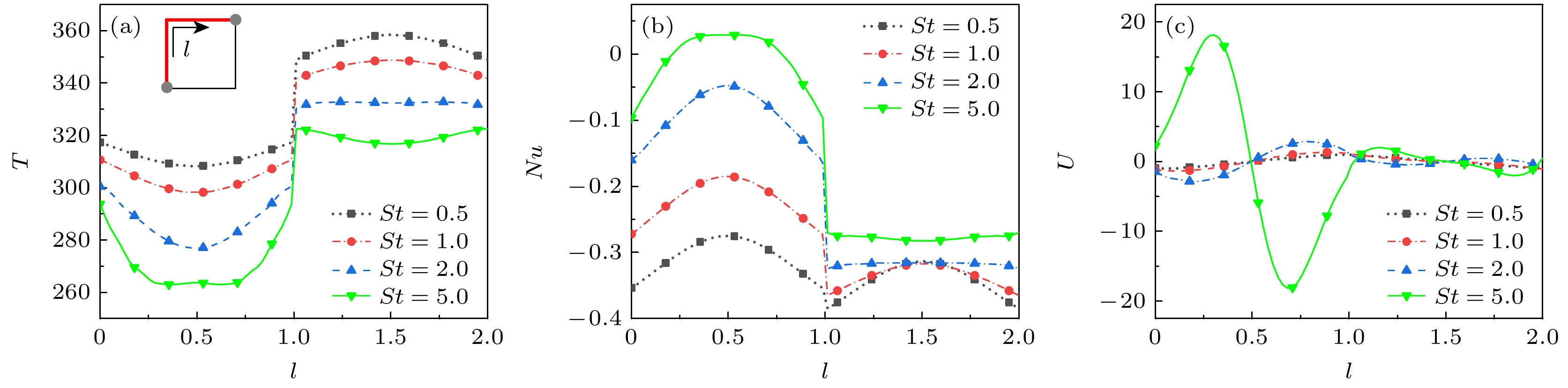
为进一步分析St对腔内流动传热强度的影响, 图7给出了t = 0时壁面处气体温度T、努塞尔数Nu和速度U的分布. 由于壁面满足不穿透条件, U为流体平行于壁面方向的速度. l为以左壁面 下角点为起点、顺时针沿左壁面向上壁面移动的 距离. 不难发现, T, Nu和U均与壁面中心呈对称或反对称分布. 左壁面中心处T取极小值, Nu与之相反. 对于上壁面, 最大T出现在中心处, Nu分布特征与T基本相同. 此外, 壁面中心处U为0, 中心两侧壁面各有一个极值, 这是由于U对称分布所致. 随着St的提高, 壁面处T单调递减, Nu和U则单调递增, 虽然热振荡加快时滑移速度增大, 但方腔中的热流线从弯曲趋于竖直, 温度分布变得平缓, 温差变小使得换热强度减小. 特别地, 当St = 5.0时, 左壁面中点附近Nu由负值转变为正值, 即传热表现为由左向右传递, 这与图4(d)中所展示的温度云图对应. 上壁面中心处T由最小变为最大; U会由负变正且急剧增大, 这是延时现象的表现.

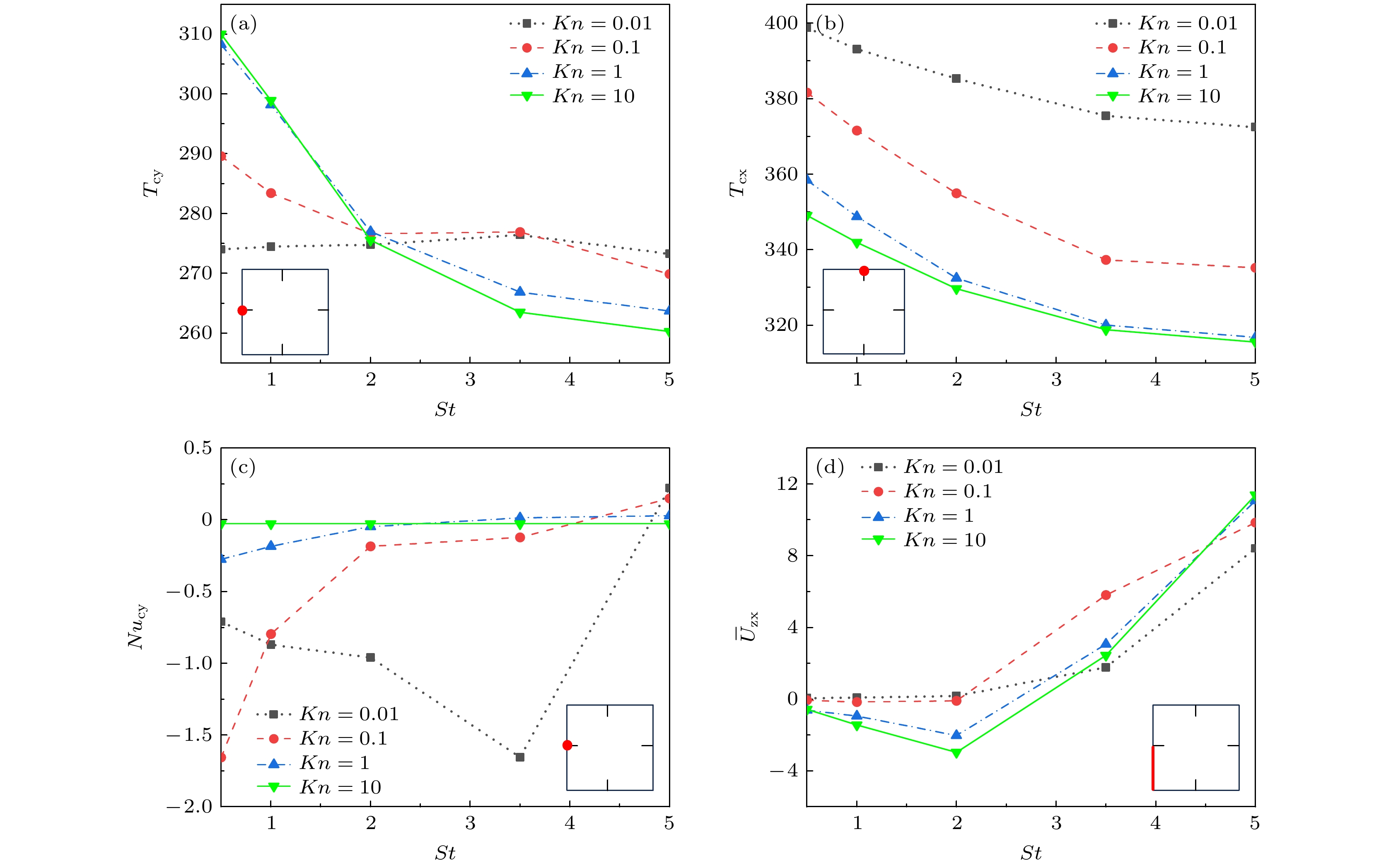
从图7中发现壁面中点附近参数随St有明显变化, 故进一步研究壁面中点处参数随St的变化情况. 图8展示了不同St和Kn下, 左、上壁面中点温度T_cy、T_cx、左壁面中点努塞尔数Nu_cy和左下半壁面平均速度$ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $. 从图8(a)—(c)可以发现, 当St增大时, T_cy和T_cx减小, Nu_cy则反之, 且均随St非线性变化, 其中温度的变化与图5中分析的结果相符. 固定St时, 增大Kn均会减小T_cx和Nu_cy, 这是由于气体变稀薄其传热能力变小所致. 特别地, 当Kn = 0.01时, 气体在接近连续流区域的传热能力较强, 气体受热量传递的迟滞效应影响较小, 致使T_cy受St的影响不大, 且Nu_cy随St的变化转为先减小到21.65附近, 再急剧升高. 在图8(d)可以看出, 随着St的提高, $ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $先略微降低, 随后在St > 2之后急剧猛增. 当固定St时, 增大Kn会增大$ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $, 这是由于气体变稀薄后, 热蠕流动增强所致.

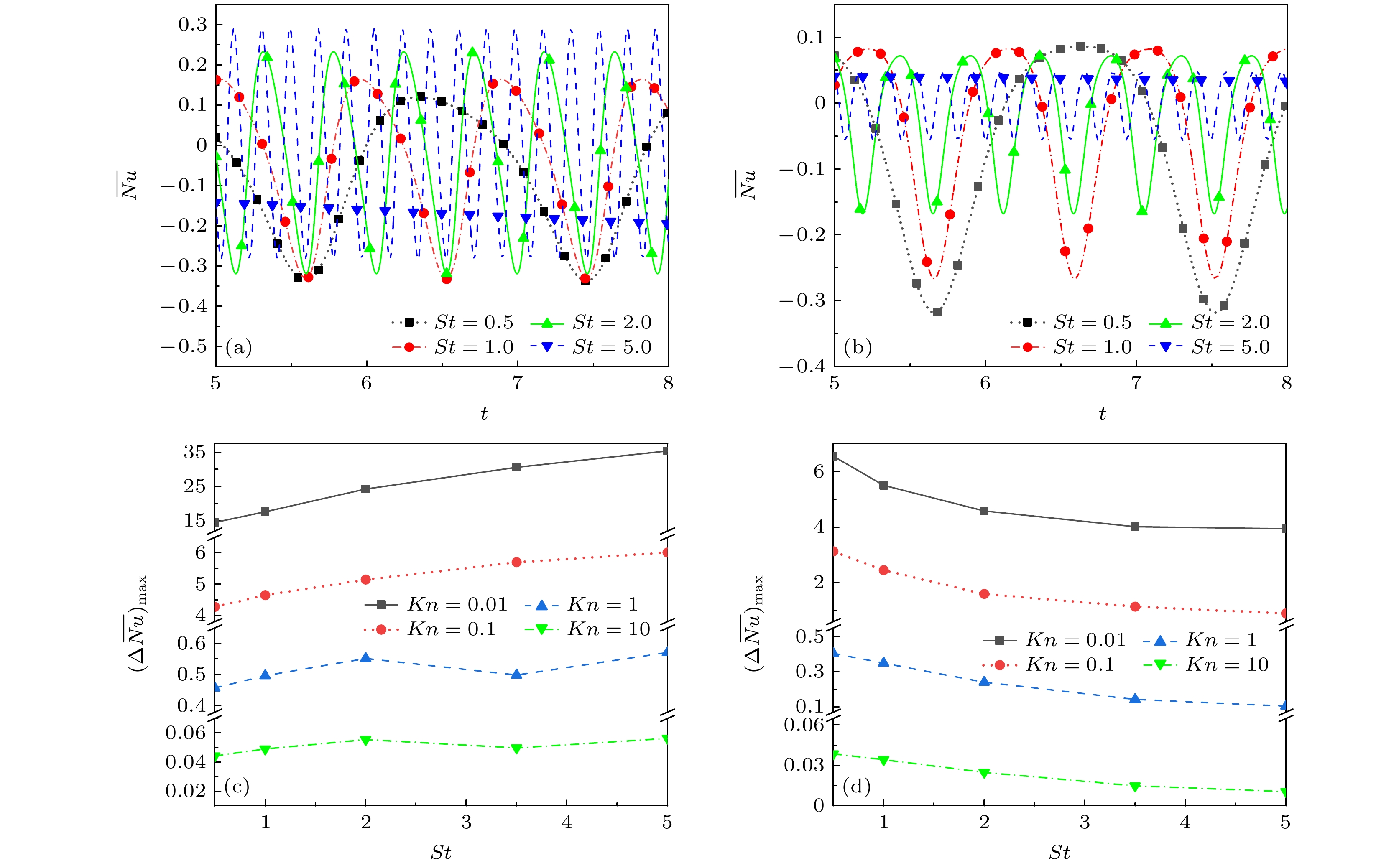
方腔内部气体与壁面间的传热强度可以用Nu来衡量. 图9给出不同St的左、下壁面平均努塞尔数$\overline{Nu} $随时间t的历程及$\overline{Nu} $的极差$ {\left(\Delta\overline{Nu}\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $. 从图9可以看出, 在不同的St下, $\overline{Nu} $的极小值均在同一时刻出现, 此刻腔内气体与壁面的换热能力最强, 且一个周期内只出现一次. 特别地, 下壁面$\overline{Nu} $的极小值均在–0.3附近. 当St增大时, 下壁面$\overline{Nu} $的峰值变大, 左壁面则反之, 这是热量传递迟滞效应的表现. 随着St增加下壁面$ {\left(\Delta\overline{Nu}\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $单调递增, 左壁面则相反. 固定St时, 随着Kn增大, 左、下壁面的$ {\left(\Delta\overline{Nu}\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $单调递减, 且当Kn增大到10时, $ {\left(\Delta\overline{Nu}\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $几乎为0, 这是因为气体之间的传热是由气体分子之间碰撞传递的, Kn增大时, 气体之间的碰撞频率降低, 换热能力下降造成的.

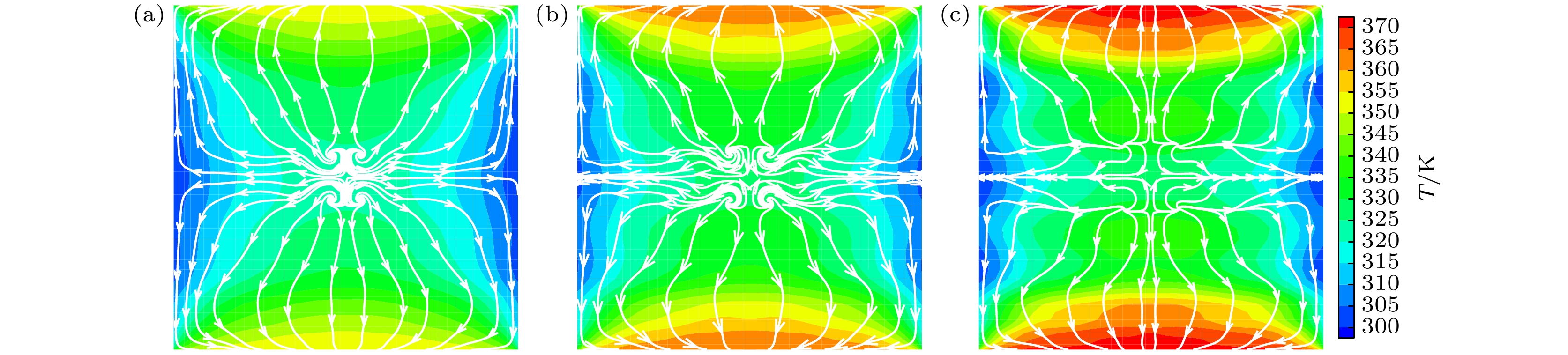
本节研究不同变温振幅A_h影响下方腔内气体流动与传热特性. 此时方腔内稀薄参数和变温频率分别固定为Kn = 1和St = 1.0. 图10展示了变温振幅A_h = 0.2, t = 0时方腔内温度场和热流线、速度场和流线的分布. 可以看出, 温度场与热流线、速度场与流线均沿方腔中心线对称. 与图4和图6的现象相似, 热流线由高温指向低温, 流线从方腔中心指向四周壁面. 方腔中心、左右壁面中心附近以及上下壁面处速度较小, 这是由于该处温差梯度较小使得热蠕流动较弱导致的. 由于A_h增大时, 腔内T和U均增大, 但是其结构基本不变, 因此这里仅给出A_h = 0.2时的情形.

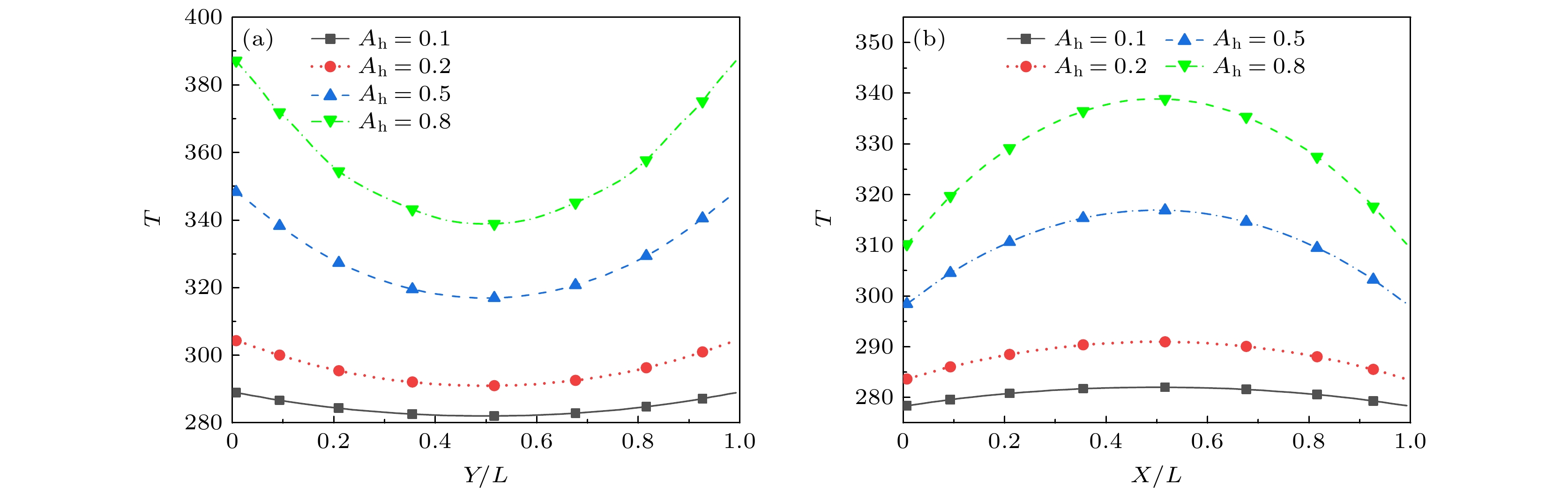
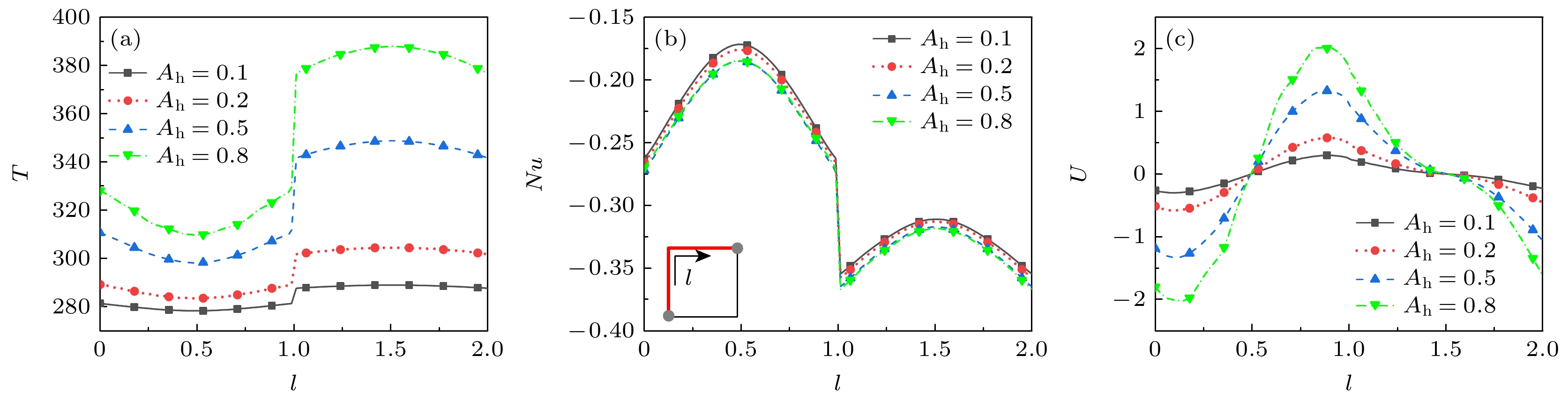
图11给出了t = 0时刻不同A_h下竖直和水平中心线上的温度分布. 如图所示, 竖直和水平中心线上T都关于方腔中心对称. 前者T中间低, 两边高, 后者T中间高, 两侧低. 随着A_h的提高, 中心线上T均单调递增, 且温度梯度变大. 特别地, 端点处气体与壁面T不一致, 表现出温度跳跃. 上下壁面中心的流体温度始终低于壁面温度, 左右壁面则相反, 这是热量传递迟滞效应的表现. 图12给出了t = 0时不同振幅A_h的壁面处气体温度T、努塞尔数Nu和速度U的分布. 可以看出, T, Nu和U均与壁面中心呈对称或反对称分布. 左壁面中心处T有极小值, 上壁面T为极大值. Nu极大值均出现在壁面中心处, 这是因为在壁面中心附近气体滑移速度较小, 热运动减弱使得换热能力下降. 速度最值出现在左壁面距中点约3/5处, 壁面中心处速度均为0. 随着A_h的提高, 壁面附近气体T和U单调递增, 而Nu有所减小.

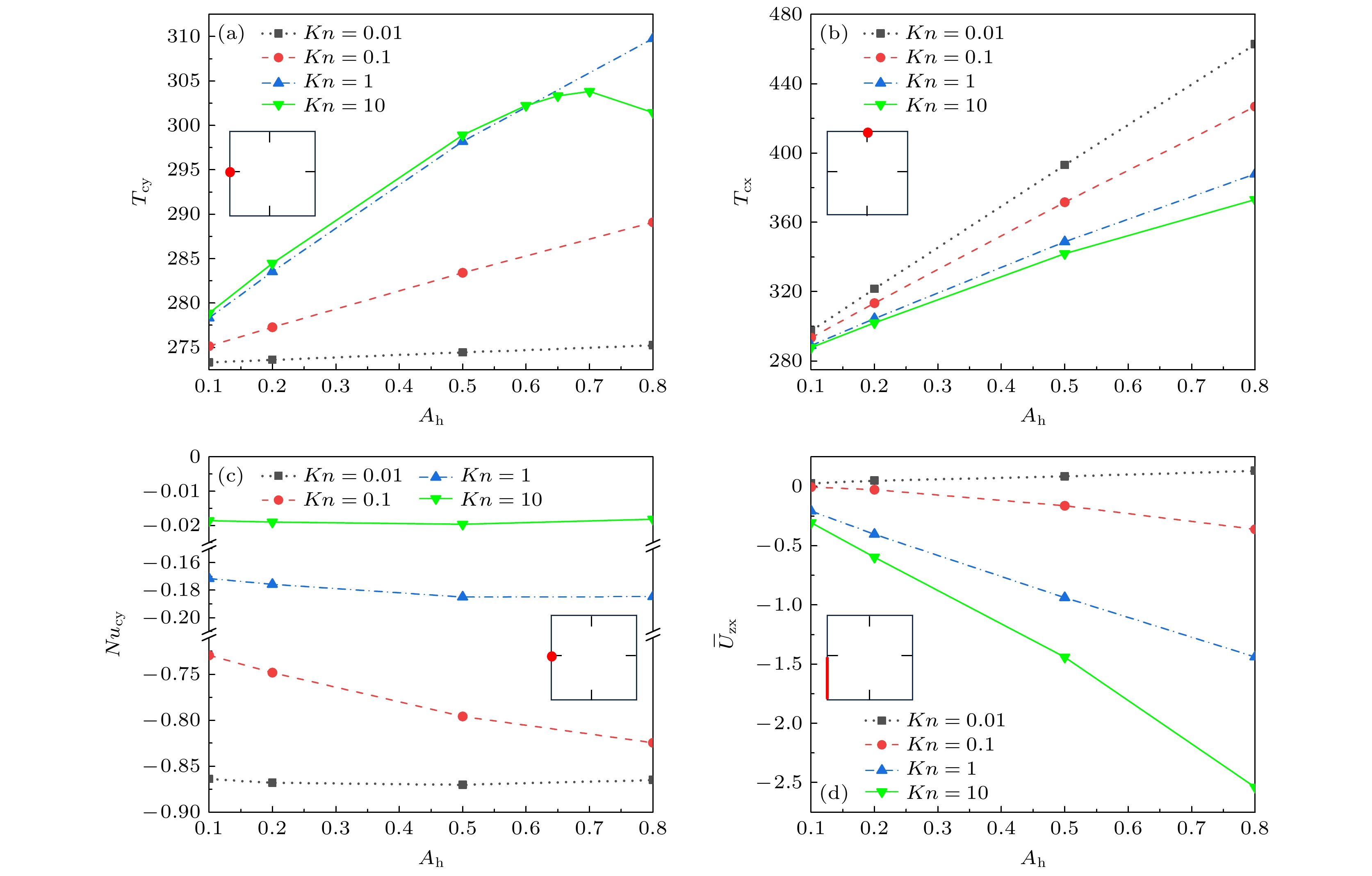
图13展示了不同A_h和Kn下, 左、上壁面中点温度T_cy、T_cx、左壁面中点努塞尔数Nu_cy和左下半壁面平局速度$ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $. 从图13中可以看出, 当A_h增大时, T_cy和T_cx呈现出线性递增, $ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $和Nu_cy则与之相反. 固定St时, 增加Kn会增大T_cy和$ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $并且减小T_cx和Nu_cy. 这是由于Kn变大时, 气体变稀薄使得自身传热能力下降, 故Nu_cy减小, 上壁面中点处气体传递热量的减小使其温度变低; Kn增大的同时, 气体的热蠕流动增强, 壁面处气体滑移速度增大, 由上、下壁面捕捉又释放出来的气体分子能够快速地传递到左壁面, 致使T_cy提高. 特别地, 当Kn = 10时, A_h超过一定值后T_cy的增大速率变小. 这里进一步给出了A_h = 0.6, 0.7和0.8时的结果. 可以看到, 随着A_h的增大T_cy先增大后减小, 并在A_h = 0.7附近出现极值. 为了解释这一现象, 图14中展示了相应的腔内温度场和流线. 壁面温变振幅A_h增大使得腔内气体温度增大. 但是同时, 水平壁面和垂直壁面间的温差增大、热蠕流动增强, 加之当Kn = 10时壁面滑移速度增大, 使得来自上、下壁面的高温气体被迅速带走, 而来自上半周期的低温气体开始集中于壁面中点处. 最终, 热蠕流与滑移流增强导致流体温度降低要更显著, 使得左壁面中点温度开始降低.

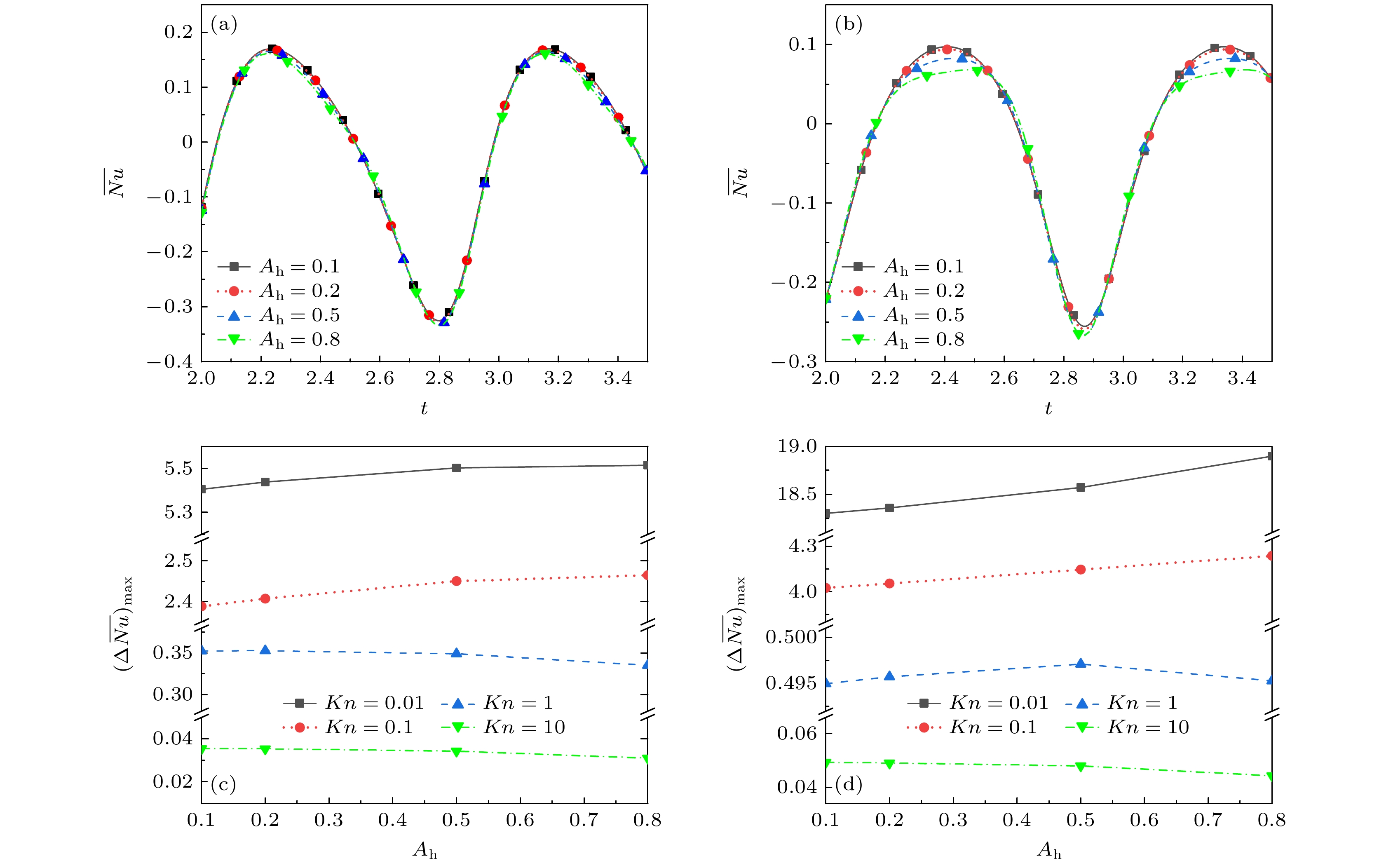
为了清楚地展示方腔内传热强度的变化, 图15给出了不同频率时左、下壁面平均努塞尔数$\overline{Nu}{\mathrm{的}} $时间历程及$\overline{Nu} $的极差$ {(\Delta\overline{Nu})}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $. 不难看出, 在不同的A_h下, $\overline{Nu} $的极值均在同一时刻出现. 随着A_h的提高, 同一时刻的$\overline{Nu} $变化甚微, 只有下壁面$\overline{Nu} $的极值略有减小, 这是因为振幅的提高使温差梯度和换热量呈倍数的提高, 但是方腔内的热流线和流线结构不发生改变, 气体在同样的换热形式下热对流强度理应相同. 从$ {(\Delta\overline{Nu})}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $随A_h的变化中也能发现, 随着A_h的改变$ {(\Delta\overline{Nu})}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $仅有微小的变化, 最大不超过5%, 可见A_h与$\overline{Nu} $没有一般依赖关系. 固定A_h时, 随着Kn增大, $ {(\Delta\overline{Nu})}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $单调递减. 特别地, 当Kn = 10时, $ \Delta N{u}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $几乎为0, 这是因为在自由分子流域, 气体分子之间接触频率较小, 热量难以依靠碰撞传递.

本文采用DUGKS方法对变温壁驱动方腔内热蠕流动过程进行了数值模拟, 探讨了变温频率和变温振幅改变对不同稀薄程度气体的流动传热特性的影响, 得出如下结论.

1) 壁面温度周期变化时, 方腔内气体流动与传热特性也随之呈现周期性变化. 但是与运动壁面驱动情况相比, 在本文研究的参数范围内未观察到反傅里叶传热现象.

2) 在振荡壁温的驱动下, 方腔内的温度场存在迟滞变化现象. 增加St将使迟滞现象更突出, 温度跳跃越大. 由于热流线表现为由热壁面流向冷壁面即常规傅里叶传热, 壁面上的温度变化与中心线上温度变化相一致, 竖直壁为中间低两边高, 水平壁则与之相反.

3) 通过提高振荡频率可以减弱壁面上的热对流强度, 且热流线从弯曲趋于竖直. 特别地, 当St = 5时方腔中心温度停留在上一周期的低温状态中, 左右壁面中点附近热流线出现反向现象, 表现为从壁面指向方腔内部.

4) St较小时, 腔内流动较为平缓, 且流动出现涡状结构. 随着St的增大, 方腔内的热蠕流动增强, 且壁面上的滑移速度增大, 但是由于迟滞现象使等温线趋于水平, 导致流动趋于平缓, 逐渐变为由上下壁面流向方腔中心.

5) 增大A_h可增强方腔内热蠕流动强度, 但是A_h的改变基本不影响方腔内的流场结构. 随着A_h增大, 腔内气体温度升高, 壁面附近温度跳跃现象越突出, 且Nu存在小幅减小.