首页
登录
注册
下载:
-
流注放电(streamer discharge)是快速发展的电离通道, 也是闪电传播预电离、高压输变线路长间隙放电的重要初始阶段[1]. 大气压条件下, 流注放电过程中可产生大量活性种, 从而在臭氧生成[2-5]、材料改性[6,7]及杀菌消毒[8,9]等领域得到广泛应用. 根据目标产物不同(如臭氧、活性态OH等), 往往在流注放电间隙中输送不同氧浓度的氮氧混合气体[10].
流注传播过程分为两个阶段: 流注从一侧电极形成后至接触另一侧电极为止的一次流注阶段(primary streamer), 一次流注接触另一侧电极后沿其路径再次发展电离的二次流注(secondary streamer)阶段[11]. 一次流注阶段流注头部电场强(约500 Td, 1 Td = 10–17 V·cm2), 发展速度快(约
$10^6\rm\, mm/ns $ ), 但持续时间短($ <50\rm\, ns $ ); 二次流注阶段通道电场较低(约100 Td), 但持续时间较长(约1 μs), 因此二次流注阶段是大部分目标产物(如臭氧等)的主要生成阶段[12]. 不同设备中, 二次流注放电特性与产物产量随氧浓度变化有较大差异[13], 研究氧浓度对二次流注的放电特性与目标产物产量影响机制具有意义.Meek[14]与Raether[15]指出, 均匀场的击穿过程是电子雪崩转化为自传播流注的过程, 其依赖于气体中的电子碰撞与光电离. 基于此, Sigmoid[16]提出二次流注本质上是由于一次流注残留通道中电子Douglas-Hamilton-Mani型附着不稳定性形成的一个或多个高场区域. 为进一步观察二次流注形成与传播过程, Ono和Oda[13]使用增强型CCD相机拍摄了针板电极正二次流注放电, 观察到二次流注形成于一次流注到达阴极后, 并沿一次流注通道向阴极方向发展, 通道长度与施加电压大致成正比. 然而, 由于流注放电过程的不稳定性, 易受紫外光、电磁波等外界因素影响, 目前对流注放电特性的测量手段仍大多局限于光学手段[17], 难以精确测量流注放电的电场、电子密度等参数及其分布.
为更进一步研究二次流注的传播特性, Eichwald等[18]在Naidis等[19]和Zhelezniak等[20]的一次流注模型基础上, 对电极采用Neumann电子流边界条件模拟二次电子源, 成功计算了二次流注的放电过程, 并与实验结果取得较好的一致性[18]. 基于此, Ono等[21]与Komuro等[22,23]在模型中加入了激发、淬灭等110余个化学反应过程, 模拟了大气压条件下二次流注过程中
$ \rm N_2(C) $ ,$ \rm N(^4 S) $ ,$ \rm O(^3 P) $ 等激发态粒子(活性种)产物的分布, 分析了针电极施加电压峰值、上升率对产物产率的影响, 并将计算出的产物分布与实际实验结果比较, 计算出的二次流注放电过程产物分布与实际测量分布较相近, 表明基于Neumann边界条件的流体模型可计算大气条件下二次流注过程中活性种的分布特性.国内外虽针对二次流注放电特性已进行了较多研究, 但局限于空气组分下的流注电场、电子密度等参数的分布, 对于不同氧浓度对目标产物生成参数的相关影响机制仍不清楚. 相同气压条件下,
$ \rm O_2 $ 分子相较于$ \rm N_2 $ 分子的碰撞电离速率常数高约50%, 同时伴随强烈的二、三体吸附效应, 对二次流注产物生成过程具有显著影响. 为此, 开发了可计算不同氧浓度氮氧混合气体中二次正流注过程的流体模型, 通过比较实验与模型中获得的20%—90%氧浓度下二次流注放电过程中阴极转移电荷量、发光强度, 验证了模型的准确性. 基于建立的数值模型, 计算了臭氧中间产物激发态氧原子$ \rm O(^3 P) $ 密度的分布, 认识了氧浓度对$ \rm O(^3 P) $ 产率的影响机制, 讨论了不同氧浓度下激发态氧原子$ \rm O(^3 P) $ 的产生与湮灭过程. -
本文采用耦合漂移-扩散方程与泊松方程的等离子体流体模型, 并使用本课题组开发的有限体积法算法进行求解[24], 控制方程如下:
其中,
$ n_s, \, v_s(E/N), \, S_s(E/N), \, \mu_s(E/N) $ 分别表示各粒子密度、移动速度、源项与迁移率, 下标$ s= {\mathrm{e, p, n}} $ 分别代表电子、正离子与负离子;$ E/N $ 表示换算电场,$ \varepsilon_0 $ 表示真空中的介电常数, e表示元电荷绝对值. 化学源项包含电子碰撞反应、二、三体吸附反应、激发反应与淬灭反应等多种反应类型, 反应速率常数基于Phelps数据库[25]通过求解Boltzmann方程获得[26], 包含110个化学反应, 具体反应列表与文献[12, 24]相同. 光电离源项$ S_{{\mathrm{ph}}} $ 基于文献[24, 27]提出的积分方法计算, 但使用本课题组开发的包含氧光子诱导光电离的数值模型. -
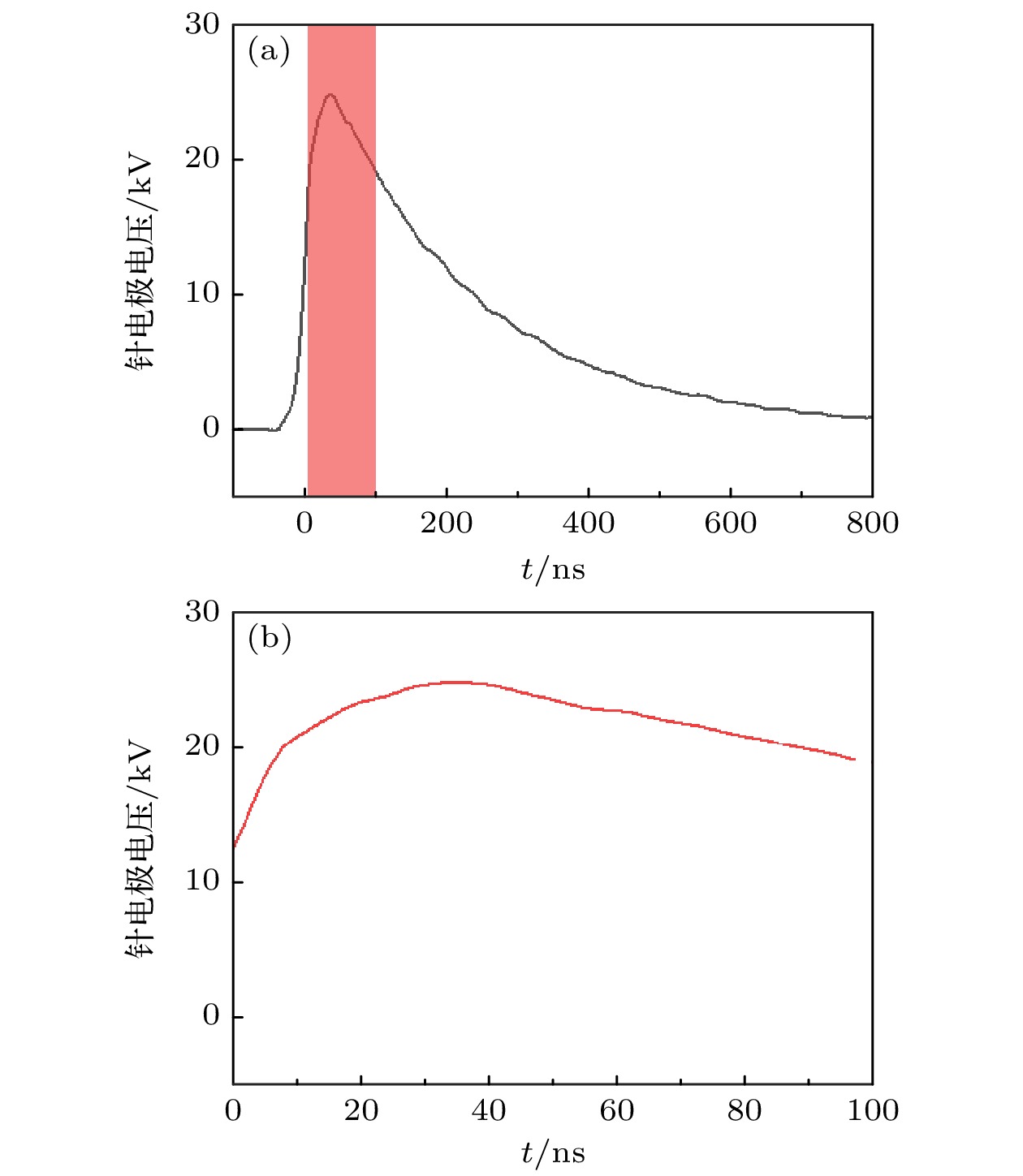
模型涉及正负粒子流与泊松电场两类边界条件: 针电极正离子通量设置为0, 负离子与电子通量采用Neumann边界, 边界施加实验中获得的实际电压波形
$ V(t) $ 如图1所示, 其极性为正, 因此模拟出的流注均为正流注; 板电极边界正负离子与电子通量均使用Neumann边界, 电压设置为0 (接地). 初始时刻使用均匀低密度背景电子$ n_{\mathrm{e}}= 1 \times 10^6\rm\, cm^{-3} $ , 正离子密度$ n_{\rm O_2^+}=n_{\rm N_2^+}=0.5 n_{\mathrm{e}} $ . -
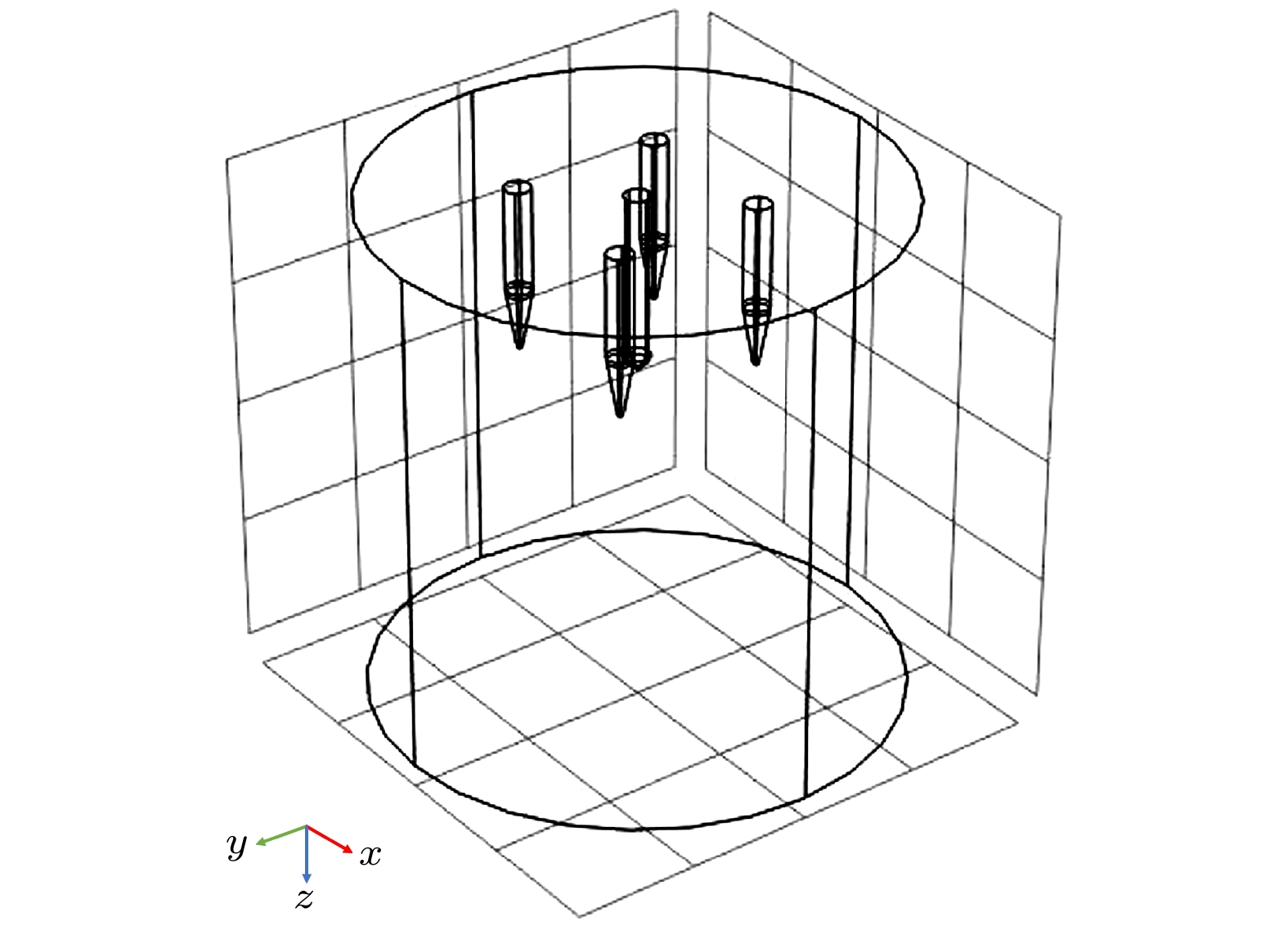
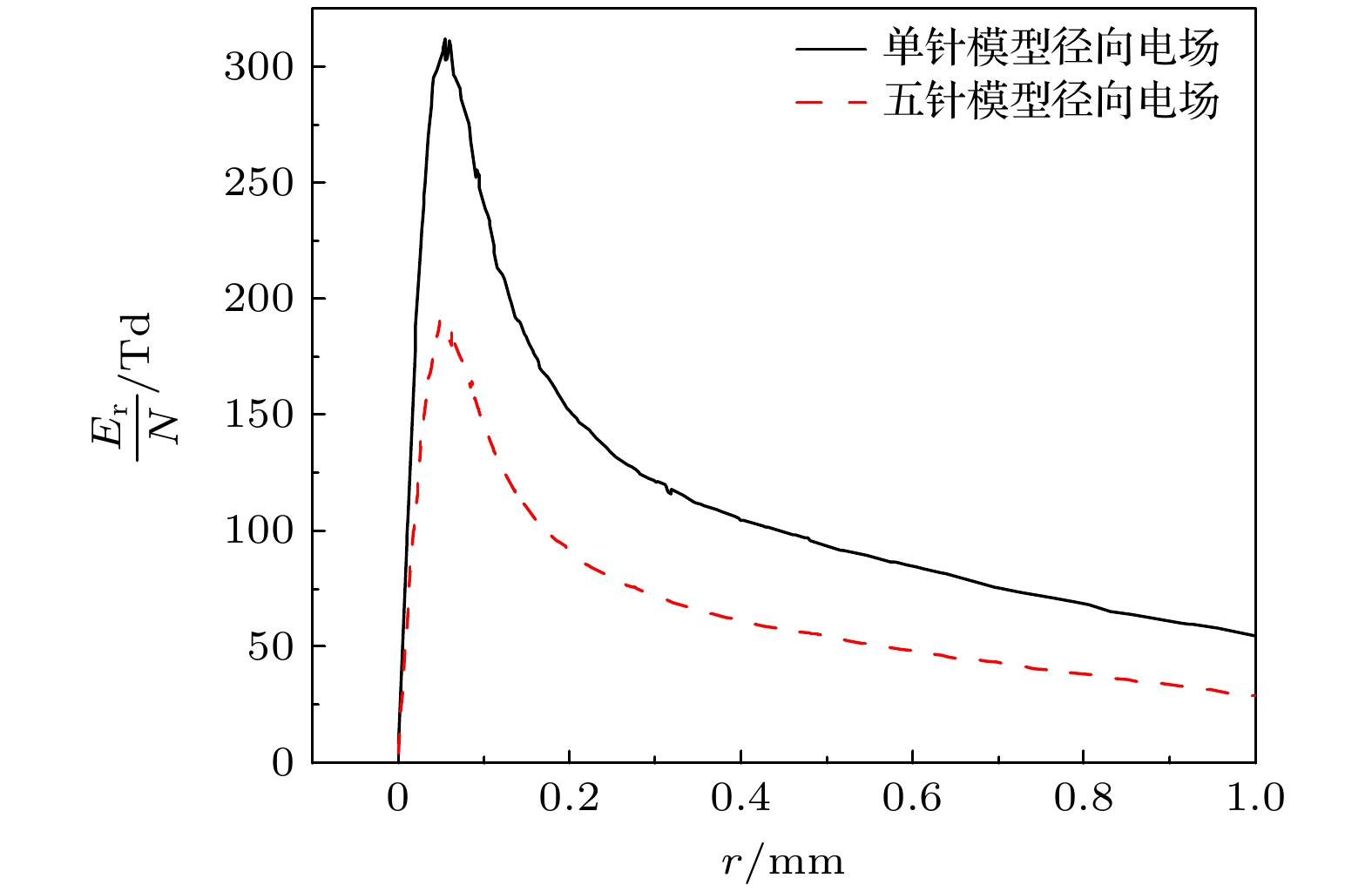
根据已有研究, 高氧浓度下模型针电极附近易出现非物理分支现象, 造成模型收敛性下降并致使计算终止, 影响平板电流与转移电荷的计算[12,23]. 非物理分支形成的主要原因为: 二维轴对称数值模型中未包含实验中主针电极周围的环绕针电极及其产生的细小流注放电通道, 计算出的背景径向电场未考虑环绕电极及流注抑制效应, 导致流注向两侧扩展. 因此, 为抑制针附近的非物理分支, 有必要量化环绕针电极对径向电场的影响. 使用多物理场仿真软件COMSOL, 建立包含环绕针电极的三维静电场模型如图2所示, 针尖z = 0 mm处的径向电场分布与忽略环绕针电极的分布对比如图3所示. 计算结果表明, 存在环绕电极情况下, 径向电场强度约为单针情况下径向电场的55%. 因此, 计算背景针电极电场时, 对单针背景电场
$ {\mathit{\boldsymbol{E}}}_{\mathrm{L }}$ 按(6)式—(8)式校正:其中,
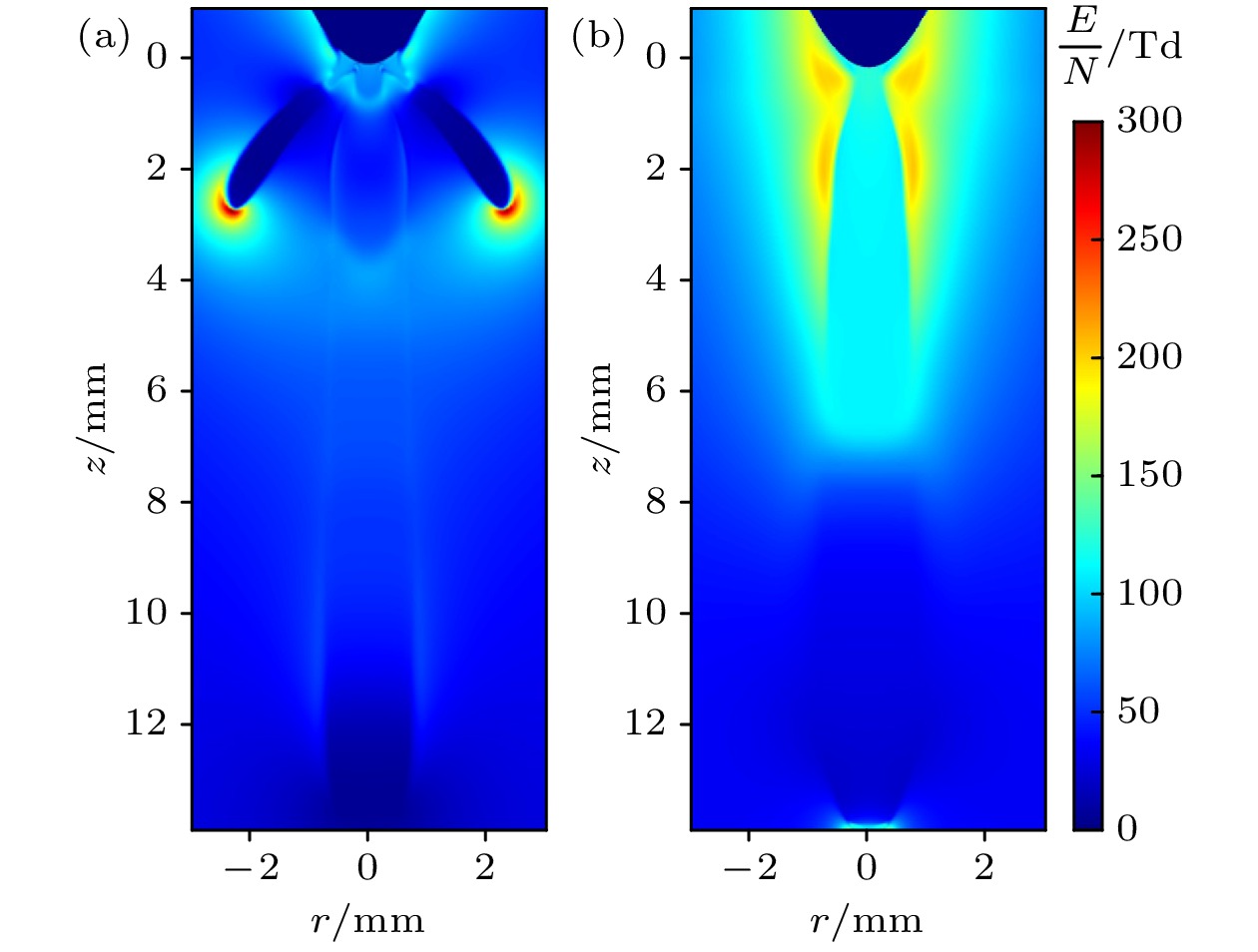
$ k_{{\mathrm{mod}}} $ 表示径向电场校正系数(在本文中取0.55).$ E_{{\mathrm{L}}r, {\mathrm{mod}}} $ ,$ E_{{\mathrm{L}}z, {\mathrm{mod}}} $ 表示校正后的针电极径向与轴向背景电场,$ E_{{\mathrm{L}}r, {\mathrm{ori}}} $ 与$ E_{{\mathrm{L}}z, {\mathrm{ori}}} $ 表示校正前单针电极的径向与轴向电场,$ S(x) $ 表示Sigmoid函数, 用于平滑修正与未修正区域过渡处的微分, 避免电场值突变造成数值发散.电场校正前后得到的流注模拟结果如图4所示, 可见本文开发的径向电场抑制方法可以有效抑制针电极附近非物理分支的形成, 计算出的二次流注更接近实验中获得的真实流注形态.
-
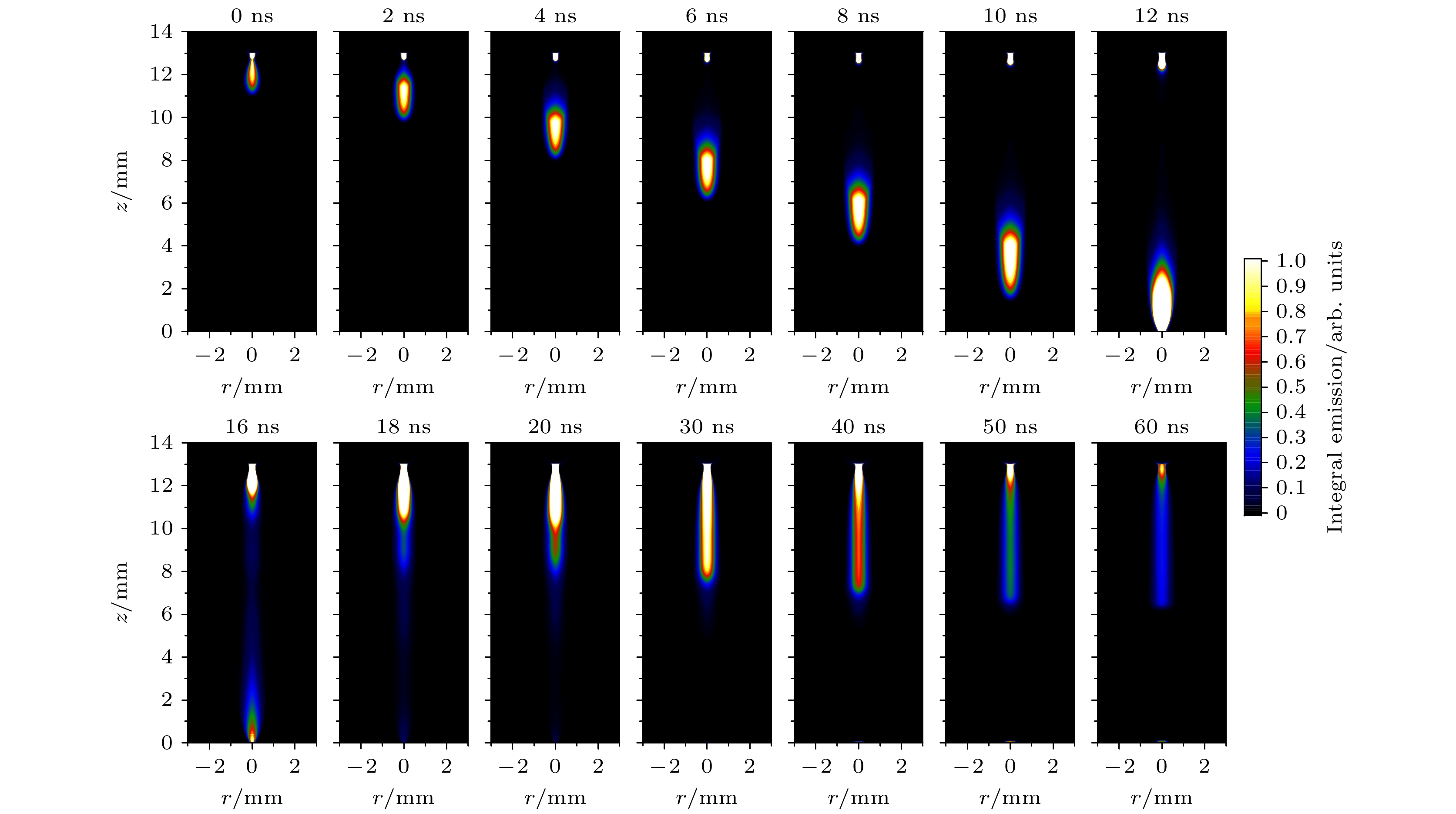
目前等离子体的主要光学观测手段依赖于增强型CCD相机(ICCD)捕获流注发展过程中产生的光子, 获得流注发光强度的分布. 对比流注通道ICCD发光图像的计算与实验结果, 对模型结果进行验证. 使用Abel积分对空气条件下0—60 ns发展过程中流注通道ICCD发光图像进行复现(具体积分方法将在3.2节介绍). 如图5所示, 修正模型计算的流注放电并未出现非物理分支现象, 一次流注约在12 ns发展值平板阴极; 二次流注产生于针电极附近, 并沿一次流注放电通道向阴极延伸, 通道直径约为0.55 mm, 长度约为8 mm, 与图6所示实验结果[4]一致.
-
氮氧混合气体中, 氧浓度变化将显著改变混合气体的碰撞截面, 从而影响流注发展特性. Komuro等[4]提供了不同氧浓度下流注电流波形参数, 使用电流线圈(Pearson, P2877, 200 MHz)测得, 时间分辨率2 ns. 本文使用0.125 ps的时间步长以提升收敛性, 若直接比较计算与测量获得电流波形, 可能由于时间分辨率的不同出现采样点偏差.
为尽可能消除时间分辨率差异的影响, 本文通过对平板电流波形
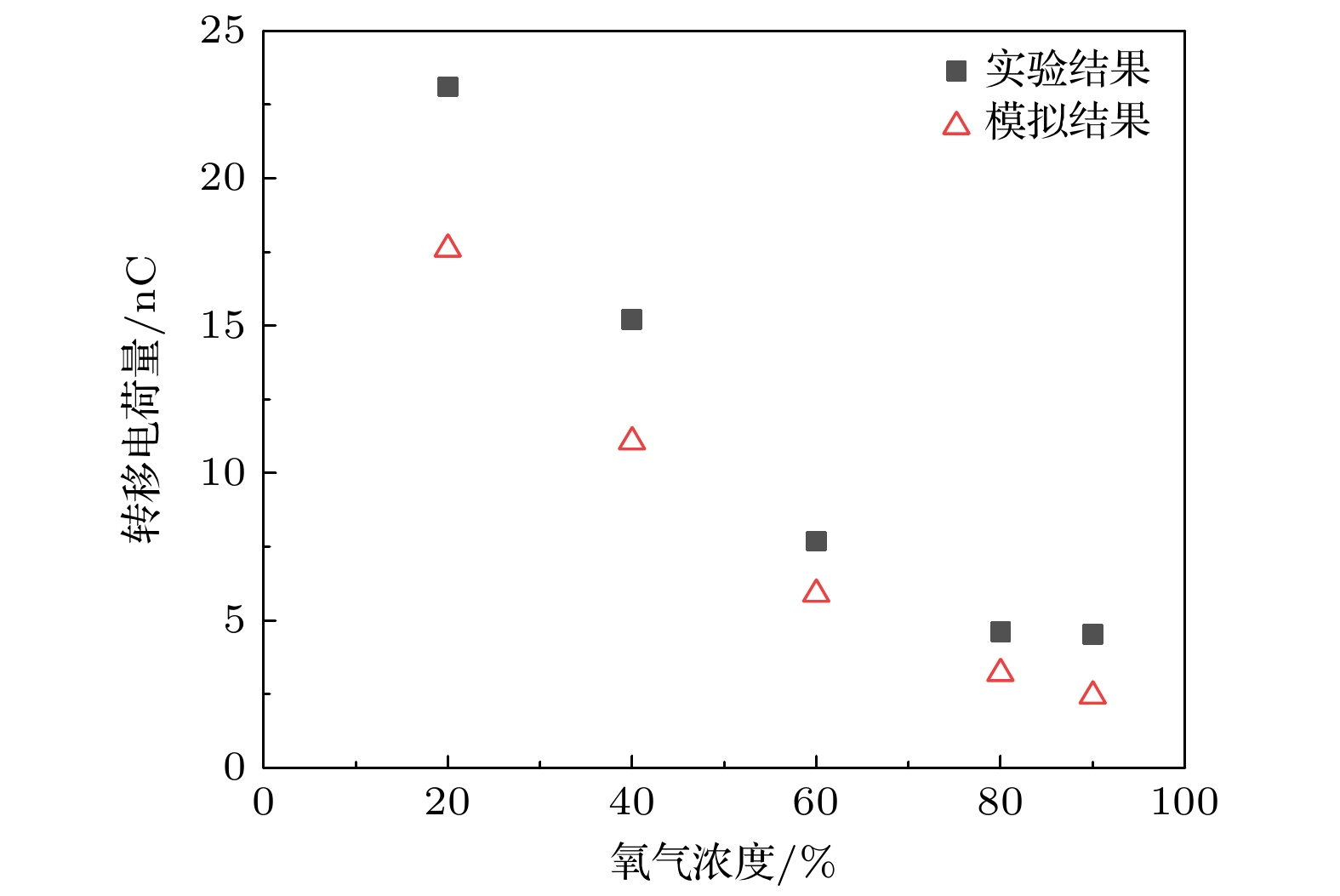
$ I_{\mathrm{p}}(t) $ 进行时间积分, 计算二次流注放电过程中转移至阴极的电荷量, 通过对比实验与仿真获得的阴极转移电荷量, 验证模型的有效性. 其中积分时间选择0—100 ns, 此时不同浓度下电流值已下降至峰值的1%左右. 通过计算与实验电流波形得到的不同氧浓度下的转移电荷量对比如图7所示, 可见, 模型与实验结果拟合较好, 平均误差在15%以内, 进一步证明了模型的有效性. 氧浓度上升时, 模型与测量获得的阴极转移电荷量均出现下降: 相比于空气条件, 90%氧浓度条件下转移电荷量下降约80%, 这是由于氧浓度上升时, 二、三体吸附作用增强, 导致电子密度下降, 转移电荷量降低. -
流注放电发展过程中, 间隙中大量自由基反应产生光子, 使用ICCD相机等光学观测手段可对其进行捕捉, 获得流注通道在时间和空间上的变化. 将捕获的光子在0—100 ns时间内进行积分, 可获得不同氧浓度下二次流注过程的发光特性[4]. 在本文建立的数值模型中, 通过计算
$ \rm N_2/O_2 $ 混合气体主要发光产物$ \rm N_2(C) $ 的生成与湮灭过程, 可获得不同氧浓度下不同时刻$ \rm N_2(C) $ 的密度分布, 并通过Abel积分复现实验中ICCD拍摄的流注发光图片. 将实验与模拟所得进行对比, 进一步验证模型的正确性.流注放电过程中的发光强度与
$ \rm N_2(C) $ 密度成正比[12], 即其中
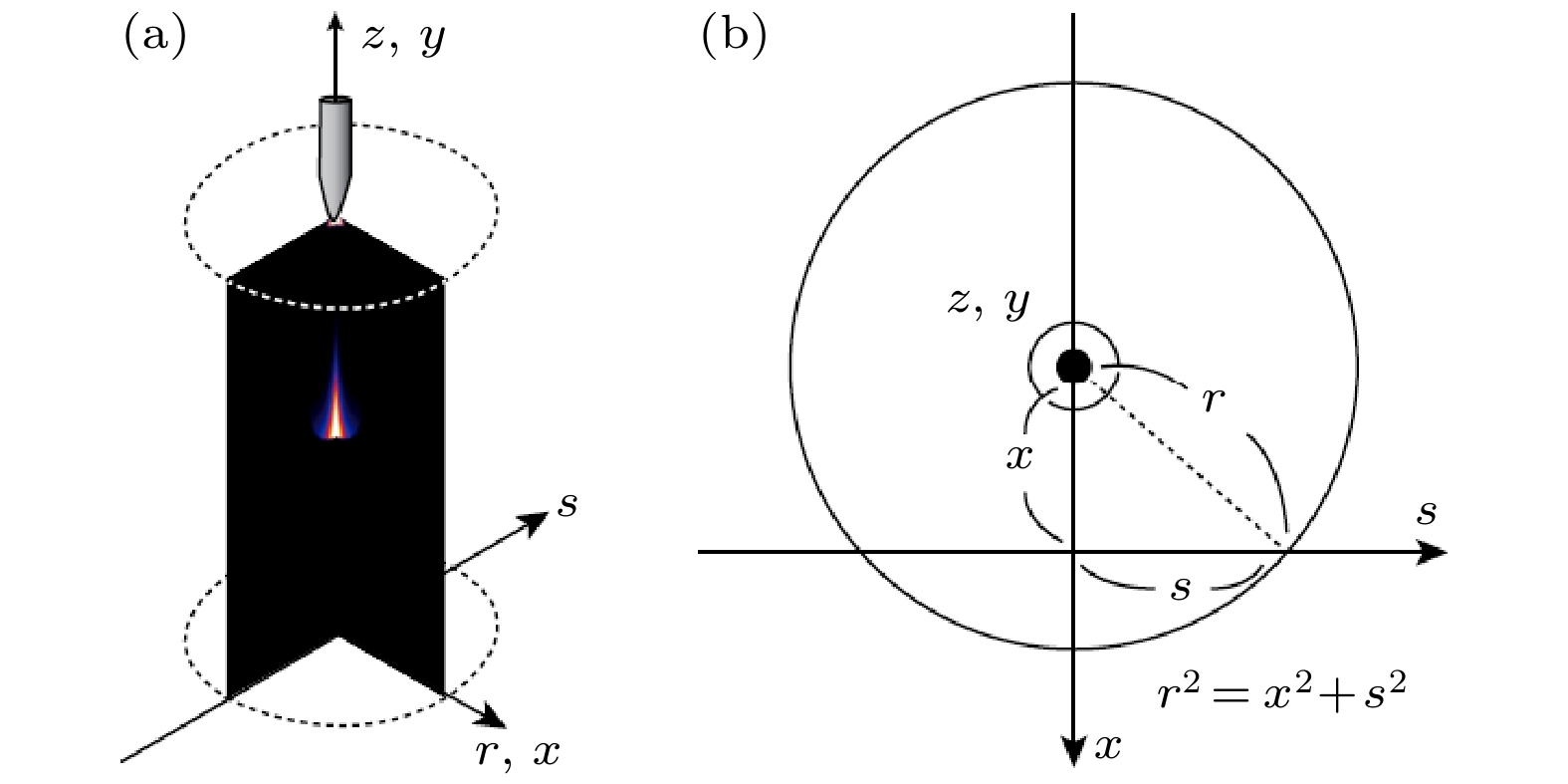
$ I_{\mathrm{k}}(r, z, t) $ 为每点的发光强度,$ n_{{\mathrm{N_2(C)}}}(r, z, t) $ 为每点处的$ \rm N_2(C) $ 密度. 本文使用的是二维轴对称模型, 如图8所示, 为复现实验ICCD拍摄结果, 需沿视线方向s计算积分, 并将其投影至一般坐标$ (x, y) $ 平面, 如(10)式:其中, 坐标对应关系为
$ r^2=x^2+s^2, \, y=z $ .$ \varPhi(x, y, t) $ 为每瞬间ICCD捕获的光子数, 实际ICCD拍摄时需要在快门开放时间$ T_{{\mathrm{gate}}} $ 内对ICCD捕获的光子数量进行积分, 在数值模型中可表示为(11)式所示的时间积分:其中
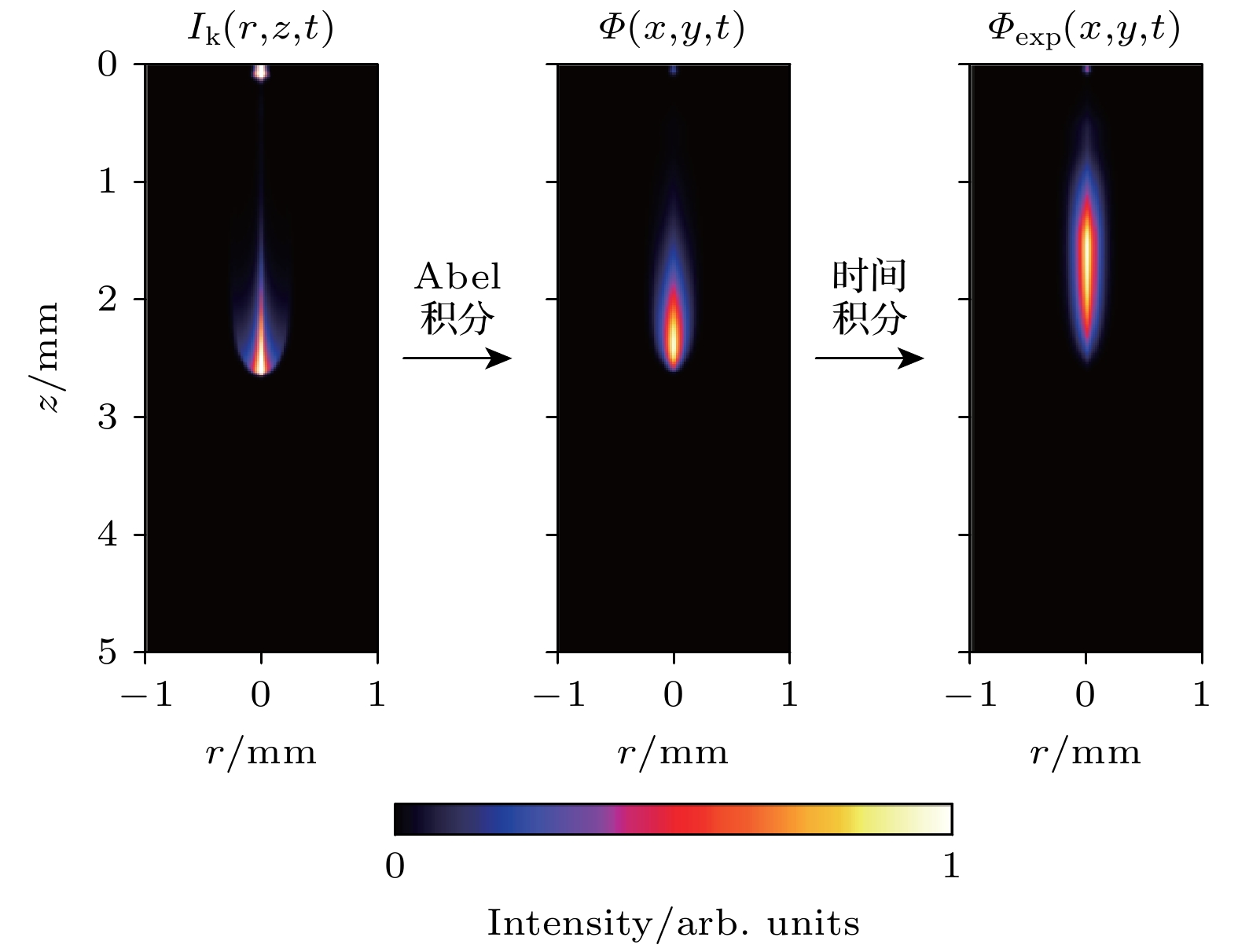
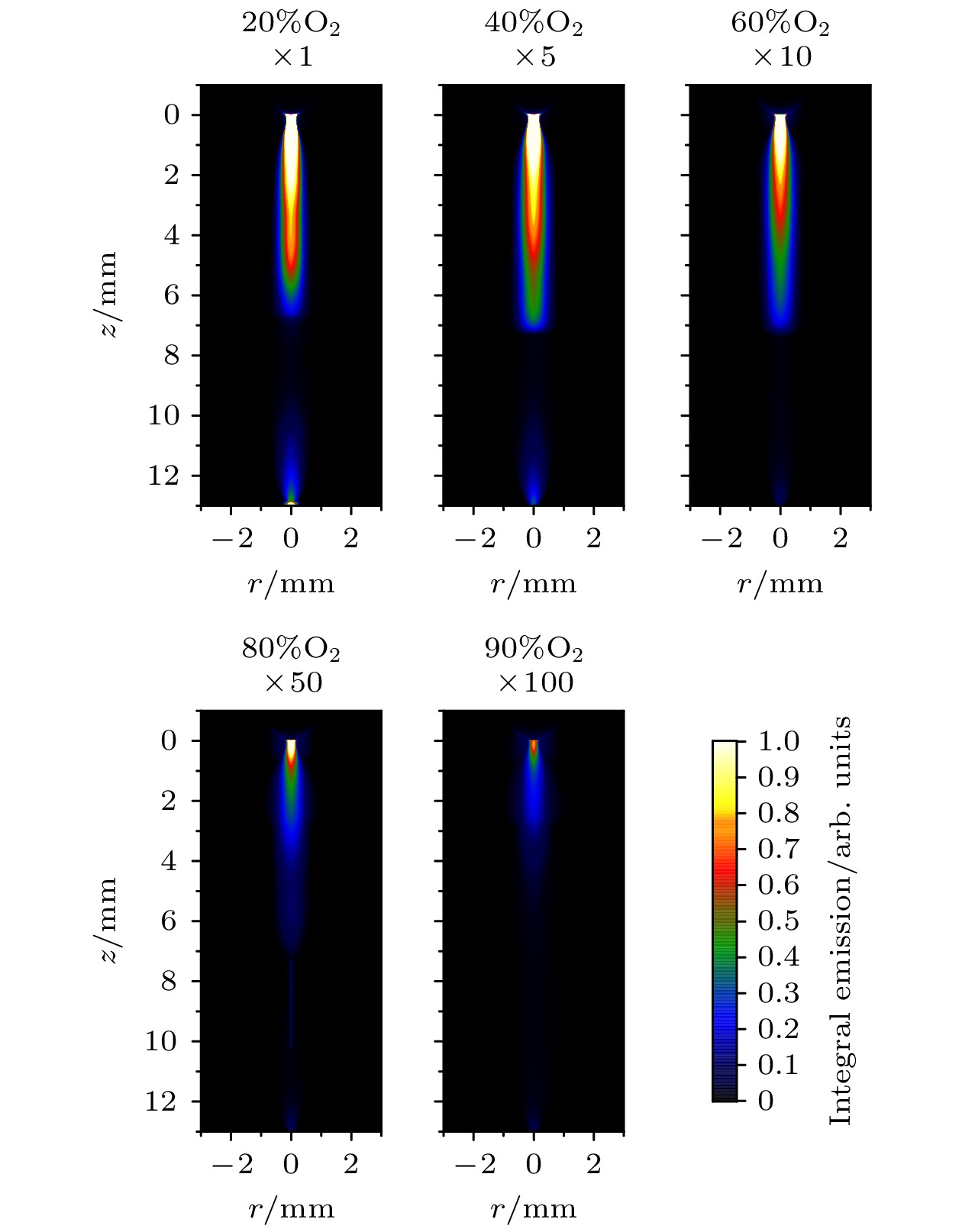
$ \varPsi_{{\mathrm{exp}}}(x, y, t) $ 为对应于实验ICCD拍摄结果积分后的光发射强度分布. 因此, 利用(9)式—(11)式, 可通过计算的$ \rm N_2(C) $ 分布, 复现实验获得的ICCD拍摄结果. 经Abel积分前后计算的发光强度对比如图9所示, 可见使用Abel及时间积分可有效还原2 ns快门时间内ICCD相机的拍摄结果.基于上述积分方式复现的ICCD相机100 ns快门时间的拍摄结果如图10所示, 可见, 氧浓度升高时, 计算出的二次流注发光强度大幅下降、通道直径大致不变, 且二次流注形态与文献[4]提供的ICCD拍摄照片拟合良好.
对0—100 ns时的二维发光结果进行二维空间积分:
可获得不同氧浓度下的总发射强度
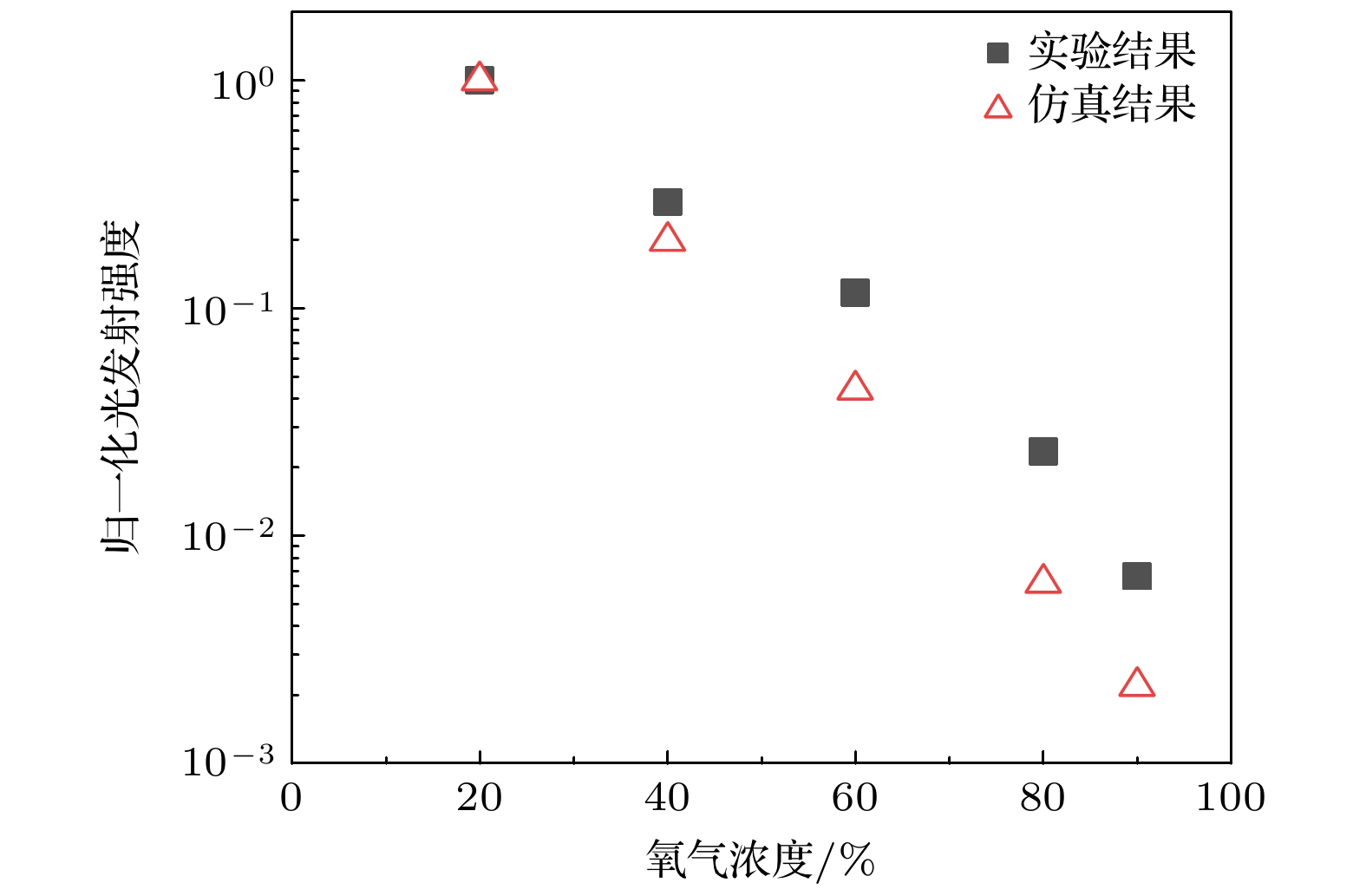
$ IT_i $ , 其中i表示氧气百分比. 对总发射强度$ IT_i $ 除以20%氧浓度下的总发光强度进行归一化处理, 图11为获得的不同氧浓度下总发光强度计算结果与实验结果的对比. 总发射强度拟合效果良好, 氧浓度由20%上升至90%时, 发射强度约下降至原来的0.2%, 这是由于二、三体吸附作用的增强, 高氧浓度下电子密度下降, 同时氮气浓度下降, 因此作为主要发光物的$ \rm N_2(C) $ 密度减小, 最终导致发光强度减弱. -
基于测量结果, 流注放电过程中
$ \rm N_2/O_2 $ 混合气体中激发态氧原子$ \mathrm{O(^3 P)} $ 的消减速率与臭氧的增加速率大致相同, 表明臭氧主要通过以下反应从$ \mathrm{O(^3 P)} $ 转化产生[21,28]:其中,
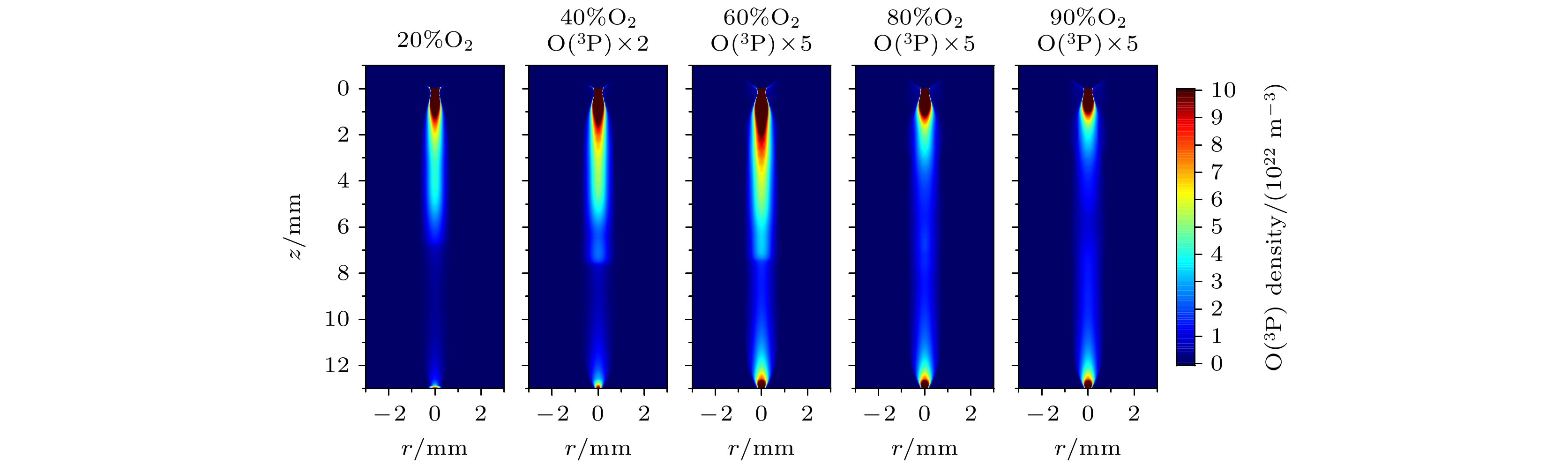
$ \rm O $ 表示激发态氧原子$ \rm O(^3 P) $ , M指混合背景气体的组分$ \rm N_2 $ 或$ \rm O_2 $ 分子. 典型速率常数$ 6.01\times 10^{-34} $ cm6/s下, 氧浓度[O2] = 20%时, 上述反应的时间常数为14 μs; [O2] = 90%时, 时间常数为3.2 μs[13,29]. 这意味着为比较模拟与实验测得的臭氧浓度, 需将模拟的计算时间由100 ns量级至少延长至14 μs, 计算时间大幅延长, 影响计算与分析效率. 相对于臭氧, 其主要中间产物$ \rm O(^3 P) $ 密度在约100 ns内即可达到稳定状态. 因此, 基于已有实验测量结果[4,13,21], 可使用流注发展过程中计算所得激发态氧原子$ \rm O(^3 P) $ 产量反映实验获得的臭氧分子产量, 无需将模型计算时间延长至10 μs量级.图12为不同氧浓度下t = 100 ns时刻激发态氧原子
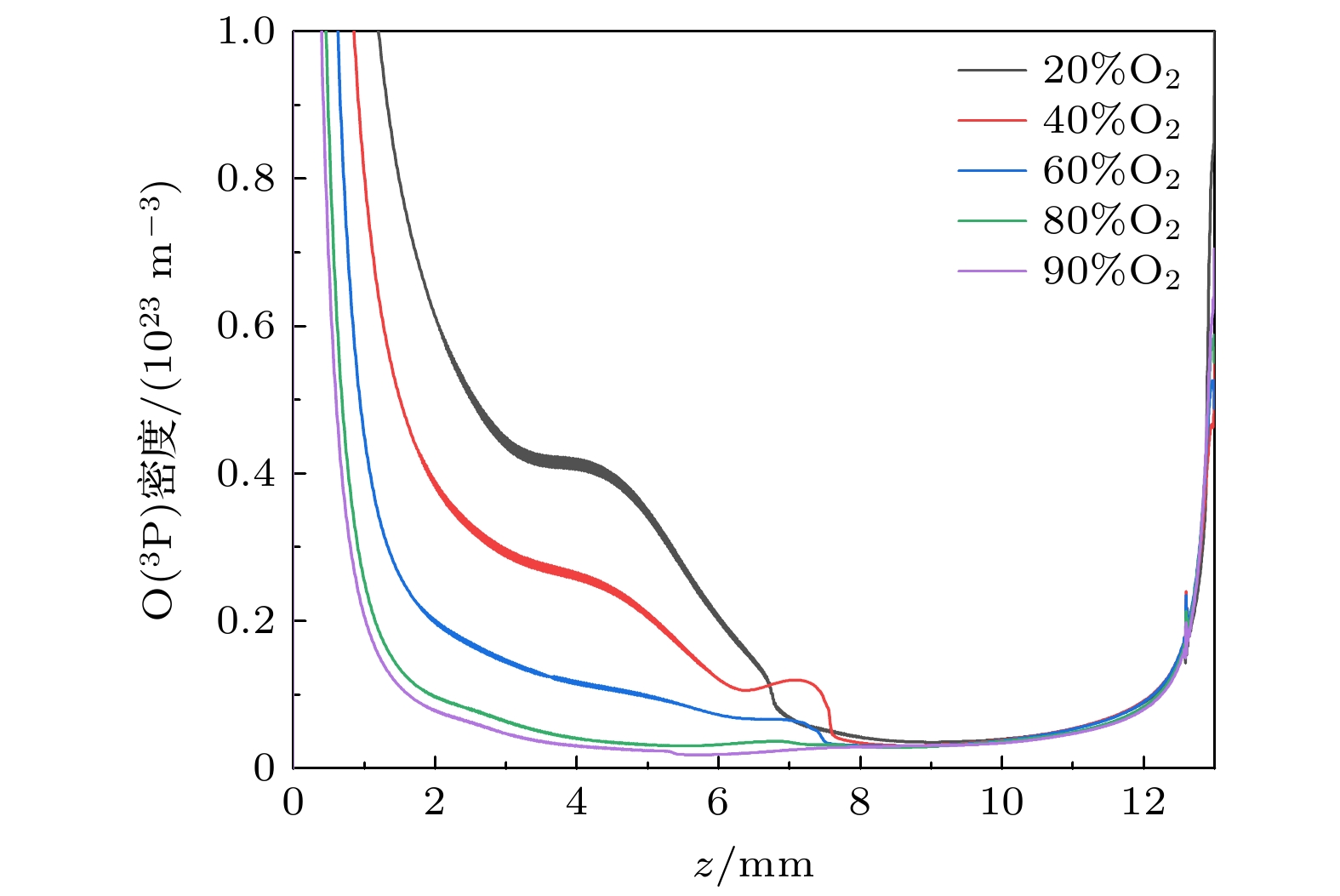
$ \mathrm{O(^3 P)} $ 的二维分布, 此时间点各氧浓度下$ \mathrm{O(^3 P)} $ 的密度均趋于稳定. 根据图12,$ \mathrm{O(^3 P)} $ 主要集中在图10所示$ z \leqslant 6\, \mathrm{mm} $ 的二次流注通道内部区域. 为进一步分析$ \mathrm{O(^3 P)} $ 的分布状态, 图13给出了不同氧浓度[O2]下,$ \mathrm{O(^3 P)} $ 沿对称轴r = 0 mm在$ z \leqslant 7\, \mathrm{mm} $ 内的一维分布. 可见, 随着氧浓度增加至90%, z = 3 mm处的密度下降约90%.在
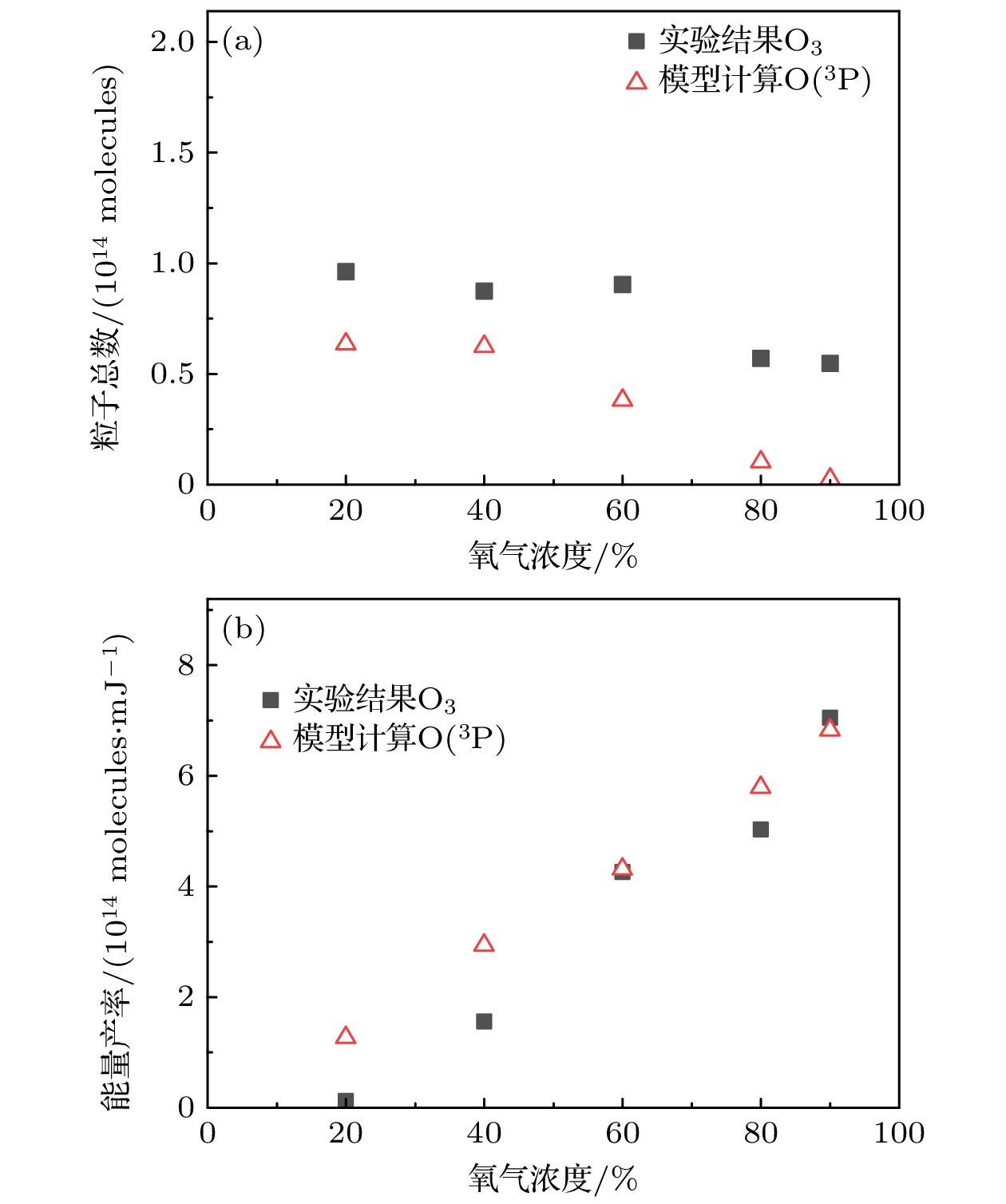
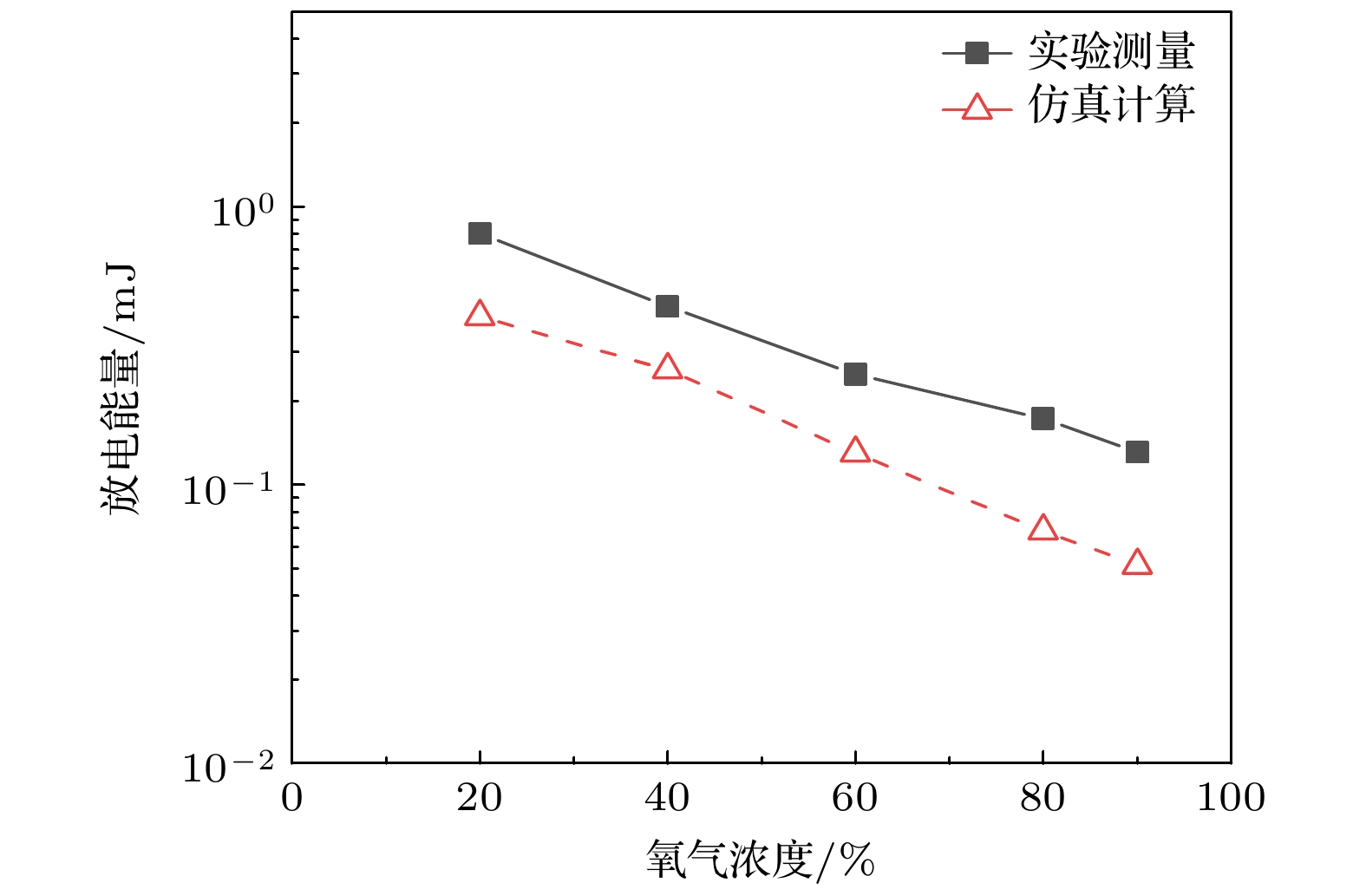
$ t=100\rm\, ns $ 时刻, 对不同氧浓度下整个计算域内$ \rm O(^3 P) $ 的密度进行积分, 获得$ \rm O(^3 P) $ 总产量, 并将其与实验中测量的$ \rm O_3 $ 总量进行比较[4], 结果如图14(a)所示. 在较高氧浓度下,$ \rm O(^3 P) $ 与实测$ \rm O_3 $ 总量均出现下降, 且模拟得到的总$ \rm O(^3 P) $ 与实测$ \rm O_3 $ 一致, 初步表明$ \rm O(^3 P) $ 反映臭氧产量的可行性. 计算不同氧浓度下放电过程的能量消耗, 获得臭氧 单位能量产率模拟与实测值如图15所示. 氧浓度由20%增加至90%时, 放电能量下降约85%, 放电能量的下降主要是电子密度下降导致电流持续时间下降导致. 基于总放电能量, 不同氧浓度下实验中$ \rm O_3 $ 与模拟中$ \rm O(^3 P) $ 单位能量产率如图14(b)所示, 氧浓度由20%增加至90%时, 实验中$ \rm O_3 $ 与计算的$ \rm O(^3 P) $ 产率均增上升3—4倍. 计算与实验获得的放电能量与单位能量产率均取得较好的一致性, 进一步证明使用计算的$ \rm O(^3 P) $ 反映真实臭氧产率的准确性.为分析氧浓度对激发态氧原子
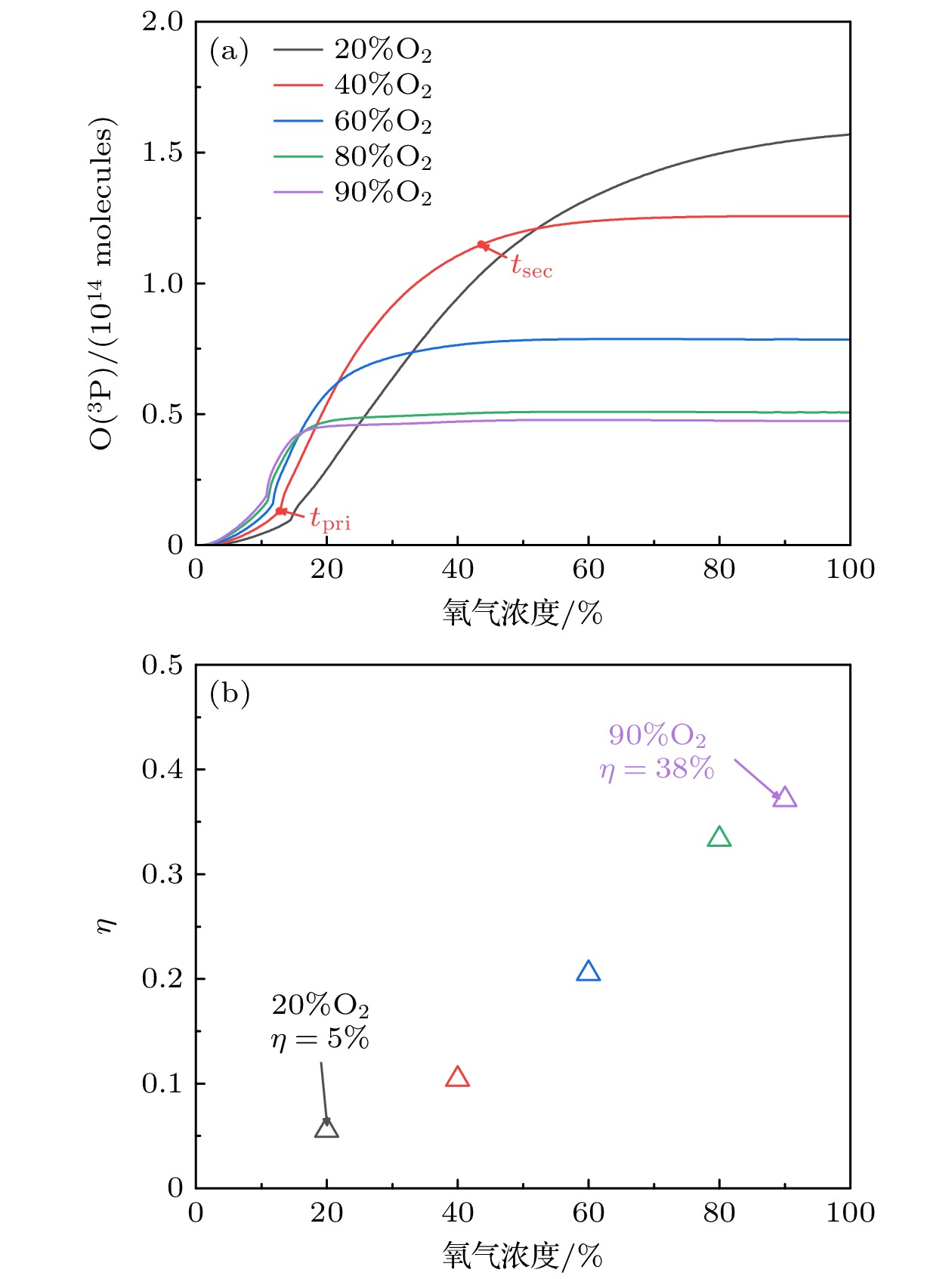
$ \rm O(^3 P) $ (臭氧)产量影响, 计算不同氧浓度下整个模拟区域内产生的$ \rm O(^3 P) $ 总量随时间的变化, 结果如图16(a)所示.$ \rm O(^3 P) $ 的产生可分为两个阶段:$ t = 0 $ —$ t_{{\mathrm{pri}}} $ 为第一阶段,$ t_{{\mathrm{pri}}} $ —$ t_{{\mathrm{sec}}} $ (板电流下降到峰值电流值的10%时的时间)为第二阶段, 分别表征一次和二次流注放电过程中$ \rm O(^3 P) $ 的产生速率.在
$ t=0 $ —$ t_{{\mathrm{pri}}} $ 期间, 一次流注由阳极(针电极)向阴极(板电极)传播, 由于传播过程中头部强电场在放电间隙中生成$ \rm O(^3 P) $ , 但其强场区域面积较小,$ \rm O(^3 P) $ 产量增加相对缓慢; 当一次流注在$ t =t_{{\mathrm{pri}}} $ 时刻与阴极接触后, 二次流注形成并开始扩展,$ \rm O(^3 P) $ 的产量继续上升, 虽然二次流注最大场强较低, 但由于其强场范围大, 相对于一次流注过程$ \rm O(^3 P) $ 总量增加速度加快[18,30,31]. 对于一次、二次流注产生的$ \rm O(^3 P) $ 数量, 当$ t\leqslant100\rm\, ns $ 时, 由于(13)式的时间常数较长,$ \rm O(^3 P) $ 的消耗反应速率较慢, 可近似忽略其消耗数量,$ \rm O(^3 P) $ 的密度逐渐增加. 氧浓度由20%增加至90%时, 一次流注产生的$ \rm O(^3 P) $ 数量上升一倍, 二次流注$ \rm O(^3 P) $ 的产量则下降约70%. 不同氧浓度下一次流注产生的$ \rm O(^3 P) $ 占总$ \rm O(^3 P) $ 产量的比例如图16(b)所示, 随氧浓度的增加, 一次流注阶段中产生的$ \rm O(^3 P) $ 所占的百分比逐渐上升. 当氧浓度为20%时, 仅约5%的$ \rm O(^3 P) $ 在一次流注阶段生成, 而当氧浓度增至90%时, 这一比例上升至约38%.进一步分析流注放电中的
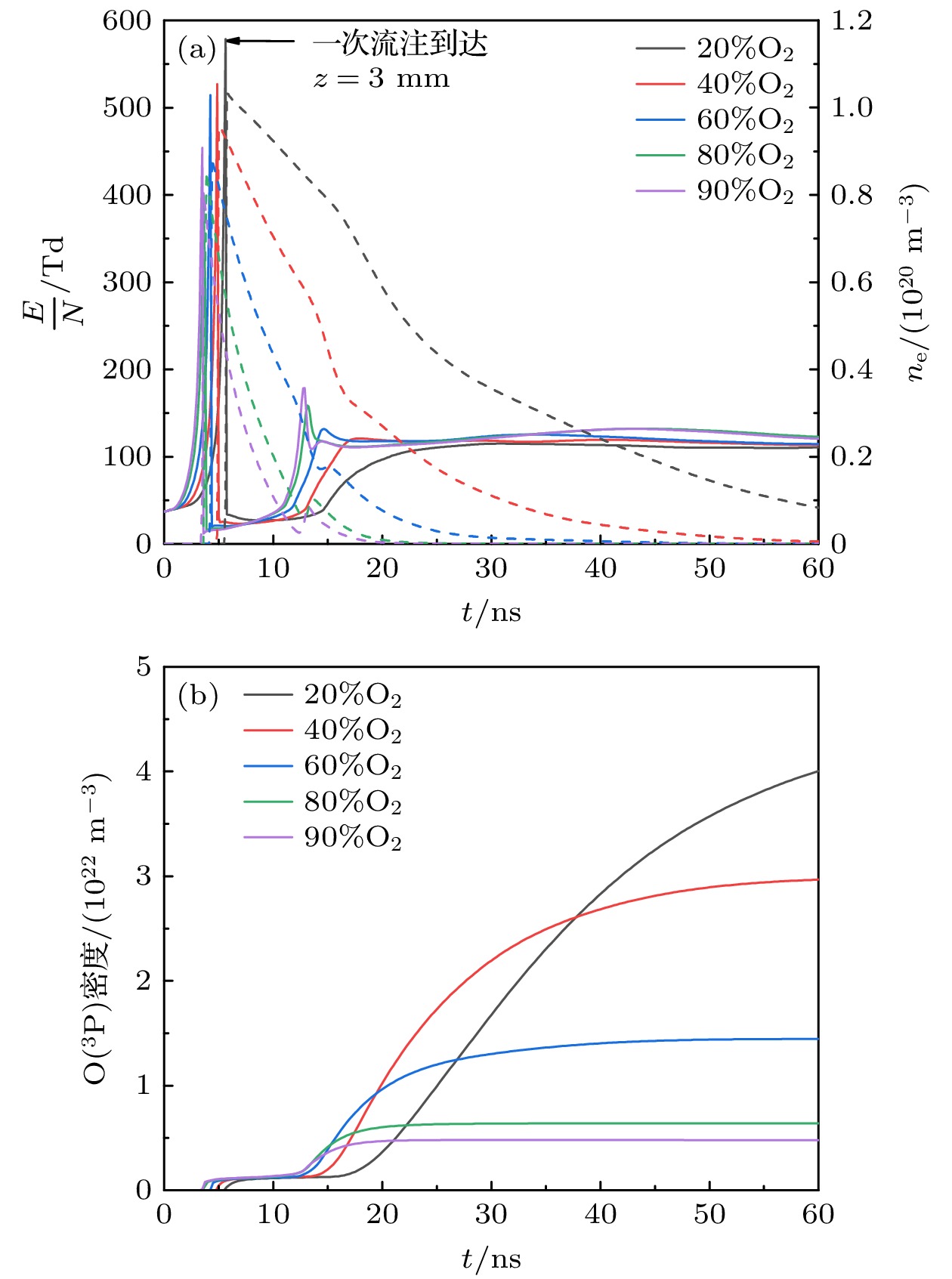
$ \rm O(^3 P) $ 产生过程, 图17(a), (b)分别表示不同氧浓度下对称轴z = 3 mm处电子密度、换算电场及$ \rm O(^3 P) $ 密度随时间的变化. 可见, 在一次流注头部接近z = 3 mm时E/N迅速增加至450—550 Td, 随后在流注头部通过后迅速减少到约20 Td. 二次流注形成并发展至z = 3 mm后, E/N再次上升至约120 Td. 图17(a)显示, 不同氧浓度下, E/N的时间变化趋势大致相同. 与此相反, 电子密度随着一次流注的通过迅速增加, 后由于低电场下的电子附着反应下降. 电子密度的下降速率依赖于与氧的电子附着反应速率, 因此高氧浓度下由于吸附作用增强, 电子密度下降速率加快. 氧浓度为20%时, 二次流注形成前氧浓度下降约30%; 而氧浓度为90%时, 二次流注发展之前, 电子密度已经减少约95%.图17(b)显示了对称轴上z = 3 mm处
$ \rm O(^3 P) $ 密度随时间的变化, 其横轴时间坐标与图17(a)相对应. 可见, 一次流注头部接近z = 3 mm处时, 场强上升,$ \rm O(^3 P) $ 开始生成, 但由于场强变化不大, 且$ \rm O(^3 P) $ 的主要激发速率对场强变化并不敏感, 各氧浓度下产量几乎相同. 然而, 二次流注形成期间,$ \rm O(^3 P) $ 的产量根据氧浓度的不同出现显著差异: 与图16(b)中呈现的结果大致一致,$ \mathrm{[O_2]} = 20{\text{%}} $ 和$ \mathrm{[O_2]} = 90{\text{%}} $ 下$ \rm O(^3 P) $ 密度分别为最大值与最小值. 因此, 二次流注中产生的$ \rm O(^3 P) $ 量随着氧浓度增加而减少的原因可解释如下: 二次流注通道内E/N强度随氧浓度变化不大, 但由于吸附作用增强, 二次流注阶段电子密度随氧浓度增加而显著下降. 由于电子密度主要决定于氧分子的二体或三体附着反应速率常数[10], 电子密度的下降速率与氧浓度的一次或二次方成比例, 因此可以预期$ \rm O(^3 P) $ 产生随氧浓度增加而减少. 进一步可解释高氧浓度下臭氧产率的变化: 对于$ \rm O(^3 P) $ 的产生, 模拟表明, 由于高氧浓度下电子密度下降速度加快, 二次流注中产生的$ \rm O(^3 P) $ 与$ \rm O(^3 P) $ 总量的比例随着氧浓度的增加而减少. 因此, 随着氧浓度的增加, 二次流注电场保持不变, 但电子的下降速率与氧浓度成比例增加, 从而导致二次流注持续时间缩短, 中间产物$ \rm O(^3 P) $ 的产量下降, 最终导致臭氧产量的下降. -
本文开发了抑制高氧浓度下数值模型中流注非物理分支的径向电场抑制方法, 基于此建立了能够模拟不同氧浓度下二次流注发展过程的数值模型, 与相关实验结果进行了对比分析; 分析了氧浓度变化对
$ \rm N_2/O_2 $ 混合物中臭氧主要中间产物的产量影响, 认识了氧浓度对$ \rm O(^3 P) $ 产率的影响机制, 讨论了不同氧浓度下激发态氧原子的产生与湮灭过程. 主要结论如下.1) 氧浓度上升带来了吸附作用的增强, 使得阴极转移电荷量降低; 当氧浓度由20%上升至90%时, 计算的转移电荷量由约17 nC下降至约2.5 nC, 约下降80%, 且模拟与计算结果平均误差小于15%.
2) 随着氧浓度增加, 二次流注阶段电子密度迅速下降. 当氧浓度达到90%时, 约90%的生成电子在二次流注形成之前湮灭. 电子密度的下降导致二次流注光发射强度减弱: 当氧浓度由20%上升至90%时, 总发光强度约下降至0.2%.
3) 氧浓度的变化显著影响臭氧主要中间产物
$ \rm O(^3 P) $ 的产生过程, 当氧浓度上升至90%时, 其产量下降约50%, 单位能量产率上升3—4倍. 产量下降的原因主要是吸附作用的增强导致的电子密度下降, 流注放电能量降低.4) 氧浓度影响臭氧中间产物
$ \rm O(^3 P) $ 的产生阶段, 低氧浓度下,$ \rm O(^3 P) $ 主要产生于二次流注阶段, 20%氧浓度下一次流注的$ \rm O(^3 P) $ 产量仅约为5%; 高氧浓度下, 一次流注阶段$ \rm O(^3 P) $ 产量占比逐渐上升, 90%氧浓度下一次流注阶段产量约占总放电过程产量的38%.
不同氧浓度混合气体二次流注放电下激发态氧原子生成特性与影响因素
Characteristics and influencing factors of excited oxygen atom generation in secondary streamer discharge of mixed gases with different oxygen concentrations
-
摘要: 流注放电被应用于消毒杀菌、臭氧生产等领域, 其中二次流注放电过程对臭氧有效生产持续时间和效率影响明显, 然而氧浓度对二次流注放电过程及目标产物产量的影响还不清楚. 为此, 开发不同氧浓度下针-板电极二次流注发展过程的流体分析模型, 解决高氧浓度下流注放电模拟的非物理分支(branch)问题, 分析氧浓度对二次正流注光发射特性的影响, 研究不同氧浓度下的阴极转移电荷量和激发态氧原子$ \rm O(^3P) $产量, 并与实验数据进行对比. 结果表明, 氧浓度由20%增加至90%后, 二次流注放电通道电子密度平均降低90%, 电场强度变化小于10%, 单次放电持续时间缩短77%, 激发态氧原子$ \rm O(^3P) $单位能量产率上升64%, 同时放电时间缩短会使产量降低50%, 但激发态氧原子$ \rm O(^3P) $单位能量产率的提高优于单次降产量. 氧浓度增大引发氧分子二、三体吸附效应增强和电子密度下降是单次放电产量下降的原因, 电子与氧分子碰撞概率提升是单位能量产率上升的原因.Abstract: Streamer discharge has been widely used in fields of sterilization, disinfection, ozone generation, etc. The secondary discharge process significantly affects the effective ozone production duration and efficiency. However, the mechanism of oxygen concentration affecting secondary discharge characteristics and the yield of target products is still unclear. To address this issue, a fluid-based analysis model of the secondary positive streamer discharge process between needle-plate electrodes under varying oxygen concentrations is developed in this work. This model considers the radial electric field and resolves potential non-physical branching issues that may arise in discharge simulations at high oxygen concentrations. In this work, the effect of oxygen concentration on the optical emission characteristics of secondary positive streamers is examined. The optical emission intensity, cathode charge transfer, and the yields of excited-state oxygen atoms (O(3P)) under different oxygen concentrations are investigated and compared with experimental data. The results show that when the oxygen concentration increases from 20% to 90%, the light emission intensity of the secondary discharge decreases by about 0.2%. At the same time, the average electron density in the discharge channel decreases by 90%, the change of electric field intensity is less than 10%, and the duration of single discharge duration is shortened by 77%. Under these conditions, the proportion of O(3P) yield originating from the primary discharge increases from 20% to 38%, and the unit energy yield of excited-state oxygen atoms O(3P) rises by 64%. Although the reduction in discharge duration results in a 50% decrease in absolute O(3P) yield, the increase in unit energy yield far compensates for the decrease in single-discharge yield. The single-discharge yield decreases with oxygen concentration increasing due to the enhanced two- and three-body adsorption effects of oxygen molecules, which reduce the electron density. Additionally, the increased collision probability between electrons and oxygen molecules further affects these characteristic changes.
-
Key words:
- streamer discharge /
- fluid simulation /
- numerical simulation /
- duration .
-
-
图 1 针电极施加的脉冲电压波形 (a) 0—800 ns的电压波形; (b) 放大x轴后0—100 ns的电压波形
Figure 1. Applied voltage
$ V(t) $ at the anode (needle) in the simulation: (a) The voltage waveform of 0–800 ns; (b) enlarged voltage waveform of 0–100 ns.
图 2 用于计算径向电场的包含环绕针电极的三维模型示意图
Figure 2. Overview of the calculation region of the three-dimensional model for calculating the distribution of the electric field near the anode.
图 3 包含环绕针电极的五针模型与单针电极三维模型针尖z = 0处径向电场对比
Figure 3. Distribution of radial electric field along z = 0 calculated via the three-dimensional simulation.
图 4 进行电场抑制前后模拟出的流注对比 (a)未进行径向电场修正; (b)进行径向电场修正后的二次流注
Figure 4. Simulated secondary streamer with and without modification: (a) Radial electric field with modification; (b) radial electric field without modification.
图 5 模拟的大气压条件下0—60 ns时间段ICCD相机拍摄的图像的流注发展过程
Figure 5. Simulated emission ICCD figure of the secondary streamer under 20%
$ \rm O_2 $ concentration from 0 to 60 ns.
图 6 实验获得的大气压条件下0—60 ns时间段ICCD相机图像的流注发展过程
Figure 6. Emission ICCD figure of the secondary streamer under 20%
$ \rm O_2 $ concentration from 0 to 60 ns in the experiment
图 7 不同氧浓度下模拟与实验获得的阴极转移电荷量对比
Figure 7. Comparison between the transferred charge calculated in the simulation and measured in the experiment.
图 8 积分坐标系之间的关系 (a)轴对称坐标系与视线方向坐标系s; (b)圆柱对称Abel坐标系
Figure 8. Relationship between integral coordinate systems: (a) Axisymmetric coordinate system with line-of-sight direction coordinate system s; (b) cylindrically symmetric Abel coordinate system
图 9 使用Abel及时间积分(快门时间2 ns)前后, 计算的发光强度对比
Figure 9. Comparison of calculated luminous intensity before and after using Abel and time integration (gate time 2 ns).
图 10 不同氧浓度下计算得出的二级流注的发射强度示意图
Figure 10. Calculated 2D emission intensity of the secondary streamer under different oxygen concentrations.
图 11 不同氧浓度下计算与实验得出的二次流注的发射总强度对比
Figure 11. Comparison of calculated and experimentally derived total emission intensities for secondary streamer at different oxygen concentrations.
图 12 不同氧浓度下二次流注过程t = 100 ns时的
$ \mathrm{O(^3 P)} $ 密度分布Figure 12. Spatial distribution of
$ \mathrm{O(^3 P)} $ at t = 100 ns during secondary streamer at different oxygen concentrations.
图 13 不同氧浓度下二次流注过程t = 100 ns时, 对称轴r = 0 mm上的
$ \mathrm{O(^3 P)} $ 密度Figure 13. Density of
$ \mathrm{O(^3 P)} $ on the axis of symmetry r = 0 mm at t = 100 ns for secondary streamer process at different oxygen concentrations.
图 14 不同氧浓度下模型计算与实验得出的二次流注的产出
$ \rm O(^3 P) $ 总量(a)与每单位能量产率对比(b)Figure 14. Comparison between the simulation and measurement results for (a) total number of measured
$ \rm O_3 $ and simulated$ \rm O(^3 P) $ molecules and (b) measured$ \rm O_3 $ and simulated$ \rm O(^3 P) $ yields.
图 16 (a) 不同氧浓度下产生的
$ \rm O(^3 P) $ 总量随时间变化; (b) 不同氧浓度下一次流注产生的$ \rm O(^3 P) $ 产量与总产量比值Figure 16. The dependence of the total amount of
$ \rm O(^3 P) $ produced on the time at various oxygen concentrations; (b) fraction of$ \rm O(^3 P) $ produced by the primary streamer to the total amount of$ \rm O(^3 P) $ production at various oxygen concentrations.
图 17 (a) 不同氧浓度下, E/N (实线)和电子密度(虚线)随时间的变化; (b)不同氧浓度下, 对称轴上z = 3 mm处的
$ \rm O(^3 P) $ 密度随时间的变化Figure 17. (a) Time dependencies of E/N (solid line) and the electron density (dashed line) under various O2 concentrations; (b) time dependencies of
$ \rm O(^3 P) $ density at z = 3 mm on the symmetric axis under various O2 concentrations. -
[1] 李晗蔚, 孙安邦, 张幸, 姚聪伟, 常正实, 张冠军 2018 物理学报 67 045101 doi: 10.7498/aps.67.20172309 Li H W, Sun A B, Zhang X, Yao C W, Chang Z S, Zhang G J 2018 Acta Phys. Sin 67 045101 doi: 10.7498/aps.67.20172309 [2] Samaranayake W, Miyahara Y, Namihira T, Katsuki S, Sakugawa T, Hackam R, Akiyama H 2000 IEEE Trans. Dielectr. Electr. Insul. 7 254 doi: 10.1109/94.841818 [3] Fukawa F, Shimomura N, Yano T, Yamanaka S, Teranishi K, Akiyama H 2008 IEEE Trans. Plasma Sci. 36 2592 doi: 10.1109/TPS.2008.2004372 [4] Komuro A, Yoshino A, Wei Z, Ono R 2023 J. Phys. D: Appl. Phys. 56 185201 doi: 10.1088/1361-6463/acc18f [5] Meher P, Deshmukh N, Mashalkar A, Kumar D 2023 AIP Conference Proceedings 2764 1 doi: 10.1063/5.0144316 [6] Wang D, Namihira T 2020 Plasma Sources Sci. Technol. 29 023001 doi: 10.1088/1361-6595/ab5bf6 [7] Li X, Sun A, Zhang G, Teunissen J 2020 Plasma Sources Sci. Technol. 29 065004 doi: 10.1088/1361-6595/ab8f75 [8] Syssoev V, Naumova M, Kuznetsov Y, Orlov A, Sukharevsky D, Makalsky L, Kukhno A 2022 Inorg. Mater. Appl. Res. 13 1380 doi: 10.1134/S2075113322050410 [9] Sisoev V, Zavyalova A, Makalsky L, Kuchno A 2021 IOP Conference Series: Earth and Environmental Science 723 042068 doi: 10.1088/1755-1315/723/4/042068 [10] Wei Z, Komuro A, Ono R 2023 Plasma Processes Polym. 21 2300113 doi: 10.1002/ppap.202300113 [11] Abahazem A, Merbahi N, Ducasse O, Eichwald O, Yousfi M 2008 IEEE Trans. Plasma Sci. 36 924 doi: 10.1109/TPS.2008.925708 [12] Ono R, Komuro A 2020 J. Phys. D: Appl. Phys. 53 035202 doi: 10.1088/1361-6463/ab4e65 [13] Ono R, Oda T 2003 J. Phys. D: Appl. Phys. 36 1952 doi: 10.1088/0022-3727/36/16/306 [14] Meek J 1940 Phys. Rev. 57 722 doi: 10.1103/PhysRev.57.722 [15] Raether H 1939 Zeitschrift für Physik 112 464 [16] Sigmond R 1984 J. Appl. Phys. 56 1355 doi: 10.1063/1.334126 [17] Nijdam S, Teunissen J, Takahashi E, Ebert U 2016 Plasma Sources Sci. Technol. 25 044001 doi: 10.1088/0963-0252/25/4/044001 [18] Eichwald O, Ducasse O, Dubois D, Abahazem A, Merbahi N, Benhenni M, Yousfi M 2008 J. Phys. D: Appl. Phys. 41 234002 doi: 10.1088/0022-3727/41/23/234002 [19] Babaeva N Y, Naidis G 1996 J. Phys. D: Appl. Phys. 29 2423 doi: 10.1088/0022-3727/29/9/029 [20] Zhelezniak M, Mnatsakanian A K, Sizykh S V 1982 High Temperature Science 20 357 [21] Ono R, Takezawa K, Oda T 2009 J. Appl. Phys. 106 043302 doi: 10.1063/1.3190530 [22] Komuro A, Ono R, Oda T 2013 J. Phys. D: Appl. Phys. 46 175206 doi: 10.1088/0022-3727/46/17/175206 [23] Komuro A, Takahashi K, Ando A 2015 J. Phys. D: Appl. Phys. 48 215203 doi: 10.1088/0022-3727/48/21/215203 [24] Wei Z, Komuro A, Ono R 2023 Plasma Sources Sci. Technol. 32 115016 doi: 10.1088/1361-6595/ad0b97 [25] Phelps and Morgan Databases, Murphy T I https://us.lxcat.net/contributors/ [2024-11-04] [26] Hagelaar G, Pitchford L C 2005 Plasma Sources Sci. Technol. 14 722 doi: 10.1088/0963-0252/14/4/011 [27] Bourdon A, Pasko V, Liu N Y, Célestin S, Ségur P, Marode E 2007 Plasma Sources Sci. Technol. 16 656 doi: 10.1088/0963-0252/16/3/026 [28] Yoshida K, Komuro A, Wada N, Naito T, Ando A 2022 J. Electrostat. 117 103716 doi: 10.1016/j.elstat.2022.103716 [29] DeMore W, Sander S, Golden D, Hampson R, Kurylo M, Howard C, Ravishankara A, Kolb C, Molina M 1997 JPL Publication 97 1 [30] Komuro A, Ono R, Oda T 2013 Plasma Sources Sci. Technol. 22 045002 doi: 10.1088/0963-0252/22/4/045002 [31] Komuro A, Takahashi K, Ando A 2017 Plasma Sources Sci. Technol. 26 065003 doi: 10.1088/1361-6595/aa638d -
计量
- 文章访问数: 210
- HTML全文浏览数: 210
- PDF下载数: 1
- 施引文献: 0