高级搜索

激光锡等离子体的状态参数分布和极紫外波段辐射的模拟研究

,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

敏琦, 王国栋, 何朝伟, 何思奇, 卢海东, 刘兴邦, 武艳红, 苏茂根, 董晨钟. 激光锡等离子体的状态参数分布和极紫外波段辐射的模拟研究[J]. 物理学报, 2025, 74(3): 033201-1. doi: 10.7498/aps.74.20241321
引用本文: 敏琦, 王国栋, 何朝伟, 何思奇, 卢海东, 刘兴邦, 武艳红, 苏茂根, 董晨钟. 激光锡等离子体的状态参数分布和极紫外波段辐射的模拟研究[J]. 物理学报, 2025, 74(3): 033201-1. doi: 10.7498/aps.74.20241321
shu
Qi MIN, Guodong WANG, Chaowei HE, Siqi HE, Haidong LU, Xingbang LIU, Yanhong WU, Maogen SU, Chenzhong DONG. Numerical simulation of state parameter distributions and extreme ultraviolet radiation in laser-produced tin plasma[J]. Acta Physica Sinica, 2025, 74(3): 033201-1. doi: 10.7498/aps.74.20241321
Citation: Qi MIN, Guodong WANG, Chaowei HE, Siqi HE, Haidong LU, Xingbang LIU, Yanhong WU, Maogen SU, Chenzhong DONG. Numerical simulation of state parameter distributions and extreme ultraviolet radiation in laser-produced tin plasma[J]. Acta Physica Sinica, 2025, 74(3): 033201-1. doi: 10.7498/aps.74.20241321
shu

激光锡等离子体的状态参数分布和极紫外波段辐射的模拟研究

  • 1.

    西北师范大学物理与电子工程学院, 甘肃省原子分子物理与功能材料重点实验室, 兰州　730070

  • 2.

    兰州工业学院计算机与人工智能学院, 兰州　730050

    • 通讯作者: E-mail: mq_lpps@nwnu.edu.cn.;  E-mail: sumg@nwnu.edu.cn.;  E-mail:dongcz@nwnu.edu.cn.

  • 中图分类号: 32.30.Jc, 52.65.-y, 52.25.-b, 52.25.Os

Numerical simulation of state parameter distributions and extreme ultraviolet radiation in laser-produced tin plasma

  • 1.

    Key Laboratory of Atomic and Molecular Physics & Functional Material of Gansu Province, College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, China

  • 2.

    School of Computer Science and Artificial Intelligence, Lanzhou Institute of Technology, Lanzhou 730050, China

    • Corresponding authors: E-mail: mq_lpps@nwnu.edu.cn.;  E-mail: sumg@nwnu.edu.cn.;  E-mail: dongcz@nwnu.edu.cn.

  • MSC: 32.30.Jc, 52.65.-y, 52.25.-b, 52.25.Os

  • 摘要: 激光锡(Sn)等离子体光源是当前先进极紫外(EUV)光刻机中最为核心的分系统, 其辐射出的13.5 nm附近2%带宽内的EUV光的功率值和稳定性是决定整个光刻机是否成功的关键指标之一. 本文针对激光Sn等离子体光源这一复杂系统, 开展了详细的关于等离子体状态参数分布以及EUV辐射光谱的数值模拟研究. 首先基于细致能级模型, 在局域热动平衡近似条件下计算得到了Sn等离子体在12—16 nm波段的辐射不透明度数据. 随后利用激光等离子体辐射流体力学程序RHDLPP, 分别模拟了纳秒激光脉冲作用于Sn平面固体靶和液滴靶所产生的等离子体的温度和电子密度等状态参数的分布. 结合辐射不透明度数据和等离子体状态数据, 利用光谱模拟后处理子程序SpeIma3D完成了平面靶等离子体的空间分辨EUV光谱以及液滴靶等离子体在60°观测角下的角分辨EUV光谱的模拟. 最后, 得到了液滴靶等离子体在13.5 nm, 2%带宽内的带内辐射强度随观测角度的变化规律. 本文获得的所有等离子体状态参数分布和EUV光谱模拟结果与现有的实验结果具有很好的一致性, 证明了RHDLPP程序在激光Sn等离子体EUV光源方面的模拟能力, 相关结果可以为EUV光刻以及国产化EUV光源的研制提供一定的支持.
    Abstract: The laser-produced Sn plasma light source is a critical component in advanced extreme ultraviolet (EUV) lithography. The power and stability of EUV radiation within a 2% bandwidth centered at 13.5 nm are key indicators that determine success of the entire lithography process .The plasma state parameter distributions and the EUV radiation spectrum for a laser-produced Sn plasma light source are numerically simulated in this work. The radiative opacity of Sn plasma within the 12–16 nm range is calculated using a detailed-level-accounting model in the local thermodynamic equilibrium approximation. Next, the temperature distribution and the electron density distribution of plasma generated by nanosecond laser pulses interacting with both a Sn planar solid target and a liquid droplet target are simulated using the radiation hydrodynamics code for laser-produced plasma, RHDLPP. By combining the radiative opacity data with the plasma state data, the spectral simulation subroutine SpeIma3D is employed to model the spatially resolved EUV spectra for the planar target plasma and the angle-resolved EUV spectra for the droplet target plasma at a 60-degree observation angle. The variation of in-band radiation intensity at 13.5 nm within the 2% bandwidth as a function of observation angle is also analyzed for the droplet-target plasma. The simulated plasma state parameter distributions and EUV spectral results closely match existing experimental data, demonstrating the ability of RHDLPP code to model laser-produced Sn plasma EUV light sources. These findings provide valuable support for the development of EUV lithography and EUV light sources.
  • 加载中

  • 图 1  激光等离子体辐射流体力学程序RHDLPP的程序框架图

    Figure 1.  Framework for the radiation hydrodynamics code RHDLPP.

    下载: 全尺寸图片 幻灯片

    图 2  SpeIma3D程序模拟激光等离子体光谱的示意图[35]

    Figure 2.  Schematic diagram of the spectrum of a laser-produced plasma simulated by the SpeIma3D program[35].

    下载: 全尺寸图片 幻灯片

    图 3  不同$ \left({T}_{{\mathrm{e}}}, {n}_{{\mathrm{e}}}\right) $下离子电荷态分布的对比结果, 其中红色柱状图代表 LTE条件下基于细致能级的结果(LTE-DLA), 蓝色柱状图代表LTE条件下基于屏蔽氢近似的结果(LTE-SH), 灰色柱状图代表non-LTE条件下基于屏蔽氢近似的结果

    Figure 3.  Comparison of ion charge state distributions under different $ \left({T}_{{\mathrm{e}}}, {n}_{{\mathrm{e}}}\right) $ conditions. The red bar chart represents results based on DLA model under LTE conditions (LTE-DLA), the blue bar chart represents results based on the screened hydrogenic approximation under LTE conditions (LTE-SH), and the gray bar chart represents results based on the screened hydrogenic approximation under non-LTE conditions.

    下载: 全尺寸图片 幻灯片

    图 4  密度为0.002 g/cm3, 温度为(a) 32 eV和(b) 20 eV 时Sn等离子体的EUV 辐射不透明度

    Figure 4.  EUV radiative opacity of Sn plasmas at a density of 0.002 g/cm3 and temperatures of (a) 32 eV, (b) 20 eV.

    下载: 全尺寸图片 幻灯片

    图 5  延迟时间10.5 ns时, 模拟和实验测量的激光Sn等离子体(a)温度和(b)电子密度在距离靶面130, 200, 300 μm 处沿着r轴的分布

    Figure 5.  Simulated and experimentally measured distributions of laser-produced Sn plasma (a) temperature and (b) electron density along the r-axis are presented at distances of 130, 200, and 300 μm from the target surface, with a delay time of 10.5 ns.

    下载: 全尺寸图片 幻灯片

    图 6  不同延迟时间下模拟的Sn等离子体温度(a)和质量密度(b)在r = 0处沿着z轴的分布

    Figure 6.  Simulated distribution of Sn plasma temperature (a) and mass density (b) along the z-axis at r = 0 for various delay times.

    下载: 全尺寸图片 幻灯片

    图 7  距离靶面130, 200, 300 μm 处激光Sn等离子体的EUV光谱[18]

    Figure 7.  The EUV spectra of laser-produced Sn plasma at 130, 200, and 300 μm from the target surface[18].

    下载: 全尺寸图片 幻灯片

    图 8  (a) 距离靶面130, 200, 300 μm 处激光Sn等离子体归一化的EUV实验光谱[18]以及(b) Sn7+—Sn14+离子的归一化发射率

    Figure 8.  (a) Normalized EUV experimental spectra of laser-produced Sn plasma at distances of 130, 200, and 300 μm from the target surface[18], and (b) normalized emissivity of Sn7+− Sn14+ ions.

    下载: 全尺寸图片 幻灯片

    图 9  延迟时间为4, 7, 10, 13 ns时, 模拟得到的Sn液滴等离子体的温度(第一行)和密度(第二行)的二维分布, 图中激光自左向右沿着z轴入射

    Figure 9.  Two-dimensional distributions of temperature (the first row) and density (the second row) of Sn droplet plasma, obtained from simulations, when the delay times is 4, 7, 10, and 13 ns. In the panel, the laser propagates along the z-axis from left to right.

    下载: 全尺寸图片 幻灯片

    图 10  观测视线与激光入射方向成60º角时, 实验测量的[12] (黑色实线)、Torretti等[12]模拟的(红色实线)以及本文利用RHDLPP程序模拟的(蓝色实线) Sn液滴等离子体的EUV光谱

    Figure 10.  The EUV spectra for the Sn droplet plasma, including the experimentally measured data[12] (black solid line), the simulation by Torretti et al. [12] (red solid line), and the simulation performed in this paper using the RHDLPP program (blue solid line). The spectra are observed at a 60º angle relative to the direction of laser incidence.

    下载: 全尺寸图片 幻灯片

    图 11  Sn液滴等离子体在13.5 nm, 2%带宽内的归一化辐射强度随观测角的变化, 其中红色实心圆表示本文的模拟结果, 蓝色虚线表示拟合曲线

    Figure 11.  Variation of the normalized radiation intensity of the Sn droplet plasma at 13.5 nm with a 2% bandwidth as a function of the observation angle. The red solid circles represent the simulation results from this paper, while the blue dashed lines correspond to the fitted curves.

    下载: 全尺寸图片 幻灯片

    表 1  14组$ \left({T}_{{\mathrm{e}}}, {n}_{{\mathrm{e}}}\right) $下的比值R、电离温度$ {T}_{Z} $、LTE条件下基于细致能级的平均电荷态$ {\left\langle{Z}\right\rangle}_{{\mathrm{LTE}}\text-1} $、LTE条件下基于屏蔽氢近似的平均电荷态$ {\left\langle{Z}\right\rangle}_{{\mathrm{LTE}}\text-2} $及non-LTE条件下基于屏蔽氢近似的平均电荷态$ {\left\langle{Z}\right\rangle}_{{\mathrm{n}}{\mathrm{o}}{\mathrm{n}}{\text{-}}{\mathrm{LTE}}} $

    Table 1.  Ratios R, ionization temperatures $ {T}_{Z} $, average charge states $ {\left\langle{Z}\right\rangle}_{{\mathrm{LTE}}\text-1} $ based on DLA model under LTE conditions, $ {\left\langle{Z}\right\rangle}_{{\mathrm{LTE}}\text-2} $ based on the screened hydrogenic approximation under LTE conditions, and $ {\left\langle{Z}\right\rangle}_{{\mathrm{n}}{\mathrm{o}}{\mathrm{n}}{\text{-}}{\mathrm{LTE}}} $ based on the screened hydrogenic approximation under non-LTE conditions for 14 sets of $ \left({T}_{{\mathrm{e}}}, {n}_{{\mathrm{e}}}\right) $ values.

    序号 $ {T}_{{\mathrm{e}}}/{\rm eV}$ $ {n}_{{\mathrm{e}}}/{\rm cm}^{-3} $ $ R $ $ {T}_{Z}/\rm eV $ $ {\left\langle{Z}\right\rangle}_{{\mathrm{LTE}}\text-1} $ $ {\left\langle{Z}\right\rangle}_{{\mathrm{LTE}}\text-2} $ $ {\left\langle{Z}\right\rangle}_{{\mathrm{n}}{\mathrm{o}}{\mathrm{n}}\text-{\mathrm{LTE}}} $
    1 38 5.10×1020 1.00754 37.72 12.57 12.60 12.60
    2 2.05×1020 1.01839 37.31 13.20 13.35 13.34
    3 5.97×1019 1.05867 35.89 13.91 14.09 14.08
    4 32 5.07×1020 1.00418 31.87 11.10 11.14 11.13
    5 1.26×1020 1.01645 31.48 12.39 12.58 12.57
    6 5.34×1019 1.03737 30.85 13.17 13.25 13.23
    7 28 3.18×1020 1.00418 27.88 10.44 10.41 10.41
    8 1.15×1020 1.0114 27.68 11.32 11.46 11.46
    9 4.31×1019 1.02944 27.20 12.14 12.39 12.37
    10 23 1.00×1020 1.00664 22.85 9.87 9.82 9.81
    11 5.26×1019 1.0125 22.72 10.37 10.39 10.38
    12 2.23×1019 1.02862 22.36 11.00 11.11 11.10
    13 20 4.77×1019 1.00851 19.83 9.40 9.30 9.29
    14 1.06×1019 1.0364 19.30 10.42 10.44 10.43
    下载: 导出CSV

    表 2  COWAN计算采用的Sn11+—Sn14+离子的组态列表

    Table 2.  Configuration list of Sn11+ to Sn14+ ions.

    离子 组态
    Sn11+ 4s24p6 + {4d3, 4d25s, 4d25d, 4d4f2, 4d4f5p, 4d5s2,
    4d5p2, 4d5d2, 4d5p5d};
    4s24p5 + {4d34f, 4d35p, 4d35f, 4d24f5s, 4d24f5d,
    4d25s5p};
    4s24p4 + {4d5, 4d45s, 4d45d, 4d34f2, 4d34f5p};
    4s24p3 + {4d54f, 4d55p, 4d44f5s, 4d44f5d};
    4s4p6 + {4d4, 4d35s, 4d35d, 4d24f2, 4d24f5p};
    4s4p5 + {4d44f, 4d45p, 4d34f5s, 4d34f5d}.
    4s24p6 + {4d24f, 4d25p, 4d25f, 4d4f5s, 4d4f5d,
    4d5s5p};
    4s24p5 + {4d4, 4d35s, 4d35d, 4d24f2, 4d25s2, 4d24f5p,
    4d25s5d};
    4s24p4 + {4d44f, 4d45p, 4d34f5s, 4d34f5d};
    4s24p3 + {4d6, 4d55s, 4d55d, 4d44f2, 4d44f5p};
    4s4p6 + {4d34f, 4d35p, 4d24f5s, 4d24f5d};
    4s4p5 + {4d5, 4d45s, 4d45d, 4d34f2, 4d34f5p}.
    Sn12+ 4s24p6 + {4d2, 4d5s, 4d5d, 4f2, 4f5p, 5s2, 5p2,
    5d2, 5p5d};
    4s24p5 + {4d24f, 4d25p, 4d25f, 4d4f5s, 4d4f5d, 4d5s5p};
    4s24p4 + {4d4, 4d35s, 4d35d, 4d24f2, 4d24f5p};
    4s24p3 + {4d44f, 4d45p, 4d34f5s, 4d34f5d};
    4s4p6 + {4d3, 4d25s, 4d25d, 4d4f2, 4d4f5p};
    4s4p5 + {4d34f, 4d35p, 4d24f5s, 4d24f5d}.
    4s24p6 + {4d4f, 4d5p, 4d5f, 4f5s, 4f5d, 5s5p};
    4s24p5 + {4d3, 4d25s, 4d25d, 4d4f2, 4d5s2, 4d4f5p, 4d5s5d};
    4s24p4 + {4d34f, 4d35p, 4d24f5s, 4d24f5d};
    4s24p3 + {4d5, 4d45s, 4d45d, 4d34f2, 4d34f5p};
    4s4p6 + {4d24f, 4d25p, 4d4f5s, 4d4f5d};
    4s4p5 + {4d4, 4d35s, 4d35d, 4d24f2, 4d24f5p}.
    Sn13+ 4s24p6 + {4d, 5s, 5d};
    4s24p5 + {4d4f, 4d5p, 4d5f, 4f5s, 4f5d, 5s5p};
    4s24p4 + {4d3, 4d25s, 4d25d, 4d4f2, 4d4f5p};
    4s24p3 + {4d34f, 4d35p, 4d24f5s, 4d24f5d};
    4s4p6 + {4d2, 4d5s, 4d5d, 4f2, 4f5p};
    4s4p5 + {4d24f, 4d25p, 4d4f5s, 4d4f5d}.
    4s24p6 + {4f, 5p, 5f};
    4s24p5 + {4d2, 4d5s, 4d5d, 4f2, 5s2, 4f5p, 5s5d};
    4s24p4 + {4d24f, 4d25p, 4d4f5s, 4d4f5d};
    4s24p3 + {4d4, 4d35s, 4d35d, 4d24f2, 4d24f5p};
    4s4p6 + {4d4f, 4d5p, 4f5s, 4f5d};
    4s4p5 + {4d3, 4d25s, 4d25d, 4d4f2, 4d4f5p}.
    Sn14+ 4s24p6;
    4s24p5 + {4f, 5p, 5f};
    4s24p4 + {4d2, 4d5s, 4d5d, 4f2, 4f5p};
    4s24p3 + {4d24f, 4d25p, 4d4f5s, 4d4f5d};
    4s4p6 + {4d, 5s, 5d};
    4s4p5 + {4d4f, 4d5p, 4f5s, 4f5d}.
    4s24p5 + {4d, 5s, 5d};
    4s24p4 + {4d4f, 4d5p, 4f5s, 4f5d};
    4s24p3 + {4d3, 4d25s, 4d25d, 4d4f2, 4d4f5p};
    4s4p6 + {4f, 5p};
    4s4p5 + {4d2, 4d5s, 4d5d, 4f2, 4f5p}.
    下载: 导出CSV
  • [1] Bakshi V 2023 Photon Sources for Lithography and Metrology (Washington: SPIE Press
    [2] Bakshi V 2018 EUV Lithography (2nd Ed.) (Washington: SPIE Press
    [3] 林楠, 杨文河, 陈韫懿, 魏鑫, 王成, 赵娇玲, 彭宇杰, 冷雨欣 2022 激光与光电子学进展 59 0922002 doi: 10.3788/LOP202259.0922002 Lin N, Yang W H, Chen Y Y, Wei X, Wang C, Zhao J L, Peng Y J, Leng X Y 2022 Laser Optoelectron. Prog. 59 0922002 doi: 10.3788/LOP202259.0922002
    [4] Versolato O O 2019 Plasma Sources Sci. Technol. 28 083001 doi: 10.1088/1361-6595/ab3302
    [5] Versolato O O, Sheil J, Witte S, Ubachs W, Hoekstra R 2022 J. Opt. 24 054014 doi: 10.1088/2040-8986/ac5a7e
    [6] Behnke L, Schupp R, Bouza Z, Bayraktar M, Mazzotta Z, Meijer R, Sheil J, Witte S, Ubachs W Hoekstra R, Versolato O O 2021 Opt. Express 29 4475 doi: 10.1364/OE.411539
    [7] Schupp R, Behnke L, Sheil J, Bouza Z, Bayraktar M, Ubachs W, Hoekstra R, Versolato O O 2021 Phys. Rev. Res. 3 013294 doi: 10.1103/PhysRevResearch.3.013294
    [8] Schupp R, Behnke L, Bouza Z, Mazzotta Z, Mostafa Y, Lassise A, Poirier L, Sheil J, Bayraktar M, Ubachs W 2021 J. Phys. D: Appl. Phys. 54 365103 doi: 10.1088/1361-6463/ac0b70
    [9] Hemminga D J, Versolato O O, Sheil J 2023 Phys. Plasmas 30 033301 doi: 10.1063/5.0125936
    [10] Hernandez-Rueda J, Liu B, Hemminga D J, Mostafa Y, Meijer R A, Kurilovich D, Basko M, Gelderblom H, Sheil J, Versolato O O 2022 Phys. Rev. Res. 4 013142 doi: 10.1103/PhysRevResearch.4.013142
    [11] Meijer R A, Kurilovich D, Eikema K S E, Versolato O O, Witte S 2022 J. Appl. Phys. 131 105905 doi: 10.1063/5.0082352
    [12] Torretti F, Sheil J, Schupp R, Basko M M, Bayraktar M, Meijer R A, Witte S, Ubachs W, Hoekstra R, Versolato O O, Neukirch A J, Colgan J 2020 Nat. Comm. 11 2334 doi: 10.1038/s41467-020-15678-y
    [13] Sheil J, Versolato O O, Neukirch A J, Colgan J 2021 J. Phys. B: At. Mol. Opt. Phys. 54 035002 doi: 10.1088/1361-6455/abcedf
    [14] 高城, 刘彦鹏, 严冠鹏, 闫杰, 陈小棋, 侯永, 靳奉涛, 吴建华, 曾交龙, 袁建民 2023 物理学报 72 183101 doi: 10.7498/aps.72.20230455 Gao C, Liu Y P, Yan G P, Yan J, Chen X Q, Hou Y, Jin F T, Wu J H, Zeng J L, Yuan J M 2023 Acta Phys. Sin. 72 183101 doi: 10.7498/aps.72.20230455
    [15] Colgan J, Kilcrease D P, Abdallah Jr J, Sherrill M E, Fontes C J, Hakel P, Armstrong G S J 2017 High Energy Density Phys. 23 133 doi: 10.1016/j.hedp.2017.03.009
    [16] Sasaki A 2024 Appl. Phys. Lett. 124 064104 doi: 10.1063/5.0187576
    [17] Fujioka S, Nishimura H, Nishihara K, Sasaki A, Sunahara A, Okuno T, Ueda N, Ando T, Tao Y, Shimada Y, Hashimoto K, Yamaura M, Shigemori K, Nakai M, Nagai K, Norimatsu T, Nishikawa T, Miyanaga N, Izawa Y, Mima K 2005 Phys. Rev. Lett. 95 235004 doi: 10.1103/PhysRevLett.95.235004
    [18] Pan Y, Tomita K, Sunahara A, Sasaki A, Nishihara K 2023 Appl. Phys. Lett. 123 204103 doi: 10.1063/5.0174185
    [19] Su M G, Min Q, Cao S Q, Sun D X, Hayden P, O’Sullivan G, Dong C Z 2017 Sci. Rep. 7 45212 doi: 10.1038/srep45212
    [20] Basko M M, Sasorov P V, Murakami M, Novikov V G, Grushin A S 2012 Plasma Phys. Control. Fusion 54 055003 doi: 10.1088/0741-3335/54/5/055003
    [21] Nishihara K, Sunahara A, Sasaki A, Nunami M, Tanuma H, Fujioka S, Shimada Y, Fujima K, Furukawa H, Kato T, Koike F, More R, Murakami M, Nishikawa T, Zhakhovskii V, Gamata K, Takata A, Ueda H, Nishikawa T, Lzawa Y, Miyanaga N, Mima K 2008 Phys. Plasmas 15 056708 doi: 10.1063/1.2907154
    [22] Sizyuk T, Hassanein A 2015 Phys. Plasmas 22 093101 doi: 10.1063/1.4929786
    [23] Koshelev K N, Ivanov V V, Novikov V G, Medvedev V, Grushin A S, KrivtsunV M 2012 J. Micro. Nanolith. Mems. 11 021112 doi: 10.1117/1.JMM.11.2.021112
    [24] Min Q, Xu Z Y, He S Q, Lu H D, Liu X B, Shen R Z, Wu Y H, Pan Q K, Zhao C X, Chen F, Su M G, Dong C Z 2024 Comput. Phys. Commun. 302 109242 doi: 10.1016/j.cpc.2024.109242
    [25] Castor J J 2004 Radiation Hydrodynamics (Cambridge: Cambridge University Press
    [26] Levermore C D, Pomraning G C 1981 Astrophysical Journal 248 321 doi: 10.1086/159157
    [27] More R M, Warren K H, Young D A, Zimmerman G B 1988 Phys. Fluids 31 3059 doi: 10.1063/1.866963
    [28] Nikiforov A F, Novikov V G, Uvarov V B 2005 Quantum-Statistical Models of Hot Dense Matter and Methods for Computation Opacity and Equation of State (Basel: Birkhauser Verlag
    [29] Heltemes T A, Moses G A 2012 Comput. Phys. Commun. 183 2629 doi: 10.1016/j.cpc.2012.07.010
    [30] Faik S, Tauschwitz A, Iosilevskiy I 2018 Comput. Phys. Commun. 227 117 doi: 10.1016/j.cpc.2018.01.008
    [31] Young D A, Corey E M 1995 J. Appl. Phys. 78 3748 doi: 10.1063/1.359955
    [32] Chung H K, Chen M H, Morgan W L, Ralchenko Y, Lee R W 2005 High Energ. Dens. Phys. 1 3 doi: 10.1016/j.hedp.2005.07.001
    [33] Min Q, Shen R Z, Su M G, Lu H D, He S Q, Liu X B, Li Y, Tao Q Q, Wu Y H, Sun D X, Cao S Q, Dong C Z 2022 J. Phys. D: Appl. Phys. 55 505205 doi: 10.1088/1361-6463/ac9c12
    [34] Magee N H, Abdallah Jr. J, Clark R E H, Cohen J S, Collins L A, Csanak G, Fontes C J, Gauger A, Keady J J, Kilcrease D P, Merts A L 1995 Astronomical Society of the Pacific Conference Series (Astrophysical Applications of Powerful New Databases, S. J. Adelman and W. L. Wiese eds.) 78 51
    [35] He S Q, Min Q, Wu Y H, Liu X B, He C W, Cao S Q, Pan Q K, Guo J, Chen F, Zhang D H, Su M G, Dong C Z 2024 Opt. Express 32 17088 doi: 10.1364/OE.522198
    [36] Rodríguez R, Florido R, Gil J M, Rubiano JG, Martel P, Mínguez E 2008 Laser Part. Beams 26 433 doi: 10.1017/S026303460800044X
    [37] Yan G P, Gao C, Hou Y, Jin F T, Li Y J, Zeng J L, Yuan J M 2024 Phys. Plasmas 31 093303 doi: 10.1063/5.0226453
    [38] Macfarlane J J 1989 Comput. Phys. Commun. 56 259 doi: 10.1016/0010-4655(89)90023-4
    [39] Busquet M 1993 Phys. Fluids B 5 4191 doi: 10.1063/1.860586
    [40] Busquet M, Colombant D, Klapisch M, Fyfe D, Gardner J 2009 High Energ. Dens. Phys. 5 270 doi: 10.1016/j.hedp.2009.05.005
    [41] Cowan R D 1981 The Theory of Atomic Structure and Spectra (California: University of California Press
    [42] Schupp R, Torretti F, Meijer R A, Bayraktar M, Scheers J, Kurilovich D, Bayerle A, Eikema K S E, Witte S, Ubachs W, Hoekstra R, Versolato1 O O 2019 Phys. Rev. Appl. 12 014010 doi: 10.1103/PhysRevApplied.12.014010
  • 加载中
图( 11) 表( 2)
计量
  • 文章访问数:  217
  • HTML全文浏览数:  217
  • PDF下载数:  7
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-09-20
  • 刊出日期:  2025-02-05

激光锡等离子体的状态参数分布和极紫外波段辐射的模拟研究

    通讯作者: E-mail: mq_lpps@nwnu.edu.cn.; 
    通讯作者: E-mail: sumg@nwnu.edu.cn.; 
    通讯作者: E-mail:dongcz@nwnu.edu.cn.
  • 1. 西北师范大学物理与电子工程学院, 甘肃省原子分子物理与功能材料重点实验室, 兰州　730070
  • 2. 兰州工业学院计算机与人工智能学院, 兰州　730050
  • 收稿日期:  2024-09-20

摘要: 激光锡(Sn)等离子体光源是当前先进极紫外(EUV)光刻机中最为核心的分系统, 其辐射出的13.5 nm附近2%带宽内的EUV光的功率值和稳定性是决定整个光刻机是否成功的关键指标之一. 本文针对激光Sn等离子体光源这一复杂系统, 开展了详细的关于等离子体状态参数分布以及EUV辐射光谱的数值模拟研究. 首先基于细致能级模型, 在局域热动平衡近似条件下计算得到了Sn等离子体在12—16 nm波段的辐射不透明度数据. 随后利用激光等离子体辐射流体力学程序RHDLPP, 分别模拟了纳秒激光脉冲作用于Sn平面固体靶和液滴靶所产生的等离子体的温度和电子密度等状态参数的分布. 结合辐射不透明度数据和等离子体状态数据, 利用光谱模拟后处理子程序SpeIma3D完成了平面靶等离子体的空间分辨EUV光谱以及液滴靶等离子体在60°观测角下的角分辨EUV光谱的模拟. 最后, 得到了液滴靶等离子体在13.5 nm, 2%带宽内的带内辐射强度随观测角度的变化规律. 本文获得的所有等离子体状态参数分布和EUV光谱模拟结果与现有的实验结果具有很好的一致性, 证明了RHDLPP程序在激光Sn等离子体EUV光源方面的模拟能力, 相关结果可以为EUV光刻以及国产化EUV光源的研制提供一定的支持.

English Abstract

    全文HTML

    1.   引　言

    • 荷兰ASML (Advanced Semiconductor Material Lithography)公司的极紫外(extreme ultraviolet, EUV)光刻机目前已用于7 nm和5 nm技术节点的芯片生产中[1,2], 这不仅标志着先进半导体制程正式进入极紫外光刻(extreme ultraviolet lithography, EUVL)时代, 同时意味着EUV光刻机已成为先进芯片大规模量产和工业化不可或缺的设备, 是未来工艺制程延续的保障. EUV光源是EUV光刻机中最为核心的分系统, 也是光刻机实现稳定运行的最大难点. ASML公司的商用EUV光刻机采用激光锡(Sn)等离子体发出的以13.5 nm为中心、2%带宽内的EUV辐射作为光源[1,2]. 为了满足大规模量产的需求, 该激光等离子体EUV光源(LPP-EUV)系统应具有被收集到中心焦点(intermediate focus, IF)处的EUV光功率高且稳定、污染低、维护成本低等性能. 其中特别是IF点处高功率、高稳定性的EUV光是决定整个光刻机是否成功的关键指标之一[1,2].

      激光Sn等离子体光源在IF点的EUV光功率由入射激光功率、EUV光转换效率(conversion efficiency, CE)、整体传输效率以及光源功率稳定性共同决定[1,2]. 其中, 光源的CE值是指EUV光的能量除以输入激光能量并换算成百分数后所得到的数值[1]. 提升CE值一直是EUV光刻光源领域最为重要的研究课题之一. 在过去的二十多年, 国内外研究人员主要从优选靶材组分及形态、优选激光源和采取预、主双脉冲方案等方面来探索提高CE的途径[1–11]. 这些措施背后所涉及的核心物理问题包括激光Sn等离子体中EUV辐射的来源和跃迁指认、EUV辐射在等离子体中的输运特性以及激光Sn等离子体的状态诊断和调控等.

      在EUV辐射的来源识别方面, 直到2020年之前国内外的主流看法都认为激光Sn等离子体的EUV光主要来自于Sn8+—Sn14+离子的退激发辐射, 涉及的跃迁应该以从单激发态4p54dm +1, 4p64dm –14f, 4p64dm –15p到基态4p64dm的单电子跃迁为主, 其中m取值0—6分别对应于Sn14+离子到Sn8+离子. 然而2020年Torretti等[12]的研究对这种看法提出了挑战. 他们对Sn11+—Sn14+离子在原有的基态和单激发态的基础上又考虑了双激发态、三激发态和更高的多重激发态的贡献[12,13]. 结果表明多重激发态之间的跃迁贡献要远远大于传统的单电子激发态到基态的跃迁. 同时, 高城等[14]在2023年基于多组态Dirac-Fock方法开展的大规模组态相互作用计算也进一步证实了这一结论. 虽然Torretti等[12]和高城等[14]的研究为理解激光Sn等离子体EUV光的辐射性质提供了新的视角, 但是这种包含了电子关联效应的大规模组态相互作用计算的结果(能级、跃迁波长和跃迁几率等)还需要更多精密实验和其他计算的验证[15,16].

      除了对等离子体中高电荷态Sn离子的辐射跃迁参数进行了细致计算之外, 研究人员还针对激光Sn等离子体的状态诊断和辐射输运特性开展了大量的实验和数值模拟研究. 例如在实验方面, Fujioka等[17]测量了Sn等离子体在9—19 nm波段的透射谱, 揭示了光学厚度对CE值的重要影响. 荷兰ARCNL (Advanced Research Center for Nanolithography)的研究团队[4–7,9,10]开展了大量基于Sn液滴的等离子体EUV光谱测量工作, 探讨了不同激光参数和液滴参数对等离子体状态以及EUV辐射强度的影响. Pan等[18]结合Thomson散射方法和发射光谱法, 联合测量了激光作用于Sn平面靶产生的等离子体的电子密度、温度以及10—18 nm波段的发射光谱. 本研究团队[19]在早期测量了不同强度的Nd:YAG激光烧蚀Sn平面靶产生的EUV光谱, 并细致分析了光谱中的自吸收特征.

      除了实验测量, 完备的数值模拟程序是进行激光Sn等离子体状态诊断和辐射特性研究的有力工具. 激光等离子体在其形成、演化及EUV辐射过程中涉及包括激光的传输与能量沉积、靶材和等离子体的动力学演化、靶材的相变、EUV辐射在等离子体内部的输运、等离子体内部各种粒子间的相互作用以及等离子体自身辐射场对宏观状态的影响等众多复杂的物理过程. 如今, 这些物理过程中的大部分都可以被高保真地建模. 然而, 开发一个能够模拟这些过程在不同空间和时间尺度上相互作用的多物理计算工具仍然是一项复杂且长期的工作. 迄今为止, 已有一些基于辐射流体力学方法的模拟程序被用来进行较大时空尺度上激光Sn等离子体的相关研究. 这些程序比较典型的有: Basko等[20]开发的任意拉格朗日-欧拉(ALE)程序RALEF-2D, 该程序是目前国际上在激光Sn等离子体EUV辐射和动力学演化特性研究方面应用最广泛的程序; Nishihara等[21]开发的二维轴对称辐射流体力学程序STAR2D; Sizyuk和Hassanein[22]开发的三维磁流体力学(MHD)程序HEIGHTS; Koshelev等[23]开发的基于欧拉方法的二维辐射流体力学程序RZLINE; 本研究团队[24]在近期开发完成的辐射流体力学程序RHDLPP. 该程序可以很好地模拟激光诱导的Sn液滴形变、激光Sn等离子体状态参数的时空分布以及激光作用于Sn平面靶或液滴靶产生的等离子体的EUV光谱.

      上述的辐射跃迁参数计算、实验测量和数值模拟程序使得人们对激光Sn等离子体的动力学演化以及EUV辐射特性有了比较清晰地认识. 但是在对LPP-EUV光源进行总体模拟时, 仍需在EUV光的辐射跃迁及输运特性的理解、数目庞大的辐射跃迁参数与大尺度等离子体模拟的耦合以及与实验测量装置尽量匹配的光谱和CE模拟等方面进行改进.

      本文针对实验上测量得到的激光Sn等离子体EUV光谱, 首先利用原子结构计算程序COWAN开展了大规模组态相互作用计算. 基于计算的高电荷态Sn离子的辐射跃迁数据, 利用细致能级模型获得了EUV波段的辐射不透明度数据. 随后利用激光等离子体辐射流体力学程序RHDLPP, 模拟了激光作用于Sn平面靶和液滴靶产生的等离子体的参数分布. 最后结合计算的等离子体状态参数和辐射不透明度数据, 利用光谱模拟后处理子程序RHDLPP-SpeIma3D完成了时间积分、空间分辨/角分辨实验光谱的模拟. 各种模拟结果与相关的实验结果具有较好的一致性.

    2.   模拟程序

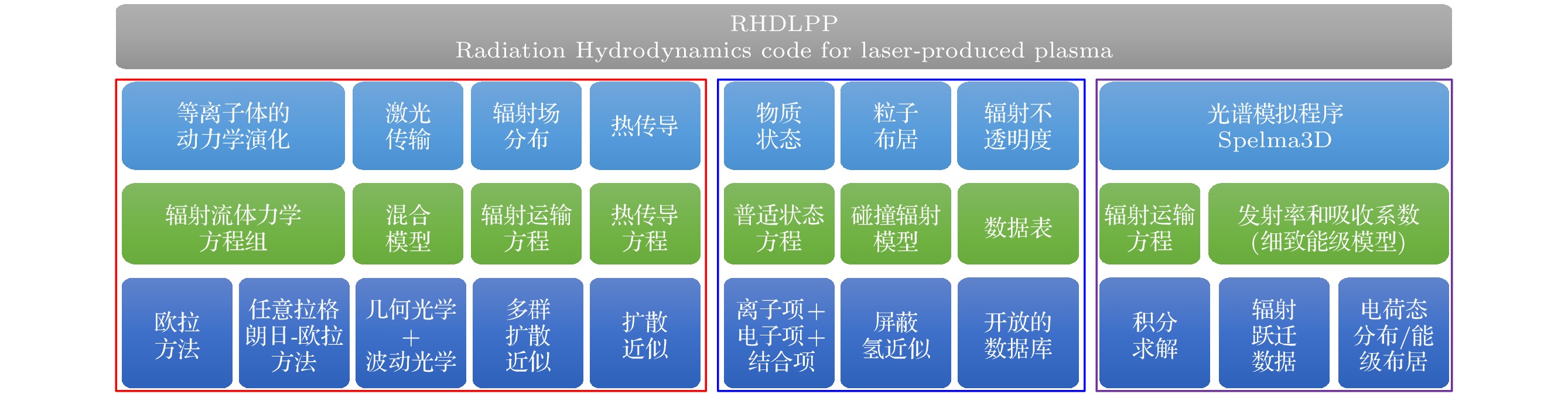
    • 对一个具有13.5 nm, 2%带宽内EUV辐射能力的激光Sn等离子体进行数值模拟需要对程序提出如下要求: 1)激光Sn等离子体在形成、演化和辐射过程中涉及丰富的物理过程, 程序需要涵盖其中的绝大多数过程; 2)构建模型的方程能够反映出相应物理过程的特性; 3) 在实验条件明确的前提下能够对已有的实验结果做出解释并模拟; 4) 具有较强的新结果预测能力和实验方案优化能力. 近年来我们开发了一套能够对激光等离子体的形成、演化和辐射等过程进行数值模拟的辐射流体力学程序RHDLPP (Radiation HydroDynamics code for Laser-Produced Plasma)[24]. 该程序考虑了激光等离子体中的大多数物理过程, 程序的框架及主要模块如图1所示. 其中将激光等离子体的形成和演化等过程分成激光传输及吸收、等离子体的演化、辐射与物质的相互作用以及热传导等4个耦合的“核心计算模块”, 如图1中红色实线框所示; 程序运行所必需的粒子布居、辐射不透明度(opacity)和物质状态参数等数据在“物理参数模块”中计算, 如蓝色实线框所示; 等离子体的光谱模拟在后处理子程序RHDLPP-SpeIma3D (该子程序还可以进行激光Sn等离子体在IF点处的EUV辐射功率和CE的计算)中完成, 如紫色实线框所示. 下面对这几个模块和子程序进行简要介绍.

      RHDLPP程序基于单流、双温(电子温度$ {T}_{{\mathrm{e}}} $=离子温度$ {T}_{{\mathrm{i}}} $≠辐射温度$ {T}_{{\mathrm{r}}} $)的辐射流体力学模型编写而成. 图1中红色实线框所示的4个核心计算模块处理的主要物理过程包括激光与靶材的相互作用及等离子体的形成、激光与等离子体的相互作用及激光的传输、等离子体的动力学演化、等离子体内部的辐射场分布及辐射与物质的相互作用、能量在等离子体内部的传导等. 这些模块中求解的方程可统一写成如下作了多群、限流扩散(flux-limited diffusion, FLD)近似的辐射流体力学方程组形式[24]:

      这里, $ \rho $, $ \boldsymbol{u} $, $ T $和$ p $分别代表物质的密度、速度、 温度和压强. $ E $是物质能量(内能加动能)密度. 电子热导率用$ {C}_{{\mathrm{e}}} $表示, $ {Q}_{{\mathrm{L}}} $代表激光加热产生的 能量源项. $ G $表示多群近似下辐射群的数目, $ g $代表各群的编号, 每个群的辐射能量密度用$ {E}_{g} $表 示. $ {B}_{g}= (15 a{T}^{4}/{{\mathrm{\pi }}}^{4})[P({x}_{g+1})-P({x}_{g})] $, 其中$ a $是辐射常数, $ P\left(x\right) $表示普朗克积分, 定义为 $ P(x)= \displaystyle\int _{0}^{x} {\rm d} x' \dfrac{x'^3}{{\rm e}^{x'} -1} $. $ {\lambda }_{g} $和$ {f}_{g} $分别为通量限制器和Eddington因子, 光速用$ c $表示.

      方程(3)和(4)中的$ {\kappa }_{{\mathrm{R}}, g} $, $ {\kappa }_{{\mathrm{P}}{\mathrm{e}}, g} $和$ {\kappa }_{{\mathrm{P}}{\mathrm{a}}, g} $分别表示第$ g $群的Rosseland平均不透明度、Planck平均发射不透明度和吸收不透明度, 具体的计算公式为

      其中$ {B}_{\nu }\left(T\right) $为温度为$ T $时的Planck分布函数; $ {\kappa }_{\nu } $和$ {j}_{\nu } $分别表示吸收系数和发射率; $ {x}_{g} $和$ {x}_{g+1} $分别为$ {x}_{g}=h{\nu }_{g}/{(k}_{{\mathrm{B}}}T) $和$ {x}_{g+1}=h{\nu }_{g+1}/({k}_{{\mathrm{B}}}T) $, $ {\nu }_{g} $和$ {\nu }_{g+1} $表示第$ g $群的光子频率上下限, $ {k}_{{\mathrm{B}}} $为玻尔兹曼常数.

      在FLD近似下, 方程(3)中的电子热通量$ {\boldsymbol{F}}_{{\mathrm{e}}}= -{C}_{{\mathrm{e}}}\nabla T $和方程(4)中的辐射通量$ {\boldsymbol{F}}_{g} $可写成如下形式[25]:

      其中方程(9)为Levermore和Pomraning[26]给出的通量限制器的形式. 方程(10)中$ f $表示可调节的通量限制器因子.

      RHDLPP程序对方程组(1)—(4)的求解有两种方法, 分别是欧拉法和任意拉格朗日-欧拉法. 这两种方法都是基于算子分裂(operator-split)格式进行数值求解, 其核心是先构建显式格式求解(1)—(4)式右端全部为0的双曲型方程, 然后构建隐式格式求解剩余的包括辐射扩散、热传导和激光源项在内的抛物型方程. 详细的数值求解方法可参考我们以前的工作[24], 在本文中不再进行细致介绍. 作为唯一的外部源项, 入射激光在靶材和等离子体中的传输及能量沉积是决定激光等离子体特性的重要因素. 在RHDLPP程序中, 我们使用了一个混合模型[24]来解决激光传输和能量沉积问题. 该模型在亚临界等离子体区域采用几何光学射线追踪方法, 而在超临界等离子体区域则求解一维的亥姆霍兹波动方程.

      图1中蓝色实线框所示的物理参数模块主要负责为程序的运行提供必需的状态参数、平均电离度、电荷态分布、辐射不透明度、吸收系数和发射系数等数据. 其中压强和内能等状态参数由物质状态模块提供. 该模块基于More等[27]提出的普适状态方程模型开发而成, 适用于电子温度10–4—106 eV、密度10–10—103 g/cm3的宽参数范围. 模块中物质的热力学量分为电子项、离子项和修正项. 电子项的贡献采用典型的托马斯-费米模型进行求解[28], 离子项的贡献采用经过标度结合能修正的Cowan模型进行求解[27,29]. 对于修正项, 在物质密度大于固体密度时采用键合修正模型[30], 而在物质密度小于固体密度时则采用Young和Corey [31]提出的软球函数模型. 另外, 模块中还可以利用麦克斯韦重构方法对气液共存亚稳态的相关热力学量进行进一步修正[30]. 平均电离度和电荷态分布利用基于屏蔽氢近似的碰撞辐射模型求解, 模型中考虑了电子碰撞激发和退激发、电子碰撞电离和三体复合、光电离和辐射复合、自电离和双电子俘获等12种原子过程[32,33]. 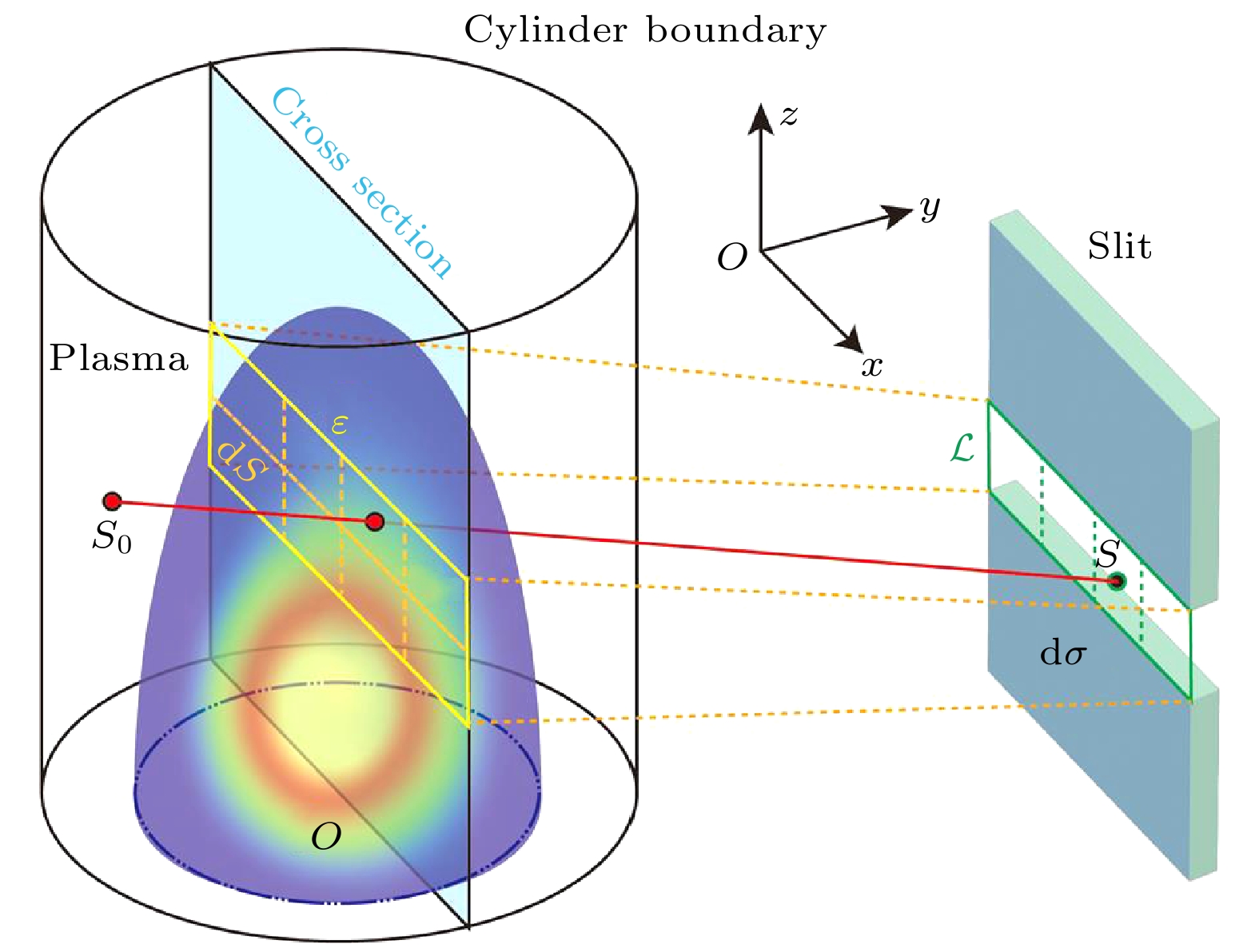方程(5)—(7)中的宽波段吸收系数和发射率来自TOPS Opacities[34]和THERMOS [28]数据库, 将这些辐射参数根据公式转换成$ {\kappa }_{{\mathrm{R}}, g} $, $ {\kappa }_{{\mathrm{P}}{\mathrm{e}}, g} $和$ {\kappa }_{{\mathrm{P}}{\mathrm{a}}, g} $等多群辐射不透明度数据后, 按温度、离子数密度和辐射群做成表格存入辐射不透明度模块中供程序调用.

      图1中紫色实线框所示为光谱模拟后处理子程序SpeIma3D[24,35]. 该子程序可以实现激光等离子体在特定波段的时空分辨光谱、角分辨光谱、积分光谱、瞬态成像以及转换效率的模拟. 程序的模拟流程可分为3步进行. 第1步, 由RHDLPP程序计算等离子体状态参数, 例如温度、电子密度和离子丰度的二维轴对称分布. 随后根据等离子体的轴对称特性, 将二维的状态参数通过绕对称轴旋转的方式转换为三维分布. 紧接着划定一个如图2中的圆柱面包围三维等离子体[35].

      第2步, 基于光谱仪狭缝和三维等离子体的方位来构建多条光线路径, 即进行光线追踪. 如图2所示, 先将谱仪狭缝离散成面积相等的面元dσ. 随后, 在等离子体内定义一个与狭缝对称的矩形区域ε. ε的大小取决于狭缝的视角和狭缝与等离子体对称轴之间的距离. 类似地, 区域ε也被划分为更小的面元, 用dS表示. 原则上需要dσ和dS的面积趋于无穷小, 然而在程序的实际编写中, dσ和dS的面积只能为有限值. 因此, 我们需要通过执行收敛性测试来确定出两个面元的最小面积. 随后用直线连接它们的几何中心就可构建出光线路径. 从图2可以看出, 每条路径的终点在狭缝表面的dσ中心. 为了确保光线穿过整个等离子体, 需将光线起点从dS的中心延伸到边界圆柱面.

      第3步, 沿着每条光线路径求解稳态辐射输运方程, 以此来计算出光线终点处任意光子频率$ \nu $所对应的辐射强度$ {I}_{\nu } $. 辐射输运方程一维积分解的形式为

      其中$ {s}_{0} $是光线的起点, 位于边界圆柱表面上; $ {I}_{\nu 0} $是起点处的辐射强度, 如果不存在外部的辐射源, 则$ {I}_{\nu 0}=0 $; $ s $表示射线的终点, 位于狭缝面元$ {\mathrm{d}}\sigma $的中心; $ {j}_{\nu } $和$ {\kappa }_{\nu } $分别表示光线路径上不同位置处的发射率和吸收系数.

      在任意时刻, 面元$ {\mathrm{d}}\sigma $从面元$ {\mathrm{d}}S $收集到的频率为$ \nu $的辐射能量$ E({\mathrm{d}}S\to {\mathrm{d}}\sigma ) $ 可以用以下方程计算:

      其中, $ {{\Delta }}S $表示面元$ {\mathrm{d}}\sigma $的大小, $ {{\Delta }}\varOmega $表示面元$ {\mathrm{d}}S $相对于$ {\mathrm{d}}\sigma $中心的立体角, $ \theta $是光线与面元$ {\mathrm{d}}\sigma $的法线之间的夹角. 最后, 通过对整个狭缝$ \mathcal{L} $和区域$ \varepsilon $进行积分, 就可以计算出在时间间隔$ {{\Delta }}t $内从区域$ \varepsilon $到达狭缝$ \mathcal{L} $的频率为$ \nu $的总辐射能量$ E(\varepsilon \to \mathcal{L}) $:

      辐射能量$ E(\varepsilon \to \mathcal{L}) $即最终的模拟光谱强度, 可用来与进行了强度定标的实验光谱比对.

    3.   Sn等离子体在EUV波段的辐射不透明度

    • 进行等离子体和光谱模拟时, 发射率与辐射不透明度是决定模拟质量的关键辐射参数. 由于激光等离子体的形成及演化过程中涉及的温度范围很宽(例如从靶材的初始温度-室温, 到等离子体的最高温度-约上百电子伏特), 因此与等离子体模拟相关的方程(5)—(7)中发射率与辐射不透明度的波长范围需从红外直至X射线波段. 而在进行光谱模拟时, 方程(11)中所需的辐射参数只涉及较窄的波段(例如本文的光谱模拟中波长范围仅从12—16 nm). 一般而言, 程序中需要先计算好方程(5)—(7)中不同温度、密度点的宽波段辐射参数, 随后从这些参数中截取出特定波段的数据来执行光 谱模拟. 在进行本文的激光Sn等离子体状态分布模拟时, 我们调用了取自THERMOS数据库[28] 的宽波段吸收系数和发射率. 然而, 这些辐射参数在EUV波段并未考虑高电荷态Sn离子多激发态之间的跃迁贡献, 若截取此类数据进行激光Sn等离子体的EUV光谱模拟将无法很好地再现实验 结果[12]. 因此, 我们在SpeIma3D光谱模拟程序中针对EUV波段的吸收系数和发射率重新进行了细致的计算.

      为了能很好地解释和匹配实验光谱中的细致结构, 我们在计算EUV波段的辐射参数时采用了精度最高的细致能级(detailed-level-accounting, DLA)模型[14]. 在DLA模型中, 对于一定温度、密度的等离子体, 在光子频率$ \nu $处, 辐射不透明度$ \rho {\kappa }_{\nu } $由束缚-束缚吸收系数$ {\mu }_{{\mathrm{b}}{\mathrm{b}}}\left(\nu \right) $、束缚-自由吸收系数$ {\mu }_{{\mathrm{b}}{\mathrm{f}}}\left(\nu \right) $、自由-自由吸收系数$ {\mu }_{{\mathrm{f}}{\mathrm{f}}}\left(\nu \right) $以及散射系数$ {\mu }_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}{\mathrm{t}}}\left(\nu \right) $共同贡献, 其表达式为[36]

      其中$ i $和$ j $代表离子$ \xi $的能级, $ {N}_{{\xi }_{i}} $是电离度为$ \xi $的离子的第$ i $个能级上的数密度, $ g $表示能级简并度, $ {f}_{{\xi }_{i, j}} $代表振子强度, $ {N}_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}} $表示总的离子数密度, 线型函数$ {\phi }_{{\xi }_{i, j}}\left(\nu \right) $采用Voigt线型, $ {\sigma }_{{\mathrm{b}}{\mathrm{f}}}\left(\nu \right) $和$ {\sigma }_{{\mathrm{f}}{\mathrm{f}}}\left(\nu \right) $分别表示光电离截面和自由-自由截面. 由于以前的工作已经表明Sn等离子体在EUV波段的总吸收系数主要来自于束缚-束缚吸收系数, 束缚-自由吸收系数和自由-自由吸收系数的贡献很小[17,37]. 因此本文中计算截面$ {\sigma }_{{\mathrm{b}}{\mathrm{f}}}\left(\nu \right) $和$ {\sigma }_{{\mathrm{f}}{\mathrm{f}}}\left(\nu \right) $时采用了比较简单的经验公式, 具体形式可参见文献[36,38], 在此不再给出. 散射系数$ {\mu }_{{\mathrm{s}}{\mathrm{c}}{\mathrm{a}}{\mathrm{t}}{\mathrm{t}}}\left(\nu \right) $通过Thomson散射截面获得[38].

      在DLA模型中计算吸收系数时, 需要知道等离子体中不同离子的电荷态分布以及每种离子在不同细致能级上的布居数. 而这些布居参数的求解又与等离子体状态密切相关. 一般来讲, 将等离子体视为处于非局域热动平衡(non-local-thermodynamic equilibrium, non-LTE)状态后建立CR模型, 进而求解大规模的速率方程组来获得各离子的能级布居是最严格的方法. 然而将这种方法应用于DLA模型计算Sn等离子体在EUV波段辐射不透明度中时会非常棘手. 主要原因是能够发出EUV辐射的Sn8+—Sn14+离子共有接近于106量级的细致能级, 如此庞大的能级数目使得我们很难完整获得相关能级间碰撞或辐射过程的动力学参数, CR模型的速率方程组求解也会变得十分困难. 鉴于此, 本文将利用局域热动平衡(local thermodynamic equilibrium, LTE)近似下的DLA模型来计算激光Sn等离子体在EUV波段的辐射不透明度. 在LTE近似下, 电荷态分布采用Saha-Boltzamnn方程计算, 能级布居满足Boltzamnn分布, 发射率$ {j}_{\nu } $与吸收系数$ {\kappa }_{\nu } $满足Kirchhoff 定律. 下面简要评估LTE近似在本文工作中的适用性.

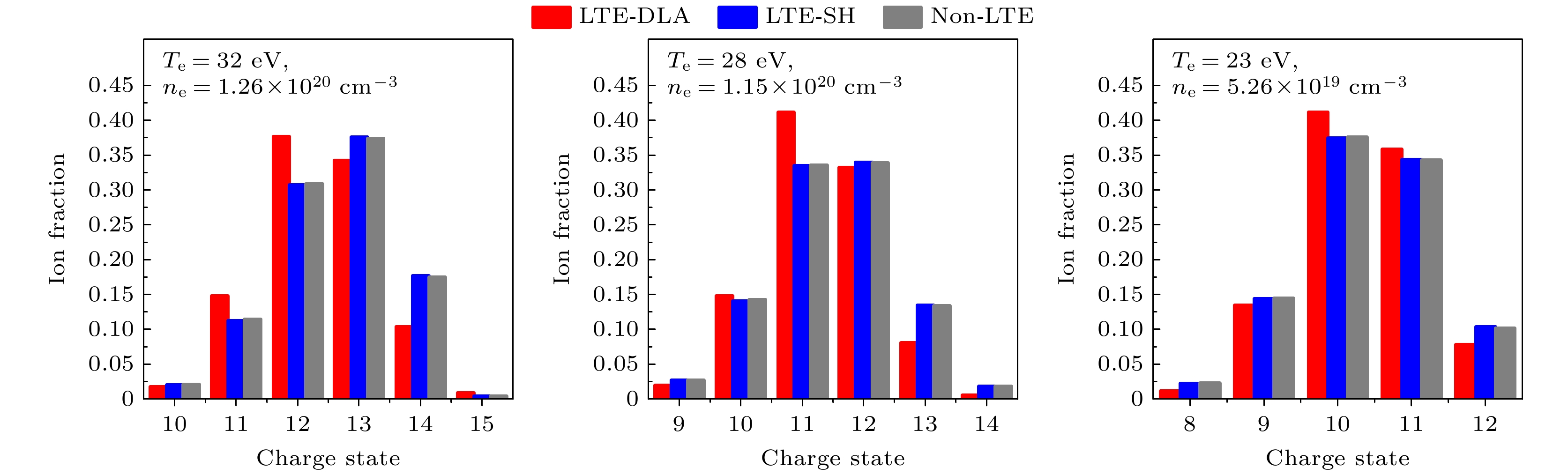
      首先, 本文中的Sn等离子体由波长为1064 nm的Nd:YAG激光产生(详见4.1节和4.2节), 这种等离子体的临界密度约为1021 cm–3, 相应的激光能量将主要沉积在临界密度附近. 该情形下等离子体中EUV辐射区域(特别是13.5 nm附近)的电子密度和温度大致在1019—1021 cm–3和20—40 eV范围[4], 此时微观粒子间的相互作用基本以碰撞过程为主. 接下来, 我们利用Busquet提出的电离温度方法(ionisation temperature method)[39,40]来进行进一步的评估. 对于温度为$ {T}_{{\mathrm{e}}} $、密度为$ \rho $的等离子体状态参数, 需要先得到一个新的电离温度$ {T}_{Z} $. 在$ \left({T}_{Z}, \rho \right) $下基于LTE近似中的Saha-Boltzamnn方程获得的电荷态分布要保证与在$ \left({T}_{{\mathrm{e}}}, \rho \right) $下利用non-LTE条件中的CR模型获得的结果一致. 另外, Busquet等[40]还给出了$ {T}_{{\mathrm{e}}} $和$ {T}_{Z} $之间的标度律公式, $ R = {T}_{{\mathrm{e}}}/{T}_{Z}\approx {[1+\left(5.36\times {10}^{13}\right){T}_{{\mathrm{e}}}^{3.5}/{n}_{{\mathrm{e}}}]}^{0.215}, $ 其中$ {n}_{{\mathrm{e}}} $表示电子密度. 利用$ {T}_{{\mathrm{e}}} $和$ {T}_{Z} $的比值$ R $可以粗略估计出LTE近似与non-LTE条件之间的偏离程度. 我们选取了14组与Nd:YAG激光产生的Sn等离子体EUV辐射相关的参数计算了比值R, 相应的结果在表1中列出. 可以看出, 在这些状态参数下$ {T}_{{\mathrm{e}}} $和$ {T}_{Z} $的比值都接近于1, 表明LTE近似基本成立.

      另外, 我们还直接对比了non-LTE和LTE条件下不同Sn离子的电荷态分布和平均电荷态. 其中, non-LTE条件下的结果利用第2节中提到的基于屏蔽氢近似的稳态CR模型进行计算, LTE条件下的结果分别利用基于屏蔽氢近似和基于细致能级的Saha-Boltzamnn方程得到. 平均电荷态在表1中的最后3列给出, 3组$ \left({T}_{{\mathrm{e}}}, {n}_{{\mathrm{e}}}\right) $下离子电荷态分布的对比结果在图3中给出. 表中$ {\left\langle{Z}\right\rangle}_{{\mathrm{LTE}}\text{-}1} $和图中红色柱状图代表 LTE条件下基于细致能级的结果, 表中$ {\left\langle{Z}\right\rangle}_{{\mathrm{LTE}}\text-2} $和图中蓝色柱状图代表LTE条件下基于屏蔽氢近似的结果, $ {\left\langle{Z}\right\rangle}_{{\mathrm{n}}{\mathrm{o}}{\mathrm{n}}\text-{\mathrm{LTE}}} $和灰色柱状图代表non-LTE条件下基于屏蔽氢近似的结果. 通过表中平均电荷态的对比可以发现, 3种方法获得的结果基本一致. 而在电荷态分布图中, 基于屏蔽氢模型的LTE和non-LTE结果非常接近, 基于细致能级模型的LTE结果则略有偏差. 这种差别来自于两种模型的精细程度, 屏蔽氢模型显然在原子结构和动力学参数计算层面上是一个非常粗略的近似. 但是, 屏蔽氢模型下LTE和non-LTE结果的高度一致仍然可以证明LTE近似适用于本文Nd:YAG激光产生的Sn等离子体的EUV辐射参数计算中.

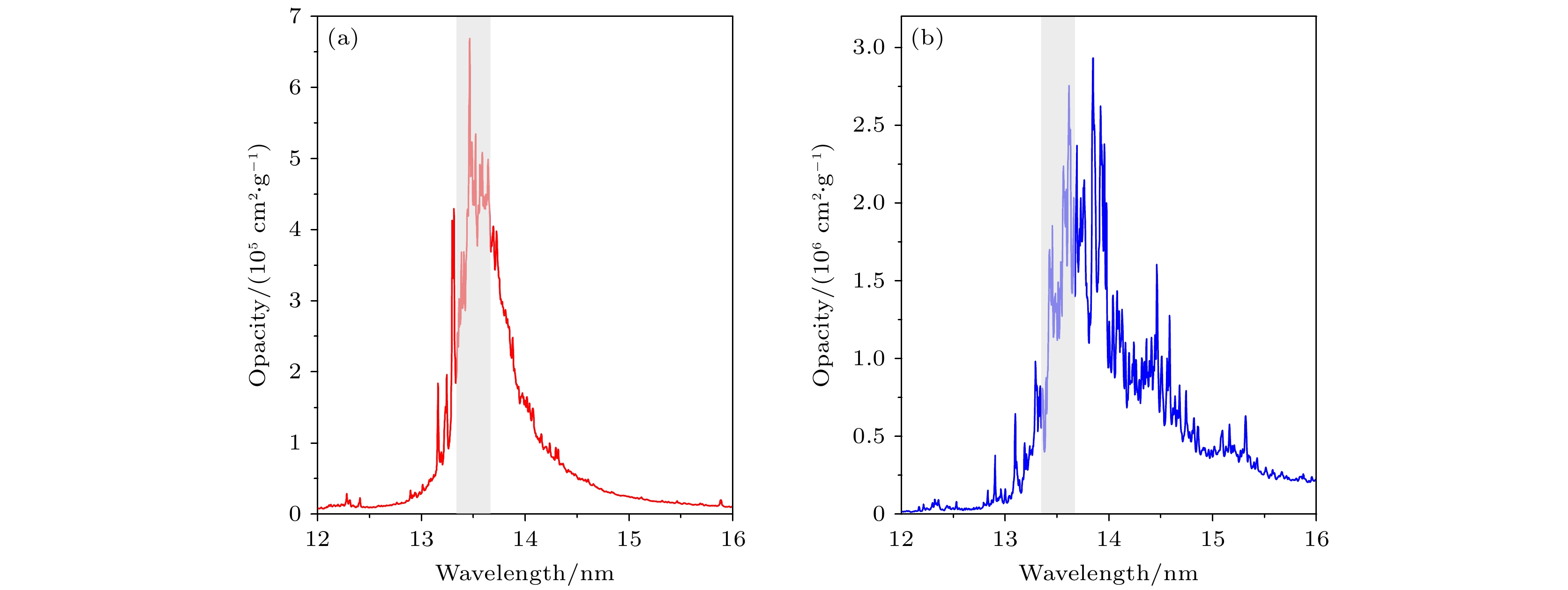
      对于(15)式束缚-束缚吸收系数$ {\mu }_{{\mathrm{b}}{\mathrm{b}}}\left(\nu \right) $中涉及的Sn离子能级和振子强度等原子参数, 本文利用原子结构计算程序COWAN[41]开展大规模的组态相互作用计算得到. 以Sn11+—Sn14+离子为例, 计算中包括的组态如表2所列.

      获得能级和振子强度等原子参数后, 使用DLA模型计算得到了波长范围12—16 nm、温度范围10—100 eV、密度范围10–6—10 g/cm3条件下Sn等离子体的辐射不透明度. 这些数据以表格的形式存储, 供SpeIma3D程序调用来进行EUV波段的光谱模拟. 图4给出了温度为32 eV(图4(a))和20 eV(图4(b))、密度为0.002 g/cm3时Sn等离子体的EUV辐射不透明度. 图中灰色阴影区域表示EUV光刻所关注的以13.5 nm为中心的2%带宽. 图4(a)条件的Sn等离子体其平均电荷态为12.6, 等离子体中占主导的离子类型为Sn11+, Sn12+, Sn13+和Sn14+, 丰度分别为0.12, 0.31, 0.37, 0.17; 而在图4(b)中, 20 eV下Sn等离子体的平均电荷态为8.8, 等离子体中占主导的离子类型为Sn7+, Sn8+, Sn9+和Sn10+, 丰度分别为0.08, 0.28, 0.41, 0.2. 在图示的波长范围内, 本文的计算结果表明单电子、双电子和三电子激发态对该波段的辐射不透明度有非常重要的贡献, 占比可达80%以上. 这与Torretti等[12]利用CATS程序和高城等[14]利用GRASP2K程序计算所得的结论基本一致. 另外, 图4(a)所示的辐射不透明度结果与Torretti等[12]的计算结果(文献[12]中的图3)也有很好的一致性.

    4.   结果与讨论

    • 获得不同温度、密度下Sn等离子体的EUV辐射不透明度数据后, 本文利用RHDLPP程序 完成了激光作用于Sn平面固体靶和球形液滴靶 产生的等离子体的参数分布计算并利用SpeIma 3D程序结合不透明度数据实现了EUV光谱的 模拟.

      • 4.1.   激光作用于Sn平面固体靶

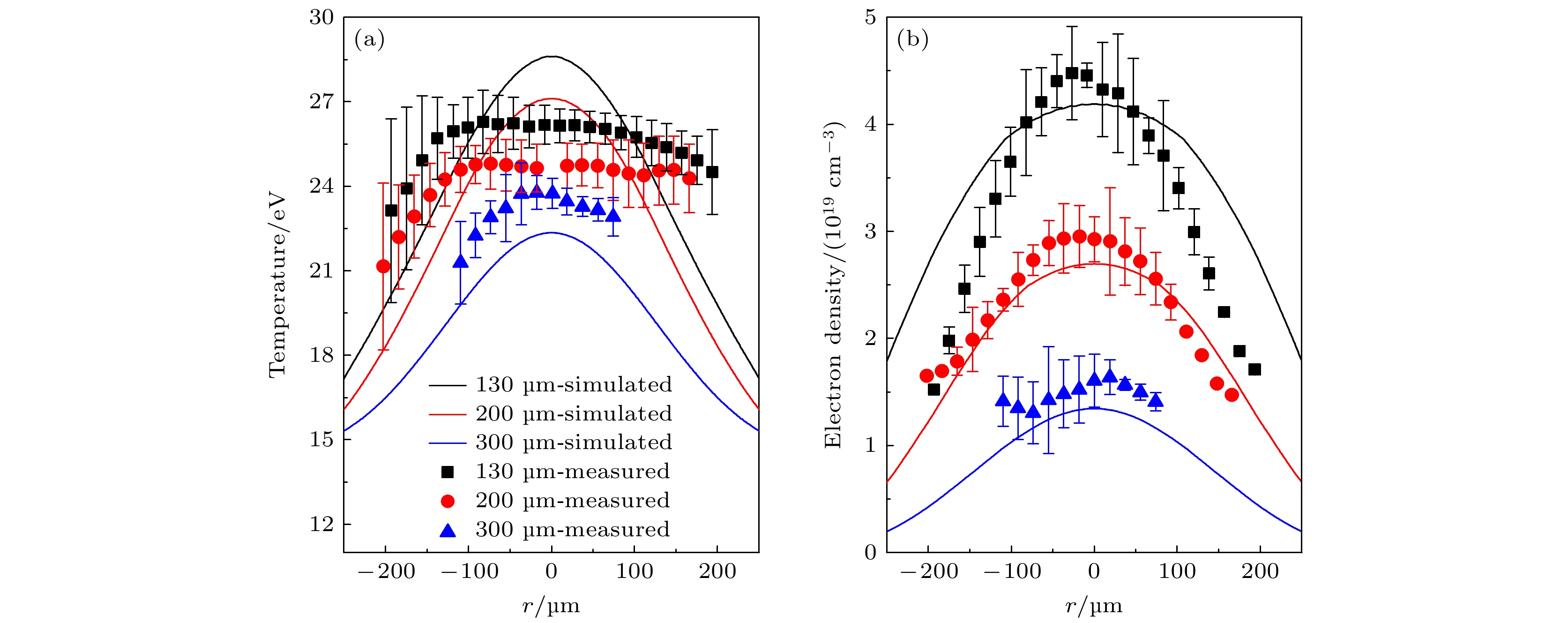
    • 该模拟中选用了一个厚度为 100 μm, 密度为 7.3 g/cm3的平面固体 Sn 靶. 背景气体设定为氢气, 密度为10–9 g/cm3. 烧蚀激光设置为在时间、空间上都为高斯型分布的Nd:YAG激光脉冲, 峰值功率密度为 3×1010 W/cm2, 半高全宽为 7 ns, 波长1.064 μm, 在靶材表面的焦斑半径为275 μm. 激光作用于靶面的时刻被定义为零时刻, 激光强度高斯分布的峰值时刻为10.5 ns. 靶材和背景气体的初始温度为300 K. 这些模拟参数与Pan等[18]结合Thomson散射法和发射光谱法联合测量激光Sn等离子体参数分布和空间分辨EUV光谱所采用的实验条件一致. 模拟在二维轴对称 (r-z)坐标系中进行, 整个计算区域设定为$ 0 < z < 900{\text{ μ}}{\mathrm{m}},\; 0 < r < 700{\text{ μ}}{\mathrm{m}} $. 固体Sn靶位于$ 0 < z < 100{\text{ μ}}{\mathrm{m}},\; 0 < r < 700{\text{ μ}}{\mathrm{m}} $的区域, 靶面位置在$ z= 100{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\text{ μ}}{\mathrm{m}} $处. 激光沿着z轴自上向下作用于靶面.

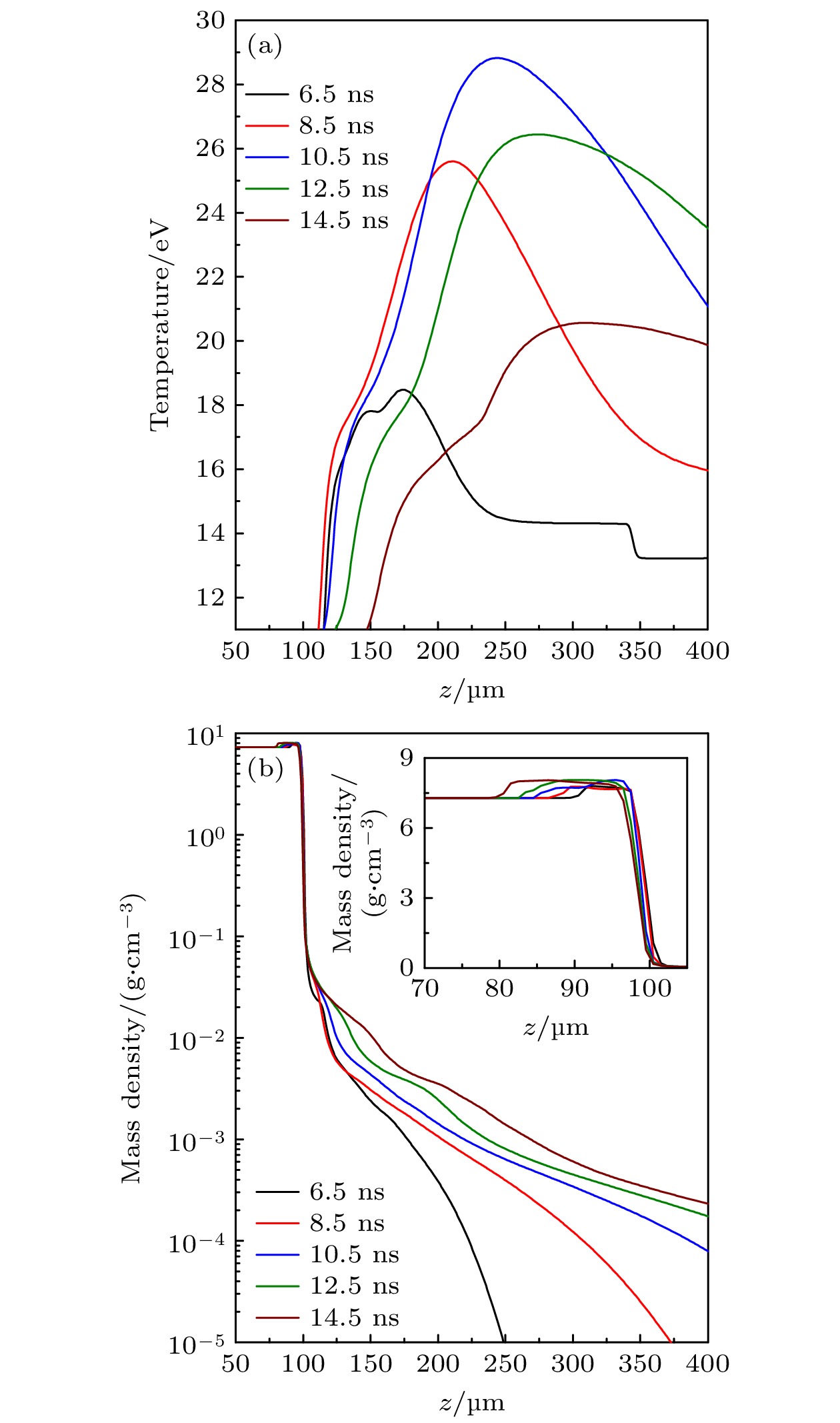
      图5展示了延迟时间为10.5 ns时激光Sn等离子体的温度和电子密度在距离靶面130, 200, 300 μm 处沿着径向(r轴)的一维分布. 图中不同颜色的实线表示本文的模拟结果, 带误差棒的黑 色方块、红色圆圈和蓝色三角形表示Pan等[18] 利用Thomson散射法测量到的实验结果(参考文献[18]中的图2(b)和图2(c)). 从图5可以看出, 模拟结果与实验结果具有较好的一致性, 这证明了RHDLPP程序在激光Sn等离子体状态参数分布模拟方面的适用性. 另外对比图5(a)的温度发现, 在距离靶面130 μm (黑色)和200 μm (红色)处模拟的温度值在$ -50{\mathrm{ }}{\text{ μ}}{\mathrm{m}} < r < 50{\text{ μ}}{\mathrm{m}} $范围内略高于实验测量值. 出现这种偏差的一个可能因素是: 程序中辐射流体力学方程组的求解调用的辐射不透明度数据来自于THERMOS数据库[28]. 这些数据在EUV波段并未细致考虑多激发态的贡献, 使得该波段的不透明度在温度为30 eV左右时偏低, 进而导致温度的模拟值过高. 为了证实这一猜想, 我们拟在后续的工作中首先细致计算考虑了多激发态贡献的6—20 nm波段的辐射不透明度数据, 随后由这些数据来替换取自THERMOS数据库[28]的辐射不透明度, 最后以替换后的数据为基础重新进行等离子体状态参数分布的模拟.

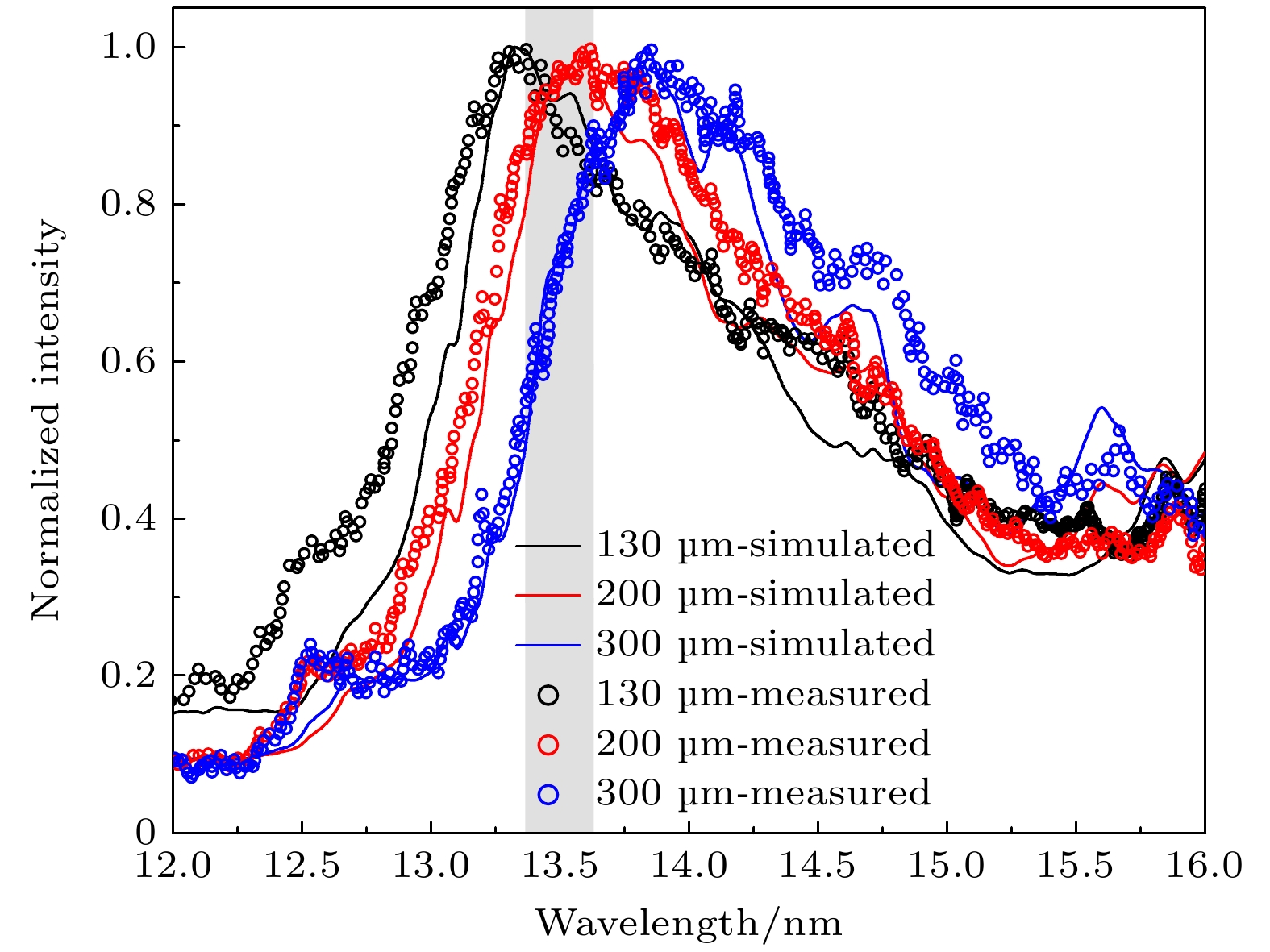
      图6给出了延迟时间为6.5, 8.5, 10.5, 12.5, 14.5 ns时模拟的激光Sn等离子体的温度和质量密度在r$ =0 $处沿着轴向(z轴)的一维分布. 从温度分布图可以看出, 最大温度值随时间的演化与激光脉冲的时间波型一致. 从初始零时刻到激光强度峰值时刻10.5 ns, 激光强度逐渐增大, 沉积在等离子体中的能量也随之升高, 这必然伴随着最大温度值的相应增大. 在10.5 ns之后, 沉积在等离子体中的激光能量开始减弱, 然而此时等离子体已具有极高的膨胀速度并且自身的辐射将损失很大一部分能量, 因此最大温度值也相应地出现了快速减小. 图6(b)中的质量密度插图清晰表现出了冲击波在靶材内部的传播, 从而形成了高密度的阵面区域. 另外, 由于激光烧蚀的持续进行以及等离子体的膨胀演化, 靶面上方等离子体区域($ z > 100{\text{ μ}}{\mathrm{m}} $)的质量密度值随着延迟时间的增大而逐渐增大.

      获得等离子体的温度和电子密度等状态参数后, 就可以将其作为输入文件由SpeIma3D程序来执行等离子体的光谱模拟. 图7给出了距离靶面130, 200, 300 μm 处激光Sn等离子体在12—16 nm波段的归一化时间积分光谱. 图中实线表示我们程序的模拟光谱, 空心圆表示Pan等[18]测量到的空间分辨光谱. 由于谱仪狭缝很窄, 各探测空间位置处的实验光谱可近似看作沿平行于靶面方向的线积分结果(具体请参见文献[18]中的图1实验测量示意图). 灰色阴影区域表示与EUV光刻应用相关的 13.5 nm附近的2%带宽. 考虑到延迟时间40 ns后等离子体的温度远低于10 eV, 此时对EUV波段的辐射再无贡献, 因此程序在光谱积分时将时间积分范围设定为0—40 ns. 从图7可以发现, 模拟光谱和实验光谱之间具有很好的一致性. 这证明了SpeIma3D程序在激光等离子体EUV光谱模拟方面的能力, 同时也证实了我们计算的Sn等离子体EUV波段的辐射不透明度、等离子体参数以及粒子布居等各种重要数据的可靠性. 另外从图7还可以看出, 从距离靶面130—300 μm的探测位置, 光谱的峰值逐渐向长波方向移动. 这与图5中不同位置下的温度和电子密度分布以及图4中的辐射不透明度分布规律一致. 距离靶面130 μm和200 μm处, 等离子体的最大温度高于25 eV, 表明等离子体中有大量的Sn10+—Sn14+离子, 这些离子发出的辐射集中在13.5 nm, 2%带宽内(如图4(a)所示). 而在距离靶面300 μm处, 等离子体的最大温度降至22 eV, 此时等离子体中以Sn7+—Sn10+离子占主导, 这些离子发出的辐射主要集中在13.5 nm, 2%带宽的右侧(如图4(b)所示).

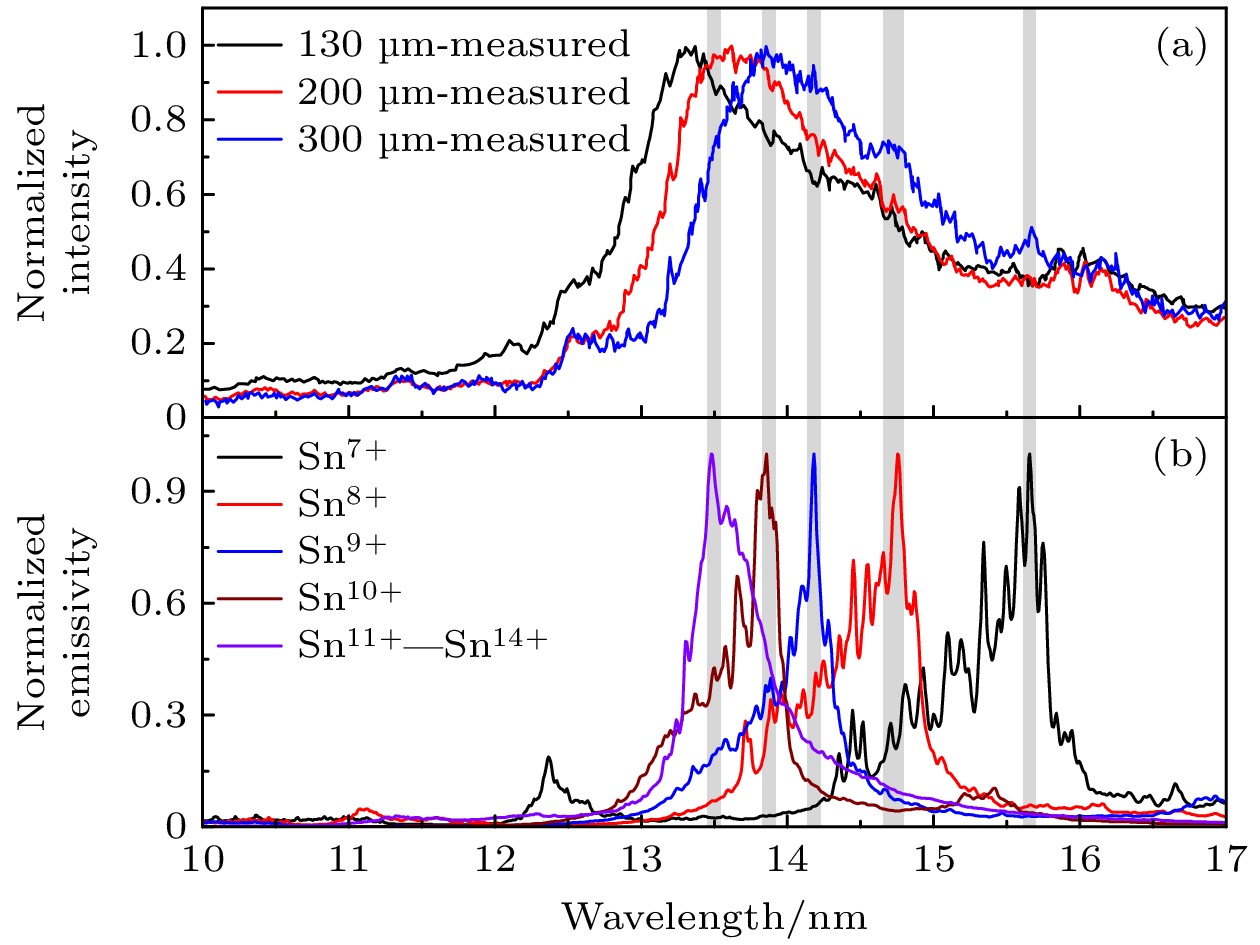
      最后, 为了对Nd:YAG激光产生的平面靶Sn等离子体的EUV辐射特性有清晰的认识, 将Sn7+—Sn14+离子的发射率与Pan等[18]测量的激光Sn等离子体在10—17 nm波段的空间分辨光谱进行了对比, 结果如图8所示. 其中, 图8(a)为3个空间位置下的归一化实验光谱, 图8(b)为Sn7+—Sn14+离子各自归一化的发射率. 由于Sn11+—Sn14+离子的发射轮廓重叠, 因此在图8(b)对这4种离子的发射率做了求和后再归一处理. 从图8可以看出, 5个浅灰色窄带标记出的是各离子发射率的最强峰位置(波长从左到右分别为13.48, 13.86, 14.18, 14.75, 15.66 nm), 然而这些最强峰对应的却是130 μm探测位置处实验光谱的凹陷结构. 表明这些理论上应具有强发射特征的EUV光子在距离靶面130 μm处沿着平行于靶面方向输运时等离子体对其有强烈的自吸收效应, 实验光谱反映出明显的自蚀特征. 200 μm探测位置处的实验光谱与130 μm处的特征相似, 而300 μm处的光谱结构却截然不同. 5个发射率的最强峰位置与300 μm探测位置处实验光谱中的小尖峰正好一一对应, 说明该位置处等离子体的自吸收效应较弱, 光谱并未表现出自蚀特征. 不同空间位置处的光谱特征与图5中所示的等离子体状态参数分布密切相关. 130 μm和200 μm处, EUV辐射区域的线长度可达350 μm左右, 并且等离子体温度和电子密度较高, 因此那些具有较大发射率和吸收系数的光子在等离子体中输运时相应的光学厚度也比较大, 光子很难全部从等离子体中逃逸出来. 而对于300 μm处, 图5反映出EUV辐射区域的线长度为200 μm左右, 等离子体温度和电子密度下降明显, 相应的光学厚度也较小, 虽然仍存在自吸收效应, 但会有部分目标EUV光子逃逸出等离子体被探测器收集. 最后, 图8(b)表明工业界关注的13.5 nm, 2%带宽内的辐射主要来自于Sn11+—Sn14+离子的贡献. 然而平面靶Sn等离子体存在的强烈自吸收效应使得相当一部分核心辐射无法到达EUV光源的中心焦点处, 光源的转换效率和辐射功率很难达到工业要求. 这是平面Sn靶无法被应用于光刻机的重要原因之一(平面靶的另外一个问题是无法很好地控制碎屑对光学元件的污染).

      • 4.2.   激光作用于Sn液滴靶

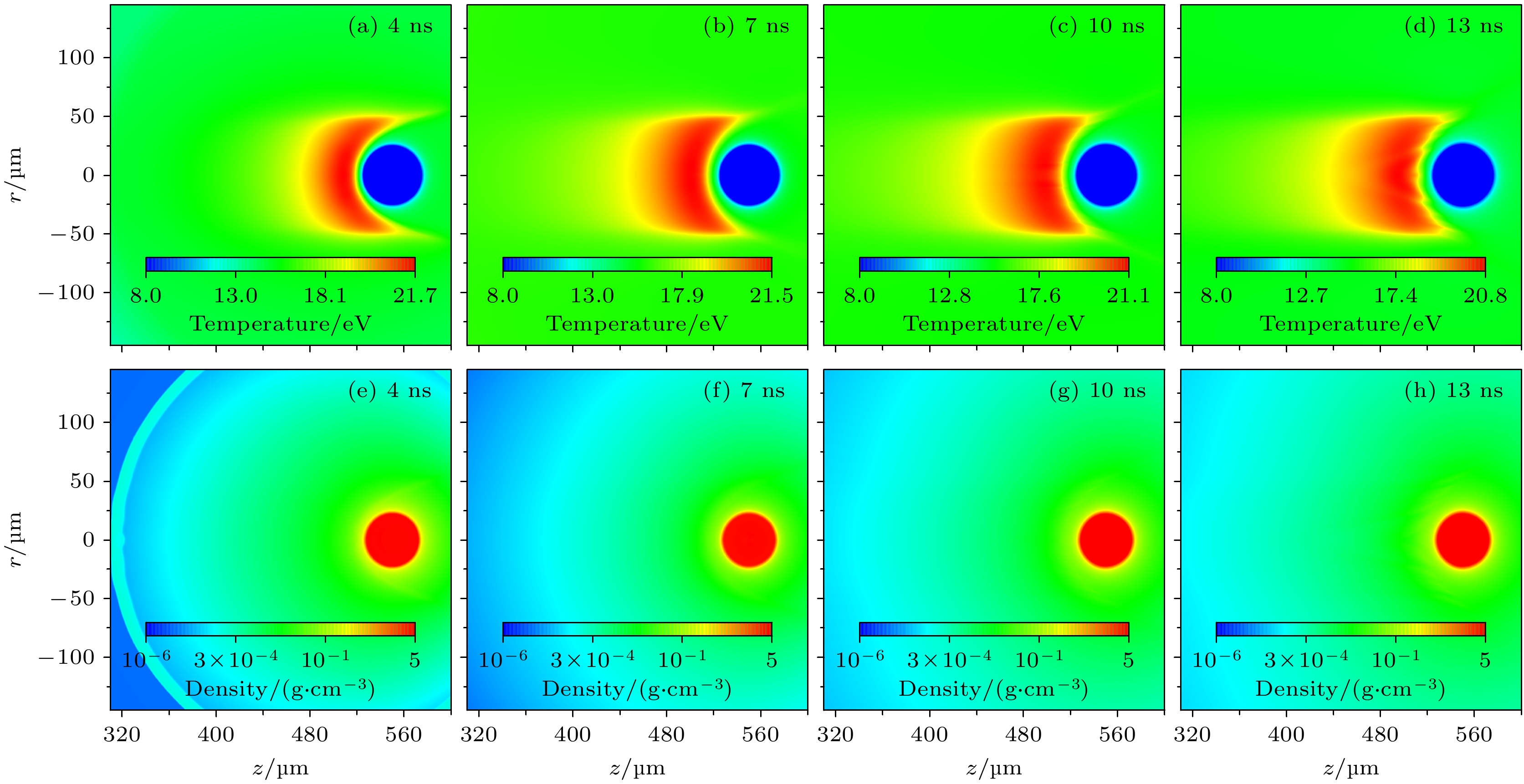
    • 目前先进的商用EUV光刻机中, 都是选用直径在几十微米量级的球形Sn液滴作为光源系统的目标靶材[4]. 本文针对激光作用于类似尺寸的Sn微滴所产生的等离子体的参数分布以及EUV光谱进行了模拟. 初始条件设置中选用了一个直径为 46 μm, 密度为 6.9 g/cm3的球形Sn液滴靶. 背景气体设定为氢气, 密度为10–7 g/cm3. 烧蚀激光设置为平顶型Nd:YAG激光脉冲, 功率密度为 4×1010 W/cm2, 脉冲持续时间为15 ns, 波长1.064 μm, 焦斑直径为 96 μm. 靶材和背景气体的初始温 度为300 K. 这些模拟参数与Torretti等[12]所采用的实验条件基本一致. 模拟同样在二维轴对称(r-z)坐标系中进行, 整个计算区域设定为$ 0 < z < 800{\text{ μ}}{\mathrm{m}},\; 0 < r < 400{\text{ μ}}{\mathrm{m}} $. 液滴Sn靶的球心位于$ r=0 $, $ z=550{\text{ μ}}{\mathrm{m}} $处. 激光沿着z轴入射.

      图9给出了延迟时间为4, 7, 10, 13 ns时, RHDLPP程序模拟得到的激光作用于Sn液滴形成的等离子体其温度和密度的二维分布. 从图9可以看出, 由于入射激光的时间波型为平顶型, 即各瞬时时刻入射的激光能量相等, 因此从4—13 ns时等离子体的温度分布基本相似, 温度最大值都为21 eV左右. 这意味着平顶型激光产生的等离子体在脉冲作用期间其状态的演化可近似认为处于稳态. 另外, 本文模拟的温度分布与Torretti等[12]利用RALEF-2D程序模拟的结果(文献[12]中的图6(a))基本一致, 这表明了RHDLPP程序同样适用于Sn液滴等离子体的参数分布模拟. 从图9中的密度分布来看, 4 ns时等离子体沿着z轴膨胀到了约320 μm处, 此时在等离子体前端具有非常明显的冲击波结构. 4 ns之后, 等离子体继续膨胀, 在图中所示的区域内密度随时间的演化基本可近似为稳态, 与温度的含时演化特征一致. 而且在激光脉冲作用期间(0—15 ns), 密度分布图中由红色所标记的液滴其形状并未发生明显的变化, 此时在液滴内部主要发生的物理过程是液滴表面的等离子体所形成的压力波的传播.

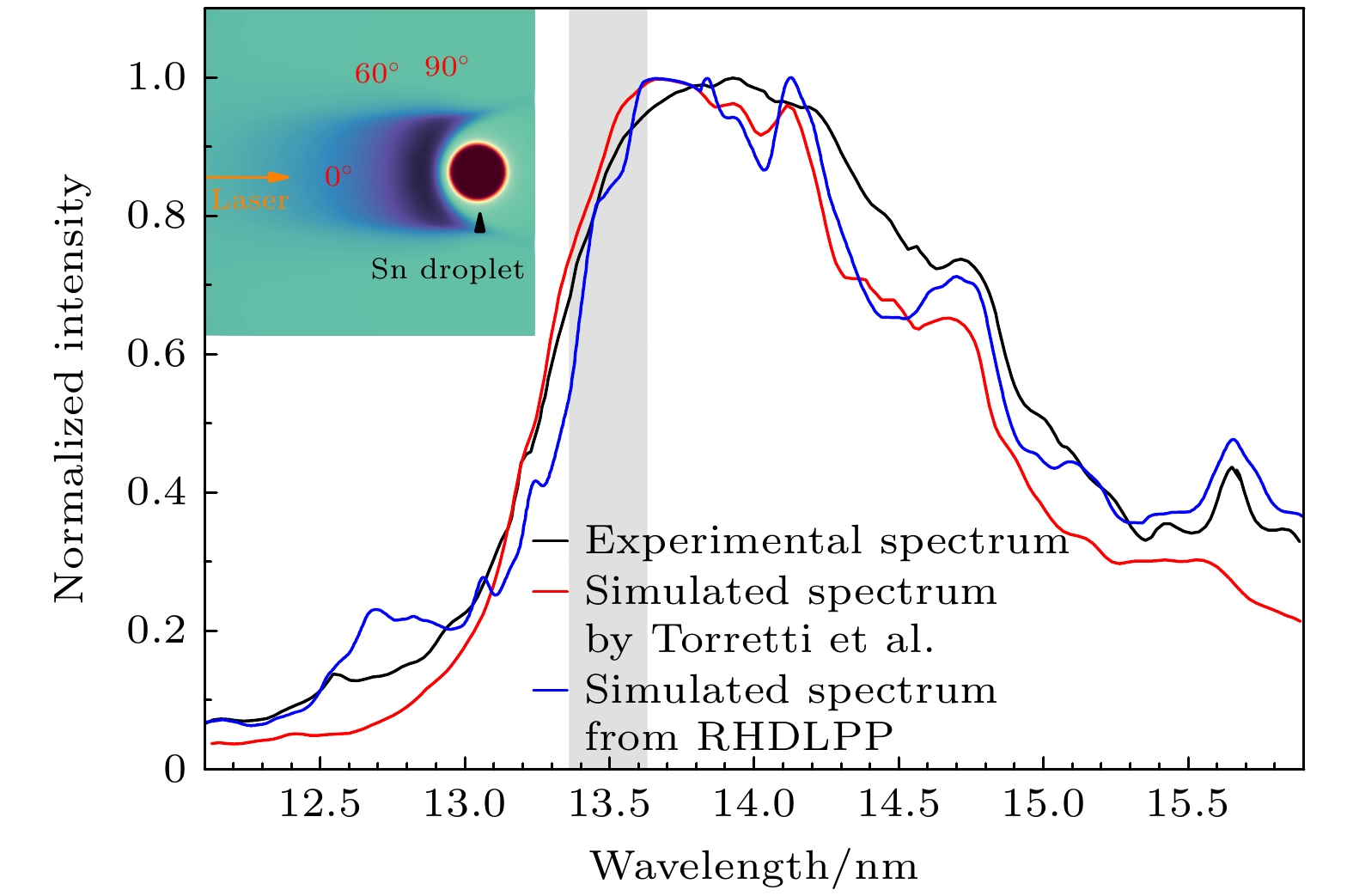
      结合液滴等离子体的状态参数以及辐射不透明度数据, 利用SpeIma3D程序进行了Sn液滴等离子体的EUV光谱模拟. 图中黑色实线表示Torretti等[12]测量到的实验光谱, 红色实线表示他们的模拟光谱, 蓝色实线代表本文的模拟光谱. 如图10插图所示, 3张光谱的观测视线与激光入射方向的夹角都为60º. 从图10可以看出, 本文的模拟光谱与Torretti等[12]的实验光谱以及模拟光谱具有很好的一致性, 这证明了SpeIma3D程序在Sn液滴等离子体EUV光谱模拟方面的能力. 另外需要说明的是, Torretti等[12]虽然也得出了与实验光谱一致性很好的模拟光谱, 但他们在模拟时作出了如下假设: 1) 等离子体是温度为20 eV、密度为0.002 g/cm3的均匀等离子体; 2) 光谱强度求解时仅进行了沿视线的一条光线上的一维积分. 与之相比, 本文的模拟完全考虑了等离子体具有的空间非均匀性, 并且在进行光谱强度积分时充分考虑了光谱仪狭缝对等离子体张开的立体角, 模拟时求和了能进入谱仪狭缝的约25万条光线的强度.

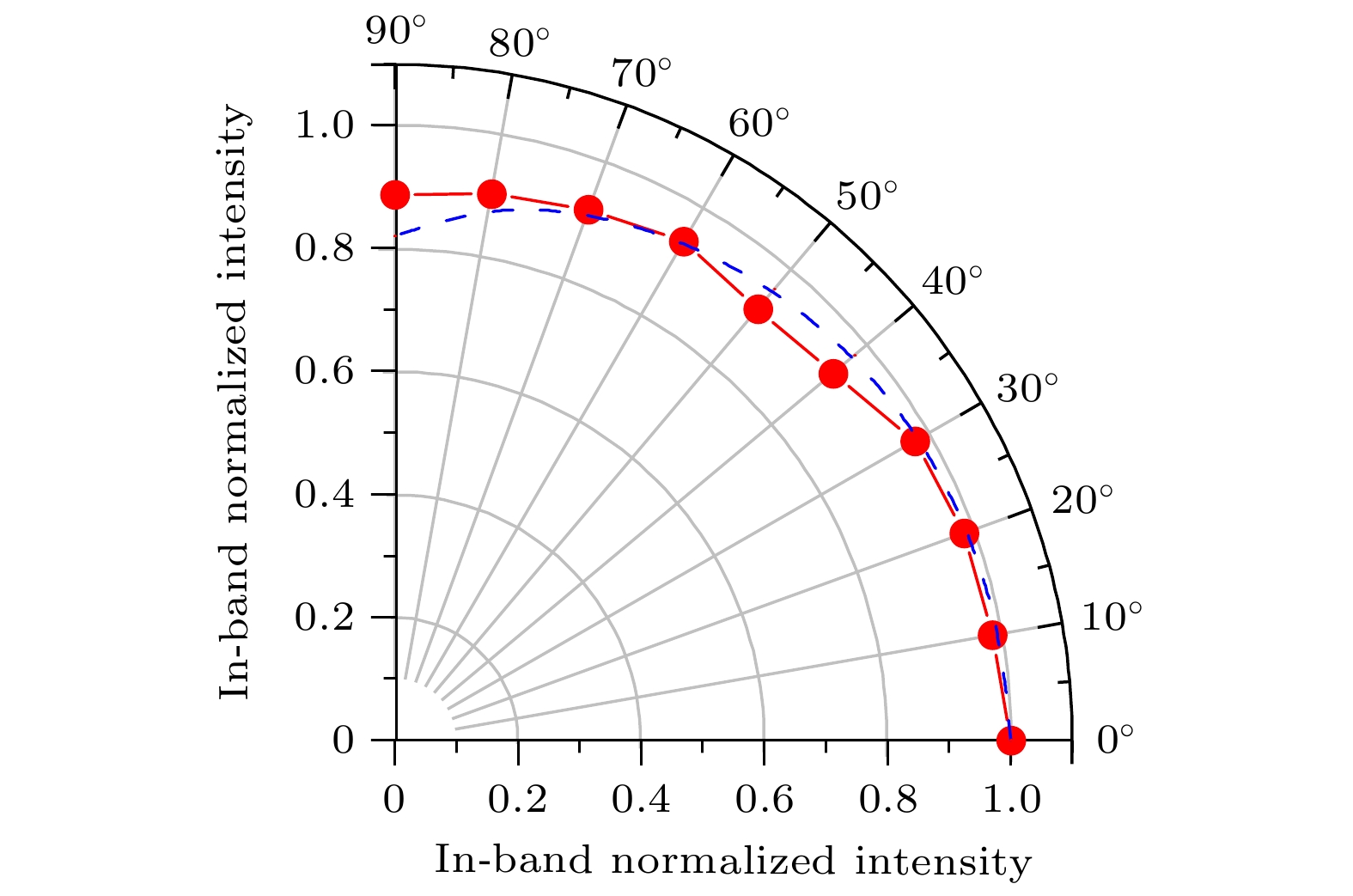
      最后, 为了测试Sn液滴等离子体EUV辐射的各向异性程度, 本文还模拟了13.5 nm, 2%带宽内的辐射强度随0º—90º观测角度的变化情况. 图11所示为归一化的带内强度随观测角的分布. 其中红色实心圆圈表示本文的模拟结果, 蓝色虚线代表拟合曲线. 文献[42]通过实验数据得到了带内强度和观测角之间的拟合公式: $ f\left(\theta \right)=\alpha +\beta {\left({\mathrm{cos}}\theta \right)}^{\gamma } $, 其中拟合参数$ \alpha =0.82 $, $ \beta =0.17 $, $ \gamma =0.6 $. 图11中的拟合曲线正是基于上述拟合公式和参数绘制而成. 可以发现本文的模拟结果与实验拟合曲线基本吻合. 图11结果可以很好地说明平顶型纳秒激光脉冲作用于Sn微滴产生的激光等离子体, 其EUV辐射基本满足各向同性假设, 即带内的辐射强度随观测角度的变化很小. 这一结论对于实验测量LPP-EUV系统在IF点处的转换效率具有重要的简化意义.

    5.   结　论

    • 本文针对在先进光刻中有重要应用的激光Sn等离子体开展了细致的数值模拟研究. 首先利用激光等离子体辐射流体力学程序RHDLPP, 分别模拟了纳秒激光脉冲作用于Sn平面固体靶和球形液滴靶所产生的等离子体的状态参数分布. 获得的等离子体温度和电子密度等模拟参数的分布与实验结果具有较好的一致性.

      同时, 利用原子结构计算程序COWAN对高电荷态Sn离子的原子结构参数开展了大规模的组态相互作用计算. 随后较为细致地评估了LTE近似在Nd:YAG激光产生的Sn等离子体中的适用性. 基于LTE近似下的DLA模型, 计算了Sn等离子体在12—16 nm波段的辐射不透明度数据. 计算结果表明多激发态对该波段的辐射不透明度有重要贡献.

      结合等离子体状态参数和辐射不透明度数据, 利用光谱模拟后处理子程序SpeIma3D给出了平面固体靶等离子体的时间积分、空间分辨EUV模拟光谱, 该结果能很好地匹配实验光谱. 最后较为细致地讨论了等离子体自吸收效应对平面靶等离子体不同空间探测位置处光谱结构的影响. 发现130 μm和200 μm处的实验光谱由于较大的等离子体光学厚度而出现了明显的自蚀结构. 在300 μm处等离子体自吸收效应较弱, 实验光谱并未表现出自蚀特征. 对于液滴靶等离子体, 利用SpeIma3D程序获得了角分辨的EUV模拟光谱以及13.5 nm, 2%带宽内的辐射强度随观测角度的分布规律. 模拟结果表明, 平顶型纳秒激光作用于Sn微滴产生的等离子体基本处于稳态、EUV辐射各向同性的状态.

      综合来看, 本文模拟的Sn等离子体的状态参数分布和EUV光谱与相关实验结果具有较好的一致性, 可以为EUV光源的设计和优化提供指导. 但仍需说明的是, 4.2节中所述条件的激光脉冲作用于Sn液滴靶产生的等离子体并不能辐射出最优的13.5 nm, 2%带宽内的EUV光. 若要使IF点的EUV辐射CE值最高, 通常要求等离子体中Sn11+—Sn14+离子占主导, 即等离子体温度须达到30 eV左右、平均电离度需为12次左右. 然而在4.2节的模拟条件下, 等离子体的最高温度仅为21 eV, 占主导的离子种类为Sn7+—Sn10+, EUV辐射的峰值位置不在带内(如图10所示). 针对这一问题, 我们将在后续的研究中重点进行更高功率密度的纳秒激光脉冲产生的等离子体以及其EUV辐射的精细模拟. 另外, 后续研究还需将本文中的EUV辐射波段范围扩展至6—20 nm, 这需要对更多不同离化度Sn离子进行更大规模的组态相互作用计算来获得相关的辐射跃迁参数以及辐射不透明度数据.

    参考文献 (42)

目录

/

返回文章
返回