首页
登录
注册
下载:
-
近几十年来, THz技术及其应用引起了广泛关注和研究[1]. THz波在许多领域具有至关重要的应用, 如THz无线通信[2]、THz时域光谱探测[3,4]和THz成像技术[5]等. 其中高效可调谐的THz源是THz应用的基础. 目前, 产生THz波的经典方法有基于电子学技术的返波振荡器[6]、自由电子激光器[7]和基于光学技术的THz气体激光器[8]、量子级联激光器[9]、光电导[10]、等离子体四波混频[11]、光整流[12,13]、非线性光学DFG[14–25]等. 其中, 非线性光学DFG由于可以产生可调谐的THz波辐射且具有较高的输出功率而被广泛关注. 目前, 非线性光学DFG产生THz源主要在非线性光学晶体中实现, 如砷化镓(GaAs)晶体[19,20]、硒化镓(GaSe)晶体[21–23]、磷化镓(GaP)晶体[24]、铌酸锂(LiNbO3)晶体[25]等. 但晶体中的非线性DFG产生THz源存在许多不足之处, 如通常大块、高质量晶体生长比较困难, 价格比较昂贵, DFG过程需要满足严格的相位匹配条件, 对晶体加工及激光技术要求比较高, 另外, 大的晶体尺寸不易集成化等. 微纳结构, 其尺寸一般在亚波长量级, 其谐振模式能将光场约束在很小的体积内, 能极大增强局域电场的能量密度, 这种增强效应不仅直接提高了非线性光学响应的效率, 还降低了实现非线性效应所需的光功率, 从而为实现高效非线性光学效应奠定了基础. 且由于基频光与非线性光作用距离很短, 通常不需要考虑相位匹配, 而日益受到关注. 此外, 利用微纳结构中的DFG产生THz源还是实现器件小型化、可集成化的重要途径. 但通常微纳结构的共振模式比较固定, 只能实现特定共振波长下的DFG, 因此难以实现可调谐的高效THz波产生, 是该领域的难点问题.
本文研究了宽波段范围内具有高Q因子的光栅-波导结构中DFG产生高效可调谐的THz辐射. 通过调控四部分光栅-波导结构相邻光栅中 其中一个的位置扰动, 可以实现准连续域束缚 态[26–32], 或者从另一角度, 实现光栅周期的加倍, 进而使得布里渊区发生折叠, 光线下方波导层中导模(guide mode, GM)色散曲线折叠到光锥上方, 形成超高Q因子的导模共振(guide mode resonance, GMR)[33]. 共振波长可以通过改变基频光的入射角调谐且高Q因子在宽波段范围内几乎保持不变, 因此可以实现在宽光谱范围内增强的、可调谐的THz波产生. 以硫化镉(cadmium sulfide, CdS)光栅-波导为例, 在横电场(transverse electric, TE)偏振光的作用下, 两束基频光光强均为100 kW/cm2时, THz的转换效率可达到10–8 W–1的量级, 为相同厚度CdS薄膜转换效率的109倍, 且通过改变两束基频光入射角的组合, 可实现任意频率THz波产生, 从而实现了在宽光谱范围内高效可调谐的THz源.
-
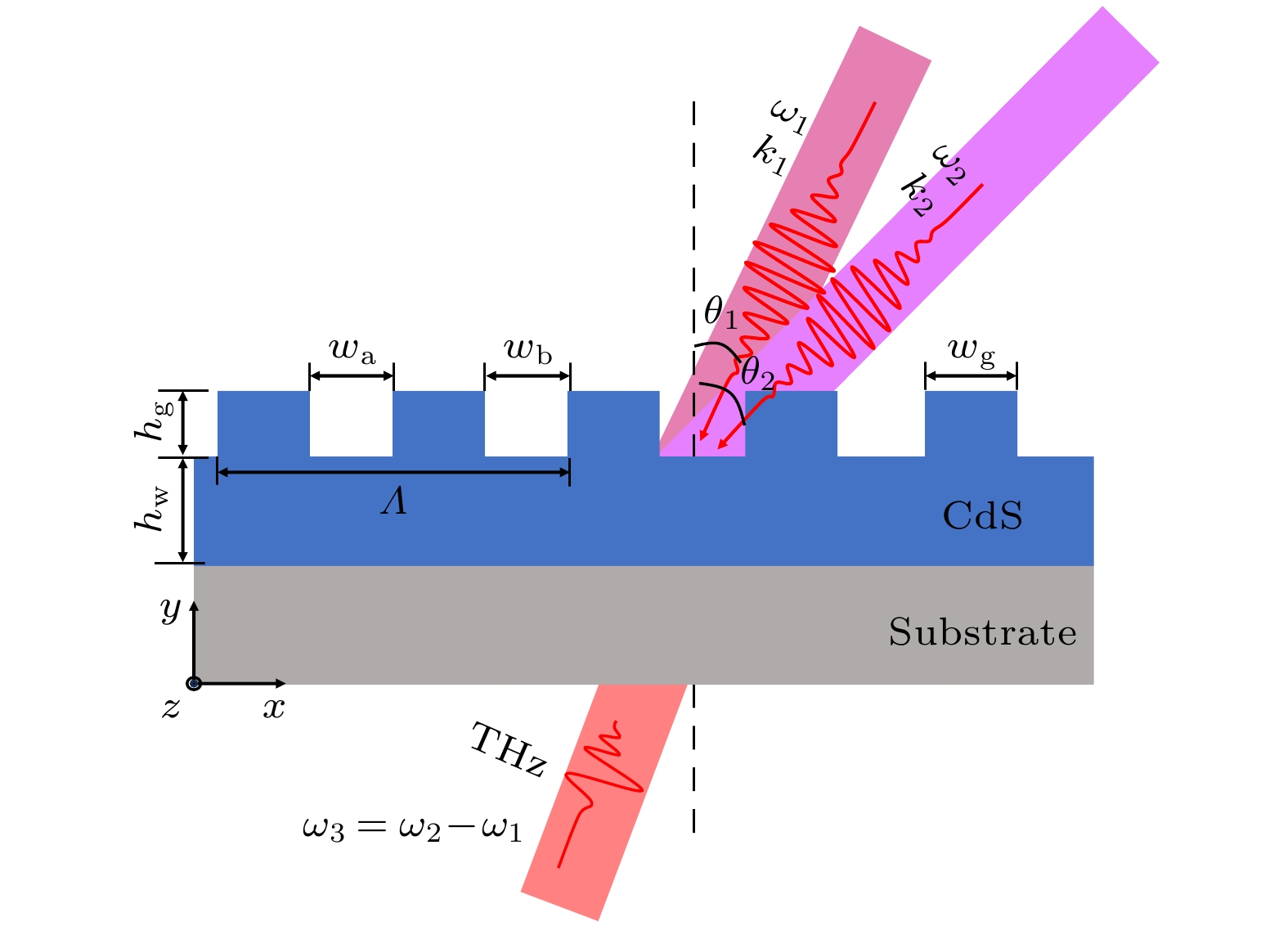
用于实现几何扰动的4部分光栅-波导结构示意图如图1所示. 4部分光栅的周期和厚度分别为Λ = 500 nm和hg = 50 nm. 光栅层的第1部分和第3部分为CdS光栅的脊, 宽度为wg, 第2部分和第4部分为空气层, 宽度分别为wa和wb, 因此光栅层的周期Λ = 2wg + wa + wb. 设wg = 0.2Λ, wa = d – ∆d, wb = d + ∆d, 其中d = 0.3Λ. 通过定义一个可调节的几何参数δ = ∆d/d, δ∈[0, 1]来反映光栅第2部分和第4部分之间的差异. 当∆d = 0, 即δ = 0时, 光栅为周期P = Λ/2的传统光栅结构. 当将第2块CdS光栅脊发生几何扰动偏离原来位置, 即∆d ≠ 0时, 光栅周期加倍. 波导层的厚度为hw = 500 nm. 由于CdS具有较高的折射率(n = 2.34)和二阶非线性系数, 本文选择CdS作为光栅层和波导层的材料. 选择二氧化硅作为衬底层材料, 其折射率ns = 1.45. 计算过程选取光栅-波导结构的一个周期作为仿真域, 入射平面是x-o-y平面. 空气域的上边界设置为光入射端口1, 二氧化硅衬底的下边界设置为端口2, 将左右边界设为Bloch-Floquet周期边界条件, 在基频模块中定义Floquet波向量kF为kFx = kx = k0sinθ, kFy = 0, 其中θ为基频光入射角, θ1和θ2分别表示基频光1和2的入射角. 上下端口外侧区域设置完美匹配层(perfectly matched layer, PML).
频域时基频场和差频场(时谐因子exp(–iωt))可表示为[34]
式中, E(ω)和E(Ω)分别为基频场和差频电场; k0 = ω/c和k2 = Ω/c分别为基频光和差频光的波矢量, 其中c为真空中的光速; μ0为真空导磁率, ε2为材料在差频场频率下的相对介电常数; ω1或者ω2分别表示频率为ω1或者ω2的基频入射光; Ω = ω2 – ω1为差频场的角频率(文中假定ω2 > ω1). 由于基频场局域场增强能够产生高效差频场, 不同于文献[35]报道, 本研究充分考虑了基频场与差频场的耦合, 当基频场频率为ω1和ω2时, 电场极化强度P (1)(ω1)和P (1)(ω2)分别表示为
二阶极化强度P (2)(Ω)表示为
其中, ε0是真空介电常数, χ(2)为CdS材料的二阶非线性极化率. 由于我们只考虑ω1和ω2的TE偏振(如图1定义的坐标, 只有Ez不为0), 所以二阶非线性极化强度P (2)(Ω)的非零分量表达式表示为
其中Ez(ω1)和Ez(ω2)分别为基频电场的z分量;
$\chi _{333}^{(2)} $ 为CdS的主要二阶极化率分量, 其大小为156 pm/V[36].利用有限元方法(comsol multiphysics)进行特征频率分析, 计算了光栅-波导结构的能带结构. 对上述耦合方程进行了数值求解, 可以得到CdS光栅-波导结构的透射光谱和差频产生THz辐射的转换效率. 如果在没有特别说明, 两个入射基频光具有相等的强度I1 = I2 = 100 kW/cm2. 由于使用二维模型, 假设光栅在第三维(z方向)的长度为单位米(1 m), 比周期大7个数量级, 从而确保其具有二维特性. 产生太赫兹波的功率定义为
其中,
$ {\boldsymbol{n}} $ 是从端口指向外的法向量, 而$ {{\boldsymbol{S}}_{{\text{THz}}}} $ 是产生THz的坡印亭矢量,$ {\text{d}}S = {\text{d}}l {\cdot} 1 [{\text{m}}] $ , dl为沿端口2边界的线元. 定义DFG转换效率为η = PDFG/(P1P2), 其中PDFG为产生THz波的功率, P1和P2为入射光功率. -
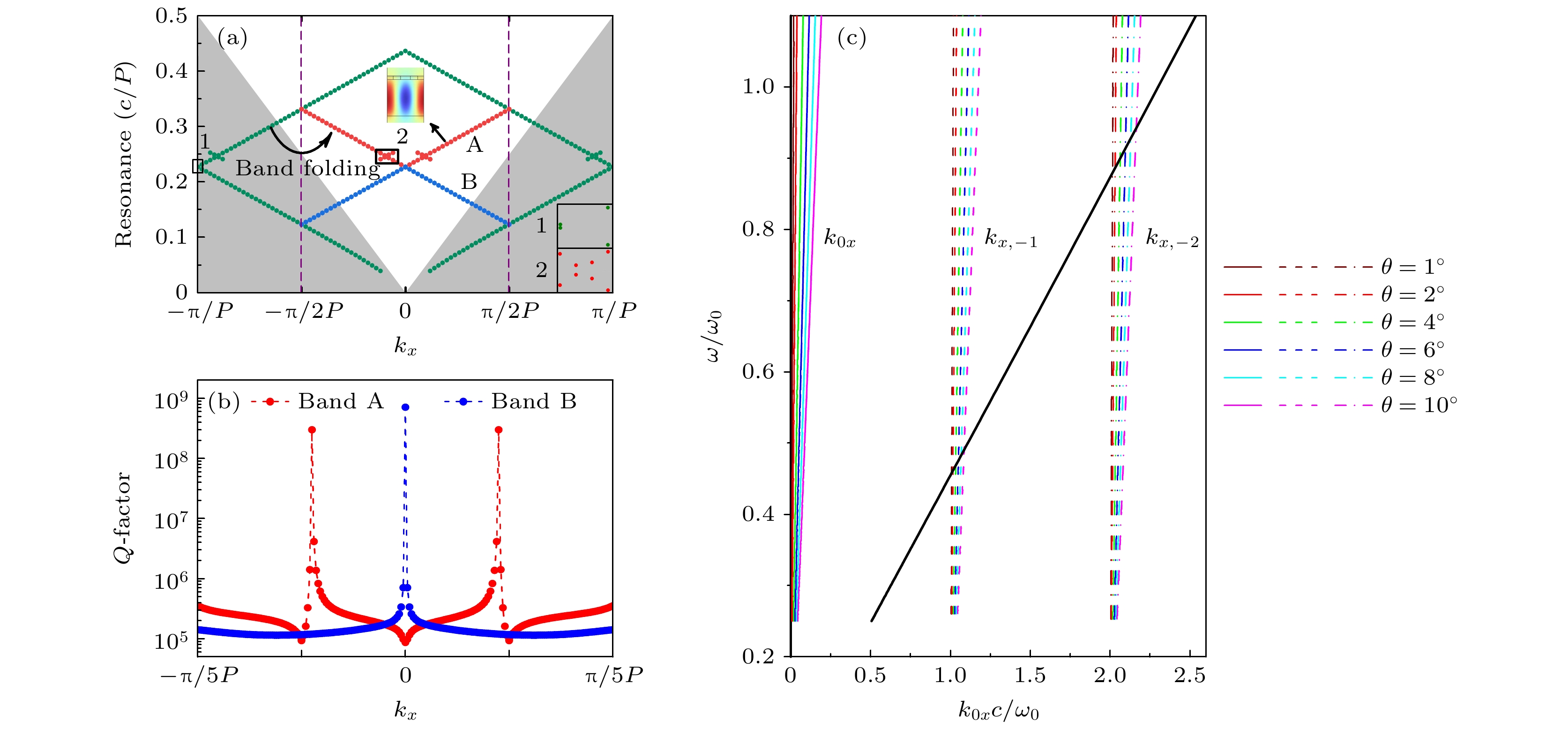
图2(a)为δ = 0.1时光栅-波导结构的能带结构. 图中的深绿色圆点表示δ = 0时周期为P = Λ/2时传统光栅-波导纳米结构中模式的能带结构. 光锥下方的一阶带表示没有向自由空间辐射, 具有无限大Q因子, 是平板中的GM模式. 泄漏模式出现在光锥上方的二阶带, 称为GMR. 当引入非零几何扰动δ时, 周期加倍, 引起第一布里渊区折叠, 导模色散曲线随之折叠到光锥线上方, 形成GMR. 如图2(b)所示, 当扰动较弱时, 两条交叉色散曲线的导波模式共振将保留原始导波模式的特性, 具有超高Q因子. 本文主要研究折叠后A带的GMR及基于A带GMR的THZ产生.
在理论上TE0导模在波导层中的色散关系可表示为[37]
其中, nw, nc, ns分别为波导层、波导上层和衬底层的折射率; hw为波导层的厚度; k0为空气中的波矢量; β为波导层模式的传播常数. TE0色散关系如图2(c)中黑实线所示, 图中ω0 = 2πc/hw, kx = k0x = k0sinθ为空气中波矢量的x方向分量, 在光栅层中写成kx = kx, i = k0sinθ – iG (i = ±1, ±2, …), 当
$ \delta \ne 0 $ 时, 纳米结构中的倒易晶格为G = 2π/Λ, 当δ = 0时, 倒易晶格变化为G ′ = 4π/Λ. 不同入射角下光栅层的kx, i如图2(c)所示. 当相位匹配条件满足kx = kx, i = k0sinθ – iG = β (图2(c)中虚线和黑色实线的交叉点)时, 波导模式能被激发. 从图2(c)可知, 只有–1和–2阶波导模式可被激发, 在不同入射角θ = 1°, 2°, 4°, 6°, 8°, 10°时纳米结构δ ≠ 0负一阶模的共振角频率ωR = 0.458ω0 (1091 nm), 0.462ω0 (1082 nm), 0.469ω0 (1066 nm), 0.476ω0 (1050 nm), 0.483ω0 (1035 nm), 0.490ω0 (1020 nm). 可见共振频率随入射角的变大而变大, 与图2(a)中A带的色散关系一致. 由于G ′ = 2G, 纳米结构δ = 0中的共振角频率与结构δ ≠ 0中的偶阶色散关系kx, 2m (m = ±1, ±2, ···)完全重合. 因此, 当可调几何参数δ由非零变为零时, 黑色实线与kx, –1的交点处的谐振模式变为暗模式, 当δ ≠ 0时, 暗模泄漏形成GMR[38,39]. -
随后计算了光栅波导结构的线性透过率及Q因子. 在入射角θ = 6°时, 几何参数δ从0到1.0变化的透射光谱如图3(a)所示. 当δ = 0.2时, 在波长λ = 1053.98 nm处获得近乎完美的反射, 对应于GMR模式. 该值比由色散关系(图2(c))确定的值要大一些. 当几何参数δ从0.2增大到1.0时, 共振谷的位置由1053.98 nm蓝移到1053.67 nm, 并且逐渐变宽, 其中当δ = 1时, 光栅变为周期为Λ的传统光栅结构. 图3(a)插图为δ = 0.2和1.0时对应共振模式下的电场Ez分布, 为明显GMR模式, 在其他入射角θ = 2°, 4°, 8°, 10°时, 相应共振态下的电场分布与θ = 6°时相似. 在相同的波导光栅结构下, 共振波长随入射角度的增加而发生蓝移, 与3.1节部分理论分析结果一致. 固定几何参数δ = 0.1, 当θ = 2°, 4°, 6°, 8°, 10°时, 共振波长分别约为1085.67, 1069.84, 1054.02, 1038.32, 1023.30 nm, 表明共振波长可以通过入射角实现可调谐性, 如图3(b)所示. 图3(b)插图所示为θ = 6°时对应共振模式下的电场Ez分布, 与图2(a)中的本征模式完全一致.
同时, 计算了不同δ时共振模式的Q因子, 定义Q = λdip/∆λ, ∆λ = |λpeak – λdip|, 其中λpeak和λdip分别为透射谱Fano线型的峰谷波长. 在θ = 6°时, 不同纳米结构的Q因子如图3(c)所示. 当δ = 1时, Q因子在1.3×103左右. 当δ逐渐减小到接近零时, Q因子迅速增大. 例如, 当δ = 0.1时, Q因子达到1.4×105; 当δ = 0.05时, Q因子达到5.8×105. 当δ = 0时, ∆λ = 0的共振峰完全消失, Q因子变为无穷大. 图3(c)插图为Q因子与δ–2呈线性关系. 共振波长与入射角的关系如图3(d)所示. 共振波长的范围很宽, 从0°时的1099.41 nm到10°时的1023.30 nm, 这为共振基频光组合差频产生可调谐THz源提供了可能. 图3(d)给出了不同入射角下共振模的Q因子变化. 可以看到, 随着入射角的增加, 共振模Q因子略有增大, 当θ = 0°时, Q因子为6.4×104, 当θ = 10°时, Q因子为5.6×105, 与图2(b)模式分析得到的结果一致. 总的来说, 在几何参数δ = 0.1的情况下, 这些共振的Q因子约为105, 保证了共振波长处光与结构之间的强相互作用产生高效非线性DFG.
-
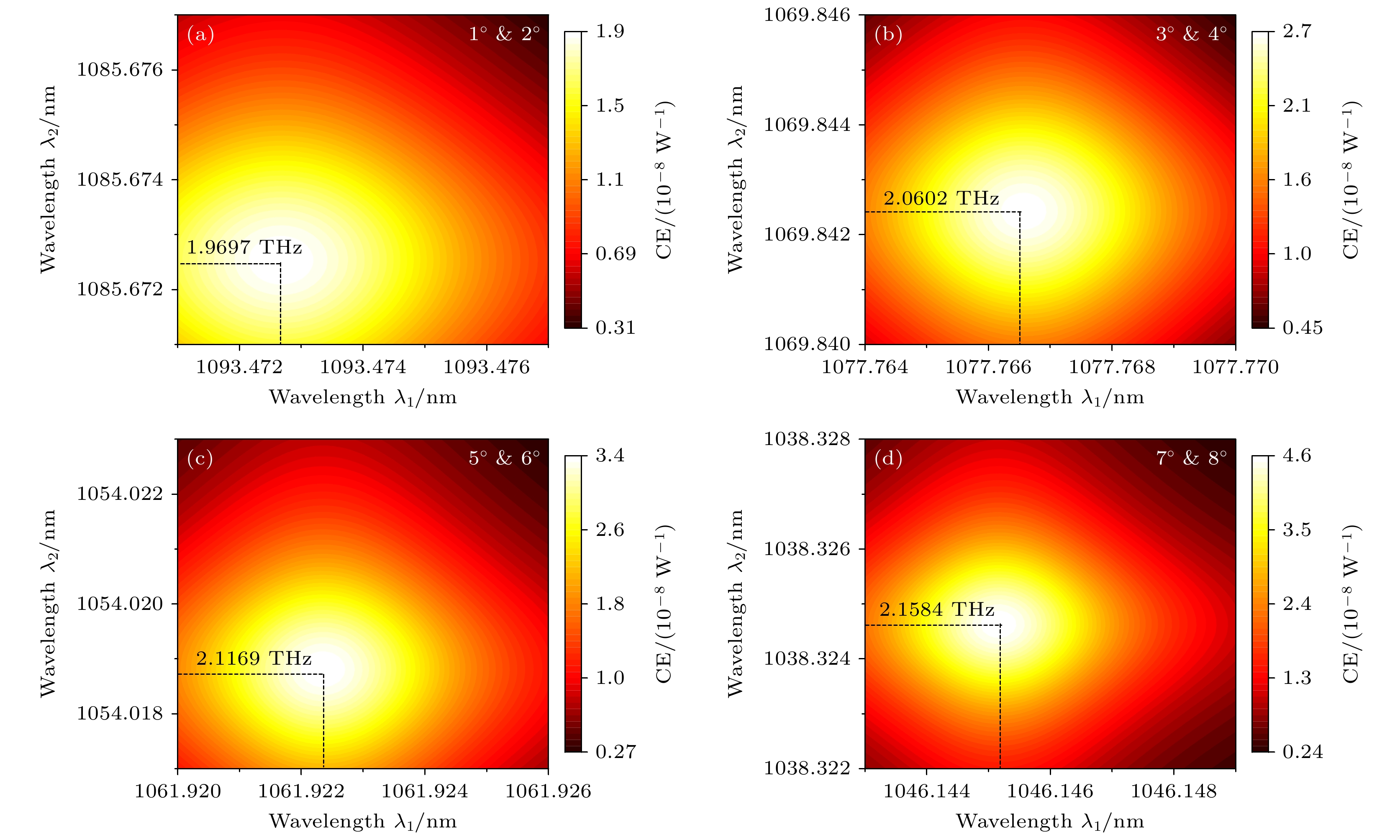
最后, 计算了非线性差频过程产生THz波. 当δ = 0.1时不同入射角下DFG转换效率对入射波长λ1和λ2的依赖关系如图4所示. 从图4(a)可以看出, 固定两束入射光的入射角分别为1°和2°, 虽然两束入射光的功率强度是恒定的, 但产生的THz转换效率与入射波长有很大的关系, 并在λ1 = 1093.4727 nm和λ2 = 1085.6725 nm时DFG转换效率达到峰值, 此时产生的光波频率为1.9697 THz, THz峰值共振带宽约为10–4 THz. 我们计算了在相同激励条件下, 相同厚度CdS薄膜中的DFG做为参照. 光栅-波导中的DFG转换效率是CdS薄膜中转换效率的109倍. 对于DFG的THz生成来说, 这种高的转换效率增强是由于两个输入光束处于GMR状态下的双重增强效应. 光栅支持GMR的主要优势在于, 共振可以通过入射角度以较大的自由度调谐到不同的波长. 如图4(b)—(d)所示, 分别选择两束光的入射角度为3°和4°, 5°和6°, 7°和8°时, 重复上述计算过程, 可以得到在入射波长分别为λ1 = 1077.7667 nm和λ2 = 1069.8424 nm, λ1 = 1061.9223 nm和λ2 = 1054.0188 nm, λ1 = 1046.1452 nm和λ2 = 1038.3247 nm时DFG转换效率达到峰值, 产生的光波频率分别为2.0602 THz, 2.1169 THz和2.1584 THz. 在相同激励条件下, DFG 的转换效率相比于平面 CdS 膜分别提高了1.5×109, 2.2×109, 3.0×109倍. 转换效率随角度的增大与Q因子随角度的增大对应, 与局域电场增强随入射角度增大相关.
如果根据图3(d)所示的入射角与共振波长的关系, 固定一束入射光的入射角为1°, 调节另一束入射光的入射角度分别为2°, 3°, 4°, 5°, 6°, 同时保持其波长相应调谐, 可以得到光波频率分别为1.9697 THz, 3.9951 THz, 6.0556 THz, 8.1454 THz和10.2625 THz的THz波, 同时可以实现在上述光波频率下获得109数量级的THz转换效率增强. 因此, 通过改变两束基频光入射角的组合, 可实现任意频率THz波产生, 从而实现了在宽光谱范围内高效可调谐的THz源.
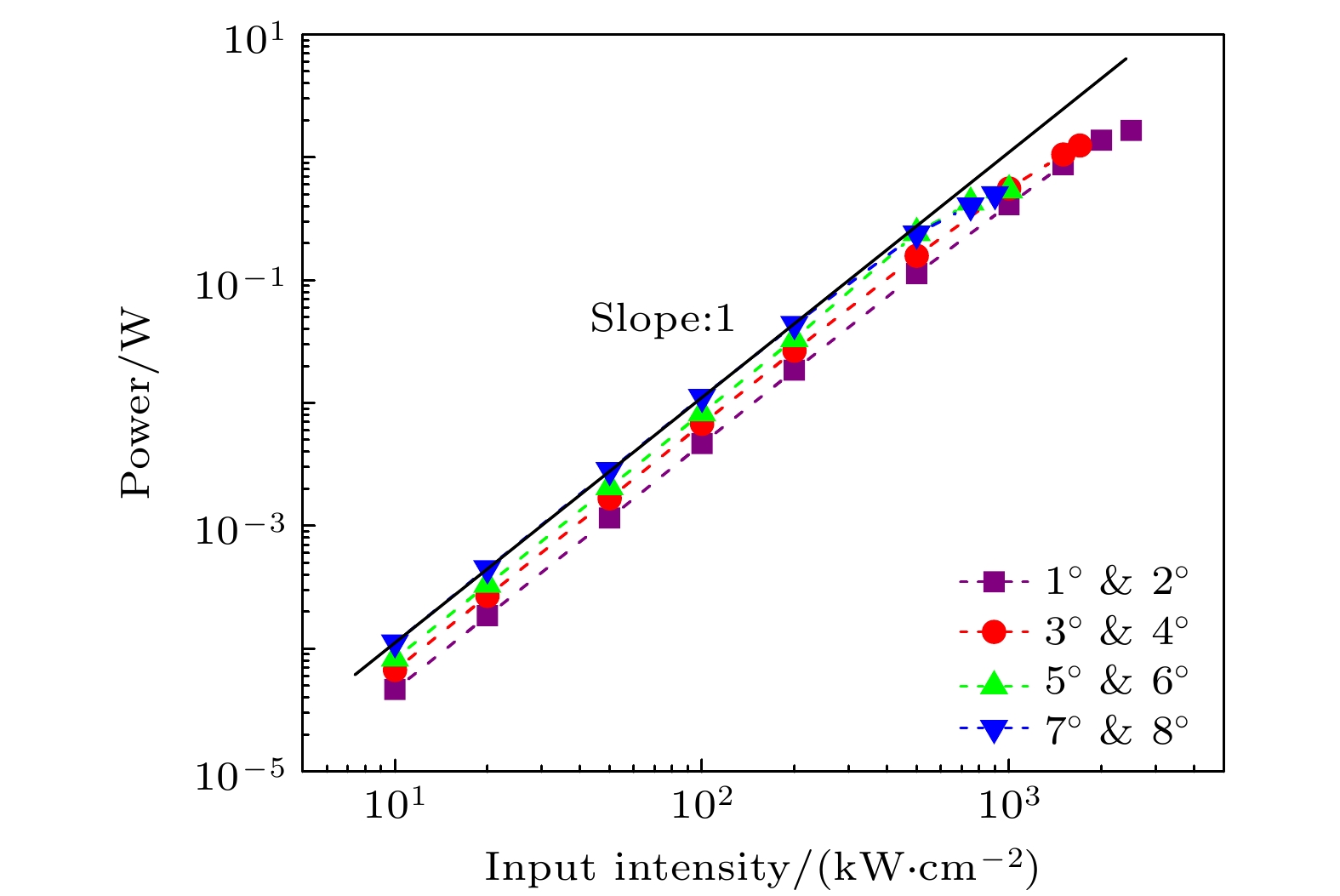
差频产生THz波的功率与入射光强的关系如图5所示. 显然地, 当基频光功率较小时, THz电场与基频场的耦合可以忽略, 符合非耗尽泵浦近似, THz功率与入射光强度的乘积符合对数斜率为1的关系. 随着基波功率的增大, 当基波场与差频场的耦合无法忽略时, THz电场与基频场的耦合会使得基频光的共振波长发生移动, 从而使得局域电场增强不再线性增大, THz功率会偏小于理论值. 此转变入射强度随两束光入射角度的增大而减小, 与Q因子和局域场增强随角度的增大而增大相关.
-
本文研究具有高Q几何扰动的CdS光栅-波导结构中非线性差频产生的高效、可调谐的THz辐射. 基频光共振波长可通过改变入射角在很宽的范围内可调且共振模均具有很高的Q因子, 从而实现了差频产生THz的波段可调性与高效性, 为微纳光子学平台产生THz源研究提供了有意义的参考.
高Q几何扰动光栅-波导结构中差频产生可调谐太赫兹辐射的数值研究
Numerical study of tunable terahertz radiation from differential frequency generation in high-Q geometrically perturbed grating waveguide structures
-
摘要: 非线性差频产生(difference frequency generation, DFG)是实现太赫兹(terahertz, THz)源的重要方式之一. 利用微纳结构的DFG产生THz源可以不考虑相位匹配, 同时是器件小型化、可集成化的重要研究方向. 借助微纳结构的共振模式增强的局域电场在宽波段范围内实现高效的、可调谐的THz源是该领域的研究重点. 本文研究了宽波段范围内具有高Q因子的光栅-波导结构中的DFG产生高效可调谐的THz辐射. 理论上, 通过调控相邻光栅中其中一个的位置扰动, 从而实现光栅周期的加倍, 进而使得布里渊区发生折叠, 光线下方波导层中导模色散曲线折叠到光锥上方, 形成超高Q因子的导模共振, 可以实现在宽光谱范围内增强的THz 产生. 以硫化镉(cadmium sulfide, CdS)光栅-波导为例, 数值研究表明, 在两束基频光光强均为100 kW/cm2时, THz的转换效率可达到10–8 W –1的量级, 为相同厚度CdS薄膜转换效率的109倍. 通过改变两束基频光入射角, 可实现不同共振基频组合, 实现任意频率THz波产生, 从而实现了在宽光谱范围内高效可调谐的THz源.Abstract: Nonlinear difference frequency generation (DFG) is a key mechanism for realizing terahertz (THz) sources. Utilization of DFG within micro- and nano-structures can circumvent the phase-matching limitations while supporting device miniaturization and integrability, thus the DFG is made a significant area of research. Enhancing the local electric fields through resonant modes in micro- and nano-structures has become a promising approach to achieving efficient and tunable THz sources across a broad wavelength range. In this work, the mechanism of DFG in high-Q-factor grating-waveguide structures for efficiently tuning THz radiation over a wide spectral range is investigated by using numerical simulations based on the finite element method (COMSOL Multiphysics). Theoretical analysis reveals that modulating the positional perturbation of one of the adjacent gratings effectively doubles the grating period, causing Brillouin zone to fold. This folding shifts the dispersion curve of the guided mode (GM) within the waveguide layer above the light cone, forming a guided mode resonance (GMR) with an ultra-high Q-factor, thereby significantly enhancing THz generation in a broad spectral range. Taking a cadmium sulfide (CdS) grating-waveguide structure for example, numerical simulations demonstrate that the THz conversion efficiency reaches an order of 10–8 W–1 when both fundamental frequency beams have an intensity of 100 kW/cm2, which is 109 times higher than the conversion efficiency of a CdS film of the same thickness. Moreover, the fundamental frequency resonance wavelength can be widely tuned by adjusting the incident angle. High-Q-factor resonance modes enable various fundamental frequency combinations by changing the incident angles of the two fundamental frequency beams, facilitating the generation of THz waves with arbitrary frequencies. This approach ultimately enables a highly efficient and tunable THz source in a wide spectral range, providing valuable insights for generating THz sources on micro- and nanophotonic platforms.
-
Key words:
- guide mode resonance /
- difference frequency generation /
- terahertz source .
-
-
图 1 四部分光栅-波导结构和光配置示意图, 其中Λ是光栅-波导结构的周期, wg是 CdS 的宽度, wa和wb是空气的宽度, hg和hw 分别是光栅层和波导层的高度
Figure 1. Schematic diagram of grating waveguide structure and light configuration. Λ is the periodicity of grating waveguide structure, wg is the width of CdS, wa and wb are the width of air, hg and hw are the height of grating layer and waveguide layer, respectively.
图 2 (a) TE偏振光照射下周期为P = Λ/2的未扰动光栅-波导结构(绿点)和几何扰动δ = 0.1、周期为Λ的光栅结构-波导结构(红点和蓝点)的能带, 插图显示了箭头所示位置的GMR模式的电场(TE)分布; (b)波段A和波段B的Q因子与kx的关系; (c)波导层中TE0导波模式的色散关系(黑色实线), 以及kx = kx, i (i = –1, –2)在不同入射角θ下的色散关系, 分别为θ = 1° (酒红色虚线)、2° (红色虚线)、4° (绿色虚线)、6° (蓝色虚线)、8° (青色虚线)、10° (品红色虚线)
Figure 2. (a) Band structure of the unperturbated grating-waveguide nanostructure of period P = Λ/2 (green dots) and geometrical perturbated δ = 0.1 grating-waveguide nanostructure of period Λ (red and blue dots). The inset shows the electric field (TE) distribution of the GMR mode at the kx as the arrow given. (b) Dependence of Q-factors of band A and B on kx. (c) Dispersion relations of the TE0 guide mode in the waveguide layer (black solid line), and kx = kx, i (i = –1, –2) under different angle of incidence θ = 1° (Wine red dashed line), 2° (red dashed lines), 4° (green dashed lines), 6° (blue dashed lines), 8° (cyan dashed lines), 10° (Magenta dashed line), respectively.
图 3 (a)不同参数δ的光栅-波导结构在入射角θ = 6°时的透射光谱, 插图分别显示了 δ = 0.2和1.0 结构中共振模式处的Ez分布; (b) δ = 0.1 的光栅-波导结构的透射率与入射角的关系, 插图显示了θ = 6°结构中共振模式处的电场Ez分布; (c) 在TE偏振光照射下, 光栅-波导结构的Q因子与δ的关系, 插图显示了Q因子与δ–2之间的线性关系, 虚线为线性拟合; (d) δ = 0.1 时, 共振波长(黑色实线)和品质因数(黑色虚线)与入射角的关系
Figure 3. (a) Transmittance spectra of grating waveguide structure of different parameter δ at the incidence angle θ = 6°. The inset shows the electric field Ez distribution at the resonance modes in the structure of δ = 0.2 and 1.0, respectively. (b) The dependence of transmittance of grating waveguide structure of δ = 0.1 on the incidence angle. The inset shows the electric field Ez distribution at the resonance modes in the structure of θ = 6°. (c) Dependence of Q-factor of the grating waveguide structure on δ under TE-polarized light irradiation. The inset shows the linear relationship between Q-factor and δ–2, and the dash line is a linear fitting. (d) The relation of resonance wavelength (solid black line) and quality factor (black dashed line) with the angle of incidence at the grating waveguide structure of δ = 0.1.
图 4 不同入射角下DFG产生的THz转换效率与入射波长的关系, 其中入射角分别为(a) 1°和2°, (b) 3°和4°, (c) 5°和6°及(d) 7°和8°
Figure 4. Generated THz conversion efficiency (CE) from DFG as a function of incident wavelength for different incidence angles. The incident angles are (a) 1° and 2°, (b) 3° and 4°, (c) 5° and 6°, and (d) 7° and 8°.
-
[1] Tonouchi M 2007 Nat. Photonics 1 97 doi: 10.1038/nphoton.2007.3 [2] Huang Y, Shen Y C, Wang J Y 2023 Engineering 22 106 doi: 10.1016/j.eng.2022.06.023 [3] Koch M, Mittleman D M, Ornik J, Castro-Camus E 2023 Nat. Rev. Methods Primers 3 48 doi: 10.1038/s43586-023-00232-z [4] Rubano A, Mou S, Marrucci L, Paparo D 2019 ACS Photonics 6 1515 doi: 10.1021/acsphotonics.9b00265 [5] Li X R, Li J X, Li Y H, Ozcan A, Jarrahi M 2023 Light Sci. Appl. 12 233 doi: 10.1038/s41377-023-01278-0 [6] Lewis R A 2014 J. Phys. D: Appl. Phys. 47 374001 doi: 10.1088/0022-3727/47/37/374001 [7] Li H T, Lu Y L, He Z G, Jia Q K, Wang L 2016 J. Infrared, Millimeter, Terahertz Waves 37 649 doi: 10.1007/s10762-016-0258-9 [8] Li Q, Li Y D, Ding S H, Wang Q 2012 J. Infrared Millim. Te. 33 548 doi: 10.1007/s10762-012-9897-7 [9] 曹俊诚, 韩英军 2024 中国激光 51 0114001 doi: 10.3788/CJL231166 Cao J C, Han Y J 2024 Chin. J. Lasers 51 0114001 doi: 10.3788/CJL231166 [10] Lai R K, Hwang J R, Norris T B, Whitaker J F 1998 Appl. Phys. Lett. 72 3100 doi: 10.1063/1.121559 [11] Upadhya P C, Fan W H, Burnett A, Cunningham J, Davies A G, Linfield E H, Lloyd-Hughes J, Castro-Camus E, Johnston M B, Beere H 2007 Opt. Lett. 32 2297 doi: 10.1364/OL.32.002297 [12] Fan W H 2011 Chin. Opt. Lett. 9 110008 doi: 10.3788/COL201109.110008 [13] Bakunov M I, Bodrov S B 2014 J. Opt. Soc. Am. B 31 2549 doi: 10.1364/JOSAB.31.002549 [14] 柴路, 牛跃, 栗岩锋, 胡明列, 王清月 2016 物理学报 65 070702 doi: 10.7498/aps.65.070702 Chai L, Niu Y, Li Y F, Hu M L, Wang Q Y 2016 Acta Phys. Sin. 65 070702 doi: 10.7498/aps.65.070702 [15] 黄敬国, 陆金星, 周炜, 童劲超, 黄志明, 褚君浩 2013 物理学报 62 120704 doi: 10.7498/aps.62.120704 Huang J G, Lu J X, Zhou W, Tong J C, Huang Z, Chu J H 2013 Acta Phys. Sin. 62 120704 doi: 10.7498/aps.62.120704 [16] 刘欢, 徐德刚, 姚建铨 2008 物理学报 57 5662 doi: 10.7498/aps.57.5662 Liu H, Xu D G, Yao J Q 2008 Acta Phys. Sin. 57 5662 doi: 10.7498/aps.57.5662 [17] 钟凯, 姚建铨, 徐德刚, 张会云, 王鹏 2011 物理学报 60 034210 doi: 10.7498/aps.60.034210 Zhong K, Yao J Q, Xu D G, Zhang H Y, Wang P 2011 Acta Phys. Sin. 60 034210 doi: 10.7498/aps.60.034210 [18] Bakunov M I, Efimenko E S, Gorelov S D, Abramovsky N A, Bodrov S B 2020 Opt. Lett. 45 3533 doi: 10.1364/OL.391871 [19] Lu Y, Wang X, Miao L, Zuo D, Cheng Z 2011 Appl. Phys. B 103 387 doi: 10.1007/s00340-010-4255-8 [20] Tochitsky S Y, Ralph J E, Sung C, Joshi C 2005 J. Appl. Phys. 98 026101 doi: 10.1063/1.1957123 [21] Zhong K, Yao J Q, Xu D G, Wang Z, Li Z Y, Zhang H Y, Wang P 2010 Opt. Commun. 283 3520 doi: 10.1016/j.optcom.2010.04.106 [22] Jiang Y, Ding Y J 2007 Appl. Phys. Lett. 91 091108 doi: 10.1063/1.2775095 [23] Shi W, Ding Y J 2005 Opt. Lett. 30 1861 doi: 10.1364/OL.30.001861 [24] Brenier A 2018 Appl. Phys. B 124 194 doi: 10.1007/s00340-018-7063-1 [25] Liu P X, Xu D G, Li J Q, Yan C, Li Z X, Wang Y Y, Yao J Q 2014 IEEE Photonics Technol. Lett. 26 494 doi: 10.1109/LPT.2014.2300172 [26] Wu F, Wu J J, Guo Z W, Jiang H T, Sun Y, Li Y H, Ren J, Chen H 2019 Phys. Rev. Appl. 12 014028 doi: 10.1103/PhysRevApplied.12.014028 [27] Ning T Y, Li X, Zhao Y, Yin L Y, Huo Y Y, Zhao L N, Yue Q Y 2020 Opt. Express 28 34024 doi: 10.1364/OE.409276 [28] Wu F, Qin M B, Xiao S Y 2022 J. Appl. Phys. 132 193101 doi: 10.1063/5.0120626 [29] Wu F, Liu T T, Long Y, Xiao S Y, Chen G Y 2023 Phys. Rev. B 107 165428 doi: 10.1103/PhysRevB.107.165428 [30] Wu F, Qi X, Luo M, Liu T T, Xiao S Y 2023 Phys. Rev. B 108 165404 doi: 10.1103/PhysRevB.108.165404 [31] Wu F, Qi X, Qin M B, Luo M, Long Y, Wu J J, Sun Y, Jiang H T, Liu T T, Xiao S Y, Chen H 2024 Phys. Rev. B 109 085436 doi: 10.1103/PhysRevB.109.085436 [32] 闫梦, 孙珂, 宁廷银, 赵丽娜, 任莹莹, 霍燕燕 2023 物理学报 72 044202 doi: 10.7498/aps.72.20221894 Yan M, Sun K, Ning T Y, Zhao L N, Ren Y Y, Huo Y Y 2023 Acta Phys. Sin. 72 044202 doi: 10.7498/aps.72.20221894 [33] Sun K L, Wei H, Chen W J, Chen Y, Cai Y J, Qiu C W, Han Z H 2023 Phys. Rev. B 107 115415 doi: 10.1103/PhysRevB.107.115415 [34] Boyd R W 2020 Nonlinear Optics (London: Academic Press [35] Jiang H, Han Z H 2022 J. Phys. D: Appl. Phys. 55 385106 doi: 10.1088/1361-6463/ac7e07 [36] Sutherland R L 2003 Handbook of Nonlinear Optics (New York: Marcel Dekker [37] Amnon Yariv, Yeh P 1984 Optical Waves in Crystals (New York: Wiley [38] Lu J, Ding B Y, Huo Y Y, Ning T Y 2018 Opt. Commun. 415 146 doi: 10.1016/j.optcom.2018.01.052 [39] Liu W X, Li Y H, Jiang H T, Lai Z Q, Chen H 2013 Opt. Lett. 38 163 doi: 10.1364/OL.38.000163 -
计量
- 文章访问数: 136
- HTML全文浏览数: 136
- PDF下载数: 1
- 施引文献: 0