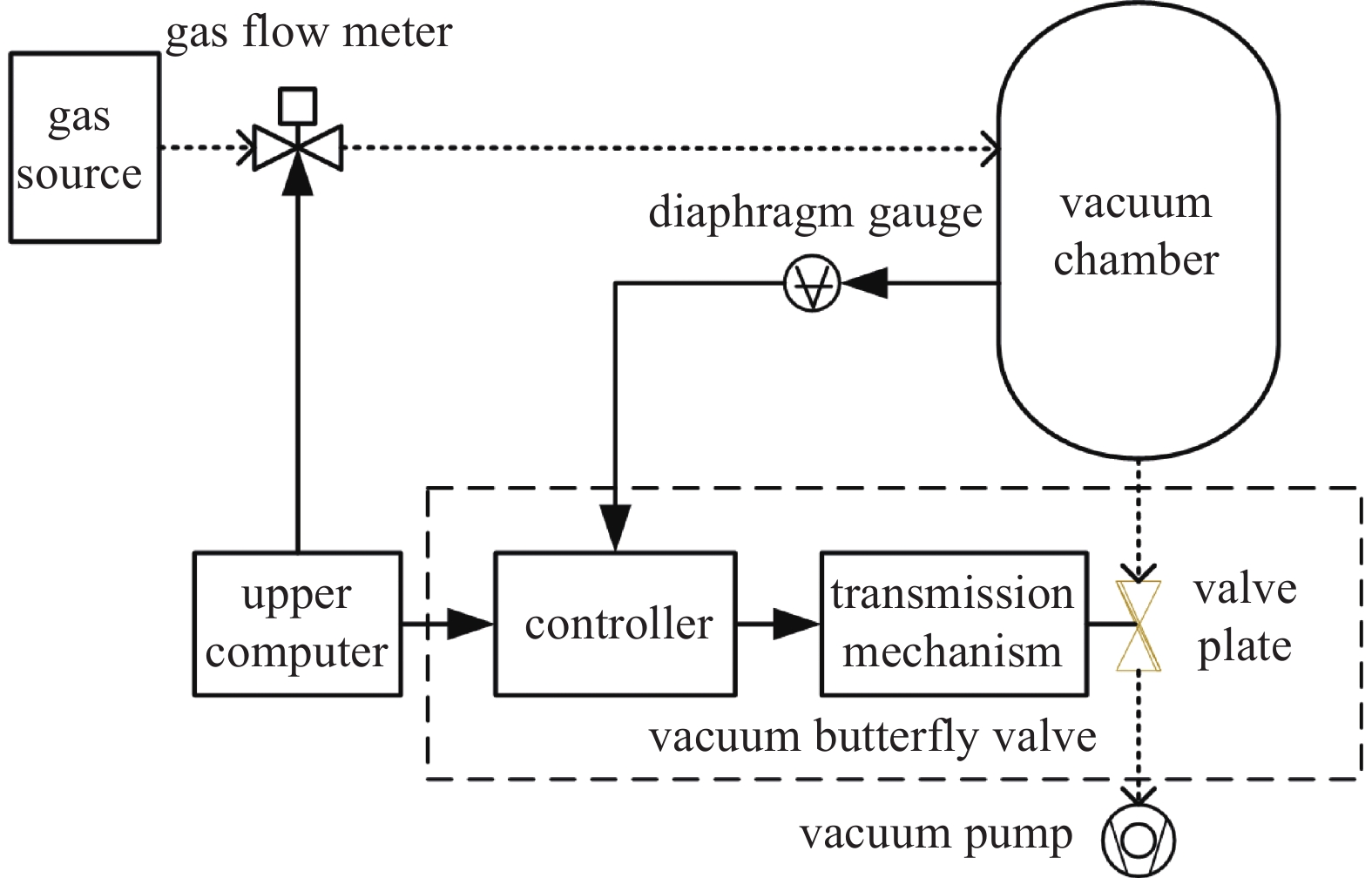
真空设备通过控制气体的流入量和流出量，来调节腔体内的气体分子数量，从而控制腔体内部压力。真空蝶阀压力控制系统的结构示意图如图1所示，其中，气体流量控制器用于控制真空设备的进气量，气体供应系统通过气体流量控制器向腔体内引入气体，从而增加腔体内的气体分子数量和提升腔内压力。真空泵则用于真空腔体的气体排出，降低腔体内部压力。薄膜真空计作为控制系统的压力传感器用于向蝶阀控制器实时反馈腔内压力。

真空蝶阀常用于真空设备压力控制的下游工艺，被安装在真空腔体与真空泵之间，控制流出腔体的气体流量。在真空设备进行调压时，真空腔体的进气量通常保持恒定，蝶阀控制器根据压力传感器实时检测的设备内部压力与给定的目标压力之间的压力误差，计算阀板的开合角度，通过执行机构改变蝶阀的气体流通面积S：

式中，r表示真空蝶阀阀板的半径；θ表示阀板的开合角度。

蝶阀的流通面积的变化使得蝶阀的气体流量发生改变，腔内气体通过蝶阀的流出量Q_out可通过式（2）计算获得：

式中，R为气体常数，T为阀前温度，p_q为阀门前压力，C_v为蝶阀流量系数，∆p为蝶阀两侧压力之差，蝶阀压差∆p的计算公式（3）如下：

式中，p_b为阀门后压力，在实际应用中，由于真空泵高效的抽气能力，阀门后压力$ p\mathrm{_b} $远低于阀门前压力p_q，因此Q_out在计算时可以转换为：

真空设备的压力是由腔内的气体分子数决定，如果气体流入量与气体流出量不能达到平衡，则引起腔内压力产生变化，腔内压力变化率$ \dot{p} $的计算公式（5）如下：

式中，Q_in为气体流入量，V为真空腔体容积，M为流过蝶阀的气体摩尔质量。

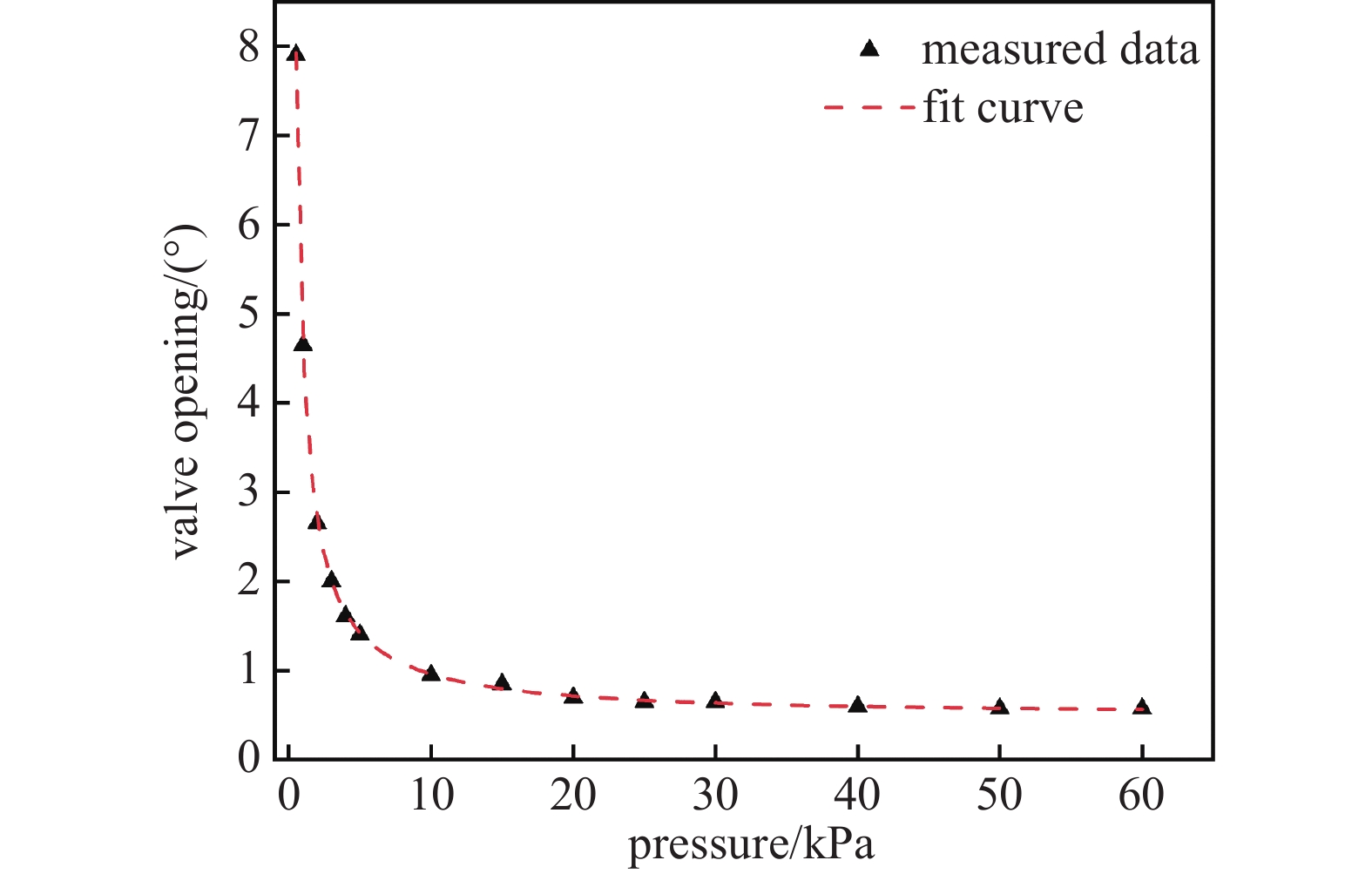
由式（4）和式（5）可知，真空蝶阀在进行控压工作时，在气体流入量Q_in、阀前温度T保持不变的情况下，通过调节蝶阀的阀板开合角度，可改变真空腔体气体流出量以及内部压力。由于蝶阀的流通特性以及气流管路其它部件阻力特性的影响，真空腔体内的压力变化与蝶阀的开度之间并非成线性关系，而是按图2的规律变化。图2是在进气量为6 L/min、真空腔体内部容积为21 L的测试环境下，通过采集腔内压力稳定时的各个压力点及对应的阀门开度测定，其表征了蝶阀压力控制系统的工作特性。进行拟合后，得到工作特性的拟合曲线，其拟合公式如下：

拟合公式的拟合优度$ {R}^{2} $为0.9984。

本文研究设计的模糊PID控制器，通过模糊控制在线调整PID控制器参数，从而提高控制系统的动态性能；并设计了校正函数，可根据上位机输入目标压力实时修正模糊控制器输出值，提高模糊PID控制算法在蝶阀压力控制系统中的适用性。

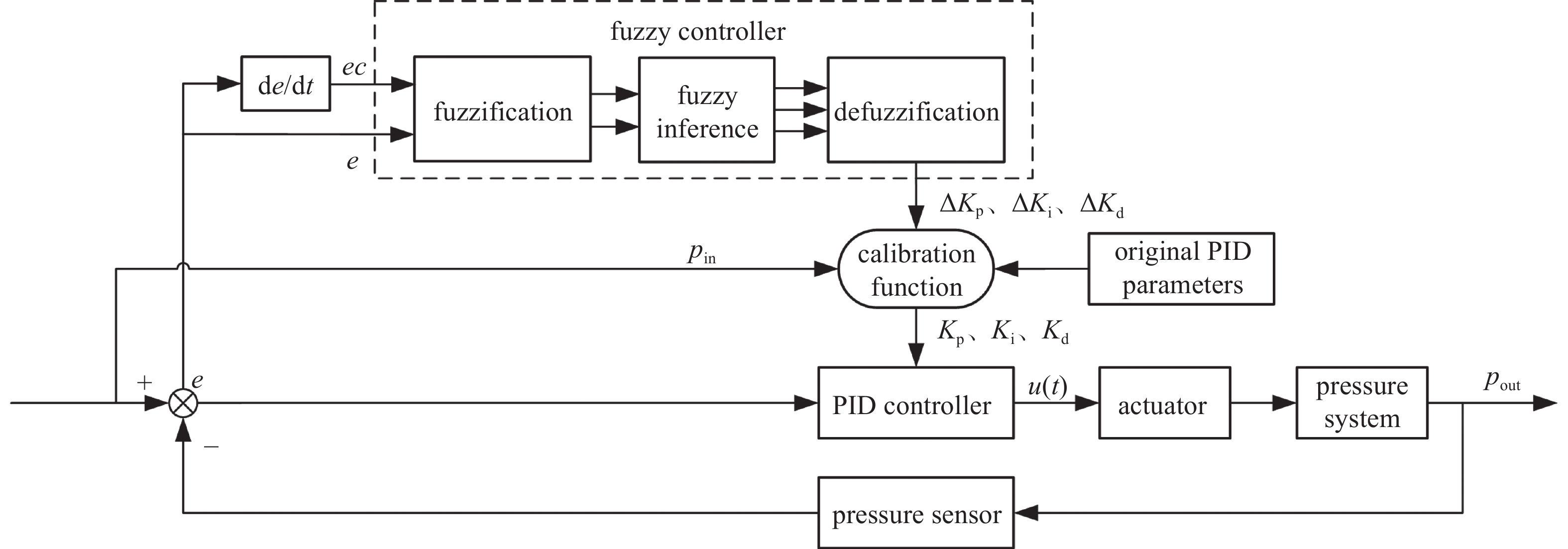
基于模糊PID的真空蝶阀压力控制系统结构图如图3所示，系统的控制器由PID控制器、模糊控制器以及校正函数组成。其中∆K_p、∆K_i、∆K_d为模糊控制器输出的PID参数调整量，K_p、K_i、K_d为经过校正函数修正后的PID控制参数，p_in为上位机给定的目标压力，u(t)为蝶阀控制器的输出信号，p_out为系统实际输出值，e(t)为控制系统的当前时刻偏差量，e(t)的计算公式如下：

经典PID控制器是通过比例、积分、微分三个部分，对反馈的实际输出量与设定的目标值的偏差进行计算。但由于蝶阀的微处理器在运算时不能对连续的模拟信号进行计算，需要输入信号进行离散化，同时为了消除调压时积分饱和带来的影响，所以采用增量型PID 控制算法^[4]，其表达式如下：

式中，∆u(t)为控制器输出量；u(t)的变化量。

对于增量式PID控制算法，在设置合适的参数K_p、K_i、K_d后，PID控制器的比例、积分、微分三个环节根据控制误差实时调节被控对象，从而使系统稳定和减小控制误差。但经典PID控制算法因为其PID参数在工作时固定，不能随环境的变化而变化^[5]，导致蝶阀压力控制系统控压时超调量大、调节时间长，其在动态性能和稳态精度上无法满足真空蝶阀高精度控压需求。

模糊PID控制器主要由模糊控制器和PID控制器两部分组成，控制系统的输入经过模糊控制器的三个环节：模糊化、模糊推理、清晰化后，实现PID控制器参数的在线自适应整定，从而使PID控制器获得更好的控制性能^[6]。

本文设计的自适应模糊PID控制器采用二输入三输出的Mamdani型模糊控制器，如图3所示，模糊控制器以真空蝶阀压力控制系统的压力误差e和压力误差变化率ec作为输入，经过模糊运算后输出PID控制器三个参数的调整量∆K_p、∆K_i、∆K_d。

模糊控制器通过模糊化，将物理论域中的压力误差e和压力误差变化率ec转化为模糊论域中的模糊值E和EC。根据真空蝶阀的实际工作压力范围，定义误差e的物理论域为[−30,30]、模糊论域为[−3,3]，其对应的量化因子设置为0.01；定义变化率ec的物理论域为[−1.5,1.5]、模糊论域为[−1,1]，其对应的量化因子设置为0.66。定义输出量∆K_p、∆K_i、∆K_d的模糊论域均为[−1,1]，对应的比例因子分别为：1、0.23、0.05。

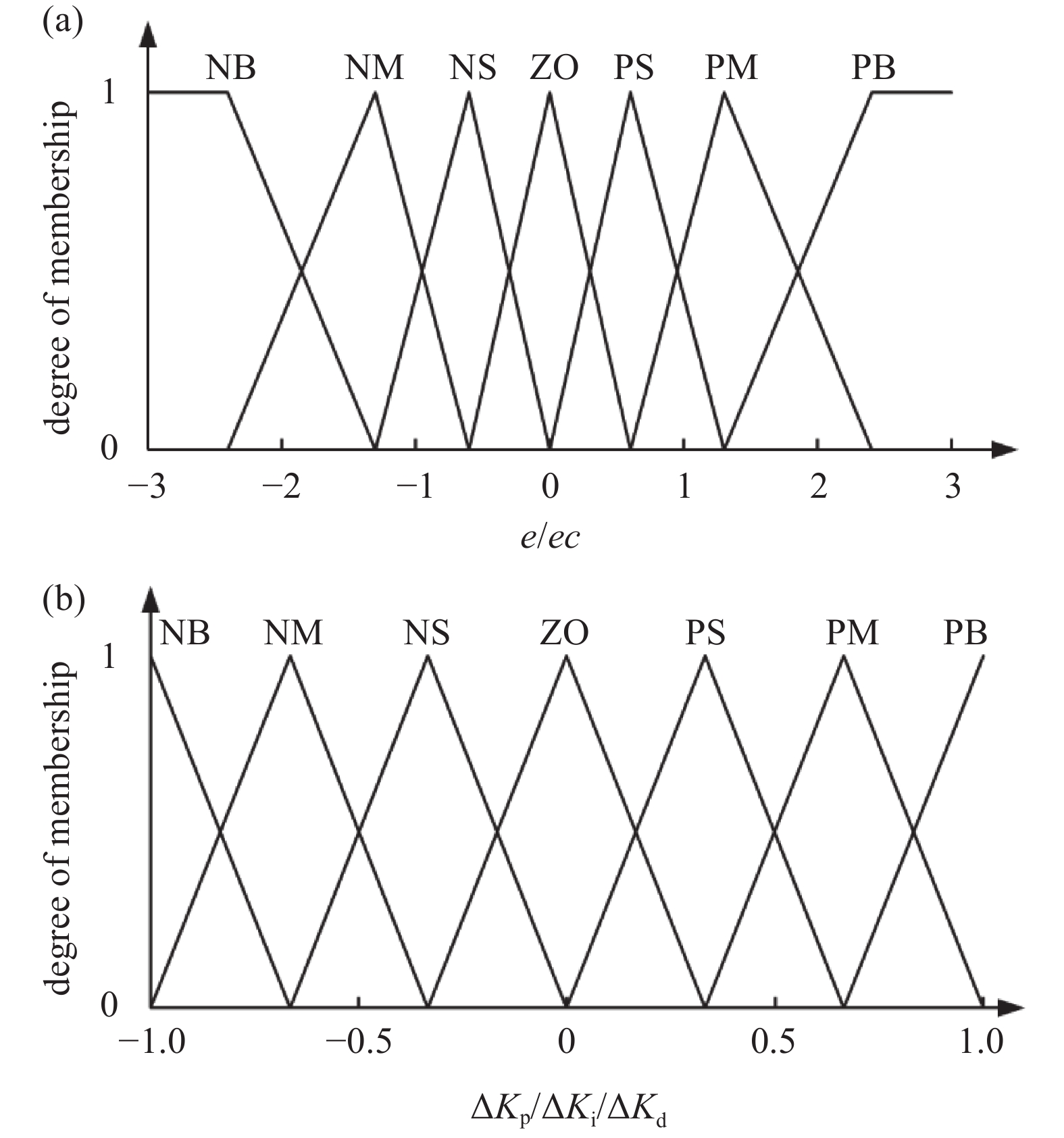
因为三角隶属函数具有运算简单、工作时内存消耗小等优点^[7]，故选择其作为输入量和输出量的隶属函数。将输入量和输出量的模糊子集均设为{NB, NM, NS, ZO, PS, PM, PB}，对应的模糊数为{−3,−2,−1,0,1,2,3}，其中：NB代表负大，NM代表负中，NS代表负小，ZO代表零，PS代表正小，PM代表正中，PB代表正大^[8-11]。输入量e、ec和输出量∆K_p、∆K_i、∆K_d对应隶属函数以及模糊子集分布如图4所示。

根据真空蝶阀压力控制系统的工程经验，分析压力误差e、压力误差变化率ec与PID控制器的三个参数之间的关系，制定以下模糊控制规则表，分别如表1、表2、表3所示。

模糊规则表中PID参数的调整原则为：当压力误差的绝对值|e|较大，但压力误差变化率ec较小时，为加快压力控制系统的响应速度，应增大K_p和K_d，同时为了避免出现超调，应减少K_i；当压力误差绝对值|e|处于中等大小，但压力误差变化率较大时，应该减小压力上升或者下降速度，则K_p不应太大，同时适当增大K_i；当压力误差的绝对值|e|较小时，为了使控制系统具有良好的稳态性能，应取较大的K_p和K_i，如果此时压力误差变化率依然较大，则为了避免震荡，应适当减小K_d。

为了使模糊控制器的输出更加平滑，文章采用目前较为常用的重心法分别对模糊推理后各输出量的模糊集合进行清晰化^[12]。其在离散域的表达式如下：

式中，U_o是输出量的精确值，F_i是模糊量化值，M_i是模糊量化值对应的隶属度值。

通过对图2分析可知，当真空设备内部处于不同压力点时，相同阀门开度变化量，引起压力变化及压力变化速率相差较大，真空设备内部压力越高，腔内压力对蝶阀的阀门开度变化越敏感。因此，真空设备内部压力与蝶阀的阀门开度之间具有强非线性。为了补偿这种强非线性的压力变化，本文基于蝶阀的压力控制特性引入了校正函数，用于对模糊控制器调整后的PID参数进行在线校正，校正后的PID三个参数如下：

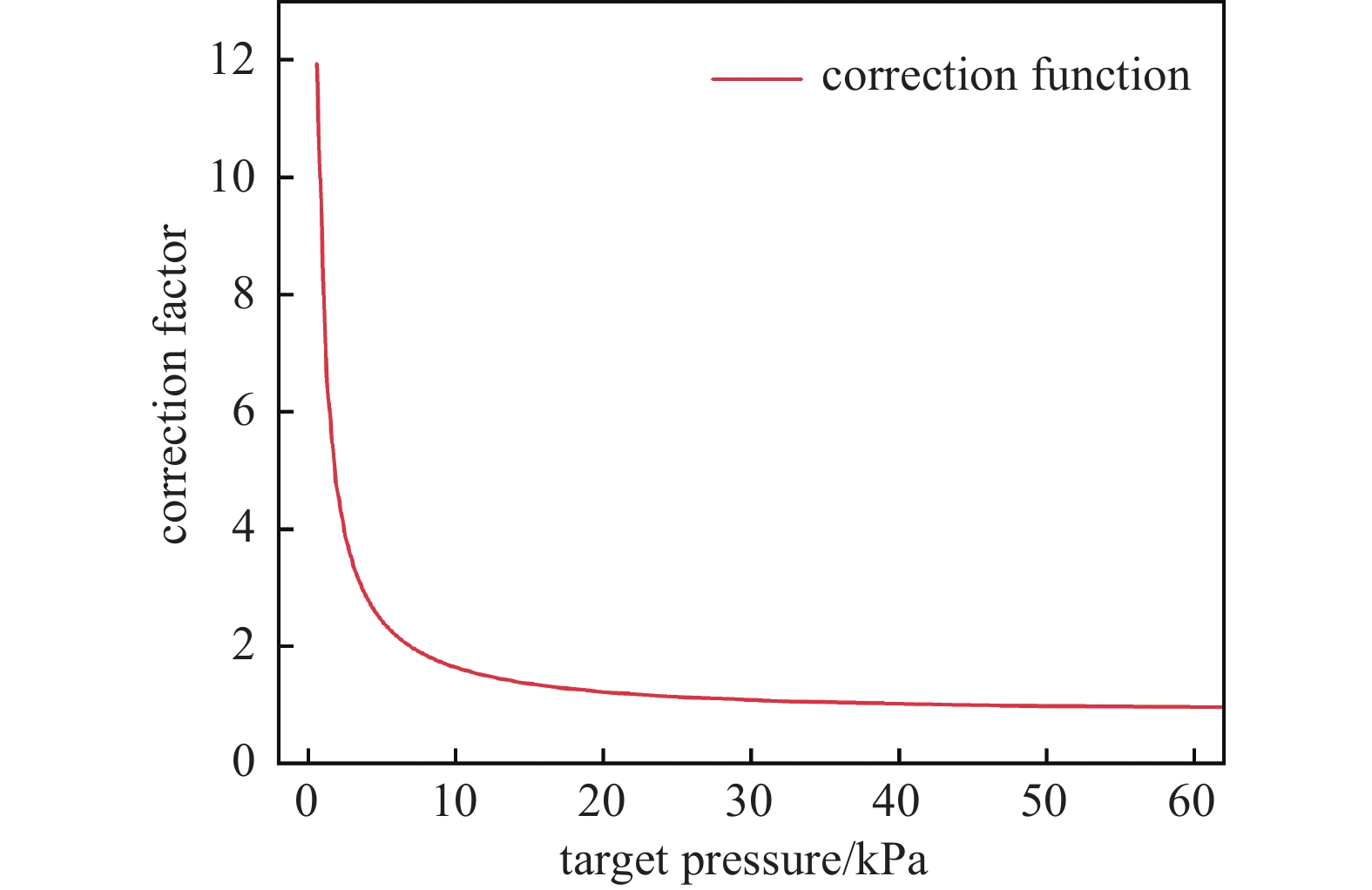
式中，K_po、K_io、K_do分别为PID参数K_p、K_i、K_d的初始值。G_k为校正函数产生的校正因子，校正因子由校正函数根据输入的目标压力计算而来，校正函数的公式如下：

式中，x为压力控制系统的目标压力，0.585是真空设备内部压力稳定在30 kPa时蝶阀的阀门开度值。由于蝶阀的控压范围主要在[0.01，30] kPa之间，所以本文以蝶阀作业时的最高压力点作为校正函数的基准点，校正函数曲线如图5所示。从图5中可看出校正因子与目标压力的关系同样具有强非线性，在压力较低时校正因子的取值较大，因此可放大低压区时控制器的输出信号，提高控制系统在低压区的敏感度和响应速度，从而改善低压时强非线性对压力控制系统造成的影响。

为了验证优化后的模糊PID控制算法在压力在蝶阀压力控制系统中的控制性能，搭建真空蝶阀压力控制系统测试平台，如图6所示。

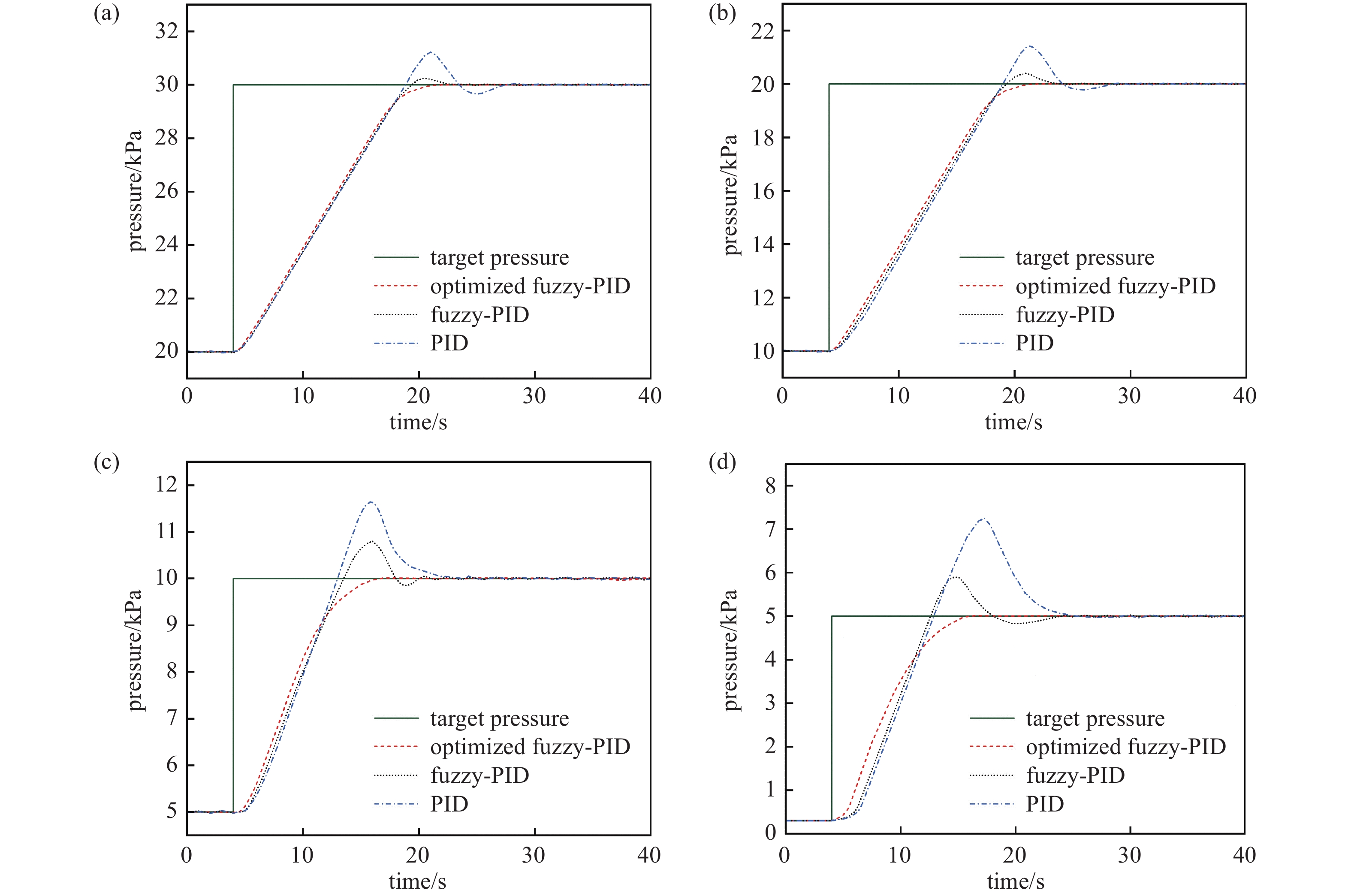
在进行算法的控制性能测试时，三种控制算法的PID控制器参数的预设值均设置为：K_po = 1.0、K_io = 0.23、K_do = 0.05。控制系统测试平台的部分参数为：薄膜真空计量程为0.1~100 kPa，真空计的输出电压为0~10 V；真空腔体容积为21 L；真空泵为干式泵，极限压强为3×10⁻² mbar；真空腔体内部温度为20℃，通入气体为高纯度氮气，进气量设置为6 L/min。图7为3种控制算法的实验结果，传统PID控制、模糊PID控制以及优化后的模糊PID控制算法在目标压力分别设置为30 kPa、20 kPa、10 kPa和5 kPa时的阶跃响应曲线,如图7所示。

从图7可以看出，由于模糊控制器是以30 kPa时的控压工程经验作为设计模糊规则的先验知识，所以在从20 kPa到30 kPa的调压过程中，模糊PID控制算法在超调量和调节时间等性能指标上远好于常规PID算法，具有较好的控制性能。但随着目标压力逐渐降低，由于控制系统强非线性带来的影响，使得模糊PID算法不仅在动态性能上出现超调量变大、调节时间变长的问题，而且控制精度也逐渐降低。而带校正函数的模糊PID控制算法受到目标压力变化的影响较小。

在不同目标压力下3种控制算法具体的控制性能指标如表4所示，其中Ts为控制系统的调节时间，σ为调压过程中的超调量，SSE为压力稳定后控制系统的稳态压力误差。由表4可看出：在目标压力较高时，优化后的模糊PID控制算法对比常规模糊PID控制和传统PID算法在调节时间上分别降低了11.8%和29.8%，稳态误差分别降低了43.3%和58.5%。随着目标压力逐渐降低，传统PID和模糊PID的控制性能逐渐变差。在目标压力降低到5 kPa时，优化后的模糊PID控制算法相较于其它两种控制算法，在调节时间上分别降低35.4%和41.9%，在稳态误差上分别降低60%和66.6%，其依旧能够保持良好的动态响应特性和控制精度。

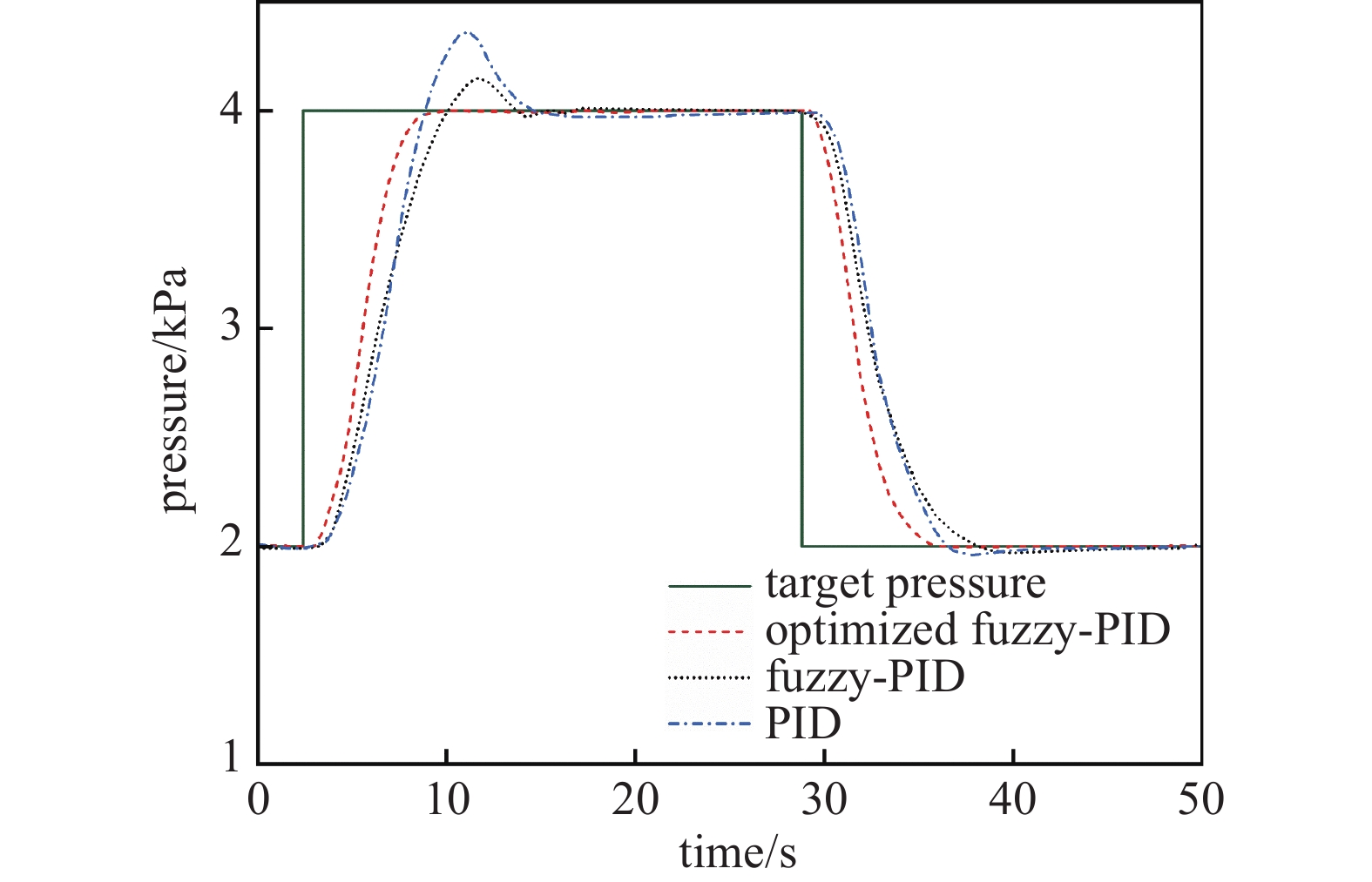
同时本文也验证了优化后的模糊PID控制器在低压时的控制性能，压力控制系统在2 kPa的低真空环境下进行了压力跟踪测试。测试结果如图8所示，在较低的压力环境下，模糊PID控制器由于受到系统的非线性影响，其控制性能大幅下降。带校正函数的模糊PID算法控制的压力系统在超调量以及调节时间上的表现要明显好于其它两种控制算法，其能够在无超调的情况下快速跟踪目标压力。

为了实现真空蝶阀压力控制系统的高精度压力控制，本文分析了真空蝶阀的控压特性，设计了模糊PID控制算法，并针对压力控制系统的强非线性设计了校正函数用于优化系统的模糊PID控制算法。实际测试结果表明，与常规的PID控制和模糊PID控制相比，使用校正函数优化后的模糊PID控制算法不仅大大减少了控制系统的调节时间和稳态误差，并且有效抑制了系统非线性带来的影响，使蝶阀在整个工作压力范围内都能保持良好的控制效果。因此，本文提出的模糊PID控制与校正函数相结合的控制算法可以用于蝶阀控压系统的压力控制，能够改善蝶阀的压力控制性能，在动态性能和控制精度等方面基本能够满足真空蝶阀控压作业的性能要求。