首页
登录
注册
-
仿星器(stellarator)通过复杂的线圈系统产生高精度的磁场来约束等离子体, 这种三维螺旋磁场位形可以在无等离子体的情况下观察到. 误差场可能源于线圈在制造过程中的形状偏差[1], 组装过程中的位置偏移[2,3]与形变, 或装置运行时所受到的电磁力和热应力作用形变. 不规则磁场的产生会导致磁面破裂, 等离子体平衡被破坏, 等离子体约束性能降低[4,5]. 因此, 评估线圈不规则性导致的误差场在高精度磁场的实现中起着关键作用.
Wendelstein7-X (W7-X) 是一种具有准力线(QI)对称磁场位形的仿星器, 其对线圈误差进行了深入研究[6]. 通过比较制造误差和组装过程中单个线圈的位移和旋转所产生的扰动对共振磁场的影响, 发现由线圈旋转产生的扰动对磁场影响最为显著[1,7]. 在其设计和制造过程中, 采用了各种先进的技术方法以实现W7-X的高精度建造、组装和误差场补偿[8]. 在大型螺旋装置(LHD)的线圈系统设计中, 分析了线圈形变所产生的不规则磁场的傅里叶分量, 并确定了线圈导体的形变允许范围. 在LHD建造完成后, 采用磁场映射方法分析了 重要的不规则效应. 结果表明, 水平位移对磁面的影响较为显著[9]. 在NCSX仿星器上[10]研究了线圈误差大小的影响, 目的是通过改变模块化线圈、环向场线圈和极向场线圈的误差值, 重新进行随机函数研究, 从而简化线圈形状. 得到了重要结论: 对靠近等离子体区域的模块化线圈进行误差控制至关重要, 但在远离等离子体的区域, 误差控制可以在一定程度上放宽[11]. 中国首台准环对称仿星器(CFQS)是一种准环对称(QA)仿星器[12–14], 该装置由西南交通大学与日本国立聚变科学研究所(NIFS)共同设计建造[15–17], 是一种类托卡马克的磁位形装置, 结合了托卡马克和仿星器的优良特性, 如新经典输运低、运行稳定不易发生大破裂、不需要等离子体电流等. 因此, 准环对称仿星器被认为是目前国际上最先进的一种磁约束位形之一. 在与其相关的研究中, 有学者对磁岛抑制及湍流输运等进行了研究[18,19]; 还有学者对其模块化线圈的错位对CFQS的磁面、旋转变换剖面、有效螺旋波纹等各种物理性质造成的影响进行了研究[2,3,20], 结果表明, 若将模块化线圈位移的幅度限制在10.0 mm以内, 则线圈的不规则性对这些物理性质的影响可忽略不计, 并且CFQS良好的新经典输运特性也将得以保持[21]. 在Zhu等[20–22]的研究中, Hessian矩阵方法[22,23]被用来识别CFQS中的重要线圈形状偏差, 并发现某些特定的线圈扰动可以显著增大n/m = 4/11的磁岛[20]. CFQS的磁场具有低阶共振扰动, 例如b42, b52和b62, 因此在其磁位形外围区域设计有2/5的磁岛偏滤器位形[24]. 但迄今为止, 尚未对由MC线圈形变引起的误差场进行过深入的探讨, 因此本文将对此进行系统研究.
-
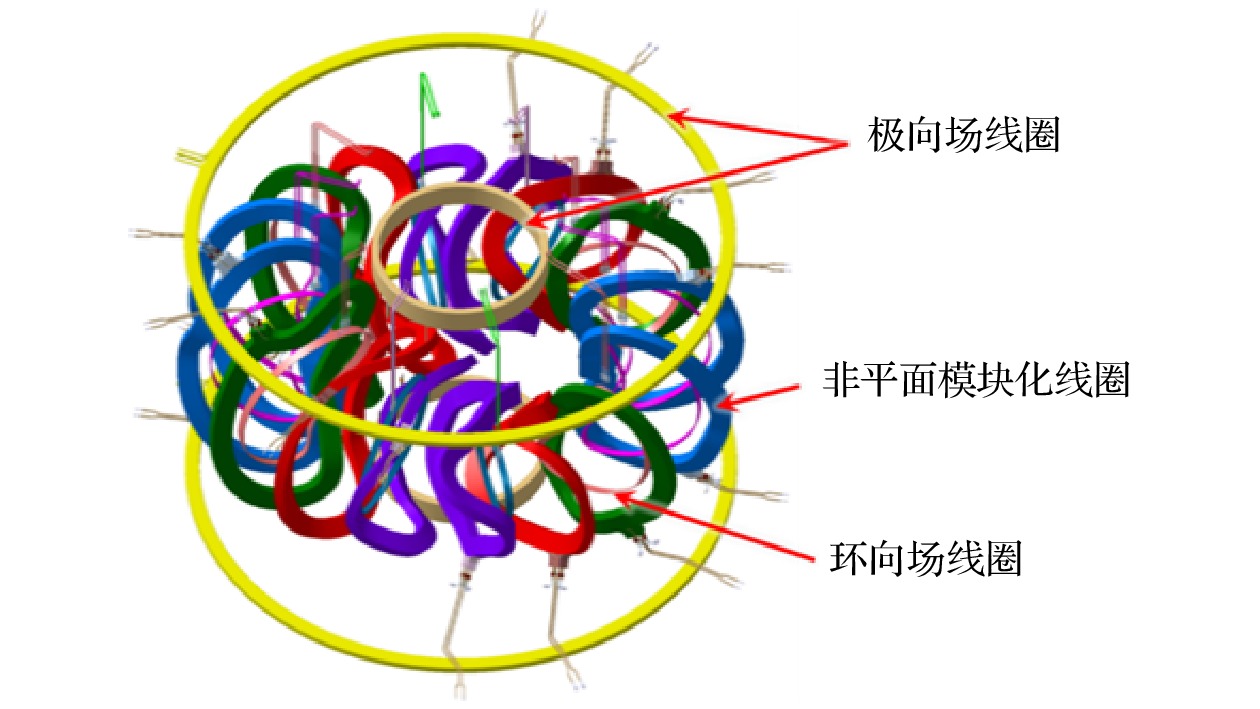
CFQS的环向周期数Np = 2、大半径R0 = 1.0 m、磁场强度Bt = 1.0 T、纵横比Ap = 4. 通过16个非平面模块化线圈来产生准环对称磁场位形[15,25]. 由于CFQS的周期性和仿星器的对称性, MC线圈系统由四组完全相同的线圈组构成. 每组线圈包含4种不同类型的线圈, 分别记为MC1, MC2, MC3和MC4. 其中, MC4形状最为复杂, 因为其扭转和曲率最大[26,27]. 为了提高磁场位形的灵活性, 设计了12个环向场线圈(TFC)和两对极向场线圈(两个PFC_IV和两个PFC_OV)[28]. TFC和PFC是简单的平面线圈, 用于控制等离子体平衡. TFC用于调整旋转变换剖面和实现磁岛偏滤器位形, 有3种不同形状的线圈, 分别为TFC_10, TFC_32和TFC_70; PFC也能起到调节磁轴位置和控制旋转变换剖面的作用[29]. CFQS的线圈系统如图1所示.
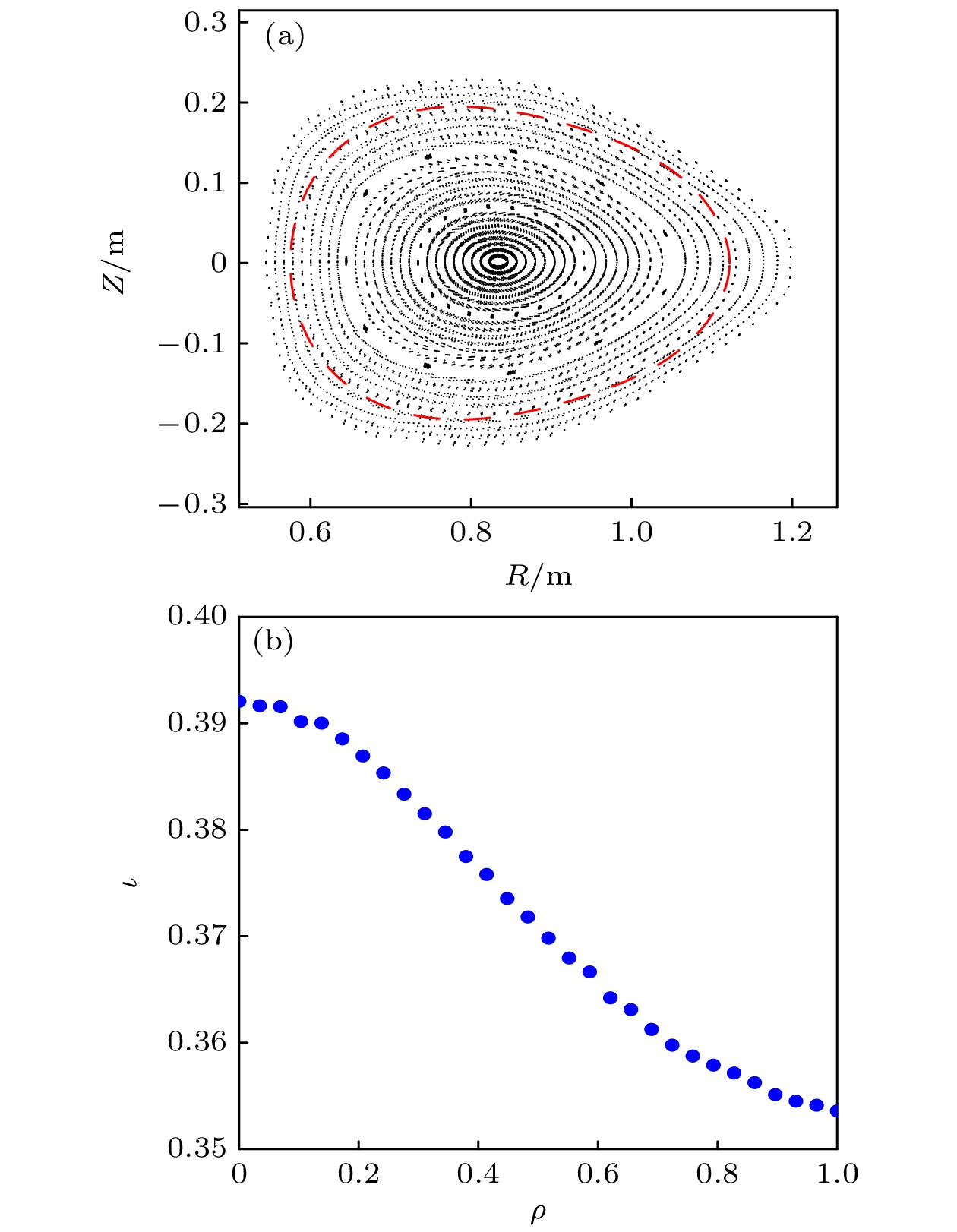
CFQS的目标磁场是一种低磁剪切的磁场, 为避免低阶有理面, 旋转变换选择了n/m = 2/5—2/6之间的值[30], 如图2所示, 其中n/m表示环向模数与极向模数的比值(仿星器的旋转变换表示和托卡马克有所不同, 后者是用安全因子q = m/n来表示). 图2(a)为通过磁力线追踪计算出理想模块化线圈产生的磁场在环向角为90°处的庞加莱截面图, 对应的旋转变换剖面如图2(b)所示. 本工作是基于真空条件下对磁场进行模拟计算. 尽管误差场可能会因为太小而无法直接观测, 但由于磁岛对误差场较为敏感, 因此能够反映出磁拓扑结构的微小变化[20]. 磁岛宽度可以用以下公式表示[31]:
其中, bmn是误差场的傅里叶分量振幅, R0是大半径,
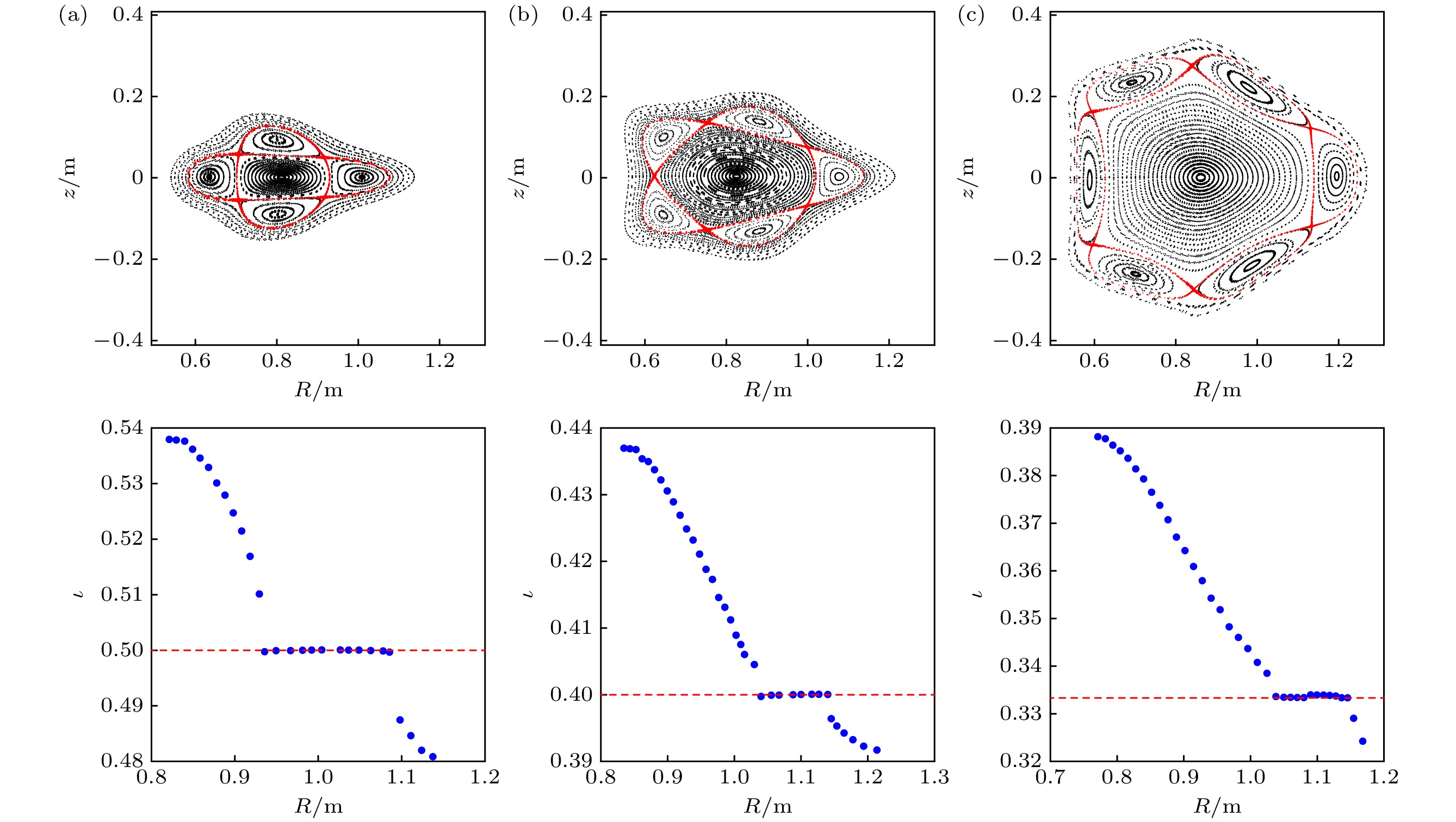
$ {\mathrm{d}}\iota /{\mathrm{d}}r $ 是有理面处的磁剪切, 其中$ r = \varPsi /{\mathrm{\pi }}{B}_{0} $ [32], Ψ是磁通量, B0是约束区域内的平均磁场强度.通过调节CFQS的线圈电流, 可以实现磁拓扑结构的灵活性, 使得旋转变换可以依次增大(或减小), 因此可以产生n/m = 2/4, 2/5和2/6这3种磁岛位形, 每种磁岛位形的线圈电流设置如表1所示. 通过磁力线追踪得到磁岛结构的庞加莱图, 通过找到岛链的X点来确定每个磁岛的边界, 并测量其径向宽度w2/4, w2/5和w2/6. 这些磁拓扑结构和相关的旋转变换剖面如图3所示, 图中, 红色虚线表示磁岛的边界, 每个岛的整体结构清晰可辨. 为了利用(1)式中磁岛的宽度变化来计算误差场, 我们将测量每个岛链中磁岛的宽度, 由于在同一个岛链中, 每一个磁岛的大小是同步且同趋势变化的, 因此选择变化最为明显的最右侧磁岛宽度变化作为代表来进行误差计算.
-
CFQS的MC线圈是用NESCOIL代码来设计的[33]. 该代码假定磁场是由分布在包围住等离子体的环形封闭面上的面电流而产生的, 所有线圈的位置都被限制在这个面上, 这个表面被称为“载流面”(CCS)或“绕组面”[34]. MC线圈的位置可以用以下方程来计算和表示:
式中, ξ和θ为线圈在CCS上的环向和极向位置,
$ \varphi $ 为极向角, m, n分别为极向模数和环向模数, Amn, Bmn, Cmn和Dmn为傅里叶系数. CCS在柱坐标下的傅里叶表示如下[33,35]:Fmn是傅里叶系数, (
$ {R}_{mn}^{{\mathrm{i}}{\mathrm{n}}} $ ,$ {Z}_{mn}^{{\mathrm{i}}{\mathrm{n}}} $ )和($ {R}_{mn}^{{\mathrm{o}}{\mathrm{u}}{\mathrm{t}}} $ ,$ {Z}_{mn}^{{\mathrm{o}}{\mathrm{u}}{\mathrm{t}}} $ )是内、外限制面的傅里叶系数.在本文的工作中MC在没有CCS扰动和有CCS扰动的两种情况下形变, 这两种情况分别可以构建面内扰动线圈和面外扰动线圈. 对于前者, CCS约束下线圈几何形状的变化可以在方程2中通过增加参数
$ {\delta }_{1} $ 和$ {\delta }_{2} $ 来实现, 扰动线圈近似表示为对于后者, 通过扰动CCS, 使得线圈的形状变化可以超出原本的CCS, 通过在(3)式中增大参数
$ {\delta }_{3} $ 来实现, 扰动线圈近似表示为在此工作中, 将每个MC线圈的最大形变范围控制在1—10 mm, 线圈的最大形变量分别随方程(4)中的
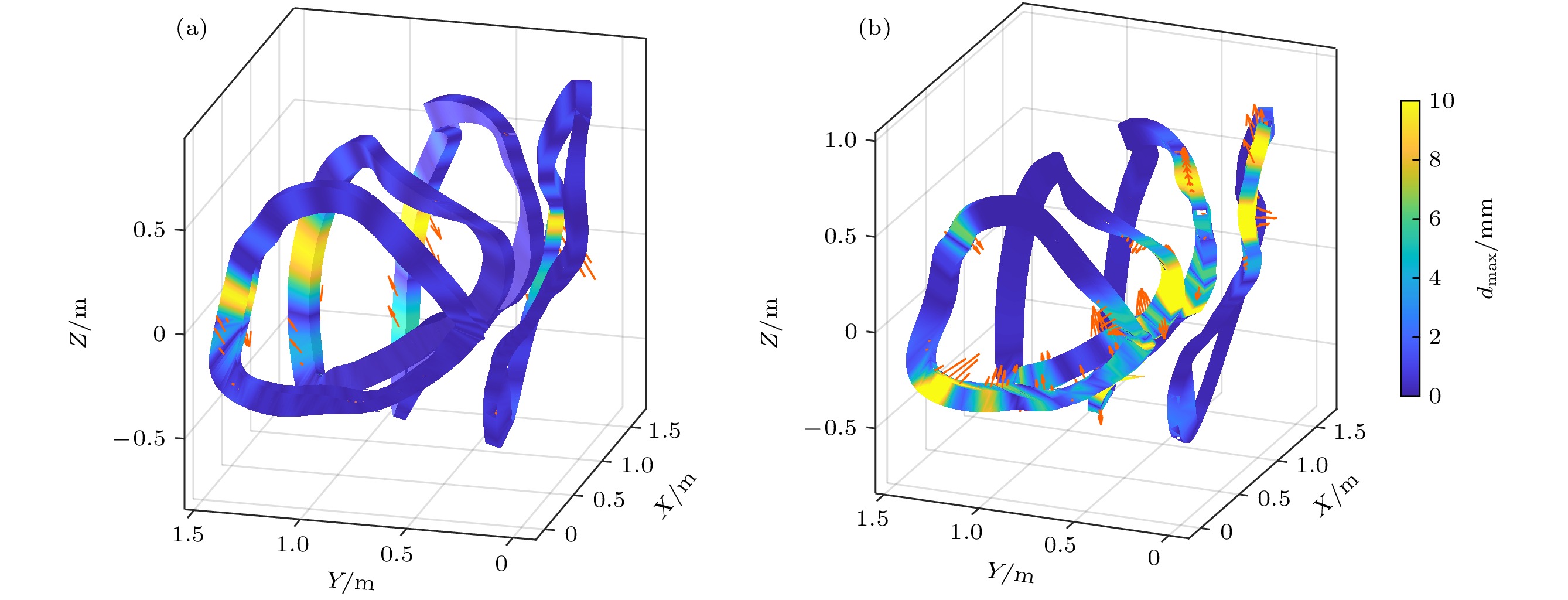
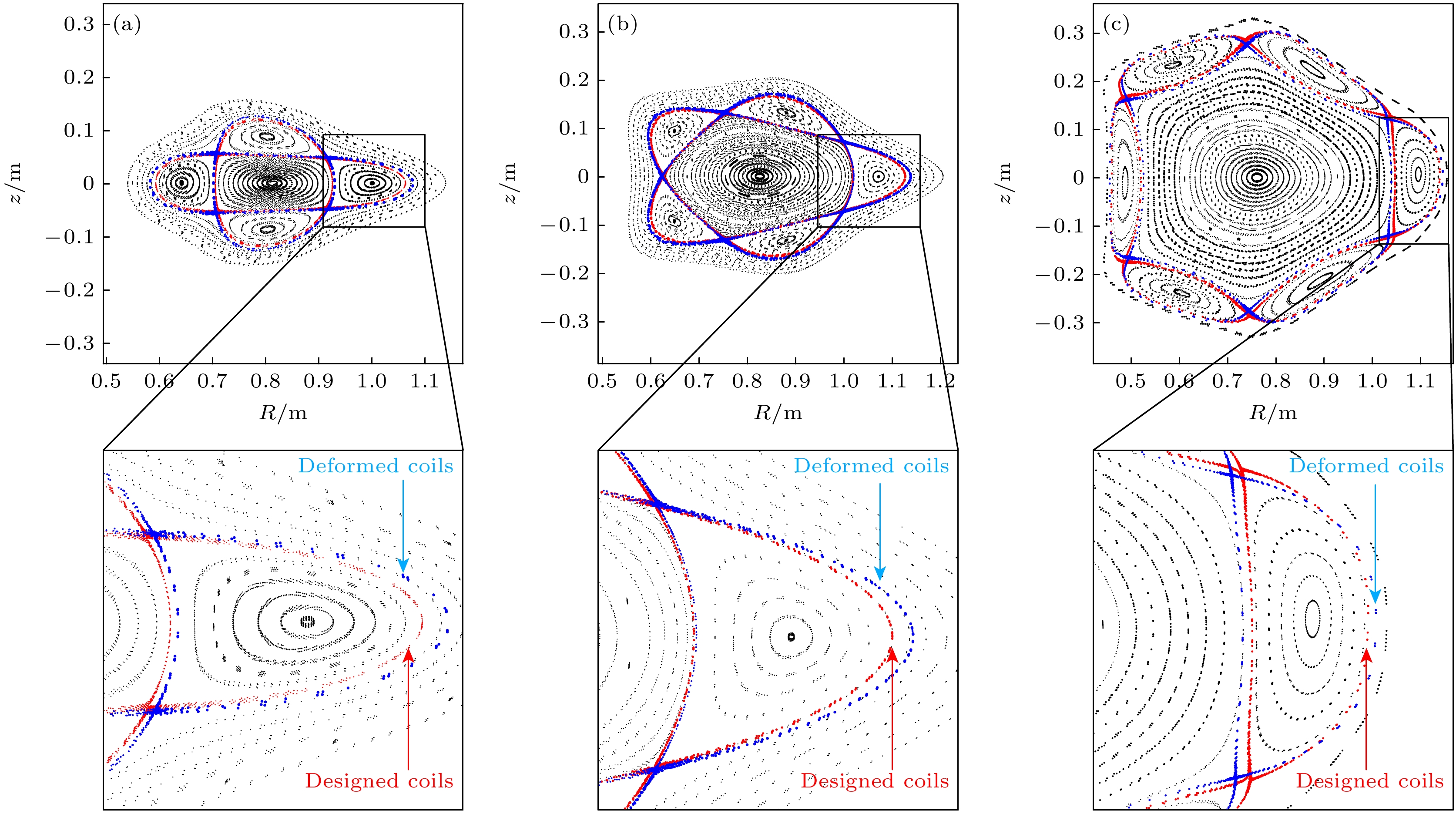
$ {\delta }_{1} $ ,$ {\delta }_{2} $ 和方程(5)中的$ {\delta }_{3} $ 而变化. 图4展示了在有CCS扰动和没有CCS扰动下的形变线圈, 最大形变量为10 mm, 线圈上的箭头表示形变方向. 由于本研究中扰动线圈仍然满足仿星器对称性和周期性, 因此图中仅给出了一组MC线圈(1/4). 图5给出了一个由MC1线圈形变而导致n/m = 2/4, 2/5和2/6磁岛宽度变化的例子, 图中红色虚线和蓝色虚线分别表示由理想线圈和形变线圈产生的岛链的边界, 原MC1与形变MC1之间的最大形状偏差距离(dmax)为10 mm, 线圈电流如表1所示. 结果表明, 形变线圈可以改变n/m = 2/4, 2/5, 2/6的磁岛宽度, 从而产生相应的共振误差场. -
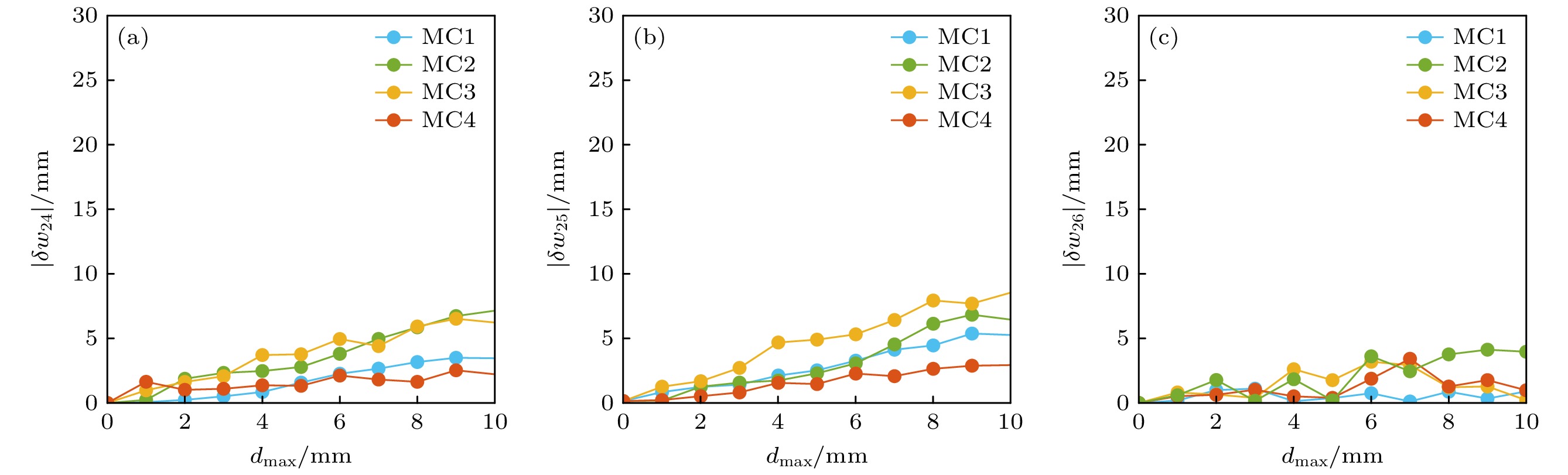
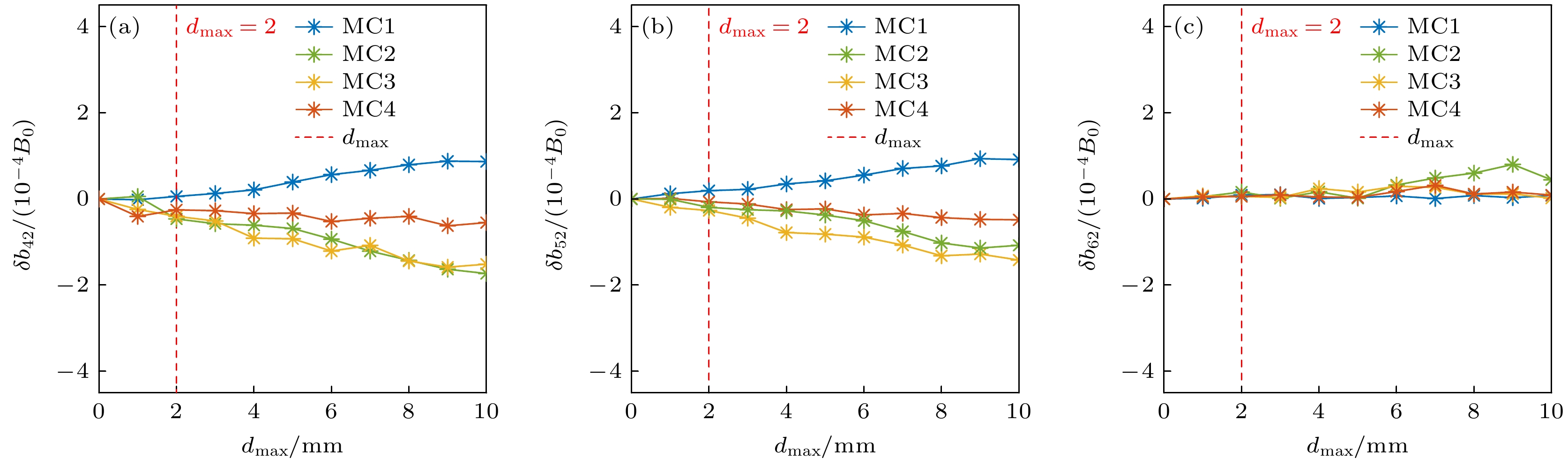
图6展示了在n/m = 2/4, 2/5, 2/6岛链中, 每个模块化线圈的最大形变量与磁岛宽度变化量的绝对值之间的关系. 每个MC线圈的扰动在CCS中是独立且受限的. 在2/4岛链中, 如图6(a)所示, 当MC1, MC2, MC3, MC4的dmax分别从0增大至10 mm时, 最右侧磁岛的宽度分别变化了3.46 mm, 7.15 mm, 6.23 mm, 2.22 mm, MC4的形状偏差对该磁拓扑结构的影响最小, 几乎可以忽略. 在图6(b)所示的2/5岛链中, 当MC1, MC2, MC3, MC4的dmax从0分别增大到10 mm时, 最右侧磁岛的宽度分别变化了5.12 mm, 6.31 mm, 8.4 mm, 2.79 mm, 依旧是MC4的影响最小. 如图6(c)所示, 2/6岛链中磁岛对线圈形变引入的误差场相较于其他两种磁岛位形来说受到影响的程度要小得多. 此外, 利用(1)式, 可以直接计算出图6中误差场振幅变化量δb42, δb52和δb62的值, 如图7(a)—(c)所示. 纵坐标为
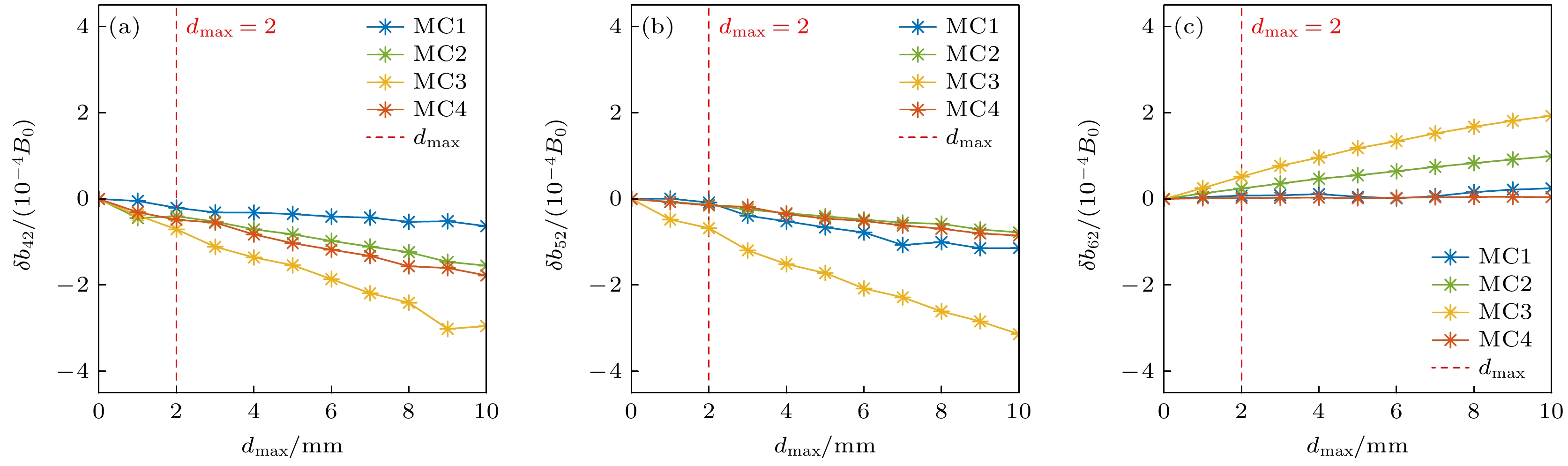
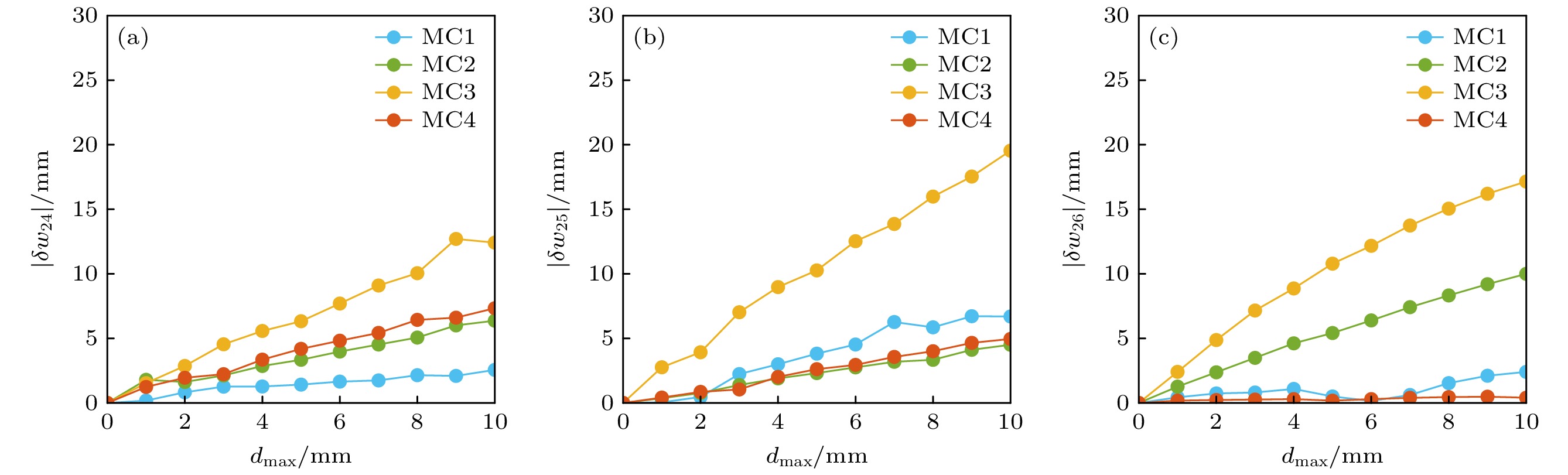
$ {\delta b}_{mn}\left({d}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}\right)/{B}_{0} = {{b}_{mn}\left({d}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}\right)}/{{B}_{0}} - {{b}_{mn}(0)}/{{B}_{0}} $ . 通过计算结果发现, δb42和δb52对MC1, MC2和MC3的面内扰动 非常敏感. 当MC1, MC2, MC3的dmax增大到10 mm时, δb42的最大值分别增加到8.8×10–5, 1.7×10–4和1.6×10–4, 而δb52的最大值分别增大到9.4×10–5, 1.1×10–4和1.4×10–4. 相比之下, δb62对线圈扰动的变化较弱. 在CFQS装置的组装和制造过程中, 我们的目标是将每种类型线圈的最大形变控制在2 mm左右(如图7和图9中, 红色虚线所示). 当线圈面内扰动dmax = 2 mm时, 产生的δb42, δb52和δb62分别为4.6×10–5, 4.4×10–5和6.0×10–5. 由于CFQS磁位形误差的设计标准为小于10–4, 因此这些误差值都是在可接受范围内的.图8和图9展示了在n/m = 2/4, 2/5和2/6岛链中, 磁岛宽度变化的绝对值和误差场与每种MC线圈最大形变量之间的关系, 此时线圈形变由理想CCS扰动而产生, 因此线圈形变扰动未受到CCS面的限制. 得出的结果与图6和图7所展示的结果相似, 例如, 在一个岛链中最右侧的磁岛宽度变化最明显; MC3的形变也会导致比其他类型线圈形变更大的误差场. 然而, 值得注意的是, 与图7中由面内扰动引起的误差场相比, 图9中线圈面外扰动引起的误差场更为显著. 在图9中, 随着MC1, MC2, MC3, MC4的dmax增大到10 mm, δb42的最大值增到6.3×10–5, 1.5×10–4, 3.0×10–4, 1.8×10–4, δb52增到1.14×10–4, 7.7×10–5, 3.1×10–4 , 8.5×10–5, δb62增到3.9×10–5, 9.9×10–5, 1.9×10–4, 4.3×10–5. 当dmax = 2 mm时, 由线圈几何形状误差引起的δb42, δb52和δb62分别为7.1×10–5, 6.7×10–5, 5.2×10–5, 这些误差仍然小于10–4, 在可接受误差范围内.
-
本研究中所采用的研究方法与Zhu等[20]所使用的有所不同. 在他们的工作中, 采用了Hessian矩阵方法来识别CFQS中的重要线圈偏差. 他们分析了4/11共振误差场, 并研究了破坏准轴对称性的敏感线圈扰动. 而在本文工作中考虑了有/无CCS扰动的两种线圈形变情况, 研究它们如何影响准环对称磁场位形. 然而, 他们的工作所得出的重要结论与我们的结论相吻合, 均发现CFQS的每个模块化线圈都应有各自的公差范围, 并且某些特定的扰动会产生显著的误差场. 此外, 我们还得出了一些新的结论, 具体如下.
1)同一种模块化线圈的形变可以同时引起n/m = 2/4, 2/5, 2/6共振误差场. 与2/6误差场相比, 2/4和2/5误差场对线圈形状偏差更为敏感.
2)误差场对MC3的扰动更加敏感, 尤其是在2/4和2/5岛链中, 而MC1和MC4的面内扰动对磁拓扑结构影响不明显, 如图6所示.
3)虽然两种情况下线圈的最大形变程度相同, 但线圈的面外扰动比面内扰动引起的误差场更为显著.
这些发现为CFQS线圈的制造和组装提供了指导: 应严格控制并减小MC3线圈的形变, 并在不敏感的MC1和MC4线圈上放宽线圈误差. 如果将允许的误差场限定在1.0×10–4内, 则MC1, MC2, MC3, MC4的最大形变可分别放宽至约7, 6, 3, 5 mm. 此外, 本研究可为CFQS的mapping实验提供准确的计算模型, 以估算磁位形误差.
仿星器的线圈形变往往是随机且不对称的, 但在本工作中的线圈形变仍然具有仿星器对称性, 因此在后续的研究中拟采用高斯过程[36]等方法对线圈进行随机形变, 获得更加符合实际情况的形变线圈, 再进一步研究线圈形变对CFQS磁拓扑结构的影响.
非常感谢祝曹祥和Samuel Lazerson的专业讨论.
中国首台准环对称仿星器中线圈形变对磁拓扑结构的影响
Influence of coil deformation on magnetic topology structure in Chinese first quasi-toroidally symmetric stellarator
-
摘要: 仿星器线圈的构形形变在制造和装配过程中是不可避免的, 这些形变会导致误差场的产生, 仿星器的磁场位形对误差场非常敏感, 严重制约等离子体的约束性能. 因此, 评估线圈形变对仿星器磁拓扑结构的影响是非常重要的研究课题. 本文研究了中国首台准环对称仿星器(CFQS)上非平面模块化线圈(MC)形变对真空场下磁拓扑结构的影响. 利用磁岛宽度变化来衡量线圈形变造成的误差场, 采用3种旋转变换(ι = 2/4, 2/5和2/6)的磁岛位形, 分别考虑了每个模块化线圈的面内扰动和面外扰动. 结果表明, 同一线圈的形变会产生不同的共振误差场, 且这些误差场的幅度各不相同; 共振误差场对每个线圈形变的敏感度不同, 最复杂线圈的面内扰动可能对磁拓扑结构的影响并不明显; 共振误差场对线圈面外扰动的灵敏度高于面内扰动的灵敏度.Abstract: In stellarators, error fields arise from the inevitable deviations in the fabrication and assembly of complex coil systems. The magnetic configurations of stellarators are predominantly generated by external coils and are highly sensitive to these error fields. Therefore, assessing the impact of coil deformations on stellarator magnetic topology is important. The purpose of this study is to explore the influence of error fields, caused by modular coil (MC) perturbations, on the magnetic topology of the Chinese First Quasi-axisymmetric Stellarator (CFQS). In this work, by changing the Fourier coefficients that represent the current-carrying surface (CCS) and the coil, two types of deformation coils, i.e. “in-surface” and “out-of-surface” disturbance on each MC can be obtained. Subsequently, three kinds of magnetic islands (ι = 2/4, 2/5 and 2/6) are used to identify coil deviations that have a significant influence on the CFQS magnetic configuration. Several important results are obtained as follows. i) The same deformation of a coil gives rise to various resonant error fields with different amplitudes. ii) The sensitivity of a resonant error field to the deformation of each coil is different. The in-surface disturbance of the most complex coil may not have a significant influence on the magnetic topology structure. iii) The sensitivity of the resonant error field to out-of-surface disturbance in the coil is higher than that to in-surface disturbance.
-
Key words:
- quasi-axisymmetric stellarator /
- coil deformations /
- error fields /
- magnetic configuration .
-
-
图 1 CFQS的线圈系统, 线圈系统包含16个非平面模块化线圈, 12个环向场线圈和4个极向场线圈
Figure 1. Main components of the CFQS coil system, the coil system includes 16 non-planar modular coils, 12 planar toroidal field coils, and 4 poloidal field coils.
图 2 (a) 由磁力线追踪计算得到的理想MC线圈产生的磁场在环向角ξ = 90°横截面处的庞加莱图(黑色虚线)和目标等离子体边界(红色虚线), 追踪的初始位置在Z = 0, R∈[0.5446, 0.8359]处, 追踪周期为270; (b) 与该磁场截面对应的旋转变换剖面, 横坐标为归一化半径
Figure 2. (a) Poincaré plots (black dots) based on tracing field lines in the magnetic configuration produced by the designed MCs and the target plasma boundary (red dashed) at the triangular-shaped cross-section, field lines with initial positions R∈ [0.5446, 0.8359] and Z = 0 are traced 270 periods; (b) the corresponding rotational transform profile with the normalized radius as its abscissa.
图 3 由理想线圈产生的n/m = 2/4 (a), 2/5 (b)和2/6 (c) 的3种磁岛位形的庞加莱截面图及旋转变换剖面, 横坐标表示从主磁轴到磁场外侧的半径, 每个磁面的追踪周期为540, 追踪的初始位置为 (a) Z = 0, R∈[0.54, 0.81]; (b) Z = 0, R∈[0.56, 0.83]; (c) Z = 0, R∈[0.44, 0.76]
Figure 3. Poincaré plots of three island configurations with n/m = 2/4 (a), 2/5 (b) and 2/6 (c) and their rotational transform profiles produced by undeformed coils, the abscissa denotes radius from the main magnetic axis to the outboard side, field lines with initial positions R∈[0.54, 0.81] and Z = 0 (a), R∈[0.56, 0.83] and Z = 0 (b), R∈[0.44, 0.76] and Z = 0 (c) are traced 540 periods.
图 4 四种不同类型MC线圈的面内(a)和面外(b)形变分布, 在MC1, MC2, MC3和MC4上设置(
$ {\delta }_{1} $ ,$ {\delta }_{2} $ ) = (0.00003, 0.0001), (0.00002, 0.00009), (0.00002, 0.00009), (0.00004, 0.000095)以产生线圈的面内扰动, 在CCS上设置$ {\delta }_{3} $ = 0.0113, 0.086, 0.094, 0.074以产生面外线圈扰动, 在这两种情况下, 每个MC的最大形变量均为10 mm,$ {\delta }_{1} $ ,$ {\delta }_{2} $ ,$ {\delta }_{3} $ 的数值均为随机选取Figure 4. Local (a) and broad (b) deformation distributions on four different types of MCs, (
$ {\delta }_{1} $ ,$ {\delta }_{2} $ ) = (0.00003, 0.0001), (0.00002, 0.00009), (0.00002, 0.00009), (0.00004, 0.000095) are set on MC1, MC2, MC3 and MC4 to produce local perturbations of coils and$ {\delta }_{3} $ = 0.0113, 0.086, 0.094, 0.074 are set on MC1, MC2, MC3, MC4 to produce broad perturbations of coils. For these two cases the maximum deformation of each MC is 10 mm.
图 5 扰动MC1线圈使其产生最大形变量为10 mm时的3种 (n/m = 2/4 (a), 2/5 (b), 2/6 (c))磁岛位形的庞加莱截图, 红色虚线和蓝色虚线分别表示由理想线圈产生的磁岛边界和MC1线圈发生形变时的磁岛边界. 场线数值与图4相同
Figure 5. Poincaré plots of three island configurations with n/m = 2/4 (a), 2/5 (b), 2/6 (c) produced by perturbed MC1 with the maximum deviations of 10 mm (other coils sustain undeformed). Red and blue dots denote boundaries of the island chains induced by designed coils and the deformed MCs. Numerical details for field line tracing are the same as shown in Fig. 4.
图 6 在n/m = 2/4(a), 2/5(b), 2/6(c)岛链中, 磁岛宽度变化量的绝对值与线圈最大形变量的关系, 每个MC线圈的形变扰动均受到载流面的限制
Figure 6. The absolute value of the magnetic island width as a function of dmax of each MC in n/m = 2/4 (a), 2/5(b) and 2/6(c) island chains, the deformations of each MC are without perturbations of CCS.
图 7 在n/m = 2/4 (a), 2/5 (b), 2/6 (c)岛链中, 误差场振幅与MC线圈最大形变量的关系, 每个MC线圈的形变扰动均受到载流面的限制
Figure 7. The amplitudes of error fields as a function of dmax of each MC in n/m = 2/4 (a), 2/5 (b) and 2/6 (c) island chains, the deformations of each MC are without perturbations of CCS.
图 9 在n/m = 2/4 (a), 2/5 (b)和2/6 (c)岛链中, 误差场振幅与MC线圈最大形变量的关系. 每个MC线圈的形变扰动均未受到载流面的限制
Figure 9. The amplitudes of error fields as a function of dmax of each MC in n/m = 2/4 (a), 2/5 (b) and 2/6 (c) island chains, the deformations of each MC are with perturbations of CCS.
图 8 在n/m = 2/4 (a), 2/5 (b), 2/6 (c)的岛链中, 磁岛宽度变化量的绝对值与MC线圈最大形变量之间的关系, 每个MC线圈的形变扰动均未受到载流面的限制
Figure 8. The absolute value of the magnetic island width as a function of dmax of each MC in n/m = 2/4 (a), 2/5 (b) and 2/6 (c) island chains. The deformations of each MC are with perturbations of CCS.
表 1 CFQS中3种磁岛位形下, 模块化线圈、环向场线圈和极向场线圈的电流设置
Table 1. Coil currents in MCs, TFCs, and PFCs for n/m = 2/4, 2/5, and 2/6 magnetic island configurations of CFQS.
磁岛位形(n/m) 2/4 2/5 2/6 线
圈
电
流IMC/kA MC1 312.5 312.5 406.3 MC2 312.5 312.5 281.6 MC3 312.5 312.5 281.6 MC4 312.5 312.5 281.6 ITFC/kA TFC_10 –60 –24 0 TFC_32 –90 –36 0 TFC_70 –90 –36 0 IPFC/kA PFC_OV 0 0 –82 PFC_IV 0 0 41 
下载: 导出CSV
-
[1] Rummel T, Risse K, Viebke H, Braeuer T, Kisslinger J 2004 IEEE Trans. Appl. Supercond. 14 1394 doi: 10.1109/TASC.2004.830584 [2] Xiong G Z, Xu Y H, Isobe M, Shimizu A, Ogawa K, Kinoshita S, Liu H F, Wang X Q, Cheng J, Liu H, Huang J, Zhang X, Zhang Y C, Yin D P, Wang A Z, Okamura S, Tang C J 2023 Plasma Phys. Control. Fusion 65 035020 doi: 10.1088/1361-6587/acb5c1 [3] Shoji M, Shimizu A, Kinoshita S, Okamura S, Xu Y H, Liu H F 2023 Plasma Fusion Res. 18 2405026 doi: 10.1585/pfr.18.2405026 [4] Boozer A H 2005 Rev. Mod. Phys. 76 1071 doi: 10.1103/RevModPhys.76.1071 [5] Waelbroeck F L 2009 Nucl. Fusion 49 104025 doi: 10.1088/0029-5515/49/10/104025 [6] Lazerson S A, Bozhenkov S, Israeli B, Otte M, Niemann H, Bykov V, Endler M, Andreeva T, Ali A, Drewelow P, Jakubowski M, Sitjes A P, Pisano F, Cannas B, W7-X Team 2018 Plasma Phys. Control. Fusion 60 124002 doi: 10.1088/1361-6587/aae96b [7] Kißlinger J, Andreevab T 2005 Fusion Eng. Des. 74 623 doi: 10.1016/j.fusengdes.2005.06.124 [8] Andreeva T, Bräuer T, Endler M, Kißlinger J, Toussaint U V 2009 Fusion Eng. Des. 84 408 doi: 10.1016/j.fusengdes.2008.12.073 [9] Yamazaki K, Yanagi N, Ji H, Kaneko H, Ohyabu N, Satow T, Morimoto S, Yamamoto J, Motojima O, the LHD Design Group 1993 Fusion Eng. Des. 20 79 doi: 10.1016/0920-3796(93)90027-F [10] Strykowsky R L, Brown T, Chrzanowski J, Cole M, Heitzenroeder P, Neilson G H, Rej D, Viol M 2009 23rd IEEE/NPSS Symposium on Fusion Engineering San Diego, CA, USA, June 01–05, 2009 p1 [11] Brooks A, Reiersen W 2003 20th IEEE/NPSS Symposium on Fusion Engineering San Diego, CA, USA, 14–17 October, 2003 p553 [12] Nührenberg J, Sindoni E, Lotz W, Troyon F, Gori S, Vaclavik J 1994 Proceedings of the Joint Varenna Lausanne International Workshop on Theory of Fusion Plasmas Varenna, Italy, August 22–26, 1994 p3 [13] Garabedian P 1996 Phys. Plasmas 3 2483 doi: 10.1063/1.871965 [14] Huang J, Nakata M, Xu Y H, Shimizu A, Isobe M, Okamura S, Liu H F, Wang X Q, Zhang X, Liu H, Cheng J, Tang C J 2022 Phys. Plasmas 29 052505 doi: 10.1063/5.0082107 [15] Xu Y H, Liu H F, Xiong G Z, Shimizu A, Kinoshita S, Isobe M, Okamura S, Nakata M, Yin D, Wan Y, Wilfred, Cooper A, Zhu C X, Liu H, Zhang X, Huang J, Wang X Q, Tang C J 2018 27th IAEA Fusion Energy Conference Ahmedabad, India, October 22–27, 2018 p5 [16] Isobe M, Shimizu A, Liu H F, Liu H, Xiong G Z, Yin D P, Ogawa K, Yoshimura Y, Nakata M, Kinoshita S, Okamura S, Tang C J, Xu Y H, the CFQS Team 2019 Plasma Fusion Res. 14 3402074 doi: 10.1585/pfr.14.3402074 [17] Wang X Q, Xu Y H, Shimizu A, Isobe M, Okamura S, Todo Y, Wang H, Liu H F, Huang J, Zhang X 2021 Nucl. Fusion 61 036021 doi: 10.1088/1741-4326/abd3ec [18] 黄捷, 李沫杉, 覃程, 王先驱 2022 物理学报 71 185202 doi: 10.7498/aps.71.20220729 Huang J, Li M S, Qin C, Wang X Q 2022 Acta Phys. Sin. 71 185202 doi: 10.7498/aps.71.20220729 [19] 苏祥, 王先驱, 符添, 许宇鸿 2023 物理学报 72 215205 doi: 10.7498/aps.72.20230546 Su X, Wang X Q, Fu T, Xu Y H 2023 Acta Phys. Sin. 72 215205 doi: 10.7498/aps.72.20230546 [20] Zhu C X, Gates D A, Hudson S R, Liu H F, Xu Y H, Shimizu A, Okamura S 2019 Nucl. Fusion 59 126007 doi: 10.1088/1741-4326/ab3a7c [21] Shimizu A, Liu H F, Kinoshita S, Isobe M, Okamura S, Ogawa K, Nakata M, Satake S, Suzuki C, Xiong G Z, Xu Y H, Liu H, Zhang X, Huang J, Wang X Q, Tang C J, Yin D P, Wan Y, the CFQS Team 2019 Plasma Fusion Res. 14 3403151 doi: 10.1585/pfr.14.3403151 [22] Zhu C X, Hudson S R, Song Y T, Wan Y X 2018 Plasma Phys. Control. Fusion 60 065008 doi: 10.1088/1361-6587/aab8c2 [23] Zhu C X, Hudson S R, Lazerson S A, Song Y T, Wan Y X 2018 Plasma Phys. Control. Fusion 60 054016 doi: 10.1088/1361-6587/aab6cb [24] Okamura S, Liu H F, Shimizu A, Kinoshita S, Isobe M, Xiong G Z, Xu Y H 2020 J. Plasma Phys. 86 815860402 doi: 10.1017/S0022377820000732 [25] Shimizu A, Kinoshita S, Isobe M, Okamura S, Ogawa K, Nakata M, Yoshimura Y, Suzuki C, Osakabe M, Murase T, Nakagawa S, Tanoue H, Xu Y H, Liu H F, Liu H, Huang J, Wang X Q, Cheng J, Xiong G Z, Tang C J, Yin D P, Wan Y 2022 Nucl. Fusion 62 016010 doi: 10.1088/1741-4326/ac369a [26] Liu H F, Shimizu A, Xu Y H, Okamura S, Kinoshita S, Isobe M, Li Y B, Xiong G Z, Wang X Q, Huang J, Cheng J, Liu H, Zhang X, Yin D P, Wang Y, Murase T, Nakagawa S, Tang C J 2021 Nucl. Fusion 61 016014 doi: 10.1088/1741-4326/abbc85 [27] Li Y B, Liu H F, Xu Y H, Shimizu A, Kinoshita S, Okamura S, Isobe X, Xiong G Z, Luo Y, Cheng J, Liu H, Wang X Q, Huang J, Zhang X, Yin D P, Wan Y, Tang C J 2020 Plasma Phys. Control. Fusion 62 125004 doi: 10.1088/1361-6587/abb9fb [28] Liu H F, Zhang J, Xu Y H, Shimizu A, Cooper W A, Okamura S, Isobe M, Wang X Q, Huang J, Cheng J, Liu H, Zhang X, Tang C J 2023 Nucl. Fusion 63 026018 doi: 10.1088/1741-4326/acadef [29] Kinoshita S, Shimizu A, Okamura S, Isobe M, Xiong G Z, Liu H F, Xu Y H, the CQFS Team 2019 Plasma Fusion Res. 14 3405097 doi: 10.1585/pfr.14.3405097 [30] Liu H F, Shimizu A, Isobe m, Okamura S, Nishimura s, Suzuki C, Xu Y H, Zhang X, Liu B , Huang J, Wang X Q, Liu H, Tang C J, Yin D P, Wan Y, the CFQS Team 2018 Plasma Fusion Res. 13 3405067 [31] Boozer A H 2015 Nucl. Fusion 55 025001 doi: 10.1088/0029-5515/55/2/025001 [32] Pedersen T S, Otte M, Lazerson S, Helander P, Bozhenkov S, Biedermann C, Klinger T, Wolf R C, Bosch F S, the Wendelstein 7-X Team 2016 Nat. Commun. 7 13493 doi: 10.1038/ncomms13493 [33] Merkel P 1987 Nucl. Fusion 27 867 doi: 10.1088/0029-5515/27/5/018 [34] Zhu C X, Hudson S R, Song Y T, Wan Y X 2018 Nucl. Fusion 58 016008 doi: 10.1088/1741-4326/aa8e0a [35] Drevlak M 1998 Fusion Technol. 33 106 doi: 10.13182/FST98-A21 [36] Wechsung F, Giuliani A, Landreman M, Cerfon A, Stadler G 2022 Plasma Phys. Control. Fusion 64 105021 -
计量
- 文章访问数: 84
- HTML全文浏览数: 84
- PDF下载数: 0
- 施引文献: 0