首页
登录
注册
-
硅通孔(through-silicon via, TSV)技术自被提出以来被认为是超越摩尔定律的关键, TSV技术允许芯片垂直堆叠, 突破了传统平面集成电路制造的限制, 实现更高的集成度; 通过缩短芯片间的互连长度, 减小互连电容和电感, 降低信号延迟和功耗, 体现出优秀的电气性能[1–4]. TSV的制造工艺决定了TSV侧壁界面具有多层材料的结构特征, 沿TSV半径方向, 材料依次为TSV填充Cu(以下简称TSV-Cu)、Cu种子层、阻挡层、绝缘层和Si基体, 构成了多层界面(以下简称TSV界面), 其中, 填充Cu和Si基体的热膨胀系数(coefficient of thermal expansion, CTE)分别为17×10–6和2.8×10–6 ℃–1, 巨大的热失配会导致TSV界面完整性问题, 而TSV界面完整性直接关系到器件的漏电和电击穿可靠性[5–8].
完整的阻挡层和绝缘层可以有效为TSV-Cu和Si基体之间提供电绝缘, 防止电流泄漏, 并且在一定程度上缓解由CTE不匹配引起的机械应力[9]. 然而, 在TSV制作和服役过程中, 温度载荷下界面的拉应力、切应力均会导致界面发生分离或开裂, 造成界面失效, 致使TSV结构发生漏电, 并加剧TSV-Cu的电迁移问题[10,11]. 此外, 典型的Bosch工艺制造形成的TSV扇贝型侧壁结构导致应力集中, 更易产生裂纹增加泄漏通道[12], 使其相对于非Bosch工艺制造出平滑侧壁结构的TSV产生更严重漏电[13], TSV漏电研究表明漏电量与TSV界面完整性密切相关.
目前, TSV绝缘层漏电机制与TSV界面完整性的关系以及漏电机制随电场强度的转变过程尚未厘清. Lin等[14]对带有TSV结构的电容器进行I-V测试, 通过拟合漏电机制发现随着电场强度的增强, 样品的漏电机制从肖特基发射机制到P-F(Poole-Frenkel)发射机制, 最终转为F-N (Fowler-Nordheim)隧穿机制, 同时发现绝缘层质量较差会导致较低电场下发生P-F发射机制, 但并未对漏电机制的转变进行详细解释, 也未考虑服役过程中温度循环造成的TSV界面缺陷如何影响TSV的漏电机制. Chen等[15]给出了TSV经历温度循环后失效模式由热致漏电失效到机械开裂失效的转变过程, 但仅给出了经历0次、100次和300次温度循环后的数据, 无法给出TSV界面状态改变的完整过程, 机制转变的支撑数据不足. 因此, 本文开展了温度循环实验, 通过Keithley 4200A-SCS对经历不同温度循环次数后的TSV样品进行I-V测试, 并结合微结构观察, 评估温度循环对TSV界面完整性及绝缘层漏电机制的影响. 最后, 通过EDS分析深入探讨了TSV漏电的根本机理.
-
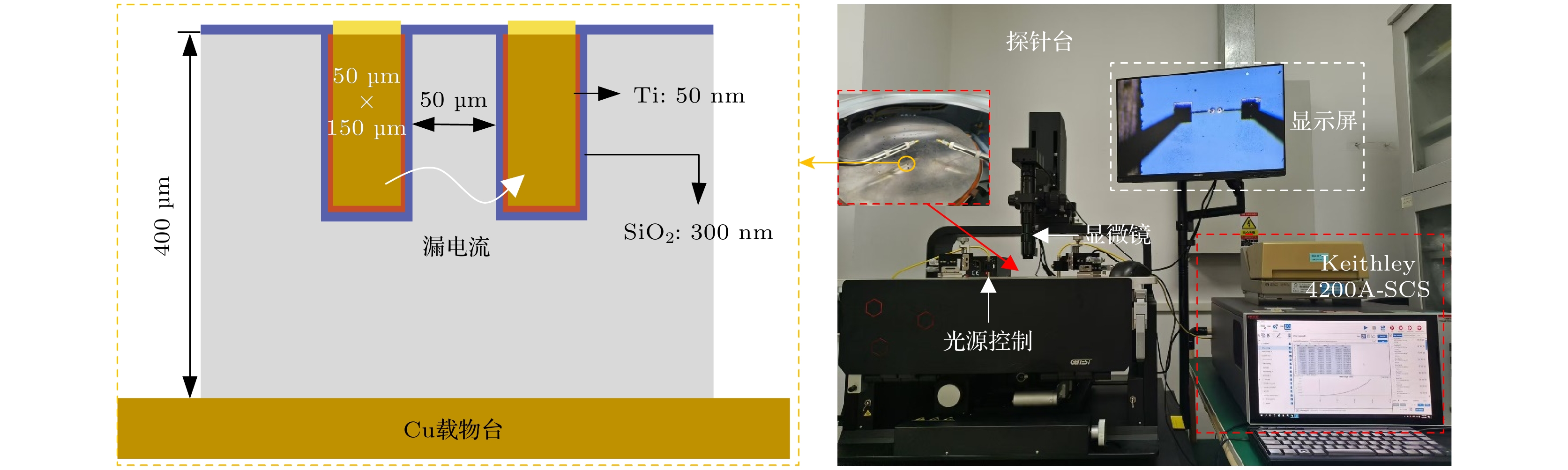
对经历不同温度循环次数后的样品进行I-V测试, 测试平台采用探针台和Keithley 4200A-SCS参数分析仪, 如图1所示, 使用20 μm晶圆探针接触Al焊盘结合4200A-SCS SMU模块实现0—30 V扫描电压的施加, 测试过程中, 两根探针通过同轴电缆与参数分析仪连接, 实现电气特性监测. 当Cu暴露在湿度较高的空气中或者当温度达到200 ℃以上时会发生氧化产生氧化铜, 针对这个问题, 本试验在样品设计方面, 整体样品表面覆盖一层SiO2绝缘层, Cu柱上方有Al焊盘覆盖, 内部铜柱处于隔绝空气状态, 在温度循环测试过程中, 客观上尽量避免Cu氧化问题; 并且在完成I-V测试后, 马上在真空环境下进行FIB切割和扫描电镜的观测.
测试样品为双盲孔TSV, 由Cu作为填充金属, Ti, SiO2和Si分别为阻挡层、绝缘层和衬底材料. 阻挡层的作用是防止高温下Cu扩散到Si基体及绝缘层中, 绝缘层的作用是将TSV中的Cu导电路径与Si基体隔离, 防止漏电流的产生, 同时阻挡层和绝缘层还可以在一定程度上缓解因Cu和Si热膨胀系数差异过大导致的热失配问题, 提高界面结合强度, 增强TSV互连结构的热机械可靠性. TSV深度150 μm, 直径50 μm, 阻挡层厚度为50 nm, 绝缘层厚度为300 nm. 采用GWS HBL-04JA高低温试验箱对样品进行温度循环试验. 参考GJB548方法1010.1-C级试验条件, 目的是研究极端高温与极端低温交替变化对器件的影响, 考虑TSV互连结构在军工及航天领域的应用, 温度范围设置为–65—150 ℃, 高低温保温时间为15 min, 温变速率为 10 ℃/min. 将所有样品分为11组, 每组有3个样品, 分别进行0, 30, 60, 90, 120, 150, 180, 210, 240, 270以及300次温度循环测试.
-
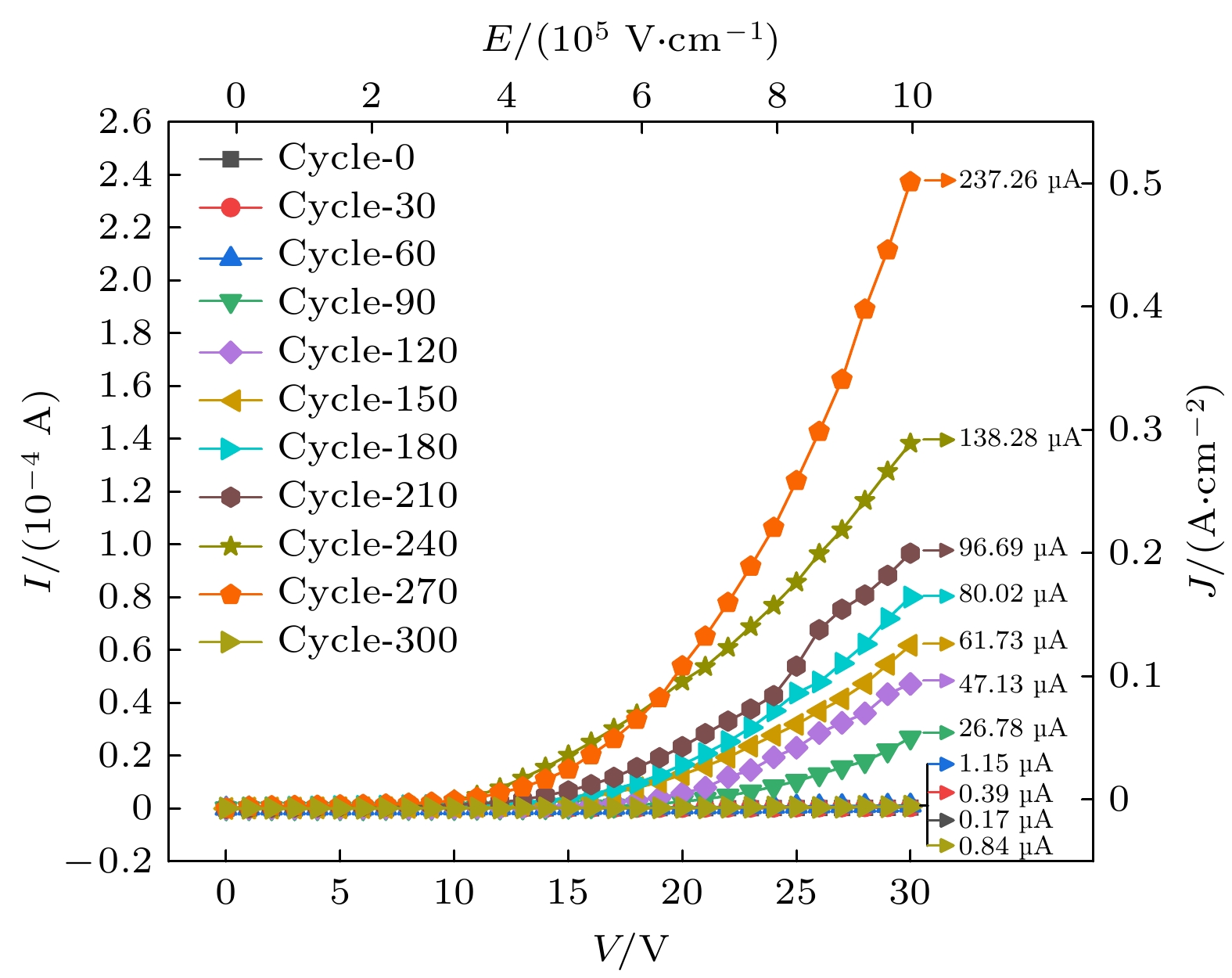
对初始状态TSV样品进行I-V测试, 当电压增大到10 V时其漏电流为1.79 nA, 参照文献[16]给出的判定标准, 10 V电压时TSV样品的漏电流小于10 nA, 意味本批次样品绝缘层质量优良. 初始状态至300次温度循环后TSV样品的I-V测试结果及计算后的电流密度-电场强度(J-E)结果如图2所示, 伴随加载电压从0 V增至30 V, 不同循环次次数后的TSV样品漏电流均呈现递增的趋势, 30 V时样品漏电流达到最大值.
图2中, 当施加扫描电压到30 V时, 初始状态TSV样品(Cycle-0)的漏电流为171.58 nA, 经受30次温度循环(Cycle-30)后, TSV样品漏电流增长到395.95 nA, 在Cycle-60时, TSV样品的漏电流增长至μA级别, 为1.53 μA, 由此可见对于本样品, 前60次温度循环并不会导致绝缘层介电性能发生较为严重的退化. 从Cycle-60 TSV样品开始, 每经历30次温度循环, TSV样品漏电流增长幅度都在20 μA左右, 这种现象一直持续到Cycle-210 TSV样品, 此阶段绝缘层介电性能退化较为稳定. Cycle-240和Cycle-270 TSV样品的漏电流出现较大的增长幅度, Cycle-240 TSV样品相较于Cycle-210样品增大了约42 μA, Cycle-270 TSV样品相较于Cycle-240 TSV样品增加了约99 μA, 此时绝缘层的介电性能退化较为严重; 但是当TSV样品经受300次温度循环后, 30 V时对应的漏电流陡然降低到0.84 μA.
-
由于TSV个体间存在差异, 每组经过温度循环的TSV样品其界面泄漏源位置并不一致. 为了观察TSV界面的最大缺陷形貌, 需要对其进行缺陷定位检测. 采用锁定热成像技术(lock-in thermography, LIT)对TSV样品进行缺陷定位, 通过热成像设备和激励源来检测TSV内部因裂纹或孔洞导致的热异常, 从而定位缺陷[17]. 使用热发射显微镜Thermal-F1, 激励电压设置为30 V, 将除TSV界面区域的温度异常点作为噪点予以排除. 经历270次温度循环的样品表面热成像图及对应的TSV界面区域的相位图和信号图分别如图3所示. 定位结果表明, TSV界面处由于缺陷发生了明显的电流泄漏.
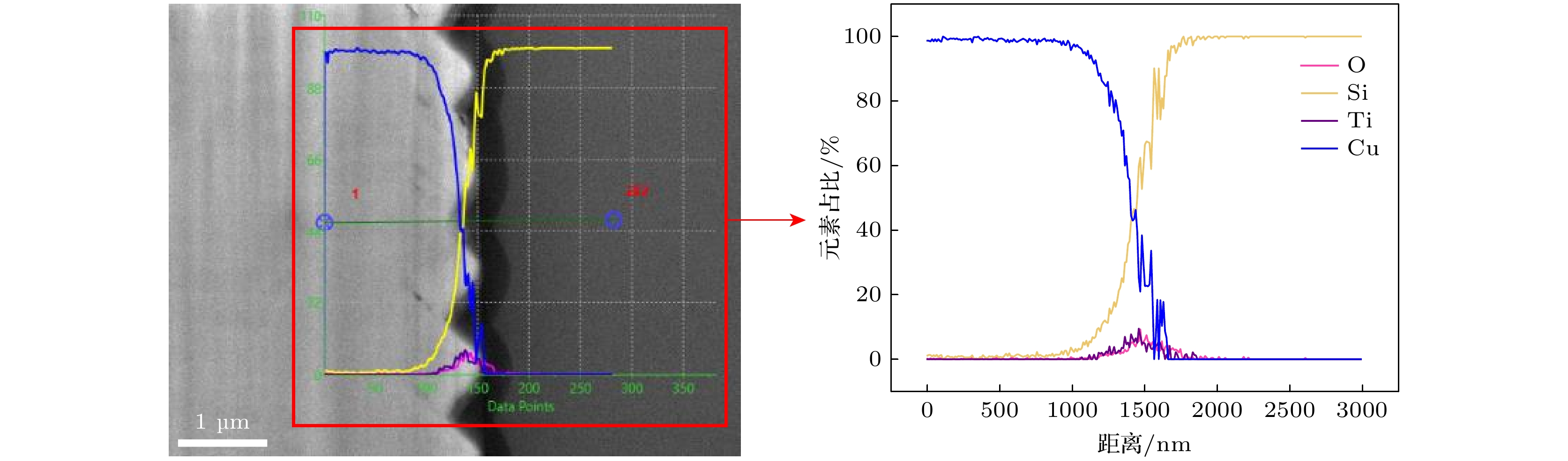
图4为通过聚焦离子束(FIB)切割TSV样品, 获得TSV界面的微观结构SEM图, 可以评估温度循环对TSV界面完整性的影响. 使用Zeiss Auriga Compact型号的FIB-SEM, 切割过程中原子束能量为30 kV, 原子束流为3 nA, 垂直击打TSV表面, 切割深度、长度和宽度分别为10, 20和10 μm. 观察过程中的电子束击打角度为52°. 图5为通过能谱仪(energy dispersive spectroscopy, EDS)对经历30次温度循环TSV样品界面的元素分析结果. 表1给出了不同温度循环次数TSV样品SiO2绝缘层中Cu元素的平均占比.
图4中, 所有TSV样品Cu柱界面附近均产生了由电镀工艺导致的空洞, 同时可以看出TSV界面损伤程度随着温度循环次数的增加逐步加剧. 在Cycle-0和Cycle-30时, TSV界面微观组织致密, 完整性良好, 未观察到明显的裂纹或严重的结构损伤, 阻挡层和绝缘层可以有效阻挡Cu原子的扩散和漏电流产生, 因此在初始阶段, 随着扫描电压的增大, TSV漏电流增长缓慢.
随着温度循环次数的增加, CTE不匹配导致Cycle-60时TSV界面阻挡层开始出现微孔洞. 在Cycle-120之后, 孔洞逐渐增大, 多个孔洞之间联合形成微裂纹, 出现明显的损伤特征; 孔洞的扩展和微裂纹的出现表明TSV界面的完整性和机械 稳定性逐步下降. EDS结果表明这些缺陷导致Cu原子大量扩散到绝缘层中, 缺陷为Cu原子提供了扩散路径, 阻挡层不能有效抑制Cu原子扩散到绝缘层中, 当Cu原子扩散到绝缘层中时, 会在绝缘层中引入漏电路径, 引起绝缘层局部电场增强, 降低绝缘层的绝缘效果, 导致漏电流增加.
在Cycle-210之后, TSV界面裂纹变得更加明显, 特别是在Cycle-300时, 已经出现了贯穿性裂纹, 这表明TSV界面损伤程度严重. 此时, TSV-Cu与Si基体之间引入了空气作为绝缘材料, 阻碍了电子在TSV-Cu与Si衬底之间的流动. 这种贯穿性裂纹有效地隔绝了漏电流的产生, 使漏电流显著下降. 同时, 贯穿性裂纹的存在也阻碍了Cu原子的扩散, 绝缘层中的Cu原子由于浓度差继续向Si衬底扩散, 导致绝缘层中Cu元素比例大幅下降.
综上可知, 温度循环从0次增至300次的过程中, TSV界面的失效模式从热致漏电(≤Cycle-270)转变为机械开裂(Cycle-300), 这种转变与TSV界面完整性的演变密切相关, 其界面从接触完好到产生微孔洞、微裂纹(加速热致漏电的产生), 最终转变为界面贯穿性裂纹(阻碍漏电流产生); EDS结果进一步表明, Cu原子扩散到绝缘层中导致的漏电路径是降低其介电性能的根本原因, 也是TSV样品产生漏电的根本机理.
-
通过对测得的I-V曲线进行漏电机制拟合分析, 可以确定绝缘层的漏电机制. 绝缘层中漏电流输运机制主要包括4种: 直接隧穿[18]、Fowler-Nordheim隧穿[19]、Poole-Frenkel(P-F)发射[20]和肖特基发射[21]. 其中, 直接隧穿在绝缘层厚度大于3.5 nm时不明显, 因此对本实验的样品来说, 直接隧穿对漏电流的贡献可以忽略不计. 此外, F-N隧穿主要在高电场(>6 MV/cm)下显现, 远高于本次实验条件, 因此本文也忽略F-N隧穿的贡献. 表2列出了其余两种漏电机制的理论公式以及对数化处理后的拟合公式. 根据拟合公式得到的漏电机制拟合曲线如图6所示.
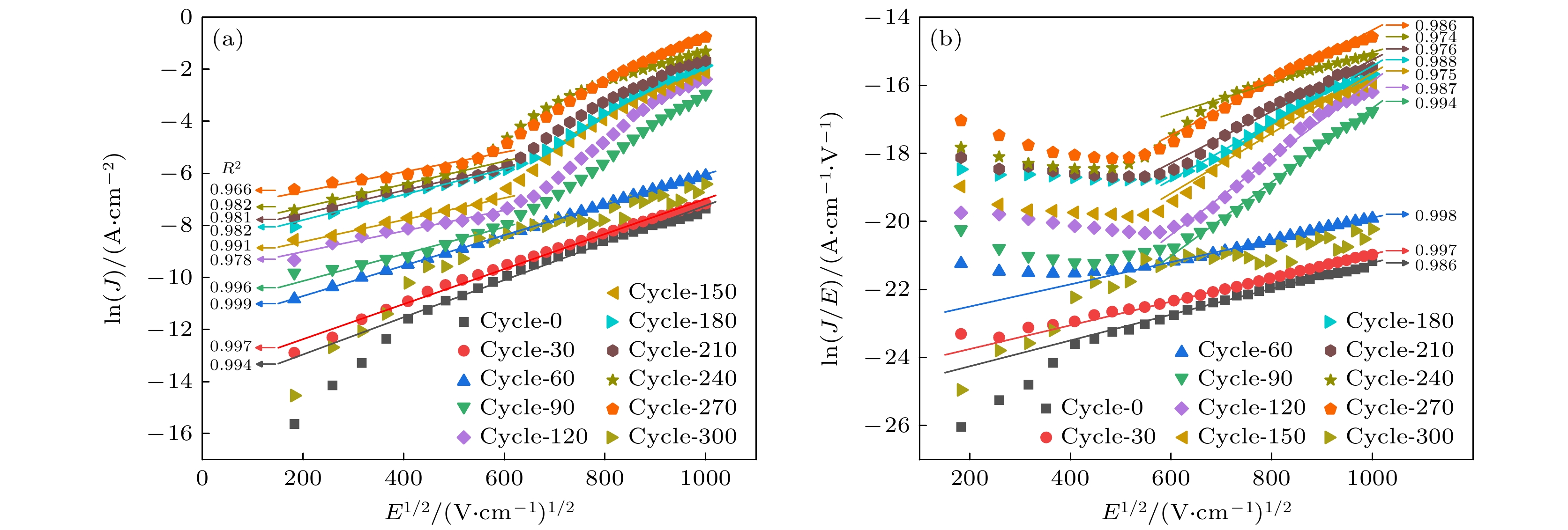
从图6(a), (b)给出的拟合优度R2值可以看出, 肖特基发射机制在整个电场范围内对Cycle-0, Cycle-30, Cycle-60 TSV样品的拟合度都很高, 分别为0.994, 0.997和0.999, 而P-F发射机制在低电场下的拟合曲线并未表现线性增函数关系, 直到当电场强度高于3.67×105 V/cm时才表现出较佳的拟合优度, 我们之前的研究也发现了这一点[15]. 当温度循环次数较少(≤Cycle-60)时, 虽然P-F发射在高电场下也有较高的拟合优度, 但是并未改变肖特基发射机制在所施加电场范围内的高拟合性, 这表明当绝缘层完整性较高时肖特基发射为TSV的漏电机制.
由图6(b)可知, Cycle-90—Cycle-270 TSV样品的P-F发射机制拟合曲线同样表现为当电场强度高于3.67×105 V/cm时才有较佳的线性增函数拟合优度. 但在图6(a)中, Cycle-90—Cycle-270TSV样品的肖特基拟合曲线与Cycle-0—Cycle-60 TSV样品的拟合曲线相比有较大的差异, 不再是单一线性曲线, 在电场强度为3.67×105 V/cm处, 拟合曲线出现明显转折点, 此点同样对应于图6(b)的Cycle-90—Cycle-270 TSV样品的P-F发射机制拟合曲线开始表现线性增长的初始点. 这表明随着温度循环次数的增加导致TSV界面完整性逐渐降低, 致使虽然在低电场下肖特基发射机制仍可以很好的拟合, 但在高电场下, TSV绝缘层的漏电机制不再是单一机制, 肖特基发射和P-F发射机制都会对TSV结构的漏电产生贡献, 并且P-F发射机制对TSV结构的漏电贡献很大以至于改变了整个电场范围内肖特基发射的单一线性关系.
肖特基发射机制是电子通过热激发克服势垒而导致的漏电, 其产生的电流依赖于温度和电场强度, 但是对温度变化更为敏感; 而P-F 发射机制是一种电场增强的热发射机制, 外部电场降低了陷阱深度, 从而增大电子的发射率, P-F发射机制对电场强度变化更为敏感, 通常在较高的电场强度下才显现出来, 这与结果分析是一致的. 随着温度循环次数的增加, 阻挡层的完整性逐渐下降, 导致更多的Cu原子在电场和温度的驱动下通过扩散机制进入绝缘层. Cu会占据SiO2绝缘层中的空位或缺陷位点, 在绝缘层或界面区域形成陷阱态. 陷阱态通过捕获和释放电荷载流子, 从而形成电荷积累区域, 导致局部电场强度增强, 进而在绝缘层内产生漏电路径. 这些高电场区域使得电子更容易通过P-F发射机制从陷阱态中逃逸. 因此, Cu扩散会显著增强P-F发射机制下的漏电流.
-
由3.3节可知, 当温度循环次数较少以及温度循环次数增加低电场条件下肖特基发射为TSV的漏电机制, TSV界面绝缘层的肖特基势垒高度是衡量绝缘层介电性能的重要参数之一, 可以表征温度循环对TSV绝缘层介电性能退化的影响程度. 因此, 将肖特基发射的公式(表2)两边取ln, 可以得出肖特基发射电流密度J和电场强度E的线性关系式(1), 其中As代表斜率, Bs代表截距:
将不同温度循环次数样品的肖特基发射拟合曲线做截距差得到:
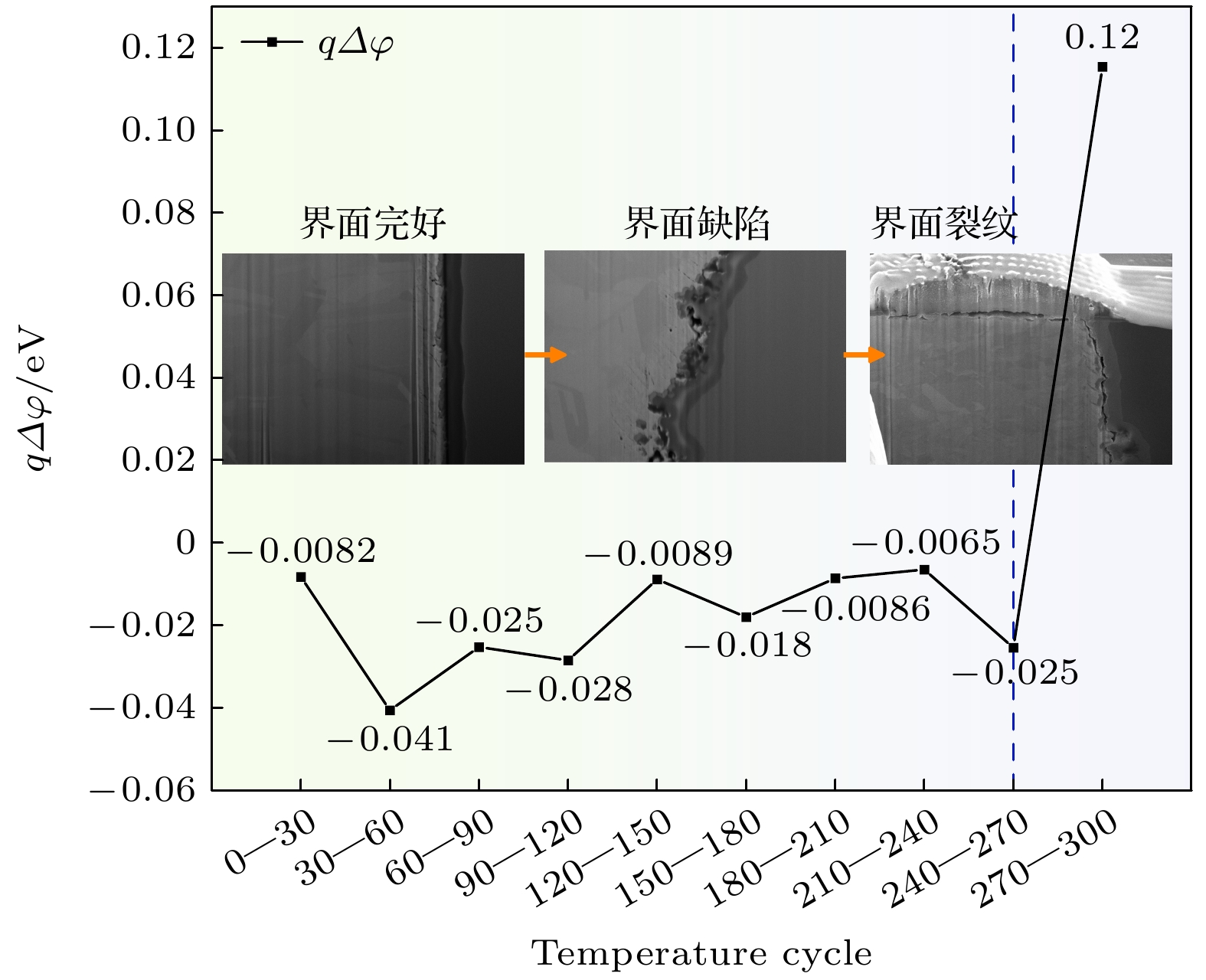
通过(2)式计算不同温度循环次数后TSV样品界面绝缘层的肖特基势垒高度变化值, 如图7所示.
图7中, 随着温度循环次数的增加, TSV样品界面绝缘层的势垒高度呈现出不同程度的下降趋势. Cycle-30 TSV样品相较于Cycle-0样品, 势垒高度仅降低0.0082 eV, 绝缘层介电性能并未出现明显的退化, 继续增至Cycle-60, 势垒高度降低0.041 eV, 绝缘层介电性能出现较大退化趋势. 分析Cycle-60 TSV样品的I-V数据发现, 其在低电场(3.67×105 V/cm)下的漏电流为10—102 nA级别, 相比Cycle-0和 Cycle-30 TSV样品的漏电流(1—10 nA)增大至少10倍, 导致其拟合漏电机制曲线时得到的截距出现较大变化. 由此可以看出即使温度循环次数较少时, TSV样品在高电场下不会产生高漏电流, 但会增大其在低电场下的漏电, 使绝缘层在低电场下的介电性能发生退化. 由于Cycle-90—Cycle-270 TSV样品是在低电场下计算的绝缘层势垒高度, 可以看出在低电场下势垒高度下降值保持在相对稳定的范围, 在此阶段, 绝缘层介电性能稳步退化, 由介电性能退化导致的漏电是270次前温度循环样品的失效机理. 由我们之前的研究发现, SiO2绝缘层势垒高度的下降, 是因为温度循环导致TSV界面SiO2绝缘层出现热致缺陷累积, 介电性能劣化. 金属中的电子在温度和电场激发下更容易跃过肖特基势垒形成漏电流.
但随着温度循环次数增加到300次, 绝缘层势垒高度相较于Cycle-270 TSV样品增加了0.12 eV, 介电性能随温度循环的退化并未出现在Cycle-300 TSV样品, 因为此时绝缘层出现由贯穿裂纹形成的空气间隙, 使漏电流减小, 其失效机制由漏电转变为机械开裂.
-
本文对经历不同温度循环次数后的TSV样品进行漏电流 I-V 测试, 通过FIB-SEM微观结构分析和 EDS 元素检测, 得到了TSV界面随温度循环次数增加的演变过程, 阐明了TSV界面完整性对铜扩散及TSV漏电流的影响, 厘清了TSV绝缘层漏电机制随电场强度的转变过程, 主要结论如下.
1)当温度循环次数小于60次时, TSV界面完整性较好, 随着温度循环次数从60次增至270次, TSV界面萌生微孔洞和微裂纹, 这些缺陷为铜扩散到绝缘层提供通道, 在绝缘层中形成漏电路径, 导致TSV热致漏电流显著增加. 伴随温度循环继续增至300次, TSV界面形成贯穿性裂纹, 阻碍了电子在TSV-Cu与Si基体间的流动, 使TSV漏电流骤减, TSV失效模式由热致漏电转变为机械开裂.
2)在温度循环次数较低(≤ Cycle-60)时, 肖特基发射是TSV绝缘层的漏电机制. 随着温度循环次数的增加(≥ Cycle-90), 绝缘层漏电机制由单一的肖特基发射转变为肖特基发射与P-F发射机制的共同作用, 特别是在高电场条件下, Cu扩散到绝缘层中形成陷阱态, 绝缘层中的高电场区域通过P-F发射机制增大电子的发射率, 使P-F发射机制对漏电的贡献显著增大.
3)随着温度循环次数的增加, TSV绝缘层内出现热致缺陷累积, TSV样品界面绝缘层的势垒高度下降, 绝缘层介电性能发生退化. 在300次温度循环后, TSV从热致漏电失效转变为机械开裂, TSV样品界面绝缘层的势垒高度增大.
温度循环对硅通孔绝缘层漏电机制的影响
Effects of temperature cycling on leakage mechanism of through-silicon via insulation layer
-
摘要: 硅通孔(TSV)作为实现三维集成电路互连的关键技术, 其侧壁界面的完整性对TSV的漏电特性至关重要. 本文开展了温度循环实验, 结合漏电流I-V测试、微观结构观察和能谱仪(EDS)元素分析, 分析了温度循环对TSV侧壁界面完整性及对绝缘层漏电机制的影响. 研究表明, 随着温度循环次数的增加, TSV阻挡层的完整性逐渐降低, 漏电流显著增加, 绝缘层的漏电机制从肖特基发射机制转变为肖特基发射与Poole-Frenkel发射机制共同作用, 这种转变在高电场条件下更为显著. 进一步的TSV界面完整性分析表明, 温度循环引起的热机械应力导致了TSV填充铜与阻挡层界面间缺陷产生, 这些缺陷促进铜原子扩散到绝缘层, 形成漏电路径, 是导致绝缘层介电性能下降的主要原因之一.Abstract: Through-silicon via (TSV), as a key technology for realizing interconnections in three-dimensional integrated circuits (3D ICs), critically depends on the integrity of its sidewall interfaces to maintain optimal leakage characteristics. In this work, the temperature cycling experiments, incorporating leakage current I-V testing, microstructural observations are conducted, and the EDS elemental analysis is made to evaluate the effects of temperature cycling on the integrity of TSV sidewall interfaces and the leakage mechanisms in the insulation layer. The results indicate that as the number of temperature cycles increases, the alternating cyclic loads progressively degrade the integrity of the TSV barrier layer, transitioning from an intact interface to the formation of micro-voids and micro-cracks, which results in a significant increase in leakage current. When through-thickness cracks appear at the interface, a sudden decrease in leakage current occurs. The TSV failure mode is transforms from thermally induced leakage to mechanical cracking. The leakage mechanism of the insulation layer transforms from the Schottky emission mechanism (Cycle≤60) into a combination of Schottky emission and Poole-Frenkel emission mechanisms (Cycle≥90), and this transformation becomes more pronounced under high electric field conditions. Further analysis of TSV interface integrity reveals that thermomechanical stress induced by temperature cycling generates defects at the interface between the TSV copper fill and the barrier layer. As thermally induced defects accumulate, the barrier height of the insulation layer continuously decreases, making it easier for electrons in the metal to overcome the Schottky barrier under thermal and electric field excitation, thereby forming leakage currents. Moreover, these defects facilitate the diffusion of copper atoms into the insulation layer, thereby forming localized high electric field regions. These high-field regions in the insulation layer increase electron emission rates through the Poole-Frenkel emission mechanism, creating leakage paths. Therefore, copper diffusion emerges as one of the primary causes of dielectric performance degradation in the insulation layer.
-
Key words:
- through silicon via /
- leakage mechanism /
- temperature cycling .
-
-
图 2 0—300次温度循环样品I-V (J-E )测试结果
Figure 2. I-V (J-E ) test results of samples after 0–300 temperature cycles.
图 4 不同温度循环次数下TSV界面微观结构图
Figure 4. Microstructure of TSV interfaces under different temperature cycling numbers.
图 6 漏电机制拟合曲线 (a) 肖特基拟合; (b) P-F拟合
Figure 6. Leakage current mechanism fitting curves: (a) Schottky fitting; (b) P-F fitting.
图 7 不同温度循环次数后绝缘层势垒高度变化值
Figure 7. Variation in insulation layer barrier height after different numbers of temperature cycles.
表 1 不同温度循环次数下绝缘层中Cu元素比例
Table 1. Cu element proportion in insulation layer under different temperature cycling numbers.
温循次数 0 30 60 90 120 150 180 210 240 270 300 Cu质量含量/% 9.19 9.22 12.55 18.07 27.44 33.59 37.16 41.98 44.19 48.29 15.85 
下载: 导出CSV
表 2 漏电机制模型
Table 2. Leakage mechanism models.
漏电机制 理论公式 拟合公式 参数说明 P-F发射 $ {J_{{\text{F-P}}}} = CE\exp \left( {\dfrac{{ - {\varphi _{\text{t}}} + q\sqrt {qE/4{\text{π}}{\varepsilon _0}{\varepsilon _{\text{r}}}} }}{{kT}}} \right) $ $ \mathrm{ln}\left(J_{\text{F-P}}/E\right)=A_{{\text{F-P}}}\sqrt{E}+B_{{\text{F-P}}} $ J 为电流密度
q 为电子电荷
E为电场强度
φt 为势陷深度
ε0 为真空介电常数
εr 为介电常数肖特基发射 ${J_{\text{S}}} = A{T^2}\exp \left( {\dfrac{{ - {\varphi _{\text{s}}} + q\sqrt {qE/4{\text{π}}{\varepsilon _0}{\varepsilon _{\text{r}}}} }}{{kT}}} \right)$ $ \mathrm{ln}J_{\text{S}}=A_{\text{S}}\sqrt{E}+B_{\text{S}} $ A 为有效理查德森常数
T 为绝对温度
φs 为肖特基势垒高度
k 为玻尔兹曼常数
下载: 导出CSV
-
[1] Wang Y K, Liu H Z, Huo L H, Li H B, Tian W C, Ji H Y, Chen S 2024 Micromachines 15 422 doi: 10.3390/mi15040422 [2] Jang Y J, Sharma A, Jung J P 2023 Materials 16 7652 doi: 10.3390/ma16247652 [3] 董刚, 武文珊, 杨银堂 2015 物理学报 64 026601 doi: 10.7498/aps.64.026601 Dong G, Wu W S, Yang Y T 2015 Acta Phys. Sin. 64 026601 doi: 10.7498/aps.64.026601 [4] 董刚, 刘荡, 石涛, 杨银堂 2015 物理学报 64 176601 doi: 10.7498/aps.64.176601 Dong G, Liu D, Shi T, Yang Y T 2015 Acta Phys. Sin. 64 176601 doi: 10.7498/aps.64.176601 [5] Fan Z W, Chen X, Wang Y S, Jiang Y, Zhang S F 2022 Microelectron. Reliab. 138 114643 doi: 10.1016/j.microrel.2022.114643 [6] Kumari V, Chandrakar S, Verma S, Majumder M K 2023 IEEE Trans. Compon. Packag. Manuf. Technol. 13 1734 doi: 10.1109/TCPMT.2023.3325222 [7] Chan J M, Lee K C, Tan C S 2018 IEEE Trans. Device Mater. Reliab. 18 520 doi: 10.1109/TDMR.2018.2880286 [8] Chan J M, Cheng X, Lee K C, Kanert W, Tan C S 2017 IEEE International Reliability Physics Symposium (IRPS) Monterey, CA, April 2–6, 2017 p4A [9] Chandrakar M, Majumder M K 2022 IEEE Trans. Compon. Packag. Manuf. Technol. 12 1832 doi: 10.1109/TCPMT.2022.3225142 [10] Gong T, Xie L L, Chen S, Lu X J, Zhao M R, Zhu J Y, Yang X F, Wang Z Z 2024 Crystals 14 37 [11] Shen Z S, Jing S Y, Heng Y Y, Yao Y F, Tu K N, Liu Y X 2023 Appl. Phys. Rev. 10 021309 doi: 10.1063/5.0139658 [12] Nakamura T, Kitada H, Mizushima Y, Maeda N, Fujimoto K, Ohba T 2012 IEEE 2011 International 3D Systems Integration Conference (3DIC) Osaka, Japan, January 31– February 2, 2012 p1 [13] Ranganathan N, Lee D Y, Youhe L, Lo G Q, Prasad K, Pey K L 2011 IEEE Trans. Compon. Packag. Manuf. Technol. 1 1497 doi: 10.1109/TCPMT.2011.2160395 [14] Lin Y, Tan C S 2018 Jpn. J. Appl. Phys. 57 07MF01 doi: 10.7567/JJAP.57.07MF01 [15] Chen S, Jian X D, Li K, Li G Y, Wang Z Z, Yang X F, Wang H Y, Fu Z W 2023 Microelectron. Reliab. 141 114889 doi: 10.1016/j.microrel.2022.114889 [16] Hung J F, Lau J H, Chen P S, Wu S H, Lai S J, Li M L, Sheu S S, Tzeng P J, Lin Z H, Ku T K, Lo W C, Kao M J 2012 IEEE 62nd Electronic Components and Technology Conference(ECTC) San Diego, CA, May 29–June 1, 2012 p564 [17] Krause M, Altmann F, Schmidt C, Petzold M, Malta D, Temple D 2011 IEEE 61st Electronic Components and Technology Conference (ECTC) Lake Buena Vista, FL, May 31–June 3, 2011 p1452 [18] Chiu F C 2014 Adv. Mater. Sci. Eng. 2014 578168 doi: 10.1155/2014/578168 [19] Fowler R H, Nordheim L 1928 Proc. R. Soc. London, Ser. A 119 173 doi: 10.1098/rspa.1928.0091 [20] Frenkel J 1938 Phys. Rev. 54 647 doi: 10.1103/PhysRev.54.647 [21] Schottky W 1939 Z. Phys. 113 367 doi: 10.1007/BF01340116 -
图( 7) 表( 2)
计量
- 文章访问数: 125
- HTML全文浏览数: 125
- PDF下载数: 1
- 施引文献: 0