机器学习是一个典型的优化问题, 其学习过程就是在参数空间中的迭代寻优过程, 将这种算法的迭代运动过程视为动力学过程是一种很自然的思路. 经过长期的发展, 动力学理论体系已十分完备, 有量子动力学、牛顿动力学、热动力学、电动力学、分子动力学, 这些动力学通过建立一组动力学方程对运动规律进行理论描述. 建立机器学习的动力学理论有望能解决这一领域缺乏理论模型的问题, 从而推进机器学习理论和应用的发展.

针对优化问题采用动力学的方法进行理论建模最早始于Metropolis等^[1]在1953年基于热力学提出的解的接收准则, 后来被Kirkpatrick等^[2]应用于求解优化问题模拟退火算法, 这是将热动力学应用于优化问题的早期尝试. 1994年Finnila等^[3]提出将目标函数视为Schrödinger方程中的势能, 从而把优化问题转化为约束态量子基态波函数问题, 这是量子动力学理论在优化问题中的首次应用. 2013年我们开始尝试提出优化问题的量子动力学框架, 研究结果表明Schrödinger方程可以有效地对优化算法的基本迭代过程进行描述^[4–7]. 量子动力学在人工智能中能成功应用的证据还包括最早实现商业应用的量子计算机D-wave, 它利用量子退火实现了对智能优化问题的成功求解^[8].

2015年Sohl-Dickstein等^[9]利用非平衡热力学思想提出了扩散概率模型(diffusion probalistic model). 随后, 扩散模型(diffusion model)得到了快速的发展, 并被广泛应用在人工智能领域. 扩散模型是动力学理论在机器学习领域成功应用的范例. 近年来动力学理论在机器学习中展现出越来越大的理论和应用价值, 并发展出基于随机微分方程的新型动力学方法^[10], 其有效性不断被实验结果证实.

机器学习的动力学理论最重要的是要建立机器学习过程的动力学方程. 由于机器学习过程是一个概率运动过程, 而量子动力学和热动力学分别 从微观和宏观两个角度描述了物质世界的概率 运动过程, 特别是量子动力学反映了物质世界最基本的运动规律. 量子动力学的核心动力学方程是Schrödinger方程, 其利用一个确定性的含时偏微分方程描述了物质世界广泛存在的概率运动规律. 这表明量子动力学可以作为描述机器学习运动过程的第一性原理. 本文通过建立机器学习的量子动力学方程, 从量子动力学角度出发展开对机器学习迭代过程的研究.

优化问题的量子动力学框架(quantum dynamics framework, QDF)最早源于2013年提出的多尺度量子谐振子算法(multi-scale quantum harmonic oscillator algorithm, MQHOA)^[6]. 随后我们对其进行了持续的研究逐步形成了优化问题的量子动力学框架, 该框架已在函数优化理论和实践中都得到了成功的应用^[11,12].

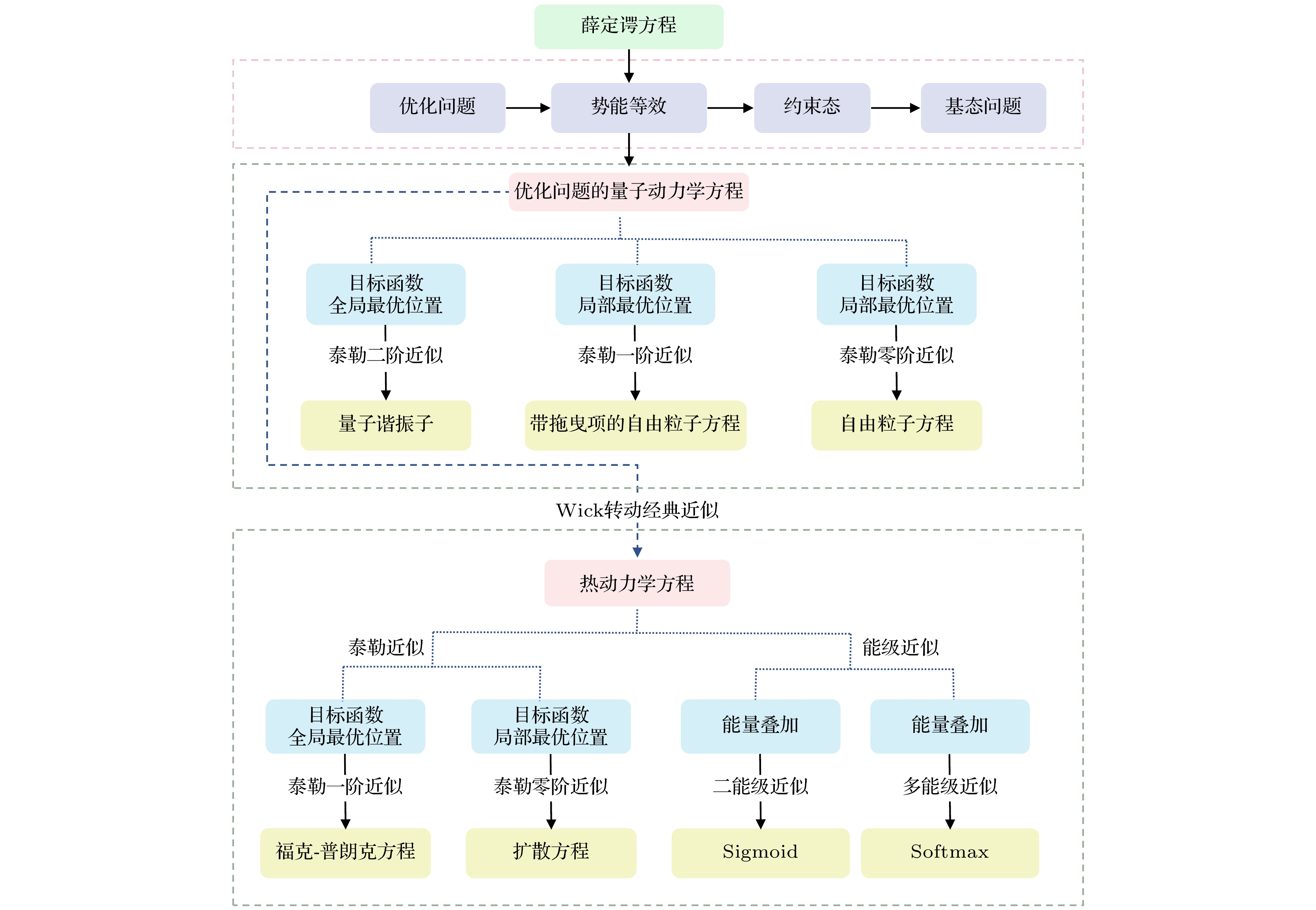
QDF的基本结构如图1所示. 量子力学的基本动力学方程为Schrödinger方程, 在研究优化问题时可以不考虑物理学中Schrödinger方程中的物理量和常数, 则Schrödinger方程可以简化为

其中D为常数, 该常数影响系统的动能大小; $ V\left( x \right) $为约束势能; $ \psi \left( x, t \right) $为粒子的波函数.

QDF的基本思想是将优化问题的迭代过程视为量子动力学过程, 将优化问题中的目标函数$ f\left( x \right) $视为Schrödinger方程中的势能项$ V\left( x \right) $, 即$ V\left( x \right) = f\left( x \right) $, 从而将优化问题转化为求解量子约束态的基态波函数问题, 相应的优化问题的量子动力学方程如下:

通过量子动力学方程, 优化问题的迭代过程转化为含时偏微分动力学方程进行描述. 其中波函数$ \psi \left( x, t \right) $的时间演化过程就是优化问题解的概率分布的演化过程.

机器学习过程也是对由大量连接权重构成的参数空间进行参数优化的过程, 其优化目标是为了寻找一个最优的连接权重组合. 通常不能直接获得参数空间优化时的目标函数, 为了和函数优化问题中的目标函数$ f\left( x \right) $区别, 这里用广义目标函数$ \zeta \left( x \right) $来形式化地表示任意问题在神经网络参数空间中目标函数的数学关系. 如果将参数空间中的广义目标函数视为Schrödinger方程中的势能项, 即进行势能等效:

则薛定谔方程转化为如下方程:

这个方程就是机器学习的量子动力学方程, 该方程的物理含义为被势能$ \zeta \left( x \right) $约束的量子束缚态系统. 根据玻恩对波函数的概率解释, 波函数$ \psi \left( x, t \right) $的模方$ {{\left| \psi \left( x, t \right) \right|}^{2}} $的意义为t时刻解的概率分布. 机器学习的过程就是波函数$ \psi \left( x, t \right) $的时间演化过程.

系统的哈密顿算符为

其中参数D决定系统动能的大小, 通过缓慢降低参数D的值可以实现系统的退火. 因此, 根据机器学习的量子动力学方程可以预测, 机器学习的迭代过程可能包含两个主要的迭代循环: 第一个迭代循环是减小D值的量子退火迭代过程, 对应于在参数空间针对广义目标函数的$ \zeta \left( x \right) $采样步长的逐步减小. D值大时, 系统动能大, 系统在基态时的零点能$ {{E}_{0}} $也大, 为了获得精确的全局最优解, 需要 逐步退火降低D值, 最后获得较低的零点能. 第二个迭代循环是同一动能下系统向基态的时间演化 过程.

建立机器学习量子动力学方程的重要意义在于以下两点: 第一, 从物理意义上将机器学习对参数的优化学习过程转化为了求解以广义目标函数$ \zeta \left( x \right) $为约束势能的量子约束态基态波函数问题; 第二, 将机器学习的迭代过程从数学上转化为严格的含时偏微分方程来表述. 由于量子物理经过一百多年的发展已具有完备且丰富的物理和数学理论体系, 可以为研究机器学习提供支持.

由于量子动力学方程的解析求解非常困难, 同时无法获得机器学习参数空间广义目标函数$ \zeta \left( x \right) $解析式, 因此采用针对广义目标函数Taylor展开的方式来对量子动力学方程进行近似分析.

参数空间的广义目标函数$ \zeta \left( x \right) $在当前位置$ {{x}_{0}} $的Taylor零阶近似为$ \zeta \left( x \right) = 0 $, 这种情况表明对广义目标函数$ \zeta \left( x \right) $的当前位置$ {{x}_{0}} $的情况一无所知. 因此, 机器学习的量子动力学方程在广义目标函数$ \zeta \left( x \right) $的0阶Taylor近似就是自由电子方程:

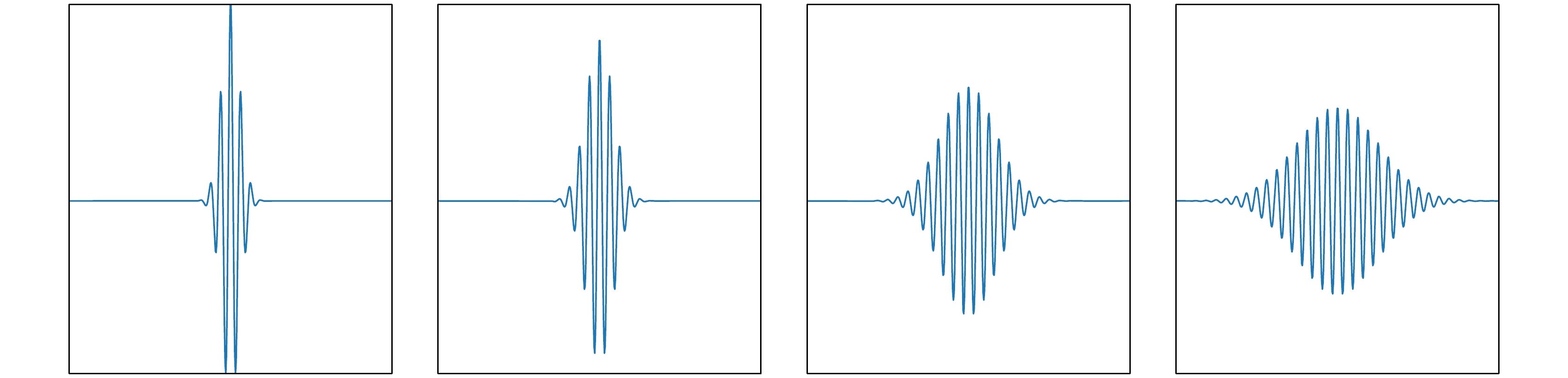
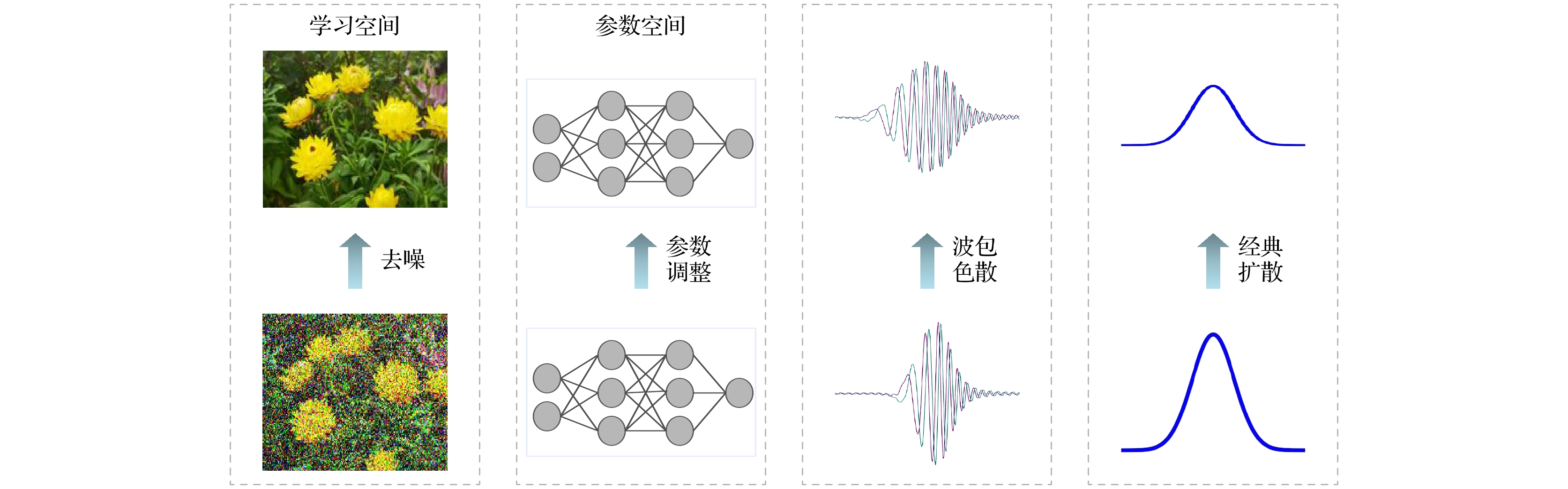
自由电子的运动未受到任何势能的约束, 所以自由电子方程中没有势能项$ \zeta \left( x \right) $. 自由电子方程相比经典的扩散方程只是多了一个表达波动性的虚数符号i, 它描述了机器学习过程中对广义目标函数$ \zeta \left( x \right) $的信息完全未知时算法的量子动力学规律.

根据量子力学中自由电子的运动理论, 0阶Taylor近似下机器学习的量子动力学过程表现为波包的色散过程. 色散过程是由于自由粒子的波函数由许多不同频率成分的态叠加组成的波包, 这些不同频率的成分随时间的演化会逐步弥散开来(如图2). 这一过程与扩散过程相似, 但却是更复杂的波包色散过程, 这正是量子动力学系统存在波粒二象性所造成的.

参数空间的广义目标函数$ \zeta \left( x \right) $在当前位置$ {{x}_{0}} $的1阶Taylor近似为$ \zeta \left( x \right)\approx \dfrac{\partial \zeta \left( {{x}_{0}} \right)}{\partial x} $, 此时机器学习的量子动力学方程为

这一方程表示电子的波包移动到$ {{x}_{0}} $位置时, 该位置约束势能$ \zeta \left( x \right) $的斜率为$ {\partial \zeta \left( {{x}_{0}} \right)}/{\partial x} $, 这一动力学过程对应于算法在参数空间通过两次采样来估计广义目标函数在$ {{x}_{0}} $位置的斜率, 从而进行梯度下降的优化操作.

量子动力学中的波包动力学过程在经典计算机中非常难以实现, 为了在经典计算机上近似实现量子动力学过程, 这里将机器学习的量子动力学方程进行Wick转动^[13]. 令虚时间$ \tau = {\rm{i}}t $, 则量子动力学方程将失去波动特性被变换为虚时间下经典的扩散反应方程:

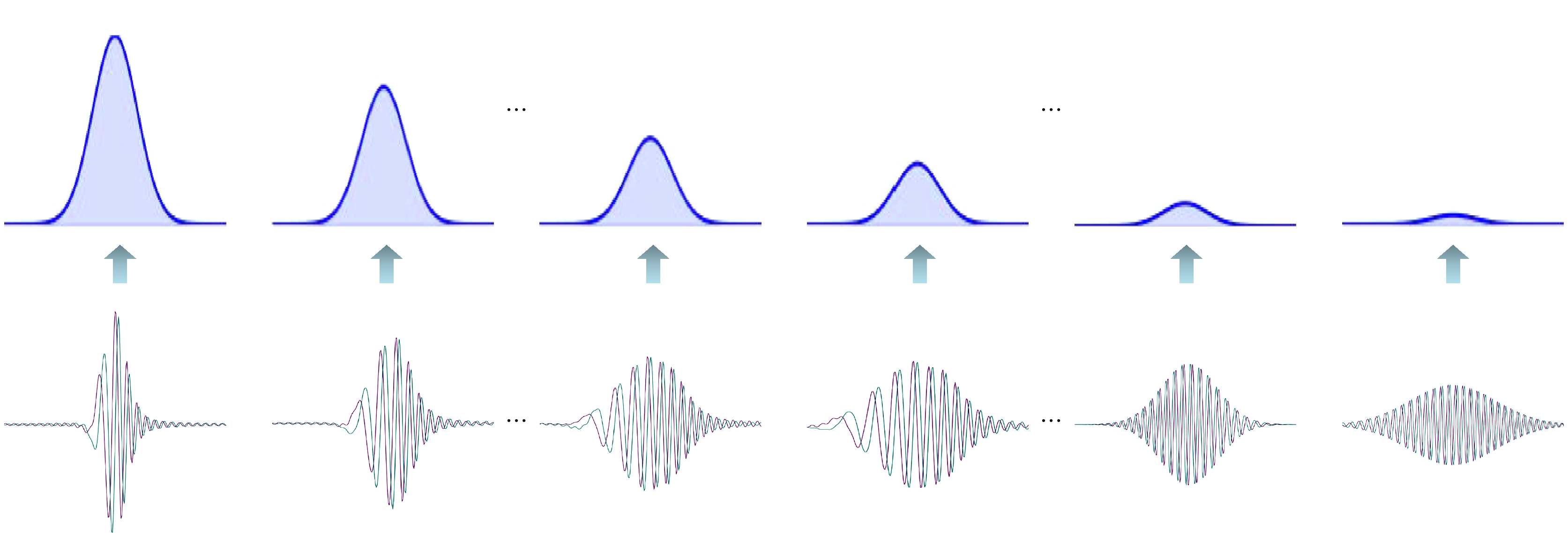
Wick转动后广义目标函数$ \zeta \left( x \right) $的0阶Taylor近似方程就由量子化的自由电子方程变换为标准的经典扩散方程:

算法的动力学过程从波包色散退化为经典扩散过程(如图3). 机器学习算法在参数空间中的采样可以采用点源的扩散过程来描述, 即扩散方程的初始条件$ \tau = 0 $时$ \psi \left( x, 0 \right) = \delta \left( x \right) $, $ \delta \left( x \right) $为狄拉克函数. 这一初始条件对应的解为格林函数, 一维扩散方程的格林函数为高斯函数:

格林函数物理意义是描述一个点源的扩散过程, 即一个位于原点0的点在τ时刻扩散到x位置的概率. 优化问题中解空间内的采样行为可以采用点源的扩散来描述. 经典的扩散过程在函数优化问题中可采用群体高斯随机行走采样的方法来实现. 这里参数D为扩散系数, D值越大系统动能越大, 对应的高斯采样的标准差越大.

从扩散方程可以得出: 如果对广义目标函数$ \zeta \left( x \right) $的信息完全未知, 机器学习的基本动力学过程就是在参数空间中进行的高斯随机扩散过程.

Wick转动后广义目标函数$ \zeta \left( x \right) $的1阶Taylor近似为Fokker-Planck方程:

其中拖拽项$ {\partial \zeta (x)}/{\partial x} $表达的是在机器学习的迭代过程中获得广义目标函数$ \zeta \left( x \right) $当前采样位置的导数. 与扩散方程描述的对广义目标函数$ \zeta \left( x \right) $完全未知的情况相比, Fokker-Planck方程描述了迭代过程中可以获得当前目标函数采样位置导数并进行梯度下降时的动力学规律. 机器学习中的Fokker-Planck方程描述了学习过程中基于高斯采样扩散的梯度下降过程. 在机器学习迭代过程中针对一个样本的学习迭代可以被映射为参数空间中针对广义目标函数$ \zeta \left( x \right) $的一次梯度下降操作.

Fokker-Planck方程中的时间变量τ和空间变量x均为连续变量, 但机器学习的迭代过程是一个离散的动力学过程, 因此采用Fokker-Planck方程的离散化形式更能准确地描述机器学习的迭代过程.

采用$ \psi _{i}^{n} $表示在时刻$ \tau = {{\tau }_{n}} $和位置$ x = {{x}_{i}} $处方程的解, 机器学习两次迭代过程的时刻分别为$ {{\tau }_{n}} $和$ {{\tau }_{n+1}} $, 则时间间隔$ \Delta \tau = {{\tau }_{n+1}}-{{\tau }_{n}} $; 两次迭代在参数空间中的位置分别为$ {{x}_{i}} $和$ {{x}_{i+1}} $, 空间位置间隔$ \Delta x = {{x}_{i+1}}-{{x}_{i}} $, 对应于参数空间广义目标函数值分别为$ \zeta \left( {{x}_{i}} \right) $和$ \zeta \left( {{x}_{i+1}} \right) $, 广义目标函数值的差$ \Delta \zeta = \zeta \left( {{x}_{i+1}} \right)-\zeta \left( {{x}_{i}} \right) $.

根据Fokker-Planck方程(11), 对时间的微分可以离散化为

方程(11)右边的动能项对位置的二阶微分可以离散化为

方程(11)右边的广义目标函数$ \zeta \left( x \right) $的Taylor二阶近似离散化为

由于在参数空间中$ \zeta \left( x \right) $的导数无法直接定义, $ {\partial \zeta ( x )}/{\partial x} $的离散形式表明可以通过在参数空间的两次采样来近似获得广义目标函数$ \zeta \left( x \right) $的梯度信息. 根据Fokker-Planck方程两边相等的关系和上面的离散化表达式可得Fokker-Planck方程的离散化形式:

变形后可得到从$ {{\tau }_{n}} $时刻到$ {{\tau }_{n+1}} $时刻的离散时间演化迭代公式:

机器学习的量子动力学方程的建立为研究机器学习的迭代过程提供了可靠的理论支持, 利用这一理论可以分析和解释机器学习中的一些核心操作和算法. 首先采用量子动力学方程对机器学习迭代过程的收敛性进行分析.

机器学习的迭代过程是一种时间演化过程, 机器学习的量子动力学方程的含时通解可以写成如下形式:

通解公式表明量子动力学方程的解是由一系列不同能级的态按概率叠加形成的叠加态. 对这一叠加态进行测量时, 叠加态将按概率坍缩到其中的一个态. 通解中的能量$ {{E}_{n}} $对应于系统的动能$ {{E}_{{\rm{d}}}} $加上势能$ {{E}_{{\rm{p}}}} $:

量子动力学方程进行Wick转动后经典扩散反应方程的通解为

求最小值的优化问题, 就可获得基态能量$ {{E}_{0}} $.

Wick转动后通解的指数部分会导致各能量对应状态随τ的演化指数衰减, 能量值$ {{E}_{n}} $越大衰减越快, 其中基态能量$ {{E}_{0}} $对应的项会以较大的概率被保留下来, 也就是说优解会被大概率保留下来. 当$ \tau \to \infty $时, 可以得到

其中$ {{c}_{0}}{{\varphi }_{0}}\left( x \right)\exp \left( -{{E}_{0}}\tau \right) $为能量最低的状态.

这一结果表明机器学习的迭代过程在$ \tau \to \infty $时是可以收敛到基态的, 即全局最优解. 这一结果也表明对机器学习的量子动力学方程进行Wick转动后, 虽然丢失了波动性, 但仍然能有效地表达算法向基态的演化收敛特性. 热动力学的时间演化过程是一个针对系统能量的低通滤波器, 低能量的状态会以较大概率被保留下来.

根据这一时间演化的收敛性和动力学方程中与动能相关的系数D的物理意义可以得出机器学习的动力学过程应包含以下两个基本迭代过程: 第一, 不断减小系数D的值以逐步降低系统的动能的退火过程, 这一过程在实际中对应于采样步长的逐步减小, 从而获得更低的基态能量$ {{E}_{0}} $, 这意味着机器学习算法应具有某种多尺度的学习过程; 第二, 在同一动能下向系统基态的时间演化过程, 这一迭代演化过程在采用Softmax或Sigmoid准则的基础上进行梯度下降操作.

同样, 利用经典扩散反应方程的通解公式可以得到机器学习中被广泛使用的Softmax和Sigmoid函数.

假设量子动力学方程进行Wick转动后经典扩散反应方程的通解是由n个能级的状态构成:

其中第k个能级τ时刻能量对应的状态为$ {{c}_{k}}{{\varphi }_{k}} (x) \times\exp (-{{E}_{k}}\tau) $.

算法演化的初始时刻$ \tau = 0 $, 此时系统状态为

由于时间τ在指数位置, 随时间的演化, 每一项的大小主要由指数项决定, 同时能量越大的状态随时间演化会衰减得越快. 当算法进行了长时间演化后, 指数项将占主导地位, 因此可以忽略非指数项的影响, 能量为$ {{E}_{k}} $的态出现的概率$ {{P}_{{{E}_{k}}}} $可以近似表示为

(23)式即为含时的Softmax函数, Softmax会随时间τ进行动力学演化, 当$ \tau = 0 $时各种状态的概率相同; 逐渐增大时间τ, 则低能量的状态出现的概率将增大; 当$ \tau \to \infty $时, 系统将趋近于能量最低的$ {{E}_{0}} $状态. 在这里Softmax实现了对系统能量的低通滤波, 以较大的概率保留了能量较小状态.

如果将系统能量进一步减少为两个, 即对系统进行二能级近似, 分别用能量$ {{E}_{\rm{a}}} $和$ {{E}_{\rm{b}}} $来表示. 假设$ {{E}_{\rm{a}}} < {{E}_{\rm{b}}} $, $ {{E}_{\rm{a}}} $为低能态对应优解, $ {{E}_{\rm{b}}} $为高能态对应差解, 则低能态$ {{E}_{\rm{a}}} $出现的概率$ {{P}_{{{E}_{\rm{a}}}}} $为

从(24)式的形式看, 在二能级近似后的概率函数就是含时的Sigmoid函数, Sigmoid函数的形状会随时间的演化发生改变. $ \Delta E $相同时, 随着时间τ的演化, 低能量状态$ {{E}_{{\rm{a}}}} $的选择概率会增大; 当$ \tau \to \infty $时, 低能量状态$ {{E}_{{\rm{a}}}} $的选择概率$ {{P}_{{{E}_{{\rm{a}}}}}} $会趋近于1.

所以根据二能级近似, 算法在迭代演化的过程中会逐步降低对差解的接受概率. 当$ \tau > 0 $且$ \Delta E > 0 $时表明算法采样到了优解, 对差解的接收概率是按相同的规律演化.

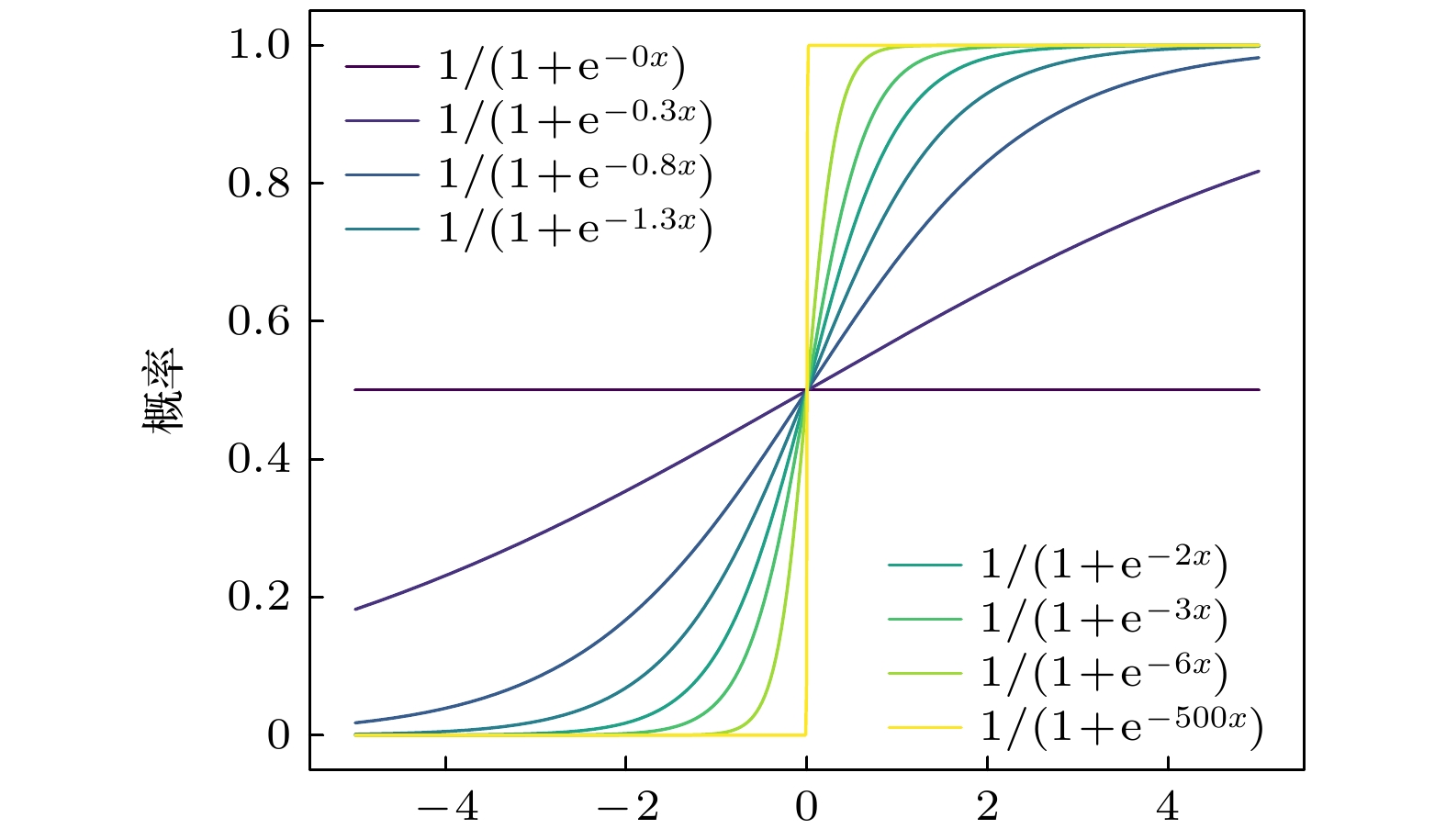
令$ \Delta E = x $, 则上述概率式就是机器学习中常见的带时间演化过程的Sigmoid激活函数:

图4给出了不同时间τ下Sigmoid函数$ S(x) $的演化图像.

扩散模型是2015年提出的一种基于热动力学理论的机器学习算法, 它在生成式人工智能等多个应用领域展现出了良好的性能和应用前景^[14–17]. 扩散模型采用对图像进行逐级添加高斯噪声后逐级对噪声图像进行去噪的高斯扩散方法来实现网络参数的学习.

针对量子动力学和扩散过程的关系早在1975年Anderson^[18]就首次根据Schrödinger方程和扩散方程的同构性提出了采用随机行走(random walk)求解分子基态波函数的扩散蒙特卡罗(diffusion Monte Carlo, DMC)方法. DMC被认为是一种获得量子系统基态能量和波函数的标准方法. 如果把一个优化问题转化为量子问题就可以采用DMC方法计算基态波函数^[19]. DMC利用了Schrödinger方程和扩散方程之间的同构性(isomorph), 模拟扩散过程推动波函数逐步向基态演化, 从而实现对目标函数全局最优解的搜索^[20].

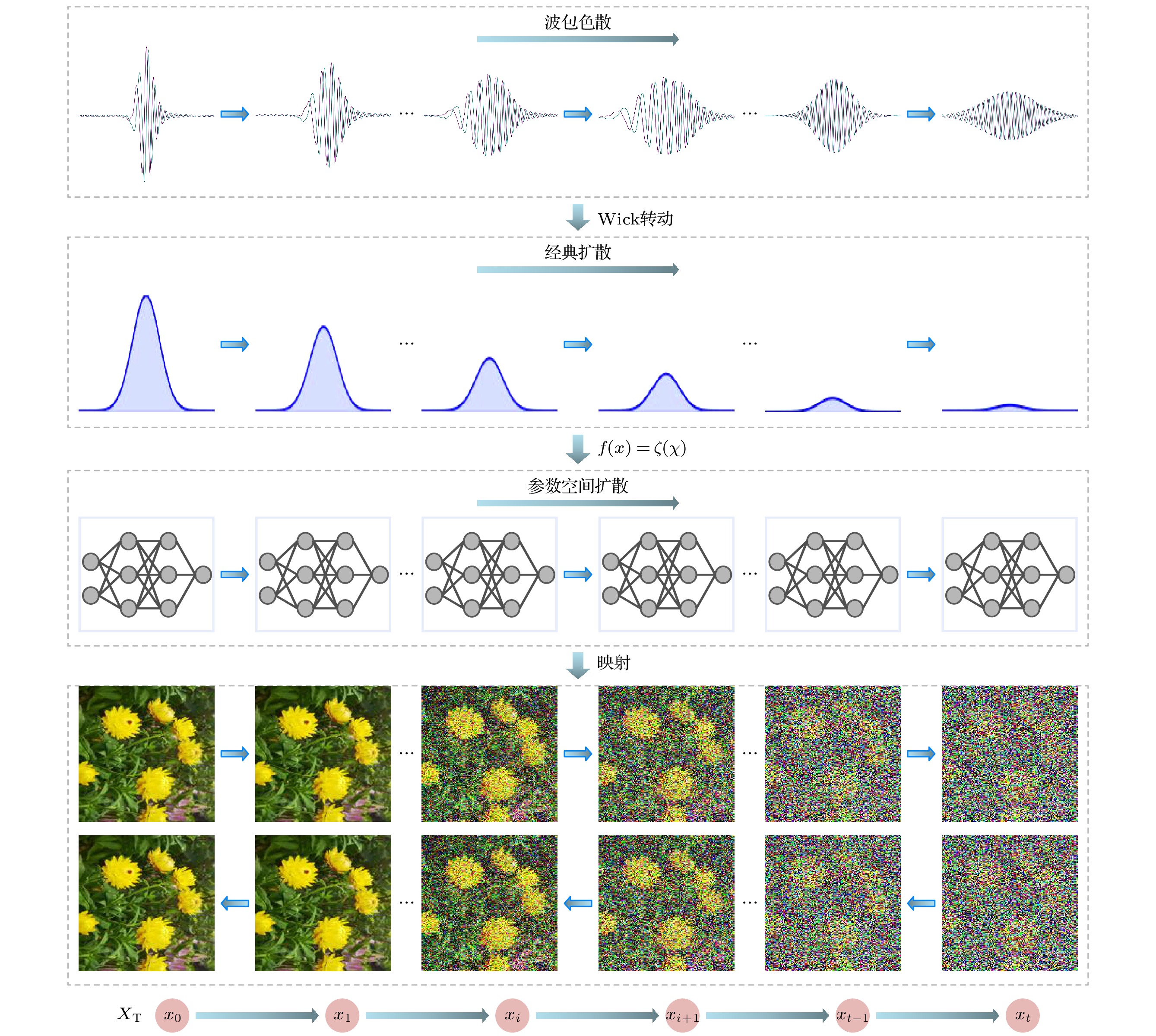
根据对机器学习量子动力学方程的分析, 经典近似后广义目标函数的0阶Taylor近似要求机器学习算法在参数空间对广义目标函数$ \zeta (x) $进行高斯采样, 1阶Taylor近似要求机器学习算法在参数空间对广义目标函数$ \zeta (x) $进行两次采样来获得对梯度的估计. 但广义目标函数$ \zeta (x) $只是对参数空间目标函数的形式化描述, 因此无法像函数优化问题一样精确地定义其采样邻域, 进而无法实现在参数空间的直接高斯采样. 所以扩散模型在学习空间中的高斯噪声扩散和去噪过程可以视为参数空间的高斯采样过程在学习空间中的近似. 如图5所示, 扩散模型通过在学习空间中的高斯噪声扩散过程间接实现了机器学习算法在参数空间中的高斯采样扩散过程, 从而解决了机器学习算法在参数空间中无法直接进行高斯采样的问题. 所以, 扩散模型的迭代过程是符合机器学习的量子动力学理论的. 根据量子动力学的理论, 扩散模型可以被认为是机器学习量子动力学经典近似下广义目标函数的0阶和1阶迭代操作. 扩散模型中的每一次去噪迭代都对应于在广义参数空间中的一次高斯采样, 一个样本的一次加噪和去噪迭代序列就对应于参数空间中一个采样点的高斯扩散采样序列.

从量子动力学的角度来看, 机器学习中的扩散模型原本是基于在参数空间中进行高斯采样的过程. 但由于在参数空间中无法定义目标函数, 直接进行高斯采样变得不可行. 因此, 扩散模型将学习空间映射到参数空间, 从而实现了在参数空间中进行高斯采样的目标. 这一方法有效地克服了参数空间中目标函数不可定义的限制, 为模型的学习和优化提供了新的理论框架.

机器学习就是利用学习空间中的训练集所形成的目标函数, 通过训练迭代实现对参数空间广义目标函数$ \zeta \left( x \right) $的优化. 机器学习的目标是对参数空间的广义目标函数进行优化, 从而获得最优的模型参数, 但通常算法无法实现在参数空间的直接采样, 所以通过学习空间向参数空间映射来间接实现针对参数空间的优化. 如图6所示, 扩散模型通过去除高斯噪声的学习过程, 间接实现了在参数空间中的高斯采样扩散过程, 完成了学习空间向参数空间中高斯采样和梯度获取的映射. 而参数空间中的高斯采样则是量子动力学理论中波包色散过程的经典近似.

同时, 根据机器学习的量子动力学, 机器学习迭代过程也应该有逐步降低动能的退火过程, 这表明在扩散模型中可能需要添加从大到小不同标准差的噪声, 从而实现系统的退火. 添加多尺度噪声的方法在扩散模型应用中的有效性目前也已被实验证明^[21]. 所以, 完整的扩散模型也应该包含两个迭代循环过程: 第一个迭代循环是高斯噪声标准差不断减小的退火过程; 第二个迭代循环是扩散演化过程.

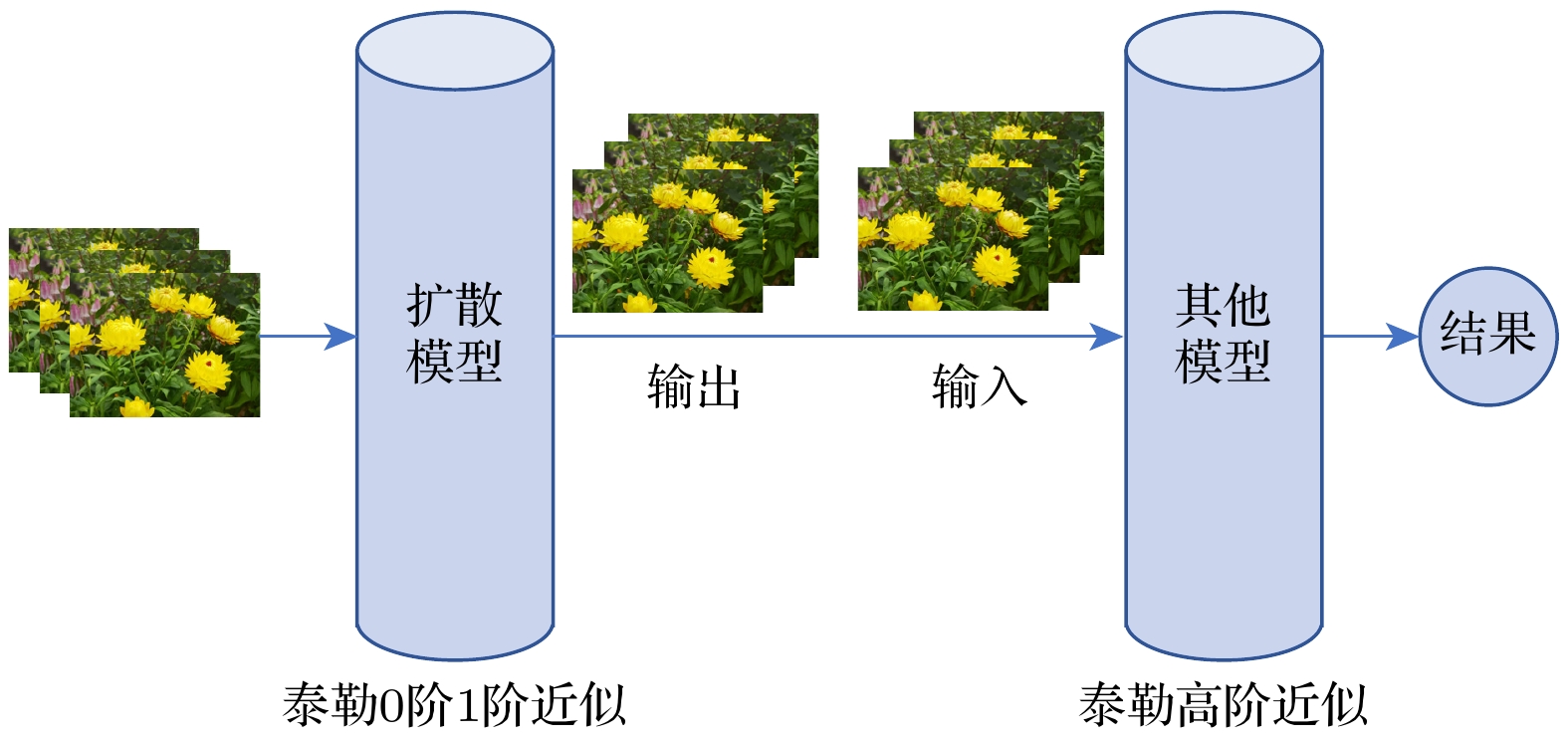
从量子动力学的角度和参数映射关系角度看扩散模型是基于目标函数0阶和1阶Taylor近似的生成式模型, 输入图像通过扩散模型后所生成的图像为经过0阶和1阶优化后的低阶推理结果, 因此, 可以将扩散模型作为其他模型数据预处理的通用模型(如图7). 原始图像首先经过扩散模型的处理, 再将扩散模型生成的输出结果作为其他模型的输入. 扩散模型在这里作为低阶推理过程完成图像的预处理, 其他模型作为高阶推理过程完成进一步推理过程. 这种新的推理结构将有可能提高整个模型的推理效果.

本文在Schrödinger方程的基础上建立了机器学习迭代过程的量子动力学方程, 并通过Wick转动将量子动力学方程与热动力学方程联系起来. 通过机器学习的量子动力学方程, 首先利用Wick转动和Taylor近似得到了机器学习的基本迭代过程; 其次, 利用方程的通解获得了机器学中常用的Softmax和Sigmoid函数, 从而在物理和数学上解释了Softmax和Sigmoid的动力学意义; 最后, 还采用量子动力学方程对扩散模型的基本迭代过程给出了动力学解释.

机器学习的量子动力学方程的建立, 将机器学习的迭代过程转化为含时偏微分方程, 实现了对机器学习过程的精确数学化描述, 从而可以充分利用量子力学和数学中成熟理论体系对机器学习展开研究. 本文的工作为建立机器学习的精确理论基础提供了一个新的研究视角和思路, 也有望为未来在量子计算机上实现人工智能算法提供理论依据^[22].