高级搜索

基于超构表面多通大容量完美矢量涡旋光束的产生及调控研究

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

张胜蓝, 田喜敏, 许军伟, 徐亚宁, 李亮, 刘杰龙. 基于超构表面多通大容量完美矢量涡旋光束的产生及调控研究[J]. 物理学报, 2025, 74(6): 064201-1. doi: 10.7498/aps.74.20241725
引用本文: 张胜蓝, 田喜敏, 许军伟, 徐亚宁, 李亮, 刘杰龙. 基于超构表面多通大容量完美矢量涡旋光束的产生及调控研究[J]. 物理学报, 2025, 74(6): 064201-1. doi: 10.7498/aps.74.20241725
shu
Shenglan ZHANG, Ximin TIAN, Junwei XU, Yaning XU, Liang LI, Jielong LIU. Generation and independent-manipulation of multi-channel high-capacity perfect vector vortex beams based on geometric metasurfaces[J]. Acta Physica Sinica, 2025, 74(6): 064201-1. doi: 10.7498/aps.74.20241725
Citation: Shenglan ZHANG, Ximin TIAN, Junwei XU, Yaning XU, Liang LI, Jielong LIU. Generation and independent-manipulation of multi-channel high-capacity perfect vector vortex beams based on geometric metasurfaces[J]. Acta Physica Sinica, 2025, 74(6): 064201-1. doi: 10.7498/aps.74.20241725
shu

基于超构表面多通大容量完美矢量涡旋光束的产生及调控研究

  • 郑州航空工业管理学院材料学院, 郑州　450046

    • 作者简介: 张胜蓝: 2016642879@qq.com .
    通讯作者: E-mail: xmtian007@zua.edu.cn.;  E-mail: xujunwei001@zua.edu.cn.; 

  • 中图分类号: 41.20.Jb

Generation and independent-manipulation of multi-channel high-capacity perfect vector vortex beams based on geometric metasurfaces

  • School of Materials Science and Engineering, Zhengzhou University of Aeronautics, Zhengzhou 450046, China

    • Corresponding authors: E-mail: xmtian007@zua.edu.cn.;  E-mail: xujunwei001@zua.edu.cn.; 

  • MSC: 41.20.Jb

  • 摘要: 完美矢量涡旋光束除具有螺旋相位、环状强度分布及非均匀偏振分布外, 其亮环半径及环宽度恒定, 不受拓扑荷数变化的影响, 且同时携带自旋角动量和轨道角动量, 因此在很多光学领域具有重要应用. 超构表面作为一种亚波长结构排列而成的平面光学器件, 能够精准调控电磁波的相位、偏振和振幅, 为集成化矢量光场调控器件的实现提供变革性解决方案. 然而, 现有超构表面在生成产生多通大容量、偏振和轨道角动量独立操控的完美矢量涡旋光束方面仍面临严峻挑战. 为此, 本文基于超构表面平台, 利用纯几何相位调制的自旋多路复用方案, 通过叠加两正交偏振完美涡旋光束, 实现了多通大容量完美矢量涡旋光束. 通过调控两正交偏振完美涡旋光束的初始相位差、振幅比及拓扑荷数, 实现了具备任意偏振阶次和偏振分布特性的完美矢量涡旋光束; 通过精心设计超构表面相位分布及光束传播路径, 生成了多重完美矢量涡旋光束阵列. 此外, 基于完美矢量涡旋光束偏振阶次和偏振态两个并行维度, 本文成功演示了一种兼具安全性高和强鲁棒性的光学信息加密方案. 该工作旨在建立一个超紧凑、稳健的平台, 以在中红外波段生成多通大容量完美矢量涡旋光束, 推动其在光学加密、粒子操控和量子光学等领域的应用.
    Abstract: Perfect vector vortex beams (PVVBs), which are characterized by spiral phase, donut-shaped intensity profile and inhomogeneous polarization of a light beam carrying spin angular momentum (SAM) and orbital angular momentum (OAM), have a constant bright ring radius and ring width which are unaffected by the changes of their carrying topological charge (TC), thus making them highly valuable in many optical fields. Metasurfaces, as planar optical devices composed of subwavelength nanostructures, can precisely control the phase, polarization, and amplitude of electromagnetic waves, providing a revolutionary solution for integrated vector field manipulation devices. However, existing metasurfaces still encounter significant challenges in generating high-capacity, polarization- and orbital angular momentum-independent controlled perfect vector vortex beams. In order to solve this problem, in this work a spin-multiplexing scheme based on pure geometric phase modulation on a metasurface platform is used to achieve high-capacity polarization- and OAM-independent controlled PVVBs. The metasurfaces with a combined phase profile of a spiral phase plate, an axicon, and a focusing (Fourier) lens are spatially encoded by rectangular Ge2Sb2Se4Te1 (GSST) nanopillar with various orientations on a CaF2 square substrate. When illuminated by circularly polarized light with opposite chirality, the metasurfaces can generate various perfect vector vortex beams (PVBs) with arbitrary topological charges. For linearly polarized incidence, the metasurface is employed to induce PVVBs by coherently superposing PVBs with spin-opposite OAM modes. The polarization states and polarization orders of the generated PVVBs can be flexibly customized by controlling the initial phase difference, amplitude ratio, and topological charges of the two orthogonal PVB components. Notably, through precisely designing the metasurface’s phase distribution and the propagation path of the generated beams, the space and polarization multiplexing can be realized in a compact manner of spatial PVVB arrays, significantly increasing both information channels and dimensions for the development of vortex communication capacity. With these findings, we demonstrate an innovative optical information encryption scheme by using a single metasurface to encode personalized polarization states and OAM in parallel channels embedded within multiple PVVBs. This work aims to establish an ultra-compact, robust platform for generating multi-channel high-capacity polarization- and OAM-independent controlled PVVBs in the mid-infrared range, and promote their applications in optical encryption, particle manipulation, and quantum optics.
  • 加载中

  • 图 1  (a)基于超构表面生成多通大容量PVVBs的效果示意图; (b) HyOPS模型; (c) 螺旋相位、锥透镜相位和双曲透镜相位叠加而成的超构表面相位剖面

    Figure 1.  (a) Schematic illustration of the metasurface-enabled generation of multi-channel high-capacity PVVBs; (b) the HyOPS model; (c) the phase profile of the metasurface obtained by combining the phases of a spiral phase plate, an axicon, and a hyperbolic metalens.

    下载: 全尺寸图片 幻灯片

    图 2  (a) 基于纯几何相位调制的自旋多路复用超构表面生成PVVB原理图; (b)最优单元结构在不同波长x-, y-LP光入射下的透射率(Txx, Tyy)和相移(ϕxx, ϕyy); (c) 超构原子在波长为4.4 μm x-LP、和y-LP光入射下产生的磁场Hy和Hx分布剖面图; (d) 当GSST纳米柱处于不同旋向角时, 最优单元结构在圆偏振光入射下的透射率和相移, 插图为纳米柱单元结构透视图和俯视图

    Figure 2.  (a) Operating principle for generating multi-channel high-capacity PVVBs by using a spin-multiplexed metasurface based on pure geometric phase modulation; (b) simulated transmission (Txx, Tyy) and phase shift (ϕxx, ϕyy) of the optimized unit cell under x- and y-polarized illumination at different wavelengths; (c) magnetic components Hy and Hx existing in GSST nanopillar excited by x-polarized and y-polarized incident light of λ = 4.4 μm; (d) calculated transmission and phase shift of the optimized unit cell under circularly polarized illumination as a function of the rotation angle of the anisotropic GSST nanopillars, with insets showing the perspective and top views of unit cells.

    下载: 全尺寸图片 幻灯片

    图 3  在x-LP光照射下, (a) 4种模式PVVBs在x-z平面上电场强度分布; (b)在焦平面上电场强度分布曲线; (c)在焦平面上亮环半径; (d)在z = 140, 200和260 μm三个横截面上的亮环半径; (e)在焦平面上的亮环宽度; (f)转化效率; (g)在HyOPS上位置分布; (h) x-LP光照射下, 4种模式PVVBs在不同偏振片下对应的电场强度分布, 斯托克斯参数(S0, S1, S2和S3)及偏振方向(Ω)

    Figure 3.  Under x-LP illumination, (a) the electric field intensity distributions of the four mode PVVBs in the x-z plane; (b) the intensity profiles at the focal plane; (c) the radii of the bright rings at the focal plane; (d) the radii of the bright rings at z = 140, 200 and 260 μm cross-sections; (e) the widths of the bright rings at the focal plane; (f) conversion efficiency; (g) their spatial distributions on the HyOPS; (h) under x-LP illumination, the electric field intensity distributions, Stokes parameters (S0, S1, S2 and S3) and polarization orientations (Ω) of the four mode PVVBs under different polarizers.

    下载: 全尺寸图片 幻灯片

    图 4  超构表面MF5在LCP光下生成RCP PVBs阵列的电场强度分布图(a)及在LP光下生成的32重PVVBs Ex分布图(b)和Ey分布图(c); (d)对应模式PVVBs的矢量场分布和偏振角度分布; (e) PVVBs代码表; (f) 编码方法和编码表; (g) 105个包含两字节的十六进制数序列; (h), (i)解密的文本信息

    Figure 4.  Electric field intensity distributions of the RCP PVB array generated by the metasurface MF5 under LCP illumination (a), and Ex (b) and Ey (c) intensity distributions of 32-fold PVVBs generated by the metasurface MF5 under LP illumination; (d) vector field distributions and polarization orientation of the corresponding mode PVVBs; (e) codebook of the PVVBs; (f) encoding method and the encoding diagram; (g) a sequence of 105 hexadecimal numbers consisting of two bytes; (h), (i) the decrypted text information.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  Mode 1—4 PVVBs对应的具体参数

    Table 1.  Specific parameters of the mode 1–4 PVVBs.

    ModeM∶Nlnlm(∆x, ∆y)/μmf/μm∆δ
    12∶1–11(0, 0)2000
    21∶2–33(0, 0)200π/2
    31∶13–3(0, 0)200π
    41∶1–66(0, 0)2003π/2
    下载: 导出CSV

    表 2  MF5的具体参数

    Table 2.  Specific parameters of the MF5.

    SCslnlm∆x/μm∆y/μmf/μm∆δ
    11–89–150350200π/15
    21/8–12–503502007π/15
    31/4–445035020010π/15
    41–881503502002π/15
    51/2–56–15025020015π/15
    61/2–66–502502006π/15
    71/8–11502502000
    81/8–2215025020014π/15
    91/4–33–1501502009π/15
    101/2–55–501502008π/15
    111/2–67501502005π/15
    121/8–2315015020013π/15
    131–78–150502003π/15
    141/4–34–505020012π/15
    151/4–45505020011π/15
    161–77150502004π/15
    171/8–11–150–5030012π/15
    181/4–44–50–503003π/15
    191/4–4550–503002π/15
    201/8–12150–503008π/15
    211/2–56–150–15030014π/15
    221/8–23–50–1503005π/15
    231/2–6650–1503006π/15
    241/2–55150–1503007π/15
    251–77–150–250300π/15
    261–78–50–2503004π/15
    271–8950–25030011π/15
    281/8–22150–25030014π/15
    291/4–33–150–35030010π/15
    301–88–50–35030015π/15
    311/2–6750–35030013π/15
    321/4–34150–3503009π/15
    下载: 导出CSV
  • [1] Guo Y H, Zhang S C, Pu M B, He Q, Jin J J, Xu M F, Zhang Y X, Gao P, Luo X G 2021 Light: Sci. Appl. 10 63 doi: 10.1038/s41377-021-00497-7
    [2] Shen Y J, Yang X L, Naidoo D, Fu X, Forbes A 2020 Optica 7 820 doi: 10.1364/OPTICA.382994
    [3] Liu Z X, Liu Y Y, Ke Y G, Liu Y C, Shu W X, Luo H L, Wen S C 2016 Photonics Res. 5 15 doi: 10.1364/PRJ.5.000015
    [4] Liu M Z, Huo P C, Zhu W Q, Zhang C, Zhang S, Song M W, Zhang S, Zhou Q W, Chen L, Lezec H 2021 Nat. Commun. 12 2230 doi: 10.1038/s41467-021-22462-z
    [5] Xu Y N, Tian X M, Xu J W, Zhang S L, Huang Y F, Li L, Liu J L, Xu K, Yu Z J, Li Z Y 2024 J. Phys. D: Appl. Phys. 57 425104 doi: 10.1088/1361-6463/ad6612
    [6] Ma Y B, Rui G H, Gu B, Cui Y P 2017 Sci. Rep. 7 14611 doi: 10.1038/s41598-017-14449-y
    [7] Shao W, Huang S J, Liu X P, Chen M S 2018 Opt. Commun. 427 545 doi: 10.1016/j.optcom.2018.06.079
    [8] Xu Y, Su X R, Chai Z, Li J L 2024 Laser Photon. Rev. 18 2300355 doi: 10.1002/lpor.202300355
    [9] Niv A A, Biener G, Kleiner V, Hasman E 2006 Opt. Express 14 4208 doi: 10.1364/OE.14.004208
    [10] Ostrovsky A S, Rickenstorff-Parrao C, Arrizón V 2013 Opt. Lett. 38 534 doi: 10.1364/OL.38.000534
    [11] Vaity P, Rusch L 2015 Opt. Lett. 40 597 doi: 10.1364/OL.40.000597
    [12] Li D L, Feng S T, Nie S P, Chang C L, Ma J, Yuan C J 2019 J. Appl. Phys. 125 073105 doi: 10.1063/1.5079850
    [13] Zou X J, Zheng G G, Yuan Q, Zang W B, Chen R, Li T Y, Li L, Wang S M, Wang Z L, Zhu S N 2020 PhotoniX 1 1 doi: 10.1186/s43074-020-00006-w
    [14] Zhang C Y, Zhang B F, Ge S K, Han C X, Wang S Z, Han Q Y, Gao W, Chu T S, Dong J, Zhang M D 2024 Opt. Express 32 31359 doi: 10.1364/OE.533691
    [15] Zhang X L, Gong Y H, Li M, Li H 2024 Opt. Express 32 8069 doi: 10.1364/OE.515968
    [16] Kim I, Ansari M A, Mehmood M Q, Kim W Q, Jang J, Zubair M, Kim Y K, Rho J 2020 Adv. Mater. 32 2004664 doi: 10.1002/adma.202004664
    [17] Huang Y F, Tian X M, Zhang S L, Xu Y N, Xu J W, Yu Z J, Jiang T, Li Z Y 2024 Opt. Lasers Eng. 183 108523 doi: 10.1016/j.optlaseng.2024.108523
    [18] He H R, Peng M Y, Cao G T, Li Y B, Liu H, Yang H 2024 Opt. Laser Technol. 180 111555 doi: 10.1016/j.optlastec.2024.111555
    [19] Liu Y C, Ke Y G, Zhou J X, Liu Y Y, Luo H L, Wen S C, Fan D Y 2017 Sci. Rep. 7 44096 doi: 10.1038/srep44096
    [20] Zhang Y C, Liu W W, Gao J, Yang X D 2018 Adv. Opt. Mater. 6 1701228 doi: 10.1002/adom.201701228
    [21] Tian S N, Qian, Z H, Guo H M 2022 Opt. Express 30 21808 doi: 10.1364/OE.461024
    [22] Liu Y, Zhou C X, Guo K L, Wei Z C, Liu H Z 2022 Opt. Express 30 30881 doi: 10.1364/OE.468616
    [23] Vogliardi A, Ruffato G, Bonaldo D, Zilio S D, Romanato F 2023 Opt. Lett. 48 4925 doi: 10.1364/OL.501239
    [24] Gu M N, Cheng C, Zhan Z J, Zhang Z H, Cui G S, Zhou Y X, Zeng X Y, Gao S, Choi D Y, Cheng C F 2024 ACS Photonics 11 204 doi: 10.1021/acsphotonics.3c01284
    [25] He J N, Wan M L, Zhang X P, Yuan S Q, Zhang L F, Wang J Q 2022 Opt. Express 30 4806 doi: 10.1364/OE.451218
    [26] Zhou T, Liu Q, Liu Y S, Zang X F 2020 Opt. Lett. 45 5941 doi: 10.1364/OL.404436
    [27] Huang K, Deng J, Leong H S, Yap S L K, Yang R B, Teng J H, Liu H 2019 Laser Photonics Rev. 13 1800289 doi: 10.1002/lpor.201800289
    [28] Xie J F, Guo H M, Zhuang S L, Hu J B 2021 Opt. Express 29 3081 doi: 10.1364/OE.413573
    [29] Zhang Z H, Li T, Jiao X F, Song G F, Xu Y 2020 Appl. Sci. 10 5716 doi: 10.3390/app10165716
  • 加载中
图( 5) 表( 2)
计量
  • 文章访问数:  49
  • HTML全文浏览数:  49
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-14
  • 刊出日期:  2025-03-20

基于超构表面多通大容量完美矢量涡旋光束的产生及调控研究

  • 收稿日期:  2024-12-14

摘要: 完美矢量涡旋光束除具有螺旋相位、环状强度分布及非均匀偏振分布外, 其亮环半径及环宽度恒定, 不受拓扑荷数变化的影响, 且同时携带自旋角动量和轨道角动量, 因此在很多光学领域具有重要应用. 超构表面作为一种亚波长结构排列而成的平面光学器件, 能够精准调控电磁波的相位、偏振和振幅, 为集成化矢量光场调控器件的实现提供变革性解决方案. 然而, 现有超构表面在生成产生多通大容量、偏振和轨道角动量独立操控的完美矢量涡旋光束方面仍面临严峻挑战. 为此, 本文基于超构表面平台, 利用纯几何相位调制的自旋多路复用方案, 通过叠加两正交偏振完美涡旋光束, 实现了多通大容量完美矢量涡旋光束. 通过调控两正交偏振完美涡旋光束的初始相位差、振幅比及拓扑荷数, 实现了具备任意偏振阶次和偏振分布特性的完美矢量涡旋光束; 通过精心设计超构表面相位分布及光束传播路径, 生成了多重完美矢量涡旋光束阵列. 此外, 基于完美矢量涡旋光束偏振阶次和偏振态两个并行维度, 本文成功演示了一种兼具安全性高和强鲁棒性的光学信息加密方案. 该工作旨在建立一个超紧凑、稳健的平台, 以在中红外波段生成多通大容量完美矢量涡旋光束, 推动其在光学加密、粒子操控和量子光学等领域的应用.

English Abstract

    全文HTML

    1.   引　言

    • 偏振和相位是光的固有特性, 灵活操纵这些特性可生成多种形式同时携带自旋角动量(spin angular momentum, SAM)和轨道角动量[1,2] (orbital angular momentum, OAM)的结构化光束. 光学涡旋光束(vortex beams, VBs), 作为一种典型结构化光束, 因其螺旋相位波前、环状强度分布及携带定量轨道角动量等特性, 吸引了众多研究者对其进行深入探索. 在光学涡旋广义存在形式中, 矢量涡旋光束(vector vortex beams, VVBs)因SAM和OAM相互作用而具有各向异性波面和偏振分布, 同时兼具涡旋光束和矢量光束特性. 对于具有不同偏振态与相位分布的矢量涡旋光束, 研究者们一般选择混合阶庞加莱球(hybrid-order poincaré sphere, HyOPS)对其进行表征[3,4], 其中南北极代表两正交圆偏振(circularly polarized, CP)涡旋光束, 球面上的点代表特定偏振态矢量涡旋光束. 相比于标量涡旋光束, 矢量涡旋光束具有更复杂的光场分布和波前结构, 在粒子操纵[5,6]、光通信[7]和量子信息[8]等领域具有重要应用.

      然而, 传统VVBs亮环半径及环宽度通常与光束所携带拓扑荷数(topological charge, TC)密切相关, 过大的拓扑荷数会导致涡旋光束中心相位奇点不稳, 强度分布明显畸变和扩散, 多模态复合传输和整体光束半径受限[9]. 2013年, Ostrovsky等[10]首次提出完美涡旋光束(perfect vortex beams, PVBs)的概念, 除具有螺旋相位及环状强度分布外, PVBs亮环半径及环宽度恒定, 不受拓扑荷数变化的影响, 且同时携带自旋角动量和轨道角动量. 2015 年, Vaity和Rusch [11]证实了对贝塞尔光束进行傅里叶变换可得到PVBs. 至此, 完美涡旋光束因其理想化且更独立的存在形式被人们广泛接受且应用到各个领域研究中. 实现矢量光场产生与调控的传统方法通常需要级联多个光学元件, 如螺旋相位板、偏振片、1/4波片、涡旋波片、空间光调制器等, 导致器件体积庞大, 缺乏灵活性, 不符合未来光子器件集成化需求. 此外, 不同光学元件之间的错位还会造成光学像差, 进而降低PVBs质量.

      超构表面, 一种由亚波长尺度超构原子周期性排列组成的二维平面结构, 能够对光场各种光学属性如振幅、偏振和相位等进行灵活高效的调控, 为光学器件小型化和集成化提供了崭新的平台, 目前已被广泛应用于成像[12,13]、光学隐身[14,15]、全息显示[16–18]及量子信息[8]等领域. 超构表面的快速发展, 为集成化矢量光场调控器件的实现提供了变革性解决方案. 如2017年, Liu等[19]通过级联3个具有不同相位机制的几何超构表面, 实现了单个PVBs. 2018年, Zhang等[20]将螺旋相位、锥透镜相位及傅里叶变换透镜相位融合进单个等离子体超构表面, 成功实现了三维聚焦PVBs. 2020年, Liu等[4]利用传输相位和几何相位共同设计超构表面, 实现了宽波段PVBs. 2022年, Tian等[21]通过单层几何相位超构表面实现了具有偏振旋转功能的PVBs. 2022年, Liu等[22]利用1/4波片超构原子构建超构表面, 实现了多通道PVBs. 完美矢量涡旋光束(perfect vector vortex beam, PVVBs)可由两正交偏振PVBs线性叠加而成, 因此同时携带自旋角动量和轨道角动量且偏振分布呈现各向异性特性. 2023年, Vogliardi等[23]利用单个超构表面, 通过巧妙设计成功实现了紧凑的单环PVVBs和双环PVVBs. Gu等[24]通过介质复合元胞超构表面实现了高效聚焦的高阶PVVBs. 然而, 由于设计机理的固有限制, 现有超构表面往往只能生成单一或少数PVBs或PVVBs, 光束集成度低、通道少, 且PVBs或PVVBs偏振和OAM难以实现多样化且独立调控. 如何突破现有设计机制的限制, 利用单一超构表面生成多通大容量、偏振和OAM独立调控的PVBs或PVVBs仍面临很大挑战.

      基于此, 本研究提出一种用于产生多通大容量、偏振和OAM独立操控PVVBs的全新方案. 该方案将螺旋相位、锥透镜相位及双曲聚焦相位集成到单一超构表面, 基于纯几何相位调制的自旋多路复用方案, 通过叠加两正交偏振PVBs, 实现了多通大容量PVVBs. 通过精准操控两正交偏振PVBs的初始相位差和振幅比, 可实现任意偏振态PVVBs; 通过调控两正交PVBs拓扑荷数, 可生成任意偏振阶次PVVBs. 为验证方案可行性, 本工作精心设计了两组超构表面: 第1组包含4个超构表面样品, 证明了所设计超构表面能够生成具备任意偏振阶次和偏振分布特性的PVVBs; 第2组为一个超构表面样品, 证明了通过精心设计超构表面相位分布及光束传播路径, 可在完全错开的聚焦平面上生成PVVBs阵列, 且每个PVVB具备特定偏振分布和偏振阶次. 此外, 作为概念性验证, 我们还设计演示了一种全新光学信息加密方案, 通过将偏振态和轨道角动量并行编码到多重PVVBs中, 实现了信息的多重加密. 该工作旨在建立一个超紧凑、稳健的超构表面平台, 以在中红外波段生成多通大容量PVVBs, 推动其在光学加密、粒子操控和量子光学等领域的应用.

    2.   基本原理及设计方案

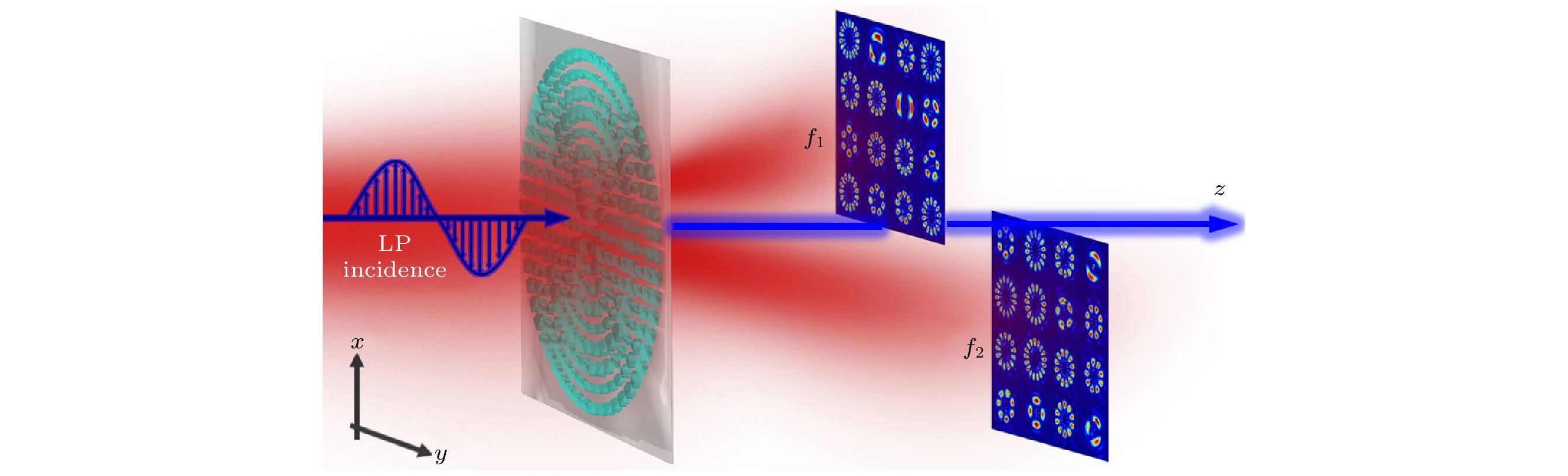
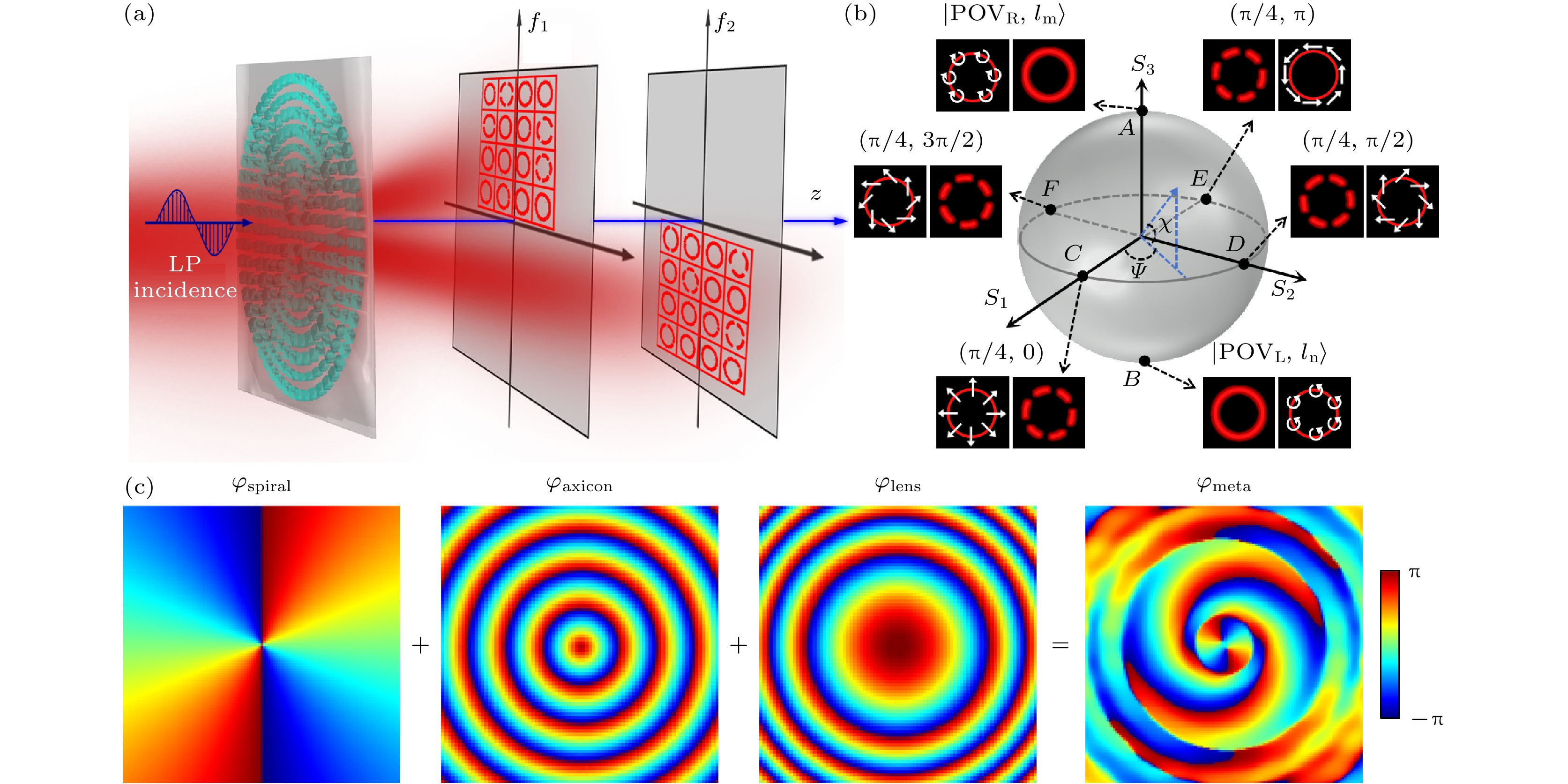
    • 图1(a)显示了利用超构表面生成多通大容量PVVBs示意图. 在线偏振光(linearly polarized light, LP light)照射下, 该超构表面能够生成多重携带个性化偏振态和偏振阶次的PVVBs, 且这些PVVBs通过预设的三维空间传播路径分布到两个完全错开的焦平面上(一个焦平面占据一二象限, 焦距为f1; 另一个焦平面占据三四象限, 焦距为f2). 图1(b)是混合阶庞加莱球, 用来表征相位和偏振各向异性的PVVBs空间分布, 其中南北极代表 两正交圆偏振PVBs, 其余点代表特定偏振分布 的PVVB. PVVB可由两正交圆偏振PVBs线性叠加而成:

      式中$\left| {{D_{m{, }n}}} \right\rangle $代表PVVB; $\left| {{\text{PV}}{{\text{B}}_{\text{R}}}, {l_m}} \right\rangle $和$\left| {{\text{PV}}{{\text{B}}_{\text{L}}}, {l_n}} \right\rangle $代表右旋和左旋圆偏振PVBs; lm, ln是各自携带的拓扑荷数; cos(χ/2)与sin(χ/2)代表两正交圆偏振PVBs振幅, ψ是两正交圆偏振PVBs之间的相位差, 其中χ∈[0, π], ψ∈[0, 2π].

      完美涡旋光束是一种光束半径与拓扑电荷无关的环形涡旋光束, 往往由高斯光束依次经过螺旋相位板、锥透镜和傅里叶变换透镜(或双曲聚焦透镜)而获得. 因此, 利用单个超构表面获取完美涡旋光束, 其相位需同时满足螺旋相位、锥透镜相位和双曲聚焦透镜相位, 如图1(c)所示. 对于自旋复用超构表面, 当右旋圆偏振光(right-handed circular polarized light, RCP light)照射时, 生成的左旋圆偏振PVB相位分布为[25]

      式中(xL, yL, f )为左旋圆偏振PVB焦点位置, λ为入射波长, ln为左旋圆偏振PVB拓扑荷数, $ \vartheta = \arctan (y/x) $为方位角, 参数d为锥透镜周期, ∆δ表示左旋和右旋圆偏振PVBs分量间初始相位差. 通过调控参数d可控制PVBs亮环半径大小; 通过调控初始相位差∆δ, 可使生成的PVVB呈现不同的偏振分布.

      当左旋圆偏振光(left-handed circular polarized light, LCP light) 照射该自旋复用超构表面时, 生成的右旋圆偏振PVB相位分布为

      式中(xR, yR, f )为右旋圆偏振PVB焦点位置, lm表示右旋圆偏振PVB拓扑荷数. 由于PVVB是由两正交圆偏振PVBs叠加而成的, 欲获得PVVB, 自旋复用超构表面须同时调控LCP和RCP入射光, 此时超构表面总相位φtotal可表示为[26]

      式中$x_{\mathrm{L}} = x_{\mathrm{R}} = \Delta x,~ y_{\mathrm{L}} = y_{\mathrm{R}} = \Delta y $.

      欲获得多重PVVBs, 自旋多路复用超构表面总相位Φtotal可表示为[26]

      式中Ms和Ns对应于两正交圆偏振PVBs幅值; S为正整数, 表示自旋复用阶数; Cs是分配给PVVBs的振幅比重因子. 需要说明的是: 1)当Ms = Ns即两正交圆偏振PVBs振幅相等叠加时, 生成圆偏振PVVB, 对应HyOPS赤道上的点, 当Ms ≠ Ns即两正交圆偏振PVBs振幅不等叠加时, 生成椭圆偏振PVVB, 对应HyOPS南北极与赤道之间的点; 2)通过调控振幅比重因子Cs值, 可使生成的多重PVVBs亮环强度保持大致相同; 3)通过设计两正交圆偏振PVBs焦点位置, 可调控PVVB空间传播路径, 生成多通大容量PVVBs, 如图1(a)所示PVVBs阵列.

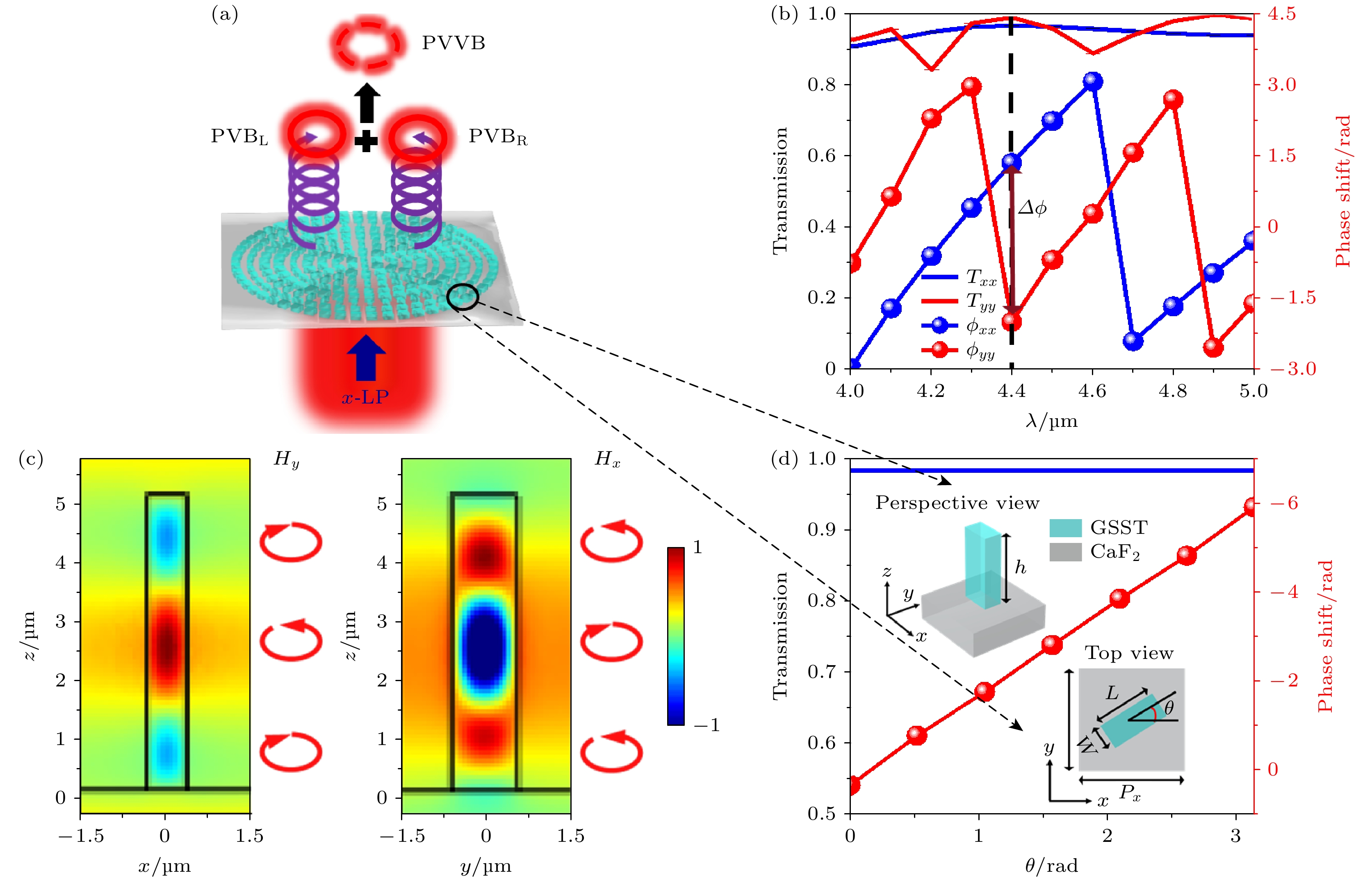
      本文基于纯几何相位调制的自旋多路复用超构表面生成多通大容量PVVBs. 当RCP光入射时, 生成左旋圆偏振PVB; 当LCP光入射时, 生成右旋圆偏振PVB; 当LP光入射时, RCP和LCP PVBs叠加即会生成PVVB, 如图2(a)所示. 图2(d)插图为所设计超构表面单元结构示意图, 单元结构(超构原子)由排列在CaF2方形衬底上各向异性Ge2Sb2Se4Te1(GSST)纳米柱组成, 其中超构原子周期Px = Py, GSST纳米柱面内尺寸为L (长度)和W (宽度), 高为h, 面内旋转角$ \theta = {\varphi _{{\text{total}}}}\left( {{\varPhi _{{\text{total}}}}} \right)/2 $. 为提高整个超构表面器件透射率, 超构表面需由半波片功能的超构原子构成, 即满足$ |{\phi _{xx}} - {\phi _{yy}}| \approx \pi $, 同时保持$ {T_{xx}} \approx {T_{yy}} \approx 1 $, ϕxx和ϕyy表示超构原子在线偏振光照射下沿长轴和短轴的透射相位, Txx和Tyy表示对应的透射率. 为验证所提方案可行性, 本文采用有限元法对超构原子进行了优化, 得到当入射波长λ = 4.4 μm, 超构原子尺寸为Px = Py = 3 μm, L = 1.1 μm, W = 0.65 μm及h = 4.8 μm时, 超构原子可实现半波片性能, 即当圆偏振光入射时, 超构原子可将其完全转化为相反手性的圆偏振透射光, 如图2(d)所示. 图2(d)还给出了当圆偏振光照射超构原子, GSST纳米柱旋转角从0变到π时, 相反手性圆偏振透射光相位从0变到2π, 振幅始终保持~1, 这进一步证实所选单元结构可实现半波片性能. 为了揭示该超构原子实现高偏振转换效率的内在机制, 图2(c)给出了该超构原子在波长λ = 4.4 μm, x线偏振(x-LP)和y线偏振(y-LP)光入射时的磁场Hy和Hx分布剖面图. 可观察到, 对于x-LP光入射, Hy磁场出现3个顺时针和逆时针交替的环形位移电流, 这对应于沿z轴垂直排列的3个反平行磁偶极子; 而对于y-LP光入射, Hx磁场出现3个沿z轴方向的反平行磁偶极子; 这种具有相反平行磁偶极子的类波导模式会产生π相位延迟, 从而使该纳米柱具有高效半波片特性[27].

    3.   结果与讨论

      3.1.   超构表面生成单模PVVB

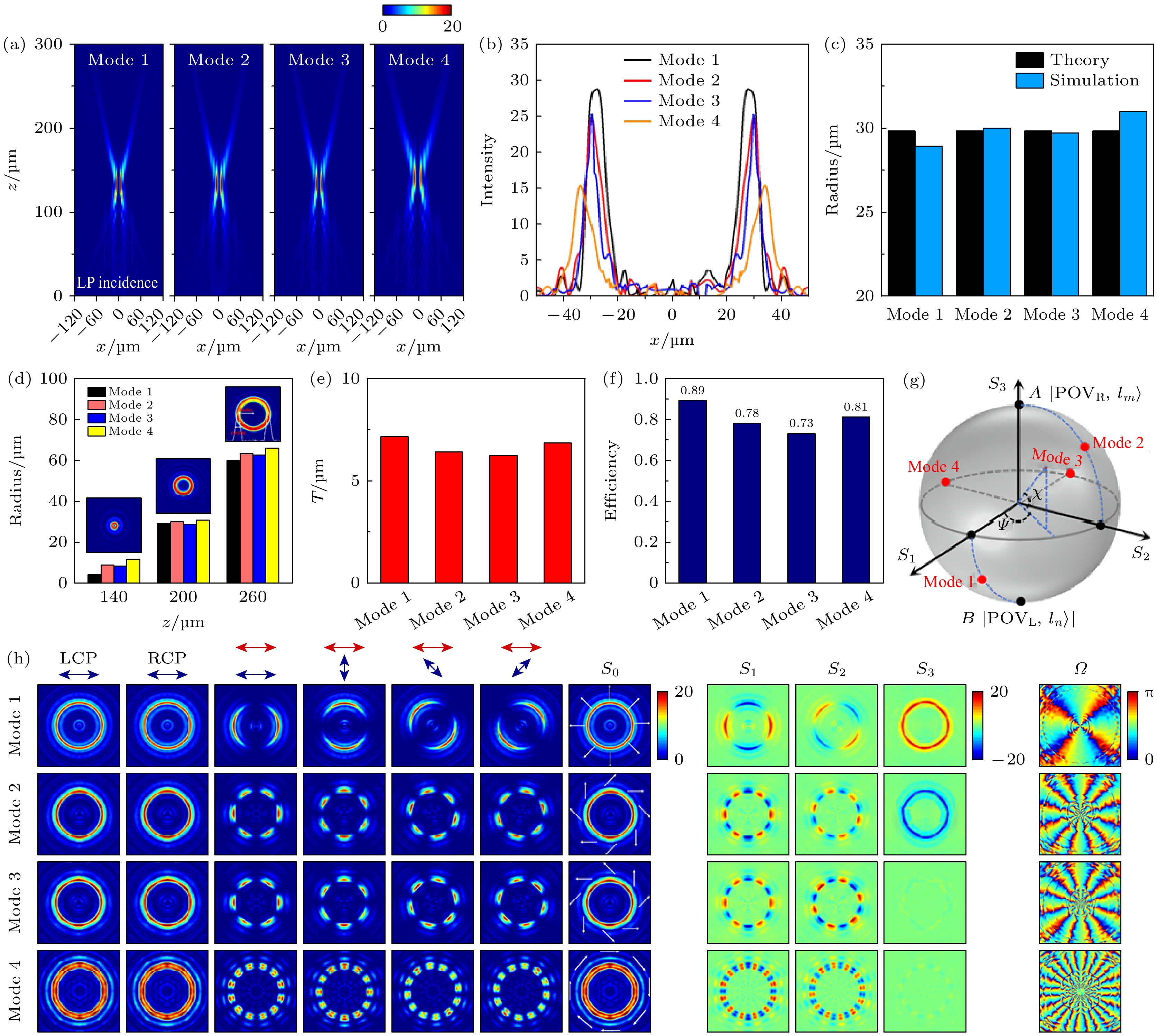
    • 本文首先设计了4个超构表面样品(MF1, MF2, MF3和MF4), 用以产生4个不同模式PVVBs (mode 1, mode 2, mode 3和mode 4). 4个超构表面设计参数见表1. 将设计参数代入(2)式—(5)式, 可推导出每个超构原子的取向角, 进而建立超构表面. 为验证所设计方法的可行性, 本文采用FDTD构建超构表面, 并对其性能进行了模拟仿真, 如图3所示. 图3(a)是4个超构表面样品在波长λ = 4.4 μm水平线偏振光照射下, 生成的PVVBs在x -z平面上的电场强度分布. 可以看到, 4种模式PVVBs在传输空间场强轮廓几乎完全相同, 与偏振阶次和拓扑荷数均无关, 说明生成了完美涡旋光束. 图3(b)是4种模式PVVBs在z = 200 μm横截面电场强度分布曲线. 两峰值间距可表示PVVBs亮环直径大小, 可得4种模式PVVBs亮环半径分别为: R1 = 27 μm, R2 = 28.4 μm, R3 = 29 μm 和R4 = 31.2 μm, 与设计理论半径值$ {R}_{1—4}= f\times NA=f\lambda /d=\text{ }29.3\text{ μm} $基本相符, 如图3(c)所示. 图3(d)是4种模式PVVBs沿z = 140 μm和z = 260 μm两个横截面的亮环半径. 可看到, 4种模式PVVBs亮环半径在传输过程中保持基本一致. 图3(e)给出了4种模式PVVBs在焦距z = 200 μm处亮环宽度, 其被定义为PVVBs电场强度分布曲线每个峰值半高全宽(full width at half-maximum, FWHM). 可看到, 4种模式PVVBs亮环宽度基本相同, 与偏振阶次和拓扑荷数均无关. 因此, 通过精心设计, 所设计超构表面在线偏振光入射下可生成不同模式的PVVBs, 且不同模式的PVVBs亮环半径和环宽均与偏振阶次和拓扑荷数无关. 转化效率可有效衡量PVVB光束发生器的性能, 其被定义为亮环强度(在焦平面上, 半径为3倍FWHM的圆上的电场强度)与入射光束强度的比值[28,29]. 如图3(f)所示, 在设计波长λ = 4.4 μm时, 4种模式的PVVBs转化效率均保持在73%以上, 其中mode 1 PVVB的转化效率更是高达89%. 这充分说明了所设计超构表面具有出色的高效转化性能.

      为确定偏振态, 本文采用不同偏振器捕获4种模式PVVBs在聚焦平面上场强分布, 如图3(h)所示. 在x -LP光照射下, 在出射端捕获的左旋或右旋偏振PVBs电场均呈环状场强分布, 且半径大小近似相等(图3(h)1-2列); 当采用水平(x -)、垂直(y-)、对角线(π/4)和反对角线(3π/4)方向的线偏振器捕获时, 4种模式PVVBs亮环轮廓大致相等, 但呈现出与线偏振器相关的各向异性偏振分布和特定数量光斑花瓣数(图3(h) 3—6列). PVVBs偏振阶次描述了在一个往返周期内光束偏振的旋转次数, 可表示为$ p = {\text{ }}({l_m} - {l_n})/2 $, 其中lm和ln表示左旋和右旋偏振PVBs的拓扑荷数. 经验证实, 使用线性偏振器进行PVVBs电场捕获时, 光斑花瓣数等于2倍偏振阶次$ \left| p \right| $. 通过观察, 4种模式PVVBs光斑花瓣数分别为2, 6, 6和12, 故偏振阶次$ \left| p \right| $为1, 3, 3和6, 与所设计左旋和右旋PVBs分量的拓扑荷数完全对应. 为进一步确定4种模式PVVBs偏振态, 图3(h)还给出了相应Stokes参数(S0, S1, S2和S3)分布和偏振方向(Ω)分布. 其中$ {S}_{0}={I}_{\text{L}}+{I}_{\text{R}}, {S}_{1}={I}_{x}-{I}_{y}, {S}_{2}={I}_{\pi /4}-{I}_{3\pi /4} $和$ {S_3} = {I_{\text{L}}}-{I_{\text{R}}} $, IL, IR, Ix, Iy, Iπ/4 和 I3π/4 分别代表PVVBs的 LCP, RCP, x-, y-, π/4 和3π/4分量场强. 由图3(h)可知, 参数S1和S2均有偶数个光斑花瓣, 且环状光斑轮廓均由最大和最小强度的光斑花瓣依次交替组成, 最大和最小强度的光斑花瓣数均为$ 2\left| p \right| $个. 参数S3反映了PVVBs是否由等量LCP和RCP PVBs分量叠加而成. 由图3(h)可知, mode 1和mode 2 PVVBs Stokes参数S3 ≠ 0, 表明mode 1和mode 2 PVVBs由不等LCP和RCP PVBs叠加而成, 为椭圆偏振特性, 分别对应HyOPS上半球面和下半球面上的点; 而mode 3和mode 4 PVVBs Stokes参数S3 = 0, 表明组成mode 3和mode 4 PVVBs的LCP和RCP PVBs权重相等, 表现为圆偏振特性, 对应于HyOPS赤道上的点. 偏振角度$ \varOmega = \arctan (S_2/S_1)/2$, 反映PVVBs偏振态. 经计算可得, 4种模式PVVBs偏振角度依次为0, π/2, π和3π/2, 对应HyOPS面上4个不同位置, 如图3(g)所示. 总之, 通过精心设计超构表面结构, 可生成具备任意偏振阶次和偏振分布特性的完美矢量涡旋光束.

      • 3.2.   基于超构表面生成PVVB阵列

    • 基于上述研究, 我们扩展了超构表面的功能, 设计出基于纯PB相位调制的超构表面样品MF5, 不仅可同时生成多重(32重) PVVBs, 而且还可精准调控每个PVVB偏振态和偏振阶次. MF5所需相位可由(5)式得到, 其中入射波长λ = 4.4 μm, 自旋多路复用阶数S = 32, 组成PVVBs的两正交偏振PVBs分量振幅比均为$M_{1—32} $∶$N_{1—32} $ = 1∶1. 为确保生成的32重PVVBs具备特定的偏振阶次和偏振分布, 且能在两个完全错开的焦平面以4×4矩阵形式排列, 我们对相关参数, 包括焦斑位置$ (\Delta x, \text{ }\Delta y, f) $、振幅比重因子Cs, 左旋和右旋偏振PVBs拓扑荷数ln和lm, 及初始相位差∆δs进行精心设置, 如表2所列. 同时为保证32重PVVBs亮环半径一致(R ≈ 30 μm), 对参数ds进行调整; 第1个焦平面上( f = 200 μm) 16重PVVBs对应$ {d_{1—16}} = \lambda {f_{1—16}}/R \approx 4.4 \times 200/30 = 29.33\text{ μm} $, 第2个焦平面上( f = 300 μm) 16重PVVBs对应$ {d_{17—32}} = \lambda {f_{17—32}}/R \approx 4.4 \times 300/30 = 44\text{ μm} $ .

      图4(a)为在LCP 光照射下, MF5在两个焦平面上生成的RCP PVBs阵列场分布图. 可观察到这些PVBs亮环半径和环宽基本一致. 图4(b), (c)是在 x-LP光入射下, MF5生成的32重PVVBs Ex和Ey分量场分布图, 可观察到这些PVVBs亮环轮廓仍保持基本一致, 但却由不同数量花瓣状光斑围绕而成, 且光斑分布不同, 说明这32重PVVBs偏振阶次不同且具备矢量特性. 通过计数花瓣状光斑数量, 可知模拟结果与理论设置完全吻合. 值得一提的是, Ex或Ey场分布图中某些PVVBs光斑数相同, 但光斑分布不同, 如图4(c)所示, 说明这些PVVBs具有相同偏振阶次和不同偏振态. 图4(d)还给出了对应模式PVVBs的矢量场分布和偏振角度分布. 可知, 位于f = 200 μm焦平面上的为一阶径向偏振分布PVVB, 位于f = 300 μm焦平面上的为一阶横向偏振分布PVVB.

      上述结果证明可在不同位置定制任意偏振分布和偏振阶次PVVBs, 且每个PVVB可独立调控, 这为光学信息传输提供了一种新加密方法. 利用PVVBs偏振态(偏振角度Ω)和偏振阶次(p)两个并行维度, 可编码出各种包含两个字节的十六进制数, 其中偏振方向Ω代表第1个字节, 偏振阶次p代表第2个字节, 因此每个PVVB代表一个包含两个字节的十六进制数. 通过设计携带n1个不同Ω值和n2个不同p值的多重PVVBs, 理论上可编码出n1×n2个包含两个字节的十六进制数. 为验证该加密方法的可行性, 图4(e)给出了包含两个字节十六进制数的编码表. 为简单起见, 偏振方向Ω范围设置为0—π, 步长为π/15, 代表十六进制数第1个字节0到F; 偏振阶次p范围设置为1—8.5, 步长为0.5, 代表十六进制数第2个字节0到F, 将偏振方向Ω和偏振阶次p任意组合, 可得到256个包含两个字节的十六进制数. MF5产生的32重PVVBs可代表32个不同的包含两个字节的十六进制数. 对这32个十六进制数值进行编码, 可覆盖标准键盘上26个英文字母和6个功能键, 如图4(f)所示. 理论上, 上述编码方法可支持任何文本信息的加密和传输, 在信息安全和通信领域具备鲁棒适用性和通用性.

      作为概念性验证, 图4(g), (h) 演示了利用上述编码方法进行信息加密与传输. 用户1将明文转换为多个包含两个字节的十六进制数的密文(图4(g)所示), 并将密文、精心设计的超构表面样品(加密信息载体)及线偏振器(密钥)一并发送给用户2. 用户2收到后, 利用波长为4.4 μm的x - LP光照射超构表面样品, 用线偏振器捕获两个焦平面上PVVBs阵列场分布(如图4(b)所示), 通过分析每个PVVBs偏振方向和偏振阶次, 得到32个包含两个字节的十六进制数, 对照如图4(f)所示的代码表, 可轻松破译每个十六进制数对应的具体加密信息. 根据双方共享的密码本, 用户2可轻松地将接收到的密文破译成文本信息, 如图4(h), (i)所示. 这种将光的轨道角动量和偏振特性通过并行通道同时整合到 PVVBs 阵列的加密和解密过程, 可有效隐藏被加密的信息, 避免信息外泄, 极大地增强了光学信息加密系统的安全性. 任何人想获得加密信息都需要同时具备加密信息载体(超构表面样品), 定制化密钥(线偏振片), 字符编码系统和密码本. 即使某人非法获得了加密信息载体和密钥, 并获得PVVBs阵列的偏振阶次和偏振角度, 但由于密码本和字符编码系统是定制化的, 也无法准确获取被加密的明文信息. 这种定制化的密码本和字符编码系统进一步增强了该光学信息加密系统的安全性.

    4.   总　结

    • 综上所述, 本文提出并验证了基于纯PB相位调制的单层全介质超构表面在中红外波段可生成多通大容量PVVBs, 且每个PVVB可独立调控, 互不干扰. PVVBs是由两正交圆偏振PVBs空间叠加而成的, 通过调控两PVBs的轨道角动量, 可实现任意偏振阶次的PVVBs; 通过调整两PVBs分量之间的相位差和振幅比, PVVBs偏振态可覆盖整个庞加莱球面. 此外, 基于PVVBs偏振阶次和偏振态两个并行维度, 本文实现了光信息加密的概念性演示. 这项工作为利用超紧凑平面纳米光子元件实现结构化光束的高效生成与控制, 并促进其在光通信、光加密、光数据存储和量子信息等领域应用奠定了基础. 需要指出的是, 这种基于纯PB相位调制的单层全介质超构表面生成多通大容量PVVBs的技术除了针对中红外单一波长外, 利用纯PB相位固有的宽带属性, 还可拓展至整个可见光波段乃至更宽的光谱范围内, 实现多光谱多通大容量PVVBs阵列; 且由于每个PVVB可独立调控, 互不干扰, 通过数学化手段还可调控PVVBs三维传输轨迹, 进一步提高集成度和信道容量; 此外, 这项技术还可与其他光学元件如全光纤、微光学阵列等进行集成, 形成更加紧凑高效的光学系统, 为利用结构化光束在其他领域如光微操作、三维光显示、光传感、光成像等方面的应用开辟新的可能性.

    参考文献 (29)

目录

/

返回文章
返回