-
自旋电子学作为一个新兴的跨学科研究领域, 结合了电子的电荷和自旋属性, 展现出独特的磁学和电学性质, 具有广泛的应用潜力, 尤其在信息存储、量子计算和磁性传感器等领域[1–3]. 近年来, 随着技术的进步, 超快自旋动力学研究成为了自旋电子学的重要前沿之一[4–7]. 超短激光脉冲引发的超快退磁、自旋输运、太赫兹发射提供了对磁性材料进行精确控制和探测的可能性, 为理解和操纵自旋流的输运过程提供了新的视角[8–13]. 另一方面, 自旋阀结构由于其磁性层之间的相互作用而展示出显著的磁电阻效应, 已经成为研究自旋输运和磁调控的理想平台[14,15]. 通过外部电流的调控, 研究人员能够操控自旋阀的磁性结构, 实现高效的自旋注入与翻转. 然而, 传统的电流驱动机制通常依赖于较长的时间周期, 往往限制了自旋动力学的实时操控能力[16].
飞秒激光脉冲作为一种极为强烈且时间尺度极短的外部调控方式, 为超快磁调控的研究开辟了新方向[17,18]. 在激光激发的自旋阀结构中, 激光脉冲能够在很短的时间内引起强烈的非平衡电子激发, 推动热电子的自旋极化转移, 进而在层间铁磁层产生超快磁动力学[19]. Rudolf等[20]利用极紫外的高次谐波探测了激光诱导Ni/Ru/Fe自旋阀结构的超快自旋动力学, 利用Ni和Fe层的铁磁或者反铁磁耦合在空间上分离其自旋动力学. 实验结果显示两个磁性层的超快磁动力学取决于其初始磁化方向的相对排列: 当Ni层和Fe层的磁化方向平行于初始方向时, 激光激发后Ni层超快退磁的同时会迅速增强Fe层的磁化强度; 而如果Fe层的初始磁化方向与Ni层反平行, 则其磁化强度会发生快速降低, 他们首次发现在该体系中超扩散自旋流参与飞秒时间尺度的自旋动力学. 随后, Turgut等[21]在相同自旋阀结构下考虑多种间隔层材料, 在Ta和W作为间隔层时, Fe层的磁化增强消失, 与Ni层同为退磁现象, 表明这些材料的自旋扩散长度较短, 导致层间自旋输运对磁化动力学的贡献减小. 不仅是金属间隔层可以产生层间自旋转移, 何为等[22]在CoFeB/MgO/CoFeB磁性隧道结中也发现了激光诱导隧穿自旋流的产生, 通过操纵热电子隧穿电流, 可以有效地控制磁性隧道结中的超快退磁过程. 这种激光诱导的超快自旋输运不仅具有比传统电流更小的时间间隔, 而且能够在纳米尺度内调节材料的磁动力学行为, 从而推动自旋电子学在高速信息处理与存储领域的应用发展.
尽管如此, 激光诱导超快磁调控仍面临许多挑战, 超快自旋流输运机制仍然存在诸多未解之谜[23,24]. 例如, Schellekens等[25]基于时间分辨磁光克尔效应测量, 研究了与之前研究类似自旋阀结构中的超快磁动力学. 他们发现, 尽管超扩散自旋流的确会对超快退磁有显著贡献, 但实验结果并不能完全重复出Rudolf等[20]观察到的Fe层瞬态磁化增强. 此外, Eschenlohr等[26]在其研究的激光强度范围内也未观察到相应的磁化增强, 并强调需要进一步的研究来优化样品设计, 深入理解界面在自旋输运中的作用. 最近, Stamm等[27]利用元素分辨的X射线光谱学对激光诱导Ni/Ru/Fe结构进行了定量测量, 对比Ni层和Fe层在不同磁化方向排列下Fe层的退磁程度, 发现退磁差别在饱和磁矩的(4.1±1.9)%, 即相对差别在24%左右, 证实了在磁化方向反平行排列下Fe层的退磁增强来源于Ni层中产生的热电子自旋流输运到Fe层中.
综上所述, 目前实验上已经对激光诱导自旋阀结构的超快自旋动力学进行了一系列探索, 但是实验结果差异较大, 且对超快热电子输运的理解仍未达成共识. 此外, 关于理论方面的研究也较为匮乏, 特别是中间层厚度、自旋衰减长度、激光吸收率等因素对层间自旋输运的影响缺乏系统性的理论分析, 亟需确定在哪些条件下可以实现最大程度的自旋转移. 本文基于超扩散自旋输运理论, 针对Ni/Ru/Fe自旋阀体系中超快自旋动力学进行了详细研究, 如图1所示. 首先, 重复出最近实验中铁磁层在不同磁化排列下的退磁差别, 并通过调节间隔层厚度, 揭示了超快自旋输运在磁动力学中的重要作用. 同时, 我们还确定了超扩散自旋流在Ru层中的自旋衰减长度. 进一步地, 通过控制激光的薄膜吸收, 得到了能够引起Fe层瞬态磁化增强的条件. 最后, 提出了一种可能的优化方案, 为激光诱导自旋阀结构在超快磁调控领域的研究提供了有力的理论支持.
-
本文采用超扩散自旋输运模型进行相关计算, 该模型成功地解释了飞秒激光脉冲诱导铁磁双层膜的超快退磁实验结果[28]. 当铁磁金属受到激光脉冲照射时, 电子吸收能量, 从费米能级(EF)以下的占据态跃迁到EF以上的能带, 成为非平衡的热电子. 这些非平衡电子的输运性质(如寿命和群速度)受到材料能带结构以及其在磁性金属中自旋取向的影响. 在Fe等铁磁材料中, 1.5 eV的光子将自旋向上3d电子激发到未占据的4s能带, 而自旋向下3d电子则跃迁至其他未占据的3d能带. 由于4s电子的群速度明显高于3d电子, 使得热电子展现出自旋依赖的速度, 这一特性最终导致了由高能热电子携带的自旋极化电流出现. 热电子的扩散还受到声子、杂质及电子间相互作用散射机制的影响. 散射类型分为弹性散射和非弹性散射两种: 弹性散射改变电子的动量但保持其能量, 而非弹性散射会导致电子的能量损失. 非弹性散射中损失的能量可传递给其他电子, 将其激发到更高的能量状态, 从而引发电子的级联效应, 促进热电子的输运.
超扩散自旋输运模型的核心方程为[28]
$ {n}_{\sigma }(E, z, t) $ 表示具有自旋$ \sigma $ 、能量E、位置z和时间t的非平衡热电子的密度. 热电子的寿命用$ {\tau }_{\sigma }(E, z) $ 表示, 该寿命由具体材料的性质决定. 有效源项$ {S}_{\sigma }^{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}}(E, z, t) $ 考虑了被散射电子和新激发电子的贡献. 算符$ \widehat{\phi } $ 和$ \widehat{I} $ 分别代表电子流算符和单位算符. 通过数值求解上述方程可以得到每个位置处电子密度随时间的变化规律. 其中, 时间依赖的磁化强度定义为自旋向上与自旋向下电子密度之差, 即$ {n}_{\sigma }^{{\mathrm{o}}{\mathrm{c}}{\mathrm{c}}}\left(z, t\right) $ 表示费米能级以下自旋为$ \sigma $ 的占据态电子密度, 这些电子的移动性远低于费米能级以上的非平衡电子, 因此它们对自旋流的贡献可以忽略不计. 自旋流密度的表达式被定义为自旋向上和自旋向下电子流密度的差, 即 -
本研究选择Ni(5)/Ru(dRu)/Fe(4)三层膜结构作为研究对象, 其中括号内数字单位为纳米, dRu = 1, 1.5, 2 nm, 与之前实验研究体系相一致[20,26,27]. 激发激光脉冲采用高斯函数进行建模, 波长为800 nm (1.5 eV), 半峰宽为30 fs, 脉冲的最大振幅在t = 0 fs时. 我们根据Stamm等[27]报道的数据设置了Ni层和Fe层的相对激光脉冲吸收率, 即A(Ni)/A(Fe) = 1.47, 并假定自旋向上和自旋向下的激发电子数相等. 在数值求解中, 非平衡热电子的能量范围从EF到EF + 1.5 eV被离散化, 能量间隔为0.125 eV. 空间网格的间隔设定为0.5 nm, 时间步长为1 fs. 激发电子自旋和能量依赖的寿命和速度可以通过基于第一性原理的多体计算得到, 相关数据已经在Zhukov等[29,30] 研究中得到了阐述. 所使用的数值计算方法也已经在之前的研究中详尽描述[31]. 为了确保普适性, 我们设定电子散射的跃迁概率与先前的研究一致[32,33].
-
首先, 保持与先前实验相同的材料厚度和激发比例, 计算Ni/Ru/Fe体系在铁磁层初始磁化方向分别为层间平行和反平行时, 激光脉冲激发后磁化强度相对于饱和磁矩变化量的时间演化关系, 如图2(a)和图2(b)所示, 并以磁化方向为反平行排列的最大磁化变化量为基准进行归一化. 为表征退磁差别, 我们使用相对变化率进行描述, 量化公式为
其中
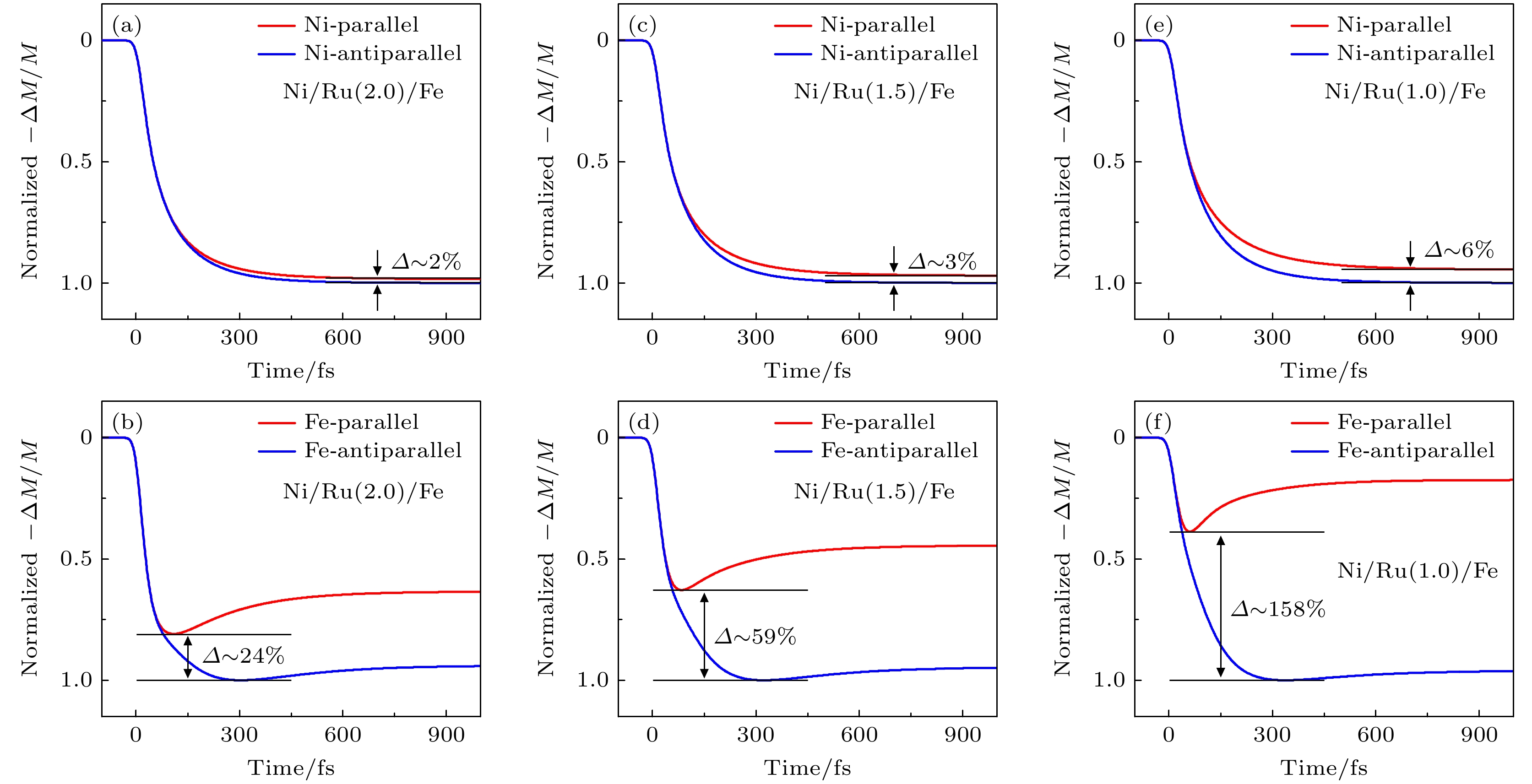
$ {(-\Delta M/M)}_{{\mathrm{P}}/{\mathrm{A}}{\mathrm{P}}} $ 为平行/反平行排列时的最大磁化变化量. 可以看到, Ni层和Fe层都表现出超快退磁现象. 特别地, Ni层最大退磁变化量在平行和反平行两种情况下的相对差别仅有$ \varDelta \sim 2{\text{%}} $ , 表明Fe层产生的自旋流对Ni层的影响较小. 相反, Fe层的最大退磁变化量在两个磁化方向下的差别达到$ \varDelta \sim 24{\text{%}} $ , 这与Stamm等[27]的实验结果相一致, 证实了Ni层产生的热电子自旋输运对Fe层磁化动力学的显著贡献. 此外, 可以看到Fe层的退磁时间也存在差别, 在平行排列下, Fe层最大退磁时间在t = 110 fs, 而在反平行排列下则为t = 304 fs, 这一明显的退磁延迟主要是源于Ni层产生的热电子在层间自旋输运时所消耗的时间. 总体上看, 两个磁性层磁化方向在平行排列时, 自旋极化热电子注入到Fe层时由于其自身自旋极化方向与Fe层相同, 从而阻止了退磁过程, 减弱其最大退磁程度, 同时使退磁恢复过程提前. 而在反平行排列下, Ni层激发的自旋流在进入Fe层后, 由于自旋极化方向与Fe层的磁化方向相反, 会进一步加剧Fe层的退磁, 导致其退磁最大值的延迟到达.进一步, 我们将间隔Ru层的厚度减小至1.5 nm和1 nm, 再次计算激光诱导的磁动力学, 如图2(c)—(f)所示. 从图2(c)—(f)可以发现随着Ru层厚度的变薄, Ni层最大退磁变化量在层间磁矩平行和反平行排列下的差别增长至
$ \varDelta \sim 3{\text{%}} $ 和$ \varDelta \sim 6{\text{%}} $ , 而Fe层的退磁差别更是增大至$ \varDelta \sim 59{\text{%}} $ 和$\varDelta \sim 158{\text{%}} $ , 这表明间隔层厚度极大地影响了热电子自旋输运的性质. 随着间隔层厚度的减小, 层间自旋流的衰减也在减弱, 使得注入至另一个磁性层的强度增强. 在三种不同间隔层厚度的体系中, 我们发现Fe层激发的热电子自旋流对Ni层退磁的影响弱于Ni层激发的热电子自旋流对Fe层退磁的影响, 这可能和激光在Ni层一侧相对较强吸收率有关. -
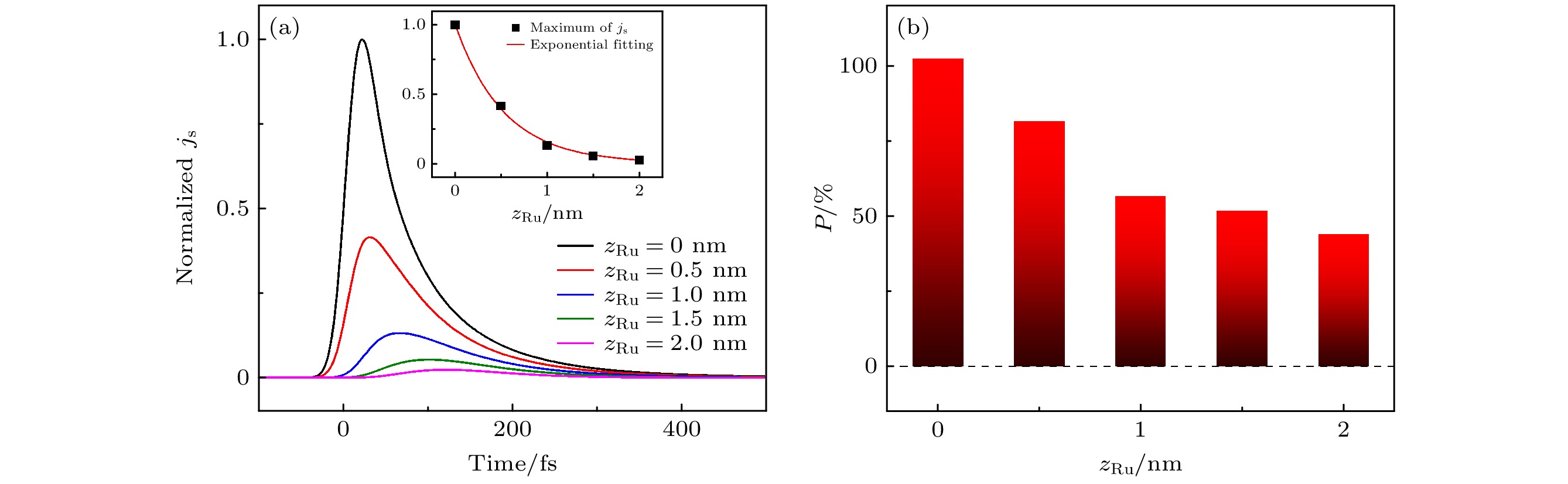
为阐明热电子自旋流在间隔层中的输运行为, 固定自旋阀结构中Ru层厚度为2 nm, 分别提取间隔层中自旋流js在距离Ni/Ru界面位置zRu处随时间的演化关系, 如图3(a)所示. 为了排除Fe层激发热电子带来的干扰, 我们仅激发了Ni层. 由图3(a)可以看到, 在Ni/Ru界面处(zRu = 0 nm), 随着激光到达Ni层, 热电子在Ni层经自旋极化后注入到Ru层, 并在几十飞秒内迅速到达最大值. 之后, 由于散射的逐渐增多而衰减, 形成一个较为缓慢的下降过程. 随着进入Ru层深度的增加, 自旋流的最大值也在快速减小, 同时由于热电子“重心”的向前扩散, 到达最大值的时刻也在延缓. 将峰值大小随热电子在Ru层移动的距离进行指数拟合, 得到其衰减长度, 如图3(a)插图. 结果显示, 热电子自旋流在Ru层的衰减长度只有0.5 nm左右, 表明其无法提供长距离的自旋输运. 值得注意, 这是指数拟合的结果, 并非热电子在不到1 nm的距离内就被完全消耗了. 进一步, 图3(b)展示了自旋流极化率在Ru层各个位置处的大小. 由图3(b)可以看到, 随着热电子在Ru层输运距离的增加, 自旋极化率也在单调降低, 表明非磁间隔层的存在并不利于热电子的自旋极化. 造成热电子自旋流强度和极化率大幅衰减的主要原因是非平衡电子在Ru层扩散中经历的多次散射, 且该散射并不依赖于电子本身的自旋取向, 最终造成了自旋和能量的损失.
-
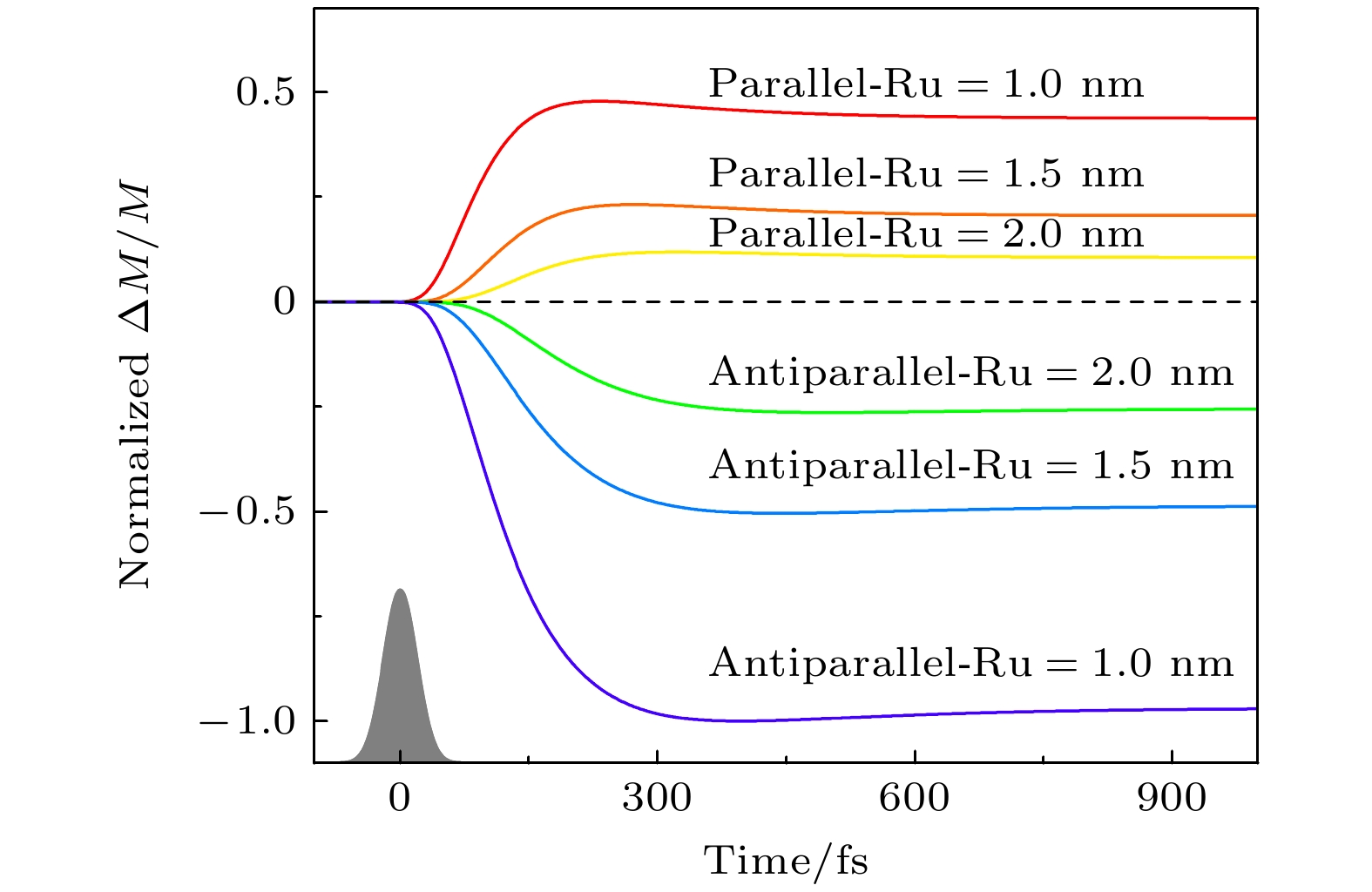
在与本研究相同的材料体系中, Rudolf等[20]此前的实验发现, Ni层与Fe层初始磁化方向平行时, 激光激发可以诱导Fe层磁化强度的瞬态增强. 然而, 在上文的结果中(如图2所示), 尽管减小间隔层厚度可以显著影响Fe层的超快磁动力学, 但只观察到Fe层的超快退磁现象. 为了解释不同实验研究组观测到Fe层磁动力学结果的差异, 通过调节激光在铁磁层的吸收率, 探讨引起Fe层超快升磁的条件. 在实验中, 不同薄膜的激光吸收率受到各种因素的影响, 并且可以通过改变激光入射角度、增加光栅等方式进行调控. 作为一个极端条件, 假定激光脉冲仅被Ni层所吸收. 图4展示了激光激发后Fe层在两种磁化方向下的磁动力学行为, 其中间隔层的厚度为dRu = 2, 1.5, 1 nm, 结果以磁化方向反平行排列下dRu = 1 nm时的最大退磁变化量为基准进行归一化. 可以看到初始磁矩方向不同的排列方式导致了Fe层出现不同的磁动力学行为, 在反平行排列下Fe层发生超快退磁; 而在平行排列下Fe层则出现了瞬态磁化增强现象, 与Rudolf等[20]实验结果定性一致. 这表明实验中Ni层的激光激发比Fe层更加显著, 且激光对Fe层磁动力学的影响强烈依赖于Ni层的激发程度. 在层间磁矩平行排列下, 激光激发Ni层产生的热电子在经历自旋输运后从间隔层注入到Fe层, 由于与自旋流极化方向同号, 导致了Fe层出现高于其饱和磁化强度的行为. 由此我们可以认为, 如果激光诱导Ni层产生的层间自旋流输运强度高于Fe层本身引起的退磁程度时, 就会出现瞬态磁化增强行为. 此外, 可以看到随间隔层厚度的减小, Fe层磁矩变化的幅度也在单调增大, 再次说明层间自旋输运对Fe层超快磁动力学的贡献受到间隔层性质的显著影响.
基于以上研究结果, 我们认为, 选择自旋扩散长度较长的金属, 如Cu, Au等[34], 可以减小热电子自旋流在间隔层输运时的散射衰减, 同时Cu层等较强的激光吸收率也可以进一步阻隔Fe层的激发, 降低其层内引起的退磁. 此外, 如果能够选择高迁移率的半金属材料作为间隔层, 也能够使热电子在输运时提升其自旋极化率. 因此在一定程度上对自旋阀结构中的层间自旋注入效率起到了增强作用.
-
本文采用超扩散自旋输运模型, 系统性研究了激光诱导Ni/Ru/Fe自旋阀结构的超快磁动力学. 首先, 通过计算Ni/Ru/Fe体系在磁性层铁磁和反铁磁耦合下激光诱导的磁动力学, 验证了最近的实验结果. 研究表明, Fe层对Ni层的退磁影响较小, 而Fe层的退磁程度和时间明显受到Ni层热电 子自旋流的显著影响, 尤其在磁矩反平行排列下, 层间自旋流进一步加剧了Fe层的退磁程度. 同时, 随着间隔层厚度的减小, 层间自旋输运的强度在逐渐增强, 从而导致Fe层退磁的相对差别显著提高. 此外, 本研究还阐明了超快升磁条件, 通过调节激光在不同薄膜间的吸收率, 发现在初始磁矩平行排列下, Ni层激发的自旋流极化方向与Fe层磁化方向一致, 抑制了Fe层的退磁过程, 导致瞬态磁化增强现象, 证明了超快自旋输运对超快升磁的关键作用. 本文结果不仅验证了热电子自旋流在铁磁层磁动力学中的重要作用, 还提出了一些优化策略. 未来, 利用具有长自旋扩散长度材料, 结合高迁移率的半金属材料作为间隔层, 有望进一步优化超快磁调控效果, 从而实现对自旋阀结构中磁性层的精确磁调控, 并为高效的磁性存储和处理器件的设计提供理论支持.
激光诱导自旋阀结构的超快自旋动力学研究
Research on ultrafast spin dynamics of laser-induced spin valve structures
-
摘要: 超快退磁的发现提供了一种使用超短激光产生超快自旋流的新手段, 从而可能更快地操纵材料磁性. 然而, 这一过程仍未被理解, 尤其是超快自旋流在层间转移中的影响因素尚不明晰. 本文利用超扩散自旋输运模型对Ni/Ru/Fe自旋阀结构体系的超快自旋输运机制进行了深入研究, 尤其关注层间自旋转移效率对铁磁层超快磁动力学的影响. 本研究计算出铁磁层在不同磁化排列下的退磁差异, 并通过调节间隔层厚度, 揭示出超快自旋输运在磁动力学中的关键作用. 此外, 还确定了热电子自旋流在间隔层中的自旋衰减长度. 通过控制激光的薄膜吸收, 进一步发现了能够引起铁磁层瞬态磁化增强的条件. 这些结果对于理解热电子自旋流的输运机制具有重要意义, 为未来控制超快自旋流提供了理论基础.Abstract: The discovery of ultrafast demagnetization has provided a new means for generating ultrafast spin currents by using an ultrashort laser, potentially enabling faster manipulation of material magnetism. This has sparked research on the transport mechanisms of ultrafast spin currents. However, the basic processes are still poorly understood, especially the factors influencing interlayer spin transfer. In this work, a superdiffusive spin transport model is used to investigate the ultrafast spin transport mechanism in the Ni/Ru/Fe spin valve system, with a particular focus on how interlayer spin transfer affects the ultrafast magnetization dynamics of the ferromagnetic layer. First, by calculating the laser-induced magnetization dynamics of the Ni/Ru/Fe system under different magnetization alignments, the recent experimental findings are validated. Further analysis shows that reducing the thickness of the Ru spacer layer will significantly enhance the spin current intensity and increase the demagnetization difference in the Fe layer, confirming the key role of the hot electron spin current generated by the Ni layer in interlayer spin transport. In addition, the spin decay length of hot electron spin currents in the spacer Ru layer is determined to be approximately 0.5 nm. This work also shows that laser-induced transient magnetization enhancement can be achieved by adjusting the relative laser absorption in the films. These results provide theoretical support for ultrafast magnetic control of future spin valve structures and contribute to the development of spintronics in high-speed information processing and storage applications.
-
Key words:
- spintronics /
- ultrafast magnetic dynamics /
- spin-polarized transport .
-

-
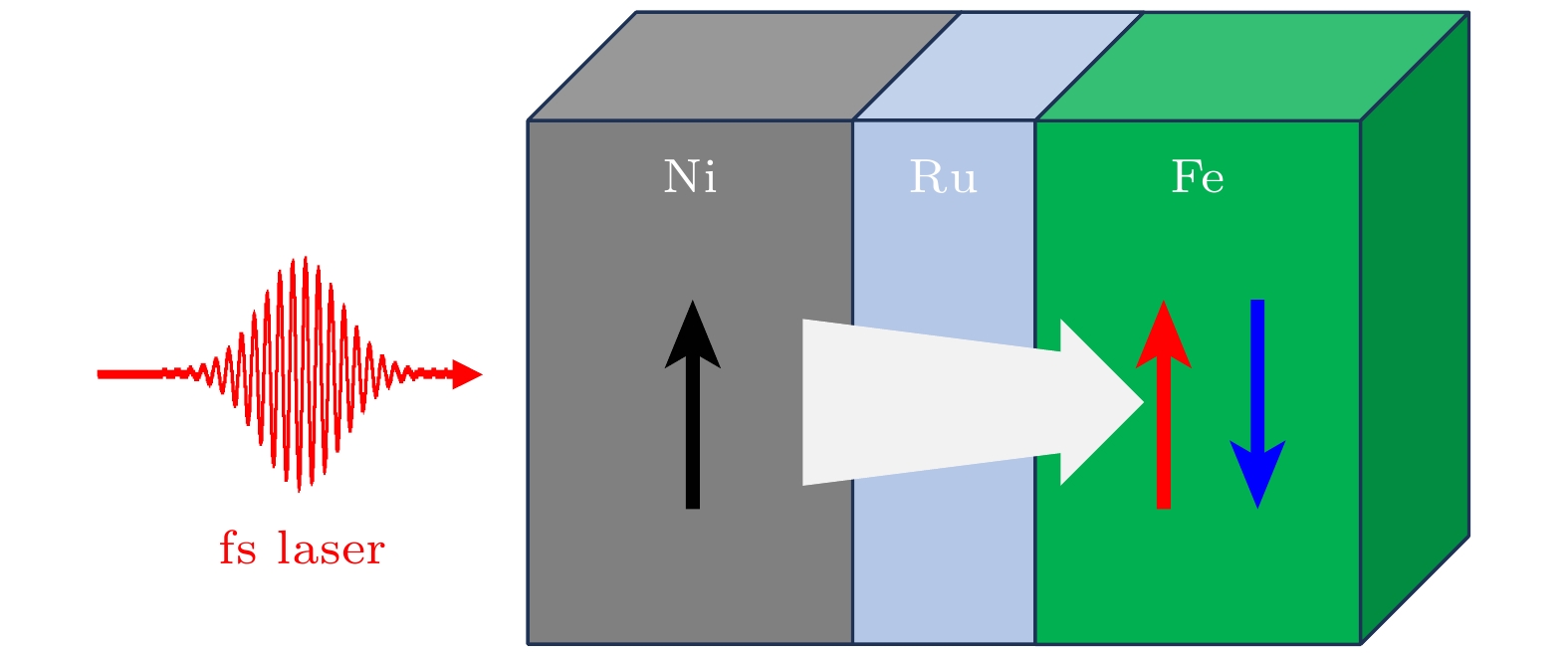
图 1 飞秒激光脉冲诱导的Ni/Ru/Fe自旋阀结构中层间自旋输运示意图. 自旋极化热电子从Ni层通过Ru层转移至Fe层, 引起超快磁动力学. Ni层和Fe层的磁化方向可以为平行或反平行排列
Figure 1. Schematic of ultrafast interlayer spin transport in a Ni/Ru/Fe trilayer structure induced by femtosecond laser pulses. Spin-polarized hot electrons transfer from the Ni layer through the Ru spacer to the Fe layer, triggering ultrafast magnetic dynamics. The magnetization directions of the Ni and Fe layers can be either parallel or antiparallel.
图 2 (a)—(f)计算得到激光激发后的磁动力学, Ni层和Fe层初始的磁化方向为平行(红线)和反平行(蓝线)排列. (a)与(b), (c)与(d), (e)与(f)分别为间隔层dRu = 2, 1.5, 1 nm厚的结果
Figure 2. (a)–(f) Calculated magnetic dynamics after laser excitation, with initial magnetization directions of the Ni and Fe layers aligned parallel (red line) and antiparallel (blue line). (a) and (b), (c) and (d), (e) and (f) show the results for spacer layer thicknesses of dRu = 2, 1.5, and 1 nm, respectively.
图 3 (a) Ru层各位置自旋流js随时间的演化曲线, 以Ni/Ru界面处最大值进行归一化, 插图是以自旋流最大值对位置进行的指数拟合; (b)为图(a)中自旋流所对应的自旋极化率
Figure 3. (a) Time evolution of the spin current js at various positions in the Ru layer, normalized to the maximum at the Ni/Ru interface. The inset shows an exponential fit of the spin current maximum values as a function of position. (b) The corresponding spin polarization of the spin current in panel (a).
图 4 计算得到不同初始磁化方向下Fe层的磁动力学行为, 其中, 飞秒激光仅激发 Ni 层产生非平衡热电子, 浅灰色阴影表示激光脉冲的时间分布
Figure 4. Calculated magnetic dynamics of Fe layer under different initial magnetization directions. The femtosecond laser excites only the Ni layer, generating nonequilibrium hot electrons. The light gray shading indicates the temporal profile of the laser pulse.
-
[1] Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, von Molnár V S, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488 doi: 10.1126/science.1065389 [2] Žutić I, Fabian J, Sarma S D 2004 Rev. Mod. Phys. 76 323 doi: 10.1103/RevModPhys.76.323 [3] Bader S D, Parkin S S P 2010 Annu. Rev. Condens. Matter Phys. 1 71 doi: 10.1146/annurev-conmatphys-070909-104123 [4] 许涌, 张帆, 张晓强, 杜寅昌, 赵海慧, 聂天晓, 吴晓君, 赵巍胜 2022 物理学报 69 200703 doi: 10.7498/aps.69.20200623 Xu Y, Zhang F, Zhang X Q, Du Y C, Zhao H H, Nie T X, Wu X J, Zhao W S 2022 Acta Phys. Sin. 69 200703 doi: 10.7498/aps.69.20200623 [5] Seifert T S, Cheng L, Wei Z X, Kampfrath T, Qi J B 2022 Appl. Phys. Lett. 120 180401 doi: 10.1063/5.0080357 [6] 芦闻天, 袁喆 2022 中国科学: 物理学 力学 天文学 52 270007 doi: 10.1360/SSPMA-2021-0350 Lu W T, Yuan Z 2022 Sci. Sin. -Phys. Mech. Astron. 52 270007 doi: 10.1360/SSPMA-2021-0350 [7] 杨旭, 冯红梅, 刘佳南, 张向群, 何为, 成昭华 2024 物理学报 73 157501 doi: 10.7498/aps.73.20240646 Yang X, Feng H M, Liu J N, Zhang X Q, He W, Cheng Z H 2024 Acta Phys. Sin. 73 157501 doi: 10.7498/aps.73.20240646 [8] Kirilyuk A, Kimel A V, Rasing T 2010 Rev. Mod. Phys. 82 2731 doi: 10.1103/RevModPhys.82.2731 [9] 李杭, 张新惠 2015 物理学报 64 177503 doi: 10.7498/aps.64.177503 Li H, Zhang X H 2015 Acta Phys. Sin. 64 177503 doi: 10.7498/aps.64.177503 [10] Liu B, Xiao HJ, Weinelt M 2023 Sci. Adv. 9 eade0286 doi: 10.1126/sciadv.ade0286 [11] Jin Z M, Guo Y Y, Peng Y, Zhang Z Y, Pang J Y, Zhang Z Z, Liu F, Ye B, Jiang Y X, Ma G H, Zhang C, Balakin A V, Shkurinov A P, Zhu Y M, Zhuang S L 2023 Adv. Phys. Res. 2 2200049 doi: 10.1002/apxr.202200049 [12] Wang C T, Liu Y M 2020 Nano Converg. 7 35 doi: 10.1186/s40580-020-00246-3 [13] Wu N, Zhang S J, Wang Y X, Meng S 2023 Prog. Surf. Sci. 98 100709 doi: 10.1016/j.progsurf.2023.100709 [14] Wu X Q, Meng H, Zhang H Y, Xu N 2021 New J. Phys. 23 103007 doi: 10.1088/1367-2630/ac1143 [15] Ghising P, Biswas C, Lee Y H 2023 Adv. Mater. 35 2209137 doi: 10.1002/adma.202209137 [16] Gusev N A, Dgheparov D I, Pugach N G, Belotelov V I 2021 Appl. Phys. Lett. 118 232601 doi: 10.1063/5.0055457 [17] Beaurepaire E, Merle J C, Daunois A, Bigot J Y 1996 Phys. Rev. Lett. 76 4250 doi: 10.1103/PhysRevLett.76.4250 [18] Stanciu C D, Hansteen F, Kimel A V, KirilyukA, Tsukamoto A, Itoh A, Rasing T 2007 Phys. Rev. Lett. 99 047601 doi: 10.1103/PhysRevLett.99.047601 [19] Malinowski G, Dalla Longa F, Rietjens J H H, Paluskar P V, Huijink R, Swagten H J M, Koopmans B 2008 Nat. Phys. 4 855 doi: 10.1038/nphys1092 [20] Rudolf D, La-O-Vorakiat C, Battiato M, Adam R, Shaw J M, Turgut E, Maldonado P, Mathias S, Grychtol P, Nembach H T, Silva T J, Aeschlimann M, Kapteyn H C, Murnane M M, Schneider C M, Oppeneer P M 2012 Nat. Commun. 3 1037 doi: 10.1038/ncomms2029 [21] Turgut E, La-o-Vorakiat C, Shaw J M, Grychtol P, Nembach H T, Rudolf D, Adam R, Aeschlimann M, Schneider C M, Silva T J, Murnane M M, Kapteyn H C, Mathias S 2013 Phys. Rev. Lett. 110 197201 doi: 10.1103/PhysRevLett.110.197201 [22] He W, Zhu T, Zhang X Q, Yang H T, Cheng Z H 2013 Sci. Rep. 3 2883 doi: 10.1038/srep02883 [23] Ji B Y, Jin Z M, Wu G J, Li J G, Wan C H, Han X F, Zhang Z Z, Ma G H, Peng Y, Zhu Y M 2023 Appl. Phys. Lett. 122 111104 doi: 10.1063/5.0141071 [24] Igarashi J, Zhang W, Remy Q, Díaz E, Lin J X, Hohlfeld J, Hehn M, Mangin S, Gorchon J, Malinowski G 2023 Nat. Mater. 22 725 doi: 10.1038/s41563-023-01499-z [25] Schellekens A J, De Vries N, Lucassen J, Koopmans B 2014 Phys. Rev. B 90 104429 doi: 10.1103/PhysRevB.90.104429 [26] Eschenlohr A, Persichetti L, Kachel T, Gabureac M, Gambardella P, Stamm C 2017 J. Phys. : Condens. Matter 29 384002 doi: 10.1088/1361-648X/aa7dd3 [27] Stamm C, Murer C, Wörnle M S, Reid A H, Higley D J, Wandel S F, Schlotter W F, Gambardella P 2020 J. Appl. Phys. 127 223902 doi: 10.1063/5.0006095 [28] Battiato M, Carva K, Oppeneer P M 2010 Phys. Rev. Lett. 105 027203 doi: 10.1103/PhysRevLett.105.027203 [29] Zhukov V P, Chulkov E V, Echenique P M 2005 Phys. Rev. B 72 155109 doi: 10.1103/PhysRevB.72.155109 [30] Zhukov V P, Chulkov E V, Echenique P M 2006 Phys. Rev. B 73 125105 doi: 10.1103/PhysRevB.73.125105 [31] Battiato M, Maldonado P, Oppeneer P M 2014 J. Appl. Phys. 115 172611 doi: 10.1063/1.4870589 [32] Battiato M, Carva K, Oppeneer P M 2012 Phys. Rev. B 86 024404 doi: 10.1103/PhysRevB.86.024404 [33] Lu W T, Yuan Z, Xu X H 2023 Sci. Chin. -Phys. Mech. Astron. 66 127511 doi: 10.1007/s11433-023-2214-9 [34] Gorchon J, Mangin S, Hehn M, Malinowski G 2022 Appl. Phys. Lett. 121 012402 doi: 10.1063/5.0097448 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: