首页
登录
注册
-
真空断路器以其长寿命、小型化与介质环保等特点被广泛应用于中压电力系统，担负着系统控制与保护任务[1]。真空断路器本体结构主要包括灭弧室与操动机构。当所在线路出现短路故障时，在灭弧室与机构协同配合下完成线路故障能量的快速泄能，期间在灭弧室中不可避免产生金属蒸气电弧，其发生、发展直至熄灭全过程的动力学演化行为直接影响真空断路器的整机性能[2]。真空灭弧室触头结构设计是调控极间电弧运动行为的有效途径之一，即通过改变触头结构改变电流流路，在极间产生横磁、纵磁或旋转磁场，进而实现极间磁场对电弧的逸散作用[3]。其中，横磁触头的工作原理是在极间产生横向磁场，驱使电弧在触头表面旋转运动，使电弧向未熔区移动，使原熔区冷却，避免电弧对触头电极产生局部烧蚀。相比于纵磁结构，横磁触头在电流过零后具有较高的弧后介质强度恢复速度，因此如何提高横磁触头系统开断能力引起广泛关注[4-5]。
在毫秒级时间和毫米级空间内真空电弧等离子体的逸散进程伴随着复杂的电、磁、热、力多物理场的耦合作用。为了揭示横磁触头与电弧互作机理，邹积岩等[6]通过建立横磁作用下的直流电弧阴极过程模型，从微观角度解释了横磁作用下电弧运动机理，并得到了粒子温度等参数与磁场之间的定量关系。修士新等[7]和段肖力等[8]建立了触头三维模型，在对比杯状横磁触头、螺旋槽型横磁触头和万字型触头极间磁场和电弧受力研究中发现，弯曲状缝隙螺旋槽型比直线状缝隙结构更有利于电流的开断；杯状型横磁触头开槽倾斜角度和触头杯的槽数越大，越有利于电弧开断，万字型触头槽隙越小越有利于电弧运动。Dullni E等[9-10]在对横磁作用下真空电弧运动特性分析中，提出了电弧运动速度的计算方法，并以实验结果进行验证，研究表明电极表面温度和电弧长度（极间距）与触头运动速度存在相关性。Kaltenecker A等[11]在对杯形横磁的实验研究中发现，伴随电极的运动过程，电弧具有不同的运动模式，且电极运动对电弧特性具有重要影响。
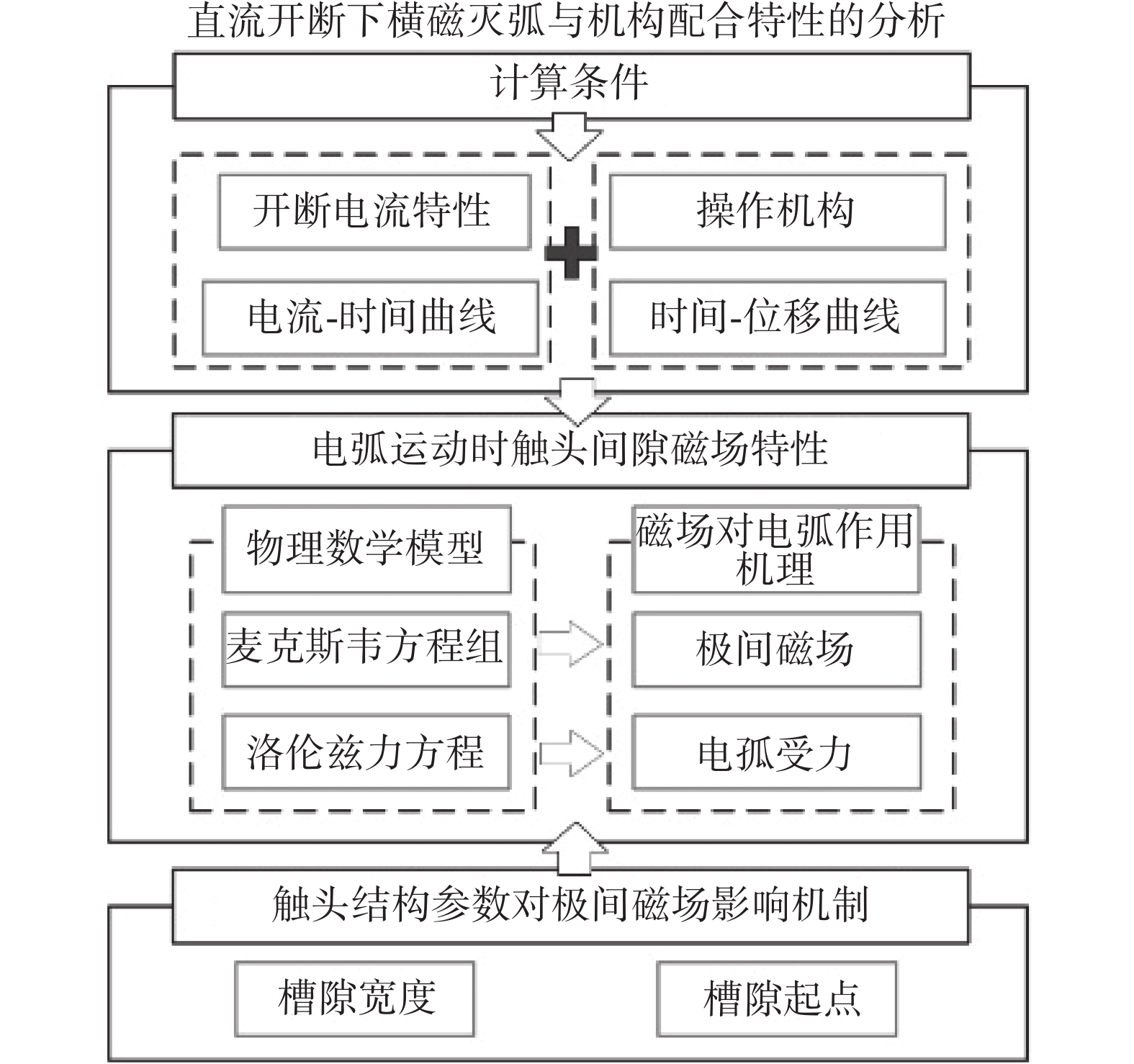
综上，为探究电极运动过程横磁触头磁场分布规律及其对电弧作用机制，以12 kV/1250 A/25 kA直流真空灭弧室横磁触头为对象，建立三维极间磁场物理数学模型，研究直流开断下操动机构速度特性和触头结构参数对极间磁场和电弧受力的作用机理（技术路线如图1所示），为设计高开断能力真空断路器触头结构提供参考。
-
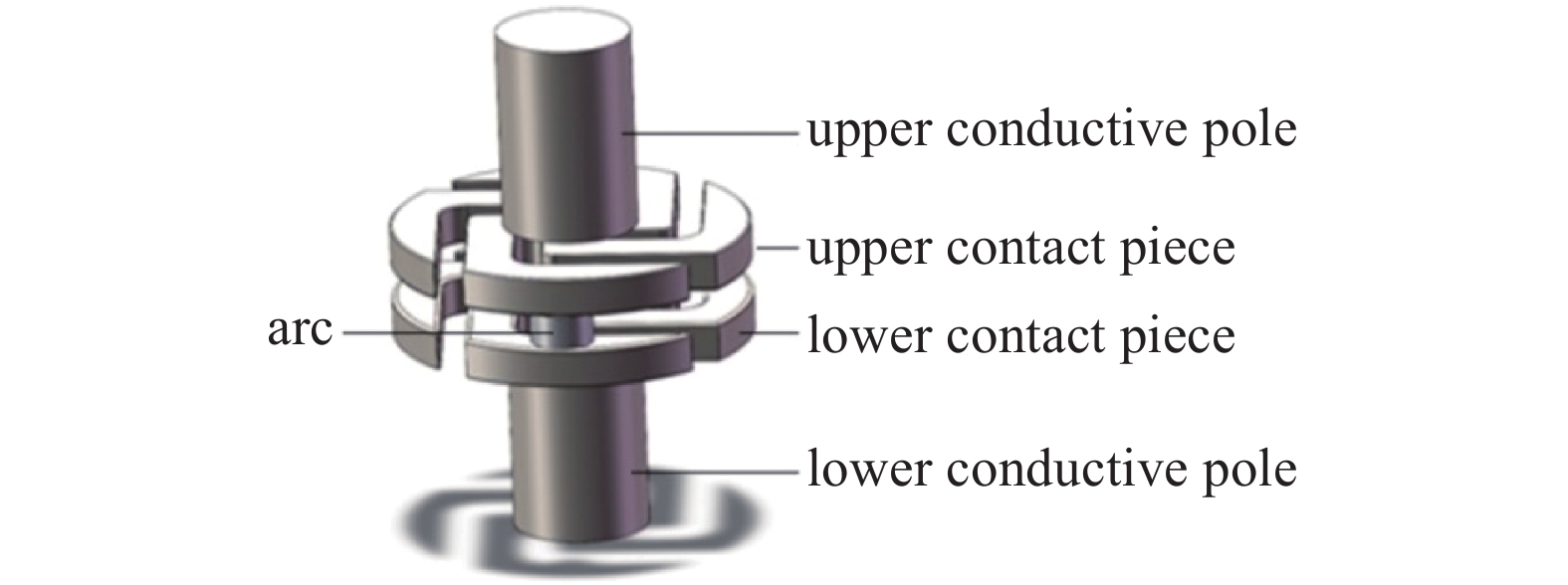
所建直流真空灭弧横磁场触头模型如图2所示，采用有限元法进行极间三维磁场分析。材料参数如表1所示。触头系统基本参数：触头直径42.0 mm；开距12.0 mm。极间电流路径：上导电杆→上触头片→电弧柱→下触头片→下导电杆。
-
触头系统电磁场[12]满足麦克斯韦方程组：
式中，
$ \rho $ 为体电荷密度，$ \mathbf{D} $ 为电位移矢量，$ \mathbf{H\mathit{\mathbf{\mathit{ }}}} $ 为磁场强度，$ \mathbf{B} $ 为磁场感应强度。采用有限元法进行电磁场求解，补充方程如下：
式中，
$ \mathbf{A} $ 为磁矢位，$ \varphi $ 为标量电位，$ \varepsilon $ 为介电常数，$ \mu $ 为真空磁导率，i为触头流过电流（电弧电流），J为电流密度。 -
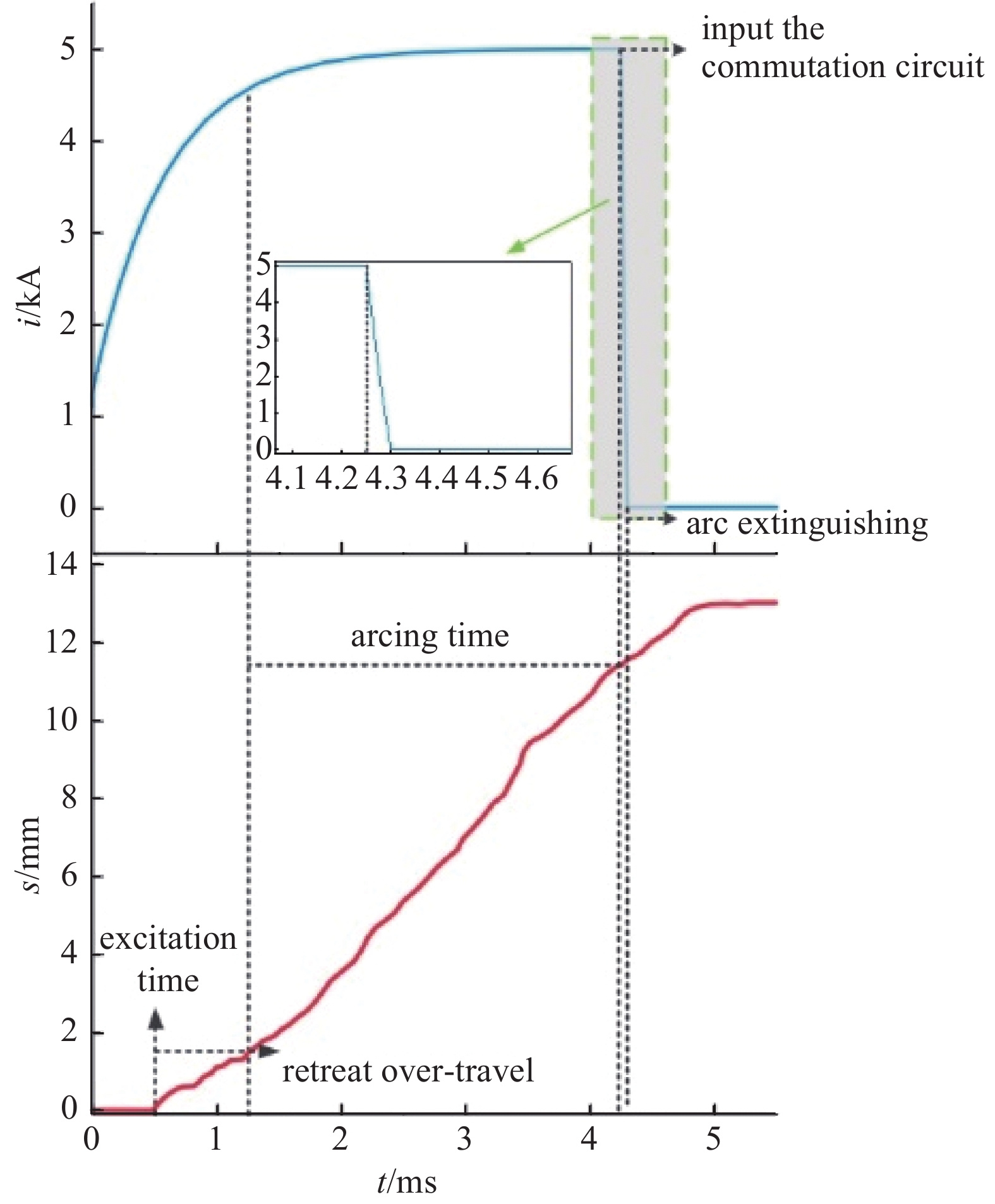
直流开断条件：依据实验所得真空断路器分闸过程位移/时间特性（如图4所示），结合电流变化，分析典型条件下的直流故障开断过程：
0 ms时，系统发生故障，故障电流快速上升，检测系统判定故障并发出分闸指令，断路器接到故障开断信号，机构未动作。
0.5 ms时，完成励磁，机构带动动触头运动，开始分闸操作。
1.25 ms时，触头刚分，极间产生金属蒸气电弧等离子体，随着机构运动，极间距增大。横磁作用下电弧在触头表面旋转。
4.25 ms时，投入换流，触头间电流迅速下降，此时极间距为10.0 mm。
4.3 ms时，电流降至为零，电弧熄灭。
5.5 ms时，完成分闸全过程。
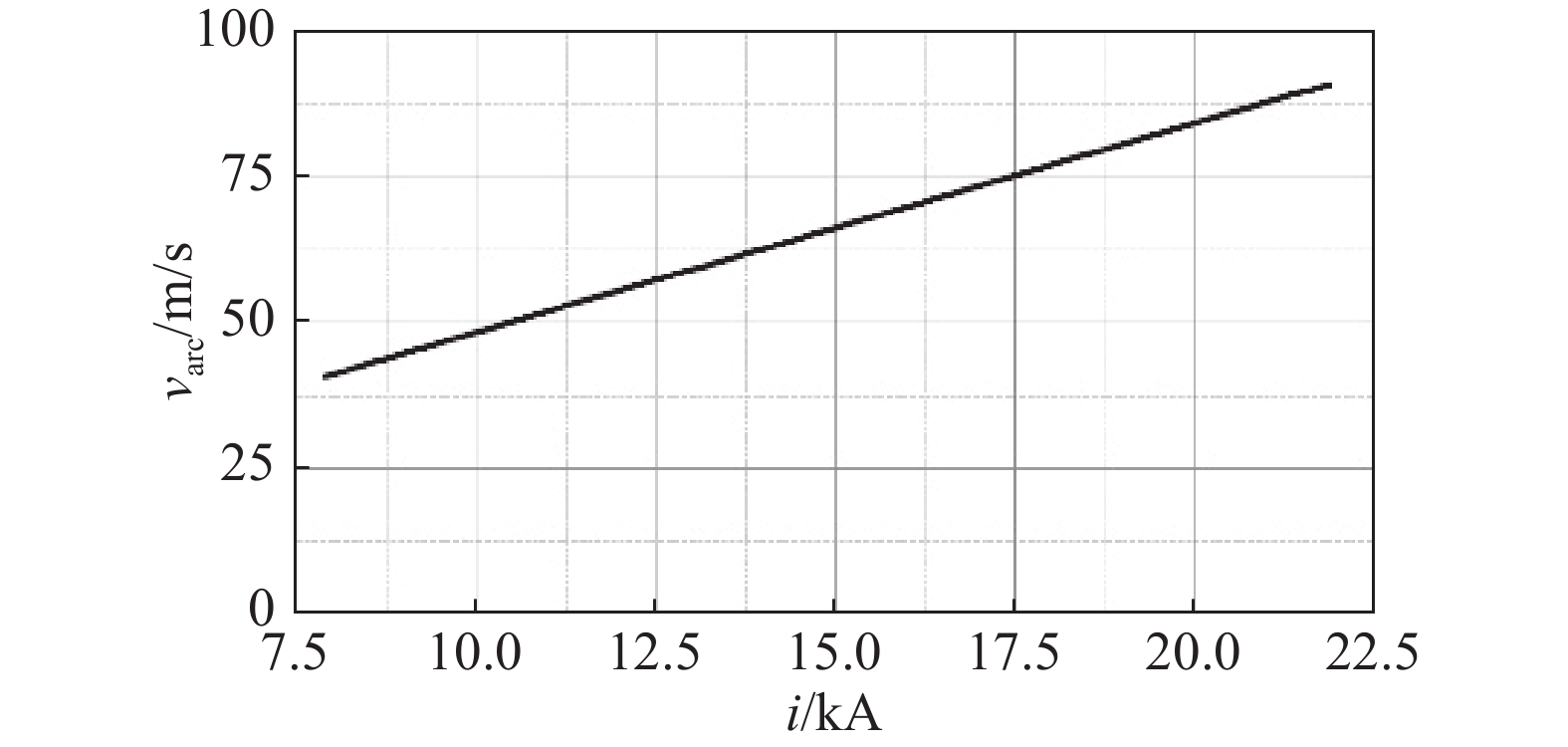
假设：燃弧电流5kA，极间距1.0 mm时，电弧刚好运动至触头边缘处；不同极间距下，触头表面温度均为Tb。计算得到在电流密度1.5×108 A/m2下，伴随开断进程的发展，电弧旋转速度如图5所示。
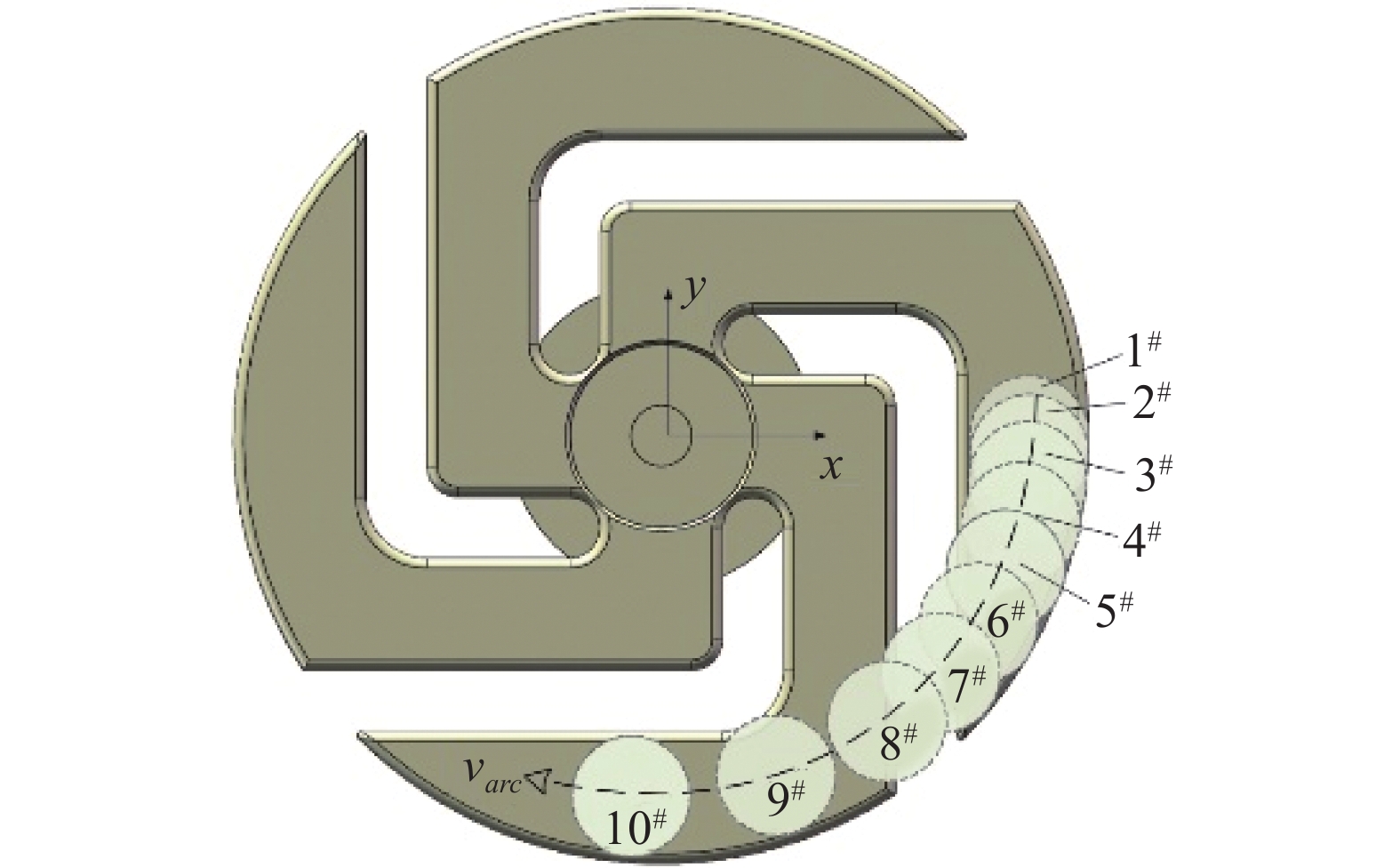
图6为万字型触头结构平面示意图，计算所得触头极间距从1.0~10.0 mm时电弧弧根运动轨迹，对应图6中“1#”~“10#”所处位置，弧柱位置坐标如表2所示。
-
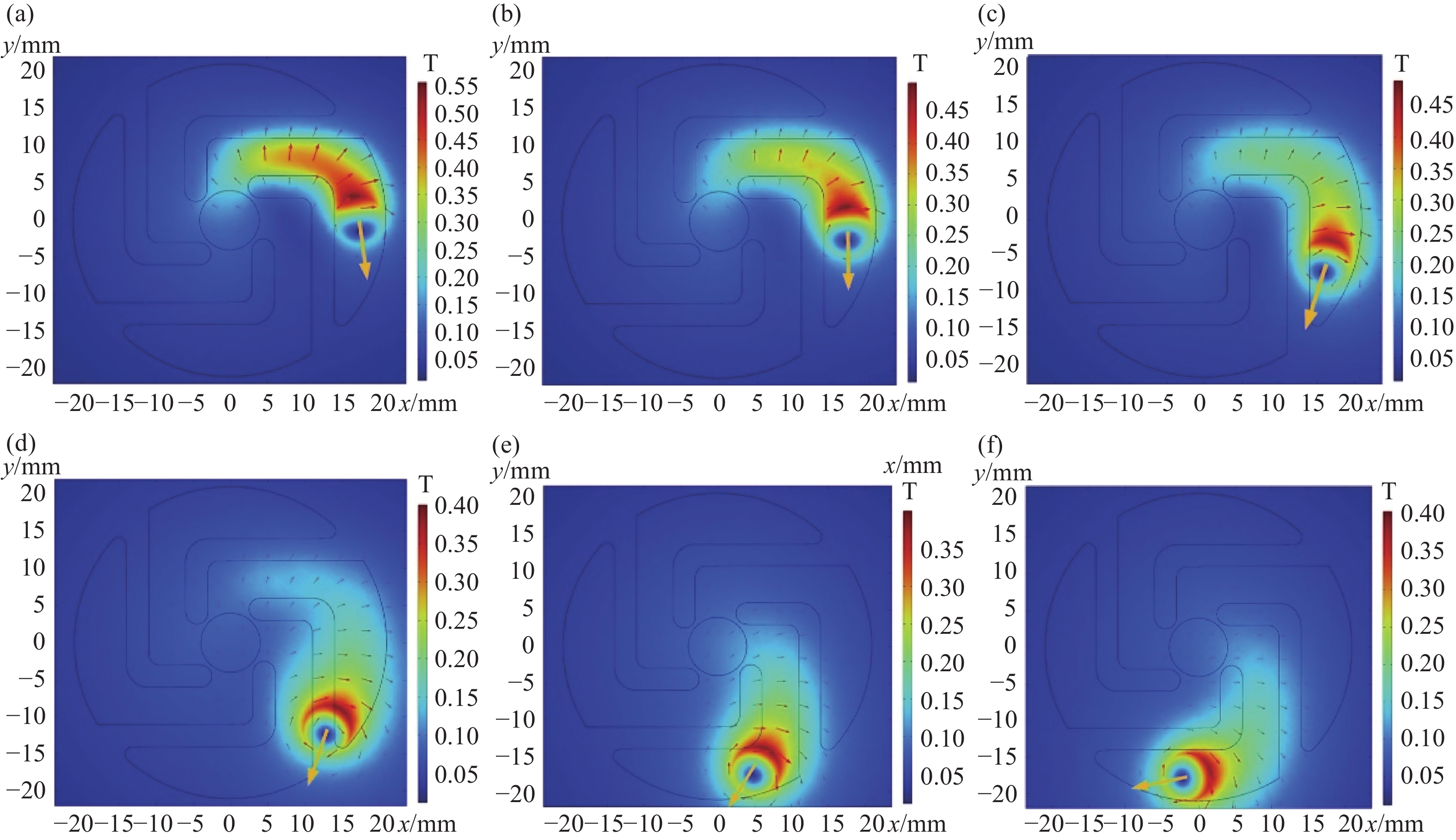
选取极间距1.0 mm、3.0 mm、5.0 mm、7.0 mm、9.0 mm及10.0 mm典型位置进行分析，如图7所示。
仿真结果表明，磁场绕弧柱旋转，驱使电弧运动。极间中心平面磁感应强度并非呈均匀分布，其最大值围绕在电弧周围，并向着四周逐渐减小；离弧柱越远，磁感应强度越小。同时，弧柱周围磁感应强度也并非呈均匀分布。
不同位置的电弧受力也不同，当电弧位于触头前端（拐点周围）时，电弧受力偏向触头外侧，防止电弧向触头中心移动；当电弧位置位于触臂末端时，对电弧磁吹力方向与触头圆周相切，驱动电弧运动；而当电弧处于触头槽隙时，所产生的磁吹方向沿着槽隙朝向触头外侧，可能导致电弧更倾向于沿着槽隙运动。
-
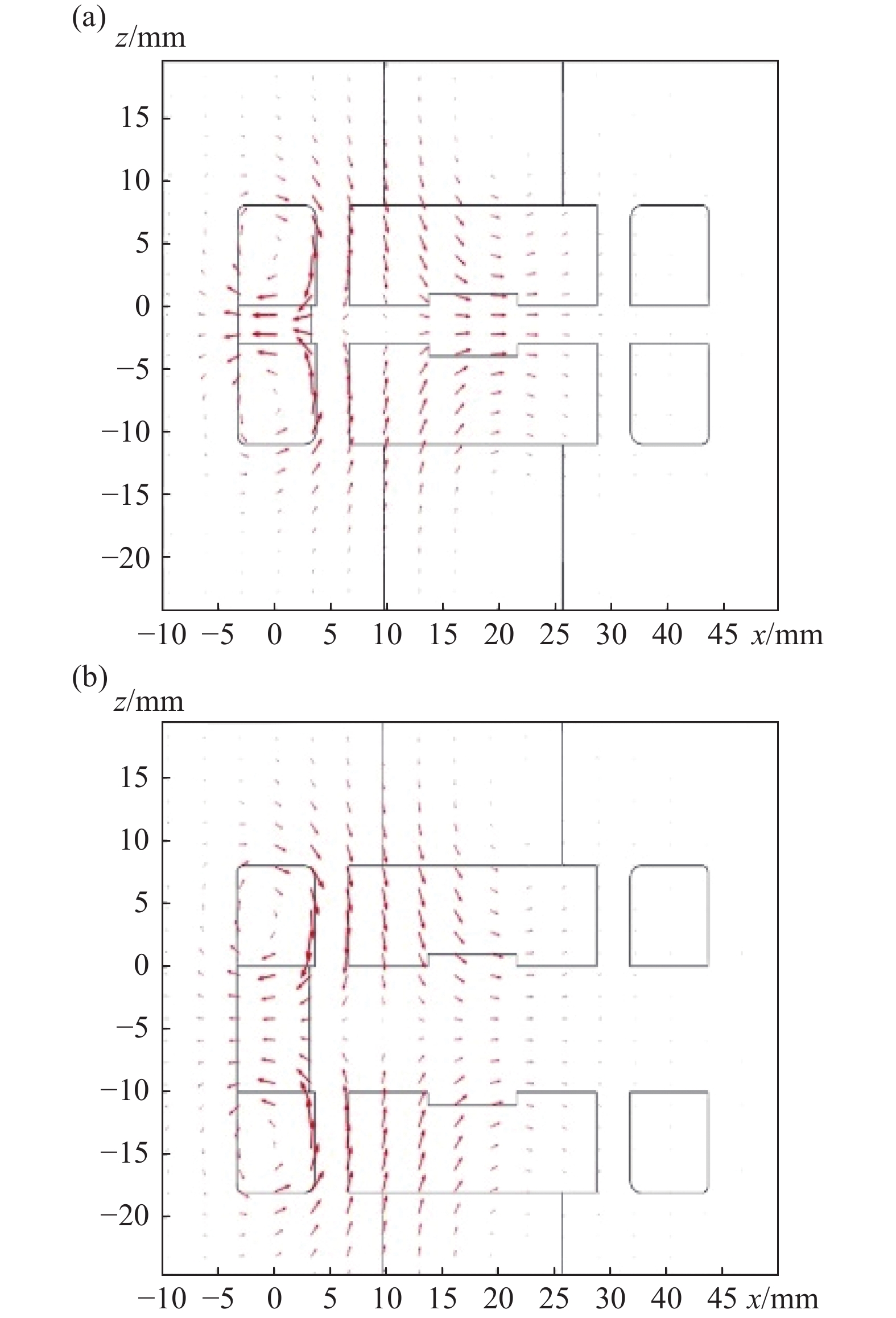
从纵切面磁感应强度看，如图8所示，箭头方向为磁场方向，箭头长度表示磁感应强度幅值，电流流经触头所产生的横向磁场磁感应强度在两侧触头处最大，并向着触头间隙中心平面逐渐减小。
在极间距为3.0 mm和10.0 mm时，电弧位置均处于触臂中心。对比触头纵切面上磁感应强度分布可知，极间距3.0 mm时，中心平面最大磁感应强度为502.9 mT；极间距10.0 mm时，中心平面最大磁感应强度为438.97 mT；极间距离的增大，会减小触头中心面的磁感应强度。
-
极间距7.0 mm之前，电弧在触头触臂上运动。由表2可知，极间距从1.0 mm增至4.0 mm时，由于极间距增加，中心平面最大磁感应强度从572.13 mT减至487.37 mT；极间距5.0 mm时，中心平面最大磁感应强度增加；极间距6.0 mm时，磁感应强度略有下降。电弧在触臂运动时，在触臂末端时触头所产生磁感应强度大于电弧在触臂前端的磁感应强度。极间距增加时，中心平面磁感应强度下降程度逐渐减小。
极间距7.0 mm时，电弧刚好运动至触头槽隙，极间中心平面磁感应强度急剧衰减，约为400.96 mT；极间距9.0 mm后，电弧离开槽隙到达触臂前端，极间中心面最大磁感应强度相比电弧在触头槽隙时有所增加，但较电弧过槽隙前磁感应强度下降明显。
-
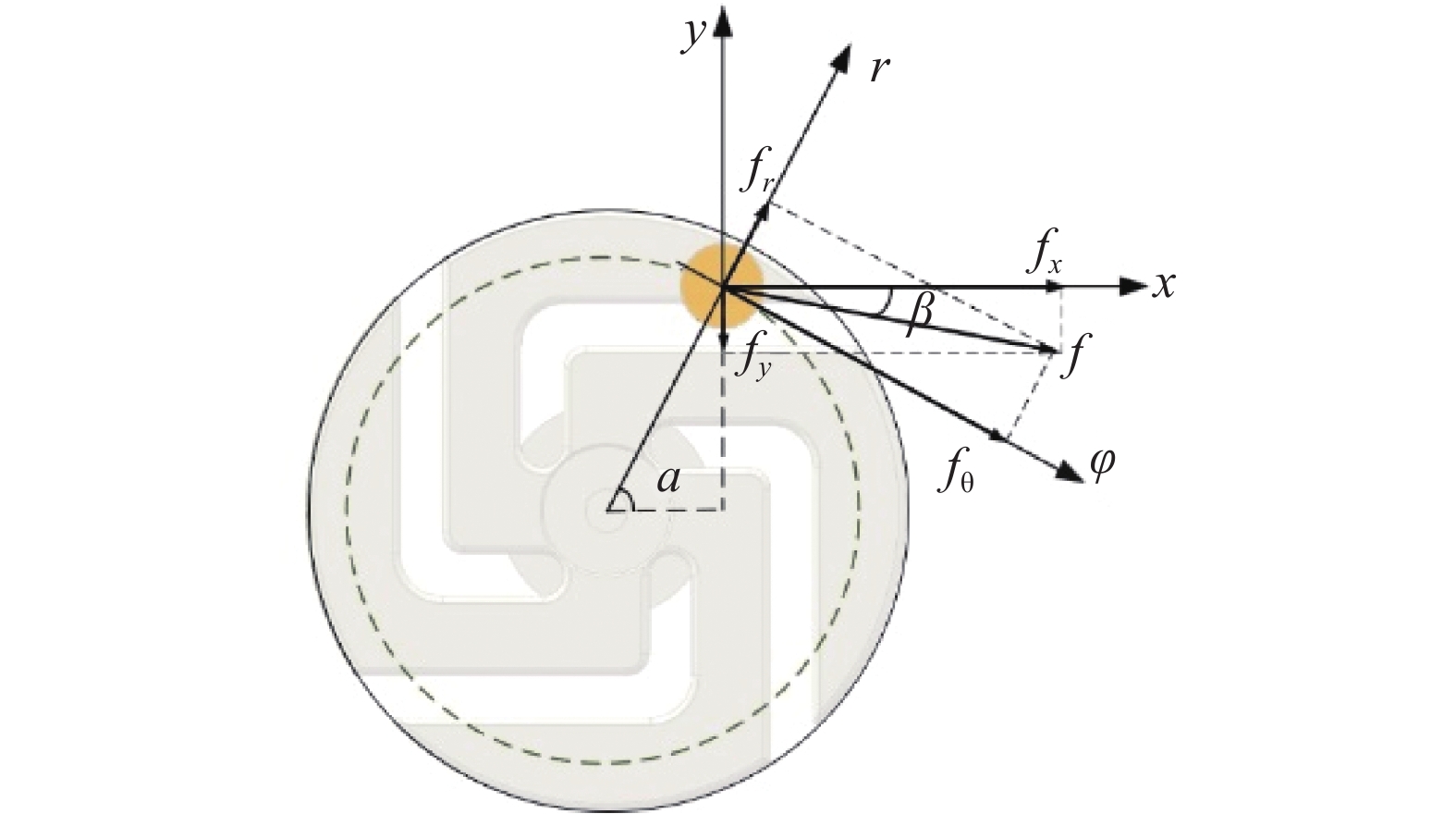
在触头极间距发生变化时，会影响电弧所处位置，导致其所受磁吹力方向不同。磁场对电弧的磁吹作用力表达式为：
由式（4）可知，磁吹力与电弧长度和磁场大小有关。
为分析电弧运动过程中磁吹力变化，计算弧柱所受磁吹力沿x、y方向分量见表3；为分析电弧在触头表面旋转运动规律，将电弧所受磁吹力x和y方向分量转换为沿圆周切向方向(θ方向)和径向方向(r方向)分量，其受力变化转换如图9所示。定义径向外法向方向和切向顺时针方向为正方向。
径向力和切向力的转换公式如下所示：
式中，α为弧柱所在位置的圆心角。
极距离在7.0 mm之前，电弧在触臂上运动，电弧所受磁吹力随着极间距增加而增加。电弧切向力随着极间距增加而不断增加，径向力在触臂拐点两侧经历了先增大后减小的变化过程，电弧到达触臂前端时，切向力达到最大而径向力最小，利于电弧在沿触臂运动的过程中最终达到一个较高切向速度以跨越槽隙。
当电弧经过触头槽隙时，即使极间距有所增加，但电弧所受磁吹力急剧衰减，主要原因是电弧运动到触头槽隙时触头间隙的磁感应强度骤减。同时电弧所受的径向力明显增加，阻碍电弧跨越槽隙。
极间距9.0 mm后，电弧重新运动至下一个触臂。由于磁感应强度和极间距增加，电弧所受磁吹力较电弧位于槽隙时有一定回升；但相较于极间距6.0 mm时仍有一定减小，这主要是由于极间磁感应强度的减小。
分析可知，刚分时刻应使机构具有较高的初速度；伴随极间距的增加，电弧很快具有较高旋转速度，以减少触头烧蚀。投入换流前，应降低机构速度，确保极间具有较高磁场强度，从而保持电弧在运动过程中具有较高加速度。
-
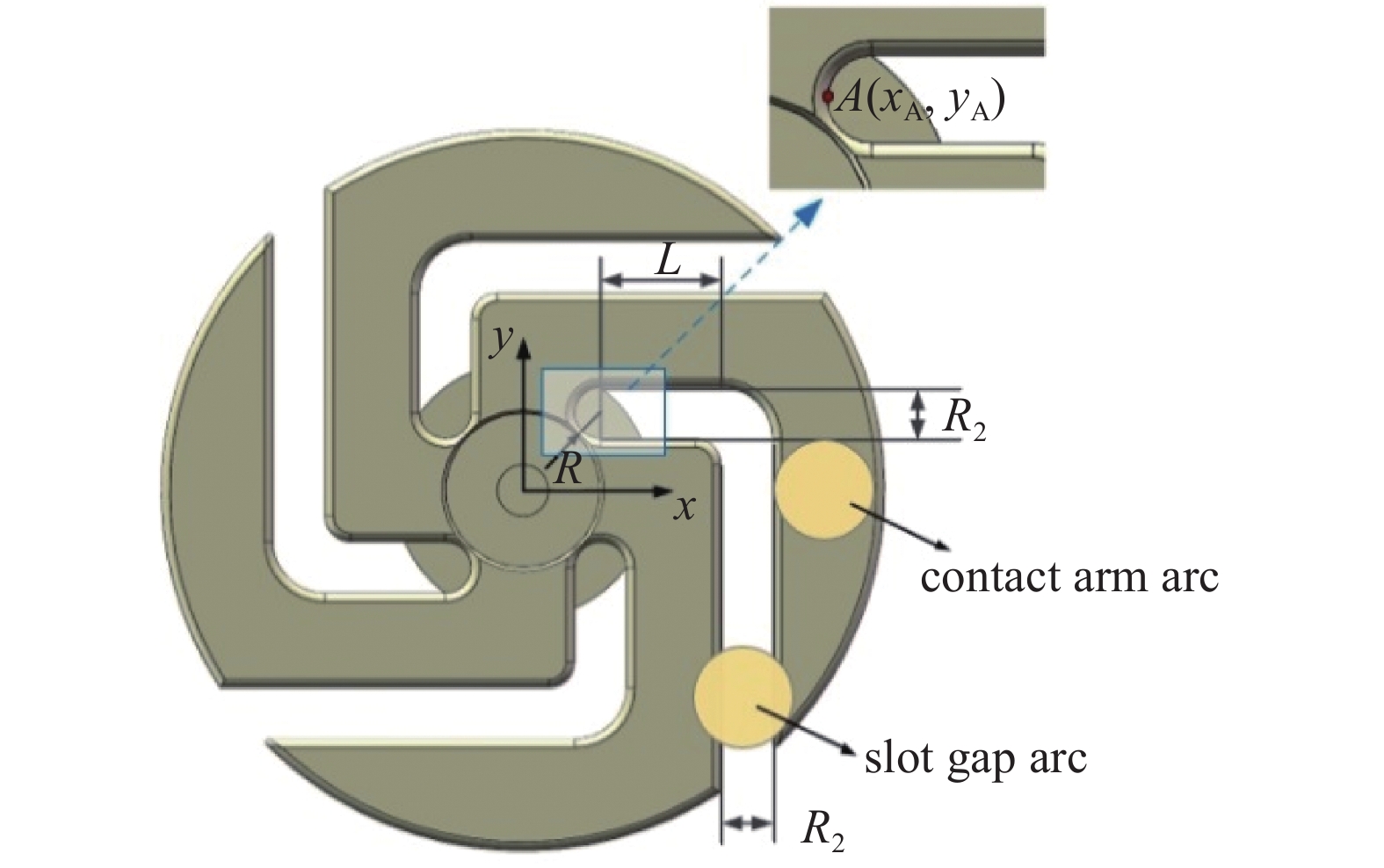
分析可知，不同电弧位置时极间磁场分布不同，电弧受力也不同，这主要源于横磁结构的设计。为减小电弧跨越槽隙的影响，有必要分析横磁触头结构对极间磁场和电弧所受磁吹力的影响。根据万字型触头的制备要求，选取主要参数如图10所示，改变槽隙起点A(xA,yA)，槽隙宽度R2研究磁场和电弧所受磁吹力的变化规律。
-
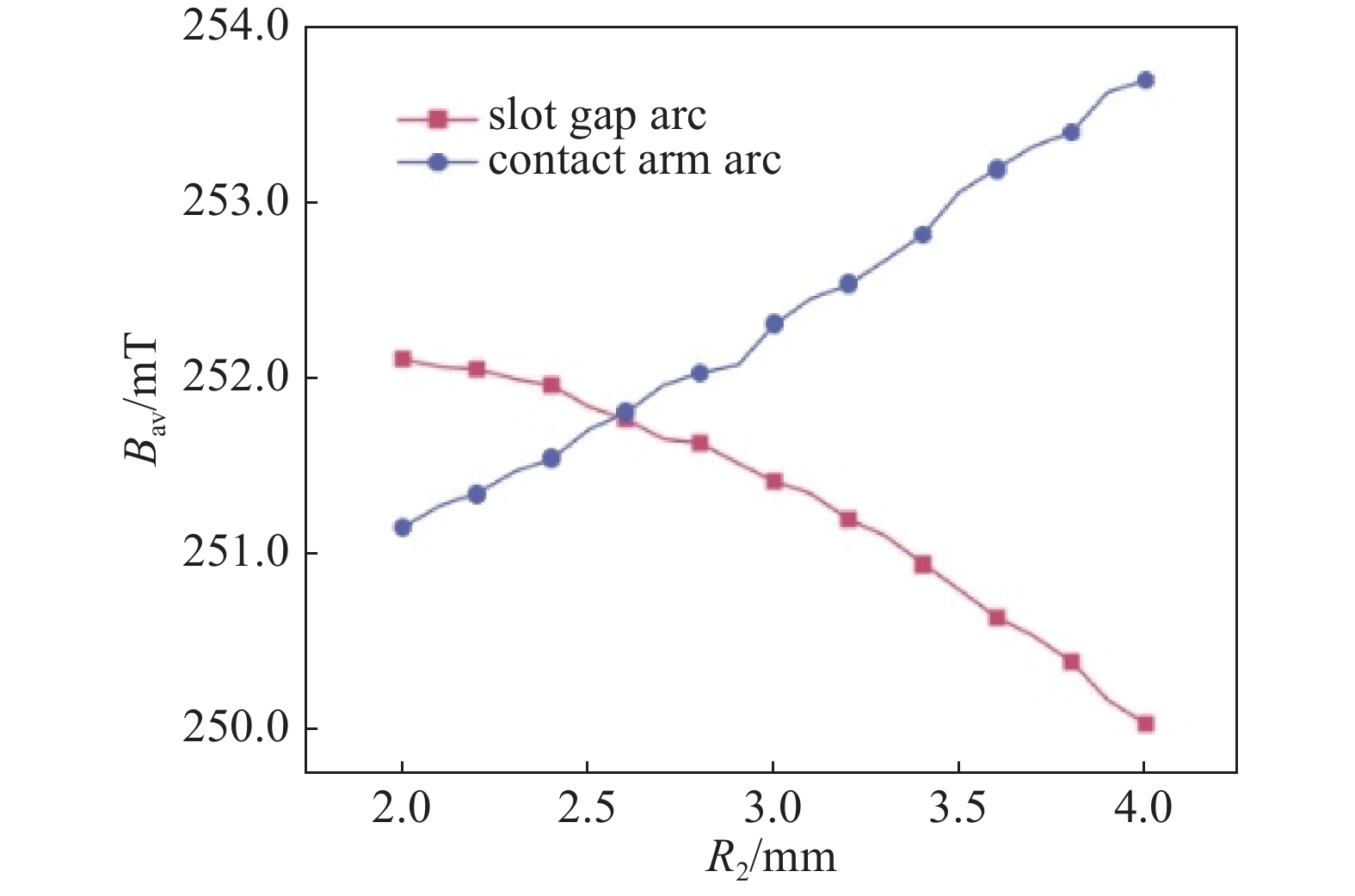
在极间距不变的前提下进行分析，选取极间距7.0 mm、xA为4.0 mm，分析电弧位于触头触臂和槽隙时槽隙宽度对极间磁场和弧柱的影响，如图11所示。电弧位置在触臂上时，随着R2增加，极间平均磁感应强度增加。原因是R2增加时，触头触臂面积渐减，电弧电流密度增强，磁感应强度增加，磁吹作用增强。而当电弧弧根位于槽隙时，R2增加磁感应强度降低。
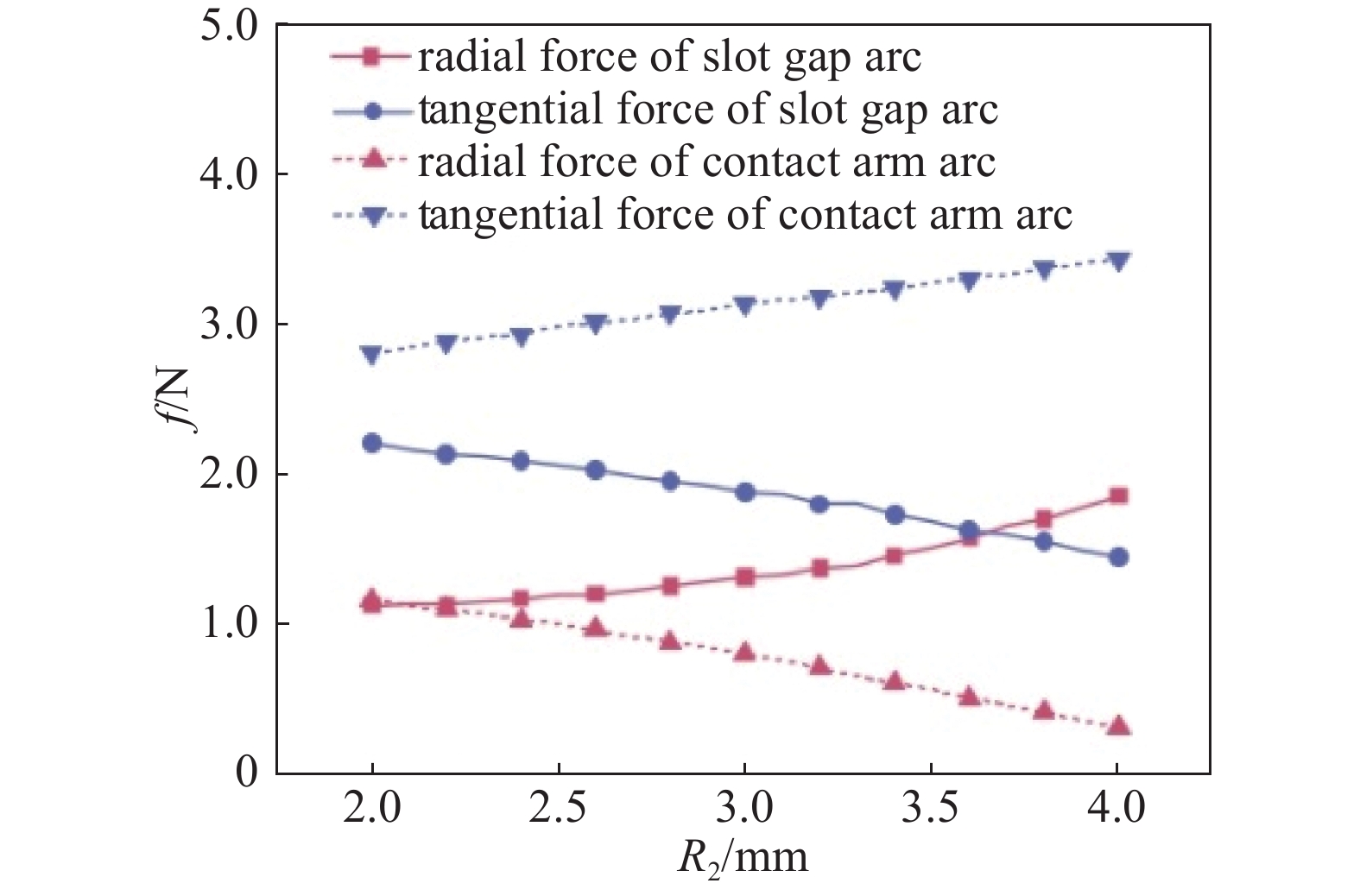
电弧所受磁吹力变化如图12所示，比对分析如下：
当电弧位于触头槽隙，R2从2.0 mm增至4.0 mm时，电弧所受磁吹力切向力逐渐减弱，径向力渐增。在R2增大到3.0 mm之后径向力增加显著，R2在3.7 mm左右，电弧位于槽隙时所受径向力大于切向力，电弧沿槽隙方向运动，跨越槽隙难度增加。
当电弧位于触臂上，触头槽隙宽度逐渐增加时，电弧所受切向力逐渐增强，径向力逐渐减弱。因此槽隙宽度增加时，电弧在触臂上的运动速度增加。
槽隙宽度越小，电弧所受切向力越大，同时径向力越小，越有利于电弧跨越槽隙；槽隙宽度减小在一定范围内可以减小槽隙对于电弧所带来的不利影响。但电弧在触臂上运动时切向力减小，电弧在触臂上的运动速度减小。
-
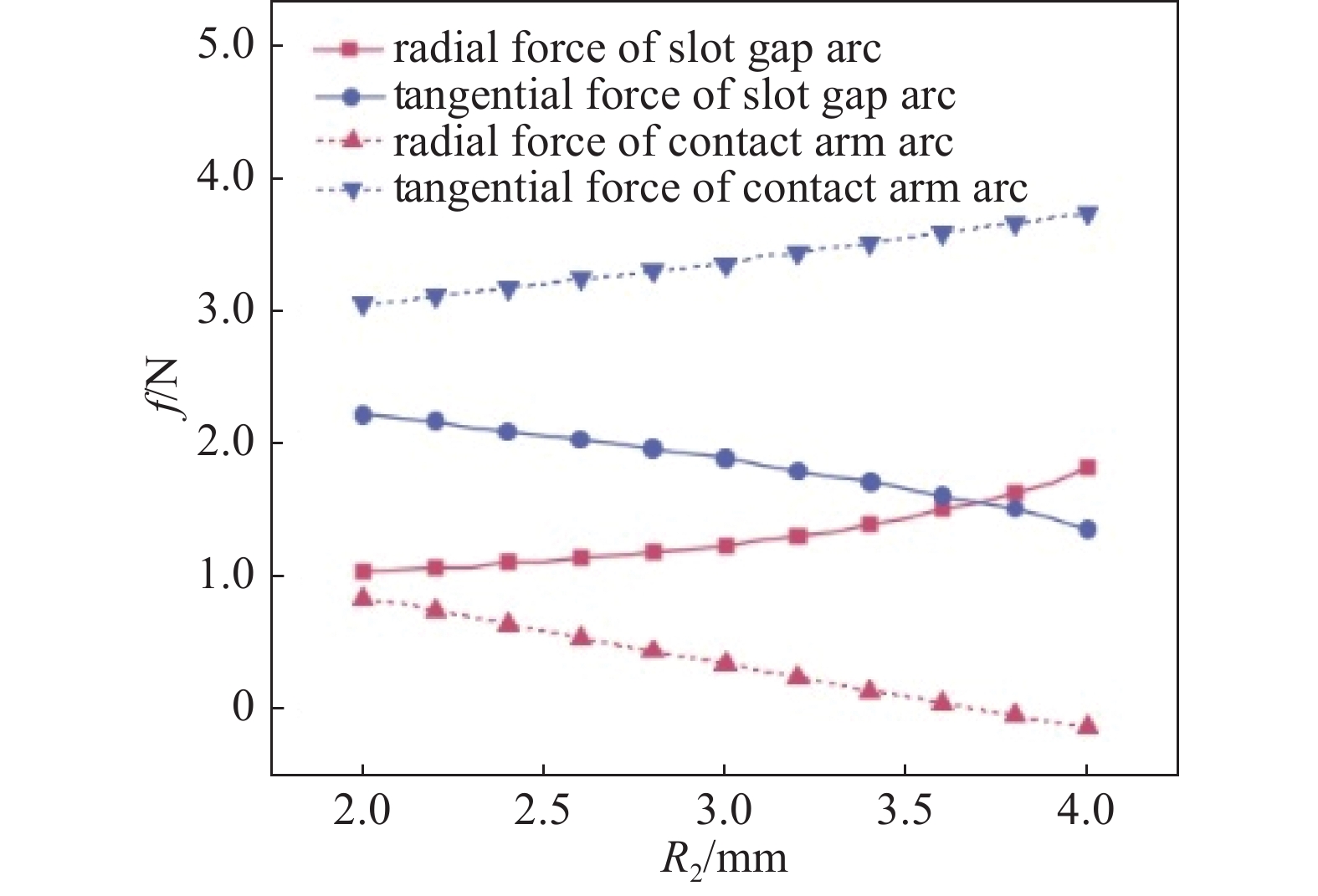
将横磁触头结构示意图中xA向触头外侧移动至5.0 mm时，改变R2大小分析电弧受力变化。如图13可知，R2从2.0 mm变化到4.0 mm的过程中，触臂电弧受切向力增加，径向力减弱；槽隙电弧受切向力减小，径向力增加，变化趋势与xA为4.0 mm时变化趋势相同。当R2大于3.7 mm左右时，触臂电弧所受径向力变为负值，可能驱使电弧向触头中心移动，不利于电弧粒子的逸散，从而降低断路器的开断性能。
相较于图12比对分析，xA为5.0 mm时，触臂电弧所受切向力始终大于xA为4.0 mm的情况，而径向力始终小于xA为4.0 mm的情况，且在R2增大的过程中，触臂电弧所受切向力和径向力的变化趋势较xA为4.0 mm更为显著；对于槽隙弧柱，将xA从4.0 mm增加至5 mm时电弧所受切向力和径向力变化不大。
分析表4可知，固定R2为3.0 mm时，xA为4.0 mm和5.0 mm两种情况下的电弧受力，随着A点向触头外侧移动，槽隙电弧所受磁吹力切向力和径向力均有减小，切向力减小了0.006 N，径向力减小了0.104 N。电弧所受切向力占磁吹力的比重明显增加。因此，将槽隙起点向触头外侧适当移动时，利于电弧跨越槽隙，增强开断性能。
通过以上分析可知槽隙起点(xA)和槽隙宽度(R2)两者均对电弧运动行为有直接影响。槽隙电弧能否成功跨越槽隙主要影响因素是R2。触臂电弧的运动速度的主要影响因素为触臂面积，触臂面积越小时，触臂电弧受到的切向力越大，切向运动速度越快，更有利于电弧围绕触头外表面做圆周运动。因此xA和R2的变化均转变为对触臂面积的影响，当改变xA和R2大小使得触臂面积减小时，电弧电流密度增加，触头极间磁场和电弧所受切向力均有增加，有利于断路器开断。但在触头面积减小到一定数值时，电弧所受径向力方向指向触头内侧，可能驱使电弧向着触头中心运动，导致断路器的开断能力降低。
-
采用有限元方法，对12 kV/1250 A/25 kA真空断路器所用万字型触头进行数值模拟与可视化分析。研究表明，电弧所受磁吹力与触头间隙磁场和电弧长度关系密切。当极间距增加时，即使触头中心面的磁场强度会减弱，但随着电弧长度增加，电弧所受磁吹力越大。在开断大电流时，可以增加触头刚分速度，使得电弧在触头表面有较高的旋转速度从而减少电弧对于触头表面的烧蚀，以提高开断性能。
仿真表明，增加xA时，电弧所受切向力占总力的比重更大，利于电弧运动，对于本研究对象（直径为42.0 mm横磁触头），xA为5.0 mm时极间磁场和电弧受力优于4.0 mm。
为探究槽隙宽度对于电弧运动的影响，设置R2在2.0~4.0 mm范围内变化，槽隙宽度越小，电弧位于槽隙时所受切向磁吹力比重越大，越有利于电弧跨越槽隙，但同时会牺牲电弧在触臂上的切向力，减小电弧在触臂上的运动速度。将触头开槽位置向外侧移动时，电弧在槽隙上的切向力和电弧在触臂上的切向力显著增加，可弥补槽隙变窄而降低触臂电弧运动速度。
直流横磁真空灭弧室电弧运动特性影响因素分析
Analysis of Influencing Factors of Arc Motion Characteristics of DC Transverse Magnetic Vacuum Interrupter
-
摘要: 在故障开断过程中，横磁真空灭弧室内部的金属蒸气电弧等离子体受横向磁场的作用沿触头表面高速运动，电弧动态演化行为直接影响真空断路器的开断性能。文章结合断路器机构运动特性曲线，建立12 kV/1250 A/25 kA真空灭弧室横磁触头系统三维磁场有限元模型，研究伴随开断进程极间磁场和电弧所受磁吹力变化规律，并探究机构运动特性对开断性能的影响。研究结果表明，提高机构速度特性可以增大电弧弧根在触头表面的旋转速度，但同时会减弱极间磁场。此外，通过仿真分析触头结构参数对电弧作用力的影响，发现将槽隙起点向触头外侧移动或减小槽隙宽度均有利于电弧跨越槽隙，减小电弧在触头表面的停滞时间，有利于提高断路器的开断能力。Abstract: During the fault breaking process, the metal vapor arc plasma in the vacuum interrupter with a transverse magnetic field moves at high speed along the contact surface, and the evolution of the arc dynamic behavior directly affects the breaking performance of the vacuum circuit breaker. In this paper, in order to study the action of magnetic blowing force on the arc during the breaking process, and to analyze the influence of the motion characteristics of the operating mechanism on the breaking performance, combing the operating mechanism characteristic of the 12 kV/1250 A/25 kA vacuum circuit breaker, a three-dimensional finite element transverse magnetic field model is established. The research results indicate that the rotational speed of the arc root on the contact surface can be increased by improving the speed characteristics of the mechanism; however, the magnetic field is correspondingly weakened. In addition, by analyzing the effect of contact structure parameters on the force exerted on the arc, it can be obtained that, moving the starting point of the slot towards the outside of the contact or reducing the slot width is beneficial for the arc to cross the slot, and the stagnation time of the arc on the contact surface can be reduced to improve the breaking capacity of the vacuum circuit breaker.
-
Key words:
- Vacuum circuit breaker /
- Vacuum arc plasma /
- Transverse magnetic field /
- Operating mechanism .
-
-
图 4 5 kA直流故障开断电流和机构位移/时间特性曲线
Figure 4. 5 kA DC fault breaking current and mechanism displacement/time characteristic curve
图 5 不同极间距下电弧速度变化（5 kA燃弧电流）
Figure 5. Arc velocity at different pole spacing (5 kA arc current)
图 6 不同极间距下电弧弧根运动轨迹示意图
Figure 6. Schematic diagram of arc root motion trajectory under different pole spacing
图 7 不同极间距下磁场分布和电弧受力示意图。（a）极间距1.0 mm，（b）极间距3.0 mm，（c）极间距5.0 mm，（d）极间距7.0 mm，（e）极间距9.0 mm，（f）极间距10.0 mm
Figure 7. Distribution of magnetic field and force at different gap distances. (a) Gap distance 1.0 mm, (b) gap distance 3.0 mm, (c) gap distance 5.0 mm, (d) gap distance 7.0 mm, (e) gap distance 9.0 mm, (f) gap distance 10.0 mm
图 8 不同极间距下磁场纵向分布。（a）极间距3.0 mm，（b）极间距10.0 mm
Figure 8. Longitudinal distribution of magnetic field at different gap distances. (a) Gap distance 3.0 mm, (b) gap distance 10.0 mm
图 9 电弧受力坐标变换示意图
Figure 9. Schematic diagram of coordinate transformation of the force exerted on the arc
图 10 横磁触头结构主要参数及弧柱位置
Figure 10. Main parameters and arc column position of transverse magnetic contact structure
图 12 弧柱受力随槽隙宽度变化（xA=4.0 mm）
Figure 12. The force exerted on the arc varying with the width of the slot gap (xA=4.0 mm)
图 13 弧柱所受磁吹力随槽隙宽度的变化（xA=5.0 mm）
Figure 13. The variation of the force exerted on the arc column with the width of the groove (xA=5.0 mm)
表 1 触头系统材料参数取值
Table 1. Material parameters of contact
结构部件与电弧区域 材料与组成 电导率/S/m 相对磁导率 导电杆 Cu 5.8×107 0.999991 触头片 CuCr25 2.8×107 1.0 电弧 Arc 2800.0 1.0 
下载: 导出CSV
表 2 触头间隙中心平面最大磁感应强度变化
Table 2. Variation of maximum magnetic induction intensity in the center plane of the contact gap
la/mm 弧柱位置与坐标 触头中心最大
磁感应强度/mT1.0 1#,（17.25，0） 572.13 2.0 2#,（17.24，−0.39） 539.34 3.0 3#,（17.202，−1.322） 507.23 4.0 4#,（16.92，−3.451） 487.57 5.0 5#,（16.26，−5.877） 497.13 6.0 6#,（15.019，−8.7297） 477.37 7.0 7#,（13.021，−11.64） 400.96 8.0 8#,（11.283，−13.426） 408.34 9.0
10.09#,（5.216，−17.447）
10#,（−1.5268，−17.68）408.21
438.93
下载: 导出CSV
表 3 不同极间距下弧柱所受磁吹力
Table 3. Magnetic blowing force on arc at different pole spacing
la/mm f/N fx/N fy/N fθ/N fr/N 1.0 0.8234 0.109 −0.816 0.816 0.109 2.0 1.4801 0.136 −1.474 1.475 0.169 3.0 2.013 0.044 −2.013 2.010 0.194 4.0 2.569 −0.339 −2.487 2.506 0.151 5.0 3.1177 −0.948 −2.970 3.116 0.093 6.0 4.1245 −1.865 −3.468 3.937 0.082 7.0 2.7226 −0.87 8 −2.577 2.521 1.028 8.0 3.0008 −1.052 −2.811 2.634 1.640 9.0 3.6073 −1.882 −3.078 2.724 2.365 10.0 3.9508 −3.869 −0.797 3.784 1.136
下载: 导出CSV
表 4 A点水平位置对电弧所受磁吹力的影响（R2=3.0 mm）
Table 4. The influence of the horizontal position of point A on the magnetic blowing force acting on the arc (R2=3.0 mm)
弧柱位置 xA/mm fθ/N fr/N 触头触臂 4.0 3.1505 0.8166 5.0 3.3802 0.3568 触头槽隙 4.0
5.01.893
1.8871.3289
1.2253
下载: 导出CSV
-
[1] 邹积岩, 陈军平, 刘晓明, 等. 真空开关技术[M]. 北京: 机械工业出版社, 2021 (in Chinese) Zou J Y, Chen J P, Liu X M, et al. Vacuum switch technology[M]. Beijing: China Machine Press, 2021 [2] Sun L, Yu L, Liu Z, et al. An opening displacement curve characteristic determined by high-current anode phenomena of a vacuum interrupter[J]. IEEE Transactions on Power Delivery,2013,28(4):2585−2593 doi: 10.1109/TPWRD.2013.2264487 [3] Wang H Y, Dong E Y, Yin G X, et al. Research on the new type of 12 kV inflatable vacuum circuit breaker[J]. Applied Mechanics and Materials,2013,397:1230−1235 [4] 王季梅. 真空开关技术与应用[M]. 北京: 机械工业出版社, 2008 (in Chinese) Wang J M. Vacuum switch technology and application[M]. Beijing: China Machine Press, 2008 [5] Schade E. Physics of high-current interruption of vacuum circuit breakers[J]. IEEE Transactions on Plasma Science,2005,33(5):1564−1575 doi: 10.1109/TPS.2005.856530 [6] 王浩, 陆金桂, 韦伦存, 等. 横向磁场作用下真空电弧阴极过程数学模型的研究[J]. 中国电机工程学报,1996,16(2):79−82 (in Chinese) Wang H, Lun J G, Wei L C, et al. Mode for the cathode mechanism in a transverse magnetic steered vacuum arc[J]. Proceedings of the CSEE,1996,16(2):79−82 [7] 修士新, 庞先海, 张敏, 等. 真空灭弧室横向磁场触头间磁吹力的计算分析[J]. 真空电子技术,2007(5):19−22 (in Chinese) doi: 10.3969/j.issn.1002-8935.2007.05.005 Xiu S X, Pang X H, Zhang M, et al. Calculation and analysis of magnetic blowing force between transverse magnetic field contacts in vacuum interrupters[J]. Vacuum Electronics,2007(5):19−22 doi: 10.3969/j.issn.1002-8935.2007.05.005 [8] 段肖力, 修士新, 吴水锋, 等. 真空开关横磁触头磁场仿真与电弧特性研究[J]. 高压电器,2017,53(3):57−63 (in Chinese) Duan X L, Xiu S X, Wu S F, et al. Simulation of magnetic field and arc characteristics of transverse magnetic contacts in vacuum switches[J]. High Voltage Apparatus,2017,53(3):57−63 [9] Dullni E. Motion of high-current vacuum arcs on spiral-type contacts[J]. IEEE Transactions on Plasma Science,1989,17(6):875−879 doi: 10.1109/27.41226 [10] Dullni E, Schade E, Shang W. Vacuum arcs driven by cross-magnetic fields (RMF)[J]. IEEE Transactions on Plasma Science,2003,31(5):902−908 doi: 10.1109/TPS.2003.818445 [11] Kaltenecker A, Schussek M. Anode-spot formation and motion of vacuum arcs[J]. IEEE Transactions on Plasma Science,1985,13(5):269−276 doi: 10.1109/TPS.1985.4316418 [12] 丁璨, 王周琳, 袁召, 等. 基于多目标灰狼优化算法与RBF神经网络的真空灭弧室触头结构优化设计[J]. 高电压技术,2024,50(2):543−550 (in Chinese) Ding C, Wang Z L, Yuan Z, et al. Optimization design of vacuum arc extinguishing chamber contact structure based on multi-objective grey wolf optimization algorithm and RBF neural network[J]. High Voltage Technology,2024,50(2):543−550 -
计量
- 文章访问数: 49
- HTML全文浏览数: 49
- PDF下载数: 0
- 施引文献: 0