-
多主元合金(multi-principal element alloys, MPEAs), 通常被称为高熵合金(high-entropy alloys, HEAs), 是一类多种元素以等原子比或近等原子比混合而成的材料. 这些合金通常形成面心立方(face-centered cubic, FCC)或体心立方(body-centered cubic, BCC)晶体结构的单相固溶体, 与传统合金中主要元素和次要元素分明的设计理念截然不同[1–6]. 多主元合金的这一创新设计理念不仅改变了合金的设计方法, 也为材料科学领域提供了新的研究思路和方向.
多主元合金因其优异的综合性能而备受关注. 例如, 它们在力学性能[7–9]、热稳定性、抗腐蚀性[10]、抗疲劳性[11]、超导性[12]和耐辐照性能[13,14]等方面表现出传统合金无法媲美的优势, 使其在航空航天、能源、电子器件等众多领域具有广泛的应用潜力. 这些卓越性能的背后, 主要得益于多主元合金的四大核心效应: 高熵效应、晶格畸变效应、缓慢扩散效应和“鸡尾酒”效应[15–17]. 其中, 晶格畸变效应在合金性能中的作用尤为重要. 研究表明, 局部晶格畸变不仅导致位错线的弯曲, 从而使得多主元合金的变形机制显著不同于传统合金, 还可能通过阻碍位错的运动, 显著增强合金的强度. 同时, 局部晶格畸变也会增大电子与声子的散射, 从而降低多主元合金的导电性和导热性[18,19].
定量评价晶格畸变对于揭示其对多主元合金性能的影响至关重要. 目前, 晶格畸变的研究主要依赖于实验技术, 如X射线衍射[20–23](X-ray diffraction, XRD)和透射电子显微镜[24–26] (transmission electron microscope, TEM), 以及基于密度泛函理论(density functional theory, DFT)的第一性原理计算和分子动力学(molecular dynamics, MD)模拟等计算方法[27–29]. 例如, Toda-Caraballo 等[27]基于元素的晶胞参数和体积模量来预测晶格畸变. 然而, 该方法在处理具有复杂微观结构或第二相析出的合金时存在局限性, 并且需要进一步的实验验证以确保预测结果的准确性. Chen等[29]通过计算弛豫后实际原子位置相对于完美晶格位置的偏离程度来描述晶格畸变, 此方法能够较好地描述合金的整体晶格畸变情况, 但在精确表征原子尺度的局域晶格畸变时仍存在一定的局限性. 此外, 一些物理模型和机器学习方法也被提出, 用以基于合金成分快速预测晶格畸变, 然而这些方法在描述电负性显著不同但原子尺寸相近的合金系统时仍然存在一定的局限性[30]. 快速且准确地预测任意合金成分的晶格畸变依旧是一个亟待解决的挑战, 这在很大程度上限制了多主元合金设计空间的探索与应用.
为了更全面地捕捉原子尺度的局域晶格畸变, 本研究采用分子动力学模拟, 并通过原子的冯·米塞斯(Von Mises)应变和体积应变作为描述符, 深入分析多主元合金中的局部晶格畸变. 这种方法能够在原子尺度上提供详细的畸变信息, 有助于深入理解多主元合金的力学性能. 我们选择了3种典型的BCC结构多主元合金作为模型材料, 即TaWNbMo, TiZrNb和Co16.67Fe36.67Ni16.67Ti0.3 (以下简称TaWNbMo, TiZrNb和CoFeNiTi), 这些合金的晶格畸变程度逐渐增大. 通过分子动力学模拟, 研究了这3种合金的原子应变特征, 包括各组分的原子应变行为、温度效应以及化学短程有序效应.
-
为了计算BCC结构下TaWNbMo, TiZrNb, CoFeNiTi合金的原子应变, 首先在每种合金中通过元素原子随机分布在晶格格点上, 构建了包含31250个原子的随机固溶体(random solid solution, RSS)结构. 使用LAMMPS软件进行分子动力学模拟[31], 采用机器学习势函数(针对Ta-W-Nb-Mo[32])和嵌入原子方法(EAM势, 针对Ti-Zr-Nb[29]和Co-Fe-Ni-Ti体系[33])来描述原子间的相互作用. 在0 K温度下, 对每种合金在其平衡体积下进行了结构优化(即使用共轭梯度法进行能量最小化), 使每个原子弛豫至局部能量最小值的稳定状态. 对于有限温度下的模拟, 我们在NPT系综(固定原子数、压力和温度)条件下运行了100 ps, 从而获得了不同温度下的原子构型. 在研究的BCC多主元合金体系中, 由于原子尺寸的显著差异, 原子会偏离理想的晶格点位, 导致晶格结构发生显著的畸变, 表现出一定程度的晶格扭曲. 所有原子构型都通过OVITOS软件进行可视化展示[34].
-
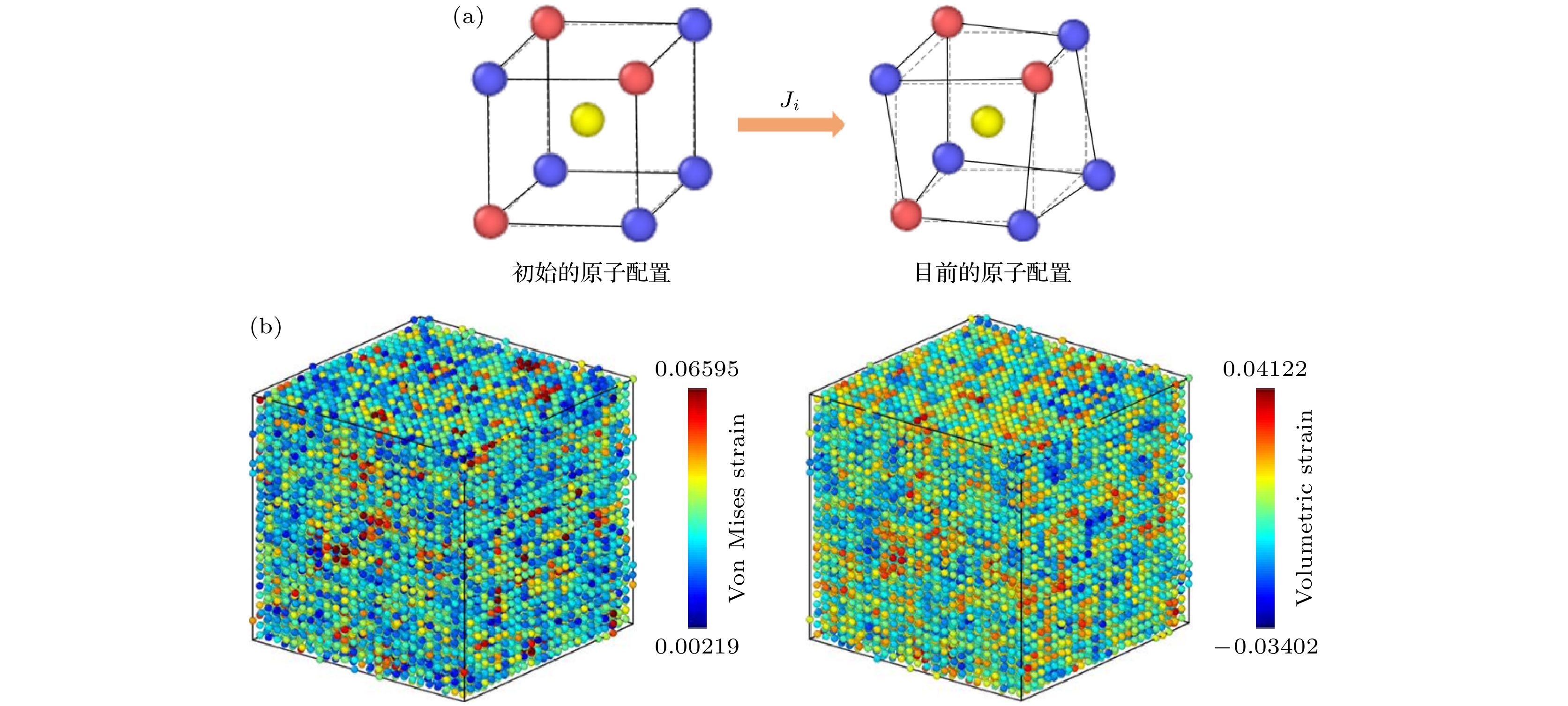
由于应变是一个相对的测量[35], 通常需要比较初始和当前的两个原子构型, 从而计算出每个原子的局部应变[36]. 定义整数
$ {N}_{i} $ 为当前构型中原子$ i $ 的最近邻数 (对于BCC晶体结构,$ {N}_{i} $ = 8). 对于原子$ i $ 的每个最近邻原子$ j $ , 它们目前的间隔为它们初始的间隔为
需要注意的是,
$ {d}_{ij} $ 和$ {d}_{ij}^{0} $ 等都被认为是行向量.如图1(a)所示, 我们寻求一个局部仿射变换矩阵
$ {J}_{i} $ , 使得换言之, 我们寻求最小的
$ {J}_{i} $ :执行上面的任意矩阵变换
$ \delta {J}_{i}^{{\mathrm{T}}} $ , 可得到:如果对于任意
$ \delta {J}_{i}^{{\mathrm{T}}} $ 上述为真, 则矩阵:换言之, 必须有:
如果定义:
可以得到简单的
拉格朗日应变矩阵计算如下:
那么可以计算第i个原子的原子体积应变:
校准到
$ {\eta }_{xx} $ =$ {\eta }_{yy} $ =$ {\eta }_{zz} $ = a, 那么其局部剪切不变量:图1(b)展示了TiZrNb合金中每个原子的
$ {\eta }_{i}^{{\mathrm{M}}{\mathrm{i}}{\mathrm{s}}{\mathrm{e}}{\mathrm{s}}} $ 和$ {\eta }_{i}^{{\mathrm{h}}{\mathrm{y}}{\mathrm{d}}{\mathrm{r}}{\mathrm{o}}} $ 的计算结果, 分别对应于原子尺度冯·米塞斯应变和体积应变. -
采用基于分子动力学的蒙特卡罗模拟(Monte Carlo, MC)方法, 以获得800 K下TiZrNb合金的局域化学有序构型[37]. MC模拟共运行了2000000步, 这相当于每个原子大约进行60次交换实验. 流程如下: I)计算初始构型的能量; II)通过随机交换两个原子获得新的构型, 每次原子交换被认为是一个MC步骤; III)对每个MC步骤得到的新构型进行能量计算; IV) 判断是否接受本次交换. 依据Metropolis算法, 新配置被接受的概率为
其中,
$ {{\Delta }}E $ 为由于原子位置的交换而引起的系统能量差,$ {k}_{{\mathrm{B}}} $ 是玻尔兹曼常数,$ {T}_{{\mathrm{M}}{\mathrm{C}}} $ 为温度. 新构型一旦被接受, 就被迭代为初始构型, 并重复上述操作. 最终, 系统能量和原子构型在经历足够数量的MC步骤之后收敛.为了描述原子对的化学偏好性, 采用经典的Warren-Cowley参数来量化局域化学有序. 其被定义为
其中,
$ k $ 表示第$ k $ 最邻近原子层,$ {N}_{ij}^{k} $ 表示在$ i $ 类原子的第$ k $ 最邻近原子层中$ j $ 原子出现的实际数量,$ {X}_{j} $ 表示合金中$ j $ 类原子的浓度,$ n $ 表示第$ k $ 最邻近原子层的原子总数.$ {\delta }_{ij}^{k} $ 的正(负)值对应于不利(有利)的i-j原子对的偏好趋势. 对于理想的随机固溶体合金而言,$ {\delta }_{ij}^{k} = 0 $ . 本文只讨论第一邻近原子层的原子对偏好, 后续论述中$ k $ 值默认为1. -
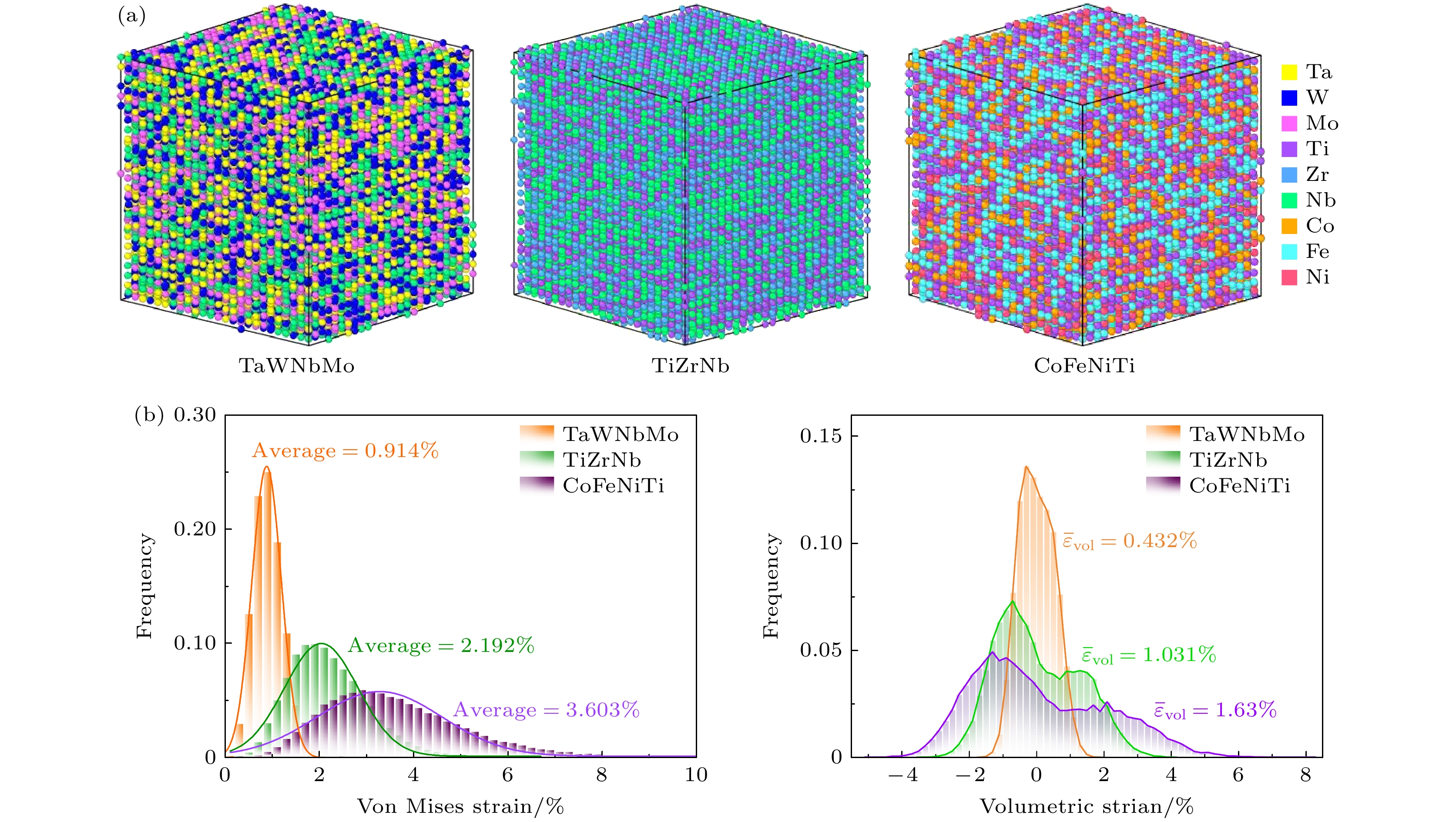
图2(a)给出TaWNbMo, TiZrNb和CoFeNiTi三种合金体系的三维原子分布模型. 通过将不同颜色映射到不同类型的元素上, 可以清晰地展示多主元合金中原子的随机分布特征. 定义变量[29]:
其中, N为构型中原子总数, (
$ {x}_{i}' , {y}_{i}' , {z}_{i}' $ )表示原子$ i $ 在完美晶格中的位置坐标, ($ {x}_{i}, {y}_{i}, {z}_{i} $ )表示原子$ i $ 结构弛豫后的位置坐标.$ {{\Delta }}d $ 表示结构松弛后原子的位置与完美晶格中相应的理想位置之间的偏差, 即反映由局部晶格畸变引起的原子位移. 用(15)式计算3种合金体系的晶格畸变, 得到$ {{\Delta }}{d}_{{\mathrm{TaWNbMo}}} = 0.042\;\text{Å} $ ,$ {{\Delta }}{d}_{{\mathrm{T}}{\mathrm{i}}{\mathrm{Z}}{\mathrm{r}}{\mathrm{N}}{\mathrm{b}}}=0.104\;\text{Å} $ ,$ {{\Delta }}{d}_{{\mathrm{C}}{\mathrm{o}}{\mathrm{F}}{\mathrm{e}}{\mathrm{N}}{\mathrm{i}}{\mathrm{T}}{\mathrm{i}}} =0.154\;\text{Å} $ , 表示3种合金的晶格畸变程度大小: TaWNbMo < TiZrNb < CoFeNiTi.此外, 由于合金中化学元素环境的复杂性, 局域晶格畸变呈现出一定的展宽分布, 并呈现类高斯形态. 图2(b)展示了这3种合金体系的冯·米塞斯应变和体积应变分布, 其中不同颜色的曲线代表不同的合金体系. 如图所示, 对于冯·米塞斯应变, TaWNbMo合金中整体的冯·米塞斯应变最小, 且其应变分布最为集中, 应变范围处于0—2%之间, 均值为0.914%; TiZrNb合金中冯·米塞斯应变分布的范围处于0—5%之间, 均值为2.192%; 而CoFeNiTi合金表现出最显著的冯·米塞斯应变特征, 应变最大值能够达到~10%, 平均应力水平为3.603%.
体积应变的负值表示体积收缩, 原子受到拉伸应力, 正值则表示体积膨胀, 原子遭受压缩应力. 为了清晰衡量3种合金体系中整体体积应变的相对大小, 对所有原子所遭受的局部体积应变的绝对值进行求和, 并计算其平均值, 定义如下:
从图2(b)可以看出, TaWNbMo, TiZrNb和CoFeNiTi的
$ {\overline{\varepsilon }}_{{\mathrm{v}}{\mathrm{o}}{\mathrm{l}}} $ 分别为0.432%, 1.031%, 1.63%, 表明3种合金中整体遭受的体积应变大小: TaWNbMo < TiZrNb < CoFeNiTi.上述结果表明, 原子冯·米塞斯应变和原子体积应变可有效描述合金的局域晶格畸变特征. 晶格畸变较小的合金体系表现出较低的冯·米塞斯应变和体积应变, 而晶格畸变较大的合金体系则表现出较高的冯·米塞斯应变和原子体积应变.
值得注意的是, TaWNbMo合金的体积应变分布曲线呈现单峰, 而TiZrNb合金和CoFeNiTi合金则呈现双峰, 且CoFeNiTi合金的双峰间距较大. 我们认为, 这一现象源于WMoNbTa合金中各组元的原子半径差异较小, 而TiZrNb和CoFeNiTi合金中原子半径差异较大. 较大体积的原子膨胀, 导致体积应变分布图中的正值部分出现一个峰; 而体积较小的原子收缩, 导致负值部分出现另一个峰. 详细讨论将在下文展开.
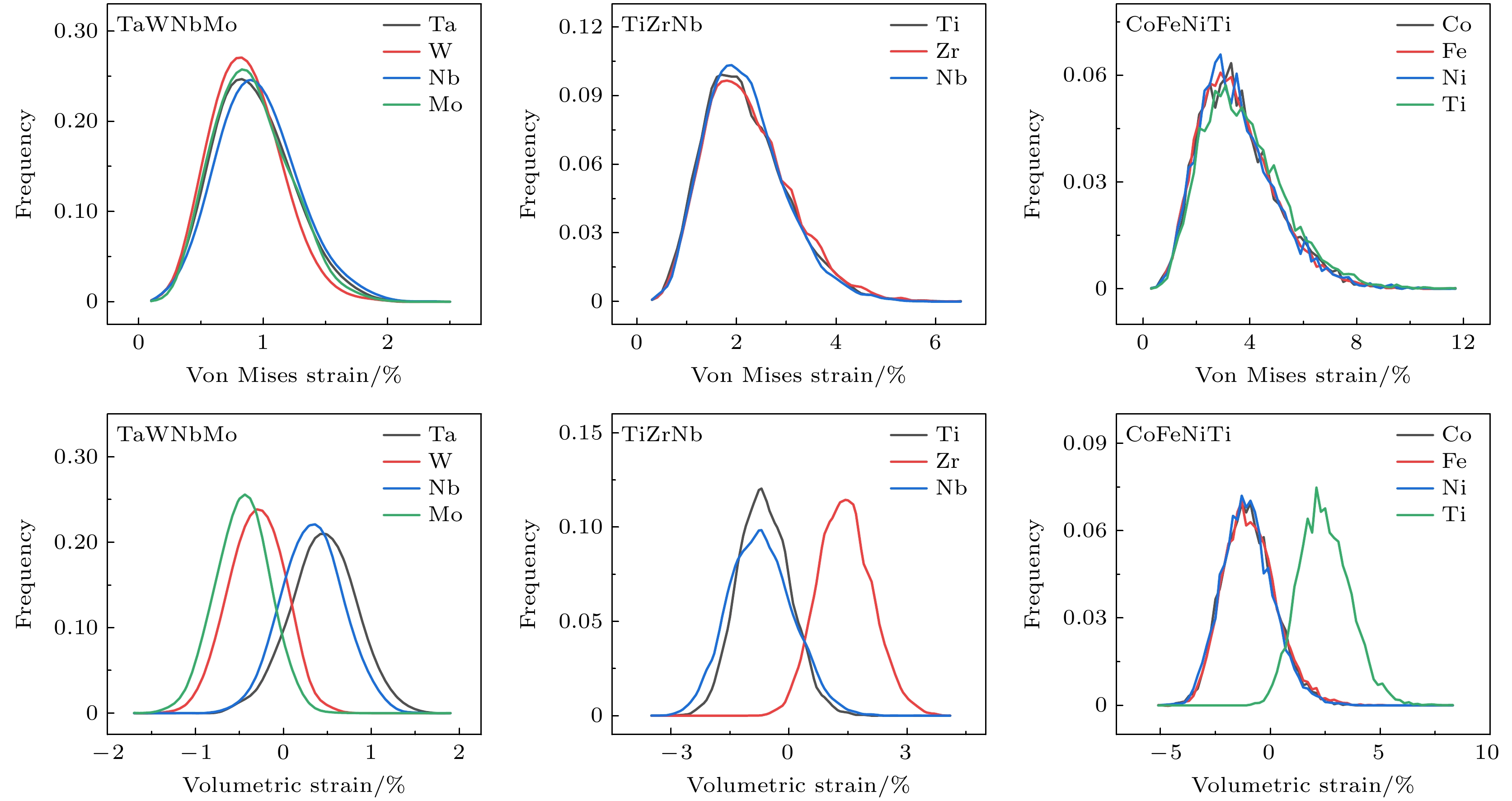
接下来, 讨论合金中原子应变是否受到元素尺寸效应的影响. 图3展示了TaWNbMo, TiZrNb和CoFeNiTi合金体系中不同组元的冯·米塞斯应变和体积应变分布情况. 对于冯·米塞斯应变, 3种合金中各组元的频率分布曲线几乎重合, 并且与对应合金体系的整体分布形态一致(见图2(b)), 这表明合金的冯·米塞斯应变几乎不受组成元素原子尺寸的影响. 即使在元素尺寸差异显著的合金体系中, 这一趋势依然成立.
然而, 在体积应变的分布上, 不同组元的频率分布表现出了明显的差异. 原子半径较小的组元主要分布在负半轴, 而原子半径较大的组元则分布在正半轴. 这表明在合金中较大尺寸的元素通常会遭受压缩应力, 而较小尺寸的元素则经历拉伸应力. 对比3种合金体系的体积应变分布图, 可发现TaWNbMo, TiZrNb和CoFeNiTi合金体系中不同组元的体积应变峰值差值分别约为1%, 3%和5%. 这一差异是由于TaWNbMo, TiZrNb和CoFeNiTi合金中组成元素间原子半径差异逐渐增大所致. 这一现象也反映了3种合金中晶格畸变的逐步增大趋势, 且与图1(b)中的结果一致.
多主元合金由于具有复杂且可调的元素化学环境[38], 使得在退火过程中常常形成化学短程有序结构. 在这一演化过程中, 化学短程有序结构导致合金元素在纳米尺度上发生显著重排, 进而对合金的微观力学性能产生重要影响[39–43]. 因此, 揭示化学短程有序结构与原子应变之间的物理关联具有重要意义.
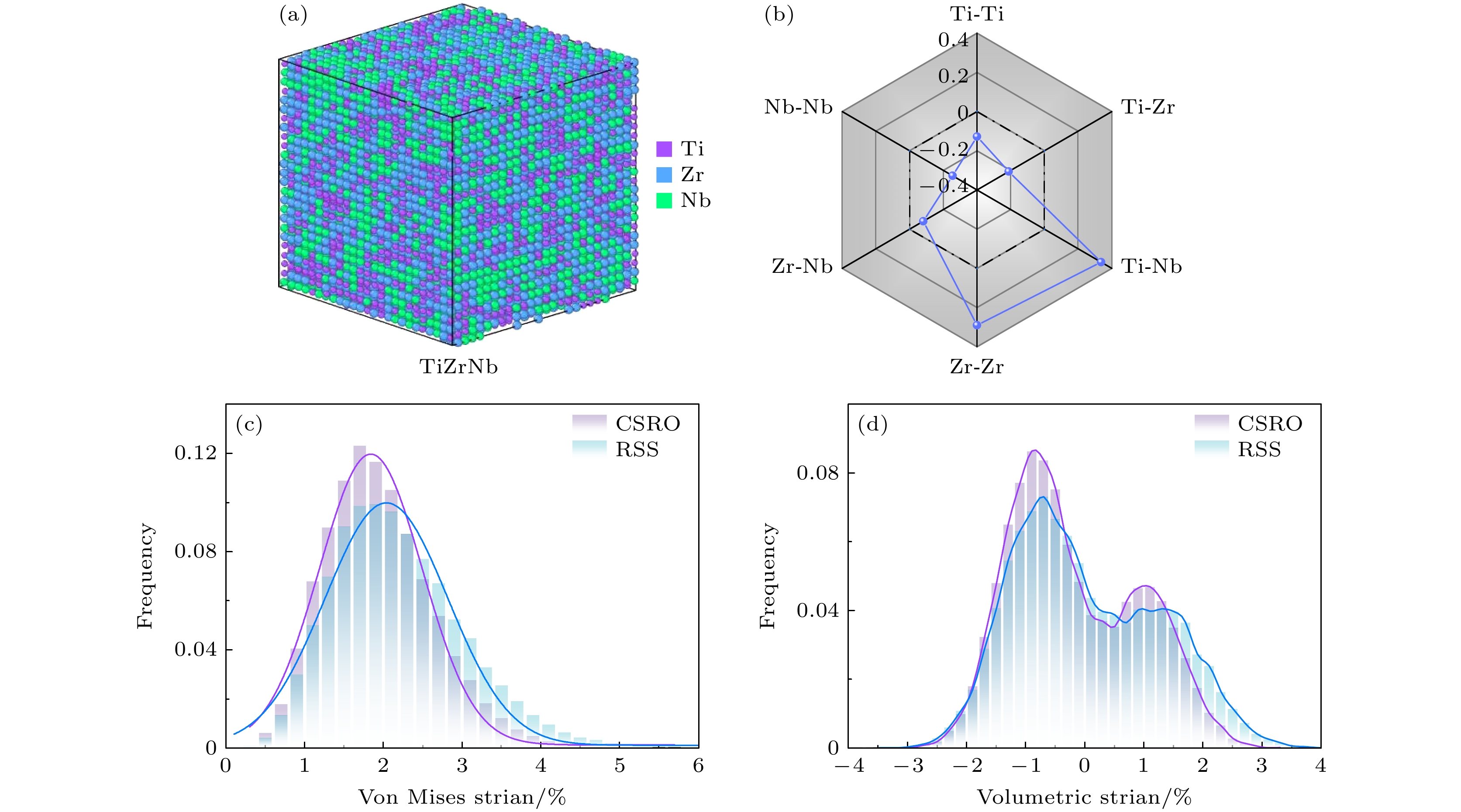
为了研究这一关联, 采用基于分子动力学的蒙特卡罗模拟获得了TiZrNb合金在800 K下的化学短程有序结构(见方法2.3). 图4(a)展示了合金的三维原子分布模型, 其中不同颜色对应不同的元素种类, 清晰地显示了合金中原子间的有序排列特征. 为了量化化学短程有序结构, 使用Warren-Cowley参数对TiZrNb合金第一邻近原子层的化学短程有序特征进行了表征. 结果如图4(b)所示, 其中
$ {\delta }_{{\mathrm{T}}{\mathrm{i}}-{\mathrm{N}}{\mathrm{b}}}^{} $ 和$ {\delta }_{{\mathrm{Z}}{\mathrm{r}}-{\mathrm{Z}}{\mathrm{r}}}^{} $ 大于零, 而$ {\delta }_{{\mathrm{T}}{\mathrm{i}}-{\mathrm{T}}{\mathrm{i}}}^{} $ ,$ {\delta }_{{\mathrm{T}}{\mathrm{i}}-{\mathrm{Z}}{\mathrm{r}}}^{} $ ,$ {\delta }_{{\mathrm{Z}}{\mathrm{r}}-{\mathrm{N}}{\mathrm{b}}}^{} $ 和$ {\delta }_{{\mathrm{N}}{\mathrm{b}}-{\mathrm{N}}{\mathrm{b}}}^{} $ 小于零, 这表明TiZrNb合金更倾向于形成Ti-Ti, Ti-Zr, Zr-Nb和Nb-Nb原子对, 而不倾向于形成Ti-Nb和Zr-Zr原子对.图4(c), (d)展示了RSS和CSRO TiZrNb构型的冯·米塞斯应变和体积应变的分布情况. 紫色柱状图表示CSRO构型的频率分布, 而蓝色柱状图代表RSS构型的频率分布. 结果表明, 相较于RSS构型, CSRO构型的冯·米塞斯应变和体积应变均较小, 且其分布更为集中. 这一现象表明, 化学短程有序结构的形成可以有效地减小合金的原子应变, 从而改变合金的整体力学性能. 在之前的研究中已经表明, 随着化学短程有序程度的增大, 晶格畸变会减小[37]. 这一发现进一步验证了采用原子应变来描述晶格畸变的方法的准确性. 这些结果为理解化学短程有序结构在多主元合金中的作用提供了有力的支持, 并为未来设计具有优异力学性能的合金材料提供了重要依据.
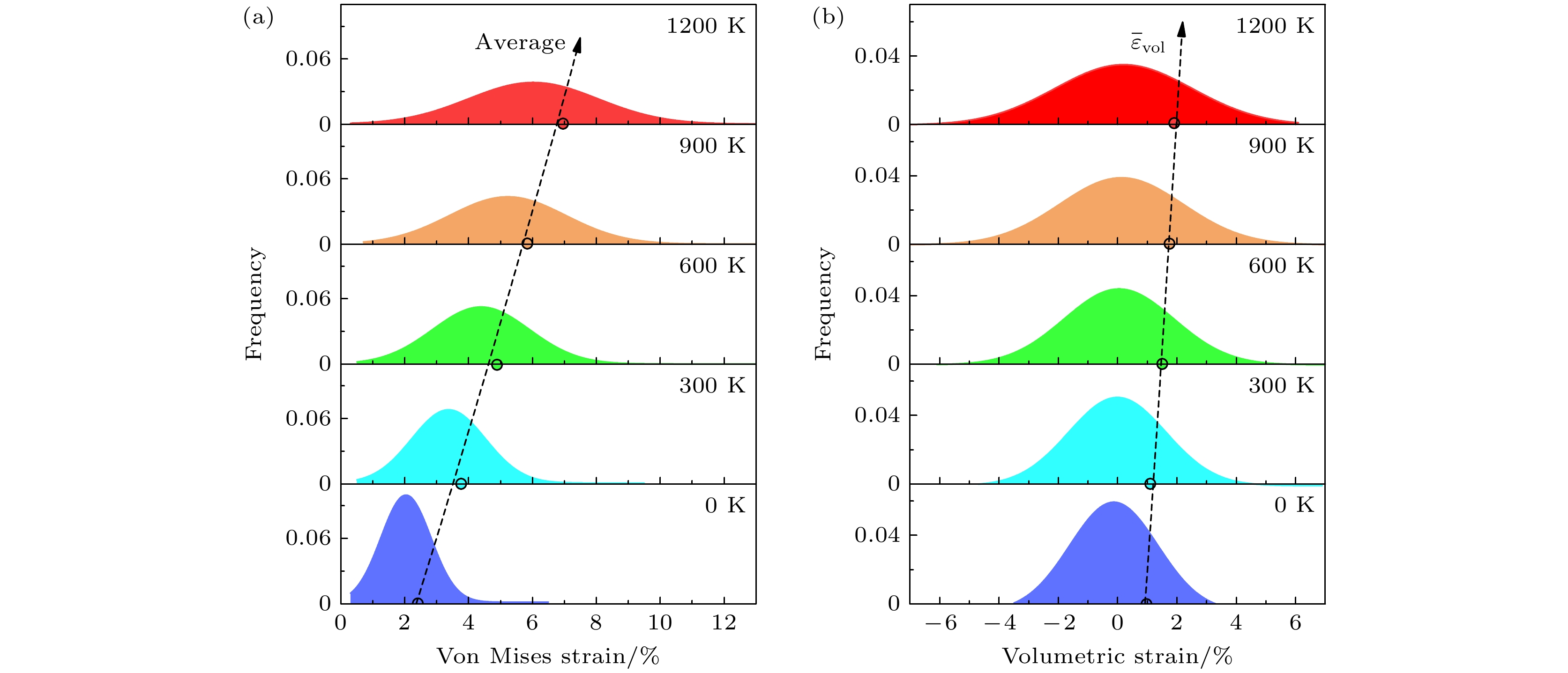
最后, 讨论温度对于合金中原子应变的影响. 我们分别计算了TiZrNb合金在0, 300, 600, 900 和1200 K下的原子应变, 结果如图5所示. 在0 K时, 冯·米塞斯应变和体积应变的分布集中在较低的应变值区间, 且应变分布较为狭窄, 表明在低温下合金中原子的局部应变较小. 随着温度的升高, 冯·米塞斯应变和体积应变的分布逐渐变宽, 且峰值向更高的应变值移动. 到1200 K时, 应变分布的峰值达到了最高应变值, 且应变分布范围显著增大. 这一变化趋势表明, 温度的升高显著增大了合金中的原子应变. 并且, 熵效应也会在高温下影响原子的局部配置. 根据图5的结果, 随着温度的升高, 冯·米塞斯应变和体积应变的分布变得更加宽广, 这与信息熵的增大相对应[38], 表明温度的升高促使合金的构型熵增大, 这一结果与已知的热力学效应一致.
图5用虚线和圆圈标记了不同温度下的绝对值平均应变, 即参数
$ {\overline{\varepsilon }}_{{\mathrm{v}}{\mathrm{o}}{\mathrm{l}}} $ . 结果显示, 随着温度的升高, 平均冯·米塞斯应变和体积应变的值逐渐增大[44], 这与实验中测量的晶格畸变与温度的变化趋势相吻合[45]. 具体而言, 冯·米塞斯应变和体积应变在1200 K时的峰值明显高于低温下的数值. 该现象可以归因于高温条件下晶格振动的加剧, 这导致原子间的相互作用变得更加剧烈, 进而增大了晶格的畸变程度和原子应变. 随着温度的升高, 冯·米塞斯应变的变化量比体积应变的大, 表明冯·米塞斯应变对温度变化更敏感. 此外, 平均原子体积应变随着温度升高而增大, 对应着此合金在高温下晶格的膨胀效应. 这一结果验证了温度在调控合金力学性能方面的重要作用, 尤其在高温环境下, 晶格畸变的增强可能对合金的整体性能产生深远影响. -
本文以体心立方结构的TaWNbMo, TiZrNb和CoFeNiTi多主元合金为模型材料, 结合分子动力学模拟, 并采用冯·米塞斯应变和体积应变作为描述符, 系统地表述了合金中原子尺度的局部晶格畸变. 同时, 深入探讨了原子半径差异、化学短程有序结构以及温度对原子应变的影响. 基于本研究的分析, 得出以下结论.
1) 冯·米塞斯应变和体积应变能够有效表征晶格畸变特征, 进一步验证了其作为晶格畸变量化工具的准确性和可靠性. 晶格畸变程度越大, 相应的冯·米塞斯应变和体积应变越大, 且应变的分布越宽广.
2)合金中原子半径差异越大, 体积应变越显著. 大半径原子通常会产生压缩应变, 而小半径原子则会产生拉伸应变. 然而, 值得注意的是, 原子半径差异对冯·米塞斯应变的影响不显著, 说明冯·米塞斯应变更受晶格畸变的直接影响, 而非单纯的原子大小差异.
3)与原子随机分布构型相比, 化学短程有序结构的形成有助于降低晶格畸变和原子应变. 化学短程有序不仅改善了合金的局部结构稳定性, 还进一步验证了使用原子应变来描述晶格畸变的有效性和准确性.
4)随着温度的升高, 多主元合金的晶格畸变程度和原子应变均逐渐增大. 这表明温度在调控合金的力学性能方面具有重要作用, 高温下晶格振动增强, 导致原子应变的显著增大.
本研究结果为多主元合金的微观力学行为提供了新的理论支持, 特别是在合金设计和性能优化方面, 能够为未来的研究和应用提供有价值的参考.
体心立方多主元合金中原子应变的计算模拟
Computational simulation of atomic strain in body-centered cubic multi-principal element alloys
-
摘要: 多主元合金, 亦称为高熵合金, 作为一种新型合金材料, 因其优异的力学性能和热稳定性在多个领域展现出巨大的应用潜力. 本文采用分子动力学模拟方法, 以3种典型的体心立方结构多主元合金——TaWNbMo, TiZrNb和CoFeNiTi为研究对象, 系统研究了合金中的原子局域晶格畸变特征及其影响因素. 通过冯·米塞斯应变和体积应变作为描述符, 定量分析了合金中原子应变的分布及其与晶格畸变的关系. 研究结果表明, 晶格畸变越大, 冯·米塞斯应变和体积应变的分布范围越广, 且应变值显著增大. 进一步分析发现, 合金中的原子半径差异、化学短程有序结构以及温度均显著影响原子应变. 具体而言, 原子半径差异越大, 体积应变越大, 而化学短程有序结构的形成有助于减小晶格畸变和原子应变. 温度的升高则会导致晶格振动加剧, 从而增大原子应变. 本文的研究为理解高熵合金的微观力学行为提供了新的视角, 并为其在高温和极端环境下的应用设计提供了理论支持.Abstract: Multi-principal element alloys (MPEAs), also known as high-entropy alloys (HEAs), are novel materials that have received significant attention due to their exceptional mechanical properties, thermal stability, and resistance to wear and corrosion. These alloys are typically composed of multiple principal elements in near-equal atomic proportions, forming solid solution phases such as face-centered cubic (FCC) or body-centered cubic (BCC) structures. Despite the promising applications, a more in-depth understanding of the atomic-level behavior, particularly, lattice distortion and atomic strain, is essential to better design and optimize these materials in extreme environments. This study focuses on systematically investigating the atomic-scale lattice distortion characteristics and their influence on atomic strain in three representative BCC-based MPEAs: TaWNbMo, TiZrNb, and CoFeNiTi. We utilize molecular dynamics (MD) simulations to explore the local atomic strain distributions in these alloys at various temperatures. Von Mises strain and volumetric strain are employed as key descriptors to quantify the atomic strain, providing a clear representation of how lattice distortion on an atomic scale influences the overall strain behavior. The study specifically addresses the effects of atomic radius differences, chemical short-range ordering, and temperature on the strain characteristics of the alloys. The results obtained indicate that an increase in lattice distortion corresponds to a broader distribution of von Mises strain and volumetric strain, with strain values significantly amplified. More precisely, alloys with larger atomic radius differences exhibit greater volumetric strain, reflecting the influence of atomic size disparity on strain distribution. Furthermore, the formation of chemical short-range order (CSRO) significantly mitigates lattice distortion and atomic strain. This finding highlights the importance of short-range atomic ordering in enhancing the stability of the alloy structures, thus potentially improving their mechanical properties. Temperature effects are also investigated, revealing that elevated temperature induces more intense atomic vibration, which in turn increases the atomic strain. The findings underscore the complex interplay between atomic-scale phenomena and macroscopic mechanical properties, offering new insights into the microscopic mechanical behavior of high-entropy alloys. This study contributes to a better understanding of the underlying mechanisms driving atomic strain and lattice distortion in MPEAs. The results provide valuable theoretical insights that can guide the design of high-performance alloys tailored for high-temperature and extreme environments. By addressing the key factors influencing atomic strain, such as atomic radius, chemical ordering, and temperature, this work lays the foundation for future research aimed at enhancing the mechanical performance of MPEAs in various industrial applications.
-

-
图 1 多主元合金中的晶格畸变及局域原子应变 (a)晶格畸变示意图, 局部仿射变换矩阵
$ {J}_{i} $ 描述了初始与当前原子构型之间的转变; (b) 0 K下TiZrNb合金中的原子应变示例, 左图为每个原子的冯·米塞斯应变, 右图为每个原子的体积应变Figure 1. Lattice distortion and local atomic strain in multi-principal element alloys: (a) Schematic of lattice distortion, where the local affine transformation matrix
$ {J}_{i} $ describes the transition from the initial to the current atomic configuration; (b) atomic strain distribution in the TiZrNb alloy at 0 K, the left panel displays the Von Mises strain for each atom, while the right panel shows the volumetric strain.图 2 不同合金体系的三维原子分布模型及其原子应变的分布 (a) TaWNbMo, TiZrNb和CoFeNiTi的三维原子分布模型; (b) 3种合金体系的冯·米塞斯应变和体积应变的分布
Figure 2. Three-dimensional atomic distribution models and atomic strain distributions in different alloy systems: (a) Three-dimensional atomic distribution models of TaWNbMo, TiZrNb, and CoFeNiTi; (b) distribution of Von Mises strain and volumetric strain for the three alloy systems.
图 3 三种合金体系中不同组元的冯·米塞斯应变和体积应变的分布, 展示了TaWNbMo, TiZrNb和CoFeNiTi三种合金体系中不同组元的冯·米塞斯应变和体积应变的分布, 每种合金中的不同组元(Ta, W, Nb, Mo, Ti, Zr, Nb, 和Co, Fe, Ni, Ti)分别绘制了应变分布图, 上半部分为冯·米塞斯应变的分布, 下半部分为体积应变的分布, 不同颜色的曲线对应于不同的元素, 反映了各组元在合金中的应变特性差异
Figure 3. Distribution of von Mises strain and volumetric strain for different elements in the TaWNbMo, TiZrNb, and CoFeNiTi alloy systems. The strain distributions for different elements (Ta, W, Nb, Mo, Ti, Zr, Nb, Co, Fe, Ni, Ti) in each alloy are shown. The upper part of the figure shows the distribution of von Mises strain, while the lower part shows the distribution of volumetric strain. The different colored curves represent different elements, reflecting the strain characteristics of each element in the alloy.
图 4 TiZrNb合金在800 K下的化学短程有序信息及其原子应变分布特征 (a)化学短程有序构型的三维原子分布模型; (b)不同原子对的Warren-Cowley参数, 展示了合金中各原子对之间的短程有序程度; (c)冯·米塞斯应变的频率分布, 分别为CSRO和RSS两种不同的化学短程有序状态下的应变分布; (d)体积应变的频率分布, 展示了不同原子对间的体积应变分布特征
Figure 4. Chemical short-range order information and atomic strain distribution characteristics of TiZrNb alloy at 800 K: (a) Three-dimensional atomic distribution model of the chemical short-range ordered configuration; (b) Warren-Cowley parameters for different atomic pairs, showing the degree of short-range order between atomic pairs in the alloy; (c) distribution of von Mises strain, showing the strain distributions under CS0 and RSS short-range order configurations; (d) frequency distribution of volumetric strain, illustrating the volumetric strain characteristics between different atomic pairs.
图 5 不同温度下TiZrNb合金的冯·米塞斯应变和体积应变频率分布图, 图中展示的温度范围从0—1200 K, 分别以不同颜色表示不同的温度状态 (a)冯·米塞斯应变的分布; (b)体积应变的分布
Figure 5. Frequency distribution of von Mises strain and volumetric strain of TiZrNb alloy at various temperatures, ranging from 0 K to 1200 K: (a) Distribution of von Mises strain; (b) distribution of volumetric strain.
-
[1] George E P, Raabe D, Ritchie R O 2019 Nat. Rev. Mater. 4 515 doi: 10.1038/s41578-019-0121-4 [2] George E P, Curtin W A, Tasan C C 2020 Acta Mater. 188 435 doi: 10.1016/j.actamat.2019.12.015 [3] Miracle D B 2017 J. Met. 69 2130 doi: 10.1007/s11837-017-2527-z [4] Pickering E J, Jones N G 2016 Int. Mater. Rev. 61 183 doi: 10.1080/09506608.2016.1180020 [5] Ma E, Ding J 2025 J. Mater. Sci. Technol. 220 233 doi: 10.1016/j.jmst.2024.09.008 [6] Yeh J W, Chen S K, Lin S J, Gan J Y, Chin T S, Shun T T, Tsau C H, Chang S Y 2004 Adv. Eng. Mater. 6 299 doi: 10.1002/adem.200300567 [7] Li Z M, Pradeep K G, Deng F, Paabe D, Tasan C C 2016 Nature 534 227 doi: 10.1038/nature17981 [8] Maresca F, Curtin W A 2020 Acta Mater. 182 235 doi: 10.1016/j.actamat.2019.10.015 [9] Gludovatz B, Hohenwarter A, Catoor D, Chang E H, George E P, Ritchie P O 2014 Science 345 1153 doi: 10.1126/science.1254581 [10] Shi Y Z, Yang B, Liaw P K 2017 Metals 7 18 doi: 10.3390/met7010018 [11] Chen P Y, Lee C, Wang S Y, Seifi M, Lewandowski J J, Dahmen K A, Jia H L, Xie X, Chen B L, Yeh J W, Tsai C W, Yuan T, Liaw P K 2018 Sci. China-Technol. Sci. 61 168 doi: 10.1007/s11431-017-9137-4 [12] Kozelj P, Vrtnik S, Jelen A, Jazbec S, Jaglicic Z, Maiti S, Feuerbacher M, Steurer W, Dolinsek J 2014 Phys. Rev. Lett. 113 107001 doi: 10.1103/PhysRevLett.113.107001 [13] Su Z X, Ding J, Song M, Jiang L, Shi Tan, Li Z M, Wang S, Gao F, Ma E Lu C Y 2023 Acta Mater. 245 118662 doi: 10.1016/j.actamat.2022.118662 [14] Zhang Z, Su Z, Zhang B, Yu Q, Ding J, Shi T, Lu C, Ritchie R O, Ma E 2023 Proc. Natl. Acad. Sci. 120 e2218673120 doi: 10.1073/pnas.2218673120 [15] Zhang Y, Zuo T, Tang T, Gao M, Dahmen K, Liaw K, Lu Z 2014 Prog. Mater. Sci. 61 1 doi: 10.1016/j.pmatsci.2013.10.001 [16] Kozak P, Sologubenko A, Steurer W 2015 Z Kristallogr Cryst Mater 230 55 doi: 10.1515/zkri-2014-1739 [17] Zhang B, Zhang Z, Xun K, Asta M, Ding J, Ma E 2024 Proc. Natl. Acad. Sci. 121 e2314248121 doi: 10.1073/pnas.2314248121 [18] Miracle D B, Senkov O N 2017 Acta Mater. 122 448 doi: 10.1016/j.actamat.2016.08.081 [19] Fan Z, Wang H, Wu Y, Liu X J, Lu Z P 2017 Mater. Res. Lett. 5 187 doi: 10.1080/21663831.2016.1244116 [20] Yeh J W, Chang S Y, Hong Y D, Chen S K, Lin S J 2007 Mater. Chem. Phys. 103 41 doi: 10.1016/j.matchemphys.2007.01.003 [21] Tong C J, Chen Y L, Chen S K, Yeh J W, Shun T T, Tsau C H, Lin S J, Chang S Y 2005 Metall. Mater. Trans. A 36 881 doi: 10.1007/s11661-005-0283-0 [22] Tsai C W, Tsai M H, Yeh J W, Yang C C 2010 J. Alloys Compd. 490 160 doi: 10.1016/j.jallcom.2009.10.088 [23] Yeh J W, Chen S K, Gan J Y, Lin S J, Chin T S, Shun T T, Tsau C H, Chang S Y 2004 Metall. Mater. Trans. A 35 2533 doi: 10.1007/s11661-006-0234-4 [24] 杨勇, 赫全锋 2021 金属学报 57 385 doi: 10.11900/0412.1961.2020.00359 Yang Y, He Q F 2021 Acta Metall. Sin. 57 385 doi: 10.11900/0412.1961.2020.00359 [25] Zou Y, Maiti S, Steurer W, Spolenak R 2014 Acta Mater. 65 85 doi: 10.1016/j.actamat.2013.11.049 [26] Santodonato L J, Zhang Y, Feygenson M, Parish C M, Gao M C, Weber R J, Neuefeind J C, Tang Z, Liaw P K 2015 Nat. Commun. 6 5964 doi: 10.1038/ncomms6964 [27] Toda-Caraballo I, Wr obel J S, Dudarev S L, Nguyen-Manh D, Rivera-Díaz-del-Castillo P E 2015 Acta Mater. 97 156 doi: 10.1016/j.actamat.2015.07.010 [28] Tian L Y, Hu Q M, Yang R, Zhao J, Johansson B, Vitos L 2015 J. Phys. Condens. Mat. 27 315702 doi: 10.1088/0953-8984/27/31/315702 [29] Chen B, Li S Z, Ding J, Ding X D, Sun J, Ma E 2023 Scr. Mater. 222 115048 doi: 10.1016/j.scriptamat.2022.115048 [30] Tandoc C, Hu Y J, Qi L, Liaw P K 2023 npj Comput. Mater. 9 53 doi: 10.1038/s41524-023-00993-x [31] Plimpton S 1995 J. Comput. Phys. 117 1 doi: 10.1006/jcph.1995.1039 [32] Yin S, Zuo Y X, Abu-Odeh A, Zhang H, Li X G, Ding J, Ong S P, Asta M, Ritchie R 2021 Nat. Commun. 12 4873 doi: 10.1038/s41467-021-25134-0 [33] Chen B, Li S Z, Ding J, Ding X D, Sun J, Ma E 2020 Proc. Natl. Acad. Sci. 117 16199 doi: 10.1073/pnas.1919136117 [34] Stukowski A 2010 Model. Simul. Mater. Sc. 18 015012 doi: 10.1088/0965-0393/18/1/015012 [35] Wang J H, Li J, Yip S, Phillpot S, Wolf D 1995 Phys. Rev. B 52 12627 doi: 10.1103/PhysRevB.52.12627 [36] Li J 2003 Model. Simul. Mater. Sci. Eng. 11 173 doi: 10.1088/0965-0393/11/2/305 [37] Wang L, Ding J, Chen S S, Jin K, Zhang Q H, Cui J X, Wang B P, Chen B, Li T Y, Ren Y, Zheng S J, Ming K S, Lu W J, Hou J H, Sha G, Liang J, Wang L, Xue Y F, Ma E 2023 Nat. Mater. 22 950 doi: 10.1038/s41563-023-01517-0 [38] Zhang M, Zhang B Z, Ding J, Ma E 2025 Scripta Mater. 259 116559 doi: 10.1016/j.scriptamat.2025.116559 [39] Ding J, Yu Q, Asta M, O. Ritchie R 2018 Proc. Natl. Acad. Sci. 115 8919 doi: 10.1073/pnas.1808660115 [40] Zhang F X, Zhao S J, Jin K, Xue H, Velisa G, Bei H, Huang R, Ko J Y P, Pagan D C, Neuefeind J C, Weber W J, Zhang Y W 2017 Phys. Rev. Lett. 118 205501 doi: 10.1103/PhysRevLett.118.205501 [41] Zhang R P, Zhao S T, Ding J, Chong Y, Jia T, Ophus C, Asta M, O. Ritchie R, Minor M A. 2020 Nature 581 283 doi: 10.1038/s41586-020-2275-z [42] Xun K H, Zhang B Z, Wang Q, Zhang Z, Ding J, Ma E 2023 J. Mater. Sci. Technol. 135 221 doi: 10.1016/j.jmst.2022.06.047 [43] Chen B, Li S Z, Ding J, Ding X D, Sun J, Ma E 2024 Acta Mater. 272 119910 doi: 10.1016/j.actamat.2024.119910 [44] He Q F, Wang J G, Chen H A, Ding Z Y, Zhou Z Q, Xiong L H, Luan J H, Pelletier J M, Qiao J C, Wang Q, Fan L L, Zeng Q S, Liu C T, Pao C W, Srolovitz D J, Yang Y 2022 Nature 602 251 doi: 10.1038/s41586-021-04309-1 [45] Tan Y Y, Chen Z J, Su M Y, Ding G, Jiang M Q, Xie Z C, Gong Y, Wu T, Wu Z H, Wang H Y, Dai L H 2022 J. Mater. Sci. Technol. 104 236 doi: 10.1016/j.jmst.2021.07.019 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: