-
铜氧化物高温超导电性的发现至今已近四十年. 大量研究结果表明, 解决高温超导问题的关键之一在于对这一体系所呈现出的各种量子物态的表征和理解[1]. 如图1所示, 铜氧化物超导体的母体化合物为具有反铁磁有序的莫特(Mott)绝缘体. 掺杂空穴或电子会抑制反铁磁序, 引发超导电性的出现. 随着载流子浓度的进一步增加, 体系会过渡到费米液体金属相. 在欠掺杂区域, 正常态中存在一个赝能隙态, 表现为电子态密度的部分损失. 在最佳掺杂和过掺杂的正常态中, 还存在奇异金属相, 其热力学及输运性质偏离费米液体行为. 此外, 铜氧化物超导体中还广泛存在电荷序关联 (charge-order correlation)
1 , 其序参量在掺杂浓度$ p = 1/8 $ 附近最强, 并与超导相存在竞争. 这些物质态的共存反映了铜氧化物中晶格、电荷、自旋和轨道等多种自由度对其低能物理性质的复杂影响. 全面理解这些物质态的产生机制及其相互关系, 成为目前研究的热点, 也是揭示高温超导机制面临的重要任务.近年来, 随着研究的不断深入, 尤其是得益于共振非弹性X射线散射实验技术的进步, 人们对铜氧化物中的电荷序有了很多新的认识. 其中包括发现覆盖相图广泛区域的短程电荷关联 (charge correlation)、电荷序的集体激发及与之相关的量子临界行为, 及电声耦合 (electron-phonon coupling) 与电荷序的关系等. 这些发现表明, 除了静态电荷序与超导相存在竞争之外, 电荷关联很可能与铜氧化物诸多奇特的正常态及超导态性质密切相关. 本文回顾了共振X射线散射对铜氧化物超导体中电荷序的研究进展, 尤其是基于具有能量分辨的非弹性散射相关的工作, 着重介绍了近年来对高温及动态电荷序关联的研究, 以及利用单轴应力对电荷序体系进行调控的实验探索. 最后, 总结了当前仍面临的主要问题, 并对未来的研究方向进行了展望.
-
一般来说, 电荷序是指材料中的价电荷产生了周期性的调制, 同时伴随着原子位置的扰动. 这种调制可以是公度的也可以是非公度的. 电荷序是一种基本的物理现象, 但其微观机制及特征具有很强的材料依赖性. 电荷序常见于低维金属材料中, 如准一维材料NbSe3[2,3]和(TaSe4)2I[4], 以及过渡金属二硫化物NbSe2[5]和TaS2[6]等二维层状材料. 在一维金属中, 费米面嵌套导致的电子不稳态可以驱动电荷密度产生新的周期性调制, 这种现象被称为电荷密度波(charge density wave, CDW)[7,8]. 该过程同时导致声子能量的软化和结构相变的发生. 在二维材料中, 上述电子态图像并不严格适用. 有研究认为, 具有动量依赖性的电声耦合对于电荷序的产生具有重要作用[9]. 相比费米面嵌套, 电声相互作用涉及到晶格和电子间的非弹性散射, 也可能引发声子的重整化和结构相变[10]. 在具有强电子关联的体系中, 存在多种相互作用的竞争, 电荷序的产生机制往往更为复杂. 本文关注的铜氧化物超导体就属于这类材料. 现有研究结果表明, 不同于上述金属材料, 铜氧化物中电子间相互作用对电荷序的产生具有重要作用. 然而, 其他机制, 包括费米面嵌套和电声耦合在其中是否起到作用, 目前仍然没有确切答案. 无法用简单费米面嵌套理解的电荷序有时也被称为“非常规电荷序”. 除了铜氧化物这种涉及多种相互作用的情况外, 引发非常规电荷序的可能机制还包括激子绝缘体[11]和姜-泰勒效应 (Jahn-Teller effect)[12]等. 关于铜氧化物中电荷序产生机制的讨论将在本文后续部分详细介绍.
-
电荷序的出现通常伴随材料多种物理性质的变化, 因此多种实验手段可以对电荷序进行直接或间接探测. 但是, 每种手段都有各自的优缺点, 需要结合起来相互补充印证. 比如电荷序的产生有可能导致费米面重构以及输运性质的改变, 因此霍尔系数和热电势等物性可能在电荷序出现时发生变化[13]. 通过输运性质的变化探测电荷序比较间接, 有时无法完全排除其他因素, 如自旋序、轨道序、拓扑序或结构相变的可能. 扫描隧道显微镜(scanning tunneling microscopy, STM)可以探测电荷序的实空间结构, 通过测量原子位置或局域电子态密度的空间调制给出电荷序的图像[14,15]. STM探测电荷序的主要局限在于其表面敏感性: 一方面, 样品表面的平整度要求比较高(原子尺度平整); 另一方面, 难以区分测量结果是来自样品的体性质还是表面态. 核磁共振(nuclear magnetic resonance, NMR)也可以在实空间探测电荷密度调制[16,17], 对局域电子结构变化具有很高的灵敏度, 并且能够反映材料的体性质. 另外, NMR测量的特征能量范围一般在微电子伏特(μeV), 对静态有序更加敏感. NMR的局限在于其测量需要在外加强磁场下进行, 可能引发物理性质的变化.
电荷序通常伴随周期性的晶格畸变. 基于这一特点, 可以利用X射线或中子衍射等手段探测晶格周期的变化, 在倒空间对电荷序进行研究. 另一方面, 利用共振X射线散射(resonant X-ray scattering, RXS)可以直接对电荷关联进行探测, 给出电荷密度空间调制的信息. 相比于非共振X射线散射, RXS具有诸多优势, 尤其是对材料中的电子态关联有着极高的敏感性, 可以基于元素或轨道选择性增强特定电子态激发过程的散射截面. 简单来说, 可以认为共振X射线散射探测电子态关联函数(correlation function), 同时其散射强度由于共振响应而增强. 这一结论可以由共振X射线散射有效理论得到[18], 同时也已被大量实验结果证实. 近年来, RXS相关实验技术的快速发展也大力促进了关联电子体系的研究进展.
-
X射线散射通过测量X光经样品散射后动量、能量和偏振的变化来探测材料内部的性质. 为了描述这一过程, 可以将体系的哈密顿量H展开为不考虑光子影响下的相互作用
$ H_0 $ 和考虑光子-电子相互作用的微扰项$ H^{\prime} $ . 光子与样品相互作用较弱时, 仅考虑光子电场与电子间的相互作用, 忽略光子的磁矩, 由N个电子构成的体系和光子的相互作用产生的微扰近似为其中e和
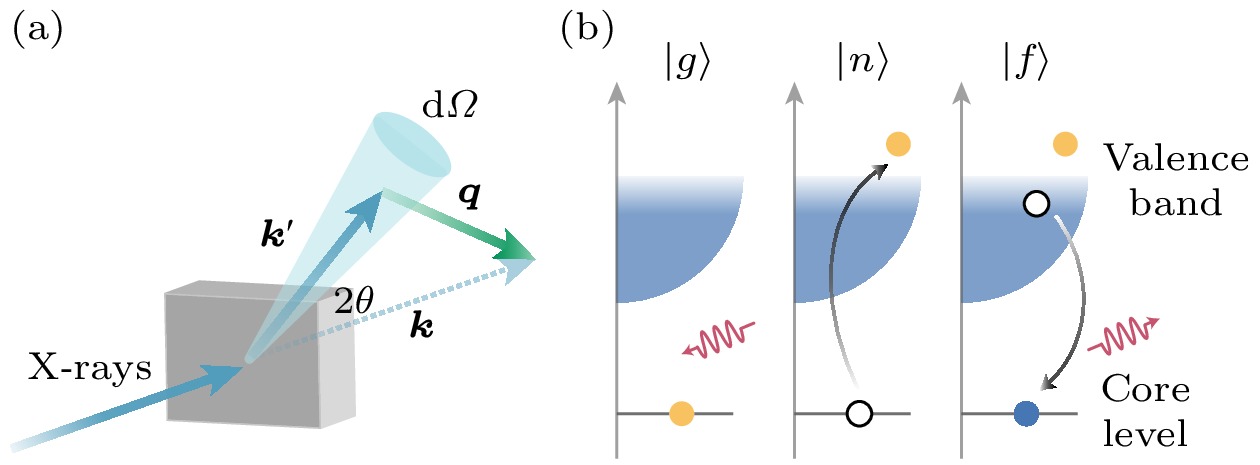
$ m_{\mathrm{e}} $ 为电子电量和静止质量,$ {\boldsymbol{p}}_j $ 和$ {\boldsymbol{r}}_j $ 为第j个电子的动量和坐标,$ {\boldsymbol{A}}\left({\boldsymbol{r}}\right) $ 为矢势. 散射过程如图2(a) 所示, 入射(出射)光子的能量、动量和偏振分别为$ \hbar\omega_{{\boldsymbol{k}}} $ ,$ \hbar{\boldsymbol{k}} $ ,$ {{\epsilon}}\; ( \hbar\omega_{{\boldsymbol{k}}^{\prime}}, \hbar{\boldsymbol{k}}^{\prime}, {{\epsilon}}^{\prime}) $ . 根据能量、动量守恒, 散射前后光子转移给样品的能量和动量分别为$ \hbar\omega=\hbar\omega_{{\boldsymbol{k}}}-\hbar\omega_{{\boldsymbol{k}}^{\prime}} $ 和$ \hbar{\boldsymbol{q}}=\hbar{\boldsymbol{k}}-\hbar{\boldsymbol{k}}^{\prime} $ , 使样品从初态$ |g\rangle $ 变化到末态$ |f\rangle $ . 考虑至二阶微扰, 该过程的微分散射截面为[18]其中
$ |G\rangle=|g\rangle\otimes|{\boldsymbol{k}}, {{\epsilon}}\rangle $ ,$ |F\rangle=|f\rangle\otimes|{\boldsymbol{k}}^{\prime}, {{\epsilon}}^{\prime}\rangle $ 和$ |n\rangle $ 分别代表样品-光子体系的初态、末态和中间态, 对应本征能量$ E_G=E_g+\hbar\omega_{{\boldsymbol{k}}} $ ,$ E_F=E_f+\hbar\omega_{{\boldsymbol{k}}^{\prime}} $ 和$ E_n $ . 散射截面中的一阶项由$ H^{\prime} $ 中$ {\boldsymbol{A}}^2 $ 项贡献, 对应非共振X射线散射(non-resonant X-ray scattering, NXS). 当入射光能量远离材料共振吸收边($ E_G= E_g+\hbar\omega_{{\boldsymbol{k}}} \not\approx E_n $ )时, 此过程占据主导, 微分散射截面近似为其中
$ r_{\mathrm{e}}= {e^2}/({4 \pi \varepsilon_0 m_{\mathrm{e}} c^2}) $ 是经典电子半径,$ p_g $ 为初态为$ |g\rangle $ 的概率. 可以看到, NXS的微分散射截面正比于动态结构因子(dynamical structure factor)$ S({\boldsymbol{q}}, \omega) $ , 即[20]在弹性散射过程中, 即
$ \hbar\omega=\hbar\omega_{{\boldsymbol{k}}}-\hbar\omega_{{\boldsymbol{k}}^{\prime}} = 0 $ 时, 该过程贡献晶体的布拉格散射(Bragg scattering).当入射光能量位于某个元素的共振吸收边, 即
$ \hbar\omega_{k}\approx E_{n}-E_{g} $ 时,$ E_G-E_n\approx 0 $ . 此时, (2)式中二阶项急剧增强并占据主导. 此过程由$ H^{\prime} $ 中相互作用的线性项$ {\boldsymbol{A}}\cdot {\boldsymbol{p}} $ 项贡献, 称为共振非弹性X射线散射(resonant inelastic X-ray scattering, RIXS), 其微分散射截面可以由Kramers-Heisenberg方程给出[18]:其中
$ T_{{\boldsymbol{k}}, {\boldsymbol{\epsilon}}} ( T_{{\boldsymbol{k}}^{\prime}, {\boldsymbol{\epsilon}}^{\prime}} )$ 是依赖于波矢和偏振的跃迁算符(transition operator),$ \varGamma_{n} $ 是中间态下芯(内壳层)空穴(core hole)寿命的倒数.$ \langle n \left|T_{{\boldsymbol{k}}, {{\epsilon}}}\right| g\rangle $ 和$ \langle f|T_{{\boldsymbol{k}}^{\prime}, {{\epsilon}}^{\prime}}^{\dagger}| n\rangle $ 分别对应X光共振吸收(X-ray absorption spectroscopy, XAS)和发射的过程. RIXS过程如图2(b)所示. 随着入射光被共振吸收, 一个芯电子被激发到外壳层的未占据态, 使样品进入一个短暂的中间态, 此时芯空穴和激发态电子会使体系产生扰动. 随后, 价带占据态的电子退激发到芯空位, 同时发射出一个光子. RIXS使样品产生价电子激发, 其动量$ \hbar{\boldsymbol{q}} $ 和能量$ \hbar\omega $ 可以通过对散射前后光子的分析确定. 根据中间态的不同, RIXS可以分为直接和间接两种过程, 这两种过程对体系的扰动方式不同, 因而会发生不同的元激发. 简单来说, 直接RIXS过程由跃迁矩阵元主导, 而间接RIXS中的元激发则是由中间态的芯空穴, 或者激发态电子和价电子间的库仑相互作用导致. 上述RIXS过程均会产生价电子激发, 因此被称为价态 (valence) RIXS. 而当中间态的芯空穴在末态被更浅壳层的芯电子填充时, 此过程产生芯电子激发, 被称为芯态 (core) RIXS. 例如过渡金属的1s2p RIXS, 其中间态的$ 1 {\mathrm{s}} $ 空穴被$ 2 {\mathrm{p }}$ 电子填充, 末态存在一个$ 2{\mathrm{ p}} $ 空穴. 关于RIXS理论更详细的介绍可以参考相关综述文章[18].目前, RIXS散射截面的计算方法主要基于简化系统的严格数值计算, 或者通过对芯空穴中间态过程进行近似来获得有效的RIXS散射截面[18], 不同方法有着各自的优缺点及适用范围. 例如基于团簇模型(cluster model)的严格对角化(exact diagonalization)计算可以有效描述局域
$ {\mathrm{dd}} $ 及电荷转移激发, 提供电子结构的有关信息[21]. 而有效RIXS理论, 包括快速碰撞近似(fast-collision approximation)[22]和费曼图(Feynman diagram)方法[23], 将复杂的RIXS响应函数以关联函数(乘以共振响应因子)形式简化表示, 对描述体系中的集体激发更加有效. -
RIXS实验的关键因素包括光通量、能量和动量分辨率、探测效率以及样品环境等. RIXS实验对光通量的需求很大, 依赖同步辐射或自由电子激光作为光源. 不同元素各个共振吸收边对谱仪工作能量范围的要求也有很大差别. 以过渡金属L边为例, 3d元素在1 keV以下, 属于软X射线 (soft X-ray) 范围, 4d元素如Ru的
$ L_3 $ 边能量约为 2.8 keV, 属于柔X射线(tender X-ray), 而5d元素如Ir的$ L_3 $ 边能量约为12.8 keV, 属于硬X射线 (hard X-ray)[25]. 相比硬X射线, 软X射线散射的应用存在一些局限, 比如覆盖倒空间范围较小 (光子能量$ \hbar\omega\approx 1\;{\mathrm{keV}} $ , 对应波矢$ {\boldsymbol{k}}\approx 0.5 $ Å$ ^{-1} $ ). 另外, 软X射线的波长远大于晶体的晶面间距, 需要使用与波长相匹配的人工光栅作为单色器和能量分析器. 此外, 低能X射线的穿透性差 (X射线在材料中的衰减大致反比于能量的三次方), 受空气散射严重, 因此软X射线谱仪的光路要求高真空环境. 共振软X射线散射也具有无法替代的优势, 比如对过渡金属及稀土氧化物体系电子态的探测和调控, 以及对薄膜材料和界面效应的研究. 本文所介绍的关于铜氧化物电荷序的RIXS研究工作基于Cu-$ L_{3} $ ($ 2 {\mathrm{p}}_{3/2} \rightarrow 3 {\mathrm{d}} $ , ~930 eV), O-K ($ 1 {\mathrm{s}} \rightarrow 2 {\mathrm{p}} $ , ~530 eV)边, 两者均属于软X射线范围. -
前文提到, 非共振X射线衍射可以通过测量晶格畸变来对电荷序的结构、周期、对称性以及相变特征等性质进行研究. (3)式和(4)式告诉我们非共振X射线散射截面正比于结构因子, 电荷序在波矢
$ {\boldsymbol{Q}} $ 处超结构衍射峰的幅度正比于$ N{\boldsymbol{Q}}\cdot \delta{\boldsymbol{r}} $ , 其中$ \delta{\boldsymbol{r}} $ 为畸变离子的位移矢量, N为该离子总电子数[63]. 利用硬X射线可以覆盖多个布里渊区, 对各个方向的电荷序超结构峰进行测量, 从而给出晶格畸变的实空间结构. 然而, 这一手段的局限在于: 1)难以区分超结构峰起源于电荷的调制还是应变场[64]; 2)电荷序引发的晶格畸变往往很小($ |\delta{\boldsymbol{r}}|\sim 10^{-3} $ Å) [63], 探测弱的超结构峰对仪器的信噪比和光通量要求很高; 3)对于薄膜样品的超结构虽然可以通过掠入射进行测量[65], 但是对实验条件要求苛刻. 相比之下, 共振X射线对电子态关联敏感, 可以依据信号对入射光是否共振响应来确定其起源于价电子还是晶格. 此外, 利用共振能量的依赖性还可以分辨不同元素, 甚至细化到价态和配位环境. 上述特点也赋予了共振X射线测量薄膜样品的独特优势: 一方面, 共振响应极大增强了散射截面; 另一方面, 元素选择性有效降低了来自衬底的背景. -
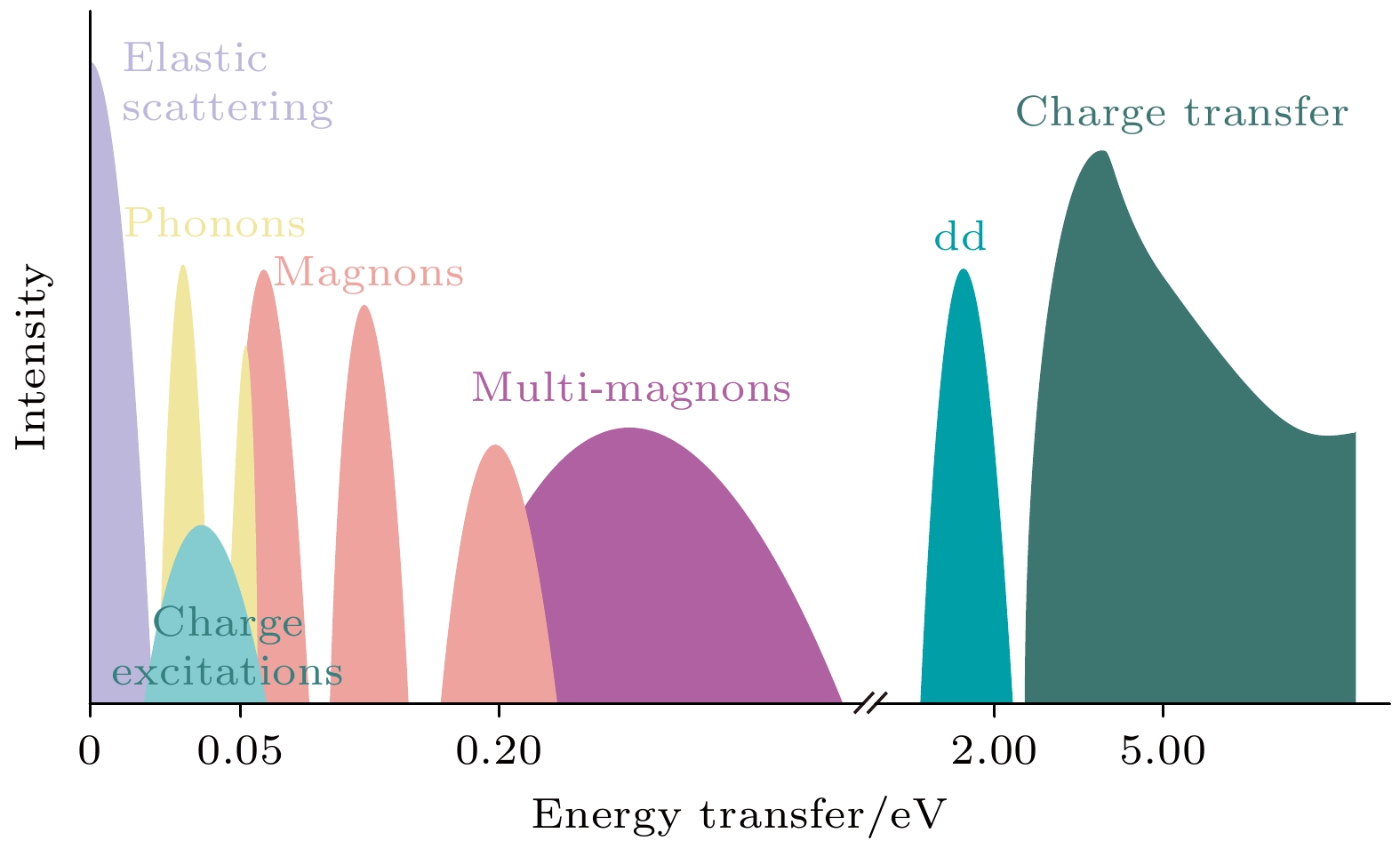
共振弹性X射线散射(resonant elastic X-ray scattering, REXS)实验中不分析出射光能量, 因此谱仪的设计更加灵活, 适合对弹性散射主导的过程进行高效探测[66]. RIXS对出射光进行能量分辨, 可以在能量-动量空间里对材料中包括晶格、电荷、自旋和轨道等多种自由度对应的元激发进行探测 (如图3示意). 原则上, 符合对称性要求的低能激发都可以通过RIXS产生, 其散射截面依赖于共振吸收边和偏振. 以测量铜氧化物常用的铜L边和氧K边为例, 铜L边对应的偶极跃迁可以直接探测dd激发. 另外, 其中间态的2p芯空穴存在较强的自旋-轨道耦合(约20 eV [67]), 自旋不再是好量子数, 因此可能产生单自旋翻转的磁激发[68]. 而氧K边具有更长的芯空穴寿命, 基于电声耦合可以产生更强的RIXS声子激发. 同时这两者都可以探测电荷关联. 相比于REXS, RIXS可以区分弹性和非弹性散射过程, (在谱仪能量分辨率范围内) 分辨静态和动态关联, 因而对探测电子态有序更为敏感. 随着近年来能量分辨率的显著提高, RIXS在铜氧化物电荷序的研究上发挥了重要作用, 包括发现电荷关联存在的普遍性, 以及和电荷序有关的电声耦合、集体电荷激发等动力学行为. 除了铜氧化物, RIXS也被有效应用在其他体系的电荷序研究上[69-72].
-
RIXS与中子散射之间存在许多共性, 同时也具备各自的优缺点, 因此被视为互补的研究手段. 本文对两者进行简单对比, 更详尽的比较可以参考综述文章[77].
1)电子态探测种类: 中子与材料中的自旋存在相互作用, 但是对电荷及轨道序关联不敏感, 只能通过相应晶格的响应间接进行探测. 由于中间态的存在, RIXS与电子的自旋、电荷及轨道自由度均可以产生耦合, 因此能够探测对应的关联函数.
2)磁激发探测种类: 两者均可探测磁性, 包括磁有序和磁激发. 然而, 中子散射依赖偶极矩(dipole-dipole)相互作用, 无法探测高阶磁激发. 相比之下, RIXS除了偶极磁激发外, 还可以探测多极(multipolar)磁激发.
3)散射截面: 中子散射的散射截面可以进行严格的解析表达, 并且正比于自旋的动态结构因子
$ S({\boldsymbol{q}}, \omega) $ . 如前文所述, RIXS产生磁激发的散射截面不仅正比于动态结构因子, 还正比于一个共振响应因子. 共振过程极大增加了电子态激发的散射截面. 因此, RIXS需要的样品量远小于中子散射. 通常非弹性中子散射实验需要几克甚至几十克样品, 而RIXS可以轻易测量不足1 mm尺寸的单晶样品, 还可以测量薄膜材料.4)穿透深度: RIXS与中子散射都属于体探测手段. 中子的穿透深度可以超过1 cm, 而RIXS的穿透深度在0.1—10 μm.
5)能量分辨率: 目前比较先进的软X射线RIXS谱仪在铜L边(约930 eV)的能量分辨率可以达到30 meV, 而中子散射的能量分辨率可达1 meV甚至更高.
-
STM, NMR和RIXS作为探测电荷序的常用谱学手段, 具有各自的特点及局限性, 前文已有介绍, 这里再作一些补充对比. STM和NMR属于局域探测手段, 能够给出局域电子结构的信息, 而RIXS测量结果则反映材料整体的关联性. 从本文后续的介绍可以看到, 通过分析RIXS散射结构因子, 也可以间接得到关于局域电子态密度的微观结构和对称性的信息. 在测量条件方面, STM对样品表面平整度的要求很高, 因此实验集中在能够通过解理获得高平整度表面的铋系铜氧化物材料上. 相比之下, NMR和RIXS作为体测量手段, 则被应用于大多数铜氧化物体系的研究.
-
1995年, Tranquada等[24]通过中子散射实验在La1.6–xNd0.4SrxCuO4 (Nd-LSCO,
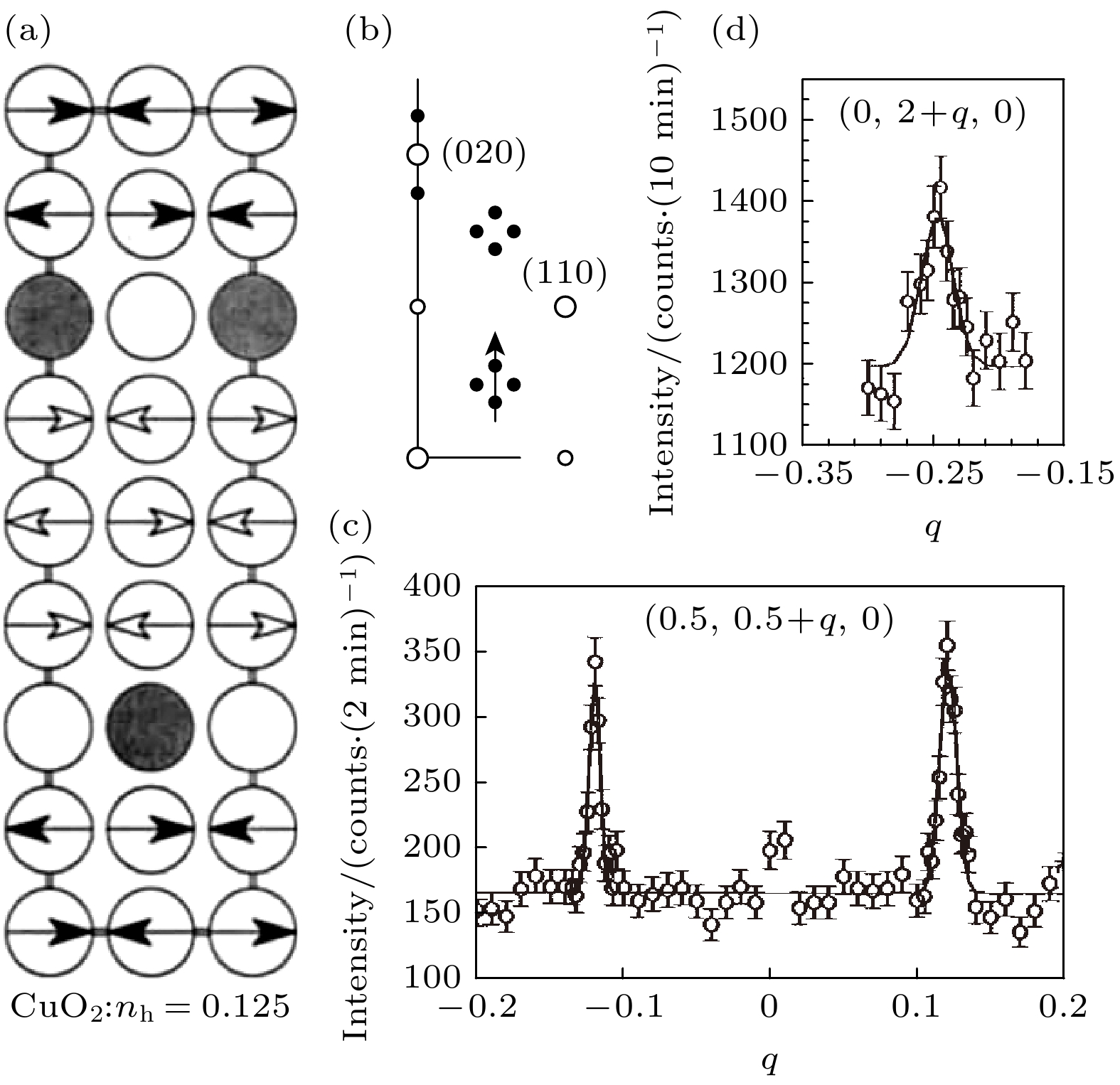
$ x = 0.12 $ )中率先发现了电荷序存在的证据, 揭开了铜氧化物超导体电荷序研究的序幕. 如图4所示, 中子散射实验在$ {\boldsymbol{Q}}_\text{CO}=(2, 2\pm\delta_\text{CO}, 0) $ 和$ {\boldsymbol{Q}}_\text{SO}=(0.5, 0.5\pm \delta_\text{SO}, 0) $ 的位置分别测量到了电荷序 (引发的晶格畸变) 和自旋序对应的衍射峰. 两种有序的波矢非公度性 (incommensurability) 满足$ \delta_\text{CO} = 2\delta_\text{SO}\approx0.25 $ , 分别对应约4和8倍晶格周期. 这一结果可以通过自旋-电荷条纹序(spin-charge stripe order)的耦合图像解释. 此外, 电荷序在$ p\approx1/8 $ 掺杂时达到 最强的现象也和条纹序的图像符合. Abbamonte 等[78]于2005年首次利用共振X射线散射测量了La1.875Ba0.125CuO4中的电荷序. 通过在O K边和Cu$ L_3 $ 边的测量, 该实验证实了O 2p和Cu 3d 电子态存在空间上的调制.2002年, Hoffman等[15]利用STM在另一类铜氧化物材料Bi2Sr2CaCu2O8+δ (Bi2212)中也发现了电荷序. 他们发现在超导态下, 外加磁场在磁通涡旋处引发棋盘状的具有4倍晶格周期的电子态调制. 这一现象也反映了电荷序和超导的竞争. 随后, 零场下STM测量也观察到了类似的电子态调制[79]. 共振X射线散射实验进一步确认了Bi2Sr2–xLaxCu2O6+δ (Bi2201)[41] 以及Bi2212[44]中电荷序的存在. YBa2Cu3O6+x (YBCO)中的电荷序最早由强磁场下的NMR实验发现[17], 随后, RIXS实验[37]和高能X射线衍射实验[36]分别在YBCO中发现了零场下非公度的二维电荷序. 此后, 共振X射线散射实验陆续在其他铜氧化物体系中发现了电荷序, 包括汞系材料HgBa2CuO4+δ (Hg1201)[50]、铊系材料Tl2Ba2CuO6+δ (Tl2201)[80] 和电子掺杂体系Nd2–xCexCuO4 (NCCO)[81]和La2–xCexCuO4 (LCCO)[82]. 这些实验结果揭示了电荷序普遍存在于铜氧化物超导体中.
-
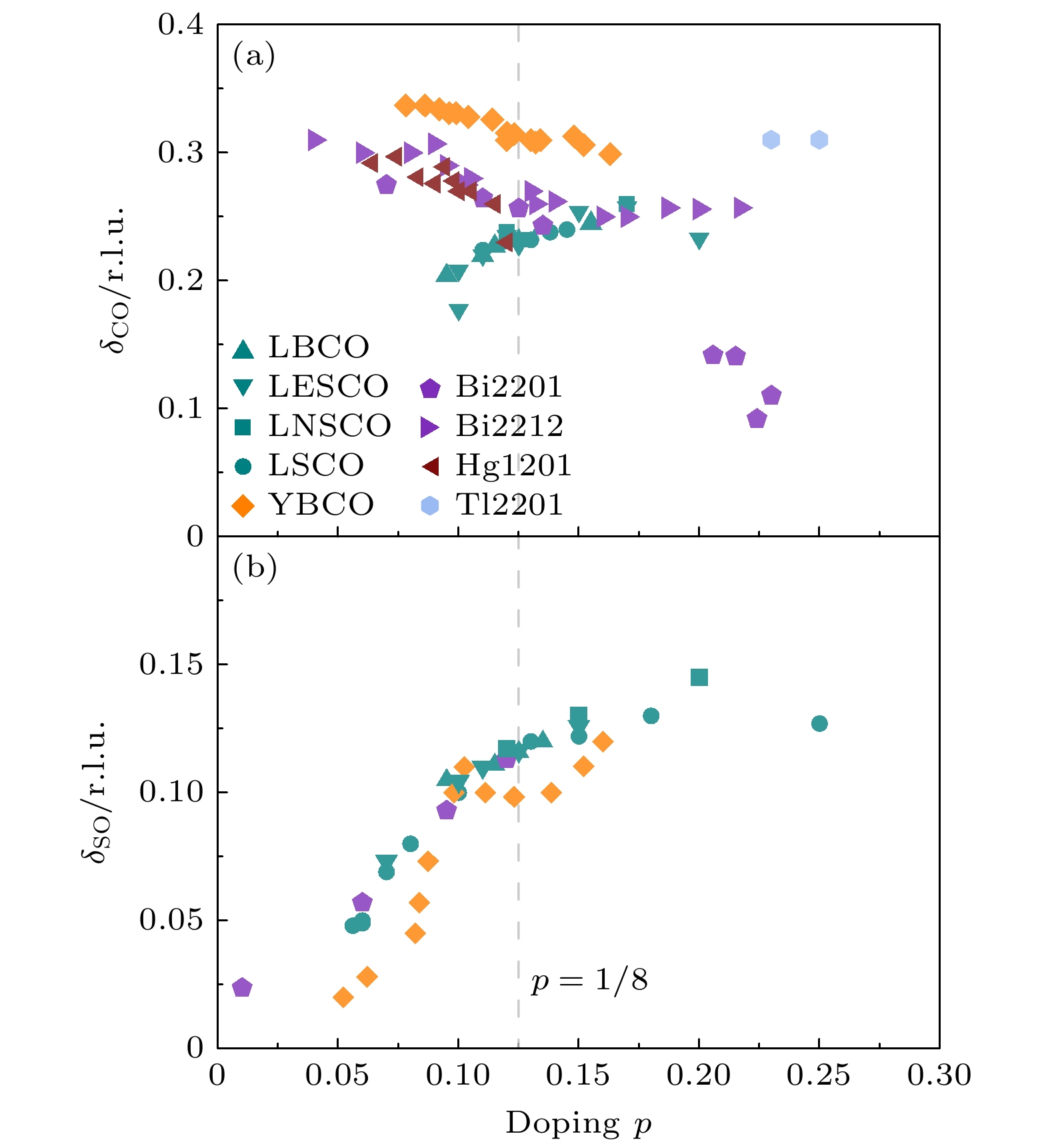
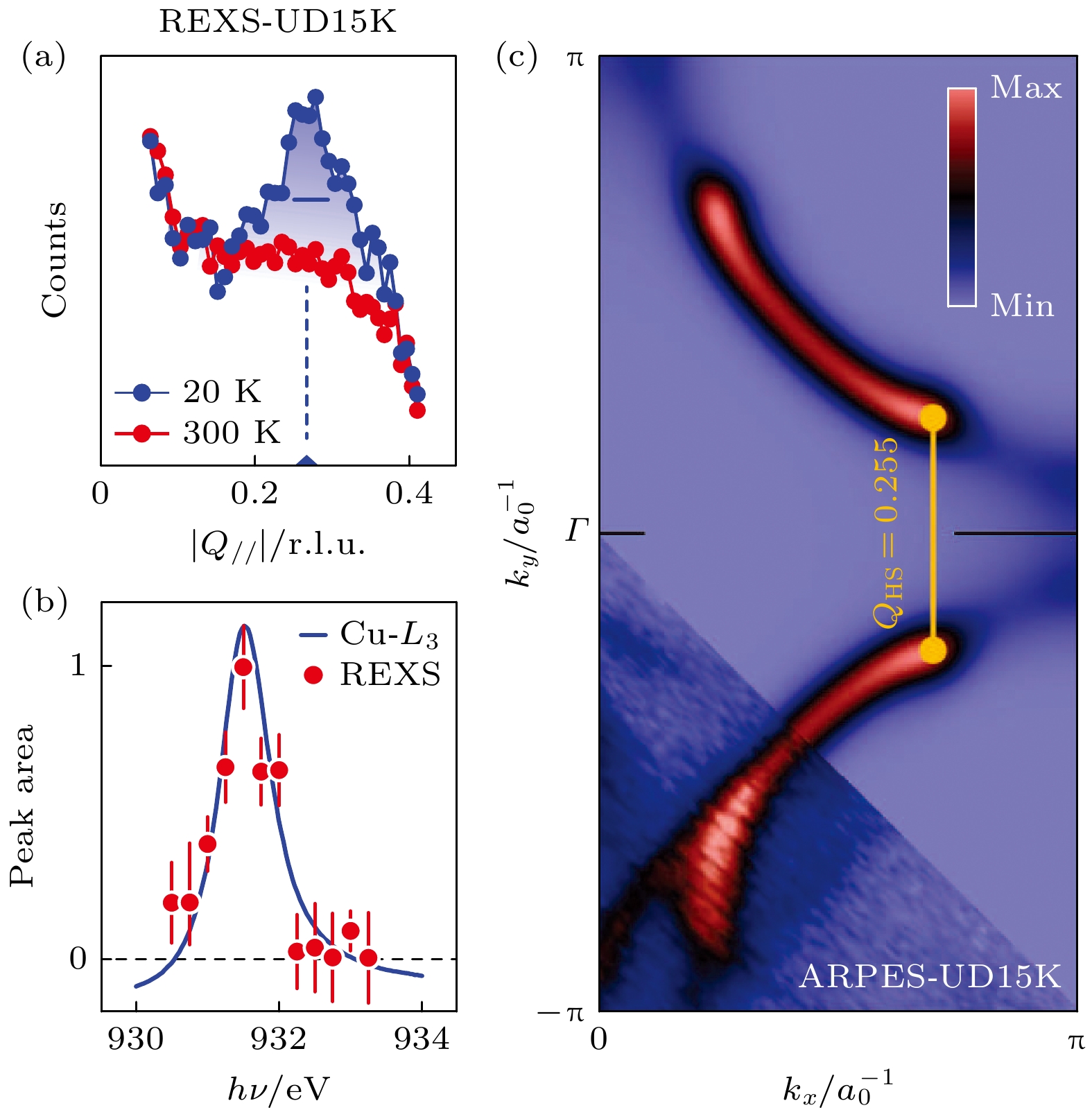
不同于镧系铜氧化物中的条纹序, 其他体系中并没有与电荷序共存的自旋序, 因而电荷序的微观图像仍未得出定论. 除了镧系铜氧化物外, 在其他空穴掺杂体系中, 电荷序波矢的大小随着空穴掺杂增加而减小, 在电子掺杂体系中随电子掺杂增加而增大 (见图5). 这一趋势与费米面的变化相符合, 因此有理论认为电荷序起源于费米面嵌套, 对应的波矢连接费米面上的反节点[83], 或者反铁磁布里渊区和费米面相交的“热点”[84-86]. 然而, 对于电荷序和费米面拓扑结构的关系仍存在争论[44,50,80,81,87]. 尽管RXS 和角分辨光电子谱(angle-resolved photoemission spectroscopy, ARPES)的对比测量发现, Bi2201体系中电荷序波矢对应赝能隙态下“费米弧”末梢的嵌套 (图6)[41], 电荷序的出现却没有在嵌套位置打开单粒子能隙. 另一方面, 欠掺杂YBCO和Hg1201等样品中观察到的量子振荡(quantum oscillation)表明, 在高场低温下, 其费米面发生了重构, 产生的电子型费米口袋大小与考虑电荷序导致的重构相符合[50], 暗示电荷序是导致费米面重构的原因. 然而, Hg1201中电荷序的面内关联长度只有几个晶格常数[50,88], 如此局域的关联难以从倒空间的图像来理解, 而后文将提到的高温动态电荷序关联的发现也与强耦合图像更加符合.
虽然这些体系里没有磁有序, 但是存在类似的自旋激发, 并且电荷序都在
$ p = 1/8 $ 掺杂附近最强. 基于这些类似条纹序的行为, 有理论提出了动态条纹序的图像[89]. 然而, 这一图像也存在实验上难以解释的现象, 比如这些体系中自旋和电荷调制的波矢随掺杂的演化没有表现出与La2–xBaxCuO4 (LBCO) 中类似的关联[39,90] (见图5总结). 另一方面, 对于电荷序局域结构的研究为理解这些现象提供了新的信息. 对Bi2212体系的STM测量表明其局域电荷密度调制是公度的, 具有4倍于晶格的周期[91]. 同时, NMR测量也表明YBCO中的电荷密度波具有公度的3倍于晶格周期的局域结构[92]. 结合这些实验现象, 可以得到一个可能的统一图像: 电子间相互作用驱动体系产生局域公度的电荷调制, 同时电子和晶格或电声相互作用起到锁定效应[19], 而费米面嵌套以及相位滑移等效应导致了电荷序在大尺度上的非公度性. 强耦合和弱耦合机制共同决定了这些体系中电荷序的性质. -
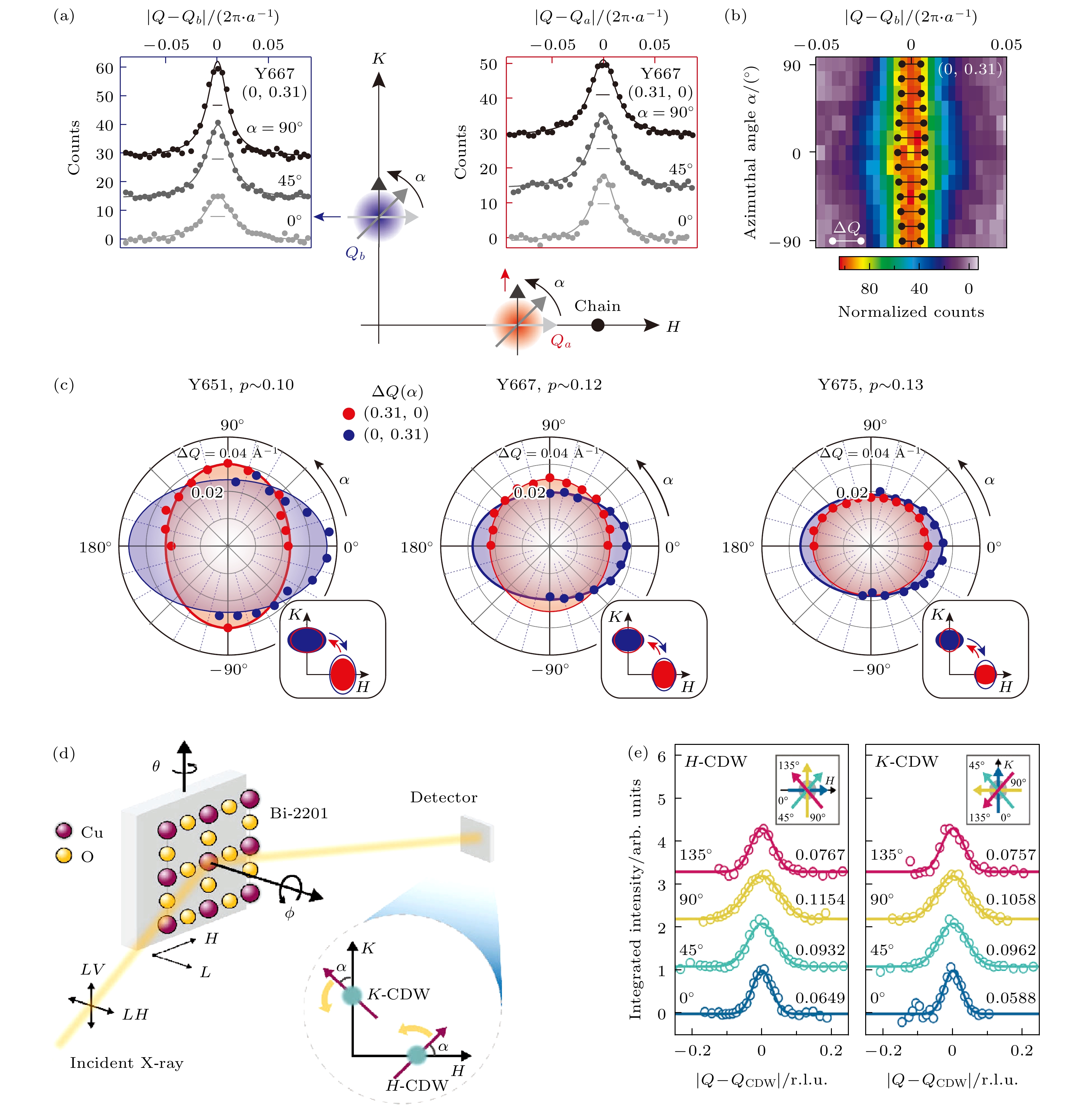
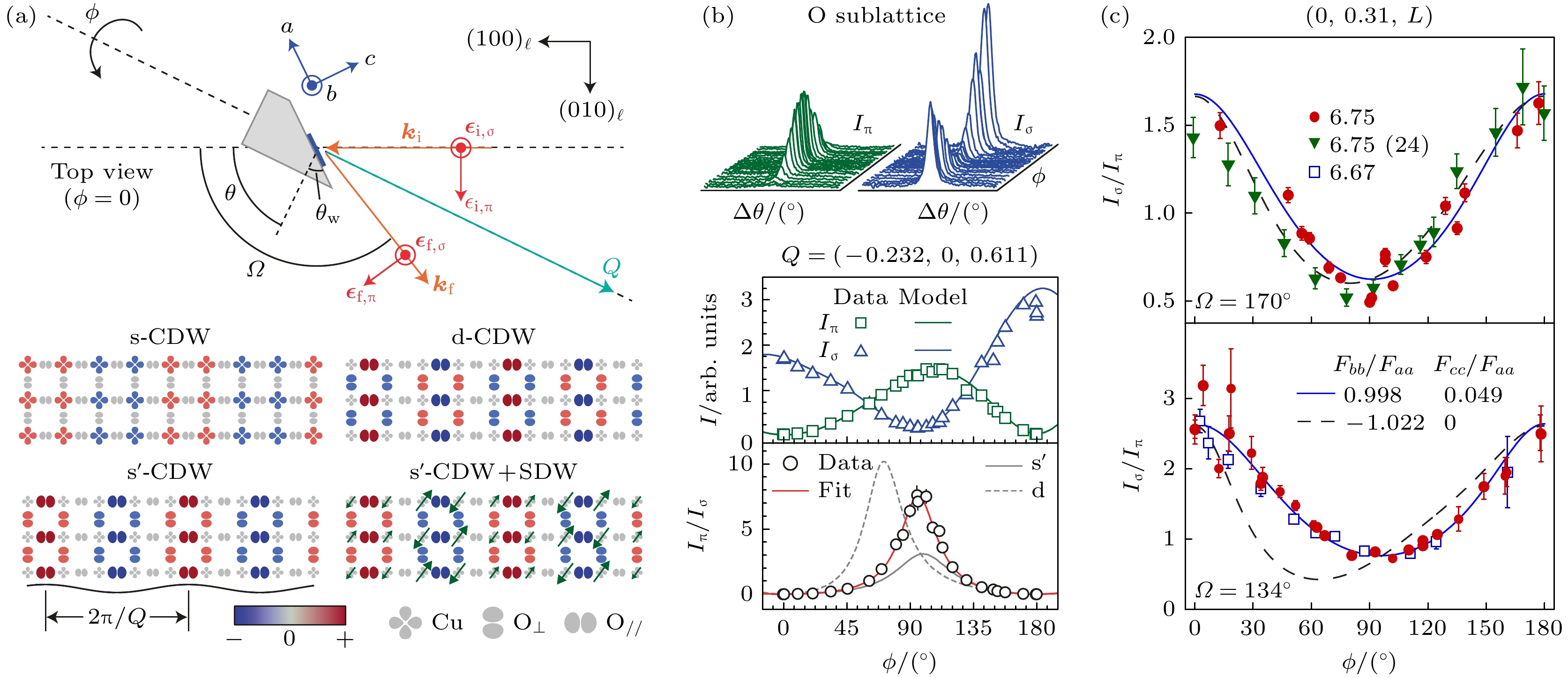
关于铜氧化物中电荷序的晶胞间(inter-unit-cell)和晶胞内(intra-unit-cell)结构均存在争议. 前者涉及的问题是电荷序具有单向 (如条纹状) 还是双向 (如棋盘状) 结构, 后者则与电荷的局域分布及对称性相关. STM对Ca2–xNaxCuO2Cl2 (Na-CCOC)和Bi2212材料的测量显示电荷序在局域上呈现单向性[93], 具有d对称性的结构因子[94,95]. 然而, 根据Bi2201的STM研究[96]及超声对YBCO的测量[97]可以认为电荷序具有双轴棋盘状结构. 高能X射线衍射对YBCO中电荷序引发晶格畸变的研究发现, 面内离子沿c方向畸变占据主导, 并且表现出d波结构因子[63]. 基于对电荷序衍射峰动量空间各向异性的分析, RXS实验指出YBCO[73]和Bi2201[74]中电荷序具有单向性的结构(图7). 由于RXS的结构因子受价电子局域对称性的影响, 通过分析散射强度还可以得到电荷序轨道对称性的信息(图8). 然而, 对YBCO的两项RXS实验分别认为其电荷序具有d波[98]和s波轨道对称性[76]. 对LBCO 的RXS研究则表明其电荷序轨道对称性最符合
$ {\mathrm{s}}^\prime $ 波的描述[75]. 电荷序的对称性可以反映电荷密度所处的价带轨道信息. 例如, d或$ {\mathrm{s}}^\prime $ 波结构意味着电荷密度分布在氧2p轨道, 而s波则表明电荷密度分布在铜3d轨道. 然而, 除了轨道对称性外, 电荷序的结构因子还可能受其他(如晶格结构)局域对称性的影响[76]. 另外, 吸收边的选择也可能会影响电荷序结构因子的确定. 例如, 铜L边可能对s波的部分更敏感. 这些因素可能共同导致了上述实验不一致的结论. 不论如何, 通过实验确定电荷序的对称性对理解电荷序的产生机制及其与超导电性的关系有着重要意义. 有理论认为, 驱动电子配对的相互作用也可能参与电荷序的产生过程[84,99]. 不难想象, 这种相互作用上的一致性会在两者序参量的对称性上有所体现. -
在铜氧化物材料中, 电荷序和超导表现出竞争关系. 但两者是同一组相互作用下的不同基态, 还是一个复合序参量的不同表现, 仍然是一个争议性的问题. 在LBCO
$ x = 1/8 $ 中, 电荷序的竞争导致体超导转变温度$ T_{\mathrm{c}} $ 被强烈抑制. 然而电阻率各项异性的测量却揭示二维超导电性与自旋序共同出现在40 K[100,101]. 这种二维超导电性被认为是配对密度波(pair-sensity-wave, PDW)超导态的体现[102]. PDW超导波函数随着条纹序产生空间调制, 层间约瑟夫森耦合产生阻挫, 因此抑制了体超导序. 在这种图像下, 电荷密度波和自旋密度波均是PDW的继承序.铜氧化物中存在PDW的一项主要实验证据来自STM实验对Bi2212中磁通涡旋附近电子态密度调制的研究[103]. 其他实验手段对铜氧化物中PDW的探索结果仍然没有定论. 例如, 对YBCO的NMR测量没有发现与CDW两倍周期相对应的调制[92]. 高能X射线衍射对YBCO的测量同样没有发现PDW存在的证据[104]. 最近, REXS实验在Sr掺杂的LBCO及Fe掺杂的LSCO中观察到在电荷序波矢一半的位置出现了具有共振依赖的弱衍射信号[105], 对应周期为电荷序两倍的电子态调制, 并且出现在电输运和磁化率测量给出的二维超导转变温度之下. 这些结果与预期的PDW衍射特征相一致, 为其存在提供了可能的证据. 值得注意的是, 该REXS实验通过背景扣除之后得到的衍射峰信号仍然十分微弱. 这一结果值得利用探测灵敏度更高的RIXS来验证. 此外, RIXS实验还可以进一步确定该信号来自准静态有序还是具有有限能量的动态关联.
除了序参量之间的耦合外, 电荷序的动力学行为也对超导具有潜在影响. 理论上, 电荷条纹序的横向涨落可以增强相邻条纹之间的约瑟夫森耦合, 导致超导的出现[106]. 在此图像下, 条纹序涨落的能量尺度对体系的基态有着重要影响. 另一方面, 也有基于弱耦合图像的理论指出铜氧化物中的电荷密度涨落可以提供d波配对所需相互作用, 从而增强超导电性[107,108]. 如图1所示, 最高
$ T_{\mathrm{c }}$ 可能对应着一个CDW的量子临界点, 其对应的电荷密度涨落不仅可能影响超导, 对载流子的散射机制也可能是导致奇异金属行为出现的原因[109,110]. 由于缺乏直接探测手段, 此前对电荷序动力学的实验研究相对较少. 随着RIXS技术的发展, 近年来出现了一系列利用RIXS研究动态电荷关联的工作. 下一节将对此作具体介绍. -
在铜氧化物电荷序研究初期, 散射及NMR实验发现电荷序出现在赝能隙特征温度
$ T^* $ 之下, 并且仅存在于$ p = 1/8 $ 附近相图很小的范围 (如图1所示), 因此电荷序被认为是由驱动赝能隙的电子态所引发的次生相. 然而, 近年来得益于RXS技术的进步, 尤其是RIXS分辨率的提高, 人们发现短程电荷关联广泛存在于铜氧化物中, 并且覆盖了温度-掺杂相图很大范围. 这一发现改写了此前对电荷序的认识, 引发了更多关于电荷涨落与超导配对[88]及正常态性质[110,112,114]之间内在关系的讨论.在镧214体系中, 自旋涨落在磁有序温度之上仍然存在, 这一现象推动了动态条纹序有关理论观点的提出[89]. 相比之下, 动态电荷关联的实验观测更加困难. 通过分析准弹性散射强度, RIXS实验对La1.875Ba0.125CuO4中电荷序的温度演化进行了研究[115], 发现条纹相内同时存在短程电荷关联与长程序, 并且短程电荷关联在条纹序转变温度之上已经存在. 对于La1.8–xEu0.2SrxCuO4 (Eu-LSCO,
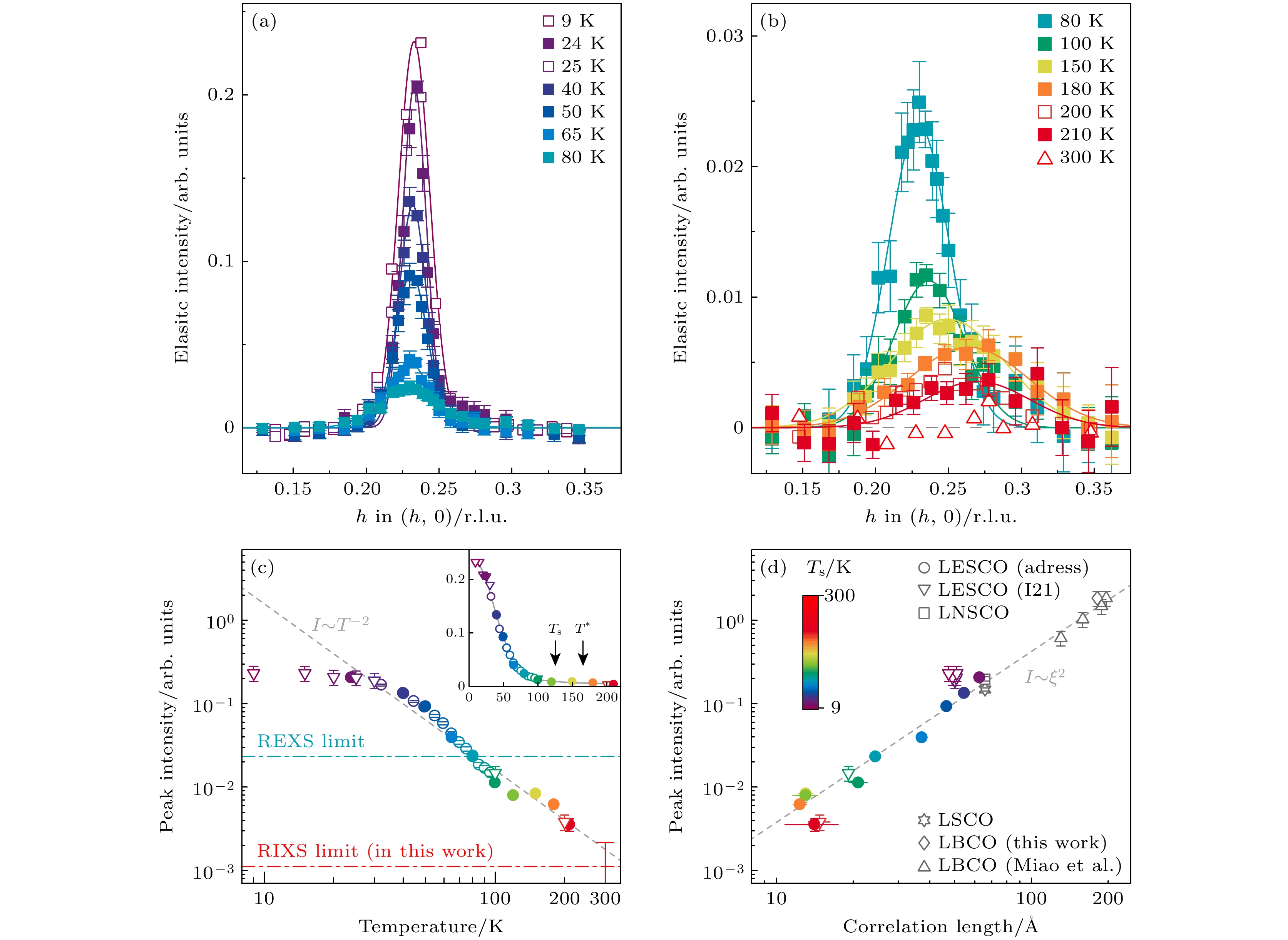
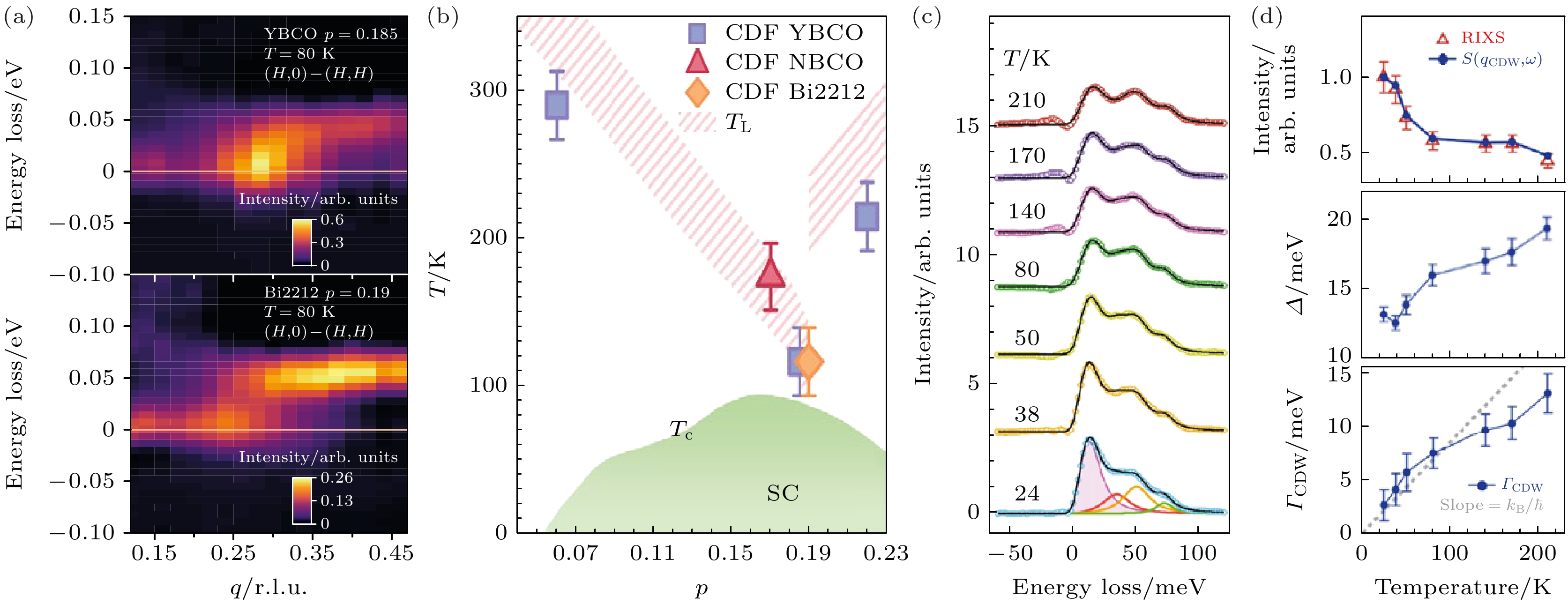
$ x = 0.125 $ )的RIXS实验发现短程电荷关联在赝能出现温度$ T^* $ 之上仍然存在[28], 表明条纹电荷关联表征了一种自发的对称性破缺趋势, 而不是赝能隙相关的次生相. 随着温度升高, 电荷关联的准弹性衍射峰逐渐变弱变宽, 直到实验测量的最高温度$ 210 $ K, 并且峰强I和关联长度ξ满足$ I\sim \xi^{2} $ (图9). 这一关系表明衍射峰的积分强度$ I\cdot\xi^{-2} $ 几乎不随温度变化. 进一步分析表明其他条纹序材料LBCO, Nd-LSCO及La2–xSrxCuO4 ($ x = 0.12 $ , LSCO)中的电荷序准弹性衍射峰均满足此关系, 随后REXS实验在掺杂覆盖$ x = 0.1 $ 至$x= 0.2 $ 的Eu-LSCO中也发现了$ I\sim \xi^{2} $ 的行为[29]. 这些结果揭示了条纹电荷关联可能存在统一描述. 不同实验也对LSCO中的高温短程电荷关联进行了研究. REXS实验发现赝能隙相内存在长程与短程电荷关联共存[116], 而其他研究则在不存在赝能隙的过掺杂样品中也发现了长程电荷序[117,118]. 更高分辨率RIXS实验发现, 具有明显温度依赖的长程电荷序在超导最佳掺杂附近消失 (图10)[34], 而短程电荷关联则在过掺杂$ x = 0.2 $ 的LSCO中仍然存在, 并且没有明显的温度依赖关系. 这些实验结果共同揭示了高温下动态条纹电荷关联的存在, 并覆盖了T-p相图的很大范围. 关于相图相悖的结论则可能源自不同能量分辨率下探测时间尺度上的差别. X射线光子关联谱(X-ray photon correlation spectroscopy, XPCS)相比非弹性散射可以在更长时间尺度上对电荷关联进行探测. 对掺杂$ x = 1/8 $ 的LBCO的XPCS研究发现条纹电荷序的畴在较长的时间尺度上(约2 h)没有显著变化[119], 说明的确存在静态电荷序. 而时间分辨的RIXS (tr-RIXS) 则在LBCO中探测到了皮秒尺度的条纹电荷涨落[120], 对应毫电子伏能量尺度, 与$ k_{\mathrm{B}}T_{\mathrm{c}} $ 相当, 表明条纹涨落可能对超导等低能物理性质产生影响.原则上RIXS可以探测电荷涨落的动态结构因子
$ S({\boldsymbol{Q}}, \omega)= (1-{\mathrm{e}}^{-\hbar \omega / k_{\text{B}} T})^{-1}\chi^{\prime\prime}({\boldsymbol{Q}}, \omega) $ , 从而得到其动态感应率的虚部$ \chi^{\prime\prime}({\boldsymbol{Q}}, \omega) $ . 然而由于RIXS散射截面包含多种激发过程的贡献, 对电荷序 涨落的实验测量面临诸多挑战. 超高分辨率铜 L边RIXS在具有短程电荷关联的Bi2212体系Bi2.2Sr1.8Ca0.8Dy0.2Cu2O8+δ中发现声子在电荷序波矢附近出现异常[45]. 其强度在略大于电荷序波矢处达到最大值, 并伴随能量的软化. 这一结果被解释为是具有色散的电荷激发与光学支声子相交时发生法诺共振(Fano resonance)的体现. 与此类似, RIXS实验在一系列具有长程或短程电荷序体系中发现, 电荷序波矢附近的声子强度及色散出现了异常, 涉及到的体系包括Eu-LSCO[19,121], Bi2201[111]和Bi2212[46] (见图11). 由于RIXS声子散射截面与电声子耦合强度有关, 对于声子强度异常的可能解释也包括电荷序相关的电声耦合强度变化[28,121]. 为了对电荷涨落进行定量分析, 需要将声子及准弹性散射对RIXS散射截面的贡献与电荷激发分离开. 如图12(a)和图12(b)所示, 针对YBCO, Nd1+xBa2–xCu3O7–δ (NBCO)及Bi2212的铜L边RIXS实验通过将$ (H, H) $ 方向的信号作为背景从$ (H, 0) $ 方向减去, 以此对低能电荷激发进行分析, 发现其特征能量尺度随掺杂及温度演化趋势与奇异金属相一致[112,122], 在相图上呈现一个楔形并在$ p = 0.19 $ 处达到最低温度(由能量尺度转化得到), 揭示了低能电荷激发与量子临界行为存在潜在联系. 对LSCO体系的超高分辨率氧K边RIXS实验[113]也发现其电荷密度激发具有类似的量子临界特征(图12(c)和图12(d)). 对Hg1201体系的RIXS实验则扣除了由多项式拟合的声子背景[88], 发现电荷激发直到接近200 meV仍然存在. 这一能量尺度与体系中顺磁振子的能量尺度相当, 暗示电荷涨落对铜氧化物体系的性质可能有着更加深刻的影响.由于受到声子散射截面的干扰, 上述实验中没有定量给出电荷密度涨落的色散关系. 事实上, 基于能带模型计算得到的RIXS声子谱与实验结果符合程度很高[23,123]. 后续研究可以将RIXS实验与计算相结合, 通过区分声子贡献得到电荷密度涨落的完整色散关系. 相应结果将帮助我们建立起关于电荷密度激发的微观描述, 明确其对铜氧化物低能物理性质的影响.
-
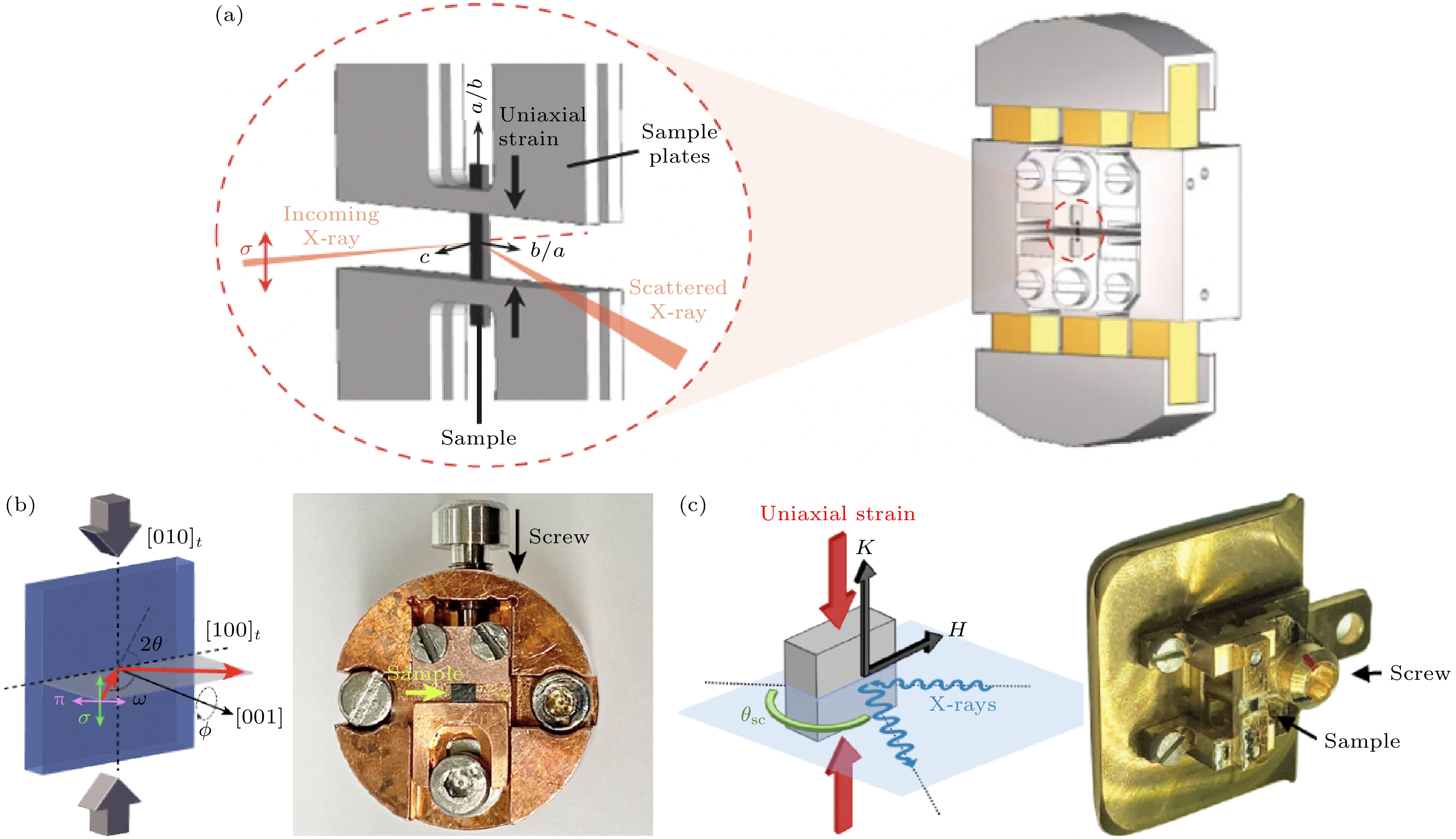
单轴应力作为一种有效的调控手段被广泛应用于量子材料的研究中. 由于软X射线散射往往需要考虑光路变化及样品解理的需求, 施加单轴应力面临更多技术问题. 近年来, 多个研究组致力于发展与软X射线散射相兼容的单轴应力样品环境(部分设计见图13), 并成功运用在铜氧化物材料的研究上.
单轴应力的一个常见效用是消除多畴的影响. 如前文所述, 铜氧化物电荷序的对称性是一个长期存在争议的问题. 在多畴的可能影响下, 具有二度旋转对称性的单轴 (如条纹序) 和四度旋转对称性的双轴 (如棋盘状) 电荷序都可以在
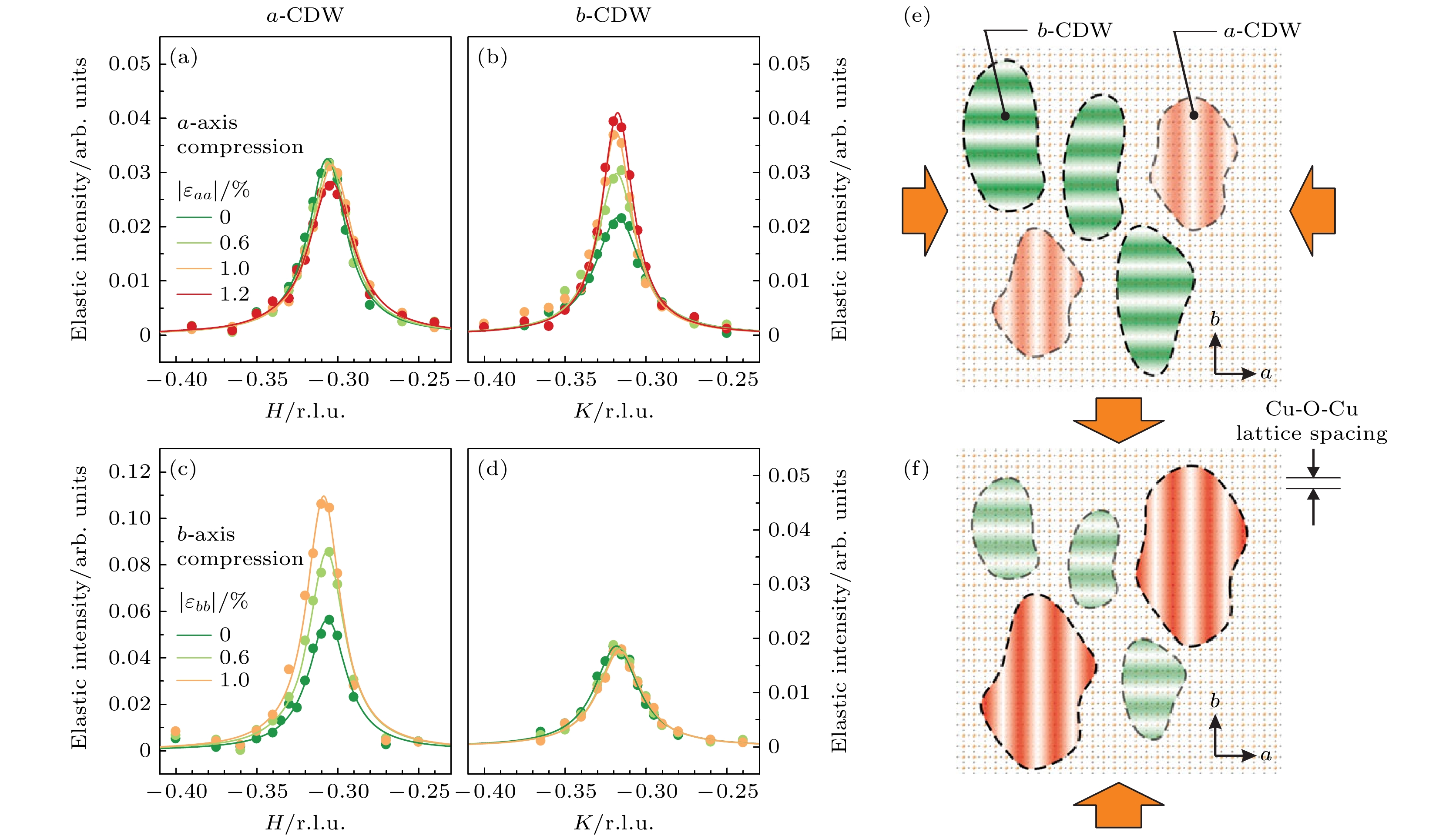
$ (H, 0) $ 和$ (0, K) $ 方向上产生X射线衍射峰, 因此难以区分. RIXS实验结合基于压电陶瓷的单轴应力装置(图13(a))对 YBa2Cu3O6.67中的电荷密度波序展开了研究[124]. 相比此前单轴压下的NXS实验[125], RIXS实验通过选择共振能量可以避免Cu—O链上的氧超结构序的影响. 如图14所示, 对面内二维电荷密度波的测量发现, 沿着晶体a方向加压会增大b方向电荷密度波的强度和关联长度, 而a方向的电荷密度波几乎不受影响. 沿着晶体b方向加压有着类似的效果, 表明两个方向的电荷密度波有着各自独立的序参量, 与棋盘状结构的描述不符.除YBCO外, 单轴应力实验还集中在镧214体系上. 通过对LSCO
$ x = 0.12 $ 单晶在铜氧面内施加沿Cu—O键方向的单轴应力, 高能X射线衍射实验发现沿着$ (K, 0) $ 方向的电荷序衍射峰被抑制消失, 而$ (H, 0) $ 方向的衍射峰强度增大了一倍[128]. 这一结果表明波矢方向相垂直的电荷序衍射峰源自于条纹序不同的畴, 而单轴应力有效消除了电荷序的多畴结构. 随后中子散射实验也确认了单轴压下可以产生单畴自旋序, 进一步确认了自旋-电荷相耦合的条纹序的微观图像[129].单轴应力还可以通过电荷序与晶格的耦合对两者进行调控. 在镧214体系中, 晶格在低温四方(low-temperature tetragonal, LTT)相内, 铜氧八面体以面内Cu—O键方向为轴产生旋转畸变(如图15(a)), 打破铜氧面四重旋转对称性的趋势与 条纹序一致, 被认为起到了稳定条纹相的作用[24]. 实验上的确在具有LTT相的LBCO, Nd-LSCO和Eu-LSCO
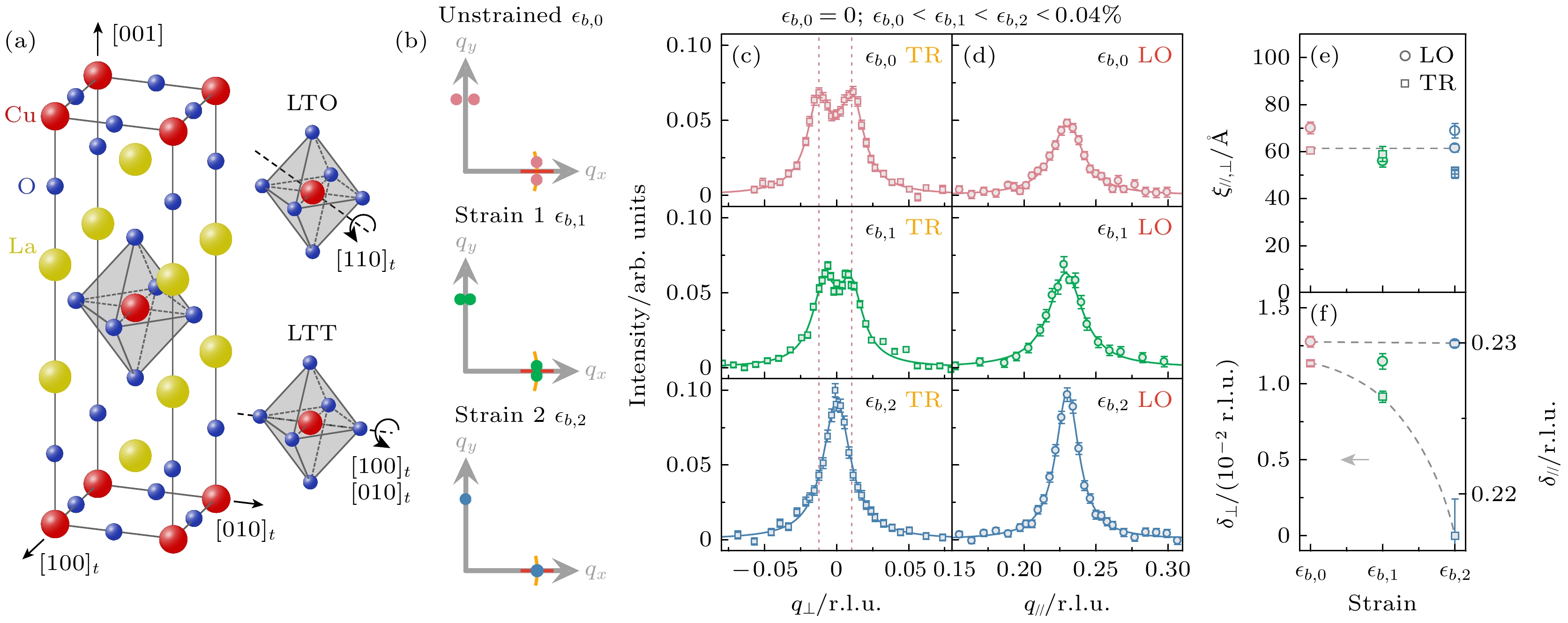
$ x = 1/8 $ 中观察到较强的静态条纹序. 而LSCO$ x = 1/8 $ 在低温下保持低温正交(low-temperature orthorhombic, LTO)相结构, 其铜氧八面体旋转畸变以面内Cu—Cu连线方向为轴(图15(a)), 与条纹序对称性破缺的方向不一致. 因此LSCO中的条纹相更有可能克服由晶格耦合带来的钉扎效应, 产生条纹相涨落. 事实上, 共振及非共振X射线散射测量均发现LSCO中的电荷序衍射峰沿横向发生劈裂[126,132], 峰值出现在非公度波矢$ \delta_{\perp}\approx 0.011 $ r.l.u. 的位置 (图15), 远远超过了由LTO相栾晶效应可能导致的劈裂程度[132]. 因此这一现象需要从条纹序自身结构来理解. 在强耦合图像下, 电荷条纹序在局域范围是公度的, 但可能存在相位的跳跃. 其横向的非公度性可以理解为横向的相位跳跃有序排列[126], 等效使得电荷条纹偏离晶轴发生了转动, 条纹序横向涨落通过这种相位跳跃实现. 有理论认为这种横向条纹涨落可以增强条纹间的约瑟夫森耦合从而促进超导电性[89].LTT和LTO正交结构分别可以视为对四重对称的铜氧面施加内在
$ B_{1 g} $ 和$ B_{2 g} $ 应力. 因此, 对LSCO外加$ B_{1 g} $ 单轴应力有可能通过增强与晶格间的耦合实现对条纹序的调控. 基于这一构想, 结合图13(b)中的装置, RIXS实验研究了LSCO$ x = 0.12 $ 中电荷序对单轴压的响应[126]. 测量发现沿晶体b (平行于面内Cu—O键)方向施加微小应力($ \epsilon < 0.04{\text{%}} $ )即可以使电荷序的横向非公度性$ \delta_{\perp} $ 逐渐减小到零, 此过程中H和K方向上的电荷序衍射峰保持对称. 微小应力即可以“锁定”条纹相的实验现象表明条纹序和晶格之间存在的耦合较弱, 产生条纹涨落需要克服的能量尺度比较低. 这一结论也与tr-RIXS观测到毫电子伏尺度的横向条纹涨落的实验结果相一致[120].LTT结构中, 相邻两层铜氧八面体旋转方向交替变化, 条纹排列的方向也互相垂直, 因此对其施加单轴应力可能会与在LTO结构中产生不同效果. REXS实验发现, 对LTT结构的Nd-LSCO
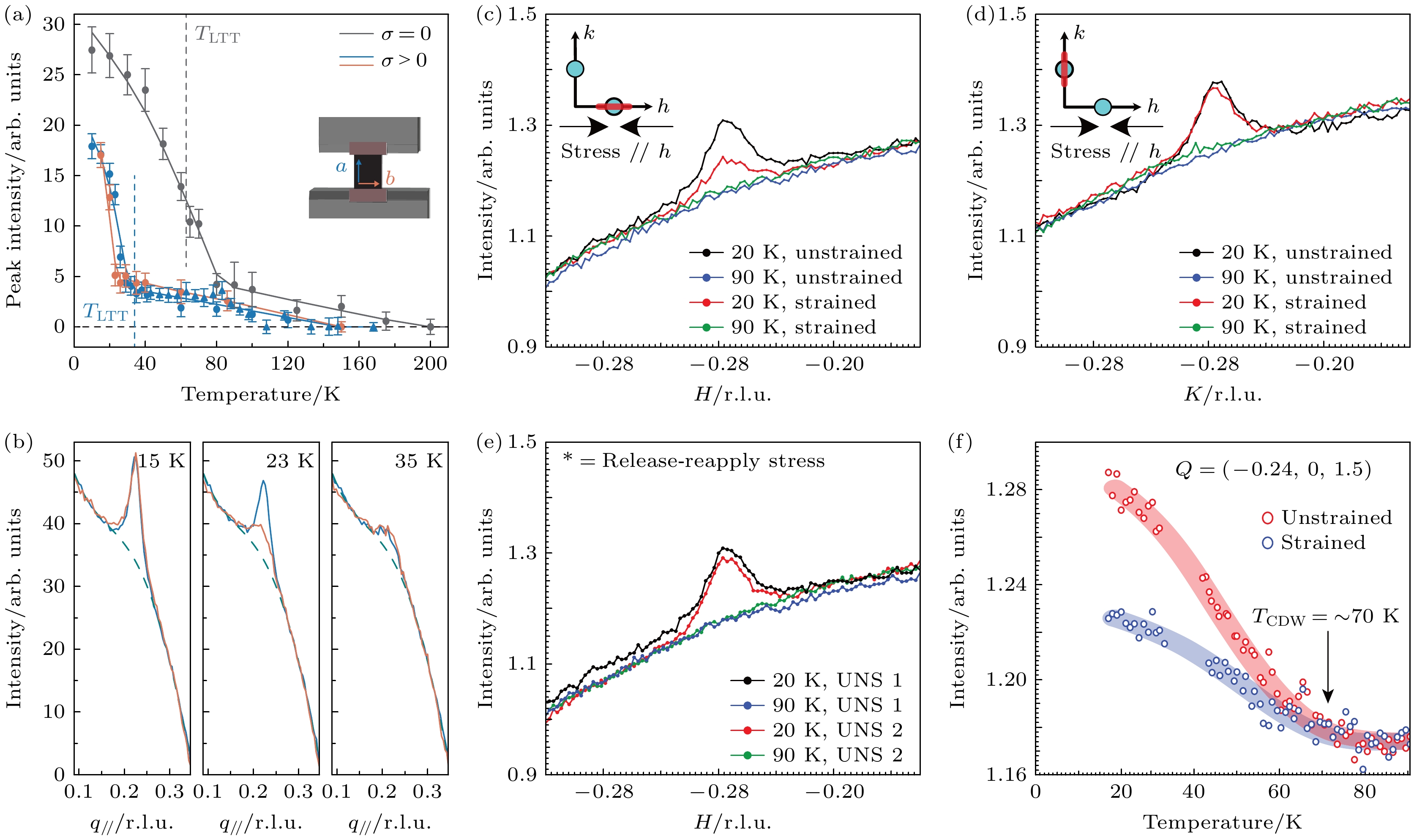
$ x = 0.125 $ 施加沿面内Cu—O键方向的单轴拉伸应力会抑制LTT结构和电荷条纹序[130]. 如图16(a)和图16(b)所示, 在$ \epsilon\approx (0.046 \pm 0.026){\text{%}} $ 的单轴拉伸应力作用下两者的相变温度分别降低了约50 K和$ 29 $ K. 两者相变温度对应力的不同响应可能源自其他竞争序(如超导)的影响. 然而, 另一项REXS实验中, 对Nd-LSCO$ x = 0.125 $ 施加沿面内Cu—O键方向的单轴压缩应力则没有观察到LTT和电荷序相变温度的变化[131]. 如图16(c)—(f), 沿H方向施加压缩应力会使该方向的电荷序衍射峰强度减小约一半, 而K方向的信号则几乎不受影响. 这一结果不同于LSCO中观察到的电荷序退栾晶的效应. 一个可能的解释是单轴压力作用下铜氧面内电子态的各项异性发生了改变, 整体表现为对电荷序的抑制. 对Nd-LSCO两项实验的不同结果有可能来自于拉伸和压缩应力效果的区别, 也可能和施加应力的大小有关. 不论如何, 上述实验共同表明利用单轴应力可以实现对电荷序的有效调控.前文提到, RIXS实验观察到电荷序波矢附近存在电荷密度涨落, 以及声子色散的异常. 这些现象的微观机制及其与电荷序之间的关系尚未明确. 为了回答这些问题, RIXS 实验进一步研究了单轴应力作用下非弹性散射的响应(应力装置见图13(c)). 通过对LSCO
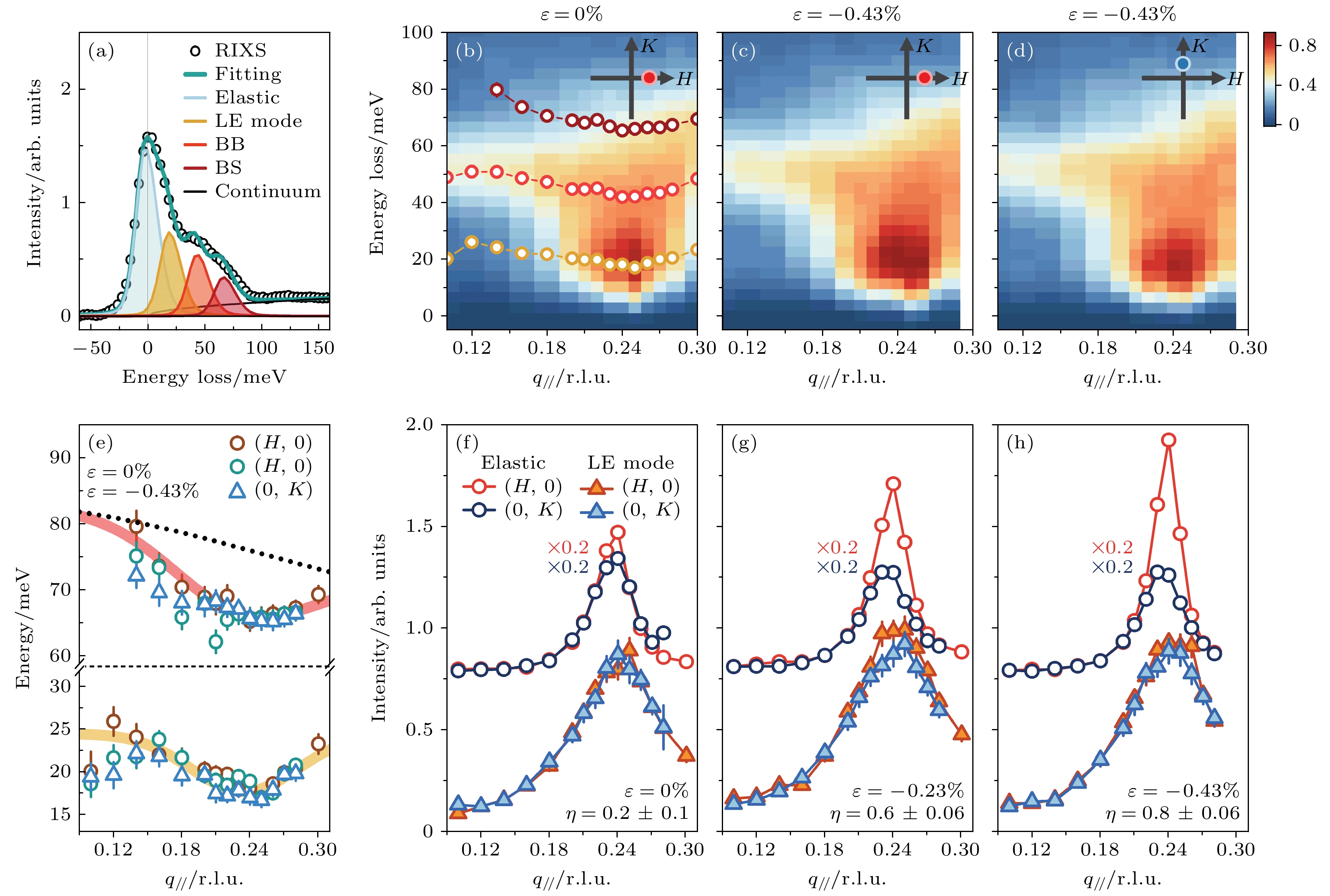
$ x = 1/8 $ 沿面内Cu—O键方向施加压缩应力, 高分辨的铜L边和氧K边的RIXS测量确认了电荷序在面内具有二重对称[127], 与此前高能X射线衍射的结果相一致[128]. 与此同时, 低能电荷激发和声子激发没有发生明显变化. 如图17所示, 在应力引发电荷序H和K方向出现明显各向异性的同时, 低能电荷激发仍保持四重对称, 而H和K方向的声子也基本一致, 70 meV附近的光学支声子在两个方向都出现色散的软化. 这些结果表明该体系中声子的异常并非由弹性电荷序引发, 支持条纹序主要起源于电子关联效应的观点.除RIXS之外, 单轴应力还可以与其他谱学测量手段相结合, 如STM和ARPES, 以研究电子态对外场的响应[133,134]. 最近的一项 ARPES 实验揭示, 在过掺杂的Pb-Bi2212中施加沿Cu—O键方向的单轴应力可以引发相列序[135]. 这种电子态旋转对称性的破缺被认为有可能来源于电荷序涨落[136]. 然而, 目前仍缺乏这些手段对铜氧化物中电荷序应力响应的直接测量. 未来相关实验的开展将有助于我们明确电荷序与外场耦合的微观机制.
-
随着同步辐射实验技术的发展, 共振X射线散射在量子材料研究领域展现出日益重要的作用. 尤其是近年来RIXS能量分辨率的大幅提高, 使我们得以对多种量子物态以及相应的元激发进行更精确的探测[137]. 本文以铜氧化物中的电荷序为代表, 介绍了近期相关的共振X射线散射研究进展, 包括针对准弹电荷关联、电声耦合与集体激发态的研究, 以及结合单轴应力进行调控的工作. 这些研究结果也指出了需要进一步解决的问题, 主要围绕以下几个方面: 1)描述铜氧化物中电荷序的统一图像; 2)电荷序和赝能隙态、超导态之间的关系; 3)电荷密度涨落的能量尺度、色散关系及其对正常态和超导态的影响. 理解这些问题需要对电荷序的相图进行更加细致的表征. 例如, 利用更高分辨RIXS将电荷序与电荷密度涨落的贡献相区分, 从而明确两者各自的演化关系. 此外, 还可以利用外场调控来拓展电荷序相图的维度. 比如, 沿垂直于铜氧面方向施加应力可以影响顶点氧的高度, 进而调节电荷序与超导之间的竞争[138]. 另外, 外加磁场也可以抑制超导, 增强电荷序. 随着技术难题的突破, 这些原位调控手段正逐步与共振X射线散射相结合, 而RIXS谱仪的能量分辨率也在持续提高, 这些实验技术的进步将为量子材料的研究打开更多新的视角.
除了铜氧化物外, 电荷序也是其他强关联电子体系的重要研究内容. 例如, 近年来新发现的镍基超导体系中也有关于电荷序存在的实验报道. 在无限层镍氧化物薄膜材料中, 共振X射线散射观察到沿着Ni—O键方向的电荷周期性调制迹象[69-71,139]. 然而, 进一步的研究表明, 该现象具有样品依赖性, 是否源于材料本征性质仍然存在争议[140]. 具有双层和三层ruddlesden-popper (RP) 结构的镍氧化物La3Ni2O7和La4Ni3O10在高压下分别展现出转变温度高达80 K和30 K的超导电性[141,142], 吸引了广泛关注. 现有的输运、缪子自旋弛豫、NMR以及RXS等实验结果表明, 常压下La3Ni2O7在低温下具有磁有序, 但是否有电荷序尚未明确[143-146]. 而在La4Ni3O10中, X射线及中子散射研究表明, 常压下存在相互交织的自旋和电荷序[147]. 考虑到La4Ni3O10的金属性, 其自旋和电荷序很可能起源于费米面嵌套, 与铜氧化物中的条纹序有着显著区别. 镍基超导家族的发现为高温超导研究提供了新的机遇, 通过与铜氧化物研究结果进行对比将帮助我们建立起对非常规超导更加全面的认识. 接下来的研究需要明确无限层和RP相镍氧化物中是否具有本征电荷序, 并确定其微观结构和对称性, 在此基础上开展高压下的研究. 另外, 最近在La3Ni2O7和La2.85Pr2.15Ni2O7薄膜中观察到了常压下
$ T_{\mathrm{c}} $ 超过40 K的超导电性[148,149], 为研究镍基超导和密度波有序的关系提供了更加理想的平台.理论计算方面, 由于共振X射线散射所涉及的高阶过程更加复杂, 如何定量描述各种RIXS激发过程仍然是一个充满挑战的问题. 现有计算方法有着各自明显的局限性. 例如, 团簇模型的严格数值计算往往受限于计算上的复杂性, 而基于有效RIXS理论得到的响应函数与关联函数的对应关系也存在疑问. 未来需要将RIXS实验测量与理论计算更加紧密结合, 促进两者共同发展.
铜氧化物超导体电荷序的共振X射线散射研究进展
Research progress of resonant X-ray scattering of charge order in cuprate superconductors
-
摘要: 非常规超导电性通常与一系列复杂的物质态相互竞争或共存. 在铜氧化物超导材料中, 存在自旋序、电荷序、赝能隙态和奇异金属相等多种物质态. 理解它们之间的关系是解决高温超导机理问题的基础. 最近的研究结果表明, 电荷序关联在铜氧化物体系中普遍存在, 并且覆盖了相图的广泛区域, 成为高温超导研究的重点. 本文总结了共振X 射线散射对铜氧化物中电荷序的研究进展, 聚焦于具有能量分辨的非弹性散射实验, 着重介绍了关于高温动态电荷序关联的研究, 以及结合单轴应力对电荷序进行调控的工作. 基于这些结果, 讨论了铜氧化物电荷序的微观机制、结构和对称性, 以及电荷序对超导和正常态的可能影响, 并对未来的研究方向进行了展望.Abstract: Unconventional superconductivity often competes or coexists with a variety of complex material states. In cuprate superconductors, there exist states including spin order, charge order, the pseudogap state, and the strange metal phase. A comprehensive understanding of their relationship is fundamental to establishing the mechanism of high-temperature superconductivity. Spin dynamics in cuprates has been extensively investigated using inelastic neutron scattering, but charge correlations remain far less understood. The latest development of resonant X-ray scattering (RXS) has been able to detect charge correlations with unprecedented sensitivity. A series of RXS studies have revealed that there universally exist the charge correlations in cuprate materials, which covers a wide range of the phase diagram. Resonant inelastic X-ray scattering (RIXS) experiments further show the dynamical behaviors of charge order. These findings highlight the important influence of charge correlations on the properties of cuprates. In this paper, we review the latest research progress in the charge order in cuprates by using RXS, with a particular emphasis on RIXS experiments. Our focus is placed on recent works on dynamical charge correlations at high temperatures as well as uniaxial strain tuning of charge order. We discuss topics including the underlying interactions, microscopic structure and symmetries, and the possible influence of charge order on both the superconducting and normal states.
-
Key words:
- cuprates /
- high-temperature superconductivity /
- charge order /
- resonant X-ray scattering .
-

-
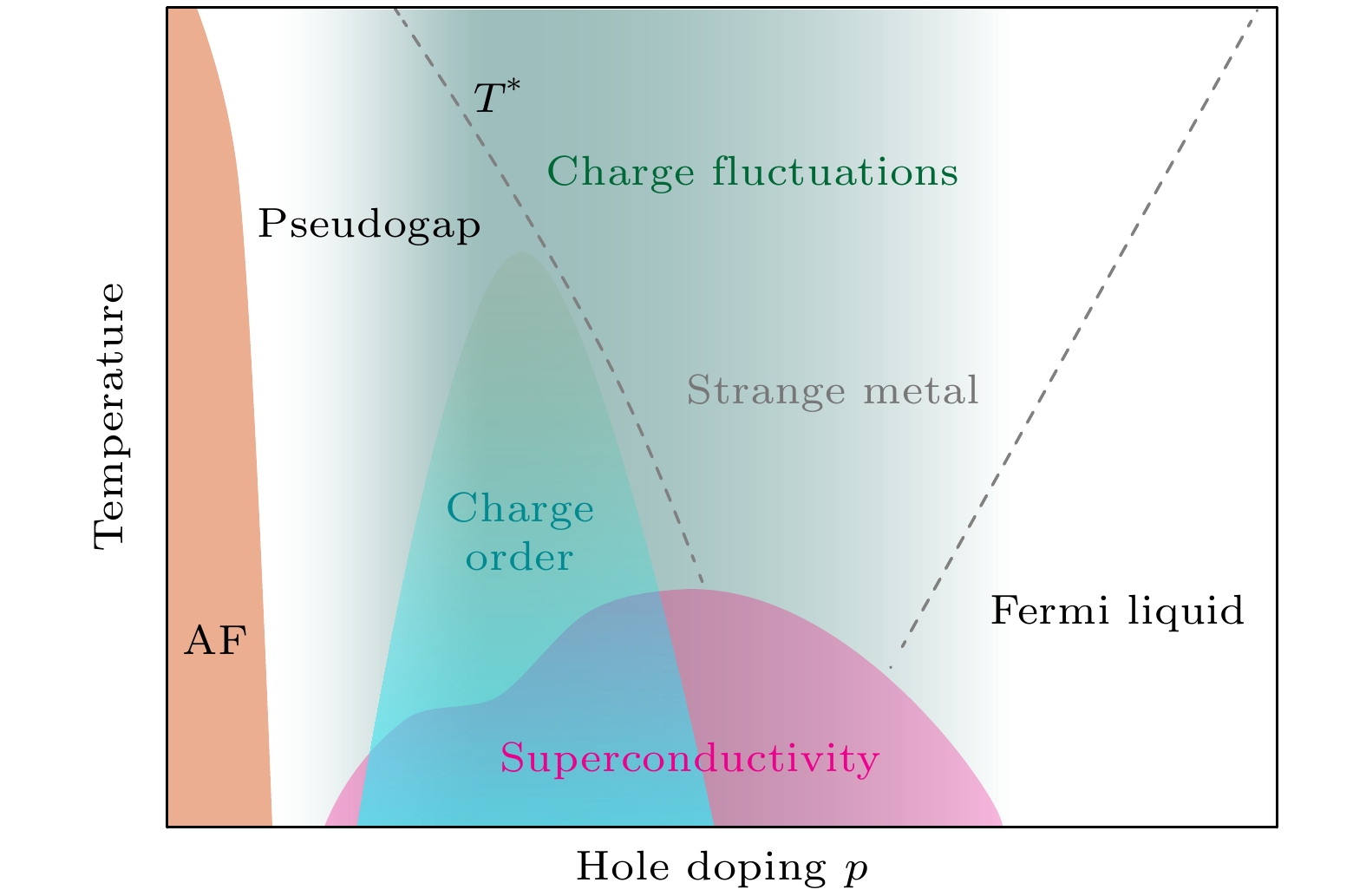
图 1 空穴型掺杂铜氧化物超导体的典型相图. 灰色长虚线标记赝能隙出现的温度
$ T^* $ . 灰色短虚线指示奇异金属和费米液体相的过渡区域. 灰绿色阴影示意电荷密度涨落出现的区域. AF表示反铁磁有序Figure 1. Typical phase diagram for hole-doped cuprates. The gray dashed line marks the pseudogap onset temperature
$T^* $ . The gray dotted line indicates the crossover from the strange metal phase to the Fermi liquid state.图 2 X射线散射原理示意图 (a)散射几何; (b)共振X射线散射过程[19]. 共振X射线将芯电子激发至价带未占据态, 使体系短暂处在具有芯空穴和激发价电子的中间态, 随后占据态的电子返回填充芯电子并发射出X射线
Figure 2. Schematic illustration of the principle of X-ray scattering: (a) Scattering geometry; (b) the process of resonant X-ray scattering[19]. Upon the absorption of an X-ray photon, a core electron is promoted to the valence state, creating a core hole and an excited valence electron in the intermediate state. In the final state, a valence electron fills the core hole, accompanied by the emission of an X-ray photon.
图 3 关联电子体系中元激发及其特征能量尺度示意图. 利用RIXS的能量分辨可以区分准弹性与非弹性散射贡献, 从而实现对电荷序的灵敏探测. 弹性散射的能量宽度取决于仪器的分辨率
Figure 3. Schematic illustration of the energy scales of elementary excitations in correlated electron systems. The energy resolution of RIXS allows for the separation of elastic from inelastic scattering processes, enhancing the sensitivity in probing charge order. The energy width of the elastic line is determined by the instrumental energy resolution.
图 4 中子散射在Nd-LSCO中观测到的条纹序衍射峰[24] (a) CuO2平面内自旋-电荷条纹模型示意图, 圆圈表示铜的位置, 箭头代表铜上的自旋, 灰色圆圈指示空穴掺杂位置; (b) 倒空间
$ (H, K, 0) $ 面内自旋和电荷序的衍射峰 (实心圆), 以及晶格的布拉格峰 (空心圆); 中子散射测量到的(c)自旋序和(d)电荷序衍射峰. 动量空间中的扫描方向如图(b)中箭头所示Figure 4. Neutron scattering observation of stripe-order reflections[24]: (a) Schematic illustration of the stripe pattern in the CuO2 plane. Circles denote the Cu sites. Arrows indicate the spins and gray circles indicate the doped holes. (b) Illustration of the
$ (H, K, 0) $ plane in the reciprocal space, where spin and charge diffraction peaks were scanned and displayed in (c) and (d), respectively.图 5 铜氧化物体系中电荷序(a)及低能自旋涨落或自旋序(b)波矢随掺杂演化关系. 数据来自X射线或中子散射的倒空间测量. 电荷序测量结果来自文献[26-52]. 自旋序或低能自旋涨落测量结果来自文献[24,26,29,53-62]
Figure 5. Doping evolution of wave vectors associated with charge (a) and low-energy spin fluctuations (b) for hole-doped cuprates, determined from X-ray or neutron scattering experiments. Data in panel (a) are taken from Refs. [26-52]. Data in panel (b) are taken from Refs. [24,26,29,53-62].
图 6 Bi2201体系中电荷序和赝能隙态下“费米弧”的嵌套[41] (a) Bi2201中共振X射线测量得到的电荷序衍射峰; (b)铜
$ L_3 $ 边电荷序的共振行为; (c) ARPES数据显示电荷序波矢量连接费米弧尖端Figure 6. Charge order and nesting of Fermi arc tips in the pseudogap state of Bi2201[41]: (a) Charge order peak in Bi2201 measured by REXS; (b) resonant behavior of charge order at the Cu
$L_3 $ -edge; (c) ARPES data showing charge ordering wave vector connects the Fermi arc-tips.图 7 YBCO和Bi2201中电荷序的单向结构[73,74] (a) YBCO中电荷序的动量结构示意图, 左右插图分别展示了H和K方向上电荷序峰部分方位角下的RXS动量扫描; (b) K方向电荷序峰强随方位角α的变化, 黑色横线表示峰宽
$ \Delta Q $ ; (c) YBa2Cu3O6.51 (Y651), YBa2Cu3O6.67 (Y667) 和 YBa2Cu3O6.75 (Y675) 中$ \Delta Q $ 随方位角α变化的极坐标图[73]; (d) Bi2201的转角RIXS实验示意图, 通过改变样品面内转角ϕ和面外转角θ实现对电荷序峰从不同方位角α进行扫描; (e) 电荷序峰沿不同角度α的动量宽度表现出各向异性[74]Figure 7. Unidirectional charge order in YBCO and Bi2201[73,74]: (a) Schematic of the momentum structure of charge order in YBCO. Left and right insets display RXS momentum scans along H and K directions at selected azimuthal angles α, respectively. (b) Intensity of the charge order peak along K as a function of azimuthal angle. Black bars indicate the peak width
$ \Delta Q $ . (c) Polar plots of$ \Delta Q $ versus α for YBa2Cu3O6.51 (Y651), YBa2Cu3O6.67 (Y667), and YBa2Cu3O6.75 (Y675)[73]. (d) Schematic of the angular-dependent RIXS experiment on Bi2201. The charge order is scanned at different azimuthal angles α by varying the in-plane and out-of-plane sample rotation angle ϕ and θ. (e) Scans at different α reveal the anisotropic structure of the charge order peaks[74].图 8 电荷序的轨道对称性[75,76] (a)共振X射线散射实验及电荷序不同轨道对称性示意图; (b) LBCO[75] 与 (c) YBCO[76]中不同极化入射光下电荷序强度的方位角依赖及模型比较[74]
Figure 8. Orbital symmetry of charge order[75,76]: (a) Schematics of the RXS geometry and different orbital symmetries of charge order; intensity of the charge order peak as a function of azimuthal angle ϕ using different incident light polarizations for (b) LBCO[75] and (c) YBCO[76].
图 9 条纹序铜氧材料的高温电荷关联[28] (a), (b) RIXS测量得到的
$ 1/8 $ 空穴掺杂Eu-LSCO中不同温度下的电荷序峰; (c) Eu-LSCO中电荷序峰强的温度依赖, 在20 K以上峰强正比于$ T^{-2} $ (灰色虚线), 插图中$ T_{\mathrm{s}} $ 和$ T^{*} $ 分别代表低温四方结构相和赝能隙态的起始温度; (d) 镧214体系中条纹电荷序峰强与关联长度的关系Figure 9. High-temperature charge correlations in stripe-ordered cuprates[28]: (a), (b) Charge order peak in Eu-LSCO at various temperatures measured by RIXS; (c) temperature evolution of the charge order peak amplitude, which decays roughly as
$T^{-2} $ (gray dashed line); (d) relationship between charge order peak amplitude and correlation length in La-214 compounds.图 10 镧系铜氧材料中的短程电荷关联[34] (a)不同能量分辨率RIXS对LSCO x = 0.145测量得到的能谱, 下图中更高的分辨率使得声子和电荷序的贡献得以区分; (b), (c) LSCO x = 0.145和x = 0.16中电荷序的温度依赖
Figure 10. Short-range charge correlations in La-based cuprates[34]: (a) RIXS spectra on LSCO x = 0.145 obtained with different energy resolutions. The improved resolution in panel (a) allows for resolving the phonon branch. (b), (c) Temperature dependence of charge order in LSCO x = 0.145 and x = 0.16.
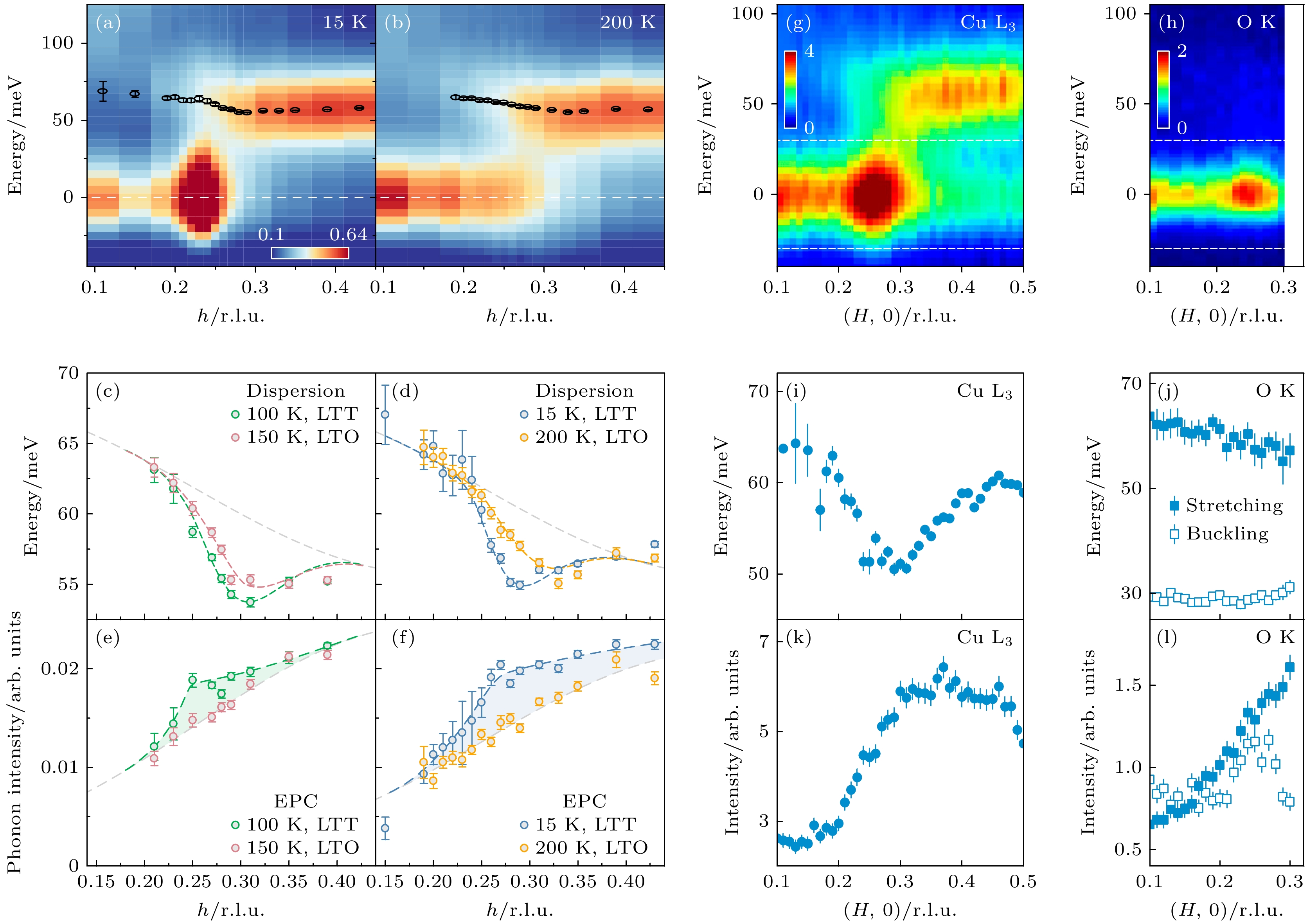
图 11 电荷序有关的RIXS声子异常[19,111] (a), (b) Eu-LSCO中15 K和200 K时电荷序波矢附近的RIXS能谱, 低温下零能量附近的信号峰来自电荷序, 黑色圆圈标记了键伸缩(bond-stretching)声子位置; (c)—(f) Eu-LSCO中电荷序波矢附近的RIXS声子软化及强度增强[19]; (g), (h) Bi2201 中电荷序波矢附近的铜L边和氧K边RIXS能谱, 氧K边具有更高能量分辨率, 因此可以分辨键伸缩和更低能量的键屈曲(bond-buckling)声子, 但是能覆盖的动量范围更小; (i)—(l) Bi2201中的RIXS声子软化及强度异常[111]
Figure 11. RIXS phonon anomaly associated with charge order[19,111]: (a), (b) RIXS spectra around the charge ordering wave vector in Eu-LSCO at 15 K and 200 K. The intense elastic peak at low temperature originates from charge order. Black dots mark the bond-stretching phonon position. (c)–(f) RIXS phonon energy softening and intensity enhancement near the charge ordering wave vector in Eu-LSCO[19]. (g), (h) Cu L-edge and O K-edge RIXS spectra around the charge ordering wave vector in Bi2201. (i)–(l) RIXS phonon softening and intensity anomaly in Bi2201[111].
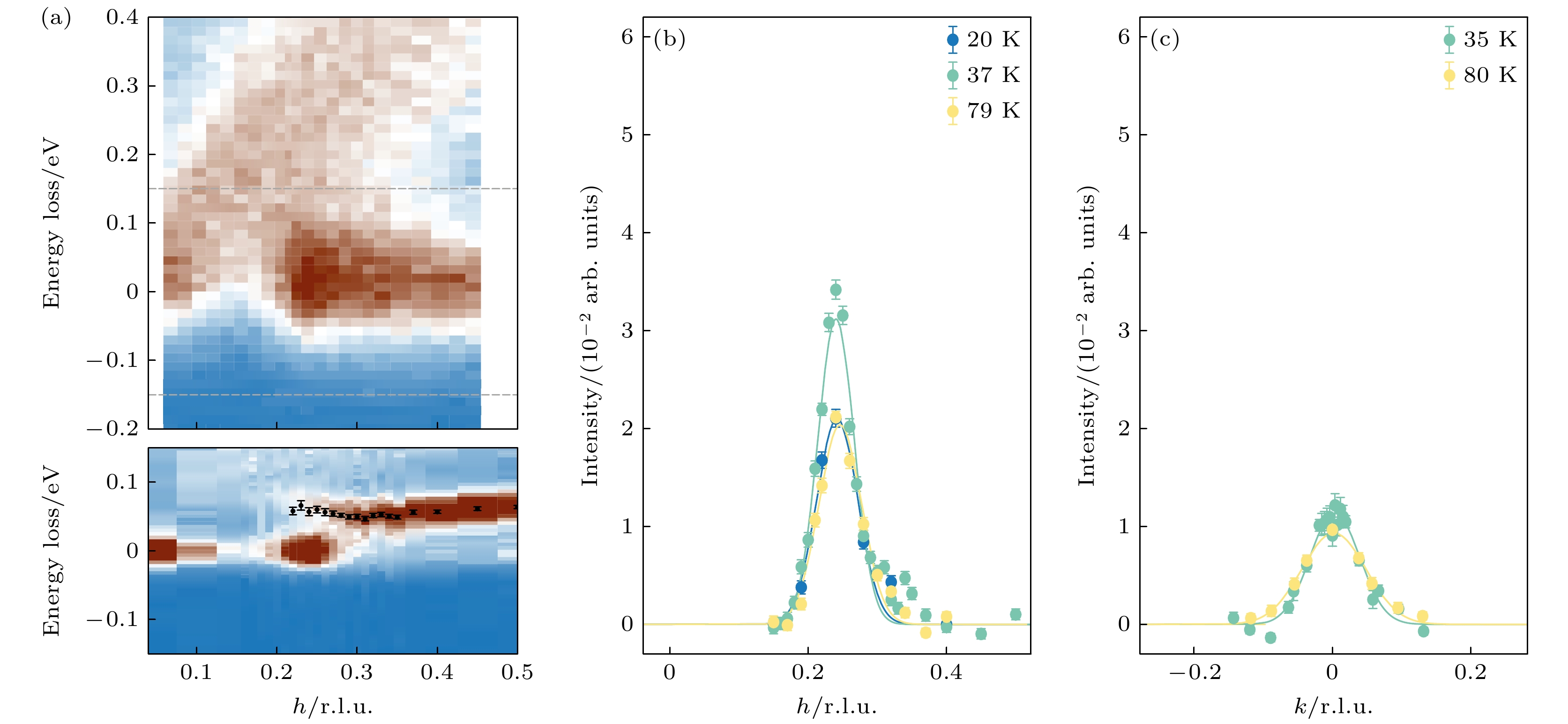
图 12 电荷密度涨落[112,113] (a) YBCO和Bi2212中
$ (H, 0) $ 和$ (H, H) $ 方向RIXS信号作差; (b)总结YBCO, NBCO及Bi2212体系中RIXS结果得到的电荷密度涨落的特征温度与空穴掺杂量的关系[112]; (c) LSCO$ x = 0.15 $ 中电荷序波矢附近不同温度下的RIXS 能谱, 100 meV以下可以分辨三支声子及更低能量的电荷激发模式; (d) LSCO$ x = 0.15 $ 中电荷激发的强度、特征能量及寿命倒数的温度依赖[113]Figure 12. Charge density fluctuations[112,113]: (a) Intensity difference between RIXS spectra taken along
$ (H, 0) $ and$ (H, H) $ directions in YBCO and Bi2212; (b) doping evolution of the characteristic temperature of charge density fluctuations obtained from RIXS data on YBCO, NBCO, and Bi2212[112]; (c) RIXS spectra around the charge ordering wave vector in LSCO$ x = 0.15 $ at different temperatures; (d) the intensity, characteristic energy, and inverse lifetime of the charge excitation as a function of temperature in in LSCO$ x = 0.15 $ [113].图 14 YBCO中二维电荷序的应力响应[124] (a) H 和 (b) K 方向电荷序对沿a方向施加应力的响应; (c) H 和 (d) K 方向电荷序对沿b方向施加应力的响应; (e), (f) 单轴应力下电荷序畴的实空间示意图
Figure 14. Strain response of the 2D charge order in YBCO[124]: (a), (b) Evolution of the charge order peaks along (a) H and (b) K directions under the a-axis compression; (c), (d) the charge order peaks along (c) H and (d) K directions under the b-axis compression. (e), (f) Schematics of the real-space charge order domains under uniaxial strain.
图 15 LSCO中应力引发的条纹序旋转[126] (a)镧214铜氧材料结构示意图[28], 左图为高温四方 (HTT) 相结构, 右图示意LTO与LTT相内铜氧八面体的旋转畸变; (b)常压及单轴压下LSCO中电荷序的动量结构示意图, 橙色和红色实线分别示意图(c)和(d)中动量空间扫描方向; (c), (d)电荷序峰的(c)横向与(d)纵向动量依赖随外加应力的变化; (e)电荷序关联长度和(f)非公度波矢随外加应力的变化关系
Figure 15. Strain-induced stripe order rotation in LSCO[126]: (a) Schematic illustration of the crystal structure of La-based cuprates[28]. Left: structure of the HTT phase; right: distortion of the CuO6 octahedra in the LTO and LTT phases. (b) Momentum structure of the charge order peak in LSCO under ambient and compressive strain. The orange and red solid lines indicate the momentum scan directions in (c) and (d), respectively. (c), (d) Strain evolution of the (c) transverse and (d) longitudinal momentum scans of charge order peak. (e) Correlation length and (f) incommensurability of charge order as a function of applied strain.
图 16 LTT结构中条纹电荷序对单轴应力的响应[130,131] (a), (b)对Nd-LSCO沿面内Cu—O键方向施加拉伸应力时LTT结构相变及电荷序的变化[130]; (c)—(f)沿面内Cu—O键方向施加压缩应力时Nd-LSCO中电荷序的变化[131]
Figure 16. Response of charge-stripe order to uniaxial strain applied in the LTT structure[130,131]: (a), (b) Evolution of charge order and LTT phase in Nd-LSCO upon the application of tensile strain along the in-plane Cu—O bond direction[130]; (c)–(f) response of charge order in Nd-LSCO to compressive strain applied along the Cu—O bond direction[131].
图 17 LSCO中电荷序及低能激发的应力响应[127] (a)代表性氧K边RIXS谱及拟合; (b)未施加应力时的动量依赖RIXS激发谱; (c), (d)外加面内Cu—O键方向压缩应力时沿(c) H (垂直于应力) 及(d) K (平行于应力) 方向的动量依赖RIXS激发谱; (e)键伸缩声子和低能电荷激发模式的色散关系的应力依赖; (f)—(h) 电荷序峰及低能电荷激发强度的应力依赖. 其中图(b)—(d)中已减去拟合得到的弹性散射信号
Figure 17. Strain response of charge order and low-energy excitations in LSCO[127]: (a) Representative RIXS spectrum fitting; (b) momentum-dependent RIXS excitations without strain application; (c), (d) RIXS excitation spectra along (c) H (perpendicular to strain) and K (parallel to strain) directions under compressive strain applied along the in-plane Cu—O bond direction; (e) strain dependence of the bond-stretching phonon and low-energy charge excitation dispersion; (f)–(h) strain dependence of the charge order and charge excitation intensities. The fitted elastic signal has been removed in panels (b)–(d).
-
[1] Keimer B, Kivelson S A, Norman M R, Uchida S, Zaanen J 2015 Nature 518 179 doi: 10.1038/nature14165 [2] Chaussy J, Haen P, Lasjaunias J C, Monceau P, Waysand G, Waintal A, Meerschaut A, Molinié P, Rouxel J 1976 Solid State Commun. 20 759 doi: 10.1016/0038-1098(76)90289-1 [3] Grüner G 1988 Rev. Mod. Phys. 60 1129 doi: 10.1103/RevModPhys.60.1129 [4] Gressier P, Guemas L, Meerschaut A 1982 Acta Cryst. B 38 2877 doi: 10.1107/S0567740882010176 [5] Weber F, Rosenkranz S, Castellan J P, Osborn R, Hott R, Heid R, Bohnen K P, Egami T, Said A H, Reznik D 2011 Phys. Rev. Lett. 107 107403 doi: 10.1103/PhysRevLett.107.107403 [6] Harper J M E, Geballe T H, DiSalvo F J 1977 Phys. Rev. B 15 2943 doi: 10.1103/PhysRevB.15.2943 [7] Peierls R E 1994 Quantum Theory of Solids (Oxford: Oxford University Press [8] Grüner G 1994 Density Waves in Solids (Reading: Addison-Wesley [9] Johannes M D, Mazin I I 2008 Phys. Rev. B 77 165135 doi: 10.1103/PhysRevB.77.165135 [10] Zhu X, Cao Y, Zhang J, Plummer E W, Guo J 2015 PNAS 112 2367 doi: 10.1073/pnas.1424791112 [11] Jérome D, Rice T M, Kohn W 1967 Phys. Rev. 158 462 doi: 10.1103/PhysRev.158.462 [12] Rossnagel K, Kipp L, Skibowski M 2002 Phys. Rev. B 65 235101 doi: 10.1103/PhysRevB.65.235101 [13] Bel R, Behnia K, Berger H 2003 Phys. Rev. Lett. 91 066602 doi: 10.1103/PhysRevLett.91.066602 [14] Hwang J, Ruan W, Chen Y, Tang S, Crommie M F, Shen Z X, Mo S K 2024 Rep. Prog. Phys. 87 044502 doi: 10.1088/1361-6633/ad36d3 [15] Hoffman J E, Hudson E W, Lang K M, Madhavan V, Eisaki H, Uchida S, Davis J C 2002 Science 295 466 doi: 10.1126/science.1066974 [16] Blinc R 1981 Phys. Rep. 79 331 doi: 10.1016/0370-1573(81)90108-3 [17] Wu T, Mayaffre H, Krämer S, Horvatic M, Berthier C, Hardy W N, Liang R, Bonn D A, Julien M 2011 Nature 477 191 doi: 10.1038/nature10345 [18] Ament L J P, van Veenendaal M, Devereaux T P, Hill J P, van den Brink J 2011 Rev. Mod. Phys. 83 705 doi: 10.1103/RevModPhys.83.705 [19] Wang Q, von Arx K, Horio M, Mukkattukavil D J, Küspert J, Sassa Y, Schmitt T, Nag A, Pyon S, Takayama T, Takagi H, Garcia-Fernandez M, Zhou K J, Chang J 2021 Sci. Adv. 7 eabg7394 doi: 10.1126/sciadv.abg7394 [20] Schülke W 2007 Electron Dynamics by Inelastic X-ray Scattering (Oxford: Oxford Universtiy Press [21] Moretti Sala M, Bisogni V, Aruta C, Balestrino G, Berger H, Brookes N B, Luca G M d, Di Castro D, Grioni M, Guarise M, Medaglia P G, Miletto Granozio F, Minola M, Perna P, Radovic M, Salluzzo M, Schmitt T, Zhou K J, Braicovich L, Ghiringhelli G 2011 New J. Phys. 13 043026 doi: 10.1088/1367-2630/13/4/043026 [22] Brink J V D, Veenendaal M V 2006 Europhys. Lett. 73 121 doi: 10.1209/epl/i2005-10366-9 [23] Devereaux T P, Shvaika A M, Wu K, Wohlfeld K, Jia C J, Wang Y, Moritz B, Chaix L, Lee W S, Shen Z X, Ghiringhelli G, Braicovich L 2016 Phys. Rev. X 6 041019 [24] Tranquada J M, Sternlieb B J, Axe J D, Nakamura Y, Uchida S 1995 Nature 375 561 doi: 10.1038/375561a0 [25] de Groot F M F, Haverkort M W, Elnaggar H, Juhin A, Zhou K J, Glatzel P 2024 Nat. Rev. Methods Primers 4 45 doi: 10.1038/s43586-024-00322-6 [26] Hücker M, V Zimmermann M, Gu G D, Xu Z J, Wen J S, Xu G, Kang H J, Zheludev A, Tranquada J M 2011 Phys. Rev. B 83 104506 doi: 10.1103/PhysRevB.83.104506 [27] Fink J, Soltwisch V, Geck J, Schierle E, Weschke E, Büchner B 2011 Phys. Rev. B 83 092503 doi: 10.1103/PhysRevB.83.092503 [28] Wang Q, Horio M, von Arx K, Shen Y, John Mukkattukavil D, Sassa Y, Ivashko O, Matt C E, Pyon S, Takayama T, Takagi H, Kurosawa T, Momono N, Oda M, Adachi T, Haidar S M, Koike Y, Tseng Y, Zhang W, Zhao J, Kummer K, Garcia-Fernandez M, Zhou K J, Christensen N B, Rønnow H M, Schmitt T, Chang J 2020 Phys. Rev. Lett. 124 187002 doi: 10.1103/PhysRevLett.124.187002 [29] Lee S, Huang E W, Johnson T A, Guo X, Husain A A, Mitrano M, Lu K, Zakrzewski A V, de la Peña G A, Peng Y, Huang H, Lee S J, Jang H, Lee J S, Joe Y I, Doriese W B, Szypryt P, Swetz D S, Chi S, Aczel A A, MacDougall G J, Kivelson S A, Fradkin E, Abbamonte P 2022 PNAS 119 e2119429119 doi: 10.1073/pnas.2119429119 [30] Wilkins S B, Dean M P M, Fink J, Hücker M, Geck J, Soltwisch V, Schierle E, Weschke E, Gu G, Uchida S, Ichikawa N, Tranquada J M, Hill J P 2011 Phys. Rev. B 84 195101 doi: 10.1103/PhysRevB.84.195101 [31] Gupta N K, McMahon C, Sutarto R, Shi T, Gong R, Wei H I, Shen K M, He F, Ma Q, Dragomir M, Gaulin B D, Hawthorn D G 2021 PNAS 118 e2106881118 doi: 10.1073/pnas.2106881118 [32] Christensen N B, Chang J, Larsen J, Fujita M, Oda M, Ido M, Momono N, Forgan E M, Holmes A T, Mesot J, Huecker M, Zimmermann M v 2014 arXiv: 1404.3192 [cond-mat.supr-con] [33] Croft T P, Lester C, Senn M S, Bombardi A, Hayden S M 2014 Phys. Rev. B 89 224513 doi: 10.1103/PhysRevB.89.224513 [34] von Arx K, Wang Q, Mustafi S, Mazzone D G, Horio M, Mukkattukavil D J, Pomjakushina E, Pyon S, Takayama T, Takagi H, Kurosawa T, Momono N, Oda M, Brookes N B, Betto D, Zhang W, Asmara T C, Tseng Y, Schmitt T, Sassa Y, Chang J 2023 npj Quantum Mater. 8 7 doi: 10.1038/s41535-023-00539-w [35] Achkar A J, Sutarto R, Mao X, He F, Frano A, Blanco-Canosa S, Le Tacon M, Ghiringhelli G, Braicovich L, Minola M, Moretti Sala M, Mazzoli C, Liang R, Bonn D A, Hardy W N, Keimer B, Sawatzky G A, Hawthorn D G 2012 Phys. Rev. Lett. 109 167001 doi: 10.1103/PhysRevLett.109.167001 [36] Chang J, Blackburn E, Holmes A T, Christensen N B, Larsen J, Mesot J, Liang R, Bonn D A, Hardy W N, Watenphul A, Zimmermann M v, Forgan E M, Hayden S M 2012 Nat. Phys. 8 871 doi: 10.1038/nphys2456 [37] Ghiringhelli G, Tacon M L, Minola M, Blanco-Canosa S, Mazzoli C, Brookes N B, Luca G M D, Frano A, Hawthorn D G, He F, Loew T, Sala M M, Peets D C, Salluzzo M, Schierle E, Sutarto R, Sawatzky G A, Weschke E, Keimer B, Braicovich L 2012 Science 337 821 doi: 10.1126/science.1223532 [38] Hücker M, Christensen N B, Holmes A T, Blackburn E, Forgan E M, Liang R, Bonn D A, Hardy W N, Gutowski O, Zimmermann M V, Hayden S M, Chang J 2014 Phys. Rev. B 90 054514 doi: 10.1103/PhysRevB.90.054514 [39] Blackburn E, Chang J, Hücker M, Holmes A T, Christensen N B, Liang R, Bonn D A, Hardy W N, Rütt U, Gutowski O, Zimmermann M V, Forgan E M, Hayden S M 2013 Phys. Rev. Lett. 110 137004 doi: 10.1103/PhysRevLett.110.137004 [40] Blanco-Canosa S, Frano A, Schierle E, Porras J, Loew T, Minola M, Bluschke M, Weschke E, Keimer B, Le Tacon M 2014 Phys. Rev. B 90 054513 doi: 10.1103/PhysRevB.90.054513 [41] Comin R, Frano A, Yee M M, Yoshida Y, Eisaki H, Schierle E, Weschke E, Sutarto R, He F, Soumyanarayanan A, He Y, Le Tacon M, Elfimov I S, Hoffman J E, Sawatzky G A, Keimer B, Damascelli A 2014 Science 343 390 doi: 10.1126/science.1242996 [42] Peng Y Y, Fumagalli R, Ding Y, Minola M, Caprara S, Betto D, Bluschke M, De Luca G M, Kummer K, Lefrançois E, Salluzzo M, Suzuki H, Le Tacon M, Zhou X J, Brookes N B, Keimer B, Braicovich L, Grilli M, Ghiringhelli G 2018 Nat. Mater. 17 697 doi: 10.1038/s41563-018-0108-3 [43] Zhang S, Li Q, Zou C, Huang H Y, Singh A, Yan H, Zhou X, Huang D J, Peng Y 2024 Phys. Rev. B 110 125108 doi: 10.1103/PhysRevB.110.125108 [44] da Silva Neto E H, Aynajian P, Frano A, Comin R, Schierle E, Weschke E, Gyenis A, Wen J, Schneeloch J, Xu Z, Ono S, Gu G, Le Tacon M, Yazdani A 2014 Science 343 393 doi: 10.1126/science.1243479 [45] Chaix L, Ghiringhelli G, Peng Y Y, Hashimoto M, Moritz B, Kummer K, Brookes N B, He Y, Chen S, Ishida S, Yoshida Y, Eisaki H, Salluzzo M, Braicovich L, Shen Z X, Devereaux T P, Lee W S 2017 Nat. Phys. 13 952 doi: 10.1038/nphys4157 [46] Lee W S, Zhou K J, Hepting M, Li J, Nag A, Walters A C, Garcia-Fernandez M, Robarts H C, Hashimoto M, Lu H, Nosarzewski B, Song D, Eisaki H, Shen Z X, Moritz B, Zaanen J, Devereaux T P 2020 Nat. Phys. 17 53 [47] Boschini F, Minola M, Sutarto R, Schierle E, Bluschke M, Das S, Yang Y, Michiardi M, Shao Y C, Feng X, Ono S, Zhong R D, Schneeloch J A, Gu G D, Weschke E, He F, Chuang Y D, Keimer B, Damascelli A, Frano A, da Silva Neto E H 2021 Nat. Commun. 12 597 doi: 10.1038/s41467-020-20824-7 [48] Lu H, Hashimoto M, Chen S D, Ishida S, Song D, Eisaki H, Nag A, Garcia-Fernandez M, Arpaia R, Ghiringhelli G, Braicovich L, Zaanen J, Moritz B, Kummer K, Brookes N B, Zhou K J, Shen Z X, Devereaux T P, Lee W S 2022 Phys. Rev. B 106 155109 doi: 10.1103/PhysRevB.106.155109 [49] Zou C, Choi J, Li Q, Ye S, Yin C, Garcia-Fernandez M, Agrestini S, Qiu Q, Cai X, Xiao Q, Zhou X, Zhou K J, Wang Y, Peng Y 2024 Nat. Commun. 15 7739 doi: 10.1038/s41467-024-52124-9 [50] Tabis W, Li Y, Tacon M L, Braicovich L, Kreyssig A, Minola M, Dellea G, Weschke E, Veit M J, Ramazanoglu M, Goldman A I, Schmitt T, Ghiringhelli G, Barišić N, Chan M K, Dorow C J, Yu G, Zhao X, Keimer B, Greven M 2014 Nat. Commun. 5 5875 doi: 10.1038/ncomms6875 [51] Campi G, Bianconi A, Poccia N, Bianconi G, Barba L, Arrighetti G, Innocenti D, Karpinski J, Zhigadlo N D, Kazakov S M, Burghammer M, Zimmermann M v, Sprung M, Ricci A 2015 Nature 525 359 doi: 10.1038/nature14987 [52] Tabis W, Yu B, Bialo I, Bluschke M, Kolodziej T, Kozlowski A, Blackburn E, Sen K, Forgan E M, Zimmermann M v, Tang Y, Weschke E, Vignolle B, Hepting M, Gretarsson H, Sutarto R, He F, Le Tacon M, Barišić N, Yu G, Greven M 2017 Phys. Rev. B 96 134510 doi: 10.1103/PhysRevB.96.134510 [53] Tranquada J M, Axe J D, Ichikawa N, Moodenbaugh A R, Nakamura Y, Uchida S 1997 Phys. Rev. Lett. 78 338 doi: 10.1103/PhysRevLett.78.338 [54] Yamada K, Lee C H, Kurahashi K, Wada J, Wakimoto S, Ueki S, Kimura H, Endoh Y, Hosoya S, Shirane G, Birgeneau R J, Greven M, Kastner M A, Kim Y J 1998 Phys. Rev. B 57 6165 doi: 10.1103/PhysRevB.57.6165 [55] Fujita M, Yamada K, Hiraka H, Gehring P M, Lee S H, Wakimoto S, Shirane G 2002 Phys. Rev. B 65 064505 doi: 10.1103/PhysRevB.65.064505 [56] Matsushita H, Kimura H, Fujita M, Yamada K, Hirota K, Endoh Y 1999 J. Phys. Chem. Solids 60 1071 doi: 10.1016/S0022-3697(99)00050-5 [57] Dai P, Mook H A, Hunt R D, Doğan F 2001 Phys. Rev. B 63 054525 doi: 10.1103/PhysRevB.63.054525 [58] Arai M, Nishijima T, Endoh Y, Egami T, Tajima S, Tomimoto K, Shiohara Y, Takahashi M, Garrett A, Bennington S M 1999 Phys. Rev. Lett. 83 608 doi: 10.1103/PhysRevLett.83.608 [59] Bourges P, Sidis Y, Fong H F, Regnault L P, Bossy J, Ivanov A, Keimer B 2000 Science 288 1234 doi: 10.1126/science.288.5469.1234 [60] Headings N S, Hayden S M, Kulda J, Babu N H, Cardwell D A 2011 Phys. Rev. B 84 104513 doi: 10.1103/PhysRevB.84.104513 [61] Haug D, Hinkov V, Sidis Y, Bourges P, Christensen N B, Ivanov A, Keller T, Lin C T, Keimer B 2010 New J. Phys. 12 105006 doi: 10.1088/1367-2630/12/10/105006 [62] Enoki M, Fujita M, Nishizaki T, Iikubo S, Singh D K, Chang S, Tranquada J M, Yamada K 2013 Phys. Rev. Lett. 110 017004 doi: 10.1103/PhysRevLett.110.017004 [63] Forgan E M, Blackburn E, Holmes A T, Briffa A K R, Chang J, Bouchenoire L, Brown S D, Liang R, Bonn D, Hardy W N, Christensen N B, Zimmermann M V, Hücker M, Hayden S M 2015 Nat. Commun. 6 10064 doi: 10.1038/ncomms10064 [64] Abbamonte P 2006 Phys. Rev. B 74 195113 doi: 10.1103/PhysRevB.74.195113 [65] Oppliger J, Küspert J, Dippel A C, Zimmermann M v, Gutowski O, Ren X, Zhou X, Zhu Z, Frison R, Wang Q, Martinelli L, Biało I, Chang J 2025 Commun. Mater. 6 3 doi: 10.1038/s43246-024-00729-4 [66] Comin R, Damascelli A 2016 Annu. Rev. Condens. Matter Phys. 7 369 doi: 10.1146/annurev-conmatphys-031115-011401 [67] de Groot F, Kotani A 2008 Core Level Spectroscopy of Solids (Boca Raton: CRC Press [68] Wang Q, Mustafi S, Fogh E, Astrakhantsev N, He Z, Biało I, Chan Y, Martinelli L, Horio M, Ivashko O, Shaik N E, von Arx K, Sassa Y, Paris E, Fischer M H, Tseng Y, Christensen N B, Galdi A, Schlom D G, Shen K M, Schmitt T, Rønnow H M, Chang J 2024 Nat. Commun. 15 5348 doi: 10.1038/s41467-024-49714-y [69] Rossi M, Osada M, Choi J, Agrestini S, Jost D, Lee Y, Lu H, Wang B Y, Lee K, Nag A, Chuang Y D, Kuo C T, Lee S J, Moritz B, Devereaux T P, Shen Z X, Lee J S, Zhou K J, Hwang H Y, Lee W S 2022 Nat. Phys. 18 869 doi: 10.1038/s41567-022-01660-6 [70] Tam C C, Choi J, Ding X, Agrestini S, Nag A, Wu M, Huang B, Luo H, Gao P, García-Fernández M, Qiao L, Zhou K J 2022 Nat. Mater. 21 1116 doi: 10.1038/s41563-022-01330-1 [71] Krieger G, Martinelli L, Zeng S, Chow L E, Kummer K, Arpaia R, Moretti Sala M, Brookes N B, Ariando A, Viart N, Salluzzo M, Ghiringhelli G, Preziosi D 2022 Phys. Rev. Lett. 129 027002 doi: 10.1103/PhysRevLett.129.027002 [72] Liu R, Zhang W, Wei Y, Tao Z, Asmara T C, Strocov V N, Schmitt T, Lu X 2023 arXiv: 2312.12749 [cond-mat.supr-con] [73] Comin R, Sutarto R, da Silva Neto E H, Chauviere L, Liang R, Hardy W N, Bonn D A, He F, Sawatzky G A, Damascelli A 2015 Science 347 1335 doi: 10.1126/science.1258399 [74] Choi J, Li J, Nag A, Pelliciari J, Robarts H, Tam C C, Walters A, Agrestini S, García-Fernández M, Song D, Eisaki H, Johnston S, Comin R, Ding H, Zhou K 2023 Adv. Mater. 36 2307515 [75] Achkar A J, He F, Sutarto R, McMahon C, Zwiebler M, Hücker M, Gu G D, Liang R, Bonn D A, Hardy W N, Geck J, Hawthorn D G 2016 Nat. Mater. 15 616 doi: 10.1038/nmat4568 [76] McMahon C, Achkar A J, da Silva Neto E H, Djianto I, Menard J, He F, Sutarto R, Comin R, Liang R, Bonn D A, Hardy W N, Damascelli A, Hawthorn D G 2020 Sci. Adv. 6 eaay0345 doi: 10.1126/sciadv.aay0345 [77] Ruixian L, Qi T, Xingye L 2022 Sci. China Phys. Mech. Astron. 52 270005 doi: 10.1360/SSPMA-2022-0058 [78] Abbamonte P, Rusydi A, Smadici S, Gu G D, Sawatzky G A, Feng D L 2005 Nat. Phys. 1 155 doi: 10.1038/nphys178 [79] Howald C, Eisaki H, Kaneko N, Greven M, Kapitulnik A 2003 Phys. Rev. B 67 014533 doi: 10.1103/PhysRevB.67.014533 [80] Tam C C, Zhu M, Ayres J, Kummer K, Yakhou-Harris F, Cooper J R, Carrington A, Hayden S M 2022 Nat. Commun. 13 570 doi: 10.1038/s41467-022-28124-y [81] da Silva Neto E H, Comin R, He F, Sutarto R, Jiang Y, Greene R L, Sawatzky G A, Damascelli A 2015 Science 347 282 doi: 10.1126/science.1256441 [82] da Silva Neto E H, Yu B, Minola M, Sutarto R, Schierle E, Boschini F, Zonno M, Bluschke M, Higgins J, Li Y, Yu G, Weschke E, He F, Le Tacon M, Greene R L, Greven M, Sawatzky G A, Keimer B, Damascelli A 2016 Sci. Adv. 2 e1600782 doi: 10.1126/sciadv.1600782 [83] Atkinson W A, Kampf A P, Bulut S 2015 New J. Phys. 17 013025 doi: 10.1088/1367-2630/17/1/013025 [84] Sachdev S, La Placa R 2013 Phys. Rev. Lett. 111 027202 doi: 10.1103/PhysRevLett.111.027202 [85] Efetov K B, Meier H, Pépin C 2013 Nat. Phys. 9 442 doi: 10.1038/nphys2641 [86] Pépin C, de Carvalho V S, Kloss T, Montiel X 2014 Phys. Rev. B 90 195207 doi: 10.1103/PhysRevB.90.195207 [87] Jang H, Asano S, Fujita M, Hashimoto M, Lu D H, Burns C A, Kao C C, Lee J S 2017 Phys. Rev. X 7 041066 [88] Yu B, Tabis W, Bialo I, Yakhou F, Brookes N B, Anderson Z, Tang Y, Yu G, Greven M 2020 Phys. Rev. X 10 021059 [89] Kivelson S A, Bindloss I P, Fradkin E, Oganesyan V, Tranquada J M, Kapitulnik A, Howald C 2003 Rev. Mod. Phys. 75 1201 doi: 10.1103/RevModPhys.75.1201 [90] Hayden S M, Tranquada J M 2024 Annu. Rev. Condens. Matter Phys. 15 215 doi: 10.1146/annurev-conmatphys-032922-094430 [91] Mesaros A, Fujita K, Edkins S D, Hamidian M H, Eisaki H, Uchida S i, Davis J C S, Lawler M J, Kim E A 2016 PNAS 113 12661 doi: 10.1073/pnas.1614247113 [92] Vinograd I, Zhou R, Hirata M, Wu T, Mayaffre H, Krämer S, Liang R, Hardy W N, Bonn D A, Julien M H 2021 Nat. Commun. 12 3274 doi: 10.1038/s41467-021-23140-w [93] Kohsaka Y, Taylor C, Fujita K, Schmidt A, Lupien C, Hanaguri T, Azuma M, Takano M, Eisaki H, Takagi H, Uchida S, Davis J C 2007 Science 315 1380 doi: 10.1126/science.1138584 [94] Fujita K, Hamidian M H, Edkins S D, Kim C K, Kohsaka Y, Azuma M, Takano M, Takagi H, Eisaki H, Uchida S i, Allais A, Lawler M J, Kim E A, Sachdev S, Davis J C S 2014 PNAS 111 E3026 doi: 10.1073/pnas.1316552111 [95] Hamidian M H, Edkins S D, Kim C K, Davis J C, Mackenzie A P, Eisaki H, Uchida S, Lawler M J, Kim E A, Sachdev S, Fujita K 2015 Nat. Phys. 12 150 [96] Wise W D, Boyer M C, Chatterjee K, Kondo T, Takeuchi T, Ikuta H, Wang Y, Hudson E W 2008 Nat. Phys. 4 696 doi: 10.1038/nphys1021 [97] LeBoeuf D, Krämer S, Hardy W N, Liang R, Bonn D A, Proust C 2012 Nat. Phys. 9 79 [98] Comin R, Sutarto R, He F, da Silva Neto E H, Chauviere L, Fraño A, Liang R, Hardy W N, Bonn D A, Yoshida Y, Eisaki H, Achkar A J, Hawthorn D G, Keimer B, Sawatzky G A, Damascelli A 2015 Nat. Mater. 14 796 doi: 10.1038/nmat4295 [99] Vojta M, Rösch O 2008 Phys. Rev. B 77 094504 doi: 10.1103/PhysRevB.77.094504 [100] Li Q, Hücker M, Gu G D, Tsvelik A M, Tranquada J M 2007 Phys. Rev. Lett. 99 067001 doi: 10.1103/PhysRevLett.99.067001 [101] Tranquada J M, Gu G D, Hücker M, Jie Q, Kang H J, Klingeler R, Li Q, Tristan N, Wen J S, Xu G Y, Xu Z J, Zhou J, Zimmermann M v 2008 Phys. Rev. B 78 174529 doi: 10.1103/PhysRevB.78.174529 [102] Agterberg D F, Davis J C S, Edkins S D, Fradkin E, Van Harlingen D J, Kivelson S A, Lee P A, Radzihovsky L, Tranquada J M, Wang Y 2020 Annu. Rev. Condens. Matter Phys. 11 231 doi: 10.1146/annurev-conmatphys-031119-050711 [103] Edkins S D, Kostin A, Fujita K, Mackenzie A P, Eisaki H, Uchida S, Sachdev S, Lawler M J, Kim E A, Séamus Davis J C, Hamidian M H 2019 Science 364 976 doi: 10.1126/science.aat1773 [104] Blackburn E, Ivashko O, Campillo E, von Zimmermann M, Liang R, Bonn D A, Hardy W N, Chang J, Forgan E M, Hayden S M 2023 arXiv: 2310.18302 [cond-mat.supr-con] [105] Lee J S, Kivelson S A, Wang T, Ikeda Y, Taniguchi T, Fujita M, Kao C C 2023 arXiv: 2310.19907 [cond-mat.supr-con] [106] Kivelson S A, Fradkin E, Emery V J 1998 Nature 393 550 doi: 10.1038/31177 [107] Wang Y, Chubukov A V 2015 Phys. Rev. B 92 125108 doi: 10.1103/PhysRevB.92.125108 [108] Castellani C, Di Castro C, Grilli M 1996 Z. Phys. B 103 137 doi: 10.1007/s002570050347 [109] Castellani C, Di Castro C, Grilli M 1995 Phys. Rev. Lett. 75 4650 doi: 10.1103/PhysRevLett.75.4650 [110] Seibold G, Arpaia R, Peng Y Y, Fumagalli R, Braicovich L, Di Castro C, Grilli M, Ghiringhelli G C, Caprara S 2021 Commun. Phys. 4 7 doi: 10.1038/s42005-020-00505-z [111] Li J, Nag A, Pelliciari J, Robarts H, Walters A, Garcia-Fernandez M, Eisaki H, Song D, Ding H, Johnston S, Comin R, Zhou K J 2020 PNAS 117 16219 doi: 10.1073/pnas.2001755117 [112] Arpaia R, Martinelli L, Sala M M, Caprara S, Nag A, Brookes N B, Camisa P, Li Q, Gao Q, Zhou X, Garcia-Fernandez M, Zhou K J, Schierle E, Bauch T, Peng Y Y, Di Castro C, Grilli M, Lombardi F, Braicovich L, Ghiringhelli G 2023 Nat. Commun. 14 7198 doi: 10.1038/s41467-023-42961-5 [113] Huang H Y, Singh A, Mou C Y, Johnston S, Kemper A F, van den Brink J, Chen P J, Lee T K, Okamoto J, Chu Y Y, Li J H, Komiya S, Komarek A C, Fujimori A, Chen C T, Huang D J 2021 Phys. Rev. X 11 041038 [114] Caprara S, Castro C D, Mirarchi G, Seibold G, Grilli M 2022 Commun. Phys. 5 10 doi: 10.1038/s42005-021-00786-y [115] Miao H, Lorenzana J, Seibold G, Peng Y Y, Amorese A, Yakhou-Harris F, Kummer K, Brookes N B, Konik R M, Thampy V, Gu G D, Ghiringhelli G, Braicovich L, Dean M P M 2017 PNAS 114 12430 doi: 10.1073/pnas.1708549114 [116] Wen J J, Huang H, Lee S J, Jang H, Knight J, Lee Y S, Fujita M, Suzuki K M, Asano S, Kivelson S A, Kao C C, Lee J S 2019 Nat. Commun. 10 3269 doi: 10.1038/s41467-019-11167-z [117] Lin J Q, Miao H, Mazzone D G, Gu G D, Nag A, Walters A C, García-Fernández M, Barbour A, Pelliciari J, Jarrige I, Oda M, Kurosawa K, Momono N, Zhou K J, Bisogni V, Liu X, Dean M P M 2020 Phys. Rev. Lett. 124 207005 doi: 10.1103/PhysRevLett.124.207005 [118] Miao H, Fabbris G, Koch R J, Mazzone D G, Nelson C S, Acevedo-Esteves R, Gu G D, Li Y, Yilimaz T, Kaznatcheev K, Vescovo E, Oda M, Kurosawa T, Momono N, Assefa T, Robinson I K, Bozin E S, Tranquada J M, Johnson P D, Dean M P M 2021 npj Quantum Mater. 6 31 doi: 10.1038/s41535-021-00327-4 [119] Chen X M, Thampy V, Mazzoli C, Barbour A M, Miao H, Gu G D, Cao Y, Tranquada J M, Dean M P M, Wilkins S B 2016 Phys. Rev. Lett. 117 167001 doi: 10.1103/PhysRevLett.117.167001 [120] Mitrano M, Lee S, Husain A A, Delacretaz L, Zhu M, de la Peña Munoz G, Sun S X L, Joe Y I, Reid A H, Wandel S F, Coslovich G, Schlotter W, van Driel T, Schneeloch J, Gu G D, Hartnoll S, Goldenfeld N, Abbamonte P 2019 Sci. Adv. 5 eaax3346 doi: 10.1126/sciadv.aax3346 [121] Peng Y Y, Husain A A, Mitrano M, Sun S X L, Johnson T A, Zakrzewski A V, MacDougall G J, Barbour A, Jarrige I, Bisogni V, Abbamonte P 2020 Phys. Rev. Lett. 125 097002 doi: 10.1103/PhysRevLett.125.097002 [122] Arpaia R, Caprara S, Fumagalli R, De Vecchi G, Peng Y Y, Andersson E, Betto D, De Luca G M, Brookes N B, Lombardi F, Salluzzo M, Braicovich L, Di Castro C, Grilli M, Ghiringhelli G 2019 Science 365 906 doi: 10.1126/science.aav1315 [123] Rossi M, Arpaia R, Fumagalli R, Moretti Sala M, Betto D, Kummer K, De Luca G M, van den Brink J, Salluzzo M, Brookes N B, Braicovich L, Ghiringhelli G 2019 Phys. Rev. Lett. 123 027001 doi: 10.1103/PhysRevLett.123.027001 [124] Kim H H, Lefrançois E, Kummer K, Fumagalli R, Brookes N B, Betto D, Nakata S, Tortora M, Porras J, Loew T, Barber M E, Braicovich L, Mackenzie A P, Hicks C W, Keimer B, Minola M, Le Tacon M 2021 Phys. Rev. Lett. 126 037002 doi: 10.1103/PhysRevLett.126.037002 [125] Kim H H, Souliou S M, Barber M E, Lefrançois E, Minola M, Tortora M, Heid R, Nandi N, Borzi R A, Garbarino G, Bosak A, Porras J, Loew T, König M, Moll P J W, Mackenzie A P, Keimer B, Hicks C W, Le Tacon M 2018 Science 362 1040 doi: 10.1126/science.aat4708 [126] Wang Q, von Arx K, Mazzone D G, Mustafi S, Horio M, Küspert J, Choi J, Bucher D, Wo H, Zhao J, Zhang W, Asmara T C, Sassa Y, Månsson M, Christensen N B, Janoschek M, Kurosawa T, Momono N, Oda M, Fischer M H, Schmitt T, Chang J 2022 Nat. Commun. 13 1795 doi: 10.1038/s41467-022-29465-4 [127] Martinelli L, Biało I, Hong X, Oppliger J, Lin C, Schaller T, Kúspert J, Fischer M H, Kurosawa T, Momono N, Oda M, Choi J, Agrestini S, Garcia-Fernandez M, Zhou K J, Wang Q, Chang J 2024 arXiv: 2406.15062 [cond-mat.str-el] [128] Choi J, Wang Q, Jöhr S, Christensen N B, Küspert J, Bucher D, Biscette D, Fischer M H, Hücker M, Kurosawa T, Momono N, Oda M, Ivashko O, Zimmermann M v, Janoschek M, Chang J 2022 Phys. Rev. Lett. 128 207002 doi: 10.1103/PhysRevLett.128.207002 [129] Simutis G, Küspert J, Wang Q, Choi J, Bucher D, Boehm M, Bourdarot F, Bertelsen M, Wang C N, Kurosawa T, Momono N, Oda M, Månsson M, Sassa Y, Janoschek M, Christensen N B, Chang J, Mazzone D G 2022 Commun. Phys. 5 296 doi: 10.1038/s42005-022-01061-4 [130] Boyle T J, Walker M, Ruiz A, Schierle E, Zhao Z, Boschini F, Sutarto R, Boyko T D, Moore W, Tamura N, He F, Weschke E, Gozar A, Peng W, Komarek A C, Damascelli A, Schüßler-Langeheine C, Frano A, da Silva Neto E H, Blanco-Canosa S 2021 Phys. Rev. Res. 3 L022004 doi: 10.1103/PhysRevResearch.3.L022004 [131] Gupta N K, Sutarto R, Gong R, Idziak S H J, Hale H, Kim Y J, Hawthorn D G 2023 Phys. Rev. B 108 L121113 doi: 10.1103/PhysRevB.108.L121113 [132] Thampy V, Dean M P M, Christensen N B, Steinke L, Islam Z, Oda M, Ido M, Momono N, Wilkins S B, Hill J P 2014 Phys. Rev. B 90 100510 doi: 10.1103/PhysRevB.90.100510 [133] Jo N H, Gati E, Pfau H 2024 Front. Electron. Mater. 4 1392760 doi: 10.3389/femat.2024.1392760 [134] Yim C M, Panja S N, Trainer C, Topping C, Heil C, Gibbs A S, Magdysyuk O V, Tsurkan V, Loidl A, Rost A W, Wahl P 2021 Nano Lett. 21 2786 doi: 10.1021/acs.nanolett.0c04821 [135] Nakata S, Horio M, Koshiishi K, Hagiwara K, Lin C, Suzuki M, Ideta S, Tanaka K, Song D, Yoshida Y, Eisaki H, Fujimori A 2021 npj Quantum Mater. 6 86 doi: 10.1038/s41535-021-00390-x [136] Nie L, Tarjus G, Kivelson S A 2014 PNAS 111 7980 doi: 10.1073/pnas.1406019111 [137] Zhou K J 2024 Acta Phys. Sin. 73 197301 doi: 10.7498/aps.73.20241009 [138] Küspert J, Biało I, Frison R, Morawietz A, Martinelli L, Choi J, Bucher D, Ivashko O, Zimmermann M V, Christensen N B, Mazzone D G, Simutis G, Turrini A A, Thomarat L, Tam D W, Janoschek M, Kurosawa T, Momono N, Oda M, Wang Q, Chang J 2024 Commun. Phys. 7 225 doi: 10.1038/s42005-024-01699-2 [139] Ren X, Sutarto R, Gao Q, Wang Q, Li J, Wang Y, Xiang T, Hu J, Chang J, Comin R, Zhou X J, Zhu Z 2024 Chin. Phys. Lett. 41 117404 doi: 10.1088/0256-307X/41/11/117404 [140] Parzyck C T, Gupta N K, Wu Y, Anil V, Bhatt L, Bouliane M, Gong R, Gregory B Z, Luo A, Sutarto R, He F, Chuang Y D, Zhou T, Herranz G, Kourkoutis L F, Singer A, Schlom D G, Hawthorn D G, Shen K M 2024 Nat. Mater. 23 486 doi: 10.1038/s41563-024-01797-0 [141] Sun H, Huo M, Hu X, Li J, Liu Z, Han Y, Tang L, Mao Z, Yang P, Wang B, Cheng J, Yao D X, Zhang G M, Wang M 2023 Nature 621 493 doi: 10.1038/s41586-023-06408-7 [142] Zhu Y, Peng D, Zhang E, Pan B, Chen X, Chen L, Ren H, Liu F, Hao Y, Li N, Xing Z, Lan F, Han J, Wang J, Jia D, Wo H, Gu Y, Gu Y, Ji L, Wang W, Gou H, Shen Y, Ying T, Chen X, Yang W, Cao H, Zheng C, Zeng Q, Guo J G, Zhao J 2024 Nature 631 531 doi: 10.1038/s41586-024-07553-3 [143] Liu Z, Sun H, Huo M, Ma X, Ji Y, Yi E, Li L, Liu H, Yu J, Zhang Z, Chen Z, Liang F, Dong H, Guo H, Zhong D, Shen B, Li S, Wang M 2022 Sci. China Phys. Mech. Astron. 66 217411 [144] Chen K, Liu X, Jiao J, Zou M, Jiang C, Li X, Luo Y, Wu Q, Zhang N, Guo Y, Shu L 2024 Phys. Rev. Lett. 132 256503 doi: 10.1103/PhysRevLett.132.256503 [145] Dan Z, Zhou Y, Huo M, Wang Y, Nie L, Wang M, Wu T, Chen X 2024 arXiv: 2402.03952 [cond-mat.supr-con] [146] Chen X, Choi J, Jiang Z, Mei J, Jiang K, Li J, Agrestini S, Garcia-Fernandez M, Sun H, Huang X, Shen D, Wang M, Hu J, Lu Y, Zhou K J, Feng D 2024 Nat. Commun. 15 9597 doi: 10.1038/s41467-024-53863-5 [147] Zhang J, Phelan D, Botana A S, Chen Y S, Zheng H, Krogstad M, Wang S G, Qiu Y, Rodriguez-Rivera J A, Osborn R, Rosenkranz S, Norman M R, Mitchell J F 2020 Nat. Commun. 11 6003 doi: 10.1038/s41467-020-19836-0 [148] Ko E K, Yu Y, Liu Y, Bhatt L, Li J, Thampy V, Kuo C T, Wang B Y, Lee Y, Lee K, Lee J S, Goodge B H, Muller D A, Hwang H Y 2024 Nature 638 935 [149] Zhou G, Lv W, Wang H, Nie Z, Chen Y, Li Y, Huang H, Chen W, Sun Y, Xue Q K, Chen Z 2024 arXiv: 2412.16622 [cond-mat.supr-con] -


 首页
首页 登录
登录 注册
注册



 下载:
下载: