高级搜索

B-样条基组方法在少电子原子结构精密计算中的应用

,  , 

downloadPDF

上一篇

下一篇

张永慧, 史庭云, 唐丽艳. B-样条基组方法在少电子原子结构精密计算中的应用[J]. 物理学报, 2025, 74(8): 083101-1. doi: 10.7498/aps.74.20241728
引用本文: 张永慧, 史庭云, 唐丽艳. B-样条基组方法在少电子原子结构精密计算中的应用[J]. 物理学报, 2025, 74(8): 083101-1. doi: 10.7498/aps.74.20241728
shu
Yonghui ZHANG, Tingyun SHI, Liyan TANG. Applications of B-spline method in precise calculation of structure of few-electron atoms[J]. Acta Physica Sinica, 2025, 74(8): 083101-1. doi: 10.7498/aps.74.20241728
Citation: Yonghui ZHANG, Tingyun SHI, Liyan TANG. Applications of B-spline method in precise calculation of structure of few-electron atoms[J]. Acta Physica Sinica, 2025, 74(8): 083101-1. doi: 10.7498/aps.74.20241728
shu

B-样条基组方法在少电子原子结构精密计算中的应用

  • 中国科学院精密测量科学与技术创新研究院, 武汉　430071

    • 通讯作者: E-mail: lytang@apm.ac.cn

  • 中图分类号: 31.15.ac, 31.15.am, 31.15.ap, 32.60.+i

Applications of B-spline method in precise calculation of structure of few-electron atoms

  • Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430071, China

    • Corresponding author: E-mail: lytang@apm.ac.cn

  • MSC: 31.15.ac, 31.15.am, 31.15.ap, 32.60.+i

  • 摘要: 少电子原子的精密光谱在基本物理理论验证、精细结构常数精确测定以及原子核性质深入探索等领域具有重要的应用价值. 随着精密测量物理学的快速发展, 人们对原子结构数据的需求已从最初的存在性确认, 转变为对高度准确性和精确性的持续追求. 为了满足精密光谱实验对高精度结构性质数据的迫切需求, 我们自主发展了一系列基于B-样条基组的高精度理论方法, 并将其成功应用于少电子原子的能级结构与外场响应性质的理论研究中. 具体而言, 实现了氦原子和类氦离子能谱的高精度确定, 为相关实验研究提供理论支撑; 实现了幻零波长的高精度理论预言, 为量子电动力学理论检验开辟了新方向; 提出了有效抑制光频移的理论方案, 为氦原子高精度光谱实验的开展提供了重要支持. 展望未来, 基于B-样条基组的高精度理论方法有望在量子态操控、核结构性质精确测定、超冷分子形成以及新物理探索等前沿领域得到广泛应用, 从而推动国内外精密测量物理领域的蓬勃发展.
    Abstract: The precise spectra of few-electron atoms plays a pivotal role in advancing fundamental physics, including the verification of quantum electrodynamics (QED) theory, the determination of the fine-structure constants, and the exploration of nuclear properties. With the rapid development of precision measurement techniques, the demand for atomic structure data has evolved from simply confirming existence to pursuing unprecedented accuracy. To meet the growing needs for precision spectroscopy experiments, we develop a series of high-precision theoretical methods based on B-spline basis sets, such as the non-relativistic configuration interaction (B-NRCI) method, the correlated B-spline basis functions (C-BSBFs) method, and the relativistic configuration interaction (B-RCI) method. These methods use the unique properties of B-spline functions, such as locality, completeness, and numerical stability, to accurately solve the Schrödinger and Dirac equations for few-electron atoms.Our methods yield significant results, particularly for helium and helium-like ions. Using these methods, we obtain accurate energies, polarizabilities, tune-out wavelengths, and magic wavelengths. Specifically, we achieve high-precision measurements of the energy spectra of helium, providing vital theoretical support for conducting related experimental researches. Additionally, we make high-precision theoretical predictions of tune-out wavelengths, paving the way for new tests of QED theory. Furthermore, we propose effective theoretical schemes to suppress Stark shifts, thereby facilitating high-precision spectroscopy experiments of heliumThe B-spline-basis methods reviewed in this paper prove exceptionally effective in high-precision calculations for few-electron atoms. These methods not only provide crucial theoretical support for precision spectroscopy experiments but also pave the new way for testing QED. Their ability to handle large-scale configuration interactions and incorporate relativistic and QED corrections makes them versatile tools for advancing atomic physics research. In the future, the high-precision theoretical methods based on B-spline basis sets are expected to be extended to cutting-edge fields, such as quantum state manipulation, determination of nuclear structure properties, formation of ultracold molecules, and exploration of new physics, thus continuously promoting the progress of precision measurement physics.
  • 加载中

  • 图 1  基于B-样条函数的多种高精度理论方法框架图

    Figure 1.  Framework diagram of various high-precision theoretical methods based on B-spline functions

    下载: 全尺寸图片 幻灯片

    图 2  在$ [0, 1000] $区间内, 10个7阶均匀分布型的B-样条函数

    Figure 2.  Ten 7th-order uniformly distributed B-spline functions within the interval $ [0, 1000] $

    下载: 全尺寸图片 幻灯片

    图 3  在$ [0, 1000] $区间内, 10个7阶指数分布型的B-样条函数

    Figure 3.  Ten 7th-order exponentially distributed B-spline functions within the interval $ [0, 1000] $

    下载: 全尺寸图片 幻灯片

    图 4  幻零波长$ \lambda_{\mathrm{t}} $和魔幻波长$ \lambda_{\mathrm{m}} $的示意图

    Figure 4.  Schematic diagram of tune-out wavelength $ \lambda_{\mathrm{t}} $ and magic wavelength $ \lambda_{\mathrm{m}} $

    下载: 全尺寸图片 幻灯片

    图 5  氦原子亚稳态413 nm幻零波长的位置

    Figure 5.  The position of the 413 nm tune-out wavelength for the metastable state of helium

    下载: 全尺寸图片 幻灯片

    图 6  氦原子413 nm幻零波长的研究历程

    Figure 6.  Research roadmap of the 413 nm tune-out wavelength for the metastable state of helium

    下载: 全尺寸图片 幻灯片

    图 7  氦原子亚稳态413 nm幻零波长的各项修正计算[49]

    Figure 7.  Contributions of various corrections to the 413 nm tune-out wavelength for the metastable state of helium [49]

    下载: 全尺寸图片 幻灯片

    图 8  氦原子$ 2\, ^3 {\mathrm{S}}_1\rightarrow 2\, ^1 {\mathrm{S}}_0 $跃迁下的魔幻波长, 其中绿色圆圈所示的位置是319.8 nm的魔幻波长

    Figure 8.  The magic wavelengths for the transition $ 2\, ^3 {\mathrm{S}}_1\rightarrow $$ 2\, ^1 {\mathrm{S}}_0 $ of helium, where the position indicated by the green circle corresponds to the 319.8 nm magic wavelength.

    下载: 全尺寸图片 幻灯片

    图 9  4He原子$ 2\, ^3 {\mathrm{S}}_1\rightarrow 3\, ^3 {\mathrm{S}}_1 $的双光子激发跃迁方案图

    Figure 9.  The two-photon excitation scheme for the $ 2\, ^3 {\mathrm{S}}_1\rightarrow $$ 3\, ^3 {\mathrm{S}}_1 $ transition of 4He.

    下载: 全尺寸图片 幻灯片

    表 1  无穷核质量下, 氦原子基态非相对论能量(原子单位)随最大分波数$ \ell_{{\mathrm{max}}}$增加的收敛性检验

    Table 1.  Convergence test for the non-relativistic energy (in a.u.) of ground-state helium with infinite nuclear mass, as the maximum partial wave $ \ell_{{\mathrm{max}}}$ increases.

    $ \ell_{{\mathrm{max}}} $ B-NRCI Method [56] $ \ell_{{\mathrm{max}}} $ C-BSBFs Method [52]
    60 –2.903724240750 1 –2.9037242683
    65 –2.903724262547 2 –2.90372437687
    70 –2.903724278413 3 –2.90372437696
    75 –2.903724290199 4 –2.903724376999
    80 –2.903724299061
    Ref. [13] –2.90372437703411960
    下载: 导出CSV

    表 2  加速度规范下, 氢原子基态贝特对数项$\beta(1 {\mathrm{s}})$(原子单位)随指数结点参数$\gamma_0$的变化. 其中, $t_1$为第一个非零结点, $E_{{\mathrm{max}}}$为中间态的最大能量值. 在计算过程中, 样条个数$N=300$, 样条阶数$k=15$, 盒子半径$R_0=200$个原子单位

    Table 2.  Values of the Bethe logarithm $\beta(1 {\mathrm{s}})$ (in a.u.) for the ground-state hydrogen in the acceleration gauge, evaluated at different knot sequences. Where $\gamma_0$ denotes the parameter of exponential knot sequences, $t_1$ represents the first interior knot point, and $E_{{\mathrm{max}}}$ indicates the highest energy. All calculations are carried out using the same set of parameters: N = 300, k = 15, and $R_0$=200 a.u.

    $ \gamma_0 $ $ t_1 $ $ E_{{\mathrm{max}}} $ $ \beta(1 {\mathrm{s}}) $
    0.005 4.10×10–1 5.76×103 2.258
    0.025 2.41×10–2 1.59×106 2.2890
    0.035 4.59×10–3 4.32×107 2.29061
    0.045 8.06×10–4 1.38×109 2.290915
    0.065 2.17×10–5 1.83×1013 2.2909796
    0.075 3.43×10–7 7.23×1015 2.29098109
    0.085 5.32×10–7 2.96×1018 2.290981330
    0.105 1.23×10–9 5.38×1020 2.2909813741
    0.115 1.84×10–10 2.36×1022 2.29098137505
    0.125 2.74×10–10 1.05×1023 2.29098137518
    0.135 4.04×10–11 4.75×1023 2.2909813752020
    0.145 5.94×10–12 2.16×1025 2.29098137520502
    0.165 1.26×10–13 4.65×1028 2.290981375205541
    0.175 1.83×10–14 2.17×1030 2.2909813752055506
    0.185 2.65×10–15 1.03×1032 2.29098137520555206
    0.195 3.82×10–16 4.86×1033 2.29098137520555227
    0.205 5.49×10–17 2.32×1035 2.290981375205552296
    0.225 1.13×10–18 5.35×1038 2.29098137520555230124
    0.235 1.60×10–19 6.31×1039 2.2909813752055523013355
    下载: 导出CSV

    表 3  不同方法计算得到的氦原子$n\, ^1 {\mathrm{S}}(n= 1—7)$态贝特对数的比较. 第二列和第三列的第一项数据来自加速度规范, 而第二项数据来自速度-加速度混合规范. 括号中的数字表示计算结果的不确定度

    Table 3.  Comparison of Bethe logarithms for the $n\, ^1 {\mathrm{S}}(n=1-7)$ states of helium obtained from different methods. The first entries in the second and third columns are from the acceleration gauge, while the second entries are from the mixed velocity-acceleration gauge. The Numbers in parentheses represent the computational uncertainties.

    State B-NRCI[65] C-BSBFs[55] Integration method[73]
    $ 1\, ^1 {\mathrm{S}} $ 4.37034(2) 4.37016022(5) 4.3701602230703(3)
    4.37014(2) 4.3701601(1)
    $ 2\, ^1 {\mathrm{S}} $ 4.36643(1) 4.36641271(1) 4.366412726417(1)
    4.366412(1) 4.3664127(1)
    $ 3\, ^1 {\mathrm{S}} $ 4.369170(1) 4.36916480(6) 4.369164860824(2)
    4.3691643(2) 4.3691648(1)
    $ 4\, ^1 {\mathrm{S}} $ 4.369893(1) 4.36989065(5) 4.369890632356(3)
    4.3698903(5) 4.3698906(1)
    $ 5\, ^1 {\mathrm{S }}$ 4.370152(3) 4.3701520(1) 4.370151796310(4)
    4.3701511(2) 4.3701519(1)
    $ 6\, ^1 {\mathrm{S }}$ 4.37027(1) 4.370267(1) 4.370266974319(5)
    4.370266(2) 4.370267(1)
    $ 7\, ^1{\mathrm{ S}} $ 4.37033(1) 4.370326(1) 4.370325261772(5)
    4.37033(1) 4.370326(1)
    下载: 导出CSV

    表 4  氦-4原子基态静电偶极极化率(原子单位)的结果比较. “NR”表示非相对论极化率, “Rel.”表示相对论极化率, “Total”表示考虑QED修正后的最终极化率. 括号中的数字表示计算结果的不确定度

    Table 4.  Comparison of the static dipole polarizability $\alpha_1(0)$ (in a.u.) for the ground state of 4He. “NR” denotes the non-relativistic polarizability, “Rel.” represents the relativistic polarizability, and “Total” stands for the final polarizability including QED corrections. The numbers in parentheses indicate the computational uncertainties.

    C-BSBFs [54] Ref. [78]
    NR 1.383809986408(2) 1.383809986408(1)
    Rel. 1.38372953306(7) 1.3837295330(1)
    Total 1.38376080(24) 1.38376077(14)
    下载: 导出CSV

    表 5  关联B-样条基组方法计算的氦-4原子$n\, ^1 {\mathrm{S}}_0(n=2—7)$和$n\, ^3 {\mathrm{S}}_1(n=2—7)$激发态的静电偶极极化率(原子单位). 对于$n\, ^3 {\mathrm{S}}_1$态的张量极化率, 斜杠前的数值对应于$n\, ^3 {\mathrm{P}}_{0, 1, 2}$中间态的贡献, 斜杠后的数值对应于$n\, ^3 {\mathrm{D}}_1$中间态的贡献. 括号中的数字为计算结果的不确定度

    Table 5.  Static dipole polarizabilities (in a.u.) calculated using the correlated B-spline basis sets for the excited $n\, ^1 {\mathrm{S}}_0(n=2-7)$ and $n\, ^3 {\mathrm{S}}_1(n=2-7)$ states of $^4$He. For the tensor polarizability of the $n\, ^3 {\mathrm{S}}_1$ states, the number before the slash corresponds to the contribution from the $n\, ^3{\mathrm{ P}}_J$ intermediate states, and the number after the slash corresponds to the contribution from the $n\, ^3 {\mathrm{D}}_1$ intermediate states. Numbers in parentheses represent computational uncertainties

    n $ \alpha_1(n\, ^1 {\mathrm{S}}_0) $ $ \alpha_1^{\mathrm{S}}(n\, ^3 {\mathrm{S}}_1) $ $ \alpha_1^{\mathrm{T}}(n\, ^3 {\mathrm{S}}_1) $
    2 800.52195(14) 315.728536(48) 0.002764488(2)/0.000726892(6)
    3 16890.5275(28) 7940.5494(13) 0.09715509(3)/–0.005470(2)
    4 135875.295(23) 68677.988(11) 0.9558(3)/–0.1189(2)
    5 669694.55(11) 351945.328(60) 5.2676(2)/–0.7829(3)
    6 2443625.15(40) 1315529.52(23) 20.654(3)/–3.291(2)
    7 7269026.8(1.2) 3977532.95(69) 64.62(3)/–10.65(3)
    下载: 导出CSV

    表 6  在激光偏振与量子轴夹角不同的情形下, 氦原子413 nm幻零波长(纳米单位)的结果比对. 第三列代表偏振方向与量子轴平行, 且初态磁量子数$M_J=0$时的情况; 第四列代表偏振方向与量子轴平行, 且初态磁量子数为$M_J=\pm 1$时的情况; 第五列代表偏振方向与量子轴垂直, 且初态量子数$M_J=\pm 1$时的情况

    Table 6.  Comparison of the 413 nm tune-out wavelength (in nm) for the $2\, ^3 {\mathrm{S}}_1$ state of 4He, with varying the initial magnetic quantum number$M_J$ values, under different angles between laser polarization and the quantization axis. The third column represents the case where the polarization direction is parallel to the quantization axis and $M_J=0$. The fourth column represents the case where the polarization direction is parallel to the quantization axis but with $M_J=\pm 1$. The fifth column represents the case where the polarization direction is perpendicular to the quantization axis, with $M_J=\pm 1$.

    Reference Method $ \alpha_1^{\mathrm{S}}(\omega)-2\alpha_1^{\mathrm{T}}(\omega) $ $ \alpha_1^{\mathrm{S}}(\omega)+\alpha_1^{\mathrm{T}}(\omega) $ $ \alpha_1^{\mathrm{S}}(\omega)-\tfrac{1}{2}\alpha_1^{\mathrm{T}}(\omega) $
    Ref. [6] Hybrid model 413.02(9)
    Ref. [89] Expt. 413.0938(9stat)(20syst)
    Ref. [47] RCI 413.080 1(4) 413.085 9(4)
    Ref. [49] RCI+NRQED 413.084 26(4) 413.090 15(4)
    Ref. [15] Expt. 413.087 08(15)
    Ref. [15] NRQED 413.087 179(6)
    Ref. [90] RCIRP 413.084 28(5) 413.090 17(3) 413.087 23(3)
    下载: 导出CSV

    表 7  氦原子$2\, ^3{\mathrm{ S}}\rightarrow 2\, ^1 {\mathrm{S}}$双禁戒跃迁下319.8 nm魔幻波长理论与实验的对比

    Table 7.  Comparison of the 319.8 nm magic wavelength between theory and experiment for the doubly forbidden transition $2\, ^3 {\mathrm{S}}\rightarrow 2\, ^1 {\mathrm{S}}$ of helium.

    Isotopes Theory Experiment
    4He 319.8153(6) nm [48] 319.81592(15)nm [96]
    3He 319.8302(7) nm [48] 319.83080(15)nm [97]
    下载: 导出CSV
  • [1] Yan Z C, Drake G W F 1995 Phys. Rev. Lett. 74 4791 doi: 10.1103/PhysRevLett.74.4791
    [2] Patkóš V, Yerokhin V A, Pachucki K 2016 Phys. Rev. A 94 052508 doi: 10.1103/PhysRevA.94.052508
    [3] Patkóš V, Yerokhin V A, Pachucki K 2017 Phys. Rev. A 95 012508 doi: 10.1103/PhysRevA.95.012508
    [4] Patkóš V, Yerokhin V A, Pachucki K 2019 Phys. Rev. A 100 042510 doi: 10.1103/PhysRevA.100.042510
    [5] Patkóš V, Yerokhin V A, Pachucki K 2021 Phys. Rev. A 103 012803 doi: 10.1103/PhysRevA.103.012803
    [6] Mitroy J, Tang L Y 2013 Phys. Rev. A 88 052515 doi: 10.1103/PhysRevA.88.052515
    [7] Pachucki K, Yerokhin V A 2010 Phys. Rev. Lett. 104 070403 doi: 10.1103/PhysRevLett.104.070403
    [8] Beyer A, Maisenbacher L, Matveev A, Pohl R, Khabarova K, Grinin A, Lamour T, Yost D C, Hänsch T W, Kolachevsky N, Udem T 2017 Science 358 79 doi: 10.1126/science.aah6677
    [9] Drake G W F, Dhindsa H S, Marton V J 2021 Phys. Rev. A 104 L060801 doi: 10.1103/PhysRevA.104.L060801
    [10] Bethe H A 1947 Phys. Rev. 72 339 doi: 10.1103/PhysRev.72.339
    [11] Karshenboim S G 2005 Phys. Rep. 422 1 doi: 10.1016/j.physrep.2005.08.008
    [12] Yerokhin V A, Pachucki K, Patkóš V 2019 Ann. Phys. 531 1800324 doi: 10.1002/andp.201800324
    [13] Drake G W F 2023 Handbook of Atomic, Molecular and Optical Physics (Cham: Springer Nature Switzerland AG 2023) pp2522–8706
    [14] Pachucki K, Patkóš V, Yerokhin V A 2017 Phys. Rev. A 95 062510 doi: 10.1103/PhysRevA.95.062510
    [15] Henson B M, Ross J A, Thomas K F, Kuhn C N, Shin D K, Hodgman S S, Zhang Y H, Tang L Y, Drake G W F, Bondy A T, Truscott A G, Baldwin K G H 2022 Science 376 199 doi: 10.1126/science.abk2502
    [16] James H M, Coolidge A S 1935 Phys. Rev. 47 700
    [17] Mitroy J, Bubin S, Horiuchi W, Suzuki Y, Adamowicz L, Cencek W, Szalewicz K, Komasa J, Blume D, Varga K 2013 Rev. Mod. Phys. 85 693 doi: 10.1103/RevModPhys.85.693
    [18] McKenzie D M, Drake G W F 1991 Phys. Rev. A 44 R6973 doi: 10.1103/PhysRevA.44.R6973
    [19] Drake G W F, Yan Z C 1992 Phys. Rev. A 46 2378 doi: 10.1103/PhysRevA.46.2378
    [20] Yan Z C, Drake G W F 1995 Phys. Rev. A 52 3711 doi: 10.1103/PhysRevA.52.3711
    [21] Yan Z, Drake G W F 1997 J. Phys. B 30 4723 doi: 10.1088/0953-4075/30/21/012
    [22] Tang L Y, Yan Z C, Shi T Y, Babb J F 2009 Phys. Rev. A 79 062712 doi: 10.1103/PhysRevA.79.062712
    [23] Rooij R V, Borbely J S, Simonet J, Hoogerland M D, Eikema K S E, Rozendaal R A, Vassen W 2011 Science 333 196 doi: 10.1126/science.1205163
    [24] Zheng X, Sun Y R, Chen J J, Jiang W, Pachucki K, Hu S M 2017 Phys. Rev. Lett. 118 063001 doi: 10.1103/PhysRevLett.118.063001
    [25] Kato K, Skinner T D G, Hessels E A 2018 Phys. Rev. Lett. 121 143002 doi: 10.1103/PhysRevLett.121.143002
    [26] Guan H, Chen S, Qi X Q, Liang S, Sun W, Zhou P, Huang Y, Zhang P P, Zhong Z X, Yan Z C, Drake G W F, Shi T Y, Gao K 2020 Phys. Rev. A 102 030801 doi: 10.1103/PhysRevA.102.030801
    [27] Sun W, Zhang P P, Zhou P P, Chen S L, Zhou Z Q, Huang Y, Qi X Q, Yan Z C, Shi T Y, Drake G W F, Zhong Z X, Guan H, Gao K L 2023 Phys. Rev. Lett. 131 103002 doi: 10.1103/PhysRevLett.131.103002
    [28] Schoenberg I J 1946 Quart. Appl. Math. 4 45 doi: 10.1090/qam/15914
    [29] Schoenberg I J 1967 On Spline Functions//Shisha O Inequalities (New York: Academic Press) pp255–291
    [30] De Boor C 1978 A Practical Guide to Splines (New York: Springer) p157
    [31] Johnson W R, Sapirstein J 1986 Phys. Rev. Lett. 57 1126 doi: 10.1103/PhysRevLett.57.1126
    [32] Johnson W R, Blundell S A, Sapirstein J 1988 Phys. Rev. A 37 307 doi: 10.1103/PhysRevA.37.307
    [33] Grant I P 1982 Phys. Rev. A 25 1230 doi: 10.1103/PhysRevA.25.1230
    [34] Fischer C F 2008 Adv. At. Mol. Opt. Phys. 55 235
    [35] Bachau H, Cormier E, Decleva P, Hansen J E, Martín F 2001 Rep. Prog. Phys. 64 1815 doi: 10.1088/0034-4885/64/12/205
    [36] Xi J H, He X H, Li B W 1992 Phys. Rev. A 46 5806 doi: 10.1103/PhysRevA.46.5806
    [37] Xi J H, Wu L J, Li B W 1993 Phys. Rev. A 47 2701 doi: 10.1103/PhysRevA.47.2701
    [38] Rao J G, Liu W Y, Li B W 1994 Phys. Rev. A 50 1916 doi: 10.1103/PhysRevA.50.1916
    [39] Qiao H X, Li B W 1999 Phys. Rev. A 60 3134 doi: 10.1103/PhysRevA.60.3134
    [40] Wu L J 1996 Phys. Rev. A 53 139 doi: 10.1103/PhysRevA.53.139
    [41] Yu K Z, Wu L J, Gou B C, Shi T Y 2004 Phys. Rev. A 70 012506 doi: 10.1103/PhysRevA.70.012506
    [42] Zhang Y H, Tang L Y, Zhang X Z, Jiang J, Mitroy J 2012 J. Chem. Phys. 136 174107 doi: 10.1063/1.4705279
    [43] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y, Mitroy J 2012 Chin. Phys. Lett. 29 063101 doi: 10.1088/0256-307X/29/6/063101
    [44] Tang L Y, Zhang Y H, Zhang X Z, Jiang J, Mitroy J 2012 Phys. Rev. A 86 012505 doi: 10.1103/PhysRevA.86.012505
    [45] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2015 Phys. Rev. A 92 012515 doi: 10.1103/PhysRevA.92.012515
    [46] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2016 Chin. Phys. B 25 103101 doi: 10.1088/1674-1056/25/10/103101
    [47] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2016 Phys. Rev. A 93 052516 doi: 10.1103/PhysRevA.93.052516
    [48] Wu F F, Yang S J, Zhang Y H, Zhang J Y, Qiao H X, Shi T Y, Tang L Y 2018 Phys. Rev. A 98 040501(R doi: 10.1103/PhysRevA.98.040501
    [49] Zhang Y H, Wu F F, Zhang P P, Tang L Y, Zhang J Y, Baldwin K G H, Shi T Y 2019 Phys. Rev. A 99 040502(R doi: 10.1103/PhysRevA.99.040502
    [50] Zhang Y H, Tang L Y, Shi T Y 2021 Phys. Rev. A 104 042817 doi: 10.1103/PhysRevA.104.042817
    [51] Zhang Y H, Tang L Y, Zhang J Y, Shi T Y 2021 Phys. Rev. A 103 032810 doi: 10.1103/PhysRevA.103.032810
    [52] Yang S J, Mei X S, Shi T Y, Qiao H X 2017 Phys. Rev. A 95 062505 doi: 10.1103/PhysRevA.95.062505
    [53] Fang H, Zhang Y H, Zhang P P, Shi T Y 2023 Phys. Rev. A 108 062818 doi: 10.1103/PhysRevA.108.062818
    [54] Fang H, Zhang Y H, Li Y T, Shi T Y 2024 Phys. Rev. A 110 062823 doi: 10.1103/PhysRevA.110.062823
    [55] Yang S J, Tang Y B, Zhao Y H, Shi T Y, Qiao H X 2019 Phys. Rev. A 100 042509 doi: 10.1103/PhysRevA.100.042509
    [56] Decleva P, Lisini A, Venuti M 1995 Int. J. Quantum Chem. 56 27 doi: 10.1002/qua.560560106
    [57] Chen M H, Cheng K T, Johnson W R 1993 Phys. Rev. A 47 3692 doi: 10.1103/PhysRevA.47.3692
    [58] Wu F F, Shi T Y, Ni W T, Tang L Y 2023 Phys. Rev. A 108 L051101 doi: 10.1103/PhysRevA.108.L051101
    [59] Lamb W E, Retherford R C 1947 Phys. Rev. 72 241 doi: 10.1103/PhysRev.72.241
    [60] Drake G W F, Martin W C 1998 Can. J. Phys. 76 679
    [61] Goldman S P 1984 Phys. Rev. A 30 1219 doi: 10.1103/PhysRevA.30.1219
    [62] Goldman S P, Drake G W F 2000 Can. J. Phys. 61 052513
    [63] Drake G W F, Goldman S P 2000 Can. J. Phys. 77 835 doi: 10.1139/p00-010
    [64] Goldman S P 1994 Phys. Rev. A 50 3039 doi: 10.1103/PhysRevA.50.3039
    [65] Zhang Y H, Shen L J, Xiao C M, Zhang J Y, Shi T Y 2020 J. Phys. B 53 135003 doi: 10.1088/1361-6455/ab8b41
    [66] Jentschura U D, Mohr P J 2005 Phys. Rev. A 72 012110 doi: 10.1103/PhysRevA.72.012110
    [67] Tang Y B, Zhong Z X, Li C B, Qiao H X, Shi T Y 2013 Phys. Rev. A 87 022510 doi: 10.1103/PhysRevA.87.022510
    [68] Kabir P K, Salpeter E E 1957 Phys. Rev. 108 1256 doi: 10.1103/PhysRev.108.1256
    [69] Dalgarno A, Stewart A L 1960 Proc. Phys. Soc. A 76 49 doi: 10.1088/0370-1328/76/1/307
    [70] Schwartz C 1961 Phys. Rev. 123 1700 doi: 10.1103/PhysRev.123.1700
    [71] Korobov V I, Korobov S V 1999 Phys. Rev. A 59 3394 doi: 10.1103/PhysRevA.59.3394
    [72] Korobov V I 2012 Phys. Rev. A 85 042514 doi: 10.1103/PhysRevA.85.042514
    [73] Korobov V I 2019 Phys. Rev. A 100 012517 doi: 10.1103/PhysRevA.100.012517
    [74] Notermans R P M J W, Rengelink R J, van Leeuwen K A H, Vassen W 2014 Phys. Rev. A 90 052508 doi: 10.1103/PhysRevA.90.052508
    [75] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637 doi: 10.1103/RevModPhys.87.637
    [76] Arora B, Sahoo B K 2014 Phys. Rev. A 89 022511 doi: 10.1103/PhysRevA.89.022511
    [77] Porsev S G, Safronova M S, Derevianko A, Clark C W 2014 Phys. Rev. A 89 022703 doi: 10.1103/PhysRevA.89.022703
    [78] Puchalski M, Piszczatowski K, Komasa J, Jeziorski B, Szalewicz K 2016 Phys. Rev. A 93 032515 doi: 10.1103/PhysRevA.93.032515
    [79] Puchalski M, Szalewicz K, Lesiuk M, Jeziorski B 2020 Phys. Rev. A 101 022505 doi: 10.1103/PhysRevA.101.022505
    [80] Dzuba V A, Flambaum V V, Sushkov O P 1997 Phys. Rev. A 56 R4357 doi: 10.1103/PhysRevA.56.R4357
    [81] Mitroy J, Safronova M S, Clark C W 2010 J. Phys. B 43 202001 doi: 10.1088/0953-4075/43/20/202001
    [82] Derevianko A, Savukov I M, Johnson W R, Plante D R 1998 Phys. Rev. A 58 4453 doi: 10.1103/PhysRevA.58.4453
    [83] Johnson W, Plante D, Sapirstein J 1995 Adv. At., Mol., Opt. Phys. 35 255
    [84] Pachucki K, Komasa J 2004 Phys. Rev. Lett. 92 213001 doi: 10.1103/PhysRevLett.92.213001
    [85] LeBlanc L J, Thywissen J H 2007 Phys. Rev. A 75 053612 doi: 10.1103/PhysRevA.75.053612
    [86] Holmgren W F, Trubko R, Hromada I, Cronin A D 2012 Phys. Rev. Lett. 109 243004 doi: 10.1103/PhysRevLett.109.243004
    [87] Copenhaver E, Cassella K, Berghaus R, Müller H 2019 Phys. Rev. A 100 063603 doi: 10.1103/PhysRevA.100.063603
    [88] Meng Z, Wang L, Han W, Liu F, Wen K, Gao C, Wang P, Chin C, Zhang J 2023 Nature 615 231 doi: 10.1038/s41586-023-05695-4
    [89] Henson B M, Khakimov R I, Dall R G, Baldwin K G H, Tang L Y, Truscott A G 2015 Phys. Rev. Lett. 115 043004 doi: 10.1103/PhysRevLett.115.043004
    [90] Lu S S, Zhang Y H, Shi T Y, Tang L Y 2025 J. Phys. B 58 035002 doi: 10.1088/1361-6455/adacbd
    [91] Katori H, Takamoto M, Pal’chikov V G, Ovsiannikov V D 2003 Phys. Rev. Lett. 91 173005 doi: 10.1103/PhysRevLett.91.173005
    [92] Takamoto M, Katori H 2003 Phys. Rev. Lett. 91 223001 doi: 10.1103/PhysRevLett.91.223001
    [93] Bothwell T, Kennedy C J, Aeppli A, Kedar D, Robinson J M, Oelker E, Staron A, Ye J 2022 Nature 602 420 doi: 10.1038/s41586-021-04349-7
    [94] Zheng X, Dolde J, Lochab V, Merriman B N, Li H, Kolkowitz 2022 Nature 602 425 doi: 10.1038/s41586-021-04344-y
    [95] McGrew W F, Zhang X, Fasano R J, Schäffer S A, Beloy K, Nicolodi D, Brown R C, Hinkley N, Milani G, Schioppo M, Yoon T H, Ludlow A D 2018 Nature 564 87 doi: 10.1038/s41586-018-0738-2
    [96] Rengelink R J, van der Werf Y, Notermans R P M J W, Jannin R, Eikema K S E, Hoogerland M D, Vassen W 2018 Nat. Phys. 14 1132 doi: 10.1038/s41567-018-0242-5
    [97] van der Werf Y, Steinebach K, Jannin R, Bethlem H L, Eikema K S E 2023 arXiv: 2306.02333v1
    [98] Thomas K F, Ross J A, Henson B M, Shin D K, Baldwin K G H, Hodgman S S, Truscott A G 2020 Phys. Rev. Lett. 125 013002 doi: 10.1103/PhysRevLett.125.013002
  • 加载中
图( 9) 表( 7)
计量
  • 文章访问数:  137
  • HTML全文浏览数:  137
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-15
  • 刊出日期:  2025-04-20

B-样条基组方法在少电子原子结构精密计算中的应用

    通讯作者: E-mail: lytang@apm.ac.cn
  • 中国科学院精密测量科学与技术创新研究院, 武汉　430071
  • 收稿日期:  2024-12-15

摘要: 少电子原子的精密光谱在基本物理理论验证、精细结构常数精确测定以及原子核性质深入探索等领域具有重要的应用价值. 随着精密测量物理学的快速发展, 人们对原子结构数据的需求已从最初的存在性确认, 转变为对高度准确性和精确性的持续追求. 为了满足精密光谱实验对高精度结构性质数据的迫切需求, 我们自主发展了一系列基于B-样条基组的高精度理论方法, 并将其成功应用于少电子原子的能级结构与外场响应性质的理论研究中. 具体而言, 实现了氦原子和类氦离子能谱的高精度确定, 为相关实验研究提供理论支撑; 实现了幻零波长的高精度理论预言, 为量子电动力学理论检验开辟了新方向; 提出了有效抑制光频移的理论方案, 为氦原子高精度光谱实验的开展提供了重要支持. 展望未来, 基于B-样条基组的高精度理论方法有望在量子态操控、核结构性质精确测定、超冷分子形成以及新物理探索等前沿领域得到广泛应用, 从而推动国内外精密测量物理领域的蓬勃发展.

English Abstract

    全文HTML

    1.   引　言

    • 随着激光冷却与囚禁技术的显著进步, 以及光学频率梳这一革命性工具的诞生, 人类对微观世界的探索能力因测量精度的极大提升而实现了前所未有的飞跃, 促使精密测量物理在21世纪的物理学领域中熠熠生辉, 成为一颗耀眼的明珠. 少电子原子凭借其电子数目少、能级结构相对简单的独特优势, 在理论上成为实现高精度计算的理想体系[1–5]. 同时, 得益于激光技术的蓬勃发展, 少电子原子在实验层面也成为精密测量物理研究的核心对象. 近年来, 围绕少电子原子精密谱的研究不仅在验证物理定律、精确测定基本物理常数方面展现出无可估量的价值, 更在探索超越标准模型的新物理领域发挥着举足轻重的作用[6–9]. 例如, 氢原子的能谱研究一直是科学发现的摇篮, 不仅催生了原子量子理论和狄拉克相对论量子力学的早期萌芽, 还极大地推动了相对论量子电动力学(QED)的发展[10]. 时至今日, 对氢原子、氦原子以及类氢、类氦等少电子原子体系进行的精密光谱研究, 依然是挖掘新的基础物理信息、拓宽科学认知边界的关键途径之一, 凸显了少电子原子结构精密计算在推动物理学进步中的核心地位[11–13].

      在少体精密测量物理领域, 理论与实验相辅相成, 共同推动着少电子原子分子精密谱研究的不断深入与广泛应用. 这一领域的进步高度依赖于高精度理论计算与精密实验测量的紧密合作, 它们共同为确定精细结构常数、里德堡常数、质子电子质量比等关键物理参数提供了坚实的基石, 并严格验证了QED理论的正确性及其适用范围[7,8,14,15]. 当前, 针对少电子原子结构的高精度理论计算, 主要采用关联高斯基方法和Hylleraas变分法[16,17]. 关联高斯基方法通过构建完备的基矢集来展开体系的波函数, 能够解析地获得哈密顿矩阵元, 从而精确求解体系的能量和波函数. 相比之下, Hylleraas方法则通过引入电子间的关联坐标来严格求解薛定谔方程, 直接获取体系的能量和波函数[18–22]. 尽管这两种方法均基于Rayleigh-Ritz变分原理, 但由于基函数的选择不同, 它们在处理具体问题时各具特色. 为了进一步提升计算精度, 需要在高精度的非相对论能量和波函数的基础上, 利用微扰理论方法逐级考虑波函数和能量的高阶修正项, 包括相对论修正和QED修正等, 这些高阶修正项在实现理论预测与实验数据在更高精度上的吻合方面发挥着至关重要的作用, 同时也为精确提取核性质提供了有力支撑[5,14,23–27].

      不同于上述的基组方法, B-样条(即basis splines, B-splines)函数因其独特的优势在原子结构计算领域备受瞩目. 这些优势包括B-样条函数的局域性、可调性、高阶连续性、正交性、近似完备性以及数值稳定性等. B-样条的概念最初由Schoenberg[28]于1946年提出, 并在1967年正式被命名为“B-样条”[29]. 在20世纪60—70年代, B-样条作为研究数学问题的有力工具风靡一时, 涌现出了许多基于B-样条的著名算法和公式[30]. 然而, B-样条真正被引入到原子物理领域的研究则要追溯到20世纪80年代. 在此期间, 国际上的Johnson, Grant, Fischer, Bachau等[31–35]率先将B-样条作为波函数展开的基组, 应用于原子结构的计算中. 在国内, 中国科学院武汉物理与数学研究所的李白文等[36–39]和吴礼金等[40, 41]率先将B-样条应用到里德堡原子的外场效应研究中, 开创了B-样条在国内原子物理领域应用的先河, 并发展了基于B-样条基组的相对论多体微扰程序, 进一步推动了相对论原子结构理论的研究.

      针对少电子原子结构的精密计算, 精密测量院原子分子外场理论组自主研发了一系列基于B-样条函数的高精度理论方法, 并将其成功应用于少电子原子结构与外场响应性质的计算中. 具体而言, 我们团队在类氢体系的研究中, 首次发展了精确求解单电子原子Dirac方程的B-样条基组方法, 高精度地获取了类氢体系的能级结构、多极极化率和长程色散系数[42–44]. 为了研究两电子原子结构性质, 我们进一步发展了基于B-样条函数的非相对论组态相互作用方法(NRCI)和相对论组态相互作用方法(RCI), 高精度计算了氦原子和锂离子低能态的动力学偶极极化率[45,46], 并实现了氦原子系列魔幻波长和幻零波长的相对论理论预言[47]. 随后, 我们不断改进RCI方法, 使其显式地包含有限核质量修正和核反冲修正, 并同时考虑了这些修正及QED修正对魔幻波长和幻零波长的影响[48,49], 实现了氦原子魔幻波长和幻零波长的高精度理论预言. 此外, 还将RCI方法推广应用于氦原子其他跃迁下的魔幻波长计算, 并提出了有效抑制氦原子Stark频移的理论方案, 为高精度实验光谱测量提供了理论支持[50,51]. 在RCI方法发展的同时, 还首次提出了关联B-样条方法, 并将其应用于低能态氦原子的静电偶极极化率计算[52–54]和贝特对数项计算[55]. 接下来将详细介绍针对两电子原子结构精密计算所发展的基于B-样条函数的系列数值理论方法.

    2.   B-样条方法的发展

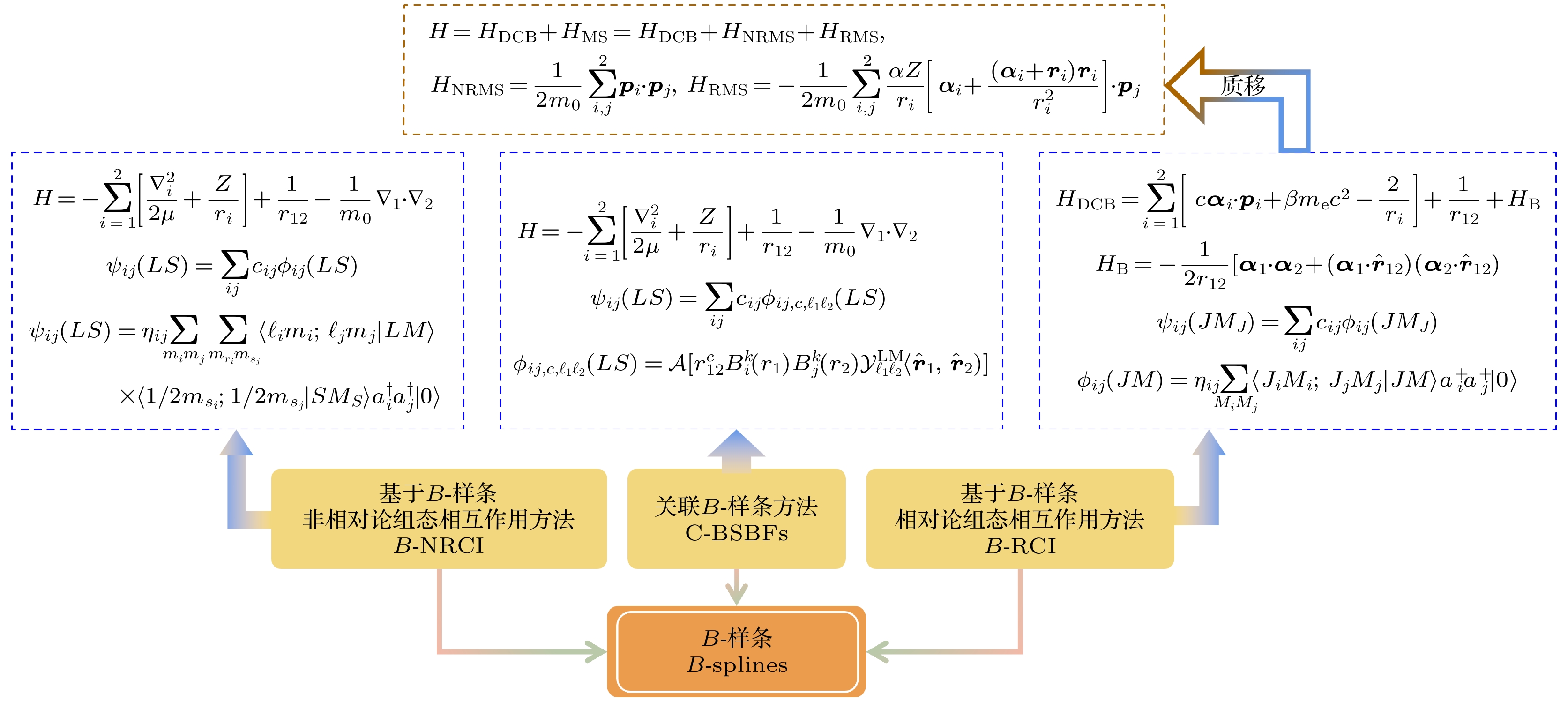
    • 图1综合展示了当前针对两电子原子体系所发展的三种高精度理论方法: 基于B-样条的非相对论组态相互作用方法(B-NRCI), 关联B-样条方法(C-BSBFs)以及基于B-样条的相对论组态相互作用方法(B-RCI). 三种方法均选择B-样条函数作为基函数. 因此, 本文首先概述B-样条函数相较于其他基函数所展现出的独特优势. 紧接着, 将逐一介绍这三种基于B-样条函数的理论方法.

      • 2.1.   B-样条函数

    • 在物理学领域, 采用有限基组方法求解薛定谔方程的历史悠久, 其核心在于将复杂的微分方程求解过程巧妙地转化为代数方程的本征值问题求解. 随着计算机技术的飞速发展, 在众多类型的基组中, “B-样条”函数凭借其独特的优势, 在原子分子物理中的应用日益广泛. 具体而言, B-样条函数展现出两大显著特性: “局域性”与“完备性”. 所谓“局域性”, 指的是每个B-样条函数仅在有限区间内非零, 这极大地简化了数值计算, 使得计算过程更加高效. 而“完备性”则确保了通过B-样条函数的线性组合, 可以逼近任意函数, 这为高精度计算提供了坚实的理论基础.

      B-样条函数是定义在有限区间$ [0, R] $内的一组分段多项式, 其递推定义式如下[30]:

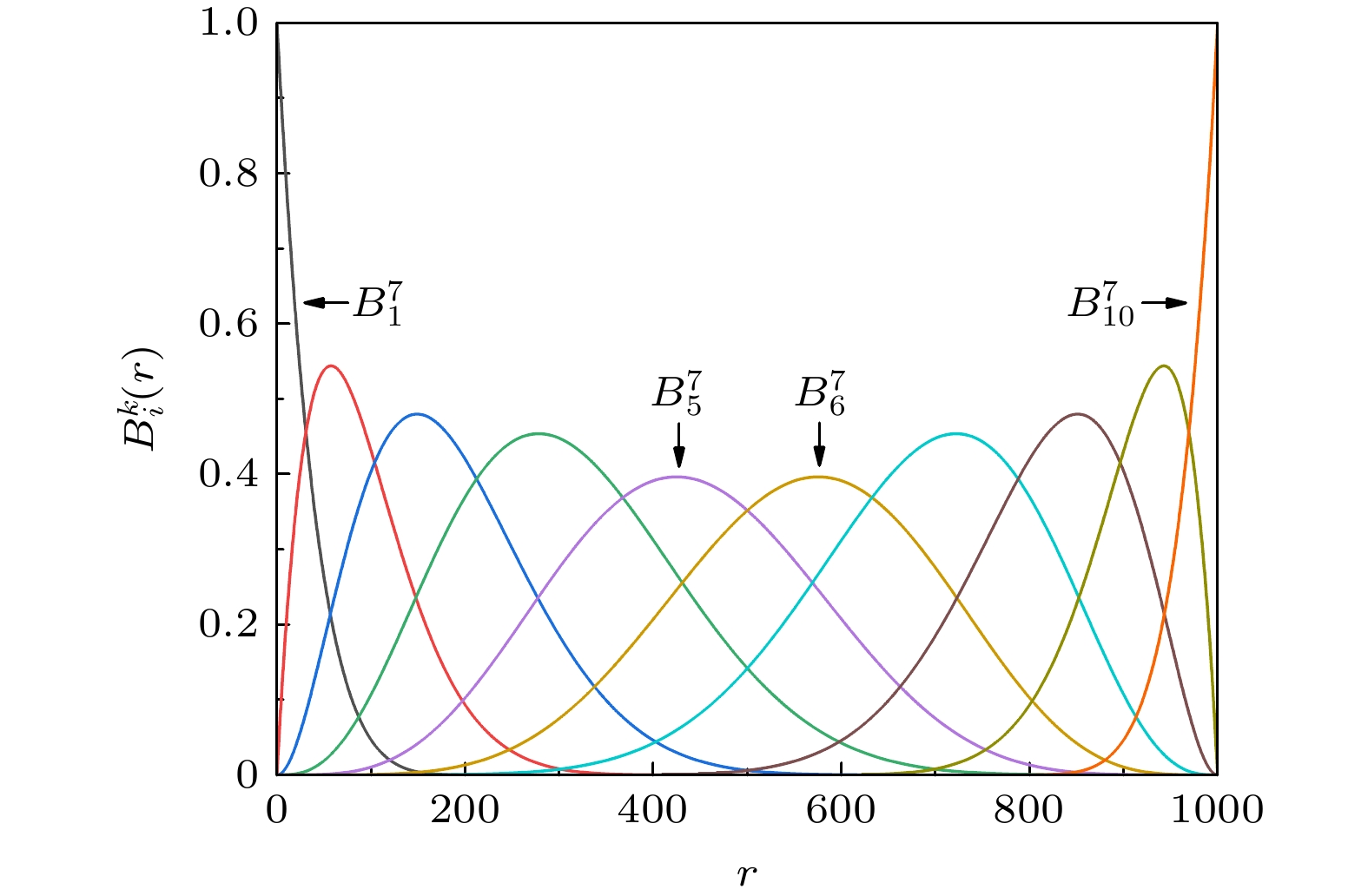
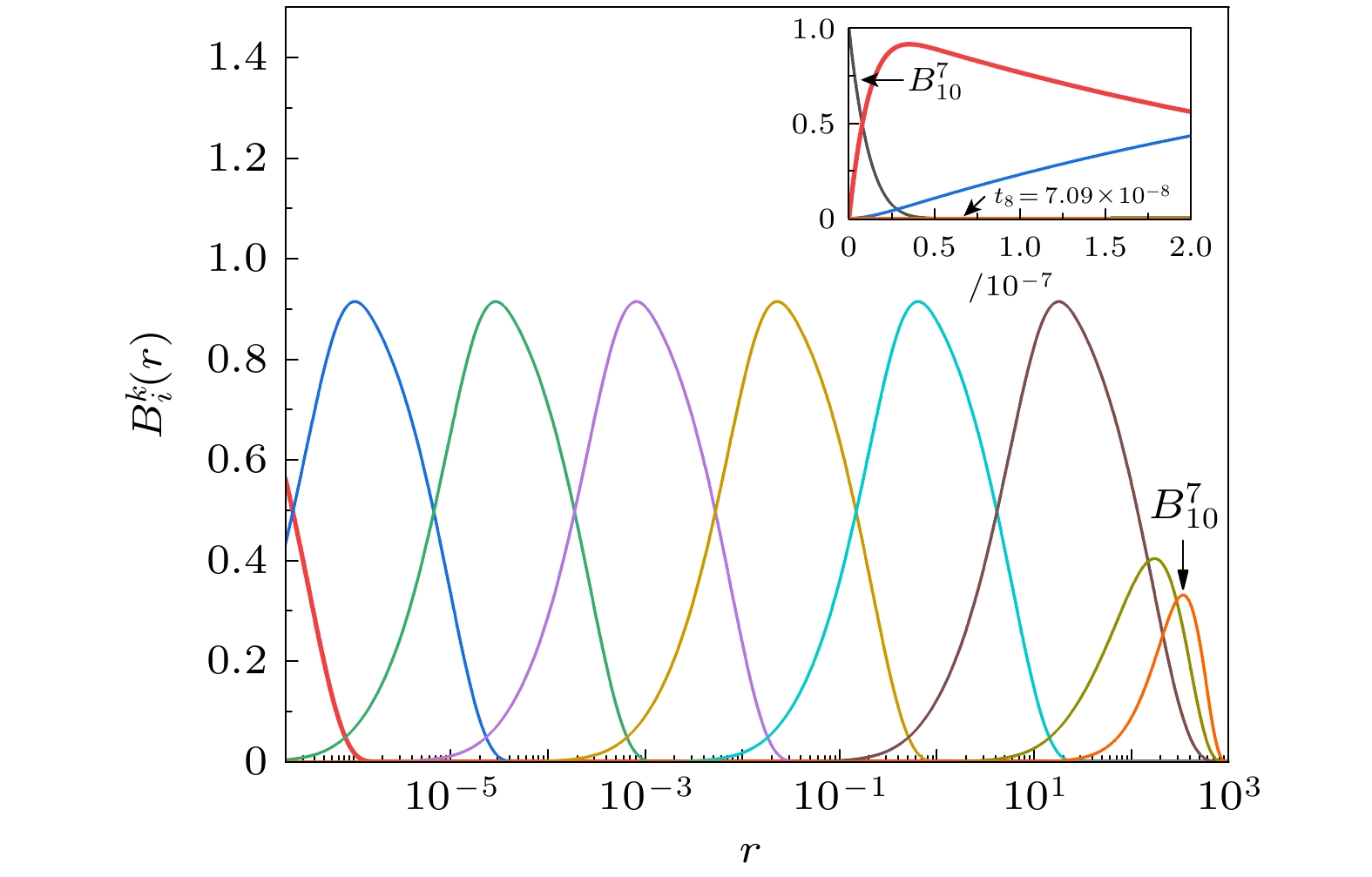
      式中, N代表B-样条的个数, 而k代表B-样条的阶数. $ {t_i} $构成了B-样条函数的结点序列, 这些结点对于确定B-样条函数的形态具有决定性作用. $ B_i^k(r) $特指第i个k阶的B-样条, 其定义域局限于结点区间$ [t_i, t_{i+k}) $, 且在此区间内, 自变量r的最高幂次为$ k-1 $. 因此, B-样条函数不仅具有高度的灵活性, 还能够在保持数值稳定性的同时, 精确地拟合原子分子的波函数.

      在实际操作中, B-样条的结点形式呈现出多样化, 主要包括线型结点序列、指数型结点序列、正弦型结点序列以及线型-抛物型结点序列等[35], 以满足不同体系的计算需求. 特别地, 在处理原子核附近的复杂波函数形式时, 指数型结点分布能够更准确地描述该区域的电子波函数性质, 因此备受青睐. 其具体的表达式如下:

      式中, 结点所在的区间被定义为$ [r_{{\mathrm{min}}}, r_{{\mathrm{max}}}] $, 该区间被n个结点$ \{t_i\} $划成$ n-1 $个子区间. $ \gamma_0 $代表指数型结点的关键参数. 为了更直观地展示在不同结点分布下B-样条函数的形态, 图2和图3分别展示了均匀分布型结点和指数型结点的B-样条函数图像. 通过对比这两个图, 可以观察到以下现象: 在均匀分布结点的样条函数图中, 左右两个端点的结点重复度均与样条阶数相同, 即均为$ k=7 $重. 特别地, 第一个样条在零点处的函数值精确地等于1, 而最后一个样条在$ R=1000 $端点处的函数值也为1. 然而, 在指数型结点分布的样条函数图中, 尽管左端点的结点重复度仍为$ k=7 $重, 但右端点的重复度却低于样条阶数, 图中展示为三重结点. 这种设计巧妙地满足了s态的径向波函数在零点处有值的特性, 同时也符合非相对论波函数在无穷远处趋于零的边界条件. 此外, 由于零点附近的样条函数分布相较于中间区域更为密集, 因此它能够更准确地描述原子核附近的电子波函数特性. 在进行相对论计算时, 若选择指数型的结点分布, 通常也会将左右两个端点均设置为k重结点, 以确保计算的准确性和可靠性.

      在求解体系的量子本征方程时, 当采用B-样条函数作为基组, 通常会遇到两类基本的积分问题: 一类是两个B-样条函数之间的积分, 另一类是B-样条函数与其导数之间的积分. 为了高效且精确地解决这些多项式积分问题, 通常采用Gaussian-Legendre积分方法[34]来进行数值计算. 该方法的核心在于精心设定高斯点和高斯系数, 确保当被积函数$ f(x) $为任意次的多项式时, 积分结果都能达到较高的精度. 在实际应用中, 通常采用区间$ [-1, 1] $上的高斯点和高斯系数进行计算. 对于其他积分区间, 可以通过简单的线性变换$ x=\dfrac{b-a}{2}t + \dfrac{b + a}{2} $, 巧妙地将积分区间映射到$ [-1, 1] $内, 从而利用已知的高斯点和高斯系数进行计算. 在确定具体积分所需的高斯点个数时, 需综合考虑Gaussian-Legendre积分的代数精度以及B-样条函数的阶数. 对于非严格分段多项式函数的积分, 只要该函数在积分区间内没有奇点, 就可以通过适当增加高斯点的个数来提高积分的计算精度.

      • 2.2.   基于B-样条的非相对论组态相互作用方法

    • 组态相互作用方法(configuration interaction, CI)是计算原子结构与外场效应的有效方法之一. 其核心思想是通过构造具有确定角动量和宇称的反对称组态波函数, 并利用这些波函数的线性组来逼近体系的真实波函数. 在CI方法中, 哈密顿矩阵元基于这些组态波函数进行计算, 并通过变分原理优化线性组合系数, 从而获得体系的能量和波函数. 因为CI方法对虚轨道空间没有任何限制, 所以具有广泛的适用性, 从而能够有效处理少电子原子和多电子原子的结构属性计算问题.

      接下来以氦原子为例, 详细介绍基于B-样条函数的非相对论组态相互作用(B-NRCI)方法, 也称传统B-样条方法. 考虑原子核质量后, 氦原子的非相对论哈密顿量可以表示为[47]

      在原子单位制下, 电子质量$ m_{\mathrm{e}}=1 $, $ m_0 $代表原子核质量. $ \mu=m_{\mathrm{e}}m_0/(m_{\mathrm{e}}+m_0) $表示电子的约化质量, 它描述了电子相对于原子核运动时的有效质量. $ r_i $为第i个电子相对于原子核的位置坐标, $ r_{12}=|\boldsymbol{r}_1-\boldsymbol{r}_2 | $表示两个电子之间的距离, $ 1/r_{12} $则代表两电子间的库仑相互作用. (3)式中最后一项代表质量极化项. 在无穷核质量情况下, 质量极化项为零.

      对于具有确定总轨道角动量L和自旋角动量S的两电子体系, 其波函数$ \psi(LS) $可以通过组态波函数$ \phi_{ij}(LS) $进行线性展开, 具体形式如下:

      而组态波函数$ \phi_{ij}(LS) $是单电子波函数的线性组合:

      其中, $ \chi(\mathit{\boldsymbol{r}}_1, \mathit{\boldsymbol{r}}_2) $代表两电子的Slater波函数, 它是通过将两电子各自的空间波函数按照特定的规则组合得到. $ \eta_{ij} $为归一化系数, 其定义如下:

      满足$ \eta_{ij}=\eta_{ji} $. Clebsch-Gordan系数$ \langle\ell_im_i; \ell_jm_j| LM\rangle $和$ \langle1/2 m_{s_i};1/2 m_{s_j}|SM_S\rangle $分别表示轨道-轨道和自旋-自旋耦合. 方程(5)中的求和部分表示对磁量子数$ m_i $, $ m_j $, $ m_{s_i} $, $ m_{s_j} $进行求和. 因此, 最终的组态波函数是与这些磁量子数无关的, 只与它们耦合后的总量子数L, M, S, $ M_S $相关. 此外, 由于Clebsch-Gordan系数具有交换对称性, 即$ \langle\ell_im_i;\ell_jm_j|LM\rangle=\langle\ell_jm_j;\ell_im_i|LM\rangle $(这一性质同样适用于自旋部分), 这一特性确保了组态波函数在电子交换下满足如下的对称性条件:

      进一步地, 根据两电子体系的哈密顿方程$ H\psi(LS)=\lambda \psi(LS) $, 应用变分原理对哈密顿矩阵方程进行处理后可得到:

      将(8)式进行化简, 可以得到如下的组态方程:

      其中, 本征能量为λ, 与之对应的本征波函数的系数为$ {c_{ij}} $. $ V_{ijk\ell} $为两电子的库仑相互作用矩阵元, 其具体展开形式为[47]

      式中, 括号里的第一项代表直接积分项, 第二项为交换积分项, 它们的具体积分形式可参考文献[45]. 在方程(9)中, $ (MP)_{ijk\ell} $为质量极化项的矩阵元, 其展开形式为

      当选用B-样条函数来展开单电子波函数时, 两电子原子的组态波函数可以表述为两个B-样条函数的直积形式, 具体如下所示:

      其中, $ \mathcal{Y}_{\ell_{1} \ell_{2}}^{L M}\left(\hat{\boldsymbol{r}}_{1}, \hat{\boldsymbol{r}}_{2}\right) $代表耦合的球谐函数.

      在处理少电子原子体系中的强关联问题时, 传统的基于B-样条函数的NRCI方法通常通过增加组态的分波数目$ \ell_1 $和$ \ell_2 $来提升数值计算的精度. 具体操作时, 预先设定一个最大分波数$ \ell_{{\mathrm{max}}} $, 然后将基函数的两个轨道角动量$ \ell_1 $和$ \ell_2 $从0逐步增加到$ \ell_{{\mathrm{max}}} $. 然而, 这种方法的效果存在局限性, 如表1所列: 即使分波数目增至80, 氦原子基态能量的收敛结果也仅能精确到7—8位有效数字, 这对于简单原子的精密计算而言远远不够. 此外, 随着分波数目的增加, 组态数目会呈现指数级增长, 导致计算量急剧上升, 对计算资源的需求大幅增加, 且难以获得理想的线性计算效率的提升.

      • 2.3.   关联B-样条基组方法

    • 为了在提高数值计算精度的同时, 兼顾计算时间和计算量的需求, 我们自主发展了关联B-样条基组方法 (C-BSBFs). 该方法的核心创新在于, 在基函数的构造中直接引入了电子-电子间的关联坐标$ r_{12} $, 其具体形式为[52]

      其中c的取值决定了是否包含关联项. 当$ c=0 $时, 它回归到传统的B-样条基函数(如方程(12)所示); 而当$ c=1 $时, 上述基函数直接包含了电子间的关联相互作用. 这意味着, C-BSBFs方法不仅充分保留了B-样条函数的优异特性, 还有效地考虑了电子间的关联效应. 因此, 在处理强关联的能态时, 该方法展现出了显著的优越性.

      表1对比了关联B-样条方法和传统B-样条NRCI方法在氦原子基态非相对论能量计算上的收敛性. 数据显示, C-BSBFs方法具有快速的收敛性, 仅用1个分波数即可达到传统B-NRCI方法使用65个分波时的能量精度. 当C-BSBFs方法使用4个分波时, 其计算结果与Hylleraas方法的结果有10位相同数字. 相比之下, 传统B-NRCI方法即使使用80个分波, 也仅能与Hylleraas变分法下的结果符合到7位有效数字. 因此, 在电子间强关联能级计算中, C-BSBFs方法能显著提升计算效率和精度.

      • 2.4.   基于B-样条的相对论组态相互作用方法

    • B-NRCI方法和C-BSBFs方法都是从薛定谔方程出发, 通过构建组态波函数来求解体系的本征方程, 但两者所获得的能量和波函数均未包含相对论修正. 为了全面考虑两电子原子中核与电子相互作用的全阶相对论效应, 我们进一步发展了基于B-样条函数的相对论组态相互作用(B-RCI)方法.

      在相对论框架下, 两电子体系的Dirac-Coulomb-Breit(DCB)哈密顿量表示为[49]

      其中, c代表光速, $ \boldsymbol{\alpha}_i $和β代表4×4的狄拉克矩阵, $ \boldsymbol{p}_i $为电子动量算符, 而$ H_{\mathrm{B}} $则是描述电子-电子之间通过交换光子产生相互作用的Breit算符. 在只考虑单光子(虚光子)交换、且没有高阶或动态修正时, Breit 相互作用算符可写为[49,57]

      在计算少电子原子的结构性质时, 考虑Breit相互作用至关重要. 以类氦的Li+离子为例, 只有包含Breit相互作用, 才能正确得到$ 2\, ^3 {\mathrm{P}} $态的精细能级结构顺序.

      对于总角动量为J、磁量子数为$ M_J $的两电子原子波函数$ \psi(JM_J) $, 可以表示为组态波函数$ \phi_{ij}(JM_J) $的线性组合:

      其中, 组态波函数的展开形式如下:

      式中$ \chi(\mathit{\boldsymbol{r}}_1, \mathit{\boldsymbol{r}}_2) $代表两电子的Slater波函数, Clebsch- Gordan系数则用于描述两电子角动量的jj耦合, 并在耦合过程中对磁量子数进行了求和. 因此, 组态波函数的最终形式与单个电子的磁量子数无关. 此外, 由于Clebsch-Gordan系数具有交换对称性, 因此所构建的组态波函数也自然满足相应的电子交换关系:

      进一步, 考虑到单电子态的总角动量量子数总是半奇数的特性, 在构建相对论组态波函数时需要遵循一条重要规则: 当体系总角动量J为奇数时, 用于构建组态波函数的两个单电子态必须是不同的. 此外, 在相对论框架下构建组态时, 需要特别注意的是, 在求解单电子Dirac方程的过程中, 会出现负能态问题. 在电学性质的计算中, 由于负能态的影响相对较小, 通常仅采用正能态来构造组态, 这种计算方式被称为no-pair计算. 然而, 在计算磁学性质时, 负能态的贡献变得显著, 有时甚至能改变数值结果的符号[58]. 因此, 为了准确描述负能态效应, 必须将负能态直接纳入组态的构建中, 这种计算方式则被称为pair计算.

      在成功构建组态波函数之后, 类似于NRCI方法, 利用变分原理对体系的哈密顿方程进行变分处理后, 进而推导出如下的相对论组态方程:

      其中, 本征能量为λ, 与之对应的本征波函数系数为$ {c_{ij}} $. 在相对论计算框架下, 两体相互作用矩阵元$ V_{ijkl} $由库仑相互作用和Breit相互作用两部分组成[47,57]:

      若不考虑Breit相互作用, 则(20)式中直接积分部分的矩阵元可以具体表达为

      若考虑Breit相互作用, 则只需把$ X_{\nu}(ijk\ell) $替换为$ X_{\nu}(ijk\ell)+M_{\nu}(ijk\ell)+N_{\nu}(ijk\ell) $, 其中$ M_{\nu}(ijk\ell) $和$ N_{\nu}(ijk\ell) $的具体表达式分别为

      (20)—(23)式中径向函数的具体展开形式可以参见文献[57].

    3.   B-样条方法的应用

      3.1.   辐射修正中Bethe-logarithm项的计算

    • 1947年, Lamb和Retherford[59]通过微波技术揭示了一个重要现象: 氢原子$ 2 {\mathrm{s}}_{1/2} $和$ 2 {\mathrm{p}}_{1/2} $态并非如Dirac理论预言的那样完全简并, 而是存在1057 MHz的能量差异. 这一现象被命名为兰姆位移(Lamb shift). 同年, Bethe基于量子化的辐射场理论, 深入探究了电子与其自身辐射的虚光子之间的相互作用所引起的电子自能修正, 并据此预测出$ 2 {\mathrm{s}}_{1/2} $和$ 2 {\mathrm{p}}_{1/2} $态之间的能量差为1040 MHz, 这一预测与实验结果相符合, 从而成功解释了兰姆位移. 兰姆移位的发现极大地推动了量子电动力学(QED)理论的发展.

      根据QED理论, 原子能级的QED修正领头项包括电子自能、真空极化、反常磁矩以及QED效应对电子-电子相互作用的修正. 对于两电子原子的能级而言, QED修正中领头项的具体表达式为[13,60]

      其中Q项定义为

      在(24)式和(25)式中, α代表精细结构常数, Z代表核电荷数, $ \langle\delta({\boldsymbol{r}}_i)\rangle $表示电子在核位置处出现的几率, $ \langle\delta({\boldsymbol{r}}_{12})\rangle $代表两个电子同时出现在同一位置的几率, γ表示欧拉常数, ϵ是以$ r_{12}=0 $为球心的半径, $ \beta(nLS) $为贝特对数项(Bethe logarithm, BL).

      随着精密测量物理领域实验精度的不断提升, 对理论计算的精度也提出了更高要求. 在计算少电子原子的结构属性时, 除了必须考虑相对论修正之外, 还需逐步考虑QED 修正. 其中, BL项作为QED领头项中的重要组成部分, 往往成为QED修正计算中不确定性的主要来源. 这是由于BL项的计算涉及对中间态的几乎发散的无限求和, 而这些求和的主要贡献来自极高的激发态. 因此, BL项的精确计算是精密结构理论研究中的关键科学问题, 对于解决少电子原子精密光谱实验与理论之间的差异起着至关重要的作用.

      值得注意的是, 尽管BL项属于量子电动力学的范畴, 但根据Bethe的计算, 它本质上反映了电子自能的非相对论部分[59]. 由于BL项是在非相对论框架下定义的, 因此我们基于非相对论量子电动力学对其进行计算. 在加速度规范下, BL项的定义为[61–63]

      其中,

      在(26)—(28)式中, $ n_0 $和$ L_0 $分别代表初态的主量子数和角动量量子数, $ |0\rangle $代表初态波函数, 对应的能量为$ E_0 $; $ |n\rangle $代表在偶极跃迁过程中所有被允许的中间态, 这些中间态既包含束缚态也包含连续态, 对应的能量为$ E_n $. $ {\boldsymbol{r}_i} $表示第i个电子相对于原子核的位置矢量.

      长久以来, BL项的精确计算一直是少电子原子精密光谱理论研究中的一大难题. 从上述表达式可以看出, BL项的主要贡献来源于高能的单双激发态. 然而, 标准的变分方法难以准确获取这些高能激发态, 导致能量带来的误差通常远大于矩阵元所带来的误差[61,63,64]. 为了解决这一问题, 我们采取了多种策略. 一方面, 致力于修正和优化各种基函数, 确保这些函数能够同时高精度地模拟低能态和高激发态. 另一方面, 利用偶极矩阵元在不同规范下的等价性, 计算不同规范下的BL项, 以进行交叉验证. 特别地, 在速度-加速度混合规范的计算中, BL项的计算甚至能够避免直接涉及能量项, 而仅依赖于波函数[64]. 此外, 在实际的数值计算过程中, 还可以利用Wigner-Eckart定理对磁量子数进行求和, 以简化BL项的表达式. 简化后的BL项在不同规范下的具体表达式可参考文献[65].

      目前, 氢原子基态、低激发态以及里德堡态的BL计算已取得显著的进展, 相关研究成果见参考文献[66,67]. 然而, 对于氦原子及类氦离子体系的研究, 早期的BL变分计算主要是基于速度规范下出发, 所得结果的有效数字仅有2—3位[68,69]. 1961年, Schwartz[70]提出了一种创新的BL积分表示方法, 该方法使得氦原子基态的BL计算结果为2.9837(40). 2000年, Drake和Goldman[63]发展了赝态求和法, 该方法显著提升了氦原子低激发态BL计算的精度, 达到9位有效数字. 随后, Korobov[71–73]对Schwartz的积分表示法进行了改进和优化, 得到了具有11—14位精确数字的氦原子基态以及高激发态的BL值.

      2013年, B-样条基组被成功地应用于氢原子的BL计算中[67], 并获得了高精度的数值结果. 该方法充分利用B-样条函数的近似完备性、局域性以及结点连续可调性等优点, 能够在加速度规范下, 同时高精度地计算出氢原子低能态和高激发态的BL 值. 具体来说, 在氢原子基态的计算中, 用450个B-样条将BL计算精度提升到24位有效数字; 而对于主量子数高达$ n=210 $的高里德堡态, 得到的BL结果也具有10位有效数字. 表2详细列出了在调节指数结点参数$ \gamma_0 $后, 第一个非零结点位置、获得的最大中间态能量与BL计算精度之间的具体关系[67]. 由表2可以发现: 随着$ \gamma_0 $增大, 第一个非零结点$ t_1 $的量级将变小, 中间态的最大能量$ E_{{\mathrm{max}}} $的量级变大, 使得最终得到的BL项的精度变高. 除此之外还发现: 第一个非零结点$ t_1 $的量级可以作为预测BL项计算精度的一个近似指标.

      为了进一步验证B-样条函数在少电子原子BL计算中的适用性, 结合CI方法将B-样条基组应用于氦原子BL的计算中. 具体计算过程如下: 首先, 采用基于B-样条函数的NRCI方法, 在速度规范、加速度规范以及速度-加速度混合规范下, 分别计算了氦原子$ n\, ^{1, 3}{\mathrm{S}}(n\leqslant8) $态的BL项. 不同规范下所得的BL结果均具有6—8位有效数字[65], 且结果相互一致, 这验证了B-样条函数下NRCI方法的可靠性. 其次, 针对强关联的单重态, 利用关联B-样条基组方法(C-BSBFs), 计算了氦原子$ n\, ^1 {\mathrm{S}}(n\leqslant10) $一系列能态在加速度规范和混合规范下的BL值. 表3选择性地给出了不同方法下氦原子单重态BL结果的对比. 从表中可以明显看出, 与Korobov[73]得到的高精度结果相比, 对于基态, 采用加速度规范下的关联样条基组方法计算得到的BL结果[55], 精度相较于传统B-NRCI方法[65]有了显著提升, 至少提高了4个数量级. 同样地, 在加速度规范下, 对于$ 2\, ^1 {\mathrm{S}} $和$ 3\, ^1 {\mathrm{S}} $态的BL结果, 关联样条基组方法也展现出了更高的精度, 相较于传统样条方法提高了3个数量级. 此外, 使用关联样条基矢进行计算时, 不同规范下的BL结果之间的符合程度也提高了1—2位有效数字.

      综合对比当前氢原子和氦原子的BL计算结果(参见文献[65,67]以及表2和表3), 可以得出以下结论: 当B-样条基组足够大时, 速度规范、加速度规范和长度规范均能得到收敛性良好的计算结果. 然而, 加速度规范的收敛速度相较于速度规范更快, 而这两种规范的结果又都优于长度规范. 此外, 关联B-样条方法相较于传统B-样条方法, 展现出更快的收敛速度和更高的数值精度. 因此, 在少电子原子结构属性的QED修正计算中, 采用在加速度规范或混合规范下的关联B-样条方法来计算BL项, 无疑是一个更为优越的策略.

      • 3.2.   极化率的计算

    • 当原子处于线偏振的外电场或激光场中时, 其能级会发生不同程度的移动, 即Stark频移. 当外电场是行波场时, 原子单个能级的Stark频移可展开为

      而当外电场是魔幻的晶格场时, 原子单个能级的Stark频移则展开为

      其中, $ \alpha_1(\omega) $和$ \gamma(\omega) $分别代表原子某个能级的动力学电偶极极化率和超极化率, $ \alpha^{{\mathrm{Q M}}}(\omega) $代表动力学电四极与磁偶极极化率之和, I表示光强强度, ω为激光场的频率, $ \varepsilon_0 $是真空介电常数, 而$ E_{\mathrm{R }}$和U则分别代表原子的反冲能量和光阱的势阱深度.

      由(29)式和(30)式可以看到, 极化率作为原子的基本结构性质, 描述了原子因感受到外电场作用而偏离正常电子云形状的程度, 也是定量分析体系Stark频移和黑体辐射频移的重要理论参数. 随着精密测量物理的兴起, 人们对极化率计算精度的要求越来越高. 这是因为高精度的原子极化率在外场效应的准确评估、魔幻光晶格实验方案的设计[74,75]、高里德堡原子有效极化势的构建[76,77]、QED理论的检验[6]、温度和压力标准的计量[78,79], 以及宇称不守恒的检验[80]等方面有着广泛而重要的应用.

      对于量子态为$ |n_{{g}}L_{{g}}M_{{g}}\rangle $的初态, 其非相对论动力学电偶极极化率可通过中间态求和方法表示[81]:

      其中, $ \alpha_1^{\mathrm{S}}(\omega) $和$ \alpha_1^{\mathrm{T}}(\omega) $分别代表标量和张量极化率, 它们的具体展开形式为[47,48]

      式中, $ f_{gn}^{(1)} $为电偶极振子强度, 其展开形式如下:

      其中, $ \triangle E_{gn}=E_n-E_g $表示初态$ |N_gL_g\rangle $与中间态$ |N_nL_n\rangle $的跃迁能量, $ T_1 $是电偶极跃迁算符. 当频率$ \omega=0 $时, 对应的极化率称为静电极化率. 关于其他多极极化率和超极化率的详细表达式, 可参考文献[22]. 此外, 对于相对论情况下极化率的普适公式, 只需将非相对论下极化率公式中的量子数L和M分别替换为量子数J和$ M_J $即可.

      对于氦原子低能态的静电极化率, 首先采用B-样条函数下的NRCI方法, 求解两电子的薛定谔方程. 然后通过中间态求和方法, 计算了在长度、速度和加速度三种规范下, 氦原子$ 2\, ^3 {\mathrm{S}} $, $ 3\, ^3 {\mathrm{S}} $, $ 2\, ^3 {\mathrm{P}} $和$ 3\, ^3 {\mathrm{P}} $的静电偶极极化率. 进一步, 利用长度规范下的振子强度和跃迁能量, 计算了$ 2\, ^3 {\mathrm{S }}$和$ 2\, ^3 {\mathrm{P}} $态到第二激发阈值, 以及$ 3\, ^3 {\mathrm{S}} $和$ 3\, ^3 {\mathrm{P}} $态到离化阈值附近的动力学偶极极化率[45]. 对比发现, 长度和速度规范下的结果符合良好, 而加速度规范下的精度相对较低[45]. 与Hylleraas方法下的结果相比, 长度和速度规范下的静电极化率符合程度分别在10–7和10–6的水平.

      其次, 针对氦原子$ 2\, ^3 {\mathrm{S}}\rightarrow3\, ^3 {\mathrm{S}} $和$ 2\, ^3 {\mathrm{S}}\rightarrow2\, ^1 {\mathrm{P}} $两条禁戒跃迁谱线, 我们发现有限核质量效应和相对论效应对谱线能量的影响相当显著. 因此, 采用B-样条函数下的RCI方法, 求解显含有限核质量算符的DCB哈密顿方程, 得到了初态及中间态的能量和波函数. 随后, 通过态求和方法计算了4He和3He体系的$ 2\, ^3 {\mathrm{S}}_1 $, $ 3\, ^3 {\mathrm{S}}_1 $和$ 2\, ^1 {\mathrm{P}}_1 $的相对论静电偶极极化率[50,51]. 目前, $ 3\, ^3 {\mathrm{S}}_1 $三重态的相对论静电偶极极化率的相对误差优于10–6, 而单重态$ 2\, ^1 {\mathrm{P}}_1 $的静电极化率相对误差在同等计算规模下仅为10–4. 值得注意的是, 在相对论极化率的计算中, 我们选择了长度规范, 以有效抑制负能态对偶极跃迁算符的影响[82,83].

      为了进一步提高单重态极化率的计算精度, 将关联B-样条基组方法应用于氦原子非相对论极化率的计算中[54]. 同时, 采用微扰方法高精度计算极化率的相对论和QED修正. 在计算过程中, 为了降低数值积分中奇异算符对波函数局域行为的要求, 采用全局算符方法[53,84]. 此外, 还采用四精度计算以提升收敛精度, 并利用标准矩阵乘法的开源程序包GEMM来提高计算效率.

      表4展示了采用关联B样条基组方法计算得到的氦原子单重态的静电偶极极化率. 通过比较可以发现: 引入关联样条基矢后, 仅需4个分波, 非相对论计算结果便能收敛到12位有效数字, 与指数关联的Slater基矢方法下的结果[78]相符合. 进一步考虑相对论修正后, 我们的结果与文献[78]中的结果具有11位相同的有效位数. 再考虑QED修正之后, 两者仍有7位相同的有效位数. 此外, 表5详细列出了氦原子激发态的极化率计算结果. 以往鲜有关于包含相对论和QED修正的激发态极化率的研究报道, 而当前计算主量子数n高达7的结果, 相对精度已达到亚ppm(1ppm = 10–6)水平. 这种既能精确处理低能态又能有效计算高激发态的能力, 再次证明了关联B样条基组方法的高精度性和广泛的适用性.

      • 3.3.   幻零波长的确定

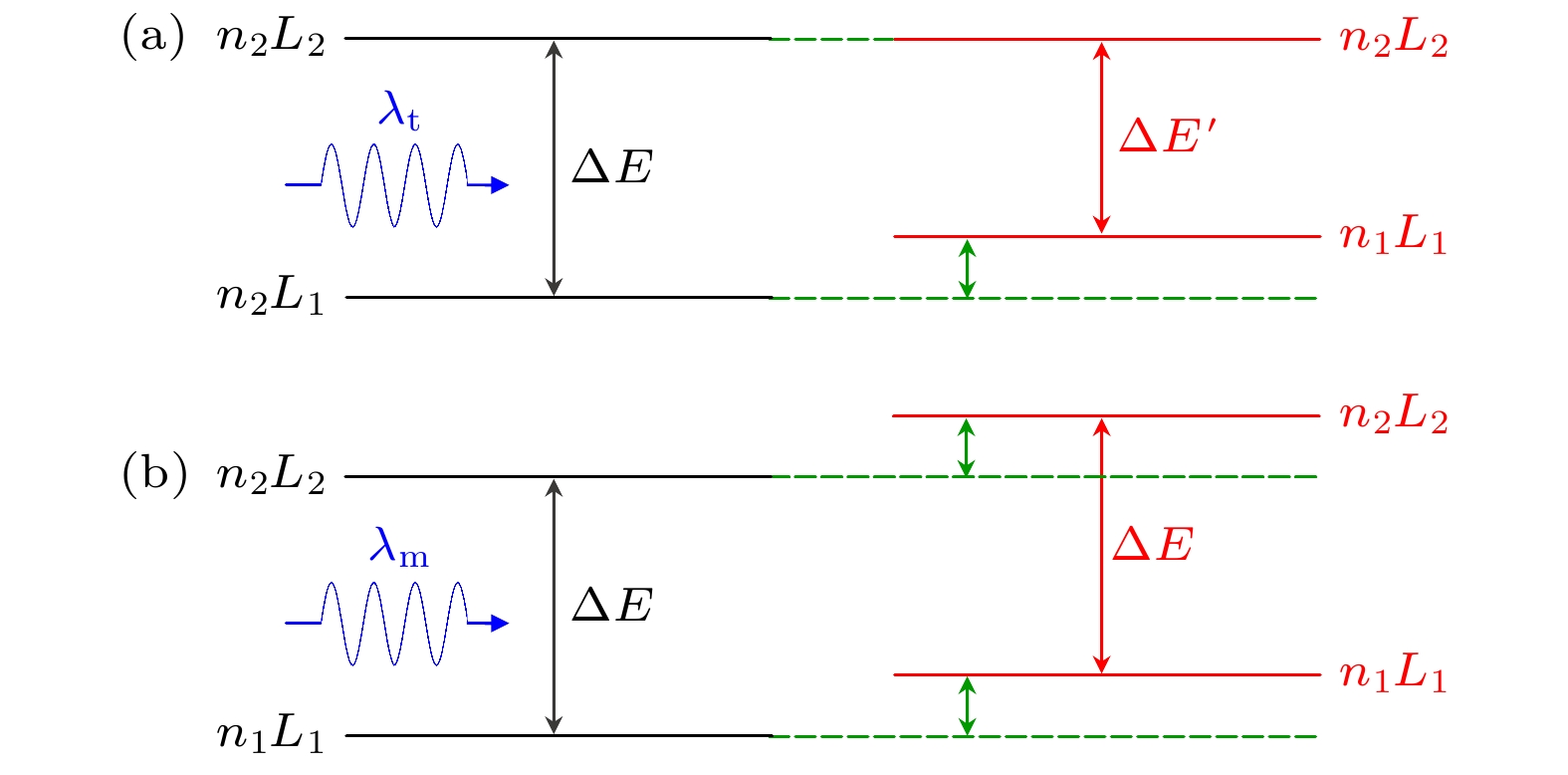
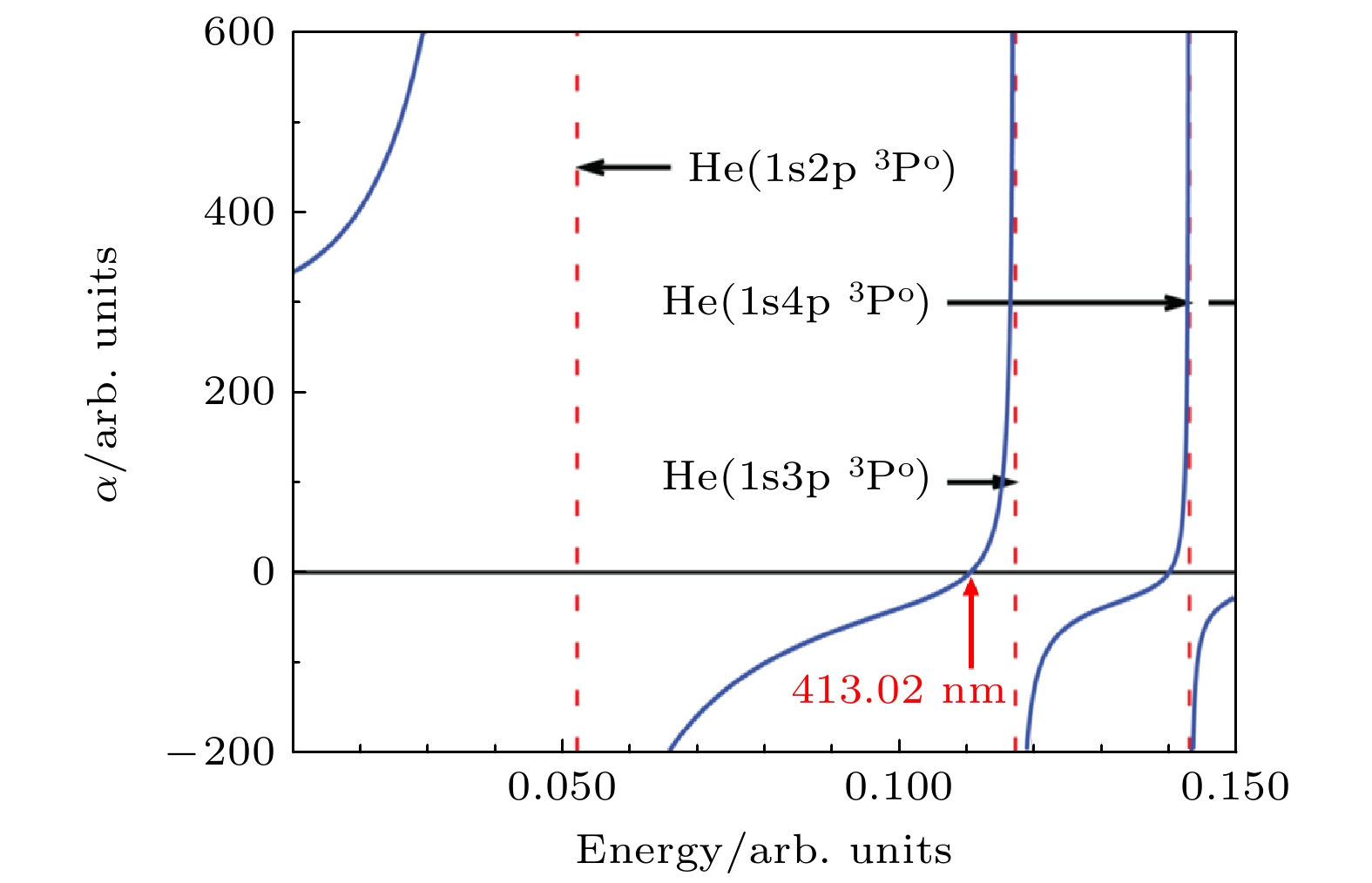
    • 幻零波长(tune-out wavelength), 指的是激光频率调制到使原子某个特定能级的ac Stark频移为零时, 该激光频率所对应的波长. 这一概念的示意图如图4(a)所示. 幻零波长最初是由Leblanc和Thywissen[85]于2007年研究单频率选择性囚禁双组分碱金属原子体系时提出的. 在理论计算中, 当高阶Stark效应的影响很小, 以致于可以忽略时, 则可以根据体系的动力学偶极极化率为零来确定幻零波长$ \lambda_{\mathrm{t}} $,

      图5展示了根据氦原子$ 2\, ^3 {\mathrm{S}}_1 $亚稳态的偶极极化率为零所确定的413 nm幻零波长的精确位置.

      值得强调的是, 幻零波长的确定与原子完整的能谱信息及一系列跃迁矩阵元密切相关. 因此, 幻零波长的高精度测定能够直接反映出人们对于原子结构性质的整体认知水平. 在幻零波长下, 原子对外部电场强度的变化变得不敏感, 彷佛“隐形”于电场之中, 这一特性使得实验上对幻零波长的测量能够达到很高的精度. 近年来, 幻零波长的高精度实验测量在多个领域展现出重要的应用, 包括原子性质的精确确定、量子态的选择与操控、精密原子干涉仪的设计以及干涉式陀螺仪的研发等. 例如, Holmgren等[86]对K原子幻零波长的测量精度达到了2 ppm, 而Copenhaver等[87]则利用原子干涉仪成功测定的7Li原子671 nm幻零波长, 精度达到了MHz水平. 这些高精度幻零波长实验测量为检验原子结构理论方法, 精确确定原子的跃迁矩阵元提供了新途径[86]. 此外, 山西大学张靖教授的研究团队[88]利用Rb原子自旋内态的幻零波长实现了超冷原子扭转双层光晶格. 2013年, Mitroy和Tang[6]首次从理论上提出利用氦原子$ 2\, ^3 {\mathrm{S}}_1 $亚稳态的413 nm幻零波长来检验原子QED理论的创新方案. 与传统的电子g因子测量, 以及少电子原子的精密光谱测量等QED理论检验方法相比, 幻零波长方案的提出为非能谱测量检验QED理论开辟了一条全新的途径.

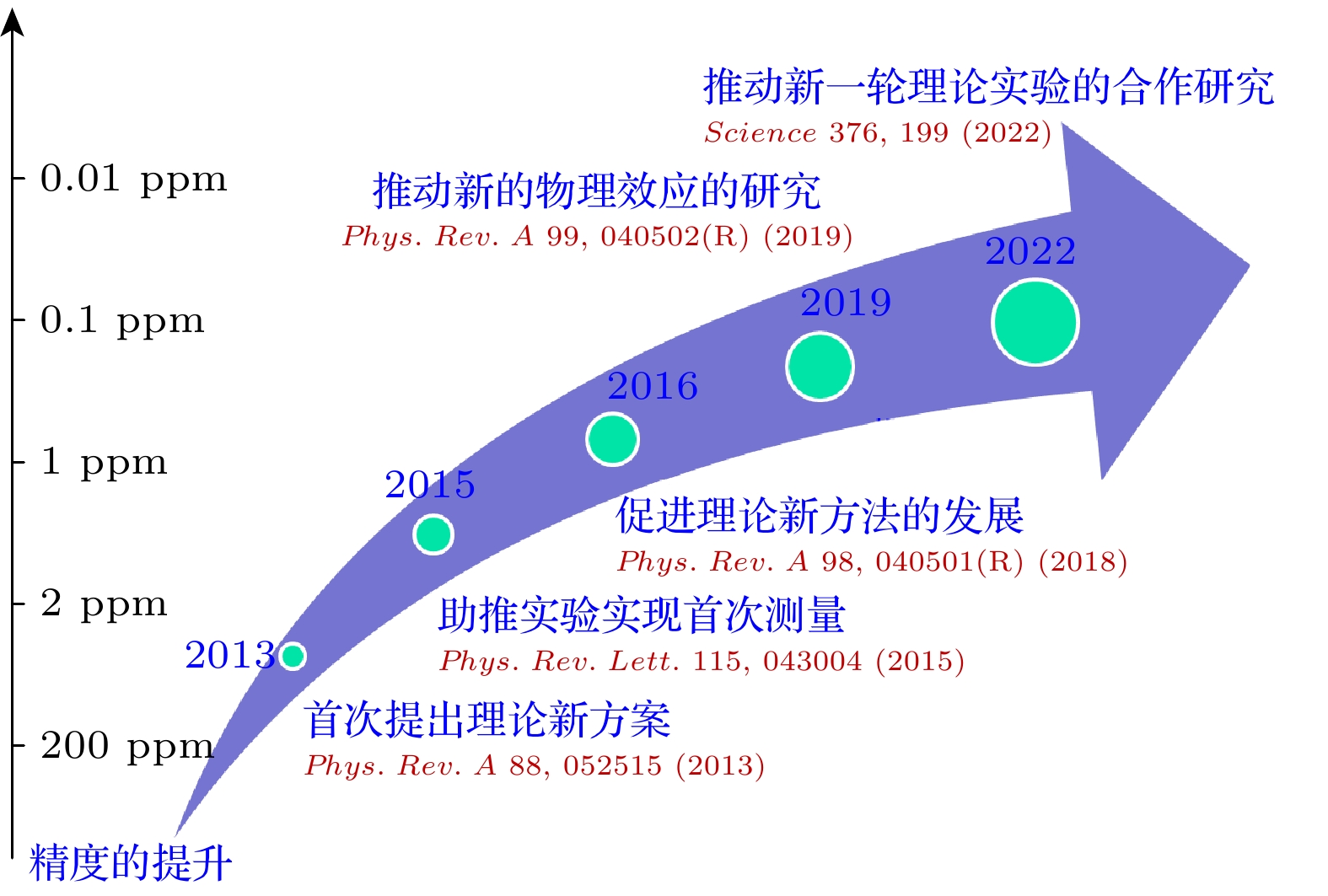
      自Mitory和Tang提出利用氦原子413 nm幻零波长来检验QED理论的提议以来, 理论与实验开展紧密合作, 致力于实现QED理论的高精度检验. 图6概述了幻零波长在理论与实验方面的研究历程. 2015年, 澳大利亚国立大学Baldwin实验团队[89]首次测量了氦原子$ 2\, ^3 {\mathrm{S}}_1 $态的413 nm 幻零波长, 测量结果为413.0938(9 stat)(20 syst) nm. 这一结果的精度相较于2013年的理论预言值413.02(9) nm [6]提高了50倍, 但两者之间存在134 ppm的差异. 该差异的主要原因在于2013年的理论预言未考虑相对论修正和QED效应. 因此, 2015—2016年, Zhang等[45,47]相继发展了基于B-样条函数的非相对论和相对论组态相互作用计算方法, 完成了有限核质量和相对论效应的计算, 给出的幻零波长从头计算结果为413.0859(4) nm, 从而将理论计算与实验测量的差异从134 ppm减小到了19 ppm. 进一步分析表明, 这19 ppm的差异主要源于理论计算中尚未考虑的QED修正. 为此, 2017—2019年, Zhang等[49]又将B-样条函数扩展应用到动力学极化率的QED修正的微扰计算中, 同时还发展了显含核反冲效应的RCI计算方法, 并评估了有限核尺寸效应对413 nm幻零波长的贡献. 详细的各项修正计算结果如图7所示, 最终得到的幻零波长结果为413.09015(4) nm. 该结果的理论误差是2015年实验误差的1/50, 但理论与实验之间仍然存在1.8σ的标准差.

      2022年, 实验与理论合作完成了对幻零波长的新一轮理论计算与实验测量[15]. 在理论方面, 从薛定谔方程出发, 利用微扰方法计算了磁化率对幻零波长的贡献, 同时考虑了电四极跃迁、电偶极跃迁高阶项以及偶极算符的相对论修正所带来的延迟效应. 最终, 幻零波长的非相对论量子电动力学 (NRQED)理论计算值为725736252(9) MHz, 其不确定度主要源于被忽略的$ \alpha^4 $阶非辐射修正和高阶QED贡献. 与2019年的理论值[49]相比, 新的NRQED计算的结果误差降低了10倍. 在实验方面, 通过振荡频率测量法来测量氦原子BEC凝聚体所感受到的偶极势的变化, 进而确定了幻零波长的实验结果为725736700(40stat, 260syst) MHz. 与2015年的实验结果相比[89], 新的实验测量精度提高了20倍. 然而, 通过对比可以发现实验所得的中心值与理论计算的中心值之间仍然存在448 MHz的差异.

      为了在相对论框架中自洽地考虑QED修正, Lu等[90]近期开发了基于B-样条函数的相对论组态相互作用结合辐射势(RCIRP)方法. 在此方法中, 辐射势算子被直接加到Dirac-Coulomb-Breit哈密顿量中, 通过单次对角化哈密顿矩阵元, 即可获取所有能量和波函数的QED修正. 进一步, 考虑当激光偏振方向与量子化轴平行或垂直的不同情况时, 计算了氦原子413 nm的幻零波长. 与NRQED的结果相比, RCIRP方法给出的QED修正与NRQED计算结果之间的相对差异小于2.5%, 详细的结果对比可参见表6. 这一结果表明, RCIRP方法在确定QED修正方面的正确性和有效性. 此外, 该方法具有极高的推广潜力, 有望被广泛应用于其他类氦体系结构与外场响应性质的QED修正计算中.

      • 3.4.   魔幻波长的计算

    • 魔幻波长指的是激光频率调制到使原子跃迁的上下能态ac Stark频移相等时, 该激光频率所对应的波长. 这一概念的示意图如图4(b)所示. 魔幻波长最初是在中性原子光晶格钟的研究中被提出来的[91,92]. 在理论上, 当高阶Stark频移的影响很小, 以致于可以忽略时, 可以根据上下能态的动力学偶极极化率相等来确定体系的魔幻波长$ \lambda_{\mathrm{m}} $[48,51],

      魔幻波长作为实验设计光晶格的重要参数, 能消除领头项的ac Stark频移, 因此高精度的魔幻波长理论预言在量子态精密调控、少体精密光谱精度的提升, 以及高精度光钟的发展中具有广泛的应用. 例如, 采用魔幻光晶格, 中性原子光钟光频移得到了有效的抑制, 系统的不确定度已全面进入$ 10^{-18} $量级[93–95].

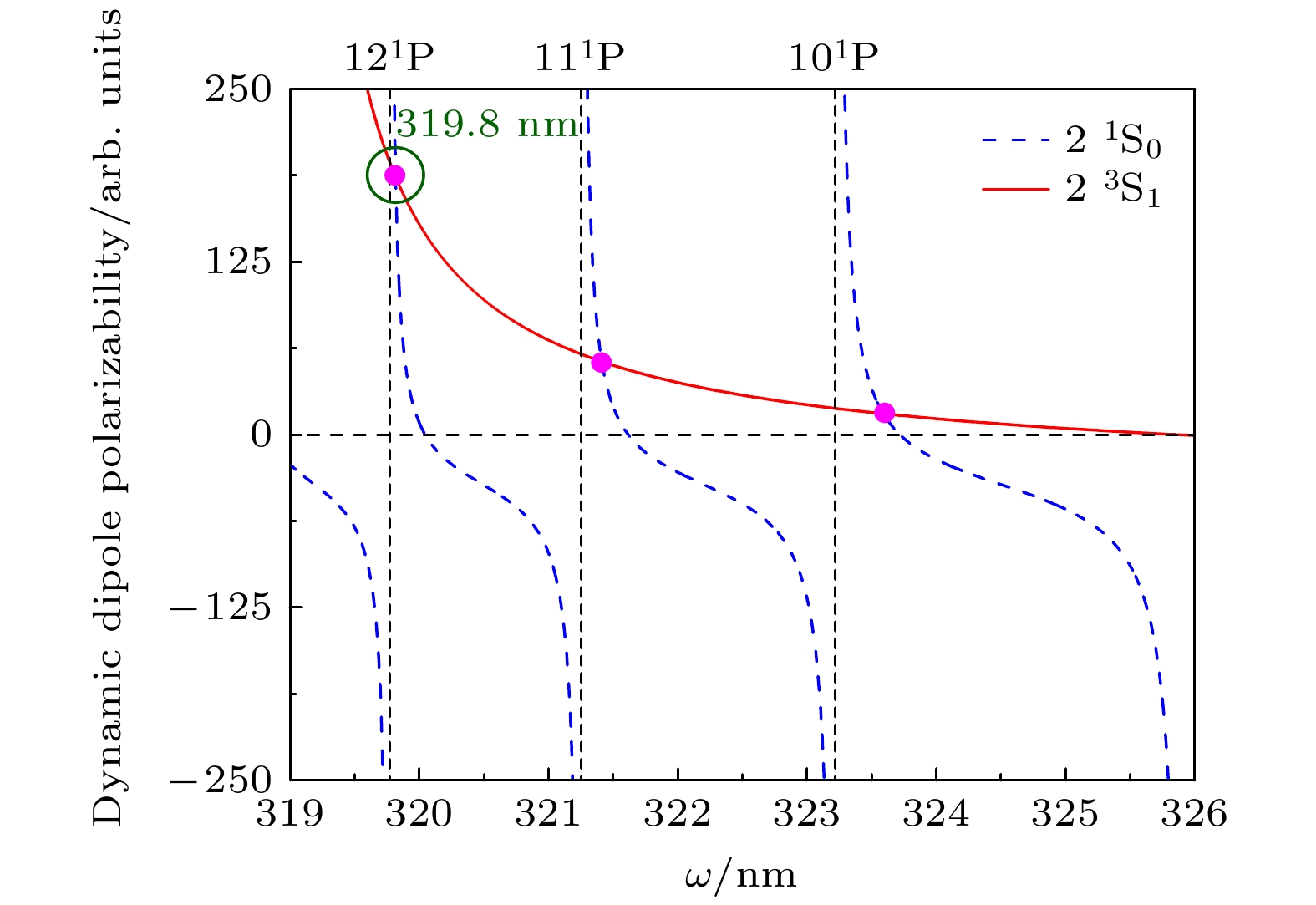
      对于氦原子体系, 类似于氢原子中著名的质子半径之谜, 目前利用氦原子$ 2\, ^3 {\mathrm{S}}\rightarrow 2\, ^1 {\mathrm{S}} $和$ 2\, ^3 {\mathrm{S}}\rightarrow 2\, ^3 {\mathrm{P}} $两条跃迁谱线定出的3He和4He的核电荷半径之间的差异达到了4个标准偏差, 这一显著差异亟需更高精度的实验测量加以解除. 为了提升$ 2\, ^3 {\mathrm{S}}_1\rightarrow 2\, ^1 {\mathrm{S}}_0 $谱线的测量精度, 荷兰阿姆斯特丹自由大学Vassen研究组[96]提出设计319.8 nm的魔幻光阱的方案, 旨在消除体系的主要误差来源中的ac Stark频移. 由于319.8 nm魔幻波长紧邻$ 2\, ^1 {\mathrm{S}}\rightarrow 12\, ^1 {\mathrm{P}} $共振线(见图8), 高精度理论预言和实验测定这一魔幻波长是极具挑战性的难题. 2018年, Wu等[48]发展了考虑有限核质量、QED修正、超精细效应的相对论组态相互作用方法, 成功实现了氦原子$ 2\, ^3 {\mathrm{S}}_1\rightarrow 2\, ^1 {\mathrm{S}}_0 $双禁戒跃迁下系列魔幻波长的高精 度理论计算. 其中4He的魔幻波长理论预言值319.8153(6) nm在2018年被Vassen小组[96]的实验测量所证实, 而3He的魔幻波长理论预言值319.8302(7) nm则在2023年同样得到了该小组的实验证实[97], 见表7. 这些高精度的魔幻波长理论预言为魔幻光偶极阱的实验设计提供了重要的参考依据, 并助力氦原子精密光谱测量的精度达到百亿分之一的水平, 为未来进一步解开氦原子不同同位素的核电荷半径方差之谜奠定了坚实的基础.

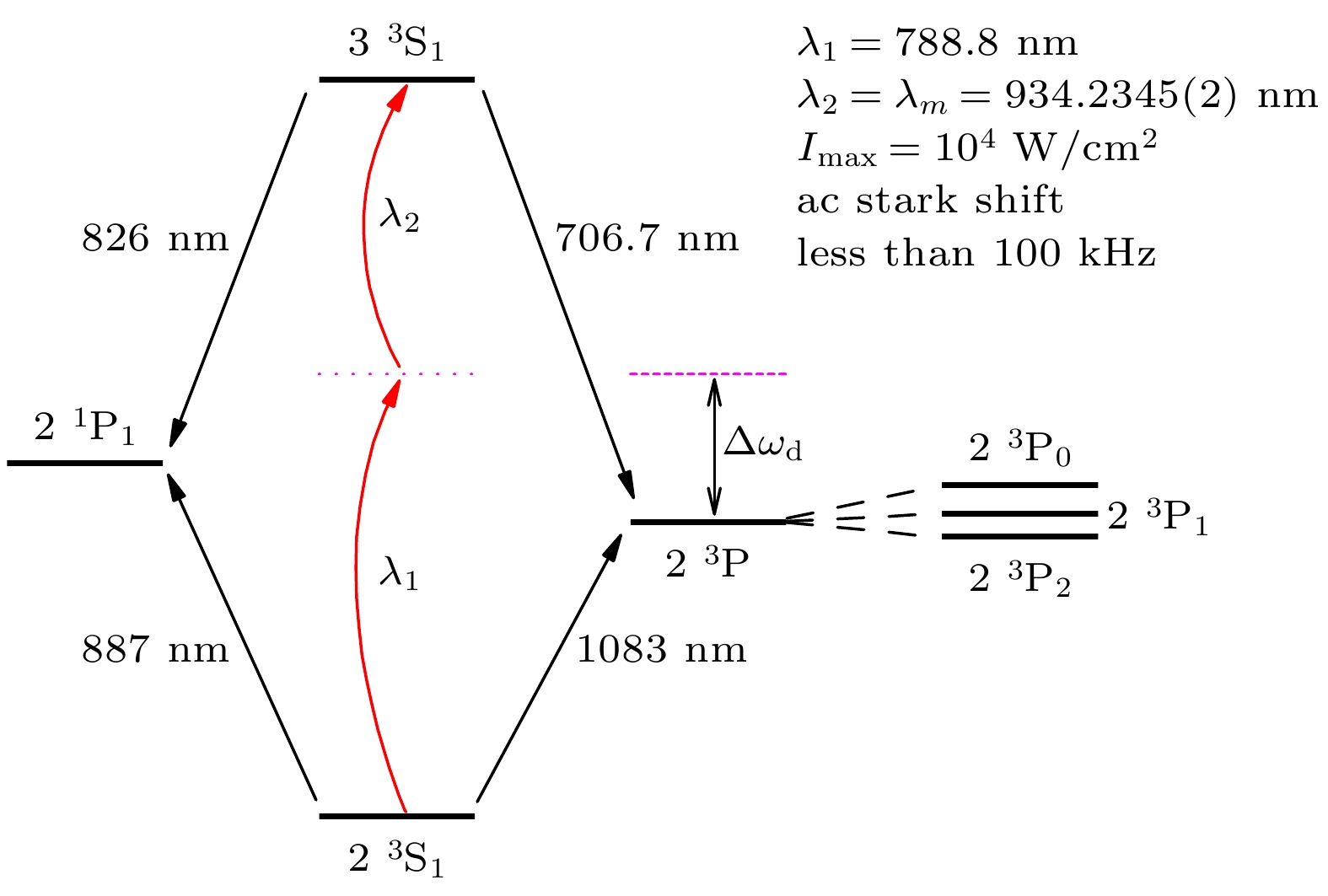
      此外, 基于高精度的RCI方法, Zhang等[45,50,51]还定出了$ 2\, ^3 {\mathrm{S}}\rightarrow2\, ^3{\mathrm{ P}} $, $ 2\, ^3 {\mathrm{S}}\rightarrow 3\, ^3 {\mathrm{P }}$, $ 3\, ^3 {\mathrm{S}}\rightarrow3\, ^3 {\mathrm{P}} $, $ 2\, ^3 {\mathrm{S}}_1\rightarrow 2\, ^1 {\mathrm{P}}_1 $, $ 2\, ^3 {\mathrm{S}}_1\rightarrow 3\, ^3 {\mathrm{S}}_1 $, $ 2\, ^3 {\mathrm{S}}_1\rightarrow 2\, ^1 {\mathrm{S}}_0 $等低能跃迁下的一系列魔幻波长. 特别地, Zhang等[45]详细分析了$ 2\, ^3 {\mathrm{S}}\rightarrow3\, ^3 {\mathrm{P }}$跃迁下的1066 nm魔幻波长的分项贡献, 发现高精度实验测量1066 nm的魔幻波长可用来反推$ 2\, ^3 {\mathrm{S}}\rightarrow 2\, ^3 {\mathrm{P}} $与$ 3\, ^3 {\mathrm{P}}\rightarrow 6\, ^3 {\mathrm{S}} $跃迁矩阵元的比值, 这为高里德堡态跃迁矩阵元的精确确定提供了新途径. 对于$ 2\, ^3 {\mathrm{S}}_1\rightarrow 3\, ^3 {\mathrm{S}}_1 $跃迁, Zhang等[50]提出采用1265 nm魔幻波长设计光偶极阱, 同时利用934 nm魔幻波长作为双色双光子跃迁的一束激发光, 以有效抑制$ 2\, ^3 {\mathrm{S}}_1\rightarrow 3\, ^3 {\mathrm{S}}_1 $精密光谱实验中的ac Stark频移的理论新方案, 见图9. 新方案中的Stark频移相比较于单光子实验中的6.9 MHz, 降低了约1/70[98]. 对于$ 2\, ^3 {\mathrm{S}}_1\rightarrow 2\, ^1 {\mathrm{P}}_1 $禁戒跃迁, Zhang等[51]发现1335.55(2)nm的魔幻波长对有限核质量、相对论修正以及QED效应敏感, 其理论计算与实验测量相结合也有望用于原子结构理论的检验.

    4.   总结与展望

    • 面向少电子原子精密光谱研究领域, 我们致力于提升其结构属性的高精度计算能力. 为此, 自主开发了一系列基于B-样条函数的理论方法, 包括非相对论组态相互作用方法、关联B-样条方法以及相对论组态相互作用方法等. 这些方法已成功应用于氦和类氦体系的结构与外场响应性质研究中, 不仅实现了QED修正领头项中贝特对数项的高精度计算, 还准确预言了氦原子的系列幻零波长和魔幻波长. 特别是氦原子413 nm的幻零波长, 其理论与实验的多次合作为QED理论的检验开辟了新方向; 而氦原子不同同位素中的319.8 nm魔幻波长也已经得到实验的逐一证实, 助力氦原子光谱测量精度达到了百亿分之一.

      B-样条基组的独立性使得大规模的组态相互作用计算成为可能. 在本文涉及的RCI双精度计算中, 最大基组规模达到了15万, 远超传统关联指数基组的计算能力. 相比之下, Hylleraas基组由于存在线性相关性的限制, 难以实现如此大规模的双精度计算. 而B-样条基组由于每个样条函数是分布在有限区间内的, 因此有效地避免了样条基组间的线性相关性问题. 本文介绍的关联B-样条基组方法, 在计算精度和效率方面均取得了显著提升: 在相同样条数目的情况下, 氦原子基态能量的计算精度提高了6个数量级, 同时基组规模减少到原来的一半. 这些改进使我们首次成功实现了氦原子低能态能级的相对论修正和QED修正的精确计算, 为两电子原子精密谱计算开辟了一条全新的路径. 未来, 我们计划将这一方法拓展至氦原子里德堡能级结构的精密计算中, 为里德堡原子的精密光谱测量、量子态操控、量子逻辑门设计以及超冷分子形成等前沿领域的研究提供理论支持. 此外, 经过并行优化的关联B-样条基组方法, 可直接推广至三电子原子和离子的精密谱计算中, 相关工作目前正在积极推进当中.

      本文还概述了利用关联B-样条基组计算氦原子低能态静态极化率(包含相对论和QED修正)的研究, 为氦原子dc Stark效应的精细刻画提供了关键参数. 未来可进一步推广到ac Stark效应的研究, 高精度预言动力学极化率、幻零波长和魔幻波长, 并与RCI计算结果进行交叉验证. 极化率计算的理论基础是二阶微扰论, 本文方法可直接推广到氦原子与类氦轻离子的二阶相对论修正的计算中. 结合已建立的贝特对数计算方法, 进一步发展贝特对数的相对论修正计算, 为两电子原子精密谱的高阶相对论和高阶QED修正计算构建更高效的理论框架.

      少电子原子的精密测量物理不仅是现代物理学的前沿阵地, 也是理论与实验紧密结合的典范. 随着测量精度要求的不断提升, 少电子原子结构的计算精度也面临更高挑战. 当前, 理论与实验之间的偏差逐渐显现, 例如, 氢原子中的质子半径之谜和氦原子同位素核电荷半径方差偏差等问题, 均反映出理论计算与实验测量之间的差距. 这些问题的根源在于当前理论方法在高阶修正方面的不足, 无论是NRQED方法还是基于B-样条的RCI方法, 均面临着高阶QED修正算子推导困难和高阶修正项数值计算的挑战. 因此, 发展束缚态高阶理论, 深入探究QED理论在低能束缚态下的非相对论极限, 成为解决这些问题的关键.

      随着深度学习技术在凝聚态物理、核物理、化学物理及生物物理等领域的广泛应用, 其在解决复杂物理问题中的潜力日益凸显. 针对少电子原子结构计算中高阶算符推导的复杂性以及当前积分算法面临的发散挑战, 未来可探索利用深度学习技术推演高阶QED算符, 并设计新型收敛算法, 以实现少电子原子结构微小效应的高精度预测. 这一方向有望成为智能时代物理学研究的重要发展趋势.

      为满足少电子原子精密测量物理领域的迫切需求, 未来我们将结合现有理论方法, 发展基于人工智能的少电子原子结构精确计算新范式, 重点解决QED高阶修正缺失的难题. 这一研究不仅为建立自主可控的高精度原子结构与外场性质理论数据库奠定了理论基础, 还将推动少电子原子在精密测量微弱场(如电磁场、重力场)及微弱物理量(如温度、压力)中的应用, 同时为暗物质探测等前沿领域提供全新的理论研究框架.

    参考文献 (98)

目录

/

返回文章
返回