首页
登录
注册
-
全息显示技术因不需要佩戴任何辅助装置, 可以提供人眼所需的全部信息, 是一种极具潜力的三维显示技术[1–4]. 随着计算机技术和计算全息显示技术的蓬勃发展[5], 计算机生成全息图(computer-generated hologram, CGH)因操作灵活和可以呈现虚拟的三维物体等优点而引起了学者的广泛关 注[6–10]. 空间光调制器(spatial light modulator, SLM)目前被广泛应用于全息图的显示, 通过将CGH加载到SLM上, 从而实现光场调制[11]. 但现有的SLM仅能实现对振幅或相位的单独调制, 为使全息图数据与SLM相匹配, 需要将其编码为振幅型或相位型全息图. 而相比于振幅型全息图, 纯相位全息图( phase-only hologram, POH)具有更高的衍射效率和无共轭像等优点[12], 因此纯相位全息图的生成算法是全息显示的主要研究方向.
传统生成纯相位全息图的方法有迭代和非迭代算法. 迭代算法有Gerchberg-Saxton (GS)算法[13]及其优化算法等, 此类算法虽然可以生成高质量的全息图, 但需多轮迭代, 耗时较长. 非迭代算法常用的有误差扩散算法[14]和双相位法[15]等, 此类算法无需迭代, 可以快速生成全息图, 但重建质量不高. 如何快速实现高质量POH成了研究的热点.
近年来, 由于深度学习神经网络具有强大的学习能力和表达能力, 能够处理大规模的数据, 可以直接从数据中学习特征表示, 为全息显示提供了新思路[16–18]. 卷积神经网络(convolutional neural network, CNN)具有强大的特征提取能力和泛化能力[19], 可以通过卷积层处理输入的图像数据, 提取复杂图像的特征信息, 被广泛应用于全息显示领域[20,21]. Horisaki等[22]用10000对均匀随机相位图及其对应的全息图作为训练数据集, 但仅能实现简单的阿拉伯数字显示. Lee等[23]用由大量基本元素(如点和圆)组成的图像作为数据集进行训练, 但经过训练的网络仅能实现小尺寸复杂全息图的生成, 且存在大量的散斑噪声. Chang等[24]用5000张图像及其对应的全息图作为训练数据集, 训练后的神经网络可以生成2K(分辨率为1920×1072)的全息图, 但由于未进行深度恢复, 丢失部分深度信息, 导致重建图像存在一定条纹伪影.
上述方法都是采用有监督的学习方式, 在训练过程中需要标记大量的目标图像和相应的全息图, 建立目标图像与其对应全息图的损失函数, 从而完成对神经网络的训练, 进而生成全息图, 重建图的质量受数据集质量的限制.
无监督学习通过在神经网络中引入物理衍射传播模型, 无需标记数据集, 可以直接生成全息图, 大大减少了时间成本, 避免了数据集质量的影响. Wu等[25]提出一种基于自编码器的卷积神经网络Holo-encoder, 将菲涅耳衍射模型引入网络中, 可以在0.15 s内生成全息图, 但由于网络单一且结构简单, 导致重建图存在大量的噪声, 重建图的峰值信噪比仅能达到23.2 dB; Shui等[26]提出一种基于角谱衍射模型的神经网络self-holo, 将神经网络分为目标生成器和相位编码器, 分别处理不同的任务, 可以在0.017 s生成纯相位全息图, 有效地减少了计算时间, 但网络的泛化能力一般, 重建图的峰值信噪比仅能达到25.08 dB; Peng等[27]提出一种相机校准波传播模型HoloNet, 模型的目标相位发生器和相位编码器分别负责不同的任务, 进一步提升了重建图像的质量, 重建图像的平均峰值信噪比能达到30 dB, 但由于体系结构复杂, 导致计算时间增加; Zhong等[28]提出一种基于角谱衍射模型的双复值卷积神经网络(complex-valued convolutional neural network, CCNN), 第一个CCNN用于处理目标振幅叠加初始相位为0的复振幅, 第二个用于处理SLM面上的复振幅信息, 该算法可以在0.015 s生成峰值信噪比大于30 dB的全息图. 由于复值网络仅需处理复振幅信息, 而非分别处理振幅和相位, 对细节的特征提取欠佳, 导致重建图存在一定的伪影.
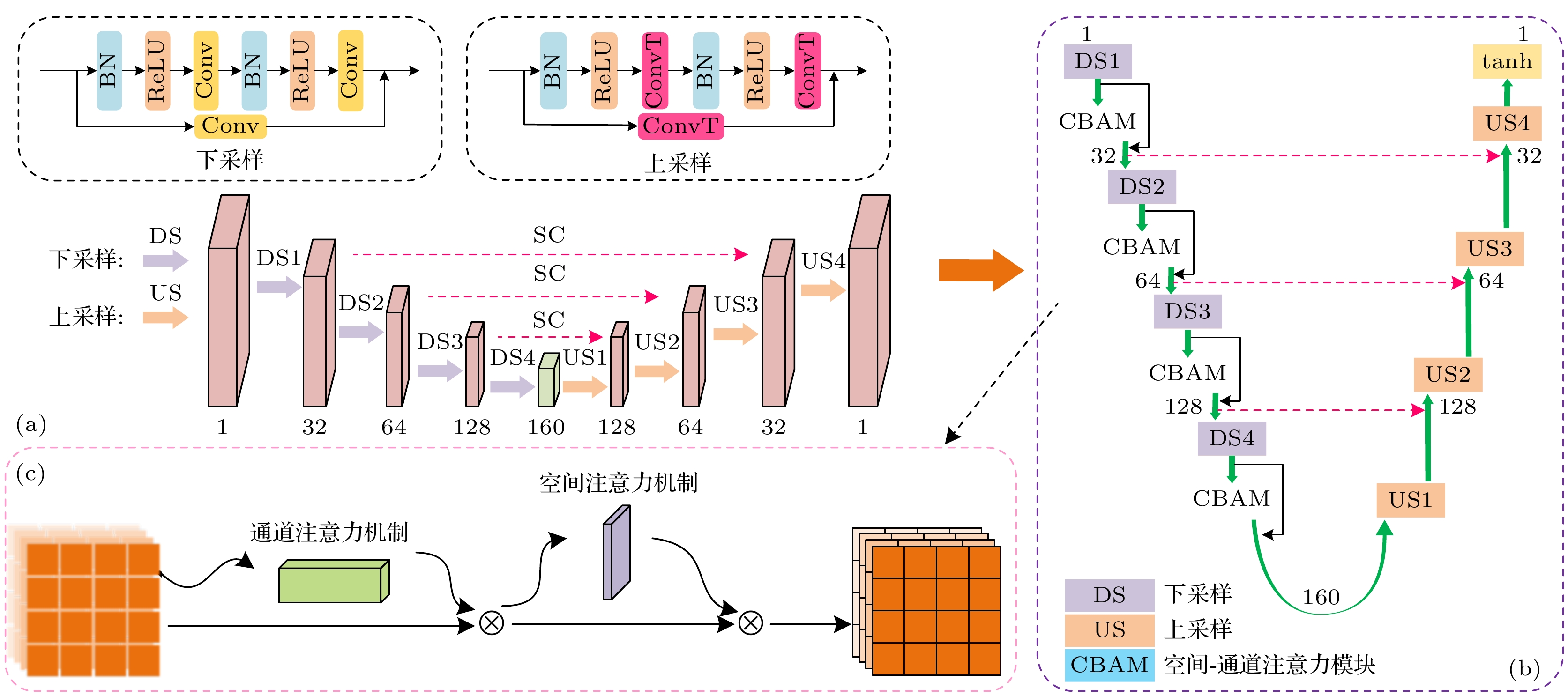
为了实现快速高质量全息图的生成, 我们提出了一种注意力卷积神经网络算法RTC-Holo. 整个网络分成相位预测网络(PP-CNN)和全息编码网络(HE-CCNN)两个模块, PP-CNN进行相位预测, HE-CCNN对SLM面的复振幅进行预测, 预测后得到的复振幅的相位用于全息编码和数值重建. 在相位预测网络PP-CNN的下采样引入空间-通道注意力机制模块(convolutional block attention module, CBAM), 在不增加计算复杂度的同时, 增强下采样的特征提取能力, 进而提升整个网络架构生成CGH的质量. 将ASM衍射传播模型嵌入到整个网络中, 避免大规模标记数据集, 以无监督学习的方式进行网络训练. 采用均方误差(mean-square error, MSE)作为损失函数, 使用Adam优化器对RTC-Holo进行更新.
-
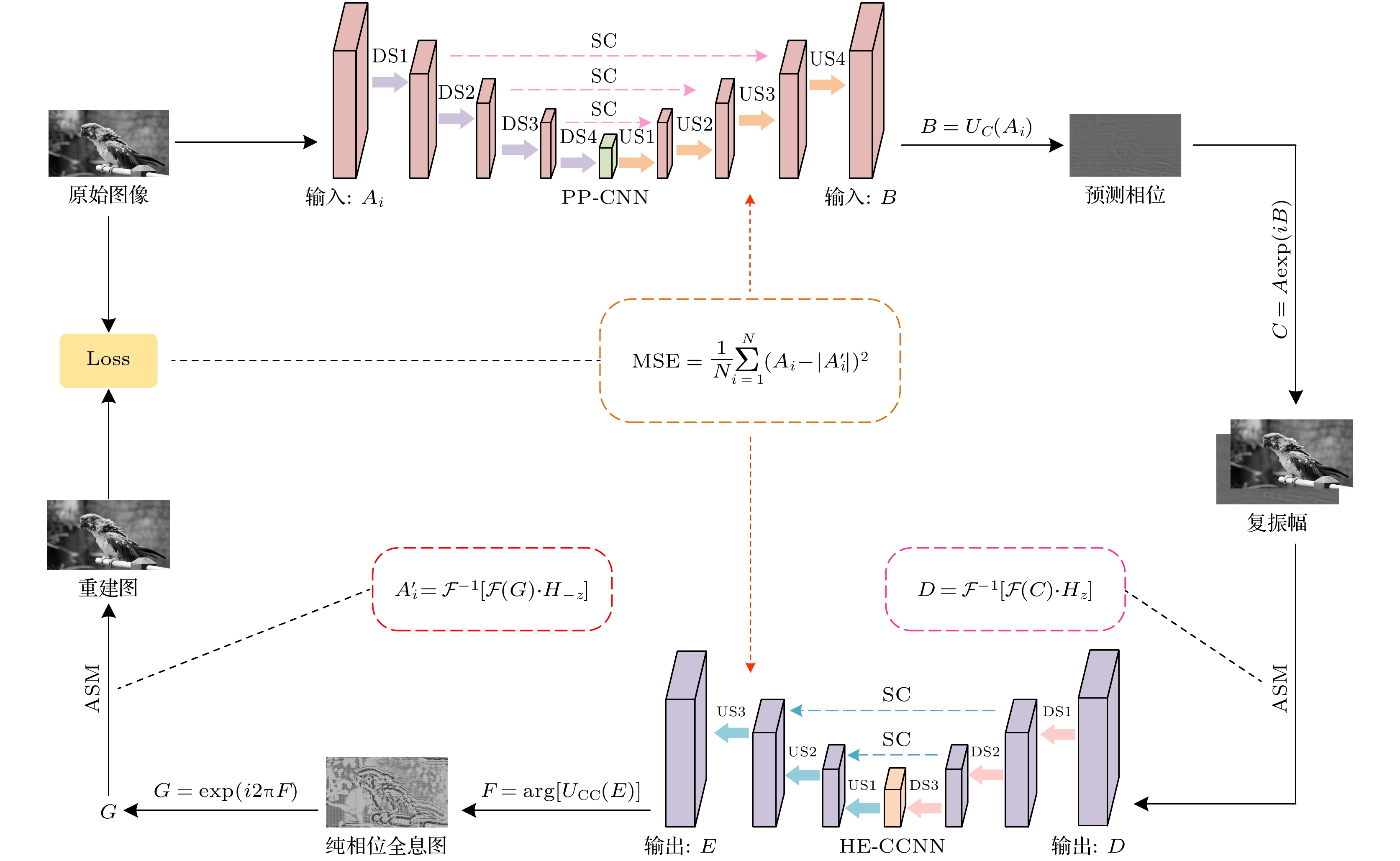
设计的神经网络架构如图1所示. 整个网络架构由一个卷积神经网络(CNN)、一个复值卷积神经网络(CCNN)和角谱(ASM)衍射传播模型组成.
两个子网络均是基于不同卷积层的轻量级网络. 相位预测网络PP-CNN通过输入的目标振幅信息预测出目标平面上的相位分布. 然后, 预测相位与目标振幅叠加得到复振幅, 通过ASM衍射传播到SLM平面. 最后, 全息编码网络HE-CCNN根据衍射信息编码出相应的纯相位全息图.
相位预测网络需要依据目标振幅预测出目标平面上的相位分布, 减轻全息编码网络的负担. 因此我们设计了轻量化CNN网络用于实现相位预测, PP-CNN如图2(a)所示. 并将空间-通道注意力机制模块(CBAM)嵌入了CNN网络架构的下采样模块, PP-CNN网络结构细节和CBAM模块结构分别如图2(b)和图2(c)所示, 在不增加计算复杂度的同时, 增强网络模型对细节的捕捉能力和提高图像特征的表达能力.
PP-CNN由4个下采样块(DS)和对应数量的上采样块(US)组成, 每个采样阶段均由相应的采样块组成. 在下采样阶段, 采用卷积层(Conv)进行下采样的特征提取, 并在下采样之间嵌入空间-通道注意力机制(CBAM)用于自适应地学习 输入特征图信息, 提高特征表达能力; 采用转置卷积层(ConvT)进行上采样, 允许上采样函数与网络的其余部分共同学习. 使用跳跃连接(SC)将学习到的信息传递到上采样的输出.
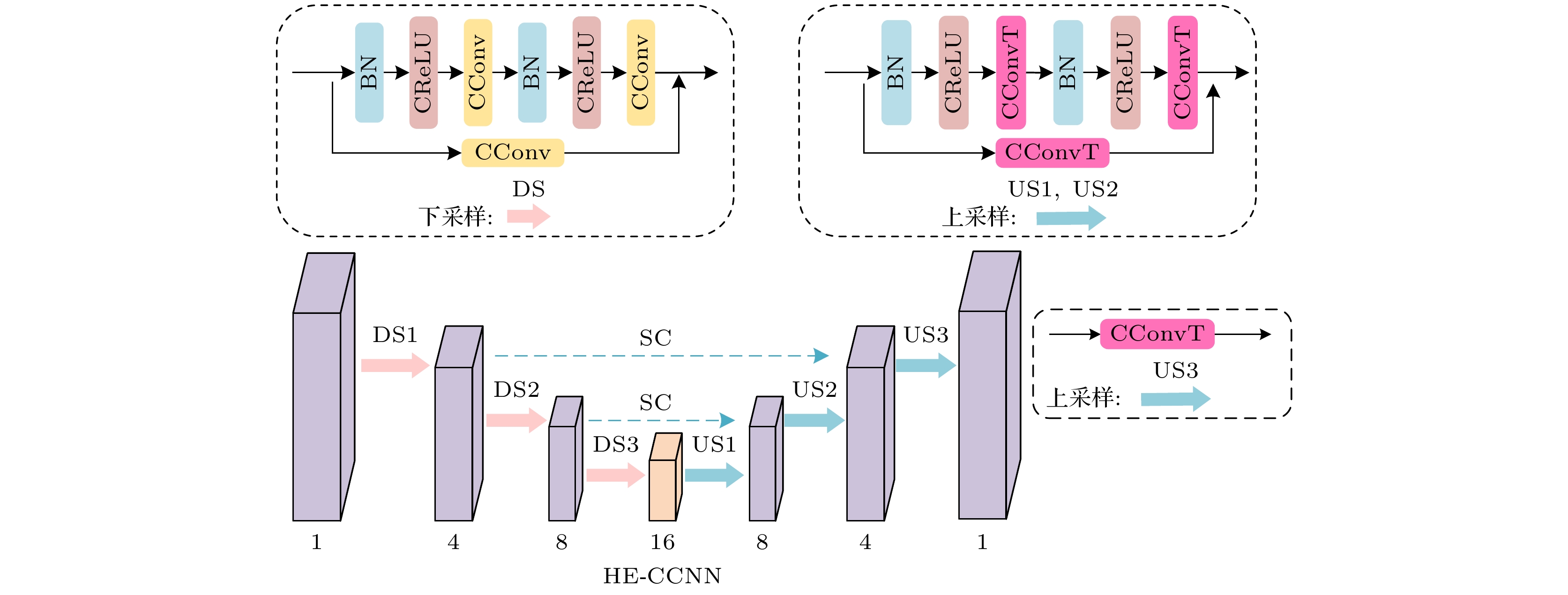
全息编码网络需要对经过ASM衍射传播到SLM平面的信息进行编码, 得到相应的纯相位全息图, 所以我们设计了结构简单、处理复值数据能力高效的CCNN网络, 其网络结构如图3所示.
HE-CCNN由复值卷积层(C-Conv)、复值ReLU层(C-ReLU)、批归一化层(BN)和复值转置卷积层(C-ConvT)组成. CCNN网络包含3个下采样块(DS)、3个上采样块(US)和跳跃连接(SC). DS块由C-Conv, C-ReLU和BN组成. US1块和US2块由BN、C-CReLU和C-ConvT组成. US3块由C-ConvT组成. SC有助于反向传播.
采用ASM传播模型用于衍射传播, 以无监督学习的方式进行训练, 避免了在训练过程中需要标记大规模的目标图像及对应的全息图, 可提高大规模数据的处理能力. 角谱衍射的反向传播仅在网络训练阶段进行, 通过对重建图和目标图像进行比较, 计算损失函数, 从而更新网络参数. 网络训练完成后, 在预测阶段, 仅在SLM平面进行了一次正向的角谱衍射传播, 这是为了将复振幅信息传播到SLM平面, 进而实现自主地预测纯相位全息图.
-
如图1所示, 假设目标振幅为
$ A $ , 利用CNN进行相位预测, 得到预测相位$ B $ , 然后将得到的相位与目标振幅$ A $ 叠加得到复振幅$ C $ .式中,
${U_{\text{C}}}( \cdot )$ 表示PP-CNN网络.复振幅
$ C $ 经ASM衍射传播后得到输入CCNN的复振幅$ D $ .式中,
$ \mathcal{F} $ 和${\mathcal{F}^{ - 1}}$ 表示二维快速傅里叶变换和逆变换;$ H_{z}\left(f_{x}, f_{y}\right) $ 表示ASM的正向传递函数;$ f_{x} $ 和$ f_{y} $ 是空间频率坐标;$ \lambda $ 是波长,$ z $ 是衍射距离.输入复振幅
$ D $ 经过CCNN后, 在SLM平面上输出复振幅$ E $ , 将输出的复振幅编码为纯相位全息图$ F $ :式中,
${U_{{\text{CC}}}}\left( \cdot \right)$ 表示HE-CCNN.纯相位全息图
$ F $ 经复振幅调制$ G $ 后, 通过ASM衍射传播得到纯相位全息图的模拟重建$ A^{\prime} $ .式中,
$ H_{z}\left(f_{x}, f_{y}\right) $ 表示ASM的逆向传递函数.采用均方误差(MSE)作为损失函数优化网络. 使用Adam优化器更新网络参数,
式中,
$ N $ 表示总像素数. -
所提的算法在Intel Xeon Gold 5220 R CPU (2.20 GHz), 32 GB RAM和NVIDIA Quadro RTX 8000 GPU (48 GB内存)进行数值仿真. 模型构建使用PyTorch 1.11.0和Python 3.9. 使用由800张2K(即分辨率为1920×1072)图像组成的DIV2K数据集训练神经网络30个循环. 在每个训练循环后, 使用由100个样本组成的DIV2K验证数据集进行评估模拟重建. SLM的像素尺寸为6.4 μm, 波长为532 nm, 衍射距离为150 mm, 学习率设置为0.001.
为了证明RTC-Holo算法的有效性与科学性, 将该方法与HoloNet, Holo-encoder和CCNNCGH在同一环境下进行了比较. 在1920×1072分辨率下, Holo-encoder, HoloNet, CCNNCGH和RTC-Holo在相同的参数条件下进行训练. 使用DIV2K的100张图片作为测试集, 采用峰值信噪比(PSNR)和结构相似性指数(structural similarity index, SSIM)作为衡量成像标准.
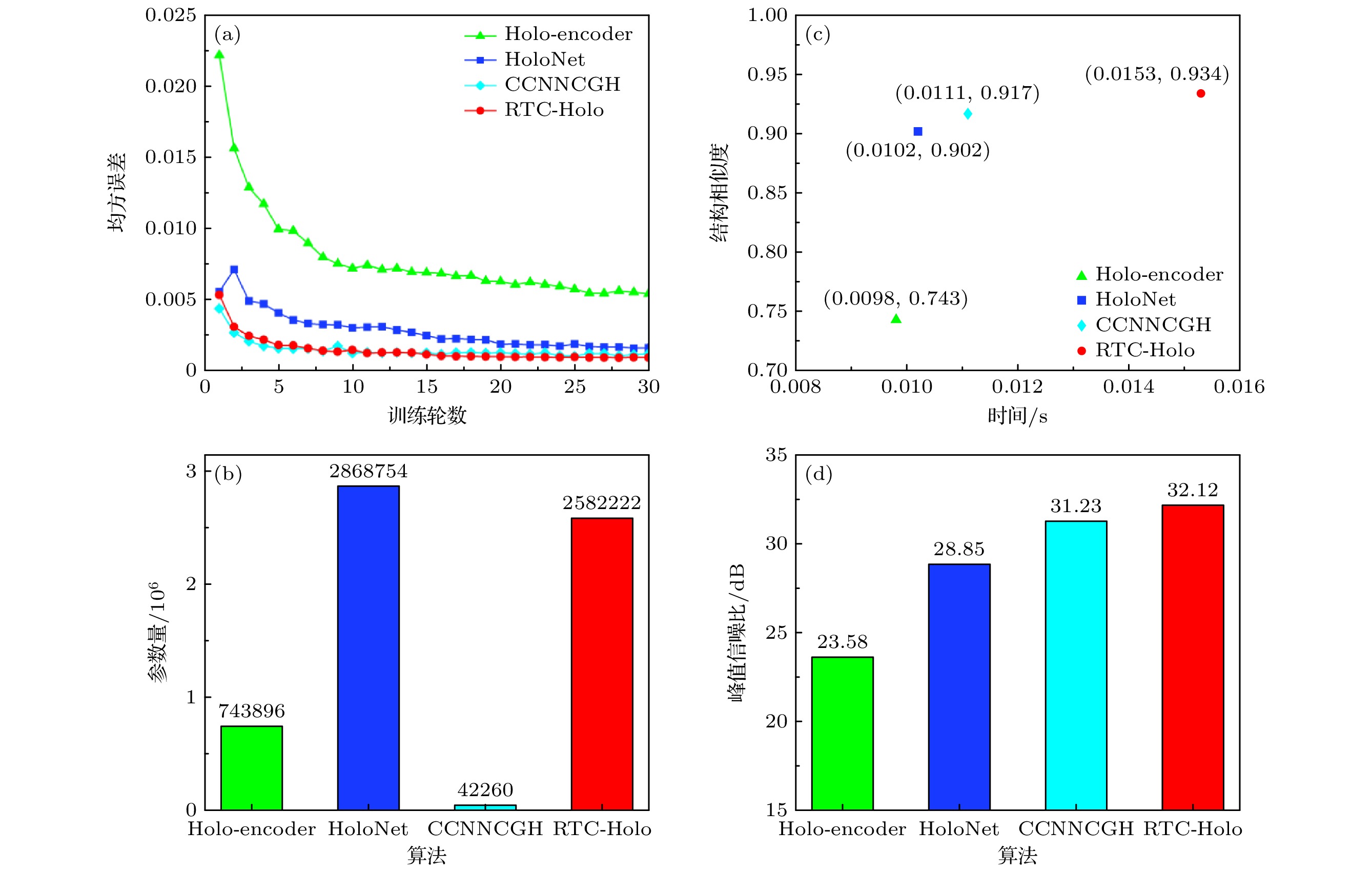
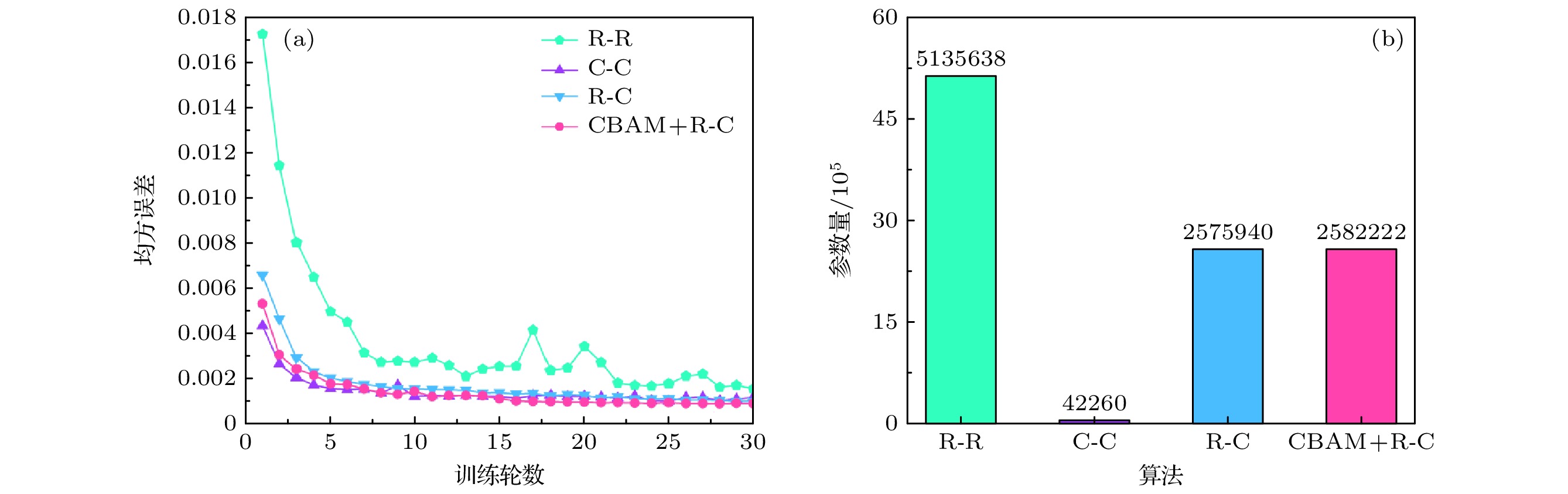
以上算法的数值仿真对比如图4所示. 图4(a)给出各算法使用验证数据集进行30轮网络训练的损失函数收敛情况, 可以看出RTC-Holo算法在同一损失函数下, 网络训练整体收敛最快. 图4(b)给出各算法参数量对比图, CCNNCGH所需的参数量最少, HoloNet所需的参数量最多, RTC-Holo所需的参数量比Holo-encoder要多, 但比HoloNet要少.
图4(c),(d)给出上述算法的PSNR、SSIM和Time的对比图, 其中PSNR, SSIM, Time均为100张图片测试集的平均值. 所提RTC-Holo算法的计算时间虽然比Holo-encoder慢了约0.005 s, 但具有更高的PSNR和SSIM, 分别提高了8.54 dB和0.191. RTC-Holo算法的计算时间比HoloNet慢了0.005 s, 但使用RTC-Holo成像的平均PSNR和SSIM分别比HoloNet提高了3.27 dB和0.032. RTC-Holo算法的计算时间比CCNNCGH慢了0.004 s, 但使用RTC-Holo成像的平均PSNR和SSIM分别比CCNNCGH提高了0.89 dB和0.017. 由此可见, 在同一数量级的运算时间上, RTC-Holo可以生成更高质量的全息图.
以上数值模拟结果说明RTC-Holo可以在保证速度的同时实现更佳的成像质量. 所提的RTC-Holo可以在0.015 s内生成高质量的2K全息图, 平均PSNR和SSIM分别为32.12 dB和0.934.
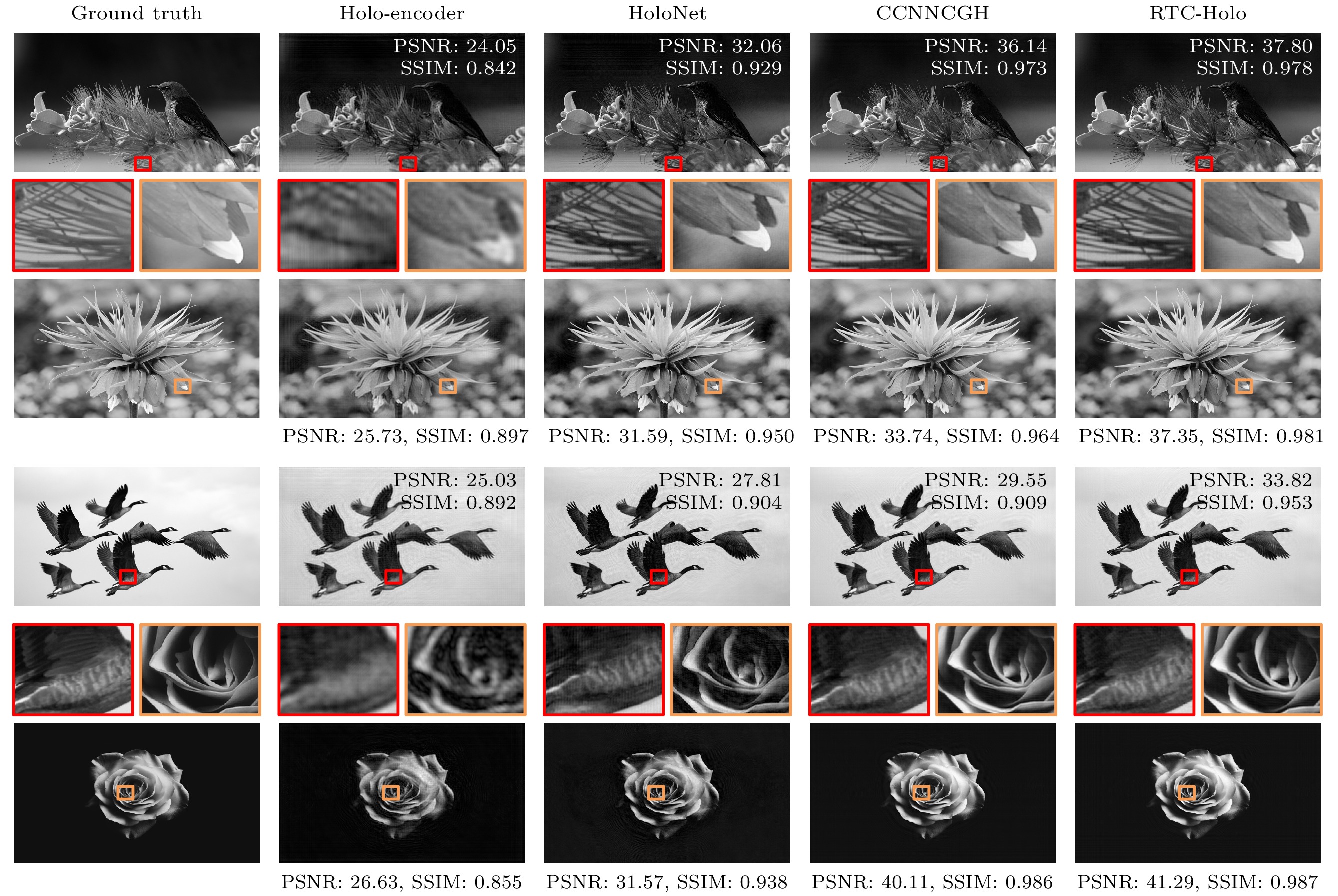
图5为1920×1072分辨率下的仿真重建图. 在相同环境下, 将我们的算法与Holo-encoder, HoloNet和CCNNCGH进行对比, 从验证集的100张图片中选取四幅图像进行测试. Holo-encoder仿真重建图像的质量偏低, 细节放大的轮廓部分模糊. HoloNet仿真重建图像的质量优于Holo-encoder, 细节放大的轮廓较清晰, 但纹理细节部分模糊. CCNNCGH仿真重建图像的质量要优于Holo-encoder和HoloNet, 但RTC-Holo仿真重建图像的质量更高, 纹理细节最清晰, 呈现出更好的显示效果.
-
为了证明实值与复值CNN结合的网络性能优于传统的双实值CNN和双复值CCNN, 对双实值R-R、双复值C-C、实-复值R-C的网络结构进行了消融实验, 而为了证明加入空间-通道注意力机制模块(CBAM)的有效性, 将加入CBAM的R-C网络与上述三个网络也进行了对比. 在相同环境下, 使用相同参数进行了上述四个网络训练, 其训练损失和参数量如图6(a)和图6(b)所示.
使用DIV2K测试数据集中的100张图片进行测试, 计算100张测试图片的平均PSNR和SSIM, 消融实验结果如表1所列. 同时从测试集中选取两张图片进行仿真重建对比, 如图7所示.
图7中R-R为双实值CNN, 第一个实值网络通过输入的目标振幅预测相位, 预测的相位与目标振幅组成复振幅经过ASM衍射传播到SLM面后, 为了避免复数作为实值CNN的输入, 把SLM面的复振幅分解为振幅和相位, 它们经cat在通道方向上进行拼接, 第二个实值网络把该拼接张量转换为相位表示.
双复值C-C网络模型使用了CCNNCGH[28]. 根据表1可以看出, 实-复值网络R-C测试结果的平均PSNR和SSIM比CCNNCGH高了0.36 dB和0.008, 比双实值网络高3.7 dB和0.034. 同时通过图7可以看出, 实-复值网络R-C仿真重建图的质量更佳, 细节更为清晰, 证明了实-复值网络结合的性能更优.
CBAM+R-C为在实值CNN中加入空间-通道注意力机制的实-复值网络结构, 即本文所提的RTC-Holo算法. 从表1信息可以看出: RTC-Holo算法的平均PSNR和SSIM比CCNNCGH高了0.89 dB和0.017, 可以看出加入CBAM注意力机制模块后, 网络性能又得到了进一步的提升. 通过图7仿真重建图的细节对比, 进一步证实了加入CBAM注意力机制模块的有效性.
-
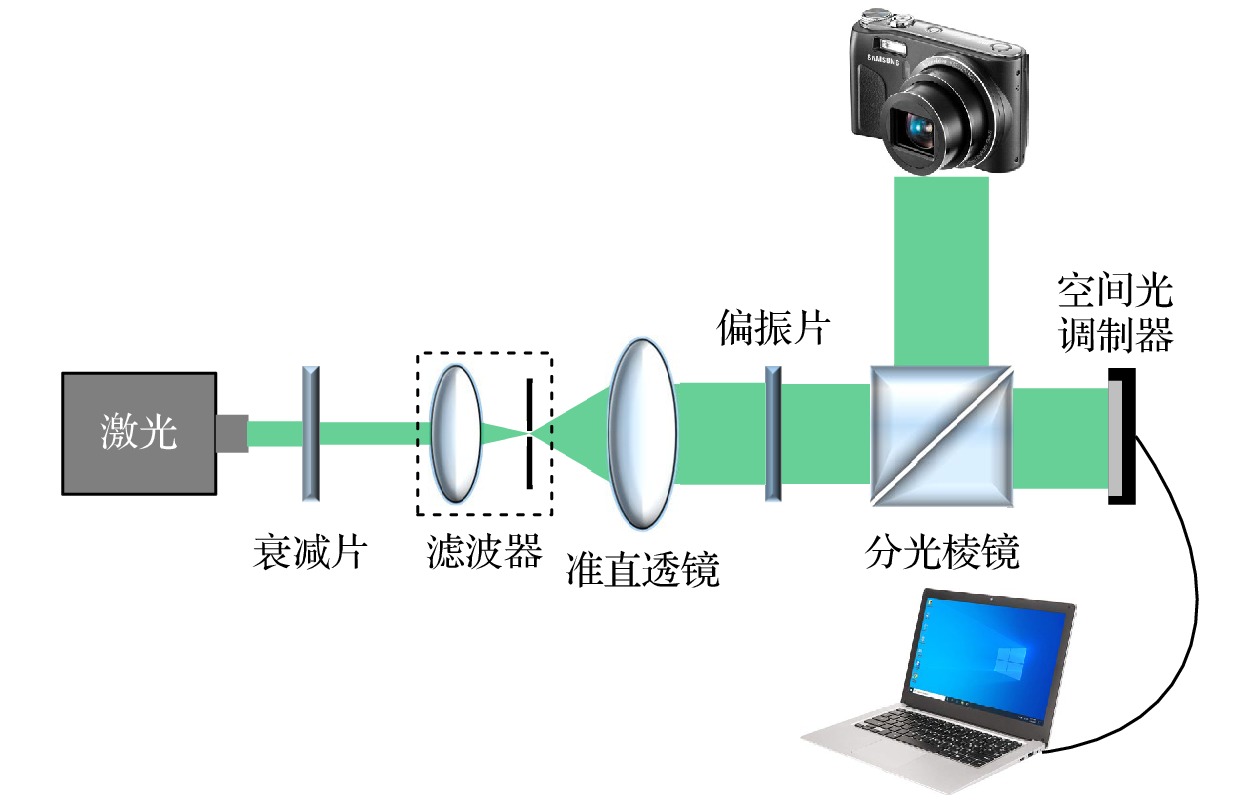
为了进一步验证所提算法的有效性, 我们搭建了光学显示系统, 如图8所示. 波长为532 nm的绿色激光经过衰减片衰减后, 通过滤波器和准直透镜进行滤波和准直, 经过偏振片控制光的偏振状态, 再使用分光棱镜BS进行光路调整, 照射到整个SLM平面, 全息图通过电脑上传到SLM中, SLM反射入射光, 使用相机捕获全息重建图. SLM分辨率为1920×1080, 像素尺寸为6.4 μm.
光学显示系统使用由Holo-encoder, HoloNet, CCNNCGH和RTC-Holo在同一环境下生成的纯相位全息图, 各算法的光学重建图如图9所示. Holo-encoder在光学重建中存在严重的噪声, 导致图像不清晰, 5倍细节放大图的轮廓十分模糊. HoloNet的重建图像质量优于Holo-encoder, 但仍存在着较多的散斑噪声, 5倍细节放大图的轮廓可以看见, 但纹理细节模糊. 与HoloNet和Holo-encoder相比, CCNNCGH重建图像的噪声较少, 在细节放大图里轮廓较清晰, 但纹理细节仍略有模糊. RTC-Holo在细节显示方面表现得更好, 重建图像的纹理和轮廓更为清晰, 质量更高. 光学重建实验进一步证明所提算法的科学性与有效性.
-
本文提出了一种注意力卷积神经网络算法RTC-Holo, 可以快速实现高质量全息图的生成. 整个网络由一个下采样嵌入CBAM模块的CNN和一个CCNN构成, 两个子网络分别负责相位预测和全息编码. RTC-Holo在保持计算速度的同时, 生成更高质量的全息图. 数值仿真与光学重建表明, 我们的方法可以快速生成高保真的2K全息图. 我们的方法为深度学习应用于实时全息显示领域提供了强有力的帮助.
基于注意力卷积神经网络的高质量全息图快速生成算法
Fast generation algorithm of high-quality holograms based on attention convolutional neural network
-
摘要: 针对目前深度学习算法难以实现快速高质量全息图的生成, 提出了一种注意力卷积神经网络算法(RTC-Holo), 在快速生成全息图的同时, 提高了全息图的生成质量. 整个网络由实值和复值卷积神经网络组成, 实值网络进行相位预测, 复值网络对空间光调制器(spatial light modulator, SLM)面的复振幅进行预测, 预测后得到的复振幅的相位用于全息编码和数值重建. 在相位预测模块的下采样阶段引入注意力机制, 增强相位预测模块下采样阶段的特征提取能力, 进而提升整个网络生成纯相位全息图的质量. 将精准的角谱衍射模型(angular spectrum method, ASM)嵌入到整个网络中, 以无监督的学习方式进行网络训练. 本文提出的算法能够在0.015 s内生成平均峰值信噪比(peak signal-to-noise ratio, PSNR)高达32.12 dB的2K (即分辨率为1920×1072)全息图. 数值仿真和光学实验验证了该方法的可行性和有效性.Abstract: In recent years, with the significant improvement of computer performance, deep learning technology has shown an explosive development trend and has been widely used in various fields. In this context, the computer-generated hologram (CGH) generation algorithm based on deep learning provides a new method for displaying the real-time high-quality holograms. The convolutional neural network is a most typical network structure in deep learning algorithms, which can automatically extract key local features from an image and construct more complex global features through operations such as convolution, pooling and full connectivity. Convolutional neural networks have been widely used in the field of holographic displays due to their powerful feature extraction and generalization abilities. Compared with the traditional iterative algorithm, the CGH algorithm based on deep learning has a significantly improved computing speed, but its image quality still needs further improving. In this paper, an attention convolutional neural network based on the angular spectrum diffraction model is proposed to improve the quality as well as the speed of generating holograms. The whole network consists of real-valued and complex-valued convolutional neural networks: the real-valued network is used for phase prediction, while the complex-valued network is used to predict the complex amplitude of the SLM surface, and the phase of the complex amplitude obtained after prediction is used for holographic coding and numerical reconstruction. An attention mechanism is embedded in the down sampling stage of the phase prediction network to improve the feature extraction capability of the whole algorithm, thus improving the quality of the generated phase-only holograms. An accurate diffraction model of the angular spectrum method is embedded in the whole network to avoid labeling the large-scale datasets, and unsupervised learning is used to train the network. The proposed algorithm can generate high-quality 2K (resolution ratio of 11920×1072) holograms within 0.015 s. The average peak signal-to-noise ratio of the reconstruction images reaches up to 32.12 dB and the average structural similarity index measure of the generated holograms can achieve a value as high as 0.934. Numerical simulations and optical experiments verify the feasibility and effectiveness of the proposed attentional convolutional neural network algorithm based on the diffraction model of angular spectrum method, which provides a powerful help for applying the deep learning theory and algorithm to the field of real-time holographic display.
-
Key words:
- holographic display /
- computer-generated holograms /
- deep learning /
- phase-only hologram .
-
-
图 1 RTC-Holo算法原理示意图
Figure 1. Schematic diagram of the principle of RTC-Holo algorithm.
图 2 PP-CNN网络结构 (a) PP-CNN; (b) PP-CNN网络结构细节; (c) CBAM模块结构
Figure 2. PP-CNN network structure: (a) PP-CNN; (b) structure details of PP-CNN; (c) structure of CBAM.
图 4 算法数值仿真对比 (a)算法30轮训练的损失函数对比折线图; (b)算法参数量对比柱状图; (c)算法SSIM-Time对比散点图; (d)算法PSNR对比柱状图
Figure 4. Algorithm numerical simulation comparison: (a) Line graph of loss function comparison for 30 training rounds of the algorithm ; (b) histogram of algorithm parameter count comparison; (c) scatter plot of algorithm SSIM-Time comparison; (d) histogram of algorithm PSNR comparison.
图 6 数值仿真对比 (a) 验证数据集30轮训练算法损失函数对比折线图; (b)算法参数对比柱状图
Figure 6. Numerical simulation comparison: (a) Line graph of algorithm loss function comparison for 30 rounds of training on the validation dataset; (b) histogram of algorithm parameter comparison.
图 9 光学重建图及细节放大图对比
Figure 9. Comparison of optical reconstruction and detailed magnification.
表 1 网络结构数值仿真对比
Table 1. Comparison of numerical simulation of network structures.
网络结构 R-R C-C R-C CBAM+R-C PSNR/dB 27.89 31.23 31.59 32.12 SSIM 0.891 0.917 0.925 0.934 
下载: 导出CSV
-
[1] Huang Q, Hou Y H, Lin F C, Li Z S, He M Y, Wang D, Wang Q H 2024 Opt. Lasers Eng. 176 108104 doi: 10.1016/j.optlaseng.2024.108104 [2] Yao Y W, Zhang Y P, Fu Q Y, Duan J L, Zhang B, Cao L C, Poon T C 2024 Opt. Lett. 49 1481 doi: 10.1364/OL.509961 [3] Chen C Y, Cheng C W, Chou T A, Chuang C H 2024 Opt. Commun. 550 130024 doi: 10.1016/j.optcom.2023.130024 [4] Huang X M, Zhou Y L, Liang H W, Zhou J Y 2024 Opt. Lasers Eng. 176 108115 doi: 10.1016/j.optlaseng.2024.108115 [5] Shigematsu O, Naruse M, Horisaki R 2024 Opt. Lett. 49 1876 doi: 10.1364/OL.516005 [6] Gu T, Han C, Qin H F, Sun K S 2024 Opt. Express 32 44358 doi: 10.1364/OE.541572 [7] Wang D, Li Z S, Zheng Y, Zhao Y R, Liu C, Xu J B, Zheng Y W, Huang Q, Chang C L, Zhang D W, Zhuang S L, Wang Q H 2024 Light: Sci. Appl. 13 62 doi: 10.1038/s41377-024-01410-8 [8] Wang Y Q, Zhang Z L, Zhao S Y, He W, Li X T, Wang X, Jie Y C, Zhao C M 2024 Opt. Laser Technol. 171 110372 doi: 10.1016/j.optlastec.2023.110372 [9] Yao Y W, Zhang Y P, Poon T C 2024 Opt. Lasers Eng. 175 108027 doi: 10.1016/j.optlaseng.2024.108027 [10] Madali N, Gilles A, Gioia P, MORIN L 2024 Opt. Express 32 2473 doi: 10.1364/OE.501085 [11] Tsai C M, Lu C N, Yu Y H, Han P, Fang Y C 2024 Opt. Lasers Eng. 174 107982. doi: 10.1016/j.optlaseng.2023.107982 [12] Zhao Y, Cao L C, Zhang H, Kong D Z, Jin G F 2015 Opt. Express 23 25440 doi: 10.1364/OE.23.025440 [13] Gerhberg R W, Saxton W O 1972 Optik 35 237 [14] Liu K X, He Z H, Cao L C 2021 Chin. Opt. Lett. 19 050501 doi: 10.3788/COL202119.050501 [15] Sui X M, He Z H, Jin G F, Cao L C 2022 Opt. Express 30 30552 doi: 10.1364/OE.463462 [16] Kiriy S A, Rymov D A, Svistunov A S, Shifrina A V, Starikov R S, Cheremkhin P A 2024 Laser Phys. Lett. 21 045201 doi: 10.1088/1612-202X/ad26eb [17] Li X Y, Han C, Zhang C 2024 Opt. Commun. 557 130353 doi: 10.1016/j.optcom.2024.130353 [18] Qin H F, Han C, Shi X, Gu T, Sun K S 2024 Opt. Express 32 44437 doi: 10.1364/OE.543792 [19] Yan X P, Liu X L, Li J Q, Hu H R, Lin M, Wang X 2024 Opt. Laser Technol. 174 110667 doi: 10.1016/j.optlastec.2024.110667 [20] Yu G W, Wang J, Yang H, Guo Z C, Wu Y 2023 Opt. Lett. 48 5351 doi: 10.1364/OL.497518 [21] Liu Q W, Chen J, Qiu B S, Wang Y T, Liu J 2023 Opt. Express 31 35908 doi: 10.1364/OE.502503 [22] Horisaki R, Takagi R, Tanida J 2018 Appl. Opt. 57 3859 doi: 10.1364/AO.57.003859 [23] Lee J, Jeong J, Cho J, Yoo D, Lee B, Lee B 2020 Opt. Express 28 27137 doi: 10.1364/OE.402317 [24] Chang C L, Wang D, Zhu D C, Li J M, Xia J, Zhang X L 2022 Opt. Lett. 47 1482 doi: 10.1364/OL.453580 [25] Wu J C, Liu K X, Sui X M, Cao L C 2021 Opt. Let. 46 2908 doi: 10.1364/OL.425485 [26] Shui X H, Zheng H D, Xia X X, Yang F R, Wang W S, Yu Y J 2022 Opt. Express 30 44814 doi: 10.1364/OE.474137 [27] Peng Y F, Choi S, Padmanaban N, Wetzstein G 2020 ACM Trans. Graphics 39 1 [28] Zhong C L, Sang X Z, Yan B B, Li H, Chen D, Qin X J, Chen S, Ye X Q 2023 IEEE Trans. Visual Comput. Graphics 30 1 -
计量
- 文章访问数: 90
- HTML全文浏览数: 90
- PDF下载数: 2
- 施引文献: 0