量子光学与凝聚态物理的交叉研究是当代物理学中的前沿方向, 尤其在探索光与物质相互作用的新奇现象及潜在应用方面具有重要意义^[1]. 近年来, 随着量子信息科学和量子计算技术的快速发展, 对量子态的精确操控和测量的要求逐步提高. 这一需求催生了多个新兴领域, 其中人工规范场和拓扑量子光学因其独特的物理性质和广阔的应用前景而备受瞩目^[2–4]. 在这些系统中, 光子的输运具有非平凡的特性, 例如基于拓扑保护边界态的光子传递可以抵抗体系中的缺陷和杂质. 此类特性有望为高鲁棒性光量子信息处理的实现提供新的方法.

与此同时, 可控的单光子散射是量子光学领域近年来的重要研究课题^[1]. 2008年, Zhou等^[5]研究了单光子在一维光子晶格中超导量子比特控制的单光子相干输运特性, 指出通过调控超导量子比特, 可以实现对单光子散射量子调控. 这个进展极大地促进了人们对于单光子散射量子调控的研究和发展^[6–26]. 2019年, Bello等^[27]进一步发现, 当超导量子比特与SSH (Su-Schrieffer-Heeger) 拓扑光子晶格相互作用时, 整个体系内部会产生新颖的束缚态和超辐射态等非传统量子光学现象. 2021年, Kim等^[28]在实验上实现了超导量子线路体系中超导量子比特和微波光子SSH拓扑晶格的耦合, 观察到手性束缚态且能够直接对拓扑边缘态进行量子控制. 这些研究不仅加深了人们对单光子在能带结构中输运机制的理解, 也可为新型量子光学器件和量子逻辑门的设计提供新的原理.

这些研究为我们在超导量子比特与SSH拓扑光子晶格系统中引入人工规范场相位提供了重要的实验基础. 在此背景下, 本文主要研究人工规范场调控下的超导量子比特-SSH拓扑光子晶格耦合体系中的单光子散射. 首先, 我们构建了一个人工规范场调控下的超导量子比特-SSH拓扑光子晶格耦合构型和理论模型, 并利用概率-振幅方法得到了反射和透射振幅的解析表达式. 通过分析, 我们揭示了人工规范场调控下的SSH拓扑光子晶格中的单光子散射具有丰富的物理特性, 包括散射系数对于$k = \pi $和上下能带具有高度对称性. 与以往研究中超导量子比特-SSH拓扑光子晶格体系中能带无关的单光子散射现象不同^[28], 我们通过调控人工规范场的相位, 能够实现能带依赖的单光子散射, 例如处于上能带的光子全透射, 同时下能带的光子全反射. 我们还证明这种散射可以不依赖晶格耦合强度, 而只依赖于晶格的拓扑性质. 这一性质可用于探测光子晶格的拓扑不变量. 最后, 我们还发现, 当超导量子比特耦合到晶胞之间及晶胞内部的光子格点时, 单光子散射的行为会发生显著变化, 甚至完全相反.

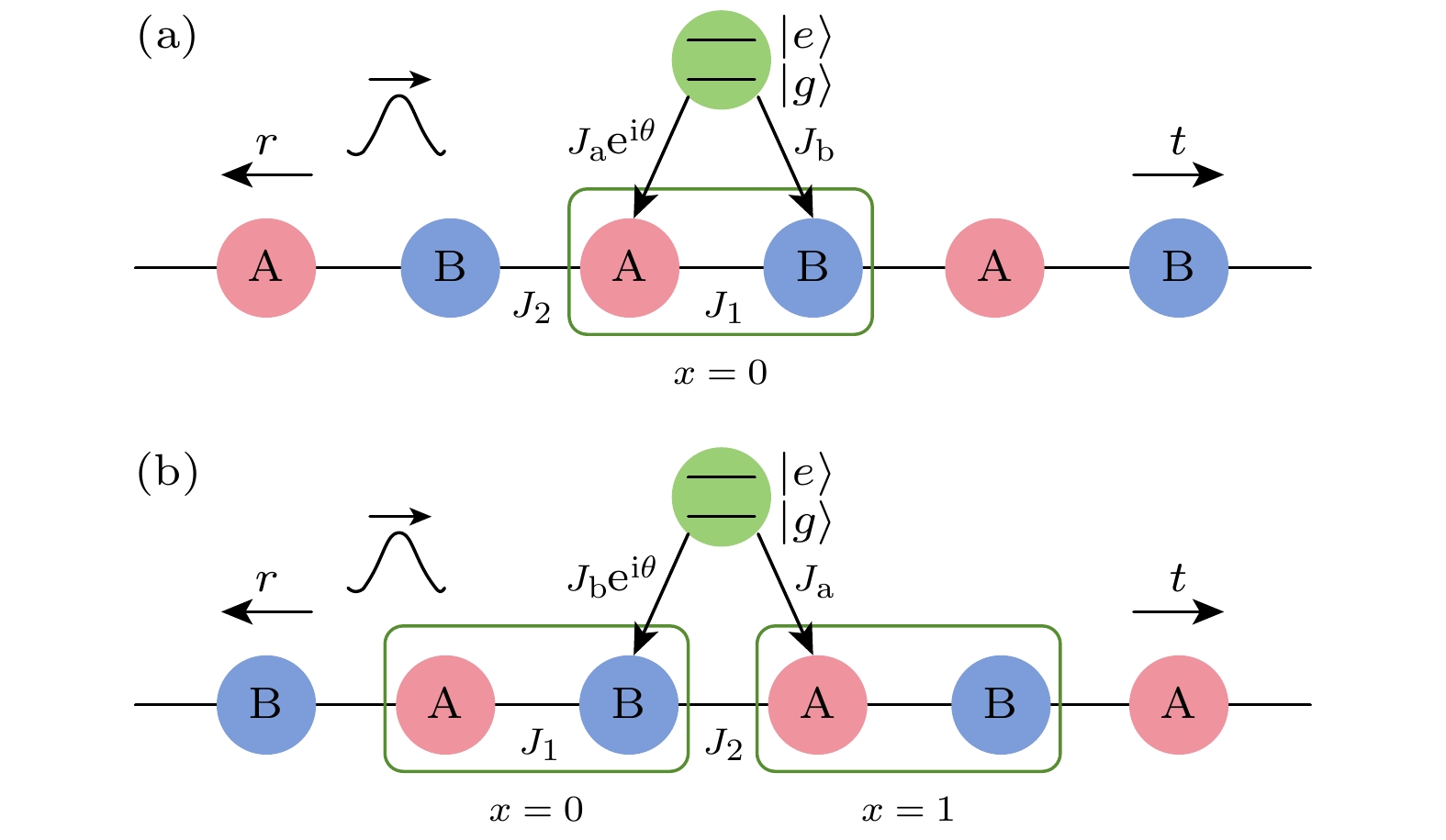
如图1所示, 考虑一个超导量子比特耦合到SSH拓扑光子晶格系统的模型. 不同于以往研究中仅与单个格点耦合的情况^[5], 本研究中的超导量子比特同时与两个格点耦合. 此外, 我们在量子比特与这两个格点构成的封闭环形结构中引入了一个人工规范场. 这种相位调制在实验中已经得到了验证, 例如Chaitali Joshi等^[29]通过在超导量子比特和传输线的耦合中加入含时调制, 实现了相位调制的耦合. 这为我们在理论模型中引入人工规范场相位提供了实验支持.

整个体系的总哈密顿量可写为如下形式:

其中${{\boldsymbol{H}}_{\text{q}}}$为超导量子比特的哈密顿量; $ {{\boldsymbol{H}}_{\text{p}}} $为SSH型光子晶格的哈密顿量; $ {{\boldsymbol{H}}_{\text{I}}} $为超导量子比特与SSH型光子晶格的相互作用哈密顿量. 超导量子比特的哈密顿量可以直接写为

其中${\omega _{\text{e}}}$是超导量子比特的激发态$\left| e \right\rangle $和基态$\left| g \right\rangle $之间的能量间隔; $ {{\boldsymbol{\sigma}} ^ + } = \left| e \right\rangle \left\langle g \right| $和$ {{\boldsymbol{\sigma}} ^ - } = \left| g \right\rangle \left\langle e \right| $分别是超导量子比特的上升算符和下降算符. SSH拓扑光子晶格的哈密顿量可以写为

其中$ {{\boldsymbol{a}}_x} $($ {{\boldsymbol{b}}_x} $)是第$x$个元胞的A(B)子晶格处光子的湮灭算符; $ {\omega _{\text{c}}} $为光子晶格A和B处的光子频率, 胞内和胞间的耦合强度分别为$ {J_1} = J\left( {1 + \delta } \right) $和$ {J_2} = J\left( {1 - \delta } \right) $, $\delta $为二聚化参数. 在本文中, 超导比特-拓扑光子晶格的耦合包含两种方式. 首先, 考虑超导比特与光子晶格$x = 0$处元胞内两个格点耦合. 在旋转波近似下, 相互作用哈密顿量可写为如下形式:

其中${J_{\text{a}}}$(${J_{\text{b}}}$)为超导比特与A(B)子晶格之间的耦合强度; $\theta $为人工规范场相位.

接下来, 我们分析SSH拓扑光子晶格的能带. 通过离散傅里叶变换, 将实空间SSH拓扑光子晶格哈密顿量, 转换成动量空间Bloch哈密顿量 ${{\boldsymbol{H}}_{\text{p}}} = \displaystyle \sum\nolimits_k {{{\boldsymbol{Q}}^\dagger }} h(k){\boldsymbol{Q}}$, 其中${\boldsymbol{Q}} = {\left( {{{\boldsymbol{a}}_k}, {{\boldsymbol{b}}_k}} \right)^{\text{T}}}$,

令$y\left( k \right) = - {J_1} - {J_2}{{\mathrm{e}}^{ -{\mathrm{ i}}k}}$. 根据(5)式, 我们可以得到SSH光子晶格的色散关系:

其中${E_ + }$和${E_ - }$分别为体系上能带和下能带的本征能量. 由于${\omega _c}$不影响本征矢, 为方便起见, 本文忽略了此项. $h\left( k \right)$的本征矢为

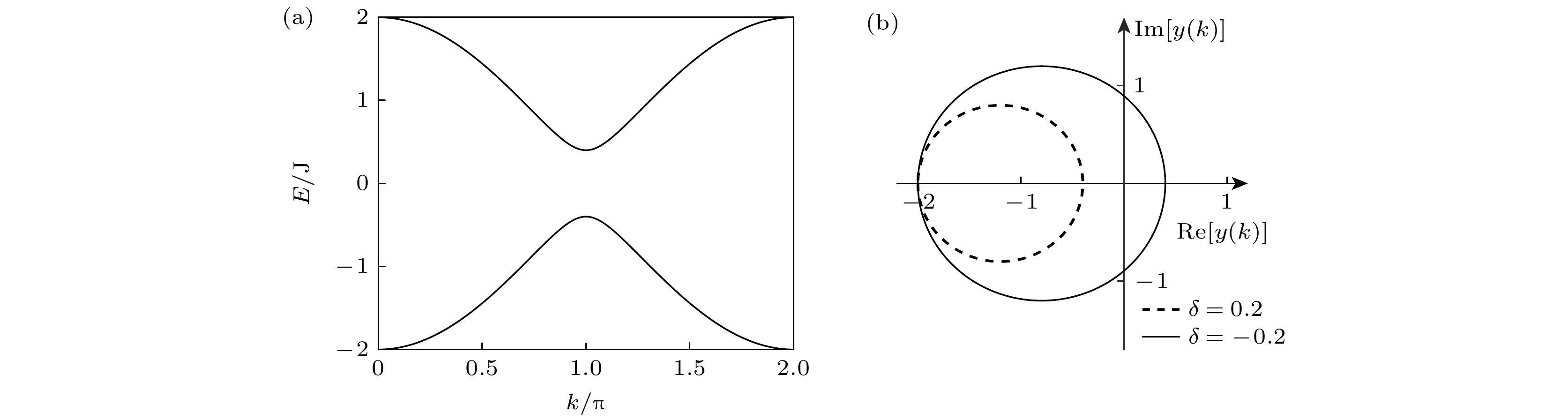
其中${\phi _ \pm } = {\mathrm{Arg}}\left[ { - \left( {{J_1} + {J_2}{{\mathrm{e}}^{ - {\mathrm{i}}k}}} \right)/{E_ \pm }} \right]$. 如图2(a)所示, 计算了$E$关于波矢$k$的示意图. 两个带之间的中间带隙为$4 J\left| \delta \right|$, 它与$\delta $的符号无关. 当$\delta = 0$时, 系统的带隙闭合, 其拓扑性质消失, 因此本文不做分析. 如图2(b)所示, 展示了动量空间哈密顿量非对角元$y\left( k \right)$的实部和虚部随波矢$k$的变化. 当$\delta \lt 0$时, 系统具有非平庸拓扑特性, 拓扑绕数为1; 当$\delta \gt 0$时, 系统的拓扑性质是平庸的, 拓扑绕数为0.

本文具体研究量子比特如何控制拓扑能带结构中的单光子散射. 在旋转坐标系下, 系统的哈密顿量可以写为

其中$\varDelta = {\omega _{\mathrm{e}}} - {\omega _{\text{c}}}$为超导比特与光场之间的失谐频率. 由于系统的总激发数算符是一个守恒量, 因此在单激发子空间中, 整个超导比特-光子晶格系统的状态可以写为

其中$\left| 0 \right\rangle $表示SSH光子晶格中的所有格点都处于真空状态; ${u_{\mathrm{e}}}$是超导比特中单个激发态对应的概率幅; ${u_{{\mathrm{A}}\left( {\text{B}} \right), k}}\left( x \right)$是在第$x$个单元的子晶格A(B)中单个光子占据的概率幅. 概率幅可以通过求解定态薛定谔方程${{\boldsymbol{H}}_{{\text{rot}}}}\left| {{\varPsi _k}} \right\rangle = {E_ \pm }\left| {{\varPsi _k}} \right\rangle $来获得. 假设一个能量为$ {E_ + } $或$ {E_ - } $的单光子最初从光子晶格的左侧注入, 如图1(a). 对于$x \ne 0$, 本征态的通解${u_{{\text{A}}, k}}(x)$和${u_{{\text{B}}, k}}(x)$可写作如下形式:

其中$r$和$t$分别为单光子反射振幅和透射振幅. 利用耦合点$x = 0$处的连续性条件, 得到如下方程:

其中${\varDelta _ \pm } = \varDelta - {E_ \pm }$. 为方便计算, 取${J_{\text{a}}} = {J_{\text{b}}} = J$. 将(10)式和(11)式代入(12)式中, 可以将该方程写为如下矩阵形式:

其中${C_1} = J\left( {1 + \delta } \right) + {J^2}{{\mathrm{e}}^{ - {\mathrm{i}}\theta }}/{\varDelta _ \pm }$, ${C_2} = {E_ \pm } + J\left( {1 - \delta } \right){{\mathrm{e}}^{ - {\mathrm{i}}\left( {k + {\phi _ \pm }} \right)}} + {J^2}{{\mathrm{e}}^{ - {\mathrm{i}}\theta }}/{\varDelta _ \pm }$. 若该方程有解, 则上述方程左边矩阵行列式值不为零. 通过直接计算, 发现上述方程在$\delta = \pm 1$或$k = 0$时无解. 因此, 在本文中, 对该参数下的散射行为不考虑. 进一步, 通过求解上述方程, 得到反射振幅和透射振幅:

由于系统能量是守恒的, 反射系数${R_ \pm } = {\left| {{r_ \pm }} \right|^2}$与透射系数${T_ \pm } = {\left| {{t_ \pm }} \right|^2}$满足${R_ \pm } + {T_ \pm } = 1$.

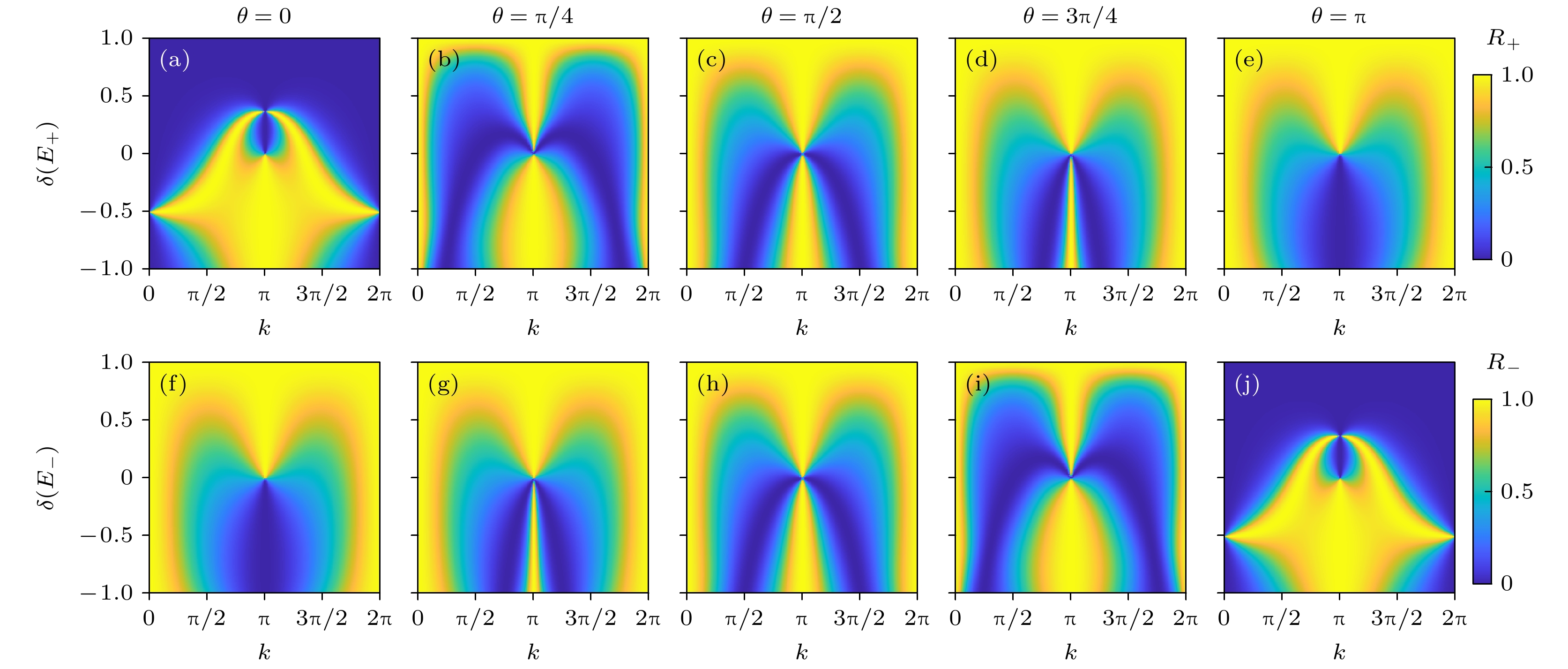
为了研究拓扑光子晶格中单光子的散射特性, 如图3所示, 我们数值计算了单光子反射系数$R$随人工规范场相位$\theta $、波矢$k$和二聚化参数$\delta $之间的关系. 为了更清晰地解释这些结果, 首先对图3中的参数设置进行说明. 在本研究中, 选择$\varDelta = 0$, 即超导量子比特的共振频率与光子晶格的频率一致. 首先, 当$\varDelta = 0$时, 模型和理论分析将更加简洁, 系统对于上下能带的行为也将会出现相应的对称性. 此时将更加关注人工规范场和拓扑结构对单光子输运的主导作用. 其次, 当量子比特的共振频率位于SSH波导能带隙中间时, 会形成手性零能模^[30]. 这些手性零能模具有拓扑保护的特性, 对系统中的缺陷和无序具有很强的鲁棒性.

在图3(a)—(e)和图3(f)—(j)中, 分别研究了输入单光子能量为$ {E_ + } $和$ {E_ - } $时的单光子反射系数. 如图3所示, 整个体系的反射系数具有丰富的对称性特性. 首先, 在不同人工规范场相位$\theta $下, 我们发现系统的反射系数$R$总是关于$k = \pi $对称. 根据

代入(14)式, 可以得到

这本质上是由SSH拓扑光子晶格能谱(图2(a))的对称性造成的; 其次, 当输入的单光子能量处于SSH拓扑光子晶格的上下能带中(${E_ + }$和${E_ + }$), 发现对应的两种反射系数也存在对称性. 根据${\varDelta _ + } = - {\varDelta _ - }$, ${\phi _ + }\left( k \right) = {\phi _ - }\left( k \right) + \pi $, 代入(14)式, 得到

这种对称是由于动量空间上下能带本征态在子晶格B中存在一个$\pi $相位差. 因此, 当施加的人工规范场相位$\theta $进一步存在一个$\pi $相位差时, 两种相位差叠加最终导致两个本征态形成相同的散射行为. 人工规范场相位$\theta = \pi /2$时, ${R_ + }\left( {\pi /2} \right) = {R_ - }\left( {\pi /2} \right)$. 如图3(c)和图3(h), 可以观察到上下能带的散射行为完全一致. 在这一特定的人工规范场相位下, 无论入射光子的能量是$ {E_ + } $还是$ {E_ - } $, 系统的散射特性都表现出完全相同的模式. 这意味着反射系数$R$不再依赖于光子的能量, 而是仅由波矢$k$和二聚化参数$\delta $决定.

图3(a)—(e)展示了当单光子能量为$ {E_ + } $时, 反射系数$R$随人工规范场相位$\theta $从0到$\pi $的动态变化. 当$\delta \lt 0$时, 整个光子晶格体系处于非平庸拓扑物态; 随着人工规范场相位$\theta $的增加, $ k = \pi $附近的全反射($R = 1$)范围逐渐缩小, 最后趋于全透射($R = 0$); 反之, 当$\delta \gt 0$时, 整个光子晶格体系处于平庸拓扑物态; 全透射范围逐渐缩小并趋于全反射. 在$k = 0$或$ 2\pi $附近时, 由全透射趋于全反射, 且全反射范围逐渐扩大. 图3(f)—(j)进一步展示了当单光子能量为$ {E_ - } $时的散射特性. 当$\delta \lt 0$, 光子晶格为非平庸拓扑时, $k = \pi $附近的全透射范围逐渐缩小并趋于全反射, 而当$\delta \gt 0$时, 光子晶格为平庸拓扑时, 全反射范围逐渐缩小并趋于全透射. 特别是在$\theta = 0$和$\theta = \pi $时, 我们观察到系统展现出完全相反的散射行为, 例如当参数$k = \pi $, $\theta = 0$, $\delta = 0.2$时, 能量为$ {E_ + } $的光子会完全反射, 能量为$ {E_ - } $的光子会完全透射. 这一现象与先前观察到的与能量无关的散射行为形成鲜明对比, 这体现了系统对于光子能量的敏感性, 揭示了人工规范场在调控光子散射路径方面的独特能力. 这些结果证明, 外加人工规范场可以为拓扑光子能带结构中单光子散射提供一种全新和丰富的调控手段.

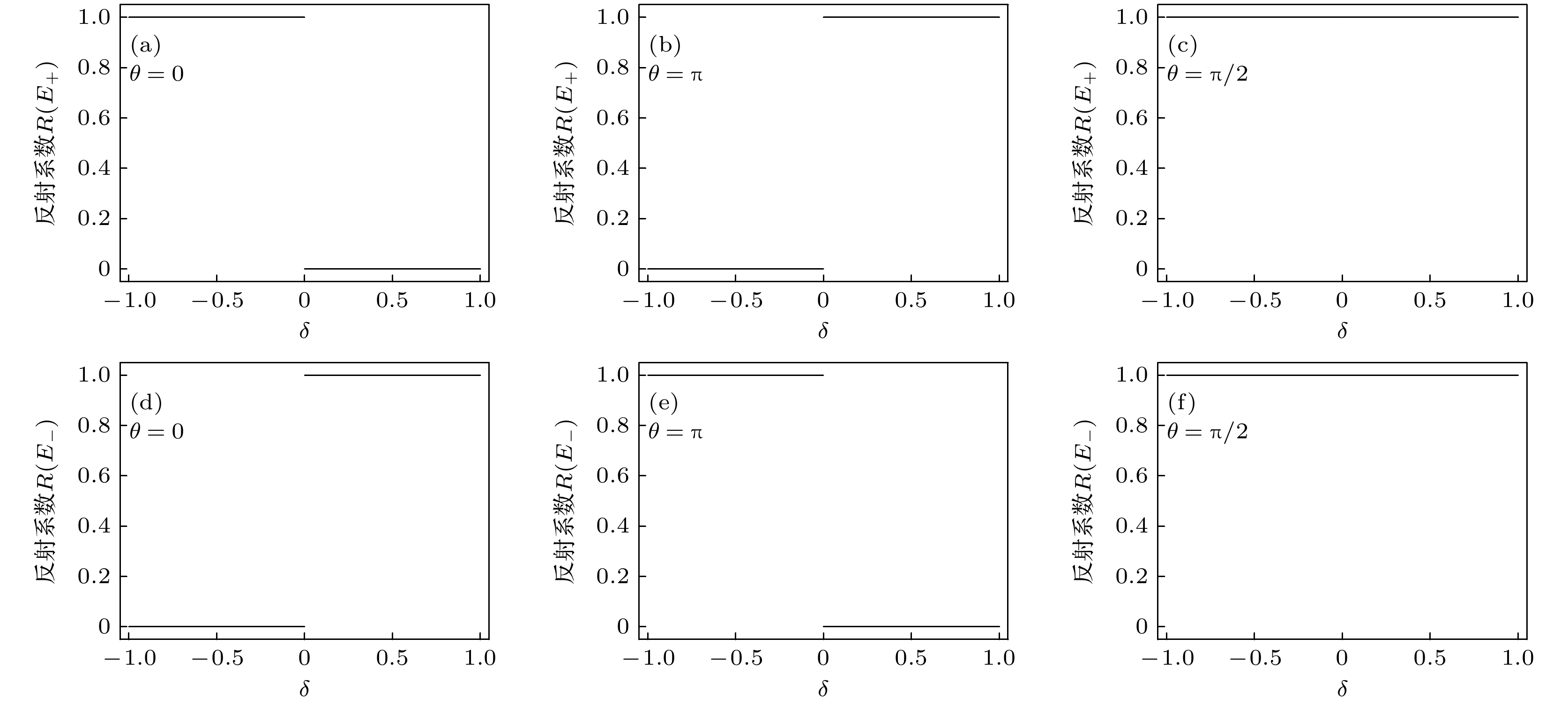
进一步, 我们发现单光子的反射系数可以用于揭示光子晶格能带结构的拓扑特性. 如图4(a)所示, 我们绘制了在$\theta = 0$, $k = \pi $, 当单光子能量为$ {E_ + } $时, 反射系数$R$关于二聚化参数$\delta $之间的图像. 我们发现, 此时反射系数$R$与$\left| \delta \right|$的大小无关, 仅取决于$\delta $的正负. 由于图4中所展示的为耦合强度为${J_{\mathrm{a}}} = {J_{\mathrm{b}}} = J = 1$, 而当改变耦合强度, 通过分析发现当且仅当在${J_{\mathrm{a}}} = {J_{\mathrm{b}}}$时, 才会出现与图4相同的散射行为. 这表明, 在特定的耦合强度条件下, 系统的散射行为与耦合强度的具体值无关, 而更多地依赖于拓扑性质和系统参数的对称性. 这一结果表明了系统对于二聚化参数$\delta $的拓扑敏感性, 即系统的反射特性在拓扑相变点附近发生了突变. 具体来说, 在$\theta = 0$的情况下, 当$\delta \lt 0$时, 反射系数等于1, 表明能量为$ {E_ + } $的光子是全反射的; 而当$\delta \gt 0$时, 反射系数等于0, 能量为$ {E_ + } $的光子是全透射的. 这种在$\delta = 0$处的突变行为是拓扑相变的一个明显标志.

如图4(a)与图4(d)和图4(b)与图4(e)所示, 在同一人工规范场相位下, 能量为$ {E_ + } $和$ {E_ - } $的系统具有完全相反的散射行为. 这一结果表明了不同的能量对应不同的拓扑响应. 图4(a)与图4(b)和图4(d)和图4(e)进一步展示了在单光子能量相同的情况下, 人工规范场相位$\theta = 0$和$\theta = \pi $的系统散射行为完全相反. 因此, 在这些情况下, 我们得到了拓扑保护的单光子散射. 此时光子的反射系数只依赖$\delta $的正负, 对于其具体的幅值具有很强的鲁棒性. 然而当$\theta \ne 0$或$\theta \ne \pi $时, 系统的散射行为与$\delta $的大小没有任何关系, 不能揭示能带的拓扑特性. 如图4(c)和图4(f)所示, 当$\theta = \pi /2$时无论$\delta $的取值如何, 系统都处于全反射状态.

为证明这些结论, 将$k = \pi $, $\theta = 0$代入(6)式, 此时

将(17)式和(18)式代入(14)式, 得到:

同理, 得出当$k = {\text{π}}$, $\theta = \pi $时, 反射系数可以写作:

其次, 可以证明当$k = {\text{π}}$, $\theta \ne 0, {\text{ \pi }}$时, 反射系数可以写作:

根据上述解析计算结果, 在$k = {\text{π}}$而$\theta $取任意其他值时, 系统只会表现出全反射现象. 只有在$k = {\text{π}}, {\text{ }}\theta = 0$或$\theta {\text{ = \pi }}$时, 系统的反射系数才会出现与拓扑相关的性质. 这等价于一个拓扑不变量, 可用于揭示光子晶格能带的拓扑性质.

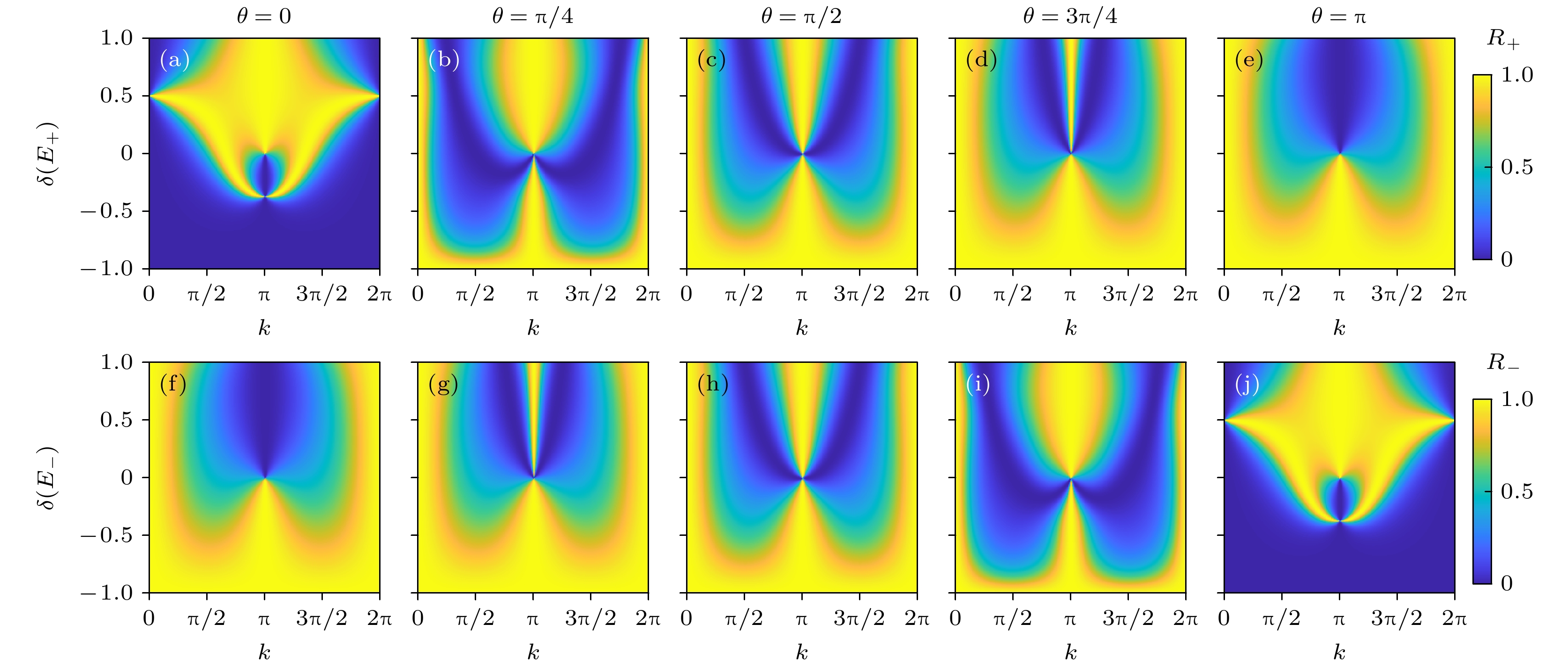
如图5所示, 进一步将超导比特与光子格点的耦合位置进一步推广至元胞之间(BA构型). 采取相同的计算方法, 可以解得反射振幅和透射振幅:

相比(14)式, 可以看出, BA和AB构型下反射振幅与透射振幅的表达式, 只存在${J_1}$与${J_2}$的相互交换. 图5(a)—(j)分别画出了在$\theta = 0$到$\theta = {\text{π}}$时左侧打入能量分别为$ {E_ + } $和$ {E_ - } $的单光子, 系统的反射系数$R$与波矢$k$以及二聚化参数$\delta $之间的关系. 可以发现, 两种构型下的反射系数在$\delta \gt 0$和$\delta \lt 0$时呈现刚好完全相反的散射行为.

具体来说, 当$\delta \gt 0$, 整个光子晶格体系处于平庸拓扑物态; 随着人工规范场相位$\theta $的增加, $ k = {\text{π}} $附近的全反射范围逐渐缩小, 最后趋于全透射. 反之, 当$\delta \gt 0$时, 整个光子晶格体系处于非平庸拓扑物态; 全透射范围逐渐缩小并趋于全反射. 这与AB构型下的散射行为变化是完全相反的. 这些结果进一步揭示了人工规范场相位对系统散射行为的调控作用.

本文深入研究了超导量子比特与SSH拓扑光子晶格系统中单光子的相干输运与散射特性, 并探讨了人工规范场在该系统中的调控作用. 通过构建理论模型, 系统地分析了超导量子比特与SSH光子晶格之间的相互作用, 推导出总哈密顿量. 本文通过求解定态薛定谔方程, 得到了反射振幅和透射振幅的解析表达式, 并进一步分析了这些表达式所揭示的物理意义. 结果说明, 系统的反射系数在不同参数条件下展现出丰富的对称性特征, 这些特征与SSH拓扑光子晶格的能谱对称性密切相关. 此外, 本文还探讨了外加人工规范场相位对散射行为的影响. 数值计算结果表明, 反射系数随人工规范场相位、波矢和二聚化参数的变化而变化, 且在特定条件下, 反射系数仅依赖于波矢和二聚化参数, 而与光子能量无关. 这一结果表明, 通过调节人工规范场, 可以灵活地控制光子的散射路径, 从而为拓扑光子能带结构中的光子输运调控提供了新的理论途径.

进一步地, 本文探讨了基于单光子散射特性的拓扑探测方法. 研究表明, 反射系数在拓扑相变点附近发生突变. 这一现象是拓扑相变的直接标志, 为拓扑性质的探测提供了有效手段. 同时, 本文还将研究推广至不同耦合位置下的超导量子比特与光子晶格系统(如BA构型), 发现系统在特定条件下表现出相反的散射行为, 进一步证实了人工规范场相位对散射行为的调控作用.

综上所述, 本文通过理论分析和数值计算, 揭示了超导量子比特与SSH拓扑光子晶格系统中单光子的输运机制和散射特性, 并系统地阐明了人工规范场对这些性质的调控机理. 这些研究结果对未来量子信息处理和拓扑光子学的发展具有重要意义. 在量子信息处理方面, 拓扑保护下的单光子散射特性可以用于实现高效的单光子源和量子比特操作, 为量子计算和量子通信提供更稳定和可靠的平台. 同时, 通过调控人工规范场, 可以实现光子在量子网络中的高效传输和路由, 减少光子在传输过程中的损耗和退相干. 在拓扑光子学领域, 单光子散射的研究为设计新型拓扑光子器件提供了理论基础, 例如基于拓扑保护的单向波导和滤波器等. 此外, 反射系数在拓扑相变点附近的突变现象为拓扑相变的探测提供了有效手段, 进一步推动了拓扑光子学的基础研究和应用拓展. 这些研究不仅为拓扑光子学和量子信息处理领域提供了新的理论视角和调控手段, 也为未来量子光学实验及基于拓扑保护的量子器件设计奠定了重要的理论基础.