超短强激光技术的巨大进步为研究光与物质的相互作用提供了新的思路. 近几十年来, 相关研究已经从基础的原子层面扩展至更为复杂的分子、二聚体, 乃至团簇领域. 超短激光脉冲已经被证明可以以亚飞秒和亚埃的时空分辨率实时监测电子和核运动^[1–6]. 在理论方面, 强场近似(SFA)理论在描述强激光场中原子分子超快动力学方面取得了巨大的成功^[7–14]. SFA理论基于量子散射矩阵理论, 以非微扰的方式处理分子体系与激光场的相互作用, 能够很好地描述分子轨道对称性、双中心干涉效应等对电离动力学的影响. 但是SFA理论也存在一定的局限性, 有待进一步完善与优化. 首先, SFA理论未将电离电子与剩余离子间的库仑相互作用纳入考量. 为解决这一问题, 研究者们将原本针对原子电离过程发展的库仑修正强场近似(CCSFA)方法^[15], 推广至分子体系^[16,17], 可以更准确地描述分子电离过程中的物理现象. 其次, 在原始的分子SFA理论中, 跃迁矩阵元的初态为无激光场时系统的本征态, 末态为受到激光场缀饰的连续态即Volkov态. 原则上讲, 原子分子电离过程不会受到原子或分子位置的影响, 即具有空间平移不变性. 但是长度规范下SFA的跃迁矩阵元中初态是平移不变的, 而末态由于激光场的缀饰, 空间平移后会产生额外项, 最终使得整个跃迁矩阵元形式并不满足空间平移不变^[18,19]. 在描述原子电离过程时可以将原子核放置在坐标系原点处, 从而避免出现额外的非物理项. 但是分子体系存在多个原子中心, 跃迁矩阵元中无法避免出现由于空间平移不变性的破坏导致的非物理项, 最终会产生错误的计算结果. 因此, 为了使得分子SFA满足空间平移不变, 需要手动为初态加入激光场缀饰项, 从而消除额外的非物理项. 这种处理方法虽然能够保证分子SFA的空间平移不变性, 并能够包含激光场对初态的影响, 比如AC Stark效应, 但是与SFA基本思想中关于初态的要求是违背的, 因此只是对特殊情况的特殊处理, 并不适用于所有分子, 故其适用范围需要仔细甄别.

另一方面, 阿秒钟方案^[6]利用近圆偏振的强飞秒激光脉冲, 巧妙地将电离电子的亚周期发射时间映射到其发射角上. 这一方法最初应用于原子, 以解决隧穿粒子在势垒区停留时间这一量子力学基本难题^[20–22]. 随后, 它又被拓展至分子系统. 在分子系统中, 分子轨道的对称性给电子动力学带来了额外的复杂性, 即使对于最简单的H₂分子也不例外^[23–26]. 相较于线偏振光, 圆偏振光在分子电离过程中展现出独特的优势. 它不仅能有效抑制再散射电子的产生, 还能减少各种干涉效应^[27–31]的影响, 使得直接电离电子的动力学过程更加纯粹和清晰. 并且人们在实验上已经获得了H₂, N₂, Ne₂二聚体等分子在(椭)圆偏振场中的二维光电子动量分布^[25,32,33], 这无疑为甄别缀饰态和非缀饰态的适用提供了很好的条件.

本文采用分子SFA方法和CCSFA方法, 对Ne₂二聚体和N₂分子在(椭)圆偏振激光场中的光电子动量分布(PMD)进行了研究, 并与已有的实验结果进行了对比. 理论分析证实, 对于核间距较大的分子, 如Ne₂二聚体, 采用缀饰态描述才能准确地呈现出二聚体的电离特征; 而对于N₂这样核间距较小的分子, 缀饰态描述则不适用.

根据分子SFA理论^[34,35], 长度规范下, 分子从初态$ \left\vert\psi_{0}({\boldsymbol{r}})\right\rangle\notag $到最终Volkov态$ \left\vert{\boldsymbol{p}}+{\boldsymbol{A}}(t)\right\rangle\ $的跃迁振幅可以表达为以下形式:

其中,

是半经典作用量. 这里, $ {\boldsymbol{E}}(t) = -\partial{\boldsymbol{A}}(t)/ \partial t $表示激光电场, 其矢势为$ {\boldsymbol{A}}(t) = A_{0}({\boldsymbol{e}}_{z}\cos \omega t - \epsilon{\boldsymbol{e}}_{x}\sin\omega t) $, $ \epsilon $是激光场的椭偏度, $ \omega $是激光角频率, $ I_{{\rm{p}}} $是电离势. 可以通过鞍点近似方法^[36,37]求解(1)式中的时间积分. 因此, 需要求解下面的鞍点方程:

因为$ I_{\rm p} > 0 $, 所以方程(3)的解$ t_{s} $为复数. $ t_{s} $的实部$ {{t}}_{{\rm{r}}} $可以理解为电离时刻, 虚部$ {{t}}_{{\rm{i}}} $可以理解为隧穿时间. 因此, 跃迁振幅可以重新写成:

在上述SFA计算过程中, 末态为自由电子在激光场中的本征态Volkov态, 即忽略了电离后电子与离子之间的库仑相互作用. 然而, 库仑场效应在电离过程中的电子动力学具有重要影响, 会导致椭圆偏振激光场中的光电子动量分布出现偏转. 因此, 人们提出了CCSFA方法, 通过经典计算获取库仑场扰动后的电子轨迹和作用量, 有效地将库仑场的影响纳入考量^[15–17]. 在CCSFA中, 跃迁振幅可以写成如下形式:

这里, $ {\tilde{\boldsymbol{p}}} $是受库仑场扰动的渐近动量. $ S'(t_{s}) $为扰动后的作用量, 由以下公式给出:

其中, $ t_{s} = t_{{\rm{r}}}+{\rm{i}} t_{{\rm{i}}} $是复数鞍点解, t_F是激光脉冲的结束时间. (6)式右边的第一个积分代表势垒下的作用量, 第二个积分代表电子离开隧穿出口后的作用量. 在这个模型中, 电子隧穿后在激光场和库仑场中的运动由牛顿方程来描述, 具体为$ {\rm{d}}{\tilde{\boldsymbol{v}}}(t)/{\rm{d}}t = {\boldsymbol{E}}(t)-\partial V({\boldsymbol{r}})/\partial {\boldsymbol{r}} $, 其中, $ {\tilde{\boldsymbol{v}}}(t) $是瞬时速度, $ V(r) = -1/r $. 电子在激光场中传播, 直到脉冲结束. 随后, 利用开普勒定律分析得到电子的最终渐近动量$ {\tilde{\boldsymbol{p}}} $. 最后, 对这些轨迹进行相干求和, 得到不同类型的分布.

前面的计算过程对于原子和分子都是相同的, 原子和分子的差别主要体现在初态波函数上. 根据玻恩-奥本海默近似, 核的运动和电子的运动是可以分开考虑的. 在固定核近似下, 初始分子电子态可以表示为原子轨道的线性组合 (LCAO)^[38], 这些原子轨道对形成对称$ (\gamma = 1) $和反对称$ (\gamma = -1) $组合:

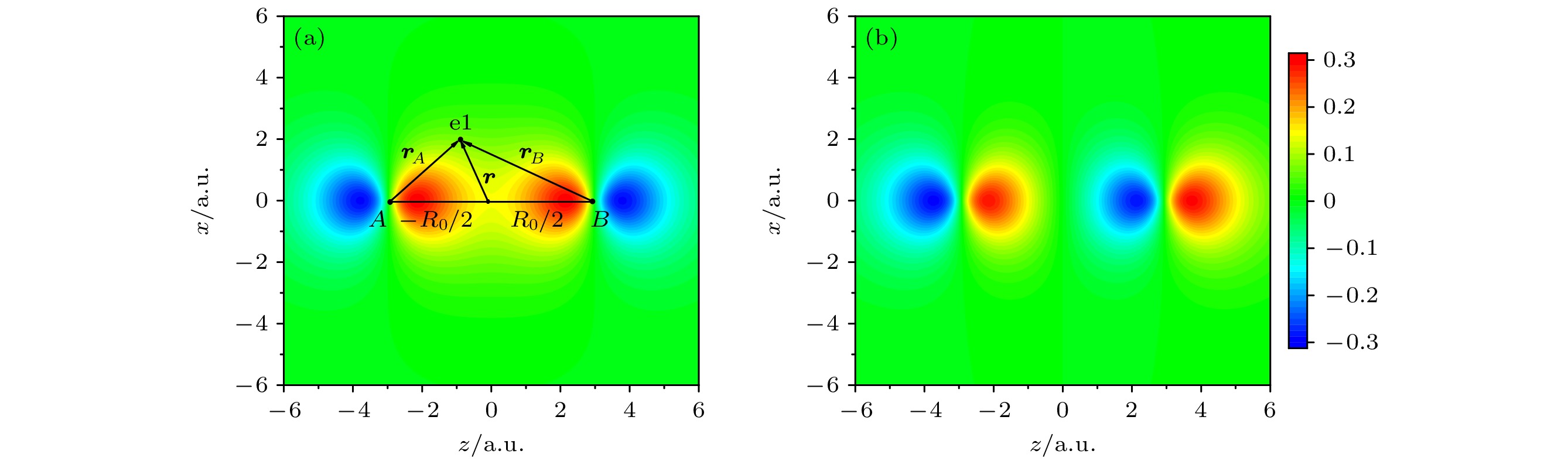
下标$ a $表示不同的原子轨道, $c_{a} $是系数, $ \psi_a $表示原子轨道波函数. 图1描绘了Ne₂二聚体的对称性轨道$ 2{\mathrm{p}}{\text{σ}}_{{\mathrm{g}}} $(图1(a))与反对称性轨道$ 2{\mathrm{p}}{\text{σ}}_{{\mathrm{u}}} $(图1(b))在(z, x)平面内的波函数空间分布情况. 图1(a)中A和B两点分别标记了两个Ne原子核的平衡位置, 它们之间的距离为$ R_0 $ = 5.86 a.u. 分子坐标系原点建立在两个核的中间处, 电子的位置矢量为$ {\boldsymbol{r}} $, 两个原子核的位置分别为$ -{\boldsymbol{R}}_0/2 $和$ {\boldsymbol{R}}_0/2 $, 电子相对于两个核的位置矢量分别为$ {\boldsymbol{r}}_{{{A}}} = {\boldsymbol{r}}+{\boldsymbol{R}}_0/2 $, $ {\boldsymbol{r}} _{{{B}}} = {\boldsymbol{r}}-{\boldsymbol{R}}_0/2 $. 双原子分子的电离可以看作是两个分别平移了$ -{\boldsymbol{R}}_0/2 $和$ {\boldsymbol{R}}_0/2 $的原子电离贡献的相干叠加. 但是需要注意的是, (1)式中的SFA跃迁矩阵元并不满足平移不变性. 例如当系统平移$ {\boldsymbol{R}}_0/2 $后, 初态满足平移不变, 但是末态为场缀饰的平面波, 会多出一项$ \exp[-{\rm{i}}({\boldsymbol{p}}+ {\boldsymbol{A}}(t))\cdot{\boldsymbol{R}}_0/2] $, 其中$ \exp(-{\rm{i}} {\boldsymbol{p}}\cdot{\boldsymbol{R}}_0/2) $为整体相位对电离没有贡献, 但是$ \exp(-{\rm{i}} {\boldsymbol{A}}(t)\cdot {\boldsymbol{R}}_0/2) $对(1)式中关于时间的积分有贡献, 会产生非物理的结果. 因此, 需要对初态进行修正以消除末态平移后的额外项, 从而确保(1)式的空间平移不变性. 这可以通过对分子初态引入光场缀饰因子$ \exp[-{\rm{i}}{\boldsymbol{A}}(t)\cdot{\boldsymbol{R}}_0/2] $来实现. 这样的初始基态称为“缀饰态”. 缀饰后的初态波函数可以写成:

那么, 方程(5) 的跃迁矩阵元$ V_{{\boldsymbol{p}}_{0}} $可以重新表示为

记$ {\boldsymbol{r}}\pm\dfrac{{\boldsymbol{R}}_{a}}{2} \to \boldsymbol r $, 则

其中,

是在分子电离过程中起重要作用的干涉项. 然而, 需要注意的是, (8)式中缀饰后的初态虽然能够保证分子SFA的空间平移不变性, 并能够包含激光场对初态的影响, 比如AC Stark效应, 但是与SFA基本思想中关于初态的要求是违背的, 因此只是对特殊情况的特殊处理, 并不适用于所有分子. 对于某些分子, 需要使用(7)式中的非缀饰态来计算才能得到正确的结果. 未考虑缀饰的初始基态, 即“非缀饰态”的$ V_{{\boldsymbol{p}}_{0}} $中的干涉项为

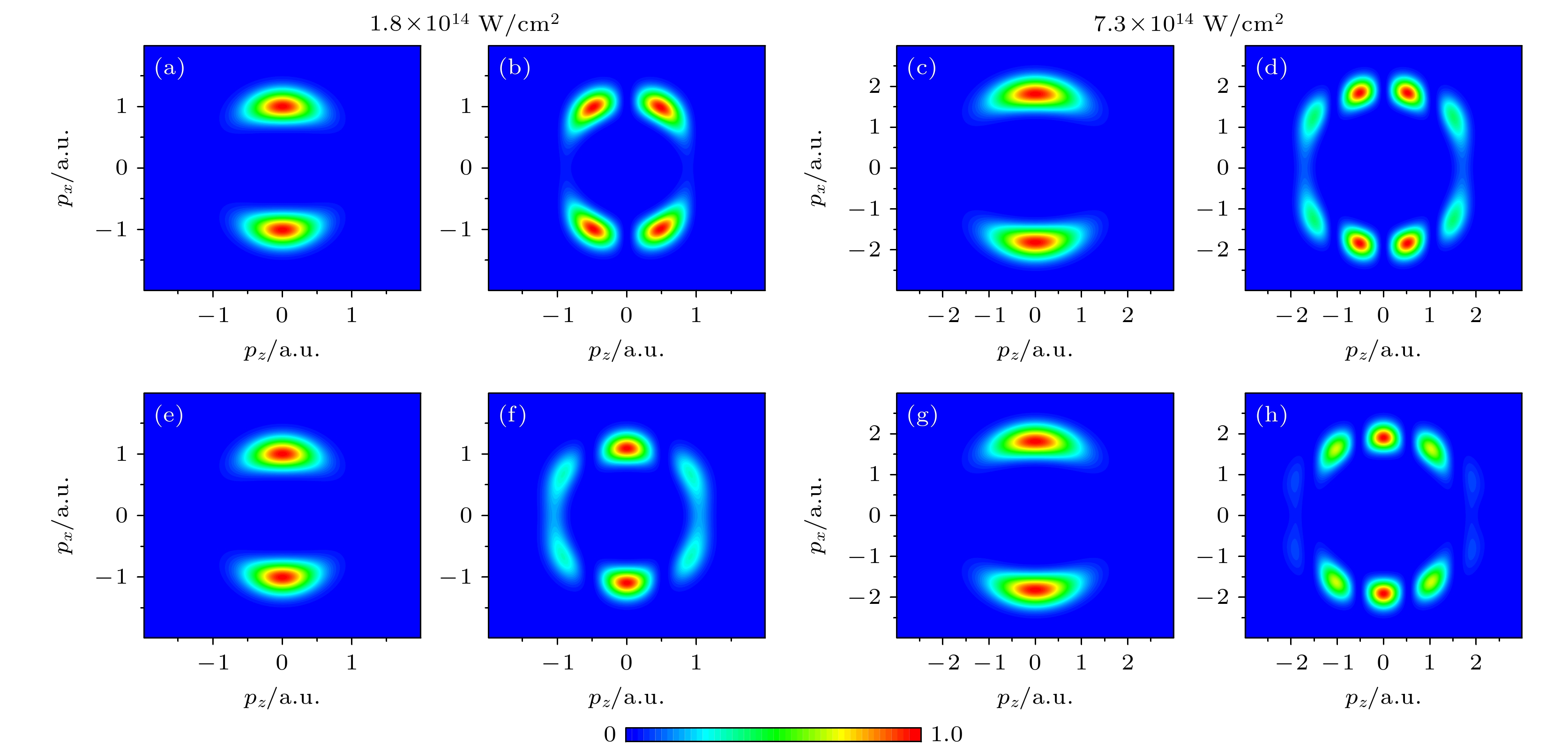
图2展示了采用SFA方法计算的Ne₂二聚体在780 nm下不同光强的圆偏振激光场中的PMD. 分子轴方向沿激光场z轴方向. 整体来说, 光强改变后电子动量分布的范围发生了变化, 但是分布的基本特征没有改变. 具体而言, 当初态为非缀饰态时, 对称轨道$ 2{\mathrm{p}}{\text{σ}}_{\rm{g}} $ (图2(a)和图2(c))和反对称轨道$2{\mathrm{p}} {\text{σ}}_{\rm{u}} $ (图2(e)和图2(g))的PMD均主要分布在$ p_{z} = 0 $轴上. 这表明在不考虑场缀饰时, Ne₂的分子轨道特性对电子动量分布没有影响. 然而, 当初态考虑了场缀饰后, 如图2(b), (d)和图2(f), (h)所示, 电子动量分布展现出了截然不同的有序干涉图样, 这些图样由一系列连续且规律的峰组成. 值得注意的是, 在$ p_{z} = 0$的位置, 对称性轨道和反对称性轨道的干涉图样呈现出完全不同的特征: 对于$ 2{\mathrm{p}}{\text{σ}}_{\rm{g}} $轨道而言, 此处分布为极小值; 而$ 2{\mathrm{p}}{\text{σ}}_{\rm{u}} $轨道则恰好相反, 此处分布为极大值. 进一步观察发现, 沿着$ p_{z} $方向, $ 2{\mathrm{p}}{\text{σ}}_{\rm{g}} $轨道和$ 2{\mathrm{p}}{\text{σ}}_{\rm{u}}$轨道的PMD都存 在严格的周期性变化. 干涉图样的数量明显更多, 但结构和条纹间距并没有发生变化. 通过与文献[32]中的实验结果(光强为$ 7.3\times 10^{14}\; {\mathrm{W/cm}}^{2} $)对比, 可以看出图2(d) 和图2(h)与实验测量的PMD符合得非常好. 因此, 对于如Ne₂这类具有大核间距的二聚体而言, 初始基态考虑缀饰效应是至关重要的. 同时, 这一发现也进一步证实了分子轨道的对称性对于干涉图样具有重要影响.

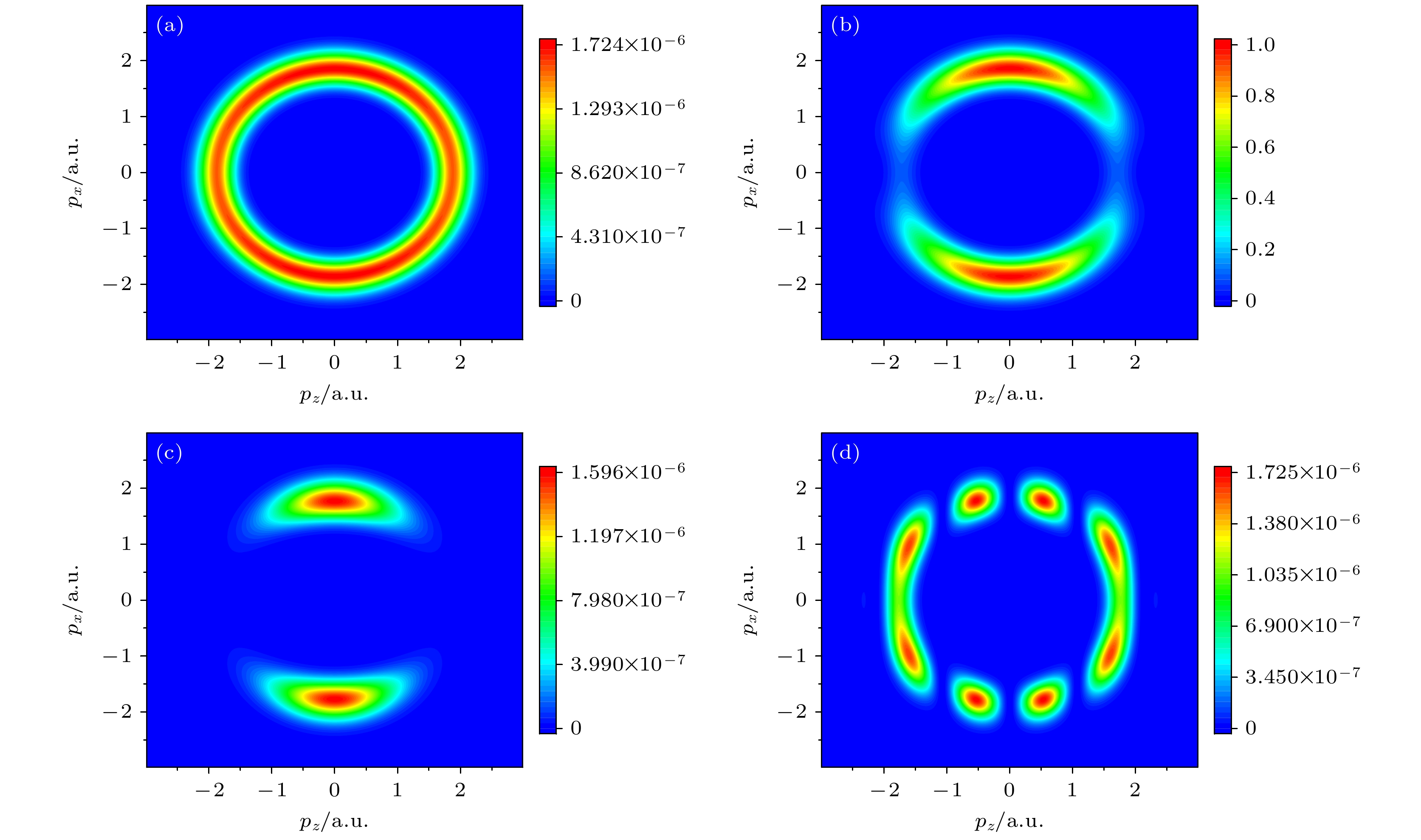
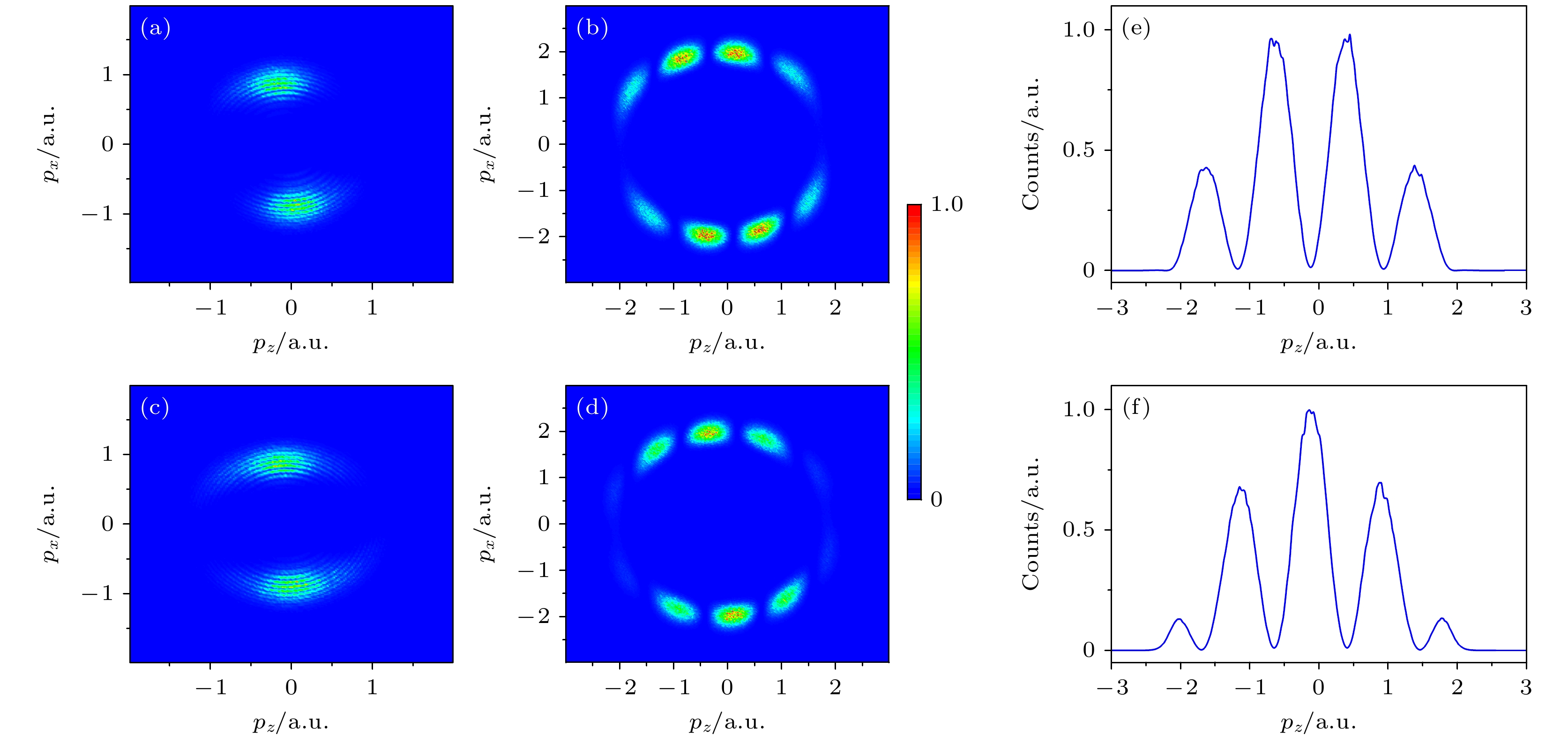
为了更深入地理解缀饰和非缀饰态动量分布差别的成因, 进一步分析了跃迁振幅中不同项对光电子分布的影响. 从(5)式可以明确看出, 分子电离的光电子产率主要由两个因素共同决定: 与初态有关的因子$ V_{p_0} $以及只与半经典电子轨迹有关的剩余项. 图3(a)展示了不考虑$ V_{p_0} $的动量分布情形. 此时, 电子动量分布呈现为一个均匀的圆形环, 这与半经典模型的预测一致, 即在圆偏振激光场中, 电子在不同方向出射的概率相同. 下面进一步分析$ V_{p_0} $中不同项对动量分布的影响. $ V_{p_0} $中包含分子干涉项以及Ne原子$2{\mathrm{p}}_z $轨道的跃迁振幅项$ \left\langle{\boldsymbol{p}}+{\boldsymbol{A}}(t_{s})\right \vert{\boldsymbol{r}} \cdot{\boldsymbol{E}}(t_{s})\left\vert\psi_{a}\right\rangle $. 图3(b)给出了仅考虑原子跃迁振幅时的动量分布, 即对应的光电子动量分布. 可以看到, 电子主要分布在$ p_{z} = 0$轴上, 没有干涉图样出现, 这种分布反映了原子$ 2{\mathrm{p}}_z $轨道的基本特性. 随后, 图3(c)和图3(d)分别给出了在图3(a)的基础上仅考虑对称性轨道的非缀饰态干涉项($ \gamma = -1 $)$ \sin[( {\boldsymbol{p}}+{\boldsymbol{A}}(t_{s}))\cdot {{{\boldsymbol{R}}_{\boldsymbol{0}}}}/{2}] $和缀饰态干涉项($ \gamma = 1 $)$ \sin({\boldsymbol{p}}\cdot {{{\boldsymbol{R}}_{\boldsymbol{0}}}}/{2}) $的动量分布. 可以明显地看出, 图3(c)中动量分布与图2(c)的结构相似, 都没有干涉结构. 而图3(d)中则呈现出明显的干涉结构, 和图2(d)中的结构一致. 这说明图2(c)和图2(d)的结构主要来自于干涉项的贡献, 与原子轨道的特性关系不大. 由于最终的动量分布可以看作是在图3(a)分布的基础上叠加分子干涉项, 而图3(a)分布为均匀分布, 因此最终的分布实际上反映了干涉项的分布. 通过对比(11)式和(12)式可以发现, 缀饰态和非缀饰态干涉项的差异主要在于三角函数中动量的不同: 前者中的动量是场关闭后的渐近动量$ {\boldsymbol{P}} $, 也就是电子的最终动量, 因此其动量分布会沿$ {\boldsymbol{R}}_0 $方向以$ R_0 $为频率振荡, 这与最终的动量分布一致. 而非缀饰态中的动量则是电离时刻的动量$ {{\boldsymbol{P}}+{\boldsymbol{A}}}(t_{s}) $, 与最终的动量分布没有直接对应关系, 这导致了非缀饰态下干涉结构的缺失.

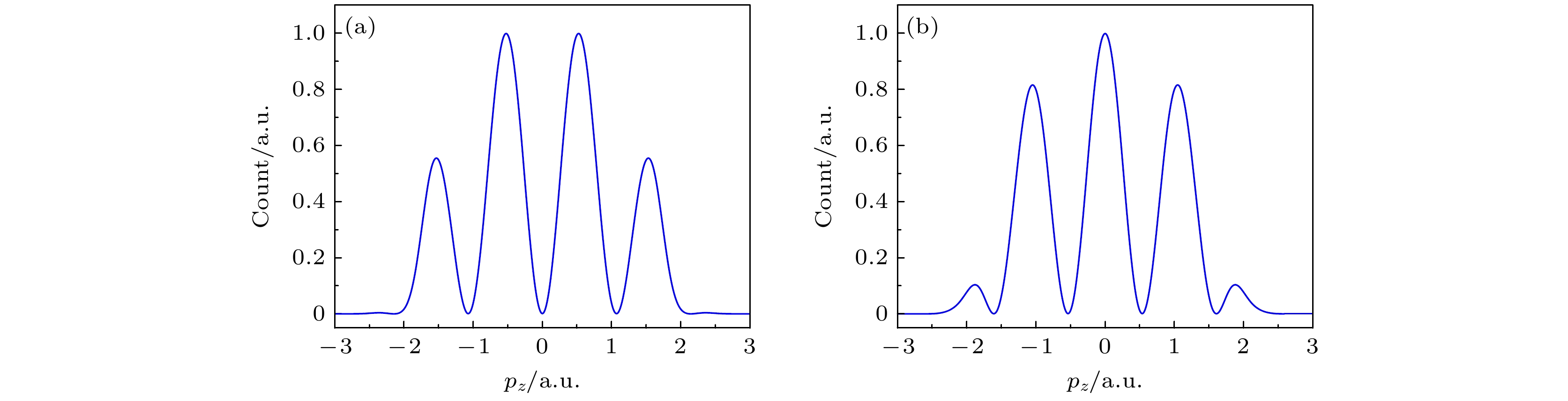
上面的分析已经表明, Ne₂二聚体在圆偏振激光场下的动量分布直接对应于缀饰态的干涉项, 因此可以根据动量分布提取分子核间距信息, 之前的研究已经证实了这种方案的可行性^[39]. 为了更加精确地提取核间距信息, 图4给出了将图2(d)和图2(h)中动量分布沿$ p_{x} $方向积分后的电离率随$ p_{z} $的变化. 图4(a)展示了对称性轨道的函数关系, 其在$ p_{z} = 0$处为极小值, 呈现出周期为1.07 a.u.的振荡行为. 而图4(b)则揭示了反对称性轨道的函数关系, 与图4(a)反相, 在$ p_{z} = 0$处为极大值, 但是振荡周期与图4(a)相同. 将这一周期代入下式:

可得R₀ = 5.87 a.u., 这与计算中用到的核间距R₀ = 5.86 a.u.相近.

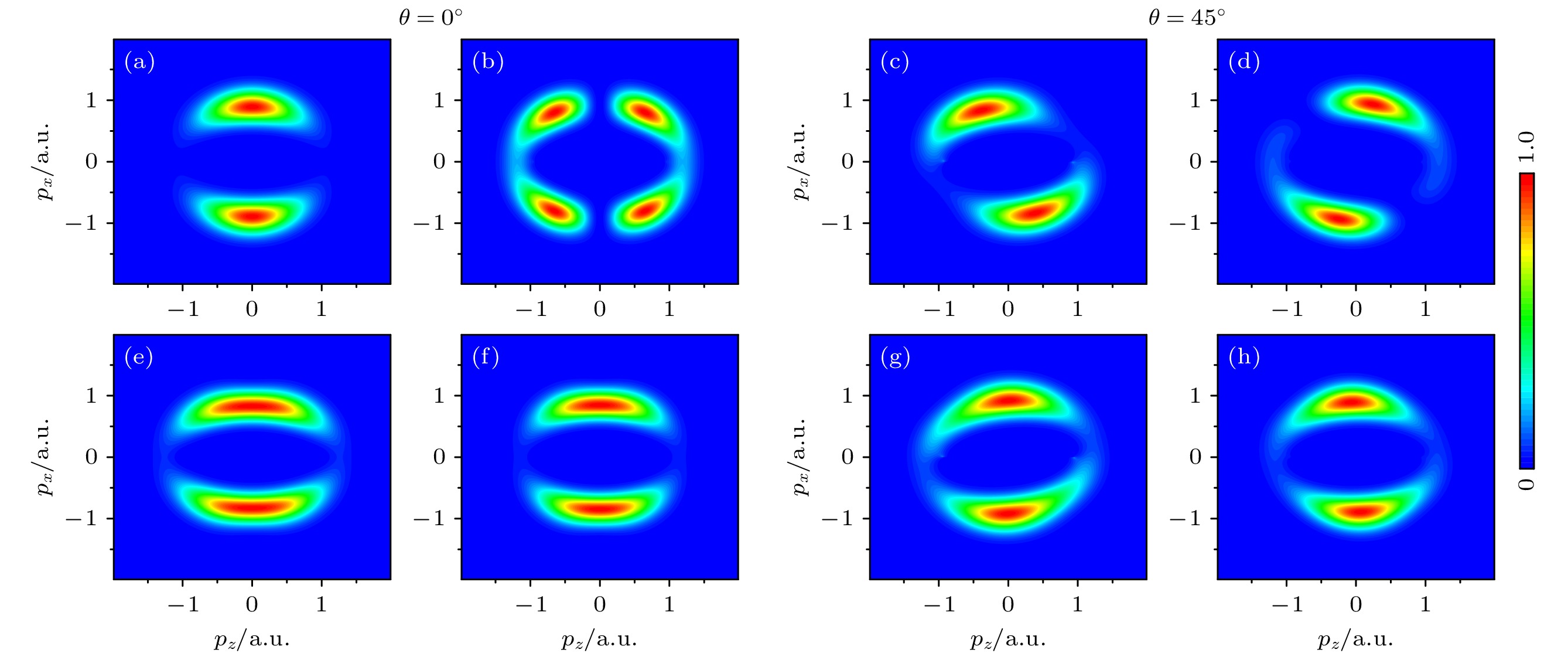
上述计算结果表明对于Ne₂这样的具有较大核间距的分子, 需要考虑缀饰态才能得到与实验一致的结果. 那么对于N₂这样的核间距较小的分子, 是否也需要采用缀饰态呢? 因此我们分析了N₂分子在椭偏振光下的光电子动量分布特性, 并将相关结果展示在图5中. 计算中采用与之前实验结果^[33]相同的参数. 激光峰值光强为$ 1.8\times10^{14}\;{\rm{W}}/{\rm{cm}}^{2} $, 波长为800 nm, 椭偏率为0.82, N—N键长设定为2.073 a.u., 分别计算了最外层占据轨道(HOMO)以及次外层占据轨道(HOMO-1)的电离. N₂的HOMO为对称的$ {\text{σ}}_{\mathrm{g}} $轨道, HOMO-1为反对称的$ {\text{π}}_{\mathrm{u}} $轨道, 波函数由Gaussian软件计算得到. 图中横轴与纵轴分别对应激光场的长轴与短轴.

图5分别呈现了N₂的HOMO和HOMO-1在不同准直角下的光电子动量分布. 图5左侧一组图展示了准直角(与激光场长轴的夹角)为$ 0^\circ $时的光电子动量分布. 具体来看, 在非缀饰态下, 图5(a)和图5(e)中的动量分布沿激光场短轴方向分布, 但HOMO-1的分布范围更宽. 这表明在不考虑场缀饰时, 小核间距分子轨道的对称性会显著影响动量分布, 这与图2中Ne₂的情况有所不同. 图5(b)和图5(f)是缀饰态的情况, 与图2(b)和图2(f) 中Ne₂的分布相比, 对称性轨道在$ {{p}}_{z} = 0 $左右两侧仍然可以观察到两个明显的峰, 而反对称性轨道, 在图5(f)中没有看到类似于图2(f)中的干涉条纹, 原因是N₂的核间距小, 对应的干涉条纹间距较大, 已经超出了动量分布的范围. 右侧一组图是在准直角为$ 45^\circ $时的光电子动量分布. 在图5(c)中, 动量分布因准直角的改变而发生了偏转, 呈现出的两个结构分别位于二、四象限, 这一结果与Yan等^[33]在2020年的实验结果一致. 而缀饰态的分布却在一、三象限, 这一结果与实验观测结果明显不同. HOMO-1的反对称性轨道$ {\text{π}}_{\mathrm{u}} $的结果并不依赖于分子缀饰态, 分布的结构相对更窄, 沿$ p_{x} $轴有些偏转. 综上所述, 对于那些核间距较小的分子而言, 选择非缀饰的初态会是更为合适的选择.

以上的分析都基于SFA的计算结果, 即忽略了电离电子受到的离子库仑势的作用. 为了更接近真实情况, 也用CCSFA方法计算了N₂和Ne₂不同分子轨道对应的光电子动量分布. 依据前面分析的结论, 在CCSFA计算中对N₂采用非缀饰态, 而对Ne₂则采用缀饰态. 图6(a)与图6(c)分别呈现了N₂的非缀饰态下HOMO和HOMO-1的动量分布. 与SFA方法所得结果(图5(a)与图5(e))相比, 可以清晰地观察到, 分布的整体结构没有发生变化, 但是发生了一定角度的偏转. 类似地, 图6(b)与图6(d) 中Ne₂缀饰态下的${\text{σ}}_{\mathrm{g }}$和$ {\text{σ}}_{\mathrm{u}} $的光电子动量分布也呈现出与图2(d)和图2(h)中同样的干涉结构, 只是发生一定角度的偏转. 由此可见, 库仑势主要导致动量分布产生一定角度的偏转, 并不会改变动量分布的结构. 类似地, 也可以根据图6中的干涉条纹来提取核间距$ {R_{0}} $. 然而, 由于干涉项中的$ {\boldsymbol{p}} $是未受到库仑势扰动的动量, 若要获取条纹宽度$\Delta{p} $, 则需首先得到未受库仑势扰动的动量分布, 这可以通过反向旋转动量分布的方式实现. 通过旋转动量分布使得图6(b)和图6(d)中的极小值和极大值位于$ p_{z} = 0$的位置, 随后, 对$ p_{x} $轴方向的电离率进行积分, 得到$ p_{z} $方向的一维动量分布, 从而获得到更精确的$ \Delta{p} $, 如图6(e)和图6(f)所示. 由于在实际情况中, 不同动量电子受到库仑势的偏转并不完全相同, 将动量分布整体偏转并不能完全消除库仑势影响. 因此图6(e)中的极大值和图6(f)中的极小值都不在$ p_{z} = 0$位置, 不过依然可以呈现出清晰的周期性振荡结构. 通过读取峰的间距$ \Delta{p} $, 再根据方程(13), 可以计算出核间距为R₀ = 5.87 a.u., 与计算中采用的核间距一致, 证明了该方法的有效性.

SFA基本思想要求初态为无场下的系统本征态, 而电离过程的空间平移不变性要求初态为激光场缀饰态, 分别对应非缀饰态和缀饰态两种形式的分子SFA理论. 本文采用SFA方法及CCSFA方法对(椭)圆偏振激光场中N₂和Ne₂分子的电离过程进行了研究, 对两种理论的适用范围进行了仔细甄别. 分别计算了两种分子的不同分子轨道在考虑和不考虑缀饰态两种情况下的光电子动量分布, 并与已有的实验结果进行了对比. 研究结果表明: 对于核间距较大的分子, 如Ne₂, 只有考虑缀饰态时计算结果才能与实验结果相符; 而对于核间距较小的分子, 如N₂, 考虑非缀饰态所得结果与实验结果一致. 因此, 我们认为非缀饰态分子SFA适合描述小核间距分子的电离过程, 而缀饰态分子SFA则适合描述大核间距分子的动力学. 这一结论对不同光强都是适用的. 上述结论的原因是, 跃迁矩阵元中由于原子中心平移导致的额外非物理项依赖于核间距的大小. 当核间距较小时, 这一额外项的效应较弱, 因此用非缀饰态就可以正确描述电离过程. 但是当核间距较大时, 这一额外项将会产生非常显著的非物理效应, 必须考虑对初态的缀饰才能将其消除, 从而得到正确的结果. 此外, 我们发现两种分子的分子轨道特性都会影响光电子动量分布. 尤其是对于Ne₂, 其光电子动量分布中的干涉结构与分子双中心干涉项直接对应, 可以从中准确提取分子核间距. 另外还发现, 库仑场效应并不会影响圆偏场中光电子分布的基本结构.