-
由于量子柴郡猫揭示了量子世界中物质与其物理属性之间灵活多变的关系, 所以引起了广泛关注. 早在2013年, 研究人员在弱测量理论的基础上发现了光子的偏振可以与本体分离[1]的现象, 并将这种物体的某一属性和本体发生分离的现象命名为量子柴郡猫. 基于这一现象, 研究人员又实现了包括光子、电子和中子等微观粒子的量子柴郡猫实验[2-12]. 能实现量子柴郡猫现象的弱测量技术[13]目前主要分为两类: 一类是利用系统与指针之间的弱耦合[13,14], 通过对指针的直接测量而间接得到系统的相关信息; 另一类则是通过系统与环境之间的弱耦合, 借助光晶格[15]和粒子干涉仪[16]进行虚数时间演化(imaginary time evolution, ITE)[7,12,17], 根据虚数时间建立起环境和系统之间的联系, 通过环境在虚数时间内的扰动得到系统的相关信息. 对于指针弱测量, 因为需要构建的随时间演化的力学量是同时与指针和系统相关的, 对指针的波函数进行直接测量时, 不会引发系统波函数的坍缩, 同时两者耦合能较为简单地构建, 所以大多应用于对单一粒子进行测量. 在两个或者多个粒子的系统中, 因为被测目标过多, 此时引入指针会导致测量和计算变得极其复杂, 而ITE并不引入额外的指针, 并且还能最大程度地保持系统的量子相干性, 所以ITE在处理多体波函数或者多量子比特波函数时有更大优势.
到目前为止, 量子柴郡猫效应在单粒子系统中已有较多研究. 例如, 在单粒子系统中, 通过无创性的弱测量实现光子的位置和自旋的分离[4]; 在退相干情况下实现光子的位置和自旋的分离[6];在混乱的环境中把系统分离出来, 实现光信号的放大[9]; 光子的本体和偏振分离以后, 在没有光子的空间中再利用弱测量使得偏振发生改变[10];实现光子的波动性和粒子性的分离, 即分别在不同的路径上测到光子的波动和粒子特性[7]; 将中子发射到硅晶体干涉仪当中, 对其位置和磁矩进行弱测量, 实现中子的位置与自旋的分离[2]以及通过晶体干涉仪, 实现中子的位置、自旋以及能量三种属性的分离[3]. 在多粒子系统中, 文献[11]和文献[12]根据光子对的波函数具有交换对称性的特点, 构建自旋和位置相关的前选态, 通过量子柴郡猫效应实现了两个光子的自旋发生永久性交换. 目前在费米子的多粒子系统中的量子柴郡猫效应的研究还尚不完善, 所以本文以自旋-1/2为例, 构建出两者关于位置和自旋的前选态, 对这两个前选态进行弱测量并提取弱值, 从而完成了在多费米子系统下的量子柴郡猫效应的数值实验.
本文的结构如下: 第2节介绍弱值的基本概念和量子柴郡猫效应中自旋-1/2原子对的理论框架; 第3节对两个自旋-1/2原子对的前选态进行弱测量, 然后再对引入延迟选择后的原子对进行弱测量; 第4节给出结论.
-
Aharonov等[13]引入名为弱值的物理量, 通过双态矢理论[18]在实验中发现, 可以通过测量得到的弱值将粒子自旋分量的测量值从1/2放大到100, 即弱值可以增大测量值. 由此可以看出, 弱值不同于传统的直接测量得到的期望值, 它是由两个不同的初末态矢与弱测量共同决定的一种数值. 假设
$ {\hat{A}} $ 为系统中任意一个可观测量, 则关于$ {\hat{A}} $ 的弱值$ {\langle}A{\rangle}_{{\mathrm{w}}} $ 可以写成:其中
$ |i{\rangle} $ 为系统的前选态,$ {|f{\rangle}} $ 为系统的后选态.$ |{i}{\rangle} $ 和$ {|f{\rangle}} $ 可以根据所测的力学量人为设定. 对于对自旋-1/2原子系统, 本文讨论对原子的位置和自旋的弱测量, 关于位置的测量算符为$ {\varPi}_{\mathrm{u}} = {|u{\rangle}}{{\langle}u|} $ 和$ {{\varPi}_{\mathrm{d}} = {|d{\rangle}}{{\langle}d|}} $ (下标u代表上路径, d代表下路径). 自旋的测量算符为$ S_z = {1}/{2}(|{\uparrow}{\rangle}{\langle}{\uparrow}|-|{\downarrow}{\rangle}{\langle}{\downarrow}|) $ (取$ \hbar = 1 $ ), 其中$ |\uparrow\rangle $ 和$ |\downarrow\rangle $ ,$ |u\rangle $ 和$ |d\rangle $ 都是彼此正交的, u和d为原子可能通过的两条路径. 此外, 量子柴郡猫效应和惠勒提出的延迟选择实验[19]共同体现了量子力学中的时间对称性原则, 即系统的性质不仅会受到过去事件的影响, 同时还会受到未来事件的影响. 文献[5]和文献[8]将量子柴郡猫效应和延迟选择结合, 分别实现了单光子和单中子在量子柴郡猫效应下的延迟选择, 以及光子和中子的本体和自旋分离. 所以本文在研究多费米子系统自旋交换的同时, 还将延迟选择引入柴郡猫实验中, 进而讨论在多费米子体系下的延迟选择与量子柴郡猫效应共同作用的结果.实验原理如图1所示, 本文考虑2个自旋-1/2的原子, 通过制备合适的前选态和后选态使得两个原子的自旋发生交换. 在前选择部分, 预设这两个粒子的前选态为线性簇态[13,20-22],
将处于此状态的两个粒子进行弱测量. 首先, 通过一个分束器使得这两个粒子分成两束, 本文将分束后通过图1中下路径的原子称为原子1, 通过上路径的原子称为原子2. 分束后的两个粒子分别进入位置密度处理器和自旋灵敏密度处理器, 这两个处理器的作用分别为模拟对粒子的位置和自旋进行虚数时间扰动. 经过扰动后, 两个粒子将进入到后选择阶段. 在后选择阶段中, 两个粒子同时且同步面临着一个双向开关, 这个开关被一个实时随机生成1或0的随机数发生器所控制. 当两个粒子来到开关处, 若发生器在此刻生成的数字为1时, 两个粒子将在后选择中获得后选态
$ {|f{\rangle}} $ ,而当两个粒子来到开关处发生器生成的数字为0时, 获得的后选态为
将前选态
$ |i\rangle $ ((2)式)和后选态$ |f\rangle $ ((3)式)与两个粒子的位置和自旋的力学量代入弱值的表达式(1)式时, 得到两个原子发生自旋交换时两原子关于位置和自旋的解析解:观测值的非零弱值表明系统确实处于该前选态和后选态上. 相反, 当弱值为零时, 表明系统不在该态上. 根据解析解的结果可以发现, 通过选定的前选态和后选态确实可以实现让原子1出现在下路径, 原子2出现在上路径的同时, 在下路径观测到原子2的自旋, 而在上路径观测到原子1的自旋.
$ \langle\varPi^1_{\mathrm{d}}\otimes S_1\rangle_{\mathrm{w}} $ 和$ \langle\varPi^2_{\mathrm{u}}\otimes S_2\rangle_{\mathrm{w}} $ 为关于α的tan函数. 这表明, 当调控参数α趋近于0, 即$ |\langle f|i \rangle|^2 $ 趋近于1时, 测量成功概率很大; 而α趋近于$ {\pi}/{2} $ 时, 可以实现弱值放大. 可以根据不同的情况设置α的值来得到预期的实验结果. 仅需要考虑α在一个周期内的取值, 即取值范围为$ \left( {0, {\pi}/{2}} \right) $ . 因为当tanα不为0时, 可以在u路径上发现原子1的自旋和在d路径上发现原子2的自旋. 说明两个原子的自旋发生了交换. 若tanα为0, 则说明两个粒子的前选态变为$ |i_{{{\mathrm{tan}}\alpha} = 0}\rangle = {{1}/{\sqrt{2}}}(|{\uparrow}_1{\downarrow}_2{\rangle}- |{\downarrow}_1{\uparrow}_2{\rangle}) |d_1 u_2\rangle $ , 自旋算符与前选态作用后的态矢会与后选态完全正交, 导致弱值总为0, 所以无需考虑α为0的情况. 同理, 当α为$ {\pi}/{2} $ 时, 测量概率即$ |\langle f|i_{{{\mathrm{tan}}\alpha} = {\pi}/{2}}\rangle|^2 $ 为0, 所以不会得到有效的测量结果, 此情况也无需考虑. 而当将前选态$ |i\rangle $ ((2)式)和后选态$ |f_2\rangle $ ((4)式)与两个粒子的位置和自旋的力学量代入弱值的表达式(1)式时, 得到两个原子不发生自旋交换时两原子关于位置和自旋的解析解, 还需说明的是, 本研究未考虑单独对自旋弱值测量的原因是两个原子的自旋是必然存在的, 无需进行单独的测量.同理, 根据弱值公式得到系统在不发生交换的情况下的解析解为
此时的弱值结果表明, 两个粒子的自旋并未发生交换, 但因初末态矢影响, 结果上与本征值略有不同, 原子2的自旋为负数. 两种不同的后选态导致最后得到的测量结果大相径庭, 这充分体现出量子世界中的时间对称性, 即使弱测量已经完成, 而在后面发生的延迟选择也影响了先前的测量.
-
第2节具体介绍了对前选态和后选态的预设与弱值的解析解的结果. 接下来详细介绍如何通过ITE的方式获取实验的数值解. ITE起源于狭义相对论中的Wick旋转[23], 目前大多应用于量子场论[24]和量子模拟[25]等不同领域. ITE是一种基于系统的扰动而不引入任何辅助指针状态的弱值提取方式. 由两个粒子的可观测量Π或
$ \varPi\otimes S $ 生成的非酉矩阵:$ {\boldsymbol{U}}(H, t) $ 的作用为对系统在虚数时间上进行演化[26], 其中H为系统的哈密顿量, H的作用是生成系统演化的算符, H的表达式为H = O, O代表可观测量. 参数t是虚数形式的时间参数, 一般不受限制. 但在ITE中, t必须足够小, 从而保证在相互作用时间内系统受到的扰动最小. ITE提取弱值的优势在于无需引入额外的仪表态, 大大简化问题, 并且在不涉及虚数的情况下, 弱值的提取依然可以通过ITE来实现, 此时哈密顿量的弱值实数部分与通过ITE得到的函数斜率成正比. 在ITE中, 施加扰动前后成功后选择的概率为$ N_0 = |{\langle}f|i{\rangle}|^2 $ 和$ N(U) = {|{\langle}f|U|i{\rangle}|^2} $ . 归一化符合率$ N(t) $ 和前两者的关系为在本实验中, 弱值与
$ N(t) $ 的函数关系为首先确定待测量系统的前选态和后选态, 从而获得
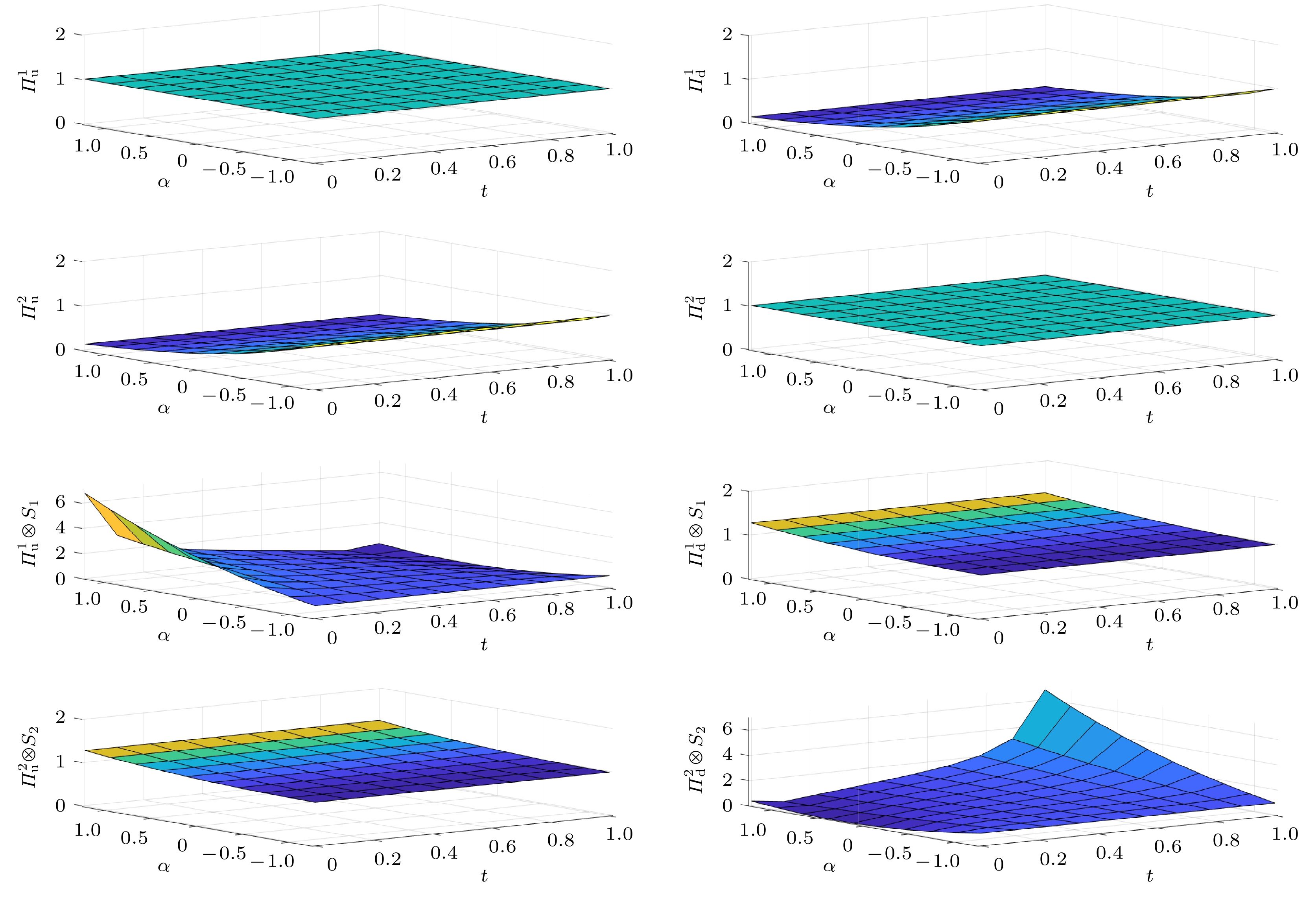
$ N_0 $ , 再将两个原子的位置与自旋的力学量分别代入$ N(U) $ 中, 就可以获得两个原子的位置与自旋的归一化符合率$ N(t) $ . 为了模拟对环境进行微扰, 虚数时间演化后获取系统的弱值. 因为位置密度处理器与自旋灵敏密度处理器是弱测量得到系统位置弱值的重要实验器件. 所以本文在弱测量部分, 假定采用一系列不同透射率(透射率T和t的关系为$ T = {\mathrm{e}}^{-2 t} $ )的位置密度处理器来模拟对位置和自旋的扰动. 根据虚数时间的演化, 透射率也随着发生变化, 分别计算出不同虚数时间情况下系统的归一化符合率. 根据这些虚数时间相关的数据点进行线性拟合得到曲线, 通过分析曲线根据(11)式得到弱值的数值解. 首先, 讨论不考虑延迟选择的情况, 即系统的后选态必为(3)式.如图2所示, 当后选态为(3)式时, 通过调控前选态的α可以获取不同的弱值结果. 将
$ \varPi^1_{\mathrm{u}} $ ,$ \varPi^2_{\mathrm{d}} $ ,$ \varPi^2_{\mathrm{u}} $ ,$ \varPi^1_{\mathrm{d}} $ ,$ \varPi^1_{\mathrm{d}}\otimes S_1 $ ,$ \varPi^2_{\mathrm{u}}\otimes S_2 $ ,$ \varPi^1_{\mathrm{d}}\otimes S_1 $ 和$ \varPi^2_{\mathrm{u}}\otimes S_2 $ 分别代入(9)式获得相关的各非酉矩阵, 再将这些非酉矩阵与通过调控α值获得的多种不同的前选态代入(10)式得到各个力学量在虚数时间演化下的归一化符合率. 在一个周期内, 即$ \alpha\in(-{\pi}/{2}, {\pi}/{2} $ ), 对于可观测量$ \varPi^1_{\mathrm{u }}$ ,$ \varPi^2_{\mathrm{d}} $ ,$ \varPi^1_{\mathrm{d}}\otimes S_1 $ 和$ \varPi^2_{\mathrm{u}}\otimes S_2 $ 的归一化符合率几乎也不受t和α影响.$ \varPi^2_{\mathrm{u }}$ 和$ \varPi^1_{\mathrm{d}} $ 的归一化符合率的变化仅和t相关. 而$ \varPi^1_{\mathrm{d}}\otimes S_1 $ 和$ \varPi^2_{\mathrm{u}}\otimes S_2 $ 的归一化符合率与t和α有一定的函数关系. 结合(5)式和(6)式的解析解可以得出,$ \varPi^1_{\mathrm{u}} $ 和$ \varPi^2_{\mathrm{d}} $ 理论上弱值结果与α无关, 但是实验结果出现了归一化符合率随α取值变小而变小的结果. 这说明环境对系统的微小相互作用可能对系统产生影响, 随着时间演化, 前选态中的参量并未因态的正交完全消除, 说明前选态的纠缠度被环境所影响而发生了改变. 对于$ \varPi^1_{\mathrm{d}}\otimes S_1 $ 和$ \varPi^2_{\mathrm{u}}\otimes S_2 $ 的N随着α变化走势相同, 而随t的变化走势相反.为了简化通过归一化符合率对弱值的提取, 本文以
$ \alpha = {\pi}/{4} $ 为例提取弱值. 此时系统的前选态为然后通过ITE提取实验的数值解与解析解进行对比. 其中, 在α取
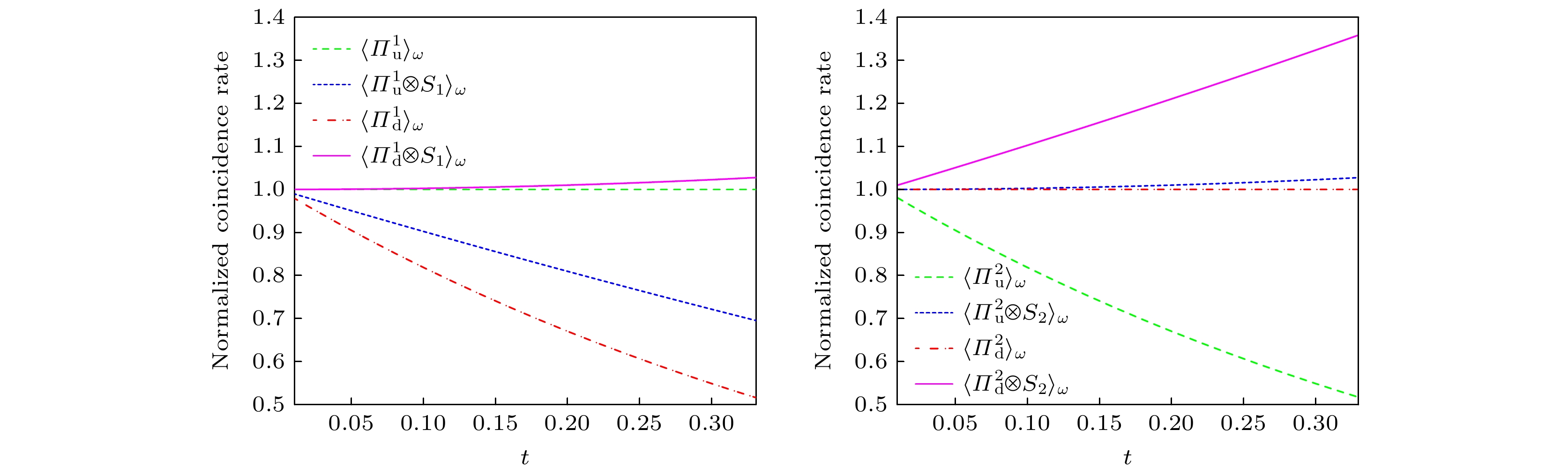
$ {\pi}/{4} $ 时, 获取各力学量归一化符合率的方法同α变化时的前选态的部分相同.如图3所示, 其中归一化符合率
$ N(t) = \dfrac{N(U)}{N_0} $ 为采样数据点的纵坐标, 时间t为横坐标, 可根据归一化后的数据点拟合出来的直线得到数值解. 系统进行ITE后得到的关于两个原子位置和自旋的$ N(t) $ 的数据. 其中,$ \langle\varPi^1_{\mathrm{u}}\rangle_{\mathrm{w}} $ ,$ \langle\varPi^2_{\mathrm{d}}\rangle_{\mathrm{w}} $ ,$ \langle\varPi^2_{\mathrm{u}}\otimes S_2\rangle_{\mathrm{w}} $ 和$ \langle\varPi^1_{\mathrm{d}}\otimes S_1\rangle_{\mathrm{w}} $ 的归一化符合率与相互作用时间t的关联性很低, 而$ \langle\varPi^2_{\mathrm{u}}\rangle_{\mathrm{w}} $ ,$ \langle\varPi^1_{\mathrm{d}}\rangle_{\mathrm{w}} $ ,$ \langle\varPi^1_{\mathrm{u}}\otimes S_1\rangle_{\mathrm{w}} $ 和$ \langle\varPi^2_{\mathrm{d}}\otimes S_2\rangle_{\mathrm{w}} $ 的归一化符合率与相互作用时间t有很明显的函数关系, 对图3中8条曲线进行线性拟合与概率校正获取弱值. 通过(10)式得到各观测量的归一化符合率, 并将各观测量的归一化符合率代入(11)式,此时就得到了通过ITE提取的弱值的数值解. 对于原子1和原子2的位置和自旋相关的纠缠态, 若对其波函数进行直接测量, 几乎很难确定两个原子所处位置和两个原子的自旋状态, 进行多次测量会得到两个原子在u和d路径出现的概率与两个原子是自旋向上或是自旋向下的概率均为1/2. 但当对系统进行弱测量(ITE)时, 得到的测量结果为原子1仅会出现在u路径, 原子2出现在d路径; 并且只能在u路径观察到原子2的自旋, 只能在d路径观察到原子1的自旋. 此时得到的数值解与第2节的解析解基本符合, 理论上验证了实验的可行性. 而当自旋交换不发生时, 根据第2节的解析解可以得出, 弱值与α并不直接相关, 但测量成功概率仍受α影响. 所以, 将延迟选择实验引入多粒子系统的量子柴郡猫效应后, 在后选择中出现两种后选态, 两个原子和自旋可以定位在不同的选择上, 通过切换不同的后选态, 两个原子本体和它们的自旋的弱值将产生不同的结果. 由于干涉仪中原子和自旋位置的测量可以独立于延迟选择过程进行, 选择一个方向进行后选择, 因此可以研究延迟选择对先前测量的影响. 为了更直接地体现出延迟选择带来的影响, 继续取
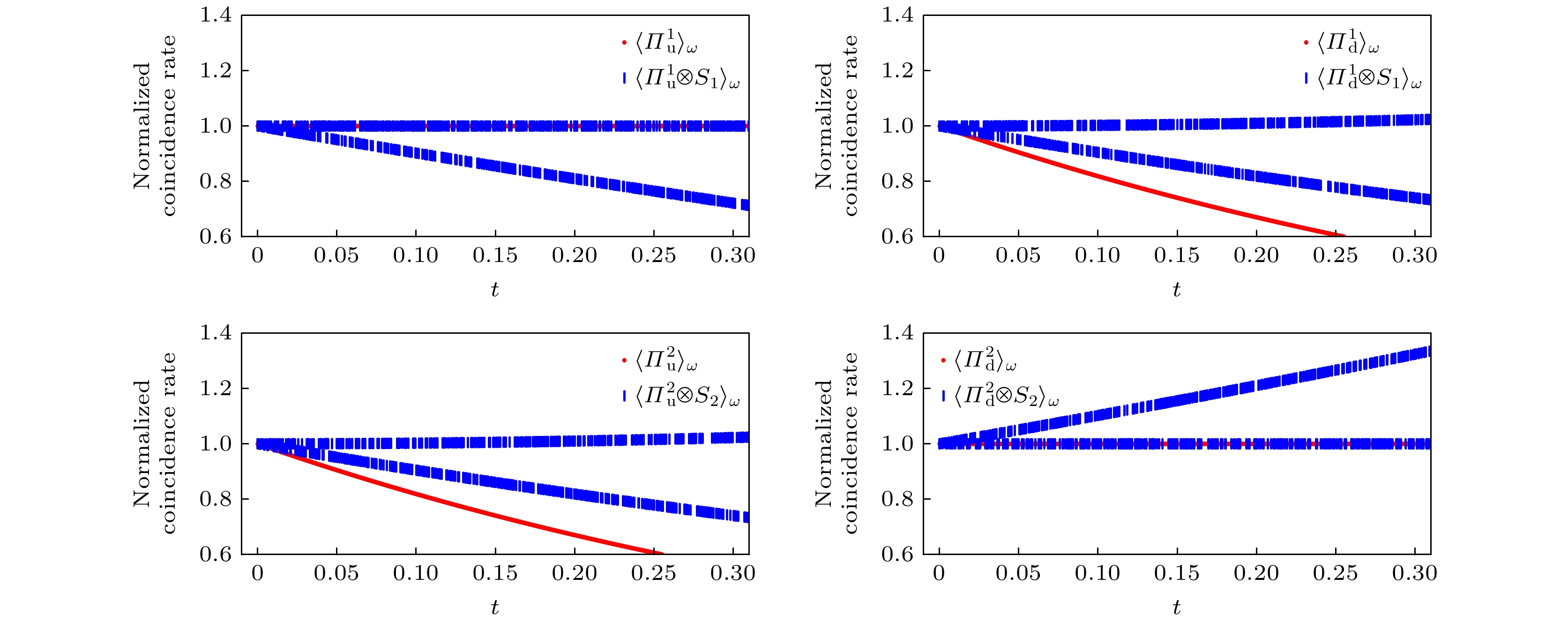
$ \alpha = {\pi}/{4} $ 计算系统的弱值.与图3相比, 图4多了一种后选择, 所以在图中不仅将不同的原子在数据上进行区分, 而且将不同的位置也做了区分, 在4个图中展示系统的归一化符合率与t之间的关系. 当两个原子自旋不发生交换时, 自旋和位置的弱值走势一致. 当自旋发生交换时, 与图4中的弱值一致, 这说明延迟选择确实对系统产生了影响, 不同的后选态影响了先前被测量过的系统. 通过不同透射率的原子获得不同的后选态后被探测器接收, 并对各点进行线性拟合后, 根据ITE获取弱值的表达式(11)式和对实验结果进行拟合, 计算得到系统在延迟选择中的数值解为
通过对比系统的数值解和解析解可以得出, 当后选态为
$ |f\rangle $ 时, 正如预期的那样, 两个原子的自旋发生了交换; 在后选择处加入延迟选择后, 在后选择部分有了一个额外的后选态, 这个后选态为$ |f_2\rangle $ . 当系统处在这个后选态时, 原子1和原子2自旋没有形成交换, 说明测量所得的数值与原子1或原子2的自身性质相对应, 此解析解和与数值解相符合, 说明费米子系统在多粒子量子柴郡猫效应中也满足时间对称性, 即彼此之间的自旋交换发生是随机的, 后选择与延迟选择共同影响了发生在测量之前的测量值. -
本文探讨了两个自旋-1/2原子系统受量子柴郡猫效应的影响, 通过构建原子的前选态和后选态, 应用ITE获取弱值, 在后选择中的延迟选择使得两个原子的自旋交换充满了随机性. 在自旋交换发生时, 它们的自旋弱值呈现出与tan函数相符合的特性, 即在实现自旋交换的同时还实现了自旋弱值放大或缩小. 放大的好处是便于在有噪声的环境或者探测器饱和的环境中更容易获得更精准的测量值, 而缩小的好处是提高测量成功概率. 可以将两者结合, 对系统进行多次测量, 从而获得更完备的测量结果. 而当两个原子获得的是不发生自旋交换的后选态时, 在量子柴郡猫效应和延迟选择效应的共同作用下, 即使系统已经经过演化, 但是自旋和位置的信息仍与系统被测量前的信息保持一致. 此外, 延迟选择实验进一步揭示了量子柴郡猫的物理内涵. 由于弱值信息的特殊性质, 只有适当的后选态才能准确提取到有用的信息. 通过属性交换实现多方通信, 并利用弱值放大提高信号的抗干扰能力, 提高信号通信效率. 基于以上特点, 我们期望这些研究成果能够在量子电路、量子通信和量子精密测量领域得到实际应用.
两个自旋-1/2原子的自旋交换
Spin exchange of two spin-1/2 atoms
-
摘要: 量子柴郡猫效应是量子力学中的一种重要现象, 它揭示物理属性与载体的可分离性, 突破了经典物理中属性必须依附于物体的固有框架, 为量子信息与量子精密测量提供了新视角. 本文基于量子柴郡猫效应, 通过前选择过程制备了一个由两个粒子组成的自旋-1/2原子系统的前选态. 对这些粒子的自旋和位置进行了量子弱测量, 并随后实施了策略性的后选择. 在后选择过程中, 设计了两个不同的后选态. 完成弱测量的粒子会沿着不同的路径演化, 最终达到不同的后选态. 最终测量结果表明, 其中一个后选态导致两个粒子的自旋发生了交换并得到了放大; 而另一个后选态则使得两个粒子即使经历了弱测量, 但状态仍然与测量前保持一致. 本研究从理论上证实了费米子系统在两体量子柴郡猫效应中的可行性, 并展示了延迟选择如何影响自旋-1/2原子系统的量子柴郡猫效应.Abstract: The quantum Cheshire cat effect is an important phenomenon in quantum mechanics that reveals the separability of physical properties from their carriers. This effect transcends the classical framework whose attributes must be inherently attached to objects, providing new perspectives for quantum information and precision measurement. According to the quantum Cheshire cat effect, we prepare a pre-selected state of a spin-1/2 atomic system composed of two particles through a pre-selection process. We conduct quantum weak measurements on the spins and positions of these two atoms and extract weak values by using the method of imaginary time evolution (ITE). Subsequently, we perform post-selection on these two atoms and design two distinct post-selected states. Initially, we calculate analytical solutions when both atoms encounter these two different post-selected states separately. Then, during the stage of obtaining weak values via ITE, we first discuss the scenario with only one post-selected state. In this case, our experimental goal is to achieve spin exchange between the two atoms. We use ITE to obtain normalized coincidence rate for the system. By linearly fitting these normalized coincidence rate, we derive numerical solutions for the weak values of the system. The comparison between the analytical solutions and numerical results indicates that they are in close agreement, demonstrating that our method promotes spin exchange between the two atoms. Next, we examine scenarios involving both post-selected states in the post-selection process. After completing weak measurements on particles, delayed-choice allows them to evolve along different paths ultimately leading to distinct post-selected states. One particular post-selected state that results in final measurement outcomes indicates that the spin exchange occurs between both particles with amplification. Conversely, the other post-selected state ensures that even after undergoing weak measurement and delayed-choice, the states of the two particles remain consistent with their pre-measurement conditions. We also compare the analytical and numerical solutions of the experiment involving delayed choice and find that they are very consistent with each other. This consistency indicates that delayed-choice indeed has a significant influence on whether the final exchange occurs. Our research theoretically confirms the feasibility of fermionic systems within bipartite quantum Cheshire cat effects and illustrates how delayed-choice influences quantum Cheshire cat effects in spin-1/2 atomic systems.
-
Key words:
- quantum information /
- weak value /
- quantum Cheshire cat .
-

-
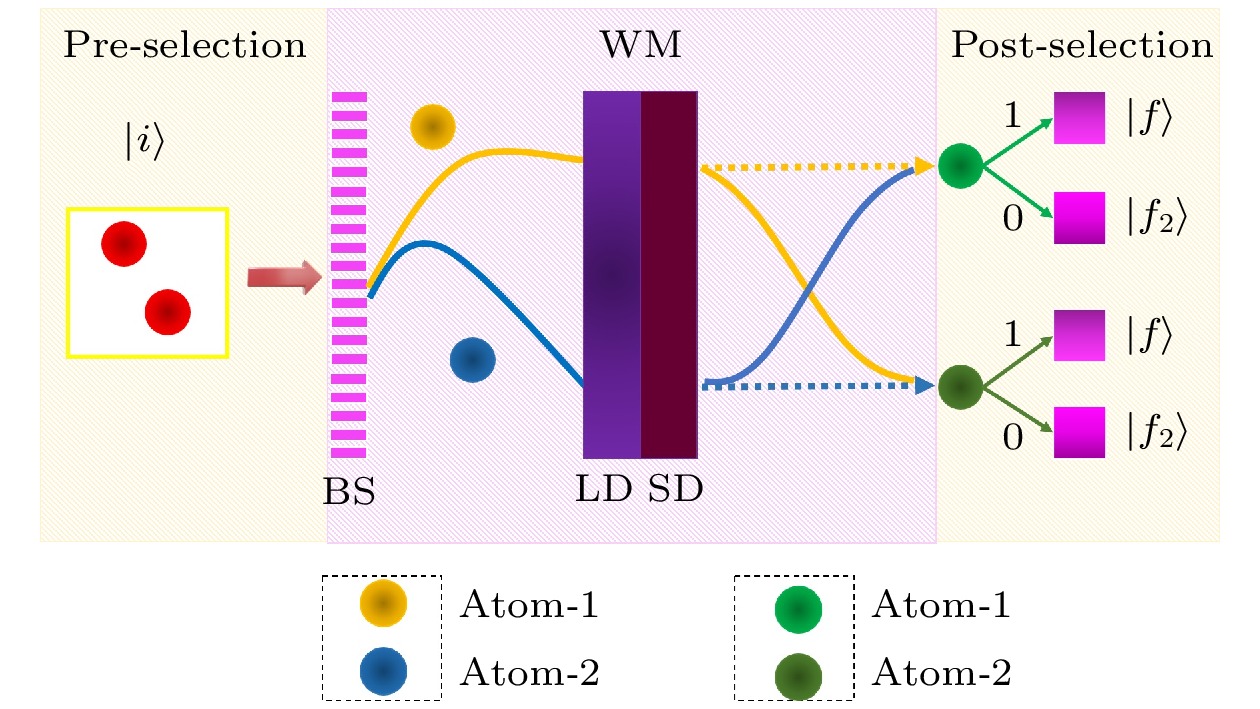
图 1 自旋-1/2原子自旋交换及自旋放大原理示意图. 在前选择部分, 制备出符合理论预期的前选态
$ |i\rangle $ . 在弱测量(WM)部分, 分束器(BS)将两个原子分束, 两个原子分束后进入位置密度处理器(LD)与自旋灵敏密度处理器(SD)中. 在后选择部分, 两个原子通过一个由1与0控制的随机开关同步进行选择, 确保两个原子同时随机获取其中一种后选态. 两个原子通过BS后, 将通过下路径的原子称为原子1, 以黄色表示; 将通过上路径的原子称为原子2, 以蓝色表示. 完成弱测量后, 用浅绿色表示原子1, 深绿色表示原子2Figure 1. Schematic diagram of spin-1/2 atomic spin exchange and spin amplification principle In the pre-selection section, prepare a pre-selected state
$ |i\rangle $ that meets theoretical expectations. In the weak measurement (WM) section, the beam splitter (BS) splits two atoms into beams, which then enter the position density processor (LD) and spin-sensitive density processor (SD). In the post-selection section, two atoms will select synchronlusly through a random switch controlled by 1 and 0, ensuring two atoms simultaneously randomly obtain one of the post-selected states. After two atoms pass through BS, the atom passing through the downward path is called atom-1, represented in yellow; the atom passing through the upper path is called atom-2, represented in blue. After completing the weak measurement, use light green to represent atom-1 and dark green to represent atom-2.图 3 在α取
$ {\pi}/{4} $ 时, 两个原子的归一化符合率N(t)随t的变化趋势. 左图为原子1的数据, 右图为原子2的数据. 因N(t)与t存在函数关系, 所以此处直接用弱值符号代表相关可观测量的N(t)Figure 3. When α takes
$ {\pi}/{4} $ , the normalized coincidence rate N(t) of two atoms varies with t. The left image shows the data for atom-1, and the right image shows the data for atom-2. Due to the functional relationship between N(t) and t, weak values are directly used here to represent the N(t) of the relevant observables. -
[1] Aharonov Y, Popescu S, Rohrlich D, Skrzypczyk P 2013 New J. Phys. 15 113015 doi: 10.1088/1367-2630/15/11/113015 [2] Denkmayr T, Geppert H, Sponar S, Lemmel H, Matzkin A, Tollaksen J, Hasegawa Y 2014 Nat. Commun. 5 4492 doi: 10.1038/ncomms5492 [3] Danner A, Geerits N, Lemmel H, Wagner R, Sponar S, Hasegawa Y 2024 Commun. Phys. 7 14 doi: 10.1038/s42005-023-01494-5 [4] Kim Y, Im D G, Kim Y S, Han S W, Moon S, Kim Y H, Cho Y W 2021 npj. Quantum. Inf. 7 13 doi: 10.1038/s41534-020-00350-6 [5] Das D, Sen U 2021 Phys. Rev. A 103 012228 doi: 10.1103/PhysRevA.103.012228 [6] Richter M, Dziewit B, Dajka J 2018 Adv. Math. Phys. 2018 7060586 doi: 10.1155/2018/7060586 [7] Li J K, Sun K, Wang Y, Hao Z Y, Liu Z H, Zhou J, Fan X Y, Chen J L, Xu J S, Li C F, Guo G C 2023 Light Sci. Appl. 12 18 doi: 10.1038/s41377-022-01063-5 [8] Wagner R, Kersten W, Lemmel H, Sponar S, Hasegawa Y 2023 Sci. Rep. 13 3865 doi: 10.1038/s41598-023-29970-6 [9] Ghoshal A, Sau S, Das D, Sen U 2023 Phys. Rev. A 107 052214 doi: 10.1103/PhysRevA.107.052214 [10] Hance J R, Ladyman J, Rarity J 2024 New J. Phys. 26 073038 doi: 10.1088/1367-2630/ad6476 [11] Das D, Pati A K 2020 New J. Phys. 22 063032 doi: 10.1088/1367-2630/ab8e5a [12] Liu Z H, Pan W W, Xu X Y, Yang M, Zhou J, Luo Z Y, Sun K, Chen J L, Xu J S, Li C F, Guo G C 2020 Nat. Commun. 11 3006 doi: 10.1038/s41467-020-16761-0 [13] Aharonov Y, Albert D Z, Vaidman L 1988 Phys. Rev. Lett. 60 1351 doi: 10.1103/PhysRevLett.60.1351 [14] Ritchie N W M, Story J G, Hulet R G 1991 Phys. Rev. Lett. 66 1107 doi: 10.1103/PhysRevLett.66.1107 [15] Bloch I, Zoller P 2006 New J. Phys. 8 E02 doi: 10.1088/1367-2630/8/8/E02 [16] Puentes G 2015 J. Phys. B. 48 245301 doi: 10.1088/0953-4075/48/24/245301 [17] Mao Y, Chaudhary M, Kondappan M, Shi J, Ilo-Okeke E O, Ivannikov V, Byrnes T 2023 Phys. Rev. Lett. 131 110602 doi: 10.1103/PhysRevLett.131.110602 [18] Aharonov Y, Bergmann P G, Lebowitz J L 1964 Phys. Rev. 134 B1410 doi: 10.1103/PhysRev.134.B1410 [19] Wheeler J A 1978 Mathematical Foundations of Quantum Theory (Amsterdam: Elsevier) pp9–48 [20] Witten E 2018 Rev. Mod. Phys. 90 045003 doi: 10.1103/RevModPhys.90.045003 [21] Amico L, Fazio R, Osterloh A, Vedral V 2008 Rev. Mod. Phys. 80 517 doi: 10.1103/RevModPhys.80.517 [22] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865 doi: 10.1103/RevModPhys.81.865 [23] Wick G C 1954 Phys. Rev. 96 1124 doi: 10.1103/PhysRev.96.1124 [24] Landsman N, van Weert C 1987 Phys. Rep. 145 141 doi: 10.1016/0370-1573(87)90121-9 [25] Xu J S, Sun K, Han Y J, Li C F, Pachos J K, Guo G C 2016 Nat. Commun. 7 13194 doi: 10.1038/ncomms13194 [26] Dressel J, Malik M, Miatto F M, Jordan A N, Boyd R W 2014 Rev. Mod. Phys. 86 307 doi: 10.1103/RevModPhys.86.307 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: