-
由于具有特殊的拓扑电子能带结构, 拓扑绝缘体作为一种新颖的物质量子态成为物理学研究的热点之一[1,2]. 拓扑绝缘体中存在由强自旋-轨道耦合引起的导带-价带反转, 以及受时间反演对称性保护的狄拉克表面态[3,4]. 在打破时间反演对称性进而使拓扑表面态被打开的情况下, 还可得到各类奇特效应, 如量子反常霍尔效应、轴子绝缘体态以及拓扑磁电效应等[5,6]. 近年来, 拓扑光子学将上述这些电子体系中的拓扑绝缘体拓展到电磁波和光学体系[7–9], 是一个快速发展的前沿领域. 通过对拓扑相变机制的深入理解和材料参数的精细调控, 可以实现对光子传输特性的精准控制, 为光子集成电路和量子信息处理技术等领域奠定基础[10–15]. 非互易光子拓扑绝缘体是拓扑光子学的重要分支, 这类材料基于时间反演对称性破缺, 能够支持稳定的拓扑边缘态[16–19]. 这些边缘态具有特殊的传输特性, 如抗弯曲传输、避免散射等, 为光子器件的设计和应用带来了新的可能性.
Casimir效应在近年受到了理论和实验上研究的广泛关注, 该效应的本质是量子真空涨落的一种宏观效果[20]. 真空涨落场在宏观边界下的电磁波模式对应的辐射压力使真空中的两物体间会存在相互吸引或排斥作用力, 研究者们对该作用力在调控微纳米尺度系统领域进行了广泛研究[21–23], 而Casimir旋转作用也存在较大开发潜力[24], 对应的Casimir扭矩也被考察应用于纳米光子和光力系统中[25]. 研究发现电子拓扑绝缘体的磁电耦合效应可增强反射系数矩阵的对角项, 进而可以调控Casimir引力和斥力[26], 研究者同样讨论了光子拓扑绝缘体实现Casimir斥力的可能性[27], 并进一步考虑其对Casimir-Polder效应的影响[28]. 近年来, 研究者考察了周期性多层结构中采用拓扑材料的系统, 如将石墨烯多层膜用于变频和电磁波的吸收[29,30], 利用多层的拓扑材料周期性结构调制Casimir效应[31], 以及发现拓扑磁电效应可以在多层结构中积累[32,33]等. 光子拓扑材料对应的多层结构要比生成电子拓扑材料多层结构要更容易实现, 而且讨论Casimir效应对应的拓扑材料需为时间反演对称性破缺的媒质, 而打破时间反演对称性在电子拓扑系统中一般较困难, 但在光子体系中则相对容易地可通过对特定材料施加磁场来实现[9]. 本文将针对基于时间反演对称性破缺的非互易光子拓扑绝缘体讨论其多层结构间的Casimir作用力. 研究发现, 在某些材料参数下存在Casimir排斥力, 确定了多层非互易性光子拓扑绝缘体系统实现排斥力并得到Casimir相互作用稳定平衡点的可能性; 光轴角度差、层数和层厚度都可作为调控多层系统间的Casimir效应的因素. 在考察改变外偏置磁场的取向以调整旋转各层的光轴角度差对Casimir效应的影响中, 还发现Casimir力随该角度差的变化趋势存在一些拐点, 因此可利用多层系统中的旋转自由度来精细调控Casimir相互作用.
-
考虑如图1展示的两组光子拓扑绝缘体多层结构组成的空间边界系统, 设其间距为L, 各单元层厚度为d. 采用宏观量子电动力学理论的格林张量方法可以计算结构间的Casimir作用力F, 其在转换为虚频
$ \omega = {\text{i}}\xi $ 下积分后的形式为[27]其中,
$ \varphi $ 角表示对所有不同方向模式的积分, k和$ \kappa $ 分别为平行和垂直于界面的波矢分量,$ {{\boldsymbol{\Re}} ^ \pm } $ 表示Fresnel反射矩阵,$ {\mathfrak{D}^ \pm } = 1 - {{\boldsymbol{\Re}} ^ \pm } \cdot {{\boldsymbol{\Re}} ^ \mp }{{\text{e}}^{ - 2\kappa L}} $ , 上角标正负号分别指代左右两组多层系统. 该计算方法普遍适用于拓扑绝缘体等各类非互易性媒质. 设多层系统中光子拓扑绝缘体的介电常数是具有非对称形式的张量:$ \overset{\lower0.5 em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\varepsilon } = \left( {{\boldsymbol{I}} - \hat y\hat y} \right){\varepsilon _x} + \hat y\hat y{\varepsilon _y} + {\varepsilon _n}\hat y \times {\boldsymbol{I}} $ , 并设媒质为磁导率为1. 上述介电常数张量是反对称的, 违反洛伦兹互易定理, 因此是时间反演对称性破缺的系统.采用传输矩阵方法来计算多层系统的反射矩阵. 因在(1)式计算中要考量不同方向
$ \varphi $ 角对应的模式以及后续考察各单元层光轴的旋转自由度(记作$\phi $ 角), 需采取xoy面在旋转上述两种角度后的旋转坐标系下的介电张量形式, 记为$ \overset{\lower0.5 em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\varepsilon }{} ' $ . 按文献[24]中对各向异性媒质内部电磁波模式的计算方法可推出光子拓扑绝缘体情况下的结果, 其中电磁场量对应方程组相应的系数矩阵可计算得到如下形式:其中
$ \varepsilon {'_{ij}} $ ($ i, j = x, y, z $ )为旋转坐标系下介电张量各元素, 而(2)式系数矩阵对应的场量方程组给出所考察系统在各个方向上的电磁学行为. 进而可计算得到光子拓扑绝缘体内部电磁波模式的波矢垂直分量其中,
Casimir效应本质上是相对论性量子场论的结果, 因此上述计算公式中会显含光速c. 根据各分界面处电磁场切向连续的边界条件, 可得到多层系统的总传输矩阵
$ {\boldsymbol{X}} = {{\boldsymbol{Q}}_{{\text{PTI}}}}{\boldsymbol{P}}_N^{ - 1}{{\boldsymbol{Q}}_{{\text{PTI}}}}{\boldsymbol{P}}_N^{ - 1}{{\boldsymbol{Q}}_{{\text{PTI}}}} \ldots $ , 其中$ {{\boldsymbol{P}}_{\text{N}}} = {\rm diag} \{{{\text{e}}^{{\text{i}}\kappa d}} , {{\text{e}}^{{\text{i}}\kappa d}} , {{\text{e}}^{ - {\text{i}}\kappa d}}, {{\text{e}}^{ - {\text{i}}\kappa d}}\} $ 是真空层传输矩阵,$ {{\boldsymbol{Q}}_{{\text{PTI}}}} = {{\boldsymbol{N}}^{ - 1}}{\boldsymbol{M}}{\boldsymbol{P}}_{M}^{ - 1}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{N}} $ 为光子拓扑绝缘体材料层对应传输矩阵, 各分矩阵形式如下:以及
$ {{\boldsymbol{P}}_{\text{M}}} = {\rm diag} \{ {{\text{e}}^{{\text{i}}k_z^{(1)}d}} ,\; {{\text{e}}^{{\text{i}}k_z^{(2)}d}} ,\; {{\text{e}}^{{\text{i}}k_z^{(3)}d}} ,\; {{\text{e}}^{{\text{i}}k_z^{(4)}d}}\} $ .$ \alpha $ ,$ \beta $ 和$ \gamma $ 分别是材料内电磁波模式的磁场x, y分量和电场y分量相对于电场x分量的比值, 由下式 给出:最后可将总传输矩阵X的各矩阵元代入计算反射矩阵:
其中
$\varDelta = {x_{11}}{x_{22}} - {x_{12}}{x_{21}}$ , 从而再代入(1)式计算多层结构光子拓扑绝缘体间的Casimir作用力. -
考察光子拓扑绝缘体的多层结构系统中可调控的Casimir吸引和排斥作用力. 以下记
$ {\omega _0} $ 为相对频率单位, 其相应的真空中波长$ \lambda $ ($ \lambda = c/{\omega _0} $ )作为空间距离的相对单位. 将对系统中Casimir引力和斥力的产生以及光子拓扑绝缘体多层结构空间参数和旋转自由度的影响进行分析和讨论. -
典型的Casimir力包括两个理想导体边界之间或两个无穷磁化板边界之间存在的Casimir引力
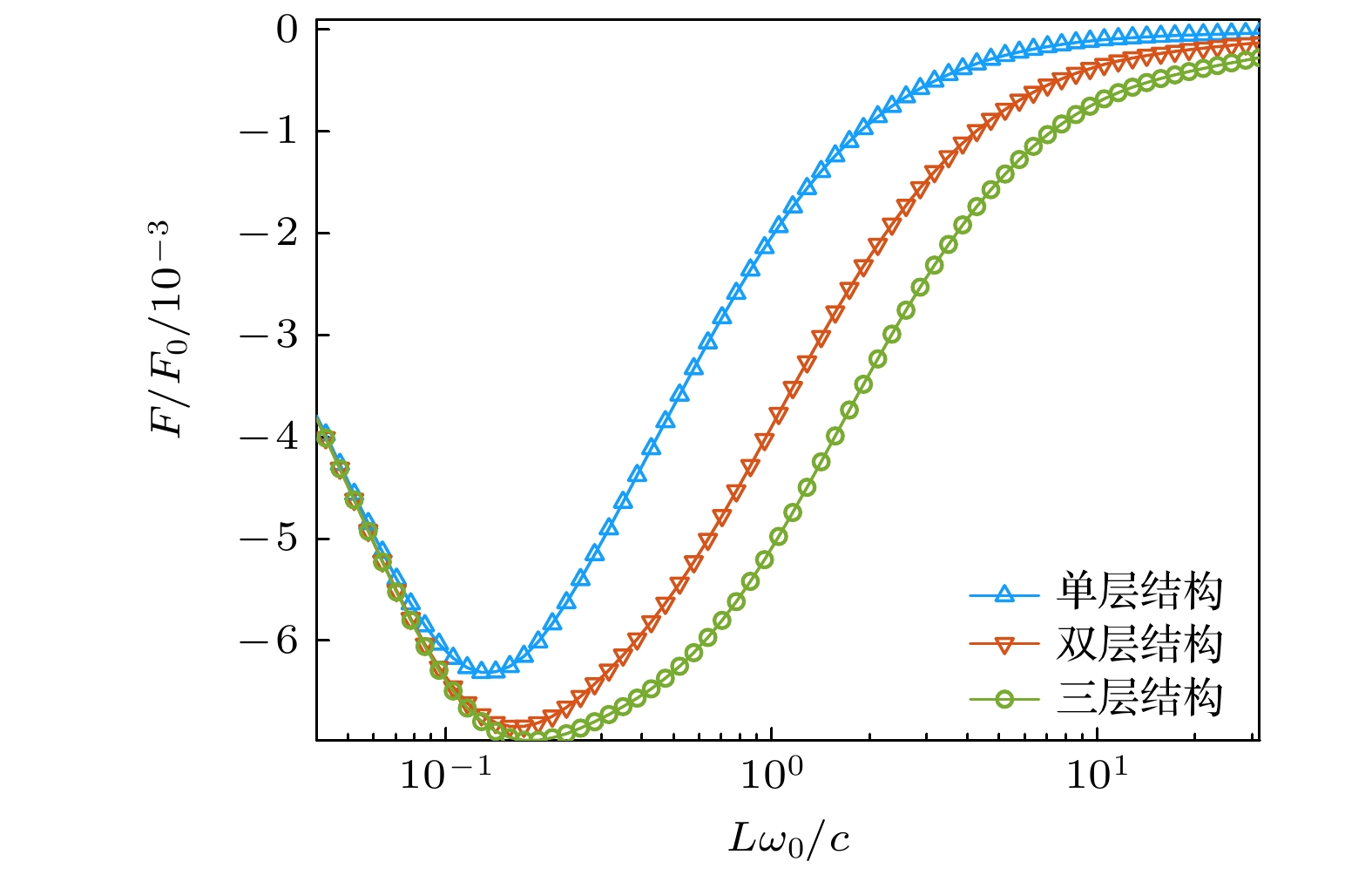
${F_0} = {{{{\text{π}}^2}\hbar c} {/ } {\left( {240{L^4}} \right)}}$ , 以及理想导体边界与无穷磁化板边界之间存在的Casimir斥力$ F_0'= {{ - 7{{\text{π}}^2}\hbar c} {/ } {\left( {1920{L^4}} \right)}} $ . 为方便分析所考察系统中的Casimir效应, 以下作用力结果以前者${F_0}$ 为基准, 也就是采取相对幅值$ F/{F_0} $ 表示. 首先考虑当左右多层光子拓扑绝缘体结构的x(x')光轴取向设置为反平行时的情况, 如图1(a)所示. 对于左右多层系统x(x')光轴为平行的情况, 将在3.2节进行讨论. 该坐标系定义下, 左右多层结构呈反镜像对称. 对应不同层数情况的Casimir作用力随多层结构间距的变化曲线如图2所示. 介电张量取值为${\varepsilon _x} = 1.1$ ,${\varepsilon _y} = 0.5$ ,${\varepsilon _n} = 1.5$ , 每个单元层厚度以及相邻单元层间的间隔均为$ 0.1\lambda $ . 从图2可以看到, 较大的距离范围下均为Casimir排斥力. 该斥力的产生, 一方面来源于光子拓扑绝缘体反射特性中交叉极化因素即反射矩阵非对角元占主导, 同时也是由于所考察的光子拓扑绝缘体空间结构满足“非镜像对称系统”这一作为产生真空中物体间Casimir斥力的条件[34]. 对于不同层数的情况, Casimir相对作用力的幅值均在间距约为0.2$ \lambda $ 前后达到极大值. 从单层结构的情况到三层结构情况对比可以看出, 随着层数的增多, Casimir斥力有明显增强, 即增加光子拓扑绝缘体材料层将对Casimir斥力产生更大的贡献, 但在长距极限或短距极限下, 不同材料层之间的差别将不再明显.继续考察当存在Casimir吸引和排斥作用力随距离转换时的情况, 如图3(a)所示. 光子拓扑绝缘体的介电常数取值为
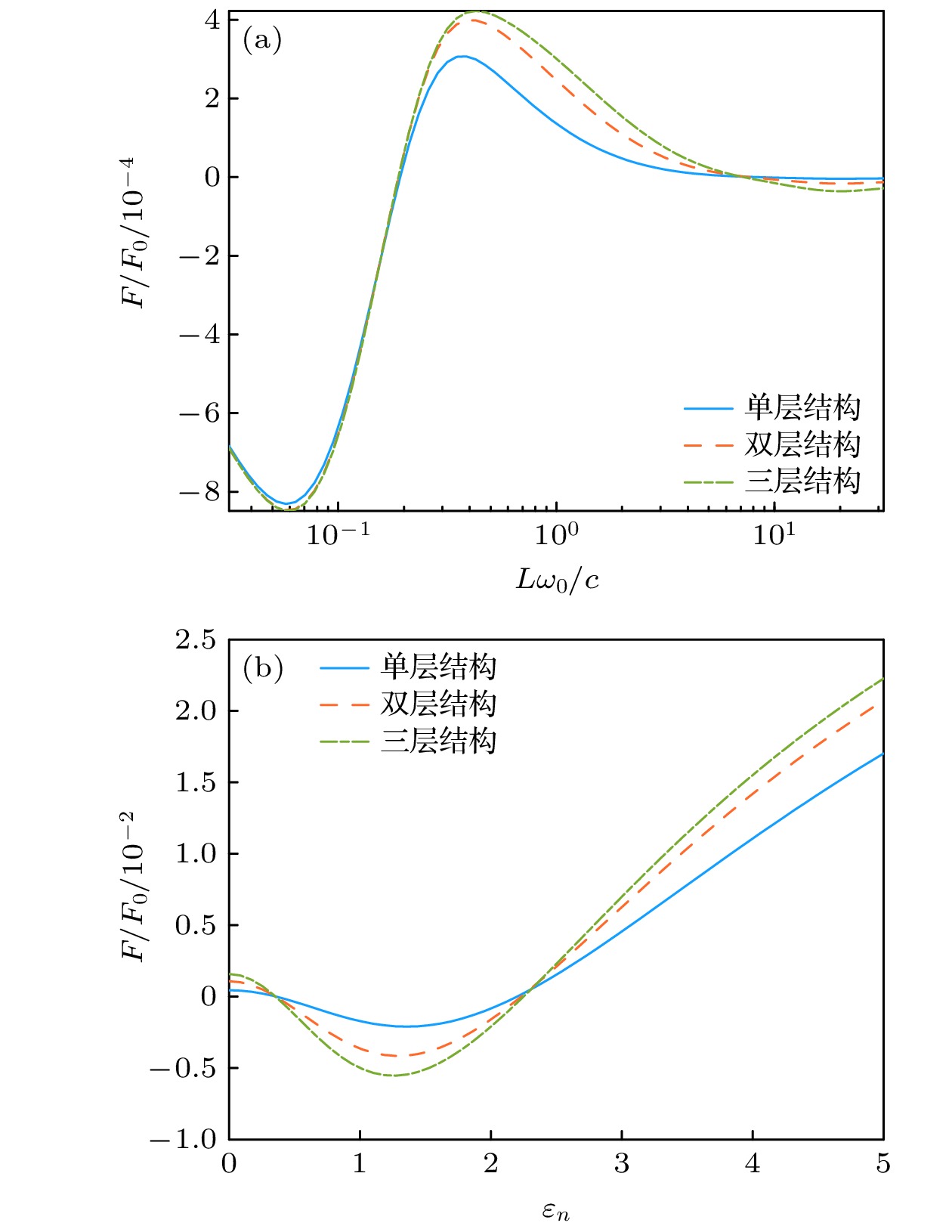
${\varepsilon _y} = 1.1$ ,${\varepsilon _n} = 1.8$ , 其他系统参数同图2中的取值. 在间距约为0.2$ \lambda $ 附近, Casimir斥力随增大的间距而转变为吸引力. 由于该转变点的Casimir相互作用附近形成了回复力, 因此该间距位置为系统在Casimir效应下的稳定平衡点. 在平衡回复力情况中, 系统的层数仍然对Casimir效应的幅值具有一定影响, 即层数越多, Casimir吸引力和排斥力的幅值都有相应的增强, 而这将使平衡位置附近的平衡回复范围增大, 使平衡点附近的稳定性更强. 另外还可注意到, 较长距下还会出现另一个平衡点, 但是属于非稳定平衡点, 即随距离增大Casimir吸引力转变为排斥力, 这种情况不会形成回复力.光子拓扑绝缘体介电张量的非对角元对产生Casimir斥力提供的贡献中占主导作用, 但其并非在任何取值下都可能得到Casimir斥力. 图3(b)为Casimir作用力在
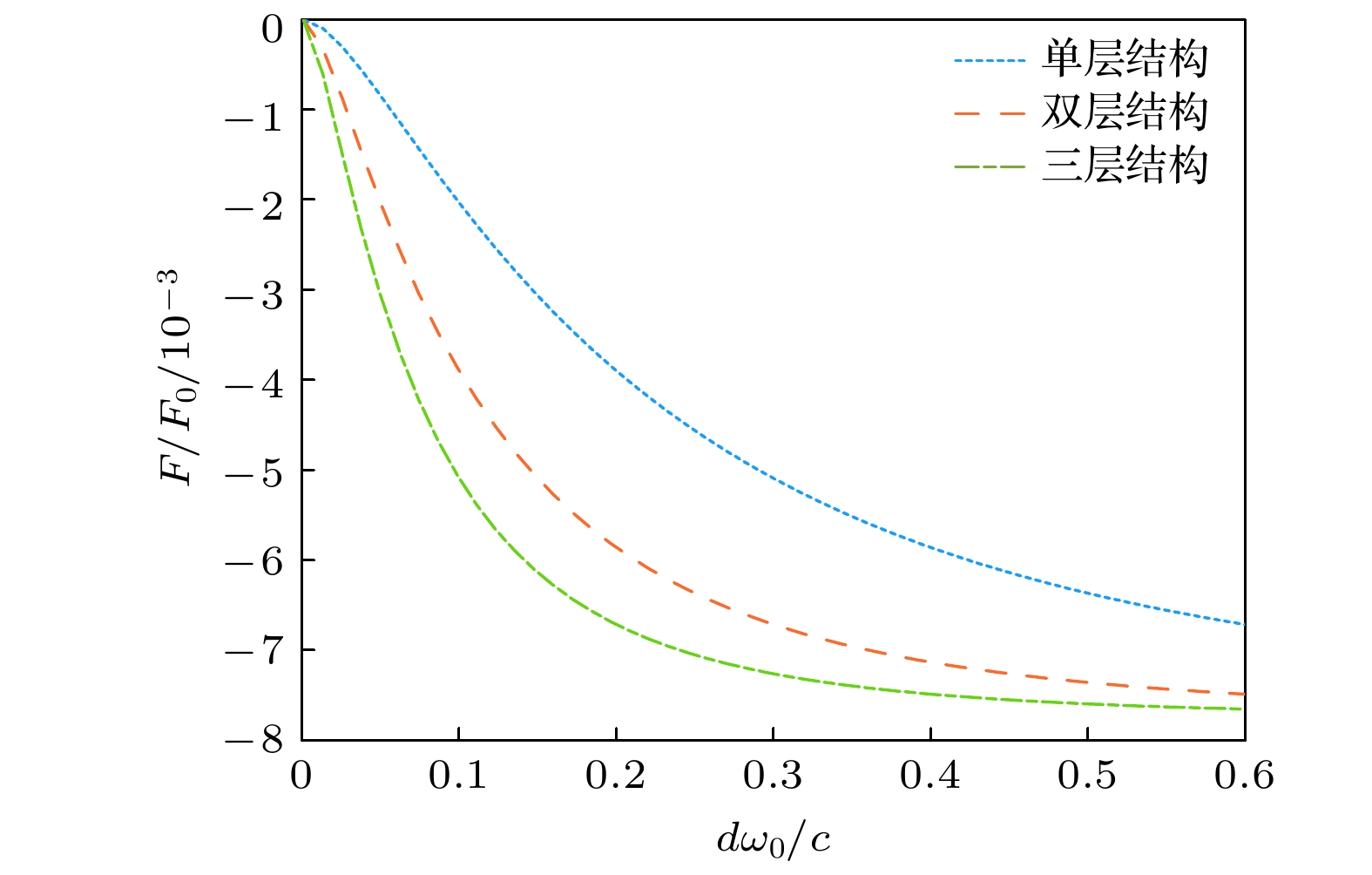
${\varepsilon _n}$ 取值影响下的变化曲线, 可以看到, 在所考察的对角矩阵元固定取值下, 介电张量非对角元仅在一定取值范围中对应系统的Casimir排斥力. 在介电张量非对角元取值不同的范围中, Casimir引力和斥力的强度随层数增加而变大, 与上述两个结果图中的规律一致. 另外, 我们也考察了多层光子拓扑绝缘体系统中的单元层厚度d对Casimir排斥力的影响, 在选取介电张量取值可对应得到系统Casimir斥力情况下, 该斥力随层厚度的变化如图4所示. 结果显示, 层越厚Casimir斥力将越强, 但对于不同层数的情况中, 层厚度对斥力的增强效果都将在厚度增大到一定程度后达到饱和. -
考虑左右多层光子拓扑绝缘体结构的x(x')光轴取向为任意角度, 设两光轴的夹角为
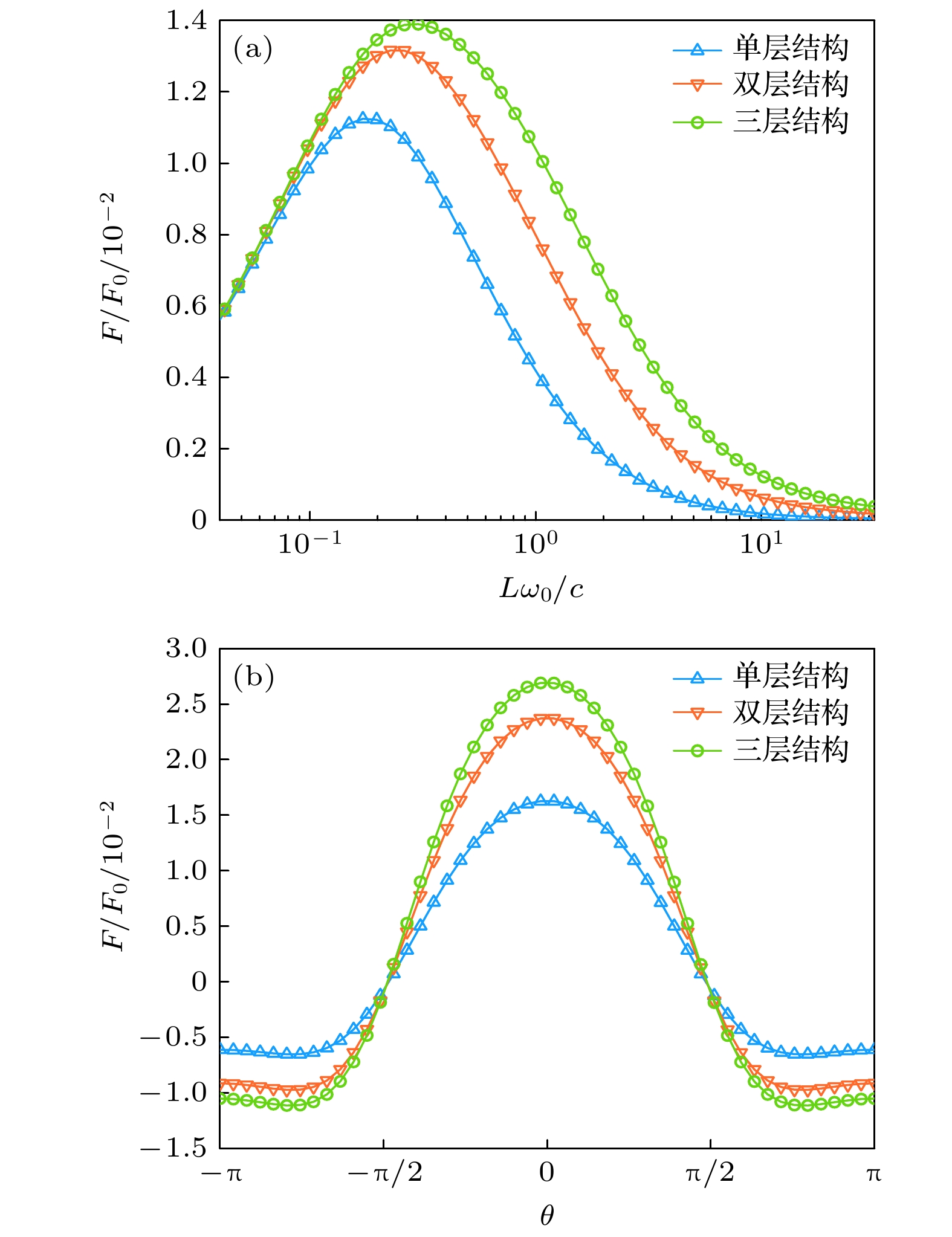
$\theta $ , 如图1(b)所示. 因此, 3.1节中所考察的左右两侧光轴取向反平行的系统结构(图1(a))则对应$\theta $ 为${\text{π}}$ 的情况. 当旋转角度$\theta $ 至0°时, 左右多层系统x(x')光轴为平行情况, 在该坐标系定义下, 左右多层结构呈镜像对称. 图5(a)给出了在这种光轴平行情况下Casimir作用力随左右结构间距的变化曲线, 其中光子拓扑绝缘体介电常数${\varepsilon _n} = 1.5$ , 其他参数同图2中的取值. 无论在长距还是短距范围, Casimir效应都体现为引力, 多层系统层数的增多也明显体现对该引力的增强效果, 因为随着层数的增多, 多次反射的贡献一般会增强, 导致两结构之间的模式增多, 从而使Casimir引力增大. 因此可以看到, 即便对于作为非互易媒质的光子拓扑绝缘体, 产生Casimir斥力的“非镜像对称系统”这一条件仍是必要的条件. 旋转夹角$\theta $ 使系统在反镜像对称情况和镜像对称情况之间连续变化, 从图5(b)可以发现, 在此过程中Casimir效应即对应在斥力和引力间进行转变. 具体来看, Casimir作用力随$\theta $ 角并不是完全的单调变化, 约在$\theta = \pm {{3{\text{π}}} {/ } 4}$ 角度处会出现Casimir斥力的极大值. 在某一角度时对应Casimir力为零, 且该角度几乎与系统层数无关, 表明光子拓扑绝缘体宏观边界对Casimir引力和斥力的贡献在该角度下相互抵消, 反射特性中的共极化与交叉极化两方面因素对Casimir效应的影响趋于平衡. 综上所述, 我们可以通过多层系统间的相对旋转来调节得到Casimir作用力的不同取向及其平衡点, 进而增加在实际微纳系统中进行探测和操控的自由度. -
在广泛研究的光子拓扑绝缘体实际材料中, 对于具有与上述讨论的参数范围相近取值的介电张量的情况, 如铁石榴石(Iron garnet)等色散类型[35–37], 将会得到Casimir斥力及其与上述讨论相类似的参数影响, 本文不再赘述. 而对于另外某些材料, 其介电常数较难取到上述讨论中产生Casimir排斥力时的数值, 而尽管如此, 对于本文考察的多层拓扑绝缘体系统, 也可以通过多层光轴取向自由度来调控Casimir作用力, 比如锑化铟(InSb)等类型的材料, 其介电响应光轴与外加偏置磁场相关, 即可利用外场对其Casimir效应进行操控. 尽管参量的频率依赖性可能会引起小尺度下紧束缚模型对凝聚态物理中电子行为的“模拟”失效, 描述该类材料电磁响应的张量形式在Casimir效应考察中仍具有一定的适用性. 此类材料中, 介电张量的色散形式为[38,39]
其中
$\omega _{\text{p}}^{2} = Nq_{\text{e}}^{2}/m{\varepsilon _0}$ 为等离子体频率,${\omega _{\text{c}}} = {B_0}{q_{\text{e}}}/m$ 为回旋频率, N,${q_{\text{e}}}$ 和m分别为自由电子密度、电量和约化质量, B0为施加在光轴x方向的外磁场,$\varGamma $ 和γ为声子和自由载流子阻尼常数,${\omega _{\text{L}}}$ 和${\omega _{\text{T}}}$ 为纵向和横向光学声子频率.考虑多层系统内部的各层光轴取向相互间均存在一定夹角, 如图1(c)所示, 并设各相邻层的光轴间夹角均为
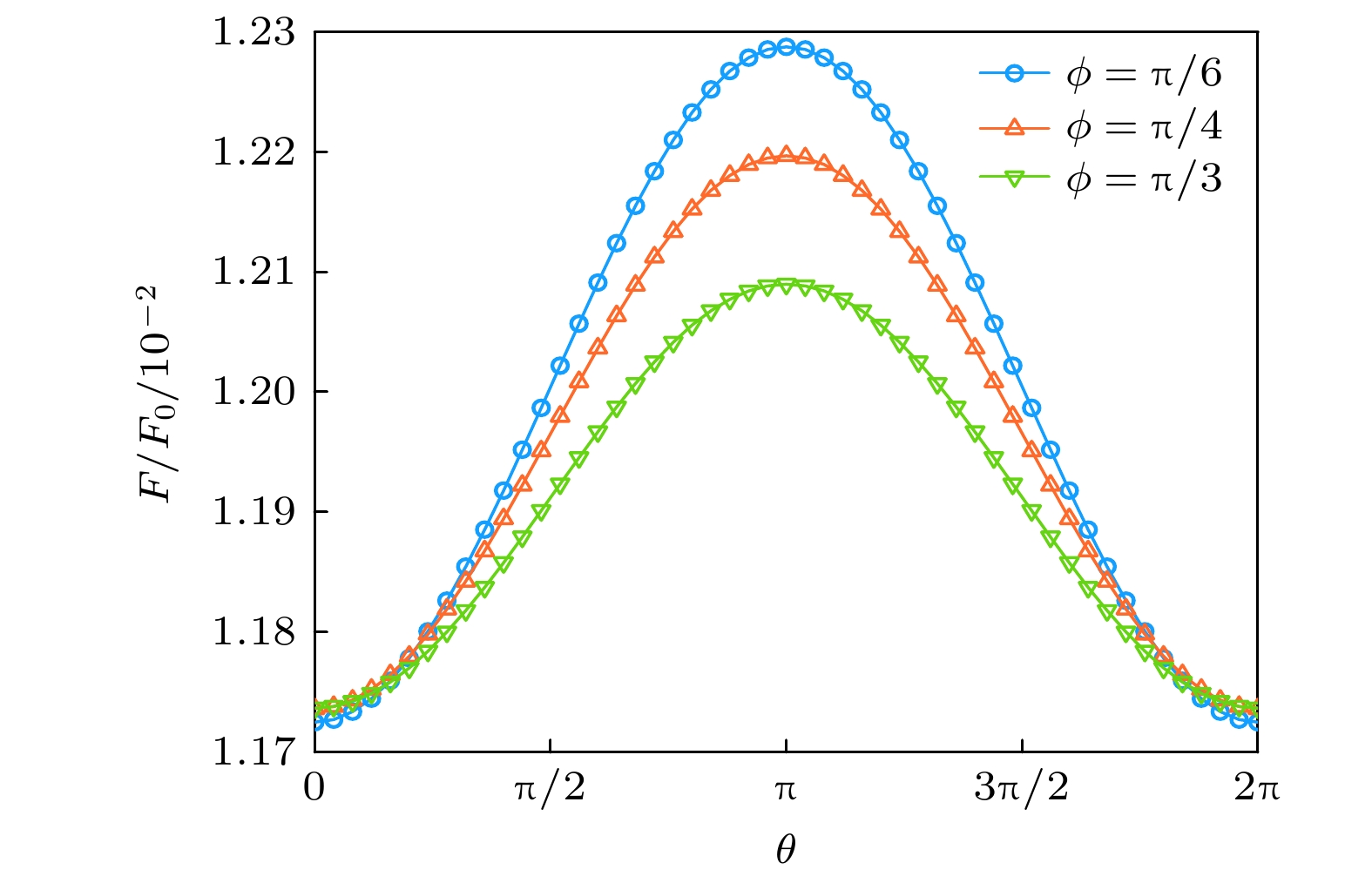
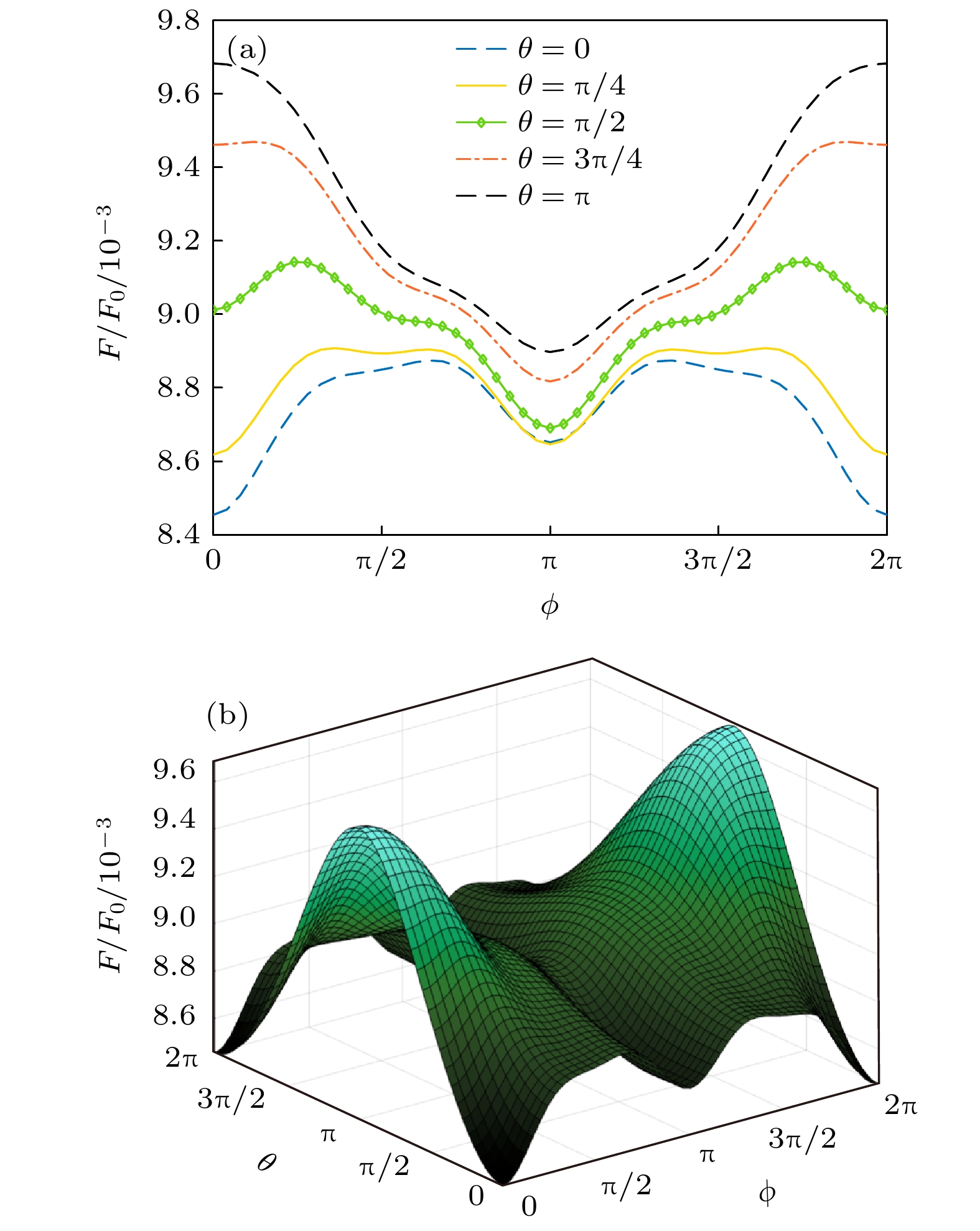
$\phi $ . 以三层结构为例, 并固定左侧结构不动, 整体旋转右侧结构, 图6为Casimir力相对幅值随两侧结构间整体旋转夹角$\theta $ 的变化图. 多层结构内部相邻层之间的光轴角度差固定, 设置为${\text{π}}/6$ ,${\text{π}}/4$ 和${\text{π}}/3$ 三种情况. 结果显示, Casimir力随两多层结构整体光轴取向夹角基本是单调递增的变化, 对于所考察的3个内部光轴夹角$\phi $ 值, 图中显示越大的$\phi $ 角一般会削弱Casimir效应, 但对于整体光轴取向夹角约在0—${\text{π}}/6$ 或$11{\text{π}}/12$ —$2{\text{π}}$ 之间时$\phi $ 角的影响则会呈现相反的影响趋势. 为更全面了解该内部光轴夹角影响的趋势, 图7给出Casimir力相对幅值随$\phi $ 角的变化曲线, 其中图7(a)中分别固定了左右多层结构之间的整体光轴取向夹角为0,${\text{π}}$ /4,${\text{π}}$ /2, 3${\text{π}}$ /4和${\text{π}}$ 时的情况, 而图7(b)给出Casimir力随着两侧结构间整体光轴取向夹角和结构内部光轴夹角变化的三维图. 对于两种夹角$\theta $ 和$\phi $ , Casimir力的变化规律都是以${\text{π}}$ 为中心而对称, 表现出相反的角度影响趋势. 而在结构内部光轴夹角为$\phi $ =${\text{π}}$ /4, 3${\text{π}}$ /4, 5${\text{π}}$ /4和7${\text{π}}$ /4位置处曲线出现拐点, Casimir力随$\phi $ 的变化趋势发生改变. 因此, 本节在3.2节基础上, 对多层系统中调控Casimir效应的可能性在旋转自由度方面扩展到结构内部层间的相对旋转. -
本文讨论了基于时间反演对称性破缺的非互易光子拓扑绝缘体多层结构间的Casimir作用力, 考察了光子拓扑绝缘体介电张量、多层系统的空间结构参数以及旋转自由度对Casimir效应的影响. 研究发现, 该多层系统中存在Casimir排斥作用力, 而且可进一步实现并调控Casimir稳定平衡回复力. 多层系统的层数和单元层厚度的增大在多数情况下可增强Casimir效应的幅值. 此外, 我们着重分析了光子拓扑绝缘体光轴角度差对Casimir作用力的调控, 通过多层系统间的整体相对旋转来调节得到Casimir作用力的不同取向及其平衡点, 而调整旋转系统内部各层间的光轴角度差对Casimir效应的影响趋势曲线中存在一些拐点, 可利用多层系统中的旋转自由度来精细调控Casimir相互作用. 本研究增加了在实际微纳系统中对物体间相互作用进行探测和操控的自由度, 以减小Casimir效应的不良影响或对该效应进行有效利用, 在此研究基础上可进一步开发光子拓扑材料对其他相关效应如动态Casimir效应等的调控作用.
光子拓扑绝缘体多层系统中的Casimir效应
Casimir effect in photonic topological insulator multilayered system
-
摘要: 光子拓扑绝缘体为光子器件的设计和应用带来了新的可能性. 本文研究了基于时间反演对称性破缺的非互易光子拓扑绝缘体多层结构间的Casimir效应. 讨论该多层系统中Casimir排斥作用力的产生, 以及Casimir稳定平衡回复力的实现和调控, 并且着重分析了光子拓扑绝缘体光轴角度差对Casimir作用力的影响. 利用多层系统间的整体相对旋转可得到Casimir作用力的不同取向及其平衡点, 而系统内部各层间的光轴角度差对Casimir效应的影响趋势中存在拐点, 因此可利用多层系统中的旋转自由度来精细控制Casimir相互作用. 本文所提供的新的操控途径和操控自由度, 在实际微纳米系统中减小Casimir效应的不良影响或利用该效应开发其对系统的调控方面具有实际意义.
-
关键词:
- 光子拓扑绝缘体 /
- Casimir效应 /
- Casimir排斥力 /
- 多层系统
Abstract: The Casimir effect has received extensive attention theoretically and experimentally in recent years. It arises from the macroscopic manifestation of quantum vacuum fluctuations, and this Casimir interaction force can be an effective means of driving and controlling components in micro-electro-mechanical system (MEMS) and nano-electromechanical system (NEMS). Due to the new possibilities provided by photonic topological insulator for designing and using photonic devices, in this work, the Casimir force between the multilayer structures of non-reciprocal photonic topological insulators with broken time-reversal symmetry is investigated, and the influences of the dielectric tensor of the photonic topological insulator, the spatial structural parameters of the multilayer system, and the rotational degree of freedom on the Casimir force are examined. It is found that there exists Casimir repulsive force in such a multilayer system, and the Casimir stable equilibrium and restoring force can be further realized and controlled. Continuous variation between anti-mirror-symmetric configuration and mirror-symmetric configuration is examined. Both the Casimir attraction and repulsion can be generally enhanced through structural optimization by increasing layer number and individual layer thickness. Furthermore, we focus on the detailed analysis of how the optical axis angle difference within the photonic topological insulator layers can be used to adjust the Casimir force. The overall relative rotation of the multilayer system may adjust the magnitude and the direction of the Casimir force, and some inflection points can be found from the influence curve of the optical axis angle difference between internal layers of the multilayer on the Casimir force, allowing the rotational degrees of freedom in the multilayer system to be used for fine-adjusting the Casimir interaction. This work introduces the enhanced degrees of freedom for probing and manipulating the interaction between small objects in micro/nano systems, thereby suppressing adverse Casimir forces and effectively using them.-
Key words:
- photonic topological insulator /
- Casimir effect /
- repulsive Casimir force /
- multilayered system .
-

-
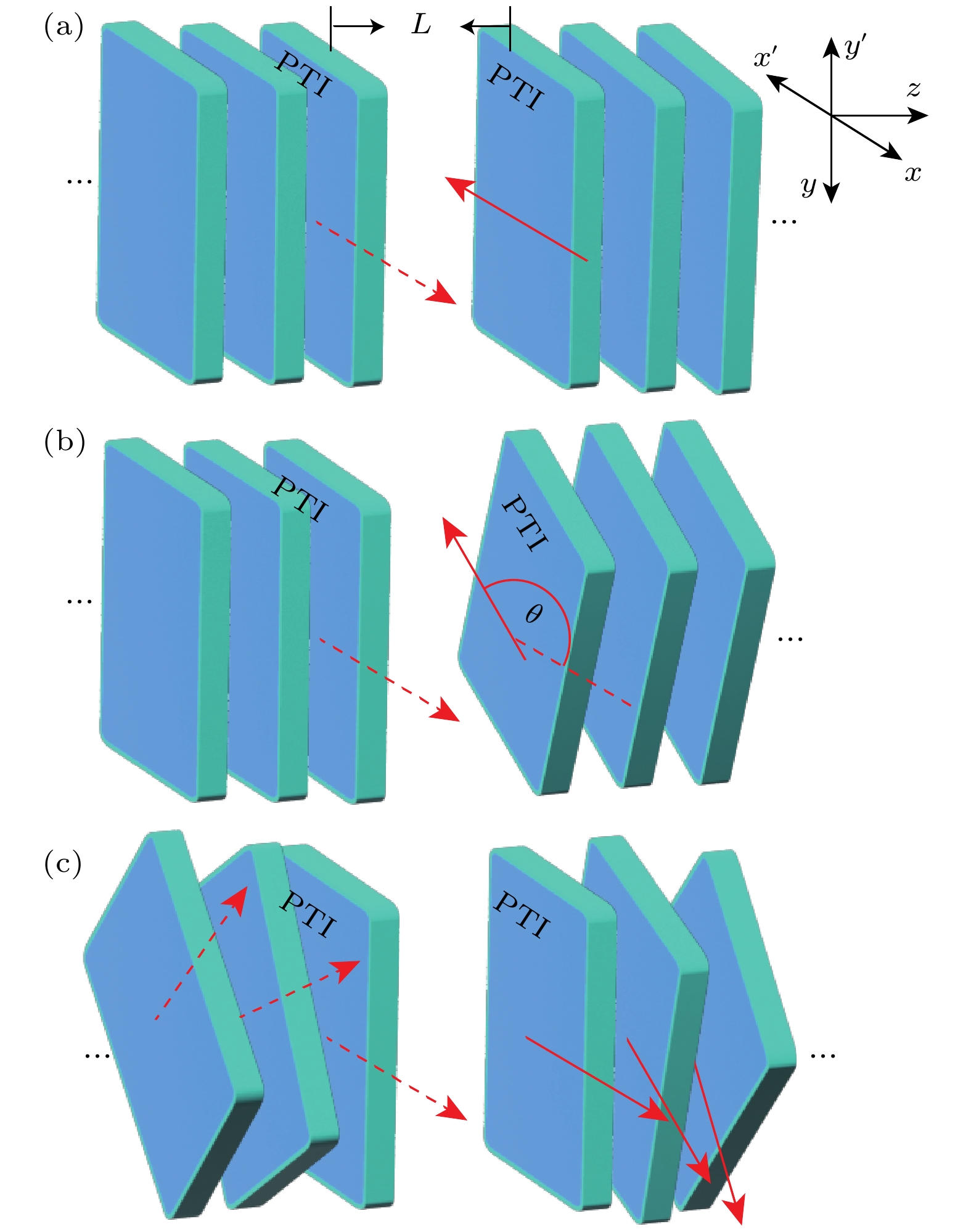
图 1 光子拓扑绝缘体多层结构间Casimir效应示意图, 其中左右多层结构间距L, 左右侧结构相应的参考系分别对应为x-y-z和x'-y'-z坐标系, 红色箭头表示光子拓扑绝缘体的x(x')方向光轴 (a) 两侧结构的该光轴反平行; (b) 两侧结构该光轴的夹角为
$\theta $ ; (c) 系统内部各层相互间也存在光轴夹角Figure 1. Sketch of the Casimir effect between multilayered structures made of photonic topological insulators, where L is the separation between two structures, x-y-z and x'-y'-z are the coordinates in the left and right structures, respectively. The red arrows indicate the x(x') optical axes of photonic topological insulators: (a) Anti-parallel on the two sides, (b) an angle
$\theta $ between the two sides; (c) exist angles between layers within the system.图 4 反镜像对称N层光子拓扑绝缘体结构(N = 1, 2, 3)间的Casimir作用力相对幅值随单元层厚度的变化, 其中结构间距L = 1.0λ, 其他系统参数同图2中的取值
Figure 4. Relative Casimir force between two N-layer photonic topological insulator structures (N = 1, 2, 3) with inversion-mirror symmetry as a function of the layer thickness, where L = 1.0λ and other parameters are the same as in Fig. 2.
图 5 N层光子拓扑绝缘体结构(N = 1, 2, 3)间的Casimir作用力相对幅值 (a)在镜像对称情况下随间距L的变化; (b)随光轴夹角
$\theta $ 的变化Figure 5. (a) Relative amplitude of Casimir force between N-layer photonic topological insulator structures (N = 1, 2, 3): (a) Variation with the separation L with mirror symmetry; (b) variation with the
$\theta $ .图 6 锑化铟三层系统间Casimir作用力相对幅值在不同 内部层间光轴夹角下随整体旋转角度
$\theta $ 的变化, 其中相 关参数为${\omega _{\text{L}}} = 3.62 \times {10^{13}} {\text{ rad/s}}$ ,${\omega _{\text{T}}} = 3.39 \times {10^{13}} {\text{ rad/s}}$ ,$\varGamma = 5.65 \times {10^{11}} {\text{ rad/s}}$ ,$\gamma = 3.39 \times {10^{12}} {\text{ rad/s}}$ ,$N = 1.07 \times $ $ {10^{17}}\;{\text{c}}{{\text{m}}^{{{ - 3}}}}$ , B = 10 T, 其他参数同图4中的取值Figure 6. Relative Casimir force between the three-layer InSb systems as a function of the overall rotation angle
$\theta $ under different optical axis angles between internal layers, where${\omega _{\text{L}}} = 3.62 \times {10^{13}}\; {\text{rad/s}}$ ,${\omega _{\text{T}}} = 3.39 \times {10^{13}} {\text{ rad/s}}$ ,$\varGamma = 5.65 \times $ $ {10^{11}} {\text{ rad/s}}$ ,$\gamma = 3.39 \times {10^{12}} {\text{ rad/s}}$ ,$N = 1.07 \times {10^{17}}\;{\text{c}}{{\text{m}}^{{{ - 3}}}}$ , B = 10 T, and other parameters are the same as in Fig. 4. -
[1] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 doi: 10.1103/RevModPhys.82.3045 [2] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 doi: 10.1103/RevModPhys.83.1057 [3] Xia Y, Qian D, Hsieh D, Wray L, Pal A, Lin H, Bansil A, Grauer D, Hor Y S, Cava R J, Hasan M Z 2009 Nat. Phys. 5 398 doi: 10.1038/nphys1274 [4] Zhang H J, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 doi: 10.1038/nphys1270 [5] Luo W, Qi X L 2013 Phys. Rev. B 87 085431 doi: 10.1103/PhysRevB.87.085431 [6] Wang P, Ge J, Li J, Liu Y, Xu Y, Wang J 2021 Innovation 2 100098 doi: 10.1016/j.xinn.2021.100098 [7] Haldane F D M, Raghu S 2008 Phys. Rev. Lett. 100 013904 doi: 10.1103/PhysRevLett.100.013904 [8] Wang Z, Chong Y, Joannopoulos J D, Soljačić M 2009 Nature 461 772 doi: 10.1038/nature08293 [9] 王子尧, 陈福家, 郗翔, 高振, 杨怡豪 2024 物理学报 73 064201 doi: 10.7498/aps.73.20231850 Wang Z Y, Chen F J, Xi X, Gao Z, Yang Y H 2024 Acta Phys. Sin 73 064201 doi: 10.7498/aps.73.20231850 [10] Wang Y, Lu Y H, Gao J, Chang Y J, Ren R J, Jiao Z Q, Zhang Z Y, Jin X M 2022 Chip 1 100003 doi: 10.1016/j.chip.2022.100003 [11] Yang Y H, Yamagami Y, Yu X B, Pitchappa P, Webber J, Zhang B L, Fujita M, Nagatsuma T, Singh R 2020 Nat. Photonics 14 446 doi: 10.1038/s41566-020-0618-9 [12] Webber J, Yamagami Y, Ducournau G, Szriftgiser P, Iyoda K, Fujita M 2021 J. Lightwave Technol. 39 7609 doi: 10.1109/JLT.2021.3107682 [13] Tschernig K, Jimenez-Galán Á, Christodoulides D N, Ivanov M, Busch K, Bandres M A, Perez-Leija A 2021 Nat. Commun. 12 1974 doi: 10.1038/s41467-021-22264-3 [14] Chen Y, He X T, Cheng Y J, Qiu H Y, Feng L T, Zhang M, Dai D X, Guo G C, Dong J W, Ren X F 2021 Phys. Rev. Lett. 126 230503 doi: 10.1103/PhysRevLett.126.230503 [15] Dai T X, Ao Y T, Bao J M, Mao J, Chi Y L, Fu Z R, You Y L, Chen X J, Zhai C H, Tang B, Yang Y, Li Z H, Yuan L Q, Gao F, Lin X, Thompson M G, O’Brien J L, Li Y, Hu X Y, Gong Q H, Wang J W 2022 Nat. Photonics 16 248 doi: 10.1038/s41566-021-00944-2 [16] Tang G J, He X T, Shi F L, Liu J W, Chen X D, Dong J W 2022 Laser Photonics Rev. 16 2100300 doi: 10.1002/lpor.202100300 [17] Lustig E, Maczewsky L J, Beck J, Biesenthal T, Heinrich M, Yang Z, Plotnik Y, Szameit A, Segev M 2022 Nature 609 931 doi: 10.1038/s41586-022-05129-7 [18] Teo H T, Xue H R, Zhang B L 2022 Phys. Rev. A 105 053510 doi: 10.1103/PhysRevA.105.053510 [19] Devi K M, Jana S, Chowdhury D R 2021 Opt. Mater. Express 11 2445 doi: 10.1364/OME.427069 [20] Casimir H B G 1948 Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen 51 793 [21] Palasantzas G, Sedighi M, Svetovoy V B 2020 Appl. Phys. Lett. 117 120501 doi: 10.1063/5.0023150 [22] Vasilyev O A, Marino E, Kluft B B, Schall P, Kondrat S 2021 Nanoscale 13 6475 doi: 10.1039/D0NR09076J [23] 周帅, 柳开鹏, 戴士为, 葛力新 2025 物理学报 74 014202 doi: 10.7498/aps.74.20241126 Zhou S, Liu K P, Dai S W, Ge L X 2025 Acta Phys. Sin 74 014202 doi: 10.7498/aps.74.20241126 [24] Zeng R, Wang C, Zeng X D, Li H Z, Yang S N, Li Q L, Yang Y P 2020 Opt. Express 28 7425 doi: 10.1364/OE.386083 [25] Küçüköz B, Kotov O V, Canales A, Polyakov A Y, Agrawal A V, Antosiewicz T J, Shegai T O 2024 Sci. Adv. 10 eadn1825 doi: 10.1126/sciadv.adn1825 [26] Grushin A G, Cortijo A 2011 Phys. Rev. Lett. 106 020403 doi: 10.1103/PhysRevLett.106.020403 [27] Fuchs S, Lindel F, Krems R V, Hanson G W, Antezza M, Buhmann S Y 2017 Phys. Rev. A 96 062505 doi: 10.1103/PhysRevA.96.062505 [28] Lindel F, Hanson G W, Antezza M, Buhmann S Y 2018 Phys. Rev. B 98 144101 doi: 10.1103/PhysRevB.98.144101 [29] Masyukov M S, Grebenchukov A N 2021 Phys. Rev. B 104 165308 doi: 10.1103/PhysRevB.104.165308 [30] Nefedov I S, Valagiannopoulos C A, Melnikov L A 2013 J. Opt. 15 114003 doi: 10.1088/2040-8978/15/11/114003 [31] Zeng R, Chen L, Nie W, Bi M, Yang Y, Zhu S 2016 Phys. Lett. A 380 2861 doi: 10.1016/j.physleta.2016.06.002 [32] Chiadini F, Fiumara V, Lakhtakia A, Scaglione A 2019 Appl. Opt. 58 1724 doi: 10.1364/AO.58.001724 [33] Zeng R, Gao T, Ni P, Fang S, Li H, Yang S, Zeng Z 2024 J. Opt. 26 075602 doi: 10.1088/2040-8986/ad4b39 [34] Kenneth O, Klich I 2006 Phys. Rev. Lett. 97 160401 doi: 10.1103/PhysRevLett.97.160401 [35] Silveirinha M G 2015 Phys. Rev. B 92 125153 doi: 10.1103/PhysRevB.92.125153 [36] Xu J, He P P, Feng D L, Luo Y M, Fan S Q, Yong K L, Tsakmakidis K L 2023 Opt. Express 31 42388 doi: 10.1364/OE.502808 [37] Holmes A M, Sabbaghi M, Hanson G W 2021 Phys. Rev. B 104 214433 doi: 10.1103/PhysRevB.104.214433 [38] Bittencourt J A 2004 Fundamentals of Plasma Physics (Springer: New York [39] Silveirinha M G, Terças H, Antezza M 2023 Phys. Rev. B 108 235154 doi: 10.1103/PhysRevB.108.235154 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: