高级搜索

第一性原理研究钒、钨固溶对碳化钼力学性能的影响

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

杨正罡, 豆尔康, 杨永, 李天瑞, 章小峰, 王昭东. 第一性原理研究钒、钨固溶对碳化钼力学性能的影响[J]. 物理学报, 2025, 74(10): 106301-1. doi: 10.7498/aps.74.20250039
引用本文: 杨正罡, 豆尔康, 杨永, 李天瑞, 章小峰, 王昭东. 第一性原理研究钒、钨固溶对碳化钼力学性能的影响[J]. 物理学报, 2025, 74(10): 106301-1. doi: 10.7498/aps.74.20250039
shu
Zhenggang YANG, Erkang DOU, Yong YANG, Tianrui LI, Xiaofeng ZHANG, Zhaodong WANG. First-principles studies of influence of V or W doping on mechanical properties of Mo2C[J]. Acta Physica Sinica, 2025, 74(10): 106301-1. doi: 10.7498/aps.74.20250039
Citation: Zhenggang YANG, Erkang DOU, Yong YANG, Tianrui LI, Xiaofeng ZHANG, Zhaodong WANG. First-principles studies of influence of V or W doping on mechanical properties of Mo2C[J]. Acta Physica Sinica, 2025, 74(10): 106301-1. doi: 10.7498/aps.74.20250039
shu

第一性原理研究钒、钨固溶对碳化钼力学性能的影响

  • 1.

    安徽工业大学冶金工程学院, 马鞍山　243000

  • 2.

    东北大学, 轧制技术及连轧自动化国家重点实验室, 沈阳　110819

    • 作者简介: 杨正罡. E-mail: yangzg200105@163.com .
    通讯作者: E-mail: yangyongboxian@163.com.; 

  • 中图分类号: 63.20.dk, 81.40.Cd, 62.20.de, 71.20.-b

First-principles studies of influence of V or W doping on mechanical properties of Mo2C

  • 1.

    School of Metallurgical Engineering, Anhui University of Technology, Ma’anshan 243000, China

  • 2.

    National Key Laboratory of Rolling Technology and Continuous Rolling Automation, Northeastern University, Shenyang 110819, China

    • Corresponding author: E-mail:yangyongboxian@163.com.; 

  • MSC: 63.20.dk, 81.40.Cd, 62.20.de, 71.20.-b

  • 摘要: 二次硬化型超高强度钢广泛应用于航空航天等领域, 弥散析出的纳米级M2C是二次硬化钢的主要强化因素. Mo是形成二次强化相Mo2C的主要元素, 可与Cr, V, W等形成复合型M2C. 为探究V, W的掺杂对Mo2C的影响, 本文基于第一性原理研究了掺杂体系的电子结构和力学性质. 研究结果表明, 掺杂V降低形成焓, 使结构更为稳定, 而掺杂W使稳定性下降. 掺杂V使韧性下降, 硬度增加. 掺杂W改善强韧性, 硬度降低更缓慢. 与C—Mo键相比, C—V键共价性弱, C—W键共价性强.
    Abstract: Secondary hardening ultra-high-strength steel is widely utilized in aerospace and other advanced engineering, with the nanoscale M2C precipitates serving as the primary strengthening factor. Mo plays a crucial role in the forming of Mo2C secondary hardening phase, which can form composite M2C precipitates with elements such as Cr, V, and W, thereby modifying the composition and properties of Mo2C. To investigate the effects of V and W doping on Mo2C, first-principles calculations are used to analyze the formation enthalpy, electronic structure, and mechanical properties of the doped systems. The CASTEP module is utilized in this study, with the Perdew-Burke-Ernzerhof (PBE) functional adopted in the generalized gradient approximation (GGA) framework. The results indicate that V doping reduces the lattice parameters and the formation enthalpy, thereby enhancing structural stability. In contrast, W doping increases the lattice parameters and lowers the formation enthalpy but leads the structural stability to decrease. In terms of mechanical properties, V doping reduces toughness while increasing hardness, whereas W doping improves the strength-toughness balance by mitigating the rate of hardness reduction. Covalent bonds are formed within the system, with V and W doping changing their characteristics: compared with the C—Mo bond, the C—V bond exhibits weaker covalency, while the C—W bond displays stronger covalency. Additionally, V doping enhances the stability of Mo—C bonds, whereas W doping reduces their stability. Charge population analysis reveals that metal atoms (Mo, V, and W) act as electron donors, while carbon atoms act as electron acceptors.
  • 加载中

  • 图 1  晶体结构以及超胞示意图　(a) Mo2C; (b) Mo8C4; (c) Mo7VC4; (d) Mo6V2C4; (e) Mo7WC4; (f) Mo6W2C4

    Figure 1.  Schematic diagram of crystal structure and the supercell: (a) Mo2C; (b) Mo8C4; (c) Mo7VC4; (d) Mo6V2C4; (e) Mo7WC4; (f) Mo6W2C4.

    下载: 全尺寸图片 幻灯片

    图 2  不同构型的弹性常数　(a) 弹性模量(B, G, E); (b) 模量比(G/B)和泊松比(ν)

    Figure 2.  Elastic constants of different configurations: (a) Elastic moduli (B, G, E); (b) modulus ratio (G/B) and Poisson’s ratio (ν).

    下载: 全尺寸图片 幻灯片

    图 3  5种构型的态密度及各原子分波态密度图　(a) Mo8C4; (b) Mo7VC4; (c) Mo6V2C4; (d) Mo7WC4; (e) Mo6W2C4. (f) 4种掺杂构型的总态密度图

    Figure 3.  Density of states for five configurations and the partial density of states for each atom: (a) Mo8C4; (b) Mo7VC4; (c) Mo6V2C4; (d) Mo7WC4; (e) Mo6W2C4. (f) Total density of states for four doped configurations.

    下载: 全尺寸图片 幻灯片

    图 4  不同构型的态密度图　(a) (Mo, V)8C4; (b) (Mo, W)8C4

    Figure 4.  The density of states for different configurations: (a) (Mo, V)8C4; (b) (Mo, W)8C4.

    下载: 全尺寸图片 幻灯片

    图 5  未掺杂构型　(a) 差分片段; (b) 差分电荷密度图

    Figure 5.  Undoped configuration: (a) Differential fragment; (b) differential charge density map.

    下载: 全尺寸图片 幻灯片

    图 6  差分电荷密度图　(a) Mo7VC4; (b) Mo6V2C4; (c) Mo7WC4; (d) Mo6W2C4

    Figure 6.  Differential charge density maps: (a) Mo7VC4; (b) Mo6V2C4; (c) Mo7WC4; (d) Mo6W2C4.

    下载: 全尺寸图片 幻灯片

    表 1  V, W掺杂前后的晶格参数a, b, c, V以及α, β, γ

    Table 1.  Lattice parameters a, b, c, volume V, and angles α, β, γ before and after doping with V and W.

    Configuration a/Å b/Å c/Å V/Å α β γ Volume expansion rate/%
    Mo2C 3.059 3.059 4.665 37.794 90.00 90.00 120.00 —
    (Mo4C2)[12] 3.056 3.056 9.331 75.476 — — — —
    (Mo2C)[13] 3.054 3.054 4.652 37.58 — — — —
    (Mo2C)[15] 3.051 3.051 4.624 37.3114 — — — —
    Mo8C4 6.108 3.054 9.346 150.996 90.06 89.98 120.00 —
    Mo7VC4 6.083 3.041 9.282 148.737 90.04 90.02 119.98 –1.50%
    Mo6V2C4 6.051 3.026 9.215 146.201 89.84 90.34 119.96 –3.18%
    Mo7WC4 6.109 3.055 9.350 151.139 90.07 89.96 119.99 0.09%
    Mo6W2C4 6.112 3.054 9.355 151.272 90.09 89.97 119.98 0.18%
    (V2C)[20] 3.045 3.045 4.409 35.4 — — — —
    (V2C)[21] 2.89 — — — — — — —
    (W2C)[20] 3.19 3.19 4.626 40.77 — — — —
    (W2C)[20] 3.060 3.060 4.703 — — — — —
    下载: 导出CSV

    表 2  不同构型的形成焓

    Table 2.  Enthalpy of formation for different configurations.

    Configuration ΔH/(eV·atom–1)
    Mo8C4 –0.131
    (Mo2C)[13] –0.113
    Mo7VC4 –0.192
    Mo6V2C4 –0.264
    Mo7WC4 –0.121
    Mo6W2C4 –0.111
    下载: 导出CSV

    表 3  不同构型的单晶弹性常数

    Table 3.  Single crystal elastic constants of different configurations.

    ConfigurationC11/GPaC12/GPaC13/GPaC33/GPaC44/GPaC66/GPa
    Mo8C4475.26119.88180.55451.77137.69178.17
    Mo7VC4481.10117.69177.65466.54134.82178.91
    Mo6V2C4473.96119.00166.23461.58141.35176.42
    Mo7WC4478.11125.91187.67459.93137.32177.95
    Mo6W2C4483.65131.41196.03468.71137.92178.09
    下载: 导出CSV

    表 4  不同构型的维氏硬度HV, Hardness (Tian)和硬度H

    Table 4.  Vickers hardness (HV), hardness (Tian), and hardness (H) of different configurations.

    ConfigurationHV/GPaHardness/GPaH/GPa
    Mo8C416.6416.5742.79
    Mo7VC416.8417.4643.00
    Mo6V2C418.1218.1341.71
    Mo7WC415.9816.0043.92
    Mo6W2C415.4315.5945.25
    下载: 导出CSV

    表 5  不同构型的弹性各向异性指数(AU, AB, AG)

    Table 5.  Elastic anisotropy indices (AU, AB, AG) of different configurations.

    ConfigurationBV/GPaGV/GPaBR/GPaGR/GPaAUAB/%AG/%
    Mo8C4262.69152.04262.30149.300.09310.07530.9073
    Mo7VC4263.86153.98263.30149.990.13520.10591.3137
    Mo6V2C4256.93155.90256.62153.640.07500.06170.7319
    Mo7WC4268.74151.14268.20148.900.07730.10170.7471
    Mo6W2C4275.88151.23275.17148.980.07790.12950.7472
    下载: 导出CSV

    表 6  不同构型的键布居

    Table 6.  Different configurations of bond population.

    Configuration Bond Number Population Length/Å
    Mo8C4
    		C—Mo80.672.1141
    C—Mo80.282.1143
    C—Mo[15]——2.118[15]
    Mo7VC4C—Mo70.692.1116
    C—Mo70.282.1131
    C4—V110.172.0367
    C3—V110.602.0380
    Mo6V2C4C—Mo60.732.1057
    C—Mo60.282.1076
    C—V20.592.0420
    C—V20.172.0675
    Mo7WC4C—Mo70.662.1152
    C—Mo70.272.1164
    C4—W110.342.1173
    C3—W110.792.1233
    Mo6W2C4C—Mo60.652.1162
    C—Mo60.262.1187
    C—W20.312.1210
    C—W20.762.1238
    下载: 导出CSV

    表 7  Mo8C4的电荷布居

    Table 7.  Charge distribution of Mo8C4.

    ConfigurationAtomspdfTotal electron/eMuliken charge/e
    Mo8C4Mo2.206.644.860.0013.700.30
    C1.443.160.000.004.60–0.60
    下载: 导出CSV

    表 9  W掺杂Mo8C4的电荷布居

    Table 9.  Charge distribution of W-doped Mo8C4.

    ConfigurationAtomTotal electron/eMuliken charge/eConfigurationAtomTotal electron/eMuliken charge/e
    Mo7WC4Mo113.700.29Mo6W2C4Mo113.700.30
    Mo213.700.31Mo213.700.30
    Mo313.700.29Mo313.720.29
    Mo413.700.30Mo413.720.29
    Mo513.700.30Mo513.660.33
    Mo613.680.32Mo613.660.33
    Mo713.660.33W127.700.29
    W127.840.27W227.700.29
    C14.60–0.60C14.60–0.60
    C24.60–0.60C24.60–0.60
    C34.62–0.61C34.62–0.62
    C44.60–0.61C44.62–0.62
    下载: 导出CSV

    表 8  V掺杂Mo8C4的电荷布居

    Table 8.  Charge distribution of V-doped Mo8C4.

    ConfigurationAtomTotal electron/eMuliken charge/eConfigurationAtomTotal electron/eMuliken charge/e
    Mo7VC4Mo113.760.24Mo6V2C4Mo113.800.20
    Mo213.700.30Mo213.800.20
    Mo313.760.24Mo313.800.21
    Mo413.720.29Mo413.800.20
    Mo513.740.26Mo513.800.21
    Mo613.780.22Mo613.800.20
    Mo713.760.25V112.380.62
    V112.380.63V212.380.62
    C14.60–0.60C14.62–0.61
    C24.60–0.60C24.62–0.61
    C34.62–0.62C34.62–0.62
    C44.62–0.61C44.62–0.61
    下载: 导出CSV
  • [1] Dahl J M, Novotny P M 1999 Adv. Mater. Processes. 155 23
    [2] Speich G R, Leslie W C 1972 Metall. Trans. 3 1043 doi: 10.1007/BF02642436
    [3] Garrison W M, Maloney J L 2005 Mater. Sci. Eng. , A 403 299 doi: 10.1016/j.msea.2005.05.021
    [4] 吴迪 2016 博士学位论文 (秦皇岛: 燕山大学) Wu D 2016 Ph. D. Dissertation (Qinhuangdao: Yanshan University
    [5] 李阿妮, 厉勇, 王春旭, 刘宪民 2007 钢铁 42 60 doi: 10.13228/j.boyuan.issn0449-749x.2007.09.020 Li A N, Li Y, Wang C X, Liu X M 2007 Iron Steel 42 60 doi: 10.13228/j.boyuan.issn0449-749x.2007.09.020
    [6] 王春旭, 张鹏杰, 高远航, 厉勇, 韩顺, 刘少尊 2020 金属热处理 45 7 doi: 10.13251/j.issn.0254-6051.2020.11.002 Wang C X, Zhang P J, Gao Y H, Li Y, Han S, Liu S Z 2020 Heat Treat. Met. 45 7 doi: 10.13251/j.issn.0254-6051.2020.11.002
    [7] Kwon H 1991 Metall. Trans. A 22 1119 doi: 10.1007/BF02661107
    [8] Kwon H, Lee K B, Yang H R, Lee J B, Kim Y S 1997 Metall. Mater. Trans. A 28 775 doi: 10.1007/s11661-997-1005-6
    [9] Lee K B, Yang H R, Kwon H 2001 Metall. Mater. Trans. A 32 1862 doi: 10.1007/s11661-001-0163-1
    [10] Lee K B, Yang H R, Kwon H 2001 Metall. Mater. Trans. A 32 1659 doi: 10.1007/s11661-001-0144-4
    [11] Speich G R, Dabkowski D S, Porter L F 1973 Metall. Trans. 4 303 doi: 10.1007/BF02649630
    [12] Liu X T, Zhou X L, Yang M S 2023 J. Mater. Sci. Mater. Electron. 34 961 doi: 10.1007/s10854-023-10364-3
    [13] Liu H L, Zhu J C, Lai Z H, Zhao R D, He D 2009 Scr. Mater. 60 949 doi: 10.1016/j.scriptamat.2009.02.010
    [14] Wang X R, Yan M F 2009 J. Wuhan Univ. Technol. Mater. Sci. Ed. 24 37 doi: 10.1007/s11595-009-7037-6
    [15] Wang X R, Yan M F, Chen H T 2009 J. Mater. Sci. Technol. 25 419 doi: 10.1179/174328408X270211
    [16] Liu Y Z, Jiang Y H, Zhou R, Liu X F, Feng J 2015 Ceram. Int. 41 5239 doi: 10.1016/j.ceramint.2014.10.167
    [17] Vanderbilt D 1990 Phys. Rev. B. 41 7892 doi: 10.1103/PhysRevB.41.7892
    [18] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865
    [19] Guo J, Feng Y L, Tang C, Wang L, Qing X L, Yang Q X, Ren X J 2022 Materials 15 4719 doi: 10.3390/ma15134719
    [20] Abderrahim F Z, Faraoun H I, Ouahrani T 2012 Physica B 407 3833 doi: 10.1016/j.physb.2012.05.070
    [21] Luo Y, Cheng C, Chen H J, Liu K, Zhou X L 2019 J. Phys. Condens. Matter 31 405703 doi: 10.1088/1361-648X/ab2847
    [22] Peng M J, Wang R F, Wu Y J, Yang A C, Duan Y H 2022 Vacuum 196 110715 doi: 10.1016/j.vacuum.2021.110715
    [23] Zhao R D, Wu F F, Liu X, Zhu J C, Zhao Z F 2016 J. Alloys Compd. 681 283 doi: 10.1016/j.jallcom.2016.03.269
    [24] Wu M M, Wen L, Tang B Y, Peng L M, Ding W J 2010 J. Alloys Compd. 506 412 doi: 10.1016/j.jallcom.2010.07.018
    [25] Jang J H, Lee C H, Heo Y U, Suh D W 2012 Acta Mater. 60 208 doi: 10.1016/j.actamat.2011.09.051
    [26] Yan M, Zhang H, Gong C, Zhang M, Gao Q 2025 J. Phys. Chem. Solids 196 112374 doi: 10.1016/j.jpcs.2024.112374
    [27] Boucetta S, Zegrar F 2013 J. Magnes. Alloys 1 128 doi: 10.1016/j.jma.2013.05.001
    [28] Gao X P, Jiang Y H, Zhou R, Feng J 2014 J. Alloys Compd. 587 819 doi: 10.1016/j.jallcom.2013.11.005
    [29] 李士明, 张启富, 邱肖盼, 张子月, 仲海峰 2022 材料保护 55 9 doi: 10.16577/j.issn.1001-1560.2022.1002 Li S M, Zhang Q F, Qiu X P, Zhang Z Y, Zhong H F 2022 Mater. Prot. 55 9 doi: 10.16577/j.issn.1001-1560.2022.1002
    [30] Chen X Q, Niu H, Li D, Li Y 2011 Intermetallics 19 1275 doi: 10.1016/j.intermet.2011.03.026
    [31] Tian Y J, Xu B, Zhao Z S 2012 Int. J. Refract. Met. Hard Mater. 33 93 doi: 10.1016/j.ijrmhm.2012.02.021
    [32] Teter D M 1998 MRS Bull. 23 22 doi: 10.1557/S0883769400031420
    [33] Haines J, Leger J M, Bocquillon G 2001 Annu. Rev. Mater. Res. 31 1 doi: 10.1146/annurev.matsci.31.1.1
    [34] 卢彩彬, 李新梅 2021 科学技术与工程 21 10646 doi: 10.3969/j.issn.1671-1815.2021.25.012 Lu C B, Li X M 2021 Sci. Techno. Eng. 21 10646 doi: 10.3969/j.issn.1671-1815.2021.25.012
    [35] Li Y F, Gao Y M, Fan Z J, Xiao B, Yue Q W, Min T, Ma S Q 2010 Phys. B: Condens. Matter. 405 1011 doi: 10.1016/j.physb.2009.10.045
  • 加载中
图( 6) 表( 9)
计量
  • 文章访问数:  36
  • HTML全文浏览数:  36
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-01-10
  • 刊出日期:  2025-05-20

第一性原理研究钒、钨固溶对碳化钼力学性能的影响

    通讯作者: E-mail: yangyongboxian@163.com.; 
    作者简介: 杨正罡. E-mail: yangzg200105@163.com
  • 1. 安徽工业大学冶金工程学院, 马鞍山　243000
  • 2. 东北大学, 轧制技术及连轧自动化国家重点实验室, 沈阳　110819
  • 收稿日期:  2025-01-10

摘要: 二次硬化型超高强度钢广泛应用于航空航天等领域, 弥散析出的纳米级M2C是二次硬化钢的主要强化因素. Mo是形成二次强化相Mo2C的主要元素, 可与Cr, V, W等形成复合型M2C. 为探究V, W的掺杂对Mo2C的影响, 本文基于第一性原理研究了掺杂体系的电子结构和力学性质. 研究结果表明, 掺杂V降低形成焓, 使结构更为稳定, 而掺杂W使稳定性下降. 掺杂V使韧性下降, 硬度增加. 掺杂W改善强韧性, 硬度降低更缓慢. 与C—Mo键相比, C—V键共价性弱, C—W键共价性强.

English Abstract

    全文HTML

    1.   引　言

    • 二次硬化钢因其强度高、韧性好, 广泛应用于航空航天等领域, 如军机起落架等[1–4]. 二次硬化钢的超高强度主要来源于板条马氏体基体及其在500 ℃左右回火后析出的碳化物[4]. Mo是形成二次强化相的主要元素[5]. 当Mo含量较低时, 二次硬化作用弱. 随Mo含量的增加, 析出的M2C数量增多, 二次硬化作用提高. 在钢铁材料领域, Mo2C一般为六方结构, 复合型M2C (例如(Mo, Cr)2C, (Mo, Cr, W)2C或(Mo, Cr, V, W)2C)[4]仍保持六方结构.

      王春旭等[6]发现AIR0509钢在535 ℃下回火4 h析出M2C并达到最佳强韧性配合. Kwon等[7,8]和Lee等[9,10]发现, W和Mo复合形成M2C可延缓峰时效, 增强二次硬化效应. Speich等[11]和Liu等[12]发现, 向Fe-Ni-Mo-C钢中添加Co可以提高M2C的成核速率, 且形成尺寸较小的M2C. Liu等[12,13]深入地分析了不同温度下Cr-Co-Mo马氏体钢中碳化物的演变, 定量表征了碳化物的类型、形态和尺寸, 发现合金钢的强韧性与这些碳化物的成分、晶体结构、热力学性质和稳定性有关. 当二次硬化钢中加入其他合金元素(Cr, V, W, Nb等), 会形成M2C从而改变Mo2C的成分和性能, 改变碳化物析出行为, 如Cr固溶于Mo2C中可以促进M2C碳化物的形成[14]. 为了给合金设计提供思路, 有必要阐明这些合金元素对Mo2C的影响.

      目前, 研究人员利用第一性原理研究了Mo2C的结构、稳定性、力学性能等参数[13,15,16]. Wang等[15]基于密度泛函理论计算了Mo2C的熔点和硬度. Liu等[16]详细分析了Mo2C的吉布斯自由能以及剪切模量、杨氏模量. Liu[13]等利用第一性原理计算了Mo2C的结构和电子性质, 并研究了Cr, Nb的掺杂对结构稳定性的影响. 结果表明, Mo2C的化学键既有共价键又有金属键. Nb是该体系的稳定元素, 而Cr则降低Mo2C的稳定性. Liu等[12]和Wang[14]等发表的第一性原理研究主要集中在Cr掺杂Mo2C的结构稳定性及力学性能上. 除Cr, Nb以外, V, W也会配分至Mo2C中形成(Mo, V, W)2C, 改变Mo2C的性能, 从而改变二次硬化钢的性能. 然而, 关于V, W掺杂Mo2C性质的研究至今鲜少报道. 本文将采用第一性原理方法对V、W掺杂Mo2C进行计算, 并通过形成焓、弹性常数来描述V, W的掺杂对Mo2C的稳定性及力学性质的影响, 通过态密度和差分电荷密度分析键合特性. 研究结果对二次硬化钢中Mo2C的进一步发展具有良好的指导作用, 为二次硬化钢成分的优化设计和新型高性能二次硬化钢材料的开发提供理论依据.

    2.   计算方法与细节

    • 本文使用CASTEP[17], 将赝势平面波与密度泛函理论(density functional theory, DFT)相结合进行第一性原理计算, 采用PBE泛函进行广义梯度近似(generalized gradient approximation, GGA)[18]. 计算中全局精度设置为fine, 默认截断能设置为421.8 eV, K点网格设置为9×9×6. 采用BFGS (Broyden-Fletcher-Goldfarb-Shanno)方法进行优化. 赝势选用OTFG ultrasoft, 比起传统的超软赝势提供更高精度. 计算过程中考虑自旋, 其他参数采用默认设置.

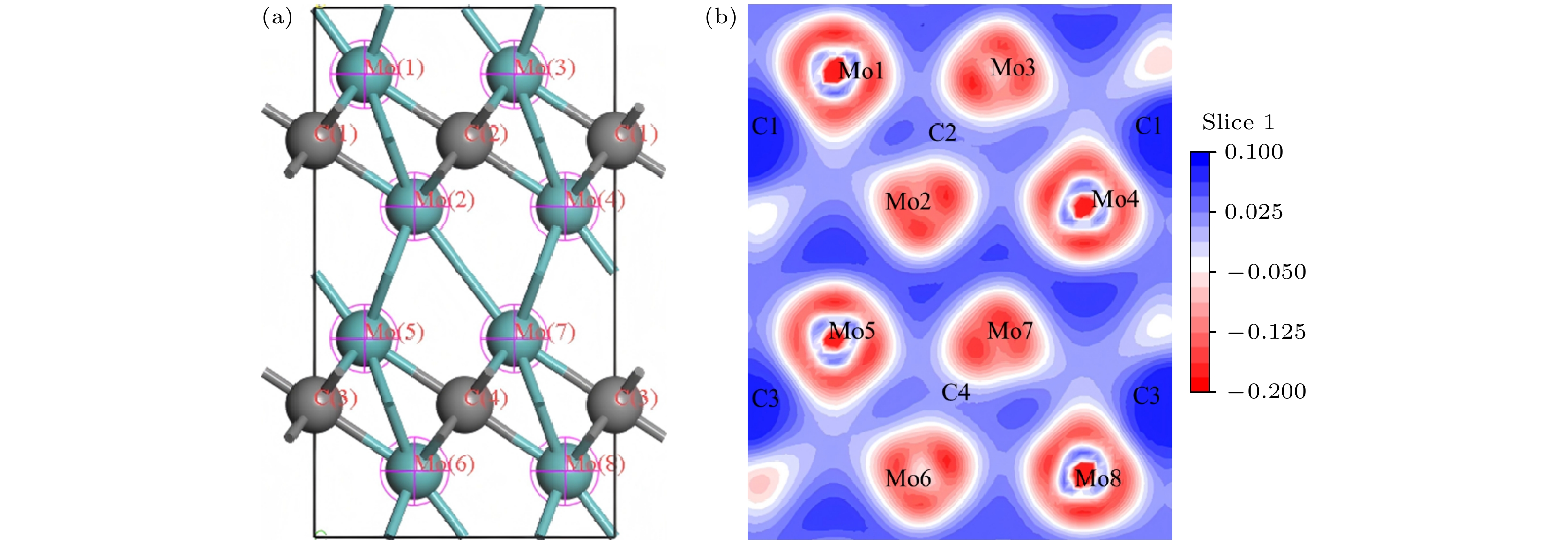
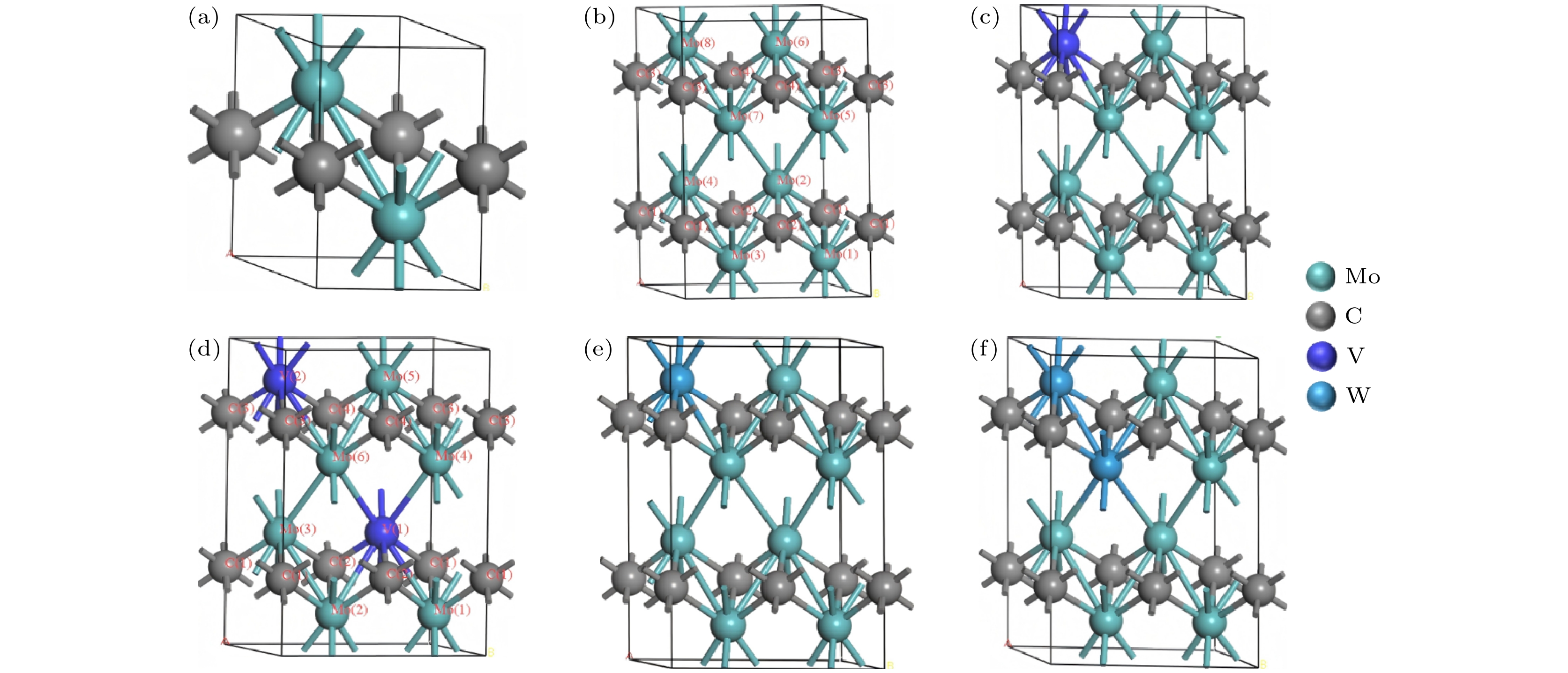
      对Mo2C进行计算[19], 晶格参数a = b = 3.073 Å, c = 4.653 Å. 由于原始晶胞只有2个Mo原子与1个C原子, Mo原子坐标(0.33, 0.67, 0.25), (0.67, 0.33, 0.75), C原子坐标为(0, 0, 0.5). 考虑2×1×2扩胞, 增加原子数目. 并考虑V, W取代Mo的位置, 不同构型的结构示意图如图1所示. 为了清楚取代位置, 给出Mo8C4及每个原子的代号, 如图1(b)所示. 此外, 单胞结构优化后, 建立超胞做掺杂计算时, 并未在掺杂之前对超胞进行结构优化, 这是因为在掺杂后, 掺杂原子会破坏结构原有的对称性, 导致结构内部的电荷重排, 原子的相对位置也会发生变化, 因此在掺杂后再进行结构优化使晶胞几何结构稳定化以及能量最小化.

    3.   结果与讨论

      3.1.   晶格参数和热力学稳定性

    • 为了了解V, W掺杂后对Mo8C4晶体结构的影响, 采用晶格参数和体积变化来反映结构的变化程度. 结构优化后Mo8C4及掺杂结构的晶格参数和体积变化率如表1所列, 可以看出掺杂前的构型结构优化后的晶格参数与文献报道值相近[12,13,15,20,21], 表明计算结果可靠. 与Mo8C4相比, 随着V含量的增加, a, b, c, V均不断减小. 而随着W含量的增加, 晶格参数及晶胞体积略微增加. V, W的掺入使晶格参数发生不同程度的变化, 其中V的掺杂对晶格参数的影响更大. 从体积变化率来看, 与Mo8C4相比, Mo6V2C4变化幅度最大, 减小幅度高达3.18%. 这是由化合物中Mo, V, W, C的原子尺寸差异引起不同程度的晶格畸变导致的. 其中V原子半径为135 pm, Mo原子半径140 pm, W原子半径141 pm, C原子半径86 pm. 这与Cr掺杂[12–14]对晶格参数的影响规律一致.

      形成焓通常用于描述热力学稳定性[22], 也可以描述合金化的能力[23]. 形成焓可由下式计算[24]:

      式中Etotal表示超胞结构的总能量; Esolid(Mo), Esolid(C), Esolid(X)分别表示单个Mo, C原子以及合金原子X(V, W)的能量, m, n, l分别表示超胞结构不同原子的数目. 用第一性原理的方法计算出单个Mo, C, V, W的值分别为–1936.199 eV, –157.558 eV, –1951.782 eV和–9252.502 eV. 计算选取构型[13,25]为体心立方(body-centered cubic, bcc) Mo, bcc V, bcc W以及金刚石C, 与文献计算值[13,26]比较吻合.

      表2列出了不同构型的形成焓的计算结果, 可以看出Mo8C4构型的形成焓与以前的计算结果吻合较好, 使本文结果更为可靠. 形成焓为负表明结构稳定, 且形成焓越小, 结构越稳定[22]. 随着V原子的掺杂, 形成焓明显减小, 表明合金化能力增强. 而随着W原子的含量增加, 形成焓增大, 表明合金化能力减弱. 晶格畸变越大, 内部弹性应变能越高, 导致合金化能力和稳定性有所差异[23]. V的掺杂导致合金化能力增强, 可能是因为与Mo相比, V的原子半径和晶格参数与C更为接近, 晶格失配率更低.

      • 3.2.   弹性常数

      3.2.1.   单晶弹性常数

    • 弹性常数是表征材料性能、估算力学性质的重要物理量. CASTEP模块[22,27]通过应力-应变法计算相应应力再通过胡克定律获得弹性刚度常数Cij及其逆矩阵弹性柔度常数Sij.

      六方晶系中独立的弹性常数有C11, C33, C44, C12, C13. 固体的力学稳定性可以根据波恩-黄昆判据来判定, 六方结构的稳定性判据[22]为C11>0, C11>C12, C11+C12>0, C44>0, (C11+C12)C33>2$ C_{13}^2 $. 根据表3中掺杂前后的单晶弹性常数, 计算后得出, 掺杂V和W前后, 几种构型均符合稳定性判据, 力学稳定.

      材料在单轴应力作用下沿a, b, c轴的线压阻力与C11, C22, C33的大小正相关[22,28]. 由表3, C11大于C33, 表明这些构型沿c轴的可压缩性大于沿a轴的可压缩性, 在a轴上更不易变形. 也表明(001)平面上的键合强度强于[001]方向. 随着W含量的增加, C11, C33一直增大, 表明Mo8C4随着W的添加, 沿a, c上更难变形, 可压缩性减小. 而随着V含量的增加, C11, C33均先增后减, 在a, c轴上可压缩性先减后增.

      • 3.2.2.   多晶弹性模量

    • 由于实际应用中晶体都以多晶形式存在, 因此考虑多晶的弹性模量更有意义. 多晶弹性模量与单晶弹性常数有关联, 可通过Voigt-Reuss-Hill近似计算[22], Voigt近似和Reuss近似分别对应模量的最大值和最小值, Hill近似代表平均值.

      引入M和C 2, 以及六方结构Voigt和Reuss近似模型计算公式如下[29]:

      式中, V和R分别表示Voigt和Reuss模型. 通过Voigt-Reuss-Hill对体积模量B、剪切模量G、杨氏模量E以及泊松比近似计算, 公式如下[27]:

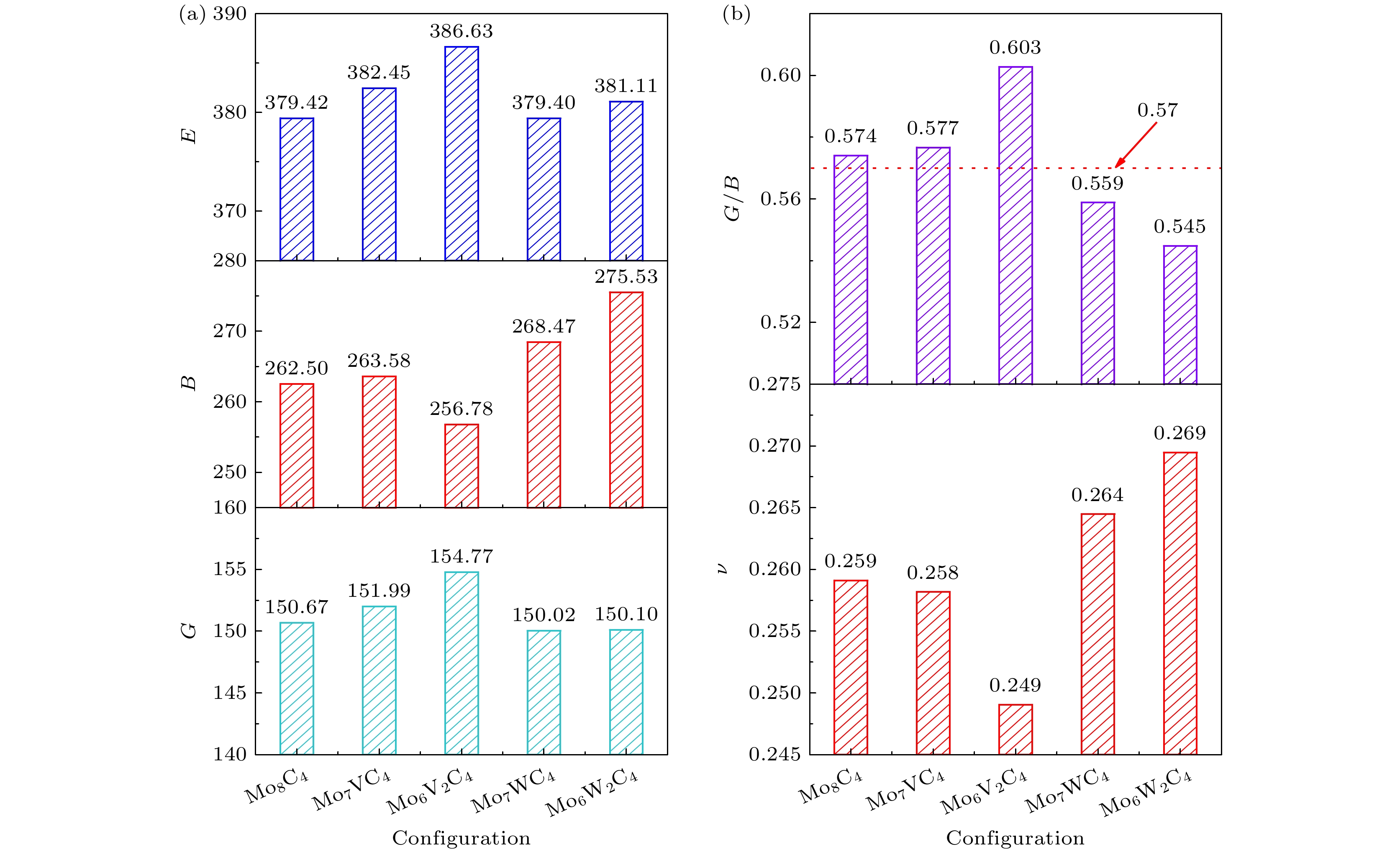
      弹性模量B, G, E的变化情况如图2(a)所示, 随着W的添加, 体积模量B增大, 在Mo6W2C4时达到最大, 约275.5 GPa. Mo7VC4的体积模量变化不大, 而继续添加V后, B明显减小. 由于B反映材料受外部压力的抗变形能力[22], 这意味着W的添加引起的晶格畸变使外力对宏观体积变化的阻力增大, 从而导致Mo8C4的可压缩性下降. 而Mo6V2C4强度最小, 最容易压缩. Mo8C4掺杂V后, 剪切模量增加, 而W的添加使剪切模量略有减小. G越大, 抗剪切应变的能力越强. 一般来说, E与刚度正相关. E越大, 越不易变形. 由图2(a)看出, 与Mo8C4相比, 掺杂W后, Mo6W2C4刚度更大, 不易变形. 而随V含量的增加, Mo8C4的刚度增加明显. 由此可知, W的添加对剪切应变能力和杨氏模量的影响很小. 有报道计算出未掺杂的Mo2C构型剪切模量为152.48 GPa[12], 体积模量为261.58 GPa[13], 与本文计算结果吻合较好.

      材料的脆韧性可以通过模量比G/B、泊松比来表征. 图2(b)给出了泊松比和模量比G/B的变化情况. 添加V后, 泊松比减小, G/B增加, 而添加W的情况则相反. 泊松比[22]反映固体横向弹性形变, 一定程度上可以预测晶体剪切形变下的稳定性, 更高的泊松比意味着更高的延展性; 而Pugh准则用G/B的边界值0.57来描述材料的塑性. 当模量比G/B > 0.57表明材料为脆性材料. 模量比越小, 韧性越好. 由此可知, 模量比与泊松比得到结果相吻合, Mo8C4为脆性材料, 添加V会使其更脆, 而掺杂W后, 韧性变强. 有报道计算出未掺杂的Mo2C构型泊松比为0.261[12], 与本文较符合.

      硬度[30]反映材料抵抗弹、塑性变形的能力. 在过去的研究中, 一些半经验模型被用于预测合金的硬度. Chen等[30]基于Pugh模量比(G/B)和剪切模量(G), 提出了一种新的半经验模型来预测多晶材料和大块金属玻璃的硬度, 该模型如下[23]:

      式中, HV为维氏硬度; k为Pugh模量比. 不同构型的维氏硬度值如表4所列, 掺杂V使维氏硬度值增大, 掺杂W使维氏硬度值减小. CASTEP基于Tian等[31]计算模型给出了Hardness, 计算结果见表4. 对Mo7VC4与Mo6V2C4, 以及Mo7WC4, Mo6W2C4之间的变化, Hardness与维氏硬度半经验模型得出的结果较为吻合. Teter[30,32]在硬度与剪切模量(G)之间建立了较好的线性相关性, 一定程度上通过剪切模量对材料硬度进行评估. 与Mo8C4相比, 添加V和W, 同样是前者数值增加, 后者减小, 但与维氏硬度的判断略有差异. 有报道说, 剪切模量与硬度的这种相关性并不总是成功的[30]. 例如碳化钨(WC)的体积模量有439 GPa、剪切模量达282 GPa, 但其硬度仅为30 GPa[30,33]. 因此添加W后, HV, Hardness (Tian 2012)[31]和G变化上的差异, 可能是G与硬度的这种相关性不太成功. 但三者也一定程度上得出同样的判断, 即与Mo8C4相比, 添加V会使硬度增加, 添加W会使硬度减小.

      此外, 硬度H与体积模量有所关联, H越大, 固体材料对弹塑性变形的抗力越强. H与B的回归拟合经验方程为[29]

      式中, H的单位为GPa. 由此得出, V的添加, 使材料抵抗弹性和塑性变形的能力先增加后减小, 而添加W, 抗弹塑性变形的能力有所增强.

      • 3.2.3.   弹性各向异性

    • 弹性各向异性通常[22]会导致微裂纹的产生和扩展. 多晶材料的体模量和剪切模量的弹性各向异性百分比被广泛应用, 使用以下三个指标来描述弹性各向异性, 即通用各向异性指数AU、压缩各向异性百分比AB和剪切各向异性百分比AG, 计算公式如下[22]:

      通过AU, AB和AG, 可以直观地确定晶体的弹性各向异性. 当AU = AB = AG = 0时, 各方向弹性模量均为各向同性, 反之则为各向异性, 偏离零的程度越大, 各向异性程度越大.

      由表5能够看出, 与Mo8C4相比, 掺杂V会导致各向异性程度增大, 掺杂W则导致各向异性程度减小. 随着V含量的增加, 各向异性程度下降, 而W含量继续增加, 导致各向异性程度略微上升, 仍低于Mo8C4. AG和AU的变化顺序一致. AB与AU表现出不同的变化顺序, 但AU比AB更准确地反映各向异性, 因为AU中同时考虑了B和G. 此外, 可以注意到, 剪切各向异性的程度远大于压缩各向异性. 随着W的掺杂, 压缩各向异性增大.

      • 3.3.   电子性质

    • 为了进一步了解这几种构型的键合情况及电子性质, 采用态密度、布居分析、差分电荷密度图作出解释.

      • 3.3.1.   态密度

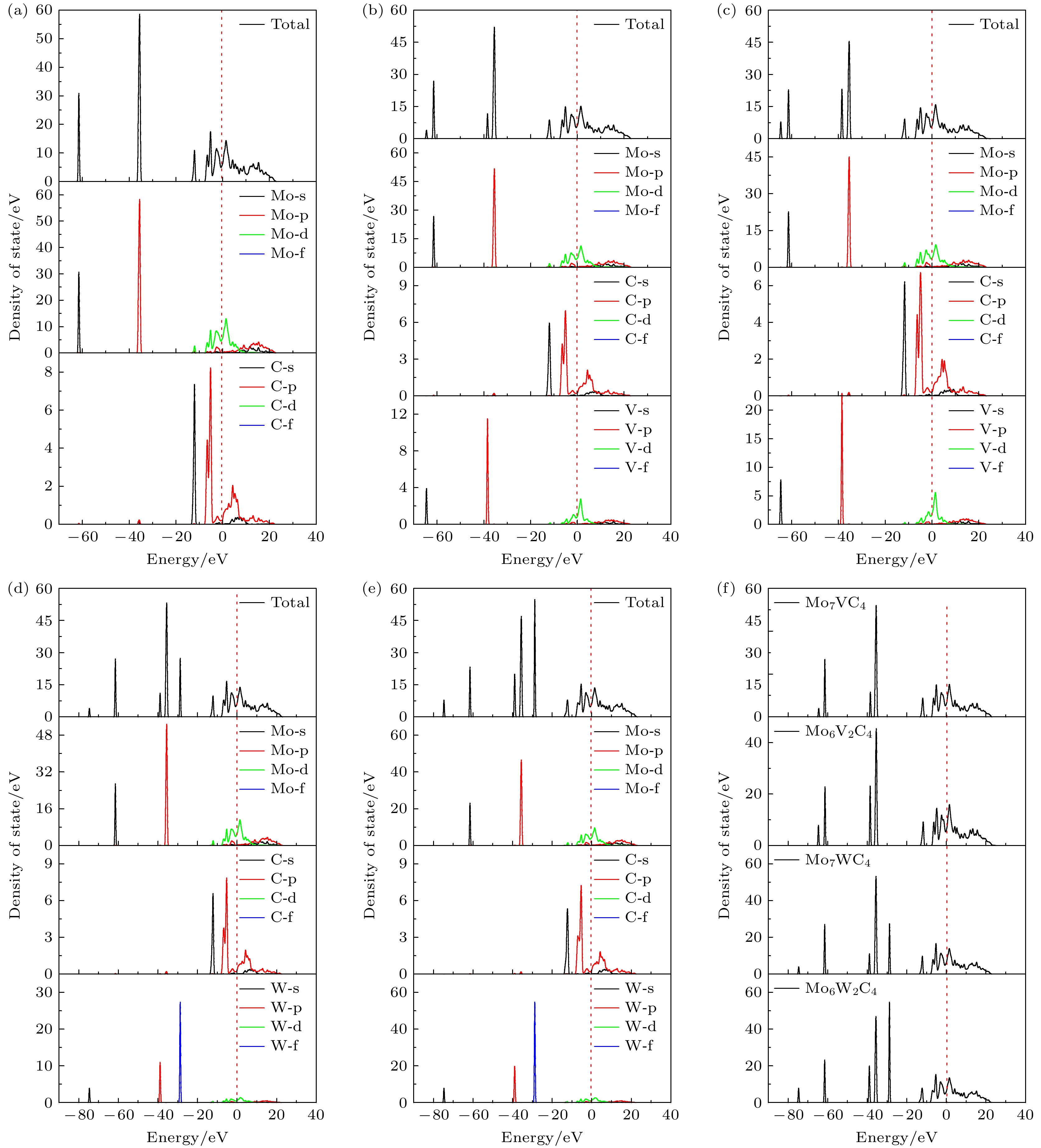
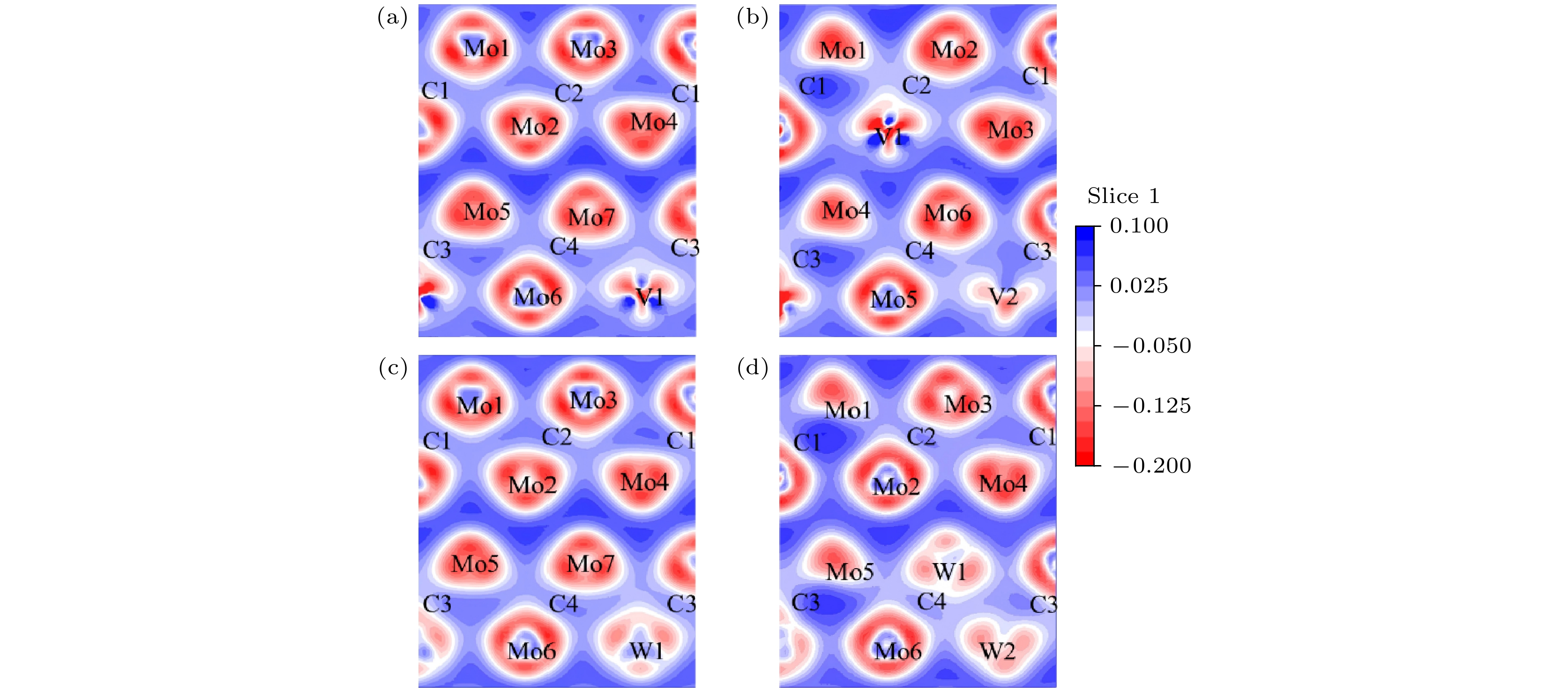
    • 采用态密度对原子间的键合情况进行定性分析. 5种构型的态密度(DOS)及分波态密度(PDOS)分别如图3(a)—(e)所示, 图3(f)为四种掺杂构型的DOS图, 0能量处的虚线表示费米能级EF. 若EF所在范围出现态密度为0, 表明该体系是绝缘体或半导体[22]. 从图3能够看出, EF所处范围, 几种构型的态密度均不为0, 没有能隙, 因此均为金属体系. 此外, 这几种构型在EF的两侧有态密度峰, 且波峰之间的态密度并不为0, 即费米能级附近出现赝能隙. 赝能隙在EF附近出现, 反映了体系稳定且存在共价键. 在能量范围内分布平均, 局域态密度峰平缓, 即类sp带, 非局域性强[34]. DOS局域尖峰则是意味着局域性强. 原子轨道成键强度大, 态密度峰平缓, 跨过能量范围大.

      由图3(a)可知, 掺杂前的态密度在费米能级附近的波峰相对平坦, 跨过能量范围大, 成键强度大. 在10—25 eV区域, 主要由Mo原子的s, p轨道和C原子的p轨道电子产生杂化, 形成Mo—C共价键. 在–3 eV和–5 eV左右, Mo的p, d轨道和C的p轨道电子杂化. C在–5 eV处波峰更为尖锐, 电荷贡献大. Mo的d轨道和C原子的s轨道在–12 eV处杂化. 在–62 eV和–35 eV附近呈现尖锐的波峰, 电荷贡献分别来自于Mo原子的s, p轨道, 局域性较强, 且–35 eV处局域性最强.

      由图3(b)和图3(c)可知, 掺杂V后, 在–65和–38 eV处增加两个小波峰, 电荷贡献分别来自于V的s, p轨道电子, 不产生杂化. 随着V原子的掺杂, Mo原子的分波态密度图中, 波峰高度有所下降, 电荷贡献有所削弱. 在–5—5 eV的区域内, Mo, V的d轨道和C的p轨道电子发生杂化, 还形成V—C键. 由图3(d)和图3(e)可知掺杂W后, W原子的s, p, f轨道电子依次在–75 eV, –39 eV, –29 eV附近产生态密度峰, 且峰值依次增大, 局域性增强. 随着W原子的掺杂, Mo原子的电荷贡献同样有所减弱, 掺杂W后Mo, W的d轨道和C的p轨道电子发生杂化, 形成W—C键. 由图3(f)可知, 随着V, W含量的增加, V, W各处波峰的电荷贡献增多, V在–40 eV处以及W在–40与–30 eV处的增加最为明显, 局域性增强.

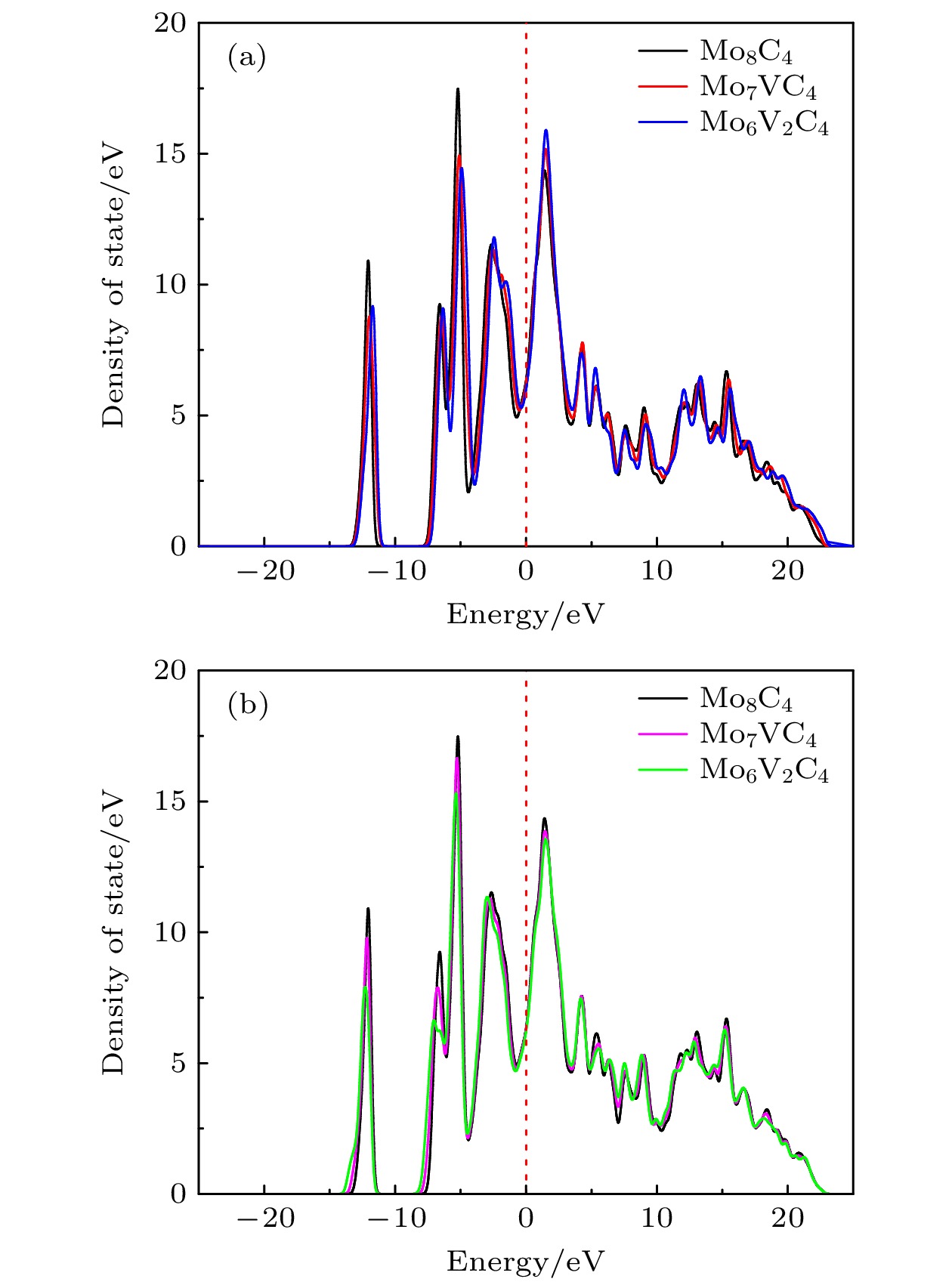
      不同构型在费米能级附近的态密度图如图4所示, 并结合图3, 可以看出掺杂后Mo原子减少, 导致多处波峰峰值降低. 但V在费米能级附近有态密度峰, 导致有波峰峰值得到提高, 而W在费米能级附近较为平缓.

      • 3.3.2.   布居分析

    • 通过电荷布居和键布居来定量分析原子间的键合情况和电荷转移, 表6给出了几种构型的键布居, 表7—表9依次是几种构型的电荷布居.

      由表6可以看出这5种构型均形成16个化学键, 从布居值来看, 每种构型形成的C—X键(X = Mo, V, W)均有一半布居值较大, 在0.7左右, 而另一半布居值较小, 在0.3左右. 这可能是由于六方结构的对称程度引起的. 一般来说, 重叠布居数越大, 共价键越强[23,35]. C—X键的布居值均为正值, 因此这5种构型所成的化学键均为共价键. 这与Cr掺杂[14], 成键类型一致. 随着V的添加, 布居值较大的Mo—C键, 其布居值会继续增大, 共价性也会越强, 而布居值较小的Mo—C键, 共价性不变. 随着V的添加, C—V键的布居值基本不变, 且与相应的C—Mo键相比, 共价性有所不如. 而W的添加, Mo—C键的布居数有所减小, 共价性减弱, 与Mo—C键相比, C—W键的布居值增加较多, 共价性增强. 此外可以注意到, 原子间距离远的形成的共价键布居值较小; 距离近的布居值大, 共价性强. 原子间相互作用减弱, 布居数减少, 使结构不稳定[14]. C—X键共价性的变化, 与结构稳定的结果相吻合.

      原子间成键长短可以对稳定性进行评估, 键长越大, 越不稳定. 从表6可以看出, 每种构型都有这个规律, 布居值大的Mo—C键, 共价性更强, 键长较小, 稳定性较高. V的添加使Mo—C键更短, 稳定性更高. W的添加使Mo—C键更长, 稳定性更低. 布居值较大的C—W键, 共价性较强, 但其键长更长, 更不稳定. C—Mo键键长约2.11 Å, 与文献[15]报道的2.118 Å吻合较好. C—V键长约2.05 Å, C—W键长约2.12 Å. 与C—Mo键相比, C—V键键长明显缩短, 稳定性更强, 而C—W键键长增大, 稳定性较弱. C—X键稳定性的差异与形成焓的计算结果相吻合, 推测C—X键稳定性的差异可能与合金化能力的差异有关.

      由表7可以看出, Mo的s, p, d轨道均有电荷贡献, 且p轨道贡献最多. 由表8和表9, Mo, V, W均失电子, C得电子. 在电荷总数上C<V<Mo<W. 这是因为W原子还在f轨道有电荷贡献, 且电荷贡献比其他轨道多出不少. 随着W掺杂, C3, C4位置得电子稍多, 这是因为W掺杂位点离C3, C4近. 随着V掺杂, Mo失电子更少; W掺杂, 则Mo失电子更多. 这是因为与Mo相比, V失电子更多, W失电子略少.

      • 3.3.3.   差分电荷密度

    • 差分电荷密度图是研究电子结构的手段之一, 可以直观地显示出成键过程中电子转移和成键情况. 标记差分片段及绘制Mo8C4的差分电荷密度图, 如图5所示. V, W掺杂后的差分电荷密度图如图6所示. 图6(a)和图6(c)中的V1, W1取代Mo8的位置, 图6(d)中的掺杂原子, 依次取代Mo7和Mo8的位置, 与前文所述一致. 差分电荷密度图中通过颜色判断电荷转移, 以及电子云堆叠形成共价键. 蓝色区域对应得电子, 代表电荷聚集; 红色区域对应失电子, 代表电荷损耗, 意味着电子不足. 而白色区域代表电荷密度基本不变. 图5为Mo8C4的差分电荷密度图, 相邻的Mo都失去电荷, 使Mo之间形成金属键. Mo原子处失电子程度具有一定的方向性. 这是因为每个Mo原子都形成一个强的Mo—C键和弱Mo—C键. 如Mo1—C1之间电荷密度差大, 形成共价键键性强, Mo1—C2键之间电荷密度差小, 形成共价键键性弱. C原子处电荷富集得电子, 电荷沿Mo—C共价键方向聚集. 从图6(a)—(d)可知, 合金原子(V, W)和Mo原子处都失电荷, C原子处得电子. 电荷沿C—X (X = V, W, Mo)共价键方向富集, 且与Mo原子相比, V原子失电子更多, W原子失电子更少, 与电荷布居相符.

    4.   结　论

    • 本文为探究V, W掺杂对Mo2C的影响, 利用第一性原理计算了晶格参数、形成焓、弹性常数和电子性质, 得出如下结论.

      1) 掺杂后的晶格参数受到掺杂原子大小的影响, 掺杂V会导致晶格参数有所减小, 而掺杂W导致晶格参数有所增加, 其中V掺杂对晶格参数的影响更大.

      2) 掺杂V会导致韧性下降, 硬度增加. 掺杂W改善强韧性, 硬度降低缓慢.

      3) C—X (X = Mo, V, W)键均为共价键, 与C—Mo键相比, C—V键共价性弱, C—W键共价性强. 掺杂V使Mo—C键稳定性更高, 并形成稳定性更高的C—V键. W的添加使Mo—C键稳定性降低. Mo, V, W均失电子, C得电子. 与Mo相比, V失电子更多, W失电子数稍少.

    参考文献 (35)

目录

/

返回文章
返回