首页
登录
注册
-
国际热核聚变实验反应堆（ITER）是由世界七方（美国、中国、俄罗斯、欧盟、日本、韩国、印度）联合投资建设的磁约束核聚变实验项目，其主要目标是建造一个能够实现自持燃烧的托卡马克反应堆[1-5]。环向场（TF）和极向场（PF）超导线圈是ITER装置主机的重要组成部分，分别用于产生约束聚变等离子体运行和控制等离子体位型所需的磁场[6]。具体而言，TF磁体线圈用于产生环向场约束聚变等离子体沿着环向运行[7]，PF磁体线圈则用于产生极向场控制等离子体位型[8]。考虑到TF 和PF 磁体线圈在ITER 装置中的核心作用，TF和PF 超导磁体线圈在制造完后，需在正式安装到装置主机前于低温测试平台开展超导磁体线圈低温性能测试，以验证超导磁体线圈的超导性能、机械稳定性、热负荷管理、电磁性能、绝缘性能、电流引线和接头的性能，以及与托卡马克系统的兼容性，低温性能测试有助于发现和解决超导磁体线圈在低温环境下可能出现的各种问题，从而为托卡马克装置的安全、可靠运行提供保障。
目前，中国的EAST超导托卡马克装置、韩国的KSTAR超导托卡马克装置、日本的JT-60SA 装置以及在建的ITER国际热核聚变堆装置，均针对TF 和PF 超导磁体线圈的测试需求，建设了低温测试平台。这些测试平台包括椭圆形和圆柱形等不同结构。无论测试平台的形状如何，冷屏始终是其核心部件，主要用于屏蔽外部环境对磁体的热负荷。低温测试平台中的冷屏一般采用主动式冷却金属冷屏，常见的结构形式有管板式和胀板式两种。例如，聚变堆关键系统综合研究基础设施 （CRAFT）的低温测试平台采用了胀板式结构冷屏[9]，而EAST装置的超导磁体低温测试平台采用了管板式冷屏结构。无论是管板式与胀板式冷屏，均具有较高的冷却效率，但它们都存在大量焊接和连接密封界面，且冷却通道里充有兆帕级压力的冷却介质，因而存在泄漏风险。此外，它们的制造难度大，制造周期长且拆卸困难。
为提高超导磁体测试效率，并减少在装拆过程中可能出现的冷却介质泄漏，ITER装置超导磁体低温测试平台（MCTB）中的冷屏设计采用了被动式冷却冷屏结构。该冷屏主要由多层绝热（MLI）组成。MLI具有薄厚度、轻质量和良好的安装与拆卸便捷性等特点，且能够有效满足最小热负荷（尤其是辐射热负荷）要求[10-11]。由于测试平台对磁体的辐射传热占总漏热的主要部分，所以，相较于管板式与胀版式冷屏，MLI具有更大的工程应用价值。
-
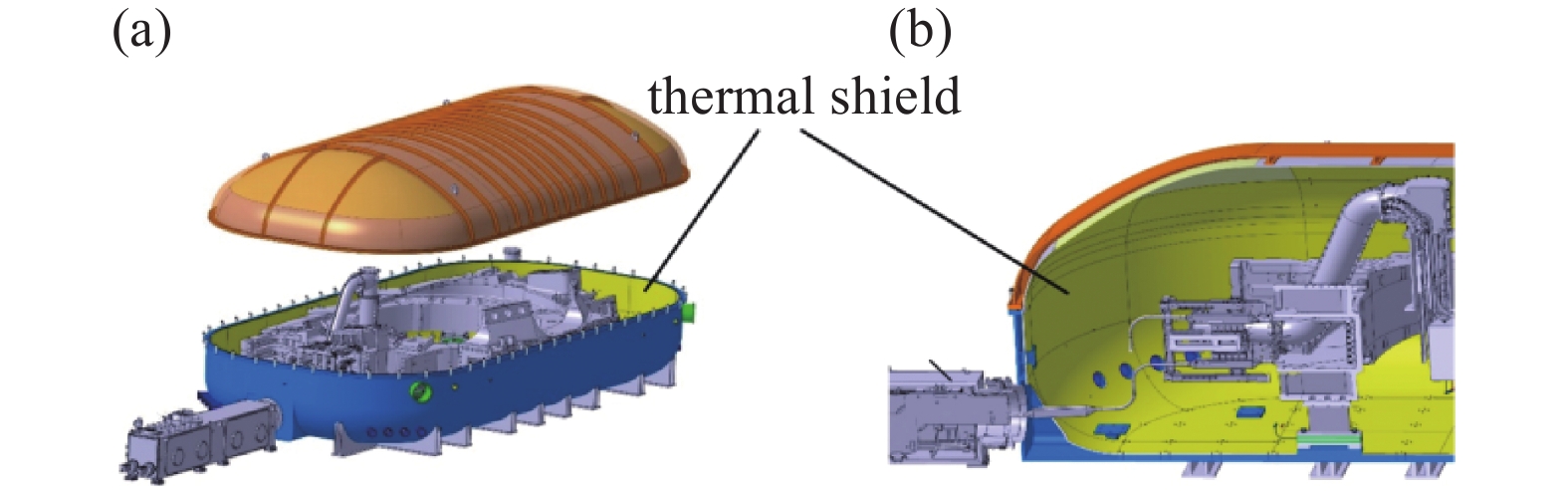
根据ITER 装置磁体线圈测试要求， MCTB 主要由杜瓦、冷屏及磁体支撑、各类连接法兰等部件组成，其总体外观尺寸为21.2 m（长）×10.5 m（宽）×6 m（高），具体结构如图1所示。
根据ITER 装置磁体低温系统制冷能力，磁体线圈测试平台的冷屏需要保证磁体在测试过程中受到的辐射热载荷不超过1 kW。此外，MCTB冷屏结构需满足超导磁体测试易安装拆卸的要求。
-
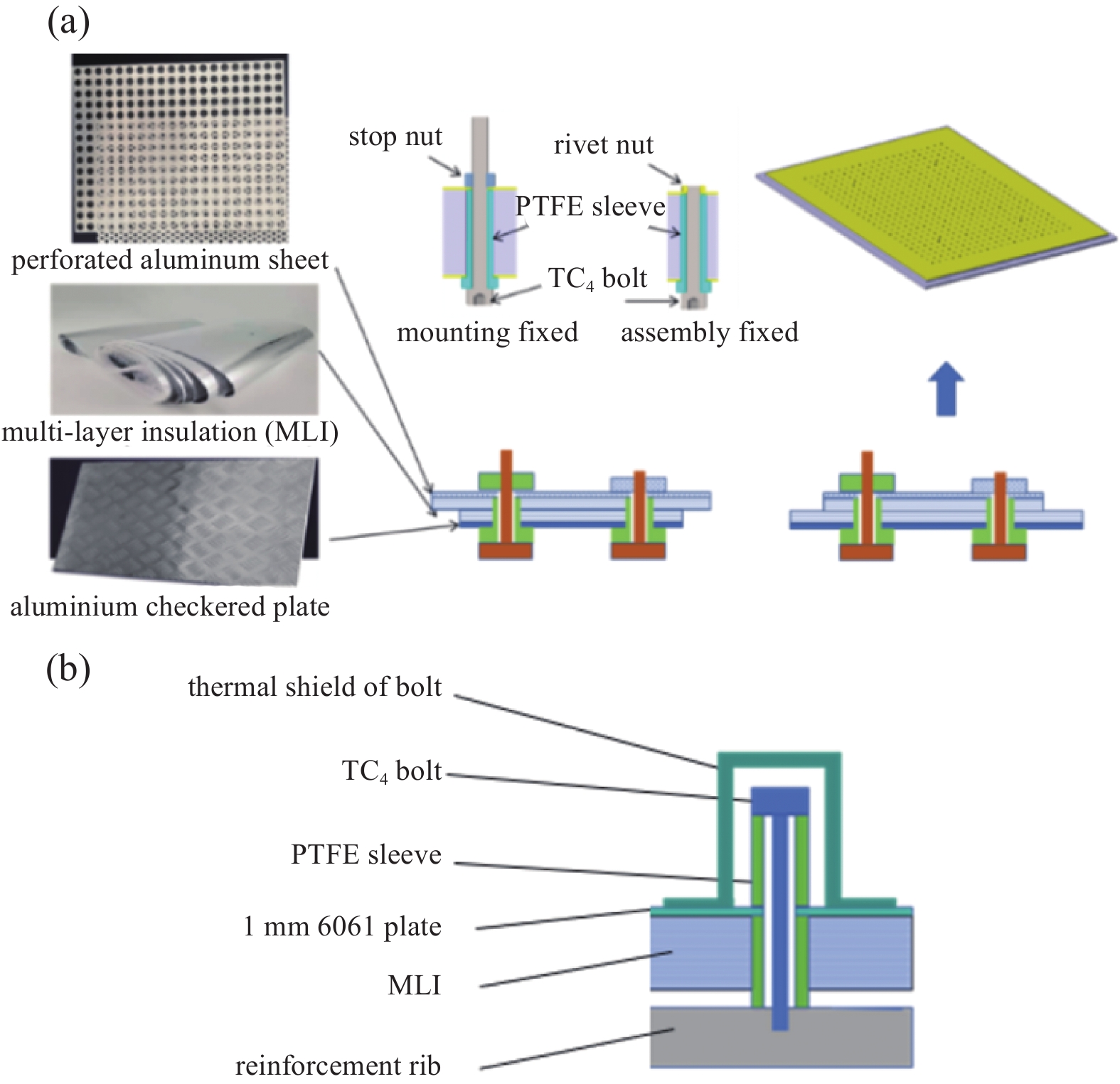
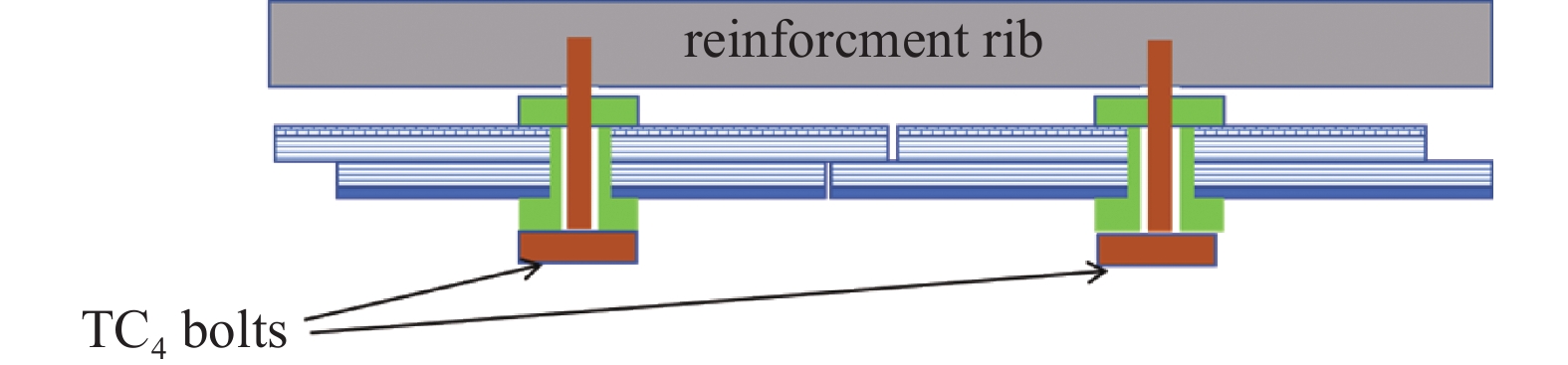
根据MCTB的外观结构，冷屏大体形状采用矩形，具体如图2所示。为了简化冷屏的安装与拆卸，冷屏被模块化设计，每个模块由铝制格栅板、MLI和穿孔铝板组成，MLI和1 mm铝板组成冷屏，通过Ti-6Al-4 V （TC4）螺栓固定在盖板上，聚四氟乙烯（PTFE）套筒起限位作用。这种设计可有效防止MLI在安装和使用过程中出现过度变形。同时，为减少螺栓头向磁体的辐射热泄漏，螺栓头上添加了冷屏。如图3所示。铝制格栅板、MLI 和穿孔铝板通过密度为10 个/m2的组装螺栓组成一个复合绝热板。复合绝热板通过密度为1 个/m2安装螺栓固定在MCTB内壁。安装完成后，移除所有组装螺栓及其对应的套筒，安装简图如图4所示。
MLI是由高反射率的反射层与低导热率的间隔层交替排列而成，反射层通常由金属箔（如铝箔）或两侧涂覆高反射材料（如铝或金）的塑料薄膜制成，由于铝成本较低，常用铝作为涂层材料。涤纶薄膜则具有低热导率、高强度和轻质量等优点，较铝箔更能有效减小横向传热[12]。此外，聚酯纤维作为间隔材料也可进一步减少多层绝热中的横向传热。因此，该多层绝热选用双面镀铝涤纶薄膜作为反射层，聚酯纤维作为间隔层。
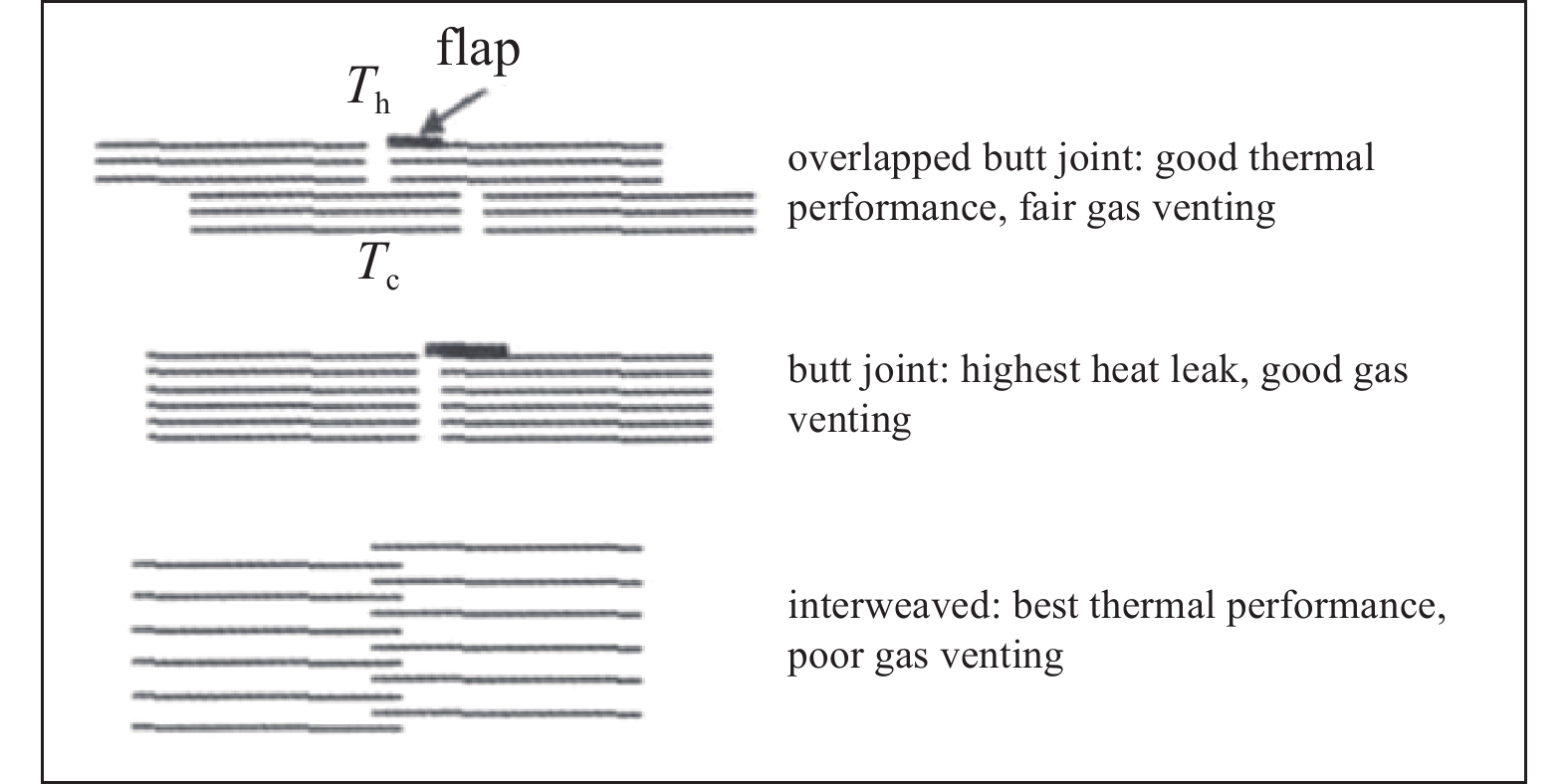
MLI的层间搭接方式会影响其绝热性能[13]，常见的结构类型包括多层交叠型，层层交替型和层层对接型，具体结构如图5所示[14]。层层交替型的导热路径复杂，其隔热性能最佳，但由于层间结构复杂，阻碍气体抽出，所以透气性能差且加工成本较高。层层对接型可以提高多层绝热层间真空度，但由于搭接处存在较大缝隙，易形成漏热通道，从而降低MLI的隔热性能。多层交叠型结合了层层交替型与层层对接型的优点，在确保良好的隔热性能的同时，非完全交错结构使其具有良好的真空条件[15]。基于此优势，该多层绝热采用多层交叠型搭接结构，并利用尼龙线与尼龙扣进行层间固定。
在MLI的制造过程中，需要严格控制每层材料的结构完整性，并根据层密度要求依次铺设间隔层和辐射层。为确保膜材排列紧密，可在铺设每一层时使用张紧滚轮调节膜材拉力，以防止膜材松弛或起皱。同时，为确保各层之间的位置精度，可在装配平台上设置标定刻度，并利用定位销固定关键点，以降低位置偏差。为进一步确保装配质量，每铺设5至10层膜材后，采用光照法检查膜材是否存在破损或缺陷，从而保证MLI的绝热性能。
-
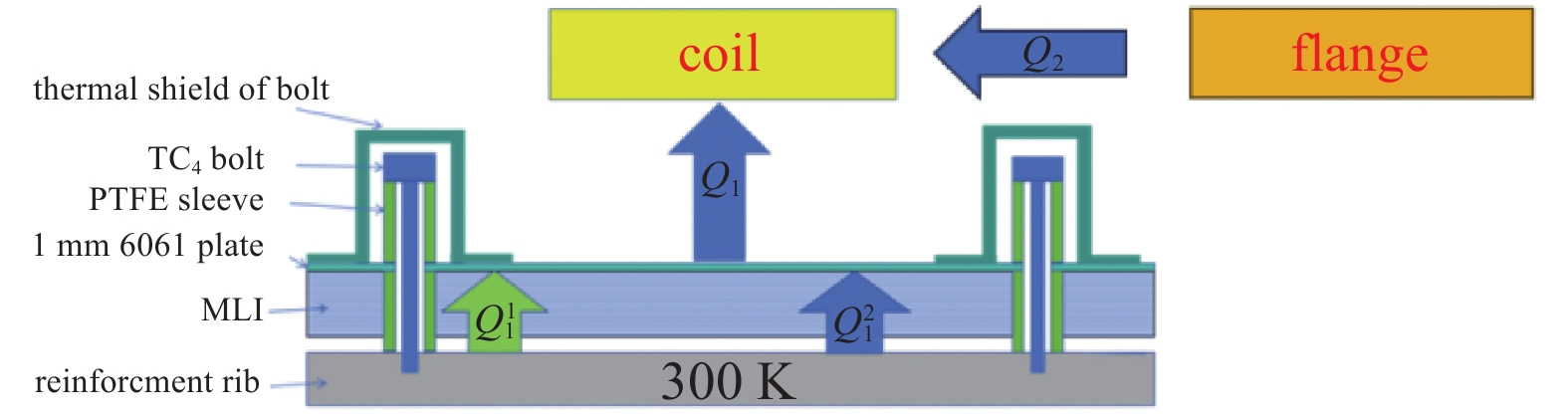
基于MCTB在使用过程中磁体辐射热载荷设计要求，磁体（TF和PF）辐射热载荷低于1 kW。磁体辐射热载荷包括冷屏辐射热载荷和法兰孔辐射热载荷两部分热量。因此，在设计冷屏过程中，冷屏对磁体辐射热载荷分析是非常有必要的，基于分析结果，优化冷屏结构，保障磁体在测试过程中能稳态运行。其中冷屏对磁体热辐射载荷分析模型如图6所示。
-
冷屏的传热分析以冷屏内侧温度为切入点。冷屏受到支架的传导热流 （
$ Q_{\mathrm{T}} $ ）和300 K壁面的传导热流 （$ Q_{\mathrm{W}} $ ），同时，冷屏向线圈辐射热量 （${Q_1}$ ）。当系统处于热平衡状态时，冷屏内侧温度将稳定在某一值。温度为
$ T_{\mathrm{T}} $ 的冷屏内侧对温度为$ T_{\mathrm{C}} $ 的线圈的辐射热流表达式为[16]：其中，
$ A_{\mathrm{C}} $ 为线圈面积，$\sigma $ 为斯特藩-玻尔兹曼常数，$ \varepsilon_{\mathrm{C}} $ 为线圈发射率，$ \varepsilon\mathrm{_T} $ 为冷屏发射率。支架对冷屏的传导热流表达式为[17]：
其中，
$A$ 为传热横截面积，$k$ 为热传导系数，TC4平均导热系数$ {k}_{1}=6.0\text{ }{\mathrm{W}}/({\mathrm{m}}·{\mathrm{K}}) $ ，PTFE平均导热系数$ {k}_{2}=0.264\text{ }{\mathrm{W}}/({\mathrm{m}}·{\mathrm{K}}) $ [18]，$ T\mathrm{_R} $ 为室温，即冷屏外侧温度，$L$ 为导热距离。壁面对冷屏的传导热流表达式为[16]：
其中，
$ A\mathrm{_T} $ 为冷屏面积，$\lambda $ 为MLI表观热传导系数，$N$ 为MLI层数，$n$ 为MLI层密度，MLI的最佳层密度约为26层/$ {\mathrm{cm}} $ [19-20]。根据热平衡原理有：
法兰对线圈的辐射热流表达式为[16]：
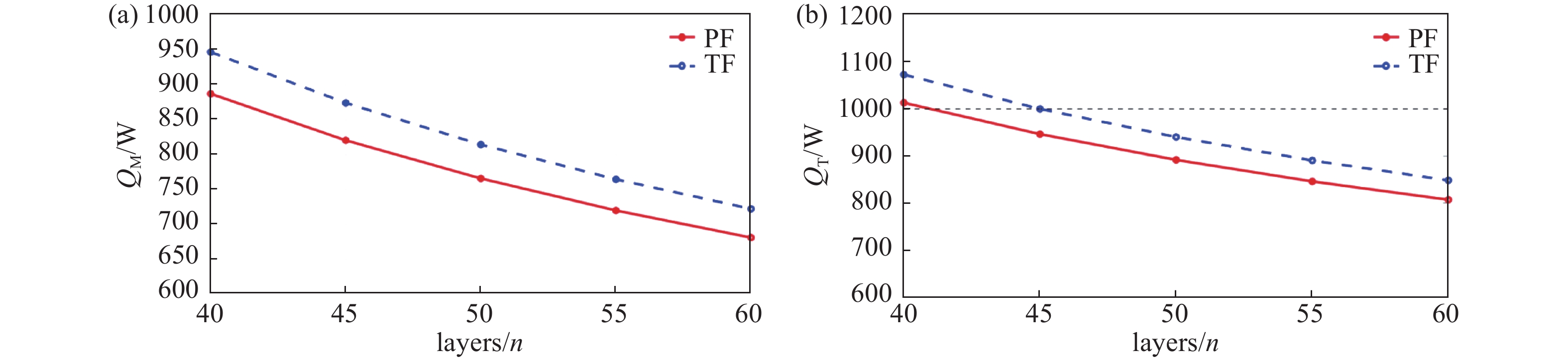
根据MCTB技术规范文件，可得边界参数并列于表1，通过MATLAB软件进行计算，计算结果列于图7。图7显示了当MLI层数大于45层时，线圈受到总漏热小于1 kW，满足技术规范文件的要求。则多层绝热采用层数
$N = 50$ ，此时MLI内侧温度$ T\mathrm{_T} $ 分别为138.35 K与147.98 K，TF和PF线圈受到的总热辐射分别为940.12 W与891.62 W。为了方便研究MLI的绝热性能，后续MLI内侧温度选择为138.35 K。 -
MLI的绝热性能直接决定低温性能测试的结果，而热流密度是衡量MLI绝热性能的关键指标。目前计算热流密度的模型有Lockheed模型、修正Lockheed模型和逐层传热模型（LBL）。其中，LBL模型因其明确的物理意义、较少的经验系数且能准确计算出MLI的层间温度分布而被广泛使用。
基于Mcintosh G E [22]提出的方法，假定存在3种无相互影响的传热机制：相邻辐射屏的辐射传热，辐射屏间的残余气体导热以及间隔物的固体导热，采用“逐层”模型来预测MLI的温度分布和热通量。
辐射换热[23]：
式中：
$\sigma $ 为黑体辐射常数，5.67×10−8 W/(m2·K4)，${T_{i + 1}}$ 为温度较高的辐射层的温度，${T_i}$ 为温度较低的辐射层的温度，${\varepsilon _{i + 1}}$ 为温度较高的辐射层的发射率，${\varepsilon _i}$ 为温度较低的辐射层的发射率。考虑到辐射屏发射率随温度变化，对于MLI中第i层材料为双层镀铝薄膜的辐射屏，其发射率
${\varepsilon _i}$ 与该辐射屏的温度${T_i}$ 呈指数关系[24]：气体导热[25]：
式中：
${C_1} = [(\gamma + 1)/(\gamma - 1)] \cdot \sqrt {R/\left( {8\pi MT} \right)} $ ，$ \gamma=C_{\mathrm{p}}/C\mathrm{_v} $ （$ C_{\mathrm{p}} $ 为定压比热容，$ C\mathrm{_v} $ 为定容比热容），$R$ 为气体常数，$T$ 为真空腔表面的温度，$M$ 为气体的摩尔质量，对于空气${C_1} = 1.1666$ ；$\alpha $ 为适应系数，对于空气$\alpha = 0.9$ ，$p$ 为气体压力，0.01 Pa。固体导热[26]：
式中：
${K_{\mathrm{s}}} = f{C_2}k/{D_x}$ ，${C_2}$ 为经验常数（对于涤纶间隔物，${C_2} = 0.008$ ），$f$ 为间隔材料的稀松程度，${D_{\mathrm{x}}}$ 为间隔物厚度，$k$ 为间隔材料的热导率，对于常用的涤纶间隔物，可通过经验公式（10）计算（其中$T$ 为热力学温度）[18]：总热流：
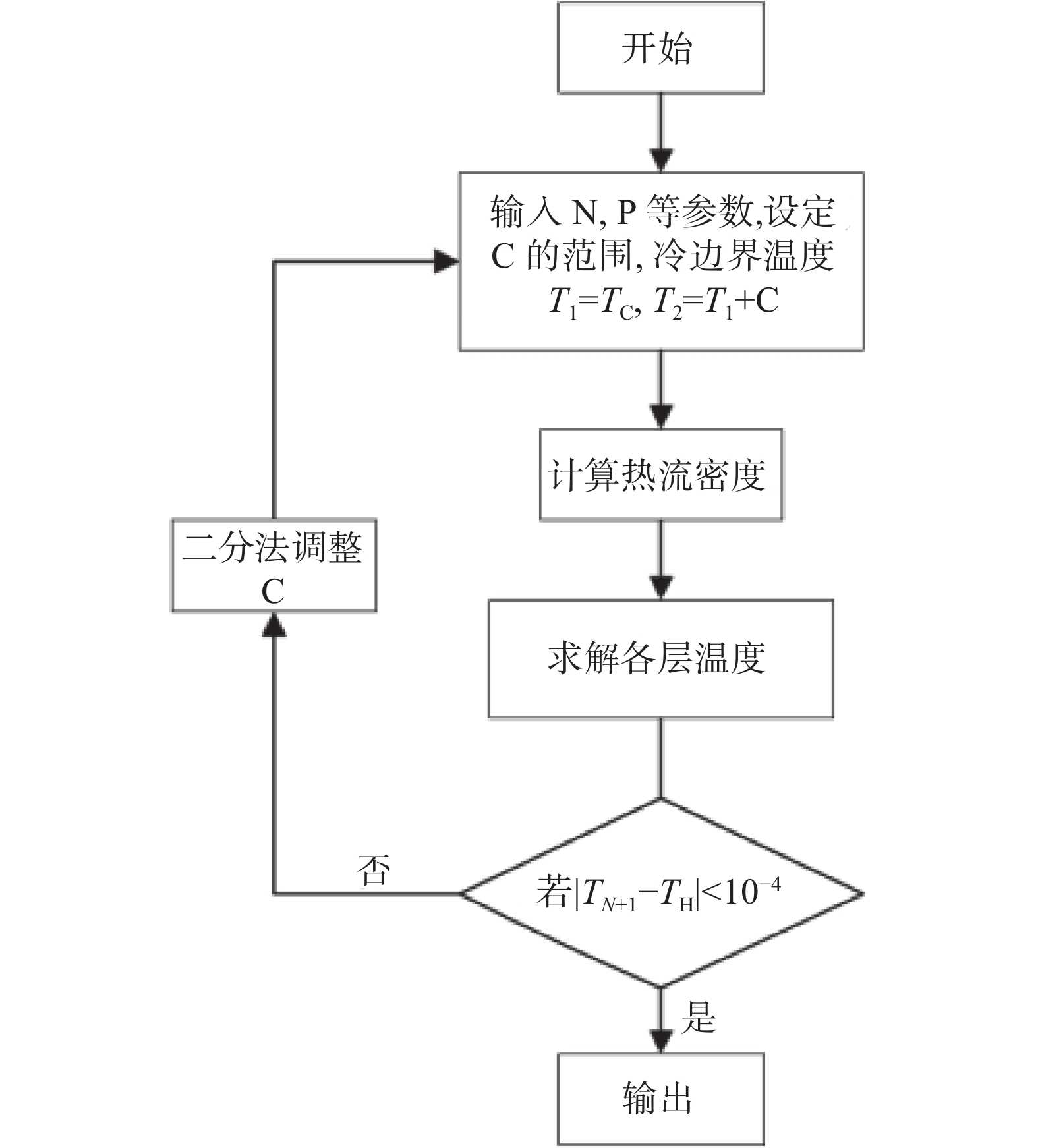
为了计算出沿绝热层厚度方向的温度分布，采用Matlab进行迭代计算，求解流程如图8所示。初始假定
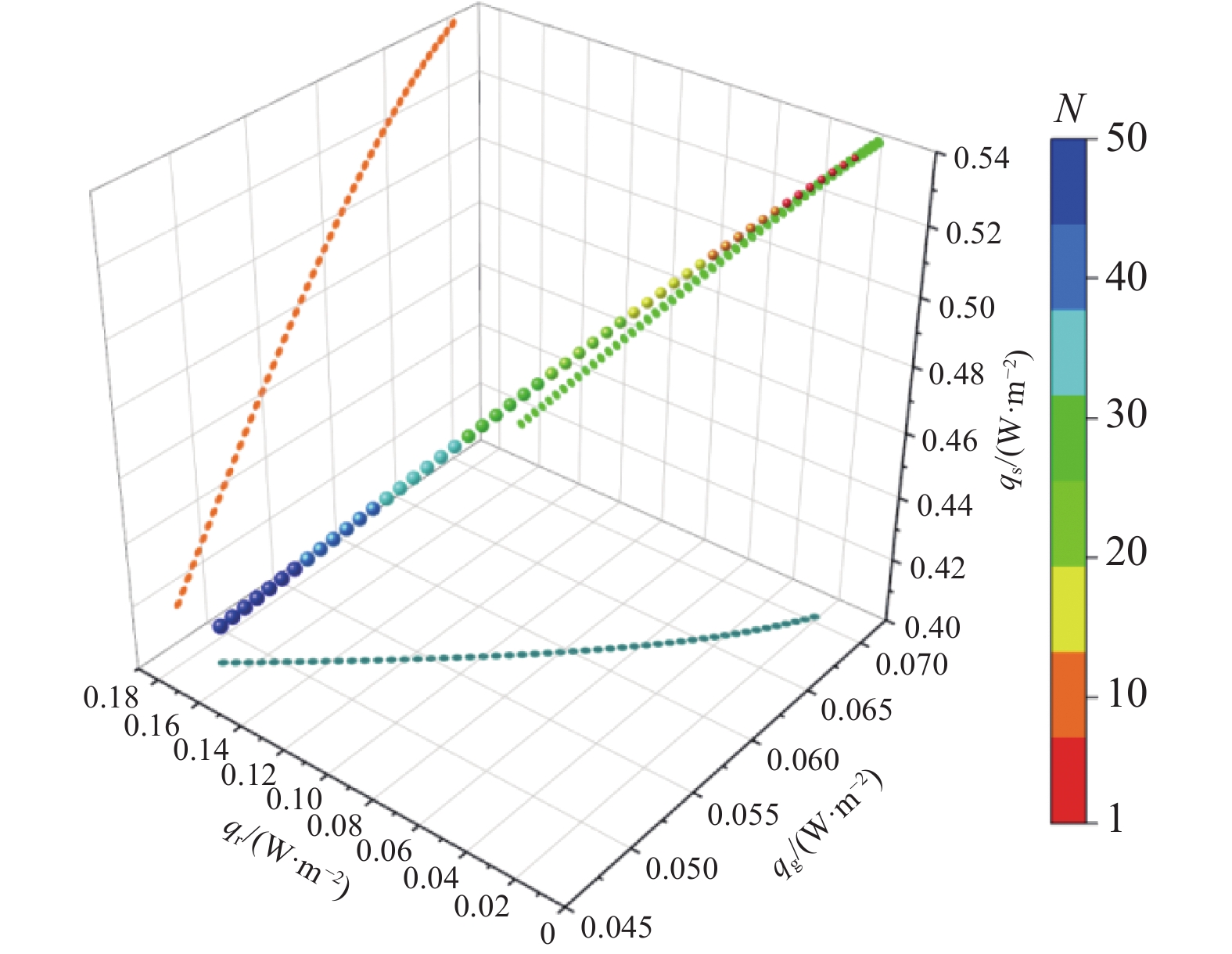
${T_2} = {T_1} + C$ ，${T_1}$ 即冷屏内侧温度，为138.35 K。$C$ 为一常数，初始假设为100，采用二分法求得最终值。根据${T_1}$ 和${T_2}$ 值求得第一层总热流密度值，再根据每层总热流密度相等计算出${T_3}$ ，${T_4}$ ······${T_{i + 1}}$ ，将计算出的${T_{i + 1}}$ 与$ T_{\mathrm{H}} $ 做比较，若温差可忽略不记，则求得的结果即为实际的温度分布。最后根据公式（8）、（9）、（11）进行计算，最终可得总热流密度为0.6292 W/m2。图9展示了MLI层间热流密度的散点图。其中，X轴、Y轴和Z轴分别表示残留气体传热热流密度（
$ q\mathrm{_g} $ ）、辐射传热热流密度（$ q_{\mathrm{r}} $ ）和固体传热热流密度（$ q\mathrm{_s} $ ）。为进一步体现温度与层数对三种传热热流密度的影响，采用球体的大小和颜色对其加以区分。具体而言，球体的大小与该层的温度成正比，温度越高，球体越大；球体的颜色表示该层的层数，其中第1层为深红色，第50层为深蓝色，颜色变化可参见图中的颜色标尺。此外，为更直观地分析各热流密度之间的变化规律，将球体投影在三个主平面内。观察XY平面（青色投影）可见，辐射传热热流密度由冷边界到热边界呈现连续且明显的上升趋势，而残余气体传热热流密度则表现出缓慢下降的趋势。观察YZ平面（绿色投影）可见，固体传热热流密度由冷边界至热边界表现出显著下降的趋势。 -
由上述分析可知，可以通过不同的密度分布来减小MLI的总热流：在靠近热边界处使用较大的层密度，在靠近冷边界处采用较小的层密度，从而形成变密度多层绝热结构（VD-MLI）。
由于VD-MLI需要实现密度的渐变分布，在制造工艺上相较于传统MLI提出了更高的要求。例如，在低密度区由于间隔层的增多会对真空度产生不利影响；在高密度区由于辐射层层间距离的减小会产生热短路风险，从而对辐射层的表面光洁度提出了更高的要求。尽管如此，VD-MLI在降低热泄漏方面具有显著优势，相关研究表明，在质量相同的情况下，VD-MLI的热泄漏量小于传统MLI的一半；而当两者性能相同时，传统MLI的重量比VD-MLI重74%[27-28]，因此，对于热负荷或质量要求高的系统，VD-MLI具有极高的应用价值。
MLI最优变密度组合为低密度区8层/cm、中密度区14层/cm、高密度区20层/cm[29]。在采用最佳变密度组合与总层数不变的情况下，选取三个结构参数（即低密度区层数A，中密度区层数B和高密度区层数C）作为试验因素，利用正交实验法研究不同密度区域的层数分布对VD-MLI性能的影响，参数水平如表2。同时，为了更好的体现VD-MLI的层密度与层数对其性能的影响，设置两组不同层密度的VD-MLI进行对照，其中D组为最优变密度组合（即内层密度：8层/cm，中间密度：14层/cm，外层密度：20层/cm），E组的内层密度为26层/cm，其余条件与D保持一致，计算结果列于表3。
由表3可以看出，在采用最优变密度组合并保证总层数为50层的情况下，随着内层层数的增加，热泄漏量逐渐降低，这是由于内层层数的增加减少了固体传热，从而整体热泄漏量下降。采用VD-MLI并使用最优变密度组合，相较于MLI的热泄漏量下降幅度较大，至少可以达到27.8％。由此可见，在绝热性能相同的前提下，VD-MLI所需的层数低于MLI，降低了冷屏安装难度。此外，在低密度区层数相同的情况下，中密度区层数越多，热泄漏量的下降幅度越显著，这是由于VD-MLI高密度区层间接触面积增大，从而增大了固体导热，此时减少高密度区层数，可以降低总热流密度。从E组数据可以得到，随着内层层数的增加，VD-MLI的性能逐渐恶化，这与D组所得到的结果是相反的，因为E组内层密度远远大于D组，层间接触面积会随着内层密度增加而增大，从而导致固体传热增强。这也验证了在密度较高区域，应采取较少的层数。
-
本文针对TF与PF磁体性能测试实验要求，针对性地设计了MCTB的冷屏结构，经初步分析，冷屏结构的总体设计是可行的，并通过采用LBL模型对MLI进行迭代求解，得到热流密度等参数，为MLI绝热性能优化提供理论支持，最后，通过对两种不同密度参数的VD-MLI进行对比分析，结果表明，采用最优密度的VD-MLI相较于传统MLI，漏热量至少下降27.8％，且在高密度区应尽量减少其层数，为磁体测试平台的冷屏设计制造提供重要参考。
大型低温测试装置的冷屏结构设计与研究
The Thermal Shield Structure of Large-Scale Cryogenic Test Facilities
-
摘要: 环向场（TF）和极向场（PF）线圈是国际热核聚变实验反应堆（International Thermonuclear Experimental Reactor， ITER）的关键部件。为了验证已制造的TF和PF线圈性能是否符合性能标准，需在安装前于低温环境中进行低温超导性能测试。根据TF和PF线圈的结构及测试要求，设计了大型低温测试装置。基于该测试装置的结构设计，采用多层绝热（MLI）作为冷屏屏蔽外部环境的热负荷，并结合线圈对测试装置的绝热性能要求及实际安装条件，对MLI的材料、搭接处理以及结构进行了设计。通过热力学分析计算，确定了MLI的最佳层数，并使用MATLAB软件对MLI的漏热量及各层温度进行了数值计算，为后续优化提供数据参考。最后，通过正交实验法对变密度多层绝热（VD-MLI）进行理论分析和数值模拟，比较了不同密度配置下VD-MLI的绝热性能与漏热趋势，为低温测试平台的冷屏设计提供了指导。
-
关键词:
- 国际热核聚变实验反应堆 /
- 大型低温测试装置 /
- 多层绝热 /
- 逐层传热模型
Abstract: The toroidal field (TF) and poloidal field (PF) coils are the key components of the International Thermonuclear Experimental Reactor (ITER). To verify whether the performance of the manufactured TF and PF coils meets the performance standards, low-temperature superconducting performance tests need to be conducted in a low-temperature environment before installation. According to the structure and testing requirements of the TF and PF coils, a large-scale low-temperature testing device was designed. Based on the structural design of the testing device, multi-layer insulation (MLI) as thermal was used to shield the thermal load from the external environment. Combined with the insulation performance requirements of the coils for the testing device and the actual installation conditions, the materials, lap joint treatment, and structure of the MLI were designed. Through thermodynamic analysis and calculation, the optimal number of MLI layers was determined, and the heat leakage and temperature of each layer of the MLI were numerically calculated using MATLAB software, providing data references for subsequent optimization. Finally, the theoretical analysis and numerical simulation of variable density multilayer insulation (VD-MLI) are carried out by the orthogonal experiment method. The thermal insulation performance and heat leakage trend of VD-MLI under different density configurations are compared, which provides guidance for thermal shield design of low temperature test platform. -
-
图 1 MCTB整体结构图及剖视图。（a）MCTB整体结构图，（b）MCTB剖视图
Figure 1. MCTB overall structure diagram and section view. (a) MCTB overall structure diagram, (b) MCTB section view
图 2 冷屏整体结构及剖视图。（a）冷屏整体结构，（b）冷屏结构剖视图
Figure 2. Thermal shield overall structure and section view. (a) Thermal shield overall structure, (b) section view of the thermal shield structure
图 3 冷屏模块化结构及安装示意图。（a）冷屏模块化组成，（b）冷屏安装结构组成
Figure 3. Modular structure and installation diagram of thermal shield. (a) Thermal shield modular composition, (b) thermal shield installation structure
图 7 TF和PF线圈热分析结果。（a）MLI对线圈的辐射热量，（b）线圈受到的总热量
Figure 7. Thermal analysis results of TF and PF coils. (a) The radiation heat of MLI to coils, (b) the total heat received by the coil
参数 TF PF 线圈面积，AC/m2 200 100 线圈温度，TC/K 4 4 线圈表面发射率， $ \varepsilon\mathrm{_C} $ 0.5 0.5 铝板表面发射率， $ \varepsilon\mathrm{_T} $ 0.1 0.1 法兰表面发射率， $ \varepsilon\mathrm{_F} $ 0.1 0.1 冷屏面积，AT/m2 580 580 法兰总面积，AF/m2 3.02 3.02 室温，TR/K 300 300 MLI表观热传导系数， $\lambda $ /W/(m·K)1.35×10−4 1.35×10−4 
下载: 导出CSV
表 2 正交实验因子与水平
Table 2. Factors and levels of orthogonal experiments
水平 低密度区
层数A/层中密度区
层数B/层高密度区
层数C/层1 9 21 20 2 10 20 21 3 11 19 15 4 15 15 19
下载: 导出CSV
表 3 热流密度计算结果
Table 3. Heat flux calculation results
序号 因素水平 D E 1 A1B1C1 0.4039 0.4770 2 A1B2C2 0.4056 0.4793 3 A1B3C3 0.4591 0.5551 4 A1B4C4 0.4676 0.5679 5 A2B1C2 0.3866 0.4617 6 A2B2C1 0.4005 0.4814 7 A2B3C4 0.4153 0.5028 8 A2B4C3 0.4878 0.6118 9 A3B1C3 0.4153 0.5101 10 A3B2C4 0.3955 0.4834 11 A3B3C1 0.3971 0.4858 12 A3B4C2 0.4239 0.5264 13 A4B1C4 0.3497 0.4466 14 A4B2C3 0.3775 0.4919 15 A4B3C2 0.3552 0.4506 16 A4B4C1 0.3846 0.5043
下载: 导出CSV
-
[1] Fantz U, Bonomo F, Fröschle M, et al. Advanced NBI beam characterization capabilities at the recently improved test facility BATMAN Upgrade[J]. Fusion Engineering and Design,2019,146:212−215 doi: 10.1016/j.fusengdes.2018.12.020 [2] Ermolenko B V, Ermolenko G V, Fetisova Y A, et al. Wind and solar PV technical potentials: measurement methodology and assessments for Russia[J]. Energy,2017,137:1001−1012 doi: 10.1016/j.energy.2017.02.050 [3] Perrault D. Status of ITER safety issues[J]. Fusion Science and Technology,2019,75(5):339−344 doi: 10.1080/15361055.2019.1594538 [4] 李建刚. 托卡马克研究的现状及发展[J]. 物理,2016,45(2):88−97 (in Chinese) doi: 10.7693/wl20160203 Li J G. The status and progress of Tokamak research[J]. Physics,2016,45(2):88−97 doi: 10.7693/wl20160203 [5] Aymar R. Status of ITER[J]. Fusion Engineering and Design,2002,61-62:5−12 doi: 10.1016/S0920-3796(02)00218-1 [6] Hussain M T, Wu Y, Qin J G, et al. Evaluating conductor design and stability performance for the conductor of high-field winding package in CFETR TF coil[J]. IEEE Transactions on Applied Superconductivity,2024,34(4):4904407 [7] Jong C T J, Mitchell N, Sborchia C. The ITER-FEAT toroidal field structures[J]. Fusion Engineering and Design,2001,58-59:165−170 doi: 10.1016/S0920-3796(01)00569-5 [8] Holtkamp N. The status of the ITER design[J]. Fusion Engineering and Design,2009,84(2−6):98−105 doi: 10.1016/j.fusengdes.2008.12.119 [9] Song X H, Guo L, Liu H J, et al. Construction and application of large superconducting magnet performance research platform[J]. IEEE Transactions on Applied Superconductivity,2024,34(5):9502204 [10] Singh D, Pandey A, Singh M K, et al. Heat radiation reduction in cryostats with multilayer insulation technique[J]. Journal of Instrumentation,2020,15(7):P07032 doi: 10.1088/1748-0221/15/07/P07032 [11] Sutheesh P M, Chollackal A. Thermal performance of multilayer insulation: a review[J]. IOP Conference Series: Materials Science and Engineering,2018,396:012061 doi: 10.1088/1757-899X/396/1/012061 [12] 刘素梅, 宋云涛, 武松涛, 等. ITER装置CTB盒冷屏绝热结构初步设计与分析[J]. 低温与超导,2008,36(3):8−10 (in Chinese) doi: 10.3969/j.issn.1001-7100.2008.03.003 Liu S M, Song Y T, Wu S T, et al. Primary design and heat transfer analysis on CTB of ITER with vacuum multilayer insulation[J]. Cryogenics and Superconductivity,2008,36(3):8−10 doi: 10.3969/j.issn.1001-7100.2008.03.003 [13] Nast T C, Frank D J, Feller J. Multilayer insulation considerations for large propellant tanks[J]. Cryogenics,2014,64:105−111 doi: 10.1016/j.cryogenics.2014.02.014 [14] Glaser P E. Thermal protection systems for liquid hydrogen tanks[R]. NASA, 1962 [15] 赵一搏, 杨汝平, 邱日尧, 等. 多层隔热结构研究进展[J]. 宇航材料工艺,2013,43(4):29−34 (in Chinese) doi: 10.3969/j.issn.1007-2330.2013.04.007 Zhao Y B, Yang R P, Qiu R Y, et al. Recent progress on multi-layer insulation structures[J]. Aerospace Materials & Technology,2013,43(4):29−34 doi: 10.3969/j.issn.1007-2330.2013.04.007 [16] 邬田华, 王晓墨, 许国良. 工程传热学(第二版)[M]. 武汉: 华中科技大学出版社, 2020: 176−179 (in Chinese)) Wu T H, Wang X M, Xu G L. Engineering heat transfer (2nd edition)[M]. Wuhan: Huazhong University of Science & Technology Press, 2020: 176−179 [17] Ekin J W. Experimental techniques for low-temperature measurements: cryostat design, material properties, and superconductor critical-current testing[M]. Oxford: Oxford University Press, 2006: 50−68 [18] Ventura G, Perfetti M. Thermal properties of solids at room and cryogenic temperatures[M]. Dordrecht: Springer, 2014: 203−209 [19] Johnson W L. Thermal performance of cryogenic multilayer insulation at various layer spacings[D]. Orlando: University of Central Florida Orlando, 2010 [20] Johnson W. Thermal analysis of low layer density multilayer insulation test results[J]. AIP Conference Proceedings,2012,1434(1):1519−1526 [21] ITER. Technical specifications for the magnet cold test cryostat[R]. France: ITER, 2024 [22] McIntosh G E. Layer by layer MLI calculation using a separated mode equation[M]//Kittel P. Advances in cryogenic engineering. Boston: Springer, 1994: 1683−1690 [23] 陈国邦, 张鹏. 低温绝热与传热技术[M]. 北京: 科学出版社, 2004: 29−31 (in Chinese) Chen G B, Zhang P. Low temperature insulation and heat transfer technology[M]. Beijing: Science Press, 2004: 29−31 [24] 周志雄. 高真空多层绝热中接触导热数值计算和实验研究[D]. 上海: 上海交通大学, 2007: 24−25 (in Chinese) Zhou Z X. Numerical calculation and experimental study on thermal contact conductance in multi-layer insulation[D]. Shanghai: Shanghai Jiaotong University, 2007: 24−25 [25] 肖志宏, 汪荣顺, 石玉美, 等. 应用逐层传热模型分析高真空多层绝热中的传热过程[J]. 真空科学与技术学报,2004,24(2):113−117 (in Chinese) doi: 10.3969/j.issn.1672-7126.2004.02.008 Xiao Z H, Wang R S, Shi Y M, et al. Theoretical analysis of heat transfer of high vacuum multi-layers[J]. Chinese Journal of Vacuum Science and Technology,2004,24(2):113−117 doi: 10.3969/j.issn.1672-7126.2004.02.008 [26] Hastings L J, Hedayat A, Brown T M. Analytical modeling and test correlation of variable density multilayer insulation for cryogenic storage[R]. Hanover: NASA, 2004 [27] Hedayat A, Hastings L J, Brown T. Analytical modeling of variable density multilayer insulation for cryogenic storage[J]. AIP Conference Proceedings,2002,613(1):1557−1564 [28] Fredrickson G O. Investigation of high-performance insulation application problems[R]. NASA, 1973 [29] 王田刚, 李延娜, 姚淑婷, 等. 变密度多层绝热最优层密度研究[J]. 低温与超导,2014,42(7):6−9,48 (in Chinese) Wang T G, Li Y N, Yao S T, et al. Study on optimal layer density of variable density multilayer insulation[J]. Cryogenics & Superconductivity,2014,42(7):6−9,48 -
图( 9) 表( 3)
计量
- 文章访问数: 38
- HTML全文浏览数: 38
- PDF下载数: 1
- 施引文献: 0