高级搜索

人工智能赋能量子通信与量子传感系统

,  ,  ,  , 

downloadPDF

上一篇

下一篇

徐佳歆, 徐乐辰, 刘靖阳, 丁华建, 王琴. 人工智能赋能量子通信与量子传感系统[J]. 物理学报, 2025, 74(12): 120301-1. doi: 10.7498/aps.74.20250322
引用本文: 徐佳歆, 徐乐辰, 刘靖阳, 丁华建, 王琴. 人工智能赋能量子通信与量子传感系统[J]. 物理学报, 2025, 74(12): 120301-1. doi: 10.7498/aps.74.20250322
shu
Jiaxin XU, Lechen XU, Jingyang LIU, Huajian DING, Qin WANG. Research progress of artificial intelligence empowered quantum communication and quantum sensing systems[J]. Acta Physica Sinica, 2025, 74(12): 120301-1. doi: 10.7498/aps.74.20250322
Citation: Jiaxin XU, Lechen XU, Jingyang LIU, Huajian DING, Qin WANG. Research progress of artificial intelligence empowered quantum communication and quantum sensing systems[J]. Acta Physica Sinica, 2025, 74(12): 120301-1. doi: 10.7498/aps.74.20250322
shu

人工智能赋能量子通信与量子传感系统

  • 1.

    南京邮电大学, 量子信息技术研究所, 南京　210003

  • 2.

    南京邮电大学, 宽带无线通信与传感网教育部重点实验室, 南京　210003

    • 作者简介: 王琴, 教授, 博士生导师. 从中国科学技术大学获得博士学位, 目前为南京邮电大学通信与信息工程学院副院长. 入选江苏省杰出青年、双创人才等人才计划, 获得江苏省光学学会青年光学科技奖、江苏省三八红旗手、全国大学生课外学术科技作品竞赛优秀指导教师等荣誉. 在量子信息领域做出了一系列创新性的科研成果, 作为第一(或通信)作者在国际物理学主要学术期刊, 如Phys. Rev. Lett.、Phys. Rev. Appl. 等发表高水平SCI论文一百多篇, 申请国际PCT专利3项, 授权国家发明专利30多项, 美国专利3项. 主持或参与多个国家级、省部级重点、重大项目, 包括国家重点研发计划“量子调控与量子信息”重点专项、国家自然科学基金重大项目、江苏省重点研发计划, 以及江苏省前沿引领计划等; 现为中国密码学会量子密码专业委员会、中国物理学会量子光学专业委员会等多个学会专业委员会委员, 担任《量子光学学报》、《量子电子学报》编委等 .
    通讯作者: E-mail: qinw@njupt.edu.cn.

  • 中图分类号: 03.67.Hk, 07.05.Mh, 03.67.Dd

Research progress of artificial intelligence empowered quantum communication and quantum sensing systems

  • 1.

    Institute of Quantum Information and Technology, Nanjing University of Posts and Telecommunications, Nanjing 210003, China

  • 2.

    Key Laboratory of Broadband Wireless Communication and Sensor Network of Ministry of Education, Nanjing University of Posts and Telecommunications, Nanjing 210003, China

    • Corresponding author: E-mail: qinw@njupt.edu.cn.

  • MSC: 03.67.Hk, 07.05.Mh, 03.67.Dd

  • 摘要: 量子通信和量子传感分别利用量子系统的独特特性, 比如量子态的叠加性或量子纠缠特性等, 能够实现信息论安全的通信以及对物理量的高精度测量. 量子通信和量子传感, 作为当前最接近实用化的两种量子技术, 成为学术界的研究热点. 然而, 这两种技术在走向实用化的过程中也面临着诸多挑战, 例如: 设备缺陷导致现实安全性问题, 环境噪声干扰大导致测量精度降低等, 使得系统的大规模部署受到严重限制. 人工智能凭借其强大的算力和数据处理能力, 已经在通信、计算和成像等领域发挥着重要作用. 本文首先综述了人工智能与量子通信和量子传感交叉领域的发展现状, 包括人工智能在量子密钥分发、量子存储、量子网络、量子传感等方向的具体结合与应用, 为提升系统的可靠性、安全性、智能化与可扩展性等方面提供了强有力的保障. 接着分析了人工智能在赋能量子通信和量子传感系统中目前存在的问题, 最后对该领域未来的发展前景进行了展望和讨论.
    Abstract: Quantum communication and quantum sensing, which leverage the unique characteristics of quantum systems, enable information-theoretically secure communication and high-precision measurement of physical quantities. They have attracted significant attention in recent research. However, they both face numerous challenges on the path to practical application. For instance, device imperfections may lead to security vulnerability, and environmental noise may significantly reduce measurement accuracy. Traditional solutions often involve high computational complexity, long processing time, and substantial hardware resource requirements, posing major obstacles to the large-scale deployment of quantum communication and quantum sensing networks. Artificial intelligence (AI), as a major technological advancement in current scientific landscape, offers powerful data processing and analytical capabilities, providing new ideas and methods for optimizing and enhancing quantum communication and sensing systems.Significant progresses have been made in applying AI to quantum communication and sensing, thus injecting new vitality into these cutting-edge technologies. In quantum communication, AI techniques have greatly improved the performance and security of quantum key distribution, quantum memory, and quantum networks through parameter optimization, real-time feedback control, and attack detection. In quantum sensing, quantum sensing technology enables ultra-high sensitivity detection of physical quantities such as time and magnetic fields. The introduction of AI has opened up new avenues for achieving high-precision and high-sensitivity quantum measurements. With AI, sensor performance is optimized, and measurement accuracy is further enhanced through data analysis.This paper also analyzes the current challenges in using AI to empower quantum communication and sensing systems, such as implementing efficient algorithm deployment and system feedback control under limited computational resources, and addressing complex task environments, dynamically changing scenarios, and multi-task coordination requirements. Finally, this paper discusses and envisions future development prospects in this field.
  • 加载中

  • 图 1  人工智能概述

    Figure 1.  An overview of artificial intelligence.

    下载: 全尺寸图片 幻灯片

    图 2  强化学习示意图

    Figure 2.  Schematic diagram of reinforcement learning.

    下载: 全尺寸图片 幻灯片

    图 3  传统扫描传输程序与使用基于LSTM模型的QKD系统的误码率对比[29]

    Figure 3.  Comparisons of QBER between applying traditional scanning-and-transmitting program and using LSTM model for the same QKD system[29].

    下载: 全尺寸图片 幻灯片

    图 4  基于支持向量回归的系统物理参数预测的基本思想[33]

    Figure 4.  Basic idea of SVR to solve the physical parameters prediction problem[33].

    下载: 全尺寸图片 幻灯片

    图 5  基于ANN的量子攻击检测模型[38]　(a)一个没有隐藏层的线性人工神经网络模型, 只能解决线性可分问题; (b)一个带有隐藏层的非线性ANN模型, 用于对不同类型的量子攻击进行分类

    Figure 5.  ANN-based quantum attack detection model[38]: (a) A linear ANN model without the hidden layer which can only solve linear separable problems; (b) a nonlinear ANN model with a hidden layer to classify different types of quantum attacks.

    下载: 全尺寸图片 幻灯片

    图 6  基于机器学习的攻击检测方案的实现过程[39]

    Figure 6.  Implementation process of a machine-learning-based attack detection scheme[39].

    下载: 全尺寸图片 幻灯片

    图 7  机器学习算法的详细流程示意图[47], 输入数据集(离散化的驱动场)不断地进行调整, 直到输出值和目标值之间的误差(强化学习算法中的反馈信号)降低到足够小的水平

    Figure 7.  Detailed schematic of the ML algorithm[47], the input dataset (discrete control laser pulse) iteratively adjusts itself until the error (feedback in training) between the estimated output and the target value becomes small enough.

    下载: 全尺寸图片 幻灯片

    图 8  量子密钥分发光网络中基于深度强化学习的路由与资源分配框架示意图[55]

    Figure 8.  An illustration of the proposed deep reinforcement learning framework for the routing and resource assignment in quantum key distribution-secured optical networks[55].

    下载: 全尺寸图片 幻灯片

    图 9  即插即用双场量子接入网络与10 G-以太网无源光网络的全共存架构[56]

    Figure 9.  Full coexistence architecture of plug-and-play twin-field QAN and 10 G-EPON[56].

    下载: 全尺寸图片 幻灯片

    图 10  深度强化学习在量子传感协议中的应用示意图, I是智能体与环境的交互; II是基于状态感知的策略网络和价值网络, 采用LSTMCells[77]

    Figure 10.  Illustration of deep reinforcement learning with (I) agent-environment interaction (II) state-aware policy and value networks with LSTMCells for quantum sensing protocols[77].

    下载: 全尺寸图片 幻灯片

    图 11  基于深度学习的量子传感示意图[80]

    Figure 11.  Schematic of deep-learning-based quantum sensing[80].

    下载: 全尺寸图片 幻灯片

    表 1  人工智能在DV-QKD中的应用对比

    Table 1.  Comparison of artificial intelligence applications in DV-QKD.

    应用领域 方法 主要贡献 参考文献
    参数优化 随机森林 预测MDI-QKD和BB84-QKD协议的最优参数 [24]
    参数优化 神经网络 直接预测QKD系统最优参数 [25]
    参数优化 极端梯度提升
    		预测TF-QKD的优化参数, 效率和准确性优于RF和BPNN [27]
    参数优化和系统校准 反向传播神经网络 预测系统最优参数, 同时通过仿真对MDI-QKD系统进行相位校准 [26]
    协议选择和参数优化 随机森林 首次将机器学习方法应用于QKD系统实现最优协议选择与系统参数优化 [28]
    相位校准 长短记忆网络 预测设备物理参数, 实时进行BB84-QKD系统的相位校准 [29]
    相位校准 长短记忆网络 预测MDI-QKD系统中两个用户的相位漂移, 实时主动补偿 [30]
    相位校准 长短记忆网络 预测TF-QKD系统相位漂移, 实现主动反馈控制 [31]
    设备缺陷和攻击检测 随机森林 实时检测设备缺陷和攻击, 准确率高达98% [32]
    下载: 导出CSV

    表 2  人工智能在CV-QKD中的应用对比

    Table 2.  Comparison of artificial intelligence applications in CV-QKD.

    应用领域 方法 主要贡献 参考文献
    参数优化 支持向量回归 预测系统物理参数, 优化QKD系统性能和安全性 [33]
    参数优化 反向传播神经网络 调整调制方差, 确保系统安全, 有效地提高了密钥率 [34]
    参数优化 机器学习框架 控制相位噪声, 优化调制方差, 实现100 km光纤通道上的密钥分发 [40]
    密钥率预测 多标签分类算法 通过多标签分类算法区分相干态, 优于现有离散调制CV-QKD协议 [35]
    密钥率预测 神经网络 快速预测离散调制CV-QKD协议的密钥率, 速度和准确性优于传统数值方法 [36,37]
    攻击检测 人工神经网络 自动识别和分类攻击类型, 准确率和召回率超过99% [38]
    攻击检测 密度聚类和多类支持向量机 高效检测量子黑客攻击, 修正密钥率高估问题, 提供更紧致的安全边界 [39]
    下载: 导出CSV

    表 3  人工智能在量子传感中的应用对比

    Table 3.  Comparison of artificial intelligence applications in quantum sensing.

    应用领域 方法 主要贡献 参考文献
    量子传感器
    校准    		 神经网络 利用神经网络处理训练数据中的不确定性, 实现接近量子极限的测量精度 [73]
    参数估计 粒子群优化 自动设计干涉仪相位估计的反馈策略, 精度接近海森伯极限, 优于传统的
    BWB策略    		 [74]
    参数估计 强化学习 训练神经网络生成适用于不同参数值的控制序列, 避免每次参数更新时
    重新优化的高计算成本    		 [75]
    量子传感器优化 强化学习 训练神经网络生成适利用强化学习的交叉熵方法优化量子传感器的动力学特性 [76]
    参数估计 深度强化学习 从几何角度推导了参数估计的 QFI 的无噪声和有噪声边界, 在无噪声和
    有噪声条件下均展现出良好的鲁棒性和样本效率    		 [77]
    参数估计 模型感知强化学习 结合贝叶斯估计和强化学习, 优化量子计量学中的实验设计, 适用于多种
    量子平台    		 [78]
    未知环境 深度学习 结合图神经网络和三角插值算法, 使光学量子传感器在未知环境中达到
    海森伯极限精度    		 [80]
    微波探测 深度学习 提出不求解主方程即可有效探测多频率微波电场的方案, 硬件要求低, 精度高 [79]
    下载: 导出CSV
  • [1] Das Sarma S, Deng D L, Duan L M 2019 Phys. Today 72 48 doi: 10.1063/PT.3.4164
    [2] Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, Vogt-Maranto L, Zdeborová L 2019 Rev. Mod. Phys. 91 045002 doi: 10.1103/RevModPhys.91.045002
    [3] Wallnöfer J, Melnikov A A, Dür W, Briegel H J 2020 PRX Quantum 1 010301 doi: 10.1103/PRXQuantum.1.010301
    [4] Kaelbling L P, Littman M L, Moore A W 1996 J. Artif. Intell. Res. 4 237 doi: 10.1613/jair.301
    [5] LeCun Y, Bengio Y, Hinton G 2015 Nature 521 436 doi: 10.1038/nature14539
    [6] Ma W, Liu Z, Kudyshev Z A, Boltasseva A, Cai W, Liu Y 2021 Nat. Photonics 15 77 doi: 10.1038/s41566-020-0685-y
    [7] Jain A K, Mao J, Mohiuddin K M 1996 Computer 29 31 doi: 10.1109/2.485891
    [8] Gers F A, Schmidhuber J, Cummins F 2000 Neural Comput. 12 2451 doi: 10.1162/089976600300015015
    [9] Cleveland W S, Devlin S J, Grosse E 1988 J. Econom. 37 87 doi: 10.1016/0304-4076(88)90077-2
    [10] Kotsiantis S B 2013 Artif. Intell. Rev. 39 261 doi: 10.1007/s10462-011-9272-4
    [11] Snoek J, Larochelle H, Adams R P 2012 Advances in Neural Information Processing Systems 25 (NIPS 2012) Lake Tahoe, USA, December 3–8, 2012 p1
    [12] Xu R, Wunsch D 2005 IEEE Trans. Neural Netw. 16 645 doi: 10.1109/TNN.2005.845141
    [13] Raymer M L, Punch W F, Goodman E D, Kuhn L A, Jain A K 2000 IEEE Trans. Evol. Comput. 4 164 doi: 10.1109/4235.850656
    [14] Dietterich T G 2000 Proceedings of the First International Workshop on Multiple Classifier Systems June 21–23, 2000 pp1–15
    [15] Bennett C H, Brassard G 1984 Proceeding of the IEEE International Conference on Computers, Systems and Signal Processing Bangalore, 1984 pp175–179
    [16] Ekert A K 1991 Phys. Rev. Lett. 67 661 doi: 10.1103/PhysRevLett.67.661
    [17] Bennett C H, Brassard G, Mermin N D 1992 Phys. Rev. Lett. 68 557 doi: 10.1103/PhysRevLett.68.557
    [18] Bennett C H 1992 Phys. Rev. Lett. 68 3121 doi: 10.1103/PhysRevLett.68.3121
    [19] Acín A, Brunner N, Gisin N, Massar S, Pironio S, Scarani V 2007 Phys. Rev. Lett. 98 230501 doi: 10.1103/PhysRevLett.98.230501
    [20] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503 doi: 10.1103/PhysRevLett.108.130503
    [21] Lucamarini M, Yuan Z L, Dynes J F, Shields A J 2018 Nature 557 400 doi: 10.1038/s41586-018-0066-6
    [22] Zeng P, Zhou H, Wu W, Ma X 2022 Nat. Commun. 13 3903 doi: 10.1038/s41467-022-31534-7
    [23] Xie Y M, Lu Y S, Weng C X, Cao X Y, Jia Z J, Bao Y, Wang Y, Fu Y, Yin H L, Chen Z B 2022 PRX Quantum 3 020315 doi: 10.1103/PRXQuantum.3.020315
    [24] Ding H J, Liu J Y, Zhang C M, Wang Q 2020 Quantum Inf. Process. 19 1 doi: 10.1007/s11128-019-2494-0
    [25] Wang W, Lo H K 2019 Phys. Rev. A 100 062334 doi: 10.1103/PhysRevA.100.062334
    [26] Lu F Y, Yin Z Q, Wang C, Cui C H, Teng J, Wang S, Chen W, Huang W, Xu B J, Guo G C, Han Z F 2019 J. Opt. Soc. Am. B 36 B92 doi: 10.1364/JOSAB.36.000B92
    [27] Dong Q, Huang G, Cui W, Jiao R 2022 Quantum Inf. Process. 21 233 doi: 10.1007/s11128-022-03579-6
    [28] Ren Z A, Chen Y P, Liu J Y, Ding H J, Wang Q 2021 IEEE Commun. Lett. 25 940 doi: 10.1109/LCOMM.2020.3040212
    [29] Liu J Y, Ding H J, Zhang C M, Xie S P, Wang Q 2019 Phys. Rev. Appl. 12 014059 doi: 10.1103/PhysRevApplied.12.014059
    [30] Zhang S W, Liu J K, Zhang C, Zhou X, Wang Q 2021 Entropy 23 1242 doi: 10.3390/e23101242
    [31] Liu J Y, Jiang Q Q, Ding H J, Ma X, Sun M S, Xu J X, Zhang C H, Xie S P, Li J, Zeng G G, Zhou X Y, Wang Q 2023 Sci. China Inf. Sci. 66 189402 doi: 10.1007/s11432-022-3619-0
    [32] Xu J X, Ma X, Liu J Y, Zhang C H, Li H W, Zhou X Y, Wang Q 2024 Sci. China Inf. Sci. 67 202501 doi: 10.1007/s11432-023-3988-x
    [33] Liu W Q, Huang P, Peng J Y, Fan J P, Zeng G H 2018 Phys. Rev. A 97 022316 doi: 10.1103/PhysRevA.97.022316
    [34] Su Y, Guo Y, Huang D 2019 Entropy 21 908 doi: 10.3390/e21090908
    [35] Liao Q, Xiao G, Zhong H, Guo Y 2020 New J. Phys. 22 083086 doi: 10.1088/1367-2630/abab3c
    [36] Zhou M G, Liu Z P, Liu W B, Li C L, Bai J L, Xue Y R, Fu Y, Yin H L 2022 Sci. Rep. 12 8879 doi: 10.1038/s41598-022-12647-x
    [37] Liu Z P, Zhou M G, Liu W B, Li C L, Gu J, Yin H L, Chen Z B 2022 Opt. Express 30 15024 doi: 10.1364/OE.455762
    [38] Mao Y Y, Huang W T, Zhong H, Wang Y J, Qin H, Guo Y, Huang D 2020 New J. Phys. 22 083073 doi: 10.1088/1367-2630/aba8d4
    [39] Ding C, Wang S, Wang Y N, Wu Z J, Sun J T, Mao Y Y 2023 Phys. Rev. A 107 062422 doi: 10.1103/PhysRevA.107.062422
    [40] Hajomer A A, Derkach I, Jain N, Chin H M, Andersen U L, Gehring T 2024 Sci. Adv. 10 eadi9474 doi: 10.1126/sciadv.adi9474
    [41] Chen Y H, Lee M J, Wang I C, Du S, Chen Y F, Chen Y C, Yu I A 2013 Phys. Rev. Lett. 110 083601 doi: 10.1103/PhysRevLett.110.083601
    [42] Reim K F, Michelberger P, Lee K C, Nunn J, Langford N K, Walmsley I A 2011 Phys. Rev. Lett. 107 053603 doi: 10.1103/PhysRevLett.107.053603
    [43] Cho Y W, Campbell G T, Everett J L, Bernu J, Higginbottom D B, Cao M T, Geng J, Robins N P, Lam P K, Buchler B C 2016 Optica 3 100 doi: 10.1364/OPTICA.3.000100
    [44] Sun M S, Zhang C H, Luo Y Z, Wang S, Liu Y, Li J, Wang Q 2025 Appl. Phys. Lett. 126 104001 doi: 10.1063/5.0255199
    [45] Meng R R, Liu X, Jin M, Zhou Z Q, Li C H, Guo G C 2024 Chip 3 100081 doi: 10.1016/j.chip.2023.100081
    [46] Leung A, Tranter A, Paul K, Everett J, Gris P V, Higginbottom D Campbell G, Lam P K, Buchler B 2018 Conference on Lasers and Electro-Optics Pacific Rim (CLEO-PR) Hong Kong, China, July 29–August 3, 2018 paper Th1D.2
    [47] Cai M, Lu Y, Xiao M, Xia K 2021 Phys. Rev. A 104 053707 doi: 10.1103/PhysRevA.104.053707
    [48] Khatri S 2021 Quantum 5 537 doi: 10.22331/q-2021-09-07-537
    [49] Reiß S D, Loock P 2023 Phys. Rev. A 108 012406 doi: 10.1103/PhysRevA.108.012406
    [50] Robertson E, Esguerra L, Meßner L, Gallego G, Wolters J 2024 Phys. Rev. Appl. 22 024026 doi: 10.1103/PhysRevApplied.22.024026
    [51] Lei Y, An H, Li Z, Hosseini M 2024 Phys. Rev. Research 6 033153 doi: 10.1103/PhysRevResearch.6.033153
    [52] Wehner S, Elkouss D, Hanson R 2018 Science 362 eaam9288 doi: 10.1126/science.aam9288
    [53] Cao Y, Zhao Y, Li Jun, Lin J, Zhang Jie, Chen J 2019 Optical Fiber Communications Conference and Exhibition (OFC) San Diego, CA, USA, March 3–7, 2019 p1
    [54] Cao Y, Zhao Y, Li Jun, Lin J, Zhang J, Chen J 2020 IEEE Trans. Netw. Serv. Manage. 17 946 doi: 10.1109/TNSM.2020.2964003
    [55] Sharma P, Gupta S, Bhatia V, Prakash S 2023 IET Quantum Commun. 4 136 doi: 10.1049/qtc2.12063
    [56] Kang J L, Zhang M H, Liu X P, He C 2024 Phys. Rev. A 109 022617 doi: 10.1103/PhysRevA.109.022617
    [57] Thielking J, Okhapkin M V, Glowacki P, Meier D M, Wense L, Seiferle B, Düllmann C E, Thirolf P G, Peik E 2018 Nature 556 321 doi: 10.1038/s41586-018-0011-8
    [58] Farooq M, Chupp T, Grange J, Tewsley-Booth A, Flay D, Kawall D, Sachdeva N, Winter P 2020 Phys. Rev. Lett. 124 223001 doi: 10.1103/PhysRevLett.124.223001
    [59] Poli N, Wang F Y, Tarallo M G, Alberti A, Prevedelli M, Tino G M 2011 Phys. Rev. Lett. 106 038501. doi: 10.1103/PhysRevLett.106.038501
    [60] Gruber A, Drabenstedt A, Tietz C, Fleury L, Wrachtrup J, Borczyskowski C V 1997 Science 276 2012 doi: 10.1126/science.276.5321.2012
    [61] Zhang H, Ma Y, Liao K, Yang W, Liu Z, Ding D, Yan H, Li W, Zhang L 2024 Sci. Bull. 69 1515 doi: 10.1016/j.scib.2024.03.032
    [62] 郭弘, 吴腾, 罗斌 2024 物理 53 27 doi: 10.7693/wl20240904 Guo H, Wu T, Luo B 2024 Physics 53 27 doi: 10.7693/wl20240904
    [63] Degen C L, Reinhard F, Cappellaro P 2017 Rev. Mod. Phys. 89 035002 doi: 10.1103/RevModPhys.89.035002
    [64] Pezzè L, Smerzi A, Oberthaler M K, Schmied R, Treutlein P 2018 Rev. Mod. Phys. 90 035005 doi: 10.1103/RevModPhys.90.035005
    [65] Chen J P, Zhang C, Liu Y, Jiang C, Zhao D F, Zhang W J, Chen F X, Li H, You L X, Wang Z, Chen Y, Wang X B, Zhang Q, Pan J W 2022 Phys. Rev. Lett. 128 180502 doi: 10.1103/PhysRevLett.128.180502
    [66] Xu Y, Wang T, Huang P, Zeng G H 2024 Research 7 0416 doi: 10.34133/research.0416
    [67] Liu S S, Tian Y, Zhang Y, Lu Z G, Wang X Y, Li Y M 2024 Optica 11 1762 doi: 10.1364/OPTICA.537655
    [68] Pirandola S, Bardhan B R, Gehring T, Weedbrook C, Lloyd S 2018 Nat. Photon. 12 724 doi: 10.1038/s41566-018-0301-6
    [69] Lawrie B J, Lett P D, Marino A M, Pooser R C 2019 ACS Photon. 6 1307 doi: 10.1021/acsphotonics.9b00250
    [70] Guo X, Breum C R, Borregaard J, Izumi S, Larsen M V, Gehring T, Christandl M, Neergaard-Nielsen J S, Andersen U L 2020 Nat. Phys. 16 281 doi: 10.1038/s41567-019-0743-x
    [71] Zhao S R, Zhang Y Z, Liu W Z, Guan J Y, Zhang W, Li C L, Bai B, Li M H, Liu Y, You L, Zhang J, Fan J, Xu F, Zhang Q, Pan J W 2021 Phys. Rev. X 11 031009 doi: 10.1103/PhysRevX.11.031009
    [72] Liu L Z, Zhang Y Z, Li Z D, Zhang R, Yin X F, Fei Y Y, Li L, Liu N L, Xu F, Chen Y A, Pan J W 2021 Nat. Photon. 15 137 doi: 10.1038/s41566-020-00718-2
    [73] Cimini V, Gianani I, Spagnolo N, Leccese F, Sciarrino F, Barbieri M 2019 Phys. Rev. Lett. 123 230502 doi: 10.1103/PhysRevLett.123.230502
    [74] Hentschel A, Sanders B C 2010 Phys. Rev. Lett. 104 063603 doi: 10.1103/PhysRevLett.104.063603
    [75] Xu H, Li J, Liu L, Wang Y, Yuan H, Wang X 2019 npj Quantum Inf. 5 82 doi: 10.1038/s41534-019-0198-z
    [76] Schuff J, Fiderer L J, Braun D 2020 New J. Phys. 22 035001 doi: 10.1088/1367-2630/ab6f1f
    [77] Xiao T L, Fan J P, Zeng G H 2022 npj Quantum Inf. 8 2 doi: 10.1038/s41534-021-00513-z
    [78] Belliardo F, Zoratti F, Marquardt F, Giovannetti V 2024 Quantum 8 1555 doi: 10.22331/q-2024-12-10-1555
    [79] Liu Z K, Zhang L H, Liu B, Zhang Z Y, Guo G C, Ding D S, Shi B S 2022 Nat. Commun. 13 1997 doi: 10.1038/s41467-022-29686-7
    [80] Zhou Z, Du Y, Yin X F, Zhao S, Tian X, Tao D 2024 Phys. Rev. Res. 6 043267 doi: 10.1103/PhysRevResearch.6.043267
  • 加载中
图( 11) 表( 3)
计量
  • 文章访问数:  133
  • HTML全文浏览数:  133
  • PDF下载数:  15
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-12
  • 刊出日期:  2025-06-20

人工智能赋能量子通信与量子传感系统

    通讯作者: E-mail: qinw@njupt.edu.cn.
    作者简介: 王琴, 教授, 博士生导师. 从中国科学技术大学获得博士学位, 目前为南京邮电大学通信与信息工程学院副院长. 入选江苏省杰出青年、双创人才等人才计划, 获得江苏省光学学会青年光学科技奖、江苏省三八红旗手、全国大学生课外学术科技作品竞赛优秀指导教师等荣誉. 在量子信息领域做出了一系列创新性的科研成果, 作为第一(或通信)作者在国际物理学主要学术期刊, 如Phys. Rev. Lett.、Phys. Rev. Appl. 等发表高水平SCI论文一百多篇, 申请国际PCT专利3项, 授权国家发明专利30多项, 美国专利3项. 主持或参与多个国家级、省部级重点、重大项目, 包括国家重点研发计划“量子调控与量子信息”重点专项、国家自然科学基金重大项目、江苏省重点研发计划, 以及江苏省前沿引领计划等; 现为中国密码学会量子密码专业委员会、中国物理学会量子光学专业委员会等多个学会专业委员会委员, 担任《量子光学学报》、《量子电子学报》编委等
  • 1. 南京邮电大学, 量子信息技术研究所, 南京　210003
  • 2. 南京邮电大学, 宽带无线通信与传感网教育部重点实验室, 南京　210003
  • 收稿日期:  2025-03-12

摘要: 量子通信和量子传感分别利用量子系统的独特特性, 比如量子态的叠加性或量子纠缠特性等, 能够实现信息论安全的通信以及对物理量的高精度测量. 量子通信和量子传感, 作为当前最接近实用化的两种量子技术, 成为学术界的研究热点. 然而, 这两种技术在走向实用化的过程中也面临着诸多挑战, 例如: 设备缺陷导致现实安全性问题, 环境噪声干扰大导致测量精度降低等, 使得系统的大规模部署受到严重限制. 人工智能凭借其强大的算力和数据处理能力, 已经在通信、计算和成像等领域发挥着重要作用. 本文首先综述了人工智能与量子通信和量子传感交叉领域的发展现状, 包括人工智能在量子密钥分发、量子存储、量子网络、量子传感等方向的具体结合与应用, 为提升系统的可靠性、安全性、智能化与可扩展性等方面提供了强有力的保障. 接着分析了人工智能在赋能量子通信和量子传感系统中目前存在的问题, 最后对该领域未来的发展前景进行了展望和讨论.

English Abstract

    全文HTML

    1.   引　言

    • 随着信息技术的飞速发展, 量子通信作为一种新型的通信技术, 因其在安全性、高效性等方面的优势, 逐渐成为通信领域的研究热点. 量子通信利用量子力学的基本原理, 如量子纠缠和不可克隆定理, 实现了信息的安全传输. 然而, 量子通信系统的实际应用面临着诸多挑战, 例如系统设备存在缺陷、大规模网络的资源分配等. 与此同时, 量子传感技术作为量子信息科学的重要分支, 也在高精度测量领域展现出巨大潜力, 但在实际应用中同样受到系统校准复杂、噪声干扰以及测量精度受限等问题的制约. 传统的解决方案通常计算复杂度高、耗时长, 且对硬件资源的需求较大, 这对大规模的量子通信和量子传感网络的部署构成了巨大挑战.

      人工智能作为当今科技领域的重要发展方向, 其强大的数据处理和分析能力为量子通信和量子传感系统的优化和提升提供了新的思路和方法. 例如, 在量子通信领域, 人工智能可以快速准确地预测出量子通信系统中的最优参数, 高效实时校准系统, 实时检测系统中可能存在的设备缺陷和攻击; 在量子传感方面, 人工智能可以为大规模量子传感器的校准提供高效、自适应且资源消耗少的解决方案, 显著提高了测量精度. 因此, 将人工智能赋能量子通信和量子传感系统, 不仅为量子通信和量子传感技术的突破提供了可能, 也为未来通信和传感技术的发展开辟了新的方向.

    2.   人工智能基础

    • 人工智能(artificial intelligence, AI)作为计算机科学的重要分支, 致力于开发能够模拟、延伸和扩展人类智能的理论、方法、技术及应用系统. 其核心在于通过数据驱动的方法, 使计算机系统能够自主地从海量数据中学习、推理和决策, 而无需显式的程序指令. 机器学习(machine learning, ML)作为人工智能的核心技术之一, 主要研究如何通过算法使计算机系统能够从数据中自动学习规律, 并利用这些规律进行预测或决策. 值得注意的是, 机器学习算法具有自适应性, 能够随着新数据的输入不断优化其性能, 从而实现预测准确率的持续提升.

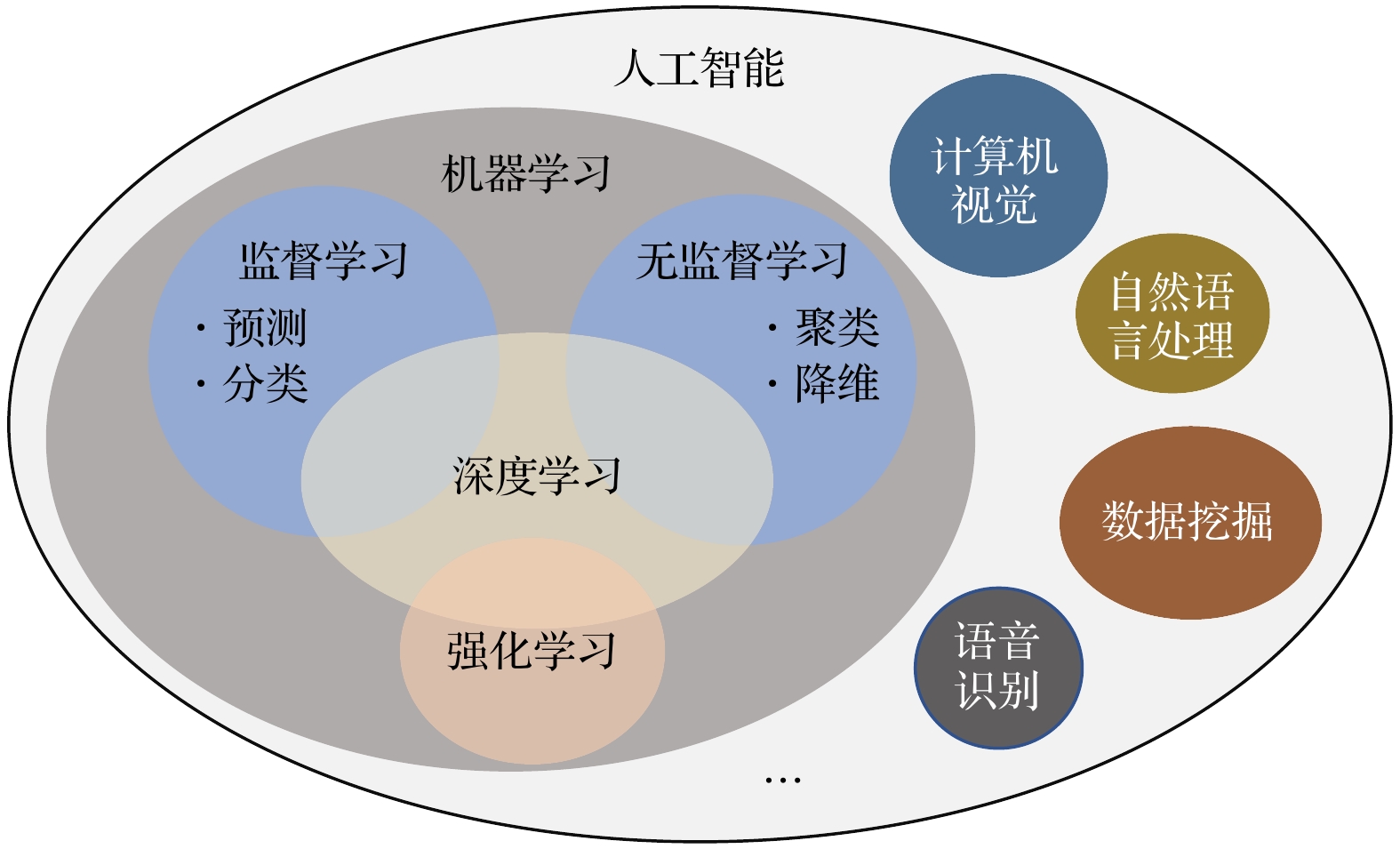
      在应用层面, 人工智能和机器学习技术已在自然科学、工程科学、生命科学、金融经济等多个领域展现出巨大的应用价值. 例如, 在物理科学中[1,2], 人工智能和机器学习为复杂实验数据的分析和物理规律的发现提供了新的方法论支持. 在量子科技领域[3], 人工智能算法被广泛应用于量子系统优化、量子态识别以及量子纠错等关键任务, 显著提升了量子信息处理的可靠性和安全性(见图1).

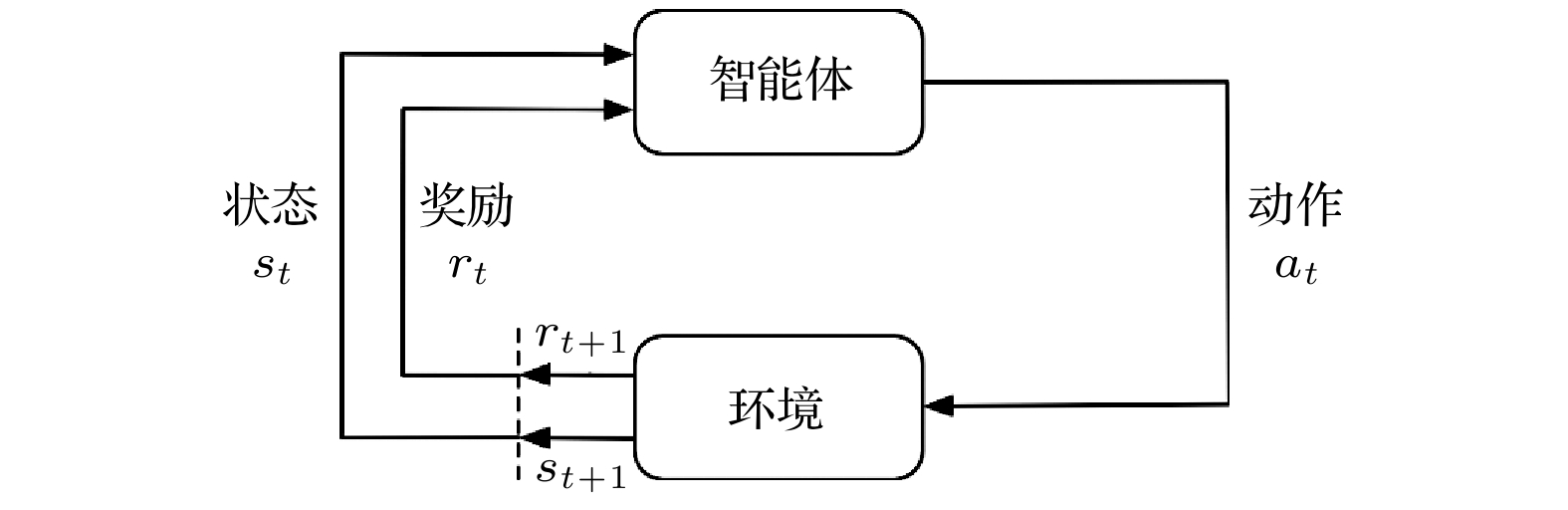
      从方法论的角度, 机器学习算法可根据其学习范式分为三大类: 监督学习、无监督学习和强化学习. 监督学习通过标注数据集进行模型训练, 建立输入与输出之间的映射关系, 适用于分类和回归任务. 无监督学习则致力于发现未标注数据中的内在结构和分布特征, 在聚类分析和降维处理等方面具有独特优势. 此外, 强化学习(reinforcement learning, RL)[4]作为一种新兴的机器学习方法, 受到行为心理学和神经科学的启发, 智能体通过与环境的持续交互, 优化决策策略或学习价值函数, 借助试错和反馈机制来最大化累积奖励, 从而逐步掌握在复杂环境中做出最优决策的能力(见图2).

      深度学习(deep learning, DL)作为机器学习的重要分支, 通过构建具有多层非线性变换的神经网络模型, 实现了对数据的高层次抽象表示. 这种多层次的特征学习机制使深度学习在处理高维、非线性数据时表现出显著优势, 在图像识别、语音处理、自然语言处理等领域取得了显著的成果[5,6]. 神经网络(neural networks, NN)[7]是一种模拟人脑神经元工作方式的复杂非线性模型, 它是深度学习的基础. 神经网络由多个神经元(也称为节点或单元)组成的层次结构, 每个神经元与前后层的神经元相连接, 通过权重和激活函数对输入进行处理, 并产生输出. 长短期记忆网络(long short-term memory, LSTM)[8]作为一种特殊的递归神经网络架构, 通过引入细胞状态和3种门控机制(遗忘门、输入门和输出门), 以便更好地控制信息的流动, 有效解决了序列数据建模中的长期依赖问题, 在时间序列预测和自然语言生成等任务中展现出卓越性能.

      从算法体系来看, 人工智能和机器学习技术涵盖了丰富的算法模型, 包括但不限于回归算法[9]、决策树算法[10]、贝叶斯算法[11]、聚类算法[12]、降维算法[13]和集成算法[14]. 这些算法模型通过有机组合和协同优化, 为复杂系统的智能决策提供了强有力的技术支撑.

      人工智能和机器学习技术的快速发展正在深刻改变科学研究范式和社会生产方式. 它们不仅革新了传统的数据处理和分析方法, 更为解决复杂系统问题提供了新的思路和工具. 在未来, 随着算法创新、算力提升和数据资源的持续积累, 人工智能和机器学习有望在更多领域实现突破性应用, 为人类社会的可持续发展注入新的动力.

    3.   人工智能在量子通信系统中的应用

      3.1.   量子密钥分发

    • 量子密钥分发(quantum key distribution, QKD)作为量子通信的核心技术之一, 基于量子力学的基本原理, 能够实现理论上无条件安全的保密通信. 该技术以光子为信息载体, 通过量子信道在通信双方之间建立共享的随机密钥串, 结合一次一密加密方案, 可构建具有信息论安全性的通信系统.

      自1984年Bennett 和Brassard[15]提出了首个QKD协议, 即BB84协议以来, 研究者们相继提出了E91协议[16]、BBM92协议[17]、B92协议[18]、设备无关量子密钥分发 (device independent QKD, DI-QKD)协议[19]等. 这些协议的安全等级、设备要求、协议过程以及实际性能等不尽相同, 为QKD在不同的应用场景中的实施提供了众多选择. 从技术实现的角度, QKD主要分为离散变量量子密钥分发(discrete-variable QKD, DV-QKD)和连续变量量子密钥分发(continuous-variable QKD, CV-QKD)两大体系. DV-QKD利用量子比特的离散态(如单光子偏振态)进行信息编码, 例如, 可以将单光子的水平偏振态和垂直偏振态分别对应二进制的0和1. 典型协议包括BB84-QKD协议, 测量设备无关量子密钥分发(measurement device independent QKD, MDI-QKD)协议[20], 双场量子密钥分发(twin-field QKD, TF-QKD)协议[21], 模式匹配量子密钥分发协议[22,23]. CV-QKD是利用量子系统的连续变量来编码信息, 例如, 通过调制光场的振幅和相位的连续值来传输密钥信息. 常见的协议包括高斯调制协议和离散调制协议.

      在实际的有限数据条件下, QKD系统的性能高度依赖于关键参数的优化, 例如X基或Z基的选择概率、信号态和诱骗态的强度等. 传统上, 这些参数的优化通常依赖于搜索算法, 虽然能够提供精确的结果, 但其计算复杂度高、耗时长, 且对硬件资源的需求较大, 这对实时QKD系统和大规模QKD网络的部署构成了显著挑战. 针对这一问题, 研究者们提出了多种基于机器学习的优化方法, 显著提升了参数优化的效率和实用性. Ding等[24]使用随机森林(random forest, RF)算法代替传统的搜索算法, 构建了一个同时适用于MDI-QKD和BB84-QKD协议的通用模型, 直接预测有限数据下基于任何给定系统条件的最优参数. 数值模拟表明, 与传统的搜索方法相比, 该方法可以达到99%以上的最优安全密钥率, 在未来的QKD应用中具有很好的应用前景. 同期, Wang和Lo[25]提出了一种使用神经网络直接预测QKD系统最优参数的方法. Lu等[26]提出了一种新颖的反向传播神经网络(back propagation neural network, BPNN), 不仅能够以更少的计算资源和更快的速度预测最优参数, 还解决了大规模MDI-QKD网络中的系统校准难题. BPNN通过利用通信过程中产生的部分丢弃数据, 实现了实时系统校准, 而无需额外设备或全面系统扫描, 显著提高了系统的实用性. 此外, Dong等[27]使用极限梯度提升(extreme gradient boosting, XGBoost)算法对TF-QKD的优化参数进行预测, 并与RF和BPNN进行了性能对比. 结果表明, XGBoost在参数预测的效率和准确性上略优于RF和BPNN, 为未来量子密钥分发网络的实时优化提供有力支持. Ren等[28]首次将机器学习方法应用于QKD系统实现最优协议选择与系统参数优化. 通过对比分析, 随机森林方法在精确性、鲁棒性和效率方面展现出显著优势, 使其成为未来大规模多用户QKD网络中实时配置最优协议和系统参数的有力候选方案.

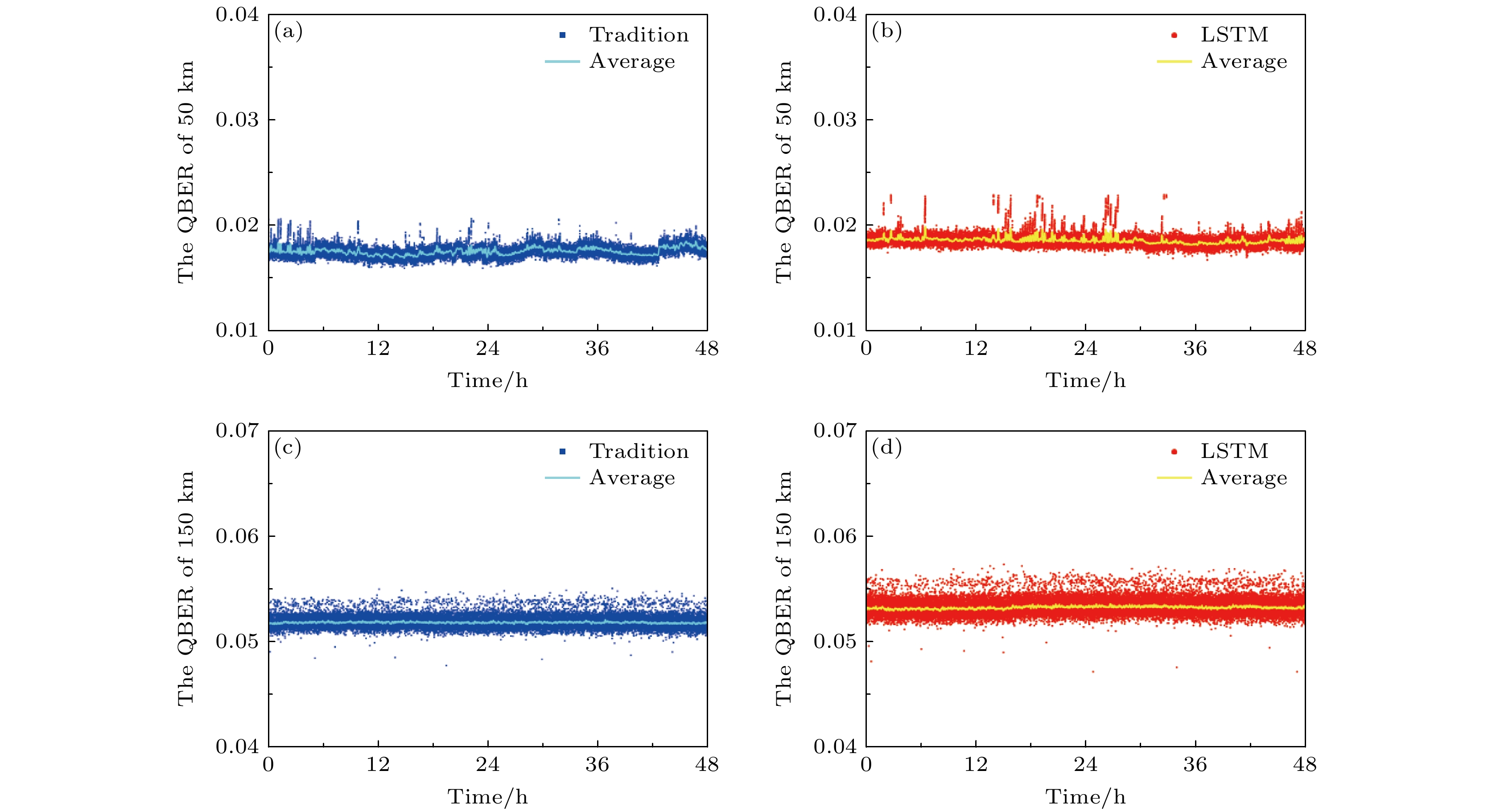
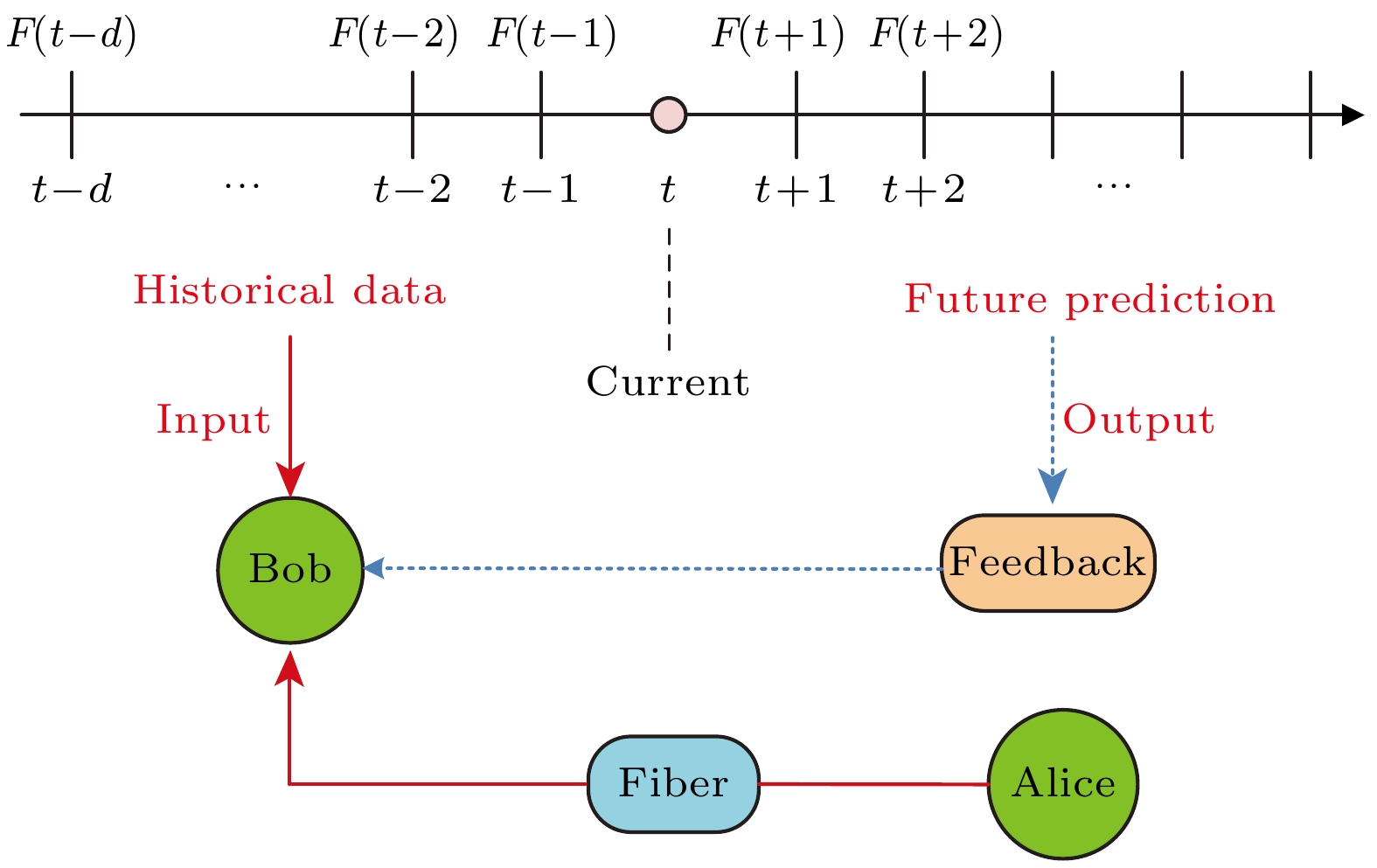
      在实际应用中, QKD系统需要高效的实时反馈控制机制, 以应对外部环境干扰和系统内部组件的不稳定性. 传统的“扫描-传输”校准方案虽然能够提供精确的参数补偿, 但校准过程需要花费大量的时间, 这会大大地降低密钥传输的效率. 为此, Liu等[29]提出了一种基于LSTM的QKD相位调制方案. 该方案通过LSTM网络提前预测设备的物理参数, 并实时进行相位校准. 在BB84-QKD系统中, 该方案在50 km和150 km的传输距离下进行了长达48 h的验证实验(见图3). 实验结果表明, 基于LSTM的QKD系统在连续运行48 h的情况下, 能够保持与传统扫描发射方案相同的量子比特误码率(quantum bit error rate, QBER)水平, 同时将传输效率至少提高了33%, 充分证明了该机器学习模型的长期可靠性和稳定性.

      为了解决测量设备或检测方面的挑战, Zhang等[30] 将LSTM模型应用于MDI-QKD系统, 成功预测了两个用户之间的相位漂移, 并实现了实时主动补偿, 显著提升了系统的参考系校准精度. TF-QKD协议因其优越的安全密钥速率和传输距离而备受关注, 但其实现依赖于精确的全局相位信息. 由于长距离光纤传输中相位波动较快, 传统的相位校准方法(如时分复用)效率低下. 针对这一问题, Liu等[31]开发了一种基于神经网络的相位漂移预测技术, 通过将双层LSTM网络加载到现场可编程门阵列(field-programmable gate array, FPGA)中, 实现了对500公里传输距离上TF-QKD系统相位漂移的准确预测和主动反馈控制, 预测效率高达85%, 极大地提升了TF-QKD系统的传输效率, 促进了高效率TF-QKD系统的实际应用.

      QKD系统的现实安全性是当前量子通信领域的研究热点. 实际设备总是存在缺陷的, 窃听者可以利用各种设备的安全风险点来获取关键信息. 目前, 各类安全分析都倾向于对每个安全风险点进行单独分析, 这给QKD系统的整体安全评估带来了很大的挑战. 现有QKD系统测评方案大多要求在进行密钥传输之前或之后对所有器件逐一做检测和标定, 不仅需要消耗大量的人力、物力, 而且会降低QKD的传输效率和实用性. Xu等[32]首次将机器学习算法引入QKD系统的实时安全监测, 实现了对不同设备缺陷和攻击的实时识别, 准确率高达98%. 该方法不仅节省了时间和成本, 更重要的是无需中断密钥传输, 为QKD系统的安全性测评提供了一种高效、实用的解决方案, 为未来量子保密通信网络的大规模应用奠定了坚实基础. 表1主要列出了目前人工智能在DV-QKD系统中的一些典型应用报道, 主要包括参数优化、相位校准、安全监测等, 并总结对比了主要贡献.

      上述都是关于人工智能在DV-QKD系统中的应用, 人工智能方法同样在CV-QKD系统中也有很多应用, 主要体现在对系统性能的优化和提升安全性. 在系统性能优化方面, 研究者们通过分析系统的物理参数波动, 如本振光强度变化、信道的扰动、环境温度的变化、器件的抖动等, 来预测和补偿相位漂移值. 这种方法在有效传输数据前插入一段双方已知的标准序列, 通过接收端数据和发送端数据对比得到相位偏移量. 然后, 利用机器学习技术, 可以建立时间和相位漂移值的预测模型. 在系统传输有效序列时, 通过此模型对相位漂移值进行预测, 作为相位补偿角度加载到发送端的相位调制器上进行相位补偿. 这种方式可以很好地分析系统相位漂移值, 并能够作为相位补偿算法进行优化. 此外, 也可以通过预测值直接对原始数据重构, 不用对相位漂移值实时进行计算, 一定程度上减少了系统开销.

      2017 年, Liu等[33]通过支持向量回归(support vector regression, SVR)模型开发了一种方法(见图4), 以优化QKD 系统的性能和实用安全性, 通过学习SVR 模型来精确预测信号物理参数的随时间变化, 其次, 利用这种预测的随时间变化的反馈来控制QKD 系统, 以实现最佳性能和实际安全性.

      2019年, Su等[34]将BPNN算法应用到CV-QKD 中的四态离散调制协议, 可以将调制方差调整到最佳值, 从而确保系统安全, 并使系统性能达到最佳, 数值结果表明, 该方案能够有效地提高密钥率. 2020 年, Liao等[35]提出了一种利用机器学习技术进行离散调制CV-QKD的新方案, 称为基于多标签学习的CV-QKD, 具体而言, 该方案将整个量子系统分为状态学习过程和状态预测过程, 前者用于训练和估计分类器, 后者用于生成最终密钥. 同时, 还设计了一种多标签分类算法, 作为区分相干态的嵌入式分类器. 先后提出了相干态的特征提取和量子分类器的相关机器学习指标, 基于多标签学习的CV-QKD方案优于其他现有的离散调制CV-QKD 协议, 如四态协议和八态协议, 也优于原始的高斯调制CV-QKD 协议, 而且随着调制方差的增大, 其性能会进一步提高. 2022年, Zhou等[36]构建了一种神经网络用于预测离散调制CV-QKD协议的密钥率, 可以根据实验参数和实验结果快速预测安全密钥率, 与传统数值方法相比, 神经网络的速度提高了几个数量级. 重要的是, 预测的密钥率不仅高度准确, 而且是安全的, 这使得离散调制CV-QKD 的安全密钥率可以在低功耗平台上实时提取, 该方案也可以扩展到快速计算其他各种非结构化量子密钥分发协议的复杂安全密钥率. 同年, Liu等[37]提出了一种结合贝叶斯优化的神经网络模型, 用于实时预测离散调制CV-QKD协议的安全密钥率. 该模型在速度上比传统数值方法快约107倍, 且预测结果具有高安全性和准确性, 能够满足移动平台等低功耗场景的需求.

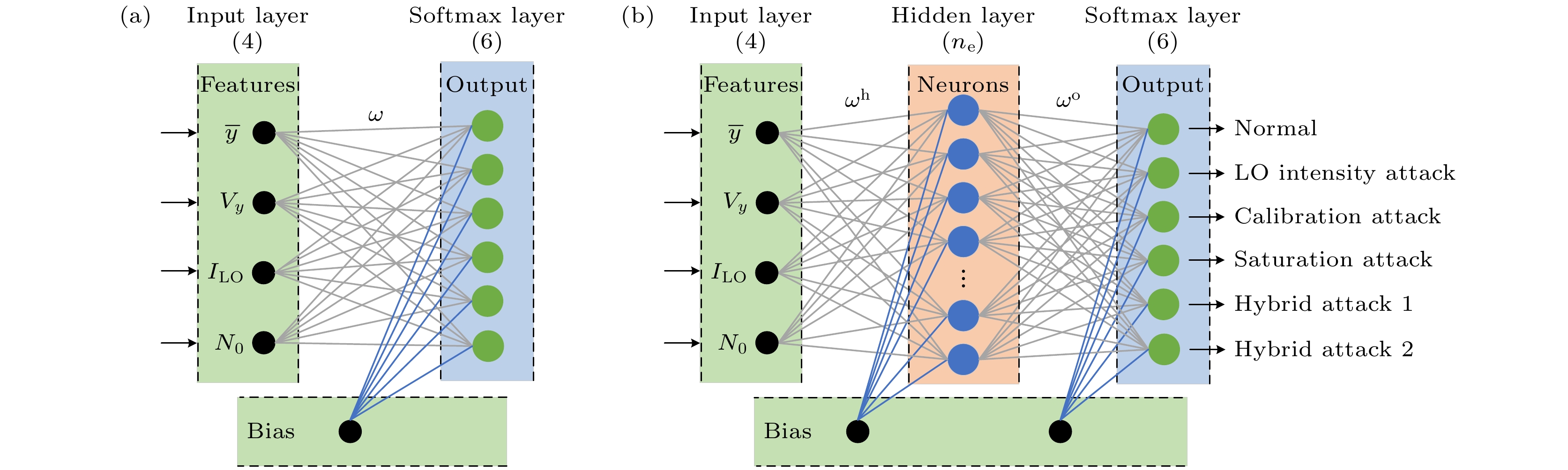
      在安全性方面, CV-QKD系统面临多种攻击策略的威胁. 现有防御方法通常依赖于实时监控模块, 但其有效性受限于额外噪声估计的准确性, 且缺乏通用性. 为此, 2020年, Mao等[38]提出了一种基于人工神经网络(artificial neural network, ANN)的量子攻击检测模型(见图5). 该模型通过分析受攻击脉冲的特征向量, 实现了对攻击类型的自动识别和分类, 准确率和召回率均超过99%, 显著提升了系统的安全性.

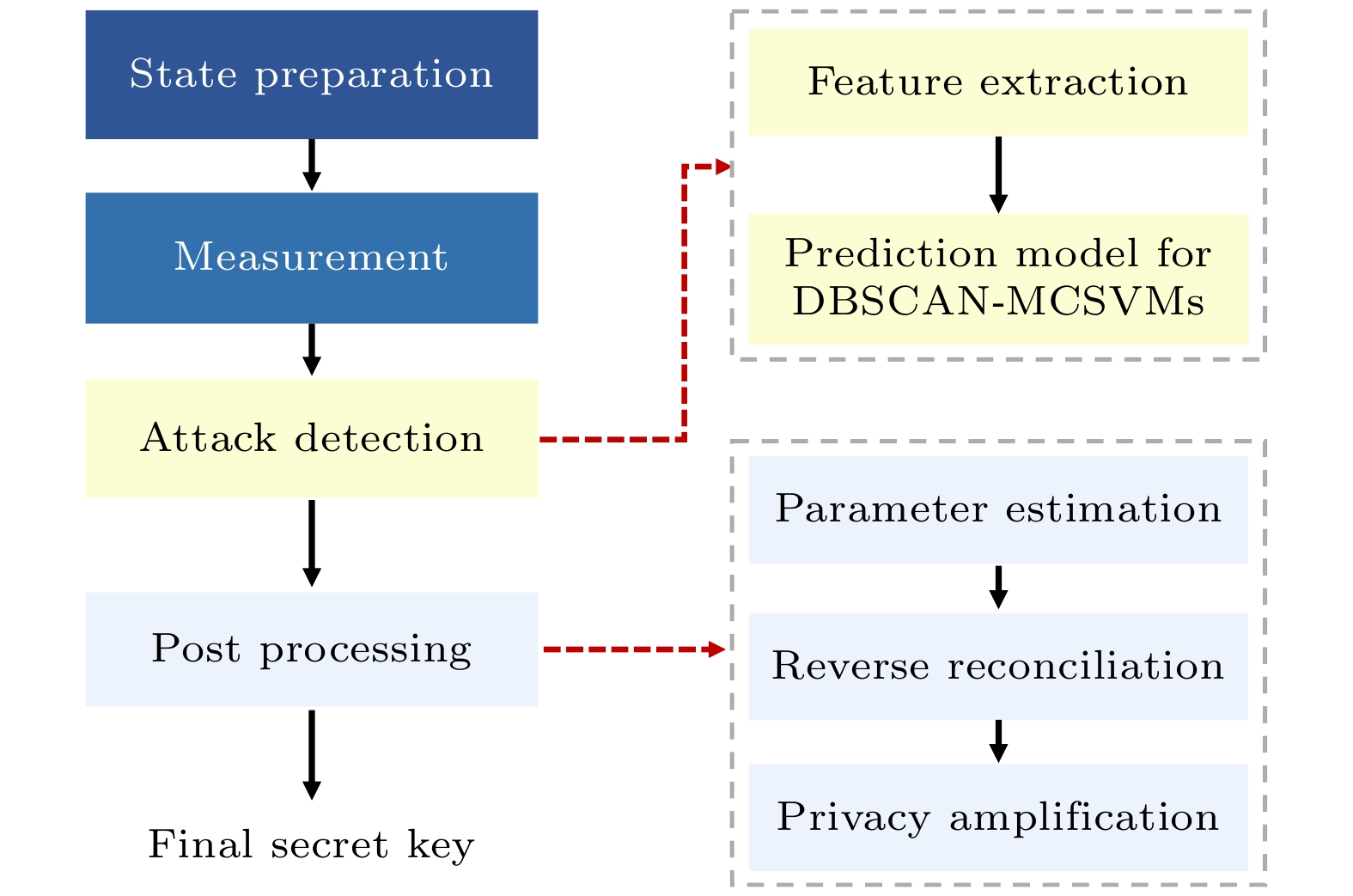
      随后, 在2023年, Ding等[39]提出了一种基于机器学习的攻击检测方案, 其实现过程见图6. 结合密度聚类(density-based spatial clustering of applications with noise, DBSCAN)和多类支持向量机(multiclass support vector machines, MCSVMs)的优势, 实现了对量子黑客攻击的高效检测. 该方案首先提取与攻击相关的特征向量, 利用DBSCAN去除噪声和异常值, 然后通过训练好的MCSVMs进行分类和预测, 实时决定是否生成最终密钥. 仿真结果表明, 该方案能够有效检测大多数攻击, 并修正了CV-QKD系统在无防御策略下的密钥率高估问题, 从而提供了更紧致的安全边界.

      在长距离CV-QKD实验方面, 传统方案通常依赖于传输本地振荡器, 这不仅增加了系统复 杂性, 还可能引入安全漏洞. Hajomer等[40]设计了一种新的长距离CV-QKD实验方案, 通过在本地生成本地振荡器, 成功实现了100 km光纤通道上的密钥分发, 总损耗为15.4 dB. 这一突破性进展通过机器学习框架控制相位噪声引起的额外噪声, 并优化调制方差, 从而实现了在有限尺寸场景下对集体攻击的安全密钥生成. 这一突破性进展不仅标志着CV-QKD技术在高损耗预算下的重要里程碑, 还为大规模安全QKD网络的部署铺平了道路. 未来, 随着量子技术的不断发展, CV-QKD有望在更多高安全性和长距离通信场景中实现广泛应用. 表2列出了人工智能在CV-QKD中的各种典型应用报道, 并总结和对比了主要贡献.

      • 3.2.   量子存储

    • 量子存储器是量子中继器的核心组成部分, 广泛应用于量子通信、量子计算和量子网络等领域, 其性能超越了仅通过被动传输所允许的范围. 量子存储的核心在于将量子态存储在物理系统中, 并在需要时按需读取. 理想的量子存储器应具备高效率、长相干时间和低噪声等特性. 常见的量子存储机制包括电磁感应透明[41]、拉曼方案[42]、梯度回波存储器[43]以及光腔反射[44]等. 其中, 基于固体系统的量子存储(如色心和稀土离子)因其稳定性、抗退相干能力和可扩展性而备受关注[45].

      为了进一步提升量子存储器的性能, 研究者们引入了机器学习技术引入了该领域, 显著提高了系统的光学深度和存储效率. Leung等[46]通过实验研究, 将机器学习与单光子技术相结合, 优化了梯度回波存储器的性能, 并探索了其在量子计算中的应用潜力. 由于冷原子集合系统的复杂性, 实现高光学深度和低温环境通常面临巨大挑战. 该方案通过强化学习优化原子捕获过程, 并开发了高消光比滤波技术, 成功从强泵浦光中分离出单光子. 这些优化措施显著提升了冷原子集合的光学深度和温度控制精度, 从而提高了梯度回波存储器的效率和相干时间.

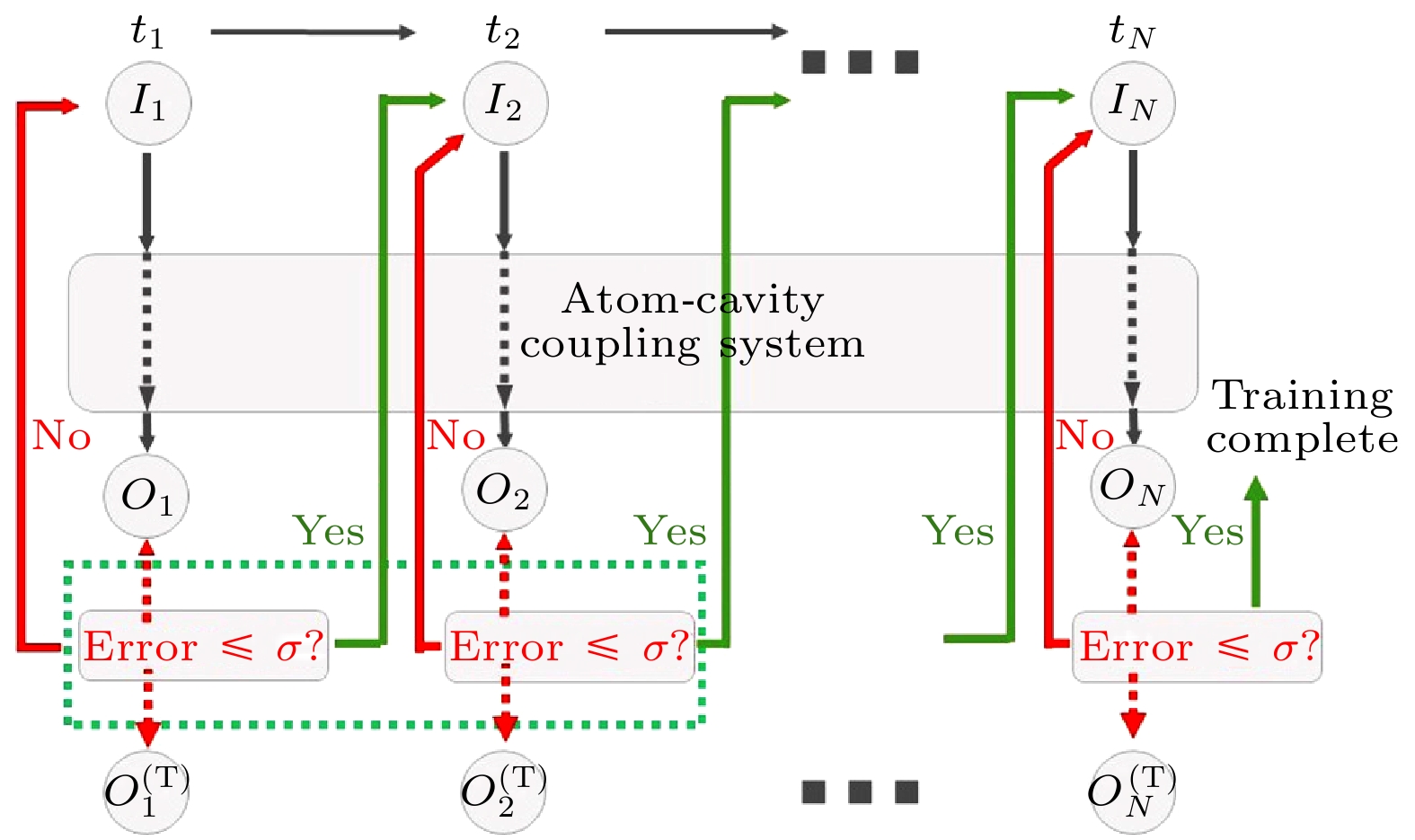
      单光子作为量子信息处理的基本单元, 其生成和存储技术对构建量子网络至关重要. 然而, 实现具有任意波包形状的单光子生成和存储仍面临诸多挑战. Cai等[47]从理论上提出了一种具有自适应过程的通用机器学习算法(见图7), 用于优化原子-腔系统, 实现了高效率和高保真度的单光子生成与存储. 该算法能够根据单光子的波函数动态调整量子系统参数, 为构建灵活可靠的量子网络提供了新的技术路径.

      尽管量子网络的研究取得了显著进展, 但量子存储器的相干时间仍然是限制其发展的关键因素. Khatri[48]提出了一种基于决策过程理论的最优纠缠分发协议设计方法, 通过动态规划或强化学习算法, 在考虑当前硬件限制(包括有限相干时间)的情况下, 优化了量子信道上的纠缠时间, 确保在信道衰减前完成终端节点间的纠缠态建立. 这一研究为量子网络的物理实现提供了重要的理论指导.

      在量子存储时间优化方面, Reiß等[49]从理论上利用强化学习技术, 实现了量子存储时间限制(即存储器截止)的动态优化, 为量子中继器状态的调整提供了灵活的策略. Robertson等[50]最近的一项研究表明, 遗传算法可以用来优化光学存储器的写入控制, 以处理高斯信号脉冲. 实验结果表明, 在不牺牲效率的前提下, 脉冲能量可减小30%, 显著提升了存储性能. 量子存储器的高存储效率和宽带特性是未来量子网络的核心要素. 尽管固态量子存储器在宽带存储方面具有优势, 但其存储效率普遍较低. 针对这一挑战, Lei等[51]通过被动优化与算法优化相结合的技术, 实验验证了将量子存储效率提升了近6倍, 并实现了高信噪比的相干和单光子级存储. 这一优化方案具有广泛的适用性, 可应用于大多数固态量子存储器, 在保持带宽的同时显著提升存储效率.

      • 3.3.   量子网络

    • 量子网络在量子信息科学中扮演着至关重要的角色, 其应用范围涵盖量子通信、量子计算和量子计量等多个领域. 实现量子网络的核心挑战之一在于将纠缠的飞行量子比特(通常以光子形式实现)分发到空间上分离的节点, 并通过量子接口或换能器将纠缠映射到静止量子比特(如基于物质的量子存储器)上. 这种分离节点的架构构成了量子网络的基础, 其中静止量子比特作为存储单元, 而飞行量子比特则充当量子信息传输的通道.

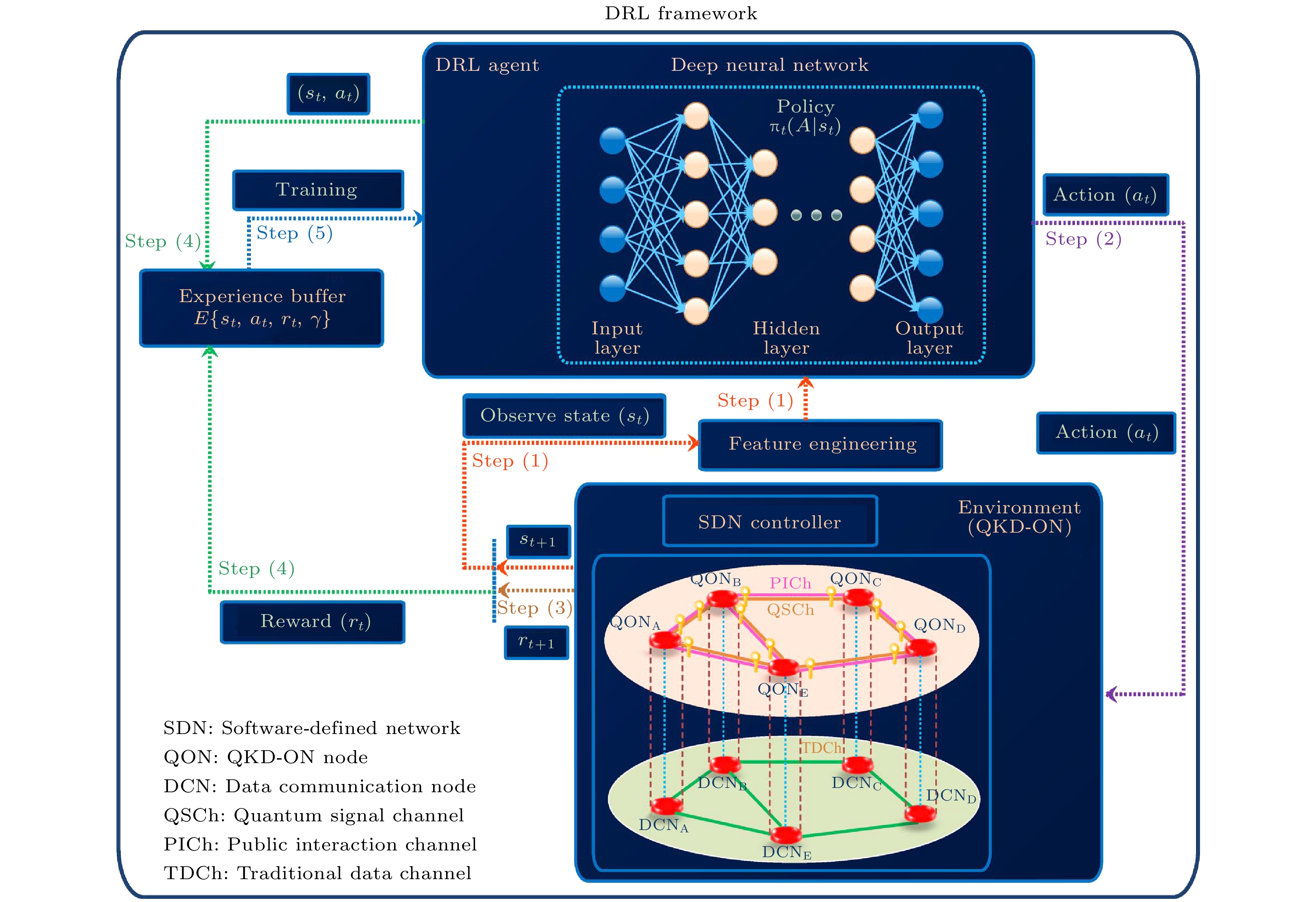
      目前, 量子网络已应用于具有可信节点的QKD中[52]. 由于QKD网络中的密钥资源具有不可复用性, 其分配方式与传统网络资源存在显著差异. 考虑到QKD网络部署的高成本和复杂性, 多租户模式成为提高未来QKD网络成本效益的重要解决方案, 尤其适用于对安全性要求较高的组织. 为优化多租户环境下的资源分配, Cao等[53]提出了一种基于强化学习的多租户密钥分配算法, 能够高效分配包括密钥在内的多种网络资源. 实验结果表明, 与随机分配、适配和最佳适配等传统启发式方法相比, 该算法在降低租户请求阻塞概率和提高密钥资源利用率方面表现优异, 将阻塞概率降低了一半以上. 此外, Cao等[54]进一步研究了量子密钥分发网络中的在线多租户配置问题, 提出了3种启发式算法(随机、适配和最佳适配的在线多租户配置算法), 并开发了一个强化学习框架以实现算法的自动优化. 比较结果显示, 在经过足够的训练迭代后, 基于强化学习的在线多租户配置算法在租户请求阻塞概率和密钥资源利用率方面显著优于启发式方法. Sharma等[55]从理论上提出了强化学习的路由与资源分配方案, 用于优化量子密钥分发安全光网络中的量子信号通道性能(见图8). 该方案的核心是通过软件定义网络控制器获取网络状态信息, 深度神经网络根据状态选择路由和资源分配策略. 通过最大化QKD光路请求数量、降低阻塞率并高效利用网络资源, 该方案相比传统方法在动态流量场景下显著提升了网络性能, 为QKD光网络的优化提供了新的有效方法.

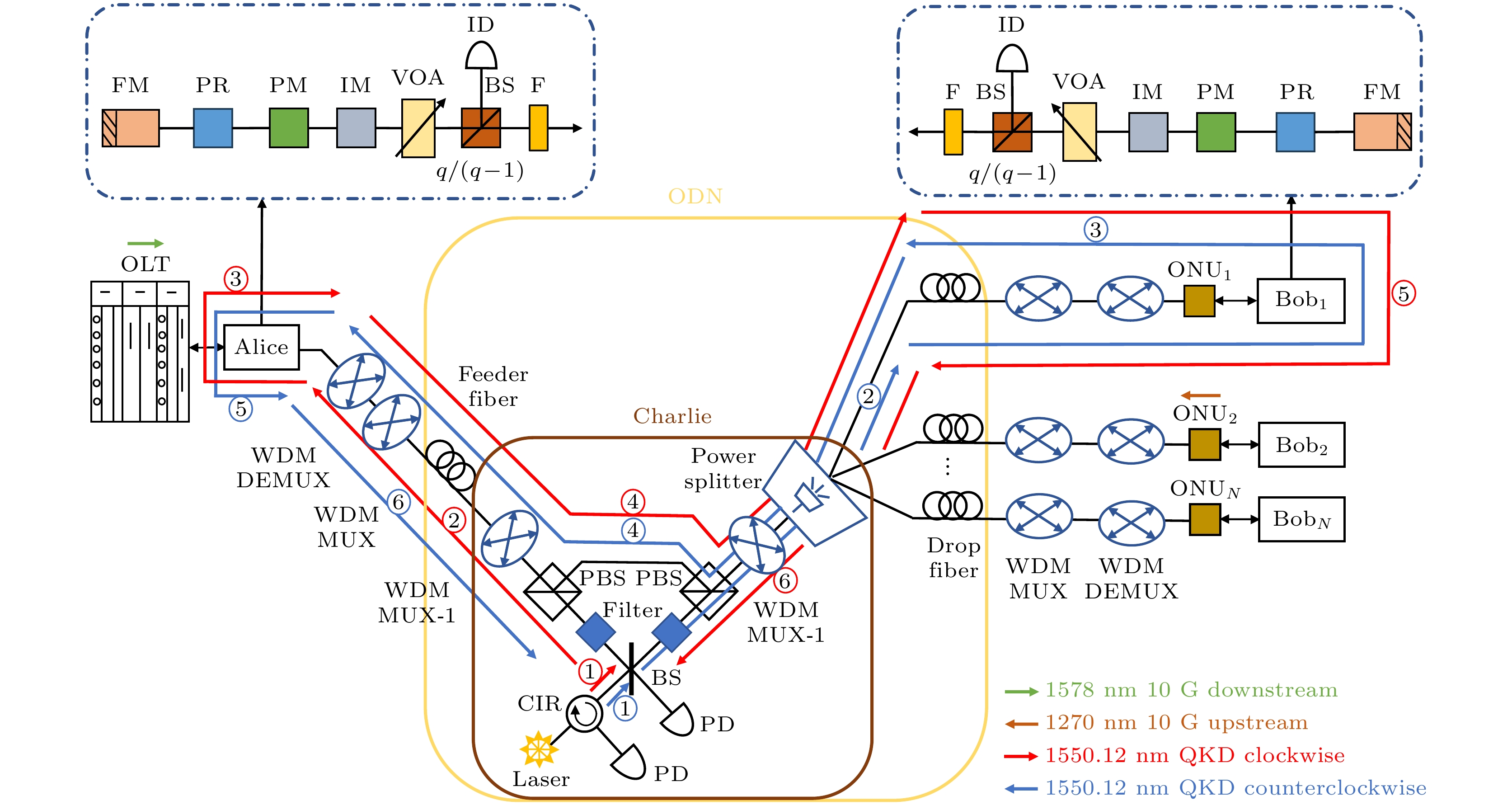
      从点对点量子密钥分发向多点通信的扩展是量子密钥分发网络大规模发展的必然趋势. 目前, 将量子接入网络(quantum access networks, QANs)集成到现有的以太网无源光网络(ethernet passive optical access networks, EPONs)中是一种相对简单且成本效益较高的实现方式. Kang等[56]提出了一种量子安全的10 Gbit/s以太网无源光网络, 实验开发并验证了一种即插即用的双场量子密钥分发架构, 仅需一个不受信任的激光器和一对共享探测器, 可支持多达64个用户(见图9). 此外, 他们还提出了一种基于机器学习的用户需求导向预测模型, 用于评估QAN的关键指标(如安全密钥率、最大馈线光纤长度等). 这种即插即用的双场量子接入网络及其机器学习辅助的实现方法, 为大规模量子接入网络的进一步实验和实际部署提供了指导.

      目前, 量子网络的发展正处于从理论研究向实际应用过渡的关键阶段. 量子存储器和可信中继作为量子网络的两大核心技术, 各有其优势和应用场景. 量子存储器的优势在于能够实现量子信息的长时间存储和按需读取, 从而增强网络的灵活性和鲁棒性. 然而, 其性能仍需进一步提升以满足大规模量子网络的需求. 相比之下, 可信中继方案在长距离量子通信中已取得显著进展, 但其依赖于物理节点的部署, 扩展性和灵活性有限. 此外, 由于需要在中间节点进行量子态的测量和重新制备, 可信中继方案的安全性也面临一定挑战. 未来, 量子网络的发展将依赖于量子存储器性能的进一步提升以及可信中继方案的优化, 以实现更高效、更安全的量子通信网络.

    4.   人工智能在量子传感系统中的应用

      4.1.   量子传感简介

    • 量子传感是一种利用量子系统、量子特性或量子现象对物理量(如磁场、电场、温度、压力等)进行高精度测量的技术. 其基于量子力学的基本原理, 特别是量子态的叠加、纠缠和量子相位演化等特性, 从而实现超越经典传感器的测量精度. 量子传感器是利用量子力学特性(如原子能级、光子态或基本粒子的自旋)进行计量的设备, 已进入实用化阶段的量子传感器的典型代表为原子钟[57]、原子磁力仪[58]、原子干涉重力仪[59]等. 同时, 以金刚石NV色心[60]、里德伯原子[61]等为平台的传感技术, 也正在逐步成为重要的发展方向.

      当前主流的量子传感技术主要可以归结为以下3类[62]: 1)使用量子物体测量物理量, 其特征是量子化的能级(量子态). 具体的例子包括来自超导、中性原子、囚禁离子或其他自旋体系中的电子能级、磁子能级、原子核能级或振动能级. 2)使用量子相干性(即具有波动属性的空间、时间叠加态)来测量物理量. 3)使用纠缠、压缩等量子资源提高测量的灵敏度或精度, 从而超越经典测量技术的统计极限. 早期的量子传感技术, 大多关注的是提升对微小物理量变化量的感知能力. 随着量子纠缠的实现以及激光技术的发展, 人们开始充分挖掘特殊量子态以及量子态操控方法在降低测量不确定度方面的巨大潜力, 这一类技术更关注的是如何在资源有限的情况下, 进一步降低待测物理量的测量不确定度. 目前, 一些量子传感方案已经在光子、原子、核磁共振及固态系统中成功演示. 相比于固体系统与原子系统[63,64], 光子具有相干时间长、不易受干扰、易于调控和容易拓展等特性, 因此光子系统针对传感任务具有天然优势, 近年来逐渐得到更广泛的关注.

      • 4.2.   量子通信系统与传感技术的结合

    • 近年来, 随着通信技术的飞速发展, 量子通信和传感技术的融合逐渐成为研究热点. 量子通信利用量子态作为信息载体, 能够实现理论上无条件安全的密钥分发. 与此同时, 传感技术也在不断发展, 分布式光纤传感技术利用光纤中的光背向散射或前向传输光的变化实现对环境变化的监测, 具有高空间分辨率和长检测范围等优点. 将量子通信系统与传统传感技术相结合, 不仅可以实现通信和传感的集成, 还能在不改变现有量子通信网络架构的情况下, 赋予通信网络环境感知能力, 为地震、滑坡等灾害的预警提供新的技术手段.

      近年来, 多个研究团队在量子通信与传感融合领域取得了重要成果. Chen等[65]在658 km光纤上实现了TF-QKD, 并利用TF-QKD系统中的频率校准链路实现了分布式振动传感. 该研究不仅拓展了量子密钥分发的距离记录, 还成功定位了振动源, 精度优于1 km. Xu等[66]提出了一种集成分布式传感和量子通信网络方案, 通过在光纤中同时实现连续变量量子密钥分发和分布式振动传感, 展示了量子通信与传感融合的潜力. 该方案在10 km标准光纤传输下, 每个用户的密钥率约为 0.7 Mbits/s, 振动响应带宽为1 Hz—2 kHz, 空间分辨率为0.2 m. Liu等[67]提出了一种集成下游量子接入网络和光纤振动传感的网络架构. 通过在单激光源的边带上同时编码8个用户的密钥信息, 并利用窄带滤波网络分离和分发密钥信息, 平均密钥率为1.94×104 bits/s, 同时实现了在100 Hz, 1 kHz和10 kHz振动频率下, 空间分辨率为131 m, 25 m和4 m的振动定位.

      然而, 传统传感技术在精度上存在局限性. 例如, 基于背向散射光的分布式光纤传感虽然能够实现较高的空间分辨率, 但由于依赖于弱光信号的反射, 其检测精度通常受到噪声的限制, 难以达到海森伯极限. 此外, 传统光纤传感技术在长距离检测时需要高功率光源(如掺铒光纤放大器), 这不仅增加了系统的复杂性和成本, 还可能对量子通信系统中的低光信号造成干扰. 相比之下, 量子传感技术利用量子态的特性, 提供了比经典测量更高的灵敏度, 能够显著提高传感精度[63,68]. 此外, 使用多光子纠缠态、单光子、压缩态等手段[69–71], 可以超越标准量子极限, 甚至在理论上接近海森伯极限.

      分布式量子传感是量子网络中一个极具潜力的研究方向, 它通过在多个测量节点的网络中执行传感任务, 能够显著提升测量的精度和效率. 与单参量量子传感相比, 分布式量子传感可以对多个参数的线性组合进行高精度测量, 分为连续变量方案[70]和离散变量方案[71,72]. 然而, 分布式量子传感仍面临一些挑战. 例如, 如何在实际应用中对任意未知待测参数实现高精度测量是一个关键问题. 未来, 随着量子纠缠技术、量子网络架构以及量子通信技术的进一步发展, 分布式量子传感技术有望在量子通信网络中实现更广泛的应用, 推动量子技术在多个领域的突破.

      • 4.3.   人工智能赋能量子传感系统

    • 近年来, 人工智能技术逐渐被引入到量子传感领域, 为量子传感器的校准、优化和性能提升提供了新的方法和思路. Cimini等[73]提出了一种基于神经网络的量子相位传感器校准方法. 该方法无需依赖复杂的理论模型来描述传感器的所有参数和噪声源, 而是通过神经网络直接对传感器进行校准. 研究发现, 神经网络能够有效处理训练数据中的不确定性, 并在实验中实现了接近量子极限的测量精度. 此外, 该方法还表现出对噪声的鲁棒性, 且可通过调整训练参数进一步优化性能. 这种方法为量子传感器的校准提供了一种高效、自适应且资源经济的解决方案, 尤其适用于大规模量子设备的校准. 此外, Hentschel和Sanders[74]的研究从理论上提出将机器学习应用于量子相位估计, 通过粒子群优化(particle swarm optimization, PSO)算法, 设计了用于干涉仪相位估计的反馈策略, 显著提高了测量精度并接近海森伯极限. 与传统的BWB (Berry-Wiseman-Breslin)策略相比, PSO生成的策略在无噪声和有噪声条件下均表现出更好的性能.

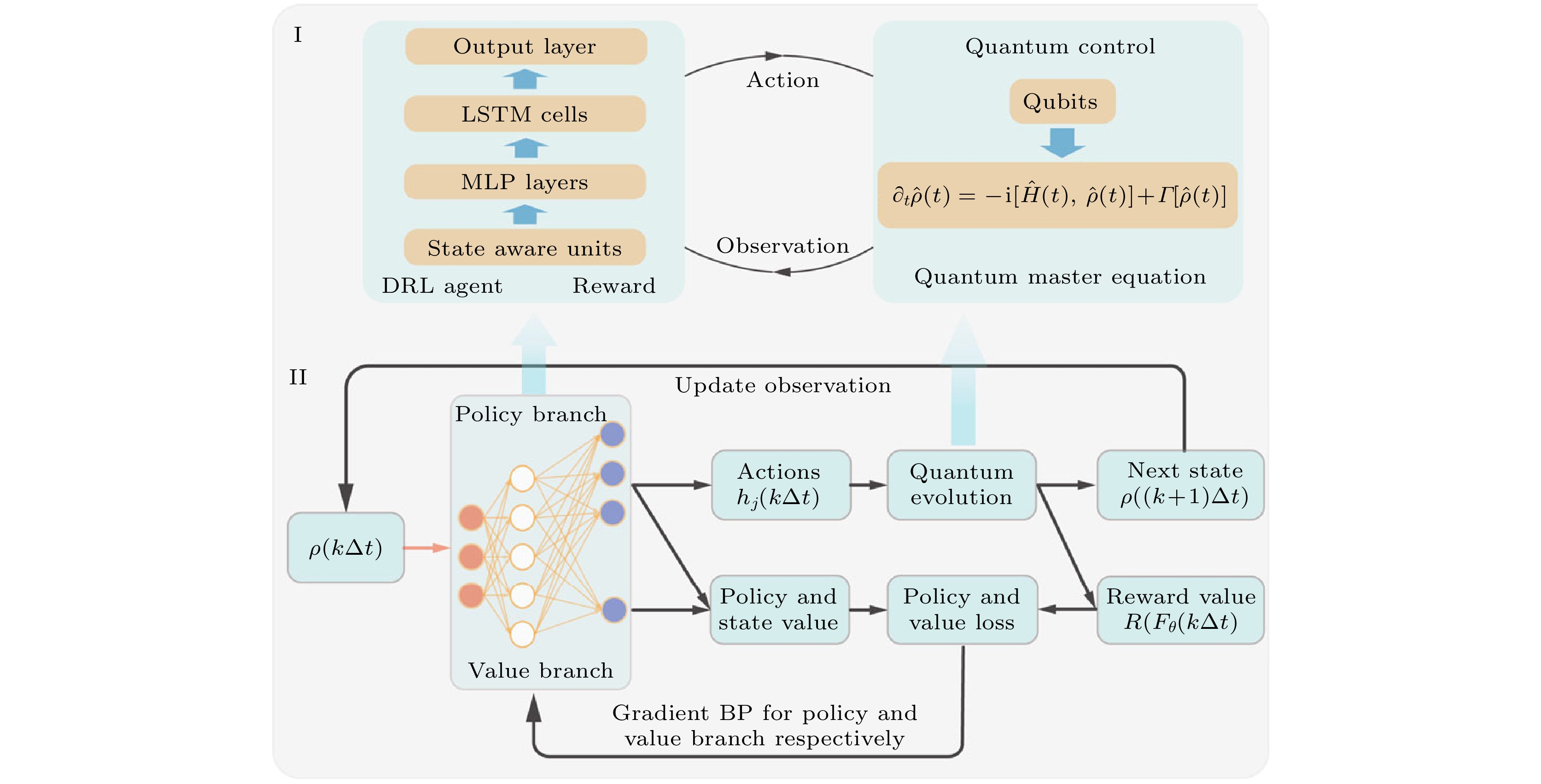
      强化学习通过智能体与环境的交互, 通过试错来优化策略, 从而实现目标. Xu等[75]的研究从理论上提出了利用强化学习来优化量子参数估计中的控制策略, 并证明了强化学习在这一领域的高效性和泛化能力. 他们通过训练神经网络来生成适用于不同参数值的控制序列, 避免了每次参数更新时重新优化的高计算成本. Schuff等[76]从理论上利用强化学习中的交叉熵方法优化量子传感器的动力学特性. 研究以量子混沌传感器为基础, 通过优化非线性控制脉冲的强度和位置, 进一步提高测量精度并对抗退相干. 与传统的周期性控制脉冲相比, 优化后的控制策略在超辐射阻尼和相位阻尼两种退相干模型下均显著提高了量子费希尔信息 (quantum Fisher information, QFI), 部分情况下灵敏度提高了超过一个数量级. 通过可视化量子态的演化, 研究揭示了强化学习采用的是一种类似于自旋压缩的策略, 这种策略能够适应超辐射阻尼的动力学特性. Xiao等[77]提出了一种基于深度强化学习的量子参数估计方案, 用于处理时间依赖的参数估计问题. 该研究从几何角度推导了参数估计的QFI的无噪声和有噪声边界, 并设计了一个与这些边界相关的奖励函数, 以加速网络训练并快速生成量子控制信号(见图10). 通过仿真验证, 该方案在无噪声和有噪声(包括退相干和自发辐射噪声)条件下均展现出良好的鲁棒性和样本效率, 并达到了理论性能极限. 此外, 该研究还评估了当参数偏离真实值时方案的可转移性, 结果表明, 该方案在时间无关参数估计中表现出色, 而在时间依赖参数估计中对噪声更为敏感.

      模型感知强化学习(model-aware reinforcement learning, MARL)进一步将物理模型的先验知识融入训练过程, 通过自动微分技术处理量子计量学中的非微分步骤, 如测量和粒子滤波的重采样. 这种方法不仅提高了策略优化的效率, 还能够处理复杂的量子系统. 例如, Belliardo等[78]从理论上开发了一个基于模型感知强化学习的框架, 用于优化量子计量学中的贝叶斯实验设计. 他们通过结合贝叶斯估计和强化学习, 实现了在多种量子平台(如NV色心和光子电路)上的高精度参数估计. 这种方法不仅在理论上具有优势, 还通过实际应用展示了其在实验设计中的高效性.

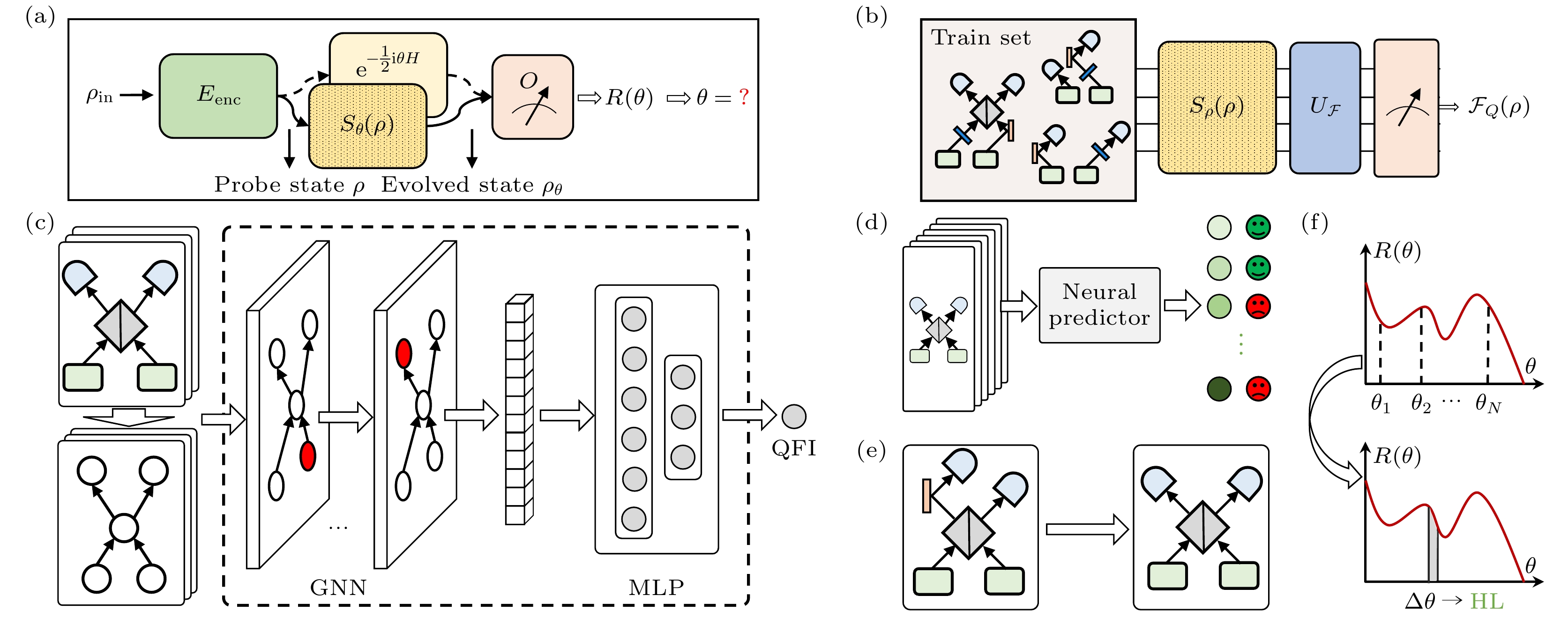
      Liu等[79]利用人工智能的方法, 实验上实现了基于里德伯原子多频率微波的精密探测, 该工作将原子传感与深度学习有机结合, 提出并实现在不求解主方程的情况下有效探测多频率微波电场的方案, 且在硬件上没有太高要求即可实现较高精度, 为传感领域与神经网络交叉结合提供了重要参考, 在通信、雷达探测等领域具有重要应用前景. Zhou等[80]提出了一种基于深度学习的光学量子传感方案, 旨在解决在未知或不受控环境中实现光学量子传感的挑战(见图11). 传统方法通常依赖于对目标系统的先验知识来达到海森伯极限的测量精度, 但在实际应用中, 这种先验知识往往难以获得. 因此, 该方案通过结合图神经网络(graph neural network, GNN)和三角插值算法, 通过数值仿真使光学量子传感器能够在未知环境中达到海森伯极限精度, 为复杂环境下的量子传感提供了新的解决方案. 表3总结了人工智能在量子传感领域的各种应用, 并进行对比.

      目前, 人工智能算法赋能量子传感领域的应用主要聚焦于单体量子传感系统. 这些系统借助神经网络、强化学习等工智能技术, 实现了传感器的高效校准、性能优化以及测量精度的显著提升. 然而, 对于分布式量子传感系统而言, 涉及多个节点之间的协同工作, 更为关键的是, 量子网络的可扩展性和稳定性构成了制约分布式量子传感技术发展的核心瓶颈. 随着节点数量的增加, 系统复杂度呈指数级上升, 导致当前分布式量子传感系统的性能提升面临很大的困难. 尽管目前尚未出现成熟的人工智能赋能分布式量子传感方案, 但面对这一复杂系统的优化需求, 发展基于人工智能的辅助设计和决策方法已成为必然趋势.

    5.   总结和展望

    • 近年来, 人工智能在量子通信和量子传感领域的应用取得了显著进展, 为这些前沿技术的发展注入了新的活力. 在量子通信方面, 人工智能技术通过优化参数、实时反馈控制以及攻击检测等手段, 极大地提升了量子密钥分发、量子存储和量子网络的性能与安全性. 在量子传感领域, 人工智能的引入为实现高精度、高灵敏度的量子测量开辟了新路径. 量子传感技术利用微观粒子的量子态变化, 能够实现对时间、磁场等物理量的超高灵敏度探测, 其精度可提升至原子尺度. 人工智能赋能量子传感, 不仅可以优化传感器的性能, 还能通过数据分析进一步提升测量精度.

      尽管人工智能在量子通信中的应用已经取得了诸多进展, 但仍面临一些挑战, 如算法的可解释性, 有些人工智能算法被认为是“黑箱”模型, 其决策过程难以解释, 这种缺乏可解释性可能会影响系量子通信系统的可靠性和安全性; 数据获取和标注的困难性, 在实际的系统中获取大量数据用来算法训练往往不是一件很容易的事等. 此外, 目前的量子通信和量子传感系统大多依赖经典的人工智能算法, 未来的研究可以进一步探索量子人工智能算法在量子通信和量子传感中的应用. 量子人工智能算法利用量子计算的叠加和纠缠特性, 有望突破经典算法的瓶颈, 实现更高效、更安全的量子通信和量子传感系统.

      量子通信和量子传感系统的小型化、芯片化以及与无人机等多场景应用的结合是也是当前研究的热点方向, 但仍面临诸多挑战. 系统的小型化和芯片化需要解决量子芯片的高成本、低集成度等问题, 同时还要确保系统的高性能和稳定性. 轻量级的芯片计算资源和存储能力可能受到限制, 而在实际的量子通信和量子传感系统中通常需要处理大量的实时数据, 如何在有限的算力条件下实现高效的算法部署和系统反馈控制, 成为亟待解决的问题. 同时, 复杂的任务环境、动态变化的场景以及多任务的协调需求, 使得人工智能辅助设计和决策成为必然趋势.

      此外, 量子通信和量子传感系统的融合是未来技术发展的重要方向. 量子通信提供了绝对安全的信息传输能力, 而量子传感则在高精度测量方面展现出巨大潜力. 两者的结合, 即“通感一体化”, 能够实现量子通信与量子传感的深度融合, 为复杂环境下的任务提供更高效、更可靠的解决方案. 例如, 量子传感技术可用于高精度的环境监测和定位导航, 而量子通信则确保这些数据的安全传输. 未来的研究需要进一步探索人工智能与量子通信及量子传感的深度融合, 开发更加高效、安全和实用的量子通信及量子传感系统, 为广泛应用奠定坚实基础.

    参考文献 (80)

目录

/

返回文章
返回