-
爆轰是极端高温
$\cal{O} $ (103 K)、高压$\cal{O} $ (10 GPa)、高爆速$ \cal{O}$ (103 m/s)物理化学反应过程, 作用时间极短$\cal{O} $ (10 μs)以至于肉眼无法全系统捕捉爆轰演化过程. 目前, 理论仍不完备, 利用实验数据倒推关键参数, 导出普适的物理规律是爆轰研究常用的方法. 然而, 爆轰的极端特征导致实验数据标定依赖于昂贵的、精密的仪器仪表, 同时超强的威力和猛度、不易全面准确评估的感度又让操作人员面临高危作业压力, 进而无法获取大量测试数据. 此外, 爆轰的非线性、多物理耦合性和强间断性, 导致基于物理守恒定律的高保真模型运算量太大, 因此感兴趣量(quantity of interest, QoI)的仿真值也是样本容量有限[1–5]. 实验/仿真样本容量不足时, 就无法保证QoI统计信息的收敛性, 只能得到粗略估计值, 会丢失关键信息. 此外, 若实验/仿真样本容量过小, 则无法直接使用基于人工神经网络的深度学习等热点机器学习方法. 基于稀疏的实验/仿真数据, 利用机器学习导出QoI的一般物理机理, 是爆轰研究的热点, 也是挑战.实验研究的另一个挑战在于爆轰演化过程中始终蕴含不确定度(uncertainty), 造成数据标定值的随机波动性. 爆轰的非线性复杂性, 导致参数、边界条件、几何区域、操作环境的微小变化都能引起QoI的剧烈振荡. 正确表征实验不确定度和评价不确定因素对QoI的影响, 能提高爆轰的认知程度. 在核能[6–9]、航天飞机[10–12]、量子力学[13]、汽车[14]等领域巨大需求的推动下, 以及美国能源部[15]、美国国防部[16]、美国空军科研办公室(AFSOR)[17]、美国海军研究实验室(NRL)[18,19]和美国机械工程师协会(American Society of Mechanical Engineers, AMSE)[20,21]等部门的倡议和资助下, 不确定度量化(uncertainty quantification, UQ)技术发展迅猛. 近年来, 国内外学者逐步开展爆轰领域UQ 研究[22–25], 但是结果异常稀少, 且研究仍集中在仿真不确定度, 对实验不确定度的研究极为罕见. 特别是, 如何定量表征高维(多物理属性)小样本爆轰实验数据的不确定度并评估其影响, 未见报道.
针对高维小样本爆轰实验数据, 单纯增加物理实验次数并不现实, 自然的想法是使用机器学习方法扩大样本容量. 但难点在于待标定数据的概率分布函数未知, 甚至有界支集(support set)未知. 另外, 高维样本点带有多个物理属性, 如何保证生成的样本点能保持不同属性之间的物理机理? Soize和Ghanem[26]于2016年提出的流形上的概率学习(probability learning on manifold, PLoM)方法耦合Itô-MCMC(Markov chain Monte Carlo, MCMC)采样和流形嵌入技术, 实现高维小样本实验数据集的有效扩容, 已经在超音速燃烧冲压发动机(scramjet)[27]、超音速喷嘴[28]、高铁节能优化[29]、失协叶盘[30]等高科技领域证明了该方法的实用性和优越性. PLoM方法的优点在于: 首先, 经典MCMC方法中, Metropolis-Hastings算法难点在于建议分布的构造凭经验, 没有普适的规律可循, 且高维采样计算成本太大[31,32]. Gibbs算法难点至于计算边际分布[33]. 相比之下, 基于Itô-MCMC的PLoM方法没有以上问题困扰, 具备高维样本生成可行性. 其次, 经典MCMC方法得到的采样虽然能够导出物理量自身的统计特征, 但是不会集中在特定的流形上, 破坏了数据的局部几何结构, 即破坏了实验样本不同物理属性之间的物理运行机理. 而PLoM方法通过使用流形嵌入方法, 发掘低维流形结构, 将基于Wiener过程驱动的耗散Hamilton系统的解空间在流形上投影, 从而生成的样本集中在耗散映射定义的非线性流形上. 不仅能导出物理量自身的统计规律, 还能更精确导出物理机理. 再次, 与经典MCMC相比, PLoM方法计算成本较低. 最后, 当高维小样本实验数据受到噪声污染时, PLoM方法表现出较强的鲁棒性.
综上所述, PLoM方法的以上特征, 成为刻画稀疏样本的高维爆轰实验数据潜在有效工具. PLoM生成的丰富的电子实验数据, 易于导出炸药的密度和爆速等物理量的概率密度函数, 还保持了不同物理属性之间的物理运行机理, 为更准确地理解爆轰动力行为打下坚实的基础.
-
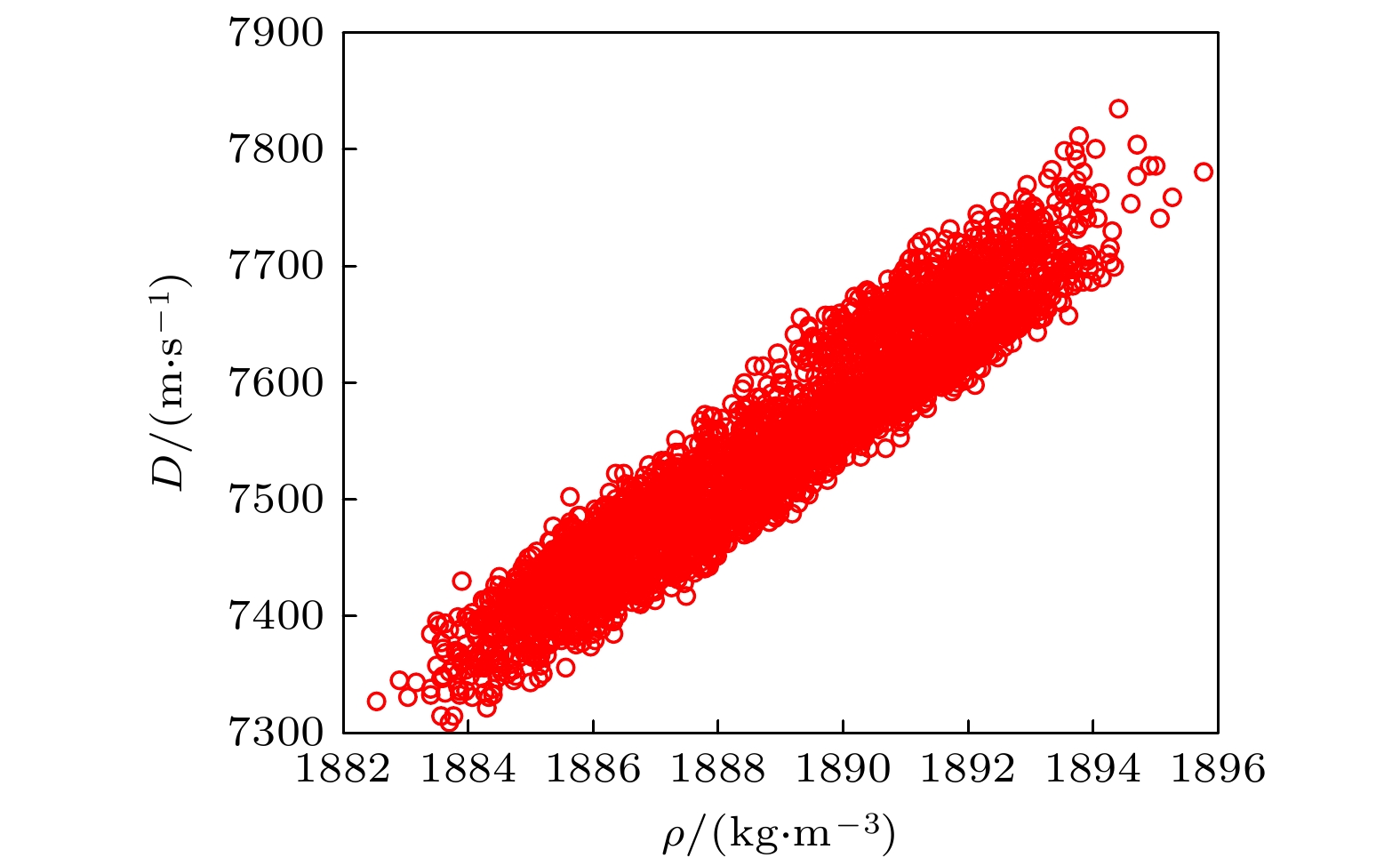
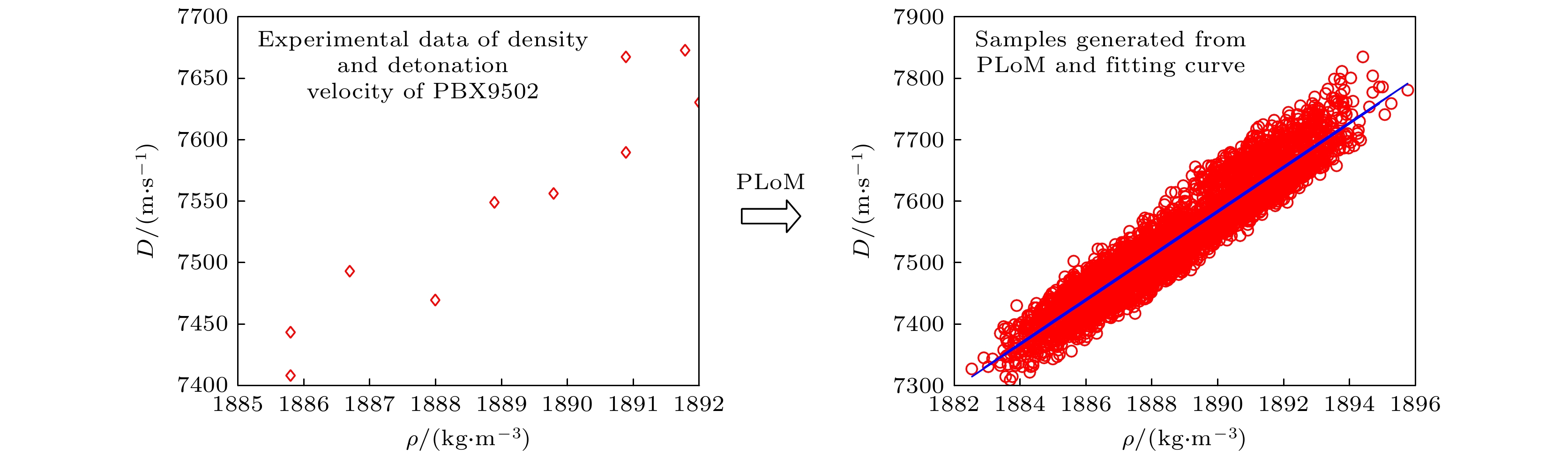
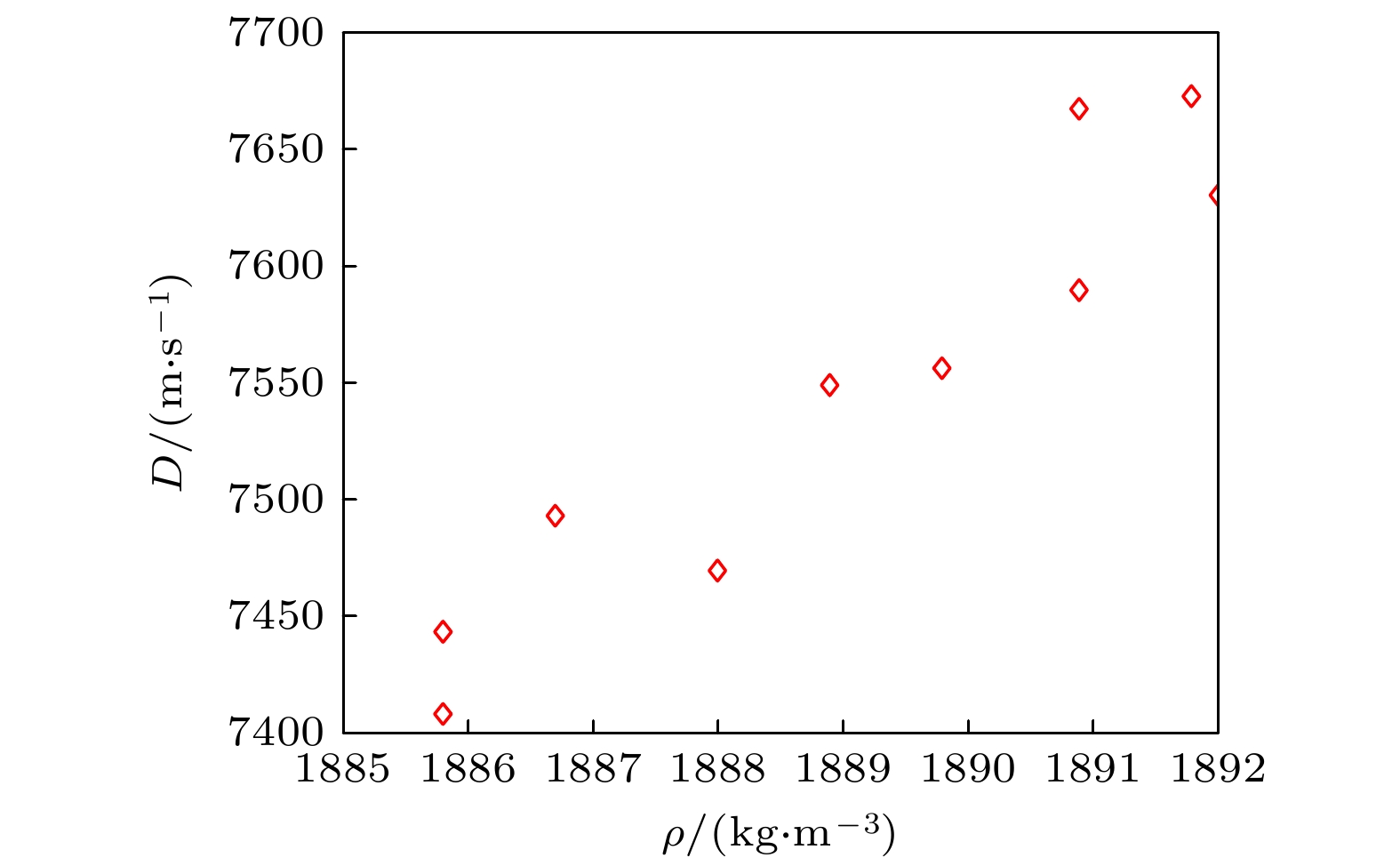
PBX9502是一款性能优越的钝感高能炸药, 在常规武器和核武器领域应用广泛. 组分为95%的TATB和5%的Kel F 800, 理论最大密度1942 kg/m3. Los Alamos国家实验室(LANL)标定的PBX9502炸药密度和爆速实验数据如图1所示[34], 其中操作环境为室温24 ℃, 药柱直径范围为8—50 mm, 由于PBX9502制备和实验标定成本较高, 导致样本容量N有限.
将图1中nd个属性的N个样本点表征为矩阵
${{\boldsymbol{X}}_{\text{d}}} \in {\mathbb{R}^{{n_{\text{d}}} \times N}}$ .${n_{\text{d}}} = 2$ 为样本点的物理属性的个数, 第1行为PBX9502的密度, 第2行为爆速, 矩阵列数N = 10为有效样本点数量.必须指出, 爆轰实验数据时刻受到到噪声污染, 因此取值并非一成不变. 如图2所示[35], 压制成型过程中产生的孔隙、空腔、扭结、裂纹、结晶使得PBX9502的密度标定值中含有不确定度[36,37]. 爆速
$D$ 的不确定度归因于操作条件限制和测量技术. 非参数统计由于理论的完备性, 成为辨识和刻画物理量的不确定度的有力工具.在概率统计的范畴内, 实验数据被认为是满足某种机理的高维随机向量的抽样. 但是实验数据服从的PDF未知. 同时, PBX9502的密度和爆速满足某种物理机理, 即随机向量的支集属于
${\mathbb{R}^{{n_{\text{d}}}}}$ 空间的有界子集, 有效抽样必须落在某种流形上. 遗憾的是, 此流形的结构未知. 接下来将利用实验数据提供的有限信息, 寻找随机向量的概率密度函数(probability density function, PDF). -
为了后续更好地应用概率方法, 首先将第2节实验数据矩阵
$ {{\boldsymbol{X}}_{\text{d}}} $ 进行伸缩变换, 得到缩比(scaling)矩阵$ \tilde {\boldsymbol{X}} = {\left[ {{{\tilde x}_{ij}}} \right]_{{n_{\mathrm{d}}} \times N}} $ , 具体步骤为式中, 算子
$ \vee , \wedge $ 定义为$a \vee b = \max \left\{ {a, b} \right\}, \; a \wedge b = \min \left\{ {a, b} \right\}$ .将矩阵
$\tilde {\boldsymbol{X}}$ 按列分块得$\tilde {\boldsymbol{X}} = \left[ {{{\tilde {\boldsymbol{x}}}_1}, {{\tilde {\boldsymbol{x}}}_2}, \cdots , {{\tilde {\boldsymbol{x}}}_N}} \right], {\tilde {\boldsymbol{x}}_i} \in {\mathbb{R}^{{n_{\text{d}}}}}, i = 1, 2, \cdots , N$ , 则$\tilde {\boldsymbol{X}}$ 的平均值向量和协方差矩阵定义为式中C的特征值和标准化特征向量
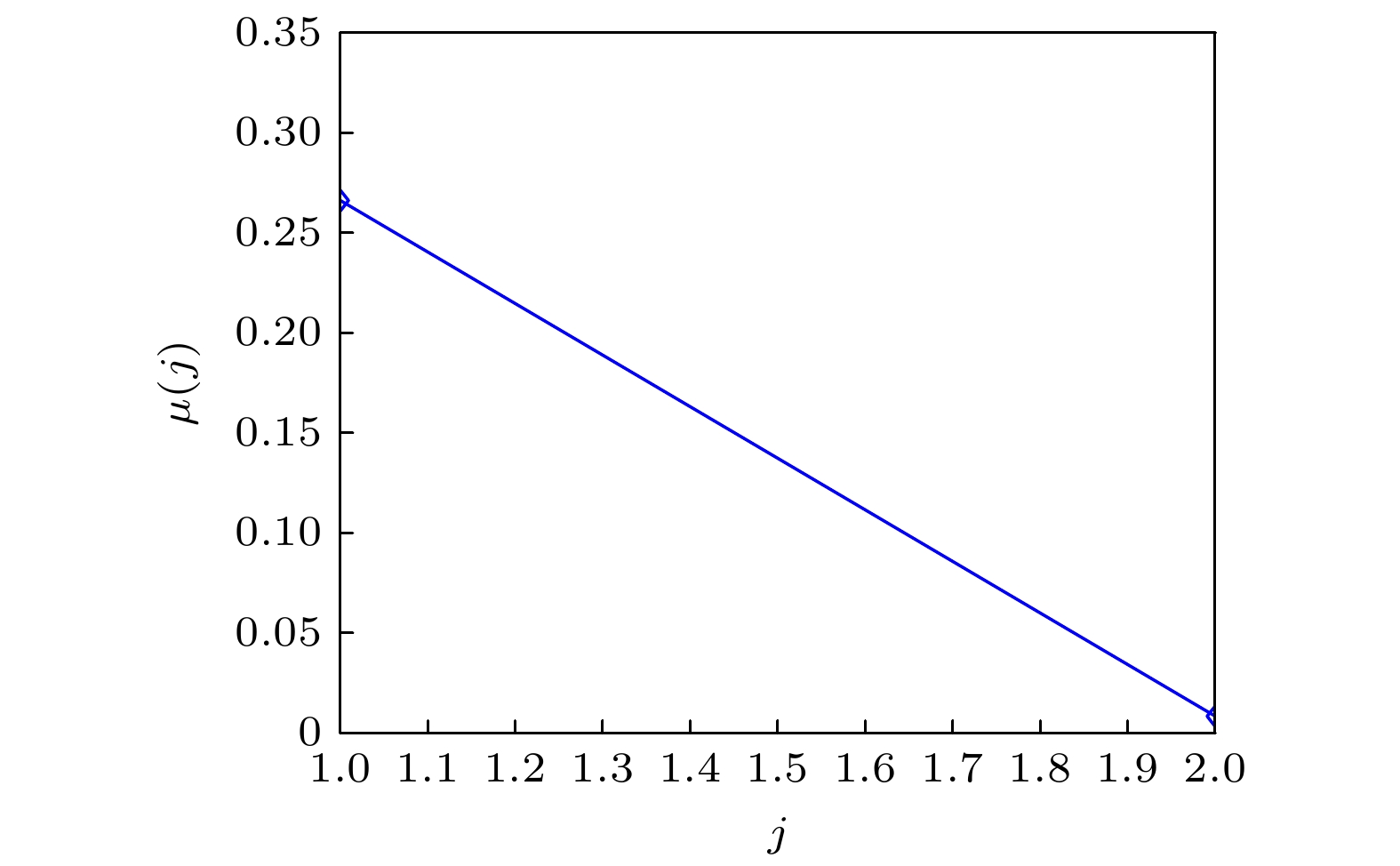
${\boldsymbol{C}}{\xi _k} = {{\boldsymbol{\mu}} _k}{\xi _k}, k = 1, 2, \cdots , {n_{\text{d}}}$ , 其中矩阵C的秩${\text{rank}}({\boldsymbol{C}}) = {\boldsymbol{\upsilon}} \leqslant {n_{\text{d}}}$ , 且$0 < {{\boldsymbol{\mu}} _1} \leqslant {{\boldsymbol{\mu}} _2} \leqslant \cdots \leqslant {{\boldsymbol{\mu }}_\upsilon }, $ ${\xi ^{\text{T}}}\xi = {{\boldsymbol{I}}_\upsilon }\; \in\; {\mathbb{R}^{\upsilon \times \upsilon }}, \xi = \left[ {{\xi _1}, {\xi _2}, \cdots , {\xi _\upsilon }} \right] \in {\mathbb{R}^{{n_{\text{d}}} \times \upsilon }}$ . 将图1中实验数据信息代入(1)式和(2)式, 计算特征值和特征向量, 得到秩${{\upsilon}} = 2$ , 特征值的具体取值见图3. -
按照主成分分析(principle component analysis, PCA)原理, 利用3.1节所得特征向量矩阵
$ {\boldsymbol{\xi }} $ , 构造随机矩阵$ {\boldsymbol{X}} \in {\mathbb{R}^{{n_{\text{d}}} \times N}} $ 的分解式为式中,
$ \bar {\boldsymbol{X}} = [{\boldsymbol{m}}, {\boldsymbol{m}}, \cdots , {\boldsymbol{m}}] \in {\mathbb{R}^{{n_{\text{d}}} \times N}} $ ,$ {\boldsymbol{\mu}} = {\text{diag}}\{ {\mu _1}, {\mu _2}, \cdots , {\mu _\upsilon }\} $ . 将$ {\boldsymbol{X}} $ 的采样点$ \tilde {\boldsymbol{X}} $ 代入(3)式, 得到$ {\boldsymbol{H}} $ 的采样点:将矩阵
$ {{\boldsymbol{\eta }}_{\text{d}}} $ 按列分块${{\boldsymbol{\eta }}_{\text{d}}} = \left[ {{\boldsymbol{\eta}} _1^{\text{d}},{\boldsymbol{ \eta}} _2^{\text{d}}, \cdots , {\boldsymbol{\eta}} _N^{\text{d}}} \right], \;{\boldsymbol{ \eta}} _i^{\text{d}} \in {\mathbb{R}^\upsilon }, i = 1, 2, \cdots , N$ , 经计算可得即(4)式生成的N个中心化、不相关样本点集
$\{ {\boldsymbol{\eta }}_1^{\text{d}},{\boldsymbol{ \eta}} _2^{\text{d}}, \cdots , {\boldsymbol{\eta}} _N^{\text{d}}\} $ .将
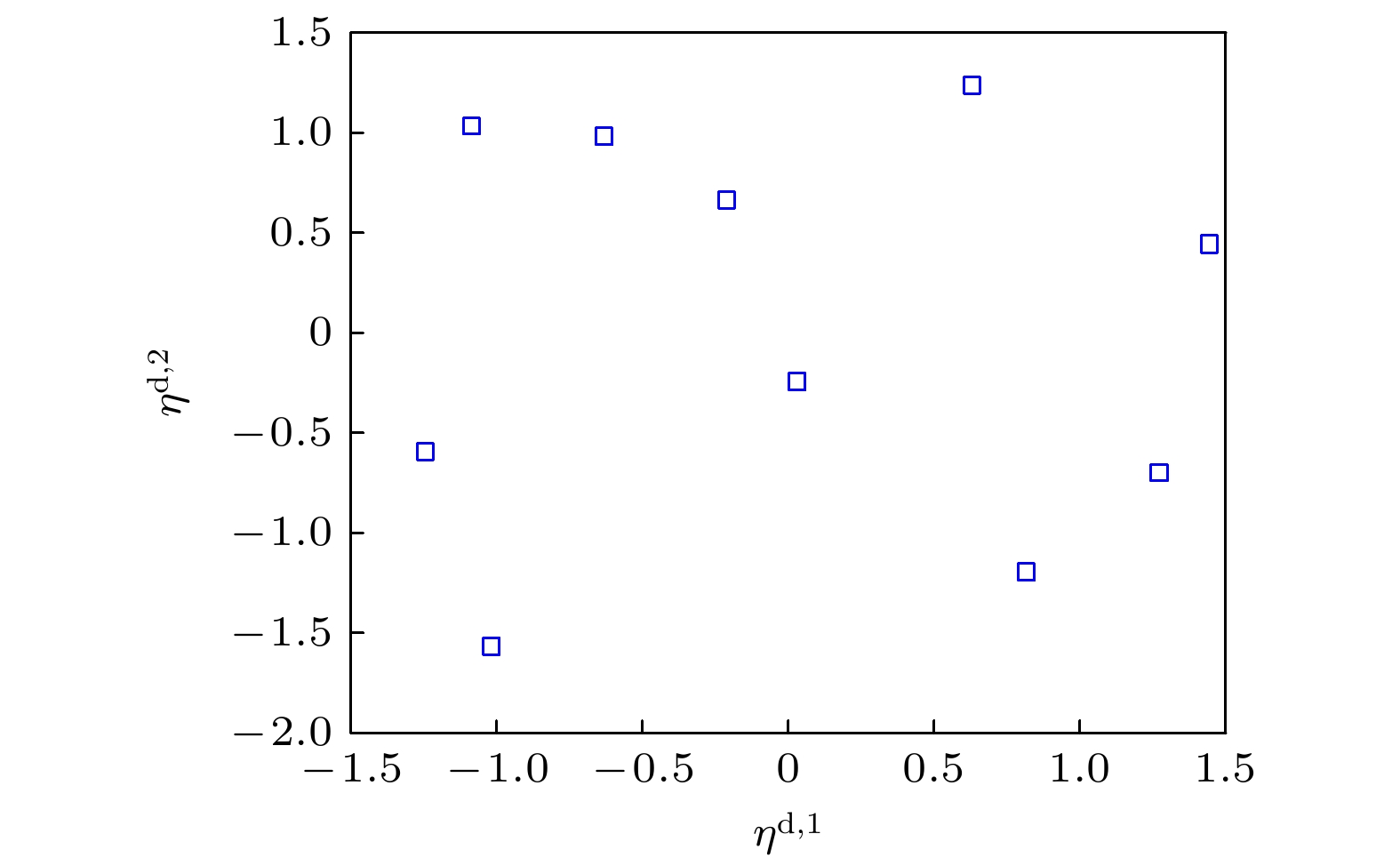
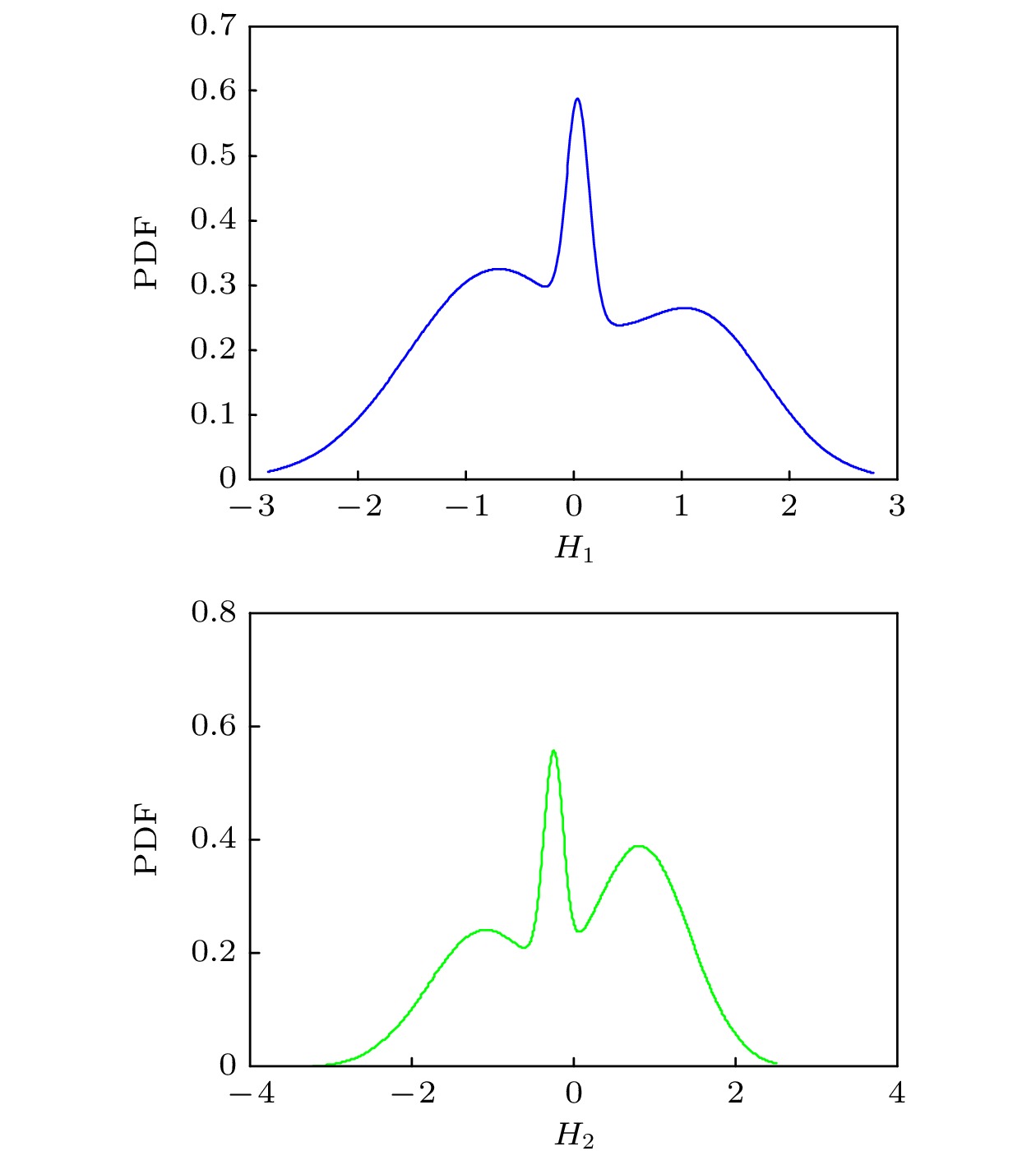
$ {\mathbb{R}^\upsilon } $ 值样本点$\{{\boldsymbol{ \eta }}_1^{\text{d}}, {\boldsymbol{\eta}} _2^{\text{d}}, \cdots ,{\boldsymbol{ \eta}} _N^{\text{d}}\} $ 作为训练集, 记做${\mathcal{D}_{{\text{train}}}} = \{ {\boldsymbol{\eta}} _1^{\text{d}},{\boldsymbol{ \eta}} _2^{\text{d}}, \cdots ,{\boldsymbol{ \eta}} _N^{\text{d}}\} $ .${\mathcal{D}_{{\text{train}}}}$ 具体信息如图4所示, 其中${{\boldsymbol{\eta}} ^{{{d}}, {1}}}$ 表示$ {{\boldsymbol{\eta}} _{\text{d}}} $ 的第1个分量,${{\boldsymbol{\eta}} ^{{{d}}, {2}}}$ 表示$ {{\boldsymbol{\eta}} _{\text{d}}} $ 的第2个分量.注1 PCA的主要目的是规范化, 而不是降维. 即将原始输入数据转化为期望为0, 协方差矩阵为单位矩阵的随机向量, 预处理后的矩阵有利于使用Gauss核密度估计.
-
Gauss核密度估计法结合训练集
${{\boldsymbol{\eta}} _{\text{d}}} = \{ {\boldsymbol{\eta}} _1^{\text{d}}, {\boldsymbol{\eta}} _2^{\text{d}}, \cdots , {\boldsymbol{\eta}} _N^{\text{d}}\} $ , 首先构造随机向量的概率模型如下:其中
$ \hat s = {s_{{\text{SB}}}}{\Big(s_{{\text{SB}}}^2 + \dfrac{{N - 1}}{N}\Big)^{ - 1/2}} $ ;$ \Vert \cdot\Vert $ 是$ {\mathbb{R}^\upsilon } $ 空间中的Euclid范数;$ {s_{{\text{SB}}}} $ 为Silverman带宽(bandwidth), 定义为$ {s_{{\text{SB}}}} = { \Big[ {\dfrac{4}{{N(2 + \upsilon )}}} \Big]^{1/(\upsilon + 4)}} $ . 由3.2节可知, 训练集${{\boldsymbol{\eta }}_{\text{d}}}$ 是中心化、不相关的矩阵, 且假设${{\boldsymbol{\eta}} _{\text{d}}}$ 的列向量相互独立, 因此(5)式构成随机向量Y的PDF. 我们假设训练集${\mathcal{D}_{{\text{train}}}}$ 是随机矩阵H的样本点, 进一步假设, 随机矩阵H的列向量相互独立, 则构成随机矩阵H的PDF. 由(5)式导出
$\mathbb{E}{\boldsymbol{H}} = {\boldsymbol{0}}, {{\mathrm{cov}}} ({\boldsymbol{H}}, {\boldsymbol{H}}) = {{\boldsymbol{I}}_\upsilon }$ ,$\mathbb{E}$ 和cov分别代表期望和协方差算子. -
定义耗散映射(diffusion map)矩阵K和B如下:
式中,
$ {b_i} = \displaystyle \sum\nolimits_{j = 1}^n {{k_{ij}}} $ ,$ {\delta _{ij}} $ 为Kronecker算子,$ {\varepsilon _{{\text{DM}}}} $ 为光滑参数. 将$ {\boldsymbol{P}} = {{\boldsymbol{B}}^{ - 1}}{\boldsymbol{K}} $ 定义为训练集${\mathcal{D}_{{\text{train}}}}$ 赋予的图(graph)上的对应随机游走(random walk)的转移矩阵, 用以产生单步转移概率.计算如下广义特征值问题
式中
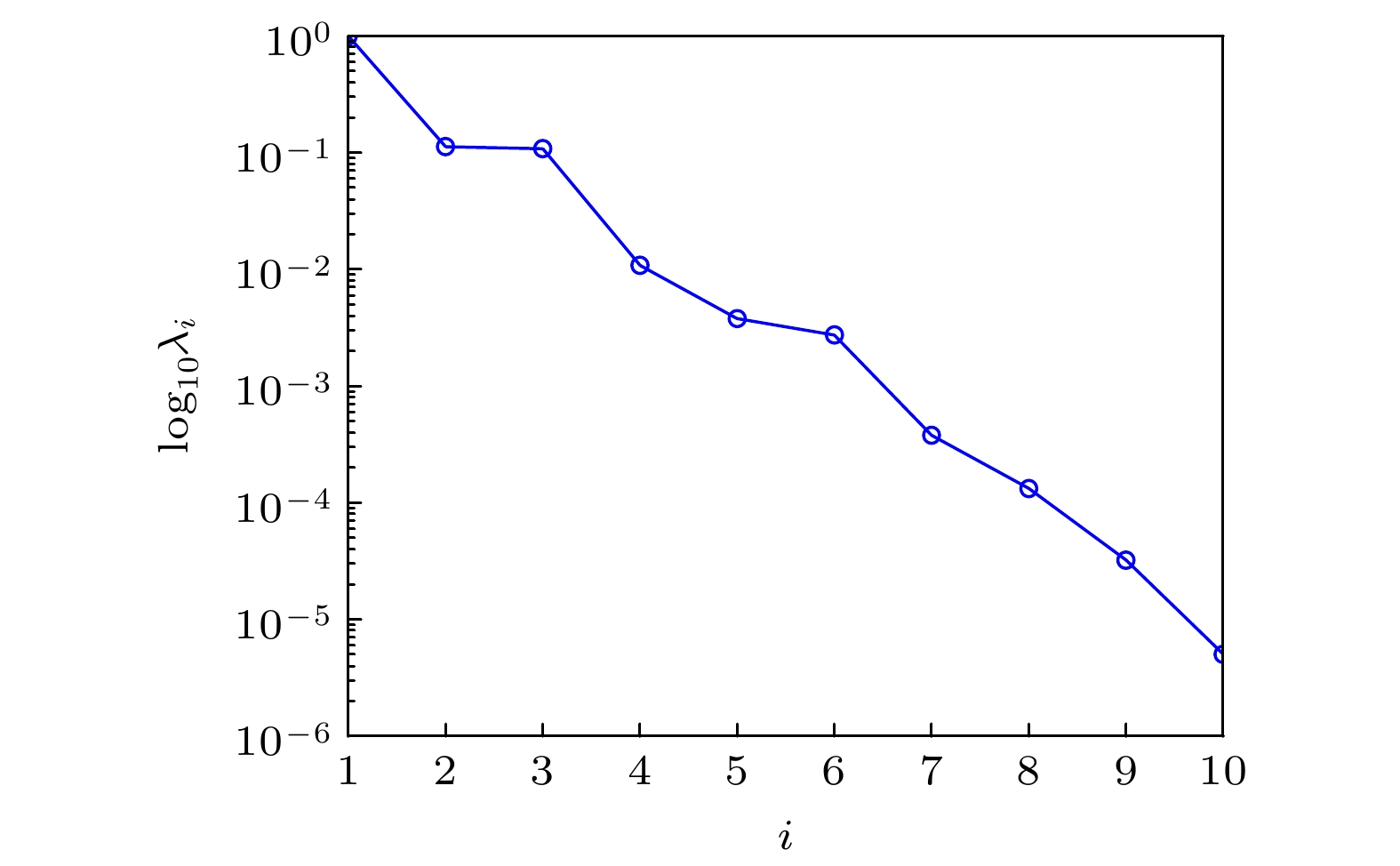
$ {\lambda _i}, {{\boldsymbol{\psi }}_i} $ 分别为满足正交化条件$ \left( {{\lambda _i}{\boldsymbol{B}}{{\boldsymbol{\psi}} _i}, {{\boldsymbol{\psi}} _j}} \right) = {\delta _{ij}}, \;i, j = 1, 2, \cdots , {n_{\text{d}}} $ 的特征值和相应的特征向量. 利用图4结果和(7)式, 计算在log10尺度下转移矩阵K的递减特征值, 结果如图5所示.构造
$ {\mathbb{R}^{{n_{\text{d}}}}} $ 空间中的耗散映射基函数$ \{ {{\boldsymbol{g}}_1}, {{\boldsymbol{g}}_2}, \cdots , {{\boldsymbol{g}}_{{n_{\text{d}}}}}\} $ 如下:降阶耗散基矩阵定义为
$ {\boldsymbol{G}} = [{{\boldsymbol{g}}_1}, {{\boldsymbol{g}}_2}, \cdots , {{\boldsymbol{g}}_m}], \; m \leqslant {n_{\text{d}}} $ , k代表转移概率的步数.注2 基矩阵依赖于
$ {\varepsilon _{{\text{DM}}}}, m $ , 而不是$ k $ , 本文选取$ k = 2 $ , 即使用两步转移概率.$ {\varepsilon _{{\text{DM}}}}, m $ 选取的标准是[38]:利用图5结果以及(7)式和(8) 式, 经计算本文中
$ {\varepsilon _{{\text{DM}}}} = 4, m = 3 $ . -
耗散映射向量生成
$ {\mathbb{R}^N} $ 中的一个子空间$ \mathcal{L}\{ {{\boldsymbol{g}}_1}, {{\boldsymbol{g}}{\boldsymbol{}}_2}, \cdots , {{\boldsymbol{g}}_m}\} $ , 通过使用投影法描述训练集${\mathcal{D}_{{\text{train}}}}$ 的局部结构. 具体而言, 给出训练矩阵的降阶表征如下:其中
$ {\boldsymbol{Z}} \in {\mathbb{R}^{\upsilon \times m}} $ , 用来生成学习集. 紧接着, 构造子空间$ \mathcal{L}\{ {{\boldsymbol{g}}_1}, {{\boldsymbol{g}}_2}, \cdots , {{\boldsymbol{g}}_m}\} $ 上的投影矩阵$ {\boldsymbol{A }}= {\boldsymbol{G}}{({{\boldsymbol{G}}^{\text{T}}}{\boldsymbol{G}})^{ - 1}} \in {\mathbb{R}^{N \times m}} $ , 进而得 -
PLoM-MCMC随机数生成器原理是将Itô随机微分方程投影到耗散映射基函数上, 即在3.4节定义的流形上采样. 设
$ {\boldsymbol{Z}}(t), {\boldsymbol{Y}}(t) \in {\mathbb{R}^{\upsilon \times N}} $ 是稳态耗散Markov过程, 表征如下:式中,
$ {\boldsymbol{Z}}(0) = {{\boldsymbol{H}}_{\text{d}}}{\boldsymbol{A}}, {\text{ }}{\boldsymbol{Y}}(0) = {\boldsymbol{KA}}, {\text{ }}{\boldsymbol{K}} \in {\mathbb{R}^{\upsilon \times N}} $ 的分量相互独立, 且服从标准正态分布, 即(11)式的初值来自于(12)式的采样.$ {\boldsymbol{W}} \in {\mathbb{R}^{\upsilon \times N}} $ 的列向量是相互独立的$ \upsilon $ 维标准Wiener过程, 并且$ \mathcal{L}({\boldsymbol{Z}}(t)) = L({\boldsymbol{Z}}(t){G^{\text{T}}}){\boldsymbol{A}} \in {\mathbb{R}^{\upsilon \times m}} $ , 泛函$ L({\boldsymbol{u}}) $ 定义为注3 随机耗散Hamilton系统(1)的解在概率意义下存在且唯一, 属于稳态、遍历的Markov过程, 不变测度为(5)式. 阻尼参数
$ {f_0} $ 以控制扩散项, 进而快速消除初值造成的瞬态振荡, 尽快到达稳态时刻, 本文选取$ {f_0} = 4 $ .等步长的Störmer-Verlet格式能有效求解Wiener过程驱动的耗散Hamilton系统(11), 此方法经Hairer等[39]改进后满足能量守恒, 格式如下:
其中
$ {\mathcal{L}_{i + {1}/{2}}} = \mathcal{L}({{\boldsymbol{{ Z}}}_{i + {1}/{2}}}) , b = {{{f_0}\Delta t}}/{4}, \;M = 30 , \Delta t = 0.238 $ 是系统(11)的离散步长.式中,
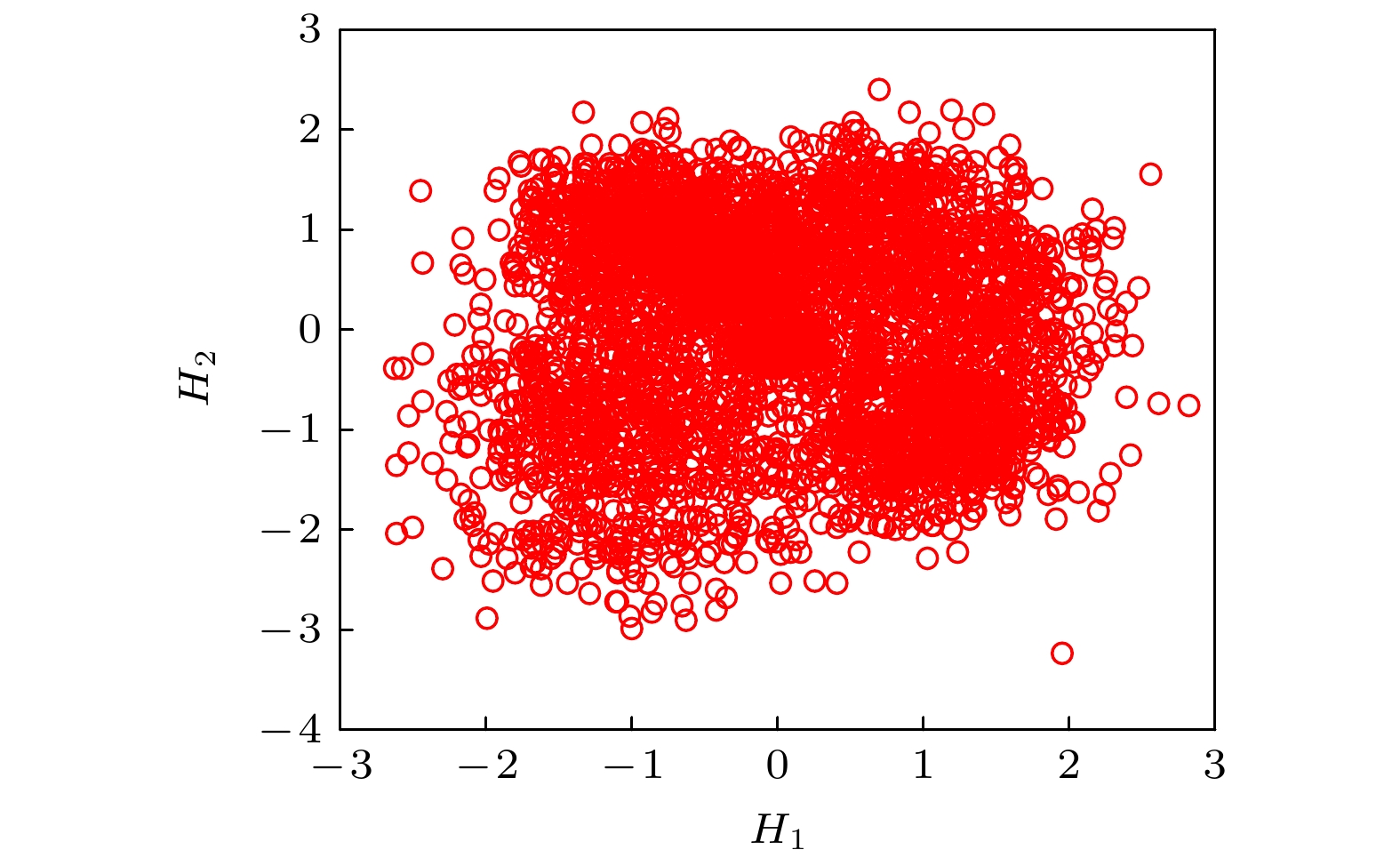
$ {M_0} = 18 $ .经计算得PLoM生成的4000个样本的学习集, 并给出H的前两个分量H1和H2的PDF, 具体结果见图6和图7.
注4 H是一个唯象中间变量, 是通过主成分分析导出的期望为0, 协方差矩阵为单位矩阵的随机向量, 即规范化随机变量. H没有物理意义, 仅仅为处理数据引入的唯象参数.
-
将图6中的样本点代入仿射变换(3), 最终生成QoI的采样点, 具体结果见图8. PLoM生成的电子实验数据样本足够丰富, 克服了实验数据的稀疏性, 是物理实验的有效替代方案. 将密度和爆速的所有采样点, 记作学习集
$ {\mathcal{D}_{{\text{learn}}}} = \{ ({\rho ^i}, {D^i}), \;i = 1, 2, \cdots , {N_{{\text{learn}}}} \} $ , 其中$ {N_{{\text{learn}}}} = 4000 $ . 从图8可以大致看出密度和爆速满足线性关系. -
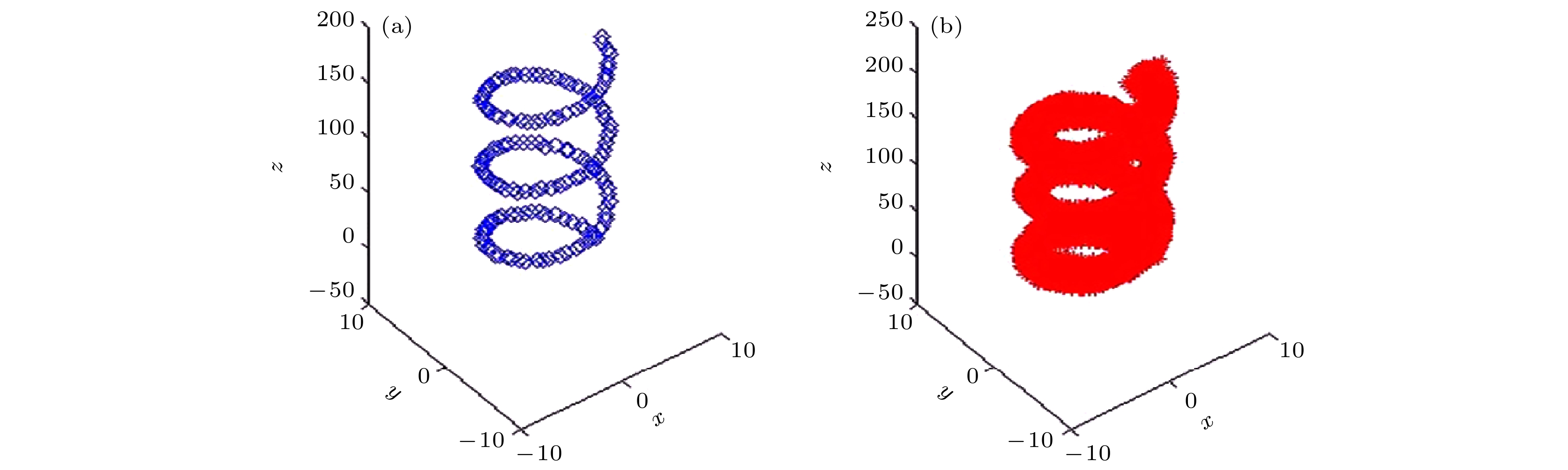
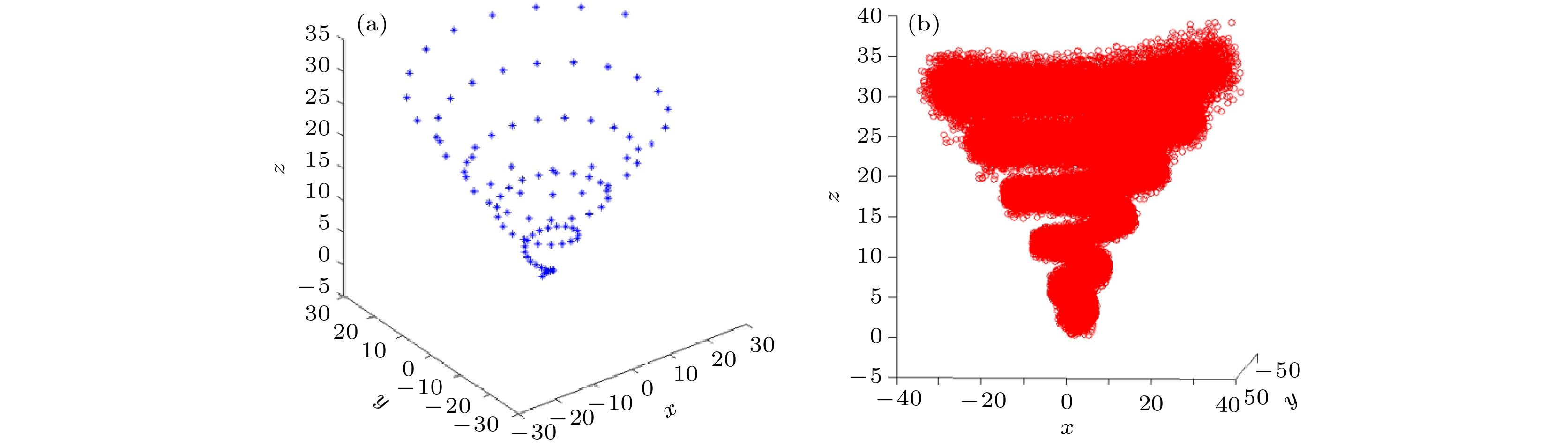
假设N个数据沿圆柱螺旋曲线施加Gauss振荡, 样本容量N = 150, 具体结果见图10(a). 必须指出, 我们事先并不知道数据的采样方法. 使用PLoM方法生成750000个样本, 具体结果见图10(b). 由图10可知, 生成的样本仍然集中在
$ {\mathbb{R}^3} $ 中的有界流形, 即螺旋曲线上, 而不是弥漫在整个$ {\mathbb{R}^3} $ 空间. 这说明PLoM方法能够保持和再现数据的几何结构, 验证了PLoM方法在数据扩容方面的有效性.为进一步验证PLoM方法的有效性, 对圆锥螺旋曲线施加Gauss噪声扰动, 得到100个数据, 具体结果见图11(a). 然后, 使用PLoM方法生成100000个样本, 具体结果见图11(b). 由图11可知, 生成的样本仍然集中在
$ {\mathbb{R}^3} $ 中对数螺旋曲线上. 这进一步说明了PLoM方法能够保持和再现数据的几何结构的能力. -
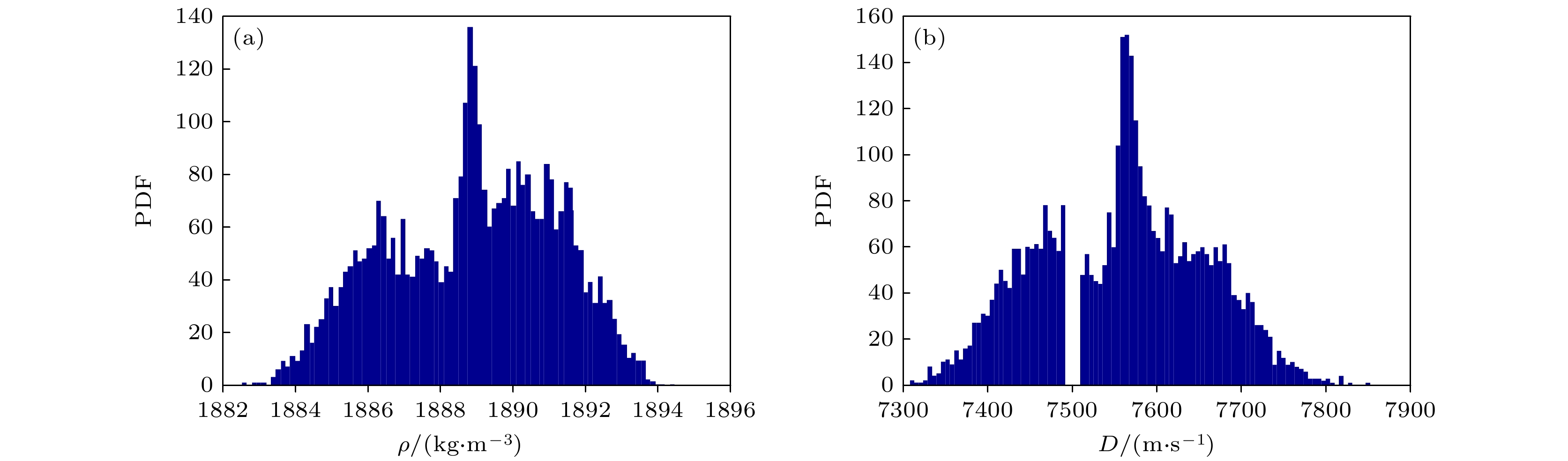
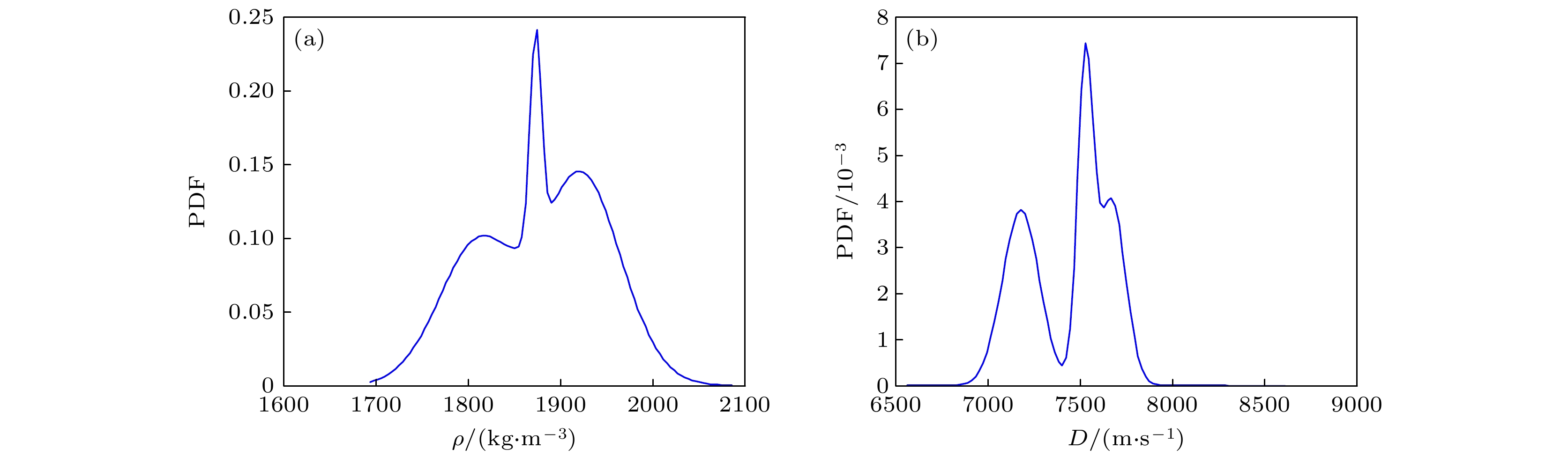
根据图8导出PBX-9502初始密度和爆速的统计直方图, 如图12所示. 当物理量样本足够丰富时, 可以使用非参数统计方法, 导出物理量的随机模型. 本文使用最大熵信息方法MaxEnt (maximum entropy information)[40,41], 导出密度和爆速的PDF, 具体结果见图13. 由图13可以看出, 密度和爆速的PDF属于一种非Gauss分布, 具有多峰态特征. 实验数据, 特别是爆速, 没有集中在某个特殊值附近. 这与实验操作时, 药柱直径取值范围较大有关.
进一步导出PBX9502的密度的期望值为1889 kg/m3和标准差为2.4 kg/m3, 变异系数为
$\dfrac{{2.4 {\text{ kg/}}{{\text{m}}^3}}}{{1889 {\text{ kg/}}{{\text{m}}^3}}} \times 100{\text{%}} = 0.13{\text{%}} $ , 95%置信区间为$[1885, 1893] {\text{ kg/}}{{\text{m}}^3}$ . 洛斯阿拉莫斯国家实验室(Los Alamos National Laboratory, LANL)国家实验室Campbel[34]标定的PBX9502的密度取值范围为(1890±5) kg/m3. 比较发现,$[1885, 1893] {\text{ kg/}}{{\text{m}}^3} \subset [1885, 1895] {\text{ kg/}}{{\text{m}}^3}$ . 因此, PLoM给出了一种密度标定方法, 且结果是可信的, PLoM生成的密度随机样本能满足工业生产和高精度仿真的要求. 与LANL的结果相比, PLoM生成的置信区间收窄了密度的标定范围. 进一步确认了PLoM生成的样本的实用性和有效性.利用矩估计法还导出爆速的期望值为7547 m/s和标准差为91 m/s, 95%置信区间为
$[7379, 7717] {\text{ m/s}}$ , 包含孙承纬院士的标定结果$7710 {\text{ m/s}}$ [1]. 这说明爆速的随机生成数也可应用于工业生产和高精度数值模拟. 同时计算得爆速的变异系数$\dfrac{{91 {\text{ m/s}}}}{{7547 {\text{ m/s}}}} \times 100{\text{%}} = 1.21{\text{%}} > 0.13{\text{%}} $ , 爆速的变异系数比密度的变异系数高一个量级, 即爆速比密度的离散程度更大. -
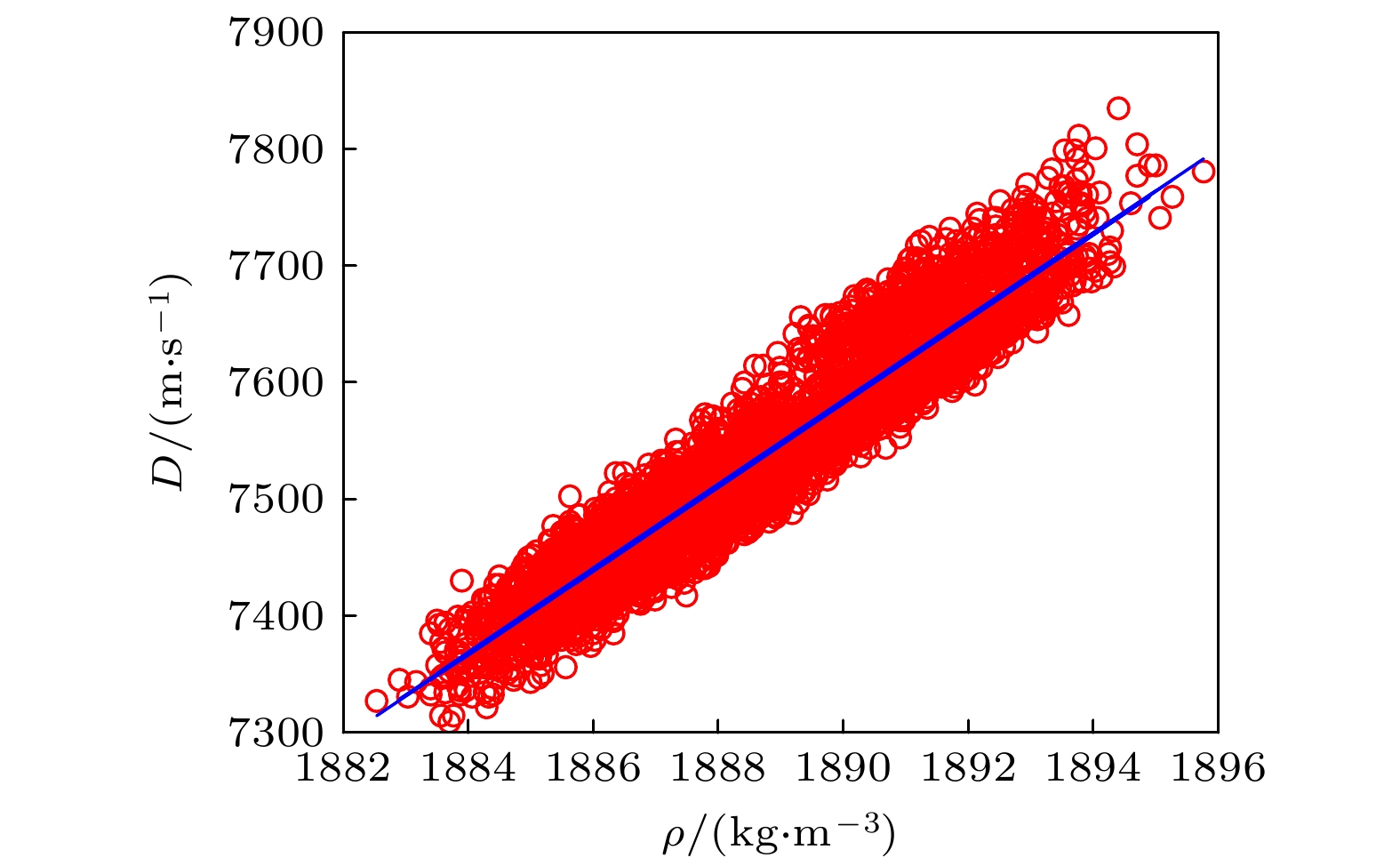
利用图8结果, 根据最小二乘法, 导出密度和爆速服从仿射关系:
其中
${\varpi _0} = 36.34, {\varpi _1} = 61119$ , 拟合曲线见图14. 从图14可以看出, PLoM生成的随机数集中在$ {\mathbb{R}^2} $ 线性有界区域. 也就是说, 在一定范围内, 爆速和密度满足线性关系, 爆速伴随着密度的增加而增加, 进一步确认了孙承纬院士的论断——“爆速和密度服从线性关系, 装药密度对爆速有极大影响”[1].进而根据(14)式导出变化率:
这意味着密度的微小变化, 能引发爆速一个量级以上的振荡, 即爆速的不确定度更大. 这与事实相符, 因为测试爆速的设备更加精密, 实验流程更加复杂[1]. 这说明了实验设计时, 保证PBX9502压制密度的精度的重要性. 压制流程不合格的PBX9502会产生灾难性的、无法预测的后果.
-
按照Chapman-Jouguet理论, 激波两侧物理量满足动量守恒定律, 即:
假设波前速度
$ {u_0} = 0 $ . 另一方面, 爆轰过程中${P_0} \ll P$ , 从而假设${P_0} = 0$ , (16)式简化为另一方面, 根据Hugoniot关系, 波后粒子速度
${u_{\text{p}}}$ 和爆速D存在线性关系:本文利用LANL实验室Gustavsen团队标定的参数[42], Hugoniot斜率
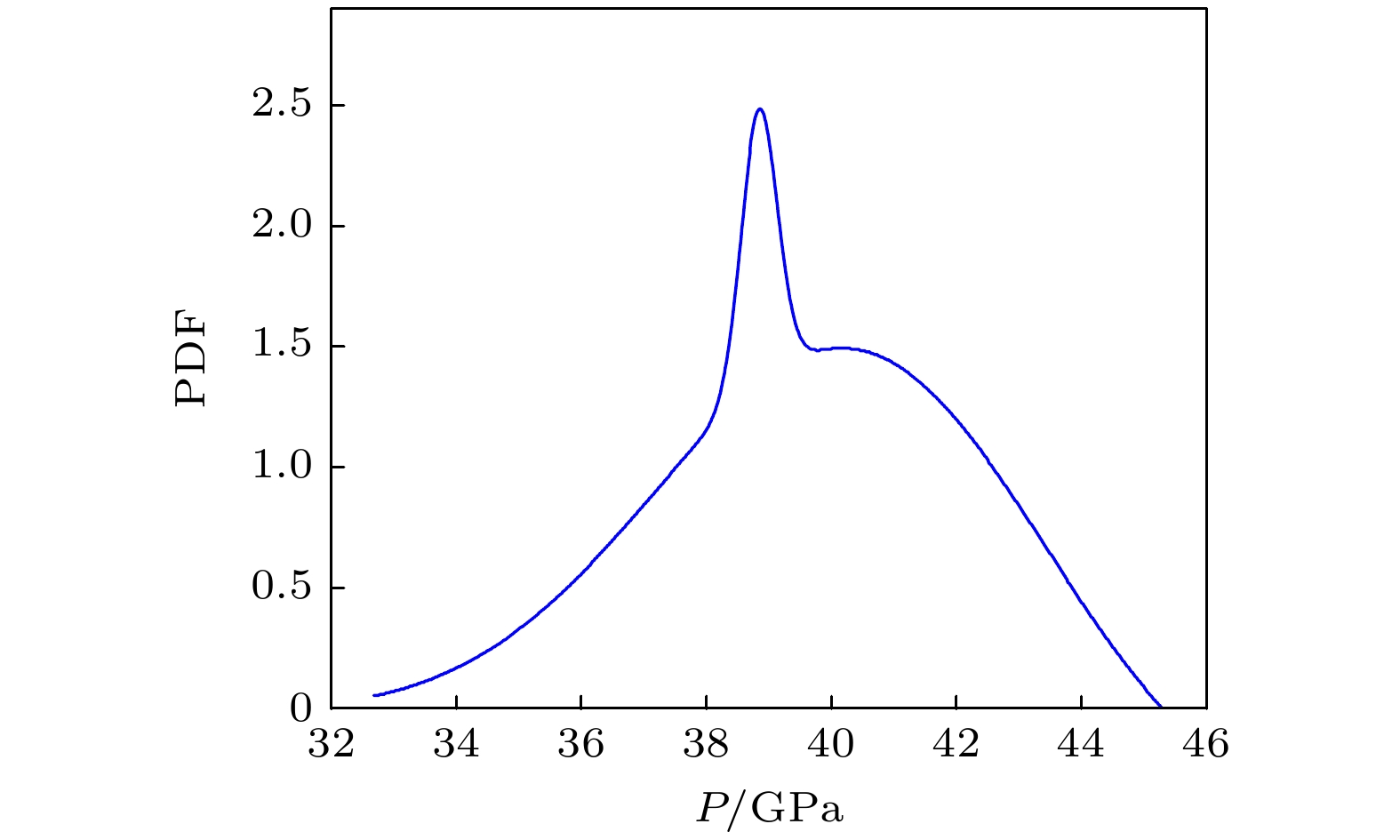
$\lambda = 1.81$ , 体积声速${c_0} = 2970 {\text{ m/s}}$ . 利用4.2.1节标定的、图13中的爆速和密度的PDF, 结合图8结果, 利用核密度估计方法得到爆压P的PDF如图15所示. 经计算得到爆压期望值为36.07 GPa, 标准差为1.61 GPa.利用图15结果, 计算得爆压的变异系数
$\dfrac{{1.61 {\text{ GPa}}}}{{36.07 {\text{ GPa}}}} \times 100{\text{%}} = 4.46{\text{%}} $ , 远大于4.2.1节爆速和密度的变异系数. 比较密度、爆速、爆压的变异系数, 研究发现密度的变异系数最小, 爆压最大, 且比密度的变异系数高一个量级. 研究结果支持孙承纬院士“爆压的离散程度较高”的论断[1].此时,
${a_3} \;= \;{{\varpi _0^2}}/{\lambda }, \;{a_2}\; =\; - 2\dfrac{{{\varpi _1}{\varpi _0}}}{\lambda } - \dfrac{{{c_0}{\varpi _0}}}{\lambda }, \;{a_1}\; = \dfrac{{{\varpi _1}{\varpi _0} + \varpi _1^2}}{\lambda }$ . (20)式表明, 爆压和密度服从非线性函数关系. 众所周知, 爆压测量的实验流程复杂, 成本较大, (20)式恰好为爆压代理模型, 为爆压标定提供了一种新的经济快捷的途径.由(20)式计算得:
$\dfrac{{{\text{d}}P}}{{{\text{d}}{\rho _0}}} = 3{a_3}\rho _0^2 + 2{a_2}{\rho _0} + {a_1}$ , 这说明PBX9502初始密度的微小变化, 能引起爆压的较大振荡, 且密度的变化对爆压的影响比爆速更大. 确认了爆压标定实验流程中, 保证炸药密度压制精度的重要性. -
PLoM方法本质上属于机器学习, 该方法将基于几何耗散的流形嵌入和Itô-MCMC结合, 实现了实验数据集的有效扩容, 丰富了样本信息. 首先将具有nd个物理属性的N个样本点当作某个随机矩阵的抽样, 用Xd表征. 再将高维小样本实验数据做缩比处理. 接着利用PCA将缩比矩阵进一步规范化, 得到训练集
$ {{\boldsymbol{\eta}} _{\text{d}}} $ . 然后, 利用容量有限的训练集和Gauss核密度估计法构造随机向量的先验PDF, 接着利用训练集$ {{\boldsymbol{\eta}} _{\text{d}}} $ 构造基于耗散映射和相应的流形以及投影矩阵. 另一方面, MCMC随机数生成器是基于Wiener过程驱动的耗散Hamilton系统, 其初值为规范化样本点构成的数据矩阵. 将Itô-MCMC抽样限制在耗散映射定义的流形上, 得到学习集. 最后使用反演变换生成密度和爆速的电子实验数据.使用的关键技术还包括: 第一, 基于训练集和几何耗散方法, 构造耗散基函数. 耗散基函数能发掘和刻画数据结构的几何特征, 探索样本聚集的流形. 第二, Itô-MCMC的不变测度与训练集的Gauss核密度估计密切相关, 结合流形嵌入方法, 将采样限制在流形上. 生成的样本, 不仅自身的概率分布符合实际, 而且保留了相关物理量的物理信息和几何结构. 第三, 使用Störmer-Verlet格式计算Wiener过程驱动的耗散Hamilton系统, 该算法易于实现并行计算, 进而急剧减少了多核计算机上的程序运行时间. 还能快速摆脱瞬态振荡, 快速到达指定不变测度的稳态响应. 最后, 通过验证算例还发现, PLoM方法受到噪声影响时, 具有抗干扰强的特点.
将PLoM生成的随机数进行统计后处理, 能得到密度和爆速的统计信息, 密度的95%置信区间包含于LANL实验室标定的取值范围. 爆速的95%置信区间包含孙承纬院士标定的数据. 说明PLoM生成的密度和爆速的随机数符合工业生产和高精度仿真的要求, 实现了稀疏实验数据的有效扩容. 增加电子实验数据后, 还导出更丰富物理信息. 与增加物理实验次数的策略相比较, 安全性高, 标定成本可以忽略不计. 研究发现, 生成的电子实验数据保持了PBX9502的密度和爆速的仿射关系. 进一步导出, 密度和爆压之间具有非线性函数关系. 结果表明, 初始密度的微小的变化, 能引起爆速和爆压的巨大振荡. 确认了爆速和爆压标定实验流程中, 保证炸药密度压制精度的重要性.
PLoM理论实际上也是一种很好的降维工具, 期间经过了两次降维, 第1次是PCA降维, 第2次是耗散映射降维. 更复杂系统的降维是我们下一步的研究目标.
基于流形上概率学习的爆轰不确定度分析
Uncertainty analysis of detonation based on probability learning on manifold
-
摘要: 爆轰实验由于操作风险高、样品制备和测试成本大等特征, 导致实验样本稀疏, 给标定待测物理量的概率分布和使用机器学习方法带来巨大的挑战. 流形上的概率学习(probability learning on manifold, PLoM)能生成丰富的、符合实用常识的、遵循实验数据物理机理的样本, 成为处理小样本的有效工具. 首先将炸药PBX9502的含有多物理属性实验数据做缩比变换, 然后, 使用主成分分析将缩比数据规范化, 并将规范化矩阵的分量作为训练集. 进而, 使用改进的多元Gauss核密度估计法表征训练集的先验概率. 紧接着利用耗散映射提炼基于训练集的非线性流形. 具体而言, 通过转移矩阵的第一个特征值和对应的特征向量构造耗散基函数和耗散映射. 其次, 将训练集作为Wiener过程驱动的Hamilton系统的初值, 先验概率作为不变测度构造Itô-MCMC随机数生成器, Störmer-Verlet格式用以求解随机耗散Hamilton方程. 最后, 采用反演变换, 实现学习集的扩容. 结果发现, PLoM能生成符合工业生产和高精度模拟需求的密度和爆速的随机数. 利用学习集导出炸药的密度和爆速服从仿射变换, 密度和爆压服从非线性关系, 密度的微小波动会引起爆速和爆压的剧烈的变化. 比较学习集的变异系数, 还发现爆压离散程度最高, 与已有研究结果相符. 所用方法具备普适性, 能推广到其他的爆轰系统.Abstract: Detonation test is affected by small experimental datasets due to high risk of implementation and the huge cost of sample production and measurement. The major challenges of limited data consist in constructing the probability distribution of physical quantities and application of machine learning. Probability learning on manifold (PLoM) can generate a large number of implementations that are consistent with practical common knowledge, while preserving potential physical mechanism these generated samples. So PLoM is viewed as an efficient tool of tackling small samples. To begin with, experimental data are assumed to be concentrated on an unknown subset of Euclidean space and can be treated as the sampling of random vector to be determined. Meanwhile, experimental problem is solved in the framework of matrix and the scaling transformation is conducted on the datasets of PBX9502 with multi-physics attributes. Then the principal component analysis is utilized to normalize the scaling matrix, and the normalization matrix is labeled as training sets. Moreover, the altered multi-dimensional Gaussian kernel density estimation is utilized for estimating the probability distribution of training set. Furthermore, diffusion map is used to discover and characterize the geometry and structure of dataset. In other words, nonlinear manifold based on the training set is constructed through diffusion map. Specifically, the first eigenvalue and corresponding eigenvector is related to the construction of diffusion basis and diffusion maps. Further, Itô-MCMC sampler is associated with dissipative Hamilton system driven by Wiener process, for which the initial condition is set to be training set, and prior probability is conceived as invariant measure. Störmer-Verlet scheme is used for solving the stochastic dissipative Hamilton equations. Finally, additional realizations of learning dataset are fulfilled through the inversion transformation. The result shows that random number generated from PLoM satisfies the requirements of industrial and high fidelity simulation. The 95% confidence interval of density is included in the range calibrated by Los Alamos National Laboratory. And the value of detonation velocity calibrated by Prof. Chengwei Sun [Sun C W, Wei Y Z, Zhou Z K 2000 Applied Detonation Physics (Beijing: National Defense Industry Press) p224] also falls into 95% confidence interval of detonation velocity generated by PLoM. It is also deduced from the learning set that density and detonation velocity satisfies the affine transformation. Furthermore, detonation pressure has nonlinear relationship with density. Tiny variation of density can lead to magnificent fluctuation of detonation pressure and detonation velocity. Detonation pressure has the largest discreetness in all the physical quantities through the comparison of variation coefficients of learning set, which coincides with the existing research results. The method used is universal enough and can be extended to other detonation systems.
-

-
-
[1] 孙承纬, 卫玉章, 周之奎 2000 应用爆轰物理 (北京: 国防工业出版社) Sun C W, Wei Y Z, Zhou Z K 2000 Applied Detonation Physics (Beijing: National Defense Industry Press [2] Mader C 1979 Numerical Modeling of Detonations (Berkeley: University of California [3] 梁霄, 王瑞利, 胡星志, 陈江涛 2023 爆炸与冲击 43 71 doi: 10.11883/bzycj-2023-0030 Liang X, Wang R L, Hu Z X, Chen J T 2023 Explos. Shock. Waves. 43 71 doi: 10.11883/bzycj-2023-0030 [4] 梁霄, 王瑞利 2024 兵工学报 45 1673 doi: 10.12382/bgxb.2022.1207 Liang X, Wang R L 2024 Acta. Arma. 45 1673 doi: 10.12382/bgxb.2022.1207 [5] Liang X, Wang R L 2020 Int. J. Uncertainty. Quantif. 10 83 doi: 10.1615/Int.J.UncertaintyQuantification.2020030630 [6] Bratton R N, Avramova M, Ivanov K 2014 Nucl. Eng. Technol. 46 313 doi: 10.5516/NET.01.2014.710 [7] Cartwright K, Pointon T, Oliver B V, Swanekamp S B, Hinshelwood D, Angus J R, Richardson A S, Mosher D 2016 Direct Electron-beam-injection Experiments for Validation of Air-chemistry Models (New Mexico: Sandia National Laboratories) SAND2016-2437C [8] Los Alamos National Laboratory 2022 Advanced Simulation and Computing Simulation Strategy Report LA-UR-22-25074 [9] 胡泽华, 叶涛, 刘雄国, 王佳 2017 物理学报 66 012801 doi: 10.7498/aps.66.012801 Hu Z H, Ye T, Liu X G, Wang J 2017 Acta. Phys. Sin. 66 012801 doi: 10.7498/aps.66.012801 [10] AIAA 1998 Guide for the Verification and Validation of Computational Fluid Dynamics Simulations (AIAA G-077-1998 [11] Clark M A, Kearns K, Overholt J L, Gross K H, Barthelemy B, Reed C 2014 Air Force Research Laboratory Test and Evaluation, Verification and Validation of Autonomous Systems Challenge Exploration Final Report Case Number 88ABW-2014-4063 [12] Hu X Z, Duan Y H, Wang R L, Liang X, Chen J T 2019 J. Verif. Valid. Uncert. 4 021006 doi: 10.1115/1.4045200 [13] 张诗琪, 杨化通 2023 物理学报 72 110303 doi: 10.7498/aps.72.20222443 Zhang S Q, Yang H T 2023 Acta. Phys. Sin. 72 110303 doi: 10.7498/aps.72.20222443 [14] Wishart J, Como S, Forgione U, Weast J, Weston L, Smart A, Nicols G, Ramesh S 2020 SAE Int. J. CAV 3 267 doi: 10.4271/12-03-04-0020 [15] Department of Energy’s NNSA 2005 Holistic, Hierarchical VVUQ as the Scientific Method for PSAAP Report LA-UR-23-32192 [16] Department of Defense 2019 Modeling and Simulation (M&S) Verification, Validation, and Accreditation (VV&A) Recommended Practices Guide (RPG) Core Document: Introduction [17] Dahm W 2010 Technology Horizons a Vision for Air Force Science & Technology During 2010-2030 Report AF/ST-TR-10-01-PR [18] Balci O 1994 Ann. Oper. Res. 53 121 doi: 10.1007/BF02136828 [19] Metzger E J, Barton N P, Smedstad O M, Ruston B C, Wallcraft A J, Whitcomb T R, Ridout J A, Franklin D S, Zamudio L, Posey P G, Reynolds C A, Phelps M 2016 Verification and Validation of a Navy ESPC Hindcast with Loosely Coupled data Assimilation American Geophysical Union A41G-0130 [20] American Society of Mechanical Engineers 2022 Verification, Validation, and Uncertainty Quantification Terminology in Computational Modeling and Simulation ASME VVUQ 1-2022 [21] Oberkampf W, Roy C 2010 Verification and Validation in Scientific Computing (Cambridge: Cambridge University Press [22] Liang X, Wang R L 2019 Def. Technol. 15 398 doi: 10.1016/j.dt.2018.11.005 [23] 王言金, 张树道, 李华, 周海兵 2016 物理学报 65 106401 doi: 10.7498/aps.65.106401 Wang Y J, Zhang S D, Li H, Zhou H B 2016 Acta. Phys. Sin. 65 106401 doi: 10.7498/aps.65.106401 [24] Park C, Nili S, Mathew J T, Ouellet F, Koneru R, Kim N, Balachandar S, Haftka R 2021 J. Verif. Valid. Uncert. 6 119007 doi: 10.1115/1.4051407 [25] 梁霄, 王瑞利 2017 物理学报 66 116401 doi: 10.7498/aps.66.116401 Liang X, Wang R L 2017 Acta. Phys. Sin. 66 116401 doi: 10.7498/aps.66.116401 [26] Soize C, Ghanem R 2016 J. Comput. Phys. 321 242 doi: 10.1016/j.jcp.2016.05.044 [27] Ghanem R, Soize C, Safta C, Huan X, Lacaze G, Oefelein J C, Najm H N 2019 J. Comput. Phys. 399 108930 doi: 10.1016/j.jcp.2019.108930 [28] Capiez-Lernout E, Ezvan O, Soize C 2024 J. Comput. Inf. Sci. Eng. 24 061006 doi: 10.1115/1.4065312 [29] Nespoulous J, Perrin G, Funfschilling C, Soize C 2024 Physics D 457 133977 doi: 10.1016/j.physd.2023.133977 [30] Capiez-Lernout E, Soize C 2022 Int. J. Non. Linear. Mech. 143 104023 doi: 10.1016/j.ijnonlinmec.2022.104023 [31] Metropolis N, Ulam S 1949 J. Am. Stat. Assoc. 44 335 doi: 10.1080/01621459.1949.10483310 [32] Hastings W 1970 Biometrika 109 57 doi: 10.1093/biomet/57.1.97 [33] Geman S, Geman D 1984 IEEE Trans. Pattern. Anal. Mach. Intell. 6 721 doi: 10.1109/TPAMI.1984.4767596 [34] Campbell A 1984 Pyrotechnics 9 183 doi: 10.1002/prep.19840090602 [35] Peterson P, Idar D 2005 Propell. Explos. Pyrot. 30 88 doi: 10.1002/prep.200400088 [36] Davis W C, Hill L G 2002 12th International Symposium Detonation San Diego, USA, August 11–16, 2002 p220 [37] Handley C, Lambourn B, Whitworth N, James H, Belfield W 2018 Appl. Phys. Rev. 5 011303 doi: 10.1063/1.5005997 [38] Coifman R, Lafon S, Lee A, Maggioni M, Nadler B, Warner F 2005 Proc. Natl. Acad. Sci. USA 102 7426 doi: 10.1073/pnas.0500334102 [39] Hairer E, Lubich C, Wanner G 2002 Geometric Numerical Integration Structure-Preserving Algorithms for Ordinary Differential Equations (Heidelberg: Springer-Verlag [40] Soize C 2008 Int. J. Numer. Methods Eng. 76 1583 doi: 10.1002/nme.2385 [41] Shannon C 1948 Bell. Syst. Tech. J. 27 623 doi: 10.1002/j.1538-7305.1948.tb00917.x [42] Gustavsen R, Sheffield S, Alcon R 2006 J. Appl. Phys. 99 114907 doi: 10.1063/1.2195191 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: