首页
登录
注册
下载:
-
大气扰动流场是指飞行器高速飞行过程中, 由于其几何和气动外形对大气介质的阻碍作用导致空气宏观运动, 从而引发大气密度异常分布的一种空气动力学现象. 作为伴随飞行器出现的固有产物, 飞行器大气扰动流场因流场内强烈的翻转气流对航空安全构成重大威胁而备受关注[1–4]. 因此人们利用电磁波技术对扰动流场进行了观测, 并逐渐形成了有效的探测手段[5]. 考虑到飞行器扰动流场的特征难以遮蔽, 且影响范围超过自身尺寸, 可基于扰动流场的探测来间接感知飞行器存在, 并有望发展成为一种新型的空中探测手段[6].
飞行器的尾涡气流是一种可探测特征, 利用多普勒效应测风技术, 通过频谱分析解算涡流的风场径向速度分布得到尾涡环量等信息[7–10]. 目前公开报道中飞行器尾流探测实验的最远探测距离为15 km[11]. 鉴于目前多类飞行器具有超声速飞行能力, 而激波-膨胀波系会产生高梯度密度跃变, 可能为光学探测提供更强的物理特异性. 例如背景纹影技术(BOS), 源于风洞实验中常用的纹影摄影技术, 利用激波产生空气介质折射率的非均匀分布, 从而使物体成像发生空间畸变的原理, 通过对比原始背景图像与畸变图像的差异来反演折射率的变化信息[12–14]. 美国宇航局(NASA)利用该技术, 以地面上稀疏沙漠植被形成的随机斑点为背景, 通过高速高分辨成像系统, 对超声速飞行器形成的激波纹影进行了清晰成像[15,16]. 实验说明了利用光学手段探测超声速飞机激波膨胀波具有可行性. 但该技术对成像背景有一定要求, 探测视场较小, 以及借助自然光无法在夜间工作等限制, 仍需要进一步突破.
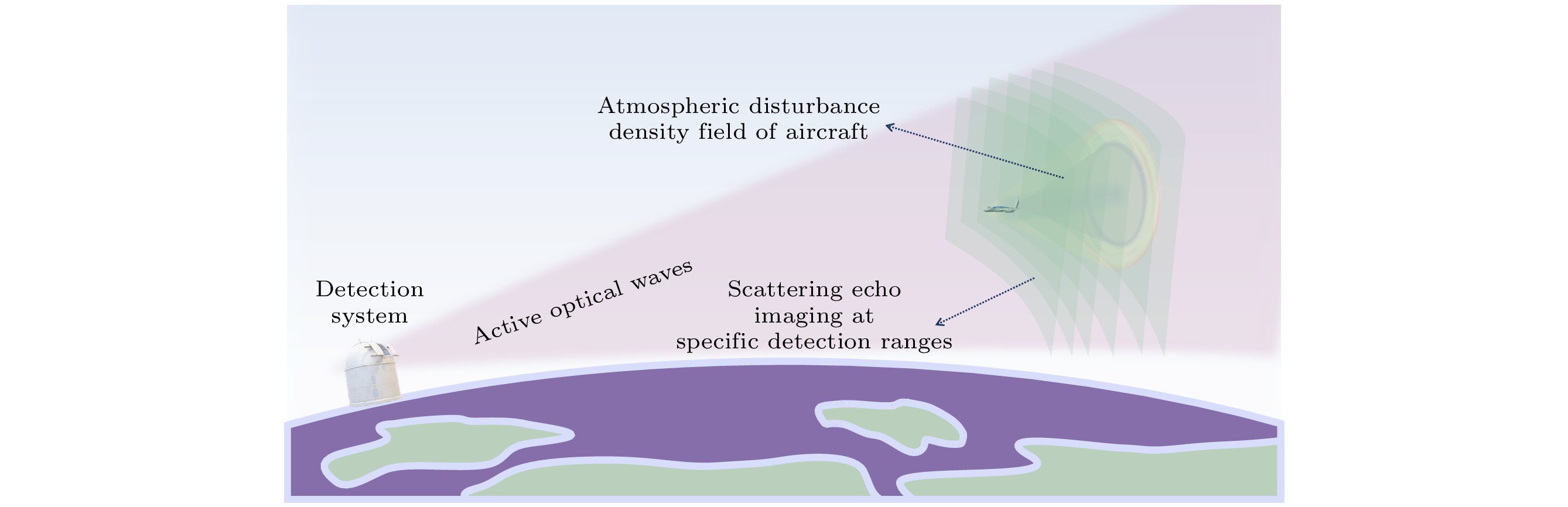
超声速飞行器形成的激波膨胀波使得流场区域内空气密度的空间分布具有显著特征. 若利用主动光源照射飞行器扰动流场区域, 鉴于大气介质密度与光散射强度之间的正相关关系, 理论上可以通过探测扰动区域的光散射强度信号, 描绘出密度分布情况, 从而提取飞行器引起的大气扰动密度场特征. 本文提出基于大气扰动密度场的飞行器探测模型构想, 基于飞行器大范围扰动流场的物理建模, 分析了流场内空气密度的分布特征, 设计了一种基于主动光源的三维层析成像探测模式. 在考虑短曝光条件下激光的二次散射作用和大气调制影响的前提下, 针对性地构建了大气扰动密度场光散射回波信号成像仿真模型. 模拟得到了不同探测位置、不同系统参数下的仿真图像. 该模型为探测系统的参数设置提供了分析工具, 并为进一步分析信号特征及发展相关探测技术奠定了基础.
-
为了分析飞行器大气扰动密度场的主要可测特征, 首先需要对扰动区域的密度分布进行建模. 由于传统的流体计算商业软件如Fluent, CFX, Phoenics等在大范围离体流场的计算较为困难, 所以采用中国科学院力学研究所自主研发的高精度数值模拟仿真软件OpenCFD-EC构建飞行器大范围离体流场空间分布模型[17–20].
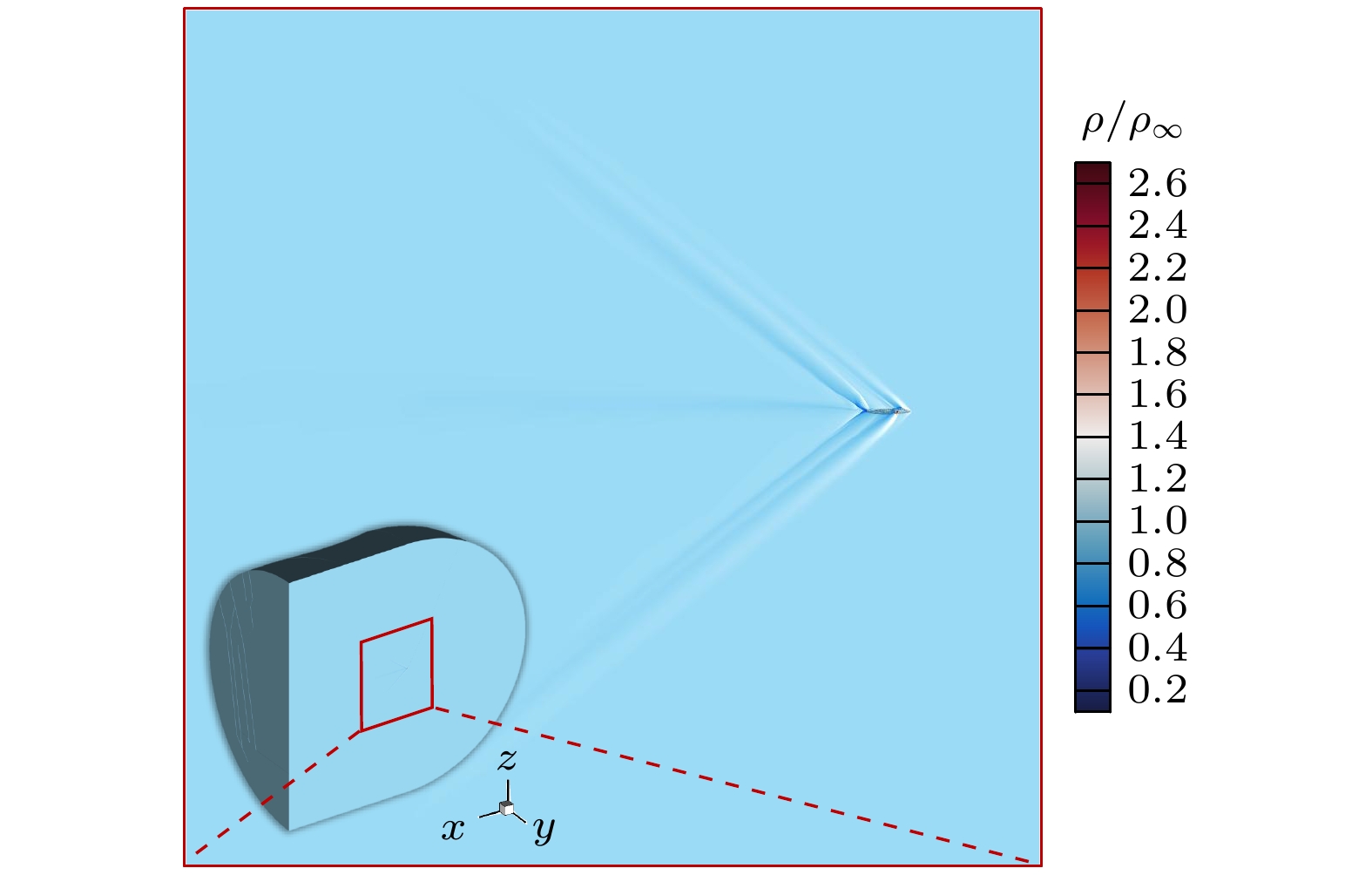
模型设置为纵向切割的半机身设计, 长度约为20 m, 翼展/机身比约为70%. 测试飞行环境为高度10 km, 巡航速度1.5Ma设置三维仿真计算条件如下: 来流速度为1.5Ma, 单位来流雷诺数Re∞/m = 1.36×104, 来流攻角为0°, 来流温度为223 K, 壁面设置为绝热壁, 流场计算区域为2 km×1 km×2 km, 计算最小网格尺寸约为2×10–4 m. 得到大气扰动密度三维云图如图1, 并以飞机尾部离体位置为原点, 飞行方向为x轴, 翼展方向为y轴, 垂直方向为z轴建立坐标系, 其中密度点云数值表示密度和背景大气的比值, ρ∞是大气背景密度.
-
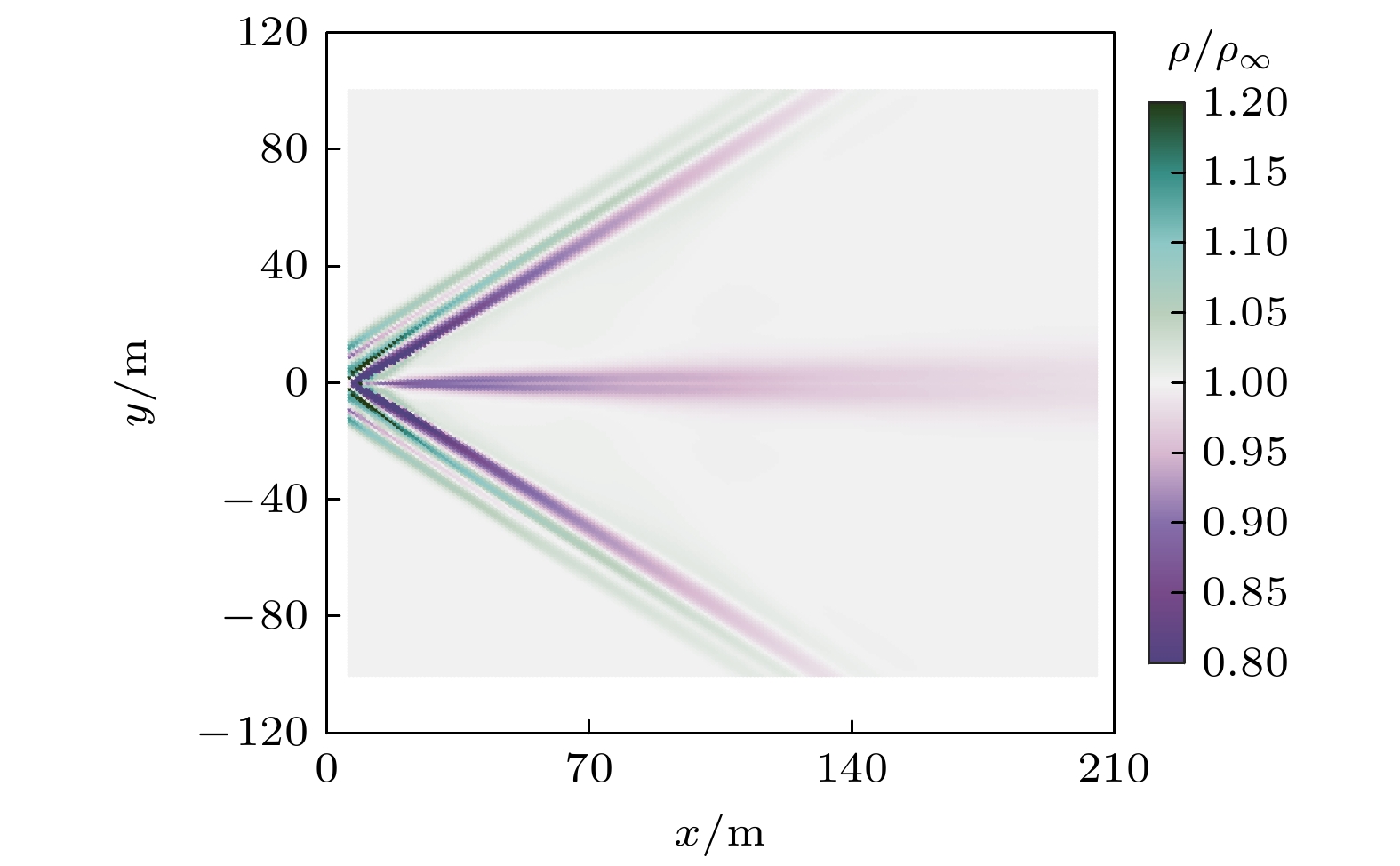
为了排除飞机本体反射对大气扰动密度场回波特征的干扰, 均选取飞机尾部离体后的扰动密度场进行分析. 马赫锥切面图是描述飞行器扰动流场的一种方式, 可以显示出高速飞行器导致的气流异常分布, 这里选取三维扰流场在y = –1 m处的侧视剖面图定性分析扰动物理场的非连续特性.
扰动密度场在图2侧视剖面图中表现为条纹状, 其中绿色表示密度值大于背景值, 紫色表示密度值小于背景值, 颜色越深与背景的差异越大, 而越接近白色与背景值越接近. 切面图呈现出紫绿相间的射线, 表明飞行器周围气流流场由多个交错的压缩波和膨胀波组成, 且在尾部存在明显的尾流. 由图2可以看出, 密度值波动最显著区域位于激波锥分界面两侧, 由高速飞行形成的激波面前侧压缩空气和后侧膨胀空气在密度值上存在极大差异.
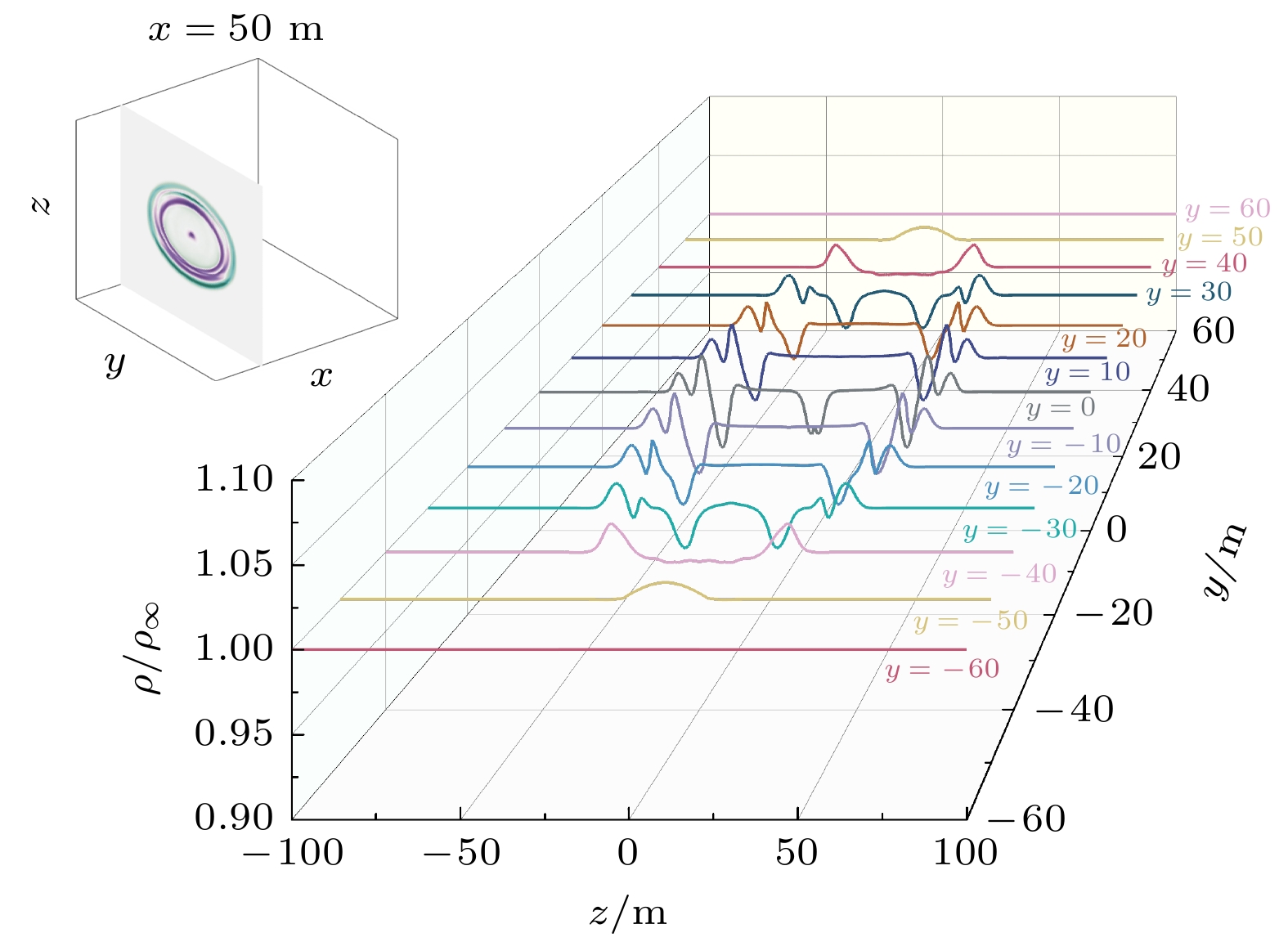
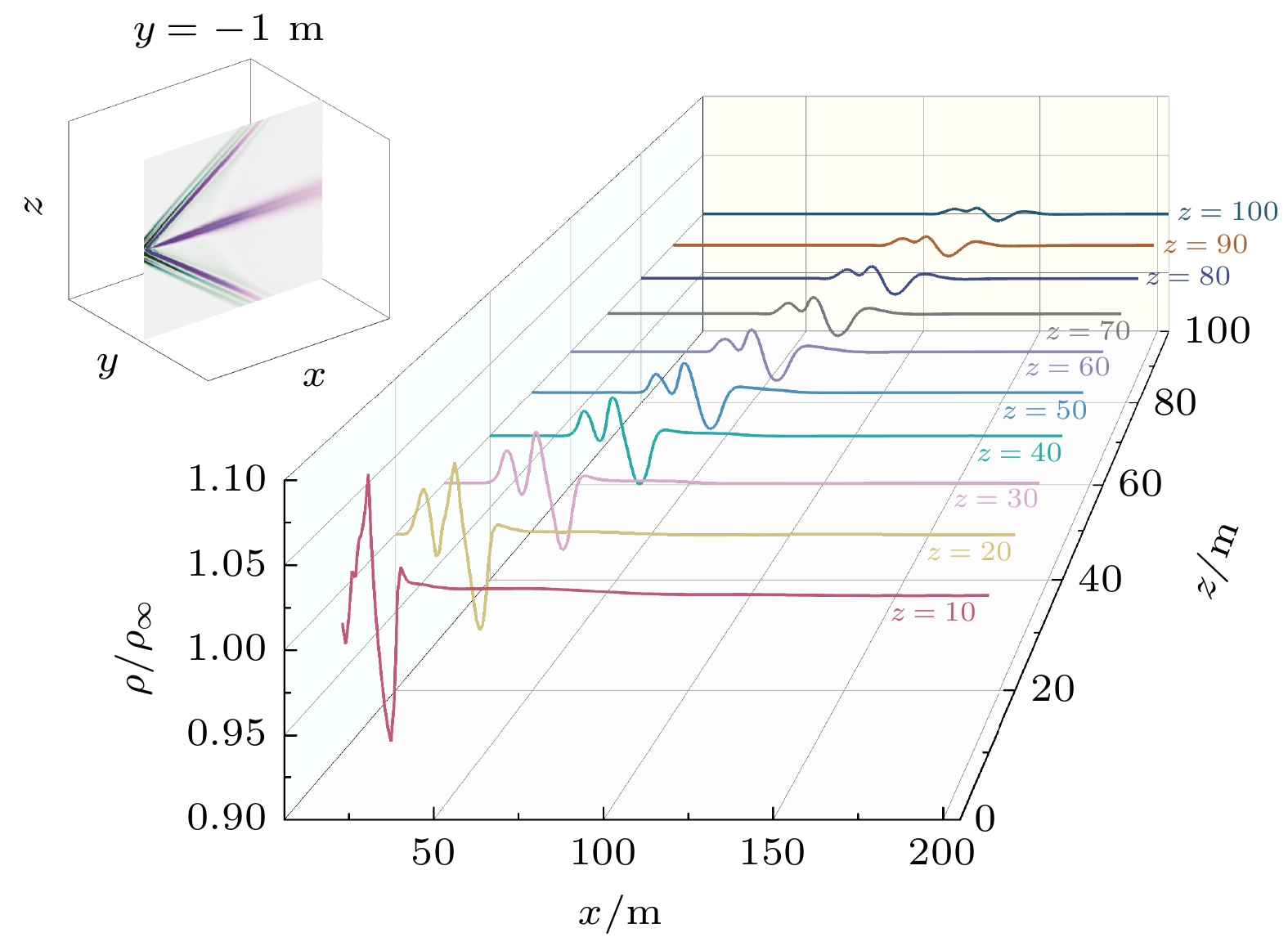
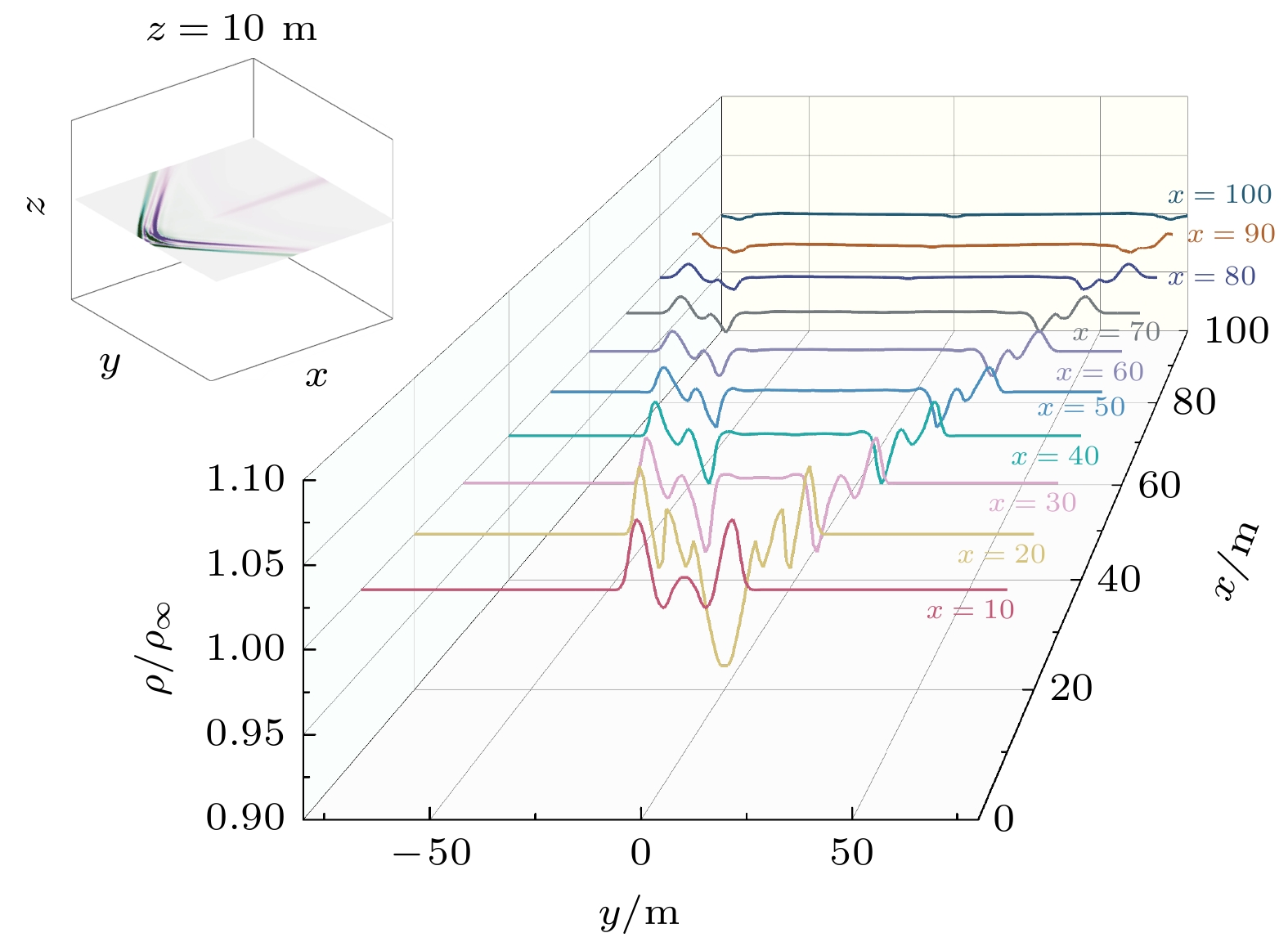
为了定量描述扰动物理场的空间衰减规律, 通过垂向、纵向、横向三个扩散方向, 选取多个位置定量分析密度比例值随扩散距离变化的结果. 其中垂向扩散分布曲线以x = 50 m为例, 见图3; 纵向扩散分布曲线以侧视图y = –1 m为例, 见图4; 横向扩散分布曲线以z = 10 m为例, 见图5.
从图3中流场整体分布来看, 飞行产生的扰动流场在正视剖面图中膨胀和挤压特征呈现出环状分布, 定量统计表明, 外圈压缩区的密度大于背景密度且出现双峰分布特征, 而中间膨胀区的密度则小于背景密度值. 结合图4的定量统计结果可得, 膨胀区密度波动的峰值绝对值稍高于压缩区. 随着扩散距离的增加, 界面两侧峰值绝对值均有所降低, 但两侧峰值相距间隔几乎保持不变, 约为9 m. 根据图5的定量统计, 飞行器扰流场的密度波动随着距飞机本体距离的增加而逐渐衰减. 综上所述, 飞行器大气扰动密度场的空间分布具有规律性的波动变化且与背景大气之间存在着明显的不同. 其特征主要为激波面前后两侧的空气密度差异存在反转, 可以作为扰动密度场的重要可测特征.
-
通过大气扰动密度场的仿真结果可得, 高速飞行器引起的大气扰动特征表现为激波锥分界面两侧的空气密度值存在显著的差异. 为了捕捉这一特征, 基于气体对光的散射回波强度与气体密度呈正相关的特性, 利用主动光源, 向空中发射激光脉冲, 接收激光脉冲在不同位置的后向散射信号, 实现对大气密度场三维空间分布的绘制. 重点关注激光脉冲经过飞行器激波界面时, 界面两侧介质因密度差异造成的激光脉冲散射回波信号差异特征.
针对该思路, 拟采用距离选通对大气扰动区域特定探测距离上光波面的散射回波进行成像探测, 实现对区域三维空间密度分布的层析成像. 探测原理如图6所示.
-
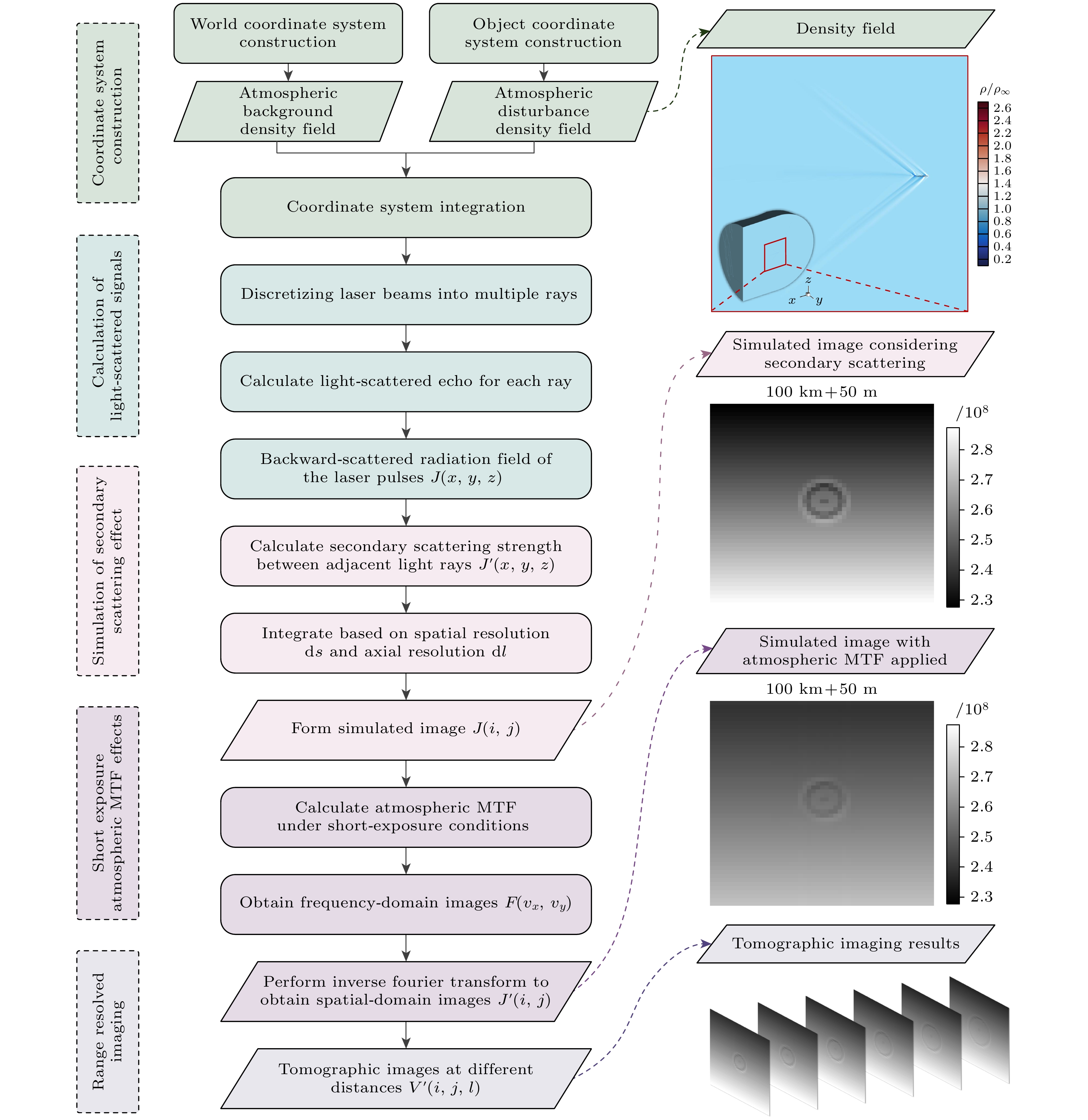
基于上述探测原理, 针对性地构建大气扰动密度场光散射回波信号成像仿真模型. 由于对扰动场的层析成像需要同步接收激光脉冲在不同探测距离上的瞬时回波信号, 需要特别考虑短曝光条件下的激光二次散射作用和大气调制作用. 大气扰动密度场光散射回波信号成像仿真模型框架和工作流程示意图7所示.
-
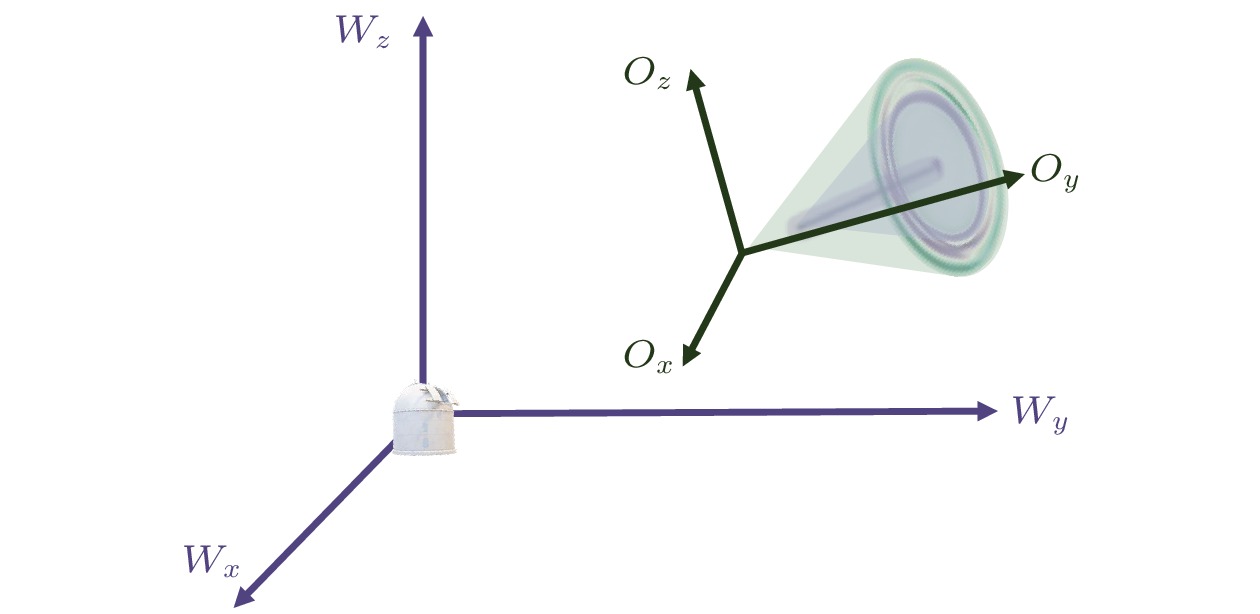
建立了以世界坐标系为主, 物体坐标系为辅的坐标系统, 见图8. 其中, 世界坐标系以探测系统为原点, 分别以正北、正西、天顶方向为x, y, z轴正方向建立右手坐标系, 并用Wxyz表示. 针对局部坐标系的建立, 以扰动流场三维仿真数据上某一点为坐标原点建立一个物体局部坐标系, 并用Oxyz表示.
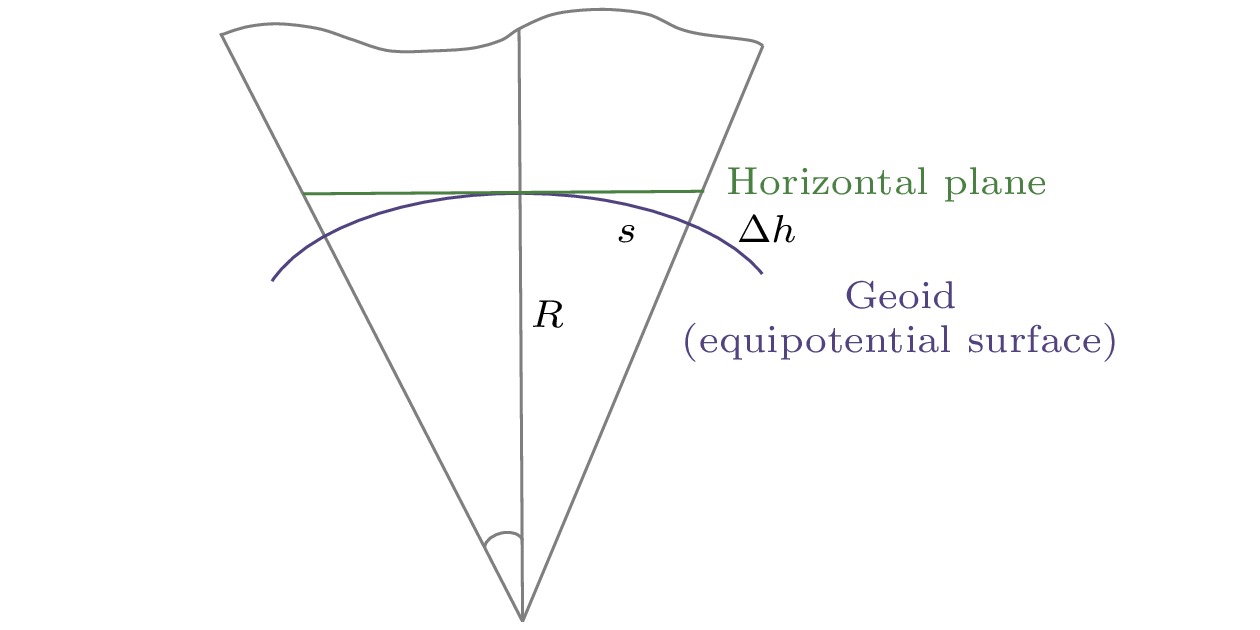
关于激光光束的描述, 使用观测天顶角与方位角表示激光入射方向并放入世界坐标系内. 关于扰动场的描述, 需注意在远距离作用时要考虑地球曲率的影响, 高差校正示意图如图9所示.
高差计算公式如下[21]:
-
针对光散射强度的计算, 可以将激光发射光束等效成无数条离散光线的集合, 依据不同位置的密度计算每条光线的散射回波信号, 模拟得激光脉冲的后向散射辐射场.
首先将激光光束离散成多条光线, 使用雷达方程分别计算每条光线经过大气扰动密度场不同位置
$(x, y, z)$ 时的光散射回波信号[22]:式中, N0为单条光线发射光子数, 由(3)式给出[23];
$ c $ 为光速;$\Delta t$ 为积分时间; C为几何因子;$ {T_{\text{t}}} $ 为发射系统透过率;$ {T_{\text{r}}} $ 为接收系统透过率; D为接收望远镜的口径;$ l $ 为距离;$ {T_{{\text{atm}}}} $ 为斜程大气透过率;$ \eta $ 为探测器量子效率; G为系统增益;$ {\beta _{\text{m}}}\left( {\lambda , {\rho _{x, y, z}}} \right) $ 为大气分子的后向散射系数,$ {\beta _{\text{a}}}\left( {\lambda , {\rho _{x, y, z}}} \right) $ 为大气气溶胶的后向散射系数, 单位为m–1·sr–1, 可根据美国标准大气模式获得, 见(4)式[24,25].式中, h是普朗克常数值为6.626276×10–34, 单位为J·s; n是光线数量;
${I_{{\text{sum}}}}$ 是激光单脉冲总能量.式中, ρx,y,z为不同位置处的大气密度; Nm为大气分子数密度; σm为单个大气分子的后向散射截面; R为干空气气体常数等于287.053, 单位为J/(kg·K); NL = 2.479×1025个/m3, 为温度296 K、压强1.013 × 105 Pa时的单位体积分子数目;
$ H $ 为海拔高度, 单位为m;$ {\rho }_{0} $ 为海平面高度大气密度, 单位kg/m3.由此, 可以获取单束光线经过扰动密度场时, 不同立体空间位置的光散射回波信号. 然后针对整束激光光束, 可将其等效成无数条离散光线的集合.
-
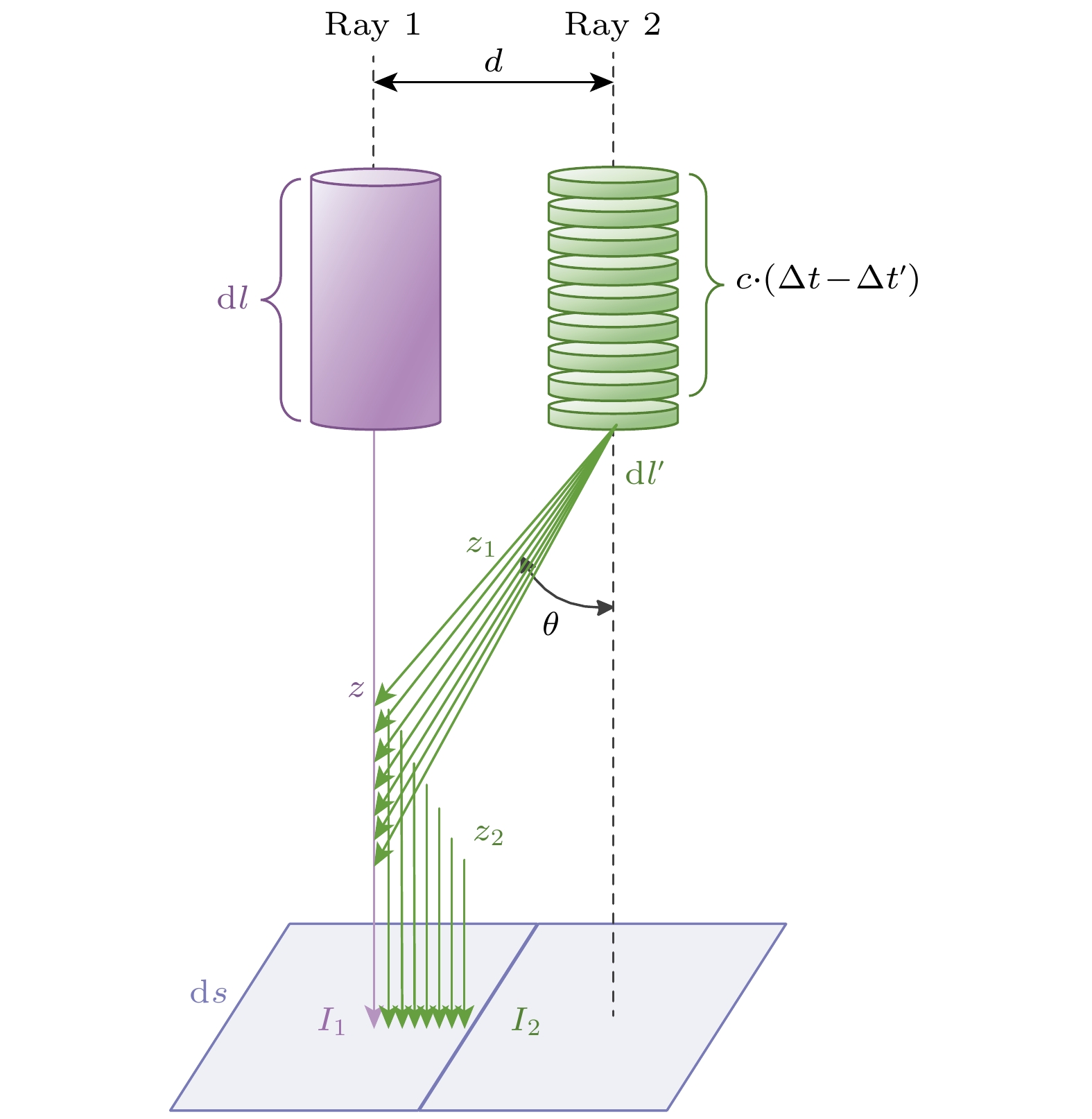
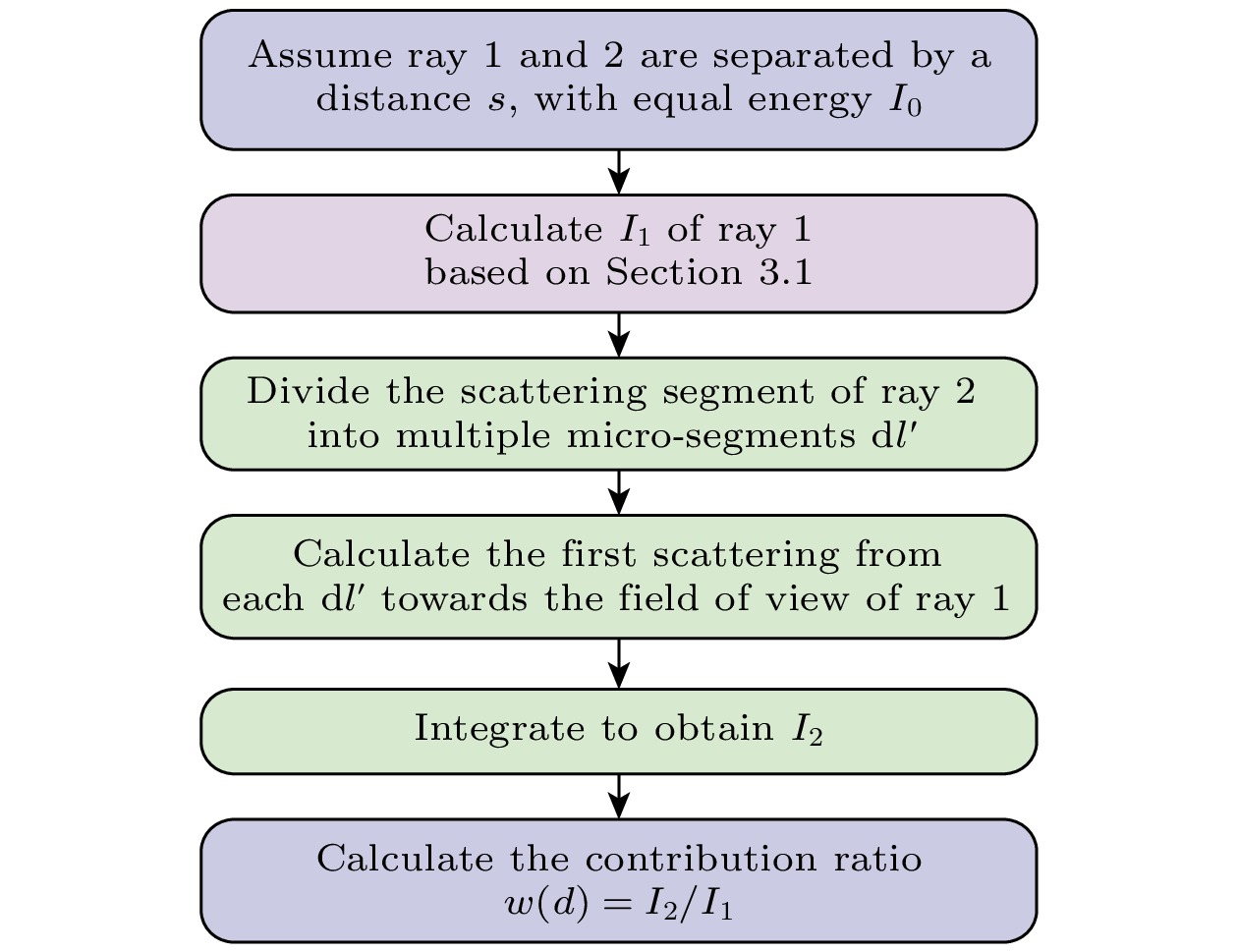
大气扰动场二次散射作用原理是: 在系统曝光门宽时限下激光脉冲与大气作用对应段dl的后向散射进入相邻瞬时视场ds内, 经过再次散射进入相邻瞬时视场, 形成二次散射辐射贡献. 计算原理见图10. 首先, 使用如下方法计算相邻光线二次散射辐射贡献比重w, 计算流程图见图11. 设定光线1与光线2的间距为d, 且两者的发射能量均为I0. 光线1的后向散射强度I1根据前述的激光雷达方程计算. 将光线2的散射路径离散为多个微分段dl', 分别对每个dl' 的一次散射辐射进行计算, 分析其在光线1视场内的贡献.
一次散射辐射为各个散射角θ方向上散射辐射的积分. 进入光线1视场的辐射形成二次散射, 且二次散射指向探测系统的辐射被接收. 由于几何关系, 二次散射角与一次散射角相同, 其计算公式如(5)式所示. 由于最终仅需计算散射辐射的比值, 故可对散射计算公式进行简化, 省略探测系统参数等常数项. 此外, 光线2的二次散射光程路径与其后向散射光程路径近似相同, 可视为受到相同的大气衰减作用, 故该部分在公式中亦省略.
式中, βm和
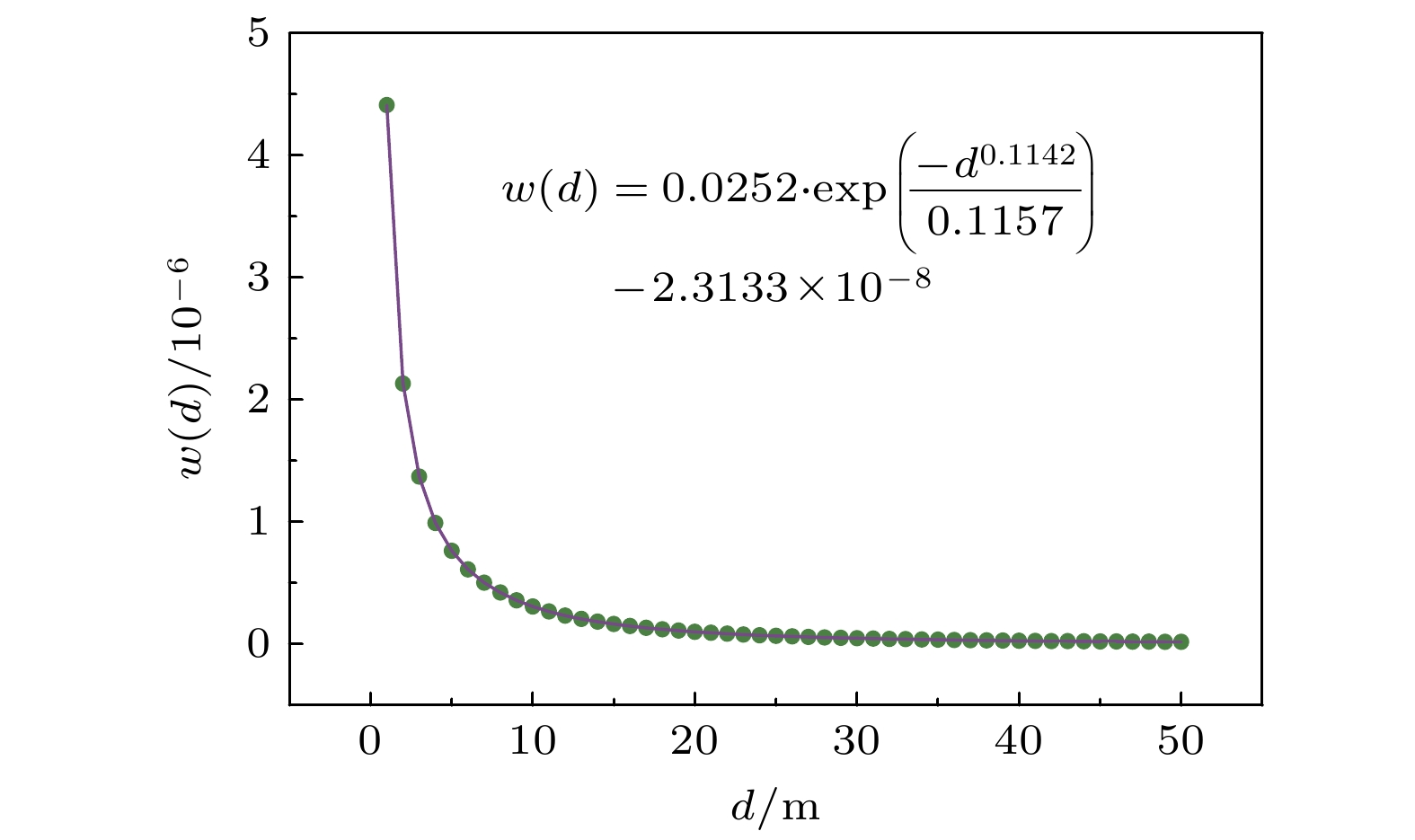
$ {\beta '_{\text{m}}} $ 分别表示一次散射系数和二次散射系数; c是光速;$ \Delta \tau $ 是探测曝光门宽,$ \Delta \tau ' $ 是微分段dl' 对应的时间;$ \Delta \tau - \Delta \tau ' $ 是探测曝光门宽剩余的时间. 由于门宽时限之外的二次散射路径是不被系统响应的, 所以(5)式计算条件是: 光线2的二次散射光程z1+z2与光线1散射光程 l 的差值应小于探测门宽剩余时间的对应光程.根据上述方法, 分别计算了光线1与光线2相距不同距离d的情况下, 光线2对光线1视场内二次散射辐射的贡献比重
$ w\left( d \right){=}{I_{2}}{\text{/}}{I_{1}} $ , 并对散点进行非线性曲线拟合, 最终得到贡献比重随距离变化的计算公式, 具体结果如图12所示. 从而得到考虑二次散射作用的单条光线的散射信号:式中, α, φ是发射光线的俯仰角和方位角.
然后, 根据成像分辨率ds和轴向分辨率dl, 将每条光线在不同位置的散射强度在探测分辨尺度内进行积分:
最后, 得到考虑二次散射效应的光散射回波信号图像, 成像示意图如图13.
-
在对成像过程的调制传递函数(modulation transfer function, MTF)进行计算时可看作由两部分组成: 大气湍流效应引起的MTF和光学成像系统本身的光学传递函数(optical transfer function, OTF).
关于大气湍流效应引起的MTF, 本文采用的距离选通激光主动成像技术属于短曝光的情况, 所以需要将大尺度漩涡引起的倾斜效应从总的湍流效应中除去, 从而得到短曝光大气MTF[26,27]:
式中,
$ \lambda $ 为激光波长; f是系统焦距; D是系统口径; 对于近场条件q = 1, 而远场条件q = 0.5;$ \omega = \sqrt {{v_x}^2 + {v_y}^2} $ 是二维空间频域的径向频率距离, 由沿x方向的频率vx和沿y方向的频率vy求得. r0是大气相干长度, 由路径上的大气折射率结构常数$ C_n^2 $ 计算得到[28]:针对光学成像系统本身的OTF, 可通过衍射置限系统下调制传递函数的表达式求解[27]:
式中,
$ \omega $ 是径向频率距离;$ {\omega _0} = D/\lambda f $ 为成像系统的截止频率, D是系统口径, λ为激光波长, f为焦距.由此, 可通过对大气散射强度信号J(i, j)作傅里叶变换, 再点乘大气MTF和理想系统OTF, 得到经传递函数作用后的频域图像F(vx, vy), 然后经傅里叶反变换得到空间域图像J'(i, j), 计算公式为
从而得到了经短曝光大气MTF作用后的成像结果, 对比结果见图14.
-
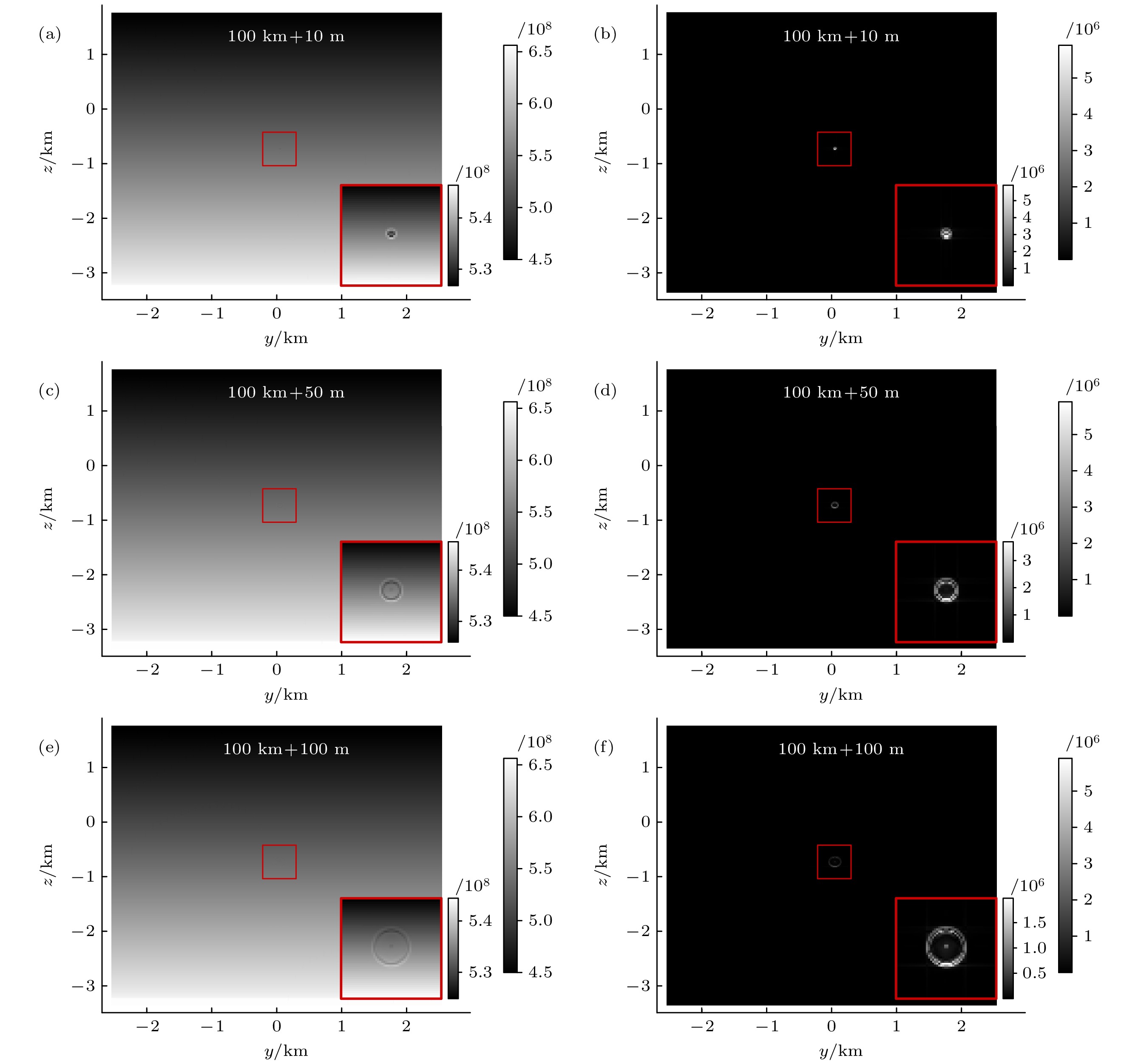
以飞机飞行高度10 km、飞行速度1.5 Ma为例, 假设探测平台高度为10 km, 在远距离100 km处发射激光脉冲, 并对大气扰动区域进行5 km×5 km的大范围成像观测. 设置在探测系统的分辨尺度为成像分辨率等于10 m, 轴向分辨率等于10 m, 瞬时视场内的脉冲能量为30 mJ, 探测波长为532 nm, 接收系统口径为0.5 m, 量子效率为70%, 发射系统和接收系统效率均为90%, 系统增益为8000, 且远距离情况下几何校正因子为1. 根据上述假设的成像系统, 仿真得到扰动大气密度场不同探测位置的层析图像如图15左列所示, 图中每个像素值的含义为经过光电倍增后探测系统输出的电计数值, 是与大气散射回波强度正相关的无量纲量; 同时获取了扰动场探测结果和与无扰动情况下的差异图像如图15右列所示, 图中每个像素值的含义为有扰动时和无扰动背景的电计数值差值, 也是无量纲量.
从图15(a)、图15(c)、图15(e)散射回波信号的层析成像结果, 可观察到大气扰动密度场在光散射层析成像中呈现出明显的环状分布, 且随着距离增加扩散面积逐渐扩大, 而光散射信号强度呈现逐渐衰减的趋势. 发现在进行大范围成像时, 大气背景密度随高度变化的影响更加显著, 使得扰动密度场特征并未明显展现, 为此取中间500 m×500 m的范围, 得到每张图像右下角的放大结果. 同时为了进一步凸显扰动信号, 获取了扰动场探测结果在无扰动情况下与背景的差异图像如图15(b)、图15(d)、图15(f)所示, 可以看出不同位置处大气散射回波强度因密度波动会存在明显差异, 说明该仿真模型可以实现将扰动流场的密度特性转换到光信号 领域.
-
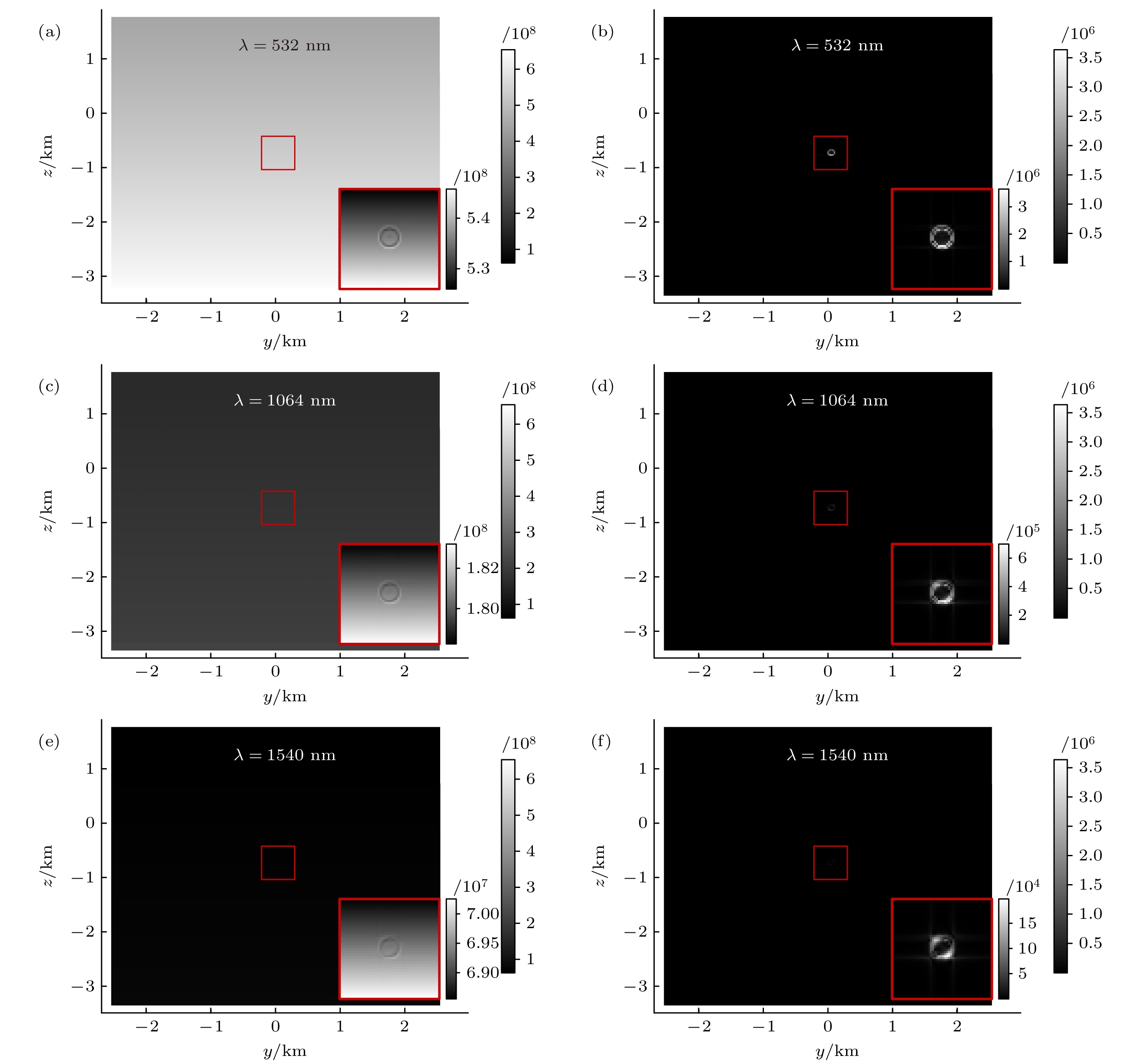
波长选择在激光雷达系统中受到散射系数和大气透过率的双重影响. 一方面, 大气散射系数与波长的4次方成反比. 另一方面, 对于光的长程传输而言, 波长越长, 大气衰减作用越小. 为了评估波长大小对于散射系数和大气透过率的矛盾问题, 可利用构建的仿真模型, 在考虑大气衰减作用的情况下, 对距离100 km处不同波长下的大气光散射回波信号强度进行计算, 并选取532, 1064, 1540 nm三个典型波段仿真得到的成像结果进行展示见图16, 其他系统参数设置同图15. 同一组大范围成像结果在相同的数据范围内进行拉伸出图, 但为了观察成像特征, 右下角的放大结果图按照各自数值进行最大-最小值拉伸.
大范围成像结果在相同数据范围内拉伸出图时, 颜色越浅代表回波信号越强, 颜色越深代表回波信号越弱. 理论上, 探测平台高度为10 km时, 受到相对较小的大气衰减影响, 结合仿真图像可知, 采用波长532 nm的激光可以平衡光散射系数与透过率之间的矛盾, 保证较强的光散射信号强度.
-
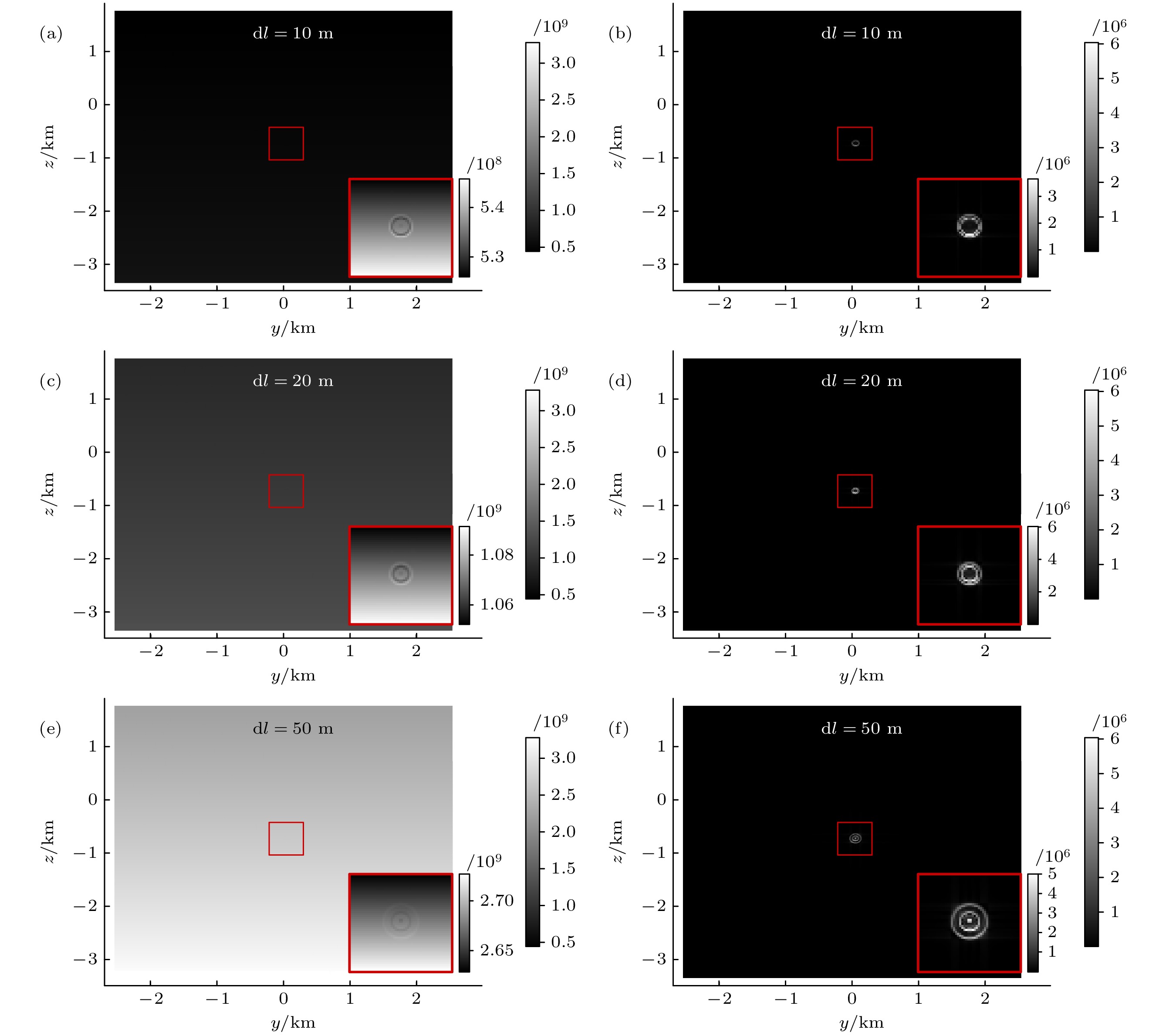
不同的轴向分辨率, 意味着不同长度的气体与激光的散射作用. 从理论上分析, 在轴向分辨率越低时, 与激光发生散射作用的气体分子越多, 散射信号强度越强, 但同时扰动场空气密度的空间波动特征越弱, 光散射信号特征也越不明显. 在成像分辨率ds设置为10 m时, 选取轴向分辨率dl为10, 20, 50 m三种情况, 其他系统参数设置同图15, 成像仿真模拟结果如图17.
通过大范围成像结果可在同一尺度下比较回波信号强度的变化, 颜色越浅代表回波信号越强. 观察图17(a)、图17(c)和图17(e)发现在轴向分辨率dl数值增大时信号强度增加, 这是因为有更多的气体分子与激光发生了散射作用. 同时比较了与无扰动背景的差异如图17(b)、图17(d)和图17(f), 观察放大后的结果发现轴向分辨率dl从10到20 m时回波信号强度数值有明显增加, 但是到50 m时数回波信号的差异减弱, 这是因为与气体分子作用的激光段长度增加时波动特征会被平滑.
-
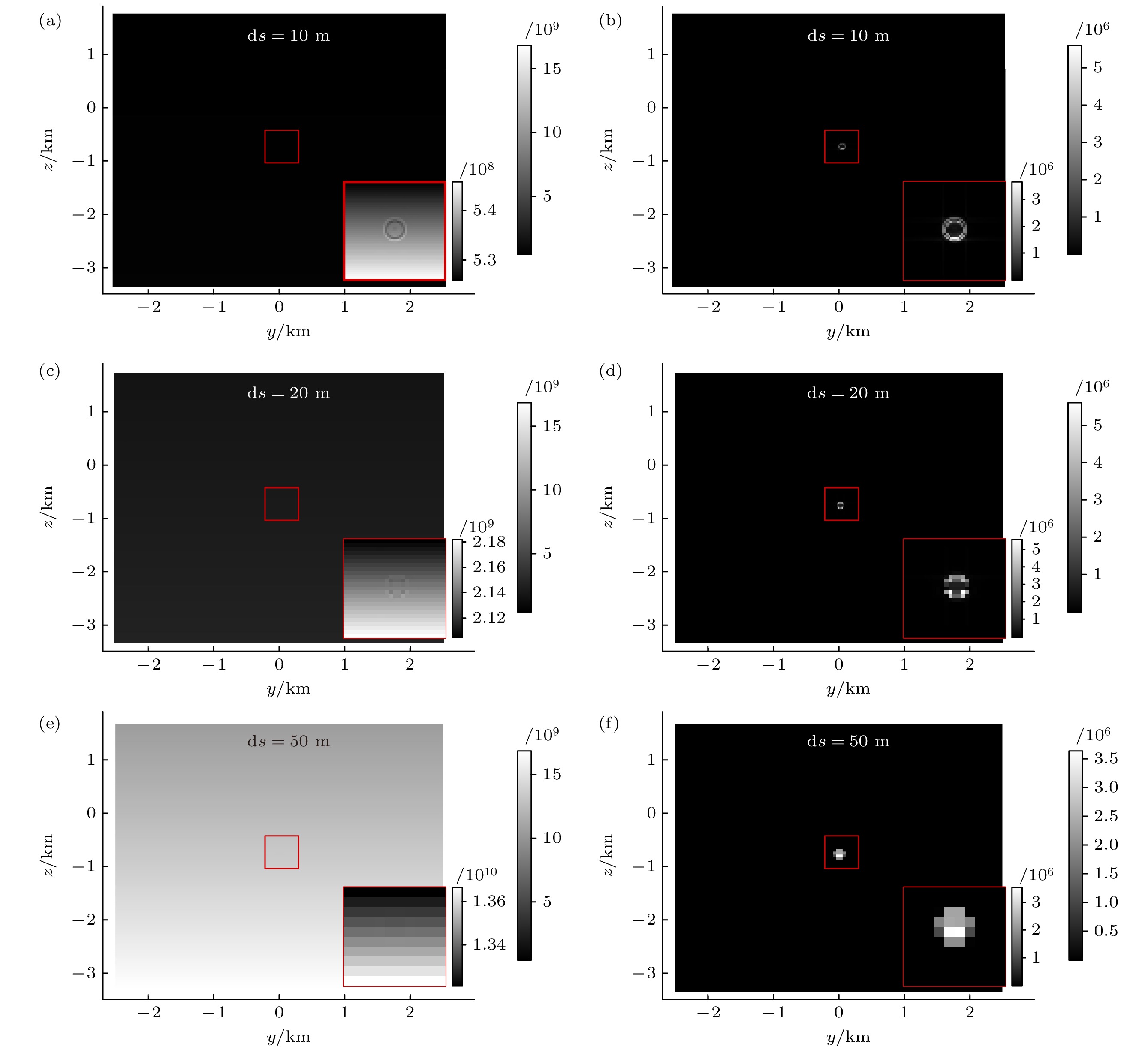
不同的成像分辨率, 意味着单个像元对应的实际成像范围不同. 在发射能量和接收口径一定的条件下, 对应的单位能量密度是一定的. 所以从理论上来说, 成像分辨率越高越能展现密度空间分布特征. 但是考虑到实际系统资源, 期望在较低分辨率下测得密度场特征. 在轴向分辨率dl设置为10 m时, 选取成像分辨率ds为10, 20, 50 m三种情况, 其他系统参数设置同图15, 成像仿真模拟结果如图18.
通过大范围成像结果可在同一尺度下比较回波信号强度的变化, 发现在成像分辨率ds增大时, 由于实际对应的成像范围增加, 所以信号强度增加, 但是单个探测单元内的密度波动会被平均, 表现在图18(a)、图18(c)和图18(e)中当成像分辨率降低至50 m时散射回波信号的波动并未展现. 同时比较了与无扰动背景的差异如图18(b)、图18(d)和图18(f), 发现在同一位置处得到的成像结果, 由于结果图的成像分辨率降低, 环状特征不明显.
-
针对大气扰动区域密度场的探测, 建立了涵盖扰动光信号生成、信号传输、回波重建及光散射成像的全仿真链路. 通过结合激光雷达方程与短曝光成像理论, 解决了短曝光条件下激光二次散射和大气MTF影响的问题, 通过去除大气湍流光学调制传递函数中大尺度漩涡引起的倾斜效应, 得到短曝光条件下湍流MTF计算方法; 通过离散光线微元不同角度散射光程长在曝光时间区间内的积分计算, 拟合了不同距离上邻近像元的二次散射辐射贡献权重, 进而构建了大气扰动密度场光散射回波成像的三维层析仿真模型.
基于该模型模拟了不同探测位置、探测波长及分辨尺度等条件下的光散射回波信号, 并分析了扰动流场的可测特征及其与无扰动背景的差异. 远距离条件下的仿真结果表明, 飞行器扰动密度场的光散射回波信号呈环状分布的图像特征. 该仿真模型可应用于探测系统参数优化、信号处理方法研究及远距离探测能力评估, 为发展基于密度扰动的飞行器探测技术提供了理论依据和技术支持.
大气扰动密度场光散射信号成像仿真方法
Imaging simulation of light scattering signals in atmospheric disturbance density fields
-
摘要: 空中飞行器在飞行过程中对邻近大气环境造成扰动, 形成明显有别于自然背景的大气密度空间分布特征. 本文提出基于大气扰动密度场远距离感知飞行器存在的构想, 针对性地设计了对大气扰动区域散射光进行三维层析成像的探测模式, 以及扰动光信号产生、传递和响应的全过程仿真链路. 重点解决了在短曝光条件和激光脉冲二次散射作用下的成像调制传递函数估算问题, 构建了飞行器扰动密度场的光散射回波成像仿真模型. 模拟了大气扰动密度场对主动光源的散射回波信号图像和与无扰动背景的差异图像, 并在此基础上讨论了不同系统参数下的仿真结果. 该模型可以为探测系统设计提供分析工具, 并为相关探测技术的发展提供基础.Abstract: During flight operations, aircraft induces atmospheric disturbances in the surrounding environment through aerodynamic interactions between its geometric configuration and ambient air medium, resulting in spatially distinct density distribution characteristics that are significantly different from natural background scenario. Considering the positive correlation between atmospheric medium density and light scattering intensity, theoretical analysis shows that detecting the light scattering intensity signals in disturbed regions can map density distributions, thereby extracting the features of aircraft-induced atmospheric disturbance density fields. Based on the concept of long-range aircraft detection through atmospheric disturbance density field characterization, a novel remote sensing method for aircraft detection is proposed in this work. Specifically, a three-dimensional tomographic imaging detection mode for scattered light in an atmospheric disturbance region is designed, and a comprehensive simulation framework covering the entire process of disturbance optical signal generation, transmission, and response is constructed. The study accomplishes the following tasks: 1) the critical challenges in estimating the imaging modulation transfer function under short-exposure conditions subjected to laser pulse secondary scattering effects are resolved, and a photon scattering echo imaging simulation model for aircraft-induced disturbance density fields is established; 2) the scattering echo signal images from active light sources in disturbed density fields and the differential images obtained under disturbed background and non-disturbed background are simulated, with simulation results under varying system parameters analyzed systematically. The research demonstrates that this simulation model can be used to optimize detection system parameters, develop signal processing methods, and assess long-range detection capabilities, thus providing both theoretical foundations and technical support for advancing aircraft detection technologies based on density disturbance characteristics.
-
Key words:
- density field /
- atmospheric disturbance /
- active detection /
- imaging simulation .
-
-
图 1 大气扰动密度场云图分布
Figure 1. Distribution of atmospheric disturbance density field cloud map.
图 2 扰动密度场侧视剖面图(以y = –1 m为例)
Figure 2. Side view profile of disturbance density field (taking y = –1 m as an example).
图 3 扰动密度场垂向扩散分布曲线(以正视图中x = 50 m为例)
Figure 3. Vertical diffusion distribution curves of disturbance density field (taking x = 50 m in the front view as an example).
图 4 扰动密度场纵向扩散分布曲线(以侧视图中y = –1 m为例)
Figure 4. Longitudinal diffusion distribution curves of disturbance density field (taking y = –1 m in the side view as an example).
图 5 扰动密度场横向扩散分布曲线(以俯视图中z = 10 m为例)
Figure 5. Lateral diffusion distribution curves of disturbance density field (taking z = 10 m in the top view as an example).
图 6 基于大气扰动密度场的探测原理示意图
Figure 6. Schematic diagram of detection principle based on atmospheric disturbance density field.
图 7 大气扰动密度场光散射回波信号成像仿真模型框架和工作流程示意图
Figure 7. Schematic diagram of the framework and workflow of the imaging simulation model for light scattering echo signals in atmospheric disturbance density field.
图 10 二次散射作用计算原理示意图
Figure 10. Schematic diagram of the calculation principle of secondary scattering effect.
图 11 二次散射作用贡献比重计算流程图
Figure 11. Flowchart of the calculation of contribution ratio of secondary scattering effect.
图 12 邻近光线二次散射贡献比随距离的变化
Figure 12. Variation curve of the contribution ratio of secondary scattering from adjacent light rays with distance.
图 13 大气扰动场光散射场回波信号成像示意图
Figure 13. Schematic diagram of echo signal imaging of light scattering field in atmospheric disturbance field.
图 14 经短曝光大气MTF作用后的成像效果
Figure 14. Imaging effect after short-exposure atmospheric MTF.
图 15 大气扰动密度场光散射层析成像探测结果图 (a), (c), (e)散射回波信号; (b), (d), (f) 与无扰动背景的差异
Figure 15. Tomographic imaging detection results of light scattering in atmospheric disturbance density field: (a), (c), (e) Scattering echo signals; (b), (d), (f) the differential images obtained by comparing disturbed and non-disturbed background.
图 16 不同波长的成像探测结果图 (a), (c), (e)散射回波信号; (b), (d), (f)与无扰动背景的差异
Figure 16. Imaging detection results at different wavelengths: (a), (c), (e) Scattering echo signals; (b), (d), (f) the differential images obtained by comparing disturbed and non-disturbed backgrounds.
图 17 不同轴向分辨率的成像探测结果图 (a), (c), (e)散射回波信号; (b), (d), (f)与无扰动背景的差异
Figure 17. Imaging detection results at different axial resolutions: (a), (c), (e) Scattering echo signals; (b), (d), (f) the differential images obtained by comparing disturbed and non-disturbed backgrounds.
-
[1] 任维贺, 张月, 苏云, 张学敏, 邓红艳, 柳祎 2022 红外与激光工程 51 20210843 doi: 10.3788/IRLA20210843 Ren W H, Zhang Y, Su Y, Zhang X M, Deng H Y, Liu Y 2022 Infrared and Laser Engineering 51 20210843 doi: 10.3788/IRLA20210843 [2] Pan W J, Jiang Y Q, Zhang Y Q 2023 Sustainability 15 6391 doi: 10.3390/su15086391 [3] Wei Z Q, Li X C, Liu F 2022 Int. J. Aeronaut. Space Sci. 23 406 doi: 10.1007/s42405-021-00437-0 [4] Liu Z R, Mao J M 2003 Chin. Phys. Lett. 20 206 doi: 10.1088/0256-307X/20/2/310 [5] 潘卫军, 栾天, 康贤彪, 张庆宇, 任杰, 张强 2019 空气动力学学报 37 511 doi: 10.7638/kqdlxxb-2018.0136 Pan, W J, Luan, T, Kang, X, Zhang Q Y, Ren, J, Zhang, Q 2019 Acta Aerodyn. Sin. 37 511 doi: 10.7638/kqdlxxb-2018.0136 [6] Garnet M, Altman A 2009 J. Aircr. 46 263 doi: 10.2514/1.38410 [7] Burnham D C, Hallock J N 2013 J. Aircr. 50 82 doi: 10.2514/1.C031715 [8] Köpp F, Rahm S, Smalikho I 2004 J. Atmos. Oceanic Technol. 21 194 doi: 10.1175/1520-0426(2004)021<0194:COAWVB>2.0.CO;2 [9] Yoshikawa E, Matayoshi N 2017 AIAA J. 55 2269 doi: 10.2514/1.J055224 [10] Gao H, Li J B, Chan P W, Hon K K, Wang X S 2018 Opt. Express 26 16377 doi: 10.1364/OE.26.016377 [11] Marshall R E, Mudukutore A, Wissel V L H, Myers T 1998 Three-Centimeter Doppler Radar Observations of Wingtip-Generated Wake Vortices in Clear Air Report No. NASA/ CR-97-206260 [12] 武宇, 易仕和, 陈植, 张庆虎, 冈敦殿 2013 物理学报 62 184702 doi: 10.7498/aps.62.184702 Wu Y, Yi S H, Chen Z, Zhang Q H, Gang D D 2013 Acta Phys. Sin. 62 184702 doi: 10.7498/aps.62.184702 [13] 易仕和, 陈植 2015 物理学报 64 199401 doi: 10.7498/aps.64.199401 Yi S, Chen Z 2015 Acta Phys. Sin. 64 199401 doi: 10.7498/aps.64.199401 [14] Sun Q, Cui W, Li Y H, Cheng B Q, Jin D, Li J 2014 Chin. Phys. B 23 075210 doi: 10.1088/1674-1056/23/7/075210 [15] Heineck J T, Banks D W, Smith N T, Schairer E T, Bean P S, Robillos T 2021 AIAA J. 59 11 doi: 10.2514/1.J059495 [16] Heineck J T, Banks D W, Schairer E T, Haering E A Jr., Bean P S 2016 AIAA Flight Testing Conference Washington, DC, USA, June 13–17, 2016 p11 [17] 李新亮 2015 航空学报 36 147 doi: 10.7527/S1000-6893.2014.0233 Li X L 2015 Acta Aeronaut. ET Astronaut. Sin. 36 147 doi: 10.7527/S1000-6893.2014.0233 [18] Yu C P, Hu R N, Yan Z, Li X L 2022 J. Fluid Mech. 940 A18 doi: 10.1017/jfm.2022.250 [19] Hu R N, Li X L, Yu C P 2023 J. Fluid Mech. 972 A14 doi: 10.1017/jfm.2023.691 [20] Hu R N, Li X L, Yu C P 2022 J. Fluid Mech. 946 A19 doi: 10.1017/jfm.2022.580 [21] 卞正富 2002 测量学 (北京: 中国农业出版社) 第17页 Bian Z F 2002 Surveying (Beijing: China Agriculture Press) p17 [22] 黄金 2024 硕士学位论文 (西安: 西安理工大学) Huang J 2024 M. S. Dissertation (Xi’an: Xi’an University of Technology [23] 崔洪鲁, 闫召爱, 张炳炎, 郭文杰, 胡雄 2020 空间科学学报 40 1046 doi: 10.11728/cjss2020.06.1046 Cui H L, Yan Z, Zhang B Y, Guo W J, Hu X 2020 Chin. J. Space Sci. 40 1046 doi: 10.11728/cjss2020.06.1046 [24] 陈胜哲 2014 博士学位论文 (北京: 北京理工大学) Chen S Z 2014 Ph. D. Dissertation (Beijing: Beijing Institute of Technology [25] 刘厚通, 陈良富, 苏林 2011 物理学报 60 064204 doi: 10.7498/aps.60.064204 Liu H T, Chen L F, Su L 2011 Acta Phys. Sin. 60 064204 doi: 10.7498/aps.60.064204 [26] 白珺, 袁艳, 苏丽娟, 孙成明 2012 现代电子技术 35 124 doi: 10.3969/j.issn.1004-373X.2012.05.035 Bai J, Yuan Y, Su L J, Sun C M 2012 Modern Electron. Tech. 35 124 doi: 10.3969/j.issn.1004-373X.2012.05.035 [27] 马雪莲 2015 光子学报 44 0601003 doi: 10.3788/gzxb20154406.0601003 Ma X L 2015 Acta Photonica Sin. 44 0601003 doi: 10.3788/gzxb20154406.0601003 [28] 陈武喝 1999 光电子·激光 10 375 doi: 10.3321/j.issn:1005-0086.1999.04.025 Chen W H 1999 J. Optoelectron. ·Laser 10 375 doi: 10.3321/j.issn:1005-0086.1999.04.025 -
计量
- 文章访问数: 63
- HTML全文浏览数: 63
- PDF下载数: 1
- 施引文献: 0