地下各向异性介质球体的电磁散射在地下目标探测^[1,2]、地质勘探^[3]和隐身技术^[4,5]等领域具有重要的应用价值. 然而, 由于各向异性介质的复杂性, 其散射特性研究面临着较大的理论与计算挑战. 目前, 数值方法如矩量法(method of moments, MOM)和有限元法(finite element method, FEM)在解决复杂几何和电磁环境中的散射问题方面表现出较强的适应性, 并在地下介质中的电磁散射问题中得到了广泛应用^[6,7]. 然而, 这些数值方法高度依赖复杂网格的离散化, 尤其在处理电大尺寸问题时, 计算时间和内存消耗显著增加, 导致计算精度和效率受到限制^[8–10].

相比之下, 球矢量波函数法作为一种能够避免网格离散化依赖的研究方法, 以其潜在的高效性和精确性, 逐渐受到关注. 然而, 现有的大多数球矢量波函数法研究主要集中于地下各向同性介质的散射问题, 且通常仅计算平面上的单点电场强度. 例如, Zamani等^[11]基于微扰法求解微粗糙界面下介质球的散射系数, 但仅适用于弱散射条件的简单介质球. Nasr等^[12]提出镜像法和多次反射法, 解决了埋地圆柱体的散射问题, 但局限于圆柱形结构; 在此基础上, Zhang等^[13]将镜像法和多次反射法以及球矢量波函数的加法定理相结合, 成功求解了埋地各向同性球体的电磁响应; Geng等^[14]进一步扩展了其方法以适应双层介质球. 然而, 上述方法均假设介质为各向同性, 没有涉及到各向异性地下介质目标的特性问题.

各向异性介质因其介电常数和磁导率以张量形式存在, 散射问题的计算复杂度显著增加, 目前相关研究主要集中在自由空间环境中. 例如, Li等^[15]基于T矩阵法研究了光学频率下各向异性粒子的散射问题, 但其适用范围仅限于小尺寸规则球体, 且仅在自由空间中有效. 樊久扬等^[16]基于快速传输矩阵法研究了单轴/双轴双各向异性媒质的电磁特性, 但该方法主要应用于相对简单的几何结构, 尚未广泛验证其在地下复杂环境中的应用. 因此, 地下各向异性介质的散射问题仍鲜有研究. 然而, 地下目标的各向异性是普遍存在的, 如地下管道的钢筋混凝土结构^[17]、地下矿藏^[18]、煤炭的分层^[19]等都是各向异性介质.

本文在前面的基础上, 给出了一种利用各向异性T矩阵法^[15]、镜像法^[11]与球矢量波函数加法定理^[20]求解地下旋电磁各向异性介质球的电磁散射问题. 与以往主要计算单点电场强度^[12–14]的研究不同, 本文的方法实现了沿各向异性介质球轴向平行的地面直线L上的电场分布求解. 为验证本文提出的球矢量波函数方法的正确性, 采用了三维电磁仿真软件FEKO进行对比分析, 该软件以其高精度和广泛应用闻名, 常用于复杂电磁散射问题的验证^[21,22]. 在计算各向异性介质时, FEKO基于FEM进行求解^[23], 但由于依赖复杂网格离散化, 尤其在大规模问题中, 计算时间和内存消耗较大. 相比之下, 本文提出的球矢量波函数方法无需网格化, 实现了更高效的计算和更快的收敛性. 结果表明, 本文提出的球矢量波函数方法与FEKO仿真结果具有高度一致性, 同时相比FEKO在计算效率上具有显著优势, 且方法更加简洁、高效.

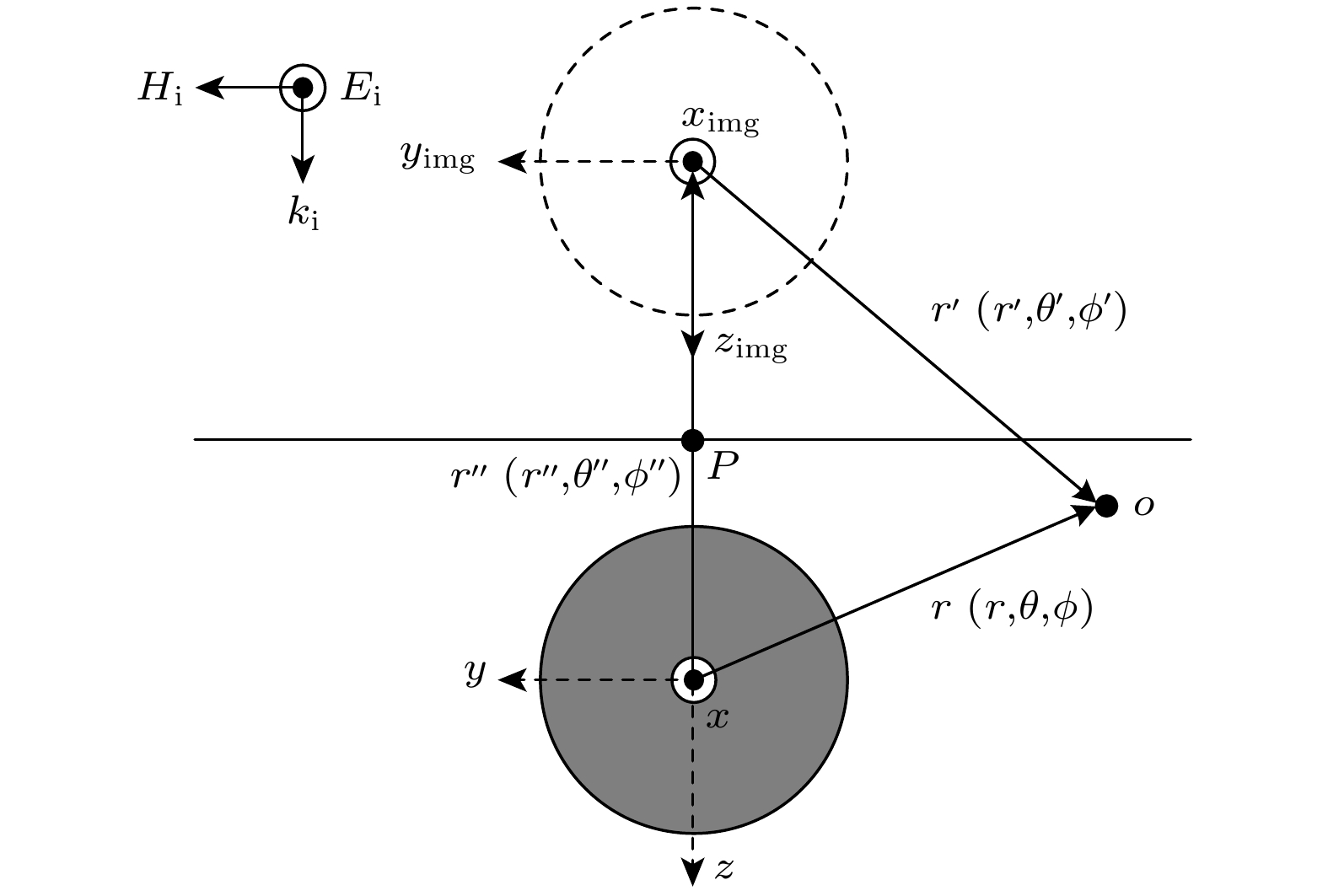
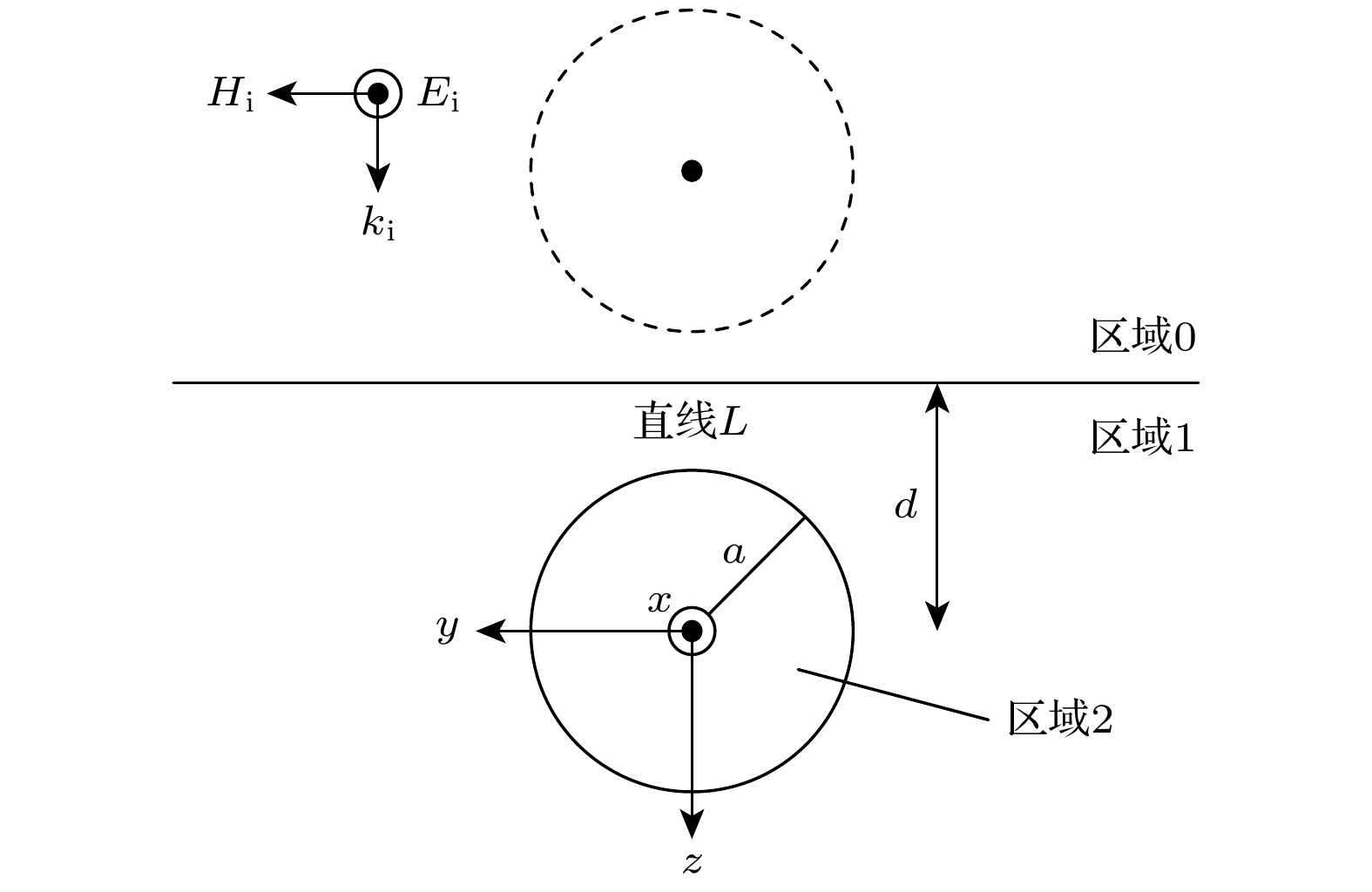
图1是地下埋藏旋电磁各向异性介质球电磁散射的几何结构. 区域0为自由空间, 区域1为具有相对介电常数$ {\varepsilon _{{\text{r1}}}} $、相对磁导率$ {\mu _{{\text{r}}1}} $和电导率$ {\sigma _1} $的各向同性导电介质, 区域2为埋藏的旋电磁各向异性球体, 其半径为$ a $和埋藏深度为$ d $. 笛卡尔坐标系的原点位于球体中心. 平面波沿z轴在区域0中传播, 入射电场沿x轴方向极化, 幅值为$ {E_0} $. 假定时间依赖性为$ \text{exp}(-\text{i}\omega t) $, 在此后分析中已不再显示.

旋电磁各向异性球的介电常数和磁导率可以表示为^[15]

其中$ {\mu _{\text{s}}} $和$ {\varepsilon _{\text{s}}} $是常数因子; $ {\mu _{\text{t}}} $表示磁导率在x轴和y轴方向上的表现; $ {\varepsilon _{\text{t}}} $表示介电常数在x轴和y轴方向上的表现; $ {\mu _{\text{g}}} $表示磁响应中的旋磁项; $ {\varepsilon _{\text{g}}} $表示电响应中的旋电项.

入射波的电场分量可表示为^[12,13]

其中$ \hat {\boldsymbol{x}} $代表沿x轴正方向的单位向量.

经地面反射和透射的电场可以表示为^[12,13]

式中, $ R $和$ T $分别表示反射系数和透射系数. 通过在$ z = - d $处应用电场和磁场切向分量的连续性条件, 可以推导出$ R $和$ T $的具体表达式^[12,13]:

式中, $ {\eta _0} = \sqrt {{{{\mu _0}} {/ } {{\varepsilon _0}}}} $和$ {\eta _1} = \sqrt {{{{\mu _1}} {/ } {{\varepsilon _1}}}} $分别是区域0和区域1的波阻抗; $ {k_0} = \omega \sqrt {{\varepsilon _0}{\mu _0}} $和$ {k_1} = \omega \sqrt {{\varepsilon _1}{\mu _1}} $分别是区域0和区域1的波数, 其中$ \omega $为角频率, $ {\varepsilon _0} $和$ {\mu _0} $分别表示区域0的介电常数和磁导率, $ \varepsilon_1=\varepsilon_0\left(\varepsilon_{\rm r1}+{\rm i}\dfrac{\sigma_1}{\omega\varepsilon_0}\right) $和$ {\mu _1} = {\mu _0}{\mu _{\rm r1}} $分别表示区域1的介电常数和磁导率.

如Li等^[15]所示, 对于旋电磁各向异性介质球的内部场求解, 可以根据麦克斯韦方程以及球矢量波函数的性质, 给出旋电磁各向异性介质球内部磁感应强度$ {{\boldsymbol{B}}_l} $, 表示为^[15]

其中k是待确定的波数, 求和式$ \displaystyle\sum\limits_{n, m} {} $中的n从1到$ + \infty $, 而m对于每个n从–n求和至n; $ {\bf{M}}_{mn}^{\left( 1 \right)}\left( {k, {\boldsymbol{r}}} \right) $和$ {\bf{N}}_{mn}^{\left( 1 \right)}\left( {k, {\boldsymbol{r}}} \right) $是各向同性介质中第一类球矢量波函数; $ {c_{mn}} $和$ {d_{mn}} $是与旋电磁各向异性介质相关的系数. 求和系数定义为$ {\overline E _{mn}} = {{\text{i}}^n}T{E_0}{C_{mn}} $, $ {C_{mn}} $的具体表达式为^[15]

磁感应强度$ {{\boldsymbol{B}}_l} $也可以表示为^[15]

基于球矢量波函数在直角坐标系下的表达式, 可以得到$ {\mu _{\text{s}}}{\overline {\boldsymbol{\mu }} ^{ - 1}} \cdot {{\bf{M}}_{mn}} $, $ {\mu _{\text{s}}}{\overline {\boldsymbol{\mu }} ^{ - 1}} \cdot {{\bf{N}}_{mn}} $, $ {\varepsilon _{\text{s}}}{\overline {\boldsymbol{\varepsilon }} ^{ - 1}} \cdot {{\bf{M}}_{mn}} $, $ {\varepsilon _{\text{s}}}{\overline {\boldsymbol{\varepsilon }} ^{ - 1}} \cdot {{\bf{N}}_{mn}} $展开成球矢量波函数的表达式, 具体表达式见文献[15]. 将(10)式两边都乘以参数$ {\mu _{\text{s}}}{\overline {\boldsymbol{\mu }} ^{ - 1}} $, 表达式如下:

其中系数$ {\overline d _{pq}} $, $ {\overline c _{pq}} $, $ {\overline \omega _{pq}} $, $ {\overline \omega _{00}} $的具体表达式见文献[15]. 对式(11)取旋度再乘以$ {\varepsilon _{\text{s}}}{\overline {\boldsymbol{\varepsilon }} ^{ - 1}} $, 可以得到如下表达式:

其中系数$ {\overline{\overline c} _{mn}} $, $ {\overline{\overline d} _{mn}} $, $ {\overline{\overline \omega } _{mn}} $, $ {\overline{\overline \omega } _{00}} $的具体表达式见文献[15]. 由麦克斯韦方程组和本构方程, 容易推导得到以下表达式:

把(12)式和(8)式代入(13)式中, 整理后可以得到如下方程:

其中系数$ {\widetilde {\widetilde d\;}_{mn}} $, $ {\widetilde {\widetilde c\,}_{mn}} $的具体表达式见文献[15]. 要让(14)式成立, 需要$ {\widetilde {\widetilde d\;}_{mn}} = 0 $, $ {\widetilde {\widetilde c\,}_{mn}} = 0 $, 可以得到一个矩阵形式:

其中$ {\lambda _l} = \dfrac{{k_{\text{s}}^{2}}}{{k_{}^2}}, $

各系数具体表达式见文献[15]. $ mn, uv $分别表示 矩阵的行和列; 用l来标注其对应的特征向量, 不 同的l值意味着代表的特征值和特征向量不同. 特征值记为$ {\lambda _l} $, 其对应的特征向量可表示为$ {\left( {{d_{mn, l}}, {c_{mn, l}}} \right)^{\text{T}}} $. 基于这些特征向量, 能够构建出一个新的函数$ {{\boldsymbol{V}}_l} $^[15]:

其中$ {k_l} = \dfrac{{{k_{\text{s}}}}}{{\sqrt {{\lambda _l}} }} $. 可以将$ {{\boldsymbol{B}}_l} $表示为^[15]

通过推导, 区域2内部的场分布可以描述为^[15]

埋地旋电磁各向异性球体上的初始入射波是穿过平面的透射波, 如(5)式表示, 可以展开成球矢量波函数的表达式^[13,15]:

展开系数$ {p_{mn}} $和$ {q_{mn}} $分别为^[24]

标准函数$ {\widetilde \pi _{mn}}\left( {\cos \theta } \right) $和$ {\widetilde \tau _{mn}}\left( {\cos \theta } \right) $的定义由文献[24]给出, 其表达式如下:

其中, $ {\mathrm{P}}_n^m\left( x \right) $是连带勒让德函数. 同时, 区域1中地下埋藏旋电磁各向异性球体散射电磁场如下所示^[15]:

根据电磁场在球表面$ r = a $处的切向连续性, 并利用勒让德函数的正交性, 可得到以下方程组^[15]:

其中, 电尺寸参数定义为$ x=\left|k_1a\right| $, 并且定义$ {m_{\text{s}}} = {{{k_{\text{s}}}}}/{{{k_1}}} , {\overline k _l} = {{{k_l}}}/{{{k_{\text{s}}}}} , {m_{\text{s}}}{\overline k _l} = {{{k_l}}}{{{k_1}}} , {\overline k _l}{m_{\text{s}}}x = {k_l}a $. Riccati- Bessel函数$ {\varPsi _n}\left( z \right) $和$ {\xi _n}\left( z \right) $可以表示为: $ {\varPsi _n}\left( z \right) = z{{\mathrm{j}}_n}\left( z \right) $, $ {\xi _n}\left( z \right) = z{\mathrm{h}}_n^{\left( 1 \right)}\left( z \right) $, 其中$ {{\mathrm{j}}_n}\left( {kr} \right) $和$ {\mathrm{h}}_n^{\left( 1 \right)}\left( {kr} \right) $分别表示第一类和第三类的球贝塞尔函数.

详细的求解过程已在文献[15]中给出. 通过求解(29)—(32)式, 可以得到散射系数$ {a_{mn}} $和$ {b_{mn}} $. 在区域1中, 反射波$ {{\boldsymbol{E}}^{{\text{r2}}}} $和$ {{\boldsymbol{H}}^{{\text{r2}}}} $沿着$ - z $方向向界面传播. 根据镜像理论^[8], 平面上的反射和透射波在$ z = - d $处的表达式如下所示:

正如Nasr等^[12]所示, 各向异性介质球的散射波在平面上的反射可以等效为各向异性介质球的镜像球对该平面波的散射(镜像法), 其地面反射场在镜像坐标系(局部坐标系)中的场分量$ {{\boldsymbol{E}}^{{\text{r3}}}} $以$ \left( {{r_{{\text{img}}}}, {\theta _{{\text{img}}}}, {\phi _{{\text{img}}}}} \right) $表示, 而在全局坐标系中, 各向异性介质球的散射场透过地平面的场分量$ {{\boldsymbol{E}}^{{\text{t3}}}} $以$ (r, \theta , \phi ) $表示. 局部坐标系的原点位于镜像球体的中心, 如图2所示. 假设自由空间的磁导率$ {\mu _0} $和各向同性导电介质的磁导率$ {\mu _1} $都为1. 在平面上点 P 处存在$ r = {r_{{\text{img}}}} = d $, $ \theta = {{\pi}} $, $ {\theta _{{\text{img}}}} = 0 $, $ \phi = {\phi _{{\text{img}}}} = 0 $. 最终得到由透射系数$ a_{mn}^{\text{t}} $, $ b_{mn}^{\text{t}} $和反射系数$ a_{mn}^{\text{r}} $, $ b_{mn}^{\text{r}} $组成的矩阵, 具体表达式如下所示:

其中, $ {m_{mn}}\left( {\theta , \phi } \right) $和$ {n_{mn}}\left( {\theta , \phi } \right) $表达式如下^[13]:

利用加法定理^[20], 可以将反射波$ {{\boldsymbol{E}}^{{\text{r3}}}} $从局部坐标系转换到全局坐标系, 其具体形式如下:

根据加法定理, 可以展开3个向量$ {\boldsymbol{r}} $, $ {\boldsymbol{r}}' $和$ {\boldsymbol{r}}'' $之间的关系, 其具体形式如下所示^[19]:

其中$ {A_{nm, vu}} $和$ {B_{nm, vu}} $表示加法定理的变换系数, 可以通过递归方法求得其具体值^[20]. 将(41)式和(42)式代入(40)式, 并与式(33)式进行比较, 可以推导出展开系数$ c_{mn}^{\text{r}} $和$ d_{mn}^{\text{r}} $的矩阵形式如下:

求解系数$ c_{mn}^{\text{r}} $和$ d_{mn}^{\text{r}} $, 将其代入(40)式, 进一步推导出全局坐标系中的反射电场. 从(21)—(33)式进行迭代, 直到在点P处收敛. P点电场的计算表达式表示如下:

为了计算沿Y轴一条直线上的电场分布, 首先确定图2中所示的固定点P处的电场. 这个过程从计算方程(29)—(32), 获得一系列的散射系数$ {a_{mn}} $和$ {b_{mn}} $开始, 然后通过一系列计算, 结合镜像方法、球面矢量波函数的加法定理和边界条件, 推导出点P处的电场. 在此基础上, 利用在点P处的电场, 计算出方程(27)和(28)中电场系数$ {a_{mn}} $和$ {b_{mn}} $. 最后, 通过得到的系数$ {a_{mn}} $和$ {b_{mn}} $, 结合位置坐标$ \left( {r, \theta , \phi } \right) $变化, 可以利用方程(27)和(28)计算平面上沿Y轴不同位置的电场分布. 这一系统化的方法能够准确描述沿L线的电场变化, 为全面理解不同位置的电场分布提供了依据, 同时有助于深入探索复杂地下环境中的散射特性.

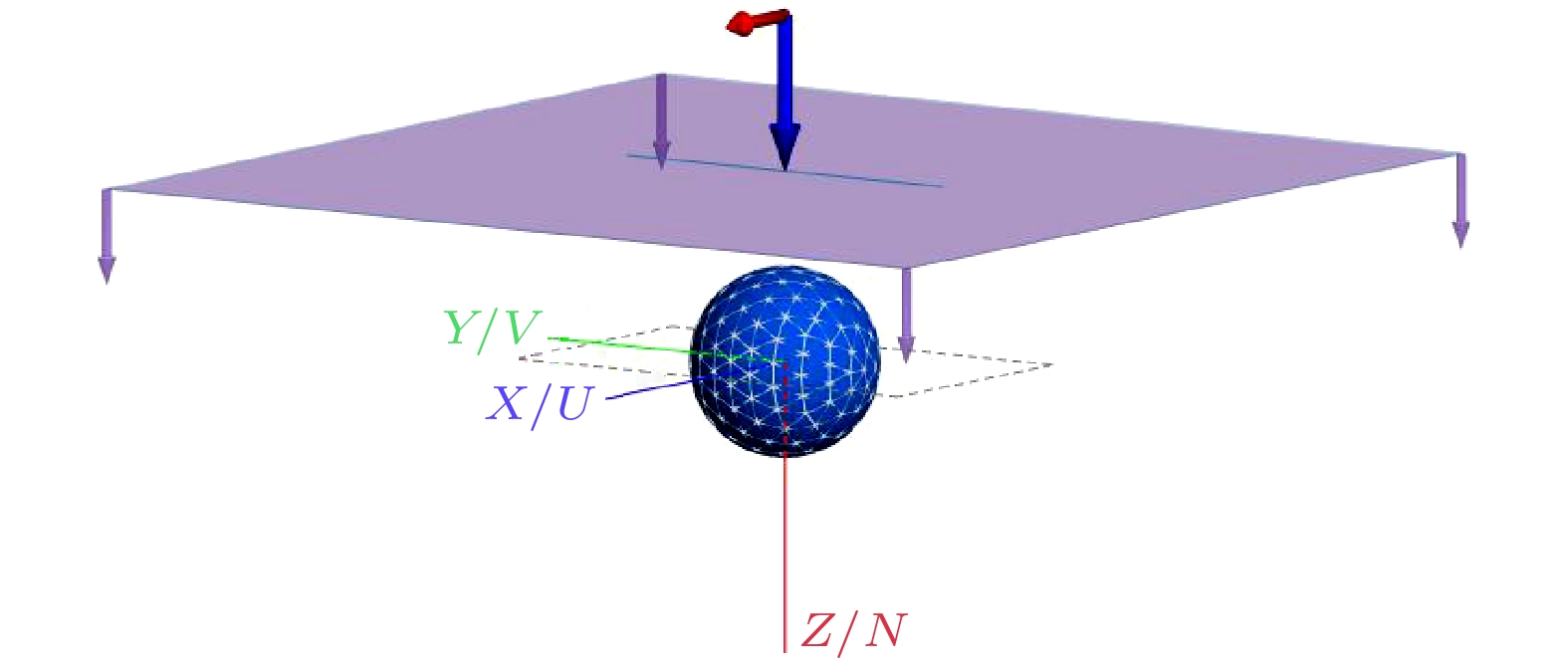
在本文的数值分析中, 选取了地平面上沿Y轴直线L(0, y, –d)上的多个离散点, 计算了各点的电场强度, 其中y的取值范围为–20—20 m. 计算工作在一台配备Intel(R) Core(TM) i7-1360P处理器和32 GB内存的笔记本电脑上完成, 基于上部分推导得到的公式, 采用FORTRAN编写程序实现了电场分布的计算, 同时给出了FEKO仿真的结果, FEKO具体仿真图如图3所示. 其中U/V/N 是局部坐标系, 分别对应水平方向、垂直方向和法向方向, 类似于局部坐标系中的X/Y/Z轴. 埋地旋电磁各向异性球体的介电常数和磁导率分别设定为$ {\varepsilon _{\text{t}}} = 15, {\varepsilon _{\text{g}}} = 2, {\varepsilon _{\text{s}}} = {\varepsilon _0}, {\mu _{\text{t}}} = 8, {\mu _{\text{g}}} = 1, {\mu _{\text{s}}} = {\mu _0} $, 区域1的相对介电常数设为$ {\varepsilon _{{\text{r1}}}} = 3 $, 相对磁导率$ {\mu _{{\text{r1}}}} = 1 $, 电导率$ {\sigma _1} $为0.002 S/m. 旋电磁各向异性介质球半径a为10 m. 上述这些参数设置在下面分析中保持不变.

通过改变入射波频率f和埋藏深度d, 得到了相应的计算结果和FEKO仿真数据, 如图4—图6所示. 此外, 针对不同参数特性, 计算了球矢量波函数解析解与FEKO仿真结果的计算时间, 具体参数如表1所列. 结果表明, 所提出的球矢量波函数方法在计算时间上显著优于FEKO仿真, 充分体现了该方法在处理特定散射问题时的高效性.

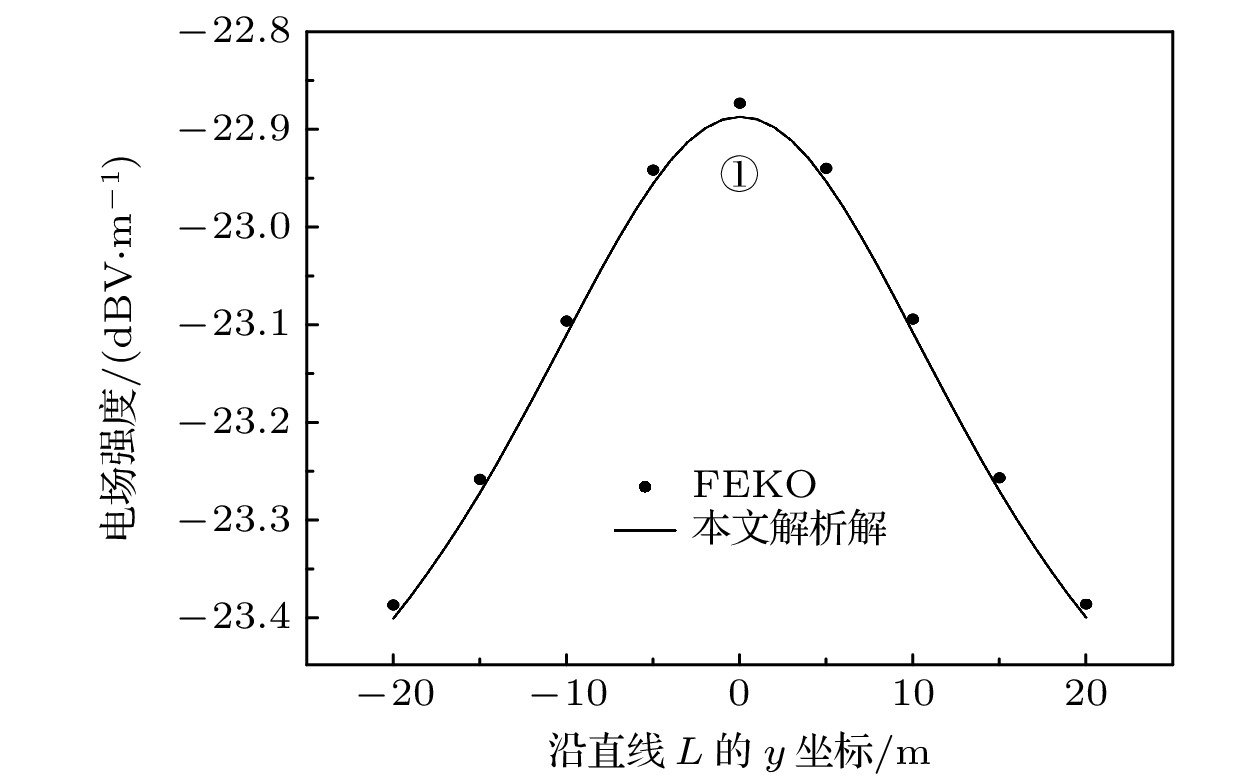
图4展示了平面上沿Y轴直线L的电场强度分布, 对比了本文提出的球矢量波函数解析解结果与FEKO仿真数据. 图中的折线代表本文球矢量波函数解析解(下文简称解析解)的计算结果, 散点则对应FEKO仿真结果. 图4的具体参数设置如下: 入射波频率f为40 kHz, 埋藏深度d为20 m.

由图4可见, 解析解与FEKO仿真结果符合较好, 平均相对误差为0.059%, 验证了所提解析解的正确性. 电场强度在y = 0处达到最大值, 并随着距离增大呈现对称性减小的趋势, 反映出球体附近电场分布的局部增强特性.

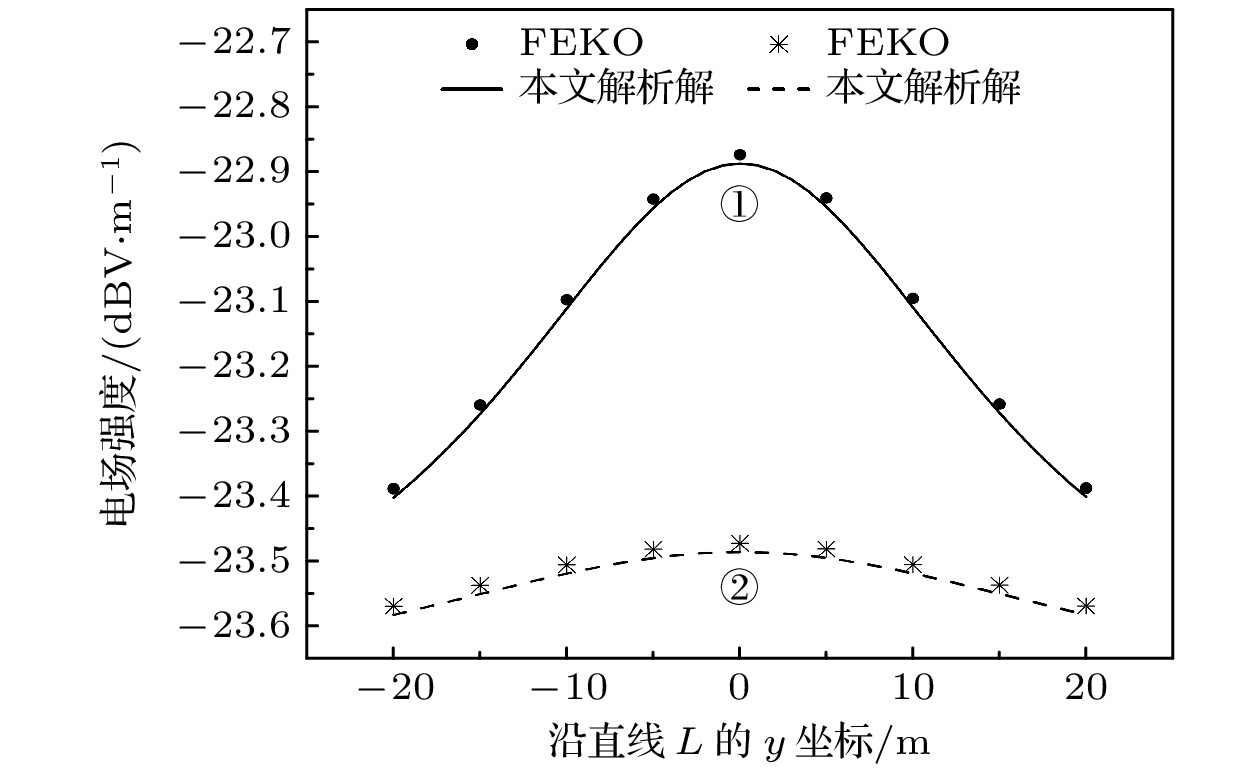
图5展示了入射波频率分别为f = 40 kHz和f = 50 kHz时, 平面上沿Y轴直线L的电场强度分布对比, 埋藏深度设置为d = 20 m. 曲线①表示频率f = 40 kHz时的电场分布, 其中黑色实线为本文解析解结果, 黑色实心圆点为FEKO仿真结果; 曲线②表示频率f = 50 kHz时的电场分布, 其中黑色虚线为本文解析解结果, 黑色星号为FEKO仿真结果.

随着入射波频率的增大, 电场强度整体呈上升趋势. 这种变化是由于在旋电磁各向异性介质球半径不变的情况下, 随着入射波的频率增大, 球目标的电尺寸随之增大, 这样所得的散射场的场强也随之增大. 从图5可以看出, 本文提出的解析解与FEKO仿真结果在不同频率下均保持高度一致. 低频f = 40 kHz(曲线①)和高频f = 50 kHz(曲线②)条件下的平均相对误差分别为0.059%和0.078%. 这表明, 本文方法在不同频率下具有良好的准确性和适用性.

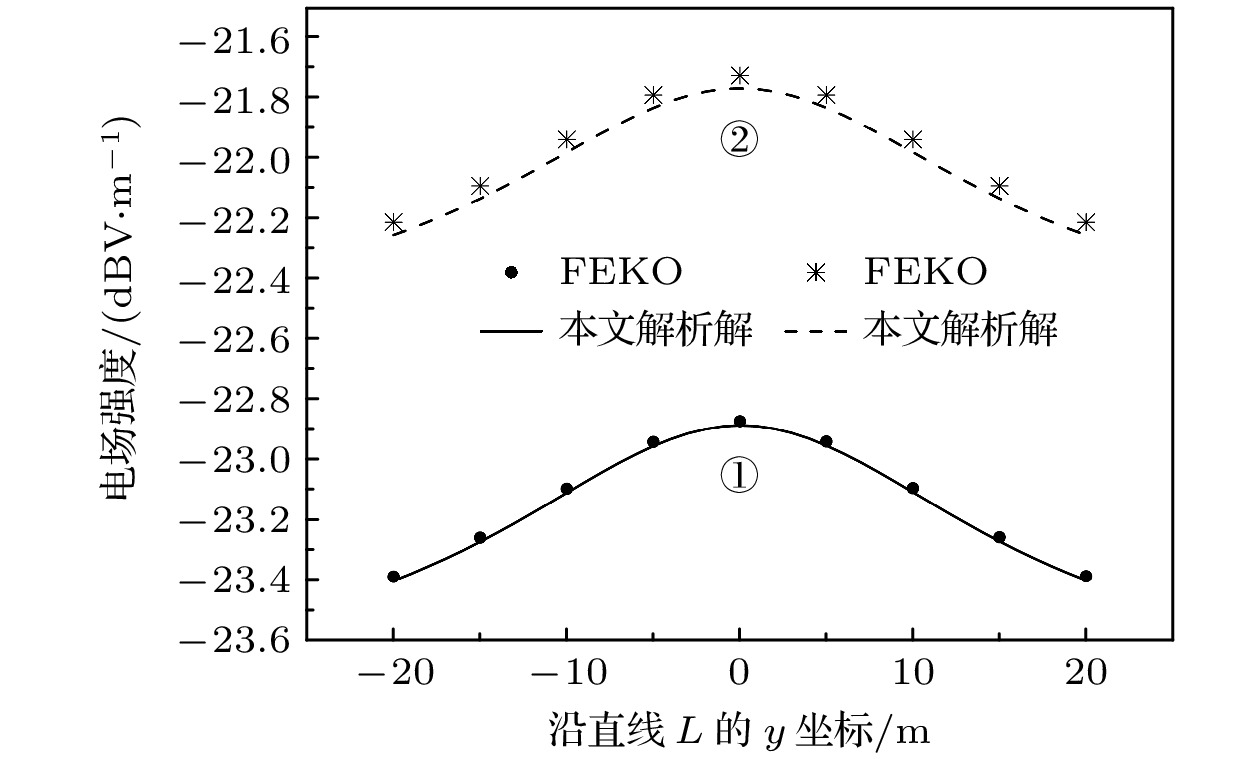
图6展示了不同埋藏深度下沿Y轴直线L的电场强度分布对比, 入射波频率设为f = 40 kHz. 其中, 曲线①表示埋藏深度d = 20 m, 黑色实线为本文提出的解析解的结果, 黑色圆点为 FEKO 仿真结果; 曲线②表示埋藏深度d = 30 m, 黑色虚线为本文解析解结果, 黑色星号为 FEKO 仿真结果.

由图6可以看出, 随着埋藏深度的增大, 电场强度整体呈现减弱趋势, 并且最大值与最小值之间的差异显著减小, 这是因为埋地深度的增大, 各向异性介质球散射场回到地面的距离变长, 其场强也就相应地减小. 深埋时电场分布更加平滑, 局部的波峰和波谷特性逐渐消失. 这主要是由于电磁波在传播过程中受到介质吸收, 能量随深度增大发生明显衰减, 同时散射波与入射波的干涉效应减弱, 导致电场分布的局部增强特性逐渐平滑化. 本文提出的解析解与FEKO仿真结果在不同埋藏深度条件下均保持高度一致, 浅埋d = 20 m (曲线①)和深埋d = 30 m (曲线②)条件下的平均相对误差分别为0.059%和0.056%, 误差极小, 充分验证了解析方法的准确性和可靠性.

本文给出了一种针对地下旋电磁各向异性介质球电磁散射问题的解析解方法, 结合T矩阵法、镜像法和球矢量波函数及其加法定理, 分析了地面上平行于球轴、沿Y轴的直线L上电场强度的分布. 和已有方法相比, 有以下特点: 首先, 在计算地下特定目标(各向异性介质球)的散射特性时, 球矢量波函数解析解结果与FEKO仿真结果高度一致, 计算效率显著提高, 验证了所提出的球矢量波函数方法在处理特定模型的准确性和高效性. 其次, 本文系统分析了入射波频率f以及埋藏深度d对电场强度分布的影响, 结果表明, 所提方法在处理不同物理参数变化时展现出较强的灵活性与适应性. 与传统解析方法^[12–14]仅能计算单点电场强度不同, 本文方法实现了平面上沿Y轴直线的电场分布计算, 显著拓展了计算范围, 提供了更为全面的电场空间分布信息. 最后需要说明的是: 本文的方法目前主要针对旋电磁各向异性介质球, 假设主轴平行于z轴, 且相关矩阵是基于这一假设构建的. 未来的研究可以进一步探讨如何将该方法推广到任意各向异性球体的散射问题, 并详细分析当主轴不平行于z轴时的计算方法. 此外, 本文所给出的矢量波函数方法目前主要适用于规则几何形状, 对于复杂几何结构或多层介质, 其适用性仍存在一定的局限性. 未来的研究还可以扩展该方法的适用范围, 针对复杂几何形状及多层介质结构中的电磁散射问题开展深入研究, 进一步提高方法的计算精度与应用广度, 以满足更复杂工程场景的需求.