-
白激光是一种超连续激光(supercontinuum, SC). 超连续激光指的是具有几百至几千纳米的超宽谱带的激光[1–3]. 白激光指的是谱带覆盖可见光波段的超连续激光. 超连续激光的产生通常通过将一个窄带入射脉冲聚焦至介质中, 使局部光强足够高, 从而激发介质中的多种非线性效应[4]. 常见的非线性机制包括: 光孤子效应[5,6]、四波混频[7]、克尔效应[8,9], 以及自相位调制(self-phase modulation, SPM)等[10–13]. 在过去10年中, 本课题组系统性地发展了基于钛宝石飞秒激光的白激光技术[14–20]. 在这些方案中, 白激光由钛宝石飞秒激光器经过多种非线性效应产生, 在获得超宽谱带的同时保留激光的特性, 如高强度和相干性. 这样的光源在多个领域具有广阔的应用前景. 其中, 多通道共聚焦显微镜、白光干涉测量以及彩色全息三维显示是三大关键潜在应用, 值得深入探索. 多通道共聚焦显微镜是一种高精度的彩色显微成像技术, 通常需要高强度激光, 并能够快速切换波长[21]. 相比传统的多种单色激光集成方案, 白激光可以更方便地切换波长, 并提供更多的颜色. 白光干涉测量是一种利用宽光谱光源通过干涉进行高精度三维表面形貌测量的技术[22]. 与传统的相干性较差的白光, 如 LED 或卤素灯相比, 白激光在该应用中可以显著提高分辨率并增强抗噪能力. 此外, 彩色全息[23]被认为是三维(three dimensional, 3D)显示技术的“圣杯”, 其原理是利用干涉条纹记录并重建光的 3D 波前. 相比于传统的单色激光(其全息图只能呈现单色), 白激光覆盖整个可见光谱, 使得彩色全息成为可能, 不仅能够扩展色彩范围, 还能提升全息图的色彩精确度.
在这些应用中, 白光干涉测量和彩色全息都需要白光具有干涉能力, 良好的空间相干性是实现干涉成像的必要前提, 是决定白激光性能和可行性的关键因素. 因此, 研究人员在选择白激光作为光源时, 必须考虑其空间相干性. 然而, 尽管已有许多超连续激光被提出, 却几乎没有对这些超连续激光空间相干性进行测量和分析的研究. 在以往仅有的少量相关研究中, 有研究仅分析了超连续激光的波前. 2018年, Kueny等[24]对一束白光超连续激光的波前进行了分析. 从实验结果看来, 该激光的波前形变较严重, 光斑呈现非圆形且光斑强度分布不均匀. 还有少部分研究仅对相干性进行模拟分析, 未进行实际的测量并提供具体的测量数据. 比如, Genty等[25]提出了一种分析白激光空间相干性的理论模型. 采用非平稳光的二阶相干理论研究超连续激光脉冲的相干特性, 展示了如何通过对单个脉冲集合的数值模拟构建时域和频域的二阶相关函数, 并提出两种便捷的模式表示方法. 该研究只停留在理论模拟分析, 仍然未进行实际的测量. 还有Melnik等[26]建立了数学模型去分析超连续激光的时间相干性. 通过理论分析和数值模拟, 揭示了连续谱的相干时间取决于输入脉冲的不同参数这一特性可归因于相干时间与相位调制系数之间的关系. 但这仍然是一项停留在模拟分析阶段的研究. 唯一涉及实际测量的研究是一项有关超连续激光相干长度测量的研究. Zeylikovich 和 Alfano[27]测得一台超连续激光在550 nm中心波长处的相干长度为1.6 μm. 然而, 该研究仅分析了超连续谱单一波长的时间相干性, 并未对超连续激光全谱段的空间相干性进行测量.
综上所述, 虽然近年来很多白激光(超连续激光)被提出, 许多研究中也都提到并验证了其宽谱带的特点[28–32]. 但是对它们作为激光的光束性能, 如波前、偏振以及相干性进行测量和分析的研究却是缺失的. 尤其是白激光的相干性并没有得到验证. 这将会限制白激光的实际应用. 为了解决这一基础光学与应用物理学中的重要问题, 本研究对本课题组近年研制出的一种高强度超平谱带白激光的空间相干特性进行了分析[18–20]. 如图1所示, 先简单介绍了该白激光的产生原理, 提供白激光同时具有白光和激光特征的理论支撑. 然后设计实验对白激光的波前强度特征、偏振特征以及空间相干性进行测量. 测量结果显示白激光继承了钛宝石飞秒激光的波前强度特征, 具有准高斯分布的波前强度, 光斑分布均匀. 白激光的偏振呈线偏振, 是激光才拥有的明显特征. 最后, 搭建杨氏双缝干涉(Young’s double-slit interferometer, YDSI)实验光路, 让白光可见光波段的8个分量分别产生干涉条纹, 测得这些条纹的平均对比度是0.77. 这表明白激光具有良好的相干性. 3个实验结果均证明白激光同时具有白光和激光的特征, 为白激光在需要使用具有高强度相干性白光领域的应用提供了有力的参考. 本实验结果将促进白激光这一优秀光源在各领域的实际应用, 推动各行业的发展.
-
白激光属于一种超连续激光, 具有超宽的谱带. 频谱覆盖了整个可见光波段的超连续激光又被称为白激光. 白激光主要是通过非线性效应产生的. 最常见的方法包括多种三阶非线性(third-order nonlinear, 3rd-NL)效应, 例如自相位调制(self-phase modulation, SPM)、四波混频和受激拉曼散射, 这通常在光子晶体光纤(photonic crystal fiber, PCF)[8]等微结构器件中实现. 然而, 单纯依赖三阶非线性效应进行谱展宽时, 往往在光谱平坦度和能量分布方面存在局限. 例如, 在展宽后的光谱中, 400 nm 附近的能量较低, 而800 nm 处(即钛宝石飞秒激光中心波长)的能量依然保持较高, 导致整个光谱呈现出明显的不均匀分布, 波长越远离中心波长, 其能量越低. 这种不平衡会限制对光谱带宽、平坦度及脉冲能量的同时优化.
在过去十年中, 本课题组提出并发展了一种新的方法, 即结合二阶(second-order nonlinear, 2nd-NL)和三阶非线性效应来产生飞秒白激光[14–20]. 通过优化了2nd-NL 和 3rd-NL 效应的单独功能及其协同作用, 最终实现了一种高性能的飞秒白激光[20]. 该激光具有高脉冲能量(~1.1 mJ)、超宽带宽和超高光谱平坦度(3 dB的衰减光谱带宽覆盖385—1080 nm, 跨越近紫外、可见光和近红外区域).
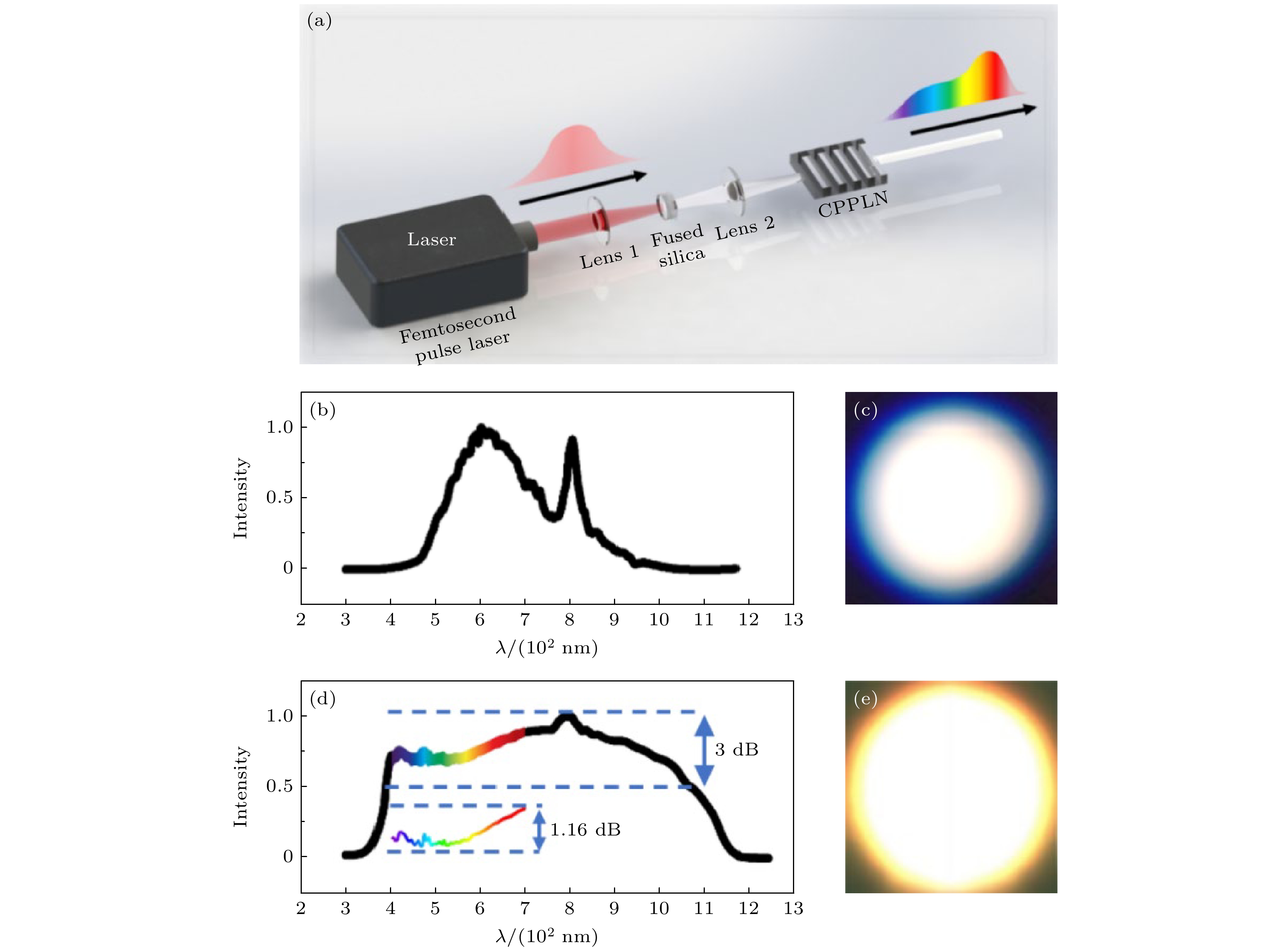
为了更好地了解该白激光的性能, 图2(a)展示了其产生原理和过程. 在该实验装置中, 本研究采用一台钛宝石飞秒激光器作为泵浦光源(脉冲能量最高可达4 mJ, 中心波长为800 nm, 脉冲宽度约为50 fs, 重复频率为1 kHz). 首先, 光束经透镜1聚焦后进入熔融石英, 并随后经透镜2聚焦进入啁啾周期极化铌酸锂晶体(chirped periodically polarized lithium niobate, CPPLN). CPPLN晶体的结构参数是结合熔融石英的输出特性专门设计的, 二者在参数配置上相辅相成, 实现了最优的协同作用, 并取得了优异的光谱展宽效果[20]. 需要强调的是, 本实验使用的高性能飞秒脉冲激光器完全由本课题组自主研制.
在实验中, 使用了一块普通的熔融石英平板(厚度8 mm)来实现三阶非线性展宽. 其中, SPM效应在展宽过程中起到了最主要的作用, 将输入的钛宝石飞秒激光(3 dB光谱带宽为20 nm)展宽为具有约300 nm, 3 dB光谱带宽的超连续白激光. 熔融石英平板后的光谱和光斑分别显示在图2(b), (c)中. 光斑呈现出蓝色调, 这是由于红色波段的凹陷所致. 为了进一步拓宽光谱并增强能量在整个带宽范围内的分布, 采用了一块自主研制的CPPLN薄板晶体(长度20 mm、厚度2 mm、宽度6 mm)能够实现准相位匹配. 该晶体利用二阶非线性效应有效地对高能量光谱成分进行转换和再分布, 使能量分布能够自适应调整, 从而显著提高光谱平坦度. 经过CPPLN后的光谱和光斑分别如图2(d), (e)所示. 由图2(d), (e)可见, 最终从熔融石英-CPPLN级联非线性光学模块输出的信号激光是一束宽谱带的、光谱平坦的白光飞秒激光.
图2(d)展示了本课题组自主研制的白激光的测量光谱, 其3 dB带宽覆盖385—1080 nm, 表明该白激光具有近700 nm的3 dB超宽带宽, 展现出超平坦的光谱特性. 图2(d)插图进一步表明, 在可见光波段(400—700 nm)内, 该白激光的光谱平坦度更佳, 在300 nm的带宽内光谱波动仅为1.16 dB, 达到了极高的高平坦度. 图2(e)显示了白激光的光斑, 呈现为均衡的白光, 并略带黄色调. 这主要是由于红光强度增强了, 使其外观类似于自然阳光. 此外, 本研究测得该白激光在可见光范围内的平均光谱能量强度为1.45 μJ/nm(或在 10 nm 带宽内约为 14.5 μJ), 其光谱功率强度在10 nm带宽内甚至可达约30 MW. 这对于白光甚至白激光而言都是一个相当高的光谱强度水平.
-
在实验中, 本研究使用8个滤波片从白激光中提取八束准单色波, 其具体参数见表1. 这8个滤波片的中心波长分别为 405 nm, 450 nm, 500 nm, 532 nm, 580 nm, 600 nm, 635 nm 和 700 nm, 覆盖整个可见光谱范围, 对应的颜色从紫蓝色、蓝色、青色、绿色、黄色、橙色到红色. 由于超窄带滤波片(如 1—3 nm 带通滤波片)价格昂贵, 本研究选择使用 10 nm 带宽的滤波片, 以提取不同波 长的光波. 通过这种方式, 能够基于这个高性能、超短脉冲、强度高且光谱极其平坦的白激光, 以简单的方法获得8束准单色激光. 这些准单色激光的性能将很好地反映白激光的整体特性.
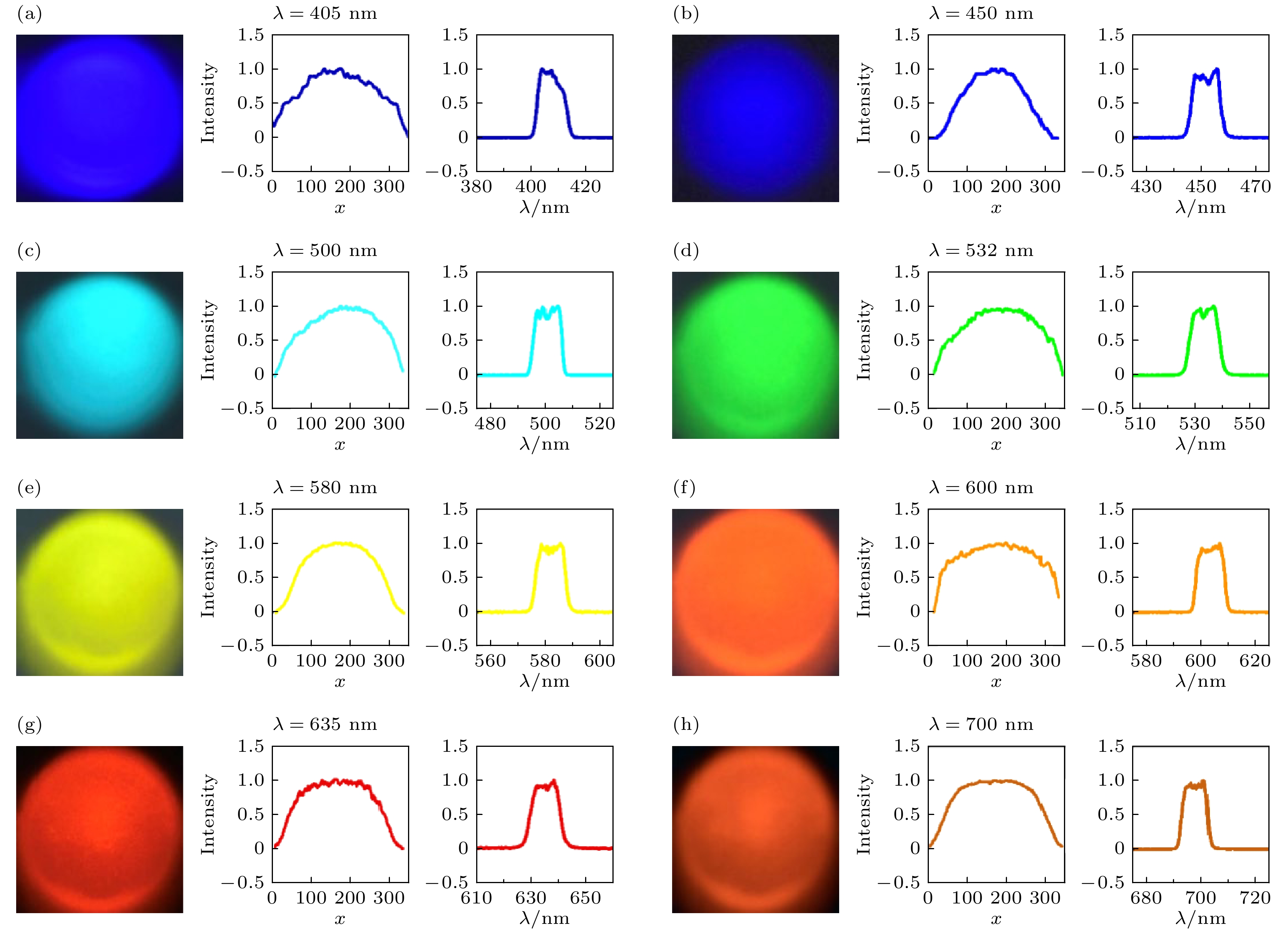
本研究首先对每束选定的准单色激光的波前强度形态进行测量. 经过准直后的光束波前强度图像由佳能数码相机拍摄, 并展示在图3(a)—(h)中. 在每个波前图像的右侧, 有两幅线状图: 中间图显示对应的光斑的线强度分布, 最右侧图则描绘光谱分布. 这些图像表明, 每束光波均形成了高质量的准高斯波前强度, 与钛宝石飞秒泵浦激光的优良高斯波前强度高度相似. 除了光束剖面的圆形光斑形状良好外, 每束选定光波在整个光束横截面上的颜色均匀性也非常出色, 未呈现明显分布不均. 这种优异的波前质量表明, 通过宏观非线性频率转换与光谱展宽模块自主研制的白激光, 在整个频率范围内展现出了卓越的均匀性. 实验结果图3表明, 这种宏观非线性光学模块不仅能够有效保持泵浦光的波前强度特性, 同时也极好地实现了其设计目标——频率转换与光谱展宽, 从而展现出卓越的整体性能. 因此, 有理由期待, 白激光也保留了泵浦光飞秒激光优良的空间相干性.
-
偏振也是激光器的重要性能之一. 一个好的激光器通常是线偏振的. 因此, 除了相干性分析外, 本研究还补充了对白激光偏振特性的分析, 使用光功率计检测通过偏光片后的八束准单色波的功率. 在偏振片后有一个衰减片, 控制最大的输出光功率低于光功率计的最大值. 当旋转偏光片时, 功率会发生变化. 对于每个波长, 记录最大功率和最小功率及其对应的角度. 具体数据详见表2. 本研究发现最大功率和最小功率之间的差异超过100倍, 并且所有对应最大功率的角度主要集中在0°, 仅有少数波长略有1°的偏差. 因此, 根据马吕斯定律, 可以认为该白激光具有良好的线偏振性质. 这个结果再次验证了本课题组白激光的优异性能.
-
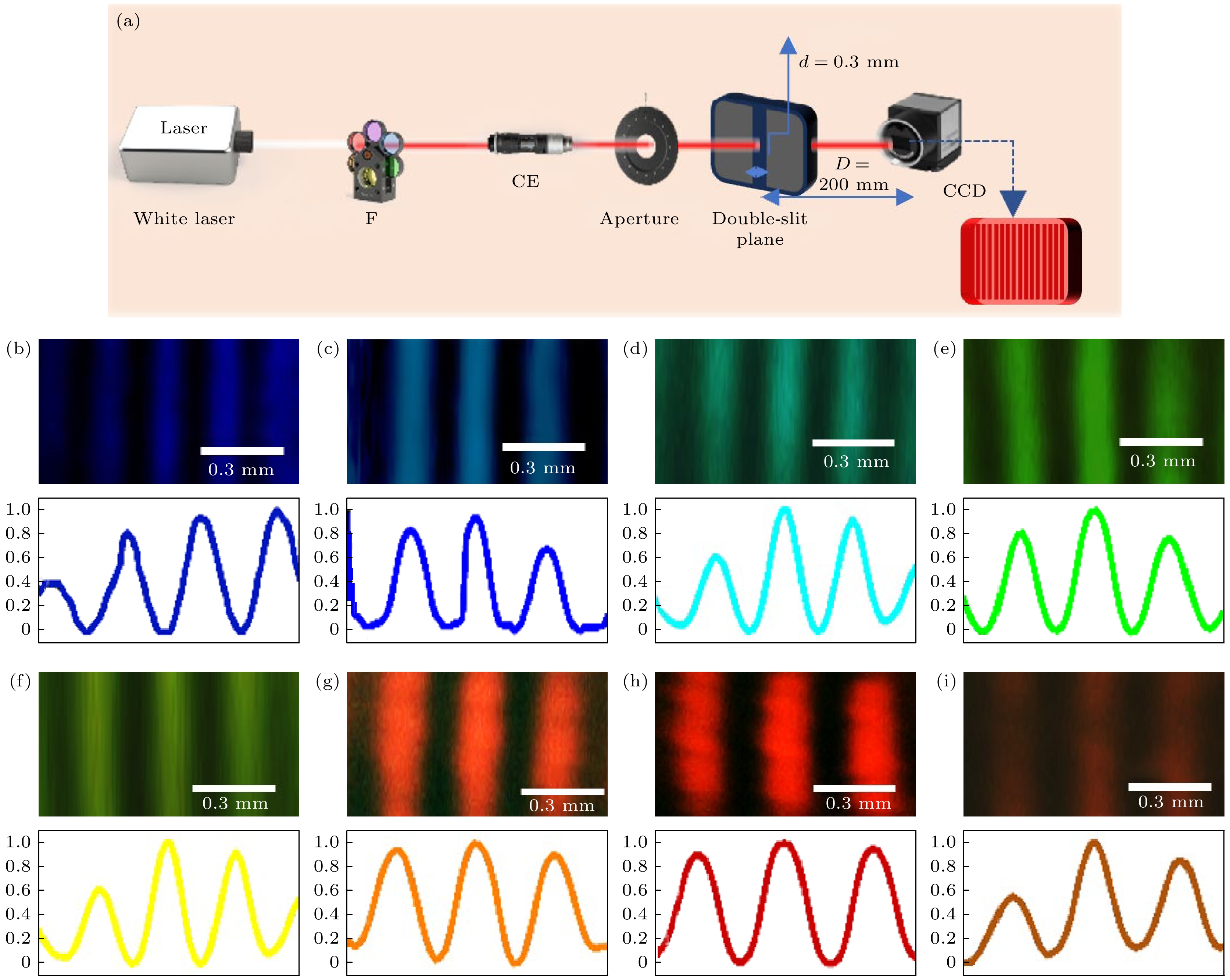
评估白激光空间相干性的需要通过干涉条纹对比度(interference fringes visibility), 实现此功能的标准实验装置是著名的YDSI. 激光束通过YDSI的两个狭缝, 产生来自不同位置的两个次级传输的衍射光束. 这两个衍射光束同时到达记录平面, 在记录平面生成干涉条纹. 图4(a)所示为本研究实验设置的光路, 类似于经典的杨氏双缝实验, 但使用了白激光和装有带通滤波片的转轮. 两个狭缝之间的空间间距d为0.3 mm. 双缝平面与CCD入口平面之间的距离D为200 mm. 根据著名的杨氏双缝干涉条纹间距公式
$ x=D\lambda /d $ , 可以计算出波长在405—700 nm之间时, 干涉条纹的间距x范围为0.27—0.47 mm. 图4(b)—(i)显示了不同波长下的干涉条纹的CCD 记录图像, 并展示了强度线图和对应的干涉条纹对比度$ \upsilon $ 值, 其定义为(条纹的最亮值-条纹的最暗值)/(条纹的最亮值+条纹的最暗值). 除了600 nm和700 nm波长外, 其他波长的光的$ \upsilon $ 在0.6—0.7之间. 大多数波长的$ \upsilon $ 均超过0.7. 此外, 所有波长的平均$ \upsilon $ 为0.77, 满足优秀相干性的要求.在可见光波段选取的8个典型波长分量中, 均在YDSI系统中观察到具有较高对比度的干涉条纹. 这表明白激光在可见光范围内具备良好的空间相干性, 可以被应用于需要相干性白光的领域. 此外, 结合这些波长分量所展现出的准高斯分布的均匀波前强度特征与一致的线性偏振状态, 可以推测在白激光的产生过程中, 非线性过程虽引发了谱展宽, 但对光束的相干性及波前质量影响较小. 这表明白激光在很大程度上保留了钛宝石飞秒激光的优良光束特性, 表现出较强的激光空间相干性. 相干性的本质是光波之间保持稳定的振幅和相位关系, 因此带宽大小会影响测量结果. 一般而言, 带宽越窄, 相干性表观上越强. 虽然本实验中因节约成本而使用了带宽为10 nm的滤波片, 属于相对较宽的窄带, 但在该条件下, 白激光各波长分量仍表现出良好的空间相干性, 这在实验结果中已有清晰的体现. 该结果也间接表明: 若在更窄带宽条件下进行测试, 有望获得更高的干涉条纹对比度, 从而展示出更好的空间相干性.
-
综上所述, 本研究实施了对课题组所自主研制的高性能白激光的激光特性, 尤其是空间相干性进行了细致的测量. 实验结果表明, 所研制的白激光在多个方面表现优异, 包括超平坦光谱分布(可见光波段内光谱波动约1.16 dB)、高光谱能量(每10 nm 带宽约14.5 μJ)、空间相干性(空间干涉条纹平均对比度约0.77)以及偏振特性(线偏振). 本研究对超宽带、超平坦白激光空间相干性的测量工作, 为需要使用白色光源的领域提供了重要的实验数据作为应用参考, 有助于推动其发展. 例如, 在显微成像领域, 激光的光谱平坦性、能量强度数据以及光波波前强度的特征可为多通道共聚焦显微镜提供参考, 因为该设备需要高强度、可快速切换波长且光斑均匀的激光源. 在层析成像领域, 空间相干性是白光干涉测量中的关键参数, 空间相干性越好测量精度越高, 但测量范围相应缩小. 不同的测量需求对应不同要求的相干性, 需要对光源的相干性特征有具体的掌握. 在全息成像领域, 干涉条纹的对比度和偏振特性至关重要. 由于全息术的基本原理依赖于干涉图案的记录, 空间干涉条纹的对比度直接影响重建图像的质量, 因此该参数对于彩色全息术具有重要的参考意义.
尽管这类高相干性、超平坦、高强度的白色激光具有巨大应用潜力, 并为多个领域提供了广阔的发展空间, 但仍需具体的性能数据以便更好地利用这一新型激光光源. 因此, 本研究对自主研制的高强度、超平坦白色激光光束的相干性进行了系统测量与分析, 为未来白激光在彩色全息、3D 表面层析、3D 彩色显示、显微成像等多个领域的实际应用提供了有价值的概念性指导, 将推动相关领域的发展.
高强度、超平坦白激光的空间相干性测量
Spatial coherence analysis of intense ultra-flat white laser
-
摘要: 白光通常被认为是非相干的, 然而, 近年来广受关注的超连续激光白激光具有激光强度高、相干性好的特点, 挑战了这一局限性. 尽管白激光已经被提出并在技术上得到了广泛的发展, 但对其光波性能, 尤其是空间相干性的具体分析却十分缺乏, 这在一定程度上限制了其实际应用. 本文对课题组2023年自主研制的由高强度飞秒激光通过二阶、三阶非线性效应展宽谱带所产生的高强度、超平坦谱带白激光开展了波前强度、偏振特性以及空间相干性的详细实验研究和分析. 通过使用带通滤波片从白激光中提取多个分量, 利用杨氏双缝干涉仪测量干涉条纹的对比度, 以评估其空间相干性. 实验结果显示, 白激光的波前强度呈准高斯分布, 光斑均匀, 是线偏振光. 白激光在杨氏双缝干涉仪中产生的可见光波段平均干涉条纹对比度是0.77, 表明其具有优异的空间相干性. 本研究将为白色激光在彩色全息、白光干涉仪表面层析、显微成像及其他需要具有一定相干性的白光的应用领域提供有价值的指导.Abstract:
White light is typically considered incoherent; however, the recently popular supercontinuum laser, also known as white laser, spans the visible spectrum and features high laser intensity and good coherence, challenging this traditional limitation. The white laser has a wide range of applications, including multi-channel confocal microscopy, color holography, and white light interferometric surface topography. Although white lasers have been proposed and developed extensively in terms of technology, specific analyses of their optical wave properties—especially spatial coherence—are still lacking. Since many applications impose certain requirements on the spatial coherence of white light, the lack of research into the spatial coherence of white lasers has, to some extent, limited their practical use. This paper presents a detailed experimental study and analysis of the wavefront intensity, polarization characteristics, and spatial coherence of the high-intensity ultra-flat spectrum white laser that was independently developed by our research group in 2023. The laser is generated by broadening the spectrum of a high-intensity Ti:sapphire femtosecond laser through second- and third-order nonlinear effects. A bandpass filter is used to extract eight components from the white laser, with a central wavelength range from 405 nm to 700 nm and a bandwidth of 10 nm for each component. By measuring the performance of these eight quasi-monochromatic lasers, the characteristics of the white laser of the entire visible spectrum can be evaluated. The CCD imaging of the collimated quasi-monochromatic laser spots reveals that their wavefront intensities exhibit a quasi-Gaussian distribution with uniform beam profiles. Polarization measurements by using polarizers at various angles show that the white laser is linearly polarized. A Young’s double-slit interferometer is used to measure the interference fringe contrast of the eight quasi-monochromatic beams to assess their spatial coherence. The experimental results show that the average interference fringe contrast of the entire visible spectrum is 0.77, and the difference between different wavelengths is very small.This indicates that the white laser has excellent spatial coherence in the visible range. The eight quasi-monochromatic lasers in the visible spectrum all exhibit quasi-Gaussian wavefront intensity distributions, linear polarization, and high spatial coherence. This indicates that the white laser inherits the excellent properties of the Ti:sapphire laser. All of these data provide valuable guidance for the application of white lasers in color holography, white light interferometric surface tomography, microscopic imaging, and other fields that require white light with a certain degree of coherence. -
Key words:
- white laser /
- spatial coherence /
- interference fringe visibility .
-

-
图 2 白激光的产生原理和基本信息 (a) 产生飞秒白激光的光路图, 该激光通过高强度钛宝石飞秒脉冲激光束经过熔融石英-CPPLN二阶与三阶非线性协同频率转换模块产生; (b)经过熔融石英平板后的光谱测量结果; (c) 经过熔融石英平板后的激光光斑; (d) 白激光的测量光谱, 展现出超平坦的光谱特性, 其中彩色带表示可见光范围, 其放大图显示在插图中; (e) 系统最终输出的白激光的光斑
Figure 2. Basic information of the white laser: (a) Schematic diagram of a homemade femtosecond white laser created by sending an intense Ti:sapphire femtosecond pulse laser beam through a fused silica-CPPLN 2nd-NL and 3rd-NL synergistic nonlinear frequency conversion module. (b) The measured spectrum of the light after the fused silica plate. (c) The spot of the laser after the fused silica plate. (d) The measured spectrum of the white laser shows the ultra-flat spectral profile. The color band represents the visible range, whose enlarged view is shown in the inset. (e) The spot of the white laser beam.
图 3 波前强度分析, 即白激光通过中心波长分别为(a) 405 nm, (b) 450 nm, (c) 500 nm, (d) 532 nm, (e) 580 nm, (f) 600 nm, (g) 635 nm, (h) 700 nm, 带宽为 10 nm 的滤波片后, 不同光谱成分的波前强度(左)、线强度分布(中)和光谱分布(右)
Figure 3. Wavefront analysis. Wavefront (left), line profile (center), and spectral profile (right) of the white laser at different spectral components in the visible band when it passes through 10 nm bandwidth filters centering at the wavelength of (a) 405 nm, (b) 450 nm, (c) 500 nm, (d) 532 nm, (e) 580 nm, (f) 600 nm, (g) 635 nm, and (h) 700 nm
图 4 杨氏双缝实验的实验结果 (a)杨氏双缝实验的光路图, 其中F为带有不同滤波片的可旋转支架, CE为光束准直扩束系统; (b)—(i) 八种波长的干涉条纹和强度线轮廓图, 其中(b) λ = 405 nm,
$ \upsilon $ = 0.86; (c) λ = 450 nm,$ \upsilon $ = 0.86; (d) λ = 500 nm,$ \upsilon $ = 0.75; (e) λ = 532 nm,$ \upsilon $ = 0.82; (f) λ = 580 nm,$ \upsilon $ = 0.77; (g) λ = 600 nm,$ \upsilon $ = 0.62; (h) λ = 635 nm,$ \upsilon $ = 0.80; (i) λ = 700 nm,$ \upsilon $ = 0.67Figure 4. Experimental results in the Young’s double-slit experiment: (a) The architecture of Young’s double-slit experiment, where F represents rotatable holder embedded with different filters, CE represents collimated beam expanding system; (b)—(i) the interference fringes and intensity line profile of the eight wavelengths, where (b) λ = 405 nm,
$ \upsilon $ = 0.86; (c) λ = 450 nm,$ \upsilon $ = 0.86; (d) λ = 500 nm,$ \upsilon $ = 0.75; (e) λ = 532 nm,$ \upsilon $ = 0.82; (f) λ = 580 nm,$ \upsilon $ = 0.77; (g) λ = 600 nm,$ \upsilon $ = 0.62; (h) λ = 635 nm,$ \upsilon $ = 0.80; (i) λ = 700 nm,$ \upsilon $ = 0.67.表 1 从白激光中提取光波所使用的滤波片的中心波长和带宽
Table 1. Central wavelength and bandwidth of the filter used to extract the light wave from the white laser.
Wavelength/nm 405 450 500 532 580 600 635 700 Bandwidth/nm 10 10 10 10 10 10 10 10 表 2 各准单色光经过滤波片后功率随偏振片角度的变化
Table 2. Power variation with polarizer angle for each quasi-monochromatic light after filtering.
$ \lambda /{\mathrm{n}}{\mathrm{m}} $ 405 450 500 532 580 600 635 700 $ {I}_{{\mathrm{max}}} /{\mathrm{\mu }}{\mathrm{W}} $ 43.7 42.5 43.5 40.1 45.7 46.8 45.0 46.2 $ {\theta }_{{\mathrm{max}}}/({}^\circ) $ 0 0 1 0 1 0 0 0 $ {I}_{{\mathrm{min}}} $ /$ {{\mu}}{\mathrm{W}} $ 0.2 0.2 0.1 0.1 0.2 0.2 0.2 0.2 $ {\theta }_{{\mathrm{min}}}/({}^\circ) $ 90 90 89 90 89 90 90 90 -
[1] Alfano R R 1990 Appl. Opt. 29 1242 doi: 10.1364/AO.29.001242 [2] Alfano R R, Shapiro S L 1970 Phys. Rev. Lett. 24 592 doi: 10.1103/PhysRevLett.24.592 [3] Fork R L, Tomlinson W J, Shank C V, Hirlimann C, Yen R, Tomlinson W J 1983 Opt. Lett. 8 1 doi: 10.1364/OL.8.000001 [4] Froehly L, Meteau J 2012 Opt. Fiber Technol. 18 411 doi: 10.1016/j.yofte.2012.08.001 [5] Travers J C, Grigorova T F, Brahms C, Belli F 2019 Nat. Photonics 13 547 doi: 10.1038/s41566-019-0416-4 [6] Elu U, Maidment L, Vamos L, Tani F, Novoa D, Frozs H, Badikov V, Badikov D, Petrov V, Russell J, Biegert J 2021 Nat. Photonics 15 277 doi: 10.1038/s41566-020-00735-1 [7] Schliesser A, Picqué N, Hänsch T W 2012 Nat. Photonics 6 440 doi: 10.1038/nphoton.2012.142 [8] Udem Th, Holzwarth R, Hänsch T W 2002 Nature 416 233 doi: 10.1038/416233a [9] Petersen C R, Møller U, Kubat I, Zhou B, Dupont S, Ramsay J, Benson T, Sujecki S, Abdel-Moneim N, Tang Z, Furniss D, Seddon A, Bang O 2014 Nat. Photonics 8 830 doi: 10.1038/nphoton.2014.213 [10] Jiang X, Joly N Y, Finger M A, Babic F, Wong K L, Travers J C, Russell J 2015 Nat. Photonics 9 133 doi: 10.1038/nphoton.2014.320 [11] He P, Liu Y Y, Zhao K, Teng H, He X K, Huang P, Huang H D, Zhong S Y, Jiang Y J, Fang S B, Hou X, Wei Z Y 2017 Opt. Lett. 42 474 doi: 10.1364/OL.42.000474 [12] Mollenauer L F, Stolen R H, Gordon J P, Tomlinson W J 1983 Opt. Lett. 8 289 doi: 10.1364/OL.8.000289 [13] Hassan M T, Luu T T, Moulet A, Raskazovskaya O, Zhokhov P, Garg M, Karpowicz N, Zheltikov A M, Pervak V, Krausz F, Goulielmakis E 2016 Nature 530 66 doi: 10.1038/nature16528 [14] Chen B Q, Ren M L, Liu R J, Zhang C, Sheng Y, Ma B Q, Li Z Y 2014 Light Sci. Appl. 3 e189 doi: 10.1038/lsa.2014.70 [15] Chen B Q, Zhang C, Hu C Y, Liu R J, Li Z Y 2015 Phys. Rev. Lett. 115 083902 doi: 10.1103/PhysRevLett.115.083902 [16] Chen B Q, Hong L H, Hu C Y, Li Z Y 2021 Research 2021 1539730 doi: 10.34133/2021/1539730 [17] Li M Z, Hong L H, Li Z Y 2022 Research 2022 9871729 doi: 10.34133/2022/9871729 [18] Hong L H, Hu C, Liu Y Y, He H J, Liu L Q, Wei Z Y, Li Z Y 2023 PhotoniX 4 11 doi: 10.1186/s43074-023-00088-2 [19] Hong L H, Liu L Q, Liu Y Y, Qian J Y, Feng R Y, Li W K, Li Y Y, Peng Y J, Leng Y X, Li R X, Li Z Y 2023 Light Sci. Appl. 12 199 doi: 10.1038/s41377-023-01256-6 [20] Hong L H, Yang H Y, Li Z Y 2023 Research 6 0210 doi: 10.34133/research.0210 [21] Knapp T, Lima N, Daigle N, Duan S, Merchant J L, Sawyer T W 2024 J. Biomed. Opt. 29 016007 doi: 10.1117/1.jbo.29.1.016007 [22] Hassan M A 2025 Appl. Opt. 64 654 doi: 10.1364/AO.546287 [23] Shimobaba T, Ito T 2003 Opt. Rev. 10 339 doi: 10.1007/s10043-003-0339-6 [24] Kueny E, Meier J, Levecq X, Varkentina N, Kärtner F X, Calendron L 2018 Opt. Express 26 31299 doi: 10.1364/OE.26.031299 [25] Genty G, Friberg A T, Turunen J 2016 Prog. Opt. 61 71 doi: 10.1016/bs.po.2015.10.002 [26] Melnik M V, Tcypkin A N, Kozlov S A 2018 Rom. J. Phys. 63 203 [27] Zeylikovich I, Alfano R R 2003 Appl. Phys. B 77 265 doi: 10.1364/fio.2003.wp2 [28] Su Y B, Fang S B, Gao Y T, Zhao K, Chang G Q, Wei Z Y 2021 Appl. Phys. Lett. 118 261102 doi: 10.1063/5.0055348 [29] Wang P, Huang J, Xie S, Troles J, Russell J 2021 Photon. Res. 9 630 doi: 10.1364/PRJ.415339 [30] Zhu X, Zhao D, Zhang B, Yang L Y, Yang Y K, Liu S, Hou J 2023 Opt. Express 31 13182 doi: 10.1364/OE.487291 [31] Chang K Y, Chen G Y, Yu H C, Liu J M 2023 Opt. Commun. 533 129281 doi: 10.1016/j.optcom.2023.129281 [32] 冯柳宾, 鲁欣, 刘晓龙, 葛绪雷, 马景龙, 李玉同, 陈黎明, 董全力, 王伟民, 滕浩, 王兆华, 盛政明, 魏志义, 贺端威, 张杰 2012 物理学报 61 174206 doi: 10.7498/aps.61.174206 Feng L B, Lu X, Liu X L, Ge X L, Ma J L, Li Y T, Chen L M, Dong Q L, Wang W M, Teng H, Wang Z H, Sheng Z M, Wei Z Y, He D W, Zhang J 2012 Acta Phys. Sin. 61 174206 doi: 10.7498/aps.61.174206 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: