高级搜索

实时熵源评估二重并行连续变量量子随机数发生器

,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

郭晓敏, 王岐岐, 罗越, 宋智杰, 李正雅, 瞿毅坤, 郭龑强, 肖连团. 实时熵源评估二重并行连续变量量子随机数发生器[J]. 物理学报, 2025, 74(12): 124202-1. doi: 10.7498/aps.74.20250333
引用本文: 郭晓敏, 王岐岐, 罗越, 宋智杰, 李正雅, 瞿毅坤, 郭龑强, 肖连团. 实时熵源评估二重并行连续变量量子随机数发生器[J]. 物理学报, 2025, 74(12): 124202-1. doi: 10.7498/aps.74.20250333
shu
Xiaomin GUO, Qiqi WANG, Yue LUO, Zhijie SONG, Zhengya LI, Yikun QU, Yanqiang GUO, Liantuan XIAO. Real-time entropy source evaluated dual-parallel continuous variable quantum random number generator[J]. Acta Physica Sinica, 2025, 74(12): 124202-1. doi: 10.7498/aps.74.20250333
Citation: Xiaomin GUO, Qiqi WANG, Yue LUO, Zhijie SONG, Zhengya LI, Yikun QU, Yanqiang GUO, Liantuan XIAO. Real-time entropy source evaluated dual-parallel continuous variable quantum random number generator[J]. Acta Physica Sinica, 2025, 74(12): 124202-1. doi: 10.7498/aps.74.20250333
shu

实时熵源评估二重并行连续变量量子随机数发生器

  • 1.

    太原理工大学新型传感器与智能控制教育部重点实验室, 太原　030024

  • 2.

    太原理工大学物理与光电工程学院, 太原　030024

    • 作者简介: 郭晓敏: guoxiaomin@tyut.edu.cn .
    通讯作者: E-mail: guoyanqiang@tyut.edu.cn.;  E-mail: xlt@sxu.edu.cn.

  • 中图分类号: 42.50.-p, 03.67.Dd, 03.65.Wj

Real-time entropy source evaluated dual-parallel continuous variable quantum random number generator

  • 1.

    Key Laboratory of Advanced Transducers and Intelligent Control System, Ministry of Education, Taiyuan University of Technology, Taiyuan 030024, China

  • 2.

    College of Physics and Optoelectronics, Taiyuan University of Technology, Taiyuan 030024, China

    • Corresponding authors: E-mail: guoyanqiang@tyut.edu.cn.;  E-mail: xlt@sxu.edu.cn.

  • MSC: 42.50.-p, 03.67.Dd, 03.65.Wj

  • 摘要: 源于量子内禀随机性的量子随机数发生器(quantum random number generator, QRNG)提供了安全性信息论可证的真随机数. 本文提出一种融合实时相空间监测与熵评估的二重并行连续变量QRNG方案, 通过动态阈值监测机制与自适应后处理矩阵规模调整技术, 同步提升QRNG安全性与生成效率, 该方案创新性地将熵源状态追踪与随机数提取优化相结合. 实验上构建基于外差探测的真空态双边带模并行提取系统, 为高精度、高速全息重构量子态和四路并行提取量子随机数提供了充足的原始数据; 高动态范围、高分辨率、矩阵规模实时可调的硬件基Toeplitz-hash后处理协调了熵源状态追踪与随机数提取优化. 在保持17 Gbit/s以上高产率的同时可有效抵御边信道攻击, 通过了NIST SP 800-22, Diehard及TestU01标准测试. 本工作为解决QRNG实时熵源可信评估难题提供了技术路径, 且该方案集成度高、扩展性好, 为量子随机数发生器走向应用提供了一种切实可行的方案.
    Abstract: Continuous-variable quantum random number generator (cv-QRNG) has attracted much attention due to its convenient state preparation and high measurement bandwidth. Chip-size integration of this type of QRNG is expectable because all components involved have been integrated on a single chip recently. Most of the existing schemes, including all existing commercial schemes, usually use a once-and-for-all approach to evaluate quantum entropy. In this work, we propose a double-level parallel cv-QRNG scheme that integrates real-time phase-space monitoring and entropy evaluation. By using dynamic threshold monitoring and self-adapting scaling of Toeplitz matrix, the security and generation rate of QRNG can be enhanced simultaneously.Experimentally, a parallel extraction system of vacuum state double quadratures and multiple sideband modes is constructed based on heterodyne, providing sufficient raw data for high-precision and high-speed tomography reconstruction of quantum entropy source and parallel extraction of QRNG. Based on the statistical analysis of data under long-term stable operation of the system, dynamic KLD-sensitive security threshold for statistical distribution of Husimi-Q function of the entropy source is established. When a weak chaotic field is injected to simulate a thermal state attack, the KLD value jumps and quickly deviates from the steady state baseline, manifesting a sensitive identification of the attack. It is worth pointing out that the threshold parameter can be dynamically optimized according to the security requirements of actual application scenarios. An FPGA-based real-time feedback Toeplitz-hash extractor employs a maximum matrix bit-width truncation method to dynamically adjust Toeplitz matrix parameters. This optimization reduces the maximum extraction ratio interval from 6% to 1.8%, with all intervals below 1% for extraction ratios ≤76%, significantly mitigating entropy losses caused by discrete adjustment of the Toeplitz matrix, and achieving a minimum extraction ratio of 16.9%. This flexibility enables the system to accurately control the response sensitivity of abnormal signals while maintaining the real-time generation of quantum random bits. Finally, real-time generation rate of 17.512 Gbit/s is attained with security parameters at the level of 10–50 and the generated random numbers passed NIST SP 800-22, Diehard, and TestU01 standard tests.This research provides a technical path for real-time assessment of entropy source security in QRNG. The proposed scheme has good integrability and scalability, presenting a feasible solution for QRNG to enter the application stage.
  • 加载中

  • 图 1  基于外差探测的多路并行实时熵评估QRNG实验方案, 其中TC为温控源, CS为电流源, LD为半导体激光器, VOA为衰减器, OPC为光学偏振器, BS1为80∶20分束器, Laser为激光源, BS2为 90∶10分束器, 90°Hybrid为90°光混频器, OPM为功率计, BHD为光电探测器, PS为功分器, M为混频器, AWG为信号发生器, LPF为滤波器, ADC为模数转换器, FPGA为现场可编程门阵列, PC为上位机

    Figure 1.  A multi-channel parallel real-time entropy evaluation QRNG experimental scheme based on heterodyne detection, where TC represents temperature-controlled source, CS represents current source, LD represents semiconductor laser, VOA represents attenuator, OPC represents optical polarizer, BS1 represents 80∶20 beam splitter, Laser represents laser source, BS2 represents 90∶10 beam splitter, 90° hybrid represents 90° optical mixer, OPM represents power meter, BHD represents photodetector, PS represents power divider, M represents mixer, AWG represents signal generator, LPF represents filter, ADC represents analog-to-digital converter, FPGA represents field programmable gate array, PC represents upper computer.

    下载: 全尺寸图片 幻灯片

    图 2  真空态双分量散粒噪声功率谱图

    Figure 2.  Vacuum-state two-component shot noise power spectrum.

    下载: 全尺寸图片 幻灯片

    图 3  后处理与熵反馈模块示意图

    Figure 3.  Schematic diagram of the post-processing and entropy feedback module.

    下载: 全尺寸图片 幻灯片

    图 4  标准NIST统计套件测试结果

    Figure 4.  Standard NIST statistical suite test results.

    下载: 全尺寸图片 幻灯片

    图 5  (a) TestU01测试结果; (b) Diehard测试结果

    Figure 5.  (a) Test results of TestU01; (b) test results of Diehard.

    下载: 全尺寸图片 幻灯片

    图 6  不同探测效率下层析精度变化曲面图　(a) η = 0.1; (b) η = 0.5; (c) η = 0.72; (d) η = 1

    Figure 6.  Performance ratio surface plot for different detection efficiency: (a) η = 0.1; (b) η = 0.5; (c) η = 0.72; (d) η = 1.

    下载: 全尺寸图片 幻灯片

    图 7  不同探测效率下层析精度变化曲面图(考虑Arthurs-Kelly误差)　(a) η = 0.1; (b) η = 0.5; (c) η = 0.72; (d) η = 1

    Figure 7.  Performance ratio surface plot considering Arthurs-Kelly error with different detection efficiency: (a) η = 0.1; (b) η = 0.5; (c) η = 0.72; (d) η = 1.

    下载: 全尺寸图片 幻灯片

    图 8  不同效率下的性能比与光子数的关系

    Figure 8.  Relationship between performance ratio and number of photons at different efficiencies.

    下载: 全尺寸图片 幻灯片

    图 9  信号方差随本振光功率的变化

    Figure 9.  Relationship of signal variance with local oscillator optical power.

    下载: 全尺寸图片 幻灯片

    图 10  实验重构结果　(a) 不同本振功率下KLD随迭代次数的变化; (b) 迭代300次的Wigner分布; (c) 不同本振功率下KLD随截断值kc的变化图; (d) 截断值kc为4的Wigner分布; (e) HET中KLD随着本振功率变化; (f) HET重构的Husimi-Q分布

    Figure 10.  Experimental reconstruction results: (a) The variation of KLD with the number of iterations at different local oscillator powers; (b) Wigner distribution with 300 iterations; (c) Variation of KLD with kc at different local oscillator powers; (d) Wigner distribution with a cut-off value of kc of 4; (e) KLD in HET with local oscillator power; (f) Husimi-Q distribution reconstructed by HET.

    下载: 全尺寸图片 幻灯片

    图 11  不同数据量下3种重构方法的KLD值

    Figure 11.  The KLD value of the three reconstruction methods under different sample sizes.

    下载: 全尺寸图片 幻灯片

    图 12  (a) 热态攻击前后的Husimi-Q 分布, 其中网格化曲线对应真空态, 彩色直方图对应热态; (b) 热态攻击前后的KLD波动图

    Figure 12.  (a) Husimi-Q distribution before and after a thermal attack, where gridded curve corresponds to vacuum state, color histogram corresponds to hot state; (b) KLD fluctuation plot before and after thermal attack.

    下载: 全尺寸图片 幻灯片

    图 13  最小熵与QSNR关系图

    Figure 13.  Graph of minimum entropy versus quantum signal-to-noise ratio.

    下载: 全尺寸图片 幻灯片

    图 14  后处理矩阵调整流程示意图

    Figure 14.  Schematic diagram of the post-processing matrix adjustment process.

    下载: 全尺寸图片 幻灯片

    图 15  可变的矩阵规模硬件实现方法

    Figure 15.  Variable matrix size implementation.

    下载: 全尺寸图片 幻灯片

    图 16  (a) 矩阵步长为128时的后处理离散提取比例; (b) 矩阵步长为32时的后处理离散提取比例

    Figure 16.  (a) Post-processing discrete extraction ratio at matrix step size of 128; (b) post-processing discrete extraction ratio at matrix step size of 32.

    下载: 全尺寸图片 幻灯片

    表 1  不同通道的关键参数

    Table 1.  Structural parameters of capillary of different kind of fluid.

    通道 条件最小熵
    /(16 bit)    		 矩阵规模
    m × n    		 后处理提
    取比/%    		 实时生
    成速率
    /(Gbit·s–1)
    X (300 MHz) 11.79 1729×2496 69.27 4.4334
    P (300 MHz) 11.71 1729×2496 69.27 4.4334
    X (800 MHz) 11.54 1729×2560 67.54 4.3226
    P (800 MHz) 11.45 1729×2560 67.54 4.3226
    下载: 导出CSV
  • [1] Wahl M, Leifgen M, Berlin M, Röhlicke T, Rahn H J, Benson O 2011 Appl. Phys. Lett. 98 171105 doi: 10.1063/1.3578456
    [2] Nie Y Q, Zhang H F, Zhang Z, Wang J, Ma X, Zhang J, Pan J W 2014 Appl. Phys. Lett. 104 051110 doi: 10.1063/1.4863224
    [3] Ma H Q, Xie Y, Wu L A 2005 Appl. Opt. 44 7760 doi: 10.1364/AO.44.007760
    [4] Aungskunsiri K, Jantarachote S, Wongpanya K, Amarit R, Punpetch P, Sumriddetchkajorn S 2023 ACS Omega 8 35085 doi: 10.1021/acsomega.3c04584
    [5] Jennewein T, Achleitner U, Weihs G, Weinfurter H, Zeilinger A 2000 Rev. Sci. Instrum. 71 1675 doi: 10.1063/1.1150518
    [6] Ren M, Wu E, Liang Y, Jian Y, Wu G, Zeng H P 2011 Phys. Rev. A 83 023820 doi: 10.1103/PhysRevA.83.023820
    [7] Xiao L T, Zhao Y T, Huang T, Zhao J M, Yin W B, Jia S T 2004 Chin. Phys. Lett. 21 489 doi: 10.1088/0256-307X/21/3/020
    [8] Eaton M, Hossameldin A, Birrittella R J, Alsing P M, Gerry C C, Dong H, Cuevas C, Pfister O 2023 Nat. Photonics 17 106 doi: 10.1038/s41566-022-01105-9
    [9] Wei W, Guo H 2009 Opt. Lett. 34 1876 doi: 10.1364/OL.34.001876
    [10] Applegate M J, Thomas O, Dynes J F, Yuan Z L, Ritchie D A, Shields A J 2015 Appl. Phys. Lett. 107 071106 doi: 10.1063/1.4928732
    [11] Guo H, Tang W Z, Liu Y, Wei W 2010 Phys. Rev. E 81 051137 doi: 10.1103/PhysRevE.81.051137
    [12] Raffaelli F, Sibson P, Kennard J E, Mahler D H, Thompson M G, Matthews J C F 2018 Opt. Express 26 19730 doi: 10.1364/OE.26.019730
    [13] Li J L, Huang Z T, Yu C L, Wu J J, Zhao T G, Zhu X W, Sun S H 2024 Opt. Express 32 5056 doi: 10.1364/OE.515390
    [14] Liu W Y, Cao Y X, Wang X Y, Li Y M 2020 Phys. Rev. A 102 032625 doi: 10.1103/PhysRevA.102.032625
    [15] Shen Y, Tian L, Zou H X 2010 Phys. Rev. A 81 063814 doi: 10.1103/PhysRevA.81.063814
    [16] Symul T, Assad S M, Lam P K 2011 Appl. Phys. Lett. 98 231103 doi: 10.1063/1.3597793
    [17] Bruynsteen C, Gehring T, Lupo C, Bauwelinck J, Yin X 2023 PRX Quantum 4 010330 doi: 10.1103/PRXQuantum.4.010330
    [18] Gehring T, Lupo C, Kordts A, Solar Nikolic D, Jain N, Rydberg T, Pedersen T B, Pirandola S, Andersen U L 2021 Nat. Commun. 12 605 doi: 10.1038/s41467-020-20813-w
    [19] Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621 doi: 10.1103/RevModPhys.84.621
    [20] Gabriel C, Wittmann C, Sych D, Dong R, Mauerer W, Andersen U L, Marquardt C, Leuchs G 2010 Nat. Photonics 4 711 doi: 10.1038/nphoton.2010.197
    [21] Guo X M, Liu R, Li P, Cheng C, Wu M, Guo Y Q 2018 Entropy 20 819 doi: 10.3390/e20110819
    [22] Haw J Y, Assad S M, Lance A M, Ng N H Y, Sharma V, Lam P K, Symul T 2015 Phys. Rev. Appl. 3 054004 doi: 10.1103/PhysRevApplied.3.054004
    [23] Guo X M, Cheng C, Wu M C, Gao Q Z, Li P, Guo Y Q 2019 Opt. Lett. 44 5566 doi: 10.1364/OL.44.005566
    [24] Kumar R, Barrios E, MacRae A, Cairns E, Huntington E H, Lvovsky A I 2012 Opt. Commun. 285 5259 doi: 10.1016/j.optcom.2012.07.103
    [25] Zheng Z Y, Zhang Y C, Huang W N, Yu S, Guo H 2019 Rev. Sci. Instrum. 90 043105 doi: 10.1063/1.5078547
    [26] Shalm L K, Zhang Y, Bienfang J C, Schlager C, Stevens M J, Mazurek M D, Abellán C, Amaya W, Mitchell M W, Alhejji M A, Fu H, Ornstein J, Mirin R P, Nam S W, Knill E 2021 Nat. Phys. 17 452 doi: 10.1038/s41567-020-01153-4
    [27] Liu Y, Zhao Q, Li M H, Guan J Y, Zhang Y, Bai B, Zhang W, Liu W Z, Wu C, Yuan X, Li H, Munro W J, Wang Z, You L, Zhang J, Ma X, Fan J, Zhang Q, Pan J W 2018 Nature 562 548 doi: 10.1038/s41586-018-0559-3
    [28] Zhang J F, Li Y, Zhao M Y, Han D M, Liu J, Wang M H, Gong Q H, Xiang Y, He Q Y, Su X L 2025 Light Sci. Appl. 14 25 doi: 10.1038/s41377-024-01641-9
    [29] Liu L J, Yang J, Wu M, Liu J L, Huang W, Li Y, Xu B J 2025 Entropy 27 68 doi: 10.3390/e27010068
    [30] Cao Z, Zhou H Y, Yuan X, Ma X F 2016 Phys. Rev. X 6 011020 doi: 10.1103/PhysRevX.6.01102
    [31] Nie Y Q, Zhou H, Bai B, Xu Q, Ma X, Zhang J, Pan J W 2024 Quantum Sci. Technol. 9 025024 doi: 10.1088/2058-9565/ad34f4
    [32] Michel T, Haw J Y, Marangon D G, Thearle O, Vallone G, Villoresi P, Lam P K, Assad S M 2019 Phys. Rev. Appl. 12 034017 doi: 10.1103/PhysRevApplied.12.034017
    [33] Pivoluska M, Plesch M, Farkas M, Ružičková N, Flegel C, Valencia N H, McCutcheon W, Malik M, Aguilar E A 2021 npj Quantum Inf. 7 1 doi: 10.1038/s41534-020-00339-1
    [34] Marangon D G, Vallone G, Villoresi P 2017 Phys. Rev. Lett. 118 060503 doi: 10.1103/PhysRevLett.118.060503
    [35] Xu B J, Chen Z Y, Li Z Y, Yang J, Su Q, Huang W, Zhang Y C, Guo H 2019 Quantum Sci. Technol. 4 025013 doi: 10.1088/2058-9565/ab0fd9
    [36] Ma X F, Yuan X, Cao Z, Qi B, Zhang Z 2016 npj Quantum Inf. 2 16021 doi: 10.1038/npjqi.2016.21
    [37] Tomamichel M, Schaffner C, Smith A, Renner R 2011 IEEE Trans. Inf. Theory 57 5524 doi: 10.1109/TIT.2011.2158473
    [38] Drahi D, Walk N, Hoban M J, Fedorov A K, Shakhovoy R, Feimov A, Kurochkin Y, Kolthammer W S, Nunn J, Barrett J, Walmsley I A 2020 Phys. Rev. X 10 041048 doi: 10.1103/PhysRevX.10.041048
    [39] Huang W N, Zhang Y C, Zheng Z Y, Li Y, Xu B J, Yu S 2020 Phys. Rev. A 102 012422 doi: 10.1103/PhysRevA.102.012422
    [40] Shi Y, Chng B, Kurtsiefer C 2016 Appl. Phys. Lett. 109 041101 doi: 10.1063/1.4959887
    [41] Lin F D, Ge W B, Song Z J, Cui X X, Guo Y Q, Guo X M, Xiao L T 2024 J. Lightwave Technol. 42 8606 doi: 10.1109/JLT.2024.3445327
    [42] Tanizawa K, Kato K, Futami F 2024 J. Lightwave Technol. 42 1209 doi: 10.1109/JLT.2024.3353268
    [43] Haylock B, Peace D, Lenzini F, Weedbrook C, Lobino M 2019 Quantum 3 141 doi: 10.22331/q-2019-05-13-141
    [44] Smithey D T, Beck M, Raymer M G, Faridani A 1993 Phys. Rev. Lett. 70 1244 doi: 10.1103/PhysRevLett.70.1244
    [45] Ourjoumtsev A, Tualle-Brouri R, Grangier P 2006 Phys. Rev. Lett. 96 213601 doi: 10.1103/PhysRevLett.96.213601
    [46] Neergaard-Nielsen J S, Nielsen B M, Hettich C, Mølmer K, Polzik E S 2006 Phys. Rev. Lett. 97 083604 doi: 10.1103/PhysRevLett.97.083604
    [47] Avesani M, Marangon D G, Vallone G, Villoresi P 2018 Nat Commun 9 5365 doi: 10.1038/s41467-018-07585-0
    [48] Shapiro J, Wagner S 1984 IEEE J. Quantum Electron. 20 803 doi: 10.1109/JQE.1984.1072470
    [49] Chaudhuri A 2021 A Tribute to the Legend of Professor C. R. Rao (Singapore: Springer) pp1–13
    [50] 任志红, 李岩, 李艳娜, 李卫东 2019 物理学报 68 040601 doi: 10.7498/aps.68.20181965 Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601 doi: 10.7498/aps.68.20181965
    [51] Arthurs E, Kelly J L 1965 Bell Syst. Tech. J. 44 725 doi: 10.1002/j.1538-7305.1965.tb01684.x
    [52] Řeháček J, Teo Y S, Hradil Z, Wallentowitz S 2015 Sci. Rep. 5 12289 doi: 10.1038/srep12289
    [53] Müller C R, Peuntinger C, Dirmeier T, Khan I, Vogl U, Marquardt C, Leuchs G, Sánchez-Soto L L, Teo Y S, Hradil Z, Řeháček J 2016 Phys. Rev. Lett. 117 070801 doi: 10.1103/PhysRevLett.117.070801
    [54] Cramér H 1949 Mathematical Methods of Statistics (Princeton: Princeton University Press) pp1–575
    [55] Hershey J R, Olsen P A 2007 IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ’07 Honolulu, HI, USA, April 15–20, 2007 pIV-317
    [56] Rached Z, Alajaji F, Campbell L L 2004 IEEE Trans. Inf. Theory 50 917 doi: 10.1109/TIT.2004.826687
    [57] Lu Y, Stuart A, Weber H 2017 SIAM/ASA J. Uncertain. Quantif. 5 1136 doi: 10.1137/16M1105384
    [58] Popescu P G, Dragomir S S, Slusanschi E I, Sta O N 2016 Electron. J. Differ. Equ. 2016 1
    [59] Wu Y, Ma X 2022 Renew. Energy 181 554 doi: 10.1016/j.renene.2021.09.067
    [60] Smithey D T, Beck M, Cooper J, Raymer M G 1993 Phys. Rev. A 48 3159 doi: 10.1103/PhysRevA.48.3159
    [61] Řeháček J, Hradil Z, Knill E, Lvovsky A I 2007 Phys. Rev. A 75 042108 doi: 10.1103/PhysRevA.75.042108
    [62] Lvovsky A I 2004 J. Opt. B: Quantum Semiclass. Opt. 6 S556 doi: 10.1088/1464-4266/6/6/014
    [63] Lvovsky A I, Raymer M G 2009 Rev. Mod. Phys. 81 299 doi: 10.1103/RevModPhys.81.299
    [64] Smith P R, Marangon D G, Lucamarini M, Yuan Z L, Shields A J 2021 Phys. Rev. Appl. 15 044044 doi: 10.1103/PhysRevApplied.15.044044
    [65] Qin H, Kumar R, Makarov V, Alléaume R 2018 Phys. Rev. A 98 012312 doi: 10.1103/PhysRevA.98.012312
    [66] Xia X, Sun J, Liu W 2023 5th International Conference on Circuits and Systems (ICCS) Huzhou, China, October 27–30, 2023 p108
    [67] Chen Z Y, Wang X Y, Yu S, Li Z Y, Guo H 2023 npj Quantum Inf. 9 28 doi: 10.1038/s41534-023-00695-8
    [68] Huang J Z, Kunz-Jacques S, Jouguet P, Weedbrook C, Yin Z Q, Wang S, Chen W, Guo G C, Han Z F 2014 Phys. Rev. A 89 032304 doi: 10.1103/PhysRevA.89.032304
    [69] Zhao Y, Fung C H F, Qi B, Chen C, Lo H K 2008 Phys. Rev. A 78 042333 doi: 10.1103/PhysRevA.78.042333
  • 加载中
图( 16) 表( 1)
计量
  • 文章访问数:  90
  • HTML全文浏览数:  90
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-13
  • 刊出日期:  2025-06-20

实时熵源评估二重并行连续变量量子随机数发生器

    通讯作者: E-mail: guoyanqiang@tyut.edu.cn.; 
    通讯作者: E-mail: xlt@sxu.edu.cn.
    作者简介: 郭晓敏: guoxiaomin@tyut.edu.cn
  • 1. 太原理工大学新型传感器与智能控制教育部重点实验室, 太原　030024
  • 2. 太原理工大学物理与光电工程学院, 太原　030024
  • 收稿日期:  2025-03-13

摘要: 源于量子内禀随机性的量子随机数发生器(quantum random number generator, QRNG)提供了安全性信息论可证的真随机数. 本文提出一种融合实时相空间监测与熵评估的二重并行连续变量QRNG方案, 通过动态阈值监测机制与自适应后处理矩阵规模调整技术, 同步提升QRNG安全性与生成效率, 该方案创新性地将熵源状态追踪与随机数提取优化相结合. 实验上构建基于外差探测的真空态双边带模并行提取系统, 为高精度、高速全息重构量子态和四路并行提取量子随机数提供了充足的原始数据; 高动态范围、高分辨率、矩阵规模实时可调的硬件基Toeplitz-hash后处理协调了熵源状态追踪与随机数提取优化. 在保持17 Gbit/s以上高产率的同时可有效抵御边信道攻击, 通过了NIST SP 800-22, Diehard及TestU01标准测试. 本工作为解决QRNG实时熵源可信评估难题提供了技术路径, 且该方案集成度高、扩展性好, 为量子随机数发生器走向应用提供了一种切实可行的方案.

English Abstract

    全文HTML

    1.   引　言

    • 量子随机数发生器(quantum random number generator, QRNG)是基于量子物理技术发展而提出的一种新型随机数生成技术. 与经典随机数发生器相比, QRNG基于量子力学内在的随机性原理, 是迄今为止唯一在理论上被严格证明可生成完全不可预测随机序列的技术. 由于真随机数在经典与量子通信领域的重要性日益凸显, 其应用范围广泛, 包括金融、工程、物理中的蒙特卡罗模拟, 以及计算机领域的大数据分析和游戏开发等, 量子随机数发生器已成为量子技术迈向实用化道路上的重要前沿领域. 近二十年来, 国内外相关研究机构探索了多种量子熵源来产生随机数, 如光子到达时间[1-4]、单光子路径选择[5-7]、光子数统计[8-10]、激光相位噪声[11-13]、量子正交分量涨落[14-18]等. 其中, 基于量子态正交分量起伏测量的连续变量量子随机数发生器(continuous variable quantum random number generator, cv-QRNG)方案因可完整建立量子熵源和量子测量过程的物理模型、可定量评估实际实现中非理想因素引入的边信息[19,20], 同时, 具有量子态易制备、高探测带宽、系统鲁棒性、可集成性强以及与现有通信设备兼容性强等优点, 尤具实用化前景[21-25].

      作为实用化量子器件, 目前, 量子随机数发生器领域的研究大多聚焦于突破更高的产率门槛和通过更全面的后验软件统计测试套件, 从设备信任程度进行归类的话, 以往大部分量子随机数产生方案都算是设备信任的类型, 包括所有现有商用的方案. 这类方案中对量子熵含量评估通常采取一劳永逸的对策, 即假设对系统进行完整描述后, 运行过程中便不再发生变化. 这样的处理显然不能连续地证明随机数发生器的安全性, 只有对QRNG系统量子条件最小熵进行最严格的、或者实时的监测, 才能保证QRNG在实际应用中的真正的安全性.

      针对现有随机数安全性测试后验性、耗时长、无法及时发现由于攻击使量子态发生改变带来的安全隐患, 近年, 国内外部分课题组提出了设备无关[26-29] (自测试)或半设备无关[30-32] (半自测试)量子随机数产生方案, 以舍弃对熵源或测量系统的信任、甚至二者皆舍的牺牲, 通过严格的, 甚至实时的最小熵先验评估, 来换取输出的量子随机数的高安全性.

      设备无关方案不对系统的硬件可靠性和环境安全性做任何假设, 而基于量子纠缠实现无漏洞贝尔测量来产生随机比特, 但实验条件严苛、系统庞大、生成速率极低, 目前最高只有Mbit/s[33]. 半设备无关量子随机数发生器则采取对熵源或量子探测一方完全不信任、另一方则完全信任的处理方式, 其代表了一种可实现相对较高产率的中间方案[34-36]. 半设备无关量子随机数发生器采取部分信任某些设备或系统组件, 简化了系统的设计和实施, 并提高了系统的性能, 通常具有更高的产生速率. 然而, 半设备无关方案仍然依赖于部分信任的设备或组件. 这仍然可能导致系统的安全性受到威胁. 因此, 在选择适当的方案时, 需要综合考虑安全性、性能以及实际应用场景的需求[37].

      2019年, Michel等[32]提出了源无关实时自测试QRNG, 即不对熵源进行任何假设, 只有量子信号探测设备是可信的. 在后处理部分, 每次自检后都通过随机的选择哈希函数实现新的后处理, 然而其仅能工作在软件平台, 随机数的产生速率仅能达到8.2 kbit/s; 2020年, Drahi等[38]提出的源无关自测试量子随机数发生器方案则利用不可信的光子源生成随机数, 并具有8.05 Gbit/s的生成速率. 生成的随机数具有严谨的可组合安全性(安全参数), 可以在多个应用中使用而不会泄漏信息. 2020年, Huang等[39]提出了一种基于本底光监控的最小熵实时校正源无关QRNG方案, 实现了超过350 Mbit/s 的随机数生成速率. 然而, 面向量子随机数发生器的实用化需求, 其安全性的信息论可证性、高的随机数产生速率、可集成性缺一不可.

      本工作提出一种实时熵评估的连续变量量子随机数产生方案. 不对设备做任何安全性假设, 而是基于对量子熵源相空间分布全息重构来实时(以时域随机抽样实现的准实时)监测系统的动态变化, 对熵源状态进行全面评估; 在计入ADC非线性效应与直流偏移的影响下建立了严格的量子条件最小熵评估模型; 基于统计偏差敏感的Kullback-Leibler散度(Kullback-Leibler divergence, KLD)精确检测量子熵源相空间Husimi-Q函数离差, 制定了量子熵含量重评估阈值; 构建了上位机熵源全息监测评估与FPGA内最小熵计算及Toeplitz-hash提取比例自适应调整的传输协议, 随机提取器矩阵规模基于最大矩阵位宽截取方法进行高动态范围、高分辨率的实时调整, 最终实现了一种实时熵评估的二重并行量子随机数产生方法. 实时安全参数保持10–50量级, 量子随机码实时产率达到17.512 Gbit/s.

      本方案相较以往的自测试QRNG方案或攻击检测方案[32,38,39], 特点在于发现量子攻击时采取实时熵含量重评估、后处理提取比例自适应调整的方式保持随机数的持续产生, 可保证QRNG的连续实时运转及高产率. 为量子随机数发生器走向应用, 应对人工智能、物联网、大数据三网融合新产业快速发展提供了一种切实可行的方案.

    2.   实时熵评估二重并行cv-QRNG实验方案与结果

    • 量子随机数安全性的根本在于其熵源的量子特性, 即使被测量子态和量子探测系统在实时生成随机数的过程中被攻击、污染, 如果采取先验的措施, 实时监测量子熵源状态, 偏差达到阈值即重新评估量子噪声熵含量并及时反馈, 实时对广义hash提取器提取比例进行相应调整, 仍然可以产生量子真随机数. 本项工作在课题组前期对实时高速连续变量量子随机数发生器研究基础上提出一种熵源实时监测反馈的二重并行cv-QRNG方案, 如图1所示.

      不同于以往基于真空态平衡零差探测(homodyne, HOM)的cv-QRNG方案[20,40-46], 采用外差探测(heterodyne, HET)[47,48]的方式, 采取这一方案的首要原因是基于HET的Husimi-Q 量子态相空间重构比基于HOM的Wigner重构对边信息的混入更敏感; 其次, Husimi-Q 重构过程无需迭代或截断优化, 样本需求量低, 显著提升重构速度的同时降低了计算复杂度, 这对于熵源实时重构评估的实现是至关重要的, 相关对比论证将在第3节给出. 更进一步, HET可同时提取真空态两个对易分量的起伏方差, 结合前期提出的连续变量量子态多频带模并行提取方案, 可实现二重熵源并行提取, 使激光器利用率、系统集成度、随机数实时产生速率显著提升.

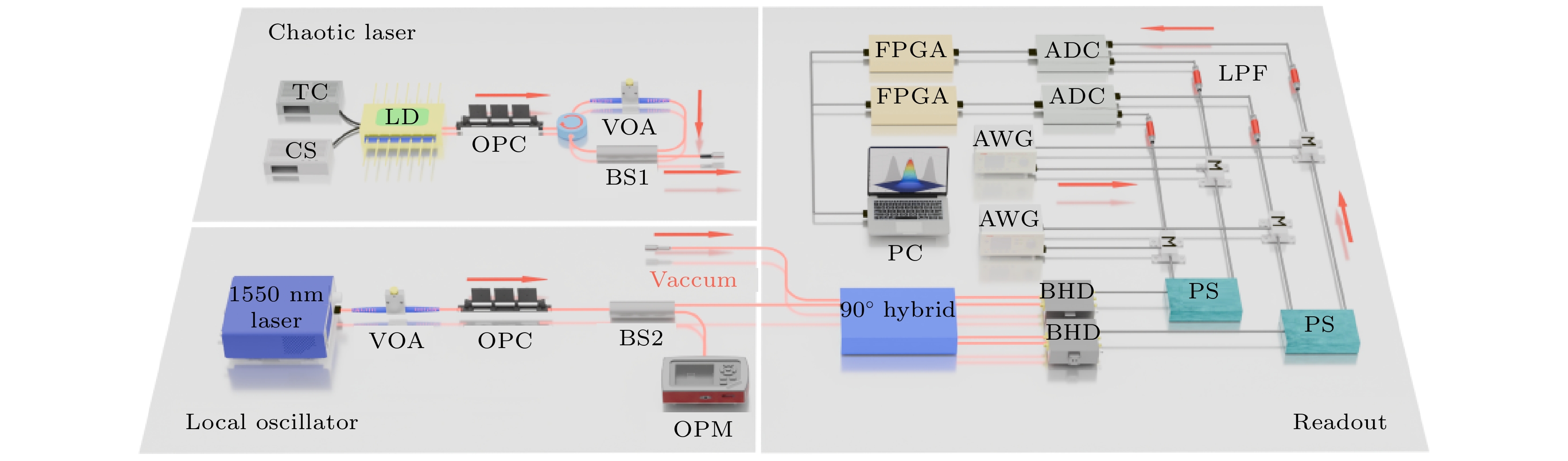
      实时熵评估二重并行cv-QRNG实验装置如图1所示. 其主要包括两个熵源: 混沌激光和真空噪声. 混沌装置在3.3节用来模拟热态攻击, 真空态噪声由HET装置进行测量, 具体地, 1550 nm 激光器输出单模激光经光纤耦合传输至可变光衰减器(VOA)精确调控功率, 偏振控制器(OPC)与偏振分束器(BS2)组合实现90∶10分束比, 较大的组分耦合入商用90°光学混频器(90° hybrid)作为真空态HET的本底光(local oscillator, LO), 较小的组分则耦合到高分辨率光功率计(OPM)用于监测本底光的功率稳定性. 光学混频器的信号端以光隔离阻隔以确保真空态输入. 在光学混频器中, 本底光与真空场发生干涉并输出π/2相位锁定信号, 经两套1.6 GHz平衡探测器(BHD, Thorlabs PDB480C)转换为电信号, 分别响应真空态的正交振幅和位相分量起伏.

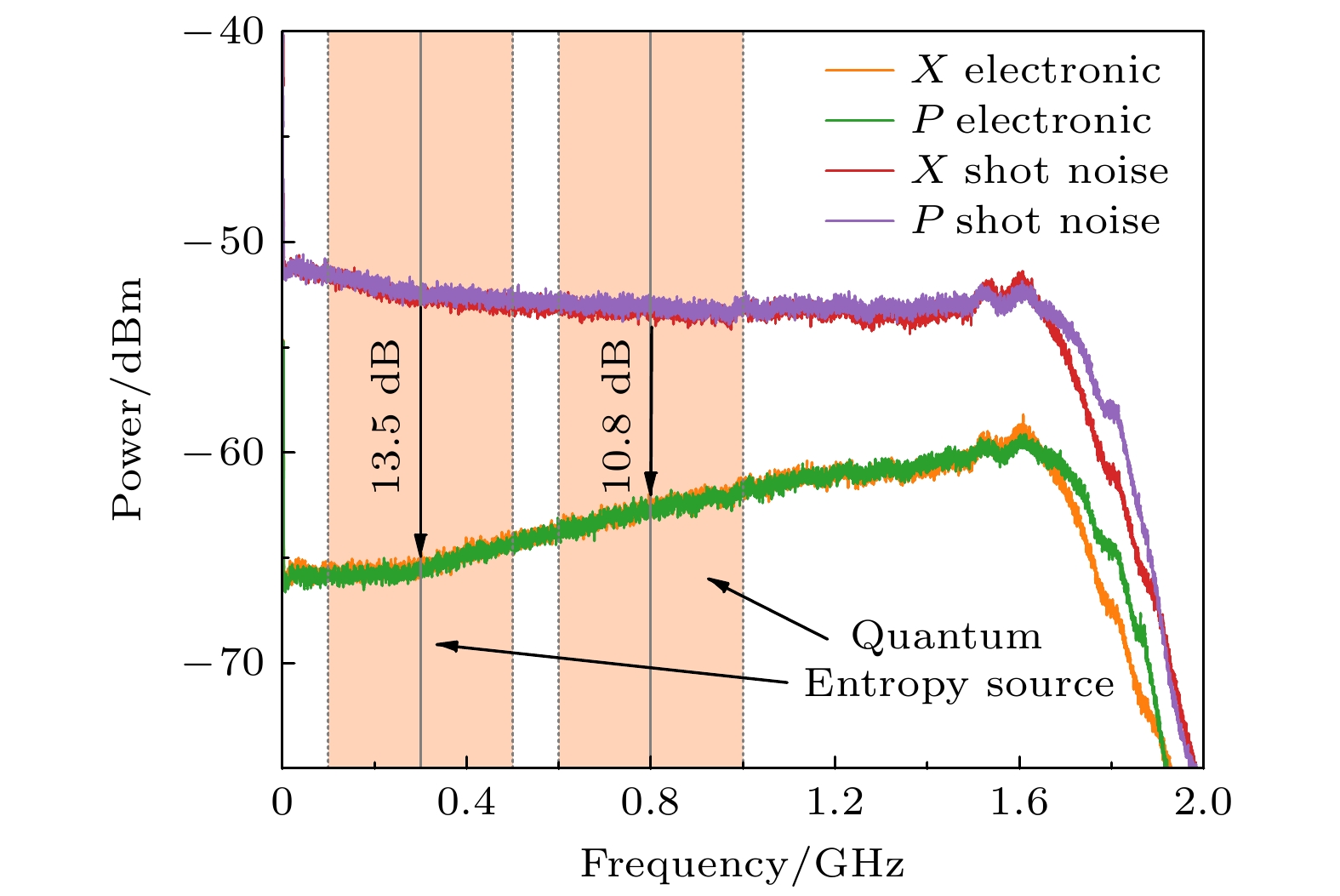
      图2所示为本底光功率控制在2 mW时宽带频谱分析仪记录的来自两路平衡探测器的真空态正交振幅和位相分量噪声功率谱. 二者具有很好的平衡性, 在较宽的频率范围内达到了10 dB以上的信噪比. 对于两个正交分量, 分别提取其两个高频边带量子模来作为量子随机数发生器的子熵源. 如图1所示, HET输出的源于真空态对易的两个正交分量起伏的光电信号分别由一个高带宽功分器(PS)等功率分为两路. 来自X分量的一个功率组分和来自P分量的一个功率组分各与300 MHz射频信号经混频器(M)进行混频, 混频后各自经一个200 MHz低通滤波器(LPF, BLP100+)滤波, 这样源于中心频率300 MHz、带宽200 MHz的真空态量子频带模的两个正交分量起伏信号便被提取出来. X分量和P分量的另一对功率组分则经800 MHz的下混频结构实现中心频率800 MHz、带宽200 MHz的两个正交分量频带模的提取. 这样, 源自真空态两个对易正交振幅分量的4个200 MHz的频带模共同为量子随机数的产生提供熵源. 信号发生器(AWG)为四路信号的下混频提供了电本振信号.

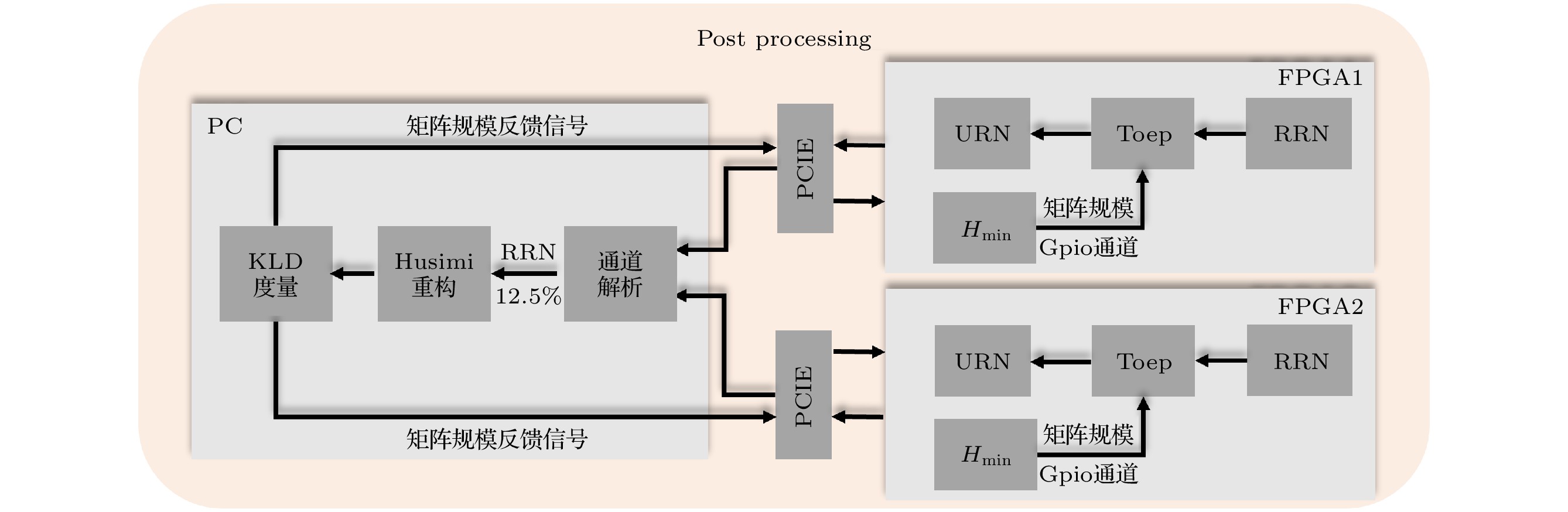
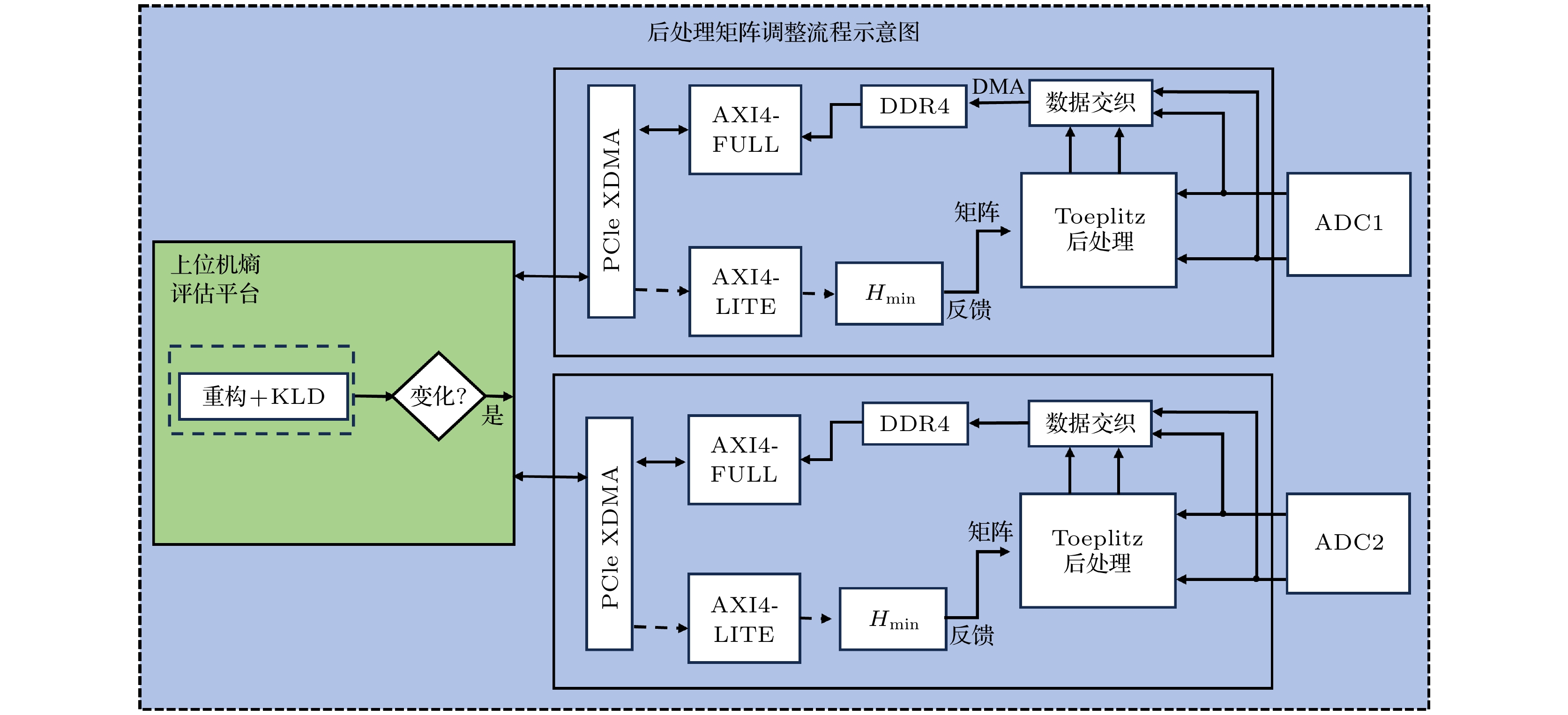
      根据Nyquist采样定律, 各路ADC的采样时钟均被设定为400 MHz. ADC量化中心频率为200 MHz的两个对易正交分量起伏光电流信号所得原始随机序列由FPGA1进行后处理. 源于中心频率为800 MHz的两个对易正交分量起伏的原始随机序列由FPGA2进行处理. AXI4 DMA(direct memory access)模块从原始随机序列中按7∶1比例随机抽取量子态全息重构所需数据, 剩余部分输入Toeplitz哈希提取器生成真随机数. 经后处理产生的真随机数与量子态重构原始数据共同构成数据流, 通过AXI4 DMA写入DDR4内存, 经PCIe传输至上位机. 基于FPGA和上位机的量子态监测评估、数据分流、实时反馈和Toeplitz矩阵调整流程如图3所示.

      上位机对读出的数据流进行相应的通道解析, Husmi重构模块选取当前一个16位原始随机数作为最大值进行循环计时, 并以此计时时间作为两次重构之间的间隔时间, 实现随机抽样重构. 将随机抽取的双分量原始数据提供给PC端实现量子态的Husimi-Q 函数重构, 并基于KLD度量实验态与理论真空态的距离. 当KLD值达到预设阈值时, 系统触发量子条件最小熵重估, 进而通过PCIe中资源消耗最少的AXI4-1ite总线将指令发送至FPGA, FPGA内CPU重新计算最小熵并将新的矩阵规模写入后处理模块, 后处理矩阵规模做相应调整. 当随机数发生器正常运作, 即KLD未触发阈值时, 量子态Husimi-Q重构及KLD计算这一熵源安全性检测始终在重复和不间断地进行中. 由于用于熵源检测的原始随机数是在随机数发生器实时运行过程中随机抽取的, 所以量子态重构监测是等效实时的. 由于每随机触发量子态Husimi-Q重构及KLD计算的同时, 亦触发FPGA内量子最小熵计算, 而基于位宽截断的矩阵规模自适应调整与随机数提取同步进行, 并不单独耗时, 所以在这个过程中涉及到的耗时过程仅限于量子态相空间Husimi-Q重构与KLD计算. 基于FPGA的Toeplitz矩阵高速高分辨率的实时调整具体方案将在第5节给出.

      依据Leftover-hash引理[37], Toeplitz矩阵维度$m \times n$与量子条件最小熵${H_{\min }}$需满足:

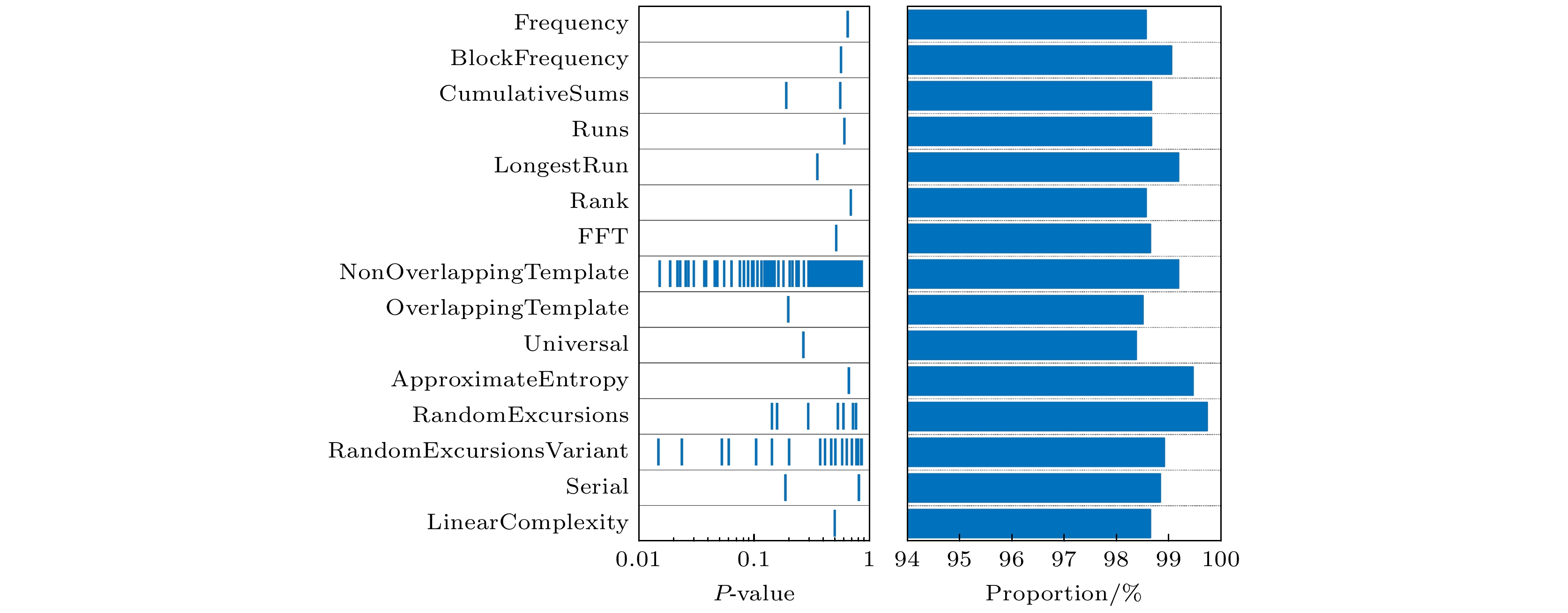
      其中, ${\varepsilon _{{\text{hash}}}}$是哈希安全参数, 在${H_{\min }}$确定的情况下, ${\varepsilon _{{\text{hash}}}}$的严格化虽可提升安全性, 但会导致提取比例的下降. 量子条件最小熵的严格评估方案将在第4节详细给出. 表1展示了安全参数选择为${10^{ - 50}}$时4个通道的关键参数, 包括量子条件最小熵含量、Toeplitz矩阵规模、量子随机数提取比例以及实时生成速率. 综合以上各路通道的随机数生成速率, 最终四通道合计获得17.512 Gbit/s的量子真随机比特输出.

      为评估最终随机序列的随机性, 对4个通道的输出序列进行NIST, Diehard, 以及TestU01测试. 首先获取了文件大小为1 Gbit的最终随机比特流, 将文件分为1000组, 每组1 Mbit进行NIST测试, NIST测试包含15种随机测试项目, 用来表征随机比特的随机性质量, 每项测试都可通过P值来反映实际的随机性指标. 如图4所示, 在α = 0.01的显著性水平下, 所有15种测试的P值均大于0.01, 各统计检验的最小通过率在0.9805607—0.9994393的置信区间内, 说明随机比特序列成功通过了所有NIST随机数统计测试项.

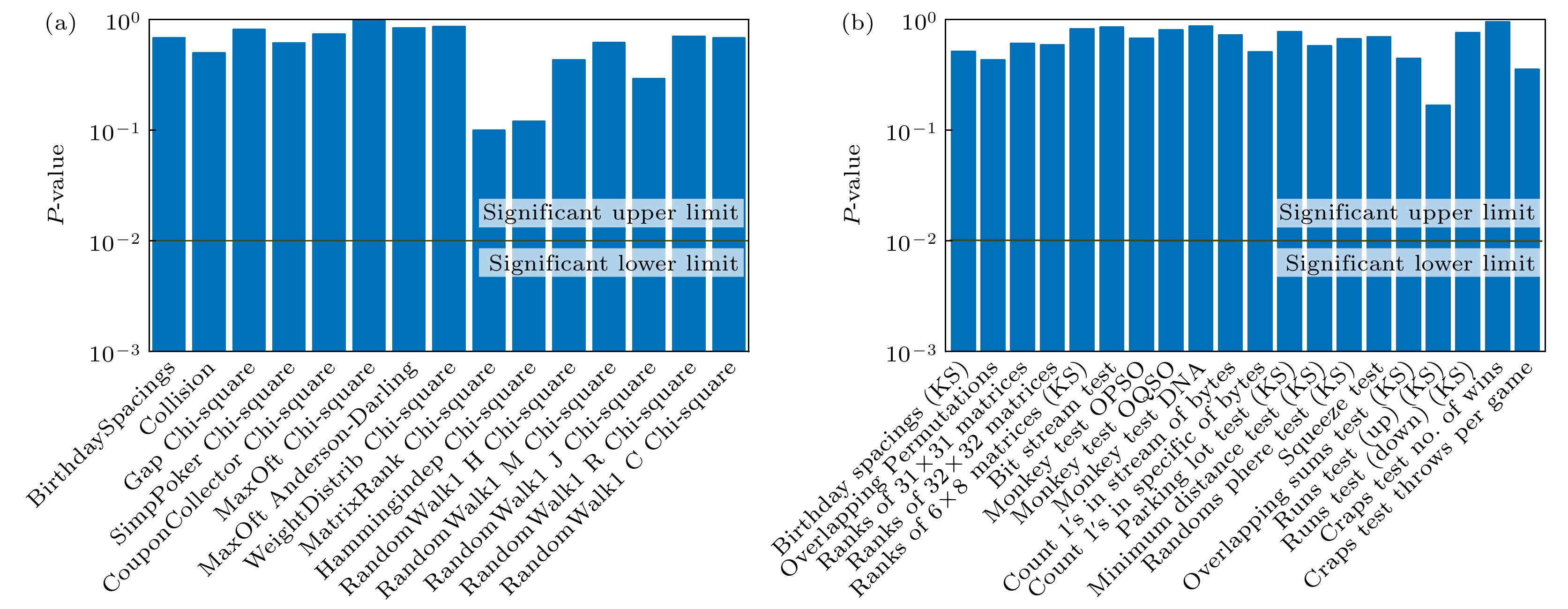
      此外, 如图5所示, 对于Diehard和TestU01测试, 各检验的P值均远大于0.01. 表明生成的量子随机数通过了所有的测试项目, 再次验证了本实时量子随机数生成方案生成的随机数具有良好的随机性.

    3.   量子态监测方案及反馈阈值设定

    • 本项工作中, 量子态相空间重构被用于评估实时QRNG的熵源的品质和安全性, 所以我们比较最典型的也是实验上可兼容于cv-QRNG的三类连续变量量子态全息重构方案: 基于HOM逆Radon变换重构量子态相空间Wigner函数, 基于HOM最大似然法重构量子态相空间Wigner函数, 基于HET的量子态相空间Husimi-Q 全息重构. 首先, 从理论上, 基于Fisher信息比较了HOM和HET的量子态协方差矩阵层析精度, 得出HET比HOM在边信息存在的情况下具有更高层析精度的判断. 进而, 具体以cv-QRNG的熵源——量子真空态, 及其在边信息干扰下呈现的热态为重构对象, 以KLD为评估指标, 从重构精度、随机数生成效率、数据量要求出发, 通过对比得出Husimi-Q 函数重构能够更准确地反映量子态的相空间分布特性, 并确定了用于重构量子态相空间分布的原始数据量最优最小值. 而KLD对各变量的敏感响应也充分保证了其作为熵源监测阈值的可靠性.

      • 3.1.   基于Fisher信息比较HOM和HET的量子态协方差矩阵层析精度

    • Fisher信息是统计学中衡量参数信息量的指标, 由Ronald Fisher提出[49], 广泛应用于估计理论和假设检验. 其数值越大, 样本所含参数信息越丰富, 估计精度越高. 量子Fisher信息则拓展到量子领域[50], 用于量化量子态参数(如密度矩阵参数)在测量过程中携带的信息量, 通过量子Fisher信息, 我们可以确定最优的量子测量方式, 从而实现对量子系统参数的精确估计. 对于多参数估计, 量子Fisher信息进一步扩展为量子Fisher信息矩阵, 其对角元给出了各参数的Fisher信息.

      理论上, Wigner函数和Husimi-Q 函数是量子态的等价表示. 对于真空态、热态等高斯态时, 量子态Wigner函数的协方差矩阵可以表示为

      其中$ \mu = 2 n + 1 $为热因子, $ n $为平均热光子数, $\lambda $为压缩因子. 考虑实际探测效率$ \eta \leqslant {1} $, 两种方案的协方差矩阵则分别为

      式中, I为单位矩阵, 两式单位矩阵系数的差异源于同时测量两个正交分量时引入的Arthurs-Kelly误差[51-53]. 由(3)式可以看出HET的协方差${{\boldsymbol{G}}_{{\text{HET}}}}$较HOM多出${\boldsymbol{I}} /(2\eta) $, 其实质上反映了额外的真空涨落, 当$ \eta {\text{ = 1}} $时该项为I/2.

      统计学通常采用Fisher信息矩阵的逆矩阵的迹$ {CR}=\text{Tr}\left\{\boldsymbol{F}^{-1}\right\} $作为评估指标, 定量比较基于上述两种测量方案对协方差矩阵的层析精度, 该指标定义了无偏估计量的Cramér-Rao 下界[49,54], 其具体表达式为

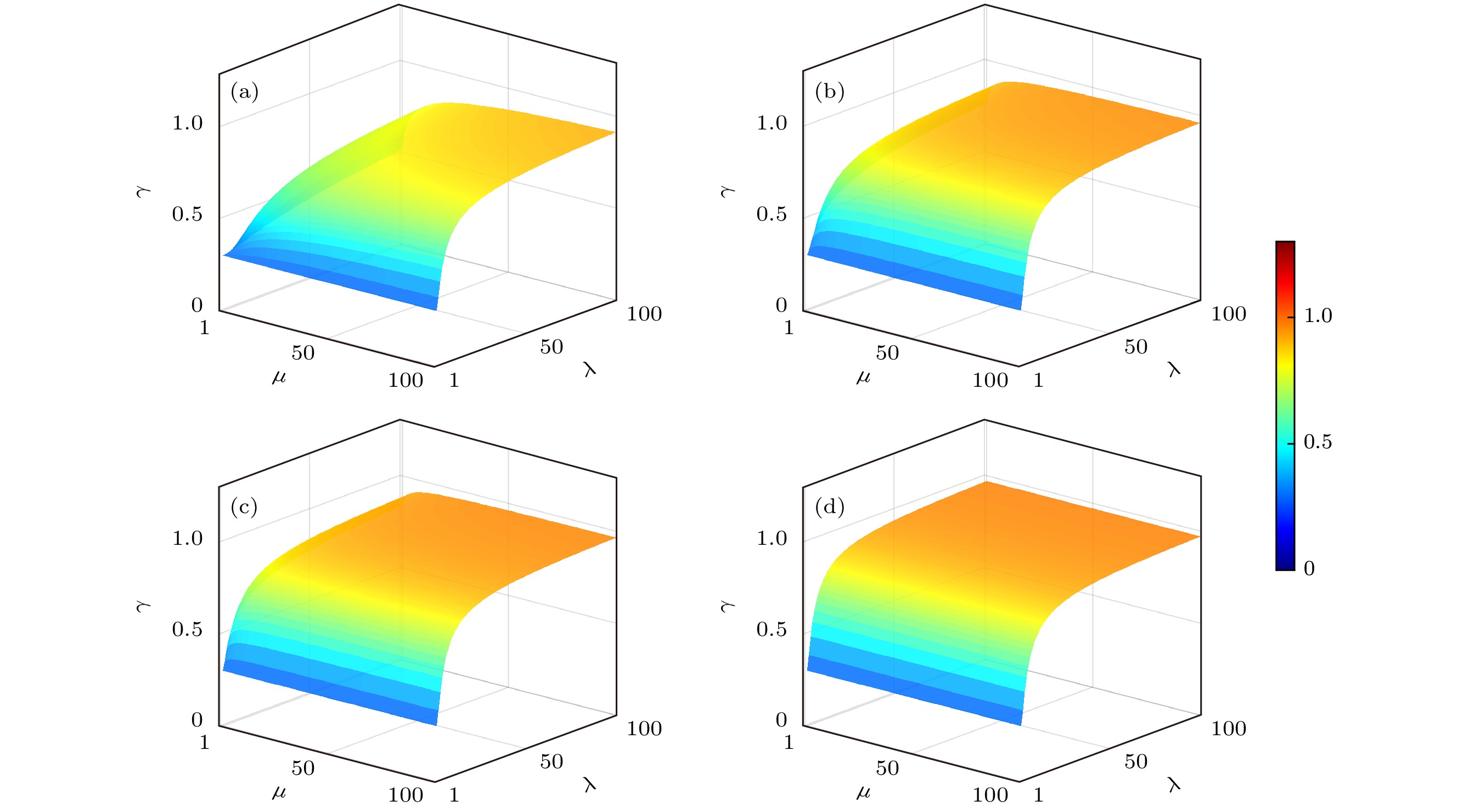
      HET与HOM层析精度比即以$ \gamma = {{C}}{{{R}}_{{\text{HET}}}}/{{C}}{{{R}}_{{\text{HOM}}}} $来评估.

      首先, 当忽略同时测量两个正交分量引入的Arthurs-Kelly误差时, 即$ {{\boldsymbol{G}}_{{\text{HOM}}}} = {{\boldsymbol{G}}_{{\text{HET}}}} $, 我们计算了各因素的影响趋势, 结果如图6所示. 探测效率分别取$ \eta = {1} $代表理想探测器的情况, $ \eta \leqslant {0}{.5} $代表效率较低的情况. $ \eta=0.72 $则代表我们的实验参数:

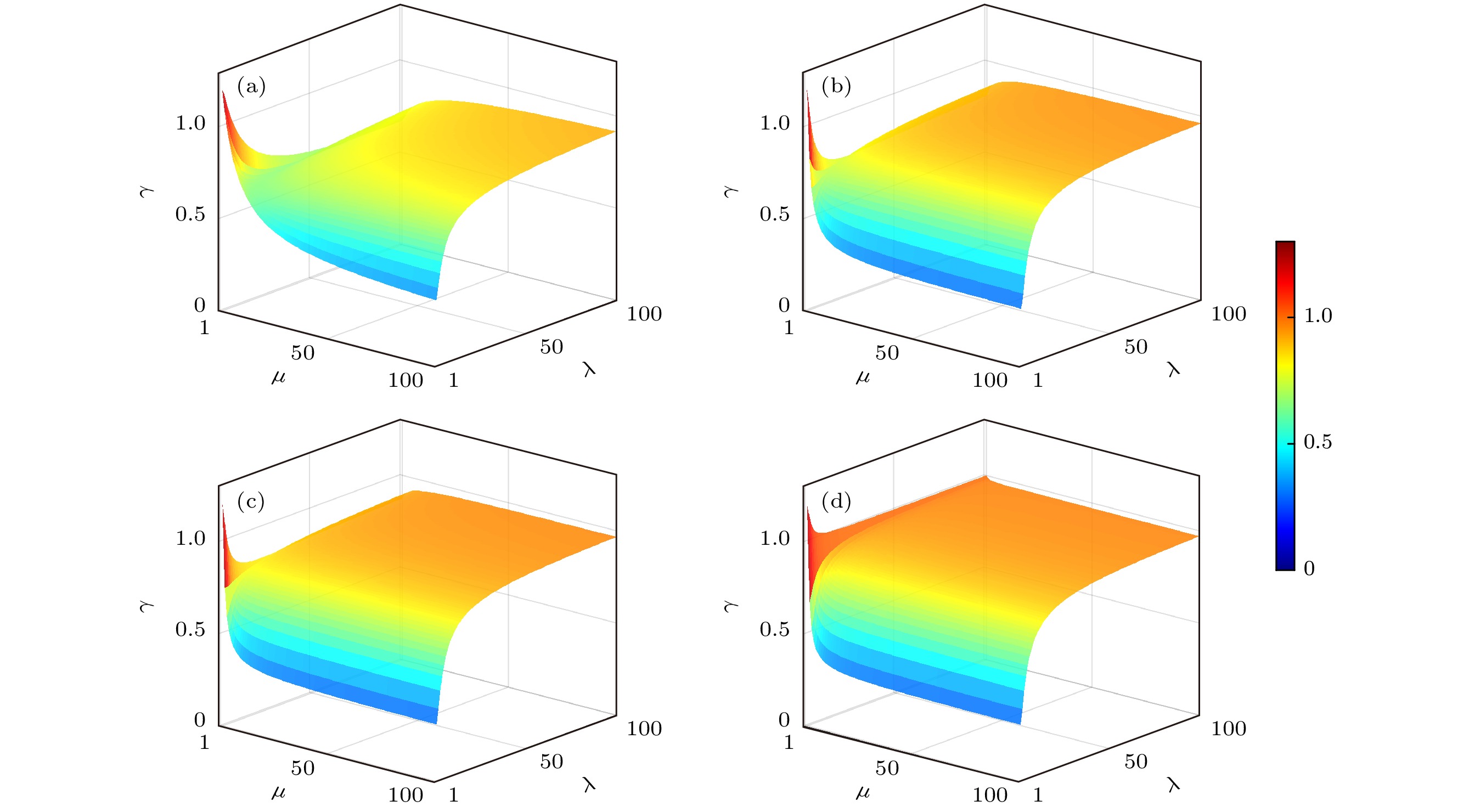
      其中e为电子电荷, $ \omega $为角频率(1550 nm), $ R $为光电二极管响应度(0.94 A·W–1, Thorlabs PDB480C). 如图6所示, 当不考虑同时测量两个正交分量引入的Arthurs-Kelly误差时, HET与HOM的层析精度比γ对压缩参数λ最为敏感, 且HET层析精度总是优于HOM的.

      图7为考虑Arthurs-Kelly误差的情况, 此时性能比γ对探测效率高度敏感. 在理想探测效率情况下, 即$\eta {\text{ = 1}}$时, 对于$\mu = 1$即理想真空态的情况, $ \gamma $始终大于1. 当$\eta {\text{ \lt 1}}$时, 只有当平均光子数接近0时, 才会出现$ \gamma $大于1的情况, 表明HET在实际场景中层析精度更高.

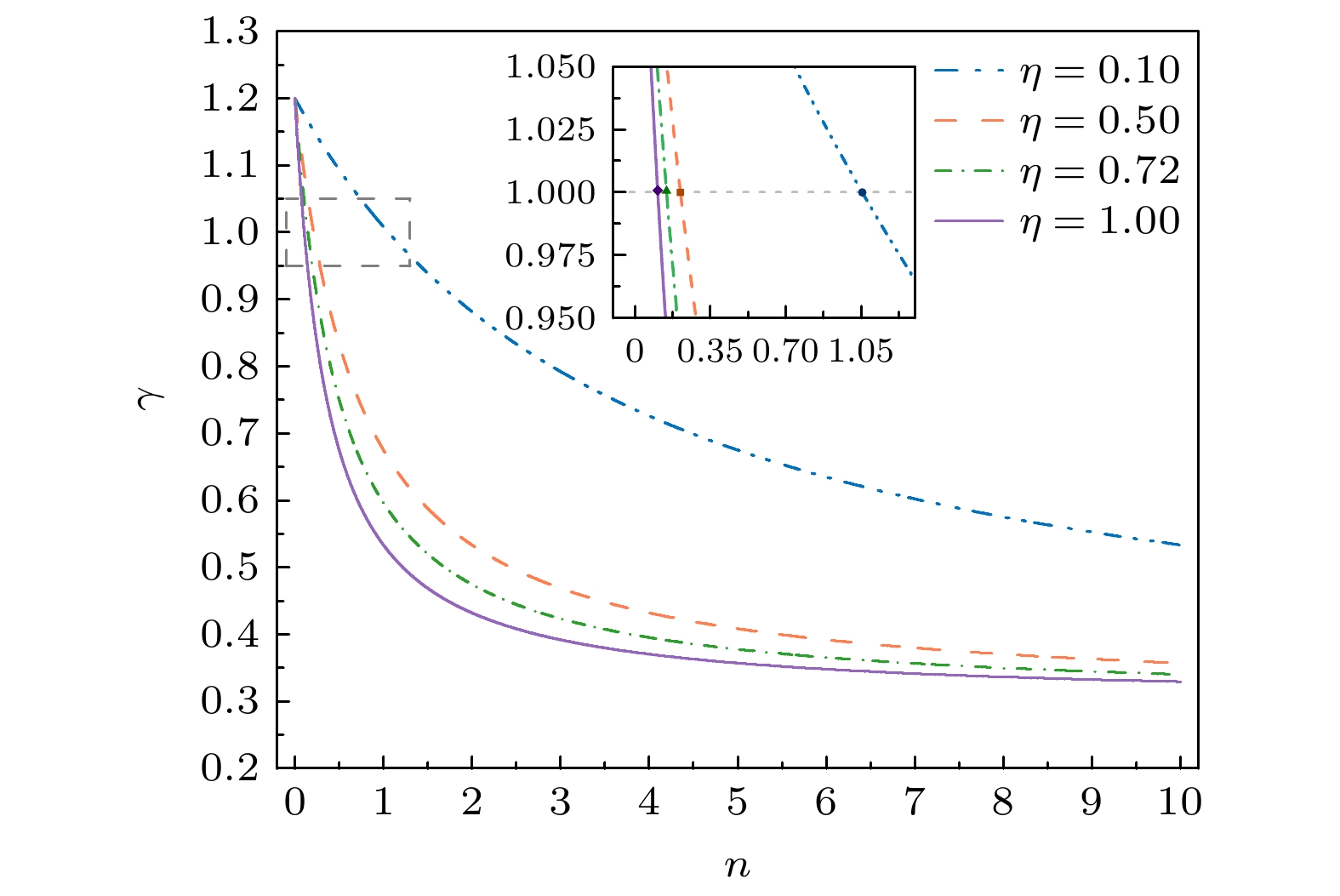
      图7显示, 实际真空态量子熵源测量情况下, 会存在一定的边信息阈值($\mu $)导致两种测量方法层析精度比的变化. 为了更加直观, 图8以平均光子数n代替热因子μ作为变量, 对比分析无量子态压缩时, 不同探测效率下两种探测方式的层析精度. 结果表明仅在热光子数极低的小范围内, HOM展现出微弱优势; 而在不同效率下平均光子数分别达到1.06, 0.21, 0.15, 0.11时HET性能超过HOM. 并且随着探测效率的提高, 外差测量的性能优势会更早显现, 表明高效率条件下外差方案可在更低热噪声水平下实现精度超越.

      • 3.2.   量子态监测全息方案选定

    • 实验上采用分布差异敏感的KLD熵, 精确评估实验测量重构的相空间分布相对纯量子态发生的变化, 对3种量子态重构方案的关键参数进行最优化, 进而对比这3种方案对量子态重构的准确度, 并研究了各方案的最小有效数据量, 为cv-QRNG量子熵源的实时监测提供了明确的方案.

      KLD通过计算两个概率分布之间的相对熵来衡量它们之间的差异, 其相对于保真度(fidelity)更具有敏感性, 在概率论和统计学中常被用于度量两个分布之间的非对称性[55-57], 在信息论中度量新的信息量[58], 在机器学习、深度学习领域中, 被广泛运用于变分自编码器、期望最大化算法、生成对抗网络[59]中, 其对于两个分布之间微小差异的敏感度更高, 更能够捕捉到细微的变化, 即使是在高维的量子态空间中也能够有效地发挥作用. 两个概率分布的KLD定义为

      其中S表示通过实验数据重构的实际分布, $ {S'} $表示真空态的理论分布, $ S\left( x \right) $和$ {S}'\left(x\right) $分别为两分布的概率密度函数. KLD值越小, 表明实验分布与理论分布越接近.

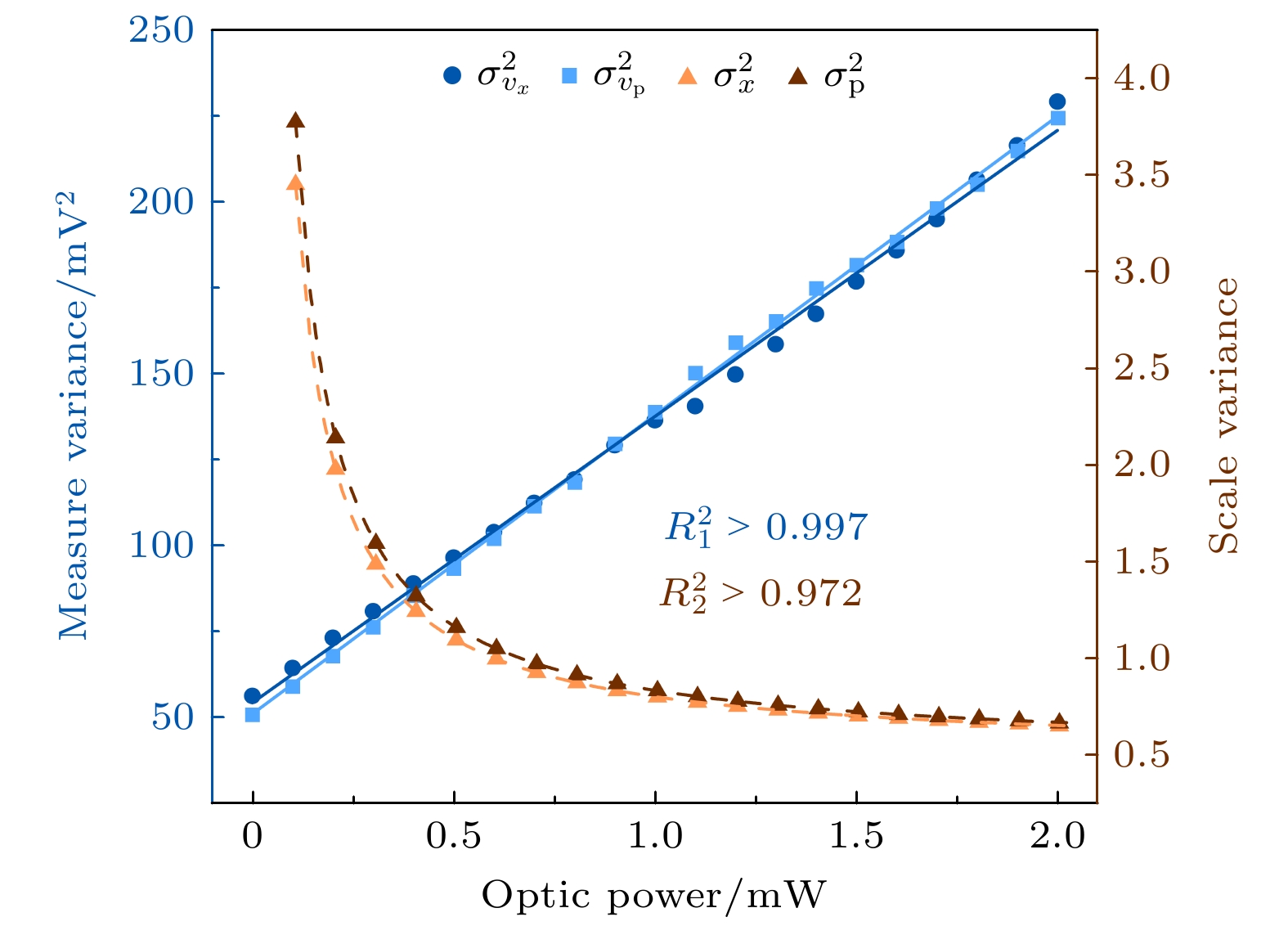
      外差探测中, LO通过相干干涉将真空波动放大至可测量范围, 此时ADC输出的光电信号是包含本振放大效应和额外噪声的物理电压值. 为重构熵源的相空间分布函数, 需将物理电压归一化为无量纲的散粒噪声单位(SNU). 这一过程基于探测器的校准实验来完成. 在校准阶段, 遮挡信号输入端确保真空态输入, 将本振功率$ {P_{{\text{LO}}}} $从0 mW提高到工作功率2 mW. 此时, 同步记录了两个探测器测量信号的方差$ \sigma _{{v_x}}^2 $和$ \sigma _{{v_{\text{p}}}}^2 $, 进行线性拟合:

      截距$ {c_{x, {\text{p}}}} $反映额外噪声对方差的贡献, 斜率$ {m_{x{\text{, p}}}} $表征LO及探测器的总增益, 图9中蓝色所示的高度线性拟合证明了探测系统的可靠性.

      根据理论模型, 散粒噪声单位方差$ \sigma _{x, {\text{p}}}^2 $与探测器电压信号方差$ \sigma _{{v_{x, {p} }}}^2 $满足如下关系:

      其中$ {k_{x, {\text{p}}}} $是待定常数, 给定理想情况下的归一化噪声方差为1/2, 通过(7)式和(8)式得到$ {k_{x, {\text{p}}}} = 2{m_{x, {\text{p}}}} $, 则相应测量电压信号数据与归一化散粒噪声单位数据之间的缩放因子为$ \sqrt {{k_{x, {\text{p}}}}{P_{{\text{LO}}}}} $, 所有电压数据都要根据这一因子缩放至散粒噪声单位. 进一步可以推出实验真空散粒噪声方差与$ {P_{{\text{LO}}}} $有如下关系:

      (9)式反映随着LO光强的增大, 电子噪声的相对贡献逐渐减小, 实验散粒噪声方差接近期望的1/2. 图9中的橙色非线性曲线为实验数据缩放到散粒噪声水平后的统计方差与$ {P_{{\text{LO}}}} $的关系, 拟合度验证了公式的理论预期.

      HOM中来自LO与信号光的两束光经过分束器合并后由探测器探测, 在这种情况下LO相位为正交测量提供了参考, 即利用两种模式之间的相位差来识别LO的相位. 得到的零差数据为该相位角下量子态的Wigner函数的边缘分布:

      在逆Radon变换算法下, 通过对不同相位$\theta \in \left[ {0, \pi} \right)$的分布进行如下变换得到对应量子态的相空间Wigner分布函数:

      其中, $K\left( x \right)$是核函数, 在数值上近似为$K\left( x \right) = \left[ {\cos \left( {{k_{\text{c}}}x} \right) + {k_{\text{c}}}x\sin \left( {{k_{\text{c}}}x} \right) - 1} \right]/{x^2}$. 这里kc为截断参数, 需要根据具体的量子态进行调整, 其值依赖于实验条件[60].

      而最大似然法通过提取合理有限维度, 多次迭代后获得与被测光场直接相关的密度矩阵$\hat \rho $, 同时不受低探测效率条件的限制, 重构结果也更接近实际物理情况[61,62]:

      其中$k$为迭代次数, $\aleph $为初始密度矩阵$ {\hat \rho ^{\left( 0 \right)}} = \aleph \left[ {{{\hat 1}}} \right] $对单位矩阵$ \left[ {\hat 1} \right] $的归一化系数. 通过迭代之后的密度矩阵来重构Wigner函数:

      其中$ \hat \rho _{st}^{\left( {k + 1} \right)} $为密度矩阵$ {\hat \rho ^{\left( {k + 1} \right)}} $对应的第s行第t列的矩阵元, 当$ s \geqslant t $时:

      其中$ {\rm L}_t^{s - t} $为连带拉盖尔多项式, 当$s \lt t$时, $ {W_{\left| s \right\rangle \left\langle t \right|}}\left( {x, p} \right) = {W^*}_{\left| s \right\rangle \left\langle t \right|}\left( {x, p} \right) $.

      HET通过双平衡探测器同步测量量子态的正交分量X 和 P, 避免了因手动调节LO与信号光的相对相位所引入的复杂性, 可以直接获取量子态的Husimi-Q 分布:

      对于具体的量子态, 如系统处于热态时, 其密度矩阵为

      其中n对应耦合进入HET系统的热态平均光子数, 则在相空间中的热态Husimi-Q 函数表示为

      当光子数为0时, 对应的Husimi-Q函数表示真空态.

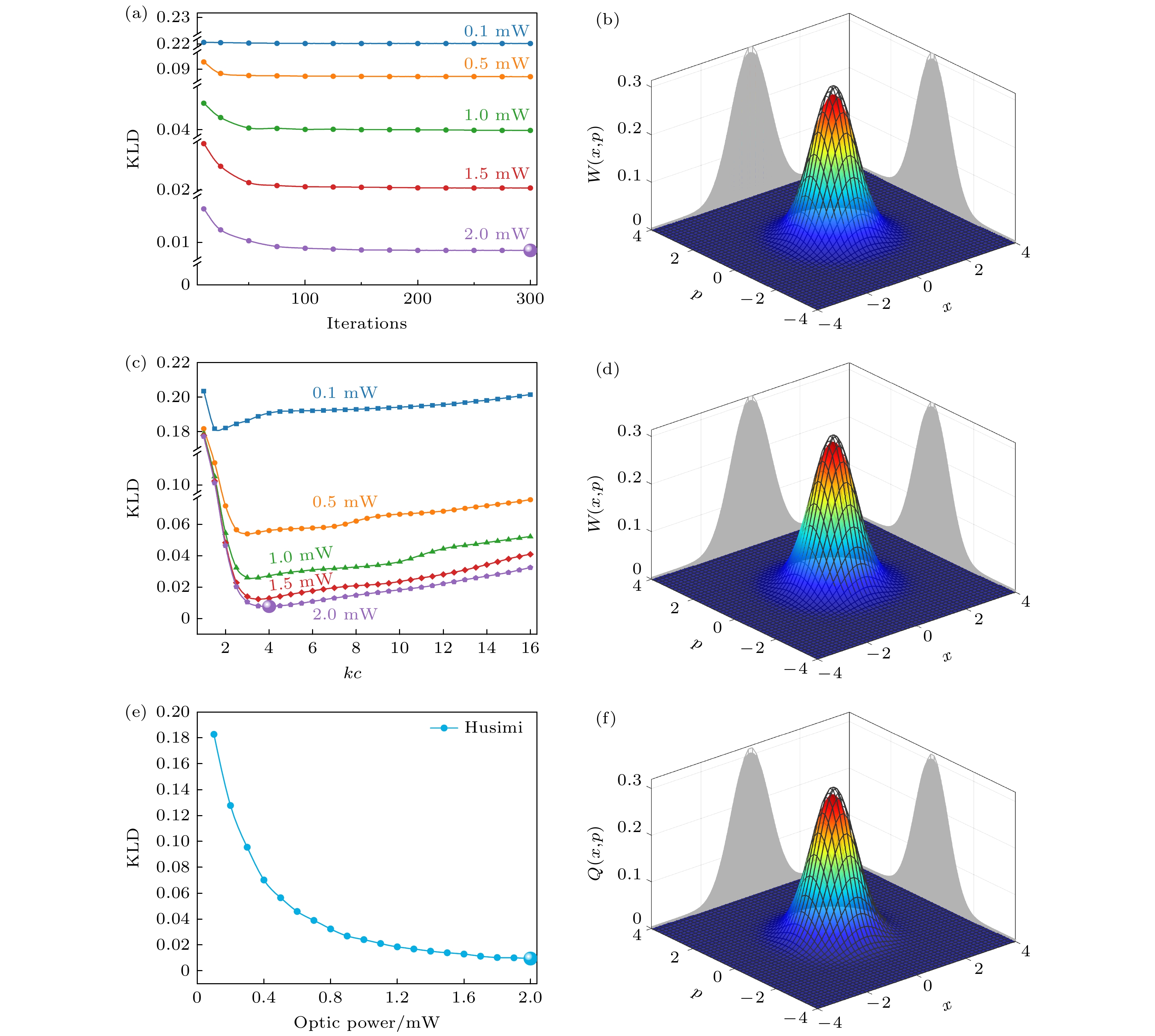
      基于实验数据与相空间正交分量缩放因子的标定结果, 分别对HOM和HET数据集实施归一化预处理, 并采用3种相空间重构方法进行量子态重构. 图10(a)展示了最大似然法重构过程中KLD随$ {P_{{\text{LO}}}} $的变化规律. 实验数据显示, KLD值随$ {P_{{\text{LO}}}} $增强呈现单调递减趋势, 这归因于高功率LO光有效抑制了系统额外噪声的干扰, 使量子噪声成为主导噪声源. 迭代次数对重构质量的影响研究表明, 当k > 200时KLD值进入收敛区域; 权衡层析精度与重构效率后, 本研究确定最佳迭代次数k = 300作为实验参数. 图10(b)展示了该参数下的重构结果, 实验方差(彩色曲面)略高于理论真空(网格包络), 阴影部分为Wigner函数在两个正交方向$X\left( {\theta = 0} \right)$和$P\left( {\theta = \pi}/2 \right)$的投影.

      在逆Radon变换法分析中, 图10(c)揭示了截断参数kc对重构质量的关键影响. 数值模拟表明, 当kc取值偏离最优区间(3 < kc < 5)时, 重构过程会产生显著数值伪影[63], 导致KLD值异常升高. 基于此, 实验选择kc = 4进行重构, 所得Wigner函数如图10(d)所示.

      图10(e)研究了$ {P_{{\text{LO}}}} $ 从0.1 mW增至2 mW时Husimi-Q函数KLD的变化. 随着功率提升, KLD呈现单调递减特性并在1.5 mW后趋于稳定. 图10(f)为最终在2 mW最优功率下获得的Husimi-Q函数重构结果, 图中清晰展现了量子态的相空间分布特征.

      在量子层析技术中, 充分的数据采样虽能更精确地刻画量子态特性, 但实际应用场景往往需权衡精度与效率. 尤其在实时性要求高的场景, 过高的数据量虽可略微提升重构精度, 却显著增加时间开销与计算资源消耗.

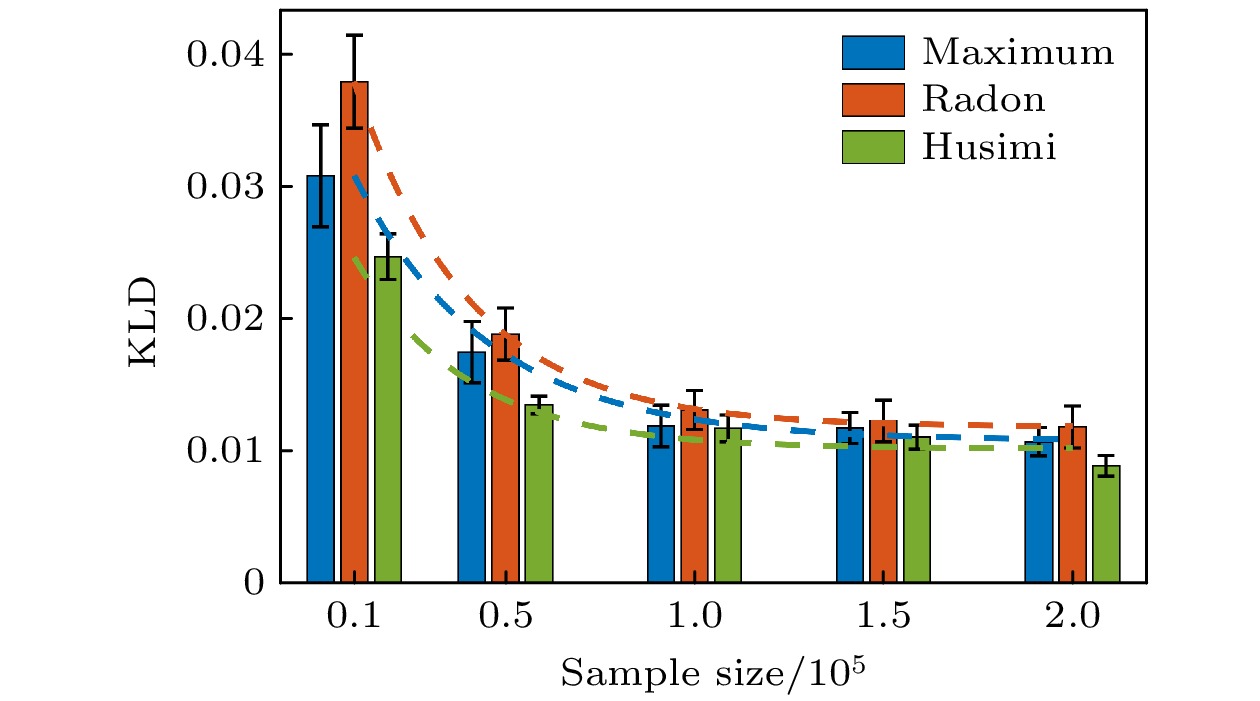
      图11展示了3种方法在不同数据量下的KLD表现. 在小样本下Husimi-Q相空间重构方法表现出显著优势, KLD更小, 误差线更短; 当样本量逐渐增大时, 所有方法性能均先提升后逐渐收敛, 但Husimi-Q仍保持最低KLD. 整体来看, Husimi-Q重构方法在所有样本量下均表现最佳, 尤其在105样本量时已接近收敛, 在资源受限时仍能保持高鲁棒性.

      • 3.3.   量子熵含量重评的反馈阈值设定

    • 量子随机数发生器相比伪或经典随机数发生器的最大区别是其有源于量子内禀随机性的物理熵源, 量子本质的起伏相对经典起伏的比例是可以基于所选用量子态的特征参数进行评估的, 这样就可以借用信息论安全的广义hash提取器(以往用于密钥分发中的私密放大), 以确定的比例从原始随机数中提取出量子真随机数, 这是所有随机数发生器中只有量子随机数发生器是安全性信息论可证的原因. 本文提出实时全息监测量子熵源的并行连续变量量子随机数产生方案, 在高速实时产生量子随机数的同时基于KLD对量子态进行监测与评估, 一旦边信息量超过一定的预设阈值, 便反馈至硬件后处理单元, 重新计算系统量子条件最小熵, 实时调整真随机提取比例, 保证实时高速生成的随机数的安全性. 所以KLD阈值的设定是关键的步骤.

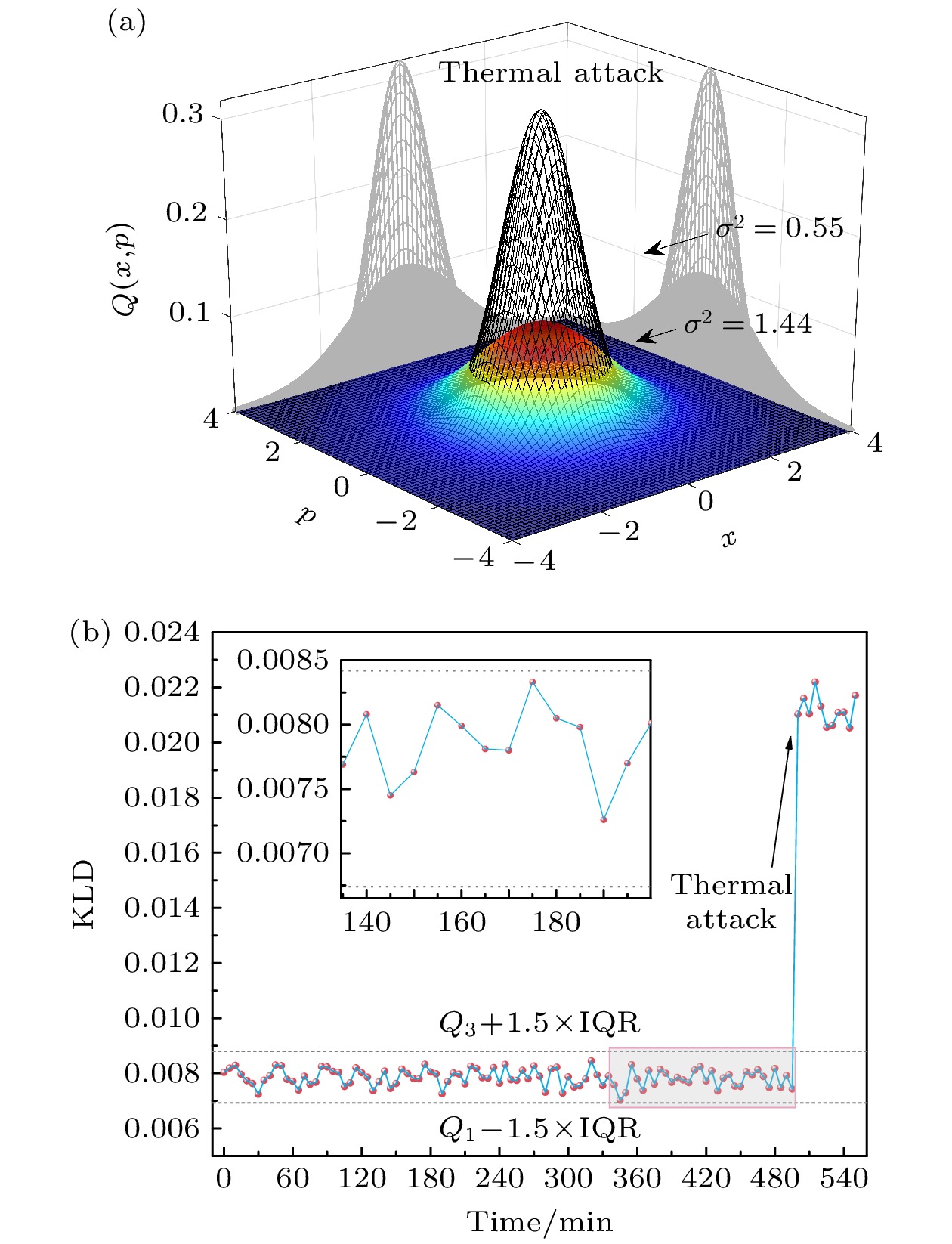
      通过混沌热态注入模拟实际系统经典噪声或外部高斯调制攻击如类似带外注入攻击[64]、饱和攻击等[65]对熵源量子态Husimi-Q 相空间畸变的影响, 并基于KLD实时监测建立动态安全阈值. 如图1混沌部分所示, 混沌光的产生基于分布式反馈半导体激光器(LD, 波长1550 nm), 通过精密温控(TC, ±0.01 ℃)和低噪声电流源(CS, ±0.1 mA)稳定激光输出, 经偏振控制器调谐后过环形器(OC)接入反馈系统反馈回路中80%的光经可调衰减器(VOA)后反馈回激光器, 形成时延为116 ns的光纤反馈回路; 剩余20%的混沌光接入主光路, 通过VOA控制耦合功率可至最小值1 μW, 对KLD变化进行分析; 混沌光与LO在90°光学混频器中干涉, 进而进入平衡探测系统和数据后处理系统.

      图12(a)为系统遭受热态攻击前后量子态层析成像对比, 相较于未遭受攻击时的真空态Husimi-Q 分布(网格化曲线), 在注入混沌光后(彩色曲面), Husimi-Q函数分布显示出高度降低、宽度增加的特性, 其方差从0.55增至1.44. 图12(b) 展示了 KLD 值的变化过程. 在系统未遭受攻击时, 通过长时间连续监测(采样间隔5 min, 数据量N = 100 组)获取系统稳态KLD波动特性, 可以看出KLD 值保持在极小范围内波动, 基于四分位距(inter quartile range, IQR)法确定了其阈值范围为[0.006925, 0.008795] (图中上下虚线). 然而, 当以微弱的1 μW混沌光注入时, KLD 值发生跃变, 快速偏离稳态基线, 说明系统量子态从真空态发生了明显转变, 可见, 以KLD评估量子态相空间Husimi-Q函统计分布变化差异, 得出熵含量重新评估阈值的方案具备良好的攻击识别能力.

      实验确定的稳态KLD阈值区间建立在对系统长期稳定运行数据的统计分析基础上, 该范围能够有效覆盖真空态量子涨落的正常波动. 值得指出的是, 该阈值参数可根据实际应用场景的安全需求进行动态优化, 在需要更高安全级别的量子通信系统中, 可通过压缩阈值上限来提升系统对微小量子态扰动的敏感度; 而对于需要兼顾误报率与检测效率的场景, 则可适当放宽阈值范围. 这种灵活性使得系统能够在保持核心检测框架的前提下, 实现对异常信号响应灵敏度的精准调控. 此外, 结合机器学习算法对历史攻击数据的学习, 可进一步构建自适应阈值模型, 使系统具备动态调整检测边界的能力, 从而在复杂攻防对抗中保持最优检测效能.

    4.   量子条件最小熵的严格评估

    • 在实际的QRNG系统中, 测量所得原始数据总是难以避免的混入由经典甚至量子边信息造成的额外噪声, 这部分噪声可能被攻击者掌控从而获得原始数据中的部分信息. 为确保后处理生成的随机序列安全可靠, 需对真空态熵源输出的随机比特数进行严格评估. 为此, 本研究在计入ADC非线性效应与直流偏移量的前提下计算系统量子条件最小熵:

      式中X为测量结果, E为攻击者可能获取的态信息. 实际探测系统产生的光电信号X为真空波动Q与额外噪声E的叠加, 其概率分布服从高斯分布:

      由于额外噪声的存在, 测量信号可等效为平均光子数为n的热态. 且总噪声方差可分解为量子散粒噪声与额外噪声的线性叠加$ \sigma _X^2 = \sigma _Q^2 + \sigma _E^2 = {g^2}(1 + 2 n) $, 其中g为系统增益, 包括LO放大与电子学增益. 则外差系统量子信噪比(quantum signal-to-noise ratio, QSNR)为${\text{QSNR}} = {Q}/{E} = 10{\log _{10}}\sigma _Q^2/\sigma _E^2$, 通常情况下, 量子噪声占据主导地位$ \left( {\sigma _Q^2 \gg \sigma _E^2} \right) $.

      在最坏情形下的安全性分析需考虑测量系统与环境之间可能的量子纠缠关联. 通过构建正交测量结果与量子边信息之间的条件概率模型, 在量子力学框架下将此类纠缠态结构纯化为双模压缩真空态(two-mode squeezed vacuum, TMSV)[19], 这是典型的高斯纠缠态. 该模型中纠缠强度由参数 δ来表征, 后续将通过优化参数 δ使系统输出的最小熵下界最大化. 在量子边信息影响下的测量分布为

      其中$ \rho _E^x $为测量量子态的密度矩阵, $ {\gamma _E} $为测量环境系统的密度算子, $\bar X$表示离散测量. 测量采样在16位ADC上进行, 采样范围为$[ - R + {{\Delta }}x/2, R - 3{{\Delta }}x/2 ]$, 选择此范围使得中间帧以0为中心, 在测量过程中, 采样信号被离散到216个帧上, 每个帧理想宽度为${{\Delta }}x = R/{2^{N - 1}}$, 然而, 在实际应用中, 由于ADC 内部电容与电阻的内在不匹配性[66], ADC会表现出一定的非线性行为, 使输出值帧宽偏离理想值. 通常采用微分非线性(differential non-linearity, DNL)来映射每帧宽的偏离程度, 具有正 DNL 会导致帧大小大于 1 LSB (least significant bit), 而具有负 DNL 会导致帧大小小于 1 LSB, 考虑ADC误差则帧宽有如下形式:

      本文基于最大$ {\text{DN}}{{\text{L}}_{\max }} = 1{\text{ LSB}} $来计算最保守的最小熵下界, 更严格来说, 在实际测量中, 测量系统中不可避免的经典噪声偏移会引入非零的直流偏压, 使得测量信号的概率分布均值非零. 另一方面, 窃听者可能通过引入直流补偿干扰测量周期. 因此在优化最小熵下界中, 需要考虑明显的直流偏移[21,22]. 本文通过加入偏移因子D来抵消这些影响. 由此得到离散化信号的概率分布:

      对于$ j = {j_{\min }} $的上边缘帧, 测量概率为

      同样对于$ j = {j_{\max }} $的下边缘帧, 有

      对于$ j_{\min }<j<j_{\max } $的中间部分, 对测量概率积分结果做如下近似:

      以此可以得到误差下的条件最小熵:

      其中,

      (27)式中第1部分通过优化纠缠强度参数$ \delta $来给出最优值, 具体的分式可展开为

      通过对$ \delta $求导并令导数为零解得最优值$ \delta = \sqrt {n\left( {n + 1} \right)} $, 代入后分式简化为

      对于第2部分, 需要对参数$ {g'} $优化, 这里通过将边帧中较高的测量概率等于高斯分布中心帧的测量概率时, 得到一个最严格下界. 由于erfc函数在定义域大于零部分递减, 显然A<C, 因此通过计算B = C来优化参数$ {g'} $, 即:

      此时通过对上述参数的优化, 得到量子条件最小熵在误差下的一个最优下界:

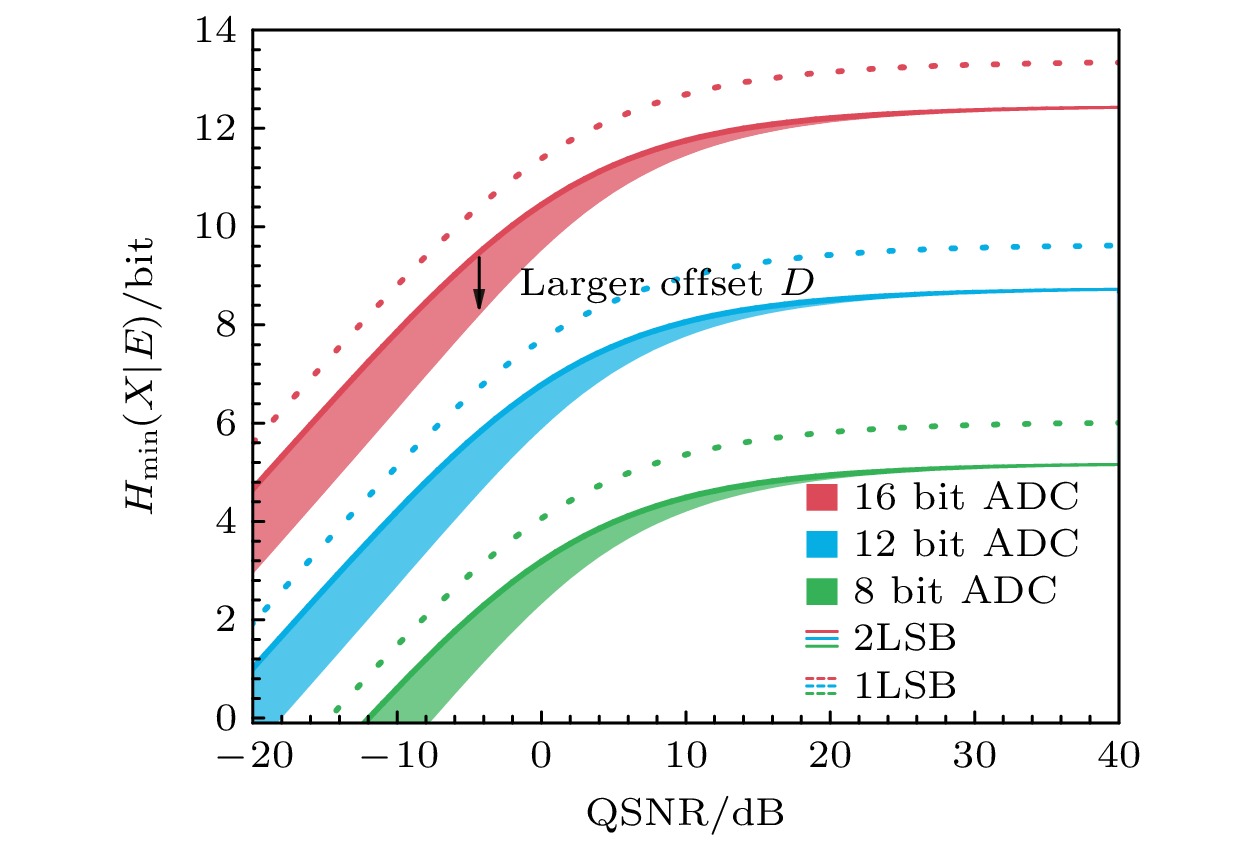
      基于以上量子条件最小熵理论模型, 图13系统性地揭示了ADC分辨率、QSNR与最小熵的定量关系, 并量化评估了直流偏移与ADC非线性效应对熵值的影响. 实验结果表明相较于较低分辨率, 采用16位ADC能够有更大的提取比特, 即便在量子信噪比为负值的极端场景下, 仍可提取${H_{{\text{min}}}}{\text{ \gt 8 bit/16 bit}}$的真随机比特, 验证了量子噪声的微观效应对熵的实质性贡献. 实验测得直流偏移$D \in \left[ {3{\sigma _{\text{E}}}, 20{\sigma _{\text{E}}}} \right]$, 应用场景中, 窃听者可能故意造成更大的直流偏移. 图中阴影部分给出了直流偏移在$3{\sigma _{\text{E}}} \leqslant D \leqslant 30{\sigma _{\text{E}}}$范围内可提取的随机位, 结果表明相较于${D_{{\text{min}}}} = 3{\sigma _{\text{E}}}$的最小偏移, 较大的直流偏移会造成提取随机比特的下降, 最大可减小2 bit. 与理想ADC $ {{\Delta }}x = 1{\text{ LSB}} $的熵值(虚线)相比, ADC的非线性误差$ {{\Delta }}x = 2{\text{ LSB}} $(实线)会导致熵值损失约1 bit. 此外, 提高量子信噪比和ADC分辨率并不能显著减轻非线性效应引起的熵值下降.

    5.   Toeplitz矩阵变化精度及调节范围

    • 真随机数的本质是不可预测、独一无二、不可再生, 所以只有实时产生、一次一密才是信息安全的真正保障, 也就是说, 面向保密通信网络飞速发展, 实时产生速率高、安全性实时监测的量子随机数发生器才能真正满足应用需求. 本文的研究目的是实时监测量子熵源、并在监测到量子攻击后, 实时反馈重新评估量子熵含量、实时调整硬件哈希后处理提取比例, 而不是直接中断随机数生成.

      在硬件实时后处理方面, 矩阵规模的实时、甚至高分辨的调整是以往报道中没有过的. 由于硬件电路是固定的, 无法像软件运算一般灵活, 为此我们创新性地提出一种最大矩阵位宽截取的方法, 即固定矩阵的输出m, 仅改变矩阵的输入n, 通过改变参与后处理的子矩阵个数实现实时的矩阵规模调整. 矩阵规模调整流程示意如图14所示. 该方案的核心参数包括Toeplitz矩阵的调节精度与动态调节范围, 前者决定系统对熵波动的响应灵敏度, 后者限定最小可实现的提取比.

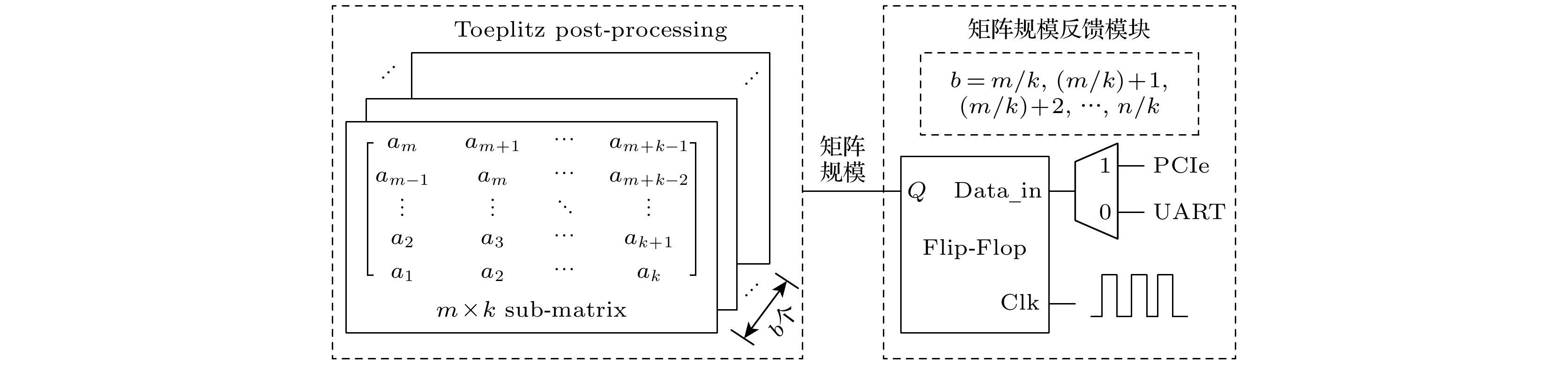
      后处理的硬件实现方法是通过将大矩阵拆分成多个规模相同的子矩阵并行运算, 在此固定m×n的Toeplitz矩阵的列数m以及m×k子矩阵的行数k, m和k的大小需要对FPGA进行资源评估后得到. 同时我们预先选择一个最大的m×n, 其代表着可以实现的最大矩阵规模, 由于m数值一定, 即其表示这后处理最低的提取比例, 包含的子矩阵个数为n/k, 将一个长度为m + n – 1比特的种子产生n/k个长度为m + k – 1的子种子. 三级并行流水线后处理包含访存、子矩阵生成及乘法和中间向量累次异或3个并行的模块; 通过同时改变访存的子矩阵个数以及累次异或的周期数可以实现实时的矩阵规模调整. 设置后处理过程中总共构建的子矩阵个数以及中间向量累次异或周期总数为b, 因量子熵源会不可避免地混入经典成分, 所以Toeplitz矩阵一般无法设置为方阵(矩阵提取比例≠100%), 则b的取值可以设置为$ \left( {m/k} \right) + 1, \left( {m/k} \right) + 2, \cdots , n/k, b $为整数.

      由于子种子的生成已经提前完成并存储于对应内存中, 我们仅需要改变以此后处理中访问内存的总次数和中间向量累次异或周期总数, 结合并行流水的思想即可完成实时动态可调的Toeplitz后处理. a组子种子在第2级存储器存放的首地址为$ y\times n/k, y = 0, 1, 2, \cdots , a-2, \text{ }a-1 $. 为满足Toeplitz矩阵的构造规则, 我们在确定一个不大于n/k 的数值b后, 需顺序地构建子矩阵. 设置每次后处理第一级访存模块的访存地址为g, g的地址取值为$ y\times n/k, (y\times n/k)+1, \cdots , (y\times n/k)+b,\; g $为整数. 此方法通过利用矩阵位宽截取的思想, 预先构造最大的矩阵, 固定矩阵的列数m, 仅修改行数n实现矩阵的实时动态调整.

      如图15所示, 每个后处理通道有着对应的矩阵规模寄存器, 在每完成一次后处理时, 每个后处理通道读取对应的寄存器, 该寄存器中锁存着系统不同后处理通道的矩阵规模b, 寄存器数值由反馈模块进行控制. 本工作中反馈模块共支持两种不同的数据反馈方式, 分别是基于PCIe的反馈方式以及基于UART的反馈方式. PCIe借助XDMA硬核通过AXI4-Lite总线对不同地址的矩阵规模寄存器进行访问, UART串口也可通过对应串口协议每次将大小为一个字节的数据传输至FPGA.

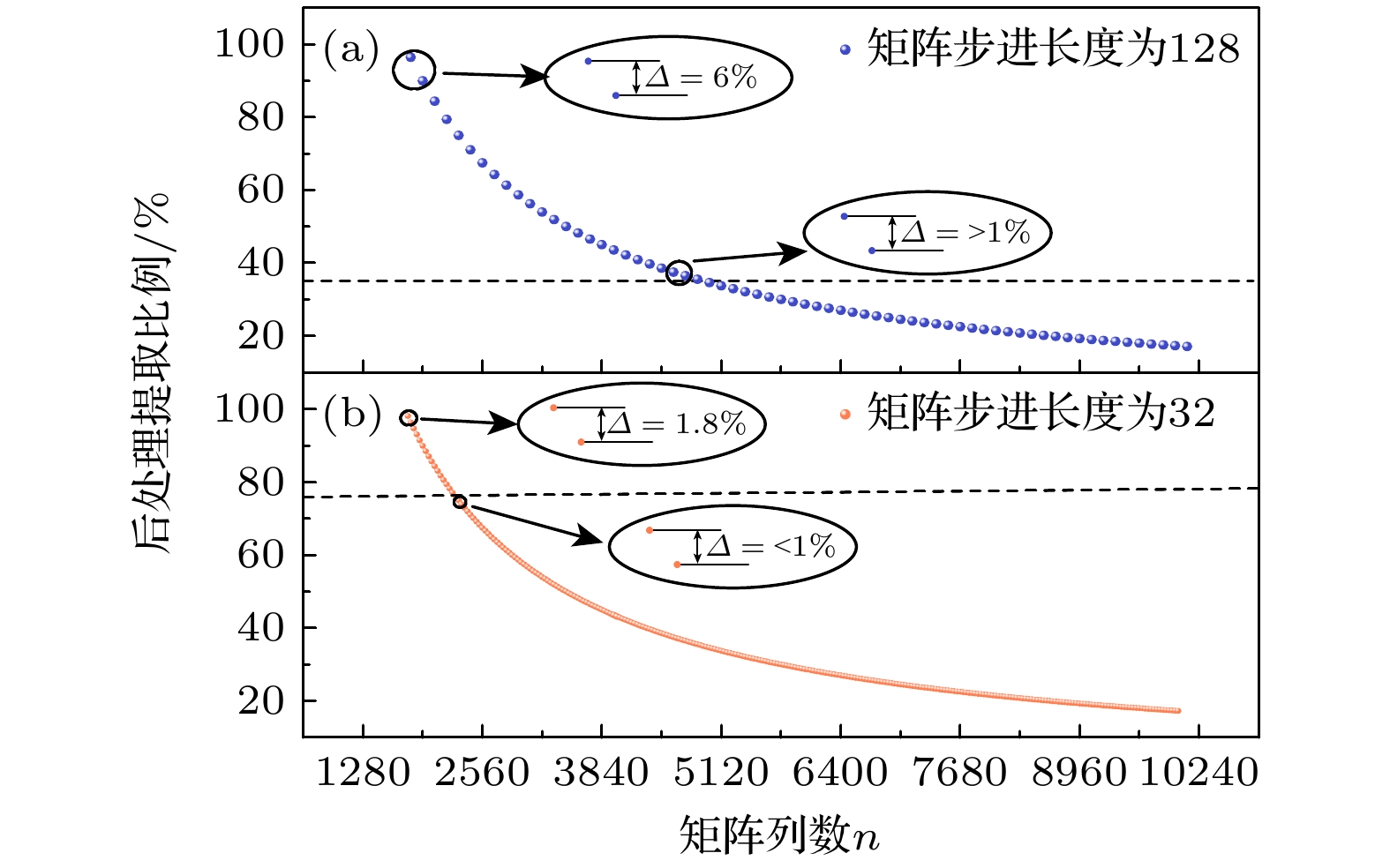
      在400 MHz采样率、16位ADC及50 MHz后处理时钟约束下, 可以得到矩阵调整步长k为128. 当后处理的m值设为1729时, 可以得到如图16(a)所示的矩阵提取比例变化图. 可以看出, 当k值较大时, 最大的提取比例间隔为6%, 随着矩阵列数n的增大, 提取比例间隔逐渐减小, 当提取比例在35%及以上时, 提取比例间隔均大于1%. 严重制约系统对微小熵波动的响应能力, 影响系统的随机数产率. 针对该问题, 本研究提出了单通道后处理内多个Toeplitz后处理模块并行架构. 通过将原始数据块k = 128分解为k' = 32的子块, 使每个处理通道内并行4个Toeplitz模块. 该设计使得矩阵规模调节步长从128缩减至32. 如图16(b)所示, 优化后最大提取比间隔从6%降至1.8%, 当提取比在76%及以下时所有间隔均小于1%, 显著缓解了离散调节导致的提取比例损失.

      本文提出矩阵规模可调的后处理模块, 矩阵行维度m = 1729由FPGA片上存储器容量直接限定, 而列维度n通过最小熵的变化来进行调整. 随机数发生器的速率由Nyquist规则${\varepsilon _{{\text{hash}}}} = {10^{ - 50}}$给出, 其中N为ADC分辨率, W为采样频率, 矩阵列数n通过Leftover-hash引理, 即采用(1)式计算. 系统量子噪声熵含量越高, n的取值越小, 真随机数的实时产生速率越高. 实际n的取值并非连续的, 而应该为硬件可实现矩阵规模调整分辨率的整数倍, 即本文所述矩阵最小调整间隔32的整数倍. 我们创新性地采用单通道后处理架构内4个Toeplitz矩阵并行的架构, 使单个后处理时钟周期内需处理的比特位128可分为4份, 即将矩阵规模调整分辨率由128提高到32, 降低了矩阵规模变化离散性造成的真随机熵损耗, 图16即呈现了这一方案前后的比较.

      而矩阵列数n的最大取值受限于FPGA硬件资源的有限, 具体主要取决于FPGA块存储器资源分布及区域布线资源的双重制约, 本文所述方案经综合协调资源分配、时序及最低提取比例约束等关键参数, 最终可实现得最大列数为n = 10176, 因此系统可实现的最低提取比例为16.9%, 也就是说我们的后处理矩阵规模实时可调方案可应对的极限情况是最小熵降低到2.876 bit/16 bit, 这对于经典噪声甚至外部攻击的情况已经具有了相当的鲁棒性, 此时单通道随机数的实时产率为1.0816 Gbit/s.

      目前的方案中采取每随机触发量子态Husimi-Q重构及KLD计算的同时, 亦触发FPGA内量子最小熵计算, 基于3.2节分析得出最小有效数据量(105)在MATLAB内做Husimi重构及KLD计算, 这一过程目前耗时约3 s, FPGA内量子最小熵计算时间已压缩至0.8 s, 而基于位宽截断的矩阵规模自适应调整与随机数提取同步进行, 并不单独耗时, 所以系统存在一个约3 s的“盲时间”. 后续我们将进一步采用深度学习的方法完成Husimi重构与KLD值之间的映射, 压缩这一“盲时间”, 进一步结合FPGA缓存单元提供真随机数储备池的方法来提供与用户之间的动态延迟, 使“盲时间”的影响消除.

    6.   结　论

    • 本文提出并实验实现了一种实时熵源监测评估的二重并行量子随机数生成方案. 基于理论及实验分析对比, 选择了重构精度最高、效率最高、数据量需求最小HET测量量子态Husimi-Q函数重构方案, 基于随机抽取原始随机数、以高维统计分布敏感的KLD熵监测熵源的准实时变化, 基于长时监测数据离差区间统计设定了反馈阈值, 构建了上位机熵源全息监测评估与FPGA内最小熵计算及Toeplitz-hash提取比例自适应调整的传输协议, 实现了高动态范围、高分辨率的矩阵规模实时可调硬件后处理, 成功实现了17.512 Gbit/s的生成速率, 安全参数${\varepsilon _{{\text{hash}}}} = {10^{ - 50}}$的量子随机数实时产生. 本项工作为解决QRNG实时熵源可信评估提供了有效方案, 且该方案涉及光源、探测系统、连续变量量子态多频模并行提取系统均有现有集成技术支持, 二重并行量子熵源提取方案随着BHD系统性能改善和FPGA后处理效率持续提升将可进一步扩展, 为量子随机数发生器应对通信网络飞速发展的应用需求提供了切实可行的方案.

      值得注意的是, 本文所述的实时熵源评估二重并行连续变量量子随机数发生器方案弥补了以往对量子熵含量评估一劳永逸的缺陷, 基于相空间全息监测了熵源的质量, 构建了量子熵含量实时重评估的方案, 最小熵计算方面目前考虑了经典噪声偏移、ADC量化误差等因素, 但是对于探测器及滤波器的有限带宽、ADC有限分辨率等因素对QRNG安全性的潜在影响尚未完善, 基于DSP算法推导连续变量量子态数字化测量结果归一化校准散 粒噪声单位[67], 将本底光带宽、电路有限带宽脉化响应、ADC有限分辨率等影响纳入到最小熵的严格评估将一种可行的方案. 同时本文通过混沌热态注入模拟实际系统经典噪声或外部高斯调制攻击等对熵源量子态的影响, 并基于KLD实时监测建立动态安全阈值. 需要强调的是, 引入此攻击的主要研究目的不是破坏QRNG的安全性, 而是希望通过实际因素的分析来验证并进一步提高本文QRNG的抗噪声鲁棒性. 因此后续研究可通过丰富对QRNG系统的攻击方式(包括熵源[68], 测量系 统[69]等)来进一步促进QRNG安全模型的完善和 发展.

    参考文献 (69)

目录

/

返回文章
返回