磁振子作为磁性材料中自旋波激发的准粒子, 近年来因其在量子信息技术、自旋电子学及微波工程等领域的应用潜力引发广泛关注^[1–3]. 基于磁振子与光子、微波谐振子及超导量子比特等多物理系统可实现的强耦合特性, 腔磁光机械系统(cavity magnon optomechanical system)已发展成为研究磁光相互作用机制、非线性动力学行为及量子器件创新设计的重要平台^[4–6]. 该系统的核心架构由光学腔场、磁振子模式与声子模式三要素构成, 其中磁光效应驱动磁振子-光子耦合, 而磁致伸缩效应则诱导磁振子-声子非线性相互作用, 这种双模态耦合机制与腔光机械系统中辐射压诱导的光力耦合具有动力学类比性^[7]. 值得一提的是, 相较于传统腔光机械系统, 腔磁光机械系统展现出高自旋密度、低耗散以及与超导量子电路等体系的高兼容性耦合能力, 使其在量子存储器、量子中继器及分布式量子计算等前沿领域展现出独特价值. 特别值得关注的是, 磁振子双稳态作为该体系的标志性非线性现象, 不仅揭示了强关联体系中自旋波的非线性演化规律, 更推动了量子器件物理的突破, 如基于该效应发展的磁振子量子比特操控方案可实现亚纳秒级门操作. 这为量子-经典混合计算架构和低功耗自旋逻辑器件的实用化奠定了理论基础^[8,9], 标志着腔磁光机械系统正从基础研究向量子工程应用实现重要跨越.

早在2010年Soykal和Flatté^[10]发现由钇铁石榴石(yttrium iron garnet, YIG)小球与单微波腔构成的腔磁光机械系统中, 强耦合相互作用的存在使磁振子可以与光子形成磁光极化子, 并在强耦合区表现出拉比劈裂. 这为磁光耦合、腔自旋量子电动力学和磁振子量子计算提供了理论支持. 研究者随后开始对腔磁光机械系统中的双稳态现象进行广泛研究^[11–14]. 2023年, Mukherjee和Jana^[13]理论研究了在含有两个YIG小球的腔磁光机械系统中克尔非线性强度、磁振子模频率失谐、光子-磁振子耦合强度和衰减率等系统参数对双稳态现象的影响. 随后Bhatt等^[14]理论研究了在调幅泵浦激光器驱动下腔磁光机械系统中的双稳态现象, 以及双稳态现象表现出的磁振子开关模式. 腔磁光机械系统实验方面的研究也取得重要突破: 李杰研究团队^[15–19]近年来连续完成了腔磁力系统中宏观量子态、压缩态及纠缠态的制备, 以及讨论了磁振子-声子的交叉克尔效应及声子模式的双稳态. Qian等^[20]实现了两个大质量YIG球体的机械振动的量子纠缠. Fabiha等^[21]通过声子-磁振子-光子耦合实现自旋波电磁纳米天线. 这些研究为探索宏观量子效应提供了腔磁光机械系统这一新的平台, 为验证宏观物体量子关联的鲁棒性提供了新的思路.

传统的磁振子双稳态研究主要集中在单腔磁光机械系统, 即在一个光学或微波腔中探讨磁光相互作用所引起的双稳态现象^[10–14,22]. 然而, 腔系统在调控自由度、远程相互作用和非线性增强方面存在局限性, 所以有必要构建新的系统突破上述局限. 双腔系统通过腔间耦合可提供更多调控参数, 例如腔-腔耦合强度、光子模式分裂、非线性克尔效应等, 从而更灵活地控制磁振子动力学行为, 成为新的研究热点^[5,6,23]. Ghasemian等^[6]通过光纤耦合含YIG铁磁球的光磁腔与超导量子比特腔构建双腔系统, 实现了腔场-腔场、磁振子-超导量子比特之间的稳态纠缠, 并通过驱动场强度和光纤耦合强度优化纠缠特性, 为量子网络节点提供了新方案. Wang等^[5]提出了一种基于宇称-时间对称的腔磁光机械系统的磁振子激光器, 进而实现低阈值磁振子激光, 且其频率可通过外加磁场进行连续调谐. 该磁振子激光可用于高灵敏磁场传感、非线性光子学和量子信息处理, 并且其可调特性使其在精密测量和片上集成光学器件中具有应用前景. 在这些研究中, 双腔结构的引入不仅可以增强系统的量子相干性, 还可以实现远程磁振子调控, 从而为非线性磁振子器件的设计提供新的可能性^[24]. 此外, 半导体量子系统(如量子点、量子阱)已广泛应用于量子光学和光子学领域, 其独特的非线性响应和可调谐特性使其成为控制磁振子动力学的理想候选者^[25–27]. 如在微波腔系统中, 半导体量子点可通过电偶极耦合或拉比振荡有效调制微波光子, 并进一步影响磁振子-光子相互作用^[26]. 因此, 研究包含半导体量子系统的双腔光磁机械系统, 探索其磁振子双稳态的形成机制及调控参数, 不仅有助于理解磁振子-光子相互作用的非线性动力学, 还可以为量子存储、量子逻辑运算和超快信息处理提供新的思路.

基于此, 本文研究了在驱动场正向输入和反向输入两种情况下, 双腔磁光机械系统中的双稳态现象. 构建了包含半导体量子点的双腔磁光机械系统, 通过求解海森伯-朗之万方程, 得到关于磁振子数(磁振子的数量, 反映自旋激发的统计分布)的三阶非线性方程. 讨论了驱动场正向和反向输入导致相同的磁振子响应需要满足的阻抗匹配条件, 以及调节隧穿耦合强度、腔与量子点的耦合强度和两腔耦合强度对双稳态现象的影响. 本研究结果将为基于磁振子的量子信息存储、非线性开关和远程相互作用调控提供新的理论支持, 有助于未来新型光磁混合量子器件的开发.

本文研究了由两个微波腔和一个YIG球组成的双腔磁光机械系统, 其中YIG球置于右侧C腔中, 如图1所示. 此外, 本文还在左侧A腔中加入了三能级量子点分子, 其中三能级量子点分子结构可通过自组织量子点技术形成^[28], 能级结构如图1(b)所示. 在腔场的作用下, 量子点中的电子从价带跃迁到导带, 形成直接激子态$\left| 2 \right\rangle $, 同时沿着生长方向引入偏置电压使得电子能在量子点间发生隧穿, 从而形成间接激子态$\left| 3 \right\rangle $, 而$\left| 1 \right\rangle $能级则是无光激发时体系所对应的基态. 各能级的本征频率分别为${\omega _a}(a = 1, {\text{ }}2, {\text{ }}3, {\text{ }}4)$. 均匀的外磁场($H$)沿z方向施加, 用来偏置YIG球. 两个微波腔场分别由驱动强度为$ {\varepsilon _1} $和$ {\varepsilon _2} $的微波场驱动. 在以频率为$ {\omega _{\text{d}}} $的旋转框架下, 体系的哈密顿量可表示为

在(1)式中$ {\hat a_i}(\hat a_i^\dagger ) $是腔模($ i = 1, {\text{ }}2 $)的湮灭(产生)算符, 并伴随着共振频率$ {\omega _i} $($ i = 1, {\text{ }}2 $). ${\sigma _{ij}} = |i\rangle \langle j| (i, j = 1, {\text{ }}2, {\text{ }}3, {\text{ }}4)$为原子算符. 算符$ \hat m $表示频率为$ {\omega _{\text{m}}} $的磁振子模, 由外部偏置磁场$ H $通过$ {\omega _{\text{m}}} = \gamma H $决定, 其中$ {\gamma {/ } {2\pi = 28{\text{ }}{\mathrm{GHz}}/T}} $是回磁比. YIG的磁晶各向异性使得不同磁化方向对应不同的能量, 其四阶非线性项$ K{\hat m^\dagger }\hat m{\hat m^\dagger }\hat m $驱动磁振子的非线性动力学. 这种各向异性通过自旋波的四波混频过程诱导了磁振子克尔效应, 克尔系数$ K = {\mu _0}{K_{{\text{an}}}}\gamma /({M^2}{V_{\text{m}}}) $表征非线性克尔效应强度, 其中$ {\mu _0} $为自由空间的磁导率, $ {K_{{\mathrm{an}}}} $为一阶各向异性常数, $ M $为饱和磁化强度, $ {V_{\text{m}}} $为YIG球的体积 ^[23,29]. $ J $为光子-光子之间的耦合率; $ g $为线性光子-磁振子之间的耦合强度, 可通过改变偏置磁场的方向或YIG球在右腔内的位置来调节. 其余的部分描述了驱动场与两个微波场以及磁振子的耦合, 并伴随着驱动场的振幅强度$ {\varepsilon _j} = \sqrt {{P_j}/\hbar {\omega _{\rm d}}} (j = 1, {\text{ }}2, {\text{ }}3) $, 其中$ {P_j} $和$ {\omega _{\rm d}} $分别为相应的输入功率和频率. 耦合参数$ {\eta _i} $($ i = 1, {\text{ }}2 $, $ {\eta _i} = {\kappa _{i, {\text{e}}}}/{\kappa _i} $)描述了驱动场和微波腔模之间的耦合, 可以连续地调节. $ {T_{\text{e}}} $, $ {g_{{\text{cq}}}} $则分别表示隧穿耦合强度以及量子点与腔场的耦合强度. 其中, 失谐量为$ {\varDelta _1} = {\omega _1} - {\omega _{\text{d}}} $, $ {\varDelta _2} = {\omega _2} - {\omega _{\text{d}}} $, $ {\varDelta _{\text{m}}} = {\omega _{\text{m}}} - {\omega _{\text{d}}} $, $ {\varDelta _3} = {\omega _3} - {\omega _{\text{d}}} $, $ {\varDelta _4} = {\omega _4} - {\omega _{\text{d}}} $.

基于体系的哈密顿量, 考虑系统的耗散和涨落. 在平均场近似^[30]下, 求解(1)式, 可以得到该系统的海森伯-郎之万运动方程:

其中, $ {\kappa _i} $表示微波腔模的总衰减率, 包含一个内部衰减率$ {\kappa _{i, 0}} $和一个外部衰减率$ {\kappa _{i, {\text{e}}}} $, 而$ {\gamma _{\text{m}}} $是磁振子模的总衰减率. ${\gamma _{ij}} = {\varGamma _i} + {\varGamma _j}$描述的是相干能级间的相干衰减率, ${\varGamma _i} = \displaystyle\sum\nolimits_{i > j} {{\varGamma _{ij}}} $描述的是能级$\left| i \right\rangle $的总衰减率, 而${\varGamma _{ij}}$则是能级$\left| i \right\rangle $到能级$\left| j \right\rangle $之间的衰减率. 在基态近似下^[31], 求解(2)式可得系统的稳态解:

首先, 本文研究正向输入的驱动场所导致的磁振子响应, 即当$ {\varepsilon _1} \ne 0 $和$ {\varepsilon _2} = 0 $, 由(3)式可得到稳态解:

其中, $\gamma \;= \;({{{\gamma _{\rm{m}}}} / 2}\; +\; {\mathrm{i}}{\varDelta _{\rm{m}}}) + {\mathrm{i}}( {2K\langle {{m^\dagger }} \rangle \langle m \rangle + K} )\; + $ $ {{g^2}( {{{{\kappa _1}} /2} + {\mathrm{i}}{\varDelta _1} + \varphi } )} / $ $[ ( {{{{\kappa _2}} / 2} + {\mathrm{i}}{\varDelta _2}} )( {{{\kappa _1}}/ 2} + $ $ {\mathrm{i}}{\varDelta _1} + \varphi ) + {J^2} ] $, $ \varphi = {{g_{\mathrm{cq}}^2} {/ } {[ {({\mathrm{i}}{\varDelta _3} + {\gamma _{21}}/2)({\mathrm{i}}{\varDelta _4} + {\gamma _{31}}/2) + T_{\mathrm{e}}^2} ]}} $. 整理稳态解, $ \langle {{m^\dagger }} \rangle \langle m \rangle = {M_1} $, $ {M_1} = \langle {{m^\dagger }} \rangle \langle m \rangle = {| {\langle m \rangle } |^2} $, 可以获得一个关于磁振子数的三阶非线性方程:

其中

随后, 本文研究反向输入的驱动场所导致的磁振子响应, 即$ {\varepsilon _1} \ne 0 $和$ {\varepsilon _2} = 0 $, 由(3)式可得到稳态解:

整理稳态解, $ \left\langle {{m^\dagger }} \right\rangle \left\langle m \right\rangle = {M_2} $, $ {M_2} = \left\langle {{m^\dagger }} \right\rangle \left\langle m \right\rangle = {\left| {\left\langle m \right\rangle } \right|^2} $, 可以获得一个关于磁振子数的三阶非线性方程:

其中$ {d_2} = {{{g^2}{\eta _2}{\kappa _2}\varepsilon _2^2\left( {\varLambda _1^2 + \varLambda _2^2} \right)} {/ } {\left( {{A^2} + {B^2}} \right)}} $.

接下来, 本文将讨论不同物理参数对该双腔磁光机械系统中磁振子数的影响. 在数值分析中, 主要物理参数选择依据参考文献[32–35], 其参数值如下: $ {\omega _{\text{m}}} = 2\pi \times 10.1{\text{ GHz}} $, $ {\kappa _2} = 2{\text{π}} \times 2.1{\text{ MHz}} $, $ {\kappa _1} = 3{\kappa _2} $, $ {\gamma _{\text{m}}} = 2{\text{π}} \times 0.1{\text{ MHz}} $, $ {\varDelta _1} = {\varDelta _2} = {\gamma _{\text{m}}} $, ${\varDelta _3} = 2{\gamma _{\text{m}}} , $ ${\varDelta _4} = 3{\gamma _{\text{m}}} , $ ${\gamma _{21}} = {\gamma _{31}} = 0.64{\text{ MHz}} , $ $K = 2\pi \times 5 \times {10^{ - 7}}{\text{ Hz}} , $ $g = 2\pi \times 41{\text{ MHz}} , $ $ {\eta _1} = {\eta _2} = 0.5 $.

首先, 比较驱动场正向输入和反向输入两种情况下磁振子数的三阶非线性方程, 可以发现区别在于磁振子数的三阶非线性方程的零阶项处. 这说明当输入的驱动场方向是相向的时, 双腔磁系统的稳态会发生变化. 然而, 当满足以下条件:

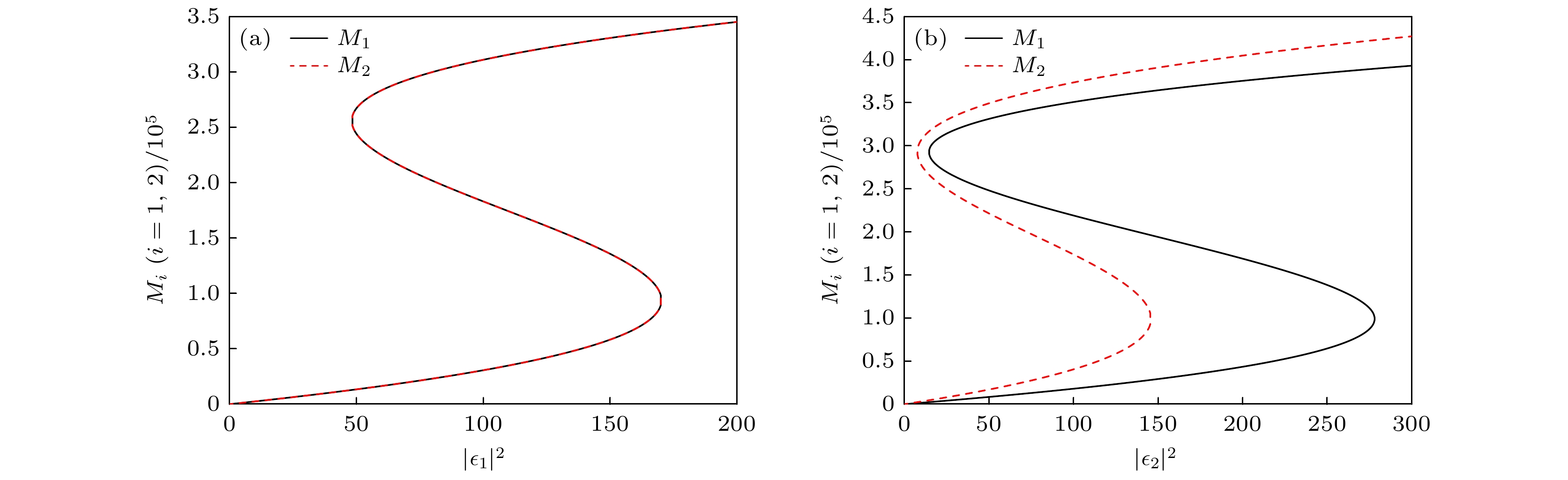
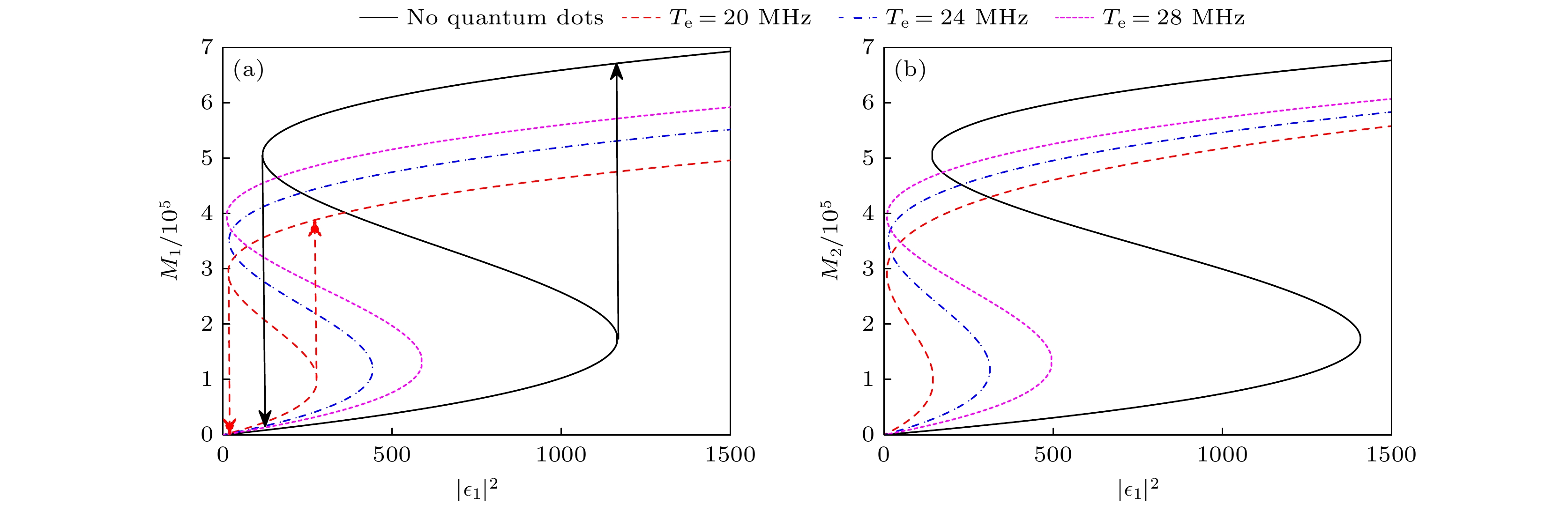
相向输入的驱动场(正向或反向输入)所导致的磁振子响应相同. 这里把(8)式看作是相同的磁振子响应的阻抗匹配条件^[9]. 如图2(a)所示, 当阻抗匹配条件被满足时, 正向和反向输入的驱动场所导致的磁振子响应是相同的, 并且磁振子数$ {M_1} $和$ {M_2} $是随着输入场的强度而同步变化. 这种对称性源自腔体之间平衡的能量交换, 抑制了方向性不对称性. 从图2(b)可以看到, 阻抗匹配条件被破坏后, 出现两种不同的双稳态曲线, 即在驱动场正向输入和反向输入两种情况下, 磁振子响应不再相同. 这是由于阻抗匹配条件被破坏将打破原有系统的对称性, 导致阈值的分歧: 正向驱动需要更高的强度, 而反向驱动则在较低强度下触发转变. 此方向性灵敏度突出了腔体介导的相位相干性在双稳态调控中的作用.

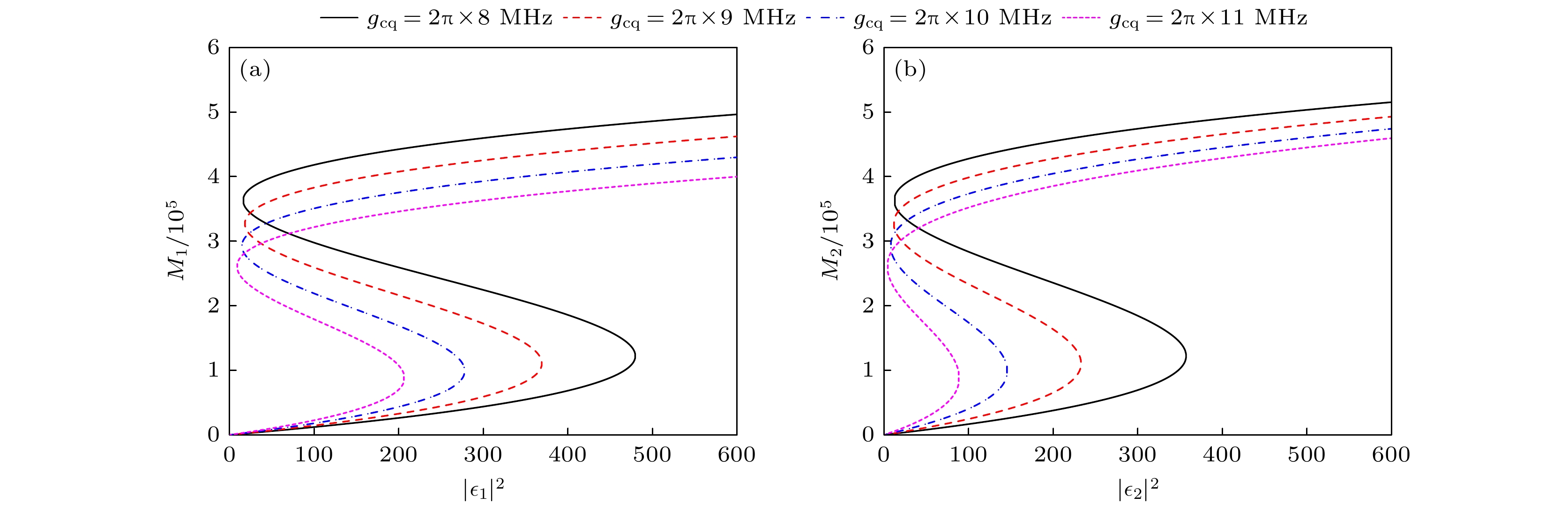
其次, 研究了不同隧穿耦合强度下磁振子数随驱动场强度(正向或反向入射)的变化曲线. 由(4)式和(6)式可知$ {g_{{\text{cq}}}} $为零时, 系统是一个不含量子点的双腔磁光机械系统. 从图3(a)和图3(b)的黑色实线可知, 在双腔磁光机械系统中出现双稳态现象, 当驱动场强度(正向或反向入射)从零开始逐步增加, 磁振子数沿着低稳态支路运动. 驱动场强度进一步增大到约为$ 1250{\text{ MHz}} $时, 磁振子数从低稳态跃迁到高稳态, 完成跃迁后磁振子数会沿着高稳态支路运动. 然而, 当驱动场强度降低到$ 110{\text{ MHz}} $左右时, 会出现磁振子数从高稳态向低稳态跃迁. 从低稳态跃迁到高稳态的转换可以看作是从“off ”状态到“on”状态的转换. 当$ {g_{{\text{cq}}}} $不为零时, 系统是一个含有三能级量子点分子的双腔磁光机械系统. 当$ {g_{{\text{cq}}}} = 2\pi \times 10{\text{ MHz}} $时(如图3所示), 在耦合系统中出现双稳态现象, 其与双腔磁光机械系统相比, 产生双稳态现象所需的驱动场强度更小, 磁振子数跃迁能在低阈值发生, 即从“off ”状态到“on”状态所需的驱动场强度更小, 如$ {T_{\text{e}}} = 20{\text{ MHz}} $时跃迁的阈值分别约为$ 25{\text{ MHz}} $和$ 275{\text{ MHz}} $. 并且, 从$ {T_{\text{e}}} = 20{\text{ MHz}} $, $ {T_{\text{e}}} = 24{\text{ MHz}} $和$ {T_{\text{e}}} = 28{\text{ MHz}} $时磁振子数随驱动场强度的变化曲线可以看出, 双稳态的阈值和磁滞回线宽度会随着隧穿耦合强度的减小而减小. 这是由于耦合系统中半导体量子点中的隧穿诱导透明(tunneling induced transparency, TIT) 效应抑制了线性吸收, 增强了光子和磁振荡之间 的非线性交互. 这种可调性源自量子点调节腔内 有效光子密度的能力, 从而动态改变光子-磁振 荡耦合强度. 由此可知, 耦合系统与双腔磁光机械系统相比能够在更低的驱动场强度下实现开关 器件, 并且还可以通过调节隧穿耦合强度对双稳态阈值和磁滞回线宽度进行控制, 实现更高的开 关精度.

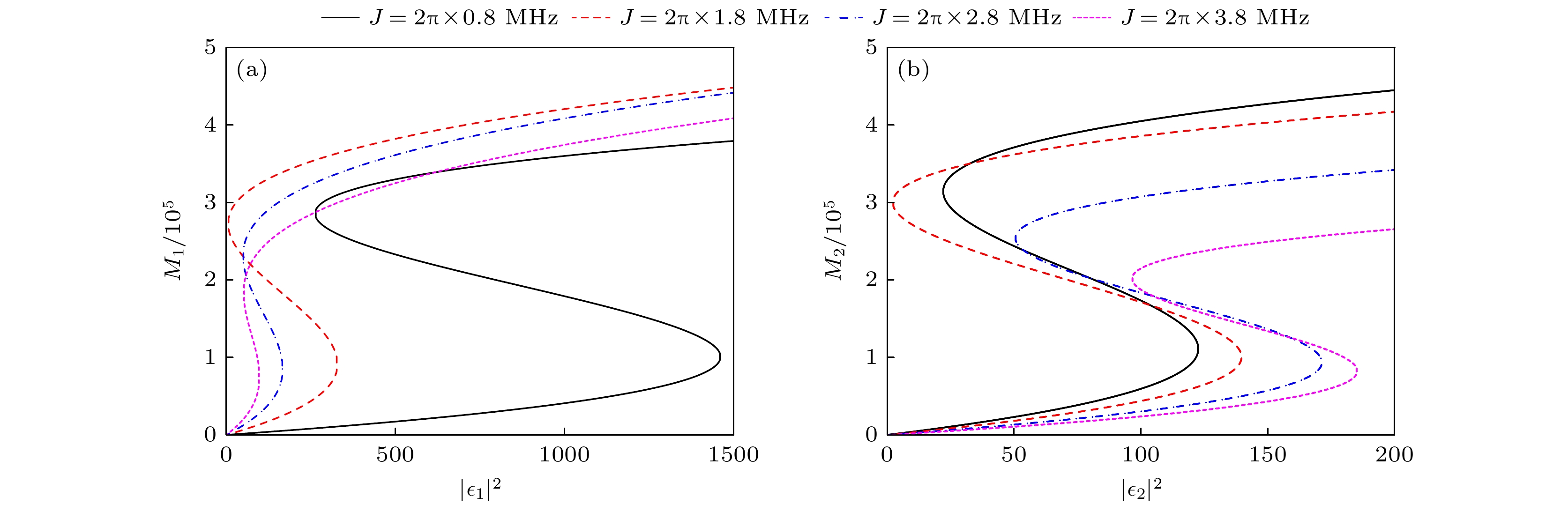
随后, 研究了腔与半导体量子点之间的耦合强度对双稳态现象的影响. 当考虑驱动场正向输入时, 从图4(a)磁振子数变化曲线可以看出, 随着驱动场强度的增加, 耦合系统中会出现磁振子双稳态现象. 双稳态的阈值和磁滞回线宽度会随着腔与半导体量子点之间的耦合强度$ {g_{{\text{cq}}}} $的不断增大而减小. 这是由于耦合系统中的半导体量子点的大偶极矩放大了腔场对磁振子振荡的有效驱动. 阈值降低意味着系统可以在较低的驱动强度下就能进入双稳态区域, 使得双稳态行为更容易触发, 也更加敏感. 而磁滞回线宽度的减小使得双稳态的转换变得更加迅速且明确. 这意味着在驱动场的强度变化过程中, 系统能够更清晰地从一个稳定的状态跳跃到另一个稳定状态, 从而增强了双稳态特性的可观察性和可操作性. 从图4(b)可以看出, 在驱动场反向输入的情况下, 出现类似的现象. 但由于阻抗匹配条件没有被满足, 所以双稳态的阈值和磁滞回线宽度会随着腔与半导体量子点之间的耦合强度$ {g_{{\text{cq}}}} $的增大而减小得更快.

最后, 还研究了两腔耦合强度对磁振子数随驱动场强度的变化曲线的影响. 从图5(a)可知, 驱动场正向输入时, 耦合系统中的磁振子双稳态曲线的阈值随着两腔之间耦合强度的增大(从$ J = 2\pi \times 0.8{\text{ MHz}} $增加到$ 2\pi \times 3.8{\text{ MHz}} $)而减小, 磁滞回线宽度与两腔之间耦合强度的变化呈现类似的趋势. 这表明耦合系统中产生双稳态现象所需的驱动场强度随着两腔之间耦合强度的增大而减小. 但由于阻抗匹配条件不被满足, 驱动场反向输入时, 如图5(b)所示, 耦合系统的双稳态阈值及磁滞回线宽度随着两腔耦合强度的变化呈现出与驱动场正向输入时不同的趋势. 在两腔低耦合情况下, 即耦合强度$ J = 2\pi \times 0.8{\text{ MHz}} $增加大$ 2\pi \times 1.8{\text{ MHz}} $时, 双稳态的阈值和磁滞回线宽度会随着两腔之间耦合强度的增大而增大. 但当耦合强度进一步增大(从$ J = 2\pi \times 1.8{\text{ MHz}} $增加到$ J = 2\pi \times 3.8{\text{ MHz}} $)时, 随着两腔之间耦合强度的增大, 双稳态的阈值和磁滞 回线宽度呈现出下降趋势. 由此可见, 通过调节两腔耦合强度可以实现对双稳态阈值和磁滞回线的控制.

本文研究了在驱动场正向输入和反向输入两种情况下, 量子点-双腔磁光机械系统中的双稳态现象. 通过对比两种情况下磁振子数的三阶非线性方程, 得出了阻抗匹配条件. 当满足该条件时, 正向和反向输入的驱动场导致的磁振子响应相同; 而当不满足阻抗匹配时, 磁振子响应则会有所不同. 具体来说, 当阻抗匹配条件不成立时, 含有三能级量子点分子的双腔磁光机械系统相比双腔磁光机械系统, 双稳态现象的出现阈值更低, 低稳态向高稳态的跃迁所需的驱动场强度也更小, 从而可以在更低的驱动场强度下实现开关功能. 此外, 本文还进一步建立了多参数协同调控模型, 揭示隧穿耦合、腔-量子点耦合及腔间耦合构成的三维调控空间, 通过调节隧穿耦合强度、腔与量子点的耦合强度及两腔耦合强度, 可以有效地控制双稳态阈值和磁滞回线宽度, 进而改变产生双稳态现象所需的驱动场强度. 该系统有望利用矢量网络分析仪在实验上探测反射谱中透射或者吸收窗口的跳变行为, 从而实验观测磁振子的双稳态效应. 这在促进数据信号传输、开关器件和存储方面具有潜力, 也可能成为大规模量子信息处理单元的组成部分. 除此之外, 该研究还可能在磁自旋电子学领域具有重要的应用价值.