首页
登录
注册
下载:
-
艾里光束具有的奇异特性驱使研究人员寻找更多基于艾里函数拓展的艾里类光束. 在此背景下, 一种被称之为艾里导数光束的宽泛光束模型应运而生[1]. 圆艾里导数光束表现出非凡的自聚焦能力, 并且其自聚焦能力随着导数阶数的增加而变强. 若圆艾里导数光束被部分阻挡, 尽管拥有自修复能力, 但其自聚焦能力还是不出所料地下降[2]. 当圆艾里导数光束嵌入啁啾时, 其自聚焦能力增强[3]. 除了上传啁啾之外, 圆艾里导数光束还可以进行其他方式的修饰, 比如上载旋转对称功率指数相位涡旋[4]. 当导数阶数为零时, 此时的艾里导数光束就是耳熟能详的艾里光束. 若导数阶数为1, 对应的艾里导数光束就是别具一格的一阶艾里导数光束. 一阶艾里导数光束在自由空间传输时会匪夷所思地衍生出艾里光束, 满足一定的条件下会产生干涉增强效应[5]. 当水平偏振的一阶艾里导数光束入射到空气-电介质界面, 在布鲁斯特角附近反射时存在显著增强的空间古斯-汉欣位移[6]. 先椭圆化后上载涡旋对一阶艾里导数光束的双重修饰也不会破坏其自聚焦能力[7]. 通过施加高阶光谱相位可调控分数薛定谔方程中一阶艾里导数光束光强峰值的位置和强度[8]. 若干个一阶艾里导数光束可以组成一阶艾里导数光束阵列[9]. 即使阵列中只有四个光束, 一阶艾里导数光束阵列仍具有自聚焦能力[10]. 环形一阶艾里导数光束阵列的自聚焦能力取决于阵列中光束的数目[11]. 环形一阶艾里导数光束阵列中引入恰当的一阶啁啾可以提高其自聚焦能力同时实现其聚焦位置后移[12]. 圆一阶艾里导数光束即使在手性介质、克尔介质和抛物线势场中传输时亦展现自聚焦特性[13-15]. 通过无量纲半径的选择[16]、涡旋的嵌入[17,18]和傅里叶空间的调制[19], 可实现圆一阶艾里导数光束自聚焦能力的调控.
艾里变换作为一种重要的光学调控手段, 能够实现高斯光束与艾里光束的相互转换[20]. 该特性推动研究人员通过艾里变换操作对多种激光束进行相位重构而成功制备出艾里类光束[21-35]. 值得注意的是, 将单个艾里变换拓展至多重艾里变换后, 能够通过多级相位调制实现新型光束的构建[36]. 然而, 现有研究对一阶艾里导数光束的特性仍存在着显著的研究空白—当前研究仅关注于其自聚焦动力学特性, 尚未系统地探究其在艾里变换作用下的演化规律. 本文通过构建一阶艾里导数光束的相位调控模型, 深入地解析艾里变换系数对光束特性的调控机制, 定量地研究变换过程中光强分布演化、质心偏移特征及光束半宽变化规律. 本项研究不仅为揭示一阶艾里导数光束的独特传播动力学特性提供理论依据, 更为拓展复杂结构光场的生成方法学开辟新的技术路径.
-
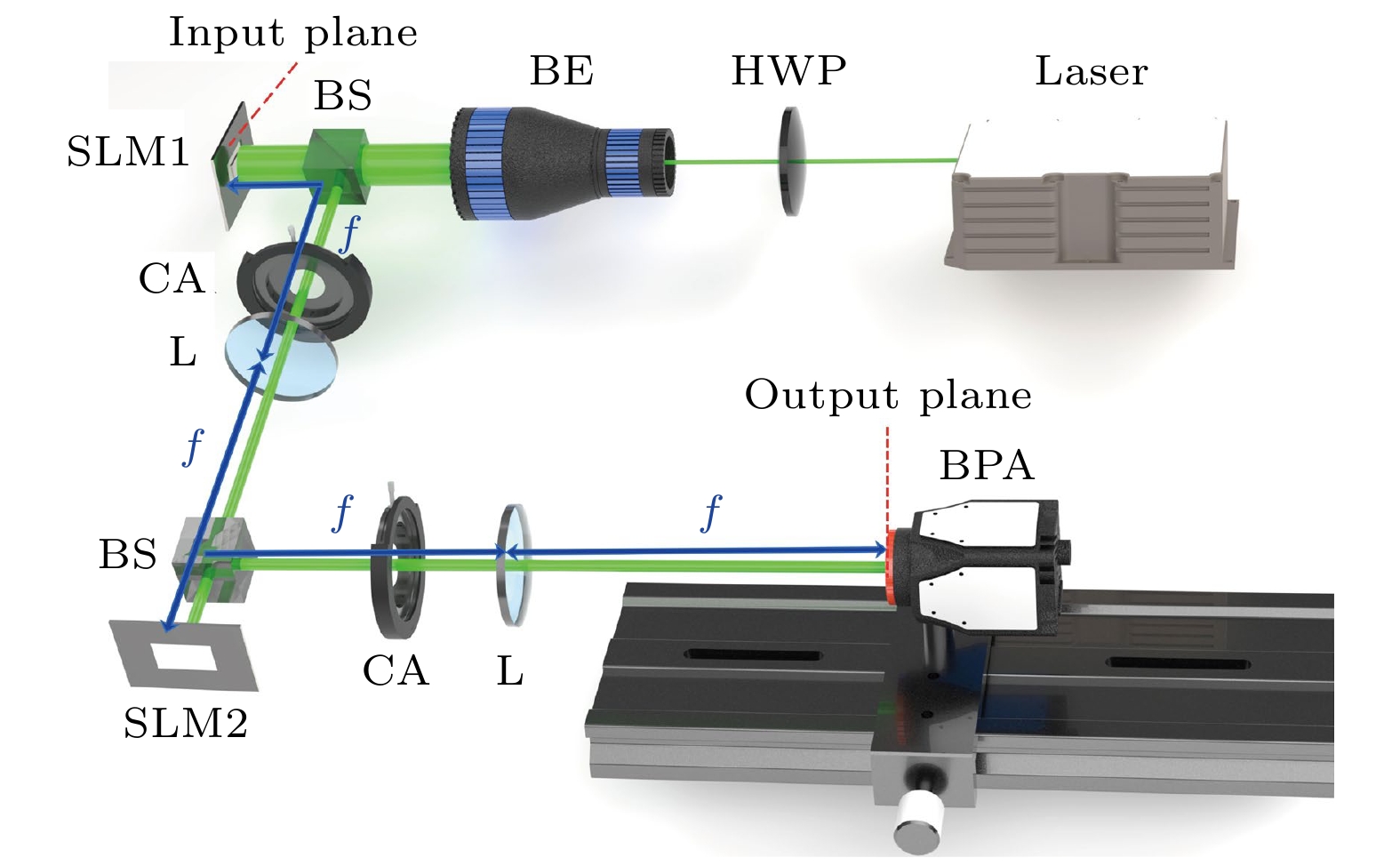
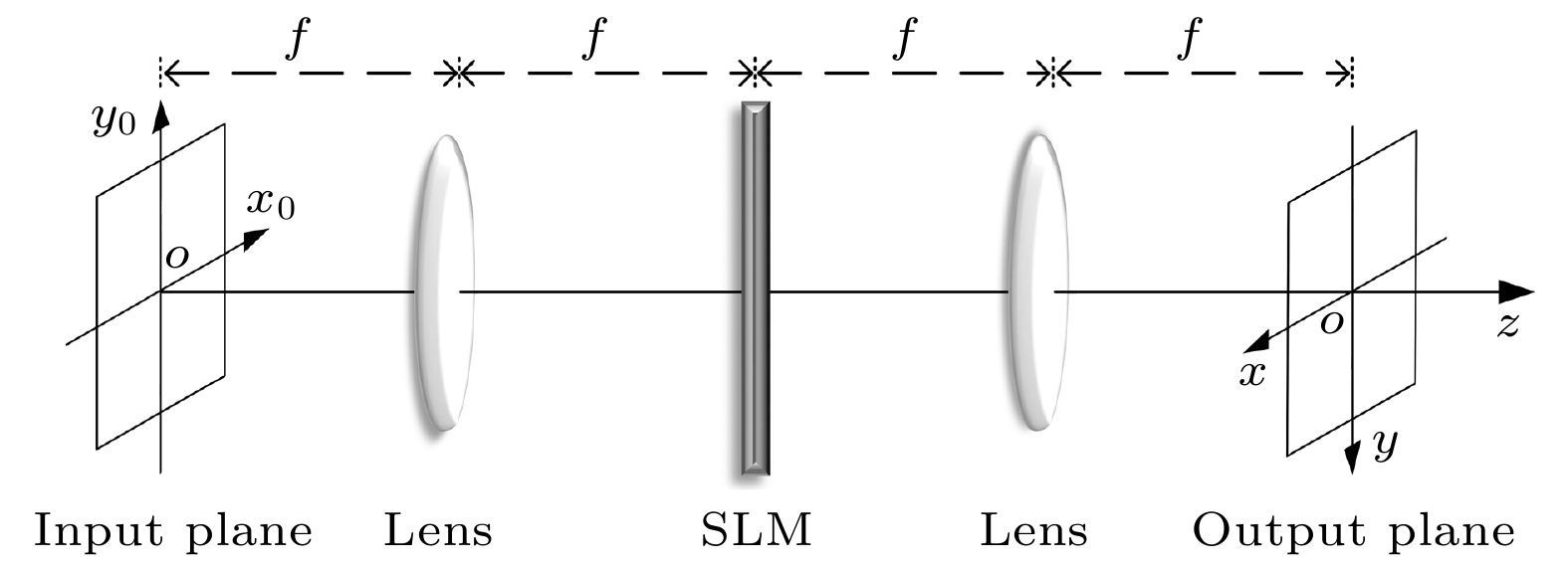
艾里变换依次由一个输入平面、一个焦距为f的薄凸透镜、一个空间光调制器(SLM)、另一个相同的薄凸透镜和一个输出平面组成, 如图1所示[20]. 输入和输出平面之间的距离为4f, 这意味着艾里变换是一个4f系统, 而SLM位于这个4f系统的中央. SLM的作用是将立方相位上载至入射光束. 第一个凸透镜放置于输入平面和SLM的中间, 而另一个凸透镜位于SLM和输出平面的中间. 因此, 艾里变换总共经历两次傅里叶变换. 在输入平面和输出平面上分别建立了直角坐标系, 从输入平面指向输出平面的垂直方向是由这两个直角坐标系共享的z轴.
-
输入平面z = 0上的输入光束是一阶艾里导数光束, 其形式为[5]
式中, x0和y0是输入平面上直角坐标系的两个横向坐标; a与w0分别为衰减因子和横向比例因子, 其中a作为模拟真实情况下光束有限能量的衰减参数, 范围为
$0 \lt a \ll 1 $ ; Ai′(·)是一阶艾里导数函数. 一阶艾里导数光束的艾里变换为[20,21]式中, x和y是输出平面上直角坐标系的两个横向坐标. b与c分别是艾里变换两个横向上的艾里系数. 由于(1)式在两个横向上是分离的, 故(2)式中的积分在两个横向上也是可分离的. 因此, 先计算x方向上的光场E(x). E(x)可表示为
式中, 上标星号表示复共轭, f1(x0)和f2(x0)分别定义为
(3)式不能通过使用现有的数学手册直接积分以获得解析结果. 然而, 通过间接的方法比如傅里叶变换法可获得(3)式的解析结果. 傅里叶变换法主要借助于如下公式[37]:
式中, F1(ξ)和F2(ξ)分别是f1(x0)和f2(x0)的傅里叶变换,
因此, 一阶艾里导数光束经艾里变换后x方向上的光场可表示为
一阶艾里导数光束经艾里变换后x方向上的光场可解析地表示为
式中, p和q是实数; u是积分变量; 辅助参数ex, gx和hx分别定义为
ex是新的横向比例因子且ex > 0, 故而b > – w0. gx是新的衰减因子, 因分子中a > 0, 故而gx > 0, 此时(11)式才有物理意义. 若b = 0时, 删去b/|b|, 则(11)式退化为(1)式. (11)式可改写为
(13)式右侧的EAi(x – d1)和EAp(x – d1)分别表示偏心艾里光束和偏心一阶艾里导数光束. 当b > –w0时, 艾里一阶导数光束的艾里变换是偏心艾里光束和偏心一阶艾里导数光束之和, 对应的权重系数分别为
$ a{b^3}/({w_0}e_x^2) $ 和–1, 偏心位置d1等于$ {a^2}{b^3}{w_0}/e_x^3 $ .当b = –w0时, 利用积分公式[37]:
(8)式可解析地表示为
式中, m是整数, Hm(·)是m阶厄米多项式;
$ w' = 2\sqrt a {w_0} $ ; EHGB表示优美厄米-高斯光束, 下标0和1表示横向模数. 当b = –w0, 艾里一阶导数光束的艾里变换为零阶与一阶偏心优美厄米-高斯光束之和, 对应的权重系数分别为1与$ 1/2 a\sqrt a $ 的, 偏心位置d2为a2w0.同理可得一阶艾里导数光束经艾里变换后y方向上的解析光场:
式中, 辅助参数ey, gy和hy分别定义为
因此, 一阶艾里导数光束经艾里变换后的光强可通过下式计算:
-
为了探究一阶艾里导数光束艾里变换后的光束特性, 下面研究其质心和光束半宽. 一阶艾里导数光束经艾里变换后x方向上的质心与光强的一阶矩有关[39-45]:
当b > –w0时, 一阶艾里导数光束经艾里变换后x方向上的质心为
式中, F3(ξ)和F4(ξ)分别是(11)式表示的E(x)与xE(x)的傅里叶变换:
当b = –w0时, 一阶艾里导数光束经艾里变换后x方向上的质心可简洁地表示为
一阶艾里导数光束经艾里变换后x方向上的光束半宽与光强的二阶矩相关[39-45]:
当b>–w0时, 一阶艾里导数光束经艾里变换后x方向上的光束半宽为
当b = –w0时, 一阶艾里导数光束经艾里变换后x方向上的光束半宽可简洁地表示为
同理可得一阶艾里导数光束经艾里变换后y方向上的质心和光束半宽:
-
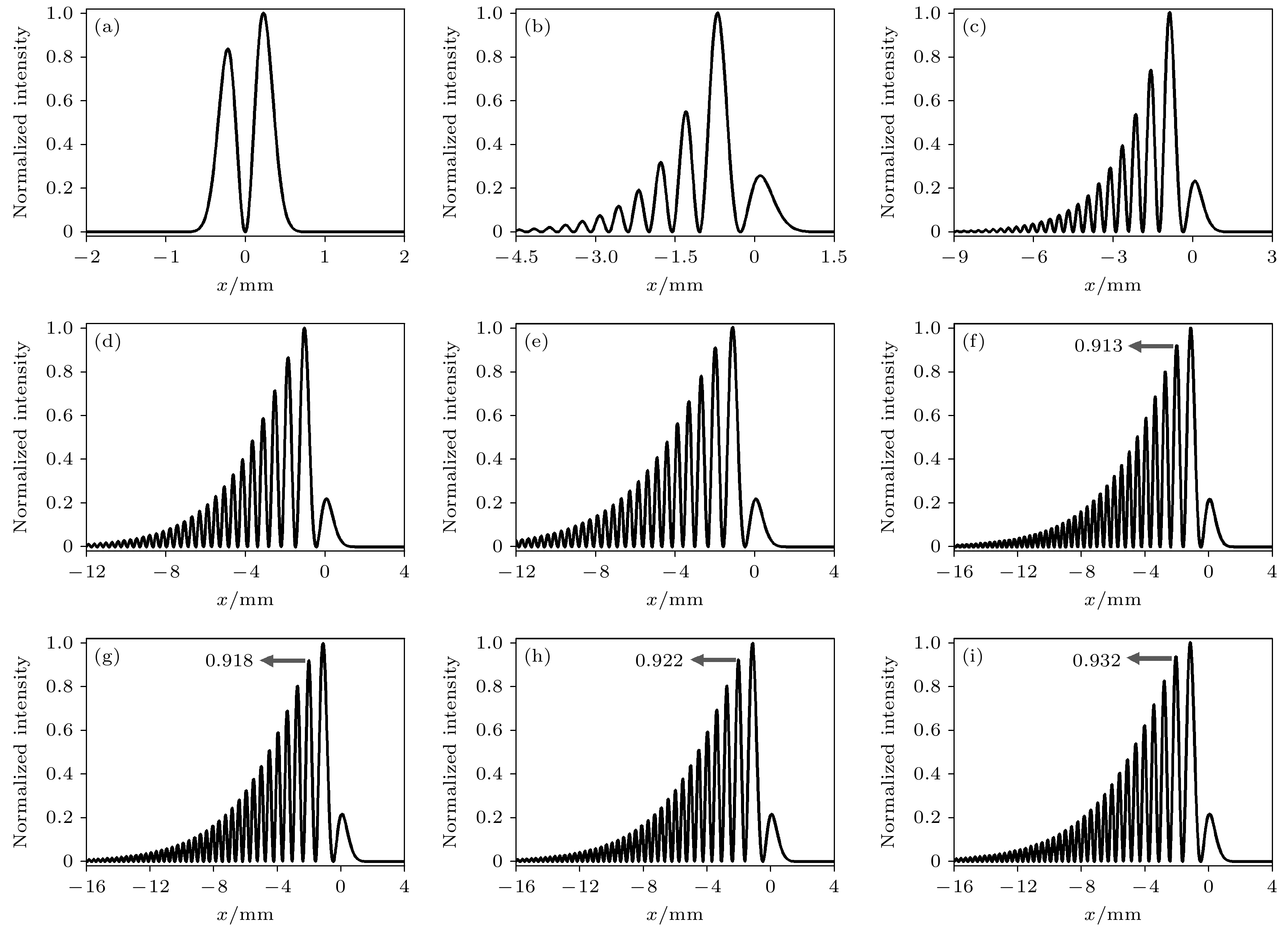
基于第2节得到的公式, 本节重点分析艾里系数对一阶艾里导数光束艾里变换的影响. 不失一般性, 一阶艾里导数光束的光束参数设置如下: a = 0.10, w0 = 0.50 mm和λ = 532 nm. 由于一阶艾里导数光束经艾里变换后两个横向光场的形式相似, 所以先研究光强在其中之一例如x方向上的演化规律. 艾里系数对一阶艾里导数光束经艾里变换后归一化光强分布的影响如图2所示. 当b = –w0 = –0.50 mm时, 归一化光强分布仅出现两个峰, 其中右峰的峰值略高于左峰, 并且两个峰值之间的谷底位于x = 0处. 当b从–0.50 mm逐渐增大但仍小于0时, 归一化光强分布的范围扩大, 峰的数目增多. 输入平面上的归一化光强分布如图2(e)所示. 为了区分图2(f)—(i), 标注了归一化光强分布中第二高峰的光强值. 随着b从–0.10 mm增大, 第二高峰和左侧剩余各峰的光强值也逐渐增大. 强的艾里特征表现在具有大量侧峰. 因此, 随着艾里系数b的增大, 一阶艾里导数光束的艾里变换拥有更强的艾里特征.
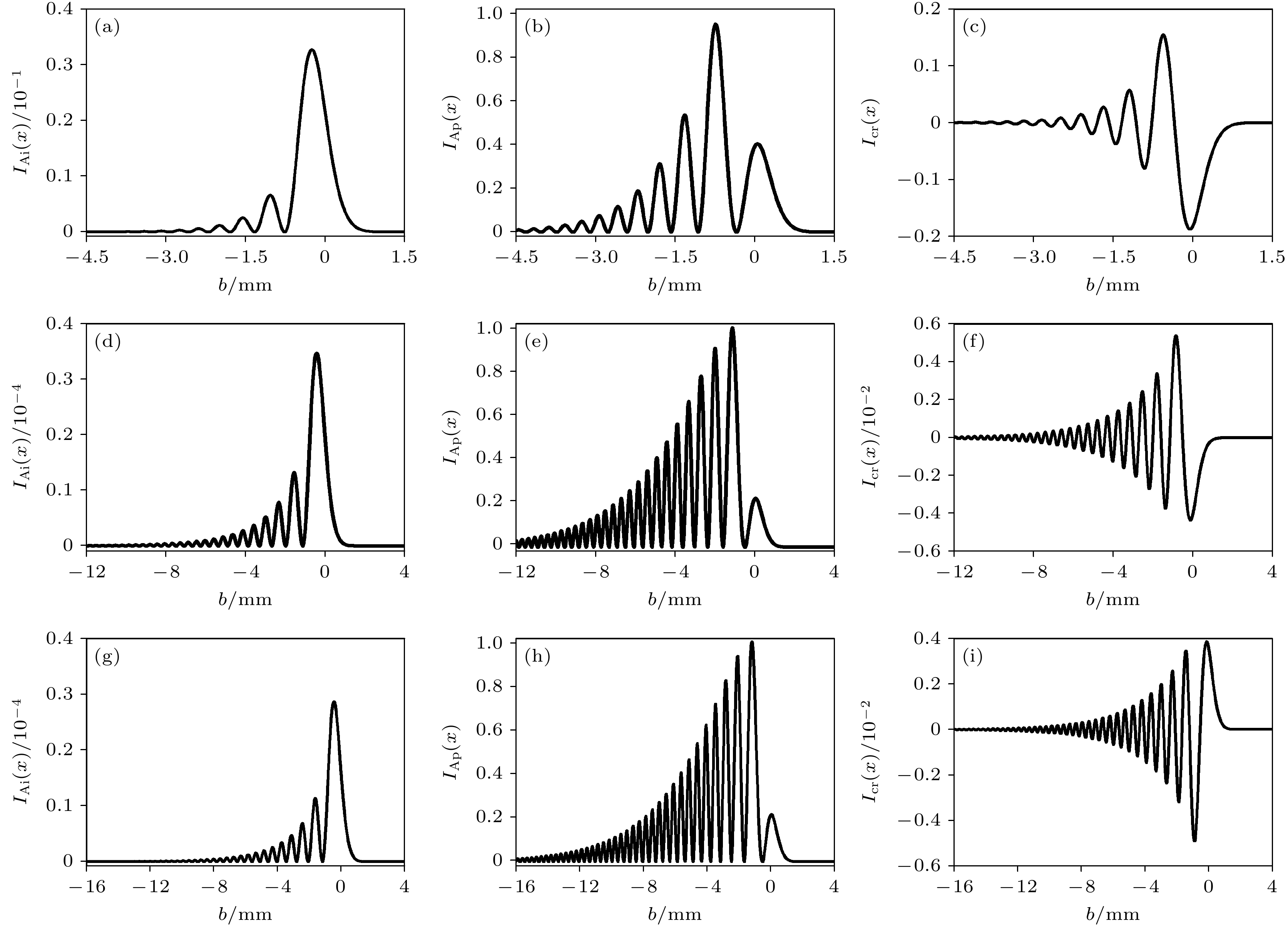
当b > –w0时, 一阶艾里导数光束经艾里变换的总光强可表示为
式中, IAi(x) = |EAi(x – d1)|2为偏心艾里光束的光强, IAp(x) = |EAp(x – d1)|2是偏心一阶艾里导数光束的光强,
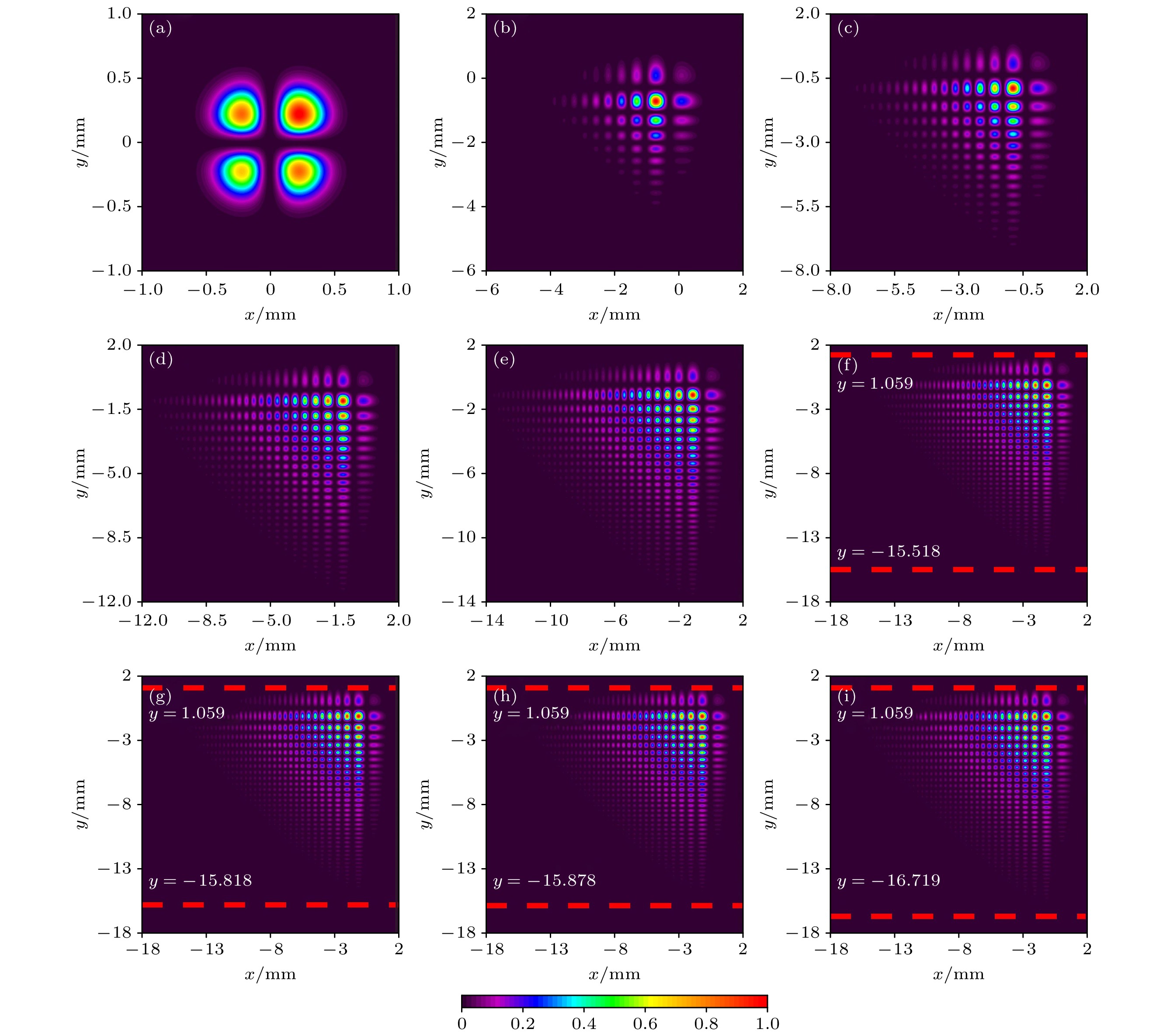
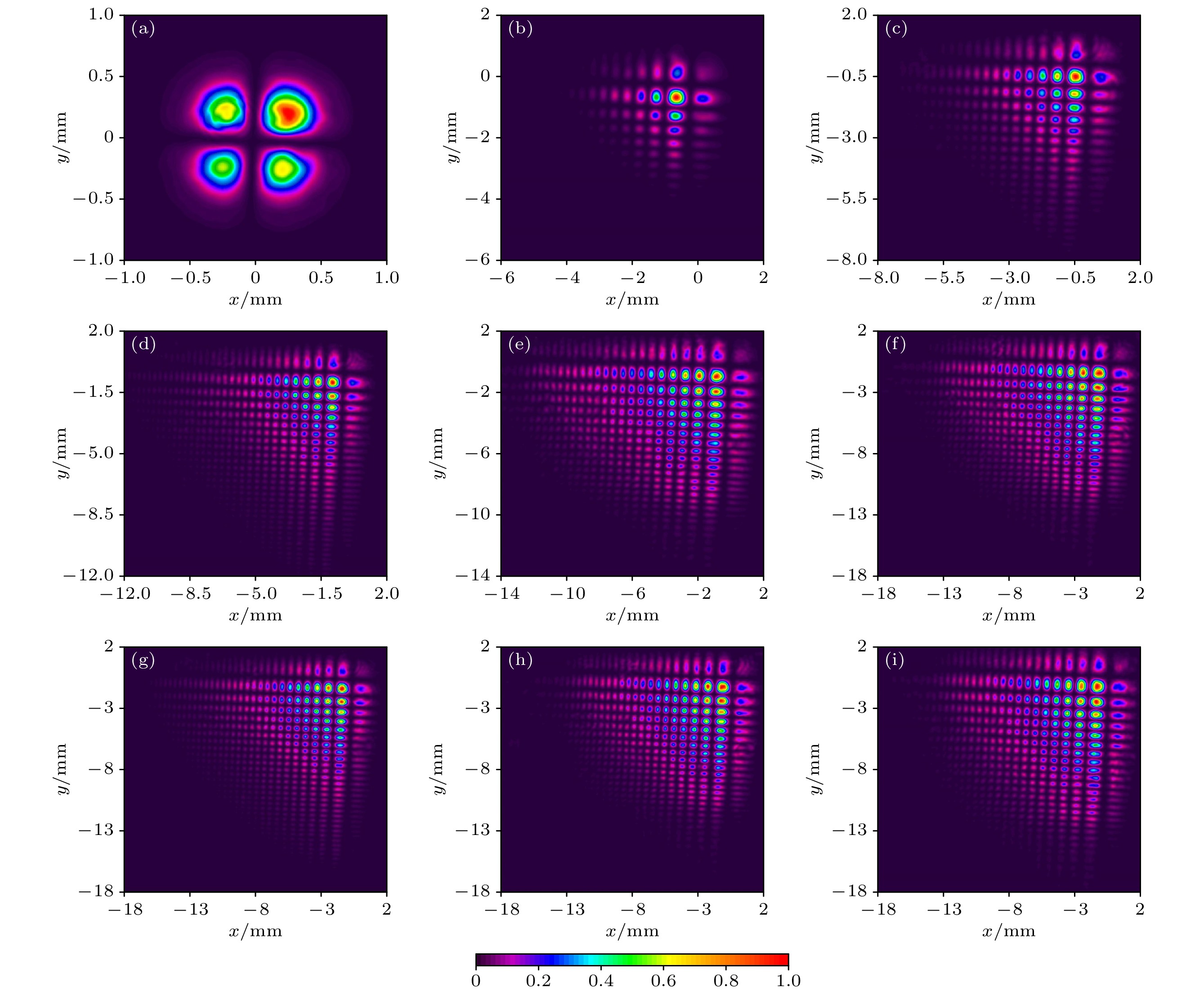
$ {I_{{\text{cr}}}}(x) = E_{{\text{{\rm Ai}}}}^ * (x - {d_1}){E_{{\text{A}}p}}(x - {d_1}) \; + E_{{\text{Ap}}}^{*} (x - {d_1}){E_{{\text{{\rm Ai}}}}}(x -{d_1}) $ 为交叉项的光强. 偏心艾里光束、偏心一阶艾里导数光束和交叉项对总光强的贡献如图3所示, 其中IAi(x), IAp(x)和Icr(x)是基于总光强的归一化后所呈现的. 当b = –0.45 mm时, IAi(x), IAp(x)和Icr(x)的最大值分别为0.03, 0.95和0.15. 当b在–w0附近时, 交叉项对总光强的贡献不能忽略. 当b = –0.20 mm和0.20 mm时, IAi(x)和Icr(x)的值微乎其微, IAp(x)几乎等同于I(x). 当b远离–w0时, 偏心艾里光束和交叉项对总光强的贡献都可以忽略不计, 并且一阶艾里导数光束的艾里变换可近似为一偏心一阶艾里导数光束, 该偏心一阶艾里导数光束与输入的一阶艾里导数光束相比, 具有更小的衰减因子和更大的横向比例因子. 这意味着通过对一阶艾里导数光束进行艾里系数远离–w0的艾里变换, 可调控其衰减因子、横向比例因子、偏心位置. 通过将单个光束升级为多光束的阵列结构, 其自聚焦能力能够得到进一步提升, 从而得到性能更高的可调节光束.其次, 探究艾里系数对一阶艾里导数光束经艾里变换后二维光强分布的影响, 如图4所示. 图4中的后4个子图标注了光强在y方向上的分布范围, 为了节省空间, 省略了单位 mm. 光强在x方向上的分布范围与在y方向上的分布范围相同, 但在图4中没有标注. 当b = c = –w0 = –0.50 mm时, 光斑由4个三个强度级别的波瓣组成, 这与四瓣高斯光束不同, 四瓣高斯光束的四瓣是同一强度等级. 因此, 一阶艾里导数光束经b = c = –w0的艾里变换后所得到的四瓣光束可作为原有四瓣高斯光束的补充和丰富, 可应用于微光学、光通信和分束技术. 当b和c逐渐从–w0增大时, 更多的波瓣逐渐出现在光强轮廓中. 当b和c从–0.10 mm增大至0.20 mm时, 光斑的变化具体表现为: 光强分布的头部位置保持不变, 而尾部位置延展(见图4(f)—(i)).
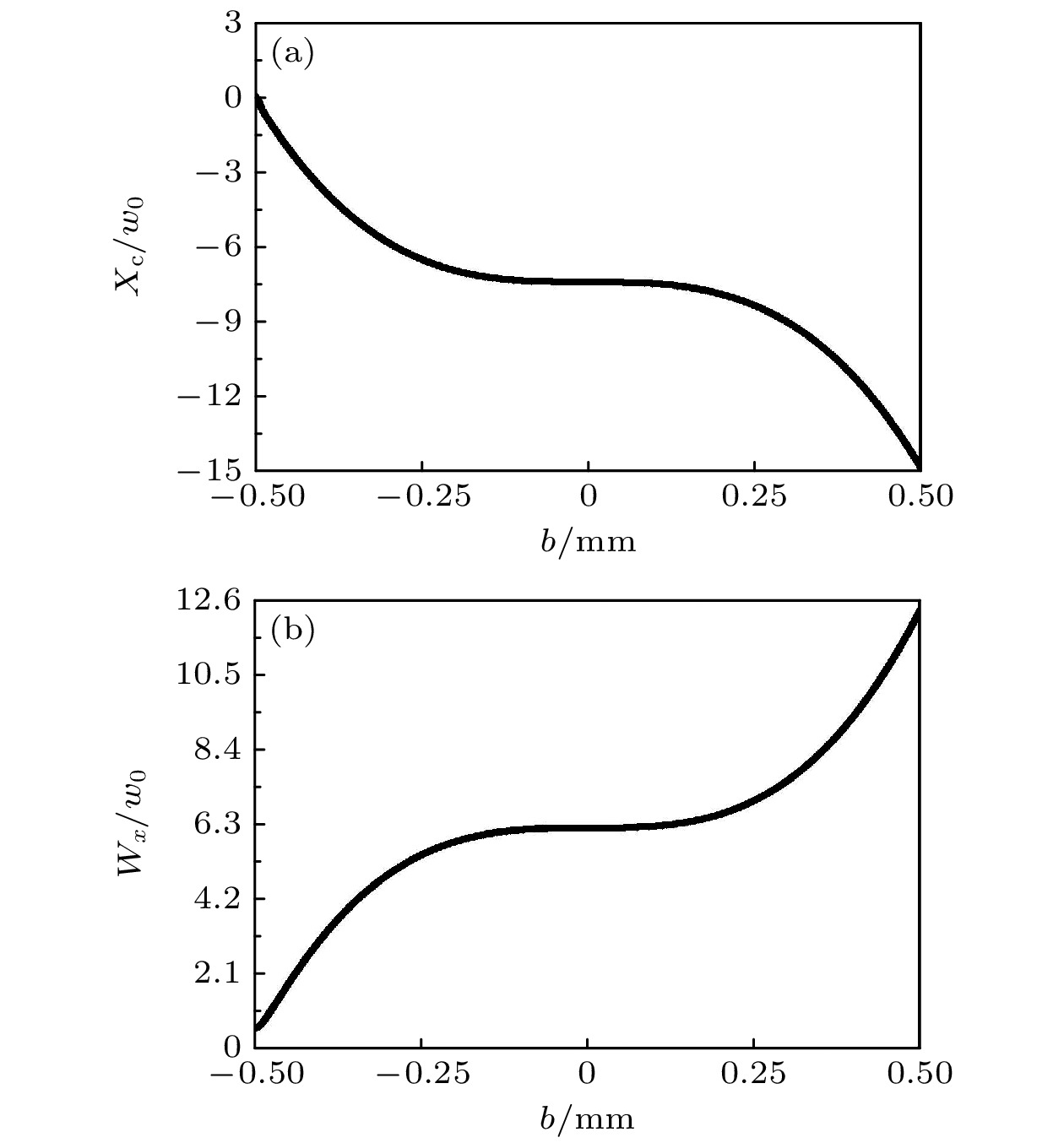
那为什么当b和c从–0.10 mm增大至0.20 mm过程中二维光强分布没有显著变化? 所以, 最后分析艾里系数对光束半宽的影响. 艾里系数b对x方向上的质心和光束半宽的影响如图5所示. 当b = –w0 = –0.50 mm时, Xc/w0 = 0.05, Wx/w0 = 0.55. 当b从–0.50 mm增大至0.50 mm这一过程中, 质心Xc经历了先快速下降、其次缓慢减小、最后迅速减小这一历程, 而光束半宽Wx经历了先快速增大、接着缓慢增大、最后迅速增大这一变化. 当b从–0.10 mm增大至0.20 mm, 光束半宽Wx恰好正处于缓慢变化的阶段. 当b = –0.10, 0.00, 0.10和 0.20 mm时, Wx/w0分别为6.13, 6.18, 6.23和6.57. 因此, 图5(b)可以很好地解释图3和图4中最后四个子图的变化.
-
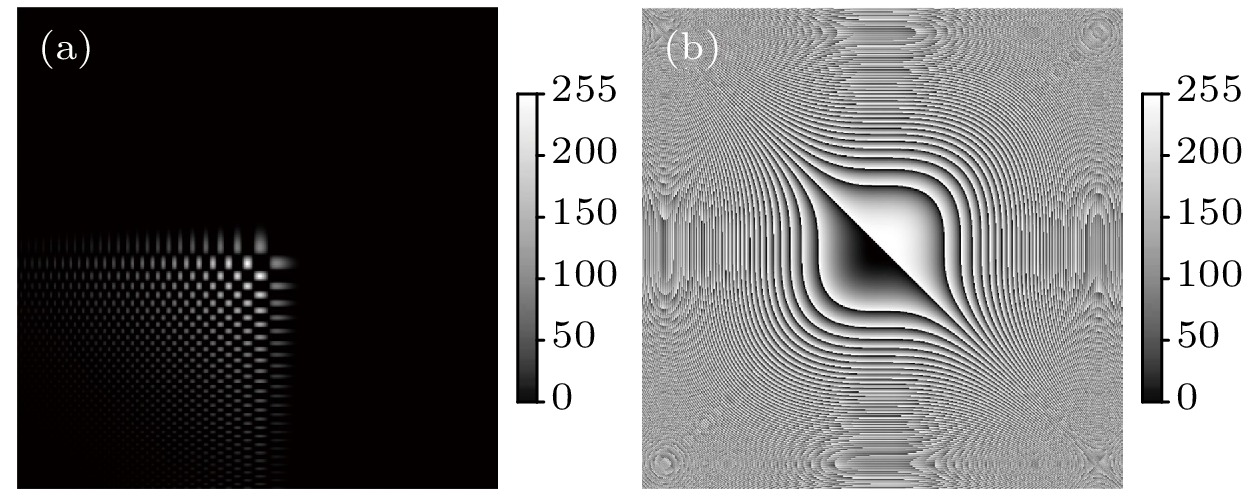
图6为一阶艾里导数光束艾里变换的实验装置示意图. 激光器用以产生532 nm的高斯种子光束; 半波片(HWP)将高斯种子光束的偏振态调整为垂直偏振; 扩束镜(BE)将通过的高斯种子光束的直径放大50倍; 分束镜(BS)将高斯种子光束一分为二, 一半继续前行, 另一半偏转90°传输. 继续前行的那一半光束进入第一个空间光调制器(SLM1; Holoeye LETO–3, 像素: 6.4 μm×6.4 μm). SLM1使用单像素棋盘法对一阶艾里导数光束的全息图进行编码, 如图7(a)所示, 0—255表示灰度等级P, 调制相位φ与灰度等级P的关系为
$ \varphi = {2\pi P}/{255} $ . 来自SLM1的反射光束就是一阶艾里导数光束. SLM1的反射表面是艾里变换的输入平面. 一阶艾里导数光束再次经过BS, 然后偏转90°进入圆型光阑(CA). CA相邻第一个薄凸透镜(L), 充当低通滤波器, 用以过滤掉源自SLM1的零阶衍射光斑. 过滤后的光束是纯的一阶艾里导数光束. 第一个薄凸透镜对一阶艾里导数光束进行傅里叶变换, 变换后的光束被第二个BS分束并进入第二个空间光调制器(受实验设备所限, 我们选用了与SLM1精度相近的可使用的SLM2; Holoeye Pluto-2, 像素: 8.0 μm×8.0 μm). SLM1和SLM2的作用不同, 前者产生一阶艾里导数光束, 后者对其进行艾里变换. 由于产生一阶艾里导数光束的要求较高, 故选用两者中精度较高的SLM1. SLM2加载了如图7(b)所示的立方相位图$ \psi (x,y) = [{k^3(b^3x^3 + c^3y^3 )/3}]/{f^3}- (2kf+\pi) $ . 从SLM2反射回来的调制光束再次穿过第二个BS, 并在偏转90°后进入第二个CA. 第二个CA过滤掉来自SLM2的零阶衍射光斑. 第二个CA后面的第二个薄凸透镜与第一个薄凸透完全相同, 其焦距f为40 cm. 第二个薄凸透镜对经第二个CA过滤的光束进行傅里叶变换, 它的后焦面是艾里变换的输出平面. 输入平面和输出平面构成一个4f系统. 最后, 光束轮廓分析仪(BPA; BGS-USB3-LT665, Ophir, 像素间距: 4.4 μm)记录一阶艾里导数光束经艾里变换后的光强分布.一阶艾里导数光束经艾里变换后的二维光强分布的实验记录如图8所示. 尽管使用了两个SLM, 但经耐心地调整光路后实验质量仍然很高. 通过对比图4和图8, 可以观察到: 随着艾里系数b和c的增大, 一阶艾里导数光束经艾里变换后二维光强分布演化的实验记录结果与理论计算结果一致.
然后, 实验测量一阶艾里导数光束艾里变换后x方向上的质心和光束半宽. x方向上的质心和光束半宽的测量过程如下. 首先, BPA记录输出光束的光强分布. 每个光强分布图分割为一个N × M光强矩阵, 每个矩阵元的光强表示为I(xi, yj), (xi, yj)表示该矩阵元的坐标, 其中i = 1, 2, 3, ···和j = 1, 2, 3, ···. 由于不同的艾里系数b和c导致不同的输出光斑尺寸, 所以每个光强分布图中N和M的具体数值也不同. 最后, 一阶艾里导数光束经艾里变换后x方向上的质心和光束半宽由以下两式计算得到:
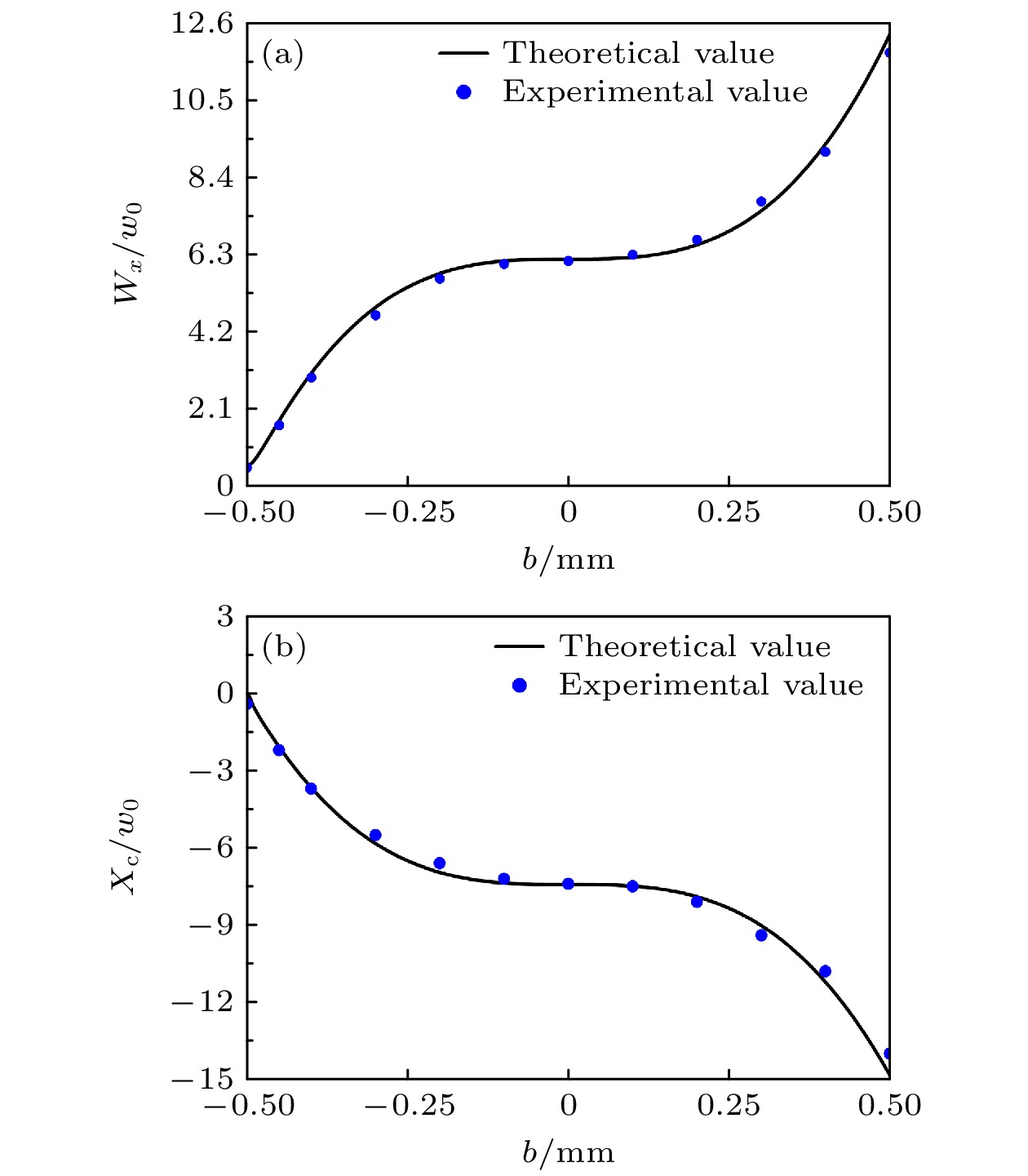
艾里系数b对一阶艾里导数光束经艾里变换后x方向上的质心和光束半宽影响的实验测量记录如图9表示, 图中的点和实线分别对应于实验值和理论值, 实验测量值与理论值相吻合, 质心和光束半宽随艾里系数b的变化呈现两边陡峭中间平坦的变化.
-
在两种情形下分别导出了一阶艾里导数光束经艾里变换后的解析光场. 第一种情形是b = c > –w0. 当b = c > –w0时, 一阶艾里导数光束的艾里变换在任意一个横向上的光场是偏心艾里光束和偏心一阶艾里导数光束之和. 当b和c逐渐远离–w0, 一阶艾里导数光束的艾里变换可近似为一偏心一阶艾里导数光束. 另一种情形是b = c = –w0. 当b = c = –w0时, 一阶艾里导数光束的艾里变换在任意一个横向上的光场是两个偏心优美厄米-高斯光束之和. 在上述两种情形下, 分别导出了一阶艾里导数光束经艾里变换后质心和光束半宽的解析表达式.
首先, 研究了艾里系数对x方向上归一化光强分布的影响. 当b从–w0开始增大时, 归一化光强分布的范围扩大, 并且出现更多的侧峰, 艾里特征增强. 在b > –w0的情况下, 分析了偏心艾里光束、偏心一阶艾里导数光束和交叉项对总光强的贡献. 当b在–w0附近时, 交叉项对总光强的贡献不能忽略. 当b远离–w0时, 偏心艾里光束和交叉项对总光强的贡献都可以忽略不计. 然后, 分析了艾里系数对二维归一化光强分布的影响. 当b和c开始从–w0增大时, 更多的波瓣逐渐出现在二维归一化光强分布中. 最后, 研究了艾里系数对质心和光束半宽的影响. 当b从–w0开始增大时, 质心经历了一个先快速减小、然后缓慢减小、最后快速减小的过程, 而光束半宽则经历了先快速增大、然后缓慢增大、最后快速增大的过程.
本文通过对一阶艾里导数光束的艾里变换实验的实现, 系统地定量表征了其光强分布、质心以及光束半宽的影响规律, 实验数据与理论计算结果呈现高度一致性. 研究证实, 经艾里变换操作的一阶艾里导数光束可以产生具有特殊形状分布的激光束, 这为复杂结构光场的制备提供了新的解决方案. 尤其值得注意的是, 当选取特征参数b = c = –w0时, 系统生成的四瓣型光束分布可以在微光学、空分复用光通信以及可编程光束分频技术等领域展现出独特的应用价值.
一阶艾里导数光束的艾里变换
Airy transformation of Airyprime beam
-
摘要: 艾里变换是一种能实现高斯光束与艾里光束相互转换的神奇光学变换. 一阶艾里导数光束, 作为艾里光束的进阶型, 在经过艾里变换后会产生怎样的光束? 这就是本文所要研究的内容. 当艾里系数大于负的横向比例因子时, 一阶艾里导数光束的艾里变换在任意一个横向上的光场是偏心艾里光束和偏心一阶艾里导数光束之和. 当艾里系数等于负的横向比例因子时, 一阶艾里导数光束的艾里变换在任意一个横向上的光场是两个偏心优美厄米-高斯光束之和. 此外, 分别导出了一阶艾里导数光束经艾里变换后的质心和光束半宽在上述两种情形下的解析表达式. 最后, 实验上实现了一阶艾里导数光束的艾里变换, 并测量了艾里系数对光强分布、质心和光束半宽的影响. 一阶艾里导数光束艾里变换的研究拓宽了特殊形态分布光束的获取途径, 有望应用于光通信和分束技术等领域.Abstract: As a remarkable optical transformation enabling mutual conversion between Gaussian and Airy beams, the Airy transformation raises intriguing questions when applied to Airyprime beam—an advanced variant of conventional Airy beam. To answer these questions, numerical simulations and experimental verification are combined in this study. The results show two different operation regimes: when the Airy coefficient exceeds the negative transverse scale factor, the Airy-transformed optical field of Airyprime beam in any transverse direction becomes equivalent to the superposition of eccentric Airy beam and eccentric Airyprime beam; when the Airy coefficient equals the negative transverse scale factor, the transformed optical field equivalently corresponds to the sum of two displaced elegant Hermite-Gaussian beams. Analytical expressions for centroid and beam half width under both regimes are rigorously derived and validated experimentally by using Airy transformation of Airyprime beams to systematically measure the influences of Airy coefficientson intensity distribution, centroid displacement, and beam half width. This investigation provides a novel method for generating complex beam profiles while enhancing the potential application value of such beams in optical communication and beam-splitting technology.
-
Key words:
- Airyprime beam /
- Airy transformation /
- Airy coefficients /
- centroid /
- beam half width .
-
-
图 2 一阶艾里导数光束经不同艾里变换后x方向上的归一化光强分布 (a) b = –0.50 mm; (b) b = –0.45 mm; (c) b = –0.40 mm; (d) b = –0.30 mm; (e) b = –0.20 mm; (f) b = –0.10 mm; (g) b = 0.00 mm; (h) b = 0.10 mm; (i) b = 0.20 mm
Figure 2. Normalized light intensity distribution in the x-direction of an Airyprime beam after different Airy transformation: (a) b = –0.50 mm; (b) b = –0.45 mm; (c) b = –0.40 mm; (d) b = –0.30 mm; (e) b = –0.20 mm; (f) b = –0.10 mm; (g) b = 0.00 mm; (h) b = 0.10 mm; (i) b = 0.20 mm.
图 3 偏心艾里光束、偏心一阶艾里导数光束和交叉项在x方向上的光强分布 (a)—(c) b = –0.45 mm; (d)—(f) b = –0.20 mm; (g)—(i) b = 0.20 mm
Figure 3. Light intensity distribution in the x -direction of the eccentric Airy beam, the eccentric Airyprime beam, and the cross term: (a)—(c) b = –0.45 mm; (d)—(f) b = –0.20 mm; (g)—(i) b = 0.20 mm.
图 4 一阶艾里导数光束经不同艾里变换后的二维归一化光强分布 (a) b = c = –0.50 mm; (b) b = c = –0.45 mm; (c) b = c = –0.40 mm; (d) b = c = –0.30 mm; (e) b = c = –0.20 mm; (f) b = c = –0.10 mm; (g) b = c = 0.00 mm; (h) b = c = 0.10 mm; (i) b = c = 0.20 mm
Figure 4. Two-dimensional normalized intensity distribution of an Airyprime beam after different Airy transformation: (a) b = c = –0.50 mm; (b) b = c = –0.45 mm; (c) b = c = –0.40 mm; (d) b = c = –0.30 mm; (e) b = c = –0.20 mm; (f) b = c = –0.10 mm; (g) b = c = 0.00 mm; (h) b = c = 0.10 mm; (i) b = c = 0.20 mm.
图 5 艾里系数b对一阶艾里导数光束经艾里变换后x方向上的质心(a)和光束半宽(b)的影响
Figure 5. Effect of the Airy coefficient b on the centroid (a) and the beam half width (b) in the x-direction of an Airyprime beam after Airy transformation.
图 6 一阶艾里导数光束艾里变换的实验装置示意图
Figure 6. Experimental setup of the Airy transformation of an Airyprime beam.
图 7 (a) 用于产生一阶艾里导数光束的相位光栅; (b) 上传到SLM2的立方相位图
Figure 7. (a) Phase grating for generation of an Airyprime beam; (b) cubic phase pattern uploaded onto SLM2.
图 8 一阶艾里导数光束经不同艾里变换后二维光强分布的实验记录 (a) b = c = –0.50 mm; (b) b = c = –0.45 mm; (c) b = c = –0.40 mm; (d) b = c = –0.30 mm; (e) b = c = –0.20 mm; (f) b = c = –0.10 mm; (g) b = c = 0.00 mm; (h) b = c = 0.10 mm; (i) b = c = 0.20 mm
Figure 8. Experimental record of two-dimensional intensity profile of an Airyprime beam after different Airy transformation: (a) b = c = –0.50 mm; (b) b = c = –0.45 mm; (c) b = c = –0.40 mm; (d) b = c = –0.30 mm; (e) b = c = –0.20 mm; (f) b = c = –0.10 mm; (g) b = c = 0.00 mm; (h) b = c = 0.10 mm; (i) b = c = 0.20 mm.
-
[1] Zang X, Dan W S, Zhou Y M, Lv H, Wang F, Cai Y J, Zhou G Q 2022 Opt. Express 30 3804 doi: 10.1364/OE.448398 [2] Kumari A, Dev V, Pal V 2024 Opt. Laser Technol. 168 109387 doi: 10.1016/j.optlastec.2023.109837 [3] Yu J, Wang Y P, Bai Z Y, Wu L P, Fu C L, Liu S, Liu Y 2023 Opt. Express 31 11053 doi: 10.1364/OE.484878 [4] Yu J, Tong S D, Long H H, Bai Z Y, Wu L P, Liu Y 2024 Opt. Express 32 6178 doi: 10.1364/OE.509568 [5] Dan W S, Zang X, Wang F, Zhou Y M, Xu Y Q, Chen R P, Zhou G Q 2022 Opt. Express 30 32704 doi: 10.1364/OE.469593 [6] Chen Z, Peng S Y, Zhang Z H, Liu J L, Meng Yang 2024 Opt. Lett. 49 6453 doi: 10.1364/OL.539499 [7] Chen D H, Mo Z W, Liang Z H, Jiang J J, Tang H L, Sun Y D, Wang Z Y, Wei Q F, Chen Y R, Deng D M 2024 Opt. Commun. 554 130109 doi: 10.1016/j.optcom.2023.130109 [8] Zhao S K, Li J C, Li T Q, Huang X W, Bai Y F, Fu X Q 2024 Laser Phys. 34 095001 doi: 10.1088/1555-6611/ad6d4d [9] Zhao S K, Huang X W, Bai Y F, Fu X Q 2024 Chaos, Solitons Fractals 187 115480 doi: 10.1016/j.chaos.2024.115480 [10] Zhou Y M, Zang X, Dan W S, Wang F, Chen R P, Zhou G Q 2023 Opt. Laser Technol. 162 109303 doi: 10.1016/j.optlastec.2023.109303 [11] Zang X, Dan W S, Wang F, Zhou Y M, Cai Y J, Zhou G Q 2022 Opt. Lett. 47 5654 doi: 10.1364/OL.476287 [12] Zang X, Dan W S, Zhou Y M, Wang F, Cai Y J, Zhou G Q 2023 Opt. Lett. 48 912 doi: 10.1364/OL.482204 [13] Wang W X, Mi Z W, Zhang L P, Wang B Y, Han K Z, Lei C X, Man Z S, Ge X L 2023 Opt. Commun. 549 129879 doi: 10.1016/j.optcom.2023.129879 [14] Yang S, Yu P X, Wu J W, Zhang X, Xu Z, Man Z S, Ge X L, Fu S G, Lei C X, Chen C D, Deng D M, Zhang L P 2023 Opt. Express 31 35685 doi: 10.1364/OE.499499 [15] Zhang L P, Yang S, Li S Y, Man Z S, Ge X L, Lei C X, He S, Zhang W F, Deng D M, Chen C D 2024 Chaos, Solitons Fractals 181 114506 doi: 10.1016/j.chaos.2024.114506 [16] He J, Dan W S, Zang X, Zhou Y M, Wang F, Cai Y J, Zhou G Q 2024 Opt. Laser Technol. 168 109932 doi: 10.1016/j.optlastec.2023.109932 [17] Zang X, Wang F, Dan W S, Zhou Y, M Zhou G Q 2022 Opt. Laser Technol. 155 108398 doi: 10.1016/j.optlastec.2022.108398 [18] Chen C D, Zhang L P, Yang S, Li S Y, Deng D M 2024 Opt. Lett. 49 2681 doi: 10.1364/OL.523374 [19] Zheng X Q, Yang Y Z, Liu Y J, Lin X J, Liang Z H, Liu J, Deng D M 2024 Opt. Lett. 49 4393 doi: 10.1364/OL.527671 [20] Jiang Y F, Huang K K, Lu X H 2012 Opt. Commun. 285 4840 doi: 10.1016/j.optcom.2012.08.003 [21] Jiang Y F, Huang K K, Lu X H 2012 J. Opt. Soc. Am. A: 29 1412 doi: 10.1364/JOSAA.29.001412 [22] Ez-zariy L, Boufalah F, Dalil-Essakali L, Belafhal A 2018 Optik 171 501 doi: 10.1016/j.ijleo.2018.06.091 [23] Yaalou M, El Halba E M, Hricha Z, Belafhal A 2019 Opt. Quantum Electron. 51 64 doi: 10.1007/s11082-019-1775-2 [24] Yaalou M, Hricha Z, El Halba E M, Belafhal A 2019 Opt. Quantum Electron. 51 308 doi: 10.1007/s11082-019-2023-5 [25] Yaalou M, Hricha Z, Lazrek M, Belafhal A 2020 J. Mod. Opt. 67 771 doi: 10.1080/09500340.2020.1769760 [26] Yaalou M, Hricha Z, Belafhal A 2020 Opt. Quantum Electron. 52 165 doi: 10.1007/s11082-020-02286-9 [27] Yaalou M, Hricha Z, Belafhal A 2020 Opt. Quantum Electron. 52 461 doi: 10.1007/s11082-020-02594-0 [28] Chu X C, Liu R J, Wang X, Han Z X, Ni Y H 2021 Opt. Appl. LI 473 doi: 10.37190/oa210401 [29] Zhang Q, Liu Z R, Wang X 2022 Results Phys. 35 105389 doi: 10.1016/j.rinp.2022.105389 [30] Huang H Q, Wu Y, Lin Z J, Xu D L, Jiang J J, Mo Z W, Yang H B, Deng D M 2022 Waves Random Complex Medium 35 5007 doi: 10.1080/17455030.2022.2066222 [31] Zhang Q, Liu Z R, Wang X 2022 Phys. Scr. 97 115502 doi: 10.1088/1402-4896/ac96d9 [32] Zhang Q, Liu Z R, Wang X 2022 Optik 251 168477 doi: 10.1016/j.ijleo.2021.168477 [33] Tang H L, Fan Z J, Ouyang S G, Mo Z W, Xu D L, Huang H Y, Deng D M 2023 Results Phys. 50 106552 doi: 10.1016/j.rinp.2023.106552 [34] Lin Q D, Zhang H, Hu Z Q, Lu X, Lu X Y, Cai Y J, Zhao C L 2023 Photonics 10 974 doi: 10.3390/photonics10090974 [35] Yaalou M, Hricha Z, Belafhal A 2023 Opt. Quantum Electron. 55 875 doi: 10.1007/s11082-023-05133-9 [36] Yaalou M, Hricha Z, Belafhal A 2023 Opt. Quantum Electron. 55 138 doi: 10.1007/s11082-022-04405-0 [37] Gradshteyn I S, Ryzhik I M 1980 Table of integrals, series, and products (New York: Academic Press [38] Vallée O, Manuel S 2010 Airy Functions and Applications to Physics (London: Imperial College Press [39] Martínez-Herrero R, Mejías P M 1993 Opt. Lett. 18 1669 doi: 10.1364/OL.18.001669 [40] Nemes G, Serna J 1998 OSA TOPS 17 200 doi: 10.1364/DLAI.1998.MQ2 [41] Mei Z R, Zhao D M 2005 Appl. Opt. 44 1381 doi: 10.1364/AO.44.001381 [42] Deng D M 2005 Phys. Lett. A 341 352 doi: 10.1016/j.physleta.2005.04.081 [43] 刘飞, 季小玲 2011 物理学报 60 014216 doi: 10.7498/aps.60.014216 Liu F, Ji X L 2011 Acta Phys. Sin. 60 014216 doi: 10.7498/aps.60.014216 [44] 余佳益, 陈亚红, 蔡阳健 2016 物理学报 65 214202 doi: 10.7498/aps.65.214202 Yu J Y, Chen Y H, Cai Y J 2016 Acta Phys. Sin. 65 214202 doi: 10.7498/aps.65.214202 [45] Mihoubi K, Bencheikh A, Manallah Ai 2018 Opt. Laser. Technol. 99 191 doi: 10.1016/j.optlastec.2017.09.002 -
计量
- 文章访问数: 71
- HTML全文浏览数: 71
- PDF下载数: 2
- 施引文献: 0