-
紫外激光具有波长短、与材料作用发热小、适合拉曼光谱分析等优异特性, 在光刻、激光加工、通信与光存储、科研与军事、生物医疗等领域有旺盛的应用需求. 紫外激光一般可由常见的可见或近红外波段激光通过磷酸二氢钾(KH2PO4, KDP)、三硼酸锂(LiB3O5, LBO)、偏硼酸钡(β-BaB2O4, BBO)等非线性晶体的三次谐波转换(third-harmonic generation, THG)获得. 这种谐波技术已较成熟, 转换效率可达50%以上, 但也存在不足, 例如: 空间光路对准要求严格; 系统难以集成, 可靠性易受环境变化影响; 晶体价格昂贵、寿命短; 在紫外波段元件薄膜易损坏. 光纤激光器光束质量好、性能稳定、体积紧凑、易于维护, 已成为全球工业激光器市场中占比最大的品种[1]. 目前, 紫外光纤激光器仍普遍采用基于晶体的频率转换技术, 即将光纤输出的长波段激光变换成空间光束, 由非线性晶体进行频率转换, 再将空间传输的紫外激光重新耦合至光纤[2,3]. 晶体模块的引入提高了光纤激光器的造价, 降低了其整体集成度与可靠性, 发展全光纤的频率转换技术具有重要的科学和现实意义.
研究者们采用不同种类光纤开展了三次谐波转换的研究, 例如常规结构的阶跃型光纤(采用掺杂的二氧化硅玻璃材料[4]或者高非线性玻璃材料[5])、椭圆纤芯光纤[6]、具有亚波长直径的光纤拉锥[7]、结构相对复杂但灵活可调的微结构光纤[8,9]等. 这些持续的工作表明, 采用多种光纤均可产生三次谐波, 但要将其发展成可实际应用的技术, 则尚需进一步的努力, 设计兼备机械性能和转换效率的特种光纤, 并降低其制备难度, 是面临的关键挑战. 此外, 掺杂玻璃材料在紫外波段传输损耗较高, 也是设计光纤时需要解决的重要问题[10]. 本文开展单包层阶跃型光纤与双包层阶跃型光纤的紫外波段三次谐波转换研究. 这两类光纤具有传输特性简单、与标准光纤连接容易等特点, 采用纯二氧化硅玻璃作纤芯材料也可使其在紫外波段有良好的透过特性. 为了与相对复杂的微结构光纤相区别, 文中将这两类光纤定义为简单结构光纤(simply-structured optical fiber, SSOF), 将详细探讨其谐波转换效率、机械性能及制备误差宽容度. 本文的研究结果对推动全光纤三次谐波转换技术的实用化具有参考价值.
-
高效的三次谐波转换要求基频波与其谐波满足相位匹配条件. 对于本文的简单结构光纤, 当纤芯直径取特定值时, 基频波的基模与三次谐波的高阶模可实现模间相位匹配(intermodal phase matching, IPM). 根据光纤理论, 各个模式的传输常数可通过本征值方程求得. 设光波在真空中的波长为
$ \lambda $ 、传输常数为$ k=2 \pi/\lambda $ , 其在光纤中的传输常数为$ \beta $ , 单包层阶跃型光纤的本征值方程为[11]其中
$ {n}_{1} $ 和$ {n}_{2} $ 分别为纤芯与包层的折射率,$ {{\mathrm{J}}}_{{\mathrm{\nu }}} $ 为第一类ν阶贝塞尔函数,$ {{\mathrm{K}}}_{\nu } $ 为第二类ν阶修正贝塞尔函数;$ U={r}_{1}{({k}^{2}{n}_{1}^{2}-{\beta }^{2})}^{1/2} $ 和$ W={r}_{1}{({\beta }^{2}-{k}^{2}{n}_{2}^{2})}^{1/2} $ 分别为纤芯与包层的归一化模式参量,$ V= {kr}_{1}{({n}_{1}^{2} - {n}_{2}^{2})}^{1/2} $ 为光纤的归一化频率($ {r}_{1} $ 为纤芯半径). 双包层阶跃型光纤的本征值方程则可表示为[12–14]其中
$ {n}_{1} $ ,$ {n}_{2} $ 和$ {n}_{3} $ 分别为纤芯、内包层和外包层的折射率,$ t={r}_{2}/{r}_{1} $ ($ {r}_{1} $ 为纤芯半径,$ {r}_{2} $ 为内包层半径),$ {s}_{ij}={n}_{i}^{2}/{n}_{j}^{2}\left(i, j=1, 2, 3\right) $ .$ {p}_{\nu } $ ,$ {q}_{\nu } $ ,$ {r}_{\nu } $ 均为贝塞尔函数的乘积形式:其中
$ {{\mathrm{Y}}}_{\nu } $ 为第二类ν阶贝塞尔函数,$ {u}_{i}^{2} = {k}^{2}n_{i}^{2} - \beta ^{2}= -{w}_{i}^{2} $ . 归一化参量可表示为$ {U}_{1}={u}_{1}{r}_{1} $ ,$ {U}_{2}={u}_{2}{r}_{1} $ ,$ {W}_{3}={w}_{3}{r}_{2} $ ,$ {V}_{12}={kr}_{1}{\left({n}_{1}^{2}-{n}_{2}^{2}\right)}^{1/2} $ ,${V}_{23}={kr}_{2}({n}_{2}^{2}- {n}_{3}^{2})^{1/2} $ , 并引入$ {\sigma }_{0}^{2}={\left(\beta \nu/k\right)}^{2} $ , (2)式中的$ {x}_{1}{, x}_{2} $ ,$ \mathfrak{I} $ 和$ \mathfrak{R} $ 可由以上参量进一步表述, 详情见文献[13]. -
假设基频波与其三次谐波在光纤中沿z方向传输, 它们的相互作用过程可由以下耦合模式方程组进行描述[7,15]:
其中
$ {A}_{1}\left(z\right) $ ,$ {A}_{3}\left(z\right) $ 分别为基频波与三次谐波的模场振幅(基频波功率$ {P}_{1}={\left|{A}_{1}\right|}^{2} $ , 三次谐波功率$ {P}_{3}={\left|{A}_{3}\right|}^{2} $ ),$ {k}_{1}=2{\mathrm{\pi }}/{\lambda }_{1} $ 为基频在真空中的传输常数,$ {n}^{\left(2\right)} $ 为光纤的非线性折射率系数,$ {\alpha }_{1} $ 和$ {\alpha }_{3} $ 则分别为基频与三次谐波在光纤中的功率损耗系数,$ {\delta \beta }_{L}={\beta }_{3}-{3\beta }_{1} $ 为它们在光纤中的传输常数失配量.(4)式包含三次谐波转换、自相位调制(self-phase modulation, SPM)与交叉相位调制(cross-phase modulation, XPM)三种非线性效应.
$ {J}_{{\mathrm{1, 2}}, {\mathrm{3, 5}}} $ 为非线性重叠积分, 其中$ {J}_{1} $ 表征基频波的SPM,$ {J}_{5} $ 表征三次谐波的SPM,$ {J}_{2} $ 表征基频波与三次谐波的XPM,$ {J}_{3} $ 则表征基频波与三次谐波之间的能量转换过程. 各非线性重叠积分由基频与三次谐波的横向电场矢量$ {\boldsymbol{F}}_{1}(x, y) $ 和$ {\boldsymbol{F}}_{3}(x, y) $ 计算如下[7]:它们与传导模式的光场分布及纤芯直径有关. SPM与XPM将使基频波与三次谐波的相位关系发生变化, 当输入的基频波功率(即泵浦功率)为
$ {P}_{0} $ 时, 该变化可用非线性传输常数失配量$ {\delta \beta }_{{\mathrm{N}}{\mathrm{L}}}\approx 3{k}_{1}{n}^{\left(2\right)}\left(2{J}_{2}-{J}_{1}\right){P}_{0} $ 进行描述. 因此, 总的传输常数失配量包括线性部分与非线性部分, 即$ {\delta \beta }_{{\mathrm{t}}}= {\delta \beta }_{{\mathrm{L}}}+{\delta \beta }_{{\mathrm{N}}{\mathrm{L}}} $ , 要在基频波与三次谐波之间实现理想相位匹配, 则要求$ {\delta \beta }_{{\mathrm{t}}}=0 $ [7,15].对长度为L的简单结构光纤, 当产生的三次谐波信号较弱(即
$ \left|{A}_{3}\right|\ll \left|{A}_{1}\right| $ )且光纤损耗可忽略时, 由(4)式可近似得[7]可见, 入射泵浦功率
$ {P}_{0} $ 、非线性重叠积分$ {J}_{3} $ 和传输常数失配量$ {\delta \beta }_{\rm t} $ 是影响三次谐波产生的3个关键参数, 在设计和优化光纤时, 需综合考虑这些因素的影响. 由(4)式描述的耦合模式方程组适用于准连续激光(脉宽为ns以上的脉冲激光可视为这种情况). 三次谐波转换效率定义为三次谐波输出功率与入射泵浦功率的比值, 即$ \eta ={P}_{3}/{P}_{0} $ . 若无特别说明, 本文提及的功率均指脉冲的峰值功率. -
对于阶跃型光纤, 纤芯直径为特定值时基频波与其三次谐波可相位匹配, 从而实现高效的能量转换. 但由于存在制造误差, 纤芯直径难以精准符合设定范围, 直径偏差会导致大的相位失配从而使谐波转换效率降低甚至无法产生. 设纤芯直径偏差沿着光纤随机发生, 幅度为ε, 采用高斯分布对其进行描述, 则有[15]
其中
$ p $ 为概率密度函数, σ为直径偏差ε的标准差. 下文将采用σ作为表征光纤随机粗糙度的参数. 设ε沿光纤在一段微小距离内是不变的, 该距离可称为粗糙度长度, 其也具有随机特性, 可用高斯分布进行描述, 更详细的分析见文献[15]. 为了简化问题, 在考虑纤芯直径随机偏差的影响时, 本文设粗糙度长度的平均值为10 μm, 标准差为1 μm, 而着重比较σ取值不同时的结果. -
已有的研究结果表明, 光纤越长, 其随机粗糙度对三次谐波转换的不良影响就越趋于显著. 因此, 文献[16]提出通过短光纤级联的方法来延长频率转换的有效作用长度. 如图1所示, 光纤级联系统包含两种光纤, 转换光纤(third-harmonic generation fiber, TF)的作用是产生三次谐波, 传导光纤(guiding fiber, GF)的作用是传输基频及谐波光信号. 设所有转换光纤长度相同(为
$ {L}_{{\mathrm{T}}{\mathrm{F}}} $ ), 所有传导光纤长度也相同(为$ {L}_{{\mathrm{G}}{\mathrm{F}}} $ ), 一段转换光纤与一段传导光纤构成一个单元, 基频波与三次谐波通过每个单元都将产生一个相位差:其中
$ {\delta \beta }_{{\mathrm{t}}}^{{\mathrm{T}}{\mathrm{F}}} $ 与$ {\delta \beta }_{{\mathrm{t}}}^{{\mathrm{G}}{\mathrm{F}}} $ 分别是转换光纤与传导光纤中的总传输常数失配量. 若该系统包含N个这样的单元, 每个单元的谐波转换效率为$ {\eta }_{0} $ , 则总效率可表示为其中
$ b={\left[\dfrac{{\mathrm{sin}} (N\cdot{\Delta \varphi }/{2})}{{\sin}({\Delta \varphi }/{2})}\right]}^{2}. $ 当$ \Delta \varphi =2 m{\mathrm{\pi }}~ (m=0, \pm 1, \pm 2, \cdots ) $ 时, b将取得最大值$ {N}^{2} $ , 即由各单元产生的三次谐波在光纤系统输出端相干叠加后增强. 传输常数失配量的线性部分是由光纤参数及光的波长、模式等决定的, 相对而言比较固定, 而非线性部分可通过入射泵浦功率进行调节. 本文将设计专门用于三次谐波转换的单包层与双包层阶跃型光纤, 并比较它们构成级联系统后的转换效果. -
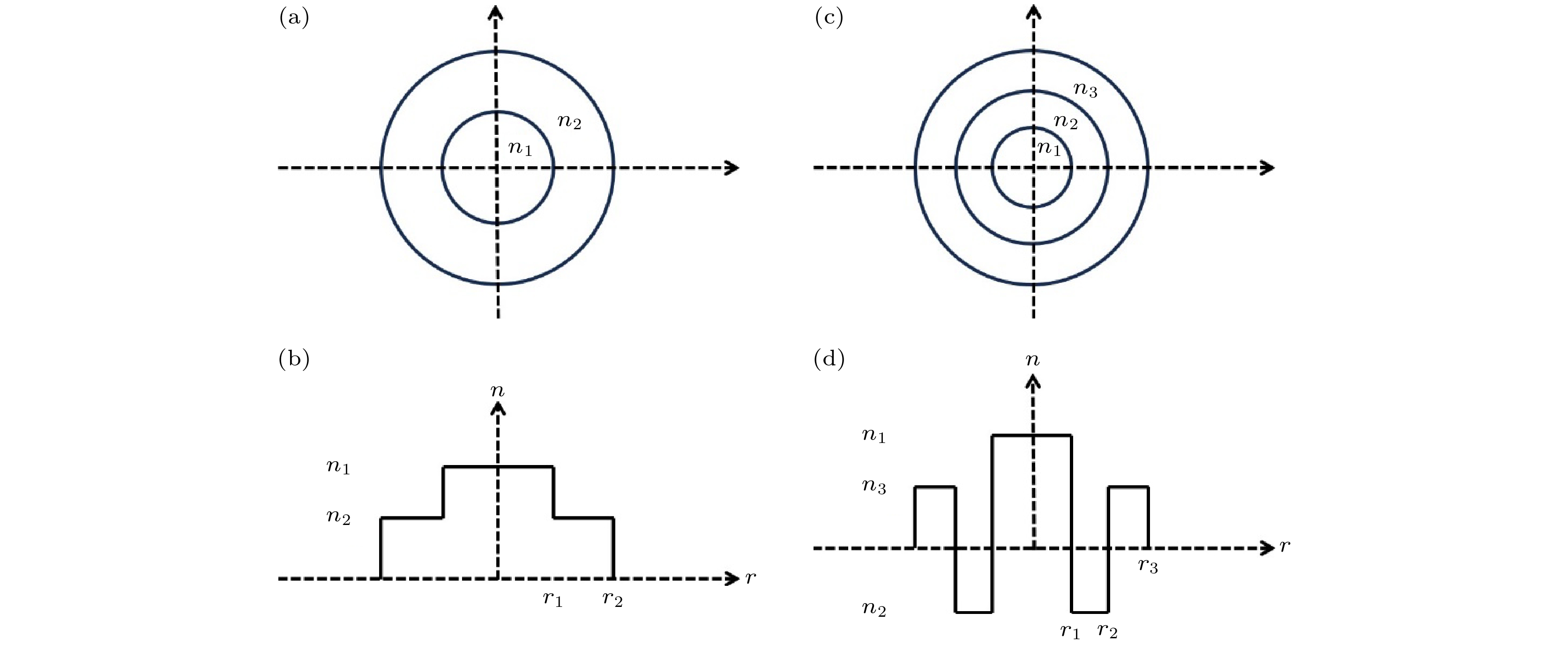
单包层光纤由折射率为n1的纤芯与折射率为n2的包层构成, 且n1 > n2, 如图2(a), (b)所示[11]. 双包层光纤由内到外依次是折射率为n1的纤芯、折射率为n2的内包层和折射率为n3的外包层, 根据3个折射率的大小关系, 双包层光纤可分为5种不同的类型, 其中n1 > n3 > n2的类型称为W型双包层光纤(W-type double-cladding fiber, WDCF), 见图2(c), (d)[12]. 分析结果表明, 光纤的数值孔径需达到一定阈值, 基频波与其三次谐波才可能实现相位匹配从而发生能量转换.
本文采用的泵浦波长
$ {\lambda }_{1}=1064\;{\mathrm{n}}{\mathrm{m}} $ , 将设计三种光纤进行三次谐波转换以获得紫外光输出. 第一种是具有高数值孔径的常规单包层光纤(conventional single-cladding fiber, CSCF), 为了降低紫外波段的传输损耗, 采用纯二氧化硅玻璃(silica)作为纤芯材料, 其非线性折射率系数$ {n}^{\left(2\right)}=2.7\times {10}^{-20}\;{{\mathrm{m}}}^{2}/{\mathrm{W}} $ , 采用掺氟二氧化硅玻璃作为固态包层[17,18], 对1 μm左右的波长, 该光纤的数值孔径$ {\rm NA}=\sqrt{{n}_{1}^{2}-{n}_{2}^{2}}=0.58 $ . 第二种是微纳光纤(microfiber, MF)[7,19], 其由标准单模光纤(如SMF-28)拉锥而成. 标准光纤的包层材料为纯二氧化硅玻璃, 直径为125 μm, 当此包层被熔融拉伸至直径小于1 μm时, 光纤原有的纤芯细至可忽略不计, 从而被拉细的包层成了新的纤芯, 而外部空气成了新的包层, 它们构成一段特殊的单包层光纤. MF的纤芯与包层折射率差大($ {{\rm NA}}=1.05 $ ), 容易满足相位匹配条件而产生三次谐波, 但机械特性较差, 光的传输也容易受外部环境的影响. 第三种为上文提到的W型双包层光纤WDCF, 其纤芯为纯二氧化硅玻璃, 内包层为掺氟二氧化硅玻璃, 外包层为氟塑料, 纤芯与内包层的数值孔径$ {{{\rm NA}}}_{12} = \sqrt{{n}_{1}^{2}-{n}_{2}^{2}} = 0.58 $ , 而纤芯与外包层的数值孔径$ {{{\rm NA}}}_{13}= \sqrt{{n}_{1}^{2}-{n}_{3}^{2}}=0.48 $ . 上述光纤材料的参数可从相关数据库查询获取[20].对泵浦波长
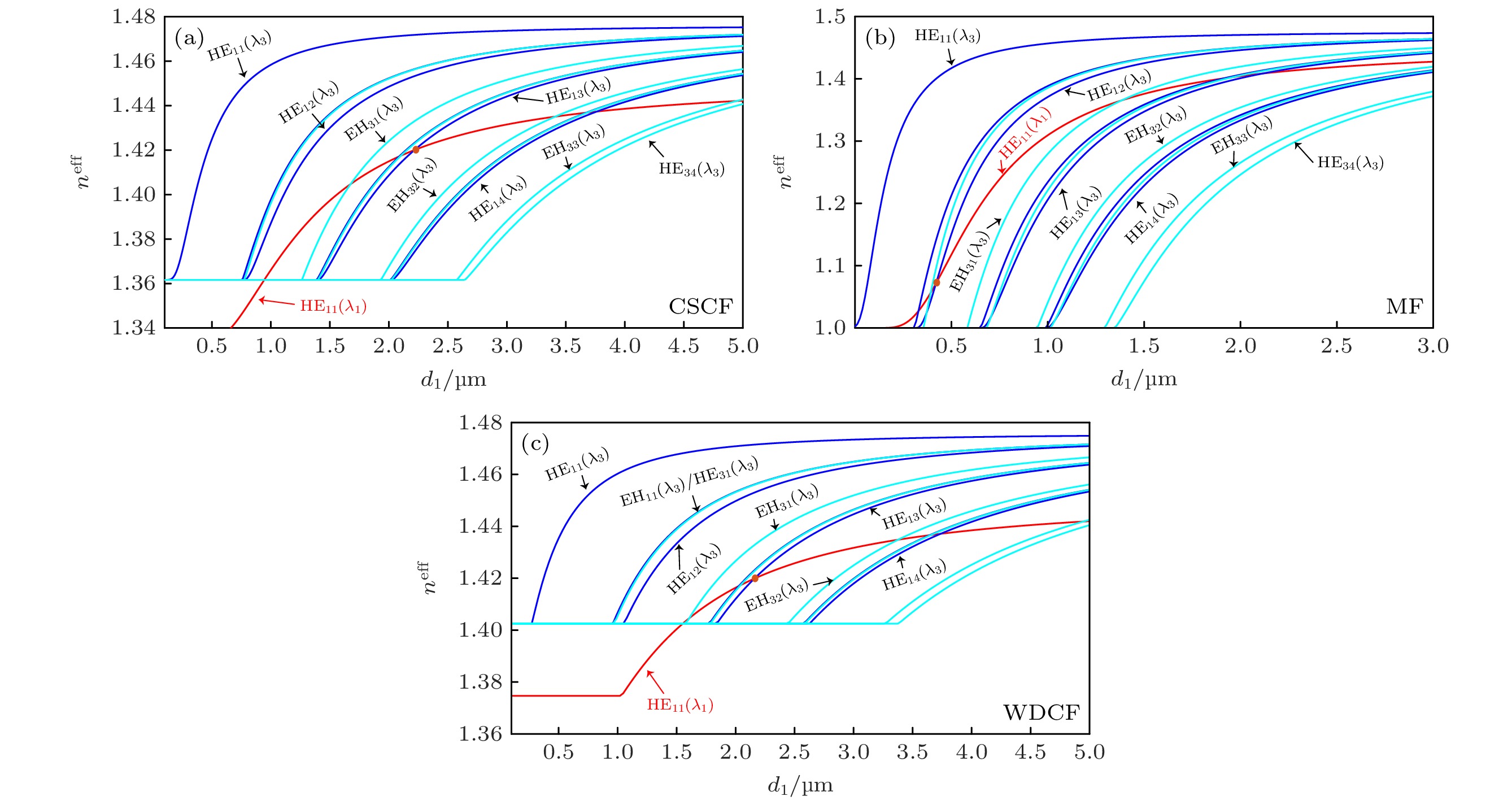
$ {\lambda }_{1}=1064\;{\mathrm{n}}{\mathrm{m}} $ , 常规单包层光纤CSCF的纤芯折射率$ {n}_{1}=1.45 $ , 包层折射率$ {n}_{2}= 1.33 $ ; 对三次谐波$ {\lambda }_{3}=355\;{\mathrm{n}}{\mathrm{m}} $ , 其纤芯和包层的折射率则分别为1.48和1.36. CSCF的包层直径设为常规的$ {d}_{2}=125 $ μm, 其纤芯直径$ {d}_{1} $ 则需根据相位匹配条件来确定. 求解(1)式所示的本征值方程, 得基频波与三次谐波各个模式在光纤中的有效折射率$ {n}^{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ , 见图3(a). 由于传输常数$ \beta = ({2{\mathrm{\pi }}}/{\lambda }){n}^{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ , 若忽略SPM与XPM引起的非线性相移, 基频波与三次谐波在$ {n}_{1}^{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}}={n}_{3}^{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ 时可实现相位匹配. 图3(a)中基频波的基模HE11(λ1)与多个三次谐波高阶模式均可相位匹配, 本文选择非线性重叠积分J3较大的模式HE13(λ3), 则CSCF的纤芯直径d1应大约为2.2 μm.微纳光纤MF的纤芯直径可类似地确定, 见图3(b). 由于具有大的数值孔径, MF对光场的束缚能力较强, 基频波的基模HE11(λ1)可与较低阶的三次谐波高阶模HE12(λ3)相位匹配, 但要求的纤芯直径小很多, 仅约0.5 μm, 不过这样的小芯径使MF的非线性参量
$ \gamma $ 显著增大[21], 所得的非线性重叠积分J3较CSCF大了将近两个数量级. 双包层光纤WDCF的纤芯直径也遵循上述过程来确定, 但需求解(2)式所示的本征值方程, 所得的有效折射率见图3(c). WDCF的相位匹配直径与CSCF相近, 但其内包层与外包层具有各自的波导场分布, 使得非线性重叠积分$ {J}_{3} $ 比CSCF大数倍. 上述三种光纤的参数信息详细列于表1中. 由于CSCF和WDCF的纤芯直径较大, 机械性能也较好, 制备及实际操控的难度较小, 将它们的长度均取为50 mm, 而将较脆弱的MF的长度设计为5 mm. 值得注意的是, 由于光场分布的对称性, 三次谐波的TM01($ {\lambda }_{3} $ ), TE01($ {\lambda }_{3} $ )和HE21($ {\lambda }_{3} $ )三种阶数较低的高阶模与基频波的基模HE11(λ1)之间的非线性重叠积分J3为零, 实际不能通过三次谐波转换而得到, 所以这三种模式在图3未画出. -
基频波与三次谐波沿光纤传输并相互作用时, SPM与XPM效应将引起非线性相移, 从而改变它们之间的相位关系. 上文在确定表1中的纤芯直径
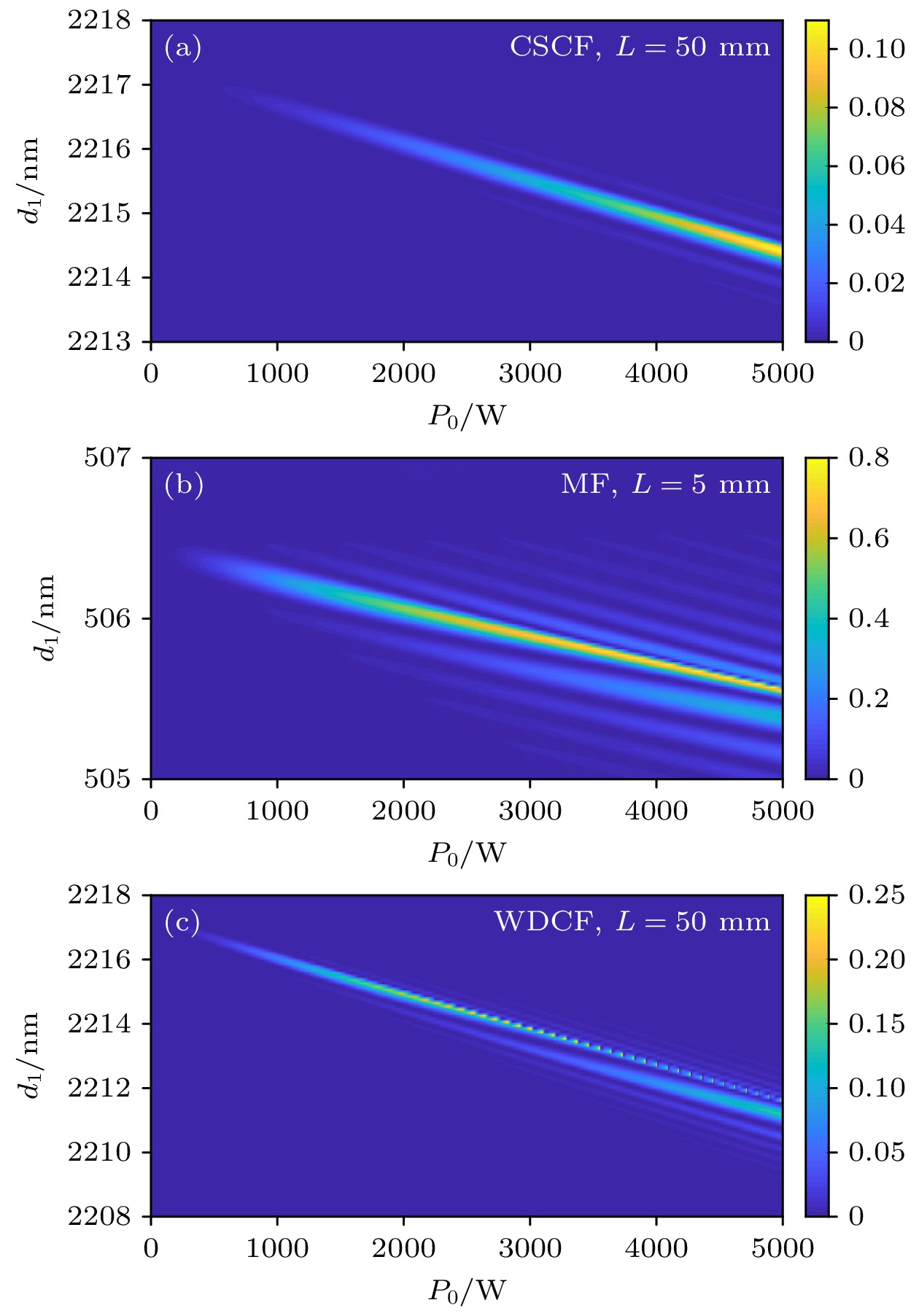
$ {d}_{1} $ 时, 并未考虑非线性相移(即忽略了非线性传输常数失配量$ {\delta \beta }_{{\mathrm{N}}{\mathrm{L}}} $ ), 这是在入射泵浦功率$ {P}_{0}=0 $ 的时候进行的初步设计. 在此基础上, 采用龙格-库达法求解(4)式所示的耦合模式方程组, 可得三次谐波转换效率与d1, P0的动态关系[22]. 图4所示为CSCF, MF和WDCF三种光纤的情况.可以发现, 随着入射泵浦功率P0升高, 满足相位匹配的纤芯直径d1在减小. 以图4(a)中的CSCF光纤为例,
$ {P}_{0}=0 $ 时得到$ {d}_{1}=2217.3\;{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ ; 若$ {P}_{0}= 2500{\;\mathrm{W}} $ , 则应调整纤芯直径为$ {d}_{1}=2216\;{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ , 此时可获得大约为2.5%的较佳转换效率; 若拟采用更高的$ {P}_{0} $ , 则应预先设计更小的$ {d}_{1} $ . 其他两种光纤也有类似的规律, 如图4(b)中的MF光纤在$ {P}_{0}= 2500\;{\mathrm{W}} $ ,$ {d}_{1}=506\;{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ 时转换效率为62.9%, 图4(c)中的WDCF光纤在$ {P}_{0} = 2500\;{\mathrm{W}} $ ,$ {d}_{1}=2214\;{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ 时转换效率为23.5%.从图4可以看出, 采用越高的泵浦功率, 可以达到的三次谐波转换效率也将越高, 但为了防止光纤损坏以及抑制受激拉曼散射等竞争性非线性过程, 通常会选择一个适宜的泵浦功率水平. 值得注意的是, 光纤在制造过程中不可避免地存在误差, 因此其纤芯直径会或多或少地偏离设计值, 而三次谐波转换对这种偏差的宽容度很小, 图4中细锐的转换效率范围清楚地表明了这一特征. 光纤制备出来后, 其直径就不可改变, 在存在偏差的情况下如何使谐波转换仍可有效发生, 是一个需要解决的重要问题. 一种常用的方法是微调泵浦光波长, 使制备好的光纤直径仍能满足相位匹配条件[19]. 根据图4, 还可以有另外一种解决方法, 即保持泵浦光波长不变, 而适应性地调节泵浦光功率, 该方法在实际中更灵活易行, 而且不会改变原本想要获得的输出波长.
-
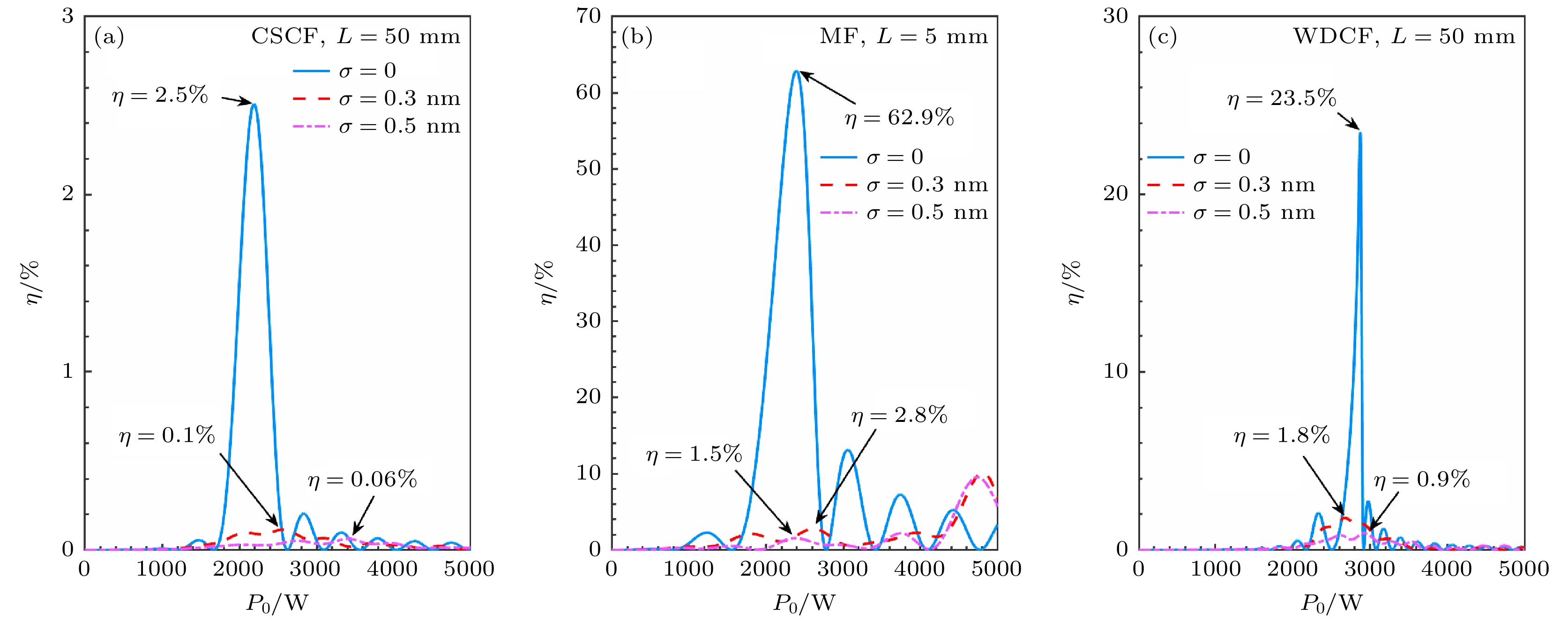
三种光纤具有不同随机粗糙度σ时的三次谐波转换效率如图5所示. 常规单包层光纤CSCF在σ = 0 时理论转换效率约2.5%; 当σ为0.3 nm时, 转换效率大幅下降至0.1%; 当σ增至0.5 nm时, 转换效率仅有0.06%. 微纳光纤MF受粗糙度的影响同样明显, 其理想转换效率可达62.9%(σ = 0), 考虑粗糙度后降至2.8%(σ = 0.3 nm)和1.5%(σ = 0.5 nm), 但依然高于CSCF. WDCF的转换效率则介于前两者之间, 其理论值为23.5%(σ = 0), 若有粗糙度则降低至1.8%(σ = 0.3 nm)和0.9%(σ = 0.5 nm).
光纤粗糙度会导致三次谐波转换效率明显 降低, 原因在于纤芯直径的波动影响总的相位失 配量
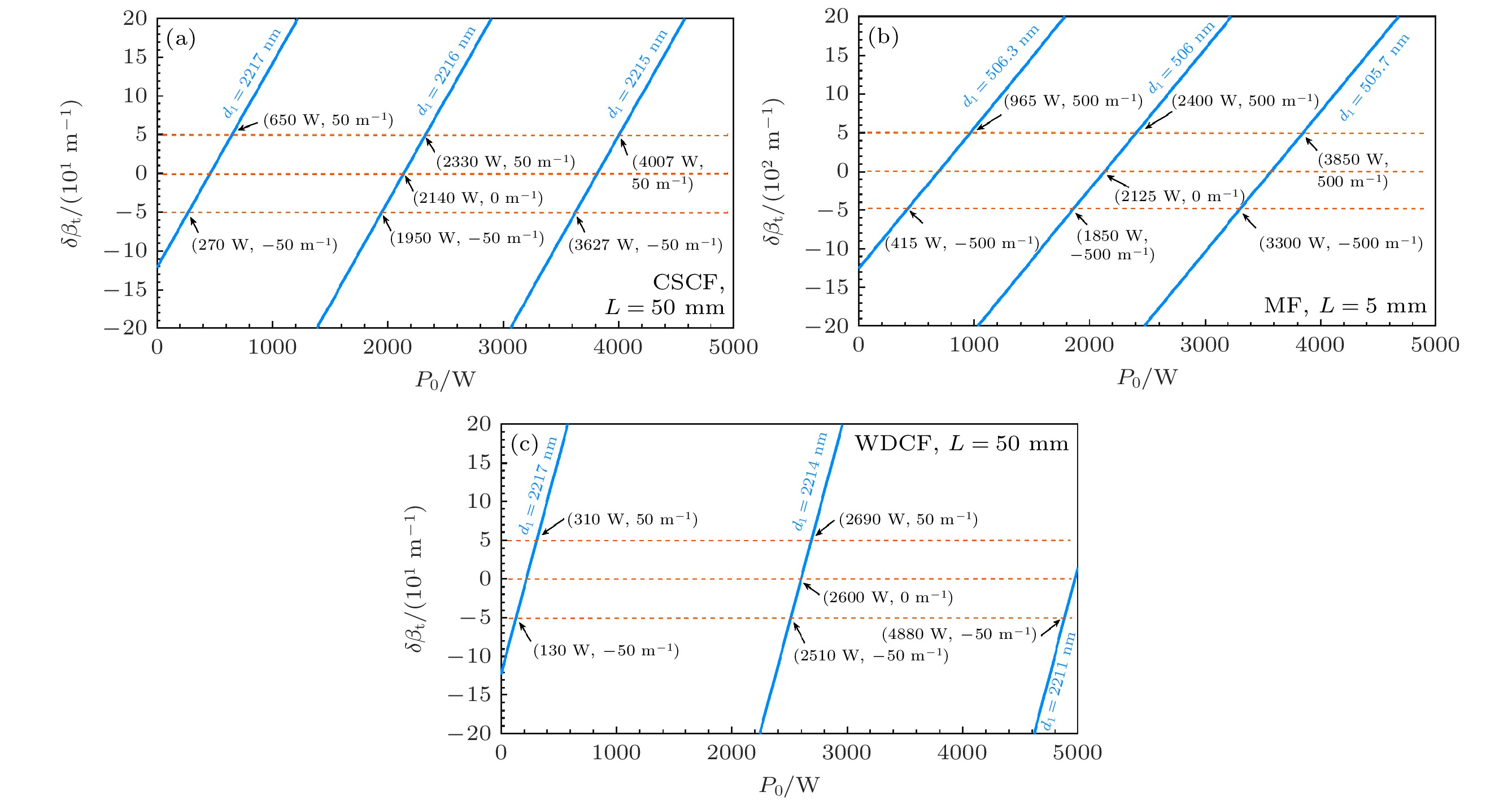
$ {\delta \beta }_{\rm t} $ [15]. 基频波与三次谐波的相干长度定义为$ {L}_{{\mathrm{c}}}= \pi/\left|{\delta \beta }_{{\mathrm{t}}}\right| $ , 它限制了频率转换光纤的有效长度. 当光纤长度不超过$ {L}_{{\mathrm{c}}} $ 时, 基频波能量转化为三次谐波能量, 后者可以沿着光纤单调增强; 而超过相干长度后, 能量转换方向周期性地变化, 三次谐波功率会发生振荡.图6(a)所示为CSCF光纤相位失配量随泵浦光功率的变化. 当纤芯直径为2216 nm, 在入射泵浦功率P0 = 2140 W处,
$ {\delta \beta }_{{\mathrm{t}}}\approx 0 $ , 理论上此时相干长度接近无穷大, 即三次谐波可以沿着光纤持 续增长; 若泵浦工作在1950—2330 W这一区间, 则有$ \left|{\delta \beta }_{{\mathrm{t}}}\right| $ $ \leqslant $ 50 m–1. 实际中光纤有制造误差, 纤芯直径可能会偏离设计值, 这时通过适应性地调节P0, 仍可使$ {\delta \beta }_{{\mathrm{t}}} $ 在一定程度上得到优化. 例如, 纤芯直径偏大为2217 nm时, 将泵浦功率向低调整到区间270—650 W, 而当纤芯直径偏小为2215 nm时, 泵浦向高调整到区间3627—4007 W. 可见, 若入射泵浦功率在0—4000 W范围内可调节, 则纤芯直径允许有±1 nm的制造误差, 这时有$ \left|{\delta \beta }_{{\mathrm{t}}}\right| $ $ \leqslant $ 50 m–1, 相干长度$ {L}_{{\mathrm{c}}} $ 约为62 mm.对微纳光纤MF和双包层光纤WDCF也可以进行类似分析, 结果见图6(b), (c). MF对制造精度的要求苛刻, 在纤芯直径设计值±0.3 nm的范围内才可将
$ \left|{\delta \beta }_{{\mathrm{t}}}\right| $ 控制在500 m–1以下, 计算出相干长度仅约6 mm. 相比较之下, WDCF的误差宽容度较大, 可在直径设计值±3 nm的范围内实现$ \left|{\delta \beta }_{{\mathrm{t}}}\right| $ $ \leqslant $ 50 m–1. 本文在对三种光纤作数值模拟时, 所采用的光纤长度均小于它们各自的相干长度. -
我们进一步用上述三种光纤构建如图1所示的级联系统, 单元数N不同时三次谐波转换效率随入射泵浦光功率的变化见图7. 各频率转换光纤TF的纤芯直径d1及长度LTF在子图中给出, 并且考虑了纤芯直径的随机波动(取粗糙度参数σ = 0.3 nm). 传导光纤则采用标准阶跃型光纤(Nufern公司的FUD-3959型号光纤), 其纤芯直径为9 μm, 并将各段长度均设为LGF = 20 cm.
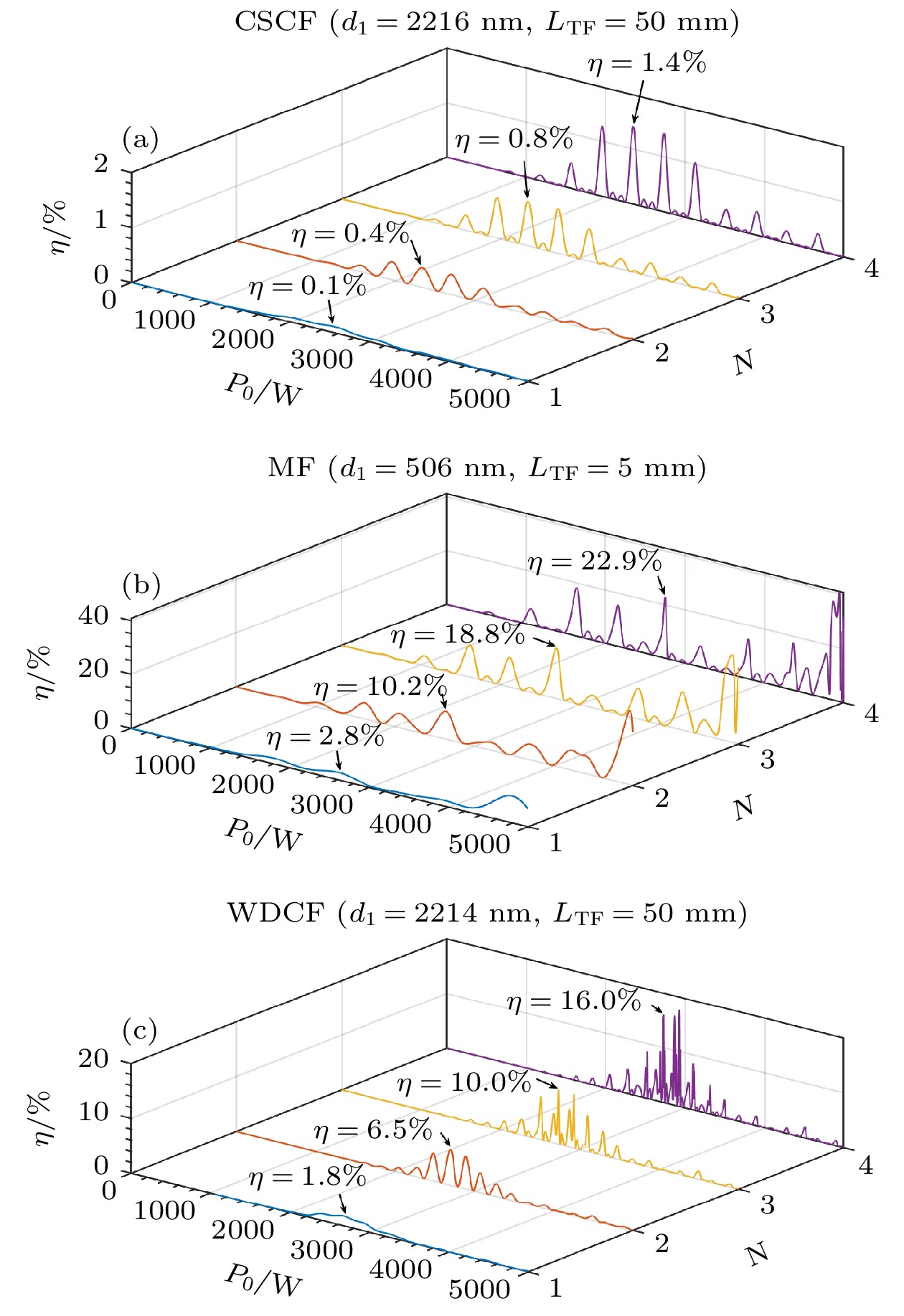
图7(a)中频率转换光纤为常规单包层光纤CSCF. 当
$ N=1 $ (即使用单根光纤)时, 最高的转换效率为$ \eta ={\eta }_{0}=0.1{\text{%}} $ ; 当$ N=2, 3, {\mathrm{ }}4 $ 时, 在0—5000 W的泵浦功率范围内, 3条转换效率曲线均出现11个主极大, 而且取得相应主极大的入射泵浦功率P0基本一致. 在3条曲线上取$ {P}_{0}\approx 2350\;{\mathrm{W}} $ 的主极大进行比较, 依次有$ \eta =0.4{\text{%}}, 0.8{\text{%}}, 1.4{\text{%}} $ , 该规律基本符合(9)式的预期, 即$ \eta \approx {{N}^{2}\cdot \eta }_{0} $ . 图7(b)所示为微纳光纤MF的情况, 级联单元数$ N=1, 2, 3, {\mathrm{ }}4 $ 时, 在$ {P}_{0}\approx 2700\;{\mathrm{W}} $ 处依次有$ \eta =2.8{\text{%}}, 10.2{\text{%}}, 18.8{\text{%}}, 22.9{\text{%}} $ ; 图7(c)为双包层光纤WDCF的情况, 级联单元数$ N=1, 2, 3, {\mathrm{ }}4 $ 时, 在$ {P}_{0}\approx 2700\;{\mathrm{W}} $ 处则有$ \eta =1.8{\text{%}}, 6.5{\text{%}}, 10.0{\text{%}}, 16.0{\text{%}} $ . 需要注意的是, 级联干涉的理论模型是在三次谐波较弱的情况下得出的, 若转换效率较高, 随着三次谐波信号增强, 该近似模型与实际的偏差会变大, 所以在图7(b), (c)中, 当$ {P}_{0} $ 较大(如超过4000 W)及级联单元数较多(如$ N=4 $ )时, 转换效率的主极大峰会变得尖锐甚至发生分裂, 图线规律性不稳定, 转换效率随N的增长也趋于饱和. -
表2归纳了三种光纤的机械强度、直径误差宽容度与转换效率. CSCF和WDCF满足相位匹配条件的纤芯直径均大于2 μm, 具有固态包层, 并可在包层外再加保护性涂覆层, 机械性能与标准光纤相近. 微纳光纤MF的纤芯直径仅约0.5 μm, 且包层为空气, 所以光纤结构脆弱, 机械性能较差. 不过, 得益于高的非线性重叠积分J3值, MF可以实现的三次谐波转换效率最高, 即使考虑纤芯直径的随机波动(σ = 0.3 nm), 采用一段5 mm长的转换光纤效率可达2%以上, 将四段这样的光纤级联, 效率则有望超过20%. 但MF对制备精度要求严苛, 即使光纤长度仅为5 mm, 纤芯直径误差宽容度也仅有±0.3 nm. WDCF的转换效率介于CSCF与MF之间, 采用一段50 mm长的光纤可接近2%, 四段进行级联时达16%. WDCF的纤芯直径误差宽容度为±3 nm, 分别是CSCF的3倍、MF的10倍. 因此, WDCF在一定程度上融合了常规单包层光纤和微纳光纤的优势, 具有较高的实际可行性.
-
纤芯与包层的折射率关系决定了基频波与三次谐波可否实现相位匹配. 分析表明, 光纤的数值孔径NA需达到一定阈值, 且NA较大时可满足相位匹配的三次谐波模式较多. 不过, 采用较大NA时, 光纤也可能支持多个基频模式. 本文中微纳光纤MF的NA为1.05, 纤芯直径约为500 nm, 可支持1064 nm的基频波单模传输. 而对于
$ {\rm NA} =0.58 $ 的CSCF光纤, 其纤芯直径约为2200 nm时还将支持TM01, TE01和HE21三种基频高阶模, 从而使参与三次谐波转换的基模HE11的功率效率降低. 在光纤设计中如何平衡这对矛盾需要进一步的研究. 另外, 根据(6)式, 转换效率与纤芯的非线性折射率系数$ {n}^{\left(2\right)} $ 成正相关, 本文讨论的三种光纤的纤芯材料均为$ {n}^{\left(2\right)} $ 较小的纯二氧化硅, 可尝试采用具有高非线性的玻璃材料设计制备光纤, 以改善光纤的综合特性.文中设计的三种光纤的实际泵浦条件可通过实验进一步确定. 文献[22]采用波长为1091 nm、脉宽为2.3 ns的MOPA泵浦直径约为520 nm、长度为8 mm的二氧化硅微纳光纤, 实验上获得了紫外波段的窄带三次谐波输出, 在峰值泵浦功率超过2600 W(对应的平均功率为1.2 W)时未观察到光纤损伤及受激拉曼散射等其他非线性频谱展宽过程. 本文采用波长相近但更常见的1064 nm作为基频, 进行三种频率转换光纤的设计, 根据理论结果, 它们在峰值泵浦功率约2700 W附近工作效果较佳, 对脉宽为ns的脉冲激光, 所需的平均泵浦功率大约在1 W量级. 微纳光纤MF的直径约为500 nm, 长度为5 mm, 预计在该功率水平仍可安全工作在窄带区, 而CSCF和WDCF的纤芯直径均大于2 μm, 应可承受更高的泵浦功率, 相关的实验研究将在后续开展.
本文的微纳光纤MF可通过熔融拉锥法由标准光纤拉制而成[19], 从标准光纤到微纳光纤腰区的过渡段为锥形光纤, 而两端保留的标准光纤可用作尾纤与其他光纤连接. 若窄带泵浦光在直径相对均匀的腰区实现相位匹配, 将产生窄带的三次谐波输出; 若泵浦光的光谱较宽, 其包含的不同波长则可在过渡区实现相位匹配, 从而产生具有一定带宽的三次谐波. 在构建光纤级联系统时, 可通过熔接将带有尾纤的各段转换光纤连接起来, 也可先获得直径较大的预光纤, 然后在商用的光纤拉锥设备上周期性地形成具有设定直径的较细的转换光纤段, 而原直径的预光纤段用作传导光纤. 当传导光纤的长度、直径等参数不同时, 三次谐波转换效率随着泵浦光功率的变化也会略有不同(如相邻峰值间隔发生改变), 但不影响级联系统的总体输出特征.
-
本文研究了三种具有简单结构的阶跃型光纤从近红外到紫外波段的三次谐波转换, 即高数值孔径单包层光纤CSCF和MF, 以及双包层光纤WDCF. 三种光纤均采用纯二氧化硅玻璃作为纤芯材料, 以便有较好的紫外透过特性, 纤芯直径则根据基频波与三次谐波的相位匹配条件确定. CSCF和WDCF均具有固态包层, 且纤芯直径可大于2 μm, 机械性能良好. MF的纤芯直径不到1 μm, 且包层为空气, 所以光纤结构脆弱, 机械性能较差. 文中通过数值模拟分析了三种光纤的谐波转换效率, 结果表明, MF光纤可以实现的转换效率最高, 采用一段MF效率可以达到2%以上, 通过光纤级联则有望超过20%, 但MF对制备精度要求严苛, 纤芯直径误差宽容度仅有±0.3 nm. CSCF的转换效率最低, 单段的效率为0.1%, 级联后约为1%的水平, 直径误差宽容度为±1 nm. WDCF的转换效率介于CSCF与MF之间, 采用一段50 mm长的光纤时接近2%, 四段级联后约为16%. WDCF的纤芯直径误差宽容度为±3 nm, 分别是CSCF的3倍和MF的10倍. 双包层光纤WDCF在一定程度上融合了常规单包层光纤CSCF和微纳光纤MF的优势, 兼备机械性能和转换效率, 并具有较低的制备难度, 为紫外波段的全光纤三次谐波转换提供了一种具有实际可行性的选择方案. 本文的结论是基于理论分析和数值模拟得出的, 后续将进一步开展相关的实验验证工作.
基于简单结构光纤的紫外波段三次谐波转换
Third-harmonic generation in ultraviolet band with simply-structured optical fibers
-
摘要: 全光纤频率转换技术具有重要的科学和现实意义, 设计兼备机械性能和转换效率的特种光纤, 并降低其制备难度, 是该技术实用化面临的关键挑战. 本文设计了具有简单结构的高数值孔径常规单包层光纤(conventional single-cladding fiber, CSCF)、微纳光纤(microfiber, MF)及W型双包层光纤(W-type double-cladding fiber, WDCF), 并通过理论分析和数值模拟比较了这三种光纤从红外到紫外波段的三次谐波转换特性. 采用1064 nm泵浦波长作设计, 谐波输出波长为355 nm. 研究结果表明, CSCF和WDCF均具有固态包层, 且纤芯直径可大于2 μm, 机械性能良好; MF光纤可以实现的转换效率最高, 但光纤结构脆弱, 机械性能较差, 且对制备精度要求严苛. WDCF融合了CSCF和MF的优势, 单段光纤的转换效率接近2%, 四段级联后约为16%, 纤芯直径误差宽容度为±3 nm, 分别是CSCF的3倍和MF的10倍, 制备难度较低, 为紫外波段的全光纤三次谐波转换提供了一种具有实际可行性的选择方案.Abstract:
Ultraviolet fiber lasers are highly desired in different fields such as lithography, laser processing, optical communications, optical storage, and biomedicine. On the other hand, all-fiber frequency conversion technology is of great significance in scientific research and practical applications, as it provides an alternative to the current solutions based on nonlinear crystals. Developing special optical fibers with both suitable mechanical performance and conversion efficiency and reducing the difficulty in their preparing are the key challenges in bringing this novel technology into practical application. In this work, three step-index optical fibers with simple structure are designed, they being a conventional single-cladding fiber (CSCF) with high numerical aperture, a microfiber (MF), and a W-type double-cladding fiber (WDCF), and the third-harmonic generation in ultraviolet band is studied by using them, respectively. The fundamental (pump) wavelength used in this work is 1064 nm and the third-harmonic wavelength is 355 nm. In order to achieve good transmission in the ultraviolet band, the cores of all three optical fibers are designed to be made of pure silica glass, and the core diameters are determined according to the phase matching condition for the fundamental wave and the third harmonic, by solving the eigenvalue equations. The cladding of CSCF is fluorine-doped silica glass, and the cladding of MF is air; for WDCF, the inner cladding and outer cladding are fluorine-doped silica glass and fluoroplastics, respectively. Both the CSCF and the WDCF have solid cladding, and their core diameters can be greater than 2 μm, so they have adequate mechanical properties. In comparison, due to the air cladding and thin core (the core diameter has to be less than 1 μm for phase matching), the MF is fragile in structure and thus its mechanical performance is rather poor. The conversion efficiencies of these three fibers are investigated in detail, by solving numerically the coupled mode equations for the pump and the third harmonic with the Runge-Kutta method. The effect of random fiber roughness (i.e. core diameter fluctuation) and enhancement in conversion efficiency by cascading the fibers are also analyzed. The results show that the conversion efficiency in MF is the highest, with an efficiency of 2% for a 5-mm-long single MF segment and over 20% for cascaded MFs; however, MF requires strict fabrication accuracy, and the tolerance of core diameter is only ± 0.3 nm. The CSCF has the lowest conversion efficiency, which is 0.1% for a 50-mm-long single segment and at the level of about 1% after cascading, and the tolerance of core diameter is ± 1 nm. The conversion efficiency of WDCF is between those of CSCF and MF, nearly 2% with a 50-mm-long segment and about 16% when four such segments are cascaded; WDCF bears core diameter tolerance of ± 3 nm, which is three times that of CSCF and 10 times that of MF. Therefore, the W-type double-cladding fiber WDCF actually integrates the advantages of conventional single-cladding fiber CSCF and microfiber MF, showing both satisfactory mechanical performance and conversion efficiency, as well as reduced fabrication difficulty, which provides a promising solution for all-fiber third-harmonic generation in the ultraviolet band. -

-
图 2 光纤折射率示意图 (a)单包层光纤的横截面; (b)单包层光纤折射率随半径的分布; (c) W型双包层光纤的横截面; (d) W型双包层光纤折射率随半径的分布
Figure 2. Refractive index diagram of optical fiber: (a) Cross-section of single-cladding fiber; (b) refractive index distribution in radius of single-cladding fiber; (c) cross-section of W-type double-cladding fiber; (d) refractive index distribution in radius of W-type double-cladding fiber.
图 3 基频波和三次谐波不同模式的有效折射率
$ {n}^{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ 与纤芯直径$ {d}_{1} $ 的关系 (a)常规单包层光纤CSCF; (b)微纳光纤MF; (c)双包层光纤WDCF, 基频波长$ {\lambda }_{1}=1064\;{\mathrm{n}}{\mathrm{m}} $ Figure 3. Dependence of effective refractive index
$ {n}^{{\mathrm{e}}{\mathrm{f}}{\mathrm{f}}} $ of the fundamental wave and the third harmonic on core diameter d1: (a) CSCF; (b) MF; (c) WDCF. The fundamental wavelength is$ {\lambda }_{1}=1064\;{\mathrm{n}}{\mathrm{m}} $ .图 6 纤芯直径不同时总相位失配量
$ {\delta \beta }_{\rm t} $ 随泵浦光功率P0的变化 (a)常规单包层光纤CSCF, 长度为50 mm, 纤芯直径分别为$ {d}_{1}=2217,\; 2216, \;2215\;{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ ; (b)微纳光纤MF, 长度为5 mm, 纤芯直径分别为$ {d}_{1}=506.3, \;506, \;505.7\;{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ ; (c)双包层光纤WDCF, 长度为50 mm, 纤芯直径分别为$ {d}_{1}= $ $ 2217, \;2214, \;2211\;{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ Figure 6. Total mismatch in propagation constant
$ {\delta \beta }_{\rm t} $ versus input pump power P0 for different core diameters: (a) CSCF in 50 mm length, core diameters are$ {d}_{1}=2217,\; 2216, $ $ 2215\;{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ ; (b) MF in 5 mm length, core diameters are$ {d}_{1}=506.3, $ $ 506, \;505.7\;{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ ; (c) WDCF in 50 mm length, core diameters are$ {d}_{1}=2217,\; 2214, \;2211{\mathrm{ }}{\mathrm{ }}{\mathrm{ }}\;{\mathrm{ }}{\mathrm{n}}{\mathrm{m}} $ .图 7 级联单元数N不同时三次谐波转换效率
$ \eta $ 随泵浦光功率P0的变化 (a)转换光纤为常规单包层光纤CSCF, 长度LTF = 50 mm; (b)转换光纤为微纳光纤MF, 长度LTF = 5 mm; (c)转换光纤为双包层光纤WDCF, 长度LTF = 50 mm. 泵浦光波长$ {\lambda }_{1}=1064\;{\mathrm{n}}{\mathrm{m}} $ , 转换光纤粗糙度σ = 0.3 nm; 传导光纤为标准阶跃型光纤(纤芯直径9 μm, 长度LGF = 20 cm)Figure 7. Third harmonic conversion efficiency versus input pump power for cascading system of different unit number N: (a) CSCF as the third-harmonic generation fiber (TF), with length LTF = 50 mm; (b) MF as the TF, with length LTF = 5 mm; (c) WDCF as the TF, with length LTF = 50 mm. The pump wavelength is
$ {\lambda }_{1}=1064\;{\mathrm{n}}{\mathrm{m}} $ , and the TFs are of roughness (σ = 0.3 nm). The guiding fibers (GFs) are standard step-index fibers (9 μm core diameter, length LGF = 20 cm).表 1 光纤的基本参数(基频波长
$ {\lambda }_{1}=1064\;{\mathrm{n}}{\mathrm{m}} $ , 三次谐波波长$ {\lambda }_{3}=355\;{\mathrm{n}}{\mathrm{m}} $ )Table 1. Basic parameters of optical fibers (fundamental wavelength
$ {\lambda }_{1} = 1064\;{\mathrm{n}}{\mathrm{m}} $ , third-harmonic wavelength$ {\lambda }_{3} = 355\;{\mathrm{n}}{\mathrm{m}} $ )基本参数 光纤类型 CSCF MF WDCF 纤芯材料 纯silica 纯silica 纯silica 内包层材料 掺氟silica 空气 掺氟silica 外包层材料 无 无 氟塑料 基频折射率[n1, n2, n3] [1.45, 1.33, —] [1.45, 1, —] [1.45, 1.33, 1.37] 三次谐波折射率[n1, n2, n3] [1.48, 1.36, —] [1.48, 1, —] [1.48, 1.36, 1.40] 基频模式 HE11(λ1) HE11(λ1) HE11(λ1) 三次谐波模式 HE13(λ3) HE12(λ3) HE13(λ3) 纤芯直径d1/nm 2217.3 506.5 2217.4 包层直径[d2, d3]/μm [125, —] [ $\infty$ , —][6, 125] 光纤长度L/mm 50 5 50 非线性重叠积分J3/μm–2 0.0092 0.7266 0.0344 基频功率损耗系数 $ {\alpha }_{1}$ /(dB·m–1)0.08 2 0.08 谐波功率损耗系数 $ {\alpha }_{3} $ /(dB·m–1)0.8 20 0.8 表 2 三种光纤的特性对比(泵浦光波长
$ {\lambda }_{1}= 1064\;{\mathrm{n}}{\mathrm{m}} $ , 光纤粗糙度σ = 0.3 nm)Table 2. Comparison of characteristics of three fibers (pump wavelength is
$ {\lambda }_{1}=1064\;{\mathrm{n}}{\mathrm{m}} $ , and the TFs are of roughness σ = 0.3 nm).特性 光纤类型 CSCF MF WDCF 机械强度 较强 弱 较强 优化的纤芯直径/nm 2216 506 2214 纤芯直径误差宽容度/nm ±1 ±0.3 ±3 $ {\eta }^{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $ (N = 1)/%0.1 2.8 1.8 $ {\eta }^{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $ (N = 4)/%1.4 22.9 16.0 -
[1] 周朴, 冷进勇, 肖虎, 马鹏飞, 许将明, 刘伟, 姚天甫, 张汉伟, 黄良金, 潘志勇 2021 中国激光 48 2000001 doi: 10.3788/CJL202148.2000001 Zhou P, Leng J Y, Xiao H, Ma P F, Xu J M, Liu W, Yao T F, Zhang H W, Huang L J, Pan Z Y 2021 Chin. J. Lasers 48 2000001 doi: 10.3788/CJL202148.2000001 [2] Lü X L, Peng Y J, Wang W Y, Zhao Y N, Zhu X Y, Leng Y X 2021 High Power Laser Sci. 9 e38 doi: 10.1017/hpl.2021.23 [3] Fu Q, Hanrahan N, Xu L, Lane S, Lin D, Jung Y, Mahajan S, Richardson D J 2021 Opt. Express 29 42485 doi: 10.1364/OE.441248 [4] Bencheikh K, Richard S, Mélin G, Krabshuis G, Gooijer F, Levenson J 2012 Opt. Lett. 37 289 doi: 10.1364/OL.37.000289 [5] Cheng T, Gao W, Liao M, Duan Z, Deng D, Matsumoto M, Misumi T, Suzuki T, Ohishi Y 2014 Opt. Lett. 39 1005 doi: 10.1364/OL.39.001005 [6] Gabriagues J 1983 Opt. Lett. 8 183 doi: 10.1364/OL.8.000183 [7] Grubsky V, Savchenko A 2005 Opt. Express 13 6798 doi: 10.1364/OPEX.13.006798 [8] Efimov A, Taylor A, Omenetto F, Knight J, Wadsworth W, Russell P 2003 Opt. Express 11 2567 doi: 10.1364/OE.11.002567 [9] 滕欢, 柴路, 王清月, 胡明列 2017 物理学报 66 044205 doi: 10.7498/aps.66.044205 Teng H, Chai L, Wang Q Y, Hu M L 2017 Acta Phys. Sin. 66 044205 doi: 10.7498/aps.66.044205 [10] Boivin M, El-Amraoui M, Ledemi Y, Morency S, Vallée R, Messaddeq Y 2014 Opt. Mater. Express 4 1740 doi: 10.1364/OME.4.001740 [11] Snyder A W, Love J D 1983 Optical Waveguide Theory (New York: Chapman and Hall) pp248–254 [12] Brunet C, Bélanger P A, Rusch L A 2016 J. Lightwave Technol. 34 3094 doi: 10.1109/JLT.2016.2561975 [13] Tsao C 1992 Optical Fibre Waveguide Analysis (New York: Oxford University Press) pp298–369 [14] Kong M, Shi B 2006 Fiber Integrated Opt. 25 305 doi: 10.1080/01468030600692859 [15] Jiang X J, Zhang D D, Lee T, Brambilla G 2018 Opt. Lett. 43 2728 doi: 10.1364/OL.43.002728 [16] Jiang X J, Chen Z N, Lee T, Brambilla G 2020 Opt. Lett. 45 3272 doi: 10.1364/OL.389998 [17] Malitson I H 1965 J. Opt. Soc. Am. 55 1205 doi: 10.1364/JOSA.55.001205 [18] Tan C Z 1998 J. Non-Cryst. Solids 223 158 doi: 10.1016/S0022-3093(97)00438-9 [19] Lee T, Jung Y, Codemard C, Ding M, Broderick N, Brambilla G 2012 Opt. Express 20 8503 doi: 10.1364/OE.20.008503 [20] Refractive Index Database https://refractiveindex.info/ [2025-1-25] [21] Agrawal G P 2019 Nonlinear Fiber Optics (London: Academic) pp476,477 [22] Jiang X J, Lee T, Chen M M, Sun Q, He J, Brambilla G 2019 Opt. Lett. 44 4191 doi: 10.1364/OL.44.004191 -


 首页
首页 登录
登录 注册
注册




 下载:
下载: