热电制冷器(thermometric cooler, TEC)广泛应用于精密光学^[1,2]、半导体激光器^[3,4]、光电测量^[5,6]等高技术领域, 其温度控制精度直接影响系统的性能. 特别是在半导体单频激光器^[7,8]、光学频率梳^[9]等应用中, 由于半导体辐射光谱^[10]以及光学材料折射率^[11]对温度敏感, TEC温控精度通常要求达到毫开尔文(简记为mK)量级, 这对控制算法的稳定性、实时性和抗干扰能力提出了极高要求. 高精度温控的前提是维持热源功率的稳定性, 在此基础上, 提高温控系统对环境变化的适应能力, 是TEC高精度温控技术面临的关键问题.

传统TEC温控系统主要采用比例-积分-微分(proportional integral derivative, PID)控制算法, 其计算简单、易于实现, 在工业温控系统中得到了广泛应用. 然而, 在需要达到mK级别的精密温控场景下, 传统PID控制策略固有的适应性不足便成为主要障碍, 使其难以满足苛刻的应用需求^[12]. 具体而言, 一方面, 由于TEC的冷却/加热特性受材料参数、环境温度和驱动电流等多种因素影响, 表现出显著的非线性特性, 这使得一组针对特定工况优化的固定PID参数难以适应不同的工作状况, 在工况变化时可能导致控制性能恶化, 表现为响应滞后、容易振荡, 最终使得控制精度下降, 暴露了其参数对工况的依赖性与缺乏自适应调整能力的问题. 另一方面, 其积分环节在追求mK级精度时面临着固有矛盾: 积分作用对于消除稳态误差、确保系统最终能精确稳定在目标值是不可或缺的, 但合适的积分增益极难选取. 若增益设置过低, 误差修正缓慢, 系统可能因热惯性或环境扰动变化而无法快速、精确地维持在目标设定点, 导致精度不达标; 若增益设置过高以保证稳态精度, 则会增加系统在目标点附近振荡的风险, 而且在控制器输出因大幅环境扰动或工况改变而饱和时, 将极易引发严重的积分饱和, 导致后续过程产生显著的超调和恢复时间. 这种控制器参数固定、积分行为模式单一的局限性, 构成了传统PID在mK级高精度、高稳定性温控应用中的主要瓶颈.

为克服传统PID控制的局限性, 学者提出了基于数学模型的预测控制^[13]、基于机器学习^[14]的智能温控, 以及基于专家系统^[15]的自适应温控等改进方法. 然而, 这些方法在高精度温控应用中仍然存在适应性问题. 预测控制依赖设定的数学模型来优化控制输入, 其控制精度受预测模型的准确性制约^[16], 同时TEC温控系统的非线性特性及外界扰动会引入预测偏差, 从而影响控制性能. 深度神经网络^[17]等数据驱动方法具备自适应性, 但高度依赖训练数据, 泛化能力较差, 难以适应复杂动态环境. 对于模糊逻辑和专家系统的方法由于依赖预设规则, 虽然在某些特定环境下有效, 但在复杂工况下同样存在适应性不足的问题.

上述改进方法将TEC温控系统作为黑箱模型处理, 然而, 在mK级高精度控制需求下, TEC在不同工作环境下的非线性效应、热传导滞后、噪声影响等因素难以通过黑箱建模精确描述. 研究表明^[18,19], TEC器件的内部电热耦合及热传导过程可通过宏观性能参数加以描述, 同时均匀热流系统易精确建立其传热方程, 因而通过准确描述TEC散热系统的内部耦合方程, 建立的等效电路模型有望获得更高的温控精度, 在此基础上, 进一步优化控制算法策略, 对提高mK级温控系统的控制精度、适应性和抗干扰能力具有重要意义. 本文在深入分析TEC内部物理机制的基础上, 重点开展了以下三方面研究工作: 建立了TEC温控系统的高精度等效电路模型, 为后续的控制算法设计奠定基础; 提出了一种带动态直流偏置的自适应PID高精度温控算法, 提升系统在复杂工况下的温度控制性能; 创新性地引入了双路温度检测机制, 以期进一步提高系统对环境扰动的抑制能力和整体温控精度.

TEC核心结构是半导体热电单元, 其两端通过铜导流片实现电路连接, 并用平板陶瓷片进行绝缘封装. TEC通电时, 其内部的物理效应可表述为

式中, $ {Q_{\text{C}}} $和$ {Q_{\text{H}}} $分别为热电单元帕尔贴效应的制冷和发热功率, 其值和热电单元自身的塞贝克系数$ {S_{\text{m}}} $、注入电流$ I $以及半导体端面温度相关, 其中$ {T_{\text{c}}} $和$ {T_{\text{h}}} $分别为半导体材料两端温度; $ {Q_{\text{J}}} $为电流在半导体材料的等效电阻上产生的焦耳热; $ {Q_{\text{F}}} $为温差引起的傅里叶热传导效应, 其中$ {K_{\text{m}}} $为半导体材料的热导率.

由(1)式可知, TEC的外部特性仅与其内部参数和注入电流相关. TEC在非极限工作条件下, 其内部参数可以用制造商提供的标准测试数据表示为^[20]

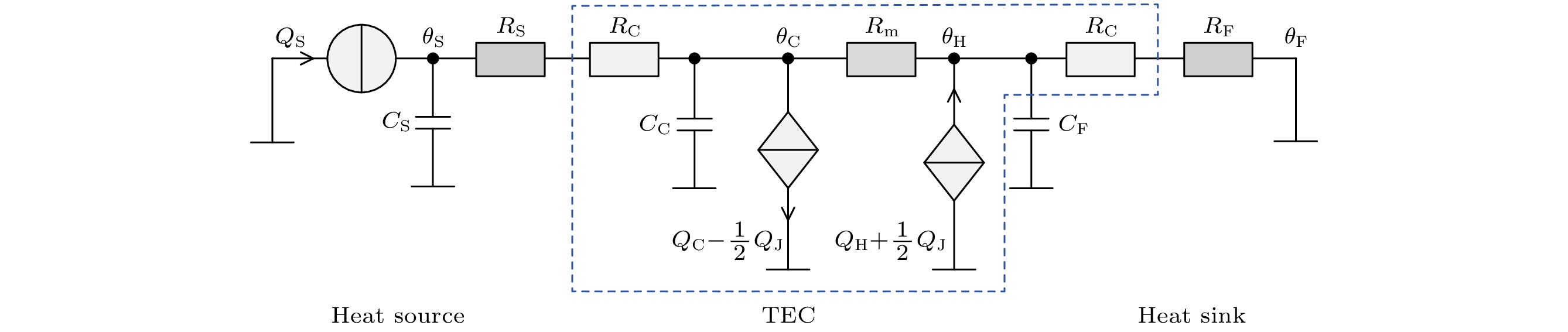
式中, $ {T_{{\text{h0}}}} $为TEC热端面温度; $ \Delta {T_{\max }} $为制冷量为零时, 最大允许输入电流$ {I_{\max }} $所对应的冷热端面的最大温差; $ {V_{\max }} $为该测试条件下对应的输入电压.

TEC温控系统结构上可简化为热源、热源热沉、TEC以及TEC热沉进行堆叠构成, 系统各模块通过传导方式实现热量传递. 忽略温控系统的 热辐射和以及与空气环境之间的自然热对流传热, 系统热量在TEC热沉端面通过水冷或风冷的强制对流形式传递给外部环境. 对于高精度温度控制研究, 其前提是热源功率稳定, 环境温度波动较小, 因而本文假设系统为一维均匀传热模式以便于采用集总等效电路模型, 通过类比传热学定律和电路理论可以建立TEC温控系统的等效电路模型如图1所示.

图1中变量$ Q $为相关热源, $ \theta $为相关节点温度, $ R $为等效热阻, $ C $为等效热容, 等效电路参考节点为环境温度. 图中虚线所围区域为TEC模块, 其下标C和m分别表示陶瓷片和半导体热电单元模块. 为简化后期数值分析复杂度, 等效电路模型做了如下简化: 1)对比热传导和热对流传热公式, 可将散热器端面的热交换系数折合成串联热阻; 2)尽管温控系统等效电路模型为高阶动态系统, 然而模型中无等效电感元件, 动态系统整体表现为过阻尼特性, 等效电路可忽略数值偏低的TEC导流片部件的电容和热阻效应; 3) TEC热端部分等效热容相对于TEC热沉热容很低, 也不予考虑; 4)同一元件的等效电容和等效电阻在电路模型中接入顺序不同, 以减少所需计算节点数量.

选用和文献[21]报道的相同的TEC元件, 其性能参数包括最大制冷量为80 W, 最大温差为72 K, 极限测试时所对应伏安值分别为17.5 V和8.5 A, 根据(2)式可计算出该TEC工作时的实际电阻值以及材料属性. 散热系统为简单的堆叠结构, 所有元件设置为具有相同的截面形状. 对于TEC非均匀散热问题, 文献[21]进行了详细研究, 该问题可通过调整等效热阻转化为均匀散热模式, 因而本文仅考虑一维均匀散热, 便于通过器件几何结构和材料属性计算其等效电阻和电容. 计算结果如表1所列, 其中陶瓷层的热导率为估计值, 其等效电容为集总参数估计值.

图1中各节点温度满足时域微分方程如下:

方程求解需要各节点温度设置初始值, 在TEC输入特定电流时, 根据(1)式可计算出等效受控电流源的输出. 当热源功率确定后, 上述微分方程组在Python环境下可通过半隐式欧拉法获得精度很高的时域数值解, 本文中计算的迭代步长设置为0.5 ms.

等效电路模型验证采用和TEC制造商相同的测试环境, 将图1中参考温度固定为323 K, 同时减小TEC两端热沉等效热阻. 考虑到温度探头的取样位置, 模拟中取$ {\theta _{\text{H}}} $和$ {\theta _{\text{F}}} $的均值作为热端温度, 同理取$ {\theta _{\text{S}}} $和$ {\theta _{\text{C}}} $的均值作为冷端温度. 热源功率设置范围从0至20 W, 在电路进入稳态后, 获取TEC冷热端温度数据绘制曲线如图2所示. 经过对比, 我们的拟合曲线和制造商测试数据基本一致, 反映出等效电路模型具有极高的可靠性.

一般地, 随着TEC制冷电流增加, 其冷热端温差会增大, 但是TEC内部的焦耳热量以及温差引起的热传导损耗都会随之增大, 进而使得TEC冷端净制冷量减小, 表现为TEC温差曲线的斜率下降. 当热源功率为零时, 在最大制冷电流作用下, 模型计算获得TEC最大温差为71.23 K, 与制造商提供的最大温差数据72 K非常接近. 此外, 在相同制冷电流下, 图2各条曲线中的温差数据与热源功率呈线性关系, 这和实际环境的测试结论一致, 也间接证明了等效电路模型的可靠性. 当热源功率为20 W时, TEC两端最大温差为54.96 K, 根据温差与热源的线性关系, 可以推算出在热源功率为80 W, 最大温差为6.13 K, 这和制造商提供的最大制冷量数据略有出入. 具体原因是该测试条件为极限测试, 模型参数会表现出更多的非线性特性, 同时我们取样冷热端温度的方法和制造商存在一定差异, 导致计算结果和制造商数据略有差异.

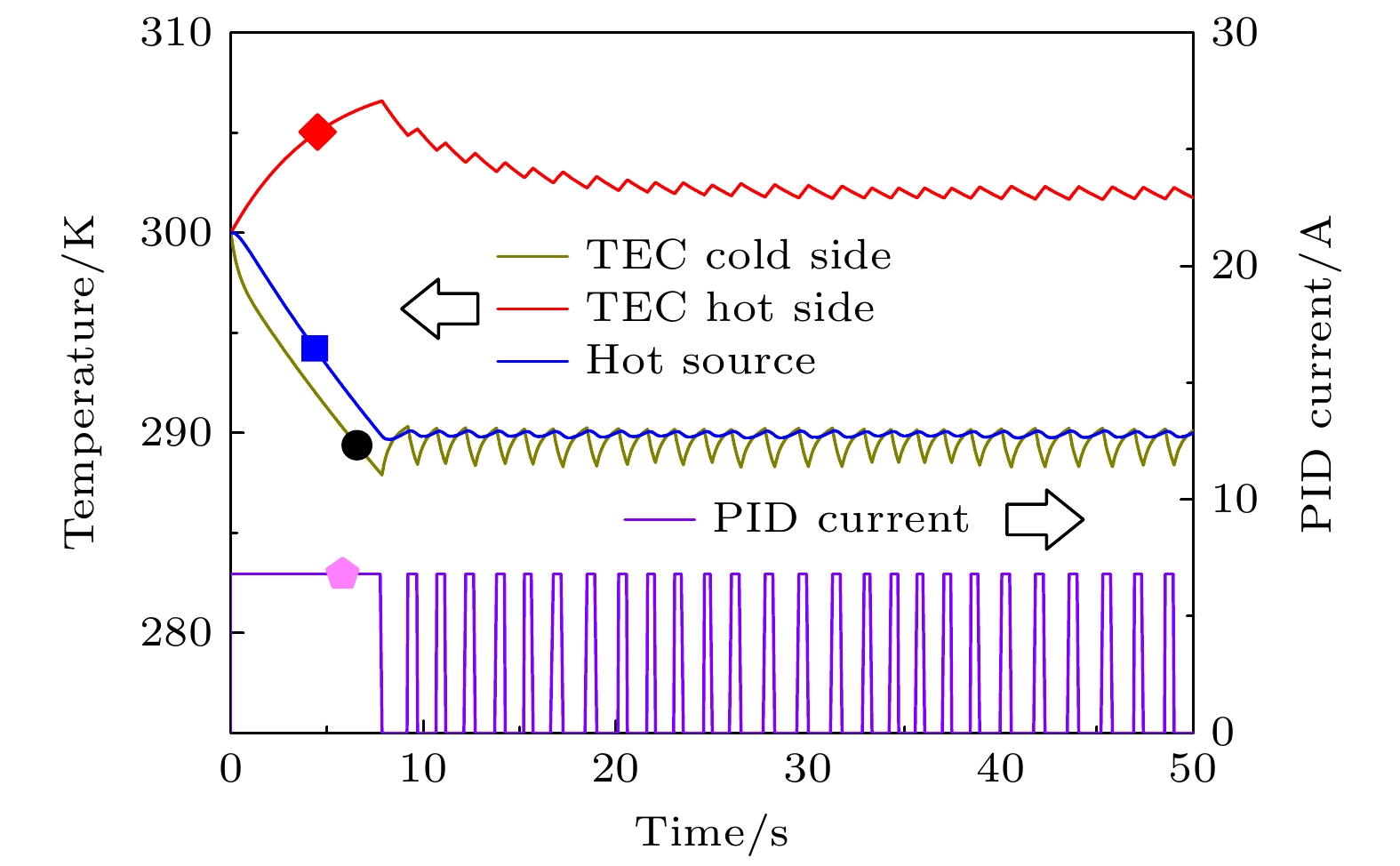
利用等效电路模型可动态分析传统PID的温控过程, 其中PID参数设置采用临界比例度法(Ziegler-Nichols). 热源功率设置为10 W, 环境温度为300 K, 散热系统初始温度和环境温度保持一致, 温控目标温度为290 K, 模拟温度传感器分别获取(3)式中各节点温度. 在实际应用中TEC不宜满负荷运作, PID设置输出电流限制为TEC最大电流的80%, 且为单向制冷模式, 即PID电流为负值时, 其输出值为零. 为保证仿真结果的可靠性, 各温度传感器设置采样精度为1 mK, 响应延迟时间为0.1 s, 具有0.5 s的低通滤波功能. 同时考虑到温控系统中也存在时间延迟和性能限制, 我们将PID算法执行频率设置为20 Hz. 除非特别说明, 后续仿真均采用相同设置.

图3各曲线反映了典型的PID温控时域过程. 在初始阶段, 由于热源当前温度与目标温度之间存在较大误差, PID为饱和输出值. TEC在PID驱动电流作用下, 其冷热端温度快速变化, 带动热源朝目标温度靠近. 当热源温度首次超过设置目标温度后, PID输出为零, 此时TEC冷端温度更低, 热源温度会继续下降. 在缺少制冷电流时, TEC冷热端之间的热传导会使冷端温度上升, 当冷端温度超过热源温度时, 热源温度也开始回升. 在热源温度高于设置值以后, PID再次输出制冷电流, 实现温度控制. 由于散热系统各模块存在较大的热容效应, 使得热源温度和TEC冷端温度曲线拐点存在明显的滞后性, 导致温控误差较大. 从图3可以看出传统PID参数易产生近似为矩形脉冲的PID饱和输出, TEC冷热端温度曲线表现为典型的RC一阶电路时变特性, 温控曲线超调量过大, 控制精度难以提高.

对于半导体单频激光器等高精度温控应用场景, 由于具有时滞特性的温度探头通常检测的是热沉温度, 因而高精度温控的前提是保持热源功率稳定, 即温控系统面临的主要问题是环境温度扰动导致的温度波动. 图3振荡曲线分析表明, 在温度达到目标温度以后, 若PID输出振荡幅度减小, 则目标温控精度会显著提高. 基于此, 我们提出了带动态直流偏置的自适应PID高精度温控技术方案.

温控系统整体方案如图4所示, 算法在具体实施中需要硬件模块记录最近数秒时段的温度检测数据和温控电流输出数据. 方案采用两套可相互转换的控制技术以保证温控系统的实时性与可靠性, 其中成熟稳定的传统PID温控实现快速粗调功能, 当检测到目标温度在设置值附近超调振荡时, 系统转换为高精度温控模式. 相应地, 如果热源功率以及温控目标温度变更等因素导致系统出现较大误差时, 系统自动转为传统PID模式. 高精度温控算法如(4)式所示:

式中, $ {I_{{\text{Out}}}}(t) $表示总的温控电流输出; $ k(t) $为两部分的权重因子, 其值和当前2 s内的绝对误差相关. $ {I_{{\text{PID}}}}(t) $为粗调时的PID分量, 其最终对输出的贡献由权重 $ \left[ {1 - k(t)} \right] $动态调整, 当系统趋于稳定时该权重减小, 有助于抑制过冲和振荡. $ {I_{{\text{Bias}}}}(t) $为动态直流偏置部分, 由(5)式描述:

式中, $ {I_{{\text{Avg5 s}}}}(t) $为近5 s内输出电流的均值; $ \beta $为直流偏置修正系数; $ {e_{{\rm{5\;s}}}}(t) $为近5 s内温控误差的均值; 表达式中第二项具有误差积分功效, 可调整动态直流偏置因子$ {I_{{\mathrm{Bias}}}}(t) $逼近当前工况下的理想稳态值.

为进一步阐明该自适应PID算法在高精度温控阶段的具体运作流程, 其核心实现步骤概述如下, 该流程在控制器每个计算周期(例如, 本仿真中为50 ms)内迭代执行:

1)判断控制模式: 首先检查是否满足从初始“快速粗调阶段”切换到“高精度自适应调节阶段”的条件. 该切换通常基于对系统状态的判断, 例如, 当检测到被控温度误差$ e(t) $穿过零点的累计次数达到预设值(如4次), 表明系统已趋于目标值附近并开始稳定或振荡时, 则启动高精度模式. 若未满足条件, 则继续执行粗调阶段的PID逻辑.

2)高精度模式计算循环: 一旦进入高精度模式, 则执行以下步骤.

① 数据获取与误差计算. 读取当前热源温度$ {\theta _{\text{S}}}(t) $, 计算与目标值$ {\theta _{{\text{Set}}}}(t) $的误差$ e(t) = {\theta _{\text{S}}}(t) - {\theta _{{\text{Set}}}}(t) $.

② 统计量计算. 更新历史数据缓冲区(误差、输出电流等), 并计算所需统计量, 主要包括: 用于计算$ {I_{{\text{Bias}}}}(t) $的近5 s平均误差$ {e_{\rm 5\; s}}(t) $和近5 s平均输出电流$ {I_{{\text{Avg5 s}}}}(t) $; 以及用于计算权重$ k(t) $的近2 s平均绝对误差$ {\left| e \right|_{{\text{Avg2 s}}}}(t) $.

③ 动态偏置项计算($ {I_{{\text{Bias}}}}(t) $). 根据(5)式计算, 此项结合了对稳态基准电流的估计和对残留稳态误差的慢积分校正(校正强度由系数$ \beta $(单位A/K)决定, 需结合具体负荷或和$ {I_{{\text{Avg5 s}}}}(t) $关联, 如0.1 A/K量级).

④ PID分量计算($ {I_{{\text{PID}}}}(t) $). 采用与初始粗调阶段相同的PID参数, 计算标准PID控制分量:

式中, $ {K_{\text{p}}} $为比例增益, $ {K_{\text{i}}} $为积分增益, $ {K_{\text{d}}} $为微分增益.

⑤ 自适应权重计算($ k(t) $). 根据近2 s平均绝对误差$ {\left| e \right|_{{\text{Avg2 s}}}}(t) $动态计算权重因子$ k(t) $$ (0 \leqslant k(t) \leqslant 1) $. $ k(t) $的计算函数确保误差大时$ k(t) \approx 0 $, 误差小时$ k(t) \approx 1 $.

⑥ 基础输出合成($ {I_{{\text{Out}}}}(t) $). 按照(4)式, 将PID分量和动态偏置分量加权组合.

⑦ 叠加双路补偿: (如果启用)将热端温度的补偿项$ {I_{{\text{Comp}}}}(t) $叠加到$ {I_{{\text{Out}}}}(t) $上($ {I_{{\text{Comp}}}}(t) $的计算细节见第3.3节最后部分).

⑧ 输出处理与执行. 对合成后的信号进行饱和限幅和单向制冷约束处理, 得到最终输出$ {I_{{\text{Tec}}}}(t) $并发送给TEC驱动单元.

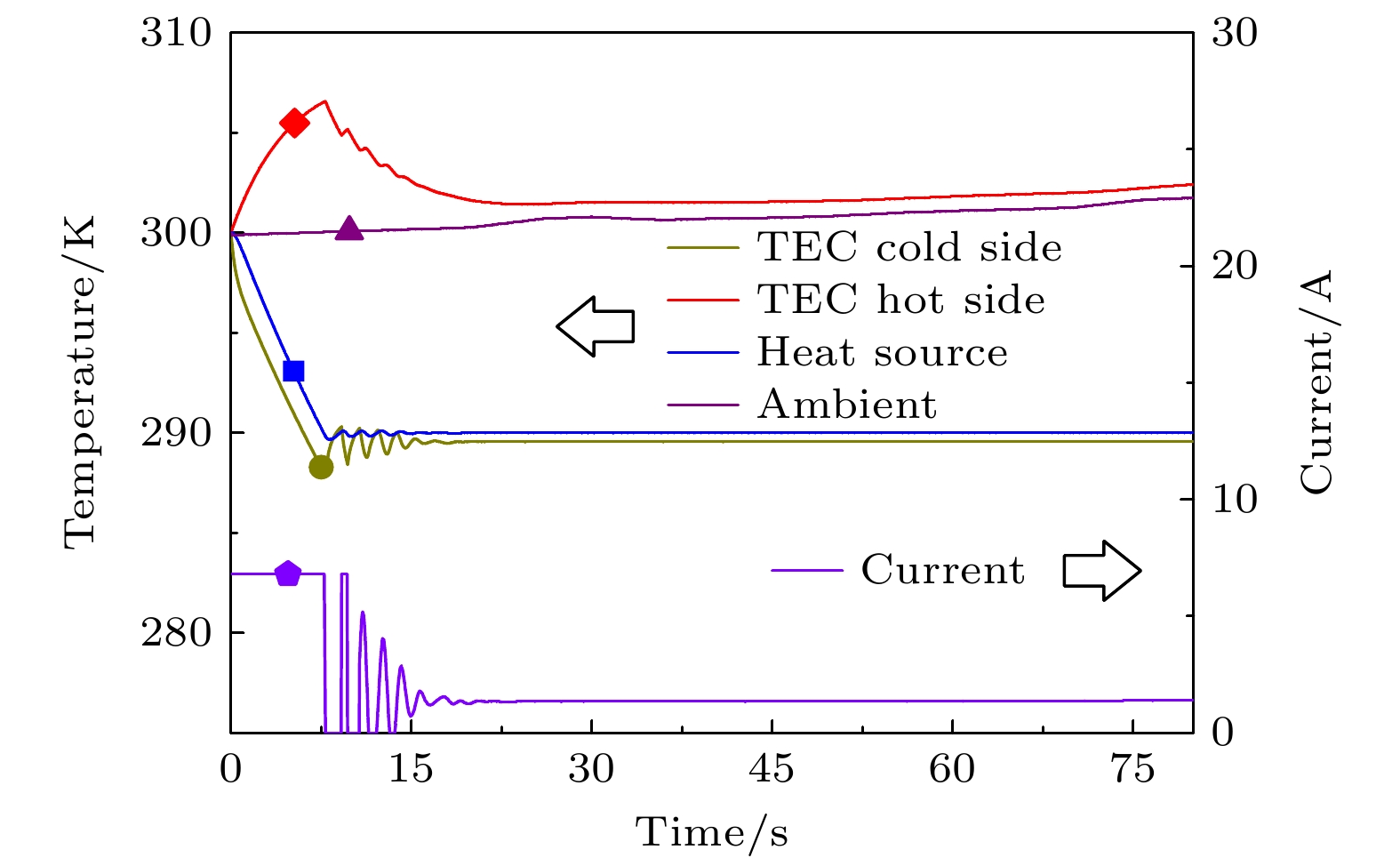
上述算法步骤构成了自适应PID高精度温度控制的核心机制. 该机制依据实时误差水平, 通过自适应权重因子$ k(t) $, 动态地结合了标准PID控制器分量$ {I_{{\text{PID}}}}(t) $的快速响应特性和动态直流偏置项$ {I_{{\text{Bias}}}}(t) $的稳态维持能力. 具体而言, 权重因子$ k(t) $使得控制器在误差较大时侧重$ {I_{{\text{PID}}}}(t) $的作用以快速收敛, 而在误差较小时则侧重$ {I_{{\text{Bias}}}}(t) $的作用以实现精确稳定. 动态偏置项$ {I_{{\text{Bias}}}}(t) $通过平均近期输出电流获得基准值, 并通过平均近期误差进行缓慢积分校正, 以此在避免积分饱和的同时消除稳态误差. 这种结构使得控制器能在不同阶段侧重不同的控制作用, 从而在保证动态响应速度的同时, 有效地提高稳态控制精度并抑制振荡.

图5为带动态直流偏置的自适应PID高精度温控的典型时域仿真图. 为保证仿真算法的适用性, 我们在传统PID测试基础上引入了环境温度扰动变化, 扰动因子由两部分叠加组成, 其一是周期为6 s, 间隔为10 s, 振幅为0.2 K的瞬时随机变量, 以检验系统对随机扰动的抑制能力; 其二是设置环境温度随时间持续增大, 以检验系统对环境温度缓变的适应能力. 图5中温控曲线前10 s的变化趋势和图3基本一致, 为传统PID控制下的快速降温过程. 当热源实际温度在设置目标附近振荡时, 算法自动切换为高精度温控模式, 由于直流偏置量和PID之间的权重与2 s内的绝对误差相关, 导致PID部分的作用不断减小, 输出制冷电流表现为阻尼振荡曲线, 并且很快收敛为缓变量. 尽管时域上环境温度和TEC热端温度变化明显, 热源温度和TEC冷端面温度在20 s后收敛为近似常数, 反映出本算法在实现高精度温度控制时, 对环境扰动也具有很好的抗干扰能力.

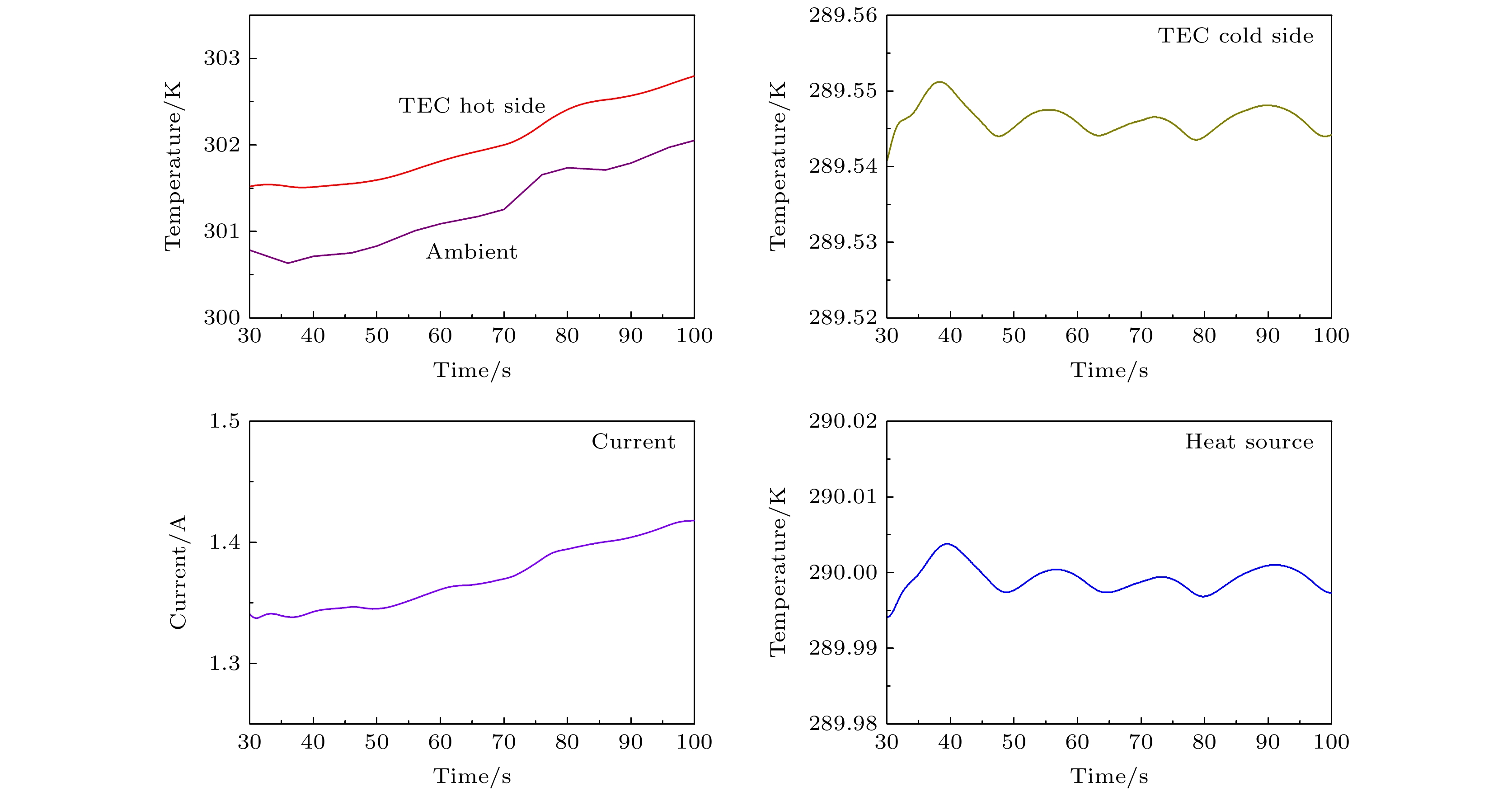
图6为图5中各时域曲线的局域放大图, 其中时间设置为30—100 s, 有利于观察温控稳定时的曲线细微变化. 在该时段中, 叠加瞬时随机扰动的环境温度增加了约1.3 K, 采用自适应PID算法(包含动态直流偏置)的温控系统输出电流也逐步增大以保持目标温度的稳定. 受高精度算法中PID部分影响, TEC冷端和热源温度也做振荡变化, 但是超调量被压缩到mK量级, 实现了高精度温度控制要求.

此外, 由于动态直流偏置中已经包含积分因子, 我们发现, $ {I_{{\text{PID}}}} $中的积分和微分因子, 对算法精度几乎没有影响, 在此基础上设置偏大的比例增益因子对整体温控精度具有更好的效果. 同时算法中传统PID温控部分, 其作用是使粗调阶段的温控曲线快速逼近目标值, 因而可以将其PID参数中的比例增益因子设置为远远大于临界比例度法的推荐值. 传统温控算法要获得高精度控制, 对后期参数调整要求较高, 而我们的算法在保留PID简洁高效的控制逻辑外, 对PID参数设置的鲁棒性较强, 有利于在各种不同场景快速实现高精度温度控制.

本文采用温控误差的标准差和最大偏差来评价高精度温控算法的效果. 由于本算法设置的动态直流偏置量为近5 s输出电流的均值和温控误差均值的叠加, 算法能很好地解决缓慢变化的环境温度扰动. 对于该类扰动, 算法仿真通常获得的标准差小于1 mK, 最大偏差约为2 mK. 基于电路模型的温控系统对误差始终为滞后补偿响应, 对于环境温度的瞬时扰动, 其引起的误差必然和扰动幅度相关. 基于此, 我们分析了环境温度瞬时扰动幅度对高精度温控的影响, 如表2中单路温度检测部分所示, 由于扰动量为随机值, 表中数据为多次仿真结果的均值.

表2数据表明, 采用带动态直流偏置的高精度温控算法可以有效地抑制环境温度的瞬时扰动, 从温控误差的标准差参数来看, 算法对环境扰动的振荡幅度近似衰减–40 db. 表2中数据变化趋势表明减小环境温度的瞬时扰动是提高温控精度的有效辅助手段, 基于此, 在实际工程应用中, 进一步提高温控精度的技术途径可以有以下两类: 1)采用两级温控系统, 前级将温控误差控制在0.1 K, 可显著地提高后级温控精度, 辛文辉等^[22]实验研究了半导体激光器的两级PID温控, 获得了和我们算法相似结论, 当外环控制精度为0.5 K时, 内环获得了10 mK的控制精度. 2)温控系统采用水冷散热时, 水冷系统要有足够水容量, 避免水温快速波动. 采用风冷散热时, 应保持系统散热系数稳定.

TEC温控系统的等效电路模型为多级RC的级联结构, 环境温度引起的扰动可视为外部输入的误差信号, 其在图1各节点引起的响应存在相位差. 时域上TEC热端部分最先响应环境扰动, 同时也会导致帕尔贴效应发热量的改变, 进一步放大误差. 由于TEC热端温度存在较大变化, 系统在硬件上可以准确检测到该变化量, 进而根据等效电路模型预测和补偿热端温度变化引起的温控误差, 理论上可进一步提高温度控制精度.

由于本文核心算法中的动态直流偏置已具备一定的扰动补偿能力, 本文在此仅对热端补偿算法进行了初步的探索性研究, 以验证其进一步提升性能的潜力. 具体的实现方式是在(4)式的基础上, 增加基于热端温度$ {\theta _{\text{H}}}(t) $变化趋势的前馈补偿电流项$ {I_{{\text{Comp}}}}(t) $, 启用该补偿机制后, 控制器总输出电流为

补偿电流项$ {I_{{\text{Comp}}}}(t) $主要是解决时域上快速变化的环境温度扰动量可能引起的较大温控误差. 该项通过分析热端温度$ {\theta _{\text{H}}}(t) $的近期变化趋势进行计算, 具体计算方法如下:

式中, $ {\theta _{\text{H}}}(\tau ) $为积分时间区间$ \left[ {t - {T_{{\rm int} }}, t} \right] $内的热端温度历史值; $ {\theta _{{\rm{H,Avg}}}}(t) $是在当前时刻$ t $计算得到的$ {\theta _{\text{H}}} $在过去一个相对较长时间窗口$ {T_{{\text{Avg}}}} $(例如$ {T_{{\text{Avg}}}} = 5{\text{ s}} $)内的滑动平均值, 它被用作评估$ {\theta _{\text{H}}} $近期变化的基准温度, 反映了其缓慢变化的趋势; $ {T_{{{\mathrm{int}}} }} $则是一个较短的积分时间窗口(例如$ {T_{{{\mathrm{int}}} }} = 2{\text{ s}} $), 其长度决定了捕捉$ {\theta _{\text{H}}} $快速变化趋势的灵敏度; $ \gamma $是一个前馈补偿系数(单位为$ {{\text{A}} {/ } {{\text{(K}} \cdot {\text{s)}}}} $, 例如$ \gamma \approx 0.1 $), 它定义了将检测到的热端温度变化趋势转化为补偿电流的比例强度, 其值需要根据系统特性进行调整. (7)式的整体作用机制在于, 通过计算实时热端温度$ {\theta _{\text{H}}}(t) $相对于其自身慢变基准$ {\theta _{{\text{H, Avg}}}}(t) $在短时间窗口$ {T_{{\rm int} }} $内的积分, 定量地捕捉并累积了热端温度的快速偏离量. 这个偏离量通常是环境发生瞬时扰动(如跳变)的早期信号, 它比主控对象$ {\theta _{\text{S}}}(t) $的误差响应更迅速. 因此, 将此积分值乘以系数$ \gamma $得到的补偿电流$ {I_{{\mathrm{Comp}}}}(t) $, 能够为系统提供一个及时的、预测性的前馈调节信号, 专门用于应对和抑制环境温度快速变化的扰动, 从而与主要处理缓变和稳态误差的$ {I_{{\text{Bias}}}}(t) $项形成功能上的有效互补, 实现更全面的扰动抑制能力. 引入热端温度补偿的改进算法后, 测试结果如表2中右侧所示, 温控精度在各种扰动幅度下均获得了较为明显改善, 其中在0.2 K小幅环境温度瞬时扰动下, 双路温度检测算法可使精度提高近一倍. 仿真分析进一步发现, 若进一步提高温度传感器的检测精度, 双路温度检测算法的控制精度还有明显的改善空间, 可实现亚mK级温控精度.

mK量级的高精度温度控制是保障半导体精密光电器件性能稳定的关键. 然而, 由于TEC的非线性特性及系统控制的滞后性, 传统控制方法难以进一步提升精度, 而将温控系统作为黑箱建模的改良技术同样面临精度和适应性限制. 实现高精度温度控制的前提是热源稳定以及环境瞬时扰动小, 而TEC温控系统的结构相对简洁, 使其更适合从系统内部出发, 分析各模块的物理约束与耦合关系, 并建立精准的系统模型.

本文基于TEC的性能参数, 引入了温控应用中的相关变量, 构建了符合实际应用场景的TEC温控系统等效电路模型. 通过与TEC制造商测试数据及传统PID温控曲线对比, 验证了所构建模型的准确性及温控算法的可靠性. 在此基础上, 本文提出了一种结合动态直流偏置的自适应PID温控算法. 仿真结果表明, 该算法对高功率热源可实现mK量级温控精度, 且对PID参数的鲁棒性较强. 同时, 研究发现抑制环境温度的瞬时扰动以及采用双路温度检测是进一步提升温控精度的有效措施. 此外, 算法核心控制逻辑简洁高效, 充分考虑了硬件性能与计算效率, 可在普通嵌入式系统上运行, 具有良好的工程应用价值.